Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermodynamic analysis of the interaction between metal vacancies and hydrogen in bulk Cu
Vasileios
Fotopoulos
 *a,
Ricardo
Grau-Crespo
*a,
Ricardo
Grau-Crespo
 b and
Alexander L.
Shluger
ac
b and
Alexander L.
Shluger
ac
aDepartment of Physics and Astronomy, University College London, Gower Street, London, WC1E 6BT, UK. E-mail: vasileios.fotis.19@ucl.ac.uk
bDepartment of Chemistry, University of Reading, Whiteknights, Reading, RG6 6DX, UK
cWPI-Advanced Institute for Materials Research (WPI-AIMR), Tohoku University, 2–1-1 Katahira, Aoba-ku, Sendai 980–8577, Japan
First published on 16th March 2023
Abstract
Using grand canonical thermodynamic analysis with inputs from DFT calculations we calculated equilibrium molar fractions of copper vacancies (VCu), H interstitials (Hi) and their complexes in bulk Cu in a wide range of temperature and hydrogen pressure values. The results show that the equilibrium molar fractions of both VCu and Hi are low in most conditions of interest, in good agreement with available experimental data. Although Hi–VCu complexes have significantly lower formation energies than the isolated defects, the low molar fraction of H is predicted to have little impact on the rise in vacancy molar fraction for external hydrogen pressures below 100 bar. Only at relatively high hydrogen pressures exceeding 10 kbar in the presence of Cu vacancies, the H molar fraction was found to reach the same order of magnitude as the molar fraction of vacancies. These results put thermodynamic limits on the hydrogen-induced vacancy clustering and void formation in bulk Cu.
1 Introduction
Effects of hydrogen on metal properties have long been a research focus.1 Whereas intentional absorption at high molar fractions can make some metal-H systems useful for hydrogen storage,2–4 H presence in metals is often detrimental and degrades their mechanical properties due to embrittlement.5 On the other hand, H incorporation can increase by several orders of magnitude the vacancy molar fraction in some metals, which is known as the superabundant vacancy (SAV) formation.6–8 SAV formation can be induced because H atoms trapped in vacancies decrease the formation energy of larger vacancy clusters.9,10 However, theoretical studies of H trapping in fcc metals have yielded inconclusive results10 regarding the role of vacancies. In particular, Lu and Kaxiras,11 who employed density functional theory (DFT) in the local density approximation, demonstrated that up to 12 H atoms may fit into a single vacancy of aluminum (Al). Ismer et al.12 have shown that up to 10 H atoms can be trapped in an Al monovacancy using the generalized gradient approximation (GGA) of DFT. Similarly, it has been reported that several H interstitials can be trapped in Pd vacancies.10,13 In Cu, DFT calculations have shown that a single Cu vacancy can trap up to 6 H atoms,14 whereas other theoretical studies have suggested that it is possible to trap up to 8 H atoms in a Cu vacancy.15Although these theoretical studies demonstrate that one metal vacancy can accommodate a significant number of H atoms, the amount of H that can be incorporated into a metal sample under different conditions remains difficult to predict because it is strongly affected by both thermodynamic and kinetic factors. In metal films, H can be introduced as a result of the use of water-based solutions during the deposition process.16,17 In such a case, H can be kinetically trapped inside the sample due to defects like dislocations and grain boundaries, which act as efficient sinks.18,19 On the other hand, H can be incorporated into a metal under H2 gas pressure at high temperatures.20 In particular, high molar fractions of H have been reported in Ni, Fe, and Pd even at temperatures of 600 K and partial H2 gas pressure of 1 bar. Experimental studies in electrodeposited (ECD) Ni have measured H molar fractions of 7 × 10−2 at high pressure values.6
Although measuring the amount of H trapped in defects remains difficult, fairly accurate predictions can be made regarding the molar fraction of incorporated H under equilibrium conditions using statistical thermodynamics.21 Davidson et al.21 conducted theoretical studies of α-Fe using DFT calculations and statistical mechanics, finding equilibrium H molar fractions of up to 10−4 at partial pressures below 1 bar. Even higher molar fractions for fcc Fe have been reported by Nazarov et al.22 However, Fe, Ni, and Pd have a much higher H solubility compared to Cu.23 Furthermore, vacancies in these metals reach molar fractions of 10−3,24 whereas in Cu, vacancy molar fractions are estimated to be one order of magnitude lower, even at high temperatures near the melting point.25 Experimental studies for ECD Cu have revealed H molar fractions of around 10−4 near the melting temperature of Cu under extreme H partial pressures exceeding 10 kbar (1 GPa).6,26 Recent theoretical studies have investigated the structure of H complexes and vacancies in Cu.15,27 However, it remains unclear how much H can be incorporated into perfect Cu lattice at more common pressures of 0.1 to 100 bar and whether SAVs can actually form under such conditions or much higher pressures and temperatures are required. Here we address these questions using theoretical simulations and statistical thermodynamics.
The first step of incorporating atomic H into Cu from the gas phase is the adsorption of H2 on Cu surfaces. As described in previous theoretical studies,28,29 this process leads to the dissociation of the H2 molecule into atomic H, which will occupy hollow sites on the Cu surface.28 This reaction was found to have a barrier of 0.50 to 0.56 eV, depending on the exposed Cu surface.29 Atomic H can then diffuse from the Cu surface into the bulk with incorporation energies ranging between 0.64 and 0.90 eV.30 As described in previous works on H in metals,9,31 the presence of H is expected to increase the concentration of metal vacancies. The increase in vacancy concentration due to the presence of H can be explained by the creation of lattice strain accomplished both by physical32 and chemical33 mechanisms. As a result of the incorporation of H, the bond strength between adjacent Cu atoms and that between neighboring host Cu atoms is expected to reduce,34 facilitating the formation of vacancies. H also interacts with thermally formed Cu vacancies and can become trapped by them.10,22,24 However, for this interaction to be significant, H has to be closer than at the second nearest neighbor (2NN) distance from a Cu vacancy.15 The formation of a Hi–VCu complex can then facilitate the diffusivity of either H31 or the whole complex.15
In this work, we neglect these dynamic processes and provide a thermodynamic analysis of the formation of H interstitials (Hi), Cu vacancies (VCu), and Hi–VCu complexes in perfect fcc Cu. By employing a combination of atomistic simulations and grand canonical statistical mechanics, we calculate the probabilities of formation of different configurations of clusters of up to 6 Cu vacancies as well as the equilibrium amount of H incorporated into perfect Cu bulk as a function of H2 partial pressure (from 0.1 to 50 kbar (5 GPa)) and temperature. The effect of Hi on the concentration of VCu at various partial pressures and temperatures was then assessed. The results show that in Cu, unlike in other metals where H is more soluble, the molar fraction of absorbed atomic H at equilibrium is expected to be relatively low. Even at H partial pressures of 100 bar and temperatures close to the melting point of Cu (H absorption increases with temperature in this system), the equilibrium molar fraction of H is orders of magnitude lower than the equilibrium molar fraction of Cu vacancies. However, at partial pressures above 10 kbar and temperatures close to the melting point of Cu, the H molar fraction approaches that of vacancies. Only at these conditions does the presence of vacancies affect the equilibrium molar fraction of H in Cu. In other words, under normal temperatures and pressures there are much more vacancies than hydrogens. Therefore hydrogen atoms are unlikely to affect the number of vacancies. At high external pressures of hydrogen, more atoms incorporate and the presence of vacancies facilitates this process further.
The paper is organized as follows: in Section 2, the technical details of the DFT and force field calculations are summarized, and the grand canonical ensemble statistical model is outlined. The computed equilibrium molar fractions of vacancies and H in bulk Cu based on the employed thermodynamic model are presented in Sections 3.1 and 3.2, respectively. In Section 3.3, we present the DFT results for vacancy–H complexes and discuss how the presence of one type of defect affects the equilibrium concentration of the other. In Section 4, a summary and conclusions are provided.
2 Methods of calculation
2.1 DFT calculations
DFT calculations were carried out for 32 and 108 atoms periodic cells using the Vienna Ab Initio Simulation Package (VASP)35–37 and the Perdew–Burke–Ernzerhof (PBE) GGA exchange–correlation functional.38 The larger supercell was used in cases where 3 or more vacancies were introduced. For the 32 and 108 atoms cells, in line with previous works,10,39 converged 6 × 6 × 6 and 4 × 4 × 4 k-point grids were used, respectively, with the 450 eV energy cutoff. Cu was treated using 11 valence electrons (3d104s1). The atomic positions were relaxed to the energy tolerance of 10−5 eV. In accordance with previous DFT studies on H trapping in transition metals,21,27 no self-interaction (+U) corrections have been used since, unlike in Cu oxides40,41 and other transition metal oxides,42 H at the examined concentrations is not affecting the nature of Cu–Cu bonding.The formation energies (per vacancy) of the vacancy clusters were calculated as:
| Eform = (En − E0 + nμCu)/n, | (1) |
2.2 Force field calculations
The embedded atom method (EAM) is commonly used to simulate the environmental dependence of atomic bonding in metals.43–46 In particular, the EAM has been widely used to investigate vacancies in metals.47,48 The EAM potential developed by Mishin et al.49 was used for all force field simulations. This potential has been fitted semiempirically and is being widely used for pure Cu systems.50,51 To carry out the EAM simulations of vacancy clusters in Cu, the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)52 was used. We used the conjugate gradient method with the force tolerance of 10−10 eV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å−1 for geometry optimization. Further cell equilibration was carried out under an isothermal–isobaric NPT ensemble at constant temperature (0 K) for 0.02 ns using a timestep of 1.0 fs.
Å−1 for geometry optimization. Further cell equilibration was carried out under an isothermal–isobaric NPT ensemble at constant temperature (0 K) for 0.02 ns using a timestep of 1.0 fs.
2.3 Enumeration of defect configurations
One of the goals of this work is to identify molar fractions of various vacancy clusters of different sizes and configurations in bulk Cu. Any configuration of vacancies located in a cubic volume of 7.23 Å × 7.23 Å × 7.23 Å comprised of 32 atoms was considered a cluster. This volume was chosen in order to limit the number of considered vacancy configurations. The Site-Occupation Disorder (SOD) code53 was used to identify non-equivalent Vn configurations by accounting for the system's symmetry. If an isometric transformation or symmetry operation that can change a cluster configuration into one that has already been discovered is found, these configurations are considered to be equivalent. Following this process, 14 V3, 72 V4, 223 V5, and 870 V6 non-equivalent configurations were identified. Using the EAM potential,49 the geometries of 500-atom cells containing each vacancy cluster configuration were fully optimized. The lowest energy configurations were then reoptimized using DFT in 108-atom simulation cells.2.4 Grand-canonical analysis
To calculate equilibrium concentrations of complex defects including inter-defect interactions, one must compare energies of non-equivalent configurations using a suitable supercell. In the typical formulation, the probability, Pm, of a given configuration (m) of lattice site substitutions or defects depends on the configuration energy, Em, and its degeneracy, Ωm, in the configurational space as follows: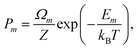 | (2) |
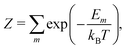 | (3) |
A more suitable approach in that case, still based on periodic DFT calculations and Boltzmann's probabilities, is to employ a grand-canonical ensemble of configurations,59 where configurations with different compositions are included via the introduction of the relevant chemical potentials. For example, the probability of the mth configuration with n Cu vacancies in the supercell may be calculated as:
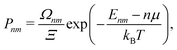 | (4) |
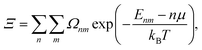 | (5) |
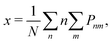 | (6) |
The same formalism can be used for the calculation of the equilibrium molar fraction of interstitial H atoms in bulk Cu. In this case, the chemical potential is a function of both temperature and of the external H2 partial pressure (p), if the crystal is considered to be in equilibrium with H2 gas:
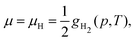 | (7) |
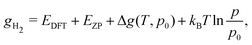 | (8) |
Finally, an ensemble of supercell configurations including both n Cu vacancies and k H interstitial atoms is considered. The probability of the mth configuration with a given (n, k) composition is given by:
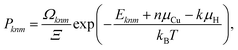 | (9) |
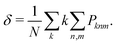 | (10) |
In the equations above, the configuration energies are taken directly from the simulations, ignoring any vibrational contributions, to avoid the huge computational cost of vibrational analysis for all configurations in the ensembles. However, vibrational contributions can sometimes be significant in the thermodynamics of defect formation in metals,24 especially when light atoms like H are involved. As a compromise, vibrational free energy corrections are introduced to the energies of the configurations involving interstitial H, by using the harmonic approximation to define a contribution from each frequency mode ν involving H:
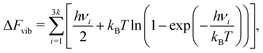 | (11) |
3 Results
3.1 Vacancy clusters and their equilibrium concentrations
The formation energies per vacancy for clusters with up to 6 vacancies are included in Fig. 1. The lowest-energy configuration for each cluster is shown in the inset images. In this and all the following structure figures, the same color code is used, with blue corresponding to Cu atoms, red representing Cu vacancies, and H atoms shown in white. Vacancies were found to form close-packed clusters, with V4 forming a stacking fault tetrahedron and V6 forming a symmetric diamond. The same lowest energy configurations have been reported for Cu vacancies by Ganchenkova et al.27 Also, in agreement with Ganchenkova et al.,27 the formation energies differ within less than 0.1 eV/vacancy for the lowest energy configurations of each cluster. As the number of vacancies increases, so does the binding energy of the clusters while the formation energy per vacancy constantly reduces. Additionally, more degenerate configurations were discovered for the V5 and V6 clusters because the number of initial non-equivalent SOD-identified configurations grows as the number of vacancies increases. To calculate the total molar fraction of vacancies at various temperatures, all the configurations shown in Fig. 1 were considered along with their degeneracy.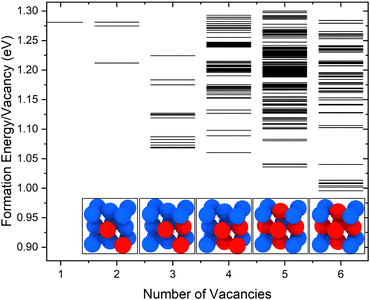 | ||
| Fig. 1 Formation energies per vacancy for V1 to V6 clusters obtained using the EAM potential.49 Inset images illustrate the lowest energy configurations for each cluster. | ||
The calculated molar fractions of the examined clusters are shown in Fig. 2(a). Molar fractions are calculated for temperatures ranging from 300 to 1400 K but Fig. 2(a) only shows molar fractions for temperatures higher than 500 K. Even at temperatures close to the melting point of Cu, one can see that V1 dominates, followed by V2, which has a molar fraction at least 3 orders of magnitude lower compared to monovacancies. Alhough a number of studies discuss the role of di-vacancies in the curvature of the Arrhenius plot in Cu,65,66 based on these results, the molar fraction of di-vacancies under equilibrium conditions will be negligible. This result is in good agreement with the di-vacancy molar fractions computed by Nordlund and Averback67 using EAM and supports their conclusion that di-vacancies, unlike other defects like self-interstitial atoms, are not expected to contribute to the curvature of the Arrhenius plots in Cu. These findings suggest that, under equilibrium conditions, bigger vacancy clusters are unlikely to form in perfect fcc Cu.
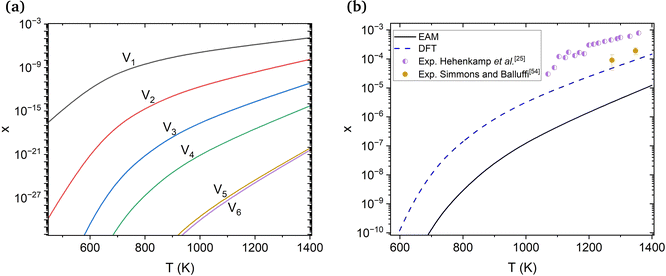 | ||
| Fig. 2 (a) Molar fractions (x) of V1–V6 vacancy clusters at varying temperatures obtained using EAM. (b) Comparison between the molar fraction obtained through DFT, EAM and experimental equilibrium molar fractions of vacancies from Hehenkamp et al.25 and Simmons and Balluffi.54 | ||
The molar fractions of monovacancies at varying temperatures calculated using EAM and DFT are compared in Fig. 2(b). Experimental vacancy molar fractions by Hehenkamp et al.25 and Simmons and Balluffi54 are also provided for reference. The DFT values are reasonably close to the experimental ones, especially the ones by Simmons and Balluffi. Hehenkamp et al. attributed the discrepancy between the two experimental methods to the length of the examined samples by Simmons and Balluffi, which resulted in an inhomogeneity in the temperatures of the samples. We also note that the molar fractions found using the potential49 are approximately one order of magnitude lower than those obtained using DFT. This potential overestimates the formation energy of a monovacancy by around 0.2 eV in comparison to experimental results, causing this discrepancy.
3.2 H concentration
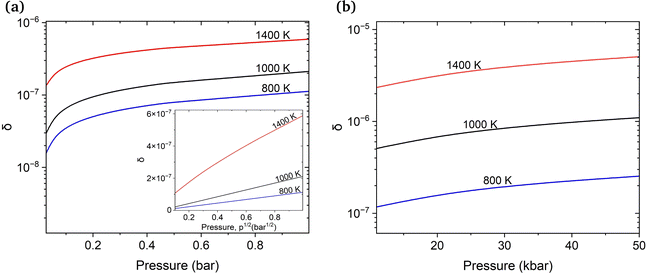
First, we estimate the molar fraction of H in perfect Cu lattice at various pressures and temperatures. Unlike previous results from Nazarov et al. for other fcc metals,22 our calculations show that H in Cu occupies interstitial octahedral rather than tetrahedral sites. This is in good agreement with the results of Ganchenkova et al.27 The calculated equilibrium molar fractions (δ) of H interstitials as functions of temperature and pressure are summarized in Fig. 3. As can be seen, in accordance with Sieverts’ law,68 the molar fraction of H at low pressures is proportional to the square root of the partial pressure (see the inset in Fig. 3(a)). Deviations from the Sieverts' law are seen at 1400 K. In the kbar range (Fig. 3(b)) the Sieverts's law is no lorger obeyed, in agreement with Evans.69 Because the H molar fraction is below 10−9 at temperatures lower than 600 K, only higher temperatures are considered. The molar fraction of H at the partial pressure range of 0.1 to 100 bar is 3 orders of magnitude lower than that of vacancies at the same temperatures. At temperatures close to the melting point of Cu and external pressure values of 1 bar, the molar fraction of H is about 10−6 and is too low to play any significant role in the formation of Cu vacancies. It increases significantly between 10 and 50 kbar (Fig. 3(b)) and for temperatures close to the melting point reaches the 10−5 range.3.3 Influence of H on the concentration of vacancies
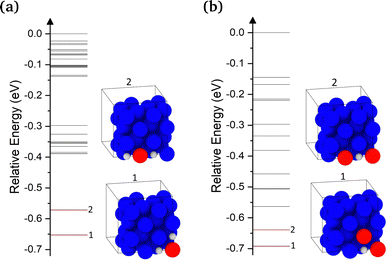
We now turn to examining the effect of H on the concentration of Cu vacancies. To achieve this, we used SOD to identify all possible 2H–V1 and 1H–V2 complex configurations. The calculated energies for the 2H–V1 and 1H–V2 complexes are shown in Fig. 4(a) and (b), respectively. Once identified, all configurations were optimized using DFT. The highest energy configuration was chosen as a reference for all energies in both plots, thus negative energies correspond to more favorable configurations. In addition, the plots include inset images of the 2 lowest energy 2H–V1 and 1H–V2 configurations. In the lowest energy configuration of 2H–V1, two H atoms are located at the two octahedral sites closest to the vacancy and are separated by 2.6 Å. In the second lowest energy configuration, the two neighboring H-occupied octahedral sites, but are now separated by 3.6 Å. The 0.1 eV energy difference between the two configurations is attributed to the weak interaction between the two interstitial H atoms.In 1H–V2 complexes, only the configurations in which the two vacancies are separated by up to a 4NN distance were examined. As seen in Fig. 4(b), the configuration with two vacancies at a distance of 2.6 Å, where the H atom occupies an octahedral site at a V–H–V coordination, thus forming a 90° angle, was found to be the most favorable. The second lowest energy configuration, in which the two vacancies were at a 3.6 Å distance, was found to be 0.05 eV higher (Fig. 4(b)). As also noted by Nazarov et al.,10 the H–VCu interaction is very short ranged. In cases where H occupied a second nearest available octahedral site from the vacancy, the gain in energy due to the H–V interaction was found to be negligible.
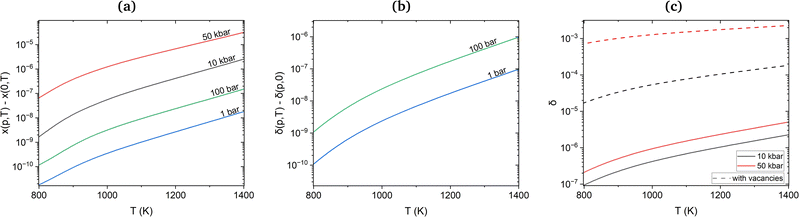
Under equilibrium conditions, monovacancies dominate over other vacancy clusters with molar fractions of 10−4 at temperatures beyond 1300 K. On the other hand, the estimated molar fraction of H in non-defective Cu is as low as 10−6 at the melting point and external partial pressure values of 1 bar. However, the interaction of H with vacancies discussed above will reduce formation energies compared to isolated H atoms and Cu vacancies. To assess the importance of this interaction, we calculated the molar fractions of H in the presence of monovacancies and di-vacancies and the molar fraction of vacancies in the presence of H. In Fig. 5(a), the molar fraction of vacancies without H is used as a reference. One can see that the difference between the plots for vacancies with and without H for partial pressures between 1 and 100 bar is indeed very small, within the 10−11 to 10−7 range. At high hydrogen pressures, between 10 and 50 kbar, the increase of the number of vacancies due to the presence of H reaches 10−5 for temperatures close to the melting point (see Fig. 5(a)) and becomes more significant.
Since the number of thermally created vacancies is much larger than that of incorporated hydrogen at normal pressure and temperature, we can expect that at high pressure an extra amount of hydrogen can be incorporated into Cu via absorption by vacancies. Indeed, the differential molar fraction of H, δ(p,T), with and without vacancies for partial pressures 1 and 100 bar in Fig. 5(b) demonstrates a moderate increase of 10−5 close to the melting point. However, for a higher pressure of 10 and 50 kbar at temperatures close to the melting point the H molar fraction increased from 1.84 × 10−4 to 2.28 × 10−3 (see Fig. 5(c)). The latter value is in a very good agreement with the experimental 2.5 × 10−3 H molar fraction at 50 kbar reported by Fukai et al.6 and reaches the same magnitude as the molar fraction of Cu vacancies.
4 Conclusions
We used a grand canonical statistical mechanics analysis to determine the molar fraction of vacancies and H in perfect bulk Cu at various temperatures and external pressure values. The study shows that V1 monovacancies dominate over other vacancy clusters up to the melting temperature of Cu, followed by V2, with molar fractions at least three orders of magnitude lower than that of the monovacancies. Without considering the presence of Cu vacancies, the molar fraction of H was found to be orders of magnitude lower than that of vacancies at the same temperatures and at hydrogen pressure values of around 1 bar. For hydrogen pressures within the kbar range and temperatures close to the melting point of Cu, H was found to reach and surpass the molar fraction of the equilibrium vacancies due to the interaction with vacancies. Further, the effect of H on the concentration of vacancies was investigated. Given the low molar fraction of H, it appeared to have little impact on the rise in vacancy molar fraction for external pressure lower than 100 bar. Likewise, vacancies were shown to have a negligible effect on the molar fraction of H. The impact of vacancies on the molar fraction of H started to become considerable at hydrogen pressure values higher than 10 kbar and temperatures close to the melting point.These findings demonstrate that, even though the presence of H promotes the formation of vacancies, this effect is insignificant in Cu because of the small amount of incorporated H. Therefore, in perfect bulk Cu under equilibrium the presence of H will start to significantly increase the molar fraction of vacancies only at hydrogen pressures exceeding 10 kbar and temperatures close to the melting point.
It is important to stress that some of the commonly used deposition methods, such as the ECD process, take place in the presence of water-based electrolyte solutions. Thus, additional H is expected to be incorporated during the deposition and can become trapped in sinks such as vacancies, dislocations or grain boundaries increasing the H molar fraction and facilitating the formation of superabundant vacancies. Further analysis under non-equilibrium conditions, where defects such as dislocations and grain boundaries are taken into account, will be required in order to fully comprehend the role of H in the SAV formation in Cu.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. L. S. acknowledges funding by EPSRC (grant EP/P013503/1). V. F. would like to acknowledge funding by EPSRC (grant EP/L015862/1) as part of the CDT in molecular modeling and materials science. Computational resources on ARCHER 2 (http://www.archer2.ac.uk) were provided via our membership in the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202, EP/R029431). V. F. and A. L. S. would like to thank Jack Strand and Tom Durrant for their useful comments and help in calculations.References
-
Y. Fukai, The Metal-Hydrogen System, Springer, 1993 Search PubMed
.
- A. Züttel, Mater. Today, 2003, 6, 24–33 CrossRef
.
- I. Jain, P. Jain and A. Jain, J. Alloys Compd., 2010, 503, 303–339 CrossRef CAS
.
- R. S. Dhayal, W. E. van Zyl and C. Liu, Dalton Trans., 2019, 48, 3531–3538 RSC
.
-
A. R. Troiano, Trans. ASM, 1960, 52, 54–80 Search PubMed
.
- Y. Fukai, M. Mizutani, S. Yokota, M. Kanazawa, Y. Miura and T. Watanabe, J. Alloys Compd., 2003, 356, 270–273 CrossRef
.
- Y. Fukai and N. Ōkuma, Phys. Rev. Lett., 1994, 73, 1640 CrossRef CAS PubMed
.
-
Y. Fukai, T. Haraguchi, E. Hayashi, Y. Ishii, Y. Kurokawa and J. Yanagawa, Defect and Diffusion Forum, 2001, pp. 1063–1068 Search PubMed
.
- J. M. Polfus, O. M. Løvvik, R. Bredesen and T. Peters, Acta Mater., 2020, 195, 708–719 CrossRef CAS
.
- R. Nazarov, T. Hickel and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 144108 CrossRef
.
- G. Lu and E. Kaxiras, Phys. Rev. Lett., 2005, 94, 155501 CrossRef PubMed
.
- L. Ismer, M. S. Park, A. Janotti and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 184110 CrossRef
.
- O. Y. Vekilova, D. Bazhanov, S. Simak and I. Abrikosov, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 024101 CrossRef
.
- Y.-W. You, X.-S. Kong, X.-B. Wu, Y.-C. Xu, Q. Fang, J. Chen, G.-N. Luo, C. Liu, B. Pan and Z. Wang, AIP Adv., 2013, 3, 012118 CrossRef CAS
.
- J.-P. Du, W. Geng, K. Arakawa, J. Li and S. Ogata, J. Phys. Chem. Lett., 2020, 11, 7015–7020 CrossRef CAS PubMed
.
- B. Bozzini, G. Giovannelli, S. Natali, B. Brevaglieri, P. Cavallotti and G. Signorelli, Eng. Failure Anal., 1999, 6, 83–92 CrossRef CAS
.
- J. Su, X. Lin, S. Zheng, R. Ning, W. Lou and W. Jin, Sep. Purif. Technol., 2017, 182, 160–165 CrossRef CAS
.
- L. Oger, B. Malard, G. Odemer, L. Peguet and C. Blanc, Mater. Des., 2019, 180, 107901 CrossRef CAS
.
- J. Li, A. Hallil, A. Metsue, A. Oudriss, J. Bouhattate and X. Feaugas, Sci. Rep., 2021, 11, 1–19 CrossRef PubMed
.
- S. Lynch, Corros. Rev., 2012, 30, 105–123 CAS
.
- E. Davidson, T. Daff, G. Csanyi and M. Finnis, Phys. Rev. Mater., 2020, 4, 063804 CrossRef CAS
.
- R. Nazarov, T. Hickel and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 224104 CrossRef
.
-
H. Wipf, Hydrogen in metals III, 1997, pp. 51–91 Search PubMed
.
- L. Bukonte, T. Ahlgren and K. Heinola, J. Appl. Phys., 2017, 121, 045102 CrossRef
.
- T. Hehenkamp, W. Berger, J.-E. Kluin, C. Lüdecke and J. Wolff, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 1998 CrossRef CAS PubMed
.
- N. Fukumuro, T. Adachi, S. Yae, H. Matsuda and Y. Fukai, Trans. IMF, 2011, 89, 198–201 CrossRef CAS
.
- M. Ganchenkova, Y. Yagodzinskyy, V. Borodin and H. Hänninen, Philos. Mag., 2014, 94, 3522–3548 CrossRef CAS
.
- K. Cao, G. Füchsel, A. W. Kleyn and L. B. Juurlink, Phys. Chem. Chem. Phys., 2018, 20, 22477–22488 RSC
.
- S. Sakong and A. Groß, Surf. Sci., 2003, 525, 107–118 CrossRef CAS
.
- C. M. Lousada and P. A. Korzhavyi, J. Mater. Sci., 2020, 55, 6623–6636 CrossRef CAS
.
- A. Metsue, A. Oudriss and X. Feaugas, Corrosion, 2019, 75, 898–902 CrossRef CAS PubMed
.
-
J. Peisl, Advances in Solid State Physics: Plenary Lectures of the 48th Annual Meeting of the German Physical Society (DPG) and of the Divisions “Semiconductor Physics” “Metal Physics” “Low Temperature Physics” “Thermodynamics and Statistical Physics” “Thin Films” “Surface Physics” “Magnetism” “Physics of Polymers” “Molecular Physics” Münster, 1984, vol. 17, pp. 45–72 Search PubMed
.
- K. Lin, Q. Li, R. Yu, J. Chen, J. P. Attfield and X. Xing, Chem. Soc. Rev., 2022, 51, 5351–5364 RSC
.
- Z. Huang, F. Chen, Q. Shen, L. Zhang and T. J. Rupert, Acta Mater., 2018, 148, 110–122 CrossRef CAS
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- R. Nazarov, T. Hickel and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 144118 CrossRef
.
- S. S. Paliwal, V. Maurya and K. B. Joshi, J. Phys.: Condens. Matter, 2020, 32, 295501 CrossRef CAS PubMed
.
- V. Maurya and K. B. Joshi, J. Phys. Chem. A, 2019, 123, 1999–2007 CrossRef CAS PubMed
.
- V. Maurya, G. Sharma and K. B. Joshi, Phys. Scr., 2021, 96, 055807 CrossRef
.
- M. S. Daw, S. M. Foiles and M. I. Baskes, Mater. Sci. Rep., 1993, 9, 251–310 CrossRef CAS
.
- M. Mendelev, M. Kramer, C. A. Becker and M. Asta, Philos. Mag., 2008, 88, 1723–1750 CrossRef CAS
.
- N. Tajima, O. Takai, Y. Kogure and M. Doyama, Comput. Mater. Sci., 1999, 14, 152–158 CrossRef CAS
.
- P. Williams, Y. Mishin and J. Hamilton, Modell. Simul. Mater. Sci. Eng., 2006, 14, 817 CrossRef CAS
.
- E. Asadi, M. A. Zaeem, A. Moitra and M. A. Tschopp, J. Phys.: Condens. Matter, 2014, 26, 115404 CrossRef PubMed
.
- D. R. Mason, D. Nguyen-Manh and C. S. Becquart, J. Phys.: Condens. Matter, 2017, 29, 505501 CrossRef CAS PubMed
.
- Y. Mishin, M. Mehl, D. Papaconstantopoulos, A. Voter and J. Kress, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 224106 CrossRef
.
-
B. Zhang, W. Hu and X. Shu, Theory of Embedded Atom Method and Its Application to Materials Science-Atomic Scale Materials Design Theory, Hunan University Publication Press, Changsha, China, 2003 Search PubMed
.
- A. Suzuki and Y. Mishin, Interface Sci., 2003, 11, 425–437 CrossRef CAS
.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
- R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. de Leeuw, J. Phys.: Condens. Matter, 2007, 19, 256201 CrossRef
.
- R. Simmons and R. Balluffi, Phys. Rev., 1963, 129, 1533 CrossRef CAS
.
- S. Benny, R. Grau-Crespo and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2009, 11, 808–815 RSC
.
- R. Grau-Crespo, N. H. de Leeuw and C. R. A. Catlow, J. Mater. Chem., 2003, 13, 2848–2850 RSC
.
- R. Grau-Crespo, N. H. de Leeuw and C. R. A. Catlow, Chem. Mater., 2004, 16, 1954–1960 CrossRef CAS
.
- I. Todorov, N. Allan, M. Y. Lavrentiev, C. Freeman, C. Mohn and J. Purton, J. Phys.: Condens. Matter, 2004, 16, S2751 CrossRef CAS
.
- R. Grau-Crespo, K. C. Smith, T. S. Fisher, N. H. de Leeuw and U. V. Waghmare, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 174117 CrossRef
.
-
D. R. Lide, CRC handbook of chemistry and physics, CRC press, 2004, vol. 85 Search PubMed
.
-
M. W. Chase, NIST-JANAF Thermochemical Tables, National Information Standards Organization (U.S.), American Chemical Society, Washington, DC, 1998, vol. 9 Search PubMed
.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406 CrossRef
.
- R. Grau-Crespo, C. R. A. Catlow and N. H. de Leeuw, J. Catal., 2007, 248, 77–88 CrossRef CAS
.
-
Y. Fukai, in The Metal-Hydrogen System, Springer, 1993, pp. 71–119 Search PubMed
.
- R. McLellan and Y. Angel, Acta Metall. Mater., 1995, 43, 3721–3725 CrossRef CAS
.
- D. Bartdorff, G. Neumann and P. Reimers, Philos. Mag. A, 1978, 38, 157–165 CrossRef CAS
.
- K. Nordlund and R. Averback, Phys. Rev. Lett., 1998, 80, 4201 CrossRef CAS
.
- A. Sieverts, Z. Metallkd., 1929, 21, 37–46 CAS
.
- M. J. Evans, Can. J. Chem., 1974, 52, 1200–1205 CrossRef CAS
.
| This journal is © the Owner Societies 2023 |