Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Temperature dependent local inhomogeneity and magnetic moments of (Li1−xFex)OHFeSe superconductors
G.
Tomassucci
 a,
L.
Tortora
a,
G. M.
Pugliese
a,
F.
Stramaglia
ab,
L.
Simonelli
a,
L.
Tortora
a,
G. M.
Pugliese
a,
F.
Stramaglia
ab,
L.
Simonelli
 c,
C.
Marini
c,
K.
Terashima
c,
C.
Marini
c,
K.
Terashima
 de,
T.
Wakita
de,
T.
Wakita
 d,
S.
Ayukawa
d,
T.
Yokoya
d,
K.
Kudo
d,
S.
Ayukawa
d,
T.
Yokoya
d,
K.
Kudo
 f,
M.
Nohara
f,
M.
Nohara
 g,
T.
Mizokawa
g,
T.
Mizokawa
 h and
N. L.
Saini
h and
N. L.
Saini
 *a
*a
aDipartimento di Fisica, Universitá di Roma “La Sapienza” – P. le Aldo Moro 2, 00185 Roma, Italy. E-mail: naurang.saini@roma1.infn.it
bMicroscopy and Magnetism Group, Swiss Light Source, Paul Scherrer Institut, Villigen, Switzerland
cCELLS – ALBA Synchrotron Radiation Facility, Carrer de la Llum 2-26, 08290, Cerdanyola del Valles, Barcelona, Spain
dResearch Institute for Interdisciplinary Science (RIIS), Okayama University, Okayama 700-8530, Japan
eNational Institute for Materials Science, Sengen 1-2-1, Tsukuba, Ibaraki 305-0047, Japan
fDepartment of Physics, Graduate School of Science, Osaka University, Toyonaka, Osaka 560-0043, Japan
gDepartment of Quantum Matter, Hiroshima University, Hiroshima 739-8530, Japan
hDepartment of Applied Physics, Waseda University, Tokyo 169-8555, Japan
First published on 2nd February 2023
Abstract
We have combined the extended X-ray absorption fine structure (EXAFS) and X-ray emission spectroscopy (XES) to investigate the local structure and the local iron magnetic moments of (Li1−xFex)OHFeSe (x∼0.2) superconductors. The local structure, studied by Fe K-edge EXAFS measurements, is found to be inhomogeneous that is characterized by different Fe–Se bond lengths. The inhomogeneous phase exhibits a peculiar temperature dependence with lattice anomalies in the local structural parameters at the critical temperature Tc (36 K) and at the spin density wave (SDW) transition temperature TN (130 K). Fe Kβ XES shows iron to be in a low spin state with the local Fe magnetic moment evolving anomalously as a function of temperature. Apart from a quantitative measurement of the local structure of (Li1−xFex)OHFeSe, providing direct evidence of nanoscale inhomogeneity, the results provide further evidence of the vital role that the coupled electronic, lattice and magnetic degrees of freedom play in the iron-based superconductors.
1. Introduction
Since the discovery of superconductivity in LaFeAsO1−xFx with a critical temperature of ∼26 K,1 iron-based superconductors (FeSCs) have attracted unprecedented attention from the scientific community due to many of their fascinating properties, resulting from a complex interplay between lattice, charge and magnetic degrees of freedom.2 In fact, besides the high-Tc superconductivity, these materials exhibit a peculiar phase diagram, with superconductivity (usually) arising from an antiferromagnetic state, often followed by a tetragonal to orthorhombic nematic transition.2–4 In general, the FeSCs are characterised by a layered structure composed of tetrahedrally coordinated FePn4(/Ch4) (where Pn stands for pnictogen and Ch for chalcogen atoms) metallic layers intercalated by a non-metallic spacer layer, giving rise to many different structures.5–7 Among all FeSCs, FeSe (11-chalcogenide), with a bulk critical temperature of ∼8 K,8 is considered an important archetype to investigate the mechanism of superconductivity in these materials.7 This is due to its relative chemical simplicity, since this system is composed of only stacked layers of tetrahedrally coordinated FeSe4.Even though the iron chalcogenides have many properties in common with other families, there are some debated differences with others.2 For example, the superconducting state in iron pnictides is reached by chemical doping and suppression of the antiferromagnetic state,9–11 while FeSe exhibits superconductivity without any magnetic ordering.3,4,7,12 Furthermore, iron chalcogenides present a complex and seemingly sensitive electronic structure, which (at least in some cases) notably lacks hole pockets on the Fermi surface at the centre of the Brillouin zone,3,13–15 contradicting the s ± symmetry scenario of the superconducting gap which is believed to have fundamental importance in explaining the superconducting pairing mechanism in the FeSC materials.
There have been several efforts made to increase Tc of the FeSe system, for example, it was found that a partial substitution of Te leads to the formation of FeSe1−xTex, which exhibits a critical temperature up to ∼15 K. However, this results in a nanoscale phase separation characterized by different iron–chalcogen bond lengths as in random alloys.16 Moreover, the Tc can be increased up to ∼37 K by applying hydrostatic pressure17 and to ∼65 K by growing single-layer FeSe on a SrTiO3 (STO) substrate.18 It has been suggested that the Tc enhancement caused by applying an external pressure is due to increased Fe 3 d and Se 4 p orbital hybridization,19,20 while that in single-layer FeSe is likely to be associated with electron doping due to the presence of O vacancies in the substrate or Se loss forming FeSe1−x.21 Nevertheless, due to the high sensitivity of FeSe to external pressure, it has been argued that chemical pressure could represent a possible control parameter for increasing Tc.7
As such, intercalation with different atomic species and molecules has been achieved, leading to a critical temperature of ∼32 K in the AxFe2−xSe2 (A = K, Cs, Rb, Tl, Tl/Rb, and Tl/K) family22–24 or ∼44 K in ammonia-intercalated Lix(NH2)y(NH3)1−yFe2Se2.25 However, understanding the effect of intercalation is not always easy, for instance, the K-intercalated 122 system KxFe2−xSe2, besides its high Tc, presents the coexistence of different electronic, magnetic and structural phases, with the superconductivity allegedly related to the lattice parameters and electronic dimensionality.26,27 In this case, the phase separation between the superconducting phase (so-called 122-phase) and the antiferromagnetic insulating phase (245-phase), characterised by  ordered Fe vacancies, makes the experimental research on the intrinsic properties of iron-chalcogenide superconductors rather difficult. Therefore, in order to study the effect of intercalation and the associated chemical pressure, it is necessary to have homogenous intercalation of FeSe, unlike the 122 system showing a microscale phase separation.
ordered Fe vacancies, makes the experimental research on the intrinsic properties of iron-chalcogenide superconductors rather difficult. Therefore, in order to study the effect of intercalation and the associated chemical pressure, it is necessary to have homogenous intercalation of FeSe, unlike the 122 system showing a microscale phase separation.
The (Li1−xFex)OHFeSe system represents a fascinating case in the intercalation chemistry of FeSe.28–32 This family of compounds consists of a stack of alternating layers of tetrahedral FeSe and (Li1−xFex)OH,33,34 with the structure of the intercalant similar to the one of LiOH (Fig. 1). In this system, the FeSe layer is responsible for the transport properties, while the (Li1−xFex)OH layer acts as a charge reservoir, with a weak hydrogen bonding interaction between the two.30 Furthermore, atomic substitution occurs with some iron cations substituting the Li sites and vice versa.30 Therefore, the presence of Li-filled Fe vacancies in the active layer may be related to Tc as high as ∼36 K.32 This shows that electron doping into the FeSe layer is similar to Li/ammonia intercalation in Lix(NH3)yFe2Se2.35,36 In addition to its high Tc superconductivity, (Li1−xFex)OHFeSe has attracted significant attention for its electronic and magnetic properties.20,34,36–38 In particular, similar to KxFe2−xSe2, (Li1−xFex)OHFeSe shows the absence of hole bands on the Fermi surface15,39 and that superconductivity appears to coexist with antiferromagnetism in the phase diagram with a spin density wave (SDW) state occurring below TN ∼ 125 K.40–42 On the other hand, unlike KxFe2−xSe2, no Fe vacancy or phase separation has been reported by diffraction experiments, making it a promising candidate to study the physical effects of intercalation in iron–chalcogenide superconductors. Recent studies40–42 confirm a peculiar relationship between structural parameters (i.e., the lattice constant c), superconductivity and magnetism. It has been argued that the superconducting and magnetic properties of this system can be tuned by changing the preparation method.20,30,31,37,43–45
 | ||
| Fig. 1 Crystal unit cell of (Li1−xFex)OHFeSe prepared using Vesta46 is displayed (left) together with the magnetic susceptibility curve showing (right) the superconducting transition temperature (Tc). In the structural unit cell the partial substitutions of Li/Fe sites are indicated by different colors. | ||
In this work, we have used the extended X-ray absorption fine structure (EXAFS) and X-ray emission spectroscopy (XES) to study the local structure of (Li1−xFex)OHFeSe and to explore correlation between superconductivity and electronic/magnetic degrees of freedom in this system. Due to the complex electronic structure of FeSC, resulting in an extreme susceptibility to external perturbations, information obtained from diffraction techniques on the average ordered structure is insufficient to fully explain the electronic properties of these materials. Therefore, it is of vital importance to probe their local structure to gain fundamental information on their physical properties. EXAFS spectroscopy, a fast and local probe,47,48 has been used to explore how the atomic displacements in (Li1−xFex)OHFeSe are affected by intercalation and temperature. On the other hand, Fe Kβ XES has been used to investigate the evolution of the local Fe magnetic moment μ, providing information on the magnetic correlations in the system. In contrast to the previous diffraction studies, the results reveal local inhomogeneity characterized by different structural configurations with a peculiar temperature dependence of the local structural parameters and local Fe magnetic moment with anomalies at Tc and TN.
2. Experimental details
Temperature dependent EXAFS and XES measurements were carried out on well-characterized single crystals of (Li1−xFex)OHFeSe prepared by a hydrothermal ion-exchange technique.41 The sample was ensured to be superconducting below ∼36.1 K Fig. 1. The CLAESS beamline49 of the 3 GeV ALBA synchrotron radiation facility in Cerdanyola del Valles (Barcelona) was used for the measurements. At the CLAESS beamline, the synchrotron radiation is emitted from a multipole wiggler composed by 12 periods and a total length of 1 m. A double crystal Si(111) monochromator was used together with platinum-coated focusing mirrors to reject higher harmonics. The measurement system contains three ionisation chambers: two for measuring the incident (I0) and transmitted (It) X-ray intensity, and one for the transmission across a reference sample. The sample, sealed in an evacuated quartz ampule, was opened in a glovebox and mounted in a He cryostat that allowed it to cool down to 10 K (±1 K) during the measurements. The measurements were performed studying Fe K-edge (7.11 keV) absorption spectra between the temperature 10 and 290 K in the transmission mode with the polarisation of the incident beam parallel to the ab plane. Fe Kβ XES measurements were carried out using a CLEAR spectrometer49,50 that is based on a diced Si(333) dynamically bent analyzer crystal and a position-sensitive Mythen detector. The data on the Fe Kβ lines were acquired by exciting the sample well above the Fe K-edge, with a total energy resolution of ∼0.9 eV. A minimum of three to four absorption/emission scans were acquired at each temperature.3. Results and discussions
The Fe K-edge X-ray absorption measurements were performed on (Li1−xFex)OHFeSe with the polarization of the beam parallel to the ab-plane (normal incidence). Fig. 2 shows the EXAFS oscillations extracted from the X-ray absorption spectra in a temperature interval of 10 to 290 K. The EXAFS oscillations were extracted using the standard procedure based on the polynomial spline fit to the pre-edge subtracted absorption spectra.47,48 The EXAFS oscillations, shown in the Fig. 2, are visible up to a high k value beyond the noise level and evolve substantially with temperature.Apart from thermal damping, we can notice some structural changes in the EXAFS oscillations (see, for example, the k-range between 7 and 9 Å−1 and between 10 and 12 Å−1), displaying a clear evolution of the local structure with temperature. The Fe K-edge EXAFS of (Li1−xFex)OHFeSe contains information on the local structure around the Fe atoms with respect to the direction of the beam polarization. The real-space view of the local structure can be obtained from Fourier transforms (FTs) of the EXAFS oscillations, providing information on the atomic distribution around the Fe sites (Fig. 3). In particular, the structure of (Li1−xFex)OHFeSe shown in Fig. 1 contains Fe sites with O atoms as the nearest-neighbours at a distance of ∼2.0 Å; the next nearest neighbours are Se (at ∼2.4 Å) followed by Fe (at ∼2.7 Å).43 The contribution of all these is observed in the FT peak structure at R ∼ 1.0–3.0 Å. To quantify the local structure parameters, the EXAFS was modelled by single scattering approximation using the standard EXAFS equation:47,48
 | (1) |
The average structure (Fig. 1) measured by diffraction experiments43 was employed as a starting model for the least-squares EXAFS fits. The EXCURVE code51 was used to calculate the backscattering amplitudes and phase shift functions. The same code was used to perform the EXAFS fits, fixing S02 and E0 (photoelectron energy zero) after a number of trials and leaving the atomic positions Ri and related Debye–Waller factors as the only free parameters. The effect of beam polarization was taken into account by introducing an effective number of neighbours considering projections of the bond distances with respect to the polarization vector of the X-ray beam, i.e., Neff,I = 3Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(θi), where θi is the angle between the polarisation vector and the direction of the bond between the absorber and scattering atoms.47,48 The number of independent data points,
cos2(θi), where θi is the angle between the polarisation vector and the direction of the bond between the absorber and scattering atoms.47,48 The number of independent data points,  , was about 20 (the interval in k space Δk = (18.0–2.3)−1 = 15.7−1 and the interval in R space ΔR = (3.0–1.0) = 2.0). Therefore, as a first approximation, a simple three-shells model considering Fe–O, Fe–Se and Fe–Fe distances was employed to perform the non-linear fitting of the EXAFS signal, assuming a homogenous effect of intercalation on the active layer. However, an unsatisfactory fit together with an unphysical outcome (inconsistent distances and near neighbor atoms) led us to consider an inhomogeneous atomic distribution around the Fe site due to Li substitution. In particular, two distances were found for both Fe–Se and Fe–Fe pairs. It should be mentioned that there is a negligible contribution of multiple scattering involving Fe–O–H in the selected R interval for the model fits and this contribution is not considered. The five-shell model fits are shown in Fig. 3 together with the corresponding experimental Fourier transforms. The k-space fits (solid line) are also included with the unfiltered EXAFS (dots) as insets for representative temperatures.
, was about 20 (the interval in k space Δk = (18.0–2.3)−1 = 15.7−1 and the interval in R space ΔR = (3.0–1.0) = 2.0). Therefore, as a first approximation, a simple three-shells model considering Fe–O, Fe–Se and Fe–Fe distances was employed to perform the non-linear fitting of the EXAFS signal, assuming a homogenous effect of intercalation on the active layer. However, an unsatisfactory fit together with an unphysical outcome (inconsistent distances and near neighbor atoms) led us to consider an inhomogeneous atomic distribution around the Fe site due to Li substitution. In particular, two distances were found for both Fe–Se and Fe–Fe pairs. It should be mentioned that there is a negligible contribution of multiple scattering involving Fe–O–H in the selected R interval for the model fits and this contribution is not considered. The five-shell model fits are shown in Fig. 3 together with the corresponding experimental Fourier transforms. The k-space fits (solid line) are also included with the unfiltered EXAFS (dots) as insets for representative temperatures.
The temperature dependence of the near neighbor distances is shown in Fig. 4. The Fe–O distance is found to be 2.03± 0.01 Å and it remains temperature independent (not shown) within the experimental uncertainties. There are two distances for Fe–Se and Fe–Fe shells: a longer Fe–Se (Fe–Se2) distance (Fig. 4 (open squares)) of approximately ∼2.40 Å, that is similar to the commonly known Fe–Se bond length in iron chalcogenides, and a shorter Fe–Se (Fe–Se1) distance of approximately ∼2.35 Å (Fig. 4 (open circles)). The probability of the shorter Fe–Se distance is estimated to be ∼45 ± 5%. Similarly, the shorter Fe–Fe (Fe–Fe1) distance (upper panel) is ∼2.67 Å (Fig. 4 (filled circles)), the usual Fe–Fe bond length in iron chalcogenides, together with a longer Fe–Fe (Fe–Fe2) distance of ∼2.94 Å. The probability of the longer Fe–Fe distance is estimated to be similar to that of the shorter Fe–Se distance (lower panel). This observation suggests that (Li1−xFex)OHFeSe is locally non homogeneous with coexisting nanoscale phases characterized by different local structure configurations. Thus, the results for the local structure provide a direct evidence of nanoscale inhomogeneity in (Li1−xFex)OHFeSe. It should be mentioned that the presence of a smaller, compressed structure had been indicated earlier (although never definitively proven) in some diffraction studies on the same material40,44 and in a sister compound (Na1−x OH)Fe1−y Se,52 originating likely from the atomic displacements in the FeSe4 tetrahedron following Li substitution in the active layer.
Looking at the temperature dependence of the local bonds, an anomaly at ∼130 K can be noticed, where the Fe–Se1 distance shows a clear change. This bond gets shorter by ∼0.04 Å. Considering the indications of antiferromagnetic spin density wave (SDW) fluctuations reported at ∼125 K,40,41,53 it is natural to associate this anomaly with SDW-like instability in the system around this temperature, indicating a correlation between the magnetic and lattice degrees of freedom in the studied system. The Fe–Se1 bond also changes in the vicinity of the superconducting transition temperature.
The local lattice anomalies can also be seen in the Se height above the Fe plane (hSe), i.e., the commonly used empirical lattice parameter to describe the correlation between the local lattice and the superconductivity in the iron-based superconductors. One can determine the hSe from a simple geometrical relationship assuming tetragonal symmetry:
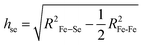 | (2) |
The Se anion heights calculated using the short and long Fe–Se distances are shown in the inset of Fig. 4. Here, the mean Fe–Fe distance has been used for Se height calculation considering a random distribution. The temperature dependence of the anion heights reflects the behaviour already observed in the anomalous bond distances with clear anomalies at ∼130 K and ∼50 K. Again, the compressed FeSe4 tetrahedra (shorter anion height) show stronger temperature dependence than the phase with a longer anion height. In fact, the shorter Se height shows a contraction upon cooling across ∼130 K followed by an elongation at ∼Tc. Although to a small extent, the longer height tends to display an opposite behavior. A similar anomaly is also observed at ∼Tc, which has become a mark of superconductivity in Fe-based superconductors.
In order to explore the evolution of the local magnetic moment in (Li1−xFex)OHFeSe, XES measurements were performed on the same sample. Fig. 5(a) displays the Fe Kβ XES image of (Li1−xFex)OHFeSe at several temperatures. The Kβ1,3 XES (3p → 1s) spectra are shown normalized with respect to the total integrated area. Here, the local magnetic moment is probed due to (3p, 3d) exchange interactions,54 modifying the Kβ XES profile and splitting between the main Kβ1,3 and the satellite Kβ′. We have included Kβ1,3 XES of Fe2O3 in which iron carries a magnetic moment of ∼4.6μB. The Kβ′ spectral weight as well as the Kβ1,3 energy show an increase with an increasing 3d spin magnetic moment.54 Thus the energy position of Kβ1,3 provides similar information on the magnetic moment as the Kβ′ satellite weight, reflecting the effective number of unpaired 3d electrons.54 The Kβ′ feature in (Li1−xFex)OHFeSe has very small intensity, suggesting iron to be in a low spin state. However, there is a small but evident energy shift in the Kβ1,3 line, observed to be shifted towards higher energy at 250 K with respect to the one at 10 K (inset of Fig. 5(a)). The differences are small but finite due to differing local Fe magnetic moments in the low spin state,54–59 suggesting non-negligible change as a function of temperature.
The local Fe magnetic moment μ can be evaluated from the integrated area of the absolute XES intensity difference with respect to a nonmagnetic reference sample.57–59 Since the goal is to study the evolution of the local magnetic moment as a function of temperature, we have used the lowest temperature XES spectrum as a reference to obtain the integrated absolute difference (IAD). Fig. 5(b)–(g) shows the XES spectra of (Li1−xFex)OHFeSe at several temperatures together with the differences with respect to the one at 10 K.
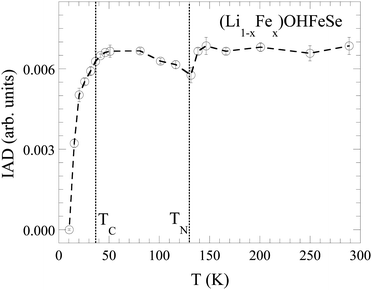
Fig. 6 shows the evolution of the IAD as a function of temperature. By cooling down, the IAD shows a small decrease, following a cusp-like anomaly and a subsequent increase below ∼130 K, before showing a sharp drop in the vicinity of the superconducting transition temperature. The sharp decrease in the IAD is an indication of quenching of the local Fe magnetic moment, similar to the one found in other iron-based superconductors.60,61 Therefore, the suppression of the magnetic moment is suggestive of its role in the superconductivity of (Li1−xFex)OHFeSe. Similar quenching of the local magnetic moment has been observed iron pnictides, however, across the collapsed tetragonal phase transition that is driven by the axial As–As distance.58,59 This is an indication of the formation of a magnetic order below TN = 130 K, already hinted by inelastic neutron scattering experiments40–42 and lowering of the local magnetic moment μ in the superconducting state. Looking at the local structure, it is clear that the local magnetic moment is related with the anion height in the system. This observation further underlines a strong magnetoelastic coupling in the iron-based superconductors with anion height being the controlling parameter.
Unlike Li/ammonia-intercalated FeSe, in which the majority of the Se atoms give rise to a compressed tetrahedron, the intercalation with LiOH is not homogeneous, showing coexistence of differently compressed FeSe-like phases. The nanoscale structural inhomogeneity also affects the electronic structure of the two phases, as observed by spatially resolved photoemission spectroscopy measurements (not shown). One question that remains open is if both of the coexisting phases are superconducting, or if superconductivity arises only in one of the two. Comparing the values of the anion height of the two phases with the critical temperature ∼36 K,62 one would expect that the superconductivity is resulting from both phases. This appears different from the case of AxFe2−ySe2, characterised by multiple coexisting crystallographic, electronic and magnetic phases,26,27,63 in which superconductivity is believed to arise from a minority metallic phase within the system. In the present case, it appears that both phases are superconducting with almost similar Tc albeit differently compressed FeSe in the anion height versus Tc phase diagram of iron-based superconductors with the Se heights of the coexisting phases being shorter and longer than the one for the optimum Tc.62
Further insight into the local disorder and bond characteristics can be gained from the EXAFS Debye Waller Factor (DWF) parameter, i.e., σi2, representing the mean square relative displacement (MSRD) of a pair of atoms. The σi2 is the sum of a temperature independent term σ02, describing the configurational disorder, and a temperature dependent term, related to the bond characteristics, i.e., σi2 = σ02 + σ2(T). The σ2(T) is well described using the correlated Einstein model,47,48,64,65 an appropriate approximation for local mode vibrations, i.e.,
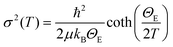 | (3) |
The σi2 values for the Fe–Se and Fe–Fe pairs as a function of temperature are shown in Fig. 7. Within the experimental uncertainties, the σi2 values are well described using the usual Einstein model (eqn 3). The shorter Fe–Se1 bond seems stiffer than the longer Fe–Se2 bond with ΘE being 350± 7 K and 331± 60 K, respectively. The static disorder appears much higher for the longer Fe–Se bond. The Einstein temperature for the Fe–Se bond in the intercalated system is somewhat higher than the one found for Fe–Se pairs in the binary FeSe compound (310 K).16 This is an indication that the intercalation and Li substitution at the Fe sites in the active layer tend to harden the Fe–Se bonds. Similarly, the Einstein temperature for the shorter Fe–Fe1 distance (Fig. 7) is higher (ΘE = 278± 10 K) than the one for the longer Fe–Fe2 bonds (ΘE = 215± 23 K) with the static disorder of the latter being much higher. Again, the ΘE of Fe–Fe bonds is slightly different from the one for the binary FeSe compound (∼268 K),16 indicating that the intercalation and Li substitution do affect the local bond network. These local structure parameters are shown in Table 1. It is worth mentioning that the noncorrelated Debye-type behavior has been reported (albeit not shown) to describe temperature dependence of σi2 in iron-based pnictides.66,67 However, considering the strong nature of the interatomic bonds and the temperature range in consideration, there is hardly any difference between the two models.
| R(Å) | Θ E (K) | σ 0 2 (Å2) | |
|---|---|---|---|
| Fe–O | 2.03 | 450 ± 150 | 0.0101(2) |
| Fe–Se1 | 2.35 | 350 ± 7 | 0.0000(1) |
| Fe–Se2 | 2.40 | 331 ± 60 | 0.0113(7) |
| Fe–Fe1 | 2.67 | 278 ± 15 | 0.0005(3) |
| Fe–Fe2 | 2.94 | 215 ± 23 | 0.0171(9) |
4. Summary and conclusions
In summary, we have presented Fe K-edge X-ray absorption (EXAFS) and emission (XES) spectroscopy measurements investigating the local structure of (Li1−xFex)OHFeSe as a function of temperature. This family of compounds consist of alternating layers of tetrahedral FeSe and (Li1−xFex)OH, with partial substitution of Fe atoms at Li sites in the intercalating layer and vice versa. EXAFS analysis reveals two distances for both Fe–Se and Fe–Fe pairs: in the case of Fe–Se, the majority of Se atoms are at a distance of ∼2.40 Å from Fe while a slightly lower number of Se is placed at a shorter distance of ∼2.35 Å. It is likely that the partial Li substitution at the Fe sites in the active layer (estimated to be up to 20%) is responsible for allowing the Se atoms to get closer to the Fe sites, effectively distorting the FeSe4 tetrahedral structure. A similar result has been found for the Fe–Fe distance to be ∼2.67 Å, while the rest of the Fe atoms are located at a distance of ∼2.94 Å. Therefore, intercalation of LiOH largely affects the active layer inducing local inhomogeneity with coexisting differently compressed tetrahedral configurations. The temperature dependence of the EXAFS Debye–Waller factors reveals that the coexisting phases are characterized by different bond stiffness.Another notable finding includes anomalous changes in the local structure parameters at the critical temperature. The anion height above the Fe plane suggests that the superconducting properties of this material may be driven by the compressed but coexisting phases since the measured anion heights correspond to the critical temperature of the system (∼36 K) in accordance with the one expected from the empirical relationship.62 Furthermore, an anomaly below ∼130 K has been observed in the local structural parameters, possibly originating from the emergence of the SDW like instability at ∼125 K. The local magnetic moment, measured by XES, shows an anomalous temperature dependence with anomalies at Tc and TN. This appears consistent with an anomalous evolution of the magnetic moment similar to the one observed in the phase separated AxFe2−ySe2 superconductor. In conclusion, a combined analysis of the local structure and the local magnetic moment in (Li1−xFex)OHFeSe reveals local inhomogeneity with nanoscale phase separation evolving anomalously with temperature.
Author contributions
N. L. S., T. Y. and M. N.: conceptualization. S. A., K. K., T. W., K. T., L. S., C. M. and N. L. S.: investigations. G. T., L. T., G. M. P., F. S., L. S., T. M. and N. L. S.: data curation and formal analysis. G. T., T. M. and N. L. S: writing, review and editing. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the ALBA staff for their assistance during the measurements. The work is a part of the executive protocol of the general agreement for cooperation between the Sapienza University of Rome and Okayama University including Waseda University. The work is partially supported by Grant-in-Aid for Scientific Research (JP20H05882, JP19H05823, JP22H01182) provided by the Japan Society for the Promotion of Science.References
- Y. Kamihara, T. Watanabe, M. Hirano and H. Hosono, J. Am. Chem. Soc., 2008, 130, 3296 CrossRef CAS PubMed
.
- R. M. Fernandes, A. I. Coldea, H. Ding, I. R. Fisher, P. J. Hirschfeld and G. Kotliar, Nature, 2022, 601, 35 CrossRef CAS PubMed
.
- A. Kreisel, P. J. Hirschfeld and B. M. Andersen, Symmetry, 2020, 12, 1402 CrossRef CAS
.
- K. Matsuura, Y. Mizukami, Y. Arai, Y. Sugimura, N. Maejima, A. Machida, T. Watanuki, T. Fukuda, T. Yajima, Z. Hiroi, K. Y. Yip, Y. C. Chan, Q. Niu, S. Hosoi, K. Ishida, K. Mukasa, S. Kasahara, J.-G. Cheng, S. K. Goh, Y. Matsuda, Y. Uwatoko and T. Shibauchi, Nat. Commun., 2017, 8, 1143 CrossRef CAS PubMed
.
- G. R. Stewart, Rev. Mod. Phys., 2011, 83, 1589 CrossRef CAS
.
- J. Paglione and R. Greene, Nat. Phys., 2010, 6, 645 Search PubMed
.
- T. Shibauchi, T. Hanaguri and Y. Matsuda, J. Phys. Soc. Jpn., 2020, 89, 102002 CrossRef
.
- F. C. Hsu, J. Y. Luo, K. W. Yeh, T. K. Chen, T. W. Huang, P. M. Wu, Y. C. Lee, Y. L. Huang, Y. Y. Chu, D. C. Yan and M. L. Wu, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 14262 CrossRef CAS PubMed
.
- C. de la Cruz, Q. Huang, J. W. Lynn, J. Li, W. Ratcliff, J. L. Zarestky, H. A. Mook, G. F. Chen, J. L. Luo, N. L. Wang and P. Dai, Nature, 2008, 453, 899 CrossRef CAS PubMed
.
- H. Hosono and K. Kuroki, Phys. C, 2015, 514, 399 CrossRef CAS
.
- X. Luo and X. Chen, Sci. China Mater., 2015, 58, 77 CrossRef CAS
.
- J. P. Sun, K. Matsuura, G. Z. Ye, Y. Mizukami, M. Shimozawa, K. Matsubayashi, M. Yamashita, T. Watashige, S. Kasahara, Y. Matsuda, J.-Q. Yan, B. C. Sales, Y. Uwatoko, J. G. Cheng and T. Shibauchi, Nat. Commun., 2016, 7, 1 Search PubMed
.
- J. J. Lee, F. T. Schmitt, R. G. Moore, S. Johnston, Y.-T. Cui, W. Li, M. Yi, Z. K. Liu, M. Hashimoto, Y. Zhang, D. H. Lu, T. P. Devereaux, D.-H. Lee and Z. X. Shen, Nature, 2014, 515, 245 CrossRef CAS PubMed
.
- D. Liu, W. Zhang, D. Mou, J. He, Y.-B. Ou, Q.-Y. Wang, Z. Li, L. Wang, L. Zhao, S. He, Y. Peng, X. Liu, C. Chen, L. Yu, G. Liu, X. Dong, J. Zhang, C. Chen, Z. Xu, J. Hu, X. Chen, X. Ma, Q. Xue and X. J. Zhou, Nat. Commun., 2012, 3, 1–6 Search PubMed
.
- X. H. Niu, R. Peng, H. C. Xu, Y. J. Yan, J. Jiang, D. F. Xu, T. L. Yu, Q. Song, Z. C. Huang, Y. X. Wang, B. P. Xie, X. F. Lu, N. Z. Wang, X. H. Chen, Z. Sun and D. L. Feng, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 060504 CrossRef
.
- B. Joseph, A. Iadecola, A. Puri, L. Simonelli, Y. Mizuguchi, Y. Takano and N. L. Saini, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 020502 CrossRef
.
- S. Medvedev, T. M. McQueen, I. A. Troyan, T. Palasyuk, M. I. Eremets, R. J. Cava, S. Naghavi, F. Casper, V. Ksenofontov, G. Wortmann and C. Felser, Nat. Mater., 2009, 8, 630 CrossRef CAS PubMed
.
- D. Huang and J. E. Hoffman, Monolayer FeSe on SrTiO3, Annu. Rev. Condens. Matter Phys., 2017, 8, 311 CrossRef CAS
.
- V. Svitlyk, M. Raba, V. Dmitriev, P. Rodire, P. Toulemonde, D. Chernyshov and M. Mezouar, Phys. Rev. B, 2017, 96, 014520 CrossRef
.
- C. V. Topping, F. K. K. Kirschner, S. J. Blundell, P. J. Baker, D. N. Woodruff, F. Schild, H. Sun and S. J. Clarke, Phys. Rev. B, 2017, 95, 134419 CrossRef
.
- S. He, J. He, W. Zhang, L. Zhao, D. Liu, X. Liu, D. Mou, Y.-B. Ou, Q.-Y. Wang, Z. Li, L. Wang, Y. Peng, Y. Liu, C. Chen, L. Yu, G. Liu, X. Dong, J. Zhang, C. Chen, Z. Xu, X. Chen, X. Ma, Q. Xue and X. J. Zhou, Nat. Mater., 2013, 12, 605 CrossRef CAS PubMed
.
- J. Guo, S. Jin, G. Wang, S. Wang, K. Zhu, T. Zhou, M. He and X. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 180520(R) CrossRef
.
- A. Krzton-Maziopa, Z. Shermadini, E. Pomjakushina, V. Pomjakushin, M. Bendele, A. Amato, R. Khasanov, H. Luetkens and K. Conder, J. Phys.: Condens. Matter, 2011, 23, 052203 CrossRef CAS PubMed
.
- A. Wang, J. Ying, Y. Yan, R. Liu, X. Luo, Z. Li, X. Wang, M. Zhang, G. Ye and P. Cheng,
et al.
, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 060512 CrossRef
.
- M. Burrard-Lucas, D. G. Free, S. J. Sedlmaier, J. D. Wright, S. J. Cassidy, Y. Hara, A. J. Corkett, T. Lancaster, P. J. Baker, S. J. Blundell and S. J. Clarke, Nat. Mater., 2013, 12, 15 CrossRef CAS PubMed
.
- A. Ricci, N. Poccia, G. Campi, B. Joseph, G. Arrighetti, L. Barba, M. Reynolds, M. Burghammer, H. Takeya, Y. Mizuguchi, Y. Takano, M. Colapietro, N. L. Saini and A. Bianconi, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 060511 CrossRef
.
- A. Ricci, N. Poccia, B. Joseph, D. Innocenti, G. Campi, A. Zozulya, F. Westermeier, A. Schavkan, F. Coneri, A. Bianconi, H. Takeya, Y. Mizuguchi, Y. Takano, T. Mizokawa, M. Sprung and N. L. Saini, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 020503 CrossRef
.
- X. Lu, N. Wang, G. Zhang, X. Luo, Z. Ma, B. Lei, F. Huang and X. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 020507 CrossRef
.
- H. K. Vivanco and E. E. Rodriguez, J. Solid State Chem., 2016, 242, 3 CrossRef CAS
.
- D. N. Woodruff, F. Schild, C. V. Topping, S. J. Cassidy, J. N. Blandy, S. J. Blundell, A. L. Thompson and S. J. Clarke, Inorg. Chem., 2016, 55, 9886 CrossRef CAS PubMed
.
- G. Hu, N. Wang, M. Shi, F. Meng, C. Shang, L. Ma, X. Luo and X. Chen, Phys. Rev. Mater., 2019, 3, 064802 CrossRef CAS
.
- L. Zhao, A. Liang, D. Yuan, Y. Hu, D. Liu, J. Huang, S. He, B. Shen, Y. Xu, X. Liu, L. Yu, G. Liu, H. Zhou, Y. Huang, X. Dong, F. Zhou, K. Liu, Z. Lu, Z. Zhao, C. Chen, Z. Xu and X. J. Zhou, Nat. Commun., 2016, 7, 1 Search PubMed
.
- G. Wang, X. Yi and X. Shi, Phys. Lett. A, 2015, 379, 2106 CrossRef CAS
.
- U. Pachmayr, F. Nitsche, H. Luetkens, S. Kamusella, F. Bruckner, R. Sarkar, H.-H. Klauss and D. Johrendt, Angew. Chem., Int. Ed., 2015, 54, 293 CrossRef CAS PubMed
.
- W. Chen, C. Zeng, E. Kaxiras and Z. Zhang, Phys. Rev. B, 2016, 93, 064517 CrossRef
.
- D. Y. Liu, Z. Sun and L. J. Zou, New J. Phys., 2017, 19, 023028 CrossRef
.
- X. Zhou and E. E. Rodriguez, Chem. Mater., 2017, 29, 5737 CrossRef CAS
.
- X. F. Lu, N. Z. Wang, H. Wu, Y. P. Wu, D. Zhao, X. Z. Zeng, X. G. Luo, T. Wu, W. Bao, G. H. Zhang, F. Q. Huang, Q. Z. Huang and X. H. Chen, Nat. Mater., 2015, 14, 325 CrossRef CAS PubMed
.
- M. Smidman, G. M. Pang, H. X. Zhou, N. Z. Wang, W. Xie, Z. F. Weng, Y. Chen, X. L. Dong, X. H. Chen, Z. X. Zhao and H. Q. Yuan, Phys. Rev. B, 2017, 96, 014504 CrossRef
.
- X. Dong, H. Zhou, H. Yang, J. Yuan, K. Jin, F. Zhou, D. Yuan, L. Wei, J. Li, X. Wang, G. Zhang and Z. Zhao, J. Am. Chem. Soc., 2015, 137, 66 CrossRef CAS PubMed
.
- X. Dong, F. Zhou and Z. Zhao, Front. Phys., 2020, 8, 586182 CrossRef
.
- Y. Mao, J. Li, Y. Huan, J. Yuan, Z.-A. Li, K. Chai, M. Ma, S. Ni, J. Tian, S. Liu, H. Zhou, F. Zhou, J. Li, G. Zhang, K. Jin, X. Dong and Z. Zhao, Chin. Phys. Lett., 2018, 35, 057402 CrossRef
.
- X. Zhou, C. K. Borg, J. W. Lynn, S. R. Saha, J. Paglione and E. E. Rodriguez, J. Mater. Chem. C, 2016, 4, 3934 RSC
.
- H. Sun, D. N. Woodruff, S. J. Cassidy, G. M. Allcroft, S. J. Sedlmaier, A. L. Thompson, P. A. Bingham, S. D. Forder, S. Cartenet, N. Mary, S. Ramos, F. R. Foronda, B. H. Williams, X. Li, S. J. Blundell and S. J. Clarke, Inorg. Chem., 2015, 54, 1958 CrossRef CAS PubMed
.
- Y. Huang, C. Wolowiec, T. Zhu, Y. Hu, L. An, Z. Li, J. C. Grossman, I. K. Schuller and S. Ren, Nano Lett., 2020, 20, 7852 CrossRef CAS PubMed
.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272 CrossRef CAS
.
-
R. Prins and D. C. Koningsberger, X-ray Absorption: Principles, Applications,Techniques of EXAFS, SEXAFS, XANES, Wiley, New York, 1988 Search PubMed
.
-
G. Bunker, Introduction to XAFS, Cambridge University Press, 2010 Search PubMed
.
- L. Simonelli, C. Marini, W. Olszewski, M. Avila Perez, N. Ramanan, G. Guilera, V. Cuartero and K. Klementiev, Cogent Phys., 2016, 3, 1231987 Search PubMed
.
- L. Simonelli, C. Marini, L. Ribo, R. Homs, J. Avila, D. Heinis, I. Preda and K. Klementiev, J. Synchrotron Radiat., 2023, 30, 235–241 CrossRef CAS PubMed
.
- S. Gurman, Interpretation of exafs data, J. Synchrotron Radiat., 1995, 2, 56 CrossRef CAS PubMed
.
- M. Guo, X. Lai, J. Deng, L. He, J. Hao, X. Tan, Y. Ren and J. Jian, Inorg. Chem., 2021, 60, 8742 CrossRef CAS PubMed
.
- G. Hu, M. Shi, W. Wang, C. Zhu, Z. Sun, J. Cui, W. Zhuo, F. Yu, X. Luo and X. Chen, Inorg. Chem., 2021, 60, 3902 CrossRef CAS PubMed
.
- P. Glatzel and U. Bergmann, Coord. Chem. Rev., 2005, 249, 65 CrossRef CAS
.
-
R. D. Cowan, The Theory of Atomic Structure and Spectra, University of California Press, Berkeley, 1981 Search PubMed
.
- G. Vankó, T. Neisius, G. Molnár, F. Renz, S. Kárpáti, A. Shukla and F. M. F. de Groot, J. Phys. Chem. B, 2006, 110, 11647 CrossRef PubMed
.
- S. Lafuerza, A. Carlantuono, M. Retegan and P. Glatzel, Inorg. Chem., 2020, 59, 12518 CrossRef CAS PubMed
.
- H. Gretarsson, S. R. Saha, T. Drye, J. Paglione, J. Kim, D. Casa, T. Gog, W. Wu, S. R. Julian and G. D. Gu, Phys. Rev. Lett., 2013, 110, 047003 CrossRef CAS PubMed
.
- H. Gretarsson, A. Lupascu, J. Kim, D. Casa, T. Gog, W. Wu, S. R. Julian, Z. J. Xu, J. S. Wen, G. D. Gu, R. H. Yuan, Z. G. Chen, N.-L. Wang, S. Khim, K. H. Kim, M. Ishikado, I. Jarrige, S. Shamoto, J.-H. Chu, I. R. Fisher and Y.-J. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 100509(R) CrossRef
.
- L. Simonelli, T. Mizokawa, M. Moretti Sala, H. Takeya, Y. Mizuguchi, Y. Takano, G. Garbarino, G. Monaco and N. L. Saini, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 214516 CrossRef
.
- F. Stramaglia, G. M. Pugliese, L. Tortora, L. Simonelli, C. Marini, W. Olszewski, S. Ishida, A. Iyo, H. Eisaki, T. Mizokawa and N. L. Saini, J. Phys. Chem. C, 2021, 125, 10810 CrossRef CAS
.
- Y. Mizuguchi, Y. Hara, K. Deguchi, S. Tsuda, T. Yamaguchi, K. Takeda, H. Kotegawa, H. Tou and Y. Takano, Supercond. Sci. Technol., 2010, 23, 054013 CrossRef
.
- A. Ricci, N. Poccia, B. Joseph, G. Arrighetti, L. Barba, J. Plaisier, G. Campi, Y. Mizuguchi, H. Takeya, Y. Takano, N. L. Saini and A. Bianconi, Supercond. Sci. Technol., 2011, 24, 082002 CrossRef
.
- E. Sevillano, H. Meuth and J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 4908 CrossRef CAS
.
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621 CrossRef CAS
.
- C. J. Zhang, H. Oyanagi, Z. H. Sun, Y. Kamihara and H. Hosono, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 214513 CrossRef
.
- C. J. Zhang, H. Oyanagi, Z. H. Sun, Y. Kamihara and H. Hosono, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 94516 CrossRef
.
| This journal is © the Owner Societies 2023 |