 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nonadiabatic wave packet dynamics and predissociation resonances in sodium hydride
Hans O.
Karlsson

Division of Scientific Computing, Department of Information Technology, Box 337, SE-751 05, Uppsala, Sweden. E-mail: Hans.Karlsson@it.uu.se
First published on 17th February 2023
Abstract
Vibrational wave packet dynamics provides an opportunity to explore the energy landscape and the population transfer between nonadiabatically coupled excited electronic states. Here the coupled nonadiabatic dynamics of the C1Σ+ and D1Σ+ states of sodium hydride (NaH) in the gas phase in the adiabatic picture is studied, using a sequence of ultra-fast laser pulses in the femtosecond region. Emergence of different population dynamics and dissociation probabilities is shown by carefully choosing the pulse wavelength, duration and time-shift between the pulses, exciting the molecule from the ground X1Σ+ state via the immediate A1Σ+ state. Quantum dynamics simulations were performed in the adiabatic picture, avoiding the adiabatic to diabatic transformation. Predissociation resonances, i.e. vibrational states with finite lifetimes, arise due to nonadiabatic couplings between bound and continuum states. Here accurate resonance energies and widths are computed providing further insight into the dissociation dynamics.
1 Introduction
With the advent of femtochemistry in the late 1980s it became possible to study chemical reactions in real time, following the breaking and making of chemical bonds as well as clocking the transition state.1,2 Laser pulses in the femtosecond region provide a balance in resolution for the nuclear dynamics between the time and energy domains. The field of femtochemistry opened up the possibility to study molecular dynamics far from the equilibrium region, necessitating the inclusion of nonadiabatic couplings between electronic states in the simulations, due to the break-down of the Born–Oppenheimer approximation.1 Furthermore, nonadiabatic couplings between bound and continuum energies on different electronic states give rise to predissociation resonances, i.e. vibrational states with finite lifetimes.3 Faster pulses, e.g. in the attosecond regime, provide a high temporal resolution but with a broad energy distribution. In the other extreme very long laser pulses, e.g. in the nanosecond regime, lead to a high resolution in energy but with a low temporal resolution.Femtosecond laser pulses give rise to a coherent superposition of vibrational states, i.e. vibrational wave packets.2 By combining several ultrafast pulses, with different wavelengths λ, pulse durations τ and time shifts T between the pulses, different regions of the potential energy landscape, as well as population transfer between electronic states, can be investigated and analyzed.1 The potential energy surfaces (PESs) and nonadiabatic couplings are computed in the adiabatic formalism using quantum chemical methodology, whereas the wave packet simulations of the nuclear dynamics normally are performed in the diabatic representation, necessitating an adiabatic to diabatic transformation.4 In a recent study Talbot et al.5 computed the accurate PES and nonadiabatic couplings for the sodium hydride (NaH) molecule. The potential energy surfaces and first-order derivative couplings were computed using equation-of-motion coupled cluster theory with single and double excitations (EOM-EE-CCSD), with core-valence polarized basis functions. In the region around 12 Å issues with the convergence of the surfaces and couplings were noted, as can be observed in the reported C and D states close to the second avoided crossing. Using the sudden approximation, vibrational wave packet dynamics on the excited electronic |A〉, |C〉 and |D〉 states were studied, using both quantum and semi-classical methods. Their simulations illustrated that the adiabatic picture can be used for the quantum and semi-classical simulations, avoiding the need for an adiabatic to diabatic transformation.
In this work the adiabatic picture is used to compute accurate predissociation resonances and quantum wave packet dynamics explicitly initiated by a sequence of femtosecond laser pulses, using the potentials, Fig. (1), and nonadiabatic couplings, Fig. (2), computed by Talbot et al.5 Similar potential energy surfaces for NaH, although no derivative couplings, were also computed by Aymar et al.6
 | ||
| Fig. 1 Potential energy surfaces of sodium hydride relevant for this work. From the study of Talbot et al.5 | ||
 | ||
| Fig. 2 Nonadiabatic couplings between the A, C and D electronic states. From the study of Talbot et al.5 | ||
The ground electronic state |X〉 of NaH has an equilibrium distance of RXeq = 1.87 Å, whereas the minimum of the first excited state |A〉 is located at RAeq = 3.19 Å. Following an excitation from the |X〉 state to the |A〉 state, a coherent wave packet will be formed composed of highly excited vibrational states, due to the shift in the equilibrium distance. The |C〉 electronic state has a local minimum at RC1 = 2.38 Å, and a global minimum at RC2 = 6.5 Å. For the |D〉 state, there is a minimum at RD1 = 2.72 Å, supporting two vibrational states, and another minima at RD2 = 12 Å. There are two avoided crossings between the |C〉 and |D〉 states. The first avoided crossing is located at Rc1 = 2.72 Å, whereas the second avoided crossing is close to Rc2 = 12 Å. Due to the different shapes and anharmonicities of the electronic states, the resulting wave packets will move with different time scales, as will be discussed below.
2 Methods
The vibronic Schrödinger equation was discretized on a grid, with a grid spacing of dR = 0.015 Å, using pseudo-spectral/sincDVR7–9 and high order finite difference10 methods. Different grid sizes, ranging from 15 Å up to 40 Å, were used to describe the wave packet dynamics and resonance states. The Hamiltonian, including nonadiabatic and time-dependent couplings, is given by5,11 | (1) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) = −iħ∇R is the momentum operator and
= −iħ∇R is the momentum operator and ![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) is the skew-symmetric matrix of first order derivative coupling vectors. The transition dipole moment is assumed to be constant and the time-dependent term Vt(t) describes the interaction with an ultrafast laser pulse in the dipole approximation.
is the skew-symmetric matrix of first order derivative coupling vectors. The transition dipole moment is assumed to be constant and the time-dependent term Vt(t) describes the interaction with an ultrafast laser pulse in the dipole approximation.
3 Predissociation resonances
The nonadiabatic coupling between the |C〉 and |D〉 electronic states leads to a bound-continuum coupling giving rise to predissociation resonances i.e. vibrational states with a finite lifetime. The nonadiabatic coupling between the |A〉 and the |C〉 and |D〉 states, respectively, also contributes to the resonance structure but with a minor effect on the resonance lifetime due to the weaker coupling strength. Earlier studies on the predissociation of the NaH molecule include radiative and predissociative decay from the A state for high rotational numbers.12 Here, the focus is on the vibrational predissociation for the coupled C and D states.The predissociation resonances are represented as complex valued energies E = Er − iEi, where the real part Er gives the position of the energy and the negative imaginary part is related to the width of the resonance Ei = Γ/2, which in turn is related to the lifetime of the resonance τres = ħ/Γ.3,13,14 To determine the resonance states, the time-independent vibronic Schrödinger equation
| Ĥ|Φ〉 = E|Φ〉 | (2) |
 where θ is the scaling angle and g(R) is a smooth function that changes from 0 to 1 around R = R0.13,15 The switching function g(R) can be of a general form as long as it is smooth; here, the shape proposed by Moiseyev13 was used. When solving for the time-independent Schrödinger equation using SES or PML, the same discretization for the kinetic energy operator
where θ is the scaling angle and g(R) is a smooth function that changes from 0 to 1 around R = R0.13,15 The switching function g(R) can be of a general form as long as it is smooth; here, the shape proposed by Moiseyev13 was used. When solving for the time-independent Schrödinger equation using SES or PML, the same discretization for the kinetic energy operator  for bound states can be used, modified by pre- and post-multiplication with the inverse of f(R) and adding a small potential term VSES(R),
for bound states can be used, modified by pre- and post-multiplication with the inverse of f(R) and adding a small potential term VSES(R),![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) SES = f−1 SES = f−1![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) f−1 + VSES f−1 + VSES | (3) |
 | (4) |
Fig. (3) displays the predissociation resonance energies and widths for the coupled |C〉 and |D〉 electronic states in relation to the respective potential energy surfaces. A close up of the |C〉 and |D〉 state resonances is given in Fig. (4). The oscillatory pattern of the resonance widths is a signature of predissociation resonances.14 For a correct description of the coupled |C〉 and |D〉 states, the widths, i.e. lifetimes, of the vibrational resonances must be considered.
 | ||
| Fig. 4 Predissociation resonances for the |C〉 and |D〉 electronic states. Note the different scales for the widths. For clarity, the same energy range is used as shown in Fig. (3). | ||
The nine highest excited vibrational resonances on the |C〉 state and the first six resonances on the |D〉 state are given in Table (1) for comparison with a previous work.5 The resonance positions compare well with the vibrational energies previously reported except for the D, 2 state which in this work is found to not be degenerate with the D, 3 state, having a slightly lower value of the energy and with a rather large width, i.e. a short lifetime, compared to the neighboring resonances. Note that the nonadiabatic coupling between the |A〉 and |C〉 electronic states also give rise to finite lifetimes also for the |C〉 vibrational states close to the dissociation limit, although with less widths than that for the |D〉 resonances due to the weaker coupling strength.
| State | Previous work5Er (eV) | This work Er (eV) | Γ/2 (meV) |
|---|---|---|---|
| C1Σ+ | |||
| 34 | 5.038 | 5.037 | 6.0 × 10−7 |
| 35 | 5.053 | 5.052 | 1.2 × 10−6 |
| 36 | 5.063 | 5.063 | 2.4 × 10−7 |
| 37 | 5.069 | 5.068 | 6.9 × 10−7 |
| 38 | 5.082 | 5.082 | 2.9 × 10−7 |
| 39 | 5.096 | 5.096 | 4.4 × 10−8 |
| 40 | 5.109 | 5.109 | 1.1 × 10−6 |
| 41 | 5.125 | 5.125 | 1.6 × 10−6 |
| 42 | 5.136 | 5.136 | 2.1 × 10−6 |
| D1Σ+ | |||
| 0 | 5.116 | 5.115 | 9.9 × 10−8 |
| 1 | 5.149 | 5.149 | 1.0 × 10−4 |
| 2 | 5.155 | 5.151 | 1.5 × 10−3 |
| 3 | 5.155 | 5.155 | 7.1 × 10−5 |
| 4 | 5.162 | 5.162 | 6.5 × 10−4 |
| 5 | 5.169 | 5.168 | 6.2 × 10−4 |
4 Wave packet dynamics
Vibrational wave packet dynamics provides a way to explore the energy landscape on the excited electronic states and the effects of the nonadiabatic couplings.1,2 By using a sequence of ultrafast laser pulses to initiate the wave packet dynamics, different regions of the potential surfaces can be explored and analyzed, e.g. with respect to population transfer, quantum interference and dissociation probabilities. Here, a two pulse, pump–probe type, scheme is used where the first pulse promotes the probability density from the ground |X〉 state to the excited |A〉 electronic state and the second pulse promotes the wave packet from the |A〉 to the coupled |C〉 and |D〉 states. The probability of dissociation from the |C〉 state depends on the laser pulse but also on the nonadiabatic coupling. The laser pulse is given by| Vt(t, t0) = E0e−(t−t0)2/α2cos(ωt) | (5) |
 | (6) |
 | (7) |
4.1 Wave packet dynamics on the electronic |A〉 state
The ultrafast pump pulse Vpump(t) gives rise to a coherent vibrational wave packet |ΨA(t)〉 by excitation from the ground vibrational state |ϕX0〉. The resulting wave packet |ΨA(t)〉 and its subsequent dynamics depend on the shape of the potential energy surface and the characteristics of the laser pulse, i.e. the wavelength λ, pulse duration τ and strength E0. Here, the strength of the pulse was chosen to be weak, i.e. around 98% of the population will remain in the electronic ground state after excitation.To determine the maximum population transfer from the |X〉 state to the |A〉 state, the population on the |A〉 state was computed as a function of wavelength, using a pump pulse with a duration of τpump = 10 fs. As seen in Fig. (5), a maximum population transfer is observed at λ = 383 nm, as noted previously.20–22
 | ||
| Fig. 5 Population on the |A〉 state as a function of the pump wavelength, using a pulse duration of τ = 10 fs. | ||
Having established an optimal wavelength for excitation, the effect of the pulse duration τ on the formation of the |ΨA(t)〉 wave packet is considered. Four different pulse lengths were used, ranging from very short (τ = 1 fs), via medium length (τ = 10 fs) to very long (τ = 25 fs and τ = 50 fs) in relation to the vibrational period of the |A〉 state. The resulting wave packet dynamics up to 200 fs as a function of pulse duration τ is shown in Fig. (6).
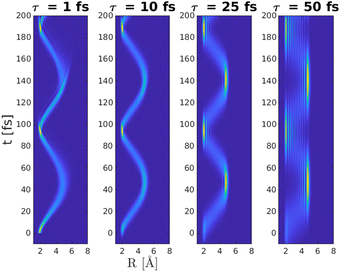 | ||
| Fig. 6 Wave packet dynamics on the |A〉 state as a function of pulse duration τ, using a wavelength of λ = 383 nm. It is noticed that the shape of the wave packet depends on the pulse duration whereas the revival time is similar Tref = 95 fs. It is further noticed that the population on the |A〉 state differ for the four different situations, as shown in Fig. (7). | ||
To understand the time-evolution of the wave packet |ΨA(t)〉, a decomposition in terms of vibrational eigenstates can be used for illustration
 | (8) |
For the pump pulse used here only bound vibrational states |ϕAn〉 will contribute to the wave packet. The coefficients cn in the superposition (8) contain the overlap between the nuclear vibrational eigenfunctions |ϕAn〉 and the ground vibrational state |ϕX0〉, as in the sudden approximation formalism, but also the effect of the ultrafast laser pulse i.e. the wavelength and pulse duration. Integrated over the duration of the pulse, the coefficients cn can be expressed as23
| cn = μ0〈ϕAn|ϕX0〉f(ω, λ) | (9) |
| f(ω, λ) = E0e−α2(ω−ωn0)2/4 | (10) |
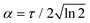 | (11) |
| ωn0 = (EAn − EX0)/ħ | (12) |
 | ||
| Fig. 7 Probability |cn|2, eqn (9), for the molecule to be in the vibrational state |ϕAn〉 as a function of vibrational energy for four different pulse durations, τ = 1 fs,τ = 10 fs, τ = 25 fs and τ = 50 fs. | ||
For a short pulse duration, τ = 1 fs, the coefficients cn are close to the Frank–Condon factors, which correlate with the sudden approximation where it is assumed that the wave packet do not move during the excitation process and the resulting weights in the wave packet are given by the overlap of the vibrational states with the initial ground vibrational state cn = 〈ϕAn|ϕX0〉. In the other extreme, τ = 50 fs, corresponding to a half vibrational period, the wave packet is dominated by a single vibrational state, in a Golden Rule type of description with an energy matching between the initial and the final states. For the excitation considered here, a duration of τ = 10 fs provides a balance between time and energy resolution. Consequently, in what follows, a pump wavelength of λpump = 383 nm and a duration of τpump = 10 fs will be used. To support the discussion in the following section, the resulting wave packet on the |A〉 state is depicted in Fig. (8).
 | ||
| Fig. 8 Probability density of the time-evolution on the A-state after a pump pulse with λpump = 383 nm and τpump = 10 fs. | ||
4.2 Nonadiabatic wave packet dynamics on the |C〉 and |D〉 electronic states
The wave packet dynamics on the coupled |C〉 and |D〉 electronic states is initiated with a second pulse Vprobe(t + T), promoting the probability density from the |A〉 state. Due to the nonadiabatic couplings, the wave packet can dissociate on the |C〉 state either directly or via the bound |D〉 state due to the nonadiabatic coupling, as illustrated by the predissociation resonances in the previous section. The resulting wave packet dynamics depends not only on the probe wavelength λprobe and pulse duration τprobe but also on the time shift T between the two pulses, since the |ΨA(t)〉 wave packet will move on the potential energy surface during the probe process. Fig. (9) depicts the population on the |C〉 and |D〉 states as a function of wavelength λprobe and time shift T directly after the probe pulse is over. From Fig. (9), it is seen that there are combinations of wavelengths λ and time shifts T where the population on the two states differs significantly. By carefully choosing the probe pulse parameters, the formation of the wave packet on the coupled states can be controlled. As the wave packet evolves in time, different regions of the coupled PES are explored with a probability of population transfer between the coupled states and for dissociation. When the wave packet is close to the crossing regions at Rc1 = 2.72 Å and Rc2 = 12 Å, part of the wave packet might be transferred between the bound |D〉 state and the unbound part of the |C〉 state, and dissociate to the Na(4s) + H(1s) limit.Four different situations were studied to showcase the effect on the dynamics and dissociation probabilities due to different wavelengths λprobe and time shifts T, as well as the importance of the nonadiabatic couplings. The four cases were as follows:
(a) λprobe = 550 nm and T = 14 fs, corresponding to the wave packet |ΨA(t)〉 being close to the first crossing region between the |C〉 and |D〉 states at the probe time T, i.e. 〈![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) 〉 = 〈ΨA(T)|
〉 = 〈ΨA(T)|![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |ΨA(T)〉 = 2.8 Å, and moving outwards, Fig.(10).
|ΨA(T)〉 = 2.8 Å, and moving outwards, Fig.(10).
(b) λprobe = 650 nm and T = 47 fs, when |ΨA(t)〉 is at the outer turning point, 〈![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) 〉 = 5 Å, Fig. (11).
〉 = 5 Å, Fig. (11).
(c) λprobe = 550 nm and T = 82 fs, when |ΨA(t)〉 is close to 〈![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) 〉 = 2.8 Å moving inwards, Fig. (12), and
〉 = 2.8 Å moving inwards, Fig. (12), and
(d) λprobe = 550 nm and T = 95 fs when |ΨA(t)〉 is at the inner turning point, 〈![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) 〉 = 1.8 Å, Fig. (13).
〉 = 1.8 Å, Fig. (13).
The |ΨD(t)〉 wave packet has a revival period of Trev ∼ 500 fs, compared to Trev ∼ 95 fs for the |ΨA(t)〉 wave packet. Furthermore, the dynamics of |ΨA(t)〉 is limited to a region in space that is less than R = 5.5 Å, whereas the motion of |ΨD(t)〉 extends beyond 25 Å. For case (a), Fig. (10), the excitation energy is above the dissociation limit for the |C〉 state and the wave packet |ΨC(t)〉 starts to dissociate. As the outgoing wave packet |ΨD(t)〉 passes the outer crossing point RC2 = 12 Å, the population is transferred to the |C〉 state, increasing the dissociation probability. A second crossing due to the inwards motion further transfer population, leading to a |ΨC(t)〉 wave packet being reflected at the inner turning point before dissociating. The second combination, (b), Fig. (11), creates wave packets close to the inner crossing region Rc1 = 2.72 Å with a mix of bound and dissociative dynamics. The initial excitation is close to 5 Å after which the wave packet quickly spreads towards both the inner and outer turning points. A partially bound state wave packet |ΨC(t)〉 is formed on the |C〉 state and each time |ΨD(t)〉 passes the outer crossing point there is a probability transfer supporting both inward and outward motions on the |C〉 state.
The parameters used in case (c), Fig. (12), where |ΨA(t)〉 moves inwards, leads to a similar population probability for the two states, one dissociative |ΨC(t)〉 and one bound |ΨD(t)〉 wave packet. The effect on the nonadiabatic coupling is clearly seen around t = 200 fs and again from t > 500 fs. The similarity to case (a) is noticed, and the excitation is taking place on a similar part of the PES but for outward (a) and inward (c) motions, respectively.
For the fourth example (d), Fig. (13), the pulse parameters are chosen such that the population on the |C〉 state initially dominates, leading to a dissociative wave packet. As |ΨC(t)〉 reaches the outer crossing point a population transfer occurs and a wave packet |ΨD(t)〉 is formed which, in turn, transfer the probability back to the |C〉 state from t > 450 fs.
From these four examples, it is seen that a very rich, both bound and dissociative, nonadiabatic wave packet dynamics can be observed depending on the nonadiabatic couplings and the choice of the pulse parameters.
5 Conclusions
In this work accurate wave packet dynamics, in the adiabatic picture, were computed for the coupled C1Σ+ and D1Σ+ states initiated by a sequence of femtosecond laser pulses. It was illustrated that the wave packet dynamics and population transfer crucially depend on the different combinations of wavelengths, durations and time-shifts between the pulses. Predissociation resonances, emerging due to the coupling between bound and continuum states, provide a complementary illustration of the nonadiabatically coupled system and showing the importance of computing resonance widths.Further studies will consider the use of optimal control for defining optimal pulse parameters to control different dissociation pathways.
Conflicts of interest
There are no conflicts to declare.References
- A. Zewail, Science, 1988, 242, 1645–1653 CrossRef CAS PubMed.
- J. Polanyi and A. Zewail, Acc. Chem. Res., 1995, 28, 119–132 CrossRef CAS.
- N. Moiseyev, P. Certain and F. Weinhold, Mol. Phys., 1978, 36, 1613–1630 CrossRef CAS.
- W. Domcke and D. R. Yarkony, in Annual Review of Physical Chemistry, ed. M. A. Johnson and T. J. Martinez, Annual Reviews, Palo Alto, 2012, vol. 63, pp. 325–352 Search PubMed.
- J. J. Talbot, M. Head-Gordon, W. H. Miller and S. J. Cotton, Phys. Chem. Chem. Phys., 2022, 24, 4820–4831 RSC.
- M. Aymar, J. Deiglmayr and O. Dulieu, Can. J. Phys., 2009, 87, 543–556 CrossRef CAS.
- C. Schwartz, J. Math. Phys., 1985, 26, 411–415 CrossRef.
- D. Colbert and W. Miller, J. Chem. Phys., 1992, 96, 1982–1991 CrossRef CAS.
- B. Fornberg, A Practical Guide to Pseusdospectral Methods, Cambridge University Press, Cambridge, 1996 Search PubMed.
- A. Nissen, H. O. Karlsson and G. Kreiss, J. Chem. Phys., 2010, 133, 054306 CrossRef PubMed.
- W. Domcke, D. Yarkony and H. Köppel, Conical intersections: electronic structure, dynamics spectroscopy, World Scientific, Singapore, 2004 Search PubMed.
- H. Telle, J. Mol. Struct., 1986, 143, 565–568 CrossRef CAS.
- N. Moiseyev, Phys. Rep., 1998, 302, 212–293 CrossRef.
- H. O. Karlsson, Eur. Phys. J. D, 2000, 11, 207–212 CrossRef CAS.
- H. O. Karlsson, J. Chem. Phys., 1998, 108, 3849–3853 CrossRef CAS.
- R. Kosloff and D. Kosloff, J. Comput. Phys., 1986, 63, 363–376 CrossRef.
- T. Park and J. Light, J. Chem. Phys., 1986, 85, 5870–5876 CrossRef CAS.
- W. T. Pollard and R. A. Friesner, J. Chem. Phys., 1994, 100, 5054–5065 CrossRef CAS.
- K. Kormann, S. Holmgren and H. O. Karlsson, J. Chem. Phys., 2008, 128, 184101 CrossRef PubMed.
- H.-Y. Huang, Y.-Y. Chang, M.-H. Liao, K.-L. Wu, T.-L. Lu, Y.-Y. Chang, C.-C. Tsai and T.-J. Whang, Chem. Phys. Lett., 2010, 493, 53–56 CrossRef CAS.
- H.-Y. Huang, T.-L. Lu, T.-J. Whang, Y.-Y. Chang and C.-C. Tsai, J. Chem. Phys., 2010, 133, 044301 CrossRef PubMed.
- C.-C. Chu, H.-Y. Huang, T.-J. Whang and C.-C. Tsai, J. Chem. Phys., 2018, 148, 114301 CrossRef PubMed.
- R. Schinke, Photodissociation dynamics, Cambridge University Press, Cambridge, 1993 Search PubMed.
| This journal is © the Owner Societies 2023 |






