Chiral symmetry breaking induced by energy dissipation†
Received
20th December 2022
, Accepted 3rd March 2023
First published on 7th March 2023
Abstract
Spontaneous chiral symmetry breaking is observed in a wide variety of systems on very different scales, from the subatomic to the cosmological. Despite its generality and importance for a large number of applications, its origin is still a matter of debate. It has been shown that the existence of a difference between the energies of the intermediate states of optical enantiomers leads to disparate production rates and thus to symmetry breaking. However, it is still unclear why this occurs. We measured for the first time the optical rotation angle of NaClO3 enantiomeric crystals in solution during their formation and found that the amount of energy needed to induce the enantiomeric excess is exactly the same as the energy dissipated per mole of solid salt calculated from the entropy production obtained from the proposed model. The irreversible nature of the process leading to entropy production thus explains the chiral symmetry breaking in the salt crystals studied. The proposed method could be used to explain the formation of self-organised structures generated by self-assembly of enantiomers arising from chiral symmetry breaking, such as those emerging in the production of advanced materials and synthetic biological tissues.
1 Introduction
Chiral structures are frequently found in nature, on scales as diverse as those of elementary particles and living beings. These structures present mirror images known as enantiomers. In some situations, the ratios of these enantiomers are similar, but in others there is an excess of one over the other, resulting in chiral symmetry breaking. Explaining why this is so is a problem of great current interest.1–6 Advances in the study of chiral symmetry breaking may have an impact in for example the production of efficient and safe medicines,7–9 the use of liquid crystals in biosensors and microlasers,9 the control of self-assembly for the production of advanced materials10 and synthetic biological tissues,11,12 and in providing a deeper understanding of the emergence of life.5,13 A key question is how self-organised structures are formed from the directed and selective self-assembly of enantiomeric constituents arising from chiral symmetry breaking that takes place outside of equilibrium and, therefore, in the presence of energy dissipation. Finding out what role dissipation plays in the symmetry-breaking process is the main objective of this article.
At equilibrium, the free energy ΔGrev required for the formation of the possible enantiomers is practically the same so the corresponding probabilities ps ∝ exp(−ΔGrev/kBT), with kB the Boltzmann constant and T the temperature, are very similar, resulting in weak or none chiral symmetry breaking. Experiments have shown that the actuation of external factors such as polarised light,14 shearing,15,16 temperature gradients17 and in general external forces driving the system out of equilibrium can lead to a significant disproportion in the concentrations of the homochiral structures (enantiomers) or even prevent their formation.3,7 In order to reproduce the experimental observations and to be able to identify optimal conditions for the intensification of the phenomenon several kinetic models considering different mechanisms have been proposed.4,6 Considering the non-equilibrium thermodynamics of the chiral symmetry breaking through the entropy production could be useful to understand also the role of energy dissipation in the process. Understanding the role of external forces in the thermodynamics and kinetics of enantiomer formation under non-equilibrium conditions is therefore of vital importance in explaining why and under what conditions chiral symmetry breaking occurs.
Fig. 1 shows a typical chiral symmetry breaking process whereby an achiral compound A gives rise to chiral D- and L-type blocks which assemble sequentially to form two different types of structures. A typical example is the formation of enantiomers of a crystal in which the mirror images of the chiral compound, levorotatory (L) and dextrorotatory (D) optical enantiomers, have the same energy but opposite optical rotation angles for polarized light. In the absence of dissipation, the ratio of the two enantiomers is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, whereas when the process takes place out of equilibrium and is therefore dissipative, the concentration of one of the enantiomers exceeds that of the other.
1, whereas when the process takes place out of equilibrium and is therefore dissipative, the concentration of one of the enantiomers exceeds that of the other.
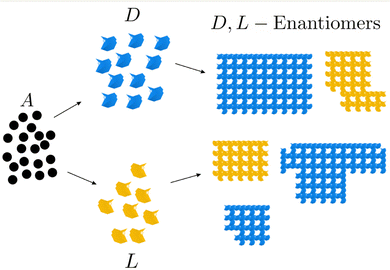 |
| | Fig. 1 Chiral symmetry breaking. The achiral compound A transforms into the chiral compounds D and L, which form D and L crystals. | |
Chiral symmetry breaking in the NaClO3 crystallisation process has been the subject of much interest in recent years.4,6,7,18 Experiments consisting of evaporating the solvent to obtain NaClO3 crystals,15 performed by stirring the sample, showed the existence of a disproportion in the concentrations of both enantiomeric crystals of NaClO3. When these experiments were performed without stirring, the concentrations of both enantiomers were found to be similar. Evaporation experiments also showed a disproportion of enantiomers in the absence of stirring but at low supersaturation of salt.7 These experiments displayed chiral symmetry breaking when the process takes place out of equilibrium, measuring the enantiomeric excess only at the end of crystallisation without providing information on the enantiomeric excess as a function of time. In these experiments, aliquots are drawn periodically, which causes the collected samples to denature as the crystals are not in contact with the system under non-equilibrium conditions.6,7 It is therefore crucial to consider the transient dynamics of the crystallisation process and to measure the in situ populations in order to understand the role of energy dissipation in chiral symmetry breaking.
In this paper, we demonstrate by modelling and experiments that the energy required to generate an enantiomeric crystal excess must be equal to the energy dissipated in the irreversible processes involved in crystallisation: heat exchange, salt diffusion, salt phase change, crystal emergence, growth and precipitation. This energy causes an increase in the free energy barrier of one of the enantiomeric crystals and, consequently, a decrease in the enantiomer formation rate which explains the enantiomeric excess. In the experiments performed, we have measured for the first time the enantiomeric excess of NaClO3 along the crystallisation process of this substance, for different non-equilibrium conditions. The model proposed provides the value of the energy responsible for the increase of the energy barrier and, therefore, of the enantiomeric excess percentage. We have found that the enantiomeric excess becomes more important when the actuating forces, temperature and activity differences, increase and therefore when energy dissipation, measured in terms of the entropy production rate, is larger. This result clearly shows the important role played by dissipation in the enantiomer formation process.
2 Chiral symmetry breaking induced by entropy production
The existence of an enantiomeric excess has been attributed to the disparity in the activation energies of both enantiomers which causes different formation rates.4,6,19 To find the reason for this mismatch, we analysed the formation of NaClO3 enantiomeric crystals. We modelled the crystallisation kinetics to find the fraction of each enantiomer and thus compute the enantiomeric excess. We also measured the optical rotation angle of the solution throughout the crystallisation process, from which the enantiomeric excess can also be obtained. The good agreement between the two results leads us to conclude that the enantiomeric excess originates from the energy dissipated in the processes of heat transfer, salt diffusion, salt phase change, crystal growth and precipitation that take place during crystallisation. This energy is absorbed by the intermediate state of one of the enantiomers increasing its free energy barrier and therefore reducing its rate of formation. The selection of the enantiomer that increases its energy barrier is random, in accordance with ref. 15. Since symmetry breaking is a stochastic process, we focus on calculating the increase of one of the activation energies. In addition, we analyse the process in terms of two reaction coordinates, where the use of two different free energy barriers and activation energies naturally arises.20,21
In Fig. 2, we illustrate the different stages of crystallisation in which the two driving forces, temperature difference ΔT between the system and its surrounding and activity difference Δz between the solid and liquid phases reach different values. Initially (Fig. 2(a)), the system is an under-saturated mixture of salt and glycerol, with Δz < 0 and a maximum value of ΔT. When the mixture comes into contact with its surroundings, it cools down to saturation point at which Δz = 0 while the salt in the liquid phase forms small clusters that maximise Δz (Fig. 2(b)). Thus, a fraction of the liquid salt undergoes a phase change that favours the formation of nuclei of one enantiomer over the other, reaching a state in which Δz > 0 and ΔT > 0 (Fig. 2(c)). Once the nuclei of the first enantiomer are formed, crystals emerge and grow and eventually redissolve bringing the system to a final state characterised by a non-racemic mixture of enantiomeric crystals in which Δz = 0 and ΔT = 0 (Fig. 2(d)).
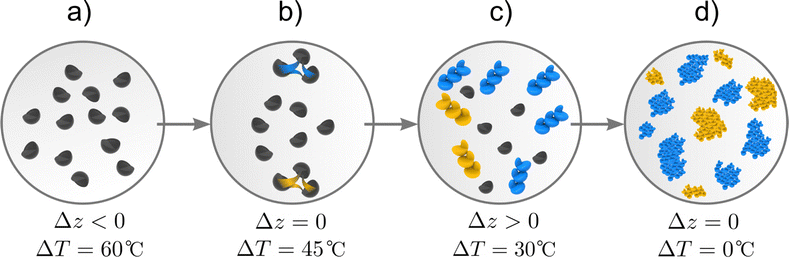 |
| | Fig. 2 Enantiomer formation process. The system is initially an under-saturated mixture of salt, denoted by small black semicircles, and glycerol (a). Temperature decrease leading to stage (b) characterised by stronger interaction among salt compounds (yellow and blue lines) thus reaching saturation. Small nuclei of both enantiomers are formed (L- and D-nuclei represented by gold and blue agglomerates respectively) in the process of phase change in which one of the enantiomers is dominant, as represented in stage (c). Finally, crystals emerge and the system reaches a state of chemical and thermal equilibrium (d) with an enantiomeric excess. | |
Fig. 2(b) highlights the fact that interactions among salt molecules in liquid state give rise to nucleation (and phase change) of the salt (Fig. 2(c)), a key point to understanding symmetry breaking. Nuclei have a crystalline structure and can adopt L and D configurations. Their growth gives rise to L and D enantiomeric crystals.
Entropy changes are due, on the one hand, to reversible heat exchange and phase change and, on the other hand, to irreversible processes that take place during crystallisation. In the former, the temperature of the system decreases and the molecular structure of the salt changes. The latter is due to the irreversible processes that take place, such as heat conduction, mass diffusion and crystal growth, resulting in a rate of entropy production. Entropy changes due to reversible processes alone do not explain the kinetics of crystallisation or the origin of chiral symmetry breaking.
To analyse the kinetics and energetics of the enantiomer formation process, we will consider that the transformation of an achiral compound A, the liquid component, into L- or D-enantiomeric crystals takes place across the standard free energy potential barrier illustrated in Fig. 3(a). In non-dissipative quasi-equilibrium processes, for which Δz ≈ 0, the state on top of the barrier A′ is common to both enantiomers, as the blue lines of Fig. 3 show. Since there is no irreversible change of the entropy, Δis = 0, the entropy change per mole is simply the reversible change Δrs. The formation of both enantiomers thus takes place along the same free-energy barrier which results in a racemic (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture.15
1) mixture.15
 |
| | Fig. 3 Free-energy landscapes in the formation of D (a) and L (b) enantiomers as a function of the reaction coordinates γL and γD. In equilibrium (Δz = 0, Δis = 0), the formation of both enantiomers from the achiral compound A takes place through the same intermediate A′. Energy barriers are represented by the continuous blue lines. Outside equilibrium (Δz > 0, Δis > 0), the energy released in the system contributes to increase the barrier of enantiomer L, denoted by the dashed red line, by an amount ΔEa = TΔisT (with ΔisT the entropy change per salt mole). The intermediate state is now A*. Increasing the barrier reduces the rate of L-enantiomer formation, thus breaking the symmetry. | |
Outside equilibrium (Fig. 3), when Δz ≠ 0 and ΔT ≠ 0, the entropy change per salt mole is Δs = Δrs + Δis, where the irreversible part contains contributions of both enantiomers: Δis = ΔisL + ΔisD. The energy dissipated in the formation of the D enantiomer is thus TΔisD (Fig. 3(a)) whereas that for the L enantiomer is TΔisL (Fig. 3(b)). The figures illustrates the fact that the formation process of both enantiomers takes place across two different free energy barriers that have different transition states (A′ and A*) whose energy difference is ΔEa = TΔisT, with ΔisT the total entropy produced per mole. This disparity in barrier height leads to different enantiomer formation rates, which explains the excess of one enantiomer over the other.4,6,19
The total entropy produced consists of the entropy produced in the formation of the enantiomers Δis and those corresponding to the remaining irreversible processes taking place in the system: heat transfer, crystal emergence, crystal growth, precipitation and diffusion. In the Theory Section, we compute the entropy production rate σ of these irreversible processes and from it the total entropy production:  , where N = NL + ND is the number of moles of solid salt, and NL and ND the number of moles of salt composing L- and D nuclei and crystals.
, where N = NL + ND is the number of moles of solid salt, and NL and ND the number of moles of salt composing L- and D nuclei and crystals.
The model we propose (see Theory Section) gives the number of moles NL and ND and from them the enantiomeric excess defined as
| | 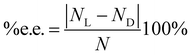 | (1) |
and the optical rotation angle
| | | α = α0(NL(h) − ND(h))/N0 | (2) |
with
α0 = 50° a reference angle,
N0 the initial amount of salt molecules and
h the height of the test tube at which measurements are taken. The comparison of the time evolution of the rotation angle obtained by the model with the experiments will be made in the Results Section.
3 Materials and methods
3.1 Experimental set up
A crucial decision was to choose glycerol as the solvent, as we needed high dielectric and thermal properties, low evaporation, high viscosity and a refractive index close to that of crystals to avoid high light scattering. The initial step of the experiment was to mix given amounts of salt and solvent in our test tube, a cylindrical quartz cuvette with an inner diameter of 20 mm, and then heat from the bottom of the mixture to ensure complete dissolution at a constant temperature. The absence of optical activity was verified once the maximum temperature was reached. Once the salt has dissolved and only the homogeneous phase is present and the temperature is constant, we turned off the heater and let the system cool down. We started measuring the optical activity and the temperature of the system until a steady state was reached and no considerable changes in optical activity were recorded. The height at which the measurements were taken varied depending on the initial salt/solvent ratio and the cooling conditions to avoid high scattering or low optical activity. In the enhanced cooling cases and for ws/wg = 0.36 in natural cooling, the measurement height was h = H/3, where H is the height of the test tube. For the remaining natural cooling cases, the height was h = H/4.
The polarimeter used is a home-built Mueller matrix polarimeter that incorporates four photoelastic modulators which allowed us to determine with high sensitivity the time-varying enantiomeric excess of the NaClO3 solution. The instrument, described in detail in ref. 22, was operated in transmission using a 405 nm laser diode (5 W) as the light source. As the photoelastic modulators operate at high frequency (∼50 kHz), this instrument can measure the 16 Mueller matrix elements of the sample simultaneously and at fast acquisition rates. In our experiments, a Mueller matrix was measured every ∼1 s during the several hours that each of the experiments lasted. An outline of our experimental setup is shown in Fig. 4. The power supply provides power to the laser and the polarisation state generator (beam generator) and polarisation state analyser (sensor) so that there is fine control of the polarisation transformation of the light after passing through the solution in the test tube. Data is transferred to and stored in a computer. To manually measure the average temperature of the solution, a thermocouple is used which is placed over the laser beam to avoid interference.
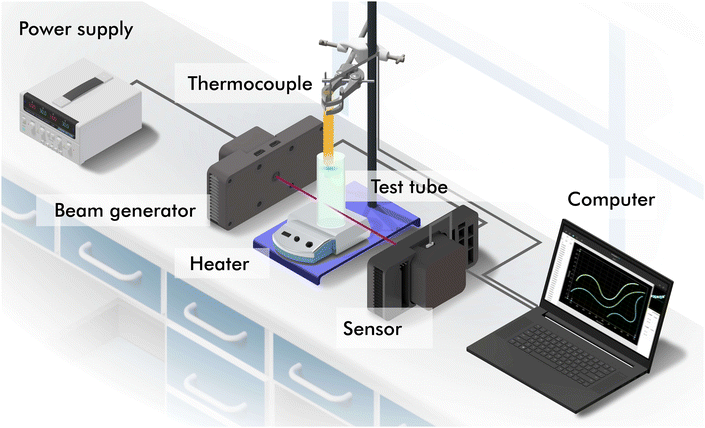 |
| | Fig. 4 Experimental set up. Devices and equipment: power supply, laser, laser and polarization state generator (beam generator), thermocouple, test tube, heater, polarization state analyzer and detector (sensor), and computer. | |
The solution was contained in a cylindrical fused quartz cell with a path length of 20 mm. When the salt was completely dissolved a clear solution was observed and the measured Mueller matrix was the 4 × 4 identity matrix, indicating that there was no optical rotation or any other optical effect. However, as the salt began to precipitate the solution became progressively hazy, until at some point Tyndall scattering became evident. Scattering could also be identified from the Mueller matrix measured by the appearance of depolarisation, as the scattered photons tend to randomise their polarisation.
The measured Mueller matrices were analysed using the differential formalism,23 which is well suited for the study of polarized light transmitted in turbid media. This method assumes that the polarisation properties of the medium have a uniform distribution along the optical path. The Mueller differential formalism can be introduced through the equation
| | 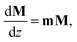 | (3) |
where the so-called differential matrix
m relates the Mueller matrix of the homogeneous anisotropic medium to its spatial derivative along the direction of light propagation (
z). A generally depolarizing Mueller matrix, satisfying
eqn (3) is
M =
emd =
eL, where
d is the optical pathlength and
L = ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M
M the accumulated differential Mueller matrix. The optical rotation of this depolarizing medium is then determined as:
| |  | (4) |
where
lij are the elements of
L. Apart from optical rotation and depolarization, no other polarimetric effect (
e.g. linear birefringence) were observed in the samples.
3.2 Theory
The model we propose describes the kinetics and energetics of enantiomeric crystal formation process which involves the solvent (glycerol) whose concentration remains practically constant, the dissolved salt and the solid salt in L- and D-configurations.
3.2.1 Mesoscopic nonequilibrium thermodynamics of the chiral symmetry-breaking.
In the first stage of the process, the dissolved salt forms small nuclei that are the precursors of the L and D nuclei of solid salt. This process takes place along reaction coordinates, (see Fig. 3).
Let ρ(γL,γD,r,t) be the probability density of finding a salt molecule in state γL or γD, at position r and time t. Salt molecules in liquid state correspond to γL = γD = 0, molecules in solid phase in L-configuration to γL = 1, while salt molecules in solid phase in D-configuration to γD = 1.
The continuity equation accounting for the evolution in time of the probability is
| |  | (5) |
with
JL and
JD the probability currents along
γL and
γD describing the emergence of the solid phase salt molecules with configurations
L and
D. On the other hand, the irreversible entropy change of the phase change process
δisph, considering local equilibrium along
γL and
γD, is
| | 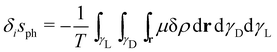 | (6) |
Taking the derivative with respect to time in
eqn (6), using the continuity equation (
eqn (5)) and integrating by parts, we obtain the entropy production rate
24 corresponding to the phase change (nuclei emergence)
| | 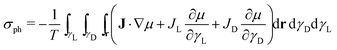 | (7) |
The expression of the currents then results from the linear coupling with the conjugate thermodynamic forces. For the diffusion current, we obtain
| |  | (8) |
where
D is the diffusion coefficient and
μ the chemical potential of the salt molecules written as
| | μ = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fρ + ϕ + ψ fρ + ϕ + ψ | (9) |
in which
f is the activity coefficient,
ϕ is the potential along the coordinates
γL and
γD, and
ψ the gravitational potential energy which depends on position
r.
The probability current corresponding to the transformation of a salt molecule in the liquid state to the solid state of configuration L is
| |  | (10) |
where
Dγ is the diffusivity along the
γ-coordinate. A similar expression is found for the current
JD. By performing a coarse-graining in
γL and
γD of the probability
ρ, one obtains the salt molar fraction:
| |  | (11) |
3.2.2 Salt phase change.
Performing a coarse-graining of eqn (5) and considering quasi-stationary currents, we obtain the molar fraction of the salt that remains in liquid state x evolves in time according to the reaction–diffusion equation| |  | (12) |
where y is the coordinate along the axis of the test tube, D the diffusion coefficient, and ṙL and ṙD the phase change rates from dissolved salt to solid salt in L- and D-configurations, respectively.
The rates ṙL and ṙD are proportional to the activity difference between solid and liquid phases or oversaturation forces ΔzL and ΔzD. The L-rate is given by
| |  | (13) |
where
k is a kinetic constant, and
Ea,L =
E0a,L + Δ
Ea the activation energy, with
E0a,L the activation energy of a quasi-equilibrium process. The forces depend on the free energy of the salt in liquid and solid states, as well as on the molar fractions of the salt in
L- and
D-configurations. The
L-oversaturation force is given by
| | 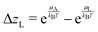 | (14) |
where the chemical potentials are
μA =
μ0A +
kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xf
xf and
μL =
μ0L +
kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xLfL
xLfL, with
f and
fL being activity coefficients accounting for the non-ideality of the salt–solvent mixture, and
xL is the molar fraction of the salt in
L-configuration. Similar equations are valid for the rate and supersaturation force corresponding to
D-configuration.
Since the oversaturation force is responsible for the phase change, when the molar fraction is less than the saturation molar fraction, x < xs, the force must be zero or undefined. In that case, the activity coefficient must be zero while for high salt concentrations f is linear in x. The activity coefficient is thus given by f = f0Θ(x − xs), with f0 a constant, which implies that the oversaturation force behaves as ΔzL ∝ x2 and therefore so do ṙL and ṙD. This behaviour is typical of an autocatalytic process, such as in the crystal formation process.4,15 To obtain fL, we use the Gibbs–Duhem equation
| | | x dμA + xL dμL + xD dμD = 0 | (15) |
in which
xD is the molar fraction of the salt in
D-configuration. The molar fractions fulfil the relation
x +
xL +
xD =
x0, with
x0 the initial molar fraction of the liquid phase.
The solid phase is composed of the small nuclei and the L- and D-crystals. The corresponding reaction–diffusion equation for the molar fraction of salt conforming the solid L-nuclei is given by
| |  | (16) |
where
ṙ(c)L is the rate at which
L-nuclei transforms into
L-crystals. An analogous equation holds for the evolution of the molar fraction
xD.
3.2.3 Crystallisation kinetics.
Self-assembly of solid nuclei leads to the formation of L- and D-crystals which may also dissolve and precipitate because their density is different from that of the solvent. Whether precipitation occurs or not depends on the size of the crystal aL and on the molar fraction of salt molecules nL making up L-crystals. The mass flux of such molecules is J(c)L = −D∂nL/∂y − kpΔρcgaL3nL, where the drift term is due to the buoyancy force,25 with kp a precipitation constant,26 Δρc the difference between the molar density of the crystal and the solvent, and g the gravity force. The corresponding balance equation is thus| |  | (17) |
The number of molecules forming a L-crystal is NL = N0nL, with N0 the initial number of salt molecules. An analogous equation holds for ND.
To find the crystal formation rate ṙ(c)L, we will describe the process in terms of the probability p(l,t) of finding a crystal of size l at time t27 which obeys the conservation law
| | 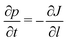 | (18) |
where
J is the crystallization current in
l-space
27,28| |  | (19) |
with
Dl a diffusivity in
l-space and
μ =
kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f(c)p
f(c)p/(
f(c)p)
eq +
ϕ the chemical potential, with
ϕ the energy required to form a crystal of size
l and
f(c) a activity coefficient. This energy consists of volume and surface contributions and is given by
ϕ = −(Δ
μ0/
vp)
l3 +
Γl2, where
vp is the specific volume of the crystal and
Γ the specific surface energy per unit of area.
27 The crystal growth rate at
l =
a0, with
a0 the nuclei size, has to be equal to the rate at which crystals emerge,
i.e.,
ṙ(c)L =
J(
a0). By knowing the amount of salt
xL necessary to make up
L-crystals, and the actual amount of salt in the
L-crystals
nL, we can obtain
J(
a0). Thus, by evaluating
eqn (19) at
l =
a0 we obtain the rate of crystal formation
| | 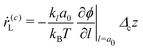 | (20) |
in which the activity difference between the
L-crystal and the
L-nuclei is
Δcz =
xL2 +
xLnL −
a0nL2/
aL, where the first contribution accounts for crystal emergence from auto-catalysis or agglomeration of the nuclei whereas the second results from absorption of nuclei on the crystals and the third corresponds to the inverse process in which smaller sizes favour the re-dissolution of the crystals in the solvent.
4 The rate of crystal formation
ṙ(c)D can be computed in a similar way.
By multiplying eqn (18) by l and integrating in l, we obtain the evolution equation of the average L-crystal size aL27
| |  | (21) |
with
ϕL =
ϕ(
aL), and
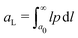
. An analogous evolution equation can be written for
D-crystals. In the presence of convection and water as a solvent, some extra consideration could be taken into account to model the kinetics of the crystal growth as shown in ref.
29.
3.2.4 Heat transfer.
The heat that the system exchanges with the environment which is at constant temperature Ts causes the temperature varies according to the equation| |  | (22) |
where cp is the specific heat of the mixture at constant pressure, U the convective heat transfer coefficient, c0 the total molar concentration, d the test tube diameter, and κ the thermal conductivity.
3.2.5 Disparity between activation energies, ΔEa.
We consider that the system exchanges heat with the environment but not mass and analyse the transition from achiral to chiral compound. The intermediate state of this transition can increase its free energy by absorbing a part of the dissipated energy, related to entropy production. The free energy change of the system ΔGT during the transition is given by the energy change of the process (from achiral to chiral) ΔG0P and the free energy change of the solvent ΔG0S (mainly due to the decrease of the internal energy as a consequence of the heat exchange with the environment):The free energy change from the achiral to the intermediate state is:| | | ΔGA–I = ΔH0A–I − TΔS0A–I + EΣ | (24) |
with H0 and S0 the standard enthalpy and entropy while the sub-index A and I correspond to achiral and intermediate state. The quantity EΣ is the absorbed energy coming from the entropy production. The free energy change from the intermediate to the chiral state is:| | | ΔGI–C = ΔH0I–C − TΔS0I–C − TΣP | (25) |
with the sub-index C referring to the chiral state (enantiomeric nuclei in this case), while ΣP is the entropy produced in the transition. The free energy change of the solvent during the transition is:| | | ΔGS = ΔH0S − TΔS0S − TΣS | (26) |
where ΣS is the entropy produced in the other processes such as heat exchange, crystal growth, diffusion and precipitation. By adding these free energy changes, we obtain the free energy change of the system:| | | ΔGT = ΔG0P + ΔG0S + EΣ − TΣ | (27) |
where Σ = ΣP + ΣS. Comparing this equation with eqn (23), we obtain the total energy absorbed by the intermediateTherefore the increment of the energy of one intermediary is| | 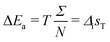 | (29) |
This energy change corresponds to the unavailable free energy of the process that does not affect the final states of the system but does affect the intermediate states. Once the system relaxes, this energy is dissipated or stored to maintain the kinetically trapped states.
3.2.6 Entropy production rates.
The energy dissipation rate (temperature times entropy production rate) of the phase change is according to non-equilibrium thermodynamics given by30,31| | | Tσph(y,t) = −(ṙLΔzL + ṙDΔzD) | (30) |
where we have neglected the contribution of diffusion since it is much smaller than that of the phase change.
The entropy production rate of the crystal growth process σg is expressed as a sum of products between fluxes (J) and forces  .25 The resulting expression of the entropy production rate considering the growing process of both enantiomeric crystals is
.25 The resulting expression of the entropy production rate considering the growing process of both enantiomeric crystals is
| |  | (31) |
Analogously, the entropy production rate due to precipitation is
| |  | (32) |
Finally, the corresponding entropy production in the heat exchange process is25
| |  | (33) |
Using eqn (30)–(33) we obtain Fig. 5 for one initial and cooling condition. We observe that heat transfer and nuclei formation are the most dissipative processes and that the supersaturation gradient is the main driving force for crystal formation,32–34 as it causes the most dissipation. This conclusion is reached in all the cases studied.
 |
| | Fig. 5 Energy dissipation rate corresponding to the different irreversible processes occurring in crystal formation as a function of time. | |
4 Results and discussion
In the experiments, we measured the optical rotation angle of the solution throughout the process, for two cooling protocols and different salt concentration values, i.e. for different values of the over-saturation force which result in different values of entropy production. The salt–solvent concentration ratio values considered, in grams of solute per grams of solvent, were: ws/wg = 0.235, ws/wg = 0.32, and ws/wg = 0.36, in the case of natural cooling, when the boundaries of the system are in contact only with the surrounding air, and ws/wg = 0.235, ws/wg = 0.30, and ws/wg = 0.36, for enhanced cooling, when the boundaries are in contact with water which has a higher cooling rate. These values were chosen so that it is guaranteed that a fraction of the salt will be in solid phase when the temperature reaches room temperature, since the equilibrium solubility at room temperature of glycerol (the solvent) is (ws/wg)s = 0.23.35
We have solved numerically eqn (12), (16), (17), (21) and (22) by using the finite-difference method in MATLAB. In this way, we obtain the molar fractions of dissolved salt x, of salt of L- and D-nuclei xL and xD, of salt in L- and D-crystals nL and nD, and the average size of L- and D-crystals aL and aD, as well as the temperature T. All these quantities are a function of position and time. We thus define NL = N0nL and ND = N0nD which are used to compute the enantiomeric excess and optical rotation angle, as shown in eqn (1) and (2). The evolution equations of the molar fractions contain the expression of the free-energy barrier ΔEa through the rates. The behaviour of these quantities is thus affected by dissipation. From eqn (30)–(33), we then compute the entropy production rate σ. Plots of temperature and average crystal size as a function of time, as well as values of the physico-chemical parameters used are given in the ESI.†
Fig. 6 depicts the evolution over time of the optical rotation angle obtained from the model and the experiments. Half of the experiments gave a negative value for the optical rotation angle, and the other half a positive value, according to ref. 15. This result confirms the random nature of the mechanism depicted in Fig. 3, where the energy-absorbing intermediate state cannot be known a priori, it can only be identified when the excitation has already taken place. Fig. 6(a) shows that for ws/wg = 0.235 the angle reaches a maximum value and then decreases because some crystals precipitate and thus fall out of the measurement range of the laser beam. For the remaining values of ws/wg, the value of the angle increases as the crystals grow. We see that the optical rotation angle takes higher values as ws/wg increases. In Fig. 6(b), we observe that in the case ws/wg = 0.30 the angle reaches a minimum value due to crystal precipitation. For ws/wg = 0.235, the angles are one to two orders of magnitude smaller than those obtained for the other salt–solvent concentration ratios.
 |
| | Fig. 6 Optical rotation angle as a function of time. (a) Natural cooling with air. (b) Enhanced cooling with air and water. Dotted lines represent experimental data whereas continuous lines stand for model results. The right y-axes show the results for the salt/solvent ratio ws/wg = 0.235 whereas the left y-axes correspond to the cases ws/wg > 0.235. | |
In Fig. 7(a and b), we represent the energy dissipation rate of: (i) heat transfer with the environment due to a temperature difference; (ii) solid nuclei formation driven by the over-saturation force; (iii) crystal growth caused by surface and volume energy differences. For both cooling protocols, a peak appears in the early stages, when the supersaturation strength reaches a maximum value. For ws/wg = 0.235, the maximum contribution to the peak comes from heat transfer as the number of nuclei is still low. Fig. 7(a) shows the presence of two peaks and one minimum whereas in Fig. 7(b) there is only one peak for each salt/solvent concentration ratio. We also observe that for enhanced cooling the peaks are slightly higher than those for natural cooling which is a consequence of the fact that in the former case, the energy barrier is higher and consequently the barrier crossing rate diminishes which leads to an increase of the enantiomer population difference, as shown in Fig. 7(c and d).
 |
| | Fig. 7 Energy dissipation rate and enantiomeric excess percentage as a function of time for different values of ws/wg: natural cooling (a and c), and enhanced cooling (b and d). | |
In Fig. 7(c and d), we plot the enantiomeric excess percentage as a function of time. In Fig. 7(c), we observe the occurrence of maxima at times similar to those at which the energy dissipation rate is minimal, reported in Fig. 7(a). Fig. 7(d) shows that the maxima of the enantiomeric excess disappear when cooling is enhanced which is a consequence of the lack of a minimum in the energy dissipation rate in Fig. 7(b). The minimum values of Tσ are found when the dissipation due to phase change decreases and heat exchange becomes the most dissipative process, as can be observed in Fig. 5. Thus, as the energy barrier of one of the enantiomers increases, the rate of phase change decreases which promotes a higher enantiomeric excess. The figure also shows that the enantiomeric excess increases with ws/wg. This is due to the fact that the oversaturation force increases thus leading to a higher energy dissipation rate, as shown in Fig. 7(a and b). Moreover, for both cooling protocols, the percentage of enantiomeric excess reaches a constant value although some crystal growth and redissolution still occur. The final enantiomeric excess percentage is higher in the case of enhanced cooling, as the energy dissipation rate is initially higher. Therefore, the early excess of one of the enantiomers, with a lower redissolution rate, causes the enantiomeric crystals to persist over time.
In Fig. 8, we show the difference between the activation energies of the enantiomers in the phase change process. We observe that at initial times, when the first nuclei are emerging, the energy difference is substantially high. This is because the energy dissipated in the system is absorbed by a small number of enantiomeric intermediates. Note that ΔEa is not defined at early times because there is no salt in the solid phase. The behaviour of this quantity is similar for both cooling conditions, but tends to be slightly higher in the enhanced cooling case. The most important difference between results for both cooling conditions is that ΔEa tends to be higher when the initial salt fraction is higher. Finally, it is important to note that ΔEa takes values lower than 1kBT in most of the process. Moreover, when ΔEa < 0.1kBT a racemic mixture is found as in the case of natural cooling (see Fig. 7).
 |
| | Fig. 8 Activation energy difference ΔEa at the phase change process for (a) natural cooling and (b) enhanced cooling. | |
5 Conclusions
Our model describes the evolution in time of the fraction of enantiomeric crystals from which we can estimate the optical rotation angle of the system with very good agreement with our measurements of this quantity as a function of time. It also allows us to compute the energy dissipated in the process as well as the enantiomeric excess. We have found that the energy required to induce the measured enantiomeric excess is exactly the same as the energy dissipated per solid salt mole computed from the model. These results show that chiral symmetry breaking in NaClO3 crystal formation is caused by the increase of the free-energy barrier of one of the enantiomers. The change in the energy levels of the intermediate state leads to unequal rates of appearance of the L- and D-enantiomeric crystals and thus to an excess of one of the enantiomers.
Our aim has been not only to show how symmetry breaking occurs, but also why. To do so, we have used a non-equilibrium thermodynamic formalism that gives us both the kinetics and the energetics of the process, and not only the kinetics, as it is usually done from the work of Kondepudi.15 The evolution equations obtained agree with those of the classical nucleation theory since we have considered the surface and volumetric energies of the crystals that contribute to the energy barrier that depends on the size of the crystals. Our evolution equations are obtained from the entropy production rate and probability conservation, showing that crystallisation and symmetry breaking are dissipative processes.
Author contributions
A. A.-R.: Designed research, performed research, analysed data, wrote the paper. J. M. R.: designed research, analysed data, wrote the paper. D. B.: designed research, analysed data. O. A.: designed experiments and contributed with new analytic tools. All authors reviewed the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
A. A.-R. and J. M. R. are grateful for financial support of MICIU (Spanish Government) under grant No. PID2021-126570NB-I00. O. A. recognises the financial support of MICIU (Spanish Government under grants No. RYC2018-024997-I and RTI2018-098410-J-I00).
References
- R. A. Hegstrom and D. K. Kondepudi, Sci. Am., 1990, 262, 108–115 CrossRef.
- P. Cintas and C. Viedma, Chirality, 2012, 24, 894–908 CrossRef CAS PubMed.
- T. Buhse, J.-M. Cruz, M. E. Noble-Terán, D. Hochberg, J. M. Ribó, J. Crusats and J.-C. Micheau, Chem. Rev., 2021, 121, 2147–2229 CrossRef CAS PubMed.
- J. M. Ribó, D. Hochberg, J. Crusats, Z. El-Hachemi and A. Moyano, J. R. Soc., Interface, 2017, 14, 20170699 CrossRef PubMed.
- H. Kuhn, Curr. Opin. Colloid Interface Sci., 2008, 13, 3–11 CrossRef CAS.
- D. K. Kondepudi and K. Asakura, Acc. Chem. Res., 2001, 34, 946–954 CrossRef CAS PubMed.
-
M. Szurgot, Crystallization and Materials Science of Modern Artificial and Natural Crystals, InTech, Rijeka, Croatia, 2012, ch. Parity Violation in Unstirred Crystallization from Achiral Solutions Search PubMed.
- M. C. Nunez, M. E. Garcia-Rubino, A. Conejo-Garcia, O. Cruz-Lopez, M. Kimatrai, M. A. Gallo, A. Espinosa and J. M. Campos, Curr. Med. Chem., 2009, 16, 2064–2074 CrossRef CAS PubMed.
- J. Jeong, Z. S. Davidson, P. J. Collings, T. C. Lubensky and A. G. Yodh, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1742–1747 CrossRef CAS PubMed.
- H.-T. Feng, C. Liu, Q. Li, H. Zhang, J. W. Y. Lam and B. Z. Tang, ACS Mater. Lett., 2019, 1, 192–202 CrossRef CAS.
- K. Jakab,
et al.
, Tissue Eng., Part A, 2008, 14, 413–421 CrossRef CAS PubMed.
- S. A. P. van Rossum, M. Tena-Solsona, J. H. van Esch, R. Eelkema and J. Boekhoven, Chem. Soc. Rev., 2017, 46, 5519–5535 RSC.
- F. Frank, Biochem. Biophys. Acta, 1953, 11, 459–463 CAS.
- A. Garay, Nature, 1968, 219, 338–340 CrossRef CAS PubMed.
- D. K. Kondepudi, R. J. Kaufman and N. Singh, Science, 1990, 250, 975–976 CrossRef CAS PubMed.
- H. Niinomi, T. Sugiyama, M. Tagawa, S. Harada, T. Ujihara, S. Uda, K. Miyamoto and T. Omatsu, Cryst. Growth Des., 2018, 18, 4230–4239 CrossRef CAS.
- J. M. Ribó, J. Crusats, Z. El-Hachemi, A. Moyano, C. Blanco and D. Hochberg, Astrobiology, 2013, 13, 132–142 CrossRef PubMed.
- C. Viedma, Phys. Rev. Lett., 2005, 94, 065504 CrossRef PubMed.
- M. Rekharsky and Y. Inoue, J. Am. Chem. Soc., 2000, 122, 4418–4435 CrossRef CAS.
- A. Arango-Restrepo, J. Rubi and D. Barragán, Phys. A, 2018, 509, 86–96 CrossRef CAS.
- A. Arango-Restrepo, D. Barragán and J. M. Rubi, J. Phys. Chem. B, 2021, 125, 1838–1845 CrossRef CAS PubMed.
- O. Arteaga, J. Freudenthal, B. Wang and B. Kahr, Appl. Opt., 2012, 51, 6805–6817 CrossRef PubMed.
- O. Arteaga, JOSA A, 2017, 34, 410–414 CrossRef PubMed.
- D. Reguera, J. M. Rubí and J. M. G. Vilar, J. Phys. Chem. B, 2005, 109, 21502–21515 CrossRef CAS PubMed.
-
S. R. De Groot and P. Mazur, Non-equilibrium thermodynamics, Courier Corporation, 2013 Search PubMed.
- A. Mersmann, Chem. Eng.
Process., 1999, 38, 345–353 CrossRef CAS.
- I. Santamaría-Holek, A. Gadomski and J. M. Rubí, J. Phys.: Condens. Matter, 2011, 23, 235101 CrossRef PubMed.
- A. Gadomski, Phys. A, 2007, 373, 43–57 CrossRef CAS.
- A. Gadomski and J. Siódmiak, Cryst. Res. Technol., 2002, 37, 281–291 CrossRef CAS.
- A. Arango-Restrepo, J. M. Rubi and D. Barragán, J. Phys. Chem. B, 2018, 122, 4937–4945 CrossRef CAS PubMed.
- A. Arango-Restrepo, D. Barragán and J. M. Rubi, Phys. Chem. Chem. Phys., 2018, 20, 4699–4707 RSC.
- M. Szurgot, Cryst. Res. Technol., 2012, 47, 109–114 CrossRef CAS.
- M. Barrett, M. McNamara, H. Hao, P. Barrett and B. Glennon, Chem. Eng. Res. Des., 2010, 88, 1108–1119 CrossRef CAS.
- H. Takiyama, Adv. Powder Technol., 2012, 23, 273–278 CrossRef CAS.
-
A. Seidell
et al.
, Solubilities of inorganic and metal organic compounds, van Nostrand, 1940 Search PubMed.
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
O.
Arteaga
b,
D.
Barragán
c and
J. M.
Rubi
*a,
O.
Arteaga
b,
D.
Barragán
c and
J. M.
Rubi
 a
a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, whereas when the process takes place out of equilibrium and is therefore dissipative, the concentration of one of the enantiomers exceeds that of the other.
1, whereas when the process takes place out of equilibrium and is therefore dissipative, the concentration of one of the enantiomers exceeds that of the other.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture.15
1) mixture.15 , where N = NL + ND is the number of moles of solid salt, and NL and ND the number of moles of salt composing L- and D nuclei and crystals.
, where N = NL + ND is the number of moles of solid salt, and NL and ND the number of moles of salt composing L- and D nuclei and crystals.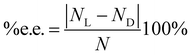
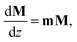
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M the accumulated differential Mueller matrix. The optical rotation of this depolarizing medium is then determined as:
M the accumulated differential Mueller matrix. The optical rotation of this depolarizing medium is then determined as:

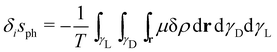
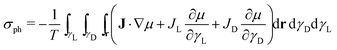

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fρ + ϕ + ψ
fρ + ϕ + ψ



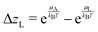
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xf and μL = μ0L + kBT
xf and μL = μ0L + kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xLfL, with f and fL being activity coefficients accounting for the non-ideality of the salt–solvent mixture, and xL is the molar fraction of the salt in L-configuration. Similar equations are valid for the rate and supersaturation force corresponding to D-configuration.
xLfL, with f and fL being activity coefficients accounting for the non-ideality of the salt–solvent mixture, and xL is the molar fraction of the salt in L-configuration. Similar equations are valid for the rate and supersaturation force corresponding to D-configuration.


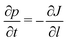

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f(c)p/(f(c)p)eq + ϕ the chemical potential, with ϕ the energy required to form a crystal of size l and f(c) a activity coefficient. This energy consists of volume and surface contributions and is given by ϕ = −(Δμ0/vp)l3 + Γl2, where vp is the specific volume of the crystal and Γ the specific surface energy per unit of area.27 The crystal growth rate at l = a0, with a0 the nuclei size, has to be equal to the rate at which crystals emerge, i.e., ṙ(c)L = J(a0). By knowing the amount of salt xL necessary to make up L-crystals, and the actual amount of salt in the L-crystals nL, we can obtain J(a0). Thus, by evaluating eqn (19) at l = a0 we obtain the rate of crystal formation
f(c)p/(f(c)p)eq + ϕ the chemical potential, with ϕ the energy required to form a crystal of size l and f(c) a activity coefficient. This energy consists of volume and surface contributions and is given by ϕ = −(Δμ0/vp)l3 + Γl2, where vp is the specific volume of the crystal and Γ the specific surface energy per unit of area.27 The crystal growth rate at l = a0, with a0 the nuclei size, has to be equal to the rate at which crystals emerge, i.e., ṙ(c)L = J(a0). By knowing the amount of salt xL necessary to make up L-crystals, and the actual amount of salt in the L-crystals nL, we can obtain J(a0). Thus, by evaluating eqn (19) at l = a0 we obtain the rate of crystal formation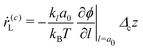

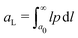 . An analogous evolution equation can be written for D-crystals. In the presence of convection and water as a solvent, some extra consideration could be taken into account to model the kinetics of the crystal growth as shown in ref. 29.
. An analogous evolution equation can be written for D-crystals. In the presence of convection and water as a solvent, some extra consideration could be taken into account to model the kinetics of the crystal growth as shown in ref. 29.

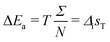
 .25 The resulting expression of the entropy production rate considering the growing process of both enantiomeric crystals is
.25 The resulting expression of the entropy production rate considering the growing process of both enantiomeric crystals is









