Vibrational spectroscopy of Cu⁺(H₂)₄: about anharmonicity and fluxionality

Abstract

The vibrational spectra of the copper(I) cation–dihydrogen complexes Cu⁺(H₂)₄, Cu⁺(D₂)₄ and Cu⁺(D₂)₃H₂ are studied using cryogenic ion trap vibrational spectroscopy in combination with quantum chemical calculations. The infrared photodissociation (IRPD) spectra (2500–7300 cm⁻¹) are assigned based on a comparison to IR spectra calculated using vibrational second-order perturbation theory (VPT2). The IRPD spectra exhibit ≈60 cm⁻¹ broad bands that lack rotational resolution, indicative of rather floppy complexes even at an ion trap temperature of 10 K. The observed vibrational features are assigned to the excitations of dihydrogen stretching fundamentals, combination bands of these fundamentals with low energy excitations as well as overtone excitations of a minimum-energy structure with C_s symmetry. The three distinct dihydrogen positions present in the structure can interconvert via pseudorotations with energy barriers less than 10 cm⁻¹, far below the zero-point vibrational energy. Ab initio Born–Oppenheimer molecular dynamics (BOMD) simulations confirm the fluxional behavior of these complexes and yield an upper limit for the timeframe of the pseudorotation on the order of 10 ps. For Cu⁺(D₂)₃H₂, the H₂ and D₂ loss channels yield different IRPD spectra indicating non-ergodic behavior.

---

1 Introduction

Transition metal cations do not only play an important role in dihydrogen activation, but also in efficient H₂/D₂ isotope separation. Recently, substantial progress has been made in developing more sustainable isotope separation methods based on selective adsorption from gaseous mixtures in porous materials.^1–5 Two effects are exploited in such materials: (a) heavier H₂ isotopologues are bound more strongly to the metal center due to their lower zero-point energy (ZPE) contribution to the adsorption energy and (b) they also exhibit a smaller effective kinetic radius as a result of their more localized probability density.^5–9 Porous materials containing undercoordinated Cu(I) adsorption sites, e.g. Cu(I)-MFU-4l, Cu(I)-MOR and Cu(I)-ZSM-5 are found to exhibit superior D₂/H₂ selectivity (>10) also at high temperatures (>77 K).^4,9,10 Understanding the binding of dihydrogen isotopologues to different Cu(I) compounds is therefore important for improving the performance of separation materials. Spectroscopic studies of hydrogen coordination to metal centers in bulk materials typically suffer from structural heterogeneity and hence difficulties in assigning the binding site. This can be avoided by performing experiments on well-defined model compounds isolated in the gas phase using the highly selective and sensitive tool of ion vibrational spectroscopy,^11–14 in particular, in the form of cryogenic ion trap vibrational spectroscopy.^15,16 Another advantage of this approach is that such model compounds are amenable to high-level computational approaches that can be used to benchmark more approximative methods applicable to extended systems.

The copper cation (Cu⁺) represents the simplest form of an under-coordinated Cu(I) site. Cu⁺–H₂ dissociation energies in Cu⁺(H₂)_n complexes have been determined by guided ion beam tandem mass spectrometry.¹⁷ Cu⁺ can bind up to four dihydrogen molecules in the first complexation shell. Sequential bond dissociation energies (BDEs) have been obtained from gas phase equilibrium constants for the reactions Cu⁺(H₂)_n → Cu⁺(H₂)_n−1 + H₂, and amount to 64, 70, 37, and 21 kJ mol⁻¹ for n = 1–4, respectively.¹⁷ Theory indicates that bonding to molecular hydrogen is largely covalent, consisting mainly of electron donation from the σ orbital of H₂ to the empty Cu⁺ 4s orbital and electron backdonation from the filled 3d_yz (dπ) orbital to the σ* orbital of H₂.¹⁷ Given the filled d-shell electron configuration ([Ar]3d¹⁰), Cu⁺ exhibits pronounced backdonation, which leads to strong binding of H₂ and which can be further enhanced by a surrounding framework.¹⁸

Beyond mass spectrometric studies, vibrational spectroscopy of small metal ion complexes provides insights into their geometric and electronic structure. Infrared photodissociation (IRPD) spectra for non-covalent metal-cation–dihydrogen complexes M⁺–H₂/D₂ (M = Li, Na, Al, Cr, Mn, Zn, Ag) have been reported by Bieske and coworkers.^19,20 The rotationally-resolved IRPD spectra indicate that all these cationic complexes adopt a C_2v T-shaped M⁺–(H₂) geometry rather than the linear M⁺–H–H structure that is preferred in the corresponding anion complexes.^20–23 The H–H stretching frequencies are red-shifted by 67 cm⁻¹ (Na⁺–H₂) to 406 cm⁻¹ (Ag⁺–H₂) relative to the frequency of a free H₂ molecule (4161 cm⁻¹).²⁴ The extent of the redshift depends on the charge and orbital interactions, which determine the balance between σ donation and π backdonation.²⁵ The strong bonding in the Cu(I)–H₂ motif is also found in neutral Cu compounds. Correspondingly red-shifted IR bands were reported at 3567 cm⁻¹ (H₂) and 2582 cm⁻¹ (D₂) for the CuH(H₂/D₂) complex in a solid hydrogen matrix.²⁶ Significant nuclear quadrupole coupling constants in dihydrogen complexes of copper fluoride (CuF) measured by microwave spectroscopy also suggest a strong interaction between the Cu(I) center of CuF and the H₂ molecule.²⁷ However, the IRPD spectrum of the Cu⁺(H₂) complex has not been reported yet, because the Cu⁺–H₂ binding energy of 64 kJ mol⁻¹ (5375 cm⁻¹)^17,28 substantially exceeds the energy of the fundamental transition of the H–H stretching vibration.

The complexes formed by molecular hydrogen and the first-row Σ-state transition metal cations Cr⁺, Mn⁺, Cu⁺, and Zn⁺ have been investigated using high-level ab initio methods. The calculations identified trends in hydrogen activation, vibrational anharmonicity, and rotational structure along the sequence of four electrostatic complexes covering the range from a relatively floppy van der Waals system (Mn⁺⋯H₂) to an almost rigid molecular ion (Cu⁺⋯H₂).²⁸ In this series, the Cu⁺ complex is predicted to exhibit the highest binding energy, the smallest anharmonicity and the most red-shifted H₂ stretching vibrational frequency (Cu⁺–H₂: 3805 cm⁻¹; Cu⁺–D₂: 2691 cm⁻¹).

Here, we report IRPD spectra of the copper–dihydrogen complexes Cu⁺(H₂)₄, Cu⁺(D₂)₄, and Cu⁺(D₂)₃H₂. The IRPD spectra are assigned based on a comparison to IR spectra calculated from second-order vibrational perturbation theory (VPT2) as well as molecular dynamics simulations. Evidence is presented for fast dihydrogen interchange (pseudorotation) that leads to a significant broadening of the vibrational bands.

2 Methods

2.1 Experimental methods

IRPD spectroscopic and mass spectrometric experiments were performed using a cryogenically cooled ion trap triple mass spectrometer described previously.^16,29,30 In brief, Cu⁺ cations are transferred to the gas phase from a 10 mM 1 : 4 methanol/water CuSO₄ solution (Sigma Aldrich: CuSO₄ 5H₂O, 99%; CH₃OH, 99.9%) using a nanospray ion source. All cations are thermalized to room temperature in a helium-filled radio frequency (RF) ion guide and mass-selected using a quadrupole mass filter. Mass-selected ⁶³Cu⁺ cations are trapped and accumulated in a linear radio-frequency (RF) ring-electrode ion trap filled with ≈1 mbar H₂/D₂ and held at 10 to 14 K. Cu⁺(H₂)_n(D₂)_m complexes are formed via three body collisions.^31,32 Every 100 ms, all ions are extracted from the trap and transferred into the time-of-flight (TOF) mass spectrometer. They are first extracted and accelerated towards the reflectron stage, separating in time and space according to their mass-to-charge ratios. After reflection, all ions are refocused into the extraction/acceleration region, where the ions of interest are irradiated by a precisely timed infrared laser pulse and subsequently re-accelerated into the linear TOF stage (IR¹MS² detection scheme).³⁰ The IRPD spectra are obtained by irradiating the ions perpendicular to the flight direction with a tunable IR laser pulse generated from an IR optical parametric oscillator/amplifier laser system (LaserVision, OPO/OPA),³³ which is pumped by an unseeded Nd:YAG laser (Continuum Surelite EX). The spectral linewidth of the IR laser radiation is 3.5 cm⁻¹. IRPD spectra are recorded by monitoring the intensity of the irradiated ions and their photofragments simultaneously using a microchannel plate (MCP) detector while continuously scanning the laser wavelength, which is monitored online using a HighFinesse WS6-600 wavelength meter. Typically, three scans were measured and averaged to obtain an IRPD spectrum. The photodissociation cross section σ_IRPD is determined as described previously.^16,29

2.2 Computational methods

Geometry optimizations using the CCSD(T) method^34,35 are performed using the Gaussian 09 D.01 program.³⁶ The def2-TZVPP basis set,³⁷ a SuperFine grid (pruned 1 75 974 for H and 2 50 974 for Cu) for the reference calculations and no frozen core, i.e. CCSD(T, Full), are used. IR spectra are computed at the minimum-energy geometry using second-order Møller–Plesset perturbation theory (MP2)^38–41 in combination with the def2-TZVPP basis set. The ZPE-corrected BDE D₀ for the reaction Cu⁺(H₂)₄ → Cu⁺(H₂)₃ + H₂ is determined using the CCSD(T)/def2-TZVPP electronic energy and the MP2/def2-TZVPP frequencies obtained within the harmonic approximation.

Vibrational frequencies and intensities are also calculated beyond the harmonic approximation using deperturbed vibrational perturbation theory (DVPT2)⁴² as implemented in the Gaussian 16 C.01 software.⁴³ From these, IR spectra are obtained by a 20 cm⁻¹ FWHM Gaussian line shape convolution. Rovibrational band profiles are simulated by using the PGopher (10.1) program.^44,45

Ab initio Born–Oppenheimer molecular dynamics (BOMD) simulations are performed on the MP2/def2-TZVPP potential energy surface using the ORCA program (version 5.0.1)^46,47 with TightSCF convergence criteria (energy change 1 × 10⁻⁸, maximum density change 1 × 10⁻⁷). The time step is set to 0.5 fs and the system is equilibrated at the targeted temperatures using a Berendsen thermostat with the time constants of 10 fs, 30 fs and 100 fs for 1, 3 and 10 k time steps, respectively. After equilibration, the thermostat is turned off and a trajectory of ≥14 k time steps (≥7 ps) is recorded. Vibrational profiles are obtained via Fourier transformation of the dipole moment autocorrelation function and yield the so-called BOMD spectrum. The spectrum is smoothed using Gaussian broadening with a FWHM of 6 cm⁻¹ and scaled by a factor of 0.932 to better fit the experimental spectrum to account for the high energy of the vibrational modes relative to the simulation temperature.

3 Results

3.1 TOF mass spectrometry

In order to characterize the stability of Cu⁺ complexes with dihydrogen we trapped and accumulated mass-selected ⁶³Cu⁺ cations in the cold ion-trap filled with dihydrogen gas. TOF spectra measured with pure H₂, pure D₂ and a 3 : 1 H₂/D₂ gas mixture in the ion trap are shown in Fig. 1 (see Fig. S1 of the ESI† for additional TOF spectra). The most intense peak in each of the TOF spectra is due to bare ⁶³Cu⁺ cations (parent ions). We observe the formation of ⁶³Cu⁺(H₂)_n complexes with up to n = 8 (Fig. 1a) and ⁶³Cu⁺(D₂)_m complexes with up to m = 5 (Fig. 1b). The complex with four dihydrogen molecules is the most abundant one in all TOF spectra, indicating its high relative stability. Hence, the sequential BDE of the fifth (vs. the fourth) dihydrogen molecule in Cu⁺(H₂/D₂)₅ is found to be considerably smaller, consistent with previous thermochemistry data at higher temperatures (>100 K).¹⁷ For the H₂/D₂ gas mixture the most abundant complex is Cu⁺(D₂)₄, followed by Cu⁺(D₂)₃H₂, even though there is three times as much H₂ than D₂ in the gas mixture. The higher probability for D₂ binding is attributed to thermodynamic control resulting from the smaller Cu⁺–D₂ (vs. Cu⁺–H₂) ZPE and hence larger BDE.

Fig. 1 TOF spectra obtained after trapping and accumulating mass-selected ⁶³Cu⁺ cations in (a) pure H₂ at 10 K, (b) pure D₂ at 14 K, and (c) a 3 : 1 gas mixture of H₂ and D₂ at 10 K. Peaks are assigned to Cu⁺(H₂)_n(D₂)_m complexes and labeled accordingly. ⁶⁵Cu⁺ cations of the naturally slightly less abundant isotope are not fully discriminated against in the quadrupole mass filter and also contribute to the TOF peak at 10.2 μs.

3.2 Energetics and PES

The global minimum-energy structure on the CCSD(T)/def2-TVZPP Born–Oppenheimer potential energy surface of Cu⁺(H₂)₄ is shown in Fig. 2a. All four H₂ molecules coordinate side-on. There is one H₂, which is substantially farther away from the Cu⁺ center (183 pm) than the other three (one at 175 pm and two at 177 pm), and which we therefore refer to as the “far H₂”. We refer to this structure as C_s-1 since there is exactly one H₂ in the mirror plane. The far H₂ rotates almost freely about the Cu–H₂ axis, as shown in Fig. 2c, with C_s-1 being a local minimum and C_s-0 a first-order saddle point only 2 cm⁻¹ higher in energy (see Fig. 2b); other than that, Cu⁺–H₂ distances and angles are very similar (see Table S1, ESI†). The energetically next-higher, second-order saddle point (+13 cm⁻¹) is C_2v-2 that connects two C_s-0 transition structures as shown in Fig. 2d. In C_2v-2, there are two pairs of equivalent H₂ molecules – of which the pair in the mirror plane (175 pm) is closer to the Cu⁺ center than the other one (181 pm). The third-order saddle point structure D_2d-0 and the fourth-order saddle point structure D_2d-4 (see Fig. 2b) are again minimally higher in energy, predicted 25 cm and 35 cm⁻¹, respectively, above C_s-1. D_2d-4 was reported as the minimum-energy structure in previous studies.¹⁷ In all structures discussed above, the H–H bond length is approximately 3 pm longer than in free H₂; it ranges from 76.6 pm (far H₂ in C_s structures) to 77.4 pm (near H₂ in C_s structures) and increases with decreasing Cu–H₂ distance.

Fig. 2 (a) CCSD(T)/def2-TZVPP minimum-energy structure of Cu⁺(H₂)₄, C_s-1; H–H and Cu–H₂ bond lengths are given in pm. (b) CCSD(T)/def2-TZVPP global minimum-energy structure and low-energy saddle point structures of Cu⁺(H₂)₄ and their electronic energies. See Fig. S2 (ESI†) for different views of these structures. (c and d) Sketch of paths along the potential energy surface of Cu⁺(H₂)₄. (c) the far H₂ (dark blue) rotates (almost) freely such that any of the near H₂ can be parallel (light blue) to the far H₂. (d) via a transition structure with C_2v symmetry, the far H₂ (saturated blue) and the near H₂ parallel to it (light blue) can interchange roles (pseudorotation).

Two higher-order saddle point structures with D_4h symmetry (see Fig. S3, ESI†) are conceivable: D_4h-4h, a completely planar structure in which the H₂ molecules lie in the σ_h plane, and D_4h-4v, where they are rotated by 90° and lie in σ_v planes. D_4h-4v and D_4h-4h are predicted 44 and 46 kJ mol⁻¹, respectively, above C_s-1, i.e. substantially above the predicted BDE, D₀ for removal of a H₂ molecules from Cu⁺(H₂)₄, 21 kJ mol⁻¹. This CCSD(T)/def2-TZVPP BDE is in reasonable agreement with the experimentally determined BDE of 19 kJ mol⁻¹ reported previously.¹⁷ The energy corresponds to a wavenumber of 1800 cm⁻¹, indicating that in our experiments a single IR photon should be sufficient to induce photodissociation.

3.3 IRPD spectroscopy

Fig. 3a shows the IRPD spectrum for Cu⁺(H₂)₄ from 2500 cm⁻¹ to 7300 cm⁻¹. The intense and broad band at 3729 cm⁻¹ (labeled a₁ in Fig. 3a) is assigned to the excitation of the fundamental transitions involving the four H₂ stretching vibrations ν_HH in agreement with previous studies on metal-cation dihydrogen complexes.^19,20,48 Although the corresponding stretching mode in free H₂ is nominally IR inactive, the metal cation induces a transition moment along the intermolecular metal–dihydrogen bond causing it to gain IR intensity.²⁰ Three smaller features (a₂–a₄) are observed at 3951, 4413 and 4640 cm⁻¹, which we attribute to the excitations of combination bands of ν_HH with the low frequency Cu⁺–H₂ modes ω_CuH2, ν^sym_HCuH and ν^asym_HCuH (see Table 1). The weak feature at 7160 cm⁻¹ (a₅) corresponds to the first overtone excitations of the ν_HH modes, indicating substantial anharmonicity considering the corresponding fundamental at 3729 cm⁻¹. All observed IRPD bands in the Cu⁺(H₂)₄ spectrum are wider than 60 cm⁻¹, much broader than the spectral bandwidth of the IR laser pulse (3.5 cm⁻¹). This could arise from rotational band contours, but band profile simulations predict considerably narrower and more structured bands (see Fig. S4 in the ESI†). Moreover, we also measured temperature-dependent IRPD spectra for Cu⁺(H₂)₄ at trap temperatures of 10 K, 20 K, 35 K and 60 K (see Fig. S4, ESI†). Their analysis further supports that there is a band broadening mechanism present that goes beyond the thermal population of rovibrational levels. Therefore, we attribute the observed band broadening to dynamic effects (see below), i.e. large-amplitude motions of the hydrogen molecules that affect ν_HH, similar to the situation in the H₃⁺(H₂)_n complexes.^49–51

Fig. 3 Comparison of the IRPD spectra of (a) Cu⁺(H₂)₄, (b) Cu⁺(D₂)₃H₂ and (c) Cu⁺(D₂)₄ to the corresponding DVPT2/MP2/def-TZVPP IR spectra of (d) Cu⁺(H₂)₄, (e) Cu⁺(D₂)₃H₂ and (f) Cu⁺(D₂)₄. Band positions and assignments to fundamental (blue), combination (orange) and overtone (green) transitions are listed in Table 1.

Table 1 Experimental IR band positions (in cm⁻¹), DVPT2/MP2/def2-TZVPP vibrational frequencies and intensities (in km mol⁻¹, in parenthesis) and band assignments for IR active vibrational modes (>0.5 km mol⁻¹)

Band	Expt.	Calc.	Assignment^a
a ν: stretching mode, ν^sym: symmetric stretching mode, ν^asym: antisymmetric stretching mode, ω: wagging mode.
Cu^+(H2)4
a1	3729	3800(4), 3790(12), 3781(18), 3751(13)	ν HH
a2	3951	3993(1), 3991(6), 3971(1), 3952(1)	ν HH + ωCuH2
a3	4413	4472(6), 4450(6), 4423(3), 4418(5), 4403(5), 4399(2), 4375(1), 4390(1)	ν HH + ν^symHCuH
a4	4640	4824(2), 4772(1), 4751(1), 4727(2), 4768(3)	ν HH + ν^asymHCuH
a5	7160	7269 (2), 7180 (1)	2νHH
		7216 (3)	ν HH + νHH
Cu^+(D2)4
b1	2678	2748 (10), 2713 (3), 2710 (13), 2691 (11)	ν DD
b2	2850	2925 (2)	ν DD + ωCuD2
b3	3183	3236 (2), 3223 (2), 3218 (1), 3206 (2), 3203 (2), 3192 (1)	ν DD + ν^symDCuD
b4	3476	3480(1), 3454(1), 3448(1), 3428(1)	ν DD + ν^asymDCuD
b5	5209	5290 (1), 5222 (0)	2νDD
		5245 (1)	ν DD + νDD
Cu^+(D2)3H2
	2674	2714 (3), 2698 (11), 2686 (10)	ν DD
	2871	2883 (0), 2865 (0), 2857 (0)	ν DD + ωCuD2
	3169	3227 (2), 3209 (1), 3201 (2), 3196 (2), 3188 (1)	ν DD + ν^symDCuD
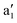
	3716	3834 (20)	ν HH

---

The spectrum for the all-D complex Cu⁺(D₂)₄ (shown in Fig. 3c) looks similar to the all-H spectrum. The main feature in the IRPD spectrum of Cu⁺(D₂)₄ is centered at 2678 cm⁻¹ (b₁). The observed frequency ratio of band a₁ (all-H) vs. b₁ (all-D) is 1.39, which is smaller than the ratio calculated from reduced masses of two H₂ isotopologues 1.41 (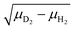), but the same as the ratio of experimental vibrational frequencies for free H₂ (4162 cm⁻¹) and D₂ (2994 cm⁻¹), indicating that the discrepancy is due to anharmonicity. Three weaker bands are found at 2850 (b₂), 3183 (b₃), and 3476 cm⁻¹ (b₄). The frequency ratios of the corresponding bands a₂/b₂, a₃/b₃ and a₄/b₄ are 1.39, 1.38 and 1.34, respectively, similar to or smaller than the a₁/b₁ ratio, in agreement with the assumption that these bands originate from combination bands involving low-frequency metal–D₂ modes. The band at 5209 cm⁻¹ (b₅) is assigned to the first overtone excitation of ν_DD. The observed b₅/a₅ ratio is 1.38, the same as the ratio determined from the first overtone excitations in the neutral dihydrogen isotopologues H₂ (8087 cm⁻¹) and D₂ (5868 cm⁻¹).⁵²

The IRPD spectrum of Cu⁺(D₂)₃H₂, measured by monitoring both H₂ loss (Cu⁺(D₂)₃ fragment) and D₂ loss (Cu⁺(D₂)₂H₂ fragment) dissociation channels, is shown in Fig. 3b. Two bands corresponding to the excitation of the ν_DD (, 2674 cm⁻¹) and the ν_HH (, 3716 cm⁻¹) fundamentals are observed with an intensity ratio of roughly 3 : 1, as could be naively expected. The two remaining features at 2871 cm⁻¹ () and 3169 cm⁻¹ () are then tentatively assigned to the excitation of combination bands involving the ν_DD stretching mode (see Fig. 3c). The IRPD spectrum obtained by exclusively monitoring the H₂ loss channel (Cu⁺(D₂)₃H₂ → Cu⁺(D₂)₃ + H₂, Fig. S5, in red, ESI†) shows similar bands, but with different intensity, indicating a non-statistical dissociation process. In particular, the relative intensity of band , corresponding to excitation of ν_HH, is substantially enhanced compared to the intensity of the bands involving ν_DD excitation, i.e. bands .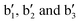

3.4 VPT2 IR spectra

The DVPT2/MP2/def-TZVPP IR spectra, which we refer to as VPT2 IR spectra from here on, of the global minimum-energy structures of Cu⁺(H₂)₄, Cu⁺(D₂)₃H₂, and Cu⁺(D₂)₄, are shown in Fig. 3d–f and band assignments to particular vibrational modes are listed in Table 1. For Cu⁺(H₂)₄ and Cu⁺(D₂)₄, they show satisfactory agreement with the experimental IRPD spectra, confirming the tentative assignments made above. Bands a₂ to a₄ (b₂ to b₄) are indeed combination bands involving the stretching modes ν_HH (ν_DD) with the Cu–dihydrogen wagging modes ω_CuH2 (ω_CuD2), the symmetric H–Cu–H stretching modes ν^sym_HCuH (ν^sym_DCuD), and the antisymmetric H–Cu–H stretching modes ν^asym_HCuH (ν^asym_DCuD), respectively. Band a₅ (b₅) corresponds to the overtone excitation 2ν_HH (2ν_DD) yielding a harmonic vibrational frequency term ω_e of 4027 cm⁻¹ (2825 cm⁻¹) and an anharmonicity constant ω_eχ_e of 149 cm⁻¹ (74 cm⁻¹), assuming a simple Morse potential. Hence the ω_e(H₂)/ω_e(D₂) ratio is indeed 1.41, the same as the ratio calculated from the reduced masses of the free H₂ isotopologues.

In contrast to the all-H and all-D complexes, the relative isotopomer contribution needs to be considered for Cu⁺(D₂)₃H₂. The lowest-energy structure of Cu⁺(D₂)₃H₂ has three isotopomers, one for each of the unique positions of H₂, and the corresponding VPT2 IR spectra are shown in Fig. S6 (ESI†). Of these three isomers, the one where H₂ occupies the far position, is lowest in energy and its spectrum is shown in Fig. 3e. The other isotopomers are predicted less than 1 kJ mol⁻¹ higher in energy and hence are expected to also contribute to the IR signal. The positions of the fundamental and combination bands in the IRPD spectrum of Cu⁺(D₂)₃H₂ are reproduced satisfactorily. However, the predicted relative band intensities, in particular those of transitions involving excitation of ν_HH, are overestimated.

3.5 Born–Oppenheimer molecular dynamics (BOMD) simulations

In light of the shallow PES, BOMD simulations were conducted to study the dynamic behavior of the dihydrogen ligands in Cu⁺(H₂)₄, and Cu⁺(D₂)₄, and Cu⁺(D₂)₃H₂. The distribution of Cu–H₂ distances in Cu⁺(H₂)₄ at different MD temperatures is shown in Fig. 4 (see also Fig. S7, ESI† for the correlation with H–H bond lengths). At an MD temperature of 15 K, two distinct Cu–H₂ distance regimes are found: ≈168 pm and ≈178 pm with corresponding H–H bond lengths of ≈78 pm and ≈77 pm, respectively. Analysis of the BOMD trajectory at 15 K (see Fig. S8a, ESI†) reveals that, most of the time, one H₂ is in the higher-distance regime (far H₂) and the other three are in the lower-distance regime (near H₂). The H₂ molecules can interchange positions via pseudorotation on a time scale of the order of 10 ps. At an elevated BOMD temperature of 50 K, the intermediate region between the two maxima is increasingly explored and at 100 K the two regimes merge completely and only a single, much broader maximum centered at 171 pm is found. Furthermore, the Cu–H₂ and H–H distances span much broader ranges at higher temperatures, indicating profound fluxionality. These parameters show a similar temperature dependence for the two other isotopologues, Cu⁺(D₂)₄ and Cu⁺(D₂)₃H₂.

Fig. 4 Histograms of the Cu–H₂ distance (in pm) in Cu⁺(H₂)₄ at different BOMD temperatures.

3.6 BOMD IR spectra

The dipole moments calculated along the BOMD trajectories are used to obtain the vibrational spectra via Fourier transformation of the autocorrelation function of the dipole moment. The resulting BOMD IR spectra are shown in Fig. 5 (and Fig. S9, ESI†). The BOMD IR spectrum of Cu⁺(H₂)₄ at 15 K (Fig. 5a) shows sharp features and two distinct peaks in the ν_HH stretching region. Weak ν_HH + ν_HCuH combination bands are predicted around 4400 cm⁻¹ and 4750 cm⁻¹. Increasing the BOMD temperature has several marked effects. First, the spectral features become broader and less distinct at 100 K (Fig. 5a) and even more so at 200 K (Fig. 5a). This suggests that the H₂ molecules increasingly explore the intermediate region between “near” and “far”, as already suggested above (see Fig. 4), and the H–H distance adapts accordingly (see Fig S7, ESI†). Consequently, broader vibrational frequency ranges for both, the high frequency and the low-frequency modes, contributing to the combination bands are explored, which translates directly into broader bands. Second, the relative IR intensity of the combination bands increases with increasing BOMD temperature. The BOMD IR spectra of Cu⁺(D₂)₄ (Fig. S9, ESI†) and of Cu⁺(D₂)₃H₂ (Fig. 5b) at different temperatures show the same trends as discussed above for Cu⁺(H₂)₄. Interestingly, the relative band intensities of the ν_DDvs. the ν_HH fundamental excitation in Fig. 5b is now better reproduced than by the “static” VPT2 IR spectrum shown in Fig. 3e and Fig. S6 (ESI†).

Fig. 5 Comparison of experimental and calculated vibrational spectra of (a) Cu⁺(H₂)₄ and of (b) Cu⁺(D₂)₃H₂: BOMD IR spectra at 15 K, 100 K and 200 K (all scaled by 0.932), and experimental IRPD spectrum.

3.7 Thermodynamic properties

According to the VPT2 calculations, anharmonic contributions add up to a total of 6 kJ mol⁻¹ for the ZPE of Cu⁺(D₂)₃(H₂) – a value much higher than what would be expected based on the values of 0.23 kJ mol⁻¹ and 0.12 kJ mol⁻¹ for free H₂ and D₂, respectively. Unlike for many systems previously studied, this even translates into a strong effect for the ZPE of the isotopologue exchange reactions. The reaction ZPE of the conversion Cu⁺(D₂)₃(H₂) + D₂ → Cu⁺(D₂)₄ + H₂ is −2.7 kJ mol⁻¹ according to the harmonic approximation, but only −0.6 kJ mol⁻¹ according to VPT2. This demonstrates that anharmonic effects play a profound role in this system. However, similar as for the harmonic approximation, we caution against taking the VPT2 result at face value. While VPT2 does consider anharmonicity and thereby explains the vibrational spectra quite well, it does not capture dynamic effects, which likely affect the thermodynamic properties of the system. Furthermore, entropy effects and therefore Gibbs energies cannot be properly accounted for at this level of theory.

4 Discussion

The broad vibrational bands of Cu⁺(H₂)₄, Cu⁺(D₂)₄, and Cu⁺(D₂)₃H₂ – which are an order of magnitude larger than the intrinsic resolution of the method – cannot be explained based on a model that combines the C_s-1 local minimum structure with internal rotations of the H₂/D₂ molecules (see also the simulation of the rovibrational lines in Fig. S4, ESI†). A careful examination of the potential energy surface of the system reveals a plausible explanation for the broad vibrational bands: Cu⁺(H₂)₄ and its isotopologues adopt a tetrahedral coordination of the ligands around the central atom. At the same time, the H₂ ligand – when binding to an undercoordinated metal cation – prefers a side-on coordination, resulting in a two-fold rotational axis. The irreconcilability of these two symmetry aspects leads to a situation with only one distinct local minimum structure, C_s-1. However, due its low symmetry, there are 192 equivalent arrangements: four possible positions of the far H₂, three possible locations of the near H₂ perpendicular to it and 2⁴ equivalent rotations of the H₂ molecules. Combined with the low-lying transition states C_s-0 and C_2v-2 (0.02 and 0.15 kJ mol⁻¹, respectively), this apparently results in a highly fluxional system, which in turn leads to the broadening of vibrational bands observed in the experiment.

This connection between fluxionality and spectral broadening is consistent with other ions (e.g. CH₅⁺), where the broad features in the vibrational spectra result from the large-amplitude motion of the internal rotation and flip motions between the numerous equivalent global minima on the PES.^53–55 The low-resolution vibrational spectra of the CH₅⁺ cation show a very broad feature for the C–H bending vibrations in the far-IR range as well as the C–H stretching vibrations in mid-IR range.^53,56 Thousands of lines in the C–H stretch region were later resolved and attributed to nuclear spin isomers of CH₅⁺ as well as the transitions from different quantum numbers.⁵⁴ We attribute the broadening of the bands associated with ν_HH to the dynamic behavior of the H₂ molecules, similar to the recently reported broadening of the low-frequency combination band in the IRPD spectrum of Cl⁻–H₂.⁵⁷ Such a broad and rotationally non-resolved ν_HH band is also found in F⁻–H₂, where it was attributed to the short life time of the excited predissociation state.⁵⁸

The different IRPD spectra obtained based on the H₂ and D₂ loss channels for Cu⁺(D₂)₃H₂ suggest that intramolecular vibrational relaxation is incomplete, i.e. ergodicity is not achieved on the photodissociation time scale and perturbed by the pseudorotations. The energy deposited initially in the H₂ oscillator preferentially leads to rupture of the Cu⁺–(H₂) rather than a Cu⁺–(D₂) bond.

Evidence of fluxionality is also found in the spectra derived from BOMD trajectories, especially for the higher simulation temperatures of 50 K and 100 K. Although a relatively rigid geometry is predicted at 15 K, we expect that, in reality, the time scale of the pseudorotation should be shorter and the fluxionality more pronounced when taking nuclear quantum effects (including tunneling) into consideration. While we find it remarkable that VPT2, which is a static method, reproduces the experimental spectra of Cu⁺(H₂)₄ and Cu⁺(D₂)₄ as well as it does, the agreement between experimental IRPD and VPT2 spectra is less convincing for the Cu⁺(D₂)₃H₂ isotopologue. This remains true even when accounting for the contributions of its different isotopomers.

Note, the nuclear spin isomers resulting from ortho- and para-dihydrogen were recently reported to play an important role in the formation and the far-IR spectroscopy of Cl⁻–(H₂) and CN⁻–(H₂) anion complexes.^21,22,57 However, the present study focuses on the near-IR spectral region and the positions of rovibrational lines from corresponding nuclear spin isomers are expected to differ by only 0.5 cm⁻¹, i.e., much smaller than the bandwidth of the IR laser pulses of ∼3.5 cm⁻¹.

The prominent anharmonicity strongly affects the thermodynamic properties of the system. This has to be considered when making statements involving the ZPE of this system. However, the pronounced effect of anharmonicity on the ZPE of isotopologue exchange reactions predicted by VPT2 is unexpected. Even if genuine, it is likely an idiosyncrasy of the present system, which limits its applicability as a model system for dihydrogen isotopologue separation in general.

5 Conclusions

We have studied the vibrational spectra of the copper cation dihydrogen complexes Cu⁺(H₂)₄, Cu⁺(D₂)₄ and Cu⁺(D₂)₃H₂ by IRPD spectroscopy and high-level theoretical calculations. Cu⁺(H₂)₄ lacks a highly symmetrical structure that reconciles the tetrahedral coordination with the two-fold rotational axis of the side-on coordinated H₂ ligands. This results in a multitude of equivalent minimum-energy structures. In combination with a shallow potential energy surface, this leads to high fluxionality, manifesting itself in very board features in the vibrational spectrum. The afforded vibrational features are assigned to excitations of H–H stretching fundamentals ν_HH, combination bands and ν_HH overtones of a minimum-energy structure with C_s symmetry. Cu⁺(D₂)₃H₂ is found to have two fragmentation channels, yielding different spectra, demonstrating non-ergodic dynamic behavior. The calculated PES indicates that the barriers for pseudorotation are less than 10 cm⁻¹, far below the ZPE. Hence, the vibrational ground state wavefunctions are delocalized and the four H₂ molecules are apparently indistinguishable. Pseudorotation in Cu⁺(D₂)₃H₂ is also studied using ab initio BOMD simulations, which confirm the fluxional behavior for Cu⁺(D₂)₃H₂ and reveal an upper limit of ≈10 ps for the time scale of H₂/D₂ exchange. The peculiarities that make Cu(H₂)₄⁺ spectroscopically interesting also complicate a deeper understanding of its thermodynamics and make it unsuitable as a model system for the fundamental understanding of adsorptive H₂ isotopologue separation in general. Future studies should therefore include systems with different ligand spheres involving, e.g., oxygen or nitrogen donor atoms and ideally only one H₂ ligand, as is commonly observed in materials considered for adsorptive H₂ isotopologue separation.

Author contributions

J. J. and T. W. contributed equally. J. J. and M. J. performed the experimental works. J. J. curated the experimental data and analysed the spectral data with DVPT2 simulations. T. W. did the potential energy surface calculations and BOMD simulations. J. J. and T. W. wrote the manuscript and prepared the figures. K. R. A. and T. H. designed the study, coordinated the project, supervised the research, contributed to the data interpretation and revised the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft (DFG), Project ID 443871192, GRK 2721: “HYDROGEN Isotopes ^1,2,3H”. J. J. acknowledges the Alexander von Humboldt-Stiftung for a postdoctoral fellowship. T. W. acknowledges the European Social Fund for a PhD fellowship. T. W. and T. H. thank the Center for Information Services and High Performance Computing (ZIH) at TU Dresden for computational resources.

References

1. R. Muhammad, S. Jee, M. Jung, J. Park, S. G. Kang, K. M. Choi and H. Oh, J. Am. Chem. Soc., 2021, 143(22), 8232–8236.
2. M. Liu, L. Zhang, M. A. Little, V. Kapil, M. Ceriotti, S. Yang, L. Ding, D. L. Holden, R. Balderas-Xicohténcatl and D. He, Science, 2019, 143(22), 8232–8236.
3. S. A. FitzGerald, C. J. Pierce, J. L. C. Rowsell, E. D. Bloch and J. A. Mason, J. Am. Chem. Soc., 2013, 135(25), 9458.
4. R. Xiong, L. Zhang, P. Li, W. Luo, T. Tang, B. Ao, G. Sang, C. Chen, X. Yan and J. Chen, Chem. Eng. J., 2020, 391, 123485.
5. H. Oh and M. Hirscher, Eur. J. Inorg. Chem., 2016, 4278.
6. I. Savchenko, B. Gu, T. Heine, J. Jakowski and S. Garashchuk, Chem. Phys. Lett., 2017, 670, 64.
7. D. Cao, J. Ren, Y. Gong, H. Huang, X. Fu, M. Chang, X. Chen, C. Xiao, D. Liu, Q. Yang, C. Zhong, S. Peng and Z. Zhang, J. Mater. Chem. A, 2020, 8(13), 6319.
8. M. Wahiduzzaman, C. F. J. Walther and T. Heine, J. Chem. Phys., 2014, 141(6), 64708.
9. J. Teufel, H. Oh, M. Hirscher, M. Wahiduzzaman, L. Zhechkov, A. Kuc, T. Heine, D. Denysenko and D. Volkmer, Adv. Mater., 2013, 25(4), 635.
10. I. Weinrauch, I. Savchenko, D. Denysenko, S. M. Souliou, H.-H. Kim, M. Le Tacon, L. L. Daemen, Y. Cheng, A. Mavrandonakis, A. J. Ramirez-Cuesta, D. Volkmer, G. Schütz, M. Hirscher and T. Heine, Nat. Commun., 2017, 8(1), 14496.
11. K. R. Asmis, A. Fielicke, G. von Helden and G. Meijer, Vibrational spectroscopy of gas-phase clusters and complexes, ed. D. Woodruff, In Atomic clusters: From gas phase to deposited. The chemical physics of solid surfaces, Elsevier, Amsterdam, Boston, 1st edn, 2007, vol. 12, pp. 327–375.
12. E. J. Bieske and O. Dopfer, Chem. Rev., 2000, 100(11), 3963.
13. J. M. Lisy, Int. Rev. Phys. Chem., 1997, 16(3), 267.
14. M. A. Duncan, Int. Rev. Phys. Chem., 2003, 22(2), 407.
15. K. R. Asmis, M. Brümmer, C. Kaposta, G. Santambrogio, G. von Helden, G. Meijer, K. Rademann and L. Wöste, Phys. Chem. Chem. Phys., 2002, 4(7), 1101.
16. N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2015, 34(1), 1.
17. P. R. Kemper, P. Weis, M. T. Bowers and P. Maitre, J. Am. Chem. Soc., 1998, 120(51), 13494.
18. P. Kozyra and W. Piskorz, Phys. Chem. Chem. Phys., 2016, 18(18), 12592.
19. V. Dryza and E. J. Bieske, Int. Rev. Phys. Chem., 2013, 32(4), 559.
20. V. Dryza, B. L. J. Poad and E. J. Bieske, Phys. Chem. Chem. Phys., 2012, 14(43), 14954.
21. F. Dahlmann, C. Lochmann, A. N. Marimuthu, M. Lara-Moreno, T. Stoecklin, P. Halvick, M. Raoult, O. Dulieu, R. Wild and S. Schlemmer, J. Chem. Phys., 2021, 155(24), 241101.
22. F. Dahlmann, P. Jusko, M. Lara-Moreno, P. Halvick, A. N. Marimuthu, T. Michaelsen, R. Wild, K. Geistlinger, S. Schlemmer and T. Stoecklin, Mol. Phys., 2022, e2085204.
23. A. A. Buchachenko, T. A. Grinev, J. Kłos, E. J. Bieske, M. M. Szczȩśniak and G. Chałasiński, J. Chem. Phys., 2003, 119(24), 12931.
24. S. L. Bragg, J. W. Brault and W. H. Smith, Astrophys. J., 1982, 263, 999.
25. G. J. Kubas, J. Org. Chem., 2014, 751, 33.
26. X. Wang, L. Andrews, L. Manceron and C. Marsden, J. Phys. Chem. A, 2003, 107(41), 8492.
27. D. J. Frohman, G. S. Grubbs, Z. Yu and S. E. Novick, Inorg. Chem., 2013, 52(2), 816.
28. D. G. Artiukhin, E. J. Bieske and A. A. Buchachenko, J. Phys. Chem. A, 2016, 120(27), 5006.
29. N. Heine and K. R. Asmis, Int. Rev. Phys. Chem., 2016, 35(3), 507.
30. M. Mayer and K. R. Asmis, J. Phys. Chem. A, 2021, 125(14), 2801.
31. M. Brümmer, C. Kaposta, G. Santambrogio and K. R. Asmis, J. Chem. Phys., 2003, 119(24), 12700.
32. D. J. Goebbert, T. Wende, R. Bergmann, G. Meijer and K. R. Asmis, J. Phys. Chem. A, 2009, 113(20), 5874.
33. W. R. Bosenberg and D. R. Guyer, J. Opt. Soc. Am. B, 1993, 10(9), 1716.
34. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87(10), 5968.
35. G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76(4), 1910.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, 2009.
37. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7(18), 3297.
38. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46(7), 618.
39. M. Head-Gordon and T. Head-Gordon, Chem. Phys. Lett., 1994, 220(1–2), 122.
40. M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166(3), 275.
41. M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153(6), 503.
42. V. Barone, J. Chem. Phys., 2005, 122(1), 14108.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, 2016.
44. C. M. Western, PGOPHER, a Program for Simulating Rotational Structure, University of Bristol, https://pgopher.chm.bris.ac.uk.
45. C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221.
46. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73.
47. M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Phys. Chem. Chem. Phys., 2013, 15(18), 6608.
48. C. Emmeluth, B. L. J. Poad, C. D. Thompson, G. H. Weddle and E. J. Bieske, J. Chem. Phys., 2007, 126(20), 204309.
49. M. A. Boyer, C. S. Chiu, D. C. McDonald, J. P. Wagner, J. E. Colley, D. S. Orr, M. A. Duncan and A. B. McCoy, J. Phys. Chem. A, 2020, 124(22), 4427.
50. T. C. Cheng, L. Jiang, K. R. Asmis, Y. Wang, J. M. Bowman, A. M. Ricks and M. A. Duncan, J. Phys. Chem. Lett., 2012, 3(21), 3160.
51. T. C. Cheng, B. Bandyopadyay, Y. Wang, S. Carter, B. J. Braams, J. M. Bowman and M. A. Duncan, J. Phys. Chem. Lett., 2010, 1(4), 758.
52. D. K. Veirs and G. M. Rosenblatt, J. Mol. Spectrosc., 1987, 121(2), 401.
53. O. Asvany, P. Padma Kumar, B. Redlich, I. Hegemann, S. Schlemmer and D. Marx, Science, 2005, 309(5738), 1219.
54. O. Asvany, K. M. T. Yamada, S. Brünken, A. Potapov and S. Schlemmer, Science, 2015, 347(6228), 1346.
55. X. Huang, A. B. McCoy, J. M. Bowman, L. M. Johnson, C. Savage, F. Dong and D. J. Nesbitt, Science, 2006, 311(5757), 60.
56. E. T. White, J. Tang and T. Oka, Science, 1999, 284(5411), 135.
57. S. Spieler, D. F. Dinu, P. Jusko, B. Bastian, M. Simpson, M. Podewitz, K. R. Liedl, S. Schlemmer, S. Brünken and R. Wester, J. Chem. Phys., 2018, 149(17), 174310.
58. D. A. Wild, R. L. Wilson, Z. M. Loh and E. J. Bieske, Chem. Phys. Lett., 2004, 393(4–6), 517.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05802b

---