High-level ab initio mapping of the multiple H-abstraction pathways of the OH + glycine reaction

Abstract

We perform a systematic search in the transition-state (TS) and product-channel complex (MIN) regions of the multi-channel OH + glycine → H₂O + H₂N–CH–COOH (CH)/HN–CH₂–COOH (NH)/H₂N–CH₂–COO (COOH) reactions. Geometry optimizations reveal {7, 3, 3} CH-TS, {2, 2, 2} CH-MIN, {17, 10, 5} NH-TS, {35, 19, 19} NH-MIN, and {6, 5, 5} COOH-TS conformers at the {MP2/3-21G, MP2/aug-cc-pVDZ, CCSD(T)-F12b/aug-cc-pVDZ} levels of theory as well as 2 additional CH-TSs based on chemical intuition. The benchmark relative energies of the TS, MIN, and product conformers are obtained by considering basis set effects up to aug-cc-pVQZ using the explicitly-correlated CCSD(T)-F12b method, post-(T) correlation up to CCSDT(Q), core correlation, scalar relativistic effects, spin–orbit coupling, and zero-point energy corrections. All the CH [ΔE_e(ΔH₀) = −38.54(−38.61) kcal mol⁻¹], NH [ΔE_e(ΔH₀) = −16.72(−17.98) kcal mol⁻¹], and COOH [ΔE_e = −4.98 kcal mol⁻¹] reactions are exothermic and proceed via shallow, usually negative, classical(adiabatic) barriers of −0.37(−0.95), −1.91(−2.48), and 1.02(−0.57) kcal mol⁻¹, respectively. In the entrance channel MRCI/aug-cc-pVTZ computations reveal several complexes with reactive(non-reactive) arrangements and binding energies of 1.0, 1.6, 3.3, (5.2 and 5.9) kcal mol⁻¹, stabilized by CH⋯OH, NH⋯OH, COOH⋯OH, (OH⋯O=C and OH⋯N) hydrogen bonds, respectively.

---

I. Introduction

The reactions of the hydroxyl radical (OH) with different organic molecules have attracted significant attention due to two main reasons.^1–17 On the one hand, the kinetics and dynamics of the OH + methane (CH₄) and ethane (C₂H₆) reactions were investigated by several experimental and theoretical studies to uncover the fundamental rules of chemistry regarding reactivity, mechanisms, bond cleavage and formation, vibrational and rotational mode specificity, energy transfer, etc.^1–9 On the other hand, reactions of the OH radical with large bio-molecules such as proteins and DNA were studied to gain an atomic and molecular level understanding of the process of oxidative stress.^10–17 UV radiation may produce free radicals in the human body, among which OH is one of the most harmful, which may react with proteins, lipids, and DNA, thereby damaging them and causing various severe diseases.^11,14,15 In the present study we aim to investigate the mechanism of the reaction of the OH radical with the simplest amino acid, glycine (H₂N–CH₂–COOH), in the gas phase, thereby connecting to the above-mentioned two different research directions. First, we plan to extend the fundamental studies of the OH + CH₄/C₂H₆ reactions^1–9 by replacing the alkane molecule with glycine, which has three different functional groups, methylene, amino, and carboxyl, all of which can react with OH. The main reaction channel of the above processes is hydrogen abstraction leading to H₂O and a dehydrogenated alkane (CH₃/C₂H₅) or glycine radical. However, unlike for OH + CH₄/C₂H₆, in the case of the OH + glycine reaction three competitive hydrogen-abstraction pathways can be studied due to the above-mentioned three different functional groups of glycine. Second, due to the fact that glycine is one of the building blocks of proteins, the OH + glycine reaction is the simplest model of oxidative stress caused by the damage of proteins by the OH radical. Of course, in order to perform realistic simulations for biochemical processes, one should also consider that such reactions occur in aqueous environments and the amino acids form peptide bonds in proteins. As we study the OH + glycine system in the gas phase, our main goal is to advance our fundamental knowledge of chemical reactivity in multi-channel reactions, and to uncover the role of several bio-chemically relevant functional groups in the reaction with a free radical without the effect of a solvent.

It is well established that gaseous glycine has 8 conformers and the lowest-energy conformer has C_s point-group symmetry as shown in Fig. 1.^18–27 The OH radical can abstract a hydrogen atom from the CH₂, NH₂, and COOH groups forming dehydrogenated glycine radicals, H₂N–CH–COOH, HN–CH₂–COOH, and H₂N–CH₂–COO, respectively. Following several incomplete, low-level electronic structure studies,^28–37 in 2020 we reported a high-level explicitly-correlated coupled-cluster- and multi-reference configuration interaction-based comprehensive mapping of the conformational space of the dehydrogenated glycine isomers revealing 4, 7, and 4 conformers for the above radicals, in order (see Fig. 2).²⁵ Thus, the reactants and the products of the OH + glycine reaction are well characterized in the literature,²⁵ however, little is known about the transition states (TSs) and complexes connecting them.^29,35 In 2001 Alvarez-Idaboy and co-workers²⁹ investigated the C–H abstraction channel using density functional theory (DFT) and the MP2 method with double- and triple-zeta Pople-type basis sets, reporting a pre-reaction complex and a transition state. In 2010 Li and co-workers³⁵ studied two minimum energy pathways of the H-abstraction process from the carbon center using various DFT functionals as well as HF and MP2 methods with the 6-311++G** basis set. In the latter study³⁵ the CCSD(T) method was also utilized for a few single-point relative energy computations. Previous work only considered the transition state of C–H abstraction and the conformational space at the TS as well as pre- and post-reaction complexes was not characterized. In the present work, we investigate hydrogen abstraction from all three functional groups and report a multi-reference ab initio description of the entrance-channel spin–orbit potentials as well as a detailed mapping of the conformational potentials in the transition-state and post-reaction complex regions of the OH + glycine system using the explicitly-correlated CCSD(T)-F12b method³⁸ considering post-(T), core correlation, scalar relativistic, and spin–orbit effects, thereby providing benchmark barrier heights, binding energies, and reaction enthalpies for the title reaction. The benchmark stationary-point properties determined in the present study allow the prediction of the mechanism of the OH + glycine multi-channel reaction and guide future global potential energy surface developments and reaction dynamics simulations. We describe the computational details in Section II, the results are presented and discussed in Section III, and the paper ends with summary and conclusions in Section IV.

Fig. 1 Conformers of glycine obtained at the CCSD(T)-F12b/aug-cc-pVDZ level of theory.^25,27

Fig. 2 Conformers of the H₂N–CH–COOH, HN–CH₂–COOH, and H₂N–CH₂–COO radicals obtained at the CCSD(T)-F12b/aug-cc-pVDZ, CCSD(T)-F12b/aug-cc-pVDZ, and MRCI/aug-cc-pVDZ levels of theory, respectively.²⁵

II. Computational details

In the first place, we search for the stationary points by chemical intuition using the second-order Møller–Plesset perturbation theory (MP2)^39,40 combined with the 3-21G basis set.⁴¹ According to from which functional group the hydrogen atom is abstracted, we distinguish 3 different reaction pathways, denoted as CH, NH, and COOH. After finding at least one minimum (except COOH) and one saddle point for each reaction channel, we perform a systematic mapping to determine the conformers of the stationary points. The method of the systematic search is presented in Fig. 3. We generate 6⁴ = 1296 initial geometries by modifying 4 torsion angles between 0° and 360° with 60° steps of the lowest-energy conformer of each saddle point and minimum obtained previously and perform geometry optimizations at the MP2/3-21G level of theory. (Note that a smaller step of 30° resulted basically in the same conformers as the 60-degree rotations in the case of cysteine as our recent study shows.⁴²) After that, we use the MP2 method with the aug-cc-pVDZ basis set⁴³ to optimize each different MP2/3-21G conformer. Furthermore, the CCSD(T)-F12b/aug-cc-pVDZ level of theory^38,43 is used for further optimizing the MP2/aug-cc-pVDZ structures. We also compute the harmonic vibrational frequencies at the two most accurate levels of theory. Furthermore, we perform CCSD(T)-F12b single-point energy computations with two different basis sets, aug-cc-pVTZ and aug-cc-pVQZ, at the CCSD(T)-F12b/aug-cc-pVDZ geometries, whose Cartesian coordinates and the corresponding vibrational frequencies are given in the ESI.†

Fig. 3 Generation of the initial 1296 structures by rotating the geometries around 4 axes by 60 degree steps.

In order to reach higher chemical accuracy, five energy corrections are taken into consideration with single-point computations using the best geometries determined at the CCSD(T)-F12b/aug-cc-pVDZ level of theory. CCSD(T),⁴⁴ CCSDT,⁴⁵ and CCSDT(Q)⁴⁶ methods with the 6-31G basis set⁴⁷ are utilized to calculate the post-CCSD(T) correlation corrections, which are obtained using the following equations:

δ[T] = CCSDT/6-31G − CCSD(T)/6-31G (1)

δ[(Q)] = CCSDT(Q)/6-31G − CCSDT/6-31G. (2)

All-electron (AE) and frozen-core (FC) computations are performed using the CCSD(T)-F12b method with the cc-pCVTZ-F12 basis set.⁴⁸ The difference between the AE and FC calculations provides the core-correction as

Δ_core = AE-CCSD(T)-F12b/cc-pCVTZ-F12 − FC-CCSD(T)-F12b/cc-pCVTZ-F12. (3)

Taking into account the scalar relativistic effects, second-order Douglas–Kroll (DK)⁴⁹ relativistic energies are calculated at the AE-CCSD(T)/aug-cc-pwCVTZ-DK level of theory⁵⁰ and for the non-relativistic energies the computations are performed at the AE-CCSD(T)/aug-cc-pwCVTZ level. The difference between the two energies provides the scalar relativistic correction:

Δ_rel = DK-AE-CCSD(T)/aug-cc-pwCVTZ-DK − AE-CCSD(T)/aug-cc-pwCVTZ. (4)

Spin–orbit (SO) corrections are computed utilizing the Breit–Pauli Hamiltonian in the interacting-states approach⁵¹ using the Davidson-corrected⁵² multi-reference configuration interaction⁵³ (MRCI+Q) method with the aug-cc-pVTZ basis set. For the MRCI calculations the active space contains 49 electrons which take place in 25 spatial orbitals keeping the 1s² core electrons of the 3 oxygen, the 2 carbon, and the nitrogen atoms frozen. The spin–orbit correction comes from the difference between the SO₁-ground-state and the non-SO₁-ground-state energies as

Δ_SO = SO₁(MRCI+Q/aug-cc-pVTZ) − non-SO₁(MRCI+Q/aug-cc-pVTZ). (5)

To describe the entrance channel, we also perform MRCI computations along different inter-atomic coordinates, keeping the geometries of the reactants fixed at their equilibrium structures, using the 3-21G, aug-cc-pVDZ, and aug-cc-pVTZ basis sets and the same active space as mentioned above. Furthermore, the SO and non-SO ground- and excited-state entrance-channel potential curves are also determined at the MRCI+Q/aug-cc-pVDZ level of theory.

To calculate the benchmark classical energies, we use the most accurate single-point energies and all of the above energy corrections. The following expression defines the benchmark classical energies:

CCSD(T)-F12b/aug-cc-pVQZ + δ[T] + δ[(Q)] + Δ_core + Δ_rel + Δ_SO, (6)

except in a few cases where any of the above terms cannot be obtained due to convergence issues. The benchmark adiabatic relative energies are the sums of the benchmark classical energies and the zero-point energy corrections (Δ_ZPE) as

CCSD(T)-F12b/aug-cc-pVQZ + δ[T] + δ[(Q)] + Δ_core + Δ_rel + Δ_SO + Δ_ZPE, (7)

where the zero-point energy corrections are obtained at the CCSD(T)-F12b/aug-cc-pVDZ level.

Note that the unrestricted Hartree–Fock (UHF)⁵⁴ reference is used at MP2⁴⁰ and post-CCSD(T) correction computations, whereas CCSD(T)-F12b, AE-CCSD(T), and DK-AE-CCSD(T) methods utilize the restricted open-shell Hartree–Fock (ROHF)⁵⁵ reference. MP2, CCSD(T)-F12b, MRCI, DK, and SO computations are executed using the MOLPRO program package.⁵⁶ The frozen-core CCSD(T), CCSDT, and CCSDT(Q) energies are determined using MRCC^57,58 within MOLPRO.

III. Results and discussion

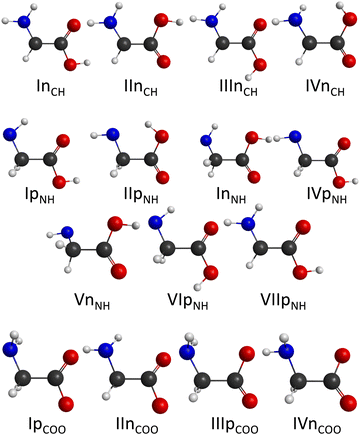
The number of initial structures that converged to a given conformer labeled by the CCSD(T)-F12b/aug-cc-pVDZ geometry is shown in Fig. 4. In the case of the CH saddle points, we determine 7 different conformers, located in a 4 kcal mol⁻¹ relative energy region, with the systematic mapping at the MP2/3-21G level, which leads to 3 conformers at the CCSD(T)-F12b/aug-cc-pVDZ level of theory. Furthermore, we identify two additional CH saddle points, III^TS_CH and V^TS_CH, by searching based on chemical intuition. We obtain 3 + 2 different CH saddle points by optimizing the MP2/3-21G geometries at the MP2/aug-cc-pVDZ level of theory, which is equal to the number of CCSD(T)-F12b/aug-cc-pVDZ conformers labeled with roman numbers reflecting their energy order. The structures of the CCSD(T)-F12b/aug-cc-pVDZ CH saddle points are visualized in Fig. 5 with increasing classical CCSD(T)-F12b/aug-cc-pVDZ energy. We can see that the lowest-energy structure (I^TS_CH) has the most intermolecular stabilizing effects, i.e., the trans-conformation of the carboxyl group and the two H-bond interactions between the amino-N and the carboxyl-H as well as between the carboxyl-O and the hydroxyl-H. The second CH saddle point (II^TS_CH) has a higher benchmark classical (adiabatic) energy by 0.37 (0.86) kcal mol⁻¹, because of the cis conformation of the carboxyl group. III^TS_CH has also a cis-carboxyl group, but in that case the amino group is in a different position, which causes an increase in energy. The carboxyl group of IV^TS_CH has also a cis configuration, but here the carbonyl-side of the carboxyl group is closer to the attacking hydroxyl group, similarly to the lowest-energy CH saddle point. The V^TS_CH conformer has the most inconvenient arrangement with 3.32 (3.05) kcal mol⁻¹ classical (adiabatic) energy relative to I^TS_CH, because of the cis-carboxyl conformation and the different position of the H of the hydroxyl group that is closer to the amino group in this case. It is important to note that at the MP2/6-311G** level of theory, as shown in ref. 29, a conformer similar to V^TS_CH is obtained, but with a carboxyl group rotated by about 180°. We have also found this carbonyl-O⋯HN bonded conformer using the MP2/3-21G level of theory. However, further optimization at the MP2/aug-cc-pVDZ level results in a fifth-order saddle point; therefore, we do not report this CH TS conformer, which may only be obtained without diffuse functions. In comparison with the conformers of glycine (Fig. 1), it is declarable that I^TS_CH is most similar to the IIn glycine conformer and II^TS_CH corresponds to the lowest-energy Ip glycine conformer. The most similar CH saddle-point conformer to the lowest-energy product conformer is II^TS_CH. In the case of the CH minima, the systematic mapping results in only 2 different conformers with similar probability and the number of these stationary points does not decrease with further optimizations. There is around 8.2 kcal mol⁻¹ between the two MP2/3-21G minima as shown in Fig. 4, whereas the benchmark classical (adiabatic) energy difference is 5.08 (4.81) kcal mol⁻¹. The CCSD(T)-F12b/aug-cc-pVDZ structures of the CH minima can be seen in Fig. 6. The difference between the two CH minima is in the conformation of the carboxyl group. Interestingly, the cis-isomer has the lower energy. I^MIN_CH is mostly similar to the IVn glycine conformer and II^MIN_CH is mostly alike the VIIIn glycine conformer. Considering the conformers of the products, the structure of the In_CH conformer is mostly identical to I^MIN_CH and IIIn_CH is similar to II^MIN_CH.

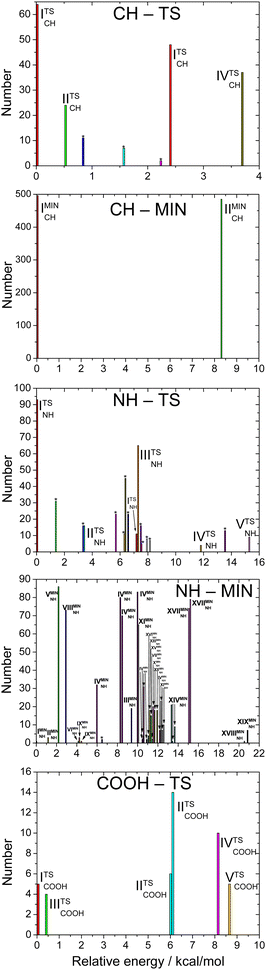Fig. 4 Number of the initial structures leading to specific conformers at the MP2/3-21G level of theory as a function of the relative energies of the conformers corresponding to transition states and minima along the different reaction pathways. The conformers are labeled based on the energy order at the CCSD(T)-F12b/aug-cc-pVDZ level. Labels * denote MP2/3-21G conformers, from which further optimizations fail to converge at a higher level of theory.

Fig. 5 Transition-state structures for H-abstraction from the CH₂ group of glycine obtained at the CCSD(T)-F12b/aug-cc-pVDZ level of theory.

Fig. 6 Structures of the product-channel complexes for H-abstraction from the CH₂ group of glycine obtained at the CCSD(T)-F12b/aug-cc-pVDZ level of theory.

With the systematic search we determine 17 different NH saddle points that lead to 10 different MP2/aug-cc-pVDZ geometries. Finally, with the CCSD(T)-F12b/aug-cc-pVDZ optimization we obtain 5 different NH saddle points (see Fig. 4). The NH saddle points extend in an energy range of 15.2 kcal mol⁻¹ at the MP2/3-21G level of theory. The benchmark CCSD(T)-F12b/aug-cc-pVDZ geometries of the NH saddle points are shown in Fig. 7. In this case, the NH saddle points with cis-carboxyl groups are more stable than the trans-isomers. It can be explained by the further position of the C-hydrogens and the carboxyl-hydrogen. The V^TS_NH conformer is definitely the highest-energy saddle point above I^TS_NH by 10.66 (10.00) kcal mol⁻¹ based on the benchmark classical (adiabatic) data, because of the lack of any stabilizing effect, whereas the first four TSs are stabilized by a H-bond between the reactant-OH and the carbonyl O. The two lowest-energy NH saddle points are similar to the Ip glycine conformer and correspond to the Ip_NH and IVp_NH conformers of the products. It is clear that III^TS_NH and IV^TS_NH saddle points are mostly identical to the VIp and VIIIn glycine isomers, respectively. Furthermore, these two TSs are mostly alike the two highest-energy product conformers based on the conformation of the carboxyl group. The highest-energy NH TS is similar to VIp and VIIIp glycine conformers, but the amino group of the saddle point is changed compared to glycine. According to the position of the outgoing H and the conformation of the carboxyl group it is declarable that the highest-energy NH saddle point is mostly comparable with the VIIp_NH conformer of the products. Most conformers are found in the case of the NH minima. With the help of the systematic mapping at the MP2/3-21G level of theory we identify 35 different structures. The further optimizations result in 19 different conformers in the cases of MP2/aug-cc-pVDZ and CCSD(T)-F12b/aug-cc-pVDZ levels of theory. The highest-energy MP2/3-21G NH minimum is at 20.9 kcal mol⁻¹ relative to the lowest-energy conformer, whereas this classical energy gap is only around 9.8 kcal mol⁻¹ at the benchmark level. The CCSD(T)-F12b/aug-cc-pVDZ conformers of the NH minima can be seen in Fig. 8. In these cases, the evolving H₂O molecule is not always near the amino group, like at the structure of the lowest-energy NH minimum (I^MIN_NH), where the H₂O molecule connects to the OH-side of the carboxyl group with a H-bond interaction. The H₂O molecule near the carboxyl group instead of the dehydrogenated amino group provides a more stable structure. The two lowest-energy NH minima, I^MIN_NH and II^MIN_NH, are mostly similar to the IVn/IVp_NH and Vn/Vn_NH conformers of glycine/product, respectively.

Fig. 7 Transition-state structures for H-abstraction from the NH₂ group of glycine obtained at the CCSD(T)-F12b/aug-cc-pVDZ level of theory.

Fig. 8 Structures of the product-channel complexes for H-abstraction from the NH₂ group of glycine obtained at the CCSD(T)-F12b/aug-cc-pVDZ level of theory.

In the carboxyl region we determine 6 different saddle points with the systematic search at the MP2/3-21G level of theory, which span an energy range of 8.6 kcal mol⁻¹ as seen in Fig. 4. Using these geometries, we obtain 5 different conformers with two more accurate levels of theory, whose benchmark classical (adiabatic) relative energies are within a range of 2.23 (3.82) kcal mol⁻¹. The CCSD(T)-F12b/aug-cc-pVDZ structures of the COOH saddle points can be seen in Fig. 9. In the geometry of the lowest-energy conformer the hydrogens of the CH₂-group are near the hydroxyl-O, which can produce an extra-stabilizing effect over the H-bond between the amino-H and one of the carboxyl oxygens. In the structures of the COOH saddle points the H-bond interaction is always between the amino-H and that of the carboxyl oxygens; there are no geometries, where the hydrogen of the reactant OH radical connects to the amino-N. It can be observed that the II^TS_COOH saddle point is similar to the lowest-energy glycine conformer and the IV^TS_COOH saddle point is mostly alike the Vn glycine conformer. Due to the position of the amino group one can predict that II^TS_COOH leads to the Ip_COO product isomer. Product-channel complexes for COOH abstraction are not found due to serious UHF convergence issues in this region. This is consistent with our previous work, where the carboxyl dehydrogenated glycine radicals could only be described using the MRCI method.²⁵

Fig. 9 Transition-state structures for H-abstraction from the COOH group of glycine obtained at the CCSD(T)-F12b/aug-cc-pVDZ level of theory.

The energetics of the OH + glycine H-abstraction reaction is shown in Fig. 10 with the help of the lowest-energy conformers indicating the benchmark classical and adiabatic relative energies. The reaction is exothermic via every reaction pathway. The lowest-energy product channel is the one when a hydrogen atom leaves the glycine from the carbon atom and joins the OH radical to form a H₂O molecule. This CH-abstraction channel (ΔE_e = −38.54 kcal mol⁻¹) is followed by the amino-dehydrogenation reaction (ΔE_e = −16.72 kcal mol⁻¹), and the carboxyl-dehydrogenation product channel (ΔE_e = −4.98 kcal mol⁻¹) with increasing energy. The global minimum of the PES corresponds to the product complex of the CH-abstraction pathway (I^MIN_CH). If we just look at the classical energies, we can see that the O-dehydrogenation pathway has a small barrier (1.02 kcal mol⁻¹), but taking the zero-point energies into account, the transition states of all the reaction channels are below the reactants in energy. Interestingly, the energy order of the transition states and product-like minima are inverted via the reaction, so the lowest-energy transition state is N-dehydrogenated, the next one is C-dehydrogenated, and the highest-energy transition state is O-dehydrogenated, though their energy difference is less than 2 kcal mol⁻¹. Thus, under thermodynamic control CH abstraction is strongly favored, however, there is no clear kinetic preference between the different pathways.

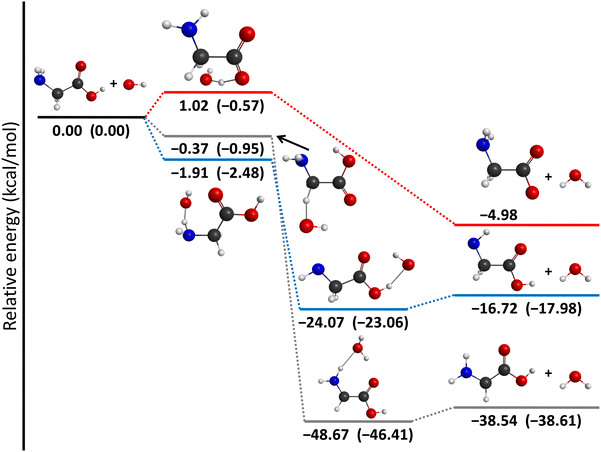Fig. 10 Schematic potential energy surface of the OH(²Π_3/2) + glycine abstraction reaction showing the most accurate classical (adiabatic) relative energies of the lowest-energy conformers of the stationary points along the different reaction pathways.

The entrance channel is studied separately because of the spin–orbit effect. In this case, we present one-dimensional potential energy curves using MRCI/3-21G, MRCI/aug-cc-pVDZ, and MRCI/aug-cc-pVTZ computations at 7 different orientations of the reactants as shown in Fig. 11. We examine cases, where the OH radical approaches the glycine molecule with its H-side, because it has the possibility to form a H-bond with the N or O atoms of glycine. Furthermore, we study attacks with the O-side of OH to map the potentials along the H-abstraction pathways. All of the one-dimensional potentials show a minimum except two orientations: where the O-side of the OH radical moves toward the O atom of the carbonyl group or the N atom in the glycine molecule. This phenomenon can be interpreted considering the repulsion between the non-bonding electrons of the O and O/N atoms. In five cases, where (1) the O of the OH radical approaches the CH₂ group, (2) the N atom of the glycine molecule is approached by the H-side of the OH radical, (3) the amino-H of the glycine molecule is approached by the O-side of the OH radical, (4) the O-side of the OH radical moves near the carboxyl-OH, and (5) the H-side of the OH radical moves toward the O of the carbonyl group, the minima are around the H-bond lengths in the range of 2–2.5 Å. Using the small 3-21G basis set with the MRCI method leads to substantially deeper minima than the computations performed at the higher MRCI/aug-cc-pVDZ and MRCI/aug-cc-pVTZ levels of theory, which are basis-set converged. In the reactive cases, when the O-side of the OH radical approaches the CH, NH, and COOH groups, the well depths are 1.0, 1.6, and 3.3 kcal mol⁻¹, respectively, at the highest MRCI/aug-cc-pVTZ level of theory. However, in the non-reactive H-side attack orientations, the minima are significantly deeper with depths of 5.9 and 5.2 kcal mol⁻¹ due to the formation of N⋯HO and carbonyl–O⋯HO hydrogen bonds, respectively, that may steer the reactants from a reactive orientation, making the reaction indirect. The right side of Fig. 11 shows the potential curves corresponding to the lowest two SO and non-SO electronic states of the OH + glycine system in the entrance channel. The experimentally-determined 0.2 kcal mol⁻¹ SO effect between the SO₁ and non-SO₁ states, which can be deduced from the measured SO splitting of the OH radical, and which is 0.18 kcal mol⁻¹ at the MRCI+Q/aug-cc-pVDZ level, can be easily seen when the distance between the reactants is large. As the reactants approach each other this effect decreases and vanishes at short interfragment distances, where the SO₁ and non-SO₁ potentials merge. Due to the small magnitude of SO splitting, its effect on the above-discussed entrance-channel properties is not significant.

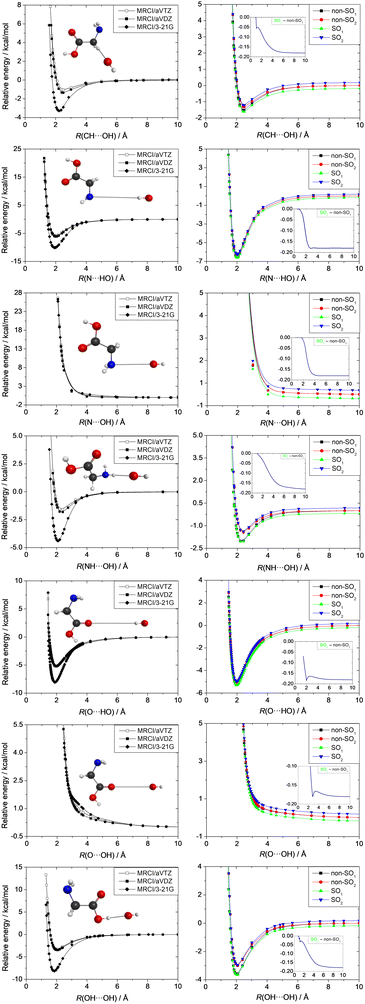Fig. 11 Entrance-channel potential energy curves of the OH + glycine system obtained at the MRCI/3-21G, MRCI/aug-cc-pVDZ, and MRCI/aug-cc-pVTZ levels of theory while the structures of the glycine and OH units are kept frozen at their equilibrium geometries. SO₁ and SO₂ denote the spin–orbit ground and excited states, whereas non-SO₁ and non-SO₂ are the non-relativistic ground and excited electronic states, respectively, obtained at the MRCI+Q/aug-cc-pVDZ level of theory. The insets show the distance dependence of the spin–orbit corrections obtained as the difference between the SO₁ and non-SO₁ energies.

The detailed numerical results of the computations can be seen in Table 1 for the saddle points and minima and in Table 2 for the product channels. It is easily noticeable that MP2 computations give very different energies in comparison with coupled-cluster theory, especially in the case of the TSs. For example, in some cases the MP2 method overestimates the energies of the more accurate CCSD(T)-F12b method even with 5 kcal mol⁻¹. Nevertheless, for the relative energies of the products MP2 is usually accurate within 0.5–1.0 kcal mol⁻¹. The energy differences between the CCSD(T)-F12b computations using different basis sets are characteristically smaller than 1 kcal mol⁻¹ and the aug-cc-pVQZ results are usually basis-set converged within 0.1–0.2 kcal mol⁻¹. The δ[T] and δ[(Q)] corrections are always negative having similar magnitudes and in most of the cases together they provide 0.2–0.3 kcal mol⁻¹ decrease in relative energy. In the case of the carboxyl TSs we can observe larger absolute values, for example, the δ[(Q)] correction is −0.57 kcal mol⁻¹ for the III^TS_COOH conformer. The core correlation and scalar relativistic corrections have only a few hundredths, in some cases a few tenths, of kcal mol⁻¹ effect; the most substantial corrections are found for the products of the CH abstraction channel and for the corresponding product complexes. The spin–orbit correction is always 0.19 kcal mol⁻¹ for every stationary point, which is in excellent agreement with the experimental value of 0.20 kcal mol⁻¹. Here it is important to note that in the case of the OH radical the spin and orbital angular momenta can also couple to the rotational angular momentum resulting in an energy shift by +0.09 kcal mol⁻¹.⁵⁹ If we assume that this rotational coupling becomes negligible when OH interacts with glycine, this so-called rotational ZPE of OH decreases all the relative energies by 0.09 kcal mol⁻¹. These rotational ZPE corrections (presumably −0.09 kcal mol⁻¹) are not incorporated into our final benchmark relative energies. Moreover, to get experimentally observable energies the vibrational ZPE corrections have to be taken into consideration. These ZPE corrections are usually 1–2 kcal mol⁻¹. Interestingly, every minimum in the product channel has a positive Δ_ZPE value and both the products and saddle points have negative ZPE corrections. Taking into account the ZPE correction the energy order of some conformers changes in a few cases. We can unambiguously declare that the I^MIN_CH conformer corresponds to the global minimum of the potential energy surface.

Table 1 Energies (kcal mol⁻¹) and additional corrections (kcal mol⁻¹) of the saddle points and minima of the OH + glycine (Ip) abstraction reaction relative to the reactants at different levels of theory

	MP2	CCSD(T)-F12b			δ[T]^e	δ[(Q)]^f	Δ core	Δ rel	Δ SO	Classical^j	Δ ZPE	Adiabatic^l
Stationary point	DZ^a	DZ^b	TZ^c	QZ^d
a MP2/aug-cc-pVDZ relative energies obtained at MP2/aug-cc-pVDZ geometries. b CCSD(T)-F12b/aug-cc-pVDZ relative energies obtained at CCSD(T)-F12b/aug-cc-pVDZ geometries. c CCSD(T)-F12b/aug-cc-pVTZ relative energies obtained at CCSD(T)-F12b/aug-cc-pVDZ geometries. d CCSD(T)-F12b/aug-cc-pVQZ relative energies obtained at CCSD(T)-F12b/aug-cc-pVDZ geometries. e CCSDT – CCSD(T) obtained with the 6-31G basis set at CCSD(T)-F12b/aug-cc-pVDZ geometries. f CCSDT(Q) – CCSDT obtained with the 6-31G basis set at CCSD(T)-F12b/aug-cc-pVDZ geometries. g Core-correlation correction obtained as the difference between all-electron and frozen-core CCSD(T)-F12b/cc-pCVTZ-F12 relative energies at CCSD(T)-F12b/aug-cc-pVDZ geometries. h Scalar relativistic effect obtained as the difference between DK-AE-CCSD(T)/aug-cc-pwCVTZ-DK and non-relativistic AE-CCSD(T)/aug-cc-pwCVTZ relative energies at CCSD(T)-F12b/aug-cc-pVDZ geometries. i Spin–orbit (SO) corrections obtained as the difference between the SO and non-SO ground-state MRCI+Q/aug-cc-pVTZ relative energies at CCSD(T)-F12b/aug-cc-pVDZ geometries. j Benchmark classical relative energy obtained as CCSD(T)-F12b/aug-cc-pVQZ + δ[T] + δ[(Q)] + Δcore + Δrel + ΔSO. k ZPE corrections obtained at CCSD(T)-F12b/aug-cc-pVDZ. l Benchmark adiabatic relative energy obtained as Classical + ΔZPE. m Benchmark classical relative energy obtained as CCSD(T)-F12b/aug-cc-pVDZ + ΔSO, because the other energy computations do not converge. n Benchmark classical relative energy obtained as CCSD(T)-F12b/aug-cc-pVDZ+ δ[T] + δ[(Q)] + ΔSO, because the other energy computations do not converge. o Benchmark classical relative energy obtained as CCSD(T)-F12b/aug-cc-pVQZ + Δcore + Δrel+ ΔSO, because the other energy computations do not converge.
I^TSCH	3.00	−0.66	−0.40	−0.27	−0.12	−0.18	−0.02	0.03	0.19	−0.37	−0.58	−0.95
II^TSCH	3.34	−0.19	—	—	—	—	—	—	0.19	0.00^m	−0.09	−0.09
III^TSCH	4.88	1.29	1.50	1.62	−0.13	−0.11	−0.04	0.03	0.19	1.56	−0.66	0.90
IV^TSCH	6.00	2.45	2.67	2.77	−0.12	−0.15	−0.03	−0.21	0.19	2.45	−1.09	1.36
V^TSCH	5.82	2.61	2.87	2.98	−0.11	−0.13	−0.01	0.03	0.19	2.95	−0.85	2.10
I^MINCH	−49.53	−48.19	−48.20	−48.26	−0.14	−0.21	−0.45	0.20	0.19	−48.67	2.26	−46.41
II^MINCH	−44.05	−43.05	−43.07	−43.11	−0.23	−0.21	−0.43	0.20	0.19	−43.59	1.99	−41.60
I^TSNH	3.06	−1.71	—	—	−0.14	−0.25	—	—	0.19	−1.91^n	−0.57	−2.48
II^TSNH	6.30	1.37	—	—	—	—	—	—	0.19	1.56^m	−1.17	0.39
III^TSNH	7.90	3.11	—	—	−0.18	−0.25	—	—	0.19	2.87^n	−0.97	1.90
IV^TSNH	11.71	6.77	—	—	—	—	—	—	0.19	6.96^m	−1.23	5.73
V^TSNH	13.74	8.56	—	—	—	—	—	—	0.19	8.75^m	−1.23	7.52
I^MINNH	−24.92	−24.50	−24.25	−24.16	−0.07	−0.10	0.00	0.07	0.19	−24.07	1.01	−23.06
II^MINNH	−24.66	−24.24	−24.01	−23.89	−0.06	−0.10	−0.01	0.07	0.19	−23.80	1.13	−22.67
III^MINNH	−24.54	−24.08	−24.93	−23.84	−0.11	−0.11	−0.05	0.07	0.19	−23.85	1.53	−22.32
IV^MINNH	−23.90	−23.28	−23.11	−23.05	−0.07	−0.11	−0.03	0.06	0.19	−23.01	0.54	−22.47
V^MINNH	−22.82	−22.86	−22.57	−22.41	−0.18	−0.17	0.00	0.07	0.19	−22.50	1.76	−20.74
VI^MINNH	−22.85	−22.56	−22.28	−22.14	−0.14	−0.13	−0.04	0.08	0.19	−22.18	1.10	−21.08
VII^MINNH	−23.00	−22.54	−22.32	−22.22	−0.07	−0.09	0.01	0.06	0.19	−22.12	0.78	−21.34
VIII^MINNH	−22.05	−22.17	−21.91	−21.75	−0.19	−0.17	0.00	0.08	0.19	−21.84	1.64	−20.20
IX^MINNH	−22.24	−21.88	−21.62	−21.49	−0.13	−0.12	−0.04	0.08	0.19	−21.51	0.83	−20.68
X^MINNH	−21.82	−21.14	−20.82	−20.70	−0.11	−0.11	−0.02	0.06	0.19	−20.69	0.27	−20.42
XI^MINNH	−21.70	−21.00	−20.81	−20.74	−0.09	−0.12	−0.01	0.06	0.19	−20.71	0.60	−20.11
XII^MINNH	−21.38	−20.78	−20.53	−20.45	−0.08	−0.10	0.00	0.05	0.19	−20.39	0.44	−19.95
XIII^MINNH	−20.98	−20.12	−19.82	−19.72	−0.07	−0.10	0.03	0.05	0.19	−19.62	0.38	−19.24
XIV^MINNH	−20.31	−19.65	−19.39	−19.30	−0.08	−0.11	0.00	0.05	0.19	−19.25	0.48	−18.77
XV^MINNH	−19.56	−19.09	−18.87	−18.77	−0.10	−0.15	0.06	0.04	0.19	−18.73	1.00	−17.73
XVI^MINNH	−19.81	−18.98	−18.64	−18.52	−0.07	−0.11	0.03	0.05	0.19	−18.43	0.12	−18.31
XVII^MINNH	−19.31	−18.74	−18.54	−18.47	−0.11	−0.11	−0.01	0.06	0.19	−18.45	0.51	−17.94
XVIII^MINNH	−15.63	−14.83	−14.46	−14.32	−0.13	−0.10	0.04	0.05	0.19	−14.27	0.27	−14.00
XIX^MINNH	−15.27	−14.77	−14.51	−14.42	−0.12	−0.10	0.02	0.05	0.19	−14.38	0.49	−13.89
I^TSCOOH	−2.72	1.51	1.52	1.61	−0.13	−0.56	−0.21	0.12	0.19	1.02	−1.59	−0.57
II^TSCOOH	7.77	1.57	1.48	1.62	—	—	0.04	−0.01	0.19	1.84^o	−0.10	1.74
III^TSCOOH	−2.29	2.07	2.09	2.19	−0.14	−0.57	−0.20	0.12	0.19	1.59	−1.67	−0.08
IV^TSCOOH	8.91	2.62	2.53	2.70	−0.35	−0.56	0.04	−0.01	0.19	2.01	0.09	2.10
V^TSCOOH	9.23	2.96	2.86	3.03	—	—	0.04	−0.01	0.19	3.25^o	0.00	3.25

---

Table 2 Energies (kcal mol⁻¹) and additional corrections (kcal mol⁻¹) of the products of the OH + glycine (Ip) abstraction reaction relative to the reactants at different levels of theory

Stationary point	MP2	CCSD(T)-F12b			δ[T]^e	δ[(Q)]^f	Δ core	Δ rel	Δ SO	Classical^j	Δ ZPE	Adiabatic^l
	DZ^a	DZ^b	TZ^c	QZ^d
a MP2/aug-cc-pVDZ relative energies obtained at MP2/aug-cc-pVDZ geometries. b CCSD(T)-F12b/aug-cc-pVDZ relative energies obtained at CCSD(T)-F12b/aug-cc-pVDZ geometries. c CCSD(T)-F12b/aug-cc-pVTZ relative energies obtained at CCSD(T)-F12b/aug-cc-pVDZ geometries. d CCSD(T)-F12b/aug-cc-pVQZ relative energies obtained at CCSD(T)-F12b/aug-cc-pVDZ geometries. e CCSDT – CCSD(T) obtained with the 6-31G basis set at CCSD(T)-F12b/aug-cc-pVDZ geometries. f CCSDT(Q) – CCSDT obtained with the 6-31G basis set at CCSD(T)-F12b/aug-cc-pVDZ geometries. g Core-correlation correction obtained as the difference between all-electron and frozen-core CCSD(T)-F12b/cc-pCVTZ-F12 relative energies at CCSD(T)-F12b/aug-cc-pVDZ geometries. h Scalar relativistic effect obtained as the difference between DK-AE-CCSD(T)/aug-cc-pwCVTZ-DK and non-relativistic AE-CCSD(T)/aug-cc-pwCVTZ relative energies at CCSD(T)-F12b/aug-cc-pVDZ geometries. i Spin–orbit (SO) corrections obtained as the difference between the SO and non-SO ground-state MRCI+Q/aug-cc-pVTZ relative energies at CCSD(T)-F12b/aug-cc-pVDZ geometries. j Benchmark classical relative energy obtained as CCSD(T)-F12b/aug-cc-pVQZ + δ[T] + δ[(Q)] + Δcore + Δrel+ ΔSO. k ZPE corrections obtained at CCSD(T)-F12b/aug-cc-pVDZ. l Benchmark adiabatic relative energy obtained as Classical + ΔZPE. m For these product radicals MRCI/aug-cc-pVDZ geometries are used and the energy computations do not converge in many cases.
H2O + InCH	−38.35	−37.75	−37.90	−38.11	−0.21	−0.20	−0.39	0.18	0.19	−38.54	−0.07	−38.61
H2O + IInCH	−36.04	−36.23	−36.33	−36.54	−0.26	−0.21	−0.38	0.18	0.19	−37.02	−0.09	−37.11
H2O + IIInCH	−32.56	−32.49	−32.64	−32.84	−0.31	−0.21	−0.37	0.17	0.19	−33.37	−0.29	−33.66
H2O + IVnCH	−26.51	−27.98	−28.05	−28.20	−0.39	−0.22	−0.29	0.15	0.19	−28.76	−0.20	−28.96
H2O + IpNH	−17.06	−16.74	−16.70	−16.75	−0.10	−0.12	0.02	0.04	0.19	−16.72	−1.26	−17.98
H2O + IIpNH	−16.25	−15.99	−15.92	−15.96	−0.23	−0.15	−0.01	0.05	0.19	−16.11	−0.98	−17.09
H2O + IIInNH	−15.28	−14.84	−14.77	−14.81	−0.08	−0.11	0.05	0.04	0.19	−14.72	−1.11	−15.83
H2O + IVpNH	−14.07	−13.49	−13.35	−13.41	−0.11	−0.11	0.04	0.04	0.19	−13.36	−1.48	−14.84
H2O + VpNH	−13.98	−13.44	−13.31	−13.35	−0.07	−0.10	0.05	0.04	0.19	−13.24	−1.36	−14.60
H2O + VIpNH	−12.03	−11.77	−11.70	−11.74	−0.16	−0.13	0.04	0.04	0.19	−11.76	−1.46	−13.22
H2O + VIIpNH	−8.05	−7.58	−7.43	−7.47	−0.16	−0.11	0.07	0.03	0.19	−7.45	−1.66	−9.11
H2O + IpCOO^m	—	—	−4.80	−4.93	—	—	−0.22	−0.02	0.19	−4.98	—	—
H2O + IInCOO^m	—	—	—	—	−0.68	−0.65	—	—	0.19	—	—	—
H2O + IIIpCOO^m	—	—	—	—	—	—	—	0.02	0.19	—	—	—
H2O + IVnCOO^m	—	—	—	—	—	—	—	—	0.19	—	—	—

---

Based on the data presented in Tables 1 and 2, we can estimate the uncertainty of the final classical and adiabatic relative energies. Considering (a) basis set errors beyond CCSD(T)-F12b/aug-cc-pVQZ (0.1–0.2 kcal mol⁻¹), (b) uncertainties of the computed T(Q), core, scalar relativistic, and SO corrections (∼0.1 kcal mol⁻¹), (c) electron correlation beyond (Q) (<0.1 kcal mol⁻¹, considering the magnitude of the T(Q) corrections), (d) non-Born–Oppenheimer effects like the diagonal BO correction (DBOC)⁶⁰ (<0.1 kcal mol⁻¹, as DBOCs are usually less than the scalar relativistic effects), and (e) the neglected anharmonicity, which may be less than 0.1 kcal mol⁻¹, i.e., 5% of the ZPE corrections of 1–2 kcal mol⁻¹, results in an uncertainty of about 0.4 kcal mol⁻¹ for both the classical and adiabatic relative energies.

IV. Summary and conclusions

Following our previous high-level ab initio studies on the conformers of amino acid, glycine and its dehydrogenated species,^25,27 we have characterized the entrance channel, transition state region, and product channel of the OH + glycine H-abstraction reaction. In the literature only two pre- and post-reaction complexes and two TSs can be found for the CH abstraction channel determined at a relatively low level of theory. In the present study we consider H abstraction from all three functional groups of glycine and perform a systematic conformational search in the TS and product-complex regions. Geometry optimizations are initiated from 1296 structures at the MP2/3-21G level, followed by further optimizations at the MP2/aug-cc-pVDZ and CCSD(T)-F12b/aug-cc-pVDZ levels of theory revealing {7, 3, 3} CH-TS, {2, 2, 2} CH-post-minimum, {17, 10, 5} NH-TS, {35, 19, 19} NH-post-minimum, and {6, 5, 5} COOH-TS conformers at the above three levels of theory, in order. For the CH abstraction TS two additional conformers are also found based on chemical intuition. As seen, the potential energy surface is more structured with the small 3-21G basis, as MP2/3-21G provides the most conformers in every region. In most cases the more accurate MP2/aug-cc-pVDZ computations significantly decrease the number of the conformers and the CCSD(T)-F12b method usually gives qualitatively the same conformers, except in the NH-TS region, as MP2 if the aug-cc-pVDZ basis is used.

The benchmark relative energies of the TS and post-minimum conformers are computed using a high-level composite approach utilizing the CCSD(T)-F12b/aug-cc-pVQZ level of theory and additive corrections of post-(T) correlation, core correlation, scalar relativity, spin–orbit effect, and zero-point energy. The benchmark ab initio results show that H abstraction is an exothermic process from every functional group and thermodynamically CH abstraction is strongly preferred over NH and the least-favored COOH abstraction. The adiabatic barriers, relative to the reactants, are slightly negative in all cases, and the kinetic preference is in the NH, CH, and COOH order. In the entrance channel H-bonded minima exist with depths of 5–6 kcal mol⁻¹ corresponding to non-reactive OH⋯N and OH⋯O=C arrangements, whereas the reactive CH⋯OH, NH⋯OH, and COOH⋯OH complexes have weaker binding energies of 1.0, 1.6, and 3.3 kcal mol⁻¹, respectively. The above findings indicate that H abstraction can occur from all three functional groups at low collision energies, where the H-bond donor character of the OH radical may steer the reactants into a non-reactive orientation, thereby making the reaction indirect. Furthermore, the little difference between the TS energies predicts that the three channels may become competitive even if the CH abstraction is thermodynamically strongly preferred. Moreover, the kinetically least preferred COOH abstraction has the deepest entrance-channel minimum along the reactive approach, which may facilitate H abstraction from this group. The present study will guide future global potential energy surface developments and dynamics simulations for the OH + glycine system, which can uncover the role of the stationary points in the mechanism and outcome of this multi-channel reaction.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank the National Research, Development and Innovation Office–NKFIH, K-125317; the Ministry of Human Capacities, Hungary grant 20391-3/2018/FEKUSTRAT; Project no. TKP2021-NVA-19, provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme; and the Momentum (Lendület) Program of the Hungarian Academy of Sciences for financial support. The authors also thank András B. Nacsa for his help with the implementation of the systematic search method.

References

1. D. L. Baulch, R. J. B. Craven, M. Din, D. D. Drysdale, S. Grant, D. J. Richardson, A. Walker and G. Watling, J. Chem. Soc., Faraday Trans. 1, 1983, 79, 689.
2. H. Lin, Y. Zhao, B. A. Ellingson, J. Pu and D. G. Truhlar, J. Am. Chem. Soc., 2005, 127, 2830.
3. B. Zhang, W. Shiu and K. Liu, J. Phys. Chem. A, 2005, 109, 8983.
4. J. Espinosa-Garcia and J. C. Corchado, Theor. Chem. Acc., 2015, 134, 6.
5. J. Li and H. Guo, J. Chem. Phys., 2015, 143, 221103.
6. H. Song, J. Li, B. Jiang, M. Yang, Y. Lu and H. Guo, J. Chem. Phys., 2014, 140, 084307.
7. N. I. Butkovskaya and D. W. Setser, Int. Rev. Phys. Chem., 2003, 22, 1.
8. B. Gruber and G. Czakó, Phys. Chem. Chem. Phys., 2020, 22, 14560.
9. C. Rangel, M. Garcia-Chamorro, J. C. Corchado and J. Espinosa-Garcia, Phys. Chem. Chem. Phys., 2020, 22, 14796.
10. I. Zs-Nagy and R. A. Floyd, Biochim. Biophys. Acta, 1984, 790, 238.
11. J. A. Imlay and S. Linn, Science, 1988, 240, 1302.
12. J. A. Simpson, S. Narita, S. Gieseg, S. Gebicki, J. M. Gebicki and R. T. Dean, Biochem. J., 1992, 282, 621.
13. V. A. Tyurin, Y. Y. Tyurina, G. G. Borisenko, T. V. Sokolova, V. B. Ritov, P. J. Quinn, M. Rose, P. Kochanek, S. H. Graham and V. E. Kagan, J. Neurochem., 2000, 75, 2178.
14. B. Lipinski, Oxid. Med. Cell. Longevity, 2011, 2011, 809696.
15. S. de M. Bandeira, L. J. S. da Fonseca, G. da S. Guedes, L. A. Rabelo, M. O. F. Goulart and S. M. L. Vasconcelos, Int. J. Mol. Sci., 2013, 14, 3265.
16. B. Niu, H. Zhang, D. Giblin, D. L. Rempel and M. L. Gross, J. Am. Soc. Mass Spectrom., 2015, 26, 843.
17. G. M. Chaban, D. Wang and W. M. Huo, J. Phys. Chem. A, 2015, 119, 377.
18. A. G. Császár, J. Am. Chem. Soc., 1992, 114, 9568.
19. A. G. Császár, J. Mol. Struct., 1995, 346, 141.
20. V. Kasalová, W. D. Allen, H. F. Schaefer III, E. Czinki and A. G. Császár, J. Comput. Chem., 2007, 28, 1373.
21. R. M. Balabin, Chem. Phys. Lett., 2009, 479, 195.
22. R. M. Balabin, J. Phys. Chem. Lett., 2010, 1, 20.
23. V. Barone, M. Biczysko, J. Bloino and C. Puzzarini, Phys. Chem. Chem. Phys., 2013, 15, 1358.
24. V. Barone, M. Biczysko, J. Bloino and C. Puzzarini, Phys. Chem. Chem. Phys., 2013, 15, 10094.
25. E. M. Orján, A. B. Nacsa and G. Czakó, J. Comput. Chem., 2020, 41, 2001.
26. R. Conte, P. L. Houston, C. Qu, J. Li and J. M. Bowman, J. Chem. Phys., 2020, 153, 244301.
27. A. B. Nacsa and G. Czakó, Phys. Chem. Chem. Phys., 2021, 23, 9663.
28. D. Yu, A. Rauk and D. A. Armstrong, J. Am. Chem. Soc., 1995, 117, 1789.
29. A. Galano, J. R. Alvarez-Idaboy, L. A. Montero and A. Vivier-Bunge, J. Comput. Chem., 2001, 22, 1138.
30. A. K. Croft, C. J. Easton and L. Radom, J. Am. Chem. Soc., 2003, 125, 4119.
31. Y. Huang, L. Guler, J. Heidbrink and H. Kenttämaa, J. Am. Chem. Soc., 2005, 127, 3973.
32. A. Mavrandonakis, S. C. Farantos and G. E. Froudakis, J. Phys. Chem. B, 2006, 110, 6048.
33. G. Yang, Y. Zu and L. Zhou, J. Phys. Org. Chem., 2008, 21, 34.
34. P. Carbonniere, A. Dargelos, I. Ciofini, C. Adamo and C. Pouchan, Phys. Chem. Chem. Phys., 2009, 11, 4375.
35. R.-J. Lin, C.-C. Wu, S. Jang and F.-Y. Li, J. Mol. Model., 2010, 16, 175.
36. J. Uranga, O. Lakuntza, E. Ramos-Cordoba, J. M. Matxain and J. I. Mujika, Phys. Chem. Chem. Phys., 2016, 18, 30972.
37. M. C. Owen, I. G. Csizmadia, B. Viskolcz and B. Strodel, Molecules, 2017, 22, 655.
38. G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104.
39. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618.
40. R. D. Amos, J. S. Andrews, N. C. Handy and P. J. Knowles, Chem. Phys. Lett., 1991, 185, 256.
41. J. S. Binkley, J. A. Pople and W. J. Hehre, J. Am. Chem. Soc., 1980, 102, 939.
42. A. B. Nacsa and G. Czakó, J. Phys. Chem. A, 2022, 126, 9667.
43. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007.
44. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479.
45. J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041.
46. M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 214105.
47. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257.
48. J. G. Hill, S. Mazumder and K. A. Peterson, J. Chem. Phys., 2010, 132, 054108.
49. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89.
50. W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48.
51. A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823.
52. S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61.
53. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803.
54. J. A. Pople and R. K. Nesbet, J. Chem. Phys., 1954, 22, 571.
55. C. C. J. Roothaan, Rev. Mod. Phys., 1960, 32, 179.
56. H.-J. Werner, P. J. Knowles, G. Knizia and F. R. Manby, M. Schütz et al., a package of ab initio programs, Molpro, version 2015.1, see https://www.molpro.net.
57. M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, B. P. Szabó, L. Gyevi-Nagy, B. Hégely, et al.Mrcc, a quantum chemical program suite, see http://www.mrcc.hu.
58. M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy and B. Hégely, et al. , J. Chem. Phys., 2020, 152, 074107.
59. M. E. Harding, J. Vázquez, B. Ruscic, A. K. Wilson, J. Gauss and J. F. Stanton, J. Chem. Phys., 2008, 128, 114111.
60. N. C. Handy, Y. Yamaguchi and H. F. Schaefer III, J. Chem. Phys., 1986, 84, 4481.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates (Å) and harmonic vibrational frequencies of all the stationary points obtained at the CCSD(T)-F12b/aug-cc-pVDZ level of theory. See DOI: https://doi.org/10.1039/d2cp03049g

---