Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mind the GAP: quantifying the breakdown of the linear vibronic coupling Hamiltonian†
Thomas J
Penfold
 and
Julien
Eng
and
Julien
Eng
 *
*
Chemistry, School of Natural and Environmental Sciences, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK. E-mail: julien.eng@newcastle.ac.uk
First published on 9th February 2023
Abstract
Excited state dynamics play a critical role across a broad range of scientific fields. Importantly, the highly non-equilibrium nature of the states generated by photoexcitation means that excited state simulations should usually include an accurate description of the coupled electronic–nuclear motion, which often requires solving the time-dependent Schrödinger equation (TDSE). One of the biggest challenges for these simulations is the requirement to calculate the PES over which the nuclei evolve. An effective approach for addressing this challenge is to use the approximate linear vibronic coupling (LVC) Hamiltonian, which enables a model potential to be parameterised using relatively few quantum chemistry calculations. However, this approach is only valid provided there are no large amplitude motions in the excited state dynamics. In this paper we introduce and deploy a metric, the global anharmonicity parameter (GAP), which can be used to assess the accuracy of an LVC potential. Following its derivation, we illustrate its utility by applying it to three molecules exhibiting different rigidity in their excited states.
1 Introduction
Quantum dynamics simulations that seek to solve the time-dependent Schrödinger equation (TDSE) are crucial for describing processes occurring in electronically excited states and therefore are the key to understanding and refining the properties of functional molecules and materials across a range of applications, such as organic light emitting diodes (OLEDS)1,2 and photovoltaics.3–5 The equations of motion governing the dynamics occurring over excited state potential energy surfaces (PES) can be solved using either traditional grid based methods, such as the multi-configurational time-dependent Hartee (MCTDH) method6,7 or trajectory based methods such as Tullys Trajectory Surface Hopping (TSH)8,9 or Gaussian basis functions (GBFs) methods.10–16 The latter being motivated by the original work of Heller,17–19 which in contrast to TSH,20,21 is able to retain a fully quantum description of the nuclear motion.Independent of the method used to evolve the nuclear wavepacket, one of the major challenges in all of these simulations is obtaining an accurate description of the high-dimensional excited state PES upon which the nuclei evolve. One approach, primarily used for traditional grid based methods is to determine global analytic functions using quantum chemistry calculations.22–24 These can be viewed as the non-Born Oppenheimer version of classical force fields and may be refined using, for example, experimental data. This is the most accurate approach, but time consuming and extremely challenging for more than a few atoms due to the size of nuclear configuration space. For trajectory based methods, most approaches exploit the spatial locality of the trajectory making it possible to calculate PES on-the-fly, and so the complicated multidimensional potential can be calculated as and when it is required25 removing the significant challenge of a priori computation of a PES. However, especially for larger molecules, this can still be challenging due to the computational scaling of the quantum chemistry methods and the large number of calculations required. The final approach, which is the focus of the present work, is to develop a model Hamiltonian, which are parameterised to match the PES around the important point on the PES, such as the Franck–Condon (FC) point. This reduces the number of quantum chemistry calculations required to map the excited state potential and can be a reliable way to calculate the excited state dynamics, especially when large amplitude motions in the excited state are absent.
In this work, we focus on the linear vibronic coupling (LVC) scheme developed by Köppel et al.26,27 which describes the excited states of a system by a series of coupled shifted harmonic oscillators. Importantly, the simplicity of this approach makes it possible parameterise an effective Hamiltonian with very few quantum chemistry calculations,28 providing a mechanism to achieve a detailed understanding of excited state dynamics through simplified models, which ultimately facilitates extraction of the critical parameters affecting function. These properties have recently been exploited to perform excited state dynamics using LVC models across a range of difference materials.1,2,29–43 While the advantage of the LVC is that it can be relatively straightforward to obtain, the disadvantage is that it becomes inaccurate for larger displacements away from the starting geometry when anharmonic effects become more important. Consequently, in the present work introduce and deploy a metric, the Global Anharmonicity Parameter (GAP), which can used to assess the accuracy of an LVC potential. Following its derivation, we illustrate and discuss its utility by applying the method to three molecular systems.
2 Methodology
2.1 Computational details
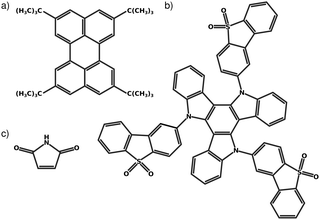
Fig. 1 shows the molecules considered in the present work. Fig. 1a is a narrowband width blue fluorescent emitter used in OLEDS, named 2,5,8,11-tetra-tert-butylperylene (TBPe).44 The rigidity of the molecule required to ensure the narrow emission spectrum makes it very suitable for the LVC treatment. Fig. 1b is a thermally activated delayed fluorescence45,46 emitter exhibiting a D–A3 structure with a triazatruxene central donor functionalized with three peripheral dibenzothiophene-S,S-dioxide acceptors abbreviated as TAT-3DBTO2 from now on.47,48Fig. 1c is Maleimide a small heterocyclic organic molecule previously studied using a quadratic vibronic coupling (QVC) Hamiltonian model.49 The level of theory used for each molecule was chosen to correspond to previous works48–50 and is described below.All parameters required for the LVC Hamiltonian, described in Section 2.2, were extracted using the VCMaker software developed in-house and available for download at ref. 51. All quantum chemistry calculations described in the following subsections were all performed with the Q-Chem 5.0 software.52,53
The Hessian of the electronic ground state and the Cartesian gradients of the first excited singlet (S1) and triplet (T1) states required for the LVC were computed at the ground state optimised geometry using the same level of theory described above. All calculations were performed in the gas phase. Cartesian coordinates of the ground and excited states optimised geometries are provided in Tables S1, S2 and S4 (ESI†).
2.2 Linear vibronic coupling
The electronic diabatic Hamiltonian elements Wn,n can be expressed by expanding W − V01 as a Taylor series expansion of the diabatic potential around a reference nuclear geometry (Q0), usually the FC geometry. V0 is a reference potential chosen accordingly to the problem. It is not restricted to a particular form but is often defined as harmonic with vibrational frequencies ωi along dimensionless normal coordinates Qi. In this case, Hamiltonian elements are expressed: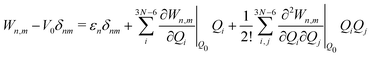 | (1) |
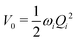 | (2) |
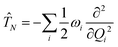 | (3) |
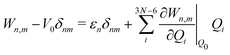 | (4) |
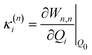 | (5) |
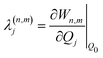 | (6) |
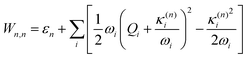 | (7) |
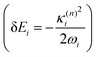 and in position
and in position 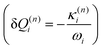 .
.
Within the LVC, the minimum of any excited state PES n is given by
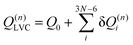 | (8) |
Eqn (8) can be rewritten in term of κ:
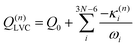 | (9) |
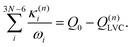 | (10) |
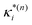 :
: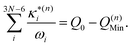 | (11) |
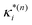 based on the excited state minima provides information at potentially larger displacements from FC. Crucially, comparing κ(n)i and
based on the excited state minima provides information at potentially larger displacements from FC. Crucially, comparing κ(n)i and 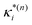 provides a direct estimate of the validity of the LVC model, i.e. in the limit the harmonic approximation holds,
provides a direct estimate of the validity of the LVC model, i.e. in the limit the harmonic approximation holds, 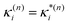 .
.
In this work we seek to develop a simple general parameter which can be used to characterise how suitable the LVC approach is. The global anharmonicity parameter (GAP) is defined as:
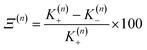 | (12) |
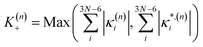 | (13) |
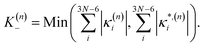 | (14) |
As these parameters are all calculated in terms of individual normal mode, Ξ can be represented in term of relative single mode anharmonicity (RSMA) ξni:
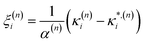 | (15) |
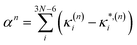 | (16) |
3 Results
3.1 TBPe
As described above, TBPe (Fig. 1a) is a narrowband fluorescent emitter44 and given the rigidity required in the molecular structure to achieve narrow emission spectra66 one would expect the LVC model to provide an accurate description of TBPe excited states. In this section we focus on the lowest excited triplet (T1) and singlet (S1) states which both exhibit π → π* excitation localised on the central aromatic moiety of TBPe. Fig. S1 (ESI†) shows the difference of electronic density associated to the S1 ← GS and T1 ← GS transitions. The minimum energy geometry of both of these states exhibit very small root-mean square deviation (RMSD: Θ) with respect to the electronic ground state optimised geometry of Θ(SMin1,GS) = 0.025 Å and Θ(TMin1,GS) = 0.029 Å, respectively.Fig. 2a shows the GAP (Ξ) and RSMA (ξ) for the S1 and T1 excited states of TBPe. The GAP of ΞS1 = 5.2% and ΞT1 = 0.4% confirms, consistent with the rigidity discussed above, the validity of the Harmonic approximation for this molecule. The RSMA shown in Fig. 2a highlights the discrete normal modes with the largest RSMA, which are in-plane motions (high frequency). Out-of-plane distortions have smaller RSMA because such motions involve a bending of the π-system which requires more energy than a collective in-plane vibration of the C–C bonds. The largest RSMA for the S1 and T1 states coincide, reflecting the similar character of the excited states.
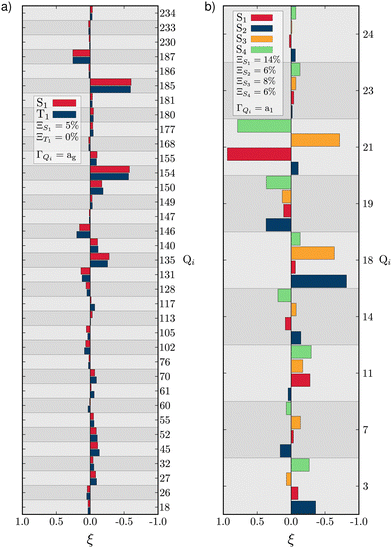 | ||
| Fig. 2 RSMA (ξ) for TBPe S1 and T1 (a) and Maleimide S1, S2, S3 and S4 (b). GAPs are shown inset. Only fully symmetric normal modes are shown. ξ for normal modes of other symmetries are shown in Tables S6 and S7 (ESI†) for TBPe and Tables S21, S22, S24 and S25 (ESI†) for Maleimide. | ||
The validity of the GAP (Ξ) approach is confirmed by the small RMSD between the optimised structures of the S1 and T1 states discussed above. In addition, the theoretical minima obtained using the displacement harmonic oscillator approach: i.e. SLVC1 and TLVC1, respectively are in very close agreement with the true minima with the RMSD of the triplet state being Θ(TMin1,TLVC1) = 0.006 Å and Θ(SMin1,SLVC1) = 0.016 Å for the singlet state. A small nuclear distortion alone is not sufficient to confirm the validity of the harmonic approximation. The relaxation energy obtained from 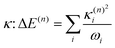 and from
and from 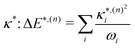 for S1 and T1 are quantitatively the same: ΔE(S1) = −0.157 eV,
for S1 and T1 are quantitatively the same: ΔE(S1) = −0.157 eV, 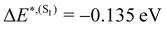 and ΔE(T1) = −0.272 eV,
and ΔE(T1) = −0.272 eV, 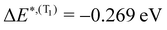 and in good agreement to the relaxation energy between the ground state optimised geometry and SMin1
and in good agreement to the relaxation energy between the ground state optimised geometry and SMin1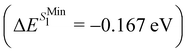 and TMin1
and TMin1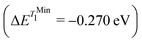 .
.
The quality of the structure and energy of the state of interest is important, however the overall electronic structure at the LVC minimum is also required to be in good agreement to the optimised minimum. Table 1 shows the comparison between the electronic structure of TBPe at the two optimised geometries SMin1 and TMin1 and their respective LVC geometries: SLVC1 and TLVC1. At both SMin1 and TMin1 the energy of S1 is very well reproduced by the LVC generated geometry with a difference of energy <0.005 eV. The energy of T1 also shows good agreement between the optimised and the LVC minima with only a small difference in energy of 0.01 eV between SMin1 and SLVC1. The maximal difference of energy is observed for the ground state energy SMin1 and SLVC1 with a difference of 0.02 eV. This is due mainly to the difference in the shape of the PES where S1 and T1 might feature shallower PES than the ground state. While this difference is negligible, it shows that for less rigid system the energetics of neighbouring states might not be is such a good agreement to the optimised minimum.
| State | SMin1 | SLVC1 | ||
|---|---|---|---|---|
| f | ΔE/eV | f | ΔE/eV | |
| S0 | — | 0.13 | — | 0.15 |
| T1 | — | 1.65 | — | 1.64 |
| S1 | 0.587 | 2.98 | 0.594 | 2.98 |
| T2 | — | 3.08 | — | 3.09 |
| T3 | — | 3.31 | — | 3.32 |
| State | TMin1 | TLVC1 | ||
|---|---|---|---|---|
| f | ΔE/eV | f | ΔE/eV | |
| S0 | — | 0.26 | — | 0.27 |
| T1 | — | 1.62 | — | 1.62 |
| S1 | 0.594 | 3.01 | 0.617 | 3.01 |
| T2 | — | 3.13 | — | 3.13 |
| T3 | — | 3.38 | — | 3.39 |
3.2 TAT-3DBTO2
Triazatruxene tris(dibenzothiophene-S,S-dioxide) TAT-3DBTO2 is a promising candidate for application in TADF OLEDs.47 It consists of a central donor moiety linked to three peripherals acceptor units through carbon–nitrogen single bonds (see Fig. 1). This type of donor–acceptor molecule features low-lying charge transfer (CT) states that typically exhibit small singlet–triplet energy gap, a requirement for the up-conversion of non-emissive triplet states in TADF.45 Indeed, after excitation the acceptor units can rotate with respect to the central donor moiety around the C–N bond (φi, see Fig. S2, ESI†) to accommodate the excited state electronic density and minimise the orbital overlap. This relaxation effectively reduces the energy gap between singlet and triplet CT states that is desirable for efficient TADF emitters.Large amplitude motions, and in particular rotations, are typically situations where harmonic potentials breakdown. At the geometry of the ground state minimum, TAT-3DBTO2 features a C3 symmetry where all three acceptors are tilted by φ = 57.29 deg with respect to the central moiety. At this geometry, the lowest triplet state T1 at E(T1) = 3.09 eV is a mix of local excitation focused on the donor and charge transfer (CT) towards all the acceptors units. In contrast, the S1 state (E(S1) = 3.62 eV) is a pure CT from the donor to all acceptors. The electronic structure of TAT-3DBTO2 at the ground state optimised geometry is reported in Table 2 and the difference of electronic density of S1 and T1 are shown in Fig. S3 (ESI†). Relaxation after excitation into S1 leads to a localisation67 of the CT towards a single acceptor and a stabilisation of the state to E(S1) = 3.32 eV (see Table 2 top right). The acceptor involved in the CT of S1 rotates around the donor–acceptor bond to a more perpendicular orientation with φ1= 77.47 deg. The other two acceptors are not involved in the excitation, remaining tilted with φ2 = 61.04 deg and φ3 = 59.84 deg. The nature of T1 changes during the relaxation in S1 to become a mixed charge transfer/locally excited state based upon the acceptor, 3 CT/3 LE(A) state at E(T1) = 3.14 eV. We report the reader to the work of Eng et al.48 for a more detailed analysis of the electronic structure.
| GS | SMin1 | ||||
|---|---|---|---|---|---|
| State | f | ΔE/eV | State | f | ΔE/eV |
| S0 | — | 0.00 | S0 | — | 0.42 |
| T1 | — | 3.09 | T1 | — | 3.14 |
| T2/T3 | — | 3.19 | S1 | 0.004 | 3.32 |
| T4 | — | 3.23 | T2 | — | 3.36 |
| T5/T6 | — | 3.42 | T3 | — | 3.45 |
| T7 | — | 3.51 | T4 | — | 3.61 |
| S1 | 0.005 | 3.62 | T5 | — | 3.62 |
| T8/T9 | — | 3.67 | T6 | — | 3.65 |
| T10 | — | 3.67 | S2 | 0.013 | 3.68 |
| S2/S3 | 0.184 | 3.67 | T7 | — | 3.78 |
| SSym1 | SLVC1 | ||||
|---|---|---|---|---|---|
| State | f | ΔE/eV | State | f | ΔE/eV |
| S0 | — | 0.18 | S0 | — | 0.46 |
| T1 | — | 3.19 | T1 | — | 3.39 |
| T2/T3 | — | 3.23 | T2 | — | 3.44 |
| T4 | — | 3.30 | T3 | — | 3.47 |
| T5/T6 | — | 3.48 | T4 | — | 3.54 |
| S1 | 0.000 | 3.50 | T5 | — | 3.71 |
| S2/S3 | 0.046 | 3.52 | T6 | — | 3.73 |
| T7 | — | 3.53 | S1 | 0.036 | 3.74 |
| T8/T9 | — | 3.60 | T7 | — | 3.78 |
| S2 | 0.048 | 3.80 | |||
| S3 | 0.092 | 3.83 | |||
The GAP for S1 is ΞS1 = 86% and therefore clearly reflects a significant breakdown of the LVC model. Due to symmetry, only fully symmetric normal modes can have κ ≠ 0, i.e. a non-zero gradient at the FC geometry and therefore the κ values calculated using the LVC will not be able to capture the symmetry breaking. In addition, because the κ* values are estimated at a structure with no symmetry (SMin1) it does not have the same constraint and may exhibit non-zero gradient along any normal modes. This is demonstrated in Fig. S4 (ESI†) as normal modes that are not a1 show non negligible RSMA. Consequently, we could expect the LVC minimum to be similar to the optimised geometry of S1 within the C3 point group symmetry (SSym1), discussed in ref. 67. The electronic structure at SSym1 is shown in Table 2 bottom left. The electronic structure at this geometry is similar as the electronic structure at GS but with the lowest excited states closer in energy. The interest of this critical structure for TADF is discussed in more details in the work of Eng et al.67 The degeneracy of states due to the C3 point group symmetry is maintained and S1 is stabilised to E(S1) = 3.50 eV and T1 is found at E(T1) = 3.19 eV. The GAP of S1 considering the set κ* taken from the SSym1 geometry 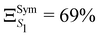 is slightly lower than ΞS1 but not sufficiently to validate the harmonic approximation.
is slightly lower than ΞS1 but not sufficiently to validate the harmonic approximation.
This analysis demonstrates that symmetry breaking is not the only reason for the breakdown of the harmonic approximation in TAT-3DBTO2. The rotational motion involved in the relaxation is not well described by normal modes of vibrations and the normal modes at the S1 minimum are too different from the set of normal modes at the FC geometry. The LVC minimum of S1 (SLVC1) shows torsion angles (φ1 = 66.59 deg, φ2 = 62.88 deg and φ3 = 60.98 deg) closer to the ones of the structure of SMin1. While SLVC1 shows an electronic structure that retains, considering numerical errors, the degeneracy pattern of the C3 symmetry with the good ordering of the electronic states, see Table 2 bottom right, the energies of the electronic states, and especially the energy of S1, are however aberrant and reflect the non-physical nature of the structure.
Compared to the S1 state, the GAP of the T1 state is smaller: ΞT1 = 53%. This is due to the predominantly LE nature of T1 at the ground state optimised geometry. π → π excitation typically lead to bond length reorganisation that involves small nuclear distortions resulting in small GAP as observed in TBPe. The mixed nature of the state means the excitation is delocalised over both the acceptors and the donor units. Modulation of the orbital overlap to minimise the state energy occurs via donor–acceptor rotation. This effect alone is not sufficient to explain the large ΞT1, in particular as torsion angle is similar for the ground state optimised geometry and the minimum of T1, i.e. φ1,2,3 = 57.29 deg and φ1 = 52.51 deg, φ2 = 54.47 deg, φ3 = 50.88 deg, respectively. The value of the torsion coordinates φ is reported for all geometries in Table S9 (ESI†). We attribute the large anharmonicity to the change of nature of the state from a LE/CT mixed nature at FC geometry to a LE(A) at the T1 minimum. The κ parameters extracted from the electronic gradient at FC describe the mixed nature of T1, while the κ* extracted from the difference of geometry, describe the diabatic 3LE(A) excited state.
The analysis of the RSMA (Fig. S4, ESI†) confirms the difference nature of S1 and T1. Indeed the normal modes with the largest ξ in S1 are normal modes within the 1000 cm−1 to 1200 cm−1 (from mode Q163 to Q201) range that are typically out of plane motions such as rotations and bending. Such motions are representative of the large localisation of the excitation occurring in S1. Conversely, the largest ξ in the T1 state are found to be normal modes with frequencies between 1600 cm−1 and 1700 cm−1 (from mode Q165 to Q194) and are C–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond stretching vibrations that are involved in the π system reorganisation that occurs during the relaxation in a π → π* electronic state.
C bond stretching vibrations that are involved in the π system reorganisation that occurs during the relaxation in a π → π* electronic state.
3.3 Maleimide
Small heterocyclic organic compounds are ideal test systems for probing theoretical concepts in photochemistry and photophysics. In this context maleimides have gained increasing interest over the past years due to a wide variety of potential applications.68–71 Recently Worth et al.49 have studied the excited state dynamics of Maleimide (see Fig. 1c) using a QVC Hamiltonian. By including four low-lying singlet excited states within the manifold of 24 vibrational modes they were able to provide a detail insight into the excited state relaxation dynamics and the vibrational modes involved.The electronic structure of Maleimide is described in detailed in ref. 49. Briefly, at the ground state optimised geometry the two lowest excited singlet states S1 and S2 are at E(S1) = 4.07 eV and E(S2) = 4.84 eV, respectively and are excitations from the oxygen lone pairs to a π* anti-bonding orbital. S3 and S4 are at E(S3) = 5.23 eV and E(S2) = 6.70 eV and correspond to excitations from a π orbital to the same π* anti-bonding orbital. The electronic structure at the ground state minimum is reported in Table S19 (ESI†), while the orbitals involved are shown in Fig. S4 (ESI†).
To estimate the GAP from the reported excited states, special attention needs to be taken while optimising each excited states. Indeed, κ and κ* must be computed at the Franck–Condon and minimum geometries of a same diabatic state, i.e. the electronic nature of the state must be the same. As reported by Worth et al. S2 and S3 electronic states cross and therefore generate two minima of different nature in the S2 PES. In order to avoid any confusion, we will refer to the adiabatic computed states as S1, S2, S3 and S4 and to the diabatic states by their electronic nature. To alleviate the notations and because the electronic transition associated to each diabatic states is population the same π orbital, we will name the diabatic states by the orbital the electron is excited from, i.e. Sn2, Sn1, Sπ1 or Sπ2.
Scans along interpolated coordinates between the ground state and optimised SMink geometries are shown in Fig. S5 (ESI†) and emphasize the crossing between Sn1 and Sπ2. Other crossings between states can be observed, but only at higher energies, therefore not affecting the minima of the potentials. The electronic structure of Maleimide at each of the excited states' minima is shown in Table S20 (ESI†).
The anharmonicity analysis yields small GAPs for each of the lowest singlet states, namely, 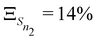 ,
, 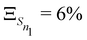 ,
, 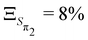 and
and 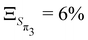 . These values are slightly larger than the values for TBPe reflecting an increase in anharmonicity despite the apparent rigidity of Maleimide. Fig. S6 (ESI†) shows the potential of the ground and four lowest excited states along the a1 normal modes, i.e. with κ ≠ 0. The curvature of the ground electronic states is systematically overestimated, especially for low-frequency normal modes. While a deviation of the curvature of the electronic excited states from the ground states frequency, can be due to vibronic coupling between excited states, a deviation of the curvature of the ground state from the LVC model is a direct signature of anharmonicity. The RSMA analysis of Maleimide is shown in Fig. 2c and d. The normal mode exhibiting the largest ξ is mode ν21 that corresponds to a symmetric stretching of C
. These values are slightly larger than the values for TBPe reflecting an increase in anharmonicity despite the apparent rigidity of Maleimide. Fig. S6 (ESI†) shows the potential of the ground and four lowest excited states along the a1 normal modes, i.e. with κ ≠ 0. The curvature of the ground electronic states is systematically overestimated, especially for low-frequency normal modes. While a deviation of the curvature of the electronic excited states from the ground states frequency, can be due to vibronic coupling between excited states, a deviation of the curvature of the ground state from the LVC model is a direct signature of anharmonicity. The RSMA analysis of Maleimide is shown in Fig. 2c and d. The normal mode exhibiting the largest ξ is mode ν21 that corresponds to a symmetric stretching of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O. The small ξ for non fully symmetric normal modes reflects the quasi-C2v symmetry of the four lowest excited state minima.
O. The small ξ for non fully symmetric normal modes reflects the quasi-C2v symmetry of the four lowest excited state minima.
While the GAP remains small, anharmonicity is clearly playing a role in these potentials. Consequently, to assess the effect of the anharmonicity especially on the excited state dynamics, we build two model diabatic Hamiltonians using the LVC approach and compare these to the Hamiltonians previously published by Worth et al.49 and constructed using a fitting procedure of the QVC approximation. The Hamiltonians include the lowest five singlet states, i.e. the ground and the four lowest excited states and either 6 or 12 normal modes, full details of the two Hamiltonian are given in Tables S25–S30 (ESI†).
Fig. 3 shows the population kinetics along the dynamics using the Hamiltonians containing 6 (dashed lines) and 12 (full lines) normal modes. In both cases, the simulations are initiated with the wavepacket vertically excited from the ground state geometry vertically into the S3 state. In the 6-modes model, ultrafast population from S3 to S2 is observed within 10 fs. The population then oscillates between the S3 and S2 states as there are no normal modes present which couple these states to the lowest S1 state. S4 is only marginally populated through the dynamics as it can only receive population from the energetically distant S2 and S1 as the S3 state is of same symmetry as S4 (A1) and therefore coupling is symmetry forbidden. In the 12-modes dynamics, the initial population transfer from S3 to S2 is still observed, but due to the inclusion of b2 mode Q20, population within S2 is quickly transferred into the S1 state. As before, S4 receives only a very small amount of population. An equilibrium between the three (S1, S2 and S3) states is reached within 50 fs with the S2 and S3 state both exhibiting ≃15% of the total population each, reflecting their near degeneracy.
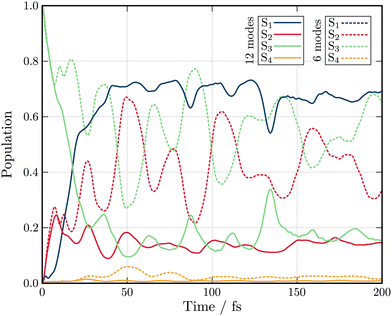 | ||
| Fig. 3 Excited state population dynamics of maleimide after excitation in S3 (1B2) state. The two models include 6 (dashed lines) and 12 (full lines) nuclear degrees of freedom. | ||
Both the 6- and 12-modes dynamics offer good agreement with dynamics reported by Worth et al.49 using the QVC approach. For the 6 model model, small differences are observed in the frequency of the oscillations observed between the S3 and S2 states which are slightly slower and larger in amplitude than those observed within the QVC approach.49 In the 12 mode model, similar differences are observed, especially in the oscillations in the population of the S1 state. While this observation could justify the usage of the LVC model for the construction of the model Hamiltonian, the topology of the excited states must be investigated.
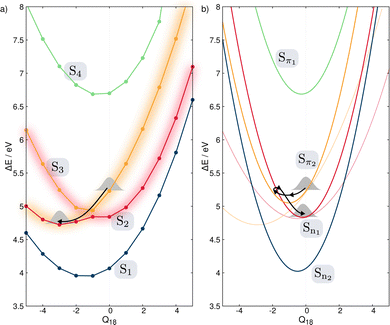
Fig. 4 shows the comparison between the computed adiabatic and the diabatic potential energy curves built using the LVC approach of S1 to S4 along normal mode Q18. This normal mode is especially important for the dynamics as it creates a conical intersection (CI) between the PES of S2 and S3. The topology of the CI (Fig. 4a) obtained from the calculated adiabatic excited state energies is peaked72,73 and consequently, a wavepacket passing through the CI originating from the FC region would end up in the minimum of diabatic state with a similar nature according to the Landau–Zener principle.74,75 In contrast the LVC potential (Fig. 4b) along this mode generates a CI topology which is sloped.72,73 Consequently, a wavepacket would end up in a different minimum exhibiting different character and dynamics. This is highlighted in Fig. 4 where the schematic arrows represent the main direction of the wavepacket upon relaxation. This emphasises that while the population kinetics of the LVC model may appear unchanged compared to a higher order expansion, suggesting that a GAP of ∼10% corresponds to a valid LVC, care must be already be taken during the interpretation of these dynamics that the similarity observed in the populations kinetics occurs for the same reason. Indeed, while quantities such as population kinetics are useful, a more rigorous assessment of the accuracy of a potential energy surface is often achieved by calculating observables such as absorption spectra. Fig. 5 shows the second absorption band of Maleimide obtained by the Fourier transform of the autocorrelation function of a wavepacket initially placed in S4. It is compared to the experimental spectrum49 and the spectrum obtained with the 12 modes Hamiltonian in ref. 49. While the spectrum obtained within the LVC approximation shows qualitative agreement with the spectrum obtained from Worth et al. it fails to reproduce the relative intensity between the peaks. The absorption peaks are also sightly shifted and the Gaussian envelope of the absorption band is not well reproduced. This can be attributed to the absence of anharmonicity in the LVC model. In this case, the calculated spectra incorporates peaks >0.5 eV above the absorption band onset, where anharmonicity will play an increasing important role, this is highlighted by the disagreement between the experimental and both calculated spectra with appears to increase with energy.
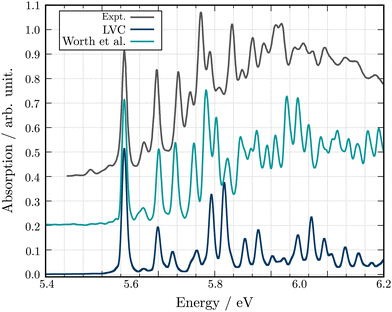 | ||
| Fig. 5 Experimental and theoretical absorption spectra for the second excitation band of Maleimide. The spectra obtained in this work is shown in blue. The spectrum extracted from the 12 modes dynamics of ref. 49 is shown in turquoise. All spectra have been shifted and scaled to align the first absorption peak in position and intensity to the experimental value. | ||
4 Conclusion
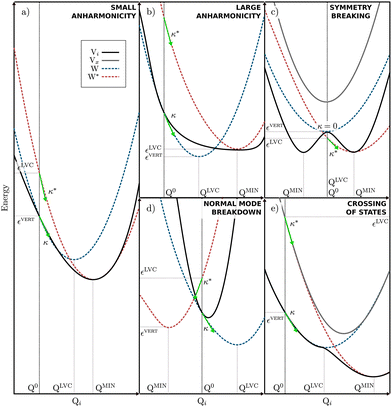
Quantum dynamics simulations are a key theoretical tool for describing processes occurring in electronically excited states, but one of the key challenges for these simulations is obtaining an accurate description of the high-dimensional excited state PES upon which the nuclei evolve. The LVC model is a very compact and efficient model which can be parameterised from relatively few quantum chemistry calculations. However, despite these advantages, the model is based upon coupled-shifted Harmonic oscillators and therefore its validity will be severely tested when larger amplitude motions are present in the excited state dynamics.For clarity shows some limiting cases of the LVC are shown in Fig. 6. Initially, Fig. 6a illustrates a situation where the LVC approach will remain valid; i.e where small anharmonicity of the potential that leads to a small Ξ. In contrast Fig. 6b–e shows four cases that will lead to a large Ξ and the breakdown of the LVC approach, namely (b) a large anharmonicity of the potential, (c) a symmetry breaking in the excited states, (d) a breakdown of the normal mode representation, i.e. the normal modes change nature between the FC and the excited state minimum geometries, and (e) the crossing of electronic states.
In this paper we have introduced and tested a metric, the Global Anharmonicity Parameter (GAP), which can be used to assess the accuracy of an LVC potential. This is based upon assessing the differences between the intrastate coupling constant, κ which can be calculated in two ways. If both yield the same results, the harmonic approximation upon which the LVC is based is valid. We have assessed the performance of this metric using three molecules, namely TBPe, TAT-3DBTO2 and Maleimide. The first two illustrate two clear examples when the LVC is valid and breakdowns, respectively. The potential for Maleimide illustrates an interesting case. Indeed, it displays a relatively small GAP, ∼10% and the excited state dynamics calculated using the LVC potential is in good agreement with those previously obtained using the QVC approach:49 However, the approximations made in the LVC change the nature of the interaction between the coupled states meaning that although the population dynamics remains very similar to higher level approaches, the mechanism leading to the dynamics is different.
In conclusion, we have demonstrated that the GAP is a useful metric for assessing the validity of the LVC approximation. From the present work, it appears that a GAP of ≥10% means any simulations using the LVC should be treated with caution. The validity of the LVC and impact of the corresponding GAP value can be assessed by calculating experimental observables, such as absorption spectra. Although further work on a broader range of systems would be required to provide insights into the effect of the magnitude of this metric, this provides an important basis for future works using the LVC approximation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
JE would like to thank Dr Thomas J. Pope, Dr Conor D. Rankine and Clelia Middleton for helping with the beta test of VCMaker. The authors would like to acknowledge the EPSRC for funding via project EP/T022442/1 and EP/V010573/1.References
- J. Gibson, A. P. Monkman and T. J. Penfold, ChemPhysChem, 2016, 17, 2956–2961 CrossRef CAS PubMed.
- T. Northey and T. Penfold, Org. Electron., 2018, 59, 45–48 CrossRef CAS.
- H. Tamura and I. Burghardt, J. Am. Chem. Soc., 2013, 135, 16364–16367 CrossRef CAS PubMed.
- H. Tamura and I. Burghardt, J. Phys. Chem. C, 2013, 117, 15020–15025 CrossRef CAS.
- H. Tamura, I. Burghardt and M. Tsukada, J. Phys. Chem. C, 2011, 115, 10205–10210 CrossRef CAS.
- M. H. Beck, A. Jäckle, G. A. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef CAS.
- H.-D. Meyer, F. Gatti and G. A. Worth, Multidimensional quantum dynamics: MCTDH theory and applications, John Wiley & Sons, 2009 Search PubMed.
- J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562–572 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- T. J. Martinez, M. Ben-Nun and R. Levine, J. Phys. Chem. A, 1996, 100, 7884–7895 CrossRef CAS.
- M. Ben-Nun and T. J. Martnez, J. Chem. Phys., 1998, 108, 7244–7257 CrossRef CAS.
- D. V. Shalashilin and M. S. Child, Chem. Phys., 2004, 304, 103–120 CrossRef CAS.
- D. V. Shalashilin, J. Chem. Phys., 2009, 130, 244101 CrossRef PubMed.
- D. V. Makhov, W. J. Glover, T. J. Martinez and D. V. Shalashilin, J. Chem. Phys., 2014, 141, 054110 CrossRef PubMed.
- G. Richings, I. Polyak, K. Spinlove, G. Worth, I. Burghardt and B. Lasorne, Int. Rev. Phys. Chem., 2015, 34, 269–308 Search PubMed.
- G. Christopoulou, A. Freibert and G. A. Worth, J. Chem. Phys., 2021, 154, 124127 CrossRef CAS PubMed.
- E. J. Heller, J. Chem. Phys., 1975, 62, 1544–1555 CrossRef CAS.
- E. J. Heller, J. Chem. Phys., 1981, 75, 2923–2931 CrossRef CAS.
- S.-Y. Lee and E. J. Heller, J. Chem. Phys., 1982, 76, 3035–3044 CrossRef CAS.
- B. F. Curchod and T. J. Martnez, Chem. Rev., 2018, 118, 3305–3336 CrossRef CAS PubMed.
- R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026–7068 CrossRef CAS PubMed.
- O. Vendrell, F. Gatti, D. Lauvergnat and H.-D. Meyer, J. Chem. Phys., 2007, 127, 184302 CrossRef PubMed.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577–606 Search PubMed.
- J. M. Bowman, G. Czako and B. Fu, Phys. Chem. Chem. Phys., 2011, 13, 8094–8111 RSC.
- B. F. Curchod, U. Rothlisberger and I. Tavernelli, ChemPhysChem, 2013, 14, 1314–1340 CrossRef CAS PubMed.
- H. Köppel, W. Domcke and L. S. Cederbaum, Conical Intersections, 2004, 323–367 Search PubMed.
- L. S. Cederbaum, H. Köppel and W. Domcke, Int. J. Quantum Chem., 2009, 20, 251–267 CrossRef.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed.
- S. Thompson, J. Eng and T. Penfold, J. Chem. Phys., 2018, 149, 014304 CrossRef CAS PubMed.
- Y. Harabuchi, J. Eng, E. Gindensperger, T. Taketsugu, S. Maeda and C. Daniel, J. Chem. Theory Comput., 2016, 12, 2335–2345 CrossRef CAS PubMed.
- J. P. Zobel, M. Heindl, F. Plasser, S. Mai and L. González, Acc. Chem. Res., 2021, 54, 3760–3771 CrossRef CAS PubMed.
- S. Mai, P. Marquetand and L. González, J. Chem. Phys., 2014, 140, 204302 CrossRef PubMed.
- S. Gómez, M. Heindl, A. Szabadi and L. González, J. Phys. Chem. A, 2019, 123, 8321–8332 CrossRef PubMed.
- G. Capano, M. Chergui, U. Rothlisberger, I. Tavernelli and T. J. Penfold, J. Phys. Chem. A, 2014, 118, 9861–9869 CrossRef CAS PubMed.
- M. Pápai, G. Vankó, T. Rozgonyi and T. J. Penfold, J. Phys. Chem. Lett., 2016, 7, 2009–2014 CrossRef PubMed.
- J. P. Zobel, T. Knoll and L. González, Chem. Sci., 2021, 12, 10791–10801 RSC.
- G. Capano, T. Penfold, M. Chergui and I. Tavernelli, Phys. Chem. Chem. Phys., 2017, 19, 19590–19600 RSC.
- M. Pápai, T. J. Penfold and K. B. Møller, J. Phys. Chem. C, 2016, 120, 17234–17241 CrossRef.
- Q. Xu, D. Aranda, M. Yaghoubi Jouybari, Y. Liu, M. Wang, J. Cerezo, R. Improta and F. Santoro, J. Phys. Chem. A, 2022, 126, 7468–7479 CrossRef CAS PubMed.
- M. Y. Jouybari, J. A. Green, R. Improta and F. Santoro, J. Phys. Chem. A, 2021, 125, 8912–8924 CrossRef CAS PubMed.
- J. A. Green, M. Yaghoubi Jouybari, H. Asha, F. Santoro and R. Improta, J. Chem. Theory Comput., 2021, 17, 4660–4674 CrossRef CAS PubMed.
- F. Aleotti, D. Aranda, M. Yaghoubi Jouybari, M. Garavelli, A. Nenov and F. Santoro, J. Chem. Phys., 2021, 154, 104106 CrossRef CAS PubMed.
- D. Aranda and F. Santoro, J. Chem. Theory Comput., 2021, 17, 1691–1700 CrossRef CAS PubMed.
- Y. Giret, J. Eng, T. Pope and T. Penfold, J. Mater. Chem. C, 2021, 9, 1362–1369 RSC.
- J. Eng and T. J. Penfold, Chem. Record, 2020, 20, 831–856 CrossRef CAS PubMed.
- J. Eng and T. J. Penfold, Commun. Chem., 2021, 4, 1–4 CrossRef PubMed.
- P. L. Dos Santos, J. S. Ward, D. G. Congrave, A. S. Batsanov, J. Eng, J. E. Stacey, T. J. Penfold, A. P. Monkman and M. R. Bryce, Adv. Sci., 2018, 5, 1700989 CrossRef PubMed.
- J. Eng, J. Hagon and T. J. Penfold, J. Mater. Chem. C, 2019, 7, 12942–12952 RSC.
- A. Lehr, S. Gómez, M. A. Parkes and G. A. Worth, Phys. Chem. Chem. Phys., 2020, 22, 25272–25283 RSC.
- Y. Giret, J. Eng, T. Pope and T. Penfold, J. Mater. Chem. C, 2021, 9, 1362–1369 RSC.
- VCMAKER, 2022, http://github.com/JulienEng/VCMaker.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. ONeill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2014, 113, 184–215 CrossRef.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- M. A. Rohrdanz, K. M. Martins and J. M. Herbert, J. Chem. Phys., 2009, 130, 054112 CrossRef PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. Hariharan and J. Pople, Mol. Phys., 1974, 27, 209–214 CrossRef CAS.
- T. J. Penfold, J. Phys. Chem. C, 2015, 119, 13535–13544 CrossRef CAS.
- E. Livshits and R. Baer, Phys. Chem. Chem. Phys., 2007, 9, 2932 RSC.
- H. Sun, C. Zhong and J.-L. Brédas, J. Chem. Theory Comput., 2015, 11, 3851–3858 CrossRef CAS PubMed.
- J. Eng, B. A. Laidlaw and T. J. Penfold, J. Comput. Chem., 2019, 40, 2191–2199 CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- S. A. Ahmad, J. Eng and T. J. Penfold, J. Mater. Chem. C, 2022, 10, 4785–4794 RSC.
- T. J. Penfold and J. Eng, ChemPhotoChem, 2021, e202200243 Search PubMed.
- J. von Sonntag and W. Knolle, J. Photochem. Photobiol., A, 2000, 136, 133–139 CrossRef.
- C. Antczak, B. Bauvois, C. Monneret and J.-C. Florent, Bioorg. Med. Chem., 2001, 9, 2843–2848 CrossRef CAS PubMed.
- D. M. Davies, C. Murray, M. Berry, A. J. Orr-Ewing and K. I. Booker-Milburn, J. Org. Chem., 2007, 72, 1449–1457 CrossRef CAS PubMed.
- L. M. Tedaldi, A. E. Aliev and J. R. Baker, Chem. Commun., 2012, 48, 4725–4727 RSC.
- D. R. Yarkony, Rev. Mod. Phys., 1996, 68, 985–1013 CrossRef CAS.
- S. Matsika, Chem. Rev., 2021, 121, 9407–9449 CrossRef CAS PubMed.
- L. Landau and E. Lifshitz, in Perspectives in Theoretical Physics, ed. L. Pitaevski, Pergamon, Amsterdam, 1992, pp. 287–297 Search PubMed.
- C. Zener and R. H. Fowler, Proc. R. Soc. London, Ser. A, 1932, 137, 696–702 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05576g |
| This journal is © the Owner Societies 2023 |