Open Access Article
Open Access ArticleZinc borate glasses: properties, structure and modelling of the composition-dependence of borate speciation†
Brian
Topper
*ab,
Doris
Möncke
 a,
Randall E.
Youngman
a,
Randall E.
Youngman
 c,
Christina
Valvi
d,
Efstratios I.
Kamitsos
c,
Christina
Valvi
d,
Efstratios I.
Kamitsos
 e and
Christos P. E.
Varsamis
e and
Christos P. E.
Varsamis
 *d
*d
aInamori School of Engineering at the New York State College of Ceramics, Alfred University, 1 Saxon Drive, Alfred, NY 14802, USA. E-mail: topper3@unm.edu
bDepartment of Physics & Astronomy and Center for High Technology Materials, University of New Mexico, Albuquerque, NM 87131, USA
cScience and Technology Division, Corning Incorporated, Corning, New York 14831, USA
dApplied Physics Laboratory, Faculty of Engineering, University of West Attica, 250 Thivon, 112 41 Egaleo, Attica, Greece. E-mail: cvars@uniwa.gr
eTheoretical and Physical Chemistry Institute, National Hellenic Research Foundation, 48 Vassileos Constantinou Avenue, 11635 Athens, Greece
First published on 3rd February 2023
Abstract
The short-range order of binary zinc borate glasses, xZnO–(1−x)B2O3, has been quantitatively described as a function of ZnO content over the entire glass forming range for the first time, to the best of our knowledge. Multiple spectroscopic techniques (11B NMR, Raman, infrared) reveal detailed structural information regarding borate speciation and network connectivity, and a new model for quantifying the molar fractions of short-range order units is proposed. A consistent thermal history dependence for the fraction of tetrahedral boron (N4) is well accounted for by the proposed model. The model predicts density within 0.1% of experimental values and N4 to within 1% of NMR values. The intermediate character of four-coordinated zinc in borate glasses of this series is evident by the far infrared profiles and the glass transition temperature behavior, which decreases non-monotonically with increasing ZnO content.
1. Introduction
Zinc borate glasses constitute an interesting binary system because of their attractive properties, like high UV transmission (below 250 nm when made from pure starting materials) and good rare-earth solubility.1–3 Long fluorescent lifetimes of rare-earth dopants have been reported for relatively high concentrations of about 10 wt% RE2O3 (RE = Tb, Eu).2,3 From a chemical point of view, zinc borates present a peculiar case in that their conventional glass forming region begins at very high modifier contents (∼54 mol% ZnO). This is higher than any other binary MO–B2O3 system, where M is a divalent cation (Mg, Ca, Sr, Ba, Cd, and Pb).4 Moreover, recent structural studies indicate that zinc borate glasses exhibit a particularly rich landscape of borate motifs.5–7 These studies and the earlier work of Krogh–Moe8 show that the glass structure is distinctly different from that of the crystalline phase commonly referred to as zinc metaborate, 4ZnO–3B2O3.9 This compound is special in its own right because 4ZnO–3B2O3 contains an O2− ion that does not belong to the borate framework but, instead, to one of the modifying Zn2+ cations. Such instances are very rare in crystalline borates, with the two other known cases being 3Bi2O3–5B2O3 where there exists one ‘free’ O atom10 and 2Bi2O3–B2O3 where there exists three ‘free’ O atoms.11 Aside from these fundamentally intriguing attributes, zinc borate glasses have intrinsic potential for applications in that, despite glass formation beginning at high loads of ZnO, the glasses display good chemical and thermal stability.1,2The earliest studies of the ZnO–B2O3 binary system focused on a systematic mapping of the phase diagram, naturally providing insights into the glass forming range.12,13 Interestingly, liquid–liquid phase separation in the melt occurs for compositions near the 1ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1B2O3 ratio.12–15 The older literature often states that the first glass forms with ∼56 mol% ZnO (∼4ZnO–3B2O3), which may be just because the 4
1B2O3 ratio.12–15 The older literature often states that the first glass forms with ∼56 mol% ZnO (∼4ZnO–3B2O3), which may be just because the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio was typically the next batched molar ratio after the 1
3 ratio was typically the next batched molar ratio after the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio in the investigators’ iterations through the composition space.12,13 However, an early report by Hamilton et al. suggests that the onset of homogenous glass formation in the xZnO–(1 − x)B2O3 system is somewhere in the range 0.52 < x ≤ 0.55.15 After general phase diagram studies, the zinc–borate glass structure was investigated, and the early studies proposed borate speciation at odds with what recent spectroscopic data indicates. For example, Harris and Bray reported an 11B nuclear magnetic resonance (NMR) study in the early 1980s and proposed that there exist no asymmetric borate entities in the studied glasses.16 In NMR studies of borates, trigonal metaborate units and trigonal pyroborate units with 1 and 2 non-bridging oxygen atoms per boron, respectively, show different chemical shifts relative to the trigonal neutral or trigonal orthoborate units with 0 and 3 non-bridging oxygen atoms, respectively.17 The former units with a mixture of bridging and non-bridging oxygen atoms are referred to as asymmetric triangular units, while the latter with either all bridging or all non-bridging oxygen atoms are referred to as symmetric triangular units. This original assessment for no asymmetric borate entities throughout the glass forming range was questioned in a recent 11B magic angle spinning (MAS) NMR study of the x = 0 glass in the ternary system xLa2O3–(55 − x)ZnO–45B2O3,7 where deconvolution of the 11B MAS NMR spectrum for the 55ZnO–45B2O3 glass showed that about half of the trigonal borate units are actually asymmetric. It is noted that the pioneering study by Harris and Bray16 was rationally based on comparison of the zinc borate NMR data with that of lithium borate NMR data, and was interpreted in the context of Krogh-Moe's model of glass structure, where the short-range structure in the vitreous state is considered as a permutation of analogous crystalline phases. Given the timing of the early Harris and Bray report,16 the conclusions of the authors were scientifically sound. Even before the recent NMR work of Januchta et al.,7 polarized Raman spectra of RE3+:4ZnO–3B2O3 glass suggested the presence of pyroborate dimers, (B2O5).18
1 ratio in the investigators’ iterations through the composition space.12,13 However, an early report by Hamilton et al. suggests that the onset of homogenous glass formation in the xZnO–(1 − x)B2O3 system is somewhere in the range 0.52 < x ≤ 0.55.15 After general phase diagram studies, the zinc–borate glass structure was investigated, and the early studies proposed borate speciation at odds with what recent spectroscopic data indicates. For example, Harris and Bray reported an 11B nuclear magnetic resonance (NMR) study in the early 1980s and proposed that there exist no asymmetric borate entities in the studied glasses.16 In NMR studies of borates, trigonal metaborate units and trigonal pyroborate units with 1 and 2 non-bridging oxygen atoms per boron, respectively, show different chemical shifts relative to the trigonal neutral or trigonal orthoborate units with 0 and 3 non-bridging oxygen atoms, respectively.17 The former units with a mixture of bridging and non-bridging oxygen atoms are referred to as asymmetric triangular units, while the latter with either all bridging or all non-bridging oxygen atoms are referred to as symmetric triangular units. This original assessment for no asymmetric borate entities throughout the glass forming range was questioned in a recent 11B magic angle spinning (MAS) NMR study of the x = 0 glass in the ternary system xLa2O3–(55 − x)ZnO–45B2O3,7 where deconvolution of the 11B MAS NMR spectrum for the 55ZnO–45B2O3 glass showed that about half of the trigonal borate units are actually asymmetric. It is noted that the pioneering study by Harris and Bray16 was rationally based on comparison of the zinc borate NMR data with that of lithium borate NMR data, and was interpreted in the context of Krogh-Moe's model of glass structure, where the short-range structure in the vitreous state is considered as a permutation of analogous crystalline phases. Given the timing of the early Harris and Bray report,16 the conclusions of the authors were scientifically sound. Even before the recent NMR work of Januchta et al.,7 polarized Raman spectra of RE3+:4ZnO–3B2O3 glass suggested the presence of pyroborate dimers, (B2O5).18
Recently, in a comprehensive overview of metaborate glasses, Möncke et al. identified the signature of boroxol rings and pyroborate species in the Raman spectrum of vitreous 55ZnO–45B2O3.6 This was explained by the disproportionation at the metaborate equilibrium into neutral and highly charged borate species, 2(BØ2O)− ⇌ (BØ3)0+ (BØO2)2− (where Ø = bridging oxygen and O = non-bridging oxygen), which was also invoked for the ZnO-rich side of the ternary glasses (50−x)ZnO–xCuO–50B2O3.5 Such behavior was observed earlier in magnesium borate glasses,19,20 and it is not surprising since Mg2+ and Zn2+ cations have comparable field strength. These high field strength divalent cations need for their coordination the high negative charge offered by bidentate ligands, such as the two non-bridging oxygen atoms of trigonal pyroborate species.
While the NMR data of Harris and Bray showed a clear decrease in tetrahedral boron–oxygen units with increasing zinc oxide content, the Raman spectra reported in a later review on borate glass structure were interpreted as indicating that zinc borate glasses with varying ZnO content have similar structures.21 Nowadays, advances in instrumentation have allowed more systematic structural investigations of borate glasses with a variety of complementary techniques including infrared (IR),20,22 Raman,23–25 NMR,26,27 UV-Visible,1 photoluminescence,3 electron paramagnetic resonance,28 X-ray diffraction (XRD),29,30 and neutron scattering.31 Despite these efforts and many others on borate glasses, a consistent description of the composition-dependence of the structure of zinc borate glasses is missing in the literature.
The key purpose of this work is to quantify borate speciation as a function of ZnO content. To this aim, we first reassess the glass forming range by melting batches of the composition xZnO–(1−x)B2O3 over the interval x = 0.50 to x = 0.73. The upper and lower limits in the glass-forming range are determined and then glasses in the entire glass-forming region are characterized in detail. The density is measured for bulk homogenous glass samples in their quenched and annealed states, and the corresponding molar volumes are calculated. Spectroscopic techniques including 11B MAS NMR, Raman scattering, and IR reflectance are employed to probe the evolution of the structural landscape with varying zinc oxide content. In parallel to a detailed spectroscopic analysis, chemical equilibria governing the observed borate speciation are employed to explicitly describe the borate network structure as a function of the ZnO mole fraction, x. Also, we have developed a model which agrees very well with results from spectroscopy, and which accurately predicts the density for a given composition x, and elucidates the role of zinc oxide as glass modifier and intermediate type oxide.32,33
2. Short-range order configuration (SROC) model
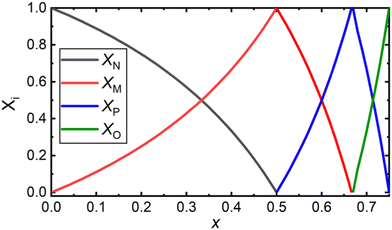
Unique to glasses, in comparison to crystals, is the ability to change continuously the composition within a glass-forming region. By their nature, crystals demand a precise molar ratio of their constituents for the manifestation of long-range order (>20 Å, “LRO”) – the absence of which is of course characteristic of the amorphous state. This missing constraint permits vitreous materials to be formed, where the short-range order (<5 Å, “SRO”) may consist of a mixture of structures of both the less- and the more-modified crystalline counterparts. Take as an example the case of a binary mixture of a metal-modifying oxide (MO) and a glass-forming oxide (GFO) for which there exist crystalline phases of the type MO–3GFO (25MO–75GFO, in mol%) and MO–GFO (50MO–50GFO, in mol%) and there is a continuous glass forming region between the compositions of these crystalline phases. In practice, if one were to look at the glass with composition e.g., 39MO–61GFO (or any other non-stoichiometric ratio in the range), most often one would consider a combination of structural units available to the less-modified MO–3GFO and to the more-modified MO–GFO compositions (i.e., the lever rule). In this way, the chemical equilibria related to the adjacent crystalline phases may be regarded as bounds of the SRO of the resulting glass. The accessible equilibria, not necessarily the exact structure of the crystalline analogue, is an important distinction because glasses often display isomerization and disproportionation of chemical species, which can be accounted for at crystalline points in composition space by mass and charge balance considerations.With this notion in mind, we will construct a general model for the structure of borate glasses. Frequently occurring crystalline phases in binary borates with MO content ≥50 mol% and distinctly different SRO are the metaborate (1MO–1B2O3), the pyroborate (2MO–1B2O3) and the orthoborate (3MO–1B2O3).4 It should be noted that alkali borates have a rather large number of crystalline phases below the metaborate composition, often characterized by their unique intermediate range order (IRO) and superstructural units, which may subsequently serve as additional nodes that would need to be considered. In any case, the SRO of any composition below metaborate (<50 mol% MO) can be considered as involving metaborate units, either tetrahedral or triangular, (BØ4)− ⇌ (BØ2O)− = (BO2)−, and neutral borate triangles, (BØ3)0 = (BO1.5)0.
Since we set out first to find a general formula of a palatable size, we consider only the modification levels of meta-, pyro-, and ortho-borate compositions. For a borate system of composition xMO–(1−x)B2O3, the SRO units will be classified as neutral N (x = 0.0, (BO1.5)0, O:B = 1.5), metaborate M (x = 0.50, (BO2)−, O:B = 2), pyroborate P (x = 0.67, (BØO2)2− = (BO2.5)2−, O:B = 2.5), and orthoborate O (x = 0.75, (BO3)3−, O:B = 3). The corresponding molar fractions should satisfy the mass balance equation:
X![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) (x) + X (x) + X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x) + X (x) + X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x) + X (x) + X![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) (x) = 1 (x) = 1 | (1) |
For simplicity, we assume that:
X![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) (x = 0.0) = X (x = 0.0) = X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x = 0.50) = X (x = 0.50) = X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x = 0.67) = X (x = 0.67) = X![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) (x = 0.75) = 1 (x = 0.75) = 1 | (2) |
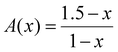 | (3) |
X![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) (x) +X (x) +X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x) = 1 (x) = 1 | (4) |
1.5X![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) (x) + 2X (x) + 2X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x) = A(x) (x) = A(x) | (5) |
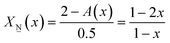 | (5a) |
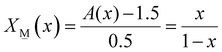 | (5b) |
X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x) + X (x) + X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x) = 1 (x) = 1 | (6) |
2X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x) + 2.5X (x) + 2.5X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x) = A(x) (x) = A(x) | (7) |
![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x) and X
(x) and X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x):
(x):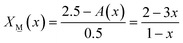 | (7a) |
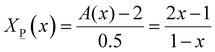 | (7b) |
X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x) + X (x) + X![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) (x) = 1 (x) = 1 | (8) |
2.5X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x) + 3X (x) + 3X![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) (x) = A(x) (x) = A(x) | (9) |
![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x) and X
(x) and X![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) (x) can be obtained as follows:
(x) can be obtained as follows: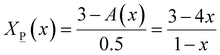 | (9a) |
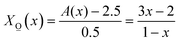 | (9b) |
The composition dependence of the molar fractions of neutral, meta-, pyro- and ortho-borate species evaluated from eqn (5a), (5b), (7a), (7b), (9a) and (9b) is presented in Fig. 1. However, as discussed in the introduction, it is known from experimental observations that in zinc borate glasses there exist N species above x = 0.50, indicating that the SRO structure cannot be accurately described in such glasses by the relations in Fig. 1. To resolve this issue, we extend the above approach by assuming that the curves of Fig. 1 represent the normalized contributions of the particular short-range order configurations (SROCs) in binary borate glasses, xMO–(1−x)B2O3, with x = 0 (X![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) ), x = 0.5 (X
), x = 0.5 (X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ), x = 0.67 (X
), x = 0.67 (X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ) and x = 0.75 (X
) and x = 0.75 (X![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) ), and use them to describe the SRO structure of any intermediate glass composition. In that sense, it is obvious that for x = 0 the corresponding SROC consists exclusively of neutral borate triangles, (BØ3)0. To give an example, for borate glass with x = 0.4, where X
), and use them to describe the SRO structure of any intermediate glass composition. In that sense, it is obvious that for x = 0 the corresponding SROC consists exclusively of neutral borate triangles, (BØ3)0. To give an example, for borate glass with x = 0.4, where X![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) = 0.33 and X
= 0.33 and X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) = 0.67 from Fig. 1, we assume that its SRO structure is a linear combination of the SROCs of glasses with x = 0 and x = 0.5 with coefficients X
= 0.67 from Fig. 1, we assume that its SRO structure is a linear combination of the SROCs of glasses with x = 0 and x = 0.5 with coefficients X![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) = 0.33 and X
= 0.33 and X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) = 0.67, respectively.
= 0.67, respectively.
In order to formulate our model, we can envision a 5-dimensional vector space where the basis is the set of the short-range order building units which are denoted as Bj where j is the number of bridging oxygen atoms per boron atom (j = 0, 1, 2, 3, 4). For a particular composition, i.e., the metaborate one where x = 0.50 and X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) = 1, the short-range order configuration, M, is a linear combination of the borate species denoted as Bj:
= 1, the short-range order configuration, M, is a linear combination of the borate species denoted as Bj:
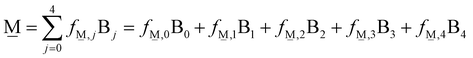 | (10) |
![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,j in our model denotes the components of the
,j in our model denotes the components of the ![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) vector in the Bj basis. Equivalently, we can represent the vector
vector in the Bj basis. Equivalently, we can represent the vector ![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) with its components, in the usual notation
with its components, in the usual notation ![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) = (f
= (f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,0,f
,0,f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,1,f
,1,f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,2,f
,2,f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,3,f
,3,f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,4). It is worthwhile noting that
,4). It is worthwhile noting that 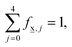 for any glass composition
for any glass composition ![[x with combining low line]](https://www.rsc.org/images/entities/char_0078_0332.gif) , and that f
, and that f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,j specifically coincides with the molar fractions of the borate units for the glass having the metaborate composition. The decomposition of the
,j specifically coincides with the molar fractions of the borate units for the glass having the metaborate composition. The decomposition of the ![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) vector is illustrated in Scheme 1, assuming that ∀j,f
vector is illustrated in Scheme 1, assuming that ∀j,f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,j = 0.2, a value that is simply selected for visualization.
,j = 0.2, a value that is simply selected for visualization.
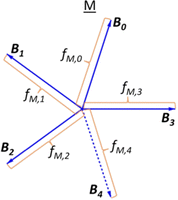 | ||
Scheme 1 Hypothetical short-range order metaborate, ![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) , configuration (SROC) where fM,j are all of equal length. , configuration (SROC) where fM,j are all of equal length. | ||
Since in the proposed model we consider only the SROCs of meta-, pyro-, and ortho-borate glasses, the interval [0,0.75) of x is divided into 3 distinct subintervals, I with x ∈ [0,0.5), II with x ∈ [0.5,0.67) and III with x ∈ [0.67,0.75). In region I contribute SROCs of type N and M, in region II contribute SROCs of type M and P, whereas in region III contribute SROCs of type P and O. With these constraints, it is always possible to evaluate the molar fraction of each particular borate entity Bj, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) j, at any value of x with the following equations:
j, at any value of x with the following equations:
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) j(x) = f j(x) = f![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) ,jX ,jX![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) + f + f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,jX ,jX![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) for 0.0 ≤ x < 0.5 for 0.0 ≤ x < 0.5 | (11a) |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) j(x) = f j(x) = f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,jX ,jX![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) + f + f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,jX ,jX![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) for 0.5 ≤ x < 0.67 for 0.5 ≤ x < 0.67 | (11b) |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) j(x) = f j(x) = f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,jX ,jX![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) + f + f![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) ,jX ,jX![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) for 0.67 ≤ x < 0.75 for 0.67 ≤ x < 0.75 | (11c) |
In the proposed model, the task at hand is then to resolve the coefficients, i.e. the array of fq,j values, for each borate unit j within each SROC q, where q ∈ {![[N with combining low line]](https://www.rsc.org/images/entities/char_004e_0332.gif) ,
,![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,
,![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,
,![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) }. In other words, one has to evaluate from experimental or theoretical investigations the borate speciation for the meta-, pyro- and ortho-borate glass compositions. Knowledge of the explicit fq,j values will then allow, in the framework of the introduced model, a direct evaluation of the short-range order structure of any glass composition.
}. In other words, one has to evaluate from experimental or theoretical investigations the borate speciation for the meta-, pyro- and ortho-borate glass compositions. Knowledge of the explicit fq,j values will then allow, in the framework of the introduced model, a direct evaluation of the short-range order structure of any glass composition.
To illustrate an example, for the glass 0.63MO–0.37B2O3 we have A(x) = 2.35 (eqn (3)) and so X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x) = 0.3 (eqn (7a)) and X
(x) = 0.3 (eqn (7a)) and X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x) = 0.7 (eqn (7b)) indicating the borate speciation should be the combination of the appropriately weighted SROCs M and P as 0.3
(x) = 0.7 (eqn (7b)) indicating the borate speciation should be the combination of the appropriately weighted SROCs M and P as 0.3![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) + 0.7
+ 0.7![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) . Now, if we assume that from experiment it is known that, M = f
. Now, if we assume that from experiment it is known that, M = f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,2B2 + f
,2B2 + f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,4B4 = 0.5B2 + 0.5B4 (Scheme 2a) and P = f
,4B4 = 0.5B2 + 0.5B4 (Scheme 2a) and P = f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,2B2 + f
,2B2 + f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,1B1 + f
,1B1 + f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,0B0 = 0.2B2 + 0.6B1 + 0.2B0 (Scheme 2b) then the short-range structure at x = 0.63 would consist of:
,0B0 = 0.2B2 + 0.6B1 + 0.2B0 (Scheme 2b) then the short-range structure at x = 0.63 would consist of:
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 0(x) = X 0(x) = X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x)f (x)f![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) ,2 + X ,2 + X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x)f (x)f![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) ,2 = 0 + 0.7 × 0.2 = 0.14 ,2 = 0 + 0.7 × 0.2 = 0.14 |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1(x) = X 1(x) = X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x)f (x)f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,1 + X ,1 + X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x)f (x)f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,1 = 0 + 0.7 × 0.6 = 0.42 ,1 = 0 + 0.7 × 0.6 = 0.42 |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2(x) = X 2(x) = X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x)f (x)f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,2 + X ,2 + X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x)f (x)f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,2 = 0.30 × 0.5 + 0.7 × 0.2 = 0.29 ,2 = 0.30 × 0.5 + 0.7 × 0.2 = 0.29 |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 3(x) = 0 3(x) = 0 |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 4(x) = X 4(x) = X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x)f (x)f![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,4 + X ,4 + X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x)f (x)f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,4 = 0.3 × 0.5 + 0 = 0.15 ,4 = 0.3 × 0.5 + 0 = 0.15 |
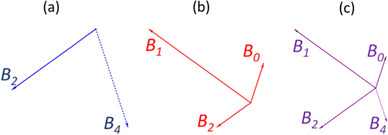 | ||
| Scheme 2 Example of the linear combination of primary SROCs M (a) and P (b) into an intermediary SROC (c) formed by the appropriately weighted sum of M and P, for the example described in the text. | ||
In this formulation, there is no strict limit on how many partitions the composition interval is divided into. Considering this, if one were to apply this to say the lithium borate system, the need to invoke additional divisions as in eqn (2) could be encountered, such as a diborate and/or pentaborate division. Regardless, a limited number of divisions are presented here to avoid unnecessary convolution and for a concise theoretical representation. Another motivation lies in the fact that the investigated Zn–borate glass family is characterized by a limited glass forming range in the interval x = [0.54,0.7].
It is important to note that this approach is valid only when the metal oxide assumes exclusively the role of a modifier in the chemical viewpoint of glass formation, and not when a modifier and network-forming role is possible, as in the case of bismuth oxide.34 The main advantage of our model is that only a limited number of glass compositions have to be analyzed in the whole glass forming range. This implies that a lower number of adjustable free parameters are required to determine the SRO as a function of composition, compared to previous infrared studies,22,35 where a deconvolution of infrared spectra into Gaussian component bands was adopted. Finally, this model can be easily extended to any glass family, like silicate, phosphate or germanate. It is underlined, though, that our approach still relies on accurate experimental data as input. Next, a detailed experimental study of the binary zinc borate system will be presented and then the model will be applied to the results obtained for the short-range order of these glasses.
3. Experimental
3.1. Glass preparation
Binary zinc borate glasses of the composition xZnO–(1−x)B2O3 were prepared by the traditional melt-quench method using as starting materials B2O3 (99.98% metals basis) and ZnO (99.9% metals basis). Stoichiometric 10 gram batches were mixed for several minutes using a pestle and mortar and transferred to a platinum crucible. The platinum crucible was then placed in a Carbolite furnace with SiC elements equilibrated at 1150 °C. After 15 minutes in the furnace, the crucible was removed and quickly swirled to promote homogenization followed by casting a small portion of the melt followed by splat quenching between two preheated metal plates. The crucible was placed back in the furnace for 5 additional minutes and then the melt was cast into a cylindrical metal mold of approximately 1 cm diameter. The samples were removed from the mold while warm and annealed at 520 °C for 1 hour. The annealing furnace was then turned off and allowed to cool slowly to room temperature. The annealed cylinders were cut into discs with thickness of less than 1 mm using a slow speed diamond saw, polished by hand with polycrystalline diamond suspension, and then dry-polished by hand as the last stage.3.2. Glass characterization
XRD measurements were taken to confirm the amorphous nature of the glass using a Bruker D2 Diffractometer with a coupled two theta scan carried out over the range from 5° to 75° with a step size of 0.02° at a rate of 1 s per step. Density measurements were obtained by the Archimedes method using kerosene as the immersion fluid. Each glass was measured 3 times and the resulting general uncertainty was ±0.001 g cm−3. Glass transition temperatures (Tg) were measured by differential scanning calorimetry (DSC) using platinum pans on a TA Instrument SDT600 DSC TGA over the temperature range 20 to 1150 °C with a heating rate of 20 °C min−1. The reported Tg values correspond to the onset of the glass transition event as identified by the intercept method and are accompanied by an estimated error of ±2 °C.11B MAS NMR measurements were made using an Agilent DD2 spectrometer in conjunction with a 16.4 T Agilent 700/54 Premium Shielded superconducting magnet, resulting in a 11B resonance frequency of 224.52 MHz. Glasses were powdered with an agate mortar and pestle, and immediately loaded into a 3.2 mm zirconia rotor for computer-controlled sample spinning at 20.0 kHz using dry, compressed nitrogen. MAS NMR data were acquired under direct polarization, using a combination of a short radio-frequency pulse width of 0.6 μs (π/12 tip angle), a 5 s recycle delay and averaging of nominally 1000 acquisitions. 11B MAS NMR data were processed in VnmrJ software (Agilent) without apodization and frequency referenced to a secondary shift standard of aqueous boric acid at 19.6 ppm relative to BF3–etherate. NMR spectra were fitted using DMFit,36 with 2nd-order quadrupolar lineshapes (Q_MAS) for BO3 resonances and mixed Gaussian/Lorentzian functions for BO4 resonances. Multiple BO3 resonances were required to adequately reproduce the trigonal boron signal and were qualitatively confirmed in 11B triple-quantum magic-angle spinning (3QMAS) NMR experiments (see below). In order to achieve meaningful and physically realistic populations for two trigonal boron sites, each was fitted using typical values for the quadrupolar coupling constant (CQ = 2.65 MHz), identical Gaussian line broadening, and quadrupolar asymmetry parameters (η) consistent with symmetric and asymmetric BO3 units.37,38 The latter parameter is most sensitive to changes in the symmetry of BO3 triangles. For symmetric BO3 resonances, the quadrupolar asymmetry parameter was fixed at η = 0.2, as is common for these sites in B-containing glasses. In the fitting of the second BO3 resonance, η was allowed to vary, ultimately reaching values in the range of 0.5 to 0.55. To accurately determine the fraction of boron in four-fold coordination,34 a small correction to the BO4 peak area was made by fitting the first set of satellite transition spinning sidebands to estimate the contribution from the hidden sideband under the central transition peak near 0 ppm.39
11B 3QMAS NMR data were collected at 16.4 T using a hypercomplex 3QMAS pulse sequence with a Z filter,40 using the same spectrometer and probe as above. The solid π/2 and 3π/2 pulse widths were optimized to 1.2 and 3.3 μs, respectively. A lower power π/2 pulse width of 20 μs was used as the soft reading pulse of the Z filter, following a storage period of 50 μs (one rotor cycle). 11B 3QMAS NMR spectra were typically obtained using 120 to 480 acquisitions at each of 80 to 128 t1 points, with a recycle delay of 0.2 s. These data were Fourier Transformed and sheared with commercial software, incorporating line broadening of 50 and 25 Hz in the MAS and isotropic dimensions, respectively. The 11B frequency was referenced to an external secondary standard of aqueous boric acid at 19.6 ppm. Isotropic projections were made by projecting the 2D datasets onto the isotropic shift axis. Curve fitting of the BO3 region of the isotropic projections was performed with two or three Gaussian peaks of similar width, providing semi-quantitative confirmation of trigonal boron speciation and their populations as obtained from analysis of the 11B MAS NMR spectra.
Raman spectra were measured in backscattering configuration on a WITech Alpha300 using a 488 nm excitation source at 20 mW power with a 50× objective and 600 g mm−1 grating over the range of approximately 90–4300 cm−1. The spectra reported are the average of 25 accumulations of measurements with 5 second integration times to provide a high signal-to-noise ratio. The spectral resolution was about 10 cm−1. Raman spectra were processed with a temperature reduction41 and then area normalized. Infrared spectra were measured in reflectance mode at a quasi-normal incidence using a dry air purge Bruker Invenio R interferometer. To obtain high quality frequency-dependent spectra, R(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ), especially in the FIR, 800 scans over the range 30–6000 cm−1 were recorded with a resolution of 4 cm−1. Absorption spectra were found by performing Kramers–Kronig analysis on the measured reflectance spectra. After extrapolating the R(
), especially in the FIR, 800 scans over the range 30–6000 cm−1 were recorded with a resolution of 4 cm−1. Absorption spectra were found by performing Kramers–Kronig analysis on the measured reflectance spectra. After extrapolating the R(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) spectra to 0 and ∞, Kramers–Kronig transformations (KKT) were performed using the Bruker OPUS software to yield the real and imaginary parts of the complex refractive index, n(
) spectra to 0 and ∞, Kramers–Kronig transformations (KKT) were performed using the Bruker OPUS software to yield the real and imaginary parts of the complex refractive index, n(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) and k(
) and k(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ), respectively, where
), respectively, where ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the frequency in cm−1. The infrared absorption coefficient is then computed via α(
is the frequency in cm−1. The infrared absorption coefficient is then computed via α(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) = 4π
) = 4π![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) k(
k(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ).
).
4. Results
4.1. Glass forming range
Homogenous, bulk glasses were found to form between x = 0.54 and x = 0.65 (Fig. S1, ESI†). The melt consisting of 50 mol% ZnO was observed to undergo liquid–liquid phase separation and the initial cast yielded a mixture of transparent glass and an opalescent material. Raman spectroscopy on these two regions identified the opalescent material as a mixture of pure B2O3 glass and boric acid, B(OH)3, in agreement with XRD studies by Ehrt2 (Fig. 2a, “x = 0.5 opalescent”). B2O3 glass was identified by its characteristic sharp, high intensity band at 808 cm−1 belonging to the ring breathing mode of the boroxol ring,42 a planar ring consisting of three boron atoms and three oxygen atoms, which in vitreous boron oxide accounts for the arrangement of roughly 75% of all boron atoms.31 In addition to the presence of the boroxol rings, characteristic of glassy boron oxide is the weak B–O stretching activity observed at about 1265 cm−1.42 Three bands expected to be useful in the identification of B(OH)3 units are present. Most visible is the intense sharp band at 886 cm−1 belonging to the symmetric stretching of orthoboric acid units, B(OH)3.42–44 Less intense are bands at 503 cm−1 attributable to the O–B–O bending of the same species and activity at 1171 cm−1 arising from the bending of B–O–H segments.43,44 In the high frequency region, various B–O stretching modes of trigonal boron units in and out of boroxol rings in pure B2O3 comprise a weak envelope that spans from the medium intensity band at 1265 cm−1 out to about 1550 cm−1.42 In Fig. 2a, a sharper feature at 1384 cm−1 could be arising from a combination of the O–B–O bending and symmetric B–O stretching of the B(OH)3 units. These results are in excellent agreement with Ehrt's XRD study of liquid–liquid phase separation in binary zinc borate.2 The Raman spectrum of the clear glass obtained from the x = 0.50 melt is visibly identical to that of the x = 0.54 glass. The difference spectrum (Fig. 2b) between x = 0.54 and the homogeneous sample obtained from the x = 0.50 melt is free of any distinguishing features, suggesting that composition x = 0.54 (7ZnO–6B2O3) may be taken, for all practical purposes, as the onset of the glass forming range.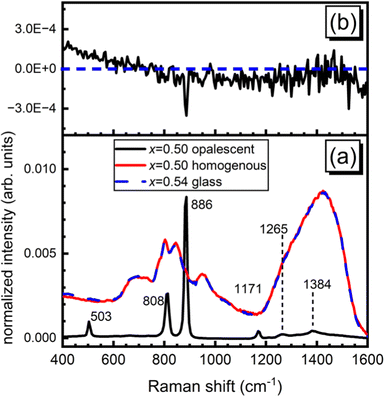 | ||
| Fig. 2 The bottom (a) presents the Raman spectra of the two components obtained from the stoichiometric metaborate composition, 50ZnO–50B2O3 (x = 0.50), compared to the Raman spectrum of x = 0.54 glass. Note the intensity of the “x = 0.50 opalescent” has been divided by a factor of 15 for comparison. The top (b) presents the difference spectrum between x = 0.54 glass and the clear glass obtained from the x = 0.50 melt. See Fig. S2 (ESI†) for infrared absorption coefficient spectrum of x = 0.50 sample. | ||
At higher zinc oxide contents, glass formation was first limited by crystallization and then prohibited alltogether by chemical separation in the melt. As observed by Harris & Bray,16 the stoichiometric zinc pyroborate (O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B = 2.5
B = 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) can form a glass if rapidly quenched, though the glass tends to crystallize during ambient cooling, and the same observation was made in this study. By increasing the melting temperature to 1200 °C and rapidly splat quenching, small regions of transparent glass were obtained for the melt with 70 mol% ZnO (x = 0.70, O:B = 2.67). However, with the quenching techniques accessible to us, the majority of the sample devitrified during cooling and glass formation was limited to a thin layer on the surface. Perhaps, complete vitrification could be accessed up to and including 70 mol% ZnO by employing the levitation melting technique.45–47 For greater than 71 mol% ZnO, chemical separation in the melt is reported.13 Our investigation supports this finding as a melt containing 73% mol% ZnO was visually observed to be phase-separated, with the bottom layer producing the strong green thermoluminescence characteristic of ZnO.48
1) can form a glass if rapidly quenched, though the glass tends to crystallize during ambient cooling, and the same observation was made in this study. By increasing the melting temperature to 1200 °C and rapidly splat quenching, small regions of transparent glass were obtained for the melt with 70 mol% ZnO (x = 0.70, O:B = 2.67). However, with the quenching techniques accessible to us, the majority of the sample devitrified during cooling and glass formation was limited to a thin layer on the surface. Perhaps, complete vitrification could be accessed up to and including 70 mol% ZnO by employing the levitation melting technique.45–47 For greater than 71 mol% ZnO, chemical separation in the melt is reported.13 Our investigation supports this finding as a melt containing 73% mol% ZnO was visually observed to be phase-separated, with the bottom layer producing the strong green thermoluminescence characteristic of ZnO.48
4.2. Glass properties
| x | 0.54 | 0.57 | 0.60 | 0.63 | 0.65 | 0.67 | 0.70 | |
|---|---|---|---|---|---|---|---|---|
| mol% B2O3 | (Batched) | 46.2 | 42.9 | 40.0 | 37.5 | 35.3 | 33.3 | 30.0 |
| mol% ZnO | 53.8 | 57.1 | 60.0 | 62.5 | 64.7 | 66.7 | 70.0 | |
| O:B | 2.08 | 2.17 | 2.25 | 2.33 | 2.42 | 2.50 | 2.67 | |
ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2O3 B2O3 |
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
|
| Density (g cm−3) | Quenched | 3.463 | 3.572 | 3.65 | 3.744 | 3.807 | 3.889 | n.m. |
| Annealed | 3.49 | 3.582 | 3.667 | 3.748 | 3.815 | — | n.m. | |
| Molar volume (cm3 mol−1) | Quenched | 21.932 | 21.371 | 21.007 | 20.558 | 20.286 | 19.917 | n.m. |
| Annealed | 21.762 | 21.312 | 20.909 | 20.536 | 20.243 | — | n.m. | |
| N 4 (NMR) | Quenched | 0.26 | 0.232 | 0.209 | 0.18 | 0.158 | 0.133 | ∼0.1 (IR) |
| Annealed | 0.286 | 0.262 | 0.231 | 0.201 | 0.17 | — | n.m. | |
| T g (°C) | Quenched | 559 | 546 | 544 | 537 | 534 | 532 | — |
| T x (°C) | Quenched | 745 | 728 | 707 | 681 | 672 | 645 | n.m. |
| T s (°C) | Quenched | 1023 | 1024 | 1019 | 1007 | 1010 | 1003 | n.m. |
| S = Tx − Tg (°C) | Quenched | 186 | 182 | 163 | 144 | 138 | 113 | n.m. |
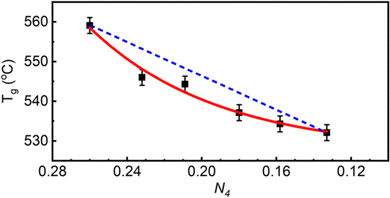
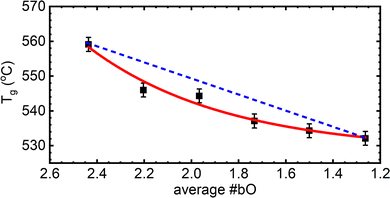
As zinc oxide is added to the 54ZnO–46B2O3 composition, the glass transition temperature, Tg, is observed to decrease (it is still higher than Tg of pure B2O3). The onset temperature of crystallization, Tx, is also found at lower temperatures; however, Tx decreases more rapidly than Tg (see Fig. S3 for experimental DSC scans, ESI†). This leads ultimately to a continuous decrease in the stability window, S = Tx − Tg, with increasing ZnO loads. The lowest relative stability at the pyroborate composition agrees well with the inability of this glass to be prepared without rapid cooling. One can infer from the trend that the stability rapidly falls off above the pyroborate (x = 0.67) composition, explaining the absence of a bulk glassy sample at x = 0.70. The stability is an important parameter in processing glasses for applications, where for example a glass may need to be brought above its Tg for shaping, such as hot pressing of a lens or fiber drawing, and so crystallization must be avoided to maintain optical integrity for most applications. Large windows between the glass transition and the onset of crystallization are desirable in this regard. Very little variation is observed in the liquidus/solidus temperature, Ts, of the compositions studied, which is in good agreement with the relatively flat nature of the zinc borate phase diagrams.12,13
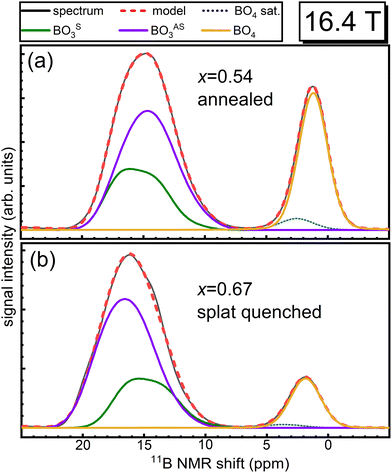
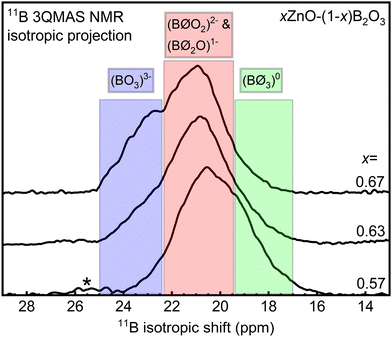
Although the fitting of multiple BO3 resonances in Fig. 3 is not necessarily unique due to substantial overlap of the two peaks, there is good agreement with the trends evidenced by the vibrational data, as discussed below. For further support, we measured the annealed x = 0.54 sample (Fig. 3a) at a lower magnetic field of 11.7 T (Fig. S6, ESI†). Two BO3 peaks with distinctly different lineshapes are present, with an η = 0.26 for BOS3 and an η = 0.45 for BOAS3. The peak areas were fixed approximately to those determined by the high field NMR experiments (Fig. 3a) while all other fitting parameters were allowed to vary. The fitting results from 16.4 T measurements reasonably simulate the experimental spectra of 11.7 T measurement, increasing our confidence in the quantitative populations of symmetric and asymmetric BO3 as determined from high-field 11B MAS NMR for the full range of glass compositions.
Analysis of tetrahedral boron in these glasses is much more direct in that we detect only a single resonance representing these polyhedra, which is well described by a mixed Gaussian/Lorentzian lineshape coexisting with a weak, underlying spinning sideband from the BO4 satellite transitions (dotted blue curves in Fig. 3). Reliable and accurate values for the fraction of four-fold coordinated boron, N4, from 11B MAS NMR spectroscopy are obtained by subtraction of this artifact from the BO4 peak intensity.
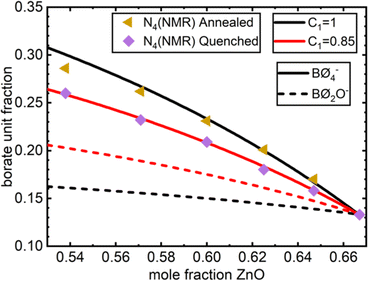
Similar to the density measurements, N4 as quantified by 11B MAS NMR (Table 1) also shows a difference between the rapidly cooled glasses obtained by splat quenching and the slowly cooled glasses obtained by casting into a pre-heated steel mold followed by annealing. NMR shows higher N4 values for the glasses that were first cast into a mold and then annealed compared to the glasses obtained from rapidly quenching the melt. The presence of four-coordinated (BØ4)− and three-coordinated (BØ2O)− borate species in borate glasses is governed by the metaborate equilibrium reaction,
| (BØ2O)− ⇆ (BØ4)− | (12) |
The temperature dependence of the structure of melts containing B2O3 has been shown to exist in boron oxide23,29,49,50 and modified borates.24,30,51–53 Pure boron oxide glass had been previously studied by Walrafen et al.49 and Hassan et al.50 as well as recently by Alderman et al.29 In all cases, the boroxol rings were observed to break down at high temperatures into non-ring trigonal borate entities. In binary sodium borates, quantitative in situ structural studies at different temperatures including Raman spectroscopy24 and X-ray diffraction30 indicate that the left-hand side of eqn (12) is favored at high temperatures and in the melt. In sodium borate glass containing 25 mol% Na2O, the N4 value can change over an order of magnitude between the glass and the melt.24 An increasing fraction of (BØ2O)− over (BØ4)− units was also observed by molecular dynamics in lithium–borate glasses with increasing temperature.54
Rapid quenching of the melt between two metal plates arrests the structure of the melt at a higher temperature, where the trigonal metaborate is favored.55 On the other hand, casting the melt into a cylindrical metal mold and allowing it to vitrify in air allows the constituents of the melt to settle into a more densely packed arrangement. Towards this direction (the goal is a lower free energy and thermodynamically favored structure, which happens to have larger N4), the equilibrium in eqn (12) shifts to favor the more compact tetrahedral metaborate unit.53 The same trend is reflected in the binary zinc borate glasses of this study by the systematically higher N4 values in the glasses with a lower fictive temperature, Tf, where we employ the traditional view56 that Tf is simply the temperature that the structure of the liquid melt is arrested at. For direct visual comparison, the 11B MAS NMR spectra for x = 0.54 are shown superimposed for the splat quenched and annealed samples in Fig. S7 (ESI†). Similar results were obtained in the early NMR study by Harris and Bray.16 The reported N4 values of zinc borate glasses for rapidly quenched samples in ref. 16 are systematically lower than the values obtained here. The glasses of that study were melted at 1400 °C, 250 °C higher than the glasses prepared in this work. This translates to an even higher fictive temperature, arresting a melt that contained a larger population of (BØ2O)− units and, thereby, possibly explaining the difference in N4 values between the two studies. Considering that Harris and Bray obtained a glass at 67 mol% ZnO content in their fast cooling but not in their slow cooling samples, just as was seen in our investigation, it seems reasonable to assume that the cooling rates they employed are comparable to those achieved here when splat quenching the melt between two metal plates. This implies that, in the glass forming range of binary zinc borates, the fraction of four coordinated boron depends on the ZnO content, the melting temperature, and the cooling rate – with the last two aspects constructing the fictive temperature.
In binary alkali borate glasses, the fraction of four-coordinated boron is directly proportional to Tg57–59 while being dependent on the amount and type of alkali addition20,60,61 and Tf.55 The formation of tetrahedral borate units with the initial addition of alkali oxide to pure B2O3 results in an increase of the glass transition temperature due to the increase in the average number of bridging oxygen atoms per boron center, Nb, which increases above 3 (the value of Nb in vitreous boron oxide).62 Eventually, further addition of alkali oxide causes the progressive depolymerization of the borate backbone by the destruction of borate tetrahedra and the formation of triangular units containing non-bridging oxygen atoms.63 A decrease in the glass transition temperature accompanies this depolymerization, but Tg does not change in a linear manner with N4. Without deeper considerations of the underlying structure in the binary zinc borate system, we can simply state that the glass transition temperature and the fraction of tetrahedral boron are both decreasing with ZnO content (see Fig. 4).
4.3. Raman spectroscopy
Unpolarized Raman spectra are shown in Fig. 5. The spectra have been reduced and area normalized, offset for clarity, and shown with vertically oriented dashed lines to highlight features we will discuss in more detail in the following text. For additional visualization, the middle and high frequency regimes are displayed overlapping in Fig. 6a and b, respectively.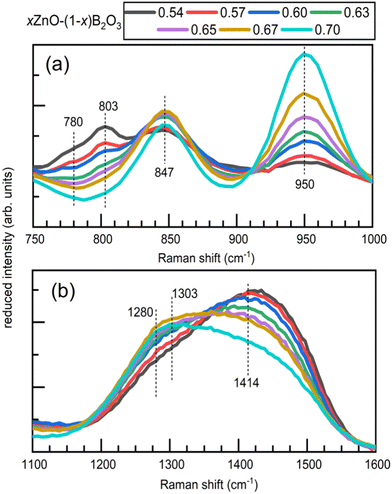 | ||
| Fig. 6 Overlapped Raman spectra for quenched glasses xZnO–(1−x)B2O3 over (a) the interval 750–1000 cm−1 and (b) the interval 1100–1600 cm−1. | ||
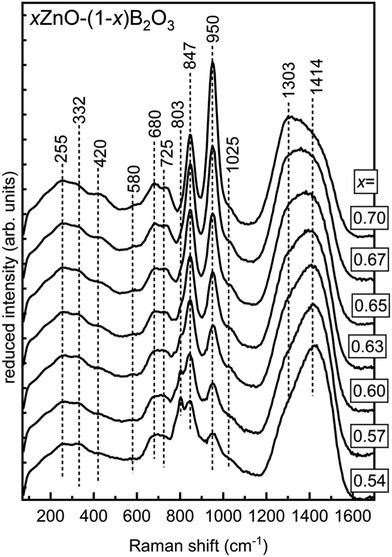
All spectra are characterized by the appearance of bands in the following spectral ranges: 1175–1600 cm−1, 750–1175 cm−1, and 450–750 cm−1. The first interval, 1175–1600 cm−1 is the most straightforward as it belongs to stretching vibrations of trigonal borate entities only (no tetrahedral modes overlapping) with the frequency highly correlated with the degree of polymerization.22,25,64,65 The middle frequency region, 750–1175 cm−1 receives its strongest contributions from the highly symmetric modes of various well-defined borate structures including boroxol rings,42 borate rings,20,66–68 pyroborate dimers,19,65 and trigonal orthoborate anions.65,69,70 In addition to the well-defined structures, asymmetric stretching of borate tetrahedra are expected to be active over most of this interval as well.68 Between 450–750 cm−1 Raman activity is primarily arising from B–O–B bending modes, with some overlap from symmetric stretching of borate tetrahedra scattering in the lower half of this region.68,71 Below 450 cm−1, Raman scattering from ZnOn polyhedra and borate network deformation modes overlap.
The spectrum of x = 0.54 is in good agreement with what has been reported by others for similar compositions.6,18,72 The most prominent feature in the lowest ZnO content glass is the sharp band with a maximum at 803 cm−1. This sharp and polarized feature is due to the ring breathing of the boroxol ring, the planar ring containing 3 boron atoms sharing 3 oxygen atoms, with all non-ring oxygen atoms also bridging to other network units.42 This structure does not have a known crystalline 100% B2O3 analogue though, after years of debate and many investigations, is now undisputed to exist as the primary superstructural unit in pure B2O3 glass.31
In pure B2O3, boroxol rings are found to coexist with non-ring trigonal borate units in roughly a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio.73,74 The B–O stretching of neutral trigonal borate units, (BØ3)0, inside and outside of ring arrangements in vitreous B2O3 contribute very weakly to a high frequency Raman envelope from about 1200–1550 cm−1.25,42 The intensity of this high frequency envelope due to (BØ3)0 is beyond an order of magnitude lower than the intensity of the boroxol ring's 803 cm−1 band. Additionally, the intensity of B–O stretching of (BØ3)0 units is substantially lower compared to that of trigonal borate units with non-bridging oxygen atoms.6,75 For these reasons, in the glasses under investigation the content of neutral borate triangles in boroxol ring arrangements cannot be unambiguously evaluated. With addition of ZnO, the 803 cm−1 feature continuously decays and ceases to be detectable beyond x = 0.65, where it is last seen as a weak shoulder.
1 ratio.73,74 The B–O stretching of neutral trigonal borate units, (BØ3)0, inside and outside of ring arrangements in vitreous B2O3 contribute very weakly to a high frequency Raman envelope from about 1200–1550 cm−1.25,42 The intensity of this high frequency envelope due to (BØ3)0 is beyond an order of magnitude lower than the intensity of the boroxol ring's 803 cm−1 band. Additionally, the intensity of B–O stretching of (BØ3)0 units is substantially lower compared to that of trigonal borate units with non-bridging oxygen atoms.6,75 For these reasons, in the glasses under investigation the content of neutral borate triangles in boroxol ring arrangements cannot be unambiguously evaluated. With addition of ZnO, the 803 cm−1 feature continuously decays and ceases to be detectable beyond x = 0.65, where it is last seen as a weak shoulder.
In the 800–900 cm−1 spectral range, the 803 cm−1 band is replaced by a sharp polarizable feature at 847 cm−1 that first appears as a shoulder in the x = 0.54 spectrum. The band increases in relative intensity until about x = 0.65, after which the intensity decays. This feature, as has been shown before, is assigned to the symmetric B–O–B stretching of pyroborates dimers, (B2O5).65,70,76,77 The growth of this feature corresponds with the increase in relative intensity of the shoulder positioned at about 1280 cm−1 observable in the x = 0.54 spectrum, which belongs to the stretching of the terminal B–O− segments of the pyroborate dimers. These band positions are in close proximity to those found in crystalline Mg2B2O5, consisting of pyroborates dimers, where the same features occur at 850 cm−1 and 1290 cm−1.19 In binary 1.2MgO–B2O3 glass, these features appear at 840 cm−1 and 1285 cm−1, respectively.19
Unlike the 847 cm−1 band, the 950 cm−1 feature continuously gains relative intensity with ZnO addition. In the glassy portion obtained from the x = 0.70 melt, this sharp feature dominates the borate region of the spectrum. This sharp and highly polarized feature arises from the symmetric stretching of the trigonal orthoborate anion, (BO3)3−. This is the structural unit of 3ZnO–B2O3 in addition to numerous other orthoborate compounds, 3MO–B2O3 where M = Li2, Na2, Ag2, Tl2, Mg, Ca, Sr.4 The feature appears at 945 cm−1 in Mg–borate glasses19 and between 935–945 cm−1 in 45Li2O–20RE2O3–35B2O3 for RE = Y, Sm, Eu, Gd, and Yb.78 In rare-earth orthoborates, the (BO3)3− anion is present in the high temperature phases even if the low temperature phase consists of tetrahedral orthoborate, (BØ2O2)3−, units;79,80 this is itself another example of the trigonal borate units being favored at high temperatures as was mentioned in Section 4.2.2. Analogous to the boroxol unit's ring breathing in the case of pure B2O3, the ν1 mode of the (BO3)3− unit dominates the spectra of orthoborate glasses consisting solely of such units.45 The site distortion inherent in the glassy state has been seen to reduce the (BO3)3− symmetry to lower than D3h.76,77 This enables all of the vibrational modes of the trigonal orthoborate anion to become both infrared and Raman active, as well as induce splitting of the ν3 and ν4 modes.81 Despite the presence of their vibrational activity, the Raman scattering intensity of the ν3 (asymmetric stretch) as well as the ν4 (in-plane bending) and ν2 (out-of-plane bending) are all weak compared to the ν1 mode. However, the activity of the asymmetric stretching of the (BO3)3− unit is the most likely culprit behind the development of a distinct maximum at 1303 cm−1 in the highest ZnO content glasses. The bending modes of the orthoborate anion occur between 600–800 cm−1 though the relative intensity of that region, even at the highest ZnO levels, strongly suggests for all binary zinc borate glasses that other borate entities are contributing significantly to the observed intensity in that frequency range.
Just above the 950 cm−1 band, a small shoulder, identified by the dash positioned at 1025 cm−1 can be seen in all spectra.20,68 This feature is most probably due to the asymmetric stretching of tetrahedral metaborate units. The corresponding symmetric stretching of the same unit may be contributing the subtle activity in the 530–580 cm−1 region that is visible to some extent in all compositions.68,71 The observation of tetrahedral boron in all zinc borate glasses is fully consistent with the result for N4 values from the NMR data (Table 1). The apparently static nature of the intensity of the feature just above 1000 cm−1 despite the decrease in N4 measured by NMR can be explained by the overlap with the high frequency tail of the ever-increasing (BO3)3− band at 950 cm−1. This feature converges to zero intensity by 1030 cm−1 in lithium–yttrium–orthoborates with 30 mol% Y2O3, where the same orthoborate anion's ν1 mode occurs at 940 cm−1 and displays a similar bandwidth to the feature here, ∼50 cm−1.70
The participation of some borate tetrahedra in 3-membered borate rings, modified boroxol rings where one (BØ3)0 is converted to a (BØ4)− by a nearby modifier, is indicated by the low frequency shoulder of the 803 cm−1 feature in glasses with x < 0.63 situated at circa 780 cm−1. To help determine the arrangement of other tetrahedral boron, we turn our attention first to their isomeric counterpart, trigonal (BØ2O)− units. The presence of trigonal metaborate entities is signaled by the varying, but consistently strong Raman activity lying above 1400 cm−1 where B–O− stretching in (BØ2O)− units existing in ring and chain configurations is seen in both crystals and glasses.64,67,68,82 The frequency of the boron oxygen stretching in trigonal metaborate units is highly sensitive to the surrounding environment.64 Main factors contributing to the position of the high frequency band of (BØ2O)− stretching modes include the intermediate range order (chain or ring configuration), the neighboring borate unit configuration (trigonal or tetrahedral), and the degree of covalency of the non-bridging oxygen with the charge balancing cation.6,52,67,68 The last case results in a red shift in the frequency such that the B–O− stretching in (BØ2O)− entities are subsequently found in the range 1300–1400 cm−1, as seen in Pb and Bi borates.6,52,83 A similar red shift is not seen for any of the B–O− stretching due to pyroborate or orthoborate units in these zinc borate glasses, so the position of the high frequency band is more likely to be explainable by the configuration and neighboring borate species.
Low field strength alkali (K, Rb, Cs) and alkaline earth (Ba) metaborates tend toward ring arrangements, while modifiers of higher field strength such as Li, Ca, and Sr tend toward chain configurations.67 The ring metaborate anion, which can be seen as a boroxol ring where all non-ring oxygen are ionically crosslinked via modifier cations to other borate units, produces spectra with a characteristic ring breathing mode between 600–650 cm−1.67 This appears alongside a rather high frequency for the terminal B–O− stretching, which is seen for example in crystals between 1550–1580 cm−1 for NaBO2 and between 1520–1550 cm−1 for Ba2Mg(B2O4)3.67 The terminal stretching of B–O− is found at lower energies in metaborate chains, such as between 1465–1500 cm−1 in α-LiBO2 and between 1455–1510 cm−1 in CaBO2.67 These exist alongside chain deformation modes scattering characteristically between 720–735 cm−1 and less intensely between 635–670 cm−1.67 These signatures of metaborate units in the mid-frequency region of 600–800 cm−1 have significant overlap with the in-plane and out-of-plane bending modes of both polymerized (BØ3)0 species and isolated (BO3)3− species.22 In addition to these individual unit vibrational modes, crystalline 2MgO–B2O3 and 2Li2O–B2O3 also display Raman activity in this region likely attributable to bending of the B–O–B connection in the (B2O5)4− dimer unit.19,65 Thus, the spectral envelope between 600–800 cm−1 contains contributions from at least 3 to 4 distinct borate arrangements in all zinc borate glasses, with some arrangements, (BØ30) and (BO3)3−, contributing more than one component. The presence of metaborate chain configurations in zinc borates seems much more probable than the presence of metaborate ring anions considering the features of Fig. 5, primarily the converging behavior of the scattering intensity above 1450 cm−1.
Now, it is necessary to consider the neighboring species of the (BØ2O)− units in chains. Only trigonal metaborate units comprise α-LiBO2 and CaBO2.67,68,82 Structures consisting of metaborate chains where trigonal and tetrahedral metaborate units alternate are known and one such compound is Ba2LiB5O10.84,85 The (BØ4)−–(BØ2O)−–(BØ4)− linkages notably impact the Raman spectrum compared to purely trigonal metaborate chains.64 In Ba2LiB5O10 the stretching modes of (BØ4)− units give rise to features at 555 cm−1 (symmetric stretch) and 969 cm−1 (asymmetric stretch)64 with an additional pair of bands seen in the reported spectrum between 1000–1100 cm−1, though their exact positions are not indicated. The characteristic chain deformation and terminal BIII–O− stretch are found at lower frequencies than the all-trigonal analogues, at 705 cm−1 and 1406 cm−1, respectively.64,67 Devitrification of lithium metaborate glass to form β′-LiBO2 showed a similar structure of alternating BIII–BIV–BIII–BIV chains.68,82 The Raman spectra of β′-LiBO2 possesses distinguishing bands at 533, 696, 933, 1045, and 1403 cm−1.82 Applying these observations to the Raman spectra of zinc borate glasses, noting consistent spectral activity between 530–580, 680, ∼1025, and 1414 cm−1, it is concluded that the majority of metaborate units, both trigonal and tetrahedral, occur in chain configurations with a large number of BIV–BIII–BIV arrangements.
This seems to be compatible with two other aspects of the structure of zinc borate glasses. First, the presence of chains can be seen as the intermediary structure between the boroxol and borate rings seen for low ZnO content with the highly charged pyro- and orthoborate species prevalent at high modifier concentration. In this way, the addition of ZnO has three possible modification mechanisms on the borate network: (a) cleaving a boroxol (3BIII) or borate ring (2BIII + 1BIV) to create a chain segment, (b) trimming a metaborate chain, creating initially chain end members and finally forming a pyroborate dimer, and (c) splitting a pyroborate dimer into two orthoborate anions. Indeed, this sequence appears entirely consistent with the progressive nature of the Raman spectra. Secondly, and perhaps more intriguing, is the tendency to form chains of alternating trigonal and tetrahedral metaborate units, which may be intimately related to the observed fictive temperature dependence on the population of tetrahedral metaborate units. As previously mentioned, the trigonal metaborate unit is favored at high temperatures.
This has recently been shown in melts consisting of Li, Sr, and Pb diborates.52 High temperature Raman investigation showed that despite the crystal structure of PbB4O786 and α-SrB4O787 both consisting of entirely tetrahedral coordinated boron (N4 = 1), the Raman spectra of the corresponding melts indicated that approximately all (BØ4)− had converted to chains of (BØ2O)− at elevated temperatures.52 Recently, X-ray Raman scattering on binary lithium borates showed that with increasing temperature above Tg, tetrahedral boron atoms were converted to trigonal boron.51 For lithium metaborate glass, N4 = 0.35, the population of tetrahedral boron was seen to decrease by about a factor of 3 at 800 °C.51 The apparent N4 dependence on fictive temperature for zinc borates can be seen as the inverse of these phenomena, where, as the temperature that the melt is arrested at is lowered, more (BØ2O)− units in the metaborate chains present in the melt will convert to (BØ4)−. Conversely, with a higher fictive temperature – due to higher melting temperatures, faster quench rates, or both – the observed structure will reflect a greater population of metaborate chain segments consisting of only (BØ2O)− units.
4.4. Infrared spectroscopy
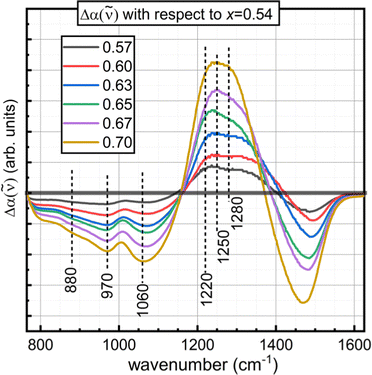
The infrared absorption coefficient spectra, a(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ), have been area normalized over the range 0–1650 cm−1 in Fig. 7 and offset for clarity. In Fig. 8, the difference is taken between the absorption profile of the indicated ZnO content with respect to the lowest homogenous glass forming composition, x = 0.54.
), have been area normalized over the range 0–1650 cm−1 in Fig. 7 and offset for clarity. In Fig. 8, the difference is taken between the absorption profile of the indicated ZnO content with respect to the lowest homogenous glass forming composition, x = 0.54.
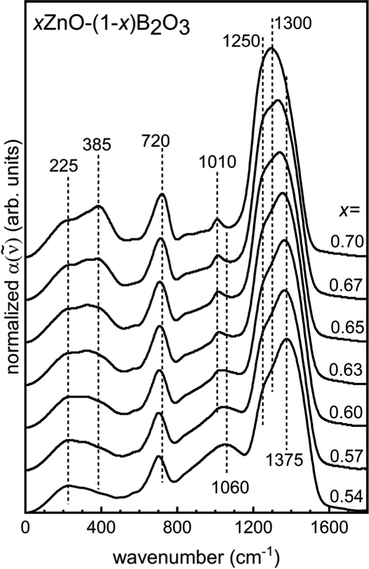 | ||
| Fig. 7 Normalized IR absorption coefficient spectra, offset for clarity, for quenched glasses xZnO–(1−x)B2O3. | ||
In the far infrared, addition of ZnO causes an increase in the relative intensity of the cation motion band as the concentration of Zn2+-oxygen sites increases. The peak maximum shifts to higher frequencies, from about 228 cm−1 for low ZnO content to about 385 cm−1 for x = 0.70. Ehrt had discussed the preference for Mn2+ and Zn2+ to be coordinated primarily 6-fold with oxygen in metaborates with significant portions of lower coordination number sites, down to 4-fold.2 This is consistent with the ∼228 cm−1 and ∼385 cm−1 peaks being attributable to ν(Zn–O) stretching in 6-fold and 4-fold coordinated Zn2+-oxygen sites, respectively, which are both observable in the spectrum of x = 0.54 with the former showing the greatest relative intensity (Fig. 7). The trend here is consistent with that of high field strength alkali and alkaline earth modifiers, as well as rare-earth sites in glasses,88–90 where increasing network depolymerization is accompanied by lower coordination numbers of the modifying cations. In binary lithium borates, in high Li2O content glasses, the 4-fold coordinated Li+ sites are abundant.22 Similarly, Mg2+–oxygen tetrahedra are posited to persist in binary Mg–borate glasses.19 For the zinc borate glasses studied here, the increase in the intensity at circa 385 cm−1 reflects the increasing population of 4-coordinated Zn2+ as the borate backbone breaks down, analogous to the case of Mg2+ and Li+, which are similar in size to Zn2+.
The next feature identifiable in all glasses is an envelope spanning from about 600–800 cm−1. This is arising from bending modes of trigonal borate entities.67 The upshift from ∼700 cm−1 to ∼720 cm−1 with increasing modifier content is consistent with the continual formation of non-bridging oxygen on trigonal borate sites observed in the Raman spectra of Section 4.3.22 Stretching modes of network polyhedra are seen between 800–1650 cm−1. The region is typically considered in two parts. The region from around 800 to about 1100–1150 cm−1 displays activity arising from tetrahedrally coordinated boron, while trigonal boron units are active in the 1100–1650 cm−1 range.6,20,22,68,70,91 As the ZnO concentration increases, the BIV bands lose relative intensity at a rate in excellent agreement with NMR. The shape of the band begins as a broad envelope with no discernible features, though a definite local maximum at 1010 cm−1 becomes characteristic of the spectra with relatively high ZnO content. The component bands that lose intensity with added ZnO are well seen in the difference spectra for glasses with x ≥ 0.57 with respect to the x = 0.54 spectrum (Fig. 8). Here, we see the loss in absorption with increasing ZnO might be attributable to a decreasing population of structures containing tetrahedral boron that exhibit infrared absorption at 880, 970, and 1060 cm−1. Ring-type superstructural units that contain one or two tetrahedral boron sites are documented to give rise to such activity.19,92 This is also in agreement with what was seen in the Raman spectra, where large borate groups containing BIV units were observed to break up with increasing network modification.
The region above 1100 cm−1 contains contributions from all trigonal borate units. The downshift in the maximum frequency is consistent with the breakdown of the percolating network.22 In the Raman spectra, it was observed that the pyroborate contribution was strongest near the nominal pyroborate stoichiometry, x = 0.67. The largest difference between the IR spectrum of x = 0.67 with respect to the x = 0.54 spectrum displays a clear maximum at about 1250 cm−1. This is seen as the shoulder in the absorption coefficient spectrum of x = 0.54 ZnO and agrees well with the position of the asymmetric B–O− stretching seen in the Raman spectra. On these grounds, it can be concluded that the asymmetric B–O− stretching from pyroborate units is infrared active in the 1240–1260 cm−1 and is Raman active at similar frequencies.
In comparing the difference spectrum for x = 0.70 relative to the difference spectrum of x = 0.67, two components seem to contribute to the maximum frequency downshift and increased symmetry observed in the high frequency band of the a(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) spectrum for x = 0.70. They appear to be absorbing in the 1200–1220 cm−1 and the 1280–1300 cm−1 range. This is in satisfactory agreement with the positions of two strong infrared active bands due to the split ν3 mode of the (BO3)3− anion that can be seen in lithium yttrium orthoborates with variable yttrium content.70 The higher frequency component shows more intense activity in both the Raman and infrared for 45Li2O–20RE2O3–35B2O3 glasses,78 as well as also in the infrared of binary bismuth borates.35 This supports the claim in Section 4.3. that the high frequency Raman band achieves a distinct maximum at 1303 cm−1 due to the weak scattering by the ν3 activity of the (BO3)3− anion.
) spectrum for x = 0.70. They appear to be absorbing in the 1200–1220 cm−1 and the 1280–1300 cm−1 range. This is in satisfactory agreement with the positions of two strong infrared active bands due to the split ν3 mode of the (BO3)3− anion that can be seen in lithium yttrium orthoborates with variable yttrium content.70 The higher frequency component shows more intense activity in both the Raman and infrared for 45Li2O–20RE2O3–35B2O3 glasses,78 as well as also in the infrared of binary bismuth borates.35 This supports the claim in Section 4.3. that the high frequency Raman band achieves a distinct maximum at 1303 cm−1 due to the weak scattering by the ν3 activity of the (BO3)3− anion.
The stretching of bridging oxygen in trigonal metaborate chains is expected to display infrared activity between 1200–1240 cm−1.22,35,76,77 Such activity could be responsible for the high difference in the absorption coefficient in this range for zinc borates below the pyroborate stoichiometry. This is reasonable on account of the absorption of asymmetric stretching of trigonal orthoborate units in this range is anticipated to be lower than that in the range 1280–1300 cm−1; but for glasses with x ≤ 0.67, the difference in absorption in the 1200–1240 cm−1 region is greater than that in the 1280–1300 cm−1 range. Despite seeing increasing concentrations of trigonal orthoborate species with additions of ZnO in the Raman spectra by the units strong ν1 band, it is likely that the 1200–1240 cm−1 region of the infrared spectra is receiving contributions from B–Ø stretching in metaborate chain configurations as well.
5. Discussion
5.1. Comparison with crystalline zinc borates
The zinc borate glass forming region is intriguing, with some reasons discussed in the introduction. Only one crystalline analogue exists in the composition space where glass formation exists, 4ZnO–3B2O3, “zinc metaborate”. The structure of zinc metaborate is comprised of entirely tetrahedral metaborate units that create B6O126− rings, for which the charge balancing zinc cations are tetrahedrally coordinated as well.9,93 The zinc polyhedra are formed by 3 oxygen ions from the borate structure and possess one ‘free’ oxygen ion each.9,93 For this reason, the compound is often written as Zn4O(BO2)6. The density of the crystal (4.22 g cm−3)93 is high relative to the glass (3.83 g cm−3, see Table 1). The difference between the glass and crystal structure for composition 4ZnO–3B2O3 has been known for some time,8 evident in the significantly lower N4 value of the glass, which was quantified almost 40 years ago.16 The infrared8 and Raman94 spectra of Zn4O(BO2)6 are consistent with the presence of tetrahedral coordinated boron. A strong band at 420 cm−1 in the Raman spectrum was interpreted as symmetric stretching of tetrahedral boron in the zinc metaborate structure and weaker activity was also reported between 420–500 cm−1.94 Activity between 900–1200 cm−1 in the Raman and infrared spectra of crystalline zinc metaborate signals the asymmetric stretching of the tetrahedral borate units.8,94 As seen in large borate groups, their complex structures yield a large number of vibrational modes and their exact identification in the broad and diffuse spectra inherent in glassy materials is ambiguous, especially with the overlap of bands belonging to other borate species. If the zinc metaborate structure is present in binary zinc borate glasses, its concentration is likely small.The other zinc borate crystal structure with tetrahedral boron is zinc diborate, ZnO–2B2O3, with the condensed “diborate ring” where two borate tetrahedra share a bridging oxygen and each (BØ4)− unit fuses to two (BØ3)0 units, that are each shared between the tetrahedra.95 This composition lies outside the region of congruent melting in the ZnO–B2O3 phase diagram.12 The diborate superstructural unit may be present in low ZnO content glasses based on the observation that the feature visible at 580 cm−1 in the high ZnO content Raman spectra evolves from a weak feature slightly lower frequency at low ZnO content, where a band is expected around 480–500 cm−1 for the diborate unit.71 In the infrared, the 970 cm−1 and 1060 cm−1 features may arise also from diborate units.95 At the same time, the decreasing intensity at 880 and 1060 cm−1 bands corresponds to the destruction of borate superstructural units containing tetrahedra, the exact nature of which is difficult to identify.19 The region of the Raman spectrum around 545 cm−1 in x = 0.54 loses relative intensity with increasing ZnO content, as N4 also decreases, and becomes a weak differentiable feature at 590 cm−1. The upshift may be due to the presence of tetrahedral boron in non-ring arrangements,71 possibly alternating with trigonal metaborate in chain configurations64,68,82 as discussed previously. The short-range order units of zinc orthoborate, 3ZnO–1B2O3, comprised of isolated (BO3)3− species,96 appear to be present in all glasses accessible from homogenous zinc borate melts.
5.2. Application of the SROC model
After the multi-faceted analysis presented in Section 4, the general model of Section 2 is applied for the first time to the zinc borate glass system to identify the aforementioned f coefficients. To account for the structural units of zinc borate glasses in xZnO–(1−x)B2O3 for x = [0.54,0.70] three SROCs need to be discerned – the metaborate![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) (x = 0.50, O:B = 2), the pyroborate
(x = 0.50, O:B = 2), the pyroborate ![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) (x = 0.67, O:B = 2.5), and the orthoborate
(x = 0.67, O:B = 2.5), and the orthoborate ![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) (x = 0.75, O:B = 3). Disproportionation at a given composition may be employed to account for species not typically found in a particular modifier content, i.e., boroxol rings present at x = 0.54 may be accounted for by a subset within
(x = 0.75, O:B = 3). Disproportionation at a given composition may be employed to account for species not typically found in a particular modifier content, i.e., boroxol rings present at x = 0.54 may be accounted for by a subset within ![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) .
.
We begin by considering the rapidly increasing intensity of the (BO3)3− symmetric stretch band in the Raman with increasing x (Fig. 6). This suggests the orthoborate SROC is described by
![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) = f = f![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) ,0B0 = BO33− ,0B0 = BO33− | (13) |
![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) ,0 = 1 and B0 is the borate structural unit contributing to the orthoborate SROC possessing 0 bridging oxygen atoms, which is the trigonal orthoborate anion. The pyroborate SROC can also be simplified to a lesser degree. The presence of boroxol and borate rings falls off rapidly (Fig. 6), and so there is not expected to be contributions of B3, trigonal units with three bO atoms, at x = 0.67 and above. With this assumption in place, the pyroborate SROC is written as
,0 = 1 and B0 is the borate structural unit contributing to the orthoborate SROC possessing 0 bridging oxygen atoms, which is the trigonal orthoborate anion. The pyroborate SROC can also be simplified to a lesser degree. The presence of boroxol and borate rings falls off rapidly (Fig. 6), and so there is not expected to be contributions of B3, trigonal units with three bO atoms, at x = 0.67 and above. With this assumption in place, the pyroborate SROC is written as![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) = f = f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,0B0 + f ,0B0 + f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,1B1 + f ,1B1 + f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,2B2 + f ,2B2 + f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,4B4. ,4B4. | (14) |
NMR gives N4 = 0.13 at x = 0.67 and so we can set f![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) ,4 = 0.13 ≈ 2/15. The presence of metaborate units at the pyroborate stoichiometry requires disproportionation of the 2 pyroborate units (in the following equation we also assume a 1
,4 = 0.13 ≈ 2/15. The presence of metaborate units at the pyroborate stoichiometry requires disproportionation of the 2 pyroborate units (in the following equation we also assume a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 metaborate formation, as will be explained below),
1 metaborate formation, as will be explained below),
 | (15) |
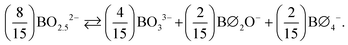 | (16) |
This does not fully account for the pyroborate SROC. We recall that the B–O–B stretching mode of the pyroborate dimer at 847 cm−1 in the Raman spectra (see Fig. 5 and 6) increases in intensity from the metaborate region to attain a maximum between x = 0.65 and x = 0.67. At the same time, there is no longer any strong evidence for the occurrence of neutral trigonal borate entities as the once observable Raman activity associated with boroxol and borate rings disappears by x = 0.67. Thus, it is reasonable to suppose that the remainder of pyroborate units do not disproportionate, that is, the equilibrium tends to the left-hand side of eqn (15). In turn, the pyroborate SROC can be explicitly written as
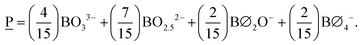 | (17) |
For the composition x = 0.67, NMR fitting (Fig. 3) quantifies the fraction of symmetric trigonal boron units, BS ((BØ3)0 + (BO3)3−) as 0.24, which is close to the predicted values of 0.267 (BO3)3− and 0.0 (BØ3)0. The trigonal asymmetric boron units with either 1 or 2 non-bridging oxygen, BAS ((BØ2O)− + (BØO2)2) is quantified by NMR to be 0.629 while the predicted fraction is 0.599. The values give confidence that the actual equilibrium governing glass formation at the pyroborate composition is that described by eqn (17).
Tending next to the metaborate SROC, NMR16 and IR6 indicate a relatively low fraction of tetrahedral boron in zinc borate glasses and the data here agrees with the earlier assessments. So, at the metaborate SROC we will start with a simple favorability of trigonal metaborate units,
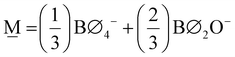 | (18) |
Ignoring the actual nature of trigonal borate units contributed by ![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) , we can evaluate the predicted fraction of four coordinated boron,
, we can evaluate the predicted fraction of four coordinated boron, 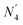 , over 0.5 ≤ x < 0.67 by
, over 0.5 ≤ x < 0.67 by 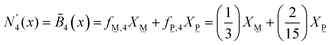 , which is eqn (11b) for j = 4 where the quantities X
, which is eqn (11b) for j = 4 where the quantities X![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) and X
and X![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) are given by eqn (7a) and (7b). In considering the N4 data from 11B NMR, the fewer borate tetrahedra in the quenched glasses implies a fictive temperature dependence of the borate unit fraction. Additionally, the difference between quenched and annealed becomes smaller approaching the pyroborate stoichiometry. To account for this, we may set a temperature dependent partition of eqn (18) such that
are given by eqn (7a) and (7b). In considering the N4 data from 11B NMR, the fewer borate tetrahedra in the quenched glasses implies a fictive temperature dependence of the borate unit fraction. Additionally, the difference between quenched and annealed becomes smaller approaching the pyroborate stoichiometry. To account for this, we may set a temperature dependent partition of eqn (18) such that
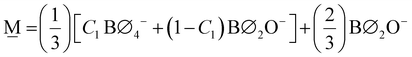 | (19) |
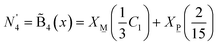 | (20) |
 represents the predicted N4 value. This prediction is compared to experimental NMR N4 values in Fig. 9 for C1 = 1 and C1 = 0.85. Also shown in Fig. 9 is the impact the C1 factor has on the trigonal metaborate contribution. For the quenched glasses, the agreement of N4 with
represents the predicted N4 value. This prediction is compared to experimental NMR N4 values in Fig. 9 for C1 = 1 and C1 = 0.85. Also shown in Fig. 9 is the impact the C1 factor has on the trigonal metaborate contribution. For the quenched glasses, the agreement of N4 with  is excellent. For the annealed glasses, there is some discrepancy between the predicted and experimental values for the glasses with the lowest ZnO content. As described in the experimental Section 3.1., all the annealed glasses were held at 520 °C for 1 hour. DSC measurements after sample preparation gives the Tg value of x = 0.54 to be 559 °C and 546 °C for x = 0.57. Therefore, it is plausible that the thermal treatments 30–40 °C below Tg could be the reason that the experimental values are lower than predicted values. In the glasses with higher ZnO content where the Tg values are lower, and thus closer to that which the one-hour thermal treatment post-casting was conducted at, the theoretical and experimental values are in superb agreement. Here, the rate of cooling from the same temperature yields quantifiable differences in the fraction of tetrahedral boron. It would be interesting to see the impact that the variation in annealing as well as melting temperate may have on the resulting N4. Indeed, on the basis of the results at hand, one cannot rule out that higher melting temperatures may introduce a similar fictive temperature dependence coefficient into the pyroborate SROC.
is excellent. For the annealed glasses, there is some discrepancy between the predicted and experimental values for the glasses with the lowest ZnO content. As described in the experimental Section 3.1., all the annealed glasses were held at 520 °C for 1 hour. DSC measurements after sample preparation gives the Tg value of x = 0.54 to be 559 °C and 546 °C for x = 0.57. Therefore, it is plausible that the thermal treatments 30–40 °C below Tg could be the reason that the experimental values are lower than predicted values. In the glasses with higher ZnO content where the Tg values are lower, and thus closer to that which the one-hour thermal treatment post-casting was conducted at, the theoretical and experimental values are in superb agreement. Here, the rate of cooling from the same temperature yields quantifiable differences in the fraction of tetrahedral boron. It would be interesting to see the impact that the variation in annealing as well as melting temperate may have on the resulting N4. Indeed, on the basis of the results at hand, one cannot rule out that higher melting temperatures may introduce a similar fictive temperature dependence coefficient into the pyroborate SROC.
Previously6,7,18 as well as here (see Fig. 5 and 6), a certain amount of disproportionation appears in the Raman spectra given the strong presence of boroxol rings and pyroborate dimers in glasses with ∼ 55 mol% ZnO. Such neutral and highly charged species close to the metaborate composition were explained by the following disproportionation of metaborate species,
| 2BØ2O− ⇄ BØ3 + BØO22− | (21) |
The experimental data suggests that approximately 75% of the trigonal borate units undergo disproportionation independent of the fictive temperature. This results in the following proposed metaborate SROC,
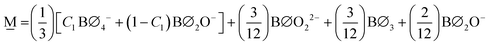 | (22) |
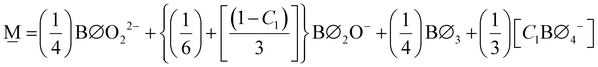 | (23) |
With our expressions for ![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif) ,
, ![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) , and
, and ![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) SROCs (eqn (23), (17) and (13), respectively) we are prepared to quantitatively estimate the fraction of short-range order structural units in binary zinc borates over the entire glass forming region. The results are presented in Table 2 and plotted in Fig. 10 as a function of ZnO content assuming annealed glasses and therefore using C1 = 1 in eqn (23). Comparing to experimental values once more, for the x = 0.54 glass, the model predicted fractions of BS = 0.253 and BAS = 0.463 while 11B NMR evaluation gives BS = 0.243 and BAS = 0.472. Overall, the agreement between the model and NMR values for symmetric and asymmetric borate entities is roughly 5%. The accuracy of the N4 determination is much better, with the agreement between predicted and NMR measured values less than 1% for the data presented in Fig. 9.
SROCs (eqn (23), (17) and (13), respectively) we are prepared to quantitatively estimate the fraction of short-range order structural units in binary zinc borates over the entire glass forming region. The results are presented in Table 2 and plotted in Fig. 10 as a function of ZnO content assuming annealed glasses and therefore using C1 = 1 in eqn (23). Comparing to experimental values once more, for the x = 0.54 glass, the model predicted fractions of BS = 0.253 and BAS = 0.463 while 11B NMR evaluation gives BS = 0.243 and BAS = 0.472. Overall, the agreement between the model and NMR values for symmetric and asymmetric borate entities is roughly 5%. The accuracy of the N4 determination is much better, with the agreement between predicted and NMR measured values less than 1% for the data presented in Fig. 9.
| x | Model | Experimental | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (BØ3)0 | (BØ2O)− | (BØO2)2− | (BO3)3− | (BØ4)− | N 4 (NMR) | ||||
| C 1 = 1 | C 1 = 0.85 | C 1 = 1 | C 1 = 0.85 | Annealed | Quenched | ||||
| a Value assigned from experimental input. b The N4 value for x = 0.700 is calculated from the infrared absorption coefficient spectrum.34 | |||||||||
| 0.538 | 0.209 | 0.161 | 0.203 | 0.286 | 0.044 | 0.300 | 0.259 | 0.286 | 0.260 |
| 0.571 | 0.167 | 0.156 | 0.189 | 0.322 | 0.088 | 0.267 | 0.234 | 0.262 | 0.232 |
| 0.600 | 0.125 | 0.150 | 0.175 | 0.358 | 0.133 | 0.233 | 0.208 | 0.231 | 0.209 |
| 0.625 | 0.083 | 0.144 | 0.161 | 0.394 | 0.178 | 0.200 | 0.183 | 0.201 | 0.180 |
| 0.647 | 0.042 | 0.139 | 0.147 | 0.430 | 0.222 | 0.167 | 0.158 | 0.170 | 0.158 |
| 0.667 | 0 | 0.133 | 0.133 | 0.465 | 0.269 | 0.133a | 0.133a | — | 0.133 |
| 0.700 | 0 | 0.089 | 0.089 | 0.311 | 0.511 | 0.089 | 0.089 | — | ∼0.1b |
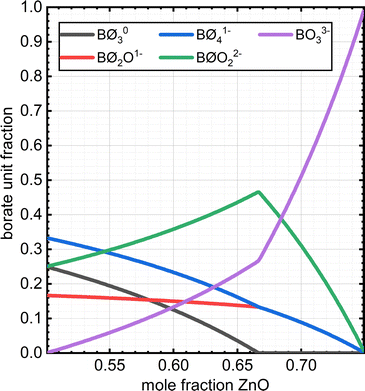 | ||
| Fig. 10 Theoretical fraction of short-range order structural units in binary zinc borate glasses taking the fictive temperature dependent constant C1 = 1. Note that beyond x = 0.667 (pyroborate composition), the fractions of trigonal metaborate, (BØ2O)−, and tetrahedral metaborate, (BØ4)−, are identical (see eqn (17) and Table 2). | ||
The trends in the trigonal boron speciation depicted in Fig. 10 agree well with the isotropic projections (high resolution dimension) from 11B 3QMAS NMR experiments at 16.4 T. Selected isotropic projections for trigonal boron only are shown in Fig. 11. The three regions depicted in Fig. 11 are based on changes in 11B isotropic chemical shift and correlations discussed by Kroeker and Stebbins.97 A shoulder around 19 ppm associated with neutral trigonal units is present for x = 0.57 and is essentially absent in the spectrum of x = 0.67. While the fully polymerized species are destroyed with the addition of ZnO, trigonal orthoborate units emerge at around 23 ppm, as seen clearly in x = 0.67.
5.3. Structure–property correlations
A successful model should accurately describe physical phenomena to have a practical use. One of the fundamental qualifications of a structural model in glass science is its ability to predict the glass density. The density of alkali and alkaline-earth borate glasses and its relation to packing and the underlying atomic structure has been studied in detail by Feller and co-workers.98–104 Different M+ and M2+ modifiers have been found to result in different volume fractions for different borate species, differing in the number of bridging oxygen associated with each borate unit.104 These volume fractions are related to the Shannon crystal radius105 of the metal cation. For Zn2+, the FIR data indicate coordination numbers span from 6 to 4. According to Shannon the values for the oxide crystal radii of ZnIV and ZnVI are 0.74 Å and 0.88 Å, respectively.105 These are close to the radii of LiIV and MgVI which are 0.73 Å and 0.86 Å, respectively.105 The volume fraction for borate units with varying degrees of polymerization has been previously determined for both Li and Mg.99,104 Without knowledge of the actual fraction of ZnIV and ZnVI species, and possibly ZnV, we make an estimation of the borate unit volume fraction for all binary xZnO–(1−x)B2O3 glasses by simply taking the mean of the volume fractions already determined for Li and Mg (Table 3).| Borate unit | j | Volume fraction (Vj) | ||
|---|---|---|---|---|
| LiIV | MgVI | Zn | ||
| BØ03 | 1 | 0.98 | 0.98 | 0.98 |
| BØ4− | 2 | 0.94 | 0.95 | 0.95 |
| BØ2O− | 3 | 1.28 | 1.26 | 1.27 |
| BØO22− | 4 | 1.61 | 1.46 | 1.54 |
| BO33− | 5 | 1.95a | N/A | 2 |
The volume fractions are calculated relative to V1 = 3.2 × 10−23 cm3,99 which corresponds to the volume of a boron atom with three bridging oxygen atoms. Values from Vj in lithium and magnesium borates are taken from a newer study104 for all units but the trigonal orthoborate unit, V5, for which only the original value from Shibata et al.99 of 1.95 is available. Here, we take the approximation V5 ≈ 2, while all other values of Vj are determined by (1/2) × (VLij + VMgj).
The mass of a given borate unit is also computed using the approach by Shibata et al.99 The mass of each structural unit, mj, is determined by the mass of the boron atom combined with the mass of the number of oxygen and zinc atoms belonging to the structural unit. These values are given in Table 4.
| Borate unit | j | B | O | Zn | Unit mass (mj) |
|---|---|---|---|---|---|
| 10.811 amu | 15.9994 amu | 65.39 amu | |||
| Number of atoms per borate unit | |||||
| BØ30 | 1 | 1 | 1.5 | 0 | 34.8 amu |
| BØ4− | 2 | 1 | 2 | 0.5 | 75.3 amu |
| BØ2O− | 3 | 1 | 2 | 0.5 | 75.3 amu |
| BØO22− | 4 | 1 | 2.5 | 1 | 116 amu |
| BO33− | 5 | 1 | 3 | 1.5 | 156 amu |
The predicted density at a given composition x, ρ'(x), is then written as
 | (24) |
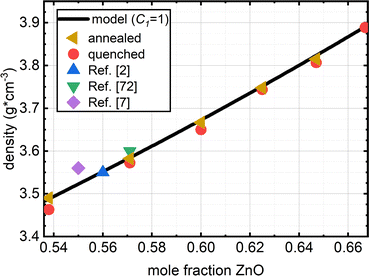 | ||
| Fig. 12 Predicted density using SRO modeled with the fictive temperature dependent constant C1 = 1 (solid black line) compared to experimental values for binary zinc borate glasses of this study (orange triangles and red circles) and other studies (blue triangle from ref. 2, green triangle from ref. 72, and purple diamond from ref. 7). | ||
Another comparison across a broader composition range is accessible via the Raman spectra. As seen in Fig. 10, the growth rate of the trigonal orthoborate (BO33−) population increases beyond the pyroborate stoichiometry, while Section 4.3 discussed the assignment of the 950 cm−1 feature to the symmetric stretching of the (BO3)3− unit. For a given vibrational mode, the spontaneous Stokes scattering intensity is linearly proportional to the population of the molecular unit exhibiting the particular vibration.25,78 The intensity of the 950 cm−1 feature is plotted against the predicted fraction of BO33− units in Fig. 13, demonstrating a strong linear correlation with an R2 value of 0.980.
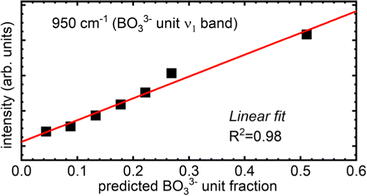 | ||
| Fig. 13 Comparison of the intensity of the Raman band at 950 cm−1 due to trigonal orthoborate units with the predicted fraction of the same (BO3)3− units. | ||
Lastly, we evaluate the predicted network connectivity to compare with glass transition temperature measurements. Taking the unit fractions from Fig. 10, the average number of bridging oxygen atoms per boron–oxygen unit, or the network connectivity, Nb is defined as
Nb(x) = 3![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 3(x) + 4 3(x) + 4![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 4(x) + 2 4(x) + 2![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2(x) + 2(x) + ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1(x) 1(x) |
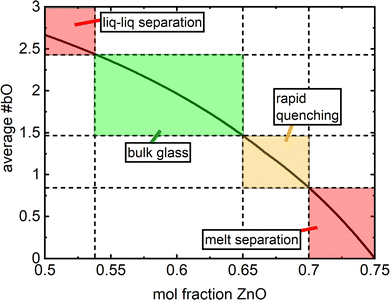 | ||
| Fig. 14 Theoretical connectivity of borate network as a function of ZnO content in binary zinc borate glasses. | ||
Taking the borate connectivity at ZnO content values corresponding to the studied compositions, the glass transition temperature is compared to the connectivity in Fig. 15. Compared to Fig. 4, in which the Tg was compared only to N4 from NMR, the average number of bO per boron exhibits a similar correlation with Tg. In both instances, the non-linear relations between the SRO borate units and the glass transition temperature are likely arising due to strong influence from the crosslinking of the intermediate zinc cations. The far infrared absorption profiles suggest an increasing fraction of ZnIV with increasing network depolymerization. With the same fixed charge in either case, the smaller radius of four-coordinated zinc yields a higher field strength for ZIV relative to ZVI (where the field strength is defined as Z = q/r2 where q is the cation charge and r is the radius). This change in zinc speciation may be working against the breakdown of interconnected borate units. Comparable to the intermediate role of alumina in silicate glasses, changing from a charge deficient network forming tetrahedron [AlØ4]− to a strong crosslinking modifier type octahedral Al3+,106 a charge deficient [ZnØ4]2− network forming type tetrahedral unit has been suggested.107 The stronger ionic crosslinking of increasing ZnIV–O–B segments appear to partially offset the destruction of covalent B–O–B linkages.
5. Conclusions
The glass forming region of the binary zinc borate system with composition xZnO–(1−x)B2O3 has been studied in detail. Liquid–liquid phase separation in the melt of the x = 0.50 composition resulted in a concentrated B2O3 material as well as a homogenous glass that was seen to be structurally identical to the glass of x = 0.54. From this, we conclude that x = 0.54 (7ZnO–6B2O3) marks the onset of the glass forming region, which was seen to extend up to x = 0.65. Through rapid splat quenching, glass formation was observed up to x = 0.70, beyond which chemical separation in the melt prevents glass formation all together. Rapidly splat quenching melts was seen to have a quantifiable impact on the tetrahedral boron population as measured by 11B MAS NMR, with slowly cooled and annealed samples having a higher N4 value than rapidly quenched and unannealed samples. In either preparation route, the N4 value decreased with increasing ZnO content.The use of 11B MAS NMR, infrared, and Raman spectroscopies provided detailed insight into the quantitative and qualitative structural aspects of binary zinc borate glasses. All spectroscopic techniques confirmed the expected depolymerization of the borate network with the addition of ZnO. For relatively low zinc oxide contents just above the metaborate stoichiometry, the structure is a robust combination of metaborate type chains mixed with an abundance of superstructural units (boroxol rings, borate rings) and highly charged borate anions (pyroborate dimers, orthoborate monomers). In these scenarios, the Zn2+ sites appear to be predominantly of the octahedral type as found by far infrared spectroscopy. With the addition of ZnO, the larger borate arrangements break down as the population of high charge density borate anions greatly increases, coinciding with an increasing population of tetrahedral Zn2+ sites. The presence of high field strength tetrahedral Zn2+ crosslinking borate anions is observed to partially offset the decrease in Tg due to the network depolymerization.
In a more general context, we have proposed a new theoretical approach to modeling the short-range order of glass forming units and successfully applied the model to the binary zinc borate system. Through a careful comparison with the existing literature of crystalline and vitreous borates, the short and intermediate range structural units have been identified qualitatively. By employing the laws of mass and charge conservation along with chemical reasoning, we have proposed for the first time, to the best of our knowledge, a complete and quantitative assessment of the short-range order structural units in the binary zinc borate glass system. The proposed model shows good agreement with actual density measurements with the estimated density within ±0.004 g cm−3 of experimental values. The model predicted fraction of tetrahedral boron is within 1% of the N4 values measured by NMR. Over the entire glass forming range from x = 0.54 to x = 0.70, the Raman intensity at 950 cm−1 due to the symmetric stretching of the trigonal orthoborate unit is linearly correlated with the model predicted fraction of the same structural unit with an R2 value of 0.98. Understanding the compositional dependence of the glass structure permits predictions of material properties, in turn allowing for a better tuning of glass composition for applications.
Author contributions
B. Topper: investigation, methodology, formal analysis, writing – original draft D. Möncke: supervision, resources, writing – review & editing R. E. Youngman: investigation, formal analysis, writing – review & editing C. Valvi: investigation E. I. Kamitsos: formal analysis, writing – review & editing, C. P. E. Varsamis: conceptualization, formal analysis, writing – review & editing, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
EIK, CPV and CV acknowledge support from “National Infrastructure in Nanotechnology, Advanced Materials and Micro-/Nanoelectronics” (MIS 5002772), co-financed by Greece and the European Union (European Regional Development Fund). BT and DM acknowledge the generosity of Dr Scott Misture (Alfred University) for permitting use of instrumentation for XRD, Raman and infrared studies. The WITec Raman data is based upon work supported by the National Science Foundation under Grant No. DMR-1626164. The publication of the article in OA mode was financially supported by HEAL-Link.References
- D. Ehrt, The Effect of ZnO, La2O3, PbO, and Bi2O3 on the properties of binary borate glasses and melts, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2006, 47(6), 669–674 CAS.
- D. Ehrt, Zinc and manganese borate glasses – Phase separation, crystallisation, photoluminescence, and structure, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2013, 54(2), 65–75 CAS.
- A. Herrmann, G. Völksch and D. Ehrt, Tb3+ as probe ion—Clustering and phase separation in borate and borosilicate glasses., Int. J. Appl. Glass Sci., 2019, 10(4), 532–545, DOI:10.1111/ijag.13209.
- A. C. Wright, Borate structures: Crystalline and vitreous, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2010, 51(1), 1–39 CAS.
- Z. Y. Yao, D. Möncke, E. I. Kamitsos, P. Houizot, F. Célarié, T. Rouxel and L. Wondraczek, Structure and Mechanical Properties of Copper-Lead and Copper-Zinc Borate Glasses., J. Non-Cryst. Solids, 2016, 435, 55–68 CrossRef CAS.
- D. Möncke, E. I. Kamitsos, D. Palles, R. Limbach, A. Winterstein-Beckmann, T. Honma, Z. Yao, T. Rouxel and L. Wondraczek, Transition and Post-Transition Metal Ions in Borate Glasses: Borate Ligand Speciation, Cluster Formation, and Their Effect on Glass Transition and Mechanical Properties, J. Chem. Phys., 2016, 145(12), 124501, DOI:10.1063/1.4962323.
- K. Januchta, R. E. Youngman, L. R. Jensen and M. M. Smedskjaer, Mechanical property optimization of a zinc borate glass by lanthanum doping, J. Non-Cryst. Solids, 2019, 520, 119461, DOI:10.1016/j.jnoncrysol.2019.119461.
- J. Krogh-Moe, The infrared spectra and the structure of some anhydrous zinc borates, Zeitschrift für Kristallographie, 1962, 117(2–3), 166–170, DOI:10.1524/zkri.1962.117.2-3.166.
- P. Smith-Verdier and S. Garcia-Blanco, Redetermination of the structure of anhydrous zinc metaborate Zn4O(BO2)6, Zeitschrift für Kristallographie – Crystalline Materials, 1980, 151(1–2), 175–177, DOI:10.1524/zkri.1980.151.1-2.175.
- A. Vegas, F. H. Cano and S. García-Blanco, Crystal structure of 3Bi2O3:5B2O3. A new type of polyborate anion (B5O11)7−, J. Solid State Chem., 1976, 17(1), 151–155, DOI:10.1016/0022-4596(76)90215-2.
- A. Hyman and A. Perloff, The crystal structure of bismuth (
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2:
2:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) borate, 2Bi2O3·B2O3, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28(7), 2007–2011, DOI:10.1107/S0567740872005436.
1) borate, 2Bi2O3·B2O3, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28(7), 2007–2011, DOI:10.1107/S0567740872005436. - D. E. Harrison and F. A. Hummel, Phase equilibria and fluorescence in the system zinc oxide-boric oxide, J. Electrochem. Soc., 1956, 103, 491–498, DOI:10.1149/1.2430391.
- E. Ingerson, G. W. Morey and O. F. Tuttle, The systems K2O–ZnO–SiO2, ZnO–B2O3–SiO2, and Zn2SiO4–Zn2GeO4, Am. J. Sci., 1948, 246(1), 31, DOI:10.2475/ajs.246.1.31.
- W. Guertler, On the limits of miscibility of boric oxide and borates in melts, Z. Anorg. Chem, 1904, 40, 225–253 CrossRef.
- E. H. Hamilton, R. M. Waxler and J. M. Nivert, Properties of zinc borosilicate glasses, J. Res. Natl. Bur. Stand., 1959, 62, 59 CrossRef CAS.
- I. Harris and P. J. Bray, B11 NMR studies of zinc borate compounds and glasses., Phys. Chem. Glasses, 1984, 25, 69–75 CAS.
- H. Eckert, Structural characterization of noncrystalline solids and glasses using Solid State NMR, Prog. Nucl. Magn. Reson. Spectrosc., 1992, 24(3), 159–293 CrossRef CAS.
- M. Bettinelli, A. Speghini, M. Ferrari and M. Montagna, Spectroscopic investigation of zinc borate glasses doped with trivalent europium ions, J. Non-Cryst. Solids, 1996, 201(3), 211–221, DOI:10.1016/0022-3093(96)00134-2.
- E. I. Kamitsos, M. A. Karakassides and G. D. Chryssikos, Vibrational spectra of magnesium-sodium-borate glasses. 2. Raman and Mid-Infrared investigation of the network structure, J. Phys. Chem., 1987, 91, 1073–1079 CrossRef CAS.
- Y. D. Yiannopoulos, G. D. Chryssikos and E. I. Kamitsos, Structure and properties of alkaline earth borate glasses, Phys. Chem. Glasses, 2001, 42(3), 164–172 CAS.
- B. N. Meera and J. Ramakrishna, Raman spectral studies of borate glasses, J. Non-Cryst. Solids, 1993, 159(1), 1–21, DOI:10.1016/0022-3093(93)91277-A.
- E. I. Kamitsos, A. P. Patsis, M. A. Karakassides and G. D. Chryssikos, Infrared reflectance spectra of lithium borate glasses, J. Non-Cryst. Solids, 1990, 126(1–2), 52–67 CrossRef CAS.
- T. Yano, N. Kunimine, S. Shibata and M. Yamane, Structural investigation of sodium borate glasses and melts by Raman spectroscopy. III. Relation between the rearrangement of super-structures and the properties of glass, J. Non-Cryst. Solids, 2003, 321(3), 157–168, DOI:10.1016/S0022-3093(03)00160-1.
- T. Yano, N. Kunimine, S. Shibata and M. Yamane, Structural investigation of sodium borate glasses and melts by Raman spectroscopy. II. Conversion between BO4 and BO2O− units at high temperature, J. Non-Cryst. Solids, 2003, 321(3), 147–156, DOI:10.1016/S0022-3093(03)00159-5.
- T. Yano, N. Kunimine, S. Shibata and M. Yamane, Structural investigation of sodium borate glasses and melts by Raman spectroscopy, J. Non-Cryst. Solids, 2003, 321(3), 137–146, DOI:10.1016/s0022-3093(03)00158-3.
- R. E. Youngman, NMR Spectroscopy in Glass Science: A Review of the Elements, Materials, 2018, 11(4), 476, DOI:10.3390/ma11040476.
- R. E. Youngman, S. Sen, L. K. Cornelius and A. J. G. Ellison, Novel structural aspects of Sb2O3–B2O3 glasses., Phys. Chem. Glasses, 2003, 44(2), 69–74 CAS.
- D. Möncke, D. Ehrt and E. I. Kamitsos, Spectroscopic study of manganese-containing borate and borosilicate glasses: Cluster formation and phase separation, Phys. Chem. Glasses, 2013, 54(1), 42–51 Search PubMed.
- O. L. Alderman, G. Ferlat, A. Baroni, M. Salanne, M. Micoulaut, C. J. Benmore, A. Lin, A. Tamalonis and J. K. R. Weber, Liquid B2O3 up to 1700 K: X-Ray diffraction and boroxol ring dissolution, J. Phys.: Condens. Matter, 2015, 27(45), 455104, DOI:10.1088/0953-8984/27/45/455104.
- O. L. G. Alderman, M. Liška, J. Macháček, C. J. Benmore, A. Lin, A. Tamalonis and J. K. R. Weber, Temperature-driven structural transitions in molten sodium borates Na2O–B2O3: X-ray diffraction, thermodynamic modeling, and implications for topological constraint theory, J. Phys. Chem. C, 2015, 120(1), 553–560, DOI:10.1021/acs.jpcc.5b10277.
- A. C. Hannon, D. I. Grimley, R. A. Hulme, A. C. Wright and R. N. Sinclair, Boroxol groups in vitreous boron oxide: New evidence from neutron diffraction and inelastic neutron scattering studies, J. Non-Cryst. Solids, 1994, 177, 299–316, DOI:10.1016/0022-3093(94)90544-4.
- W. Vogel, Glass Chemistry, Springer-Verlag, 2 edn, 1992 Search PubMed.
- D. Möncke, B. Topper and A. G. Clare, Glass as a State of Matter—The “newer” Glass Families from Organic, Metallic, Ionic to Non-silicate Oxide and Non-oxide Glasses, Rev. Mineral. Geochem., 2022, 87(1), 1039–1088, DOI:10.2138/rmg.2022.87.23.
- B. Topper, E. T. Tsekrekas, L. Greiner, R. E. Youngman, E. I. Kamitsos and D. Möncke, The dual role of bismuth in Li2O-Bi2O3–B2O3 glasses along the orthoborate join., J. Am. Ceram. Soc., 2022, 105(12), 7302–7320, DOI:10.1111/jace.18699.
- C. P. E. Varsamis, N. Makris, C. Valvi and E. I. Kamitsos, Short-range structure, the role of bismuth and property–structure correlations in bismuth borate glasses, Phys. Chem. Chem. Phys., 2021, 23(16), 10006–10020, 10.1039/D1CP00301A.
- D. Massiot, F. Fayon, M. Capron, I. King, S. Le Calvé, B. Alonso, J. O. Durand, B. Bujoli, Z. Gan and G. Hoatson, Modelling one-and two-dimensional solid-state NMR spectra, Magn. Reson. Chem., 2002, 40(1), 70–76, DOI:10.1002/mrc.984.
- P. M. Aguiar and S. Kroeker, Boron speciation and non-bridging oxygens in high-alkali borate glasses, J. Non-Cryst. Solids, 2007, 353(18–21), 1834–1839, DOI:10.1016/j.jnoncrysol.2007.02.013.
- H. Bradtmüller, B. M. Cerrutti, M. T. Souza, E. D. Zanotto and H. Eckert, Structural characterization of boron-containing glassy and semi-crystalline Biosilicate® by multinuclear NMR, J. Non-Cryst. Solids, 2019, 505, 390–399, DOI:10.1016/j.jnoncrysol.2018.10.045.
- D. Massiot, C. Bessada, J. Coutures and F. Taulelle, A quantitative study of 27Al MAS NMR in crystalline YAG, J. Magn. Reson., 1990, 90(2), 231–242 CAS.
- J.-P. Amoureux, C. Fernandez and S. Steuernagel, Z Filtering in MQMAS NMR, J. Magn. Reson., Ser. A, 1996, 123(1), 116–118 CrossRef CAS PubMed.
- F. L. Galeener and P. N. Sen, Theory for the first-order vibrational spectra of disordered solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17(4), 1928–1933, DOI:10.1103/PhysRevB.17.1928.
- C. F. Windisch and W. M. Risen, Vibrational spectra of oxygen- and boron-isotopically substituted B2O3 glasses, J. Non-Cryst. Solids, 1982, 48(2), 307–323, DOI:10.1016/0022-3093(82)90168-5.
- J. L. George and R. K. Brow, In-situ characterization of borate glass dissolution kinetics by μ-Raman spectroscopy, J. Non-Cryst. Solids, 2015, 426, 116–124, DOI:10.1016/j.jnoncrysol.2015.07.003.
- S. Yamauchi and S. Doi, Raman spectroscopic study on the behavior of boric acid in wood, J. Wood Sci., 2003, 49(3), 227–234, DOI:10.1007/s10086-002-0466-x.
- S. Sasaki, A. Masuno, K. Ohara, Y. Yanaba, H. Inoue, Y. Watanabe and S. Kohara, Structural origin of additional infrared transparency and enhanced glass-forming ability in rare-earth-rich borate glasses without B–O networks, Inorg. Chem., 2020, 59(19), 13942–13951, DOI:10.1021/acs.inorgchem.0c01567.
- A. Masuno, Functionalities in unconventional oxide glasses prepared using a levitation technique, J. Ceram. Soc. Jpn., 2022, 130(8), 563–574, DOI:10.2109/jcersj2.2.
- S. K. Wilke, O. L. Alderman, C. J. Benmore, J. Neuefeind and R. Weber, Octahedral oxide glass network in ambient pressure neodymium titanate, Sci. Rep., 2022, 12(1), 1–17, DOI:10.1038/s41598-022-12342-x.
- V. A. Nikitenko and A. I. Tereshchenko, Photo- and thermoluminescence excitation spectra of zinc oxide single crystals, J. Appl. Spectrosc., 1979, 30(5), 599–602, DOI:10.1007/BF00608421.
- G. E. Walrafen, M. S. Hokmabadi, P. N. Krishnan, S. Guha and R. G. Munro, Low frequency Raman Scattering from Vitreous and Molten B2O3, J. Chem. Phys., 1983, 79, 3609–3620, DOI:10.1063/1.446297.
- A. K. Hassan, L. M. Torell, L. Borjesson and H. Doweidar, Structural changes of B2O3 through the liquid-glass transition range: A Raman-scattering study, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(22), 12797–12805, DOI:10.1103/physrevb.45.12797.
- G. Lelong, L. Cormier, L. Hennet, F. Michel, J.-P. Rueff, J. M. Ablett and G. Monaco, Lithium borates from the glass to the melt: A temperature-induced structural transformation viewed from the boron and oxygen atoms, Inorg. Chem., 2021, 60(2), 798–806, DOI:10.1021/acs.inorgchem.0c02844.
- A. A. Sobol, V. E. Shukshin and A. I. Zaitsev, Raman spectroscopy of crystalline, glassy, and molten states of lead diborate, Opt. Spectrosc., 2016, 121(6), 810–818, DOI:10.1134/S0030400X16120249.
- E. I. Kamitsos and M. A. Karakassides, Effect of melt temperature on glass structure, Phys. Chem. Glasses, 1989, 30(6), 235–236 CAS.
- C.-P. E. Varsamis, A. Vegiri and E. I. Kamitsos, Molecular dynamics investigation of lithium borate glasses: local structure and ion dynamics, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65(10), 104203, DOI:10.1103/PhysRevB.65.104203.
- P. M. Machowski, C. P. E. Varsamis and E. I. Kamitsos, Dependence of sodium borate glass structure on depth from the sample surface, J. Non-Cryst. Solids, 2004, 345–346, 213–218, DOI:10.1016/j.jnoncrysol.2004.08.025.
- A. Q. Tool and C. G. Eichlin, Variations caused in the heating curves of glass by heat treatment, J. Am. Ceram. Soc., 1931, 14(4), 276–308, DOI:10.1111/j.1151-2916.1931.tb16602.x.
- S. Kroeker, P. M. Aguiar, A. Cerquiera, J. Okoro, W. Clarida, J. Doerr, M. Olesiuk, G. Ongie, M. Affatigato and S. A. Feller, Alkali dependence of tetrahedral boron in alkali borate glasses, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2006, 47(4), 393–396 CAS.
- Y. H. Yun and P. J. Bray, B11 Nuclear Magnetic Resonance studies of Li2O–B2O3 glasses of high Li2O content, J. Non-Cryst. Solids, 1981, 44, 227–237, DOI:10.1016/0022-3093(81)90025-9.
- M. Affatigato, S. Feller, E. J. Khaw, D. Feil, B. Teoh and O. Matthews, The glass transition temperature of lithium and lithium-sodium borate glasses over wide ranges of composition, Phys. Chem. Glasses, 1990, 31, 19–24 CAS.
- E. I. Kamitsos, Modifying role of alkali-metal cations in borate glass networks, J. Phys. Chem., 1989, 93(4), 1604–1611, DOI:10.1021/j100341a083.
- E. I. Kamitsos, G. D. Chryssikos and M. A. Karakassides, Glass transition phenomena and cation vibrations in alkali borate glasses, Phys. Chem. Glasses, 1988, 29(3), 121–126 CAS.
- E. Kamitsos, A. Patsis and G. D. Chryssikos, Infrared reflectance investigation of alkali diborate glasses, J. Non-Cryst. Solids, 1993, 152(2–3), 246–257, DOI:10.1016/0022-3093(93)90258-Y.
- B. Topper and D. Möncke, Structure and Properties of Borate Glasses, in Phosphate and Borate Bioactive Glasses, The Royal Society of Chemistry, 2022, pp. 162–191 Search PubMed.
- G. D. Chryssikos, Bond length Raman frequency correlations in borate crystals, J. Raman Spectrosc., 1991, 22, 645–650, DOI:10.1002/jrs.1250221109.
- E. I. Kamitsos, M. A. Karakassides and G. D. Chryssikos, A vibrational study of lithium borate glasses with high Li2O content., Phys. Chem. Glasses, 1987, 28(5), 203–209 CAS.
- W. L. Konijnendijk and J. M. Stevels, The structure of borate glasses studied by Raman scattering, J. Non-Cryst. Solids, 1975, 18, 307–331, DOI:10.1016/0022-3093(75)90137-4.
- E. I. Kamitsos and G. D. Chryssikos, Borate glass structure by Raman and infrared spectroscopies, J. Mol. Struct., 1991, 247, 1–16, DOI:10.1016/0022-2860(91)87058-p.
- G. D. Chryssikos, J. A. Kapoutsis, E. I. Kamitsos, A. J. Patsis and A. J. Pappin, Lithium-sodium metaborate glasses: structural aspects and vitrification chemistry, J. Non-Cryst. Solids, 1994, 167(1), 92–105, DOI:10.1016/0022-3093(94)90372-7.
- G. D. Chryssikos, E. I. Kamitsos, A. P. Patsis and M. A. Karakassides, On the structure of alkali borate glasses approaching the orthoborate composition, Mater. Sci. Eng., B, 1990, 7(1), 1–4, DOI:10.1016/0921-5107(90)90002-S.
- B. Topper, N. S. Tagiara, A. Herrmann, E. I. Kamitsos and D. Möncke, Yttrium and rare-earth modified lithium orthoborates: glass formation and vibrational activity, J. Non-Cryst. Solids, 2022, 575, 121152, DOI:10.1016/j.jnoncrysol.2021.121152.
- E. I. Kamitsos, M. A. Karakassides and G. Chryssikos, Structure of borate glasses. Part 1. Raman study of caesium, rubidium, and potassium borate glasses, Phys. Chem. Glasses, 1989, 30(6), 229–234 CAS.
- L. Del Longo, M. Ferrari, E. Zanghellini, M. Bettinelli, J. A. Capobianco, M. Montagna and F. Rossi, Optical spectroscopy of zinc borate glass activated by Pr3+ ions., J. Non-Cryst. Solids, 1998, 231(1), 178–188, DOI:10.1016/S0022-3093(98)00409-8.
- G. Ferlat, T. Charpentier, A. P. Seitsonen, A. Takada, M. Lazzeri, L. Cormier, G. Calas and F. Mauri, Boroxol rings in liquid and vitreous B2O3 from first principles, Phys. Rev. Lett., 2008, 101(6), 065504, DOI:10.1103/PhysRevLett.101.065504.
- R. Youngman and J. Zwanziger, Multiple boron sites in borate glass detected with dynamic angle spinning nuclear magnetic resonance, J. Non-Cryst. Solids, 1994, 168(3), 293–297, DOI:10.1016/0022-3093(94)90342-5.
- F. L. Galeener, J. C. J. Mikkelsen, R. H. Geils and W. J. Mosby, The relative Raman cross sections of vitreous SiO2, GeO2, B2O3, and P2O5, Appl. Phys. Lett., 1978, 32(1), 34–36, DOI:10.1063/1.89823.
- A. Winterstein-Beckmann, D. Moncke, D. Palles, E. I. Kamitsos and L. Wondraczek, Structure and properties of orthoborate glasses in the Eu2O3-(Sr,Eu)O-B2O3 quaternary, J. Phys. Chem. B, 2015, 119(7), 3259–3272, DOI:10.1021/jp5120465.
- A. Winterstein-Beckmann, D. Möncke, D. Palles, E. I. Kamitsos and L. Wondraczek, Structure–property correlations in highly modified Sr, Mn-borate glasses, J. Non-Cryst. Solids, 2013, 376, 165–174, DOI:10.1016/j.jnoncrysol.2013.05.029.
- B. Topper, On the structure of lithium and strontium borate glasses modified with yttrium and rare-earth cations investigated by, vibrational spectroscopy, Alfred University, 2020 Search PubMed.
- J. Plewa and T. Jüstel, Phase Transition of YBO3, J. Therm. Anal. Calorim., 2007, 88(2), 531, DOI:10.1007/s10973-006-8029-9.
- G. X. Gu, D. Wang, X. S. Lv, S. M. Wan, J. L. You, Q. L. Zhang and S. T. Yin, In situ study on the structural transition in YBO3 through Raman spectroscopy, Mater. Chem. Phys., 2011, 131(1–2), 274–277, DOI:10.1016/j.matchemphys.2011.09.041.
- R. S. Drago, Physical Methods in Inorganic Chemistry, University of Illinois-Urbana: Reinhold Publishing Corp., 1965 Search PubMed.
- G. D. Chryssikos, E. I. Kamitsos, A. P. Patsis, M. S. Bitsis and M. A. Karakassides, The devitrification of lithium metaborate: polymorphism and glass formation, J. Non-Cryst. Solids, 1990, 126(1), 42–51, DOI:10.1016/0022-3093(90)91022-J.
- K. I. Chatzipanagis, N. S. Tagiara, E. I. Kamitsos, N. Barrow, I. Slagle, R. Wilson, T. Greiner, M. Jesuit, N. Leonard and A. Phillips, Structure of lead borate glasses by Raman, 11B MAS, and 207Pb NMR spectroscopies., J. Non-Cryst. Solids, 2022, 589, 121660, DOI:10.1016/j.jnoncrysol.2022.121660.
- Q.-Z. Huang, G.-F. Wang and J.-K. Liang, Phase equilibrium relation of BaB2O4–Li2B2O4 and BaB2O4–Li2O sections in the ternary system BaO–Li2O–B2O3, Acta Phys. Sin., 1984, 33, 76 CrossRef CAS.
- R. W. Smith and D. A. Keszler, The pentaborate Ba2LiB5O10, Mater. Res. Bull., 1989, 24(6), 725–731, DOI:10.1016/0025-5408(89)90089-5.
- H. F. McMurdie, X-ray studies of compounds in the systems PbO–B2O3 and K2O–PbO–SiO2, J. Res. Natl. Bur. Stand., 1941, 26, 489 CrossRef CAS.
- J. Krogh-Moe, The crystal structure of strontium diborate, SrO–2B2O3, Acta Chem. Scand., 1964, 18, 2055–2060 CrossRef CAS.
- U. Hoppe, R. K. Brow, D. Ilieva, P. Jóvári and A. C. Hannon, Structure of rare-earth phosphate glasses by X-ray and neutron diffraction, J. Non-Cryst. Solids, 2005, 351(40), 3179–3190, DOI:10.1016/j.jnoncrysol.2005.08.016.
- J. Felsche, Rare-earth silicates with the apatite structure, J. Solid State Chem., 1972, 5(2), 266–275, DOI:10.1016/0022-4596(72)90039-4.
- J. Wang, W. S. Brocklesby, J. R. Lincoln, J. E. Townsend and D. N. Payne, Local structures of rare-earth ions in glasses: the ‘crystal-chemistry’ approach, J. Non-Cryst. Solids, 1993, 163(3), 261–267, DOI:10.1016/0022-3093(93)91303-K.
- E. I. Kamitsos, Infrared Spectroscopy of Glasses, in Modern Glass Characterization, ed. M. Affatigato, The American Ceramic Society and John Wiley & Sons, Inc., 2015, pp. 1–42 Search PubMed.
- J. Krogh-Moe, Interpretation of the infra-red spectra of boron oxide and alkali borate glasses, Phys. Chem. Glasses, 1965, 6(2), 46–54 CAS.
- P. Smith, S. Garcia-Blanco and L. Rivoir, The crystal structure of anhydrous zinc metaborate Zn4O(BO2)6, Zeitschrift für Kristallographie, 1964, 119(5–6), 375–383, DOI:10.1524/zkri.1964.119.5-6.375.
- A. F. Murray and D. J. Lockwood, Raman spectrum of Zn4O(BO2)6, J. Phys. C – Solid State Phys., 1976, 9(19), 3691–3700, DOI:10.1088/0022-3719/9/19/020.
- M. Martinez-Ripoll, S. Martínez-Carrera and S. García-Blanco, The crystal structure of zinc diborate ZnB4O7, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1971, 27(3), 672–677, DOI:10.1107/S0567740871002759.
- S. García-Blanco and J. Fayos, The crystal structure of zinc orthoborate, Zn3(BO3)2, Zeitschrift Fur Kristallographie, 1968, 127, 145–159, DOI:10.1524/zkri.1968.127.16.145.
- S. Kroeker and J. F. Stebbins, Three-coordinated boron-11 chemical shifts in borates, Inorg. Chem., 2001, 40(24), 6239–6246, DOI:10.1021/ic010305u.
- S. Feller, Borate Glasses, in Springer Handbook of Glass, ed. J. D. Musgraves, J. Hu and L. Calvez, Springer International Publishing, Cham, 2019, pp. 505–524 Search PubMed.
- M. Shibata, C. Sanchez, H. Patel, S. A. Feller, J. Stark, G. Sumcad and J. Kasper, The density of lithium borate glasses related to atomic arrangements, J. Non-Cryst. Solids, 1986, 85(1–2), 29–41, DOI:10.1016/0022-3093(86)90076-1.
- A. Karki, S. A. Feller, H. P. Lim, J. Stark, C. Sanchez and M. Shibata, The density of sodium-borate glasses related to atomic arrangements, J. Non-Cryst. Solids, 1987, 92(1), 11–19, DOI:10.1016/S0022-3093(87)80355-1.
- H. C. Lim and S. Feller, The density of low metal content rubidium, cesium, silver, and thallium borate glasses related to atomic arrangements, J. Non-Cryst. Solids, 1987, 94(1), 36–44, DOI:10.1016/S0022-3093(87)80258-2.
- H. P. Lim, A. Karki, S. Feller, J. E. Kasper and G. Sumcad, The density of potassium borate glasses related to atomic arrangements, J. Non-Cryst. Solids, 1987, 91(3), 324–332, DOI:10.1016/S0022-3093(87)80343-5.
- S. Kapoor, H. Bola George, A. Betzen, M. Affatigato and S. Feller, Physical properties of barium borate glasses determined over a wide range of compositions, J. Non-Cryst. Solids, 2000, 270(1), 215–222, DOI:10.1016/S0022-3093(00)00061-2.
- N. P. Lower, J. L. McRae, H. A. Feller, A. R. Betzen, S. Kapoor, M. Affatigato and S. A. Feller, Physical properties of alkaline-earth and alkali borate glasses prepared over and extended range of compositions, J. Non-Cryst. Solids, 2001, 293–295, 559–675 Search PubMed.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Found. Adv., 1976, 32(5), 751–767, DOI:10.1107/S0567739476001551.
- N. Sawangboon, A. Nizamutdinova, T. Uesbeck, R. Limbach, E. Meechoowas, K. Tapasa, D. Möncke, L. Wondraczek, E. I. Kamitsos, L. van Wüllen and D. S. Brauer, Modification of silicophosphate glass composition, structure and properties via crucible material and melting conditions, Int. J. Appl. Glass Sci., 2019, 11, 46–57, DOI:10.1111/ijag.13958.
- D. Ehrt and S. Flügel, Properties of zinc silicate glasses and melts, Mater. Sci. Eng., A, 2011, 1(8), 312–320, DOI:10.17265/2161-6213/2011.08.002.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05517a |
| This journal is © the Owner Societies 2023 |