Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Role of electron localisation in H adsorption and hydride formation in the Mg basal plane under aqueous corrosion: a first-principles study†
Bingxin
Li
 a,
Chengcheng
Xiao
a,
Chengcheng
Xiao
 a,
Nicholas M.
Harrison
ab,
Richard M.
Fogarty
a and
Andrew P.
Horsfield
a,
Nicholas M.
Harrison
ab,
Richard M.
Fogarty
a and
Andrew P.
Horsfield
 *a
*a
aThomas Young Centre, Department of Materials, Imperial College London, Exhibition Road, London SW7 2AZ, UK. E-mail: a.horsfield@imperial.ac.uk
bDepartment of Chemistry, Imperial College London, 82 Wood Lane, London W12 0BZ, UK
First published on 1st February 2023
Abstract
Understanding hydrogen-metal interactions is important in various fields of surface science, including the aqueous corrosion of metals. The interaction between atomic H and a Mg surface is a key process for the formation of sub-surface Mg hydride, which may play an important role in Mg aqueous corrosion. In the present work, we performed first-principles Density Functional Theory (DFT) calculations to study the mechanisms for hydrogen adsorption and crystalline Mg hydride formation under aqueous conditions. The Electron Localisation Function (ELF) is found to be a promising indicator for predicting stable H adsorption in the Mg surface. It is found that H adsorption and hydride layer formation is dominated by high ELF adsorption sites. Our calculations suggest that the on-surface adsorption of atomic H, OH radicals and atomic O could enhance the electron localisation at specific sites in the sub-surface region, thus forming effective H traps locally. This is predicted to result in the formation of a thermodynamically stable sub-surface hydride layer, which is a potential precursor of the crucial hydride corrosion product of magnesium.
1 Introduction
The interaction of reactive atomic or molecular hydrogen with various metal surfaces has spawned great interest as a result of its significance in numerous industries and applications.1–3 Understanding the basic principle of H adsorption, dissociation and desorption on metal surfaces is of high priority for improving the efficiency of H-related heterogeneous catalytic reactions and enhancing the productivity of hydrogen fuel cells or hydrogen storage.4,5 Among a large number of metals, the hydrogen–Mg interaction has been extensively investigated because Mg is a promising inexpensive material for large-scale hydrogen storage.6–8 In addition, it has been suggested that the study of the interplay between H atoms or H2 molecules and the Mg surfaces also has a practical significance in revealing the mechanism of Mg aqueous corrosion.9,10Mg, as the lightest engineering metal, is widely used in the automobile sectors (Mg–Al based alloys, such as AM50) and clinical medicine (Mg–Zn binary alloys) thanks to its high mechanical strength and benign biocompatibility.11,12 However, further applications of Mg and its alloys have been restricted by their poor corrosion resistance in a humid environment. Under aqueous conditions, Mg rapidly corrodes and reacts with water molecules, generates hydrogen gas and forms a dark corrosion film on the metal surface.13 This surface film is generally a porous bi-layer structure which is composed of an inner MgO layer with a Mg(OH)2-rich outer layer.14,15 Due to a large number of pores and cracks in the corrosion film, it only provides limited protection to the bulk Mg from further corrosion. Several observed corrosion phenomena of Mg, such as the negative difference effect (NDE) and the hydrogen evolution reaction (HER) kinetics, have been attributed to the on-surface corrosion product formed during aqueous corrosion.16,17
In addition to the basic corrosion product (MgO and Mg(OH)2) in the surface film, crystalline Mg hydride, which is produced initially from the H–Mg surface interaction, also forms and plays a role in aqueous Mg corrosion. Liu et al. observed the presence of this Mg hydride underneath the surface layer of high purity Mg after being corroded by distilled water.18 A crystalline Mg hydride structure is also found enriched in the β-phase of Mg–Al based alloys, whose formation could be attributed to atomic H adsorption and diffusion into the bulk Mg.19 Because the calculated energy barrier for H atoms diffusing from the top surface of Mg to the bulk phase is smaller (0.7 eV) than that of the hydrogen evolution reaction (approximately 1.04 eV) on the Mg basal plane, the adsorbed H atoms are highly mobile and could penetrate the surface to form a crystalline Mg hydride or a hydride-like structure underneath the metal surface.9,20,21 Moreover, the Pourbaix diagram of Mg–H2O shows that this Mg hydride phase could form in the whole pH range under a cathodic potential.22 This finding is supported by some previous studies: under cathodic polarisation, the corrosion-related current density (Ic) of Mg is composed of the cathodic hydrogen evolution density (Ih) and the MgH2-formation current density (Im).23 Binns et al. also verified that the MgH2 layer is found underneath the top surface of the Mg sample that is pre-treated cathodically, and concluded that MgH2 might have the ability to enhance the anodic hydrogen evolution during aqueous corrosion through its decomposition, and thus form a filiform corrosion morphology.24 In a previous ab initio study, Jiang et al. found a stable sub-surface hydride-like tri-layer structure (H–Mg–H) in a hydrogen environment (Mg surface interacting with hydrogen gas), which could be the structure of a precursor to MgH2.25
Although various experimental and simulation results demonstrate the existence of crystalline MgH2, or a hydride-like layer, underneath the Mg surface during aqueous corrosion, the atomic scale formation mechanism of this Mg hydride structure under aqueous conditions at the open circuit potential (OCP) is still unclear. Furthermore, the influence of the surface adsorption state (with different surface adsorbates, such as atomic H, OH radicals and atomic O) on the formation of the sub-surface hydride structure also requires further detailed investigation. In the present study, we applied first-principles calculations (in the density functional framework) to explore the hydrogen adsorption and hydride formation mechanisms at Mg surfaces with different adsorption states. Finding low energy structures formally involves searching the very large phase space of all possible surface compositions and structures. We discovered that the electron localisation function (ELF) is a good indicator that can be used to predict the energetically favourable positions for H adsorption within Mg surfaces, and the formation of sub-surface hydride structures is dominated by this ELF-oriented H adsorption. We also found that the on-surface adsorption could influence the ELF pattern of the surface, thus altering the sub-surface H adsorption. The theoretical basis and computational details are reviewed in Section 2. The results for H adsorption on a pristine/hydride/hydroxylated/oxidised Mg (0001) surface are demonstrated and discussed in Section 3, and the conclusions of the paper are given in Section 4.
2 Theory and methods
2.1 Theory of the electron localisation function (ELF)
In this paper, we demonstrate that the electron localisation function (ELF) can be a good predictor for the possible adsorption sites of small adsorbates on Mg surfaces.The ELF was introduced by Becke and Edgecombe to identify covalent bonds in simple molecular systems.26 As a measure of the degree of Pauli exclusion at a point in space, the ELF is calculated as the probability of finding an electron in the vicinity of another like-spin electron.27 The formula of the ELF proposed by Becke and Edgecombe can be written as:
 | (1) |
 | (2) |
 . The denominator in eqn (2), τUEGσ, is the same as the numerator but calculated for a uniform electron gas with the same local density.
. The denominator in eqn (2), τUEGσ, is the same as the numerator but calculated for a uniform electron gas with the same local density.
The numerator in eqn (2) is sometimes also called the Pauli kinetic energy density Dσ for it signifies the degree of Pauli exclusion at a point in space.31 A small Dσ indicates a small probability of finding a second like-spin electron near the reference point (high Pauli exclusion) thus suggesting that the electron is highly localised around that particular region in the space. The employment of the kinetic energy density of the uniform electron gas (D0σ) serves as a reference to Dσ, and the final form of eqn (1) restricts the value of ELF to be between 0 and 1. The upper limit of 1 of the ELF denotes complete electron localisation (such as a point charge in space), and an ELF value of 0.5 corresponds to having the same degree of localisation as a homogeneous electron gas with the same local density. Therefore, the higher the ELF value, the more localised the electrons. The position of a local ELF maximum is sometimes also denoted as an attractor. Such attractors behave like electrophiles, such as protons.32
The ELF has been demonstrated to be a powerful tool to differentiate the nature of chemical bonds for many materials.32,33 At the same time, the ELF has also been used to investigate the electron distribution of metal surfaces with different packing patterns.34,35 The chemisorption bonds between metal surfaces and some isoelectronic species can also be investigated using the ELF.36 There have been reports showing that the ELF can be used to predict the position of hydrogen atoms in hydrides.37,38 For instance, the ELF pattern of the pure Ca substructure can be used to predict the possible H positions in its hydride form CaH2, indicating that high ELF regions have a high probability of attracting hydrogen atoms.32 It has also been found recently that removing the on-surface hydrogen from the (110) surface of Mg hydride could form a high ELF region which is localised at the position of the H vacancy.39 Furthermore, the ELF has been shown to be independent of the particular computational method used, such as basis sets and pseudopotentials.40 As a result, the ELF is a promising and reliable instrument for analysing the possible H adsorption sites in metal surfaces.
2.2 Computational methods
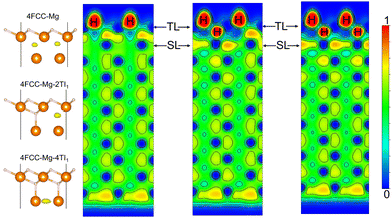
To simulate the chemisorption processes on a Mg surface, first-principles calculations based on the DFT formalism were performed as implemented in the Vienna Ab Initio Software Package (VASP).41,42 The Projector Augmented-Wave (PAW) method with the frozen core approximation was employed to model the electronic wavefunctions where Mg's 3s, O's 2s and 2p, and H's 1s are treated as valence electrons.43,44 A kinetic-energy cutoff of 700 eV was used for the plane-wave expansion of the valence wavefunctions of systems that contain Mg and H. For systems that have Mg, H and O, a tighter 750 eV cutoff was used to to ensure the total energy converges within 1 meV per atom. Electronic exchange and correlation were described using the Perdew–Burke–Ernzerhof (PBE) variant of the generalized gradient approximation (GGA).45 For the Mg (0001) surface, the Brillouin-zone was sufficiently sampled by a Γ-centred 8 × 8 × 1 Monkhorst–Pack k-point mesh with the total energy per unit cell converges within 5 meV.46 The electronic minimisation process was deemed converged when a total energy difference of 0.01 meV (per unit cell) between two steps was achieved. The atomic positions were fully relaxed to a force tolerance of 1 meV Å−1.The Mg (0001) surface was modelled by a p(2 × 2) slab prototype. The slab is selected as 11-layer thick so that the interaction between both sides of the slab becomes negligible and the surface energy converges within 0.1 meV Å−2. This periodic surface unit cell is also large enough along the x and y directions to allow the simulation of chemisorbtion with surface coverages ranging from 0.25 monolayer (ML) to 1 monolayer (ML). The lattice parameters of the slab were 6.40 × 6.40 × 45.83 Å3, which were determined from the cell optimization of the bulk Mg cell. To eliminate spurious interactions between image structures due to periodic boundary conditions, a vacuum of 20 Å was added in the z-direction (surface normal direction). We added H, O, and OH as adsorbates to the available surface adsorption sites and sub-surface interstitial sites (Fig. 1) on one side of the slab. This asymmetric configuration leads to a dipole moment in the unit cell, which was countered by adding a dipole layer in the vacuum.47 For the on-surface adsorption, the surface fcc and hcp hollow sites were considered to be potentially occupied by H, O and OH radicals. For the sub-surface interstitial sites, we took only H uptake into account because of the small size of H and its high mobility in the Mg substrate.48
For the surface with a sub-monolayer coverage of H, OH, or O, we chose a consistent reference (an H2 molecule, a clean Mg basal plane, and a water molecule) when calculating the adsorption energy per adsorbate. The adsorption energy 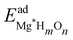 is given by
is given by
 | (3) |
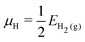 | (4) |
| μO = EH2O(g) − 2μH | (5) |
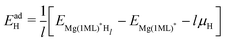 | (6) |
Here EMg(1ML)*Hl is the total energy of the Mg (0001) surfaces (fully covered with H, OH, or O) whose sub-surface interstitial sites are occupied by H atoms, and EMg(1ML)* is the energy of the reference fully covered Mg surfaces. l is the number of sub-surface H atoms per unit cell. A negative H adsorption energy indicates that the sub-surface hydrogen adsorption, at a certain interstitial site within the fully covered Mg surfaces, is exothermic compared with a H2 gas molecule, thus suggesting a stable H sub-surface structure in the Mg basal plane.
We note that zero-point energy (ZPE) was not included in our adsorption energy calculations. A previous study has demonstrated that for the hydrogen dissociative adsorption on the Mg basal plane, the difference in ZPE between one H atom in the H2 gas and adsorbed on to the Mg (0001) surface is less than 2 meV.25 This insignificant ZPE change for H thus contributes little to the total adsorption energy. Similarly, it has been found that the ZPE difference between O and OH adsorption on the metal surface is approximately 15 meV, suggesting that it has negligible influence on the adsorption energy differences reported here.50,51 Based on these findings, we deemed that it is unnecessary to include ZPE correction in the current study. We also verified that introducing the solvent effect in our calculations barely alters the adsorption patterns and the most stable adsorption phases (ESI†). Thus, ignoring the solvent effect in our calculations does not change the conclusions.
3 Results and discussion
3.1 H adsorption on or below the Mg (0001) Surface
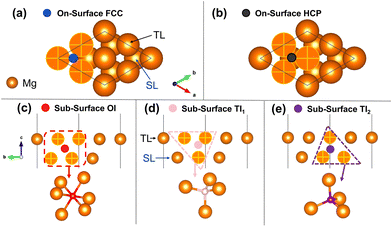
In this section, we investigate H adsorption on a Mg (0001) surface from our DFT calculations. At low H coverage (less than 1 ML), the favourable adsorption sites for H are on-surface fcc and hcp sites. For the surfaces pre-covered with 1 ML H, sub-surface H adsorption becomes thermodynamically stable. By analysing the ELF pattern for the clean Mg surface and for the H pre-covered surface, we find that ELF is a promising indicator for determining the possible stable adsorption sites for H in a Mg surface.Using the pristine surface and H2 gas as references, the adsorption energies of H in the three sub-surface sites considered are all positive for all H coverages. This demonstrates that sub-surface H adsorption is thermodynamically unfavourable at low H concentrations under the Mg (0001) surface. The tetrahedral-I adsorption configuration is only stable for a H coverage larger than 0.75 ML, below which it automatically relaxed into the surface hcp configuration after geometry optimisation. Therefore, only the adsorption energies for higher coverage are shown for the tetrahedral-I adsorption in Fig. 2. The H adsorption energy suggests that when the surface H concentration is low, H preferentially adsorbs onto the Mg (0001) surface instead of penetrating into the sub-surface. This finding of selective H adsorption preference based on H concentration is consistent with previous works.25,52
To understand why a hydrogen atom tends to bind to the on-surface hollow sites rather than the sub-surface interstitial sites, we considered four different energy components that contribute to the total adsorption energy, namely the H2 dissociation energy, the lattice distortion energy, the ELF-related energy and the Coulomb interaction energy, and estimated the individual contribution of each component. Because the H2 molecule is set as the reference, the dissociation energy of the H2 molecule is a dominating constituent that increases the adsorption energy. The DFT-calculated value for the H2 bond (breaking an H2 molecule into two H atoms) is approximately 3.36 eV per H, which is close to the value calculated by Kresse of 3.40 eV per H.53 In addition to the energy penalty caused by breaking the H–H bond, inserting H into the Mg surface requires a distortion of the surface structure due to the non-negligible size of the H atoms. The energy of this distortion (sometimes also called the deformation energy) can be calculated as54
 | (7) |
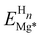 is the energy of the distorted (by n H atoms) Mg slab computed without the H atom(s) present and EMg* is the total energy of a relaxed pristine Mg (0001) slab. Table 1 shows the calculated distortion energy for the Mg (0001) surface with H at certain coverages in different sites. For the on-surface adsorptions, the distortion energy per H atom decreases with an increase in H coverage, and the contribution of the distortion energy to the total adsorption energy is diminished. The distortion energy of fcc adsorption is larger than that for hcp at all coverages. This distortion energy difference between fcc and hcp plays a more significant role in the total adsorption energy difference at low H coverage (less than 0.50 ML). At higher coverage, the difference in total adsorption energy between fcc and hcp is far larger than the difference in distortion energy (at 1 ML, the difference in total adsorption energy is approximately 93 meV while the difference in distortion energy is only 1.3 meV), indicating that there are other energy components that dominate the overall difference. The distortion energy for the sub-surface tetrahedral adsorption increases with a larger H coverage, and is significantly larger than that of the on-surface and octahedral interstitial (OI) adsorptions. For the H adsorbed in the OI site, the distortion energy is relatively low when the coverage is less than 0.5 ML. However, the total adsorption energy of OI adsorption is much more positive than the on-surface adsorption, where the distortion energy is larger than the OI adsorption at 0.25 ML and 0.5 ML. This significant positive adsorption energy of the OI adsorption could be attributed to the lack of other essential energy lowering contributions, such as the H-electron interaction, and will be explained specifically in the following.
is the energy of the distorted (by n H atoms) Mg slab computed without the H atom(s) present and EMg* is the total energy of a relaxed pristine Mg (0001) slab. Table 1 shows the calculated distortion energy for the Mg (0001) surface with H at certain coverages in different sites. For the on-surface adsorptions, the distortion energy per H atom decreases with an increase in H coverage, and the contribution of the distortion energy to the total adsorption energy is diminished. The distortion energy of fcc adsorption is larger than that for hcp at all coverages. This distortion energy difference between fcc and hcp plays a more significant role in the total adsorption energy difference at low H coverage (less than 0.50 ML). At higher coverage, the difference in total adsorption energy between fcc and hcp is far larger than the difference in distortion energy (at 1 ML, the difference in total adsorption energy is approximately 93 meV while the difference in distortion energy is only 1.3 meV), indicating that there are other energy components that dominate the overall difference. The distortion energy for the sub-surface tetrahedral adsorption increases with a larger H coverage, and is significantly larger than that of the on-surface and octahedral interstitial (OI) adsorptions. For the H adsorbed in the OI site, the distortion energy is relatively low when the coverage is less than 0.5 ML. However, the total adsorption energy of OI adsorption is much more positive than the on-surface adsorption, where the distortion energy is larger than the OI adsorption at 0.25 ML and 0.5 ML. This significant positive adsorption energy of the OI adsorption could be attributed to the lack of other essential energy lowering contributions, such as the H-electron interaction, and will be explained specifically in the following.
| θ H (ML) | fcc | hcp | OI | TI1 | TI2 |
|---|---|---|---|---|---|
| 0.25 | 8.6 (−16.7) | 13.4 (7.1) | 3.7 (284.5) | — | 21.1 (87.5) |
| 0.50 | 5.3 (−54.8) | 9.1 (−11.4) | 6.3 (277.9) | — | 21.4 (97.6) |
| 0.75 | 2.6 (−96.0) | 4.4 (−27.4) | 11.7 (247.0) | 33.6 (367.9) | 23.2 (97.9) |
| 1.00 | 2.1 (−136.3) | 3.4 (−43.0) | 18.0 (215.0) | 79.4 (467.0) | 29.0 (87.7) |
For hydrogen adsorption on Mg surfaces, the H-electron interaction contributes negatively to the H adsorption energy. This is caused by the fact that H has a higher electronegativity (2.1) than Mg (1.3).55 When put in Mg cages, H atoms tend to form H− and leave Mg in positively charged states.56 As one might expect the magnitude of the H-electron attractive interaction in the Mg surfaces is position sensitive: i.e. this interaction is more prominent at the positions where electrons are more localised. Fig. 3 shows the electron localisation function distribution within the Mg (0001) surface. The planar average ELF along Z-axis and the side-view contour both indicate a higher ELF value (a maximum of 0.68 on the planar averaged plot) near the on-surface region compared to the sub-surface and bulk regions. This on-surface electron localisation enhancement of a Mg (0001) surface stems from the changes in the local coordination of the top-layer atoms. Due to this enhanced electron localisation near the on-surface region, a stronger H-electron interaction is to be expected, and thus H atoms are more likely to be located in the on-surface adsorption sites than the sub-surface and bulk regions under low concentration. This conclusion is consistent with the calculated H adsorption energies: the H adsorption energies of the on-surface fcc and hcp adsorption sites are more negative than other sub-surface adsorptions. We thus deduce that the H-electron interaction energy should be positively correlated to the local ELF value.
Table 2 shows the ELF value at different H adsorption sites of Mg (0001) surfaces. The onsite ELF values of the on-surface fcc, hcp and the sub-surface TI1 and TI2 sites are all larger than 0.5, confirming that electrons at these positions are more localised than those in the uniform electron gas (free electrons). These localised electrons at specific adsorption sites act as proton-attractors and lower the adsorption energy by increasing the local H-electron attractive interaction. For the OI site, the small local ELF value suggests that electrons are as delocalised and metallic-like as in the free-electron gas. Therefore, the H-electron interaction at the OI site is weaker than at other sites, which leads to notable positive adsorption energy of the OI adsorption even though the related distortion energy is relatively small.
| Mg (0001) surface | fcc | hcp | OI | TI1 | TI2 |
|---|---|---|---|---|---|
| ELF value | 0.666 | 0.785 | 0.349 | 0.687 | 0.673 |
Although it is clear that the ELF is an indicator of the local H-electron interaction, and thus of the low energy adsorptions sites within the Mg surface, it is a local property and does not provide an estimate of the long-range Coulomb interactions. Consequently, the relationship between the ELF value at an adsorption site and the total adsorption energy do not have a perfect one-to-one correspondence for systems with ionic-character: the Mg–H bond is closer to an ionic bond according to a previous study of the Mg–H system.57 For instance, the H adsorption energy of the fcc site is more negative than that of the hcp site despite the ELF value at the fcc site being smaller than that of the hcp site. This apparent discrepancy is due to the long-range Coulomb interactions between the hydride and Mg ions, which is an additional energy-lowering constituent for the total adsorption energy. We opted to estimate the long-range Coulomb interaction through the Ewald method which splits the electrostatic energy into the real-space and the reciprocal-space terms respectively.58 The charge–charge interaction energy Eqij is calculated using the Bader charges of ions and estimated through the Pymatgen library.59,60
Fig. 4(a) shows the relative Coulomb interaction energies (which are calibrated by the Coulomb energy of the octahedral adsorption, with a value of −10.89 eV) of the Mg–H (0.25 ML) system with H at different adsorption sites. Although the ELF of the on-surface fcc is smaller than that of hcp (but of similar magnitude), the Coulomb interaction energy of one H at the fcc site of the Mg (0001) surface is greater than for one H in the hcp case, which results in a more negative adsorption energy. Likewise, despite the sub-surface TI2 site possessing the third largest ELF value among all adsorption sites, the total adsorption energy for H at this site is still energetically unfavourable due to the small Coulomb interaction. We conclude that the Coulomb interaction plays a dominant role in determining the most stable H-adsorption site on the Mg surface when the ELF values for the candidate sites are of similar magnitude. However, a high Coulomb interaction is not a sufficient condition for stable H adsorption if the ELF value is smaller than 0.5. For the OI adsorption, the large coulomb interaction fails to cancel the larger energy penalty which is due to the lack of electron localisation at this site.
To demonstrate the connection between the ELF value and the energy, we estimated the ELF-related energy from the adsorption energy remainder found by subtracting from the total adsorption energy the H2 dissociation energy, lattice distortion energy and the Coulomb interaction energy. Because the calculated Coulomb interaction energy only includes the contribution from the monopole–monopole interaction, ignoring the dipole–dipole and dipole–monopole interactions, the estimated long-range interaction energy carries an error. Consequently, instead of focusing on the absolute adsorption energy remainder, we calibrated the energy remainder for different adsorption sites with the most positive one (that of the OI adsorption) to underline the variation of the ELF with its energy contribution. Fig. 4(b) illustrates the relationship between the calibrated adsorption energy remainder and the corresponding ELF value. The linear regression with a negative slope indicates that a higher onsite ELF value leads to a more negative energy term, thus suggesting a stronger H-electron interaction locally. This observation supports our observation that the H-electron interaction energy and the local ELF value are correlated positively, and the localised electrons can reasonably be treated as a proton-attractor.
Overall, the ELF is a reliable indicator for predicting the possible stable adsorption site for H in the Mg (0001) surface. This is because the ELF value is positively correlated to the adsorption energy, with the higher the value the larger the H-electron interaction, and thus the more negative the corresponding energy. To fully determine the most energetically favourable site we also need to consider the structure distortion energy and the Coulomb interaction. However, the position with the largest ELF value within the Mg surface has a high probability of being a stable adsorption site, which could also be thought of as an effective trap for capturing H from the environment. In addition to predicting the position of H traps in a pristine Mg (0001) surface, we also demonstrated that the ELF could forecast the possible adsorption sites for H in a defective Mg surface in the ESI.†
Fig. 5 illustrates the sub-surface H adsorption energy at different interstitial sites in the 1 ML H (fcc) covered Mg (0001) surface. To demonstrate the influence of the surface adsorption state on the sub-surface H adsorption, we chose the H covered Mg (0001) surface and H2 gas molecule as the references for calculating the H adsorption energy. As the sub-surface H coverage increases, the TI1 adsorption remains energetically favourable having the most negative adsorption energy among the three sub-surface adsorption sites. The adsorption energies of the OI and TI2 adsorption are positive across all coverages, indicating an unstable H adsorption site, as compared with the H covered Mg surface and gaseous H2. This adsorption energy pattern demonstrates that when the Mg (0001) surface is covered by 1 ML H at the most energetically favourable on-surface site (fcc), the sub-surface H adsorption in the TI1 site could be feasible, thereby forming a stable H–Mg–H tri-layer structure at 2 ML H coverage. This H(fcc)–Mg(TL)–H(TI1) tri-layer structure (shown in Fig. 5) was also discovered in a previous theoretical study, and is considered a prospective precursor of the magnesium hydride which forms underneath the Mg surface.25 Moreover, the presence of the sub-surface Mg hydride structure was also detected experimentally in the cathodically charged Mg specimen during its aqueous corrosion.24 The X-ray diffraction spectra of the corroded specimen monitored the presence of the crystalline Mg hydride by detecting additional peaks that are expected for MgH2. The secondary ion mass spectrometry image further located the Mg hydride in the sub-surface region of the specimen. In this sense, the pre-adsorbed on-surface fcc H could enhance the stability of the sub-surface H adsorption at some particular regions within the Mg basal plane, thus forming a sub-surface hydride-like structure.
As mentioned previously, the ELF could be a rational indicator for predicting the stable H adsorption sites in the Mg surface. We now investigate the mechanism of the stabilizing of the sub-surface TI1 H adsorption by the on-surface H layer in the Mg surface by studying the evolution of the ELF in the sub-surface region of the Mg (0001) surface with the increase of the fcc H coverage from 0 to 1 ML. Fig. 6 shows the planar average ELF of the Mg (0001) surface with different fcc H coverage along the Z-axis. With the increase of the on-surface fcc H coverage, the planar average ELF peak which is located above the top surface gradually decreases. In contrast, the ELF peak in between the top layer and the second layer of the Mg surface is enhanced significantly due to the introduction of the on-surface fcc H. This enhanced ELF peak in the planar-average plot can be correlated with a newly formed ELF maximum (as shown in Fig. 6 isosurface plot) at the sub-surface TI1 sites.
Table 3 demonstrates that the onsite ELF value changes at different sub-surface interstitial sites during the formation of the 1 ML on-surface fcc H layer. For the two tetrahedral interstitial sites, the onsite ELF values both increase from the pristine Mg surface to a surface with the fcc sites fully covered with H. The onsite ELF value of the octahedral interstitial site reaches a maximum of 0.493 when the on-surface H coverage is 0.25 ML, and finally drops to a similar value as that of the clean surface when the fcc H ML forms. This indicates that the on-surface fcc H is incapable of enhancing the electron localisation above the critical value (0.5) at the octahedral site. Across all on-surface H coverages, the TI1 site possesses the largest ELF value among the three sub-surface interstitial sites, which is consistent with the local ELF maximum found in the ELF isosurface plot. On the basis of the ELF augmentation at the TI1 site, the H-electron interaction is strengthened significantly at this interstitial site. Accordingly, the H adsorption energy at the TI1 sites of a Mg (0001) surface is presumed to be negative because of the on-surface H adsorption, which agrees with the aforementioned result in Fig. 5. In this regard, ELF provides a reliable insight into predicting the stable H adsorption sites within Mg surfaces.
| fcc-H coverage (ML) | 0 | 0.25 | 0.50 | 0.75 | 1.00 |
| Octahedral (OI) | 0.349 | 0.493 | 0.465 | 0.420 | 0.367 |
| Tetrahedral-I (TI1) | 0.687 | 0.734 | 0.743 | 0.805 | 0.816 |
| Tetrahedral-II (TI2) | 0.673 | 0.691 | 0.711 | 0.712 | 0.740 |
Fig. 7 shows the ELF contour map for the Mg (0001) surface with the fcc sites occupied by H and with different H coverages in the sub-surface TI1 sites. When the sub-surface sites lack H atoms, the pre-adsorbed H atoms at fcc sites consume the electrons spread on the top surface, promoting the formation of a new ELF maximum in the sub-surface TI1 site. The subsequent occupation of these interlayer ELF maxima with H is thus energetically favourable and modifies the surface ELF pattern further. Before the sub-surface TI1 sites are fully occupied, H uptake at one TI1 site (ELF maximum position) can enhance the electron localisation at the neighbour TI1 sites. Once the sub-surface TI1 sites are completely occupied by H, the entire H(fcc)–Mg(TL)–H(TI1) tri-layer structure forms with electrons in the sub-surface region being depleted. This electron depletion is shown in the rightmost schematic in Fig. 7: the ELF value between the top layer and the second layer is approximately 0. We also note that a newly-created ELF maximum is located at the hcp hollow site of the second layer, which is similar to the position of the ELF maximum on a clean Mg (0001) surface. The ELF pattern of the stoichiometric H–Mg–H tri-layer structure indicates that ionic Mg–H bonds are built within the tri-layer, thus leading to a chemically complete structure which could be separated from the bulk Mg. Therefore, a novel almost-clean Mg surface is created underneath the tri-layer structure, with the ELF maximum positioned in the regular hcp sites. A newly formed ELF maximum in the second Mg layer is a reactive site for subsequent H adsorption, thus providing an energetically feasible path for continuously forming more H–Mg–H tri-layer structures within the Mg surface. This ELF-driven H adsorption in the Mg (0001) surface could be a possible mechanism for the growth of bulk phase MgH2 within the bulk of Mg.
3.2 H Adsorption below the hydroxylated or oxidised Mg (0001) surface
In the previous section, we demonstrated that the ELF maximum and high ELF sites within the Mg surface are potential adsorption sites for H. The on-surface H adsorption alters the ELF pattern of the underlying Mg surface with new ELF maxima developing within the sub-surface region, leading to thermodynamically stable H adsorption at the sub-surface interstitial sites. However, during aqueous corrosion of Mg, a hydrogen atom is more likely to escape from the surface as H2 rather than being adsorbed on the surface.61 In a humid environment, the bare Mg surface tends to be covered by oxygen atoms or hydroxyl groups produced by water dissociation at the surface. We now explore the ELF pattern evolution and the sub-surface H adsorption of the hydroxylated and oxidised Mg (0001) surfaces. We found that the on-surface fcc and hcp sites are the most energetically favourable for OH and O adsorption, respectively. The on-surface OH or O adsorption can enhance the ELF value at a sub-surface interstitial site, resulting in stable sub-surface H adsorption in the hydroxylated or oxidised Mg (0001) surface.Despite the OH radical having a similar electronegativity to the O atom (with a value in the range from 2.2 to 3.2, with the precise value depending on the structure and strength of the H bonding), the OH adsorption on the Mg (0001) surface shows an identical pattern to the H adsorption rather than the O adsorption, with the fcc site being more favourable than the hcp site.63 The enhanced ELF-related energy in the OH adsorption case narrows the difference in adsorption energy between the fcc and hcp sites, but does not play an equally significant role in the total adsorption energy as in O adsorption. This indicates that the energetically favourable hcp adsorption for the O atom is not only stabilized by the increased O-electron interaction (enhanced electronegativity of the adsorbate) but also settled by other important contributions.
To determine additional causes for the stabilisation of the O hcp adsorption, we investigated the lattice distortion energy for the Mg surface with O and OH radicals at hcp and fcc sites, respectively. Fig. 9(a) shows that the distortion energy for O adsorption at both hcp and fcc sites is larger than that for OH adsorption at all coverages. This is because the OH radical is adsorbed above the top layer of the surface with a distance of approximately 1 Å, which introduces limited lateral lattice distortion. The O adsorption on the Mg (0001) surface is generally in-plane adsorption with O just located in the top layer, and induces a larger lateral lattice distortion and an enhanced distortion energy. For the OH adsorption, the distortion energies for the fcc and the hcp adsorption sites both decrease with the increase of the coverage. In addition, the OH adsorption at the hcp site possesses a slightly higher distortion energy than the OH adsorption at the fcc site when the coverage is smaller than 1 ML. At 1 ML coverage, the distortion energy for OH adsorption reduces to approximately zero because of the high symmetry of the fully covered surface, which is similar to H adsorption. The distortion energy for O adsorption at an hcp site is 4 and 5 times larger than that of the OH hcp/fcc adsorption at 0.25 ML coverage and decays to zero rapidly as the coverage increases. By contrast, the O adsorbed at the on-surface fcc site introduces a strongly increasing distortion energy with respect to the increasing coverage. According to the distortion energy difference between O adsorption at the hcp and fcc sites shown in Fig. 9(a), this distortion energy difference for the O adsorption contributes significantly to the total adsorption energy difference between these two sites. Unlike the H adsorption and the OH adsorption, the hcp adsorption for O results in a smaller lattice distortion energy compared with the fcc adsorption, which also stabilises the onsite hcp O adsorption in addition to the enhanced adsorbate-electron interactions.
The remarkable distortion energy for the O adsorption at fcc sites could contribute to the large layer spacing between the top layer (TL) and the second layer (SL) of the surface. Fig. 9(b) shows the variation of the TL-SL spacing (distance change referenced to the clean surface) for the Mg surface with O and OH adsorbed at different sites. The O adsorption at fcc sites induces a significant layer separation between the top layer and the second layer of the Mg (0001) surface with increased coverage. At 0.25 ML, the TL-SL layer spacing for O and OH adsorption at both hcp and fcc sites is at a similar small level. As the coverage increases, the subsequent adsorption for the OH radicals at hcp and fcc sites and O at hcp sites alter the layer spacing by 5% or less. However, the layer spacing for the Mg surface with O adsorbed at fcc sites increases significantly as more O is adsorbed onto the surface, reaching a maximum of 28% at 1 ML coverage: this indicates a significant layer separation between the top Mg–O layer and the substrate. Such a large layer spacing results in distortion energy that is far larger than for O adsorption at hcp sites. Therefore, for O adsorption, the hcp sites are more stable as a consequence of a higher onsite ELF value (larger O-electron interaction) and a negligible lattice distortion (layer separation) compared with the fcc sites.
The ELF pattern of the hydroxylated and oxidised Mg (0001) surface suggests a possible explanation for the unique layer separation (large layer spacing) for O adsorption at fcc sites. As shown in Fig. 10, the ELF contour patterns for the OH adsorption demonstrate that the on-surface OH radicals partially consume the electrons of the top layer Mg both for the fcc and hcp sites: OH only requires 1 electron and it is slightly above the top atomic layer. Thus, there are still numerous electrons distributed in the sub-surface region underneath the top layer. These remaining electrons can connect the top-layer Mg atoms with the second layer by forming chemical bonds, thus restricting the TL-SL spacing and diminishing the related distortion energy. However, for the O adsorption, the on-surface O depletes more electrons within the top layer because one O atom requires two electrons to form a stable anion and the O is adsorbed just in the top layer with an insignificant vertical displacement.
The ELF contour map for O adsorption at a hcp site demonstrates the decrease of the sub-surface electrons compared with OH adsorption. Although the sub-surface electrons are depleted more completely by the adsorbed hcp O atoms, a chemical bond between the adsorbed O and the Mg atom directly underneath is visible in the contour map. This O–Mg bond plays a similar role as the inter-layer electrons, which connect the top layer atoms to the substrate and reduce the layer spacing, thus clarifying the small layer spacing for the O adsorption at hcp sites. However, the O adsorption at fcc sites lacks this essential Mg–O bond because of the layer configuration. The ELF contour map shows that the topmost Mg–O layer interacts weakly with the second-layer Mg atoms, with fewer electrons remaining in the sub-surface region and no evident chemical bonding between the O and SL Mg atoms. In this case, the weak electronic interaction between the atoms in the top layer and the second layer contributes to the large layer separation when O is adsorbed on fcc sites, and the lattice distortion energy is related to this lattice distortion, thereby destabilising the O adsorption at this site.
In addition, the on-surface OH radicals and O atoms also modify the ELF pattern of the pristine Mg (0001) surface and generate new ELF maxima in the sub-surface region in the same way that the on-surface H atoms do. Considering the two most stable adsorption patterns for the OH and O adsorption on the Mg surface (adsorption at fcc and hcp sites), the isosurface plot and the ELF contour map illustrate that OH at an on-surface fcc site introduces a new ELF maximum at the sub-surface TI1 site, whereas the O at an hcp site creates a new maximum at the sub-surface TI2 site (also close to the hcp site in the second Mg layer). These novel sub-surface ELF maxima are possible locations within the hydroxylated or oxidised Mg surface for adsorbing additional H atoms. Thus, in a humid environment, where the Mg surface is generally covered by OH and O groups, sub-surface H adsorption and the formation of a Mg hydride-like layer could occur.
Fig. 11(a) illustrates the adsorption energy for the sub-surface H within the Mg (0001) surface covered with 1 ML of OH at fcc sites. At all H coverages in the sub-surface region, the TI1 interstitial is the most stable site among the three sub-surface sites, with negative adsorption energy for placing H atoms at this site of the hydroxylated surface. For H adsorption at the OI and TI2 sites, the positive adsorption energy indicates an unstable H uptake at these interstitial sites in the OH covered Mg surface. This sub-surface H adsorption energy pattern agrees well with the ELF pattern within the Mg (0001) surface covered by OH at fcc sites: the electron localisation at the sub-surface TI1 site is enhanced significantly by the on-surface OH radicals at fcc sites, thereby suggesting a potentially spontaneous H adsorption. Therefore, a stable OH(fcc)–Mg–H(TI1) tri-layer that has an identical configuration to the aforementioned H(fcc)–Mg–H(TI1) tri-layer structure forms within the Mg substrate. This can be understood because the adsorption of OH at fcc sites on the Mg surface has an equivalent influence on the ELF distribution in the surface as the H adsorption at fcc sites. Likewise, the OH(fcc)–Mg–H(TI1) tri-layer is also a chemically completed structure, with the inter-layer electrons depleted adequately by the on-surface OH radicals and the sub-surface H atoms. After adding H atoms at the TI1 site of the Mg surface covered with OH at fcc sites, a novel ELF maximum could be found at the hcp hollow site within the second Mg surface layer, which suggests that more H atoms are likely to be adsorbed at the reconstructed pristine Mg surface underneath the tri-layer structure.
For the sub-surface H adsorption in the Mg (0001) surface covered with O at hcp sites, the OI and the TI2 sites are both thermodynamically stable locations for H atoms at all coverages up to 1 ML. H adsorption at the TI1 site is energetically favourable at a H coverage of less than 0.60 ML. Amongst three sub-surface H adsorption sites in the oxidised Mg (0001) surface, the TI2 site is the most stable with the most negative adsorption energy. This active H adsorption site is just the ELF maximum generated by the on-surface O atoms at hcp sites in the Mg (0001) surface, thus confirming again that the ELF is a good indicator for predicting possible adsorption sites for H in the Mg surface. Based on the ELF contour map for the O(hcp)–Mg–H(TI2) structure, the sub-surface H further consumes the remaining inter-layer electrons within the Mg surface, and also weakens the chemical bond between the O and the underneath Mg. However, the adsorbed H at the TI2 site connects to the top Mg atom with a H–Mg bond, and prevents the separation of the topmost Mg–O layer from the bulk phase. In addition, the introduction of the sub-surface H in the hcp-O covered Mg surface establishes a new ELF maximum at the TI2 interstitial between the second and the third Mg layer. This ELF evolution within the oxidised Mg surface thus indicates the possible energetically favourable pathway of forming the H–Mg–H layers within the bulk phase. Consequently, we conclude that the sub-surface Mg hydride-like layer (H–Mg–H structure) could form during Mg aqueous corrosion within the Mg surface covered by O and OH (from water dissociation) following an ELF-driven H adsorption mechanism.
4 Conclusions
In conclusion, we have studied hydrogen adsorption and hydride layer formation mechanism within the Mg (0001) surface using density functional theory calculations. We discovered that atomic H tends to be adsorbed in the high Electron Localisation Function (ELF) adsorption site within the Mg surface. By decomposing the total H adsorption energy in the Mg (0001) surface, we found that the onsite ELF value at each adsorption site is linearly correlated to the ELF-related adsorption energy. This confirms that the ELF is a reliable predictor of the H adsorption structure. The ELF maxima region within the surface could also be treated as an effective hydrogen trap. At low H coverage, fcc sites are the most stable adsorption sites on the Mg basal plane due to the joint effect of the ELF (H-electron interaction) and the Coulomb interactions. When the surface is pre-adsorbed with 1 ML of H at fcc sites, the electron localisation at the sub-surface TI1 is significantly enhanced, leading to energetically favourable sub-surface H adsorption and a stable H(fcc)–Mg–H(TI1) tri-layer structure.For the on-surface adsorption of OH radicals and atomic O, both the ELF (adsorbate–electron interaction) and the lattice distortion can influence the stable adsorption pattern (fcc sites and hcp sites are the most stable on-surface adsorption sites for OH and O, respectively). The ELF pattern in the sub-surface region of the Mg-basal plane could also be modified by the on-surface OH and O atoms, thus stabilising the sub-surface H adsorption and resulting in the formation of similar OH(fcc)–Mg–H(TI1) structure for the hydroxylate Mg surface and O(hcp)–Mg–H(TI2) structure for the oxidised Mg surface.
The adsorbate generated ELF variation within the Mg (0001) surface drives sub-surface H adsorption and the formation of the hydride layer (or its precursor) underneath the topmost Mg layer, thus illustrating the underlying mechanism for the Mg hydride formation during the aqueous corrosion at the open circuit potential. Because the formation of the sub-surface hydride is dominated by the electron localisation within the Mg surface, it is possible to control the electron localisation thereby modulating the formation of the hydride. For instance, modifying the metal surface state by doping, introducing defects or adsorbing other radicals could change the electron localisation of the metal with the formation of new ELF maxima, which could further prompt the hydride formation. Furthermore, charging the surface or applying external strain/stress on the metal could also alter the electron localisation, thus tuning the formation of the hydride. This finding lays a foundation for understanding the significance of the Mg hydride crystalline structure in Mg aqueous corrosion, and for further revealing the nature of some enigmatic phenomena in the Mg corrosion, such as the negative difference effect.
Author contributions
Bingxin Li: conceptualisation, methodology, investigation, formal analysis, visualisation, writing – original draft, writing – review & editing. Chengcheng Xiao: conceptualisation, methodology, formal analysis, software, writing – review & editing. Nicholas M. Harrison: methodology, investigation, formal analysis, supervision, writing – review & editing. Richard M. Fogarty: formal analysis, writing – review & editing. Andrew P. Horsfield: methodology, investigation, formal analysis, supervision, writing – review & editing, software acquisition.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
B. X. L. and C. C. X. acknowledge the China Scholarship Council and Imperial College London for funding via a PhD scholarship under Grant No. (2019)205. R. M. F. gratefully acknowledges funding from EPSRC under Grant No. EP/R005419/1. We acknowledge the Thomas Young Centre under grant number TYC-101. The calculations were performed on the high performance computing facilities of Imperial College London, https://doi.org/10.14469/hpc/2232.References
- K. Christmann, Surf. Sci. Rep., 1988, 9, 1–163 CrossRef.
- M. S. Hofman, D. Z. Wang, Y. Yang and B. E. Koel, Surf. Sci. Rep., 2018, 73, 153–189 CrossRef CAS.
- P. Sprunger and E. Plummer, Surf. Sci., 1994, 307, 118–123 CrossRef.
- J. Guo and P. Chen, Acc. Chem. Res., 2021, 54, 2434–2444 CrossRef CAS PubMed.
- B. Sakintuna, F. Lamari-Darkrim and M. Hirscher, Int. J. Hydrogen Energy, 2007, 32, 1121–1140 CrossRef CAS.
- I. Jain, C. Lal and A. Jain, Int. J. Hydrogen Energy, 2010, 35, 5133–5144 CrossRef CAS.
- Q. Luo, J. Li, B. Li, B. Liu, H. Shao and Q. Li, J. Magnesium Alloys, 2019, 7, 58–71 CrossRef CAS.
- Y. Shang, C. Pistidda, G. Gizer, T. Klassen and M. Dornheim, J. Magnesium Alloys, 2021, 9, 1837–1860 CrossRef CAS.
- K. S. Williams, V. Rodriguez-Santiago and J. W. Andzelm, Electrochim. Acta, 2016, 210, 261–270 CrossRef CAS.
- J. A. Yuwono, C. D. Taylor, G. Frankel, N. Birbilis and S. Fajardo, Electrochem. Commun., 2019, 104, 106482 CrossRef CAS.
- R. Wang, A. Eliezer and E. Gutman, Mater. Sci. Eng., A, 2003, 355, 201–207 CrossRef.
- S. Zhang, X. Zhang, C. Zhao, J. Li, Y. Song, C. Xie, H. Tao, Y. Zhang, Y. He and Y. Jiang, et al. , Acta Biomater., 2010, 6, 626–640 CrossRef CAS PubMed.
- S. Fajardo, C. Glover, G. Williams and G. Frankel, Electrochim. Acta, 2016, 212, 510–521 CrossRef CAS.
- M. Taheri, M. Danaie and J. Kish, J. Electrochem. Soc., 2013, 161, C89 CrossRef.
- M. Taheri, J. Kish, N. Birbilis, M. Danaie, E. A. McNally and J. R. McDermid, Electrochim. Acta, 2014, 116, 396–403 CrossRef CAS.
- S. Salleh, S. Thomas, J. Yuwono, K. Venkatesan and N. Birbilis, Electrochim. Acta, 2015, 161, 144–152 CrossRef CAS.
- Z. Shi, G. Song and A. Atrens, Surf. Coat. Technol., 2006, 201, 492–503 CrossRef CAS.
- M. Liu, P. Schmutz, S. Zanna, A. Seyeux, H. Ardelean, G. Song, A. Atrens and P. Marcus, Corros. Sci., 2010, 52, 562–578 CrossRef CAS.
- J. Chen, J. Wang, E. Han and W. Ke, Mater. Sci. Eng., A, 2008, 488, 428–434 CrossRef.
- S. Surendralal, M. Todorova, M. W. Finnis and J. Neugebauer, Phys. Rev. Lett., 2018, 120, 246801 CrossRef CAS PubMed.
- Z. Han, H. Chen and S. Zhou, Appl. Surf. Sci., 2017, 394, 371–377 CrossRef CAS.
- J. Chen, J. Dong, J. Wang, E. Han and W. Ke, Corros. Sci., 2008, 50, 3610–3614 CrossRef CAS.
- S. Xu, J. Dong and W. Ke, Int. J. Corros., 2010, 2010, 934867–934871 Search PubMed.
- W. Jeffrey Binns, F. Zargarzadah, V. Dehnavi, J. Chen, J. J. Noël and D. W. Shoesmith, Corrosion, 2019, 75, 58–68 CrossRef PubMed.
- T. Jiang, L.-X. Sun and W.-X. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 035416 CrossRef.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- A. Savin, O. Jepsen, J. Flad, O. K. Andersen, H. Preuss and H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1992, 31, 187–188 CrossRef.
- R. J. Clements, J. C. Womack and C.-K. Skylaris, Electron. Struct., 2020, 2, 027001 CrossRef CAS.
- C. V. Weizsäcker, Zeitschrift für Physik, 1935, 96, 431–458 CrossRef.
- F. Della Sala, E. Fabiano and L. A. Constantin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 035126 CrossRef.
- B. Patra, S. Jana, L. A. Constantin and P. Samal, Phys. Rev. B, 2019, 100, 155140 CrossRef CAS.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS.
- A. Savin, A. Becke, J. Flad, R. Nesper, H. Preuss and H. Von Schnering, Angew. Chem., Int. Ed. Engl., 1991, 30, 409–412 CrossRef.
- L. De Santis and R. Resta, Surf. Sci., 2000, 450, 126–132 CrossRef CAS.
- R. Rousseau and D. Marx, Chem. – Eur. J., 2000, 6, 2982–2993 CrossRef CAS PubMed.
- F. Ample, D. Curulla, F. Fuster, A. Clotet and J. M. Ricart, Surf. Sci., 2002, 497, 139–154 CrossRef CAS.
- D. A. Lang, J. V. Zaikina, D. D. Lovingood, T. E. Gedris and S. E. Latturner, J. Am. Chem. Soc., 2010, 132, 17523–17530 CrossRef CAS PubMed.
- R. Nesper and S. Wengert, Chem. – Eur. J., 1997, 3, 985–991 CrossRef CAS.
- S. Dong, C. Li, J. Wang, H. Liu, Z. Ding, Z. Gao, W. Yang, W. Lv, L. Wei and Y. Wu, et al. , J. Mater. Chem. A, 2022, 10, 22363–22372 RSC.
- P. Fuentealba, E. Chamorro and J. C. Santos, Theoretical and Computational Chemistry, Elsevier, 2007, vol. 19, pp. 57–85 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067 CrossRef CAS PubMed.
- J. Renner and H. Grabke, Zeitschrift fur Metallkunde, 1978, 69, 639–642 CAS.
- M. Todorova and J. Neugebauer, Phys. Rev. Appl., 2014, 1, 014001 CrossRef CAS.
- M. Yan, Z.-Q. Huang, Y. Zhang and C.-R. Chang, Phys. Chem. Chem. Phys., 2017, 19, 2364–2371 RSC.
- A. B. Anderson, J. Uddin and R. Jinnouchi, J. Phys. Chem. C, 2010, 114, 14946–14952 CrossRef CAS.
- G.-X. Wu, S.-X. Liu, J.-Y. Zhang, Y.-Q. Wu, L. Qian, K.-C. Chou and X.-H. Bao, Trans. Nonferrous Met. Soc. China, 2009, 19, 383–388 CrossRef CAS.
- G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8295 CrossRef CAS.
- R. Staub, M. Iannuzzi, R. Z. Khaliullin and S. N. Steinmann, J. Chem. Theory Comput., 2018, 15, 265–275 CrossRef PubMed.
- A. L. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215–221 CrossRef CAS.
- T. Würger, C. Feiler, G. B. Vonbun-Feldbauer, M. L. Zheludkevich and R. H. Meißner, Sci. Rep., 2020, 10, 1–11 CrossRef PubMed.
- T. Noritake, M. Aoki, S. Towata, Y. Seno, Y. Hirose, E. Nishibori, M. Takata and M. Sakata, Appl. Phys. Lett., 2002, 81, 2008–2010 CrossRef CAS.
- D. Wang, J. Liu, J. Zhang, S. Raza, X. Chen and C.-L. Jia, Comput. Mater. Sci., 2019, 162, 314–321 CrossRef CAS.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- C. D. Taylor, J. Electrochem. Soc., 2016, 163, C602 CrossRef CAS.
- R. J. Ouellette and J. D. Rawn, Principles of Organic Chemistry, Academic Press, 2015 Search PubMed.
- T. M. Krygowski and H. Szatyłowicz, J. Phys. Chem. A, 2006, 110, 7232–7236 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05242c |
| This journal is © the Owner Societies 2023 |




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: