Modeling of minimal systems based on ATP-Zn coordination for chemically fueled self-assembly

Abstract

Following nature's example, there is currently strong interest in using adenosine 5′-triphosphate (ATP) as a fuel for the self-assembly of functional materials with transient/non-equilibrium behaviours. These hold great promise for applications, e.g. in catalysis and drug delivery. In a recent seminal work [Maiti et al., Nat. Chem., 2016, 8, 725], binding of ATP to the metallosurfactant zinc hexadecyl-1,4,7-triazacyclononane ([ZnC₁₆ TACN]²⁺) was exploited to produce ATP-fueled transient vesicles. Crucial to the complex formation is the ability of ATP to bind to the metal ion. As a first step to unveil the key elements underlying this process, we investigate the interaction of ATP with Zn²⁺ and with methyl-1,4,7-triazacyclononane ([ZnCH₃ TACN]²⁺), using all-atom molecular dynamics simulations. The free energy landscape of the complex formation is sampled using well-tempered metadynamics with three collective variables, corresponding to the coordination numbers of Zn²⁺ with the oxygen atoms of the three phosphate groups. We find that the structure of the ternary complex is controlled by direct triphosphate coordination to zinc, with a minor role played by the interactions between ATP and CH₃ TACN which, however, may be important for the build-up of supramolecular assemblies.

---

1 Introduction

Adenosine 5′ triphosphate (ATP) serves as the primary energy source in living organisms and as a signaling molecule. It is involved in biological processes such as the operation of molecular machines and the synthesis of nucleotides and proteins. The multifaceted role of ATP in nature has inspired the design of a new generation of environment friendly smart materials. Structure and amphipathic character make ATP an excellent template for supramolecular assemblies and functional nanomaterials.¹ Crucial to this purpose is the ability of ATP to bind metal ions, which is primarily due to the high metal affinity of the triphosphate chain, although also the sugar oxygens and the aromatic nitrogens may act as binding sites.² Metal ions, besides introducing specific functionalities, may influence the self-stacking tendency of the base, promoting aggregation either via specific bridging interactions or non-specific charge screening.³ Moreover, they mediate the interaction with auxiliary ligands, for instance, amines and aromatic molecules,³ thus providing a flexible means to tune the structural and functional properties of the building blocks.^4,5 Of special interest in this context is the prospect of using ATP to obtain temporal control over the chemical functions associated with the assembled state:^6–9 ATP can trigger assembly and disassembly or can act as a chemical fuel to power a non-equilibrium process. These developments are inspired by the dynamical growth/depolymerization of actin filaments fueled by the hydrolysis of ATP to ADP. Recently, there have been several attempts to implement analogous principles in synthetic systems, to obtain materials that hold great promise for application, e.g. in catalysis,¹⁰ in biosensors, in detergent formulations and drug delivery.¹¹ Implementation of this concept was proposed in a seminal work,¹² where ATP was used to induce the formation of vesicular nanoreactors in water solutions of a metallosurfactant [ZnC_n TACN]²⁺ made of an alkyl chain (C_n) linked to a macrocycle (1,4,7-triazacyclononane, TACN), forming a complex with Zn²⁺. The hydrolysis of the nucleotide was then exploited to control the lifetime of vesicles.

Zn²⁺ has a flexible chemistry, since it can accommodate nitrogen, oxygen, sulfur and halogen atoms, thanks to its borderline hard/soft character.¹³ It may also form complexes in several coordination states, e.g. with water molecules, unlike other ions such as Mg²⁺.¹⁴ The closed-shell electronic configuration ([Ar] 3d¹⁰ 4s⁰) prevents ligand field stabilization and, consequently, several ligands and different geometries may define Zn²⁺ coordination. In aqueous solutions, free Zn²⁺ is mainly octahedrally coordinated to six water molecules,¹⁵ while in enzymes, it is found in tetrahedral, penta- or hexa-coordinated arrangements.¹⁴ Zn²⁺ can coordinate to polyaminic ligands to form stable complexes that can bind to phosphate, which is an attractive feature for use in ATP promoted and fueled self-assembly.² Detailed insight into the structural and energetic aspects of the binding is a prerequisite for understanding the mechanistic aspects of ATP-templated assembly and disassembly and achieving full control of the functionality of aggregates. Given the biological relevance of ATP, it is somehow surprising that a number of questions still remain unanswered. Although in the literature there are studies of Zn²⁺ coordination to the active site of proteins,¹⁶ no analogous knowledge exists for the coordination of Zn²⁺ to free ATP in water. The problem is far from trivial since the triphosphate moiety has several binding sites, which can eventually host the metal, leading to various coordination modes. The interaction of divalent metals with ATP has been the subject of numerous investigations, with thermodynamic and spectroscopic techniques, such as NMR and infrared/Raman. However, the large majority of these studies date to the 80s of last century and focus on complexes with Mg²⁺, while only in some cases, other ions, such as Ca²⁺, Ni²⁺, Zn²⁺, Mn²⁺, Co²⁺ or Cu²⁺, were considered. Since the early days, ³¹P NMR experiments, which probe changes in the environment of phosphorus atoms, have been used to investigate metal binding to the triphosphate chain. Qualitatively similar effects have been observed for the various metals: all resonances exhibit a downfield shift, but to a different extent for the three phosphorus atoms, larger for Pβ, smaller for Pγ and even smaller for Pα (see Fig. 1 for the atom labels).^17–21 Different interpretations of these data have been provided: on one hand, assuming a direct relation between the change of P-resonance and the degree of coordination, monodentate or bidentate binding to Pβ and Pγ was inferred, excluding the Pα contact.^17,21 On the other hand, given the strong sensitivity of ³¹P NMR resonances to torsional and bond angles of the polyphosphate chain, it was proposed that the differences between Pα, Pβ and Pγ would indicate geometrical and conformational changes,²² rather than purely electronic factors, associated with the binding of divalent cations to the phospho-oxyanions. In summary, although experimental data provide a clear indication of binding, they are insufficient to provide a detailed description of ATP–metal coordination.^18,20,23 Most of the experiments are relatively old, and novel insights could be obtained by state-of-the-art spectroscopic techniques, such as nonlinear 2D-IR spectroscopy, which was found to be a sensitive probe of phosphate–ion interactions.^24,25 It may be worth mentioning that ³¹PNMR was used also to characterize the binding of ATP to Zn²⁺ complexes with synthetic ligands, such as polyamine macrocycles,^26,27 and the experimental results were consistent with those for ATP–metal in water, whereas ¹H NMR measurements suggested the presence of additional ATP–ligand interactions.²⁷ It has been proposed that also adenine N7 (see Fig. S5a, ESI† for atom label) is involved in ATP–metal binding. In the case of ATP–Zn²⁺ complexes, a shift of H8 (see Fig. S5a, ESI† for atom label) resonance in the ¹H NMR spectra has been interpreted as an indication of such involvement.^{3,17,19,20,22,28} Two types of “macrochelate” or “closed” structures, with intramolecular metal–N7 interactions, were suggested: in one, the βγ phosphate-coordinated metal binds the innnersphere to N7, while in the other, the αβγ phosphate-coordinated metal establishes outersphere N7 binding.²⁹

Fig. 1 Systems investigated in this study: (a) adenosine 5′-triphosphate (ATP); (b) methyl triphosphate (MTP); and (c) complex of zinc with methyl-1,4,7-triazacyclononane ([ZnCH₃TACN]²⁺).

Computer simulations can be a valuable means to shed light on the structural and energetic features of binding. The challenge is the simultaneous inclusion of quantum mechanical aspects of coordinate bonding, entropic effects due to hydration and conformational degrees of freedom, and long-range electrostatics due to the presence of highly charged moieties. Density functional theory (DFT) calculations, either in a vacuum or in the presence of a few water molecules, provide detailed information on the geometry and energy of single coordination states, but cannot adequately sample conformational and solvation degrees of freedom. This could be achieved by ab initio molecular dynamics (AIMD) simulations, but their high computational cost poses a severe limitation to the extent of sampling. This problem is overcome by all-atom molecular dynamics (MD), whose reliability, however, depends on the quality of the force field (FF) that is used. Both DFT calculations^30–34 and all-atom simulations, in water^35,36 and in a protein environment,^37–40 have been applied to the study of ATP binding to Mg²⁺, with somewhat controversial results. Much less attention has been paid to other cations, mostly to investigate their effect on hydrolysis, using DFT calculations,^31–33 also at the QM/MM level,⁴¹ as well as, in a recent AIMD study.⁴² However, we are not aware of computational studies of the binding of free ATP to Zn²⁺ in water. Here, we have used all-atom MD simulations to investigate the interaction of ATP with Zn²⁺ and with methyl-1,4,7-triazacyclononane (CH₃ TACN) in water. To evaluate the role of the nucleoside, we have performed additional simulations where ATP was replaced by methyl triphosphate (MTP). The time scale of a ligand and water exchange with a metal is not accessible by standard simulations, for instance, water exchange in the first solvation shell of Mg²⁺ has been estimated to occur on timescales of the order of microseconds.⁴³ Therefore, we have resorted to enhanced sampling techniques^36,40 to explore binding modes and conformational states of the complexes. We find that the structure of the ternary complex is controlled by direct triphosphate binding to zinc and the favoured coordination modes are primarily dictated by the conformational preferences of the triphosphate chain. A minor role in the stabilization of ternary complexes is played by the interactions between ATP and CH₃ TACN which, however, may be important for the build-up of supramolecular assemblies.

2 Methods

MD simulations were carried out using LAMMPS^44,45 and the Colvars module⁴⁶ was employed for well-tempered metadynamics (WT-MTD).⁴⁷ Periodic boundary conditions and initial configurations with direct contact between triphosphate and Zn²⁺ were assumed, unless otherwise specified. Velocity Verlet algorithm⁴⁸ with a timestep of 1 fs was used to integrate the equations of motions. O–H bonds and H–O–H angles of water were constrained through the SHAKE algorithm.⁴⁹ All systems were equilibrated for 20 ns in the NPT ensemble at a temperature of 300 K and a pressure of 1 atm, whereas WT-MTD was performed in the NVT ensemble at a temperature of 300 K. The molecular composition and the length of the WT-MTD simulations for all the systems are reported in Tables S5–S8 and S10 (ESI†). The Nose–Hoover thermostat^50,51 and a barostat⁵² were used with a damping period of 100 fs and 1000 fs, respectively. Electrostatic interactions were computed with the Ewald summation method. Reweighting was performed with the Plumed plugin.⁵³ Trajectory visualization was done with VMD.⁵⁴

2.1 Force fields

OPLS-AA/MM FF was employed for ATP and MTP using the parameterization of Robertson et al.,⁵⁵ where the −4 ionization state is assumed for triphosphate, as appropriate at pH = 7.⁵⁶ For CH₃ TACN, we used the parametrization of Price et al.⁵⁷ and for Zn²⁺ non-bonded parameters reported by Stote and Karplus.⁵⁸ An alternative parametrization for Zn²⁺, using the dummy model by Duarte et al.,⁵⁹ has been used to assess the impact of metal details. Zn–N distances in [ZnCH₃ TACN]²⁺ were constrained to equilibrium values, evaluated from a standard simulation, to prevent dissociation of the complex when a bias potential was applied (Table S4, ESI†). The TIP3P model of water was used.⁶⁰

2.2 Well-tempered metadynamics

We used WT-MTD to calculate free energy surfaces (FESs) as a function of the coordination number (c.n.) between Zn²⁺ and Oj (j = α, β, γ), the oxygens linked to each of the phosphorus atoms, Pj. This is computed according to the function defined in the Colvar module⁴⁶where N_j is the number of oxygens associated with Pj, x_Zn and x_ji are the coordinates of Zn²⁺ and of the ith oxygen linked to Pj, respectively; d₀ is the switching distance to define an interatomic contact and the combination of n and m values tunes the smoothness of the function. We used n = 6 and m = 12, and d₀ = 2.70 Å. This choice is based on the first peak of the Zn–Oj radial distribution function of the bound system and allowed us to exclude Zn–Oj pairs corresponding to the second peak. In all simulations, a half-harmonic constraint was applied to the Zn–P distance to prevent diffusion of Zn²⁺ over 10.2 Å far away from the center of mass of phosphorus atoms and, thus, to reduce the sampling of unbound configurations. Also, upper boundary value of c.n.s was enforced at c.n. = 2.4. For an x variable centered in x′, the confining potential is defined aswhere K = k/w² is a rescaled force constant, with w, the grid width where the variable is defined (Table S4, ESI†).

A plugin of PLUMED version 1.3 was employed to reweight the biased probability distribution as a function of geometrical or coordination parameters.⁶¹ This procedure was used to evaluate the free energy as a function of angles and dihedrals, Zn–adenine distance, and Zn–O coordination numbers for water oxygens. For the latter, the same definition and the same parameters as for phosphate oxygens were adopted.

For all biased simulations, the initial hill height was set to 0.2 kcal mol⁻¹, the hill width (2σ) to 0.2 and the bias factor to 15. A new hill was added every 500 fs and the range of all biased collective variables (CVs) was discretized in grids of width w = 0.1 (Table S4, ESI†).

Standard MD simulations were performed for [ZnCH₃ TACN]²⁺ (Table S3, ESI†) as well as for free ATP in water (Table S2, ESI†), to characterize the Zn–TACN interaction and to get reference data for the unbound nucleotide, respectively. Detailed settings of simulations are available in the ESI.†

2.3 Naming of coordination modes

In agreement with the current literature, coordination modes will be indicated by a sequence of Greek letters, each referring to the triphosphate coordination site. For instance, αγ is a bidentate configuration, where the metal is coordinated to one Oα and one Oγ oxygen, whereas αγγ denotes tridentate binding, involving one Oα and two Oγ oxygens.

3 Results and discussion

3.1 Sampling strategy: well-tempered metadynamics to explore Zn²⁺ coordination to the phosphate groups

An accurate structural and energetic description of the binding of ATP and MTP to Zn²⁺ in water represents a challenging task, because of the presence of various coordination modes, separated by high barriers. The slow degrees of freedom can be efficiently explored employing WT-MTD, provided that effective CVs are identified. In our case, a simple CV, such as the distance between Zn²⁺ and Pβ, turned out to be inadequate to distinguish binding modes, since the flexibility of triphosphate allows several coordination states to correspond to the same distance. As a better unambiguous choice, we selected the coordination numbers of Zn²⁺ to the oxygens linked to each of the three phosphorus atoms. As a starting point in the WT-MTD simulations, we generally chose configurations with Zn²⁺ directly coordinated to triphosphate oxygens. To assess the presence of hysteresis effects in the sampling, for MTP–[ZnCH₃ TACN]²⁺ we ran an additional WT-MTD simulation starting from a configuration with water-mediated triphosphate–Zn²⁺ coordination (Table S8, ESI†). Comparing the results of the two simulations, we can estimate an uncertainty on free energies which is generally lower than 0.5 kcal mol⁻¹ (Table S1, ESI†), at least for the most stable binding states. Some higher energy binding modes are affected by larger uncertainty, possibly due to a less efficient sampling, as occurs for the unbound state, which corresponds to several different configurations.

3.2 ATP–Zn²⁺ and MTP–Zn²⁺

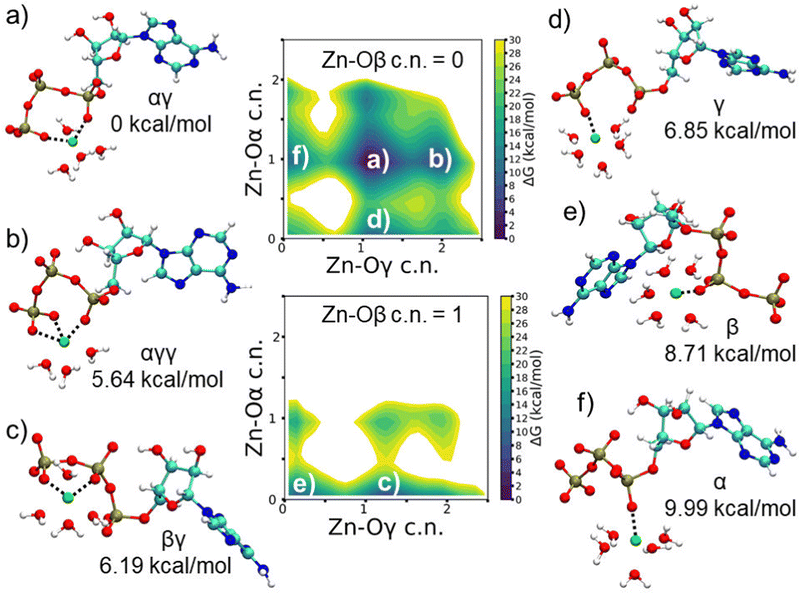
Fig. S9a and b (ESI†) show the time evolution of the free energy for the different coordination modes of ATP–Zn²⁺ in water along a WT-MTD trajectory (Table S5, ESI†). The free energy landscape is determined by a delicate balance of charge–charge interactions (Zn–O attraction and O–O repulsion), entropic penalty related to conformational constraints upon binding and entropic gain due to the release of solvation water. Very long trajectories were required to reach convergence of the free energy, although the relative order of the minima corresponding to the coordination states remained almost unaltered over time. The global minimum corresponds to bidentate αγ coordination and lies about 14 kcal mol⁻¹ below the unbound state. The next binding modes, about 5 kcal mol⁻¹ higher, are tridentate αγγ, bidentate βγ and monodentate γ. Then, there are the other monodentate coordination states, first β and then α; the relative order of these states arguably reflects the increasing steric constraints as the Zn–O contact is closer to the nucleoside. Most of the tridentate modes and some of the bidentate ones are very high in energy, higher than the unbound state, so they will not be further discussed. It is interesting to notice that, starting from the global minimum, with two Zn–O contacts, the introduction of a third, additional contact, yields a significant increase in free energy.

Fig. 2 shows the FESs of ATP–Zn²⁺ in water as a function of the Zn–Oα and Zn–Oγ coordination numbers, in the absence of Zn–Oβ contacts (upper panel) and in the presence of one Zn–Oβ contact (lower panel). The FES for the Zn–Oβ coordination number equal to two is not reported, as it corresponds to states which are higher in energy than the unbound state (Fig. S9a, ESI†). Fig. 2 shows also representative snapshots of the six lowest free energy minima. We can see that in all cases there is direct ion-contact; although not shown in the figure, for the βγ mode also a Zn–Oα contact mediated by a water molecule is found, as already reported in the literature.³ In all the configurations, irrespective of the specific binding mode, Zn²⁺ is six-fold coordinated, with water oxygens completing the coordination shell (Fig. 3), as usually found for Zn²⁺ in classical FF-based simulations.⁶²

Fig. 2 FES of ATP–Zn²⁺ in water, obtained by WT-MTD, as a function of Zn–Oα and Zn–Oγ c.n.s in the absence (top) and in the presence (bottom) of the single Zn–Oβ coordination. States with two Zn–Oβ contacts are disregarded as higher in energy. (a)–(f) Representative configurations for minima lying within 10 kcal mol⁻¹ from the global minimum.

Fig. 3 FES of ATP–Zn²⁺ as a function of c.n. of Zn²⁺ to water and triphosphate oxygens, reconstructed from WT-MTD run.

Although the interactions with phosphate oxygens are recognized as the main driving mechanism for ATP binding to divalent metals,³ it has been suggested that for Zn²⁺ also the interaction with the N7 atom of adenine (see Fig. S5a, ESI† for atom label) could play some role. However, the relevance of such interaction and its mechanism (direct or water-mediated) remains debated.^{3,17,19,20,22,28} In our simulations, we find that, regardless of the coordination mode, the Zn–N7 distance is always larger than 4 Å (see e.g. Fig. S5, ESI†). To further investigate the influence of adenosine on metal coordination, we performed additional WT-MTD simulation for MTP–Zn²⁺ (Table S6, ESI†), where the nucleobase is replaced by a simple methyl group, and we did not find specific effects of the nucleoside on the energetics and geometry of coordination (Fig. S4, S6 and S9a–d, ESI†).

The main criticism that is generally brought against non-bonded models for metal ions is the fact that there are no parameters reproducing both structural and thermodynamic experimental quantities.⁶³ To check the effect of the parametrization on Zn²⁺ interactions, we performed an additional WT-MTD simulation for ATP–Zn²⁺ using the model proposed by Duarte et al.⁵⁹ for the metal (Table S10, ESI†). This introduces dummy centers in an octahedral arrangement around Zn²⁺ to set the directionality of metal–ligand interactions. A detailed analysis of the simulation results is reported in Section S7 of the ESI.† As in the simulation based on the parametrization by Stote and Karplus, we did not observe any evidence of Zn²⁺ coordination to N7 of adenine; in fact, also in this case, the Zn²⁺–N7 distance remains above 4 Å (Fig. S11, ESI†).

3.3 Conformational properties of the triphosphate chain

The triphosphate chain is highly flexible, hence conformational degrees of freedom are expected to play a role in metal binding. Fig. 4 shows the free energy as a function of the bend angle defined by the three phosphorus atoms, Pα–Pβ–Pγ, which can be taken as a descriptor of the chain conformation. For the free nucleotide in water, the minimum is around 105°, and the free energy profile is not strongly modified when ATP is bound to Zn²⁺ in the βγ coordination mode, although the minimum is shifted towards more extended conformations. In contrast, the binding of the metal in the αγ mode leads to smaller values of the bend angle and narrowing of its distribution, with an even stronger effect for the αγγ coordination. This would suggest an unfavourable torsional strain in clamp conformations (αγγ and αγ), which is not easy to reconcile with the stability of the αγ coordination.

Fig. 4 Free energy profile as a function of the angle between the phosphorus atoms of ATP (Pα–Pβ–Pγ), calculated from standard MD simulation of the free nucleotide in water (dashed line) and by reweighting of WT-MTD run for the αγ (red solid), αγγ (blue solid) and βγ (green solid) coordination modes of ATP–Zn²⁺ in water.

To get further insight, we analysed the torsional properties of the triphosphate backbone. The plots in Fig. 5(a)–(g) show FESs and free energy profiles as a function of the dihedral angles defining the chain conformation (ω_i with i = 1–5, see Fig. 5(h)), for free ATP and for the αγ and βγ coordination modes. Analogous results are shown in Fig. S2 (ESI†) for the αγγ coordination. Fig. 5 evidences the flexibility of triphosphate, with different sensitivity of the various dihedrals to the binding state. In fact, on moving from the unbound state to the αγ coordination, the FESs for the torsional angles centered on Pα (ω₁ and ω₂) maintain their main features, although the height of barriers increases. In contrast, the FESs for the next dihedrals, ω₃ and ω₄, show a significant change. In particular ω₃, which in the unbound state does not exhibit significant barriers to rotation, is strongly restricted around the cis conformation upon αγ binding. The free energy profile for the torsional angle around the last phosphodiester bond of the chain (ω₅) has threefold symmetry, with minima corresponding to eclipsed conformations, which minimize the electrostatic repulsion between the PβO₂ group and the three equivalent Oγ atoms. The introduction of further contact, from bidentate αγ to tridentate αγγ, has the main effect of shifting the minima of the free energy for the last chain dihedral (ω₅) to staggered conformations (Fig. S2c, ESI†). There is also a slight change of the FESs for the dihedrals centered on Pα and Pβ (Fig. S2a and b, ESI†), which is in agreement with the small narrowing of the Pα–Pβ–Pγ angle shown in Fig. 4. More significant changes are observed in moving from αγ (Fig. 5(b), (e) and (g)) to βγ (Fig. 5(c), (f) and (g)) coordination. In particular, these concern the dihedrals centered on Pβ and Pγ, directly involved in metal coordination, which is constrained to narrow minima, separated by high barriers. This implies an increase in chain stiffness when oxygens linked to Pβ are coordinated to the metal, compared to clamp configurations (αγ and αγγ). It may be worth recalling that the geometry around phosphorus atoms strongly affects ³¹P chemical shifts.^64,65 Thus, the special sensitivity to coordination of the dihedrals centered on Pβ, compared to those centered on Pα and Pγ^64,65 could explain the much larger changes in ³¹P NMR chemical shift observed for this site upon metal binding.^17,22,23

Fig. 5 FES as a function of dihedral angles ω₁–ω₄ of triphosphate (a), (d) for free ATP and (b), (e) for αγ and (c), (f) for βγ coordinated ATP–Zn²⁺ in water. (g) Free energy profile as a function of the dihedral ω₅ (average over the three oxygens), for free ATP (black dashed), αγ (red solid) and βγ (green solid) coordinated ATP–Zn²⁺ in water. Data from standard MD simulation of ATP and from reweighting of WT-MTD run for ATP–Zn²⁺. (h) Definition of the dihedral angles of triphosphate. Cis and trans conformations correspond to 0° and 180°, respectively. For 1D free energy profiles of all dihedrals, see Fig. S3 (ESI†).

Using the dummy model for Zn²⁺,⁵⁹ we found that clamp configurations are around 10 kcal mol⁻¹ below extended ones (Fig. S10, ESI†) and the FES obtained for triphosphate dihedrals in the lowest free energy minima (αγ, αγγ and βγ) are similar to those obtained with the Stote and Karplus model (Fig. S12–S15, ESI†).⁵⁸ These results suggest that the coordination of Zn²⁺ to ATP is primarily dictated by the parametrization of intra- and intermolecular interactions of the triphosphate chain. Within these conformational preferences, the stabilization of αγγ and the destabilization of all monodentate coordination modes, predicted by the dummy model, are a consequence of a stronger tendency of Zn²⁺ to establish contacts with triphosphate oxygens than with water oxygens (Fig. S16, ESI†).

3.4 Including the metal ligand: ATP–[ZnCH₃ TACN]²⁺ and MTP–[ZnCH₃ TACN]²⁺

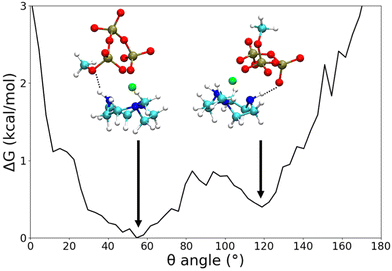
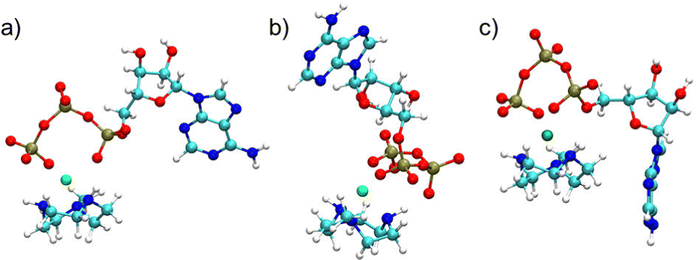
Preliminary standard MD simulations of Zn²⁺ and CH₃ TACN in water showed that the metal is coordinated to the three nitrogens of TACN in a well-defined geometry, with oxygen atoms of three water molecules to complete the hexacoordination (see Fig. S1 and Table S9, ESI†). Thus, in subsequent studies of ATP or MTP and metallosurfactant in water, Zn²⁺ coordinated to TACN and constrained in its equilibrium geometry was assumed. WT-MTD simulations of ATP–[ZnCH₃ TACN]²⁺ (Table S7, ESI†) and MTP–[ZnCH₃ TACN]²⁺ (Table S8, ESI†) in water, starting from water mediated and ion contact configurations respectively and using again the c.n.s of Zn²⁺ to phosphate oxygens as CVs, did not show dramatic effects of the CH₃ TACN ligand on the binding mode; see, for instance, the plots of the time evolution of the free energy minima along the WT-MTD trajectories for ATP–[ZnCH₃ TACN]²⁺ (Fig. S9e and f, ESI†). Irrespective of the presence of ligands, the global minimum corresponds to the αγ coordination and is quite lower in energy (5–7 kcal mol⁻¹) than the next αγγ, βγ and γ binding states. Comparing the results obtained with and without the CH₃ TACN ligand, one can notice, however, that in the former case, fluctuations of the free energy are generally larger, and there is some relative stabilization/destabilization of minima lying within the ranges of the order of 1 kcal mol⁻¹. These differences can be eventually ascribed to a rougher FES, due to the presence of additional binding modes between ATP and TACN, which lie within close energies. Analogous considerations can be made for MTP–[ZnCH₃ TACN]²⁺ (Fig. S9g and h, ESI†).

Typical structures of the αγ coordination state of ATP–[ZnCH₃ TACN]²⁺ and MTP–[ZnCH₃ TACN]²⁺ are shown in Fig. 6(c) and (d), and for comparison, also the structures of the corresponding complexes with free Zn²⁺ are reported in Fig. 6(a) and (b). Even though not sufficient to significantly perturb the coordination scheme, which is dictated by the strong interaction between triphosphate and zinc, interactions involving the ligand can contribute to the stabilization of bound states. Fig. 7 shows the free energy profile of MTP–[ZnCH₃ TACN]²⁺ in the αγ coordination, as a function of the angle (θ) between the normals to the plane of the nitrogens of TACN and the plane of phosphorus atoms of triphosphate. The minima correspond to different geometries, which both exhibit hydrogen bonds between phosphate oxygens and aminic hydrogens of the macrocycle. Additional interactions involving the ligand become even more important in the case of ATP and are expected to play a role in the architecture of self-assembled structures. As an example we show in Fig. 8 different configurations of αγ coordinated ATP–[ZnCH₃ TACN]²⁺, with and without direct contact between ATP and TACN. Further effects can be induced by substituents in the macrocycle, able to trigger specific and non-specific interactions with the adenine or the sugar moiety, such as the long alkyl chain bound to the tertiary nitrogen of TACN, that was employed in ref. 12.

Fig. 6 Representative structures of (a) ATP–Zn²⁺, (b) MTP–Zn²⁺, (c) ATP–[ZnCH₃TACN]²⁺, (d) MTP–[ZnCH₃TACN]²⁺ in water, in the global free energy minimum that corresponds to the αγ coordination mode.

Fig. 7 Free energy profile of MTP–[ZnCH₃ TACN]²⁺ as a function of the angle (θ) between the normals to the planes defined by the nitrogens of TACN and by the phosphorus atoms of triphosphate, calculated by reweighting of WT-MTD trajectories.

Fig. 8 Different configurations of αγ coordinated ATP–[ZnCH₃ TACN]²⁺: (a) without direct ATP–TACN interaction; (b) with a hydrogen bond between Oβ and an aminic hydrogen of TACN and (c) with direct interaction between adenine and TACN.

4 Conclusions

In this work, we investigated the binding of ATP to Zn²⁺, in both its free aqueous form and in complex with CH₃ TACN. Using well-tempered metadynamics simulations in combination with suitable collective variables based on coordination numbers, we could obtain a detailed picture of the free energy landscape of the bound systems.

From our results, it clearly emerges that the driving force behind the binding is the interaction between the charged phosphate groups and the metal cation. Although this could be expected, a clear description of the structure and energetics of the complexes is not obvious due to the presence of different binding sites in the flexible triphosphate chain. The most stable coordination is characterized by Zn²⁺ binding to the phosphate chain in a bidentate mode with direct contact to the oxygens linked to the α and γ phosphates. Different coordination types with one or two contacts, although possible, lay ∼10 k_B T higher in the free energy landscape. The relative stability of Zn²⁺–triphosphate coordination modes seems to be dictated primarily by the conformational preferences of the triphosphate chain of ATP. “Clamp” configurations (αγ and αγγ) are favoured over more extended ones (such as βγ). These results are robust with respect to the parametrization of the Zn²⁺ ion; in fact, we did not observe significant changes upon the replacement of a non-bonded soft-sphere model with an octahedral dummy model.

A thorough conformational analysis points to a special impact of metal coordination on the torsional angle distribution around Pβ, which is in agreement with a pronounced shift of resonance observed upon binding in the ³¹P NMR spectra of ATP. We do not observe specific interactions of Zn²⁺ with the nucleobase in the complex formation. This conclusion is further supported by the fact that the nature (geometry and coordination) and the order of the lower lying energy states do not change when in the simulations the nucleoside is replaced by a simpler methyl group. The role of the ligand was also addressed in the simulation of the ATP–[ZnCH₃ TACN]²⁺ system. Although interactions between the triphosphate oxygens and the aminic hydrogens of TACN are occasionally found, they do not play a key role in the stabilization of the complex. Our investigation represents a first step towards the detailed characterization at the atomistic level of the minimal aggregates of ATP, Zn²⁺ and CH₃ TACN, and provides the basis for the development of a system-specific chemically informed model, which will allow us to afford coarse grained simulations of the assembly/disassembly processes.

Author contributions

E. R.: conceptualization, investigation, formal analysis, and writing – original draft. A. F., M. S.: conceptualization, writing – review & editing, supervision, and resources.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Parts of this research were conducted using the supercomputer MOGON 2 and advisory services offered by Johannes Gutenberg-University Mainz (http://hpc.uni-mainz.de), which is a member of the AHRP (Alliance for High Performance Computing in Rhineland-Palatinate, http://www.ahrp.info) and the Gauss Alliance e.V. The authors gratefully acknowledge the computing time granted on the supercomputer MOGON 2 at Johannes Gutenberg-University Mainz (http://hpc.uni-mainz.de) and the C3P HPC facility of the Department of Chemical Sciences of the University of Padova. This project has received funding from the Deutsche Forschungsgemeinschaft under the TRR146 project (project A4). M. S. acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germanys Excellence Strategy-EXC 2033-390677874-RESOLV. E. R. acknowledges a PhD scholarship from the University of Padova. The authors thank prof. L. J. Prins for fruitful discussions.

Notes and references

1. P. Zhou, R. Shi, J. Feng Yao, C. Fang Sheng and H. Li, Coord. Chem. Rev., 2015, 292, 107–143.
2. A. E. Hargrove, S. Nieto, T. Zhang, J. L. Sessler and E. V. Anslyn, Chem. Rev., 2011, 111, 6603–6782.
3. H. Sigel and R. Griesser, Chem. Soc. Rev., 2005, 34, 875–900.
4. S. H. Jung, K. Y. Kim, J. H. Lee, C. J. Moon, N. S. Han, S.-J. Park, D. Kang, J. K. Song, S. S. Lee, M. Y. Choi, J. Jaworski and J. H. Jung, ACS Appl. Mater. Interfaces, 2017, 9, 722–729.
5. S. Dhiman, A. Jain and S. J. George, Angew. Chem., Int. Ed., 2017, 56, 1329–1333.
6. M. Kumar, P. Brocorens, C. Tonnelé, D. Beljonne, M. Surin and S. J. George, Nat. Commun., 2014, 5, 5793.
7. C. Pezzato and L. Prins, Nat. Commun., 2015, 6, 7790.
8. J. Deng and A. Walther, Adv. Mater., 2020, 32, 2002629.
9. A. Mishra, S. Dhiman and S. J. George, Angew. Chem., Int. Ed., 2021, 60, 2740–2756.
10. R. R. Mahato, E. Shandilya, B. Dasgupta and S. Maiti, ACS Catal., 2021, 11, 8504–8509.
11. Y. Altay, S. Cao, H. Che, L. K. E. A. Abdelmohsen and J. C. M. van Hest, Biomacromolecules, 2019, 20, 4053–4064.
12. S. Maiti, I. Fortunati, C. Ferrante, P. Scrimin and L. J. Prins, Nat. Chem., 2016, 8, 725–731.
13. J. P. Glusker, Adv. Protein Chem., 1991, 42, 1–76.
14. C. W. Bock, A. K. Katz and J. P. Glusker, J. Am. Chem. Soc., 1995, 117, 3754–3765.
15. M. Q. Fatmi, T. S. Hofer, B. R. Randolf and B. M. Rode, J. Chem. Phys., 2005, 123, 054514.
16. W. Maret, J. Inorg. Biochem., 2012, 111, 110–116.
17. M. Cohn and T. R. Hughes, J. Biol. Chem., 1962, 237, 176–181.
18. E. K. Jaffe and M. Cohn, Biochem., 1978, 17, 652–657.
19. J. L. Bock, J. Inorg. Biochem., 1980, 12, 119–130.
20. E. O. Bishop, S. J. Kimber, D. Orchard and B. E. Smith, Biochim. Biophys. Acta, 1981, 635, 63–72.
21. D. Dong, J. Zeng, F. Huang and Y. Ma, Asian J. Chem., 2014, 26, 6243–6248.
22. M. Cohn, Ann. N. Y. Acad. Sci., 1990, 603, 151–164.
23. F. Ramirez and J. F. Marecek, Biochim. Biophys. Acta, 1980, 589, 21–29.
24. B. P. Fingerhut, J. Schauss, A. Kundu and T. Elsaesser, Z. Phys. Chem., 2020, 234, 1453–1474.
25. B. P. Fingerhut, Chem. Commun., 2021, 57, 12880–12897.
26. C. Bazzicalupi, A. Bencini, A. Bianchi, A. Danesi, C. Giorgi, C. Lodeiro, F. Pina, S. Santarelli and B. Valtancoli, Chem. Commun., 2005, 2630–2632.
27. C. Bazzicalupi, A. Bencini, A. Bianchi, A. Danesi, E. Faggi, C. Giorgi, C. Lodeiro, E. Oliveira, F. Pina and B. Valtancoli, Inorg. Chim. Acta, 2008, 361, 3410–3419.
28. K. H. Scheller and H. Sigel, J. Am. Chem. Soc., 1983, 105, 5891–5900.
29. Y. H. Mariam and R. B. Martin, Inorg. Chim. Acta, 1979, 35, 23–28.
30. J. Akola and R. O. Jones, J. Phys. Chem. B, 2003, 107, 11774–11783.
31. T. Dudev, C. Grauffel and C. Lim, Sci. Rep., 2017, 7, 42377.
32. T. Dudev, C. Grauffel, S.-T. D. Hsu and C. Lim, J. Chem. Theory Comput., 2018, 14, 3311–3320.
33. C. Grauffel, T. Dudev and C. Lim, J. Chem. Theory Comput., 2019, 15, 6992–7003.
34. R. Saxena, V. B. K. S. P. K. Avanigadda, R. Singh and V. Agarwal, Int. J. Quantum Chem., 2021, 121, e26615.
35. J. C. Liao, S. Sun, D. Chandler and G. Oster, Eur. Biophys. J., 2004, 33, 29–37.
36. D. Branduardi, F. Marinelli and J. D. Faraldo-Gomez, J. Comput. Chem., 2016, 37, 575–586.
37. A. Bojovschi, M. S. Liu and R. J. Sadus, J. Chem. Phys., 2012, 137, 075101.
38. C. P. M. Scipion, U. Ghoshdastider, F. J. Ferrer, T. Y. Yuen, J. Wongsantichon and R. C. Robinsona, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10345–10350.
39. D. N. Shalaeva, D. A. Cherepanov, M. Y. Galperin, A. V. Golovin and A. Y. Mulkidjanian, eLife, 2018, 7, e37373.
40. F. P. Buelens, H. Leonov, B. L. D. Groot and H. Grubmüller, J. Chem. Theory Comput., 2021, 17, 1922–1930.
41. S. C. Kamerlin and A. Warshel, J. Phys. Chem. B, 2009, 113, 15692–15698.
42. G. Cassone, D. Chille, V. M. Nardo, O. Giuffre, R. C. Ponterio, J. Sponer, S. Trusso, F. Saija and C. Foti, Dalton Trans., 2020, 49, 6302–6311.
43. A. Bleuzen, P.-A. Pittet, L. Helm and A. E. Merbach, Magn. Reson. Chem., 1997, 35, 765–773.
44. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
45. https://www.lammps.org/ .
46. G. Fiorin, M. L. Klein and J. Hénin, Mol. Phys., 2013, 111, 3345–3362.
47. A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603.
48. L. Verlet, Phys. Rev., 1967, 159, 98–103.
49. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
50. S. Nosé, Mol. Phys., 1984, 52, 255–268.
51. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
52. G. Martyna, D. Tobias and M. Klein, J. Chem. Phys., 1994, 101, 4177–4189.
53. M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci, R. A. Broglia and M. Parrinello, Comput. Phys. Commun., 2009, 180, 1961–1972.
54. https://www.ks.uiuc.edu/Research/vmd/vmd-1.9.3/ .
55. M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, Chem. Phys. Lett., 2017, 683, 276–280.
56. F. Peral and E. Gallego, Biophys. Chem., 2000, 85, 79–92.
57. M. L. P. Price, D. Ostrovsky and W. L. Jorgensen, J. Comput. Chem., 2001, 22, 1340–1352.
58. R. H. Stote and M. Karplus, Proteins: Struct., Funct., Bioinf., 1995, 23, 12–31.
59. F. Duarte, P. Bauer, A. Barrozo, B. A. Amrein, M. Purg, J. Åqvist and S. C. L. Kamerlin, J. Phys. Chem. B, 2104, 118, 4351–4362.
60. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
61. M. Bonomi, A. Barducci and M. Parrinello, J. Comput. Chem., 2009, 30, 1615–1621.
62. E. Ahlstrand, K. Hermansson and R. Friedman, J. Phys. Chem. A, 2017, 121, 2643–2654.
63. P. Li, B. P. Roberts, D. K. Chakravorty, J. Kenneth and M. Merz, J. Chem. Theory Comput., 2013, 9, 2733–2748.
64. F. R. Prado, C. Giessner-Prettre, B. Pullman and J.-P. Daudey, J. Am. Chem. Soc., 1979, 101, 1737–1742.
65. D. G. Gorenstein, Annu. Rev. Biophys. Bioeng., 1981, 10, 355–386.

---

Footnote

† Electronic supplementary information (ESI) available: Simulation details, additional free energy surfaces and conformational analysis. See DOI: https://doi.org/10.1039/d2cp05516c

---