 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Towards structural reconstruction from X-ray spectra†
Anton
Vladyka
 *a,
Christoph J.
Sahle
*a,
Christoph J.
Sahle
 b and
Johannes
Niskanen
b and
Johannes
Niskanen
 a
a
aUniversity of Turku, Department of Physics and Astronomy, 20014 Turun yliopisto, Finland. E-mail: anton.vladyka@utu.fi; johannes.niskanen@utu.fi
bEuropean Synchrotron Radiation Source, 71 Avenue des Martyrs, 38000 Grenoble, France. E-mail: christoph.sahle@esrf.fr
First published on 15th February 2023
Abstract
We report a statistical analysis of Ge K-edge X-ray emission spectra simulated for amorphous GeO2 at elevated pressures. We find that employing machine learning approaches we can reliably predict the statistical moments of the Kβ′′ and Kβ2 peaks in the spectrum from the Coulomb matrix descriptor with a training set of ∼ 104 samples. Spectral-significance-guided dimensionality reduction techniques allow us to construct an approximate inverse mapping from spectral moments to pseudo-Coulomb matrices. When applying this to the moments of the ensemble-mean spectrum, we obtain distances from the active site that match closely to those of the ensemble mean and which moreover reproduce the pressure-induced coordination change in amorphous GeO2. With this approach utilizing emulator-based component analysis, we are able to filter out the artificially complete structural information available from simulated snapshots, and quantitatively analyse structural changes that can be inferred from the changes in the Kβ emission spectrum alone.
1 Introduction
Core-level spectroscopy provides information of structure of matter at the atomic level, and the constituent methods are applied from standard material characterization to conceptually new experiments at large-scale facilities such as free-electron lasers. Although reference data helps, interpretation of core-level spectra is not always straightforward, especially in the case of soft condensed or amorphous matter where ensemble statistics plays a drastic role.1–7 Studies of this statistical nature, and the implied repeated function evaluations, could benefit from machine learning (ML), application of which to core-level spectra has been studied rather intensively lately.8–15 In general, when working with atomic resolution studies have raised the need to engineer features for both structure16–20 and spectra.13,19The pressure dependent evolution of the germanium coordination by oxygen in glassy GeO2 has been a long standing subject of study.21–24 Besides applications of amorphous GeO2 in technical glasses, the increased sensitivity of a-GeO2 to pressure compared to amorphous SiO2 motivates the study of structural changes similar to those expected to occur in the pressurized analogue glass a-SiO2 but at greatly reduced absolute pressures. Detailed knowledge of the compaction mechanisms in these simple glasses will have direct consequences for our understanding of geological, geochemical, and geophysical processes involving more complex silicate glasses and melts.
X-ray emission spectra (XES) of GeO2 is an inviting case for development of spectroscopic analysis for soft and amorphous condensed matter. First, large spectroscopic changes with changing local structure are known to exist.24 Second, simulations are known to reproduce the observed ensemble-mean effects well.25 Third, XES is local-occupied-orbital derived and a few orbital-bonding neighbor atoms are expected to be decisive for the spectrum outcome. This would result in a minimal set of structural parameters needed to predict XES. Last, owing to the chemical simplicity and simple bonding topology due to non-molecular structure, this system has promise to be reproduced by ML with the limited number of data points that the condensed phase allows. Namely, for such systems the electronic simulation needs to account for multi-electron effects in numerous interacting atoms - typically on the level of density functional theory. As a consequence, the number of individual structural data points for spectroscopy can be expected to be ∼ 104 in an extensive contemporary simulation.
In this work, we focus on Ge Kβ XES calculations of amorphous GeO2 at elevated pressures. Our previous work on the water molecule indicated that predicting spectral features is easier than predicting structural features.14 In the condensed phase, where the structural features to be predicted are more numerous, the task is arguably even more complicated. As a solution to this dilemma, we build a procedure on spectrum prediction for structures, dimensionality reduction and iterative optimization algorithms. This approach is possible because the evaluation of a ML model requires much less computational resources than the corresponding quantum mechanical calculation does. We predict statistical moments of XES lines from a Coulomb matrix16 that describes the local atomic structure around the site of characteristic X-ray emission. Next, we study obtainable structural information for the occurring spectral changes in the pressure progression of the XES by emulator-based component analysis (ECA).15 Last, we investigate an approximate solution to the spectrum-to-structure inverse problem by first transforming it into an optimization task in the dimension-reduced ECA space, followed by expansion to the full multi-dimensional Coulomb matrix. A dedicated evaluation data set allows for assessment of performance of the approach in each of the aforementioned tasks.
2 Methods
After ionisation from a Ge 1s orbital, the electronic system is left in a highly excited state, which decays by either Auger decay or by emission of a photon, accompanied by a transition of an electron from a higher-energy orbital. For germanium, transitions from 3p to 1s orbital give rise to so called Kβ emission spectra. Since the Ge 3p orbitals constitute valence orbitals, Ge Kβ XES is highly sensitive to chemical bonding of the active Ge site.We study data of amorphous GeO2 from statistical spectral simulations over a range of 11 pressure values from 0 GPa to 120 GPa. These XES spectra, simulated using the OCEAN code26,27 (version 2.5.2), are based on real-space configurations from ab initio molecular dynamics simulations reported earlier by Du et al.28 We used the Quantum ESPRESSO program package (version 5.0)29,30 for sampling the ground state wave functions and electron densities at the gamma point with a plane wave cutoff of 100 Ry (see Ref. 25 for more details). Transition matrix elements are then calculated using the Haydock recursion method31 as implemented in the OCEAN code using a Lorentzian width of 1.0 eV for the continued fraction. At each pressure point, Ge Kβ XES spectra of 18 structurally uncorrelated AIMD simulation snapshots containing 72 GeO2 formula units were calculated for each Ge atom. For 5 pressure points only 17 out of 18 snapshots yielded spectra in a finite time frame due to convergence issues, resulting in 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 896 XES spectra. The spectra of individual Ge sites were aligned and normalized for each pressure to yield a constant Kβ5 line peak position and intensity in its ensemble average spectrum.
896 XES spectra. The spectra of individual Ge sites were aligned and normalized for each pressure to yield a constant Kβ5 line peak position and intensity in its ensemble average spectrum.
Even though extensive from a statistical simulation viewpoint, the available dataset is still rather limited for sophisticated ML algorithms. In this case, using a descriptive numerics allows for condensing structural and spectral information to a few parameters, resulting in an improvement of ML performance. We apply descriptors to both the spectrum and the atomic structure of the system (see below).
2.1 Spectral-line descriptor
The XES spectrum is given as a function presenting intensity against photon energy in eV (I = I(E)). For a distinguishable peak in the spectrum, we use raw moments defined as follows: | (1) |
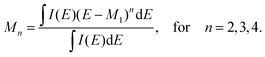 | (2) |
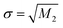 (eV), skewness sk =M3/σ3 and excess kurtosis ex = M4/σ4 − 3. These descriptors are referred to as “spectral moments”, and are presented as a vector m throughout the manuscript. In this work, 4 moments were calculated for both Kβ′′ and Kβ2 peaks, which resulted in 8 descriptors per spectrum.
(eV), skewness sk =M3/σ3 and excess kurtosis ex = M4/σ4 − 3. These descriptors are referred to as “spectral moments”, and are presented as a vector m throughout the manuscript. In this work, 4 moments were calculated for both Kβ′′ and Kβ2 peaks, which resulted in 8 descriptors per spectrum.
2.2 Structural descriptors
As the structural descriptor we use the Coulomb matrix,16 the elements of which are defined as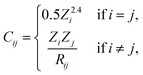 | (3) |
The definition of the Coulomb matrix implies that it can be inverted to a distance matrix containing interatomic distances by
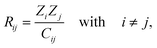 | (4) |
To check the performance of the Coulomb matrix descriptor against a many-body-tensor-representation32 spirited descriptor, we used snapshot-wise evaluated radial distribution functions (RDF) from the active site. Although similar predictive power was obtained via the RDF, its performance in the later steps of the analysis (spectral coverage of decomposition) was inferior to that of the Coulomb matrix.
2.3 Algorithms
The structural and spectral data are presented as feature-wise standardized matrices![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) and
and ![[M with combining tilde]](https://www.rsc.org/images/entities/b_char_004d_0303.gif) , respectively (individual data points
, respectively (individual data points ![[p with combining tilde]](https://www.rsc.org/images/entities/b_char_0070_0303.gif) and
and ![[m with combining tilde]](https://www.rsc.org/images/entities/b_char_006d_0303.gif) occupy rows in these matrices). The analysis algorithms aim at discovering the correlations between the two data sets, for which we first applied the emulator-based component analysis (ECA) method as described in ref. 15. This algorithm relies on a machine-learning based emulator for spectral features at a vector of structural descriptors, that may be previously unseen to it. The algorithm uses projection of structural data on a subspace so that projected data maximize the generalized covered spectral variance (R2 score) when a prediction is made using the emulator. Here, ECA is applied to standardized Coulomb matrix parameters
occupy rows in these matrices). The analysis algorithms aim at discovering the correlations between the two data sets, for which we first applied the emulator-based component analysis (ECA) method as described in ref. 15. This algorithm relies on a machine-learning based emulator for spectral features at a vector of structural descriptors, that may be previously unseen to it. The algorithm uses projection of structural data on a subspace so that projected data maximize the generalized covered spectral variance (R2 score) when a prediction is made using the emulator. Here, ECA is applied to standardized Coulomb matrix parameters ![[p with combining tilde]](https://www.rsc.org/images/entities/b_char_0070_0303.gif) and the corresponding standardized spectral moments
and the corresponding standardized spectral moments ![[M with combining tilde]](https://www.rsc.org/images/entities/b_char_004d_0303.gif) . The decomposition algorithm results in orthonormal standardized-structural-parameter-space vectors ṽ1,ṽ2,… so that spectral moments
. The decomposition algorithm results in orthonormal standardized-structural-parameter-space vectors ṽ1,ṽ2,… so that spectral moments ![[m with combining tilde]](https://www.rsc.org/images/entities/b_char_006d_0303.gif) emu = Semu(
emu = Semu(![[p with combining tilde]](https://www.rsc.org/images/entities/b_char_0070_0303.gif) (k)) for projections
(k)) for projections | (5) |
![[p with combining tilde]](https://www.rsc.org/images/entities/b_char_0070_0303.gif) at the given rank k. Scores ti are coordinates of the approximate point
at the given rank k. Scores ti are coordinates of the approximate point ![[p with combining tilde]](https://www.rsc.org/images/entities/b_char_0070_0303.gif) (k) in the k-dimensional subspace.
(k) in the k-dimensional subspace.
The ECA method requires an emulator capable of predicting spectral moments for new structural data points. As an emulator, a trained multilayer perceptron (MLP) with 2 hidden layers and 64 neurons in each layer was used. We dedicated 80% of data for training, and 20% for evaluation of the prediction. Overall, all configurations of MLPs with 2–3 hidden layers and 64 or 128 neurons were evaluated on the training dataset (∼11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 spectra) using mean squared error as a training metric.
000 spectra) using mean squared error as a training metric.
For comparison, we used partial least squares fitting based on singular value decomposition (PLSSVD)33 as applied to the X-ray spectroscopic problem in ref. 15. The PLSSVD algorithm relies on projections of spectral and structural feature vectors on latent variables between which a linear fit is made. The method results in an approximation of the data up to rank k
 | (6) |
![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) U(i),
U(i),![[M with combining tilde]](https://www.rsc.org/images/entities/b_char_004d_0303.gif) V(i)). The orthonormal basis vectors are obtained from a singular value decomposition of the covariance matrix of the data cov(
V(i)). The orthonormal basis vectors are obtained from a singular value decomposition of the covariance matrix of the data cov(![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) ,
,![[M with combining tilde]](https://www.rsc.org/images/entities/b_char_004d_0303.gif) ) =
) =![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) T
T![[M with combining tilde]](https://www.rsc.org/images/entities/b_char_004d_0303.gif) ; ordering along descending magnitude of the singular values λi is applied. For analysis using the PLSSVD algorithm, the same evaluation data set as for ECA was used.
; ordering along descending magnitude of the singular values λi is applied. For analysis using the PLSSVD algorithm, the same evaluation data set as for ECA was used.
3 Results
The ensemble-averaged Ge Kβ XES of GeO2 shows a transition induced by pressure, as seen in Fig. 2. Even though a smooth progression of the spectrum as a function of pressure is observed, the underlying statistical variation in the condensed-phase XES is large.3,5,25 This is manifested by gray shading in Fig. 2 that shows the minimum–maximum variation of intensity in the data set. We proceed with our analysis for the two lines with clear pressure dependence: the Kβ′′ and the Kβ2.Fig. 3a–c present structures and spectra of three individual snapshots at pressures of 0, 30, and 120 GPa, respectively. Fig. 3d–k in turn show the prediction and training performance of the chosen MLP for these descriptors. In the figure, perfect match between known and predicted data lie on the diagonal dashed line. Furthermore, the positions of the three illustrated spectra of Fig. 3a–c, as well as the mean moment values for each pressure point against moment values of the known mean spectrum are indicated by crosses.
The spectra and their statistical moments show a clear trend as a function of pressure. Moreover, the overall quality of the prediction performance yields Pearson correlation coefficients above 0.94. The pressure-induced progression in the spectra is transferred into spectral moments, for which the ML task proved to be easier than predicting spectra as vectors of channel-wise-listed intensity values (see Fig. S2, ESI†). Analogously with simple intensity prediction, spectral moments of an ensemble-averaged spectrum can be estimated by the mean of predicted moments to a good accuracy (see crosses in Fig. 3d–k). However, this is an approximate finding instead of a mathematical equality.
For the evaluation data set, some 77% of generalized covered spectral variance (R2 score) can be explained by only a single ECA component ṽ1 (83% with two components {ṽ1,ṽ2}). These components represent individually standardized elements of a Coulomb matrix unrolled to 153-dimensional vectors (for {ṽ1,ṽ2} rolled back to the standardized Coulomb matrix differences, see Fig. S3, ESI†) For PLSSVD, corresponding spectral variance coverages were 73% and 77% for one and two components, respectively. The added contribution of the second component indicates a rapid drop of improvement in higher ranks.
Before entering the inverse problem, it is instructive to analyse the decomposition of first rank i.e. along the path ![[p with combining tilde]](https://www.rsc.org/images/entities/b_char_0070_0303.gif) (1) = t1ṽ1. Since the emulator provides the nonlinear response to the input vector, ECA is able to mimic the behavior of the moments more closely than PLSSVD, which is linear by definition (for the spectral moments along t1 see Fig. S4, ESI†). For this reason, dimensionality reduction by ECA will be better adjusted to the spectral response; even with inaccuracies in prediction by the emulator, higher covered spectral variance is still obtained than from PLSSVD. For a majority of the atoms, both PLS and ECA trajectories follow the pressure-wise ensemble mean interatomic distances R0i from the active Ge site along the path (Fig. S5, ESI†). However, for atoms Ge3, Ge4, O3, O4 and O7 the ECA trajectories show a different behavior, which indicates that the role of these atoms in deciding the spectral outcome is low compared to other atoms.
(1) = t1ṽ1. Since the emulator provides the nonlinear response to the input vector, ECA is able to mimic the behavior of the moments more closely than PLSSVD, which is linear by definition (for the spectral moments along t1 see Fig. S4, ESI†). For this reason, dimensionality reduction by ECA will be better adjusted to the spectral response; even with inaccuracies in prediction by the emulator, higher covered spectral variance is still obtained than from PLSSVD. For a majority of the atoms, both PLS and ECA trajectories follow the pressure-wise ensemble mean interatomic distances R0i from the active Ge site along the path (Fig. S5, ESI†). However, for atoms Ge3, Ge4, O3, O4 and O7 the ECA trajectories show a different behavior, which indicates that the role of these atoms in deciding the spectral outcome is low compared to other atoms.
The interpretation of spectra would ideally lead to structures constructed from the spectroscopic information. However, already with a few number of degrees of freedom (here 153) this problem is tedious. In line with findings in ref. 14, training an emulator to directly predict the Coulomb matrix from the spectral moments was not successful with the model selection grid, data and descriptors used here (the mean Pearson correlation coefficient of 0.33 was obtained). Therefore we looked at approaches that would rely on spectrum prediction by an emulator, that has in general better performance. However, an emulator-based approach of iteratively fitting the parameters ![[p with combining tilde]](https://www.rsc.org/images/entities/b_char_0070_0303.gif) to yield the 8 desired spectral moments proved also to be an unstable high-dimensional problem, that we were unable to solve. Instead, fitting a few ECA component scores for matching spectral moments is a much simpler task that could be solved.
to yield the 8 desired spectral moments proved also to be an unstable high-dimensional problem, that we were unable to solve. Instead, fitting a few ECA component scores for matching spectral moments is a much simpler task that could be solved.
We searched for the coordinates t in the standardized dimension-reduced space by minimization of the least-squares error
 | (7) |
 with given standardized spectral moments
with given standardized spectral moments ![[m with combining tilde]](https://www.rsc.org/images/entities/b_char_006d_0303.gif) . Here,
. Here, ![[S with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0053_0303.gif) emu(
emu(![[p with combining tilde]](https://www.rsc.org/images/entities/b_char_0070_0303.gif) ) is the standardized output of the moment emulator. We limit the study to two components t1 and t2.
) is the standardized output of the moment emulator. We limit the study to two components t1 and t2.
Fig. 4 shows coordinates t = (t1,t2) for each point from the evaluation data set from fitting of eqn (7). Deduced coordinates for the set of moments of each mean-ensemble spectrum (blue line) are in a good agreement with projections of known mean points (black line) for a given pressure ensemble on the same subspace. It appears though, that this reconstruction of the scores ti misses the second component, possibly due to the fact that the component is already insignificant and the emulator is known to be imperfect. Knowledge of scores ti allows construction of an approximate Coulomb matrix ![[p with combining tilde]](https://www.rsc.org/images/entities/b_char_0070_0303.gif) as a linear combination up to rank k. The absolute p is obtained after inverse standardization, as are C and R.
as a linear combination up to rank k. The absolute p is obtained after inverse standardization, as are C and R.
Even though the mean interatomic distances are not necessarily obtainable from mean Coulomb matrix elements, and even though this matrix is not necessarily obtainable from the spectral moments of the ensemble-mean spectrum (which closely match with the ensemble mean of the spectral moments), we find both to be the case. Fig. 5 depicts the reconstructed atomic distances from the spectral moments with one-dimensional and two-dimensional ECA space, indicating rapid convergence. Moreover, the reconstruction is at least qualitatively correct as seen from comparison with the known values for the evaluation data set, the most notable discrepancy being the 5th closest O atom at low pressures. This behavior can be understood in terms of reduced sensitivity of the spectra to these atomic distances; the first ECA component does not capture the drastic relative change in the parameter value (Fig. S5, ESI†), and even the second component does not fix this shortcoming. Likewise, for the overall match on the data set, the vector ṽ1 results in underestimation of O6 distance at large t1 (high pressures), which leads to the line crossings in Fig. 5a. However, the pressure-induced coordination change from 4-coordinated Ge to 6-coordinated Ge21 is clearly discernible around the pressure of 10 GPa by the increase of the Ge–O separation for the first four oxygen atoms and the concomitant decrease of Ge–O distance for the fifth and sixth nearest oxygen neighbor. We note that while the first row of the constructed Coulomb matrix represent ensemble-averaged distances, the structure constructed from the mean Coulomb matrix is nonsensical.
4 Discussion
With the limited data available it is essential to have structural and spectral descriptors that are linkable by rather simple MLPs. Consequently, the used descriptors dictate the analysis to follow. While the relative positions of atoms for a Coulomb matrix can be evaluated (see ESI†), there is dropout of more remote, potentially significant atoms. Furthermore, the observation that spectral moments are more suitable than tabulated intensities complicates spectral analysis as they may not be applicable in all cases, e.g. when clearly distinct and identifiable peaks are not formed for all data points.Instead of more direct approaches, approximate solution of the inverse problem by reconstruction of the first ECA components proved to be a feasible task to solve by optimization. It is natural to select these parameters so that they explain most spectral variance. As a result converging expansion of less and less relevant degrees of freedom are added and finally, irrelevant are identified and filtered out. Imperfection of emulator and incompleteness of the basis are likely reasons for the crossings of lines in Fig. 5a.
Structural analysis of the AIMD trajectory results in a complete analysis of structural changes across the data set. However, this information does not indicate what can be concluded based on the XES alone, as the sensitivity of core-level spectra to structural parameters may vary greatly.15,34 A parameter without an effect on a spectrum certainly cannot be expected to be reconstructed from it, and thus spectral insensitivity to a structural degree of freedom presents a danger of misinterpretation. The design of ECA means that a spectrally irrelevant structural degree of freedom obtains zero projection in the basis vector and is, in principle, omitted in subsequent analyses. Therefore, effects shown by ECA, and analysis based on it, can be considered to be inferred from a spectrum and its change. This reasoning is supported by Fig. 5, where the magnitudes of change from 0 GPa to 120 GPa in the known distance curves mostly exceed those of the predicted ones. For the end-to-end difference oxygens O3 and O4 with negligible (< 0.05 Å) total change exceed that of the known data. Depending on details of an analysis other - rather minor - violations to the tendency can be found in the data.
For the 17 atoms and 11 pressures, the mean absolute deviation from the known ensemble-mean distances for 2-component decomposition was 0.091 Å for ECA and notably 0.051 Å for PLSSVD with which we also carried out the analysis (see Fig. S7–S9, ESI†). We interpret the better performance of PLSSVD to be due to more emphasis placed on structural variance in the method, whereas ECA focuses strictly on spectral significance. Thus PLS is allowed to know more from the simulated structural parameter space than the spectra alone would allow. However, the method undoubtedly benefited of the choice of descriptors by ML studies, making the data suitable for a linear model. In addition, imperfection of ECA results come from the imperfection of the emulator.
Since the studied XES involves transitions of electrons from the occupied valence to localized deep core levels, the associated transition matrix elements become naturally limited to the immediate neighbourhood of the active atomic site. The occupied valence orbitals, in turn, can be expected to participate in chemical bonding, and thus to render these transitions sensitive to e.g. coordination number of the active site. It is an interesting yet open question to which degree the findings presented here generalize in other systems, and specifically to those posed by XES of high-pressure science. When assuming no exceptionality for GeO2 studied here, these spectra are potent of delivering far more structural information than it may at first seem.
5 Conclusions
For Ge Kβ XES of GeO2 at elevated pressures, Coulomb matrix and statistical moments of spectral peaks prove to be descriptors feasible to be linked by machine-learning applications with ∼ 104 simulated data points. We find the statistical moments of ensemble mean spectra to match closely with the ensemble mean of individually predicted moments. Dimensionality reduction by the ECA decomposition technique provides a means for a stable approximate solution of a spectroscopic inverse problem. We find the first row of a Coulomb matrix reconstructed from the spectral moments of the ensemble-mean spectrum to represent that obtained from ensemble-mean interatomic distances from the active site. Therefore, without a strict mathematical necessity, we find that these distances can be reconstructed to a good accuracy from the ensemble mean spectral statistical moments.Decomposition of structural sensitivity of spectra reduces the number of free parameters to be solved in the inversion problem, to only a few that have been chosen a priori for their spectral significance. The basis vectors of such decomposition span a subspace of degrees of freedom with most spectral response, and therefore reconstruction via this subspace will show structural effects with true inference from the change of spectra. This prevents spectrally irrelevant structural information, available in a simulation work, from affecting the analysis. Partial least squares fitting such as PLSSVD offers a usable and much lighter alternative where machine learning is not feasible, but the method is not as strict in spectrum-only inference.
Data availability
Underlying data (MD structures, corresponding XES spectra) and analysis scripts are available via request from the authors.Author contributions
A. V. data analysis, machine learning, writing the manuscript; C. J. S. simulations, data curation, writing the manuscript; J. N. research design, data curation and its assistive analysis, funding, writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Academy of Finland is acknowledged for funding via project 331234. The European Synchrotron Radiation Facility is thanked for providing computing resources.References
- P. Wernet, D. Nordlund, U. Bergmann, M. Cavalleri, M. Odelius, H. Ogasawara, L. Näslund, T. K. Hirsch, L. Ojamäe, P. Glatzel, L. G. M. Pettersson and A. Nilsson, Science, 2004, 304, 995–999 CrossRef CAS PubMed.
- N. Ottosson, K. J. Børve, D. Spångberg, H. Bergersen, L. J. Sæthre, M. Faubel, W. Pokapanich, G. Öhrwall, O. Björneholm and B. Winter, J. Am. Chem. Soc., 2011, 133, 3120–3130 CrossRef CAS PubMed.
- J. Niskanen, C. J. Sahle, K. O. Ruotsalainen, H. Müller, M. Kavčič, M. Žitnik, K. Bučar, M. Petric, M. Hakala and S. Huotari, Sci. Rep., 2016, 6, 21012 CrossRef CAS PubMed.
- J. Niskanen, C. J. Sahle, K. Gilmore, F. Uhlig, J. Smiatek and A. Föhlisch, Phys. Rev. E, 2017, 96, 013319 CrossRef PubMed.
- J. Niskanen, M. Fondell, C. J. Sahle, S. Eckert, R. M. Jay, K. Gilmore, A. Pietzsch, M. Dantz, X. Lu and D. E. McNally, et al. , Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 4058–4063 CrossRef CAS PubMed.
- V. Vaz da Cruz, F. Gelmukhanov, S. Eckert, M. Iannuzzi, E. Ertan, A. Pietzsch, R. C. Couto, J. Niskanen, M. Fondell and M. Dantz, et al. , Nat. Commun., 2019, 10, 1–9 CrossRef CAS PubMed.
- A. Pietzsch, J. Niskanen, V. V. da Cruz, R. Büchner, S. Eckert, M. Fondell, R. M. Jay, X. Lu, D. McNally, T. Schmitt and A. Föhlisch, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2118101119 CrossRef CAS PubMed.
- J. Timoshenko, A. Anspoks, A. Cintins, A. Kuzmin, J. Purans and A. I. Frenkel, Phys. Rev. Lett., 2018, 120, 225502 CrossRef CAS PubMed.
- J. Timoshenko and A. I. Frenkel, ACS Catal., 2019, 9, 10192–10211 CrossRef CAS.
- M. R. Carbone, S. Yoo, M. Topsakal and D. Lu, Phys. Rev. Mater., 2019, 3, 033604 CrossRef CAS.
- M. R. Carbone, M. Topsakal, D. Lu and S. Yoo, Phys. Rev. Lett., 2020, 124, 156401 CrossRef CAS PubMed.
- C. D. Rankine, M. M. M. Madkhali and T. J. Penfold, J. Phys. Chem. A, 2020, 124, 4263–4270 CrossRef CAS PubMed.
- S. A. Guda, A. S. Algasov, A. A. Guda, A. Martini, A. N. Kravtsova, A. L. Bugaev, L. V. Guda and A. V. Soldatov, J. Surf. Invest.: X-Ray, Synchrotron Neutron Tech., 2021, 15, 934–938 CrossRef CAS.
- J. Niskanen, A. Vladyka, J. A. Kettunen and C. J. Sahle, J. Electron Spectrosc. Relat. Phenom., 2022, 260, 147243 CrossRef CAS.
- J. Niskanen, A. Vladyka, J. Niemi and C. J. Sahle, R. Soc. Open Sci., 2022, 9, 220093 CrossRef CAS PubMed.
- M. Rupp, A. Tkatchenko, K. R. Müller and O. A. Von Lilienfeld, Phys. Rev. Lett., 2012, 108, 1–5 CrossRef PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 1–16 Search PubMed.
- J. Timoshenko, D. Lu, Y. Lin and A. I. Frenkel, J. Phys. Chem. Lett., 2017, 8, 5091–5098 CrossRef CAS PubMed.
- K. Ghosh, A. Stuke, M. Todorović, P. B. Jørgensen, M. N. Schmidt, A. Vehtari and P. Rinke, Adv. Sci., 2019, 6, 1801367 CrossRef PubMed.
- M. F. Langer, A. Goeßmann and M. Rupp, npj Comput. Mater., 2022, 8, 41 CrossRef.
- M. Guthrie, C. Tulk, C. Benmore, J. Xu, J. Yarger, D. Klug, J. Tse, H. Mao and R. Hemley, Phys. Rev. Lett., 2004, 93, 115502 CrossRef CAS PubMed.
- G. Lelong, L. Cormier, G. Ferlat, V. Giordano, G. Henderson, A. Shukla and G. Calas, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 134202 CrossRef.
- Y. Kono, C. Kenney-Benson, D. Ikuta, Y. Shibazaki, Y. Wang and G. Shen, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 3436–3441 CrossRef CAS PubMed.
- G. Spiekermann, M. Harder, K. Gilmore, P. Zalden, C. J. Sahle, S. Petitgirard, M. Wilke, N. Biedermann, C. Weis, W. Morgenroth, J. S. Tse, E. Kulik, N. Nishiyama, H. Yavaş and C. Sternemann, Phys. Rev. X, 2019, 9, 011025 CAS.
- G. Spiekermann, C. J. Sahle, J. Niskanen, K. Gilmore, S. Petitgirard, C. Sternemann, J. S. Tse and M. Murakami, J. Phys. Chem. Lett., 2023, 14, 1848–1853 CrossRef PubMed.
- J. Vinson, J. Rehr, J. Kas and E. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115106 CrossRef PubMed.
- K. Gilmore, J. Vinson, E. L. Shirley, D. Prendergast, C. D. Pemmaraju, J. J. Kas, F. D. Vila and J. J. Rehr, Comput. Phys. Commun., 2015, 197, 109–117 CrossRef CAS.
- X. Du and J. S. Tse, J. Phys. Chem. B, 2017, 121, 10726–10732 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- Quantum ESPRESSO, https://www.quantum-espresso.org.
- R. Haydock, V. Heine and M. Kelly, J. Phys. C-Solid State Phys., 1975, 8, 2591 CrossRef.
- H. Huo and M. Rupp, Mach. Learn. Sci. Technol., 2022, 3, 045017 CrossRef.
- F. L. Bookstein, P. D. Sampson, A. P. Streissguth and H. M. Barr, Dev. Psychol., 1996, 32, 404–415 Search PubMed.
- T. G. Bergmann, M. O. Welzel and C. R. Jacob, Chem. Sci., 2020, 11, 1862–1877 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05420e |
| This journal is © the Owner Societies 2023 |





