Healing double vacancy defects on graphene: reconstruction by C₂ adsorption

Abstract

Graphene has emerged as an exciting material because of its widespread applications resulting from its unique properties. Nano-scale engineering of graphene's structure is one of the most active research areas aimed at introducing functionalities to improve the performance or endow the graphene lattice with novel properties. In this regard, conversion between the hexagon and non-hexagon rings becomes an exciting tool to tune the electronic structure of graphene due to the distinct electronic structure and functionalities induced in graphene by each type of ring. This Density Functional Theory (DFT) study is an in-depth look at the adsorption-induced conversion of pentagon–octagon–pentagon rings to hexagon rings, and systematically investigates the possibility of the conversion of pentagon–octagon–pentagon rings to pentagon–heptagon pair rings. Moreover, the bottlenecks for these atomic-level conversions in the lattice structure of graphene and the influence of heteroatom doping on the mechanisms of these transformations are established.

---

Introduction

Graphene has emerged as an exciting material because of its widespread applications resulting from its unique properties. Nano-scale engineering of graphene mainly aims to introduce functionalities for improving its performance. The main structural characteristics of graphene are determined by the synthesis method and can be further modified through post-processing.^1–4 Atomically precise graphene can be synthesized via bottom-up approaches,^5–7 top-down^8–11 and mixed methods.^12–16 Moreover, in almost all kinds of graphene synthesis methods, the generation of structural defects is unavoidable.¹⁷

Defects on the one hand reduce carrier mobility by scattering the electron waves, and on the other hand they tend to increase the band gap,¹⁸ leading to chemical reactivity and catalytic properties,¹⁹ as well as changing the mechanical strength, thermal conductivity and electrical conductivity of the ideal graphene sheet.^20–23 Structural defects play a key role in the activity of graphene as metal-free catalysts and as commercial catalysts.¹⁹ Since a specific balance between different properties may be required for each particular graphene functionality, engineering of the defect density by post-processing methods can become an essential tool to control the performance of a particular graphene sample for a target application, particularly in catalysis.

Among various types of structural defects, carbon vacancies (in particular single and double vacancies, SV and DV) and Stone–Wales (SW) defects contribute to changes in the electronic structure of the pristine graphene by incorporating non-hexagonal rings and subsequently perturbing the extended sp² system.²⁴ These imperfections may be recovered by providing suitable carbon sources to fill the vacancies and by 90° rotation of the central C–C bond in the SW defect, which can be achieved under specific reaction conditions.

The SW defect, also called the (5-7-7-5) defect, is the most uncomplex topological defect in graphene, formed by a 90° rotation of a C–C bond in the hexagonal carbon network. The formation energy of (5-7-7-5) has been reported to be an approximately 5 eV endothermic process, with a formation barrier of almost 10 eV.²⁵ This means SW defects are not likely to form at typical reaction temperatures of graphene processes, well below 1000 °C. Hence, once the SW defect is created in the graphene synthesis process, it should be stable in subsequent treatment and applications of graphene.²⁶ The formation barrier decreases to 3.7 eV if the graphene contains hydrogen or hydroxyl groups on the two carbon atoms placed at the center of the SW defect after formation.²⁷ To the best of our knowledge, there is no attempt in the literature to facilitate the SW defect formation through an exothermic adsorption process, requiring a less stable starting material compared to pristine graphene.

The abundance of DV defects compared to reactive and unstable odd-number carbon vacancies which contain a dangling bond makes it more interesting in the case of controlled atomic-scale engineering of the graphene lattice. Regarding carbon-vacancy defects, the formation energy of a double-vacancy, DV (8.7 eV), is lower than the formation energy of two isolated single-vacancies, SVs (2 × 7.5 eV). Moreover, the migration energies of SV and DV are 1.7 and 7 eV, respectively, indicating the measurable mobility of SVs and relative immobility of DVs at the usual temperatures of graphene processes.²⁸ Hence, DVs can be produced either in the synthesis or the post-synthesis of graphene, and also by coalescence of two SVs at relatively large temperatures. As an example, DVs could be created upon reduction of graphene oxide. It has been proved that epoxy groups line up on the graphene oxide basal plane and leave the graphene surface in the form of CO₂; hence a series of nearby single vacancies can be produced, which can subsequently coalesce to form lined up DVs.²⁹ These data indicate the importance of DVs over SVs expected in real defective graphene samples.

Considering the various procedures proposed in the literature for healing the structural imperfections of graphene i.e., annealing, self-healing, metal-assisted healing, and healing by adsorption,³ the latter is particularly fascinating due to the diverse range of adsorbate molecular structures. Since adsorption is the first step in catalysis, this DV healing pathway is also relevant from the point of view of the activity of defective graphene as catalysts. Indeed, the structure of adsorbate affects its interaction with defective graphene and subsequently dictates the thermodynamics and kinetics of the healing process. Healing by adsorption can be facilitated by selecting reactive adsorbates or by stabilizing the subsequent transition state via appropriate selection of the adsorbate/adsorbent pairs, while a high temperature condition is essential to speed up lattice movements and relaxation at defective sites in the other healing methods.

Toward a more detailed study of graphene healing by adsorbates, Liu et al. provided atomic-scale scanning tunnelling microscopy (STM) images of defect sites during soot formation.³⁰ Exposure of nanoscale holes on highly ordered pyrolytic graphite to acetylene at 625 K resulted in forming graphitic and amorphous carbonaceous materials at the edge of holes. The authors suggested that defect healing in graphene nanostructures at moderate temperature should be possible by the interaction of the adsorbent with unsaturated hydrocarbons. Meanwhile, acetylene-assisted enhanced graphitization in graphene or graphene oxide at temperatures ranging from 600 to 1000 °C was reported in some studies.^31–34

To understand the mechanism of graphene healing by adsorbates, Wang et al. investigated computationally the interaction of ethylene and acetylene with DV in a hydrogen-terminated flake of graphene.³⁵ Their results indicate barriers of 120.5 and 106.7 kJ mol⁻¹ for the adsorption of ethylene and acetylene on a DV. In the case of ethylene, barriers for the formation of two new carbon–carbon bonds and subsequent hydrogen transfer were calculated as 88.3 and 56.9 kJ mol⁻¹. In the case of acetylene, the barrier for the carbon–carbon bond formation on a DV is only 11.3 kJ mol⁻¹. It was suggested that during the high-temperature growth of graphene, ethylene and acetylene act as both the carbon source and defect healing agents. The same authors also studied the mechanism of healing in carbon nanotubes by ethylene and acetylene, although the details on the preferred orientation of carbon sources on DV were not mentioned.³⁶

Using vdW-DFT calculations, Zhang et al. found that the potential energy decreases when acetylene moves from the edge to the center of DV, suggesting that the center of DV is energetically more favourable for acetylene adsorption. Moreover, they reported that acetylene fills DV in graphene with no energy barrier, which is in compliance with previous studies.³⁷

Recently, Kang et al. investigated the adsorption of acetylene and water on DV to understand the mechanism of acetylene hydration to produce acetaldehyde catalysed by defective graphene. The shared C–C bond between the eight-member ring and six-member ring of DV was the active site, with preferential adsorption of acetylene, in competition with water.³⁸

Starting from these precedents, a detailed mechanistic study is presented in this study to shed light on the preferred orientation and physi- or chemi-sorption of C₂ hydrocarbons at DV on graphene. Depending on this preference, the C₂-hydrocarbon may heal DV or convert DV to SW defects after removing the hydrogens, a possibility that has not been previously considered. The hydrogen removal mechanism is not considered in this study. The importance of the former is in the case of repairing the graphene structure and recovering the properties of the original hexagonal carbon network, while the importance of the latter is in the case of inducing tailor-made active sites to catalyse target reactions. Indeed, its high surface area and tunable structure make graphene a multi-advantage platform for advanced material design. Recently,^39–42 it has been proved that the presence of non-hexagonal rings alone and in combination with nitrogen doping induces graphene catalytic activity similar to metals in oxygen reduction reactions. The main sources of non-hexagonal rings in graphene are intrinsic defects such as Stone–Wales (SW) defects which are formed during graphene synthesis.

This study is indeed an initial attempt to evaluate the possibility of SW formation via a mechanism other than carbon–carbon bond rotation, which is an endothermic reaction. In other words, we tried to introduce a new mechanism for SW defect formation.

Since semimetal graphene with well-arranged SW defects is the most stable graphene allotrope known to date,⁴³ it may be possible in the future to increase the density of SW defects more than other defects such as vacancies in graphene, with the corresponding implications in catalysis. When the density of vacancies increases they tend to coalesce and produce holes or sheet termination in graphene.

This paper is aimed to perform an in-depth mechanistic study on the interaction of C₂-hydrocarbons with defective graphene using periodic vdW-DFT calculations. Furthermore, the determinant structural characteristics, affecting the minimum energy paths (MEPs) of the studied reactions, were explored. Finally, we attempted to find how MEPs are changed by justifying the structural characteristics of the optimized geometries. Considering the calculated barrier energies we concluded that the new suggested mechanism for SW defect formation, which is exothermic, is more probable and significantly feasible in the presence of pyridinic nitrogen at the edge of double carbon vacancies. It should be noted that to the best of our knowledge there is no attempt in the literature to suggest a new mechanism for SW defect formation in addition to carbon–carbon bond rotation.

Computational methods

All periodic DFT calculations were performed using the plane-wave self-field consistent Quantum Espresso package.^44,45 The generalized gradient approximation (GGA) with the Perdew, Burke and Enzerhof (PBE) functional modified for solids was employed to calculate the exchange correlation energies of the different structures.^46,47 The plane-wave expansion of the wave functions is set to a kinetic energy cutoff of 400 eV. The k-points grid employed is set to 5 × 5 × 1 with the k-points automatically generated using the Monkhorst–Pack grid.⁴⁸ In order to achieve accurate electronic convergence, a Gaussian smearing of 0.01 Ry was applied. A 4 × 4 × 1 super-cell of graphene consisting of 32 carbon atoms was considered as a model. To make sure that 4 × 4 supercells are large enough to prevent the interaction between cells, the formation energies of double carbon vacancy defects in 4 × 4 and 6 × 6 supercells were calculated and compared, not only with each other but also with those reported in the literature for different size supercells (see the ESI†). The distance between two adjacent graphene layers was kept at 20 Å to minimize the interactions between them. To consider the effect of van der Waals (vdW) forces on the interaction of C₂-hydrogarbons and graphene based structures, the long-range-dispersion-corrected Grimme D3 method was taken into account.⁴⁹ For structure relaxation, the atomic positions were fully optimized until the maximum force on each atom was less than 10⁻⁴ eV Å⁻¹, and the convergence criteria for energy was set to 10⁻⁶ eV. To establish minimum energy paths, the reaction coordinates were scanned carefully using convergence criteria of 10⁻⁴ eV for energy. Then, the barrier energies of elementary reactions were recalculated using the Nudged Elastic Band (NEB) method.^50,51 The adsorption energy E_ads was defined using the energy of graphene based material GBM, (E_GBM), the energy of ethylene or acetylene (E_Eth/Ace) and the energy of a stable structure with the hydrocarbon adsorbed on GBM (E_GBM/Eth/Ace), as follows:

E_ads = E(_GBM/Eth/Ace) − E_GBM − E_Eth/Ace

Results and discussion

For ease of discussion and according to Fig. 1 the four under coordinated carbon atoms at the edge of DV in graphene were labelled G₁ to G₄, ethylene carbons were labelled E₁ and E₂, and acetylene carbons were labelled A₁ and A₂.

Fig. 1 Schematic illustration of two possible alignments, DVH and DVP, of C₂-hydrocarbons to approach DV on graphene. G₁, G₂, G₃, and G₄ correspond to undercoordinated carbon atoms in graphene. A₁ and A₂ correspond to the acetylene carbon atoms. E₁ and E₂ correspond to the ethylene carbon atoms. G₁G₂ and G₃G₄ are semi-bonds formed due to the DV reconstruction. The new bonds between G_i and A_j/E_k carbon atoms are highlighted in green.

Each carbon atom in the graphene lattice is surrounded by three carbon atoms. Removing the two neighbouring carbons from the graphene lattice introduces four extremely reactive under coordinated carbon atoms, which can be stabilized through reconstruction. This reconstruction lowers the energy of graphene containing a DV defect by 189 kJ mol⁻¹ compared to the unreconstructed one via compressing the distance between two nearest under coordinated carbons (G₁G₂ and G₃G₄ in Fig. 1) from 2.5 Å to 1.8 Å. In this study, all calculations were done starting from reconstructed DV as the most stable state of the initial DV on graphene.

Depending on the alignment of the C₂ molecule axis with respect to the two omitted carbon atoms axis of DV, there are two possible orientations for chemisorption of C₂-hydrocarbons on DV in graphene, termed here as horizontal (DVH) and perpendicular (DVP). As shown in Fig. 1, the DVH interaction of C₂-hydrocarbons with DV converts 5-8-5 rings to 6-6-6-6 rings and heals the DV. On the other hand, the DVP interaction converts 5-8-5 rings to 5-7-7-5 rings and creates a SW defect. These transformations are accompanied by the formation of four new bonds (green coloured in Fig. 1) between the C₂-hydrocarbons and the defective graphene.

The minimum energy paths (MEPs) for the reactions of reconstructed DV with ethylene, starting from the two distinct initial orientations (DVH, DVP) of adsorbates on DV, were calculated using the plane-wave DFT method. Fig. 2 is a schematic representation of the MEPs of ethylene reactions through DVH and DVP approaches, whose corresponding geometries are shown in Fig. 3 and 4, respectively (see Tables S1 and S2 in the ESI† for more details on MEPs and the relevant geometries).

Fig. 2 Schematic minimum energy path for ethylene interaction with DV on graphene. (a) to (g) geometries for DVH mechanism are illustrated in Fig. 3(a) to (i) and geometries for the DVP mechanism are illustrated in Fig. 4(a) to (i). See the ESI† for more details on geometries corresponding to each step and Table 1 for energies.

Fig. 3 DVH mechanism of ethylene interaction with DV, which results in conversion of 5-8-5 rings to 6-6-6-6 rings. Distances are in Å. (a) Reactants, (b) TS1, (c) chemisorption, (d) TS2, (e) local minimum, (f) TS3, and (g) product: PG-4H. See the ESI† for details on geometries corresponding to each step and Table 1 for energies.

Fig. 4 DVP mechanism of ethylene to DV, which results in conversion of 5-8-5 rings to 5-7-7-5 rings. Distances are in Å. (a) Reactants, (b) TS1, (c) chemisorption, (d) TS2, (e) local minimum, (f) TS3, (g) local minimum, (h) TS4 and (i) product: SWG-4H. See the ESI† for details on geometries corresponding to each step and Table 1 for energies.

The zero-energy corresponds to the noninteracting ethylene and the reconstructed DV. By approaching ethylene to DV on the graphene surface, a physisorption and then a chemisorption occurs and consequently, the C₂-hydrocarbon fills the DV. The energy values for all labelled steps in Fig. 2 are summarized in Table 1.

Table 1 Energies (kJ mol⁻¹) of the different steps of the reaction of ethylene with DV

GBM	Approach	Physisorption	Barrier I	Chemisorption	Barrier II	Local Min	Barrier III	Local Min	Barrier IV	Local Min
a The geometries corresponding to this path shown in Fig. 3(a) to (g). b The geometries corresponding to this path shown in Fig. 4(a) to (i).
DV	DVH^a	−93.6 (Fig. 3a)	56.9 (Fig. 3b)	−199.8 (Fig. 3c)	126.4 (Fig. 3d)	−367.5 (Fig. 3e)	38.0 (Fig. 3f)	−632.1 (Fig. 3g)	—	—
DV	DVP^b	−91.9 (Fig. 4a)	134.9 (Fig. 4b)	−275.0 (Fig. 4c)	80.3 (Fig. 4d)	−325.1 (Fig. 4e)	136.0 (Fig. 4f)	−471.1 (Fig. 4g)	223.0 (Fig. 4h)	−321.4 (Fig. 4i)

---

Interaction of ethylene with DV

In the DVH approach of ethylene to DV upon ethylene chemisorption, the interacting graphene carbons (G₁G₃) reduce their distance (from 3.02 to 2.79 Å) to form new bonds with ethylene, and as a consequence of this strain, G₁G₂ and G₃G₄ distances increase from 1.79 to 2.11 Å (Fig. 3a–c). On the other hand, in the DVP approach, upon ethylene chemisorption, the G₁G₂ distance expands to 2.81 Å to compensate the induced strain in the created heptagon ring (Fig. 4a–c). The larger distance between the nonbonded carbons (G₂G₄, 2.98 Å, Fig. 3c) in the DVH approach with respect to the G₃G₄ distance (2.08 Å, Fig. 4c) in the DVP approach, induces less stabilized nonbonded carbons in DVH, making this chemisorption energetically less favourable (−199.8 kJ mol⁻¹) than in DVP (−275.0 kJ mol⁻¹). On the other hand, the barrier energy for chemisorption through the DVP approach is larger than that of the DVH approach by 78 kJ mol⁻¹ (134.9 versus 56.9 kJ mol⁻¹, Table 1) due to the less stable transition state of the former resulting from the stress-induced seven-membered ring formation. After ethylene chemisorption, the E₁E₂ bond length increases to 1.57 Å (DVH) and 1.53 Å (DVP), almost similar to a C–C single bond length (Fig. 3c and 4c).

Therefore, the chemisorption of ethylene on DV through DVP is energetically more favourable, however, the barrier energy for this transformation is higher compared to that of the DVH approach.

First hydrogen transfer. First hydrogen transfer from chemisorbed ethylene to DV corresponds to the steps shown in (c), (d), and (e) in Fig. 3 and 4. The presence of reactive carbons in graphene can assist the hydrogen transfer from chemisorbed ethylene to graphene. Ethylene chemisorption through the DVH and DVP approach show different effects on the reactivity of nonbonded carbon atoms at the edge of DV. By approaching E₂H₄ to G₄ in DVH, the G₃G₄ distance reduces in the transition state (from 2.11 to 1.80 Å, Fig. 3c and d). However, by approaching E₁H₃ to G₃ in DVP, the G₃G₄ distance increases (from 2.08 to 2.26 Å, Fig. 4c and d), making the two carbenes more reactive in DVP than in the DVH mechanism and facilitating the first hydrogen transfer in DVP compared to DVH. The energy barrier for the first hydrogen transfer from E₁H₃ to G₃ in DVP is 80.3 kJ mol⁻¹ (Table 1). During this hydrogen transfer, the G₃G₄ distance increases from 2.08 Å to 2.82 Å (Fig. 4c and e), removing the stabilization effect of G₃ on G₄. As a result, the E₁G₄ distance reduces to 1.82 Å, ejecting the –CH₂– group of ethylene out of plane and preventing simultaneous E₁G₃ bond formation (Fig. 4e). On the other hand, the energy barrier for first hydrogen transfer from E₂H₄ to G₄ in DVH is 126.4 kJ mol⁻¹ and at the same time, not only E₂G₄ but also E₂G₃ bonds are formed (Table 1 and Fig. 3e).

Second hydrogen transfer. Second hydrogen transfer from ethylene to graphene corresponds to steps (e), (f), and (g) in Fig. 3 and 4. In the DVH mechanism, after transfer of H4 from E2 to G4 (Fig. 3e), the stress induced by the E₂G₄ bond formation increases the G₁G₂ distance to 2.44 Å and makes G₂ less stabilized, which subsequently facilitates H₂ transfer, from E₁ to G₂. This hydrogen transfer is further facilitated by the more electron-donating effect of the neighbouring CH (E₂H₃) on E₁ (Fig. 3e) compared to the less electron donating effect of the neighbouring CH₂ (E₁H₁H₂) on E₂ during the first hydrogen transfer (Fig. 3c). Therefore, the barrier for the second hydrogen transfer from chemisorbed ethylene to graphene is only 38.0 kJ mol⁻¹, compared to 126.4 kJ mol⁻¹ in the first hydrogen transfer step (Table 1). Furthermore, the second hydrogen transfer is accompanied with E₁G₂ bond formation.

In contrast, for the DVP mechanism, the barrier for this step (transfer of H₄ from E₂ to G₄) is as high as 136.0 kJ mol⁻¹ since no additional C–C bonds (neither E₁G₃ nor E₂G₄) are formed (Fig. 4e–g). The formation of these C–C bonds requires an additional step (Fig. 4g–i) which is not needed in the DVH mechanism. The initially large E₁G₃ and E₂G₄ distances (Fig. 4g) make the formation of these bonds 149.7 kJ mol⁻¹ endothermic with a barrier of 223 kJ mol⁻¹ (Table 1). Therefore, overall, when using ethylene it will be less likely to transfer 5-8-5 rings to 5-7-7-5 rings and ethylene will be more prone to heal the DV defect in graphene through the DVH mechanism.

There are two main bottlenecks for converting 5-8-5 rings to 5-7-7-5 rings with ethylene: DV reconstruction and hydrogen transfer. The former makes the initial structure less reactive and the latter causes some inconvenience by imposing additional steps towards defect healing. The reconstruction is predicted to be tuneable by heteroatom doping and it may be more reasonable to replace ethylene by acetylene as the carbon source to eliminate the difficulties caused by additional hydrogen transfer steps.

Interaction of acetylene with DV. Using acetylene as the carbon source instead of ethylene saves the two steps of hydrogen transfer. In a similar way to the previous section, the MEPs of acetylene reactions (Fig. 5) through DVH and DVP approaches and corresponding geometries are shown in Fig. 6 and 7 (see also Tables S3 and S4 in the ESI†). The preferred mechanism for acetylene adsorption on a double vacancy is DVH. Acetylene is able to simultaneously stabilize the four under coordinated graphene carbons (G₁–G₄) at the edge of DV and directly repair the DV with an energy barrier of 58 kJ mol⁻¹ (Fig. 6 and Table 2).

Fig. 5 Minimum energy path for acetylene interaction with DV on graphene. (a) to (c) the geometries for DVH are illustrated in Fig. 6(a) to (c); geometries for DVP are illustrated in Fig. 7(a) to (e). See the ESI† for details on geometries corresponding to each step and Table 2 for energies.

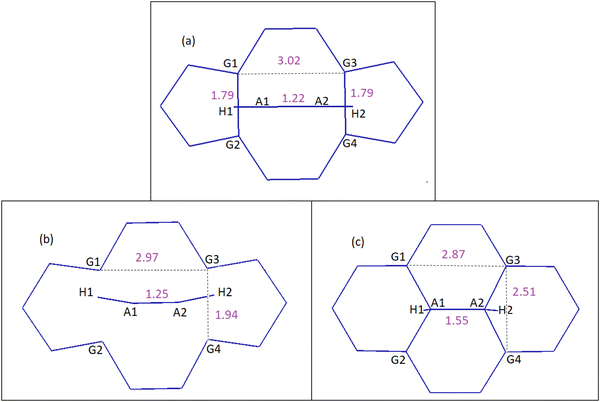Fig. 6 DVH mechanism of acetylene to DV, which results in conversion of 5-8-5 rings to 6-6-6-6 rings. Distances are in Å. (a) Reactants, (b) TS1 and (c) product: PG-2H. See the ESI† for details on the geometries corresponding to each step and Table 2 for energies.

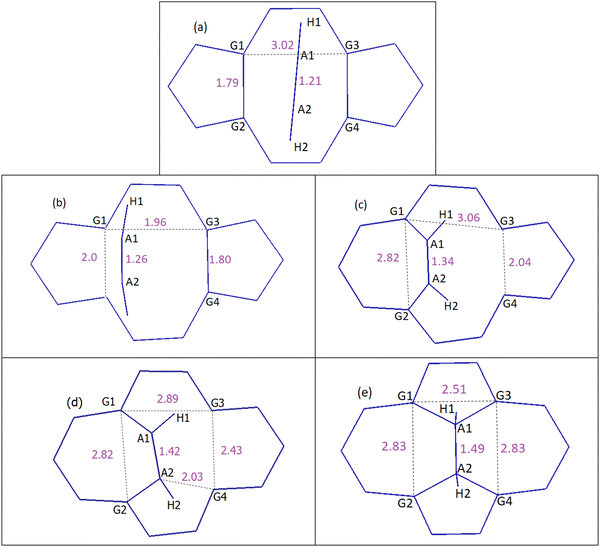Fig. 7 DVP mechanism of acetylene to DV, which results in the conversion of 5-8-5 rings to 5-7-7-5 rings. Distances are in Å. (a) Reactants, (b) TS1, (c) chemisorption, (d) TS2 and (e) product: SW-2H. See the ESI† for details on geometries corresponding to each step and Table 2 for energies.

Table 2 Energies (kJ mol⁻¹) of the different steps of the reaction of acetylene with DVs (* = No data)

GBM	Approach	Physisorption	Barrier I	Chemisorption	Barrier II	Local Min	Barrier III	Product
a The geometries corresponding to this path shown in Fig. 6(a) to (c). b The geometries corresponding to this path shown in Fig. 7(a) to (e). c Acetylene is chemisorbed on G1 and G2. d Acetylene is chemisorbed on G3 and N.
DV	DVH^a	−90.8 (Fig. 6a)	58.0 (Fig. 6b)	—	—	—	—	−933.2 (Fig. 6c)
NP	DVH	−89.6	14.0	—	—	—	—	−911.6
NG1	DVH	−88.2	104.2	—	—	—	—	−853.3
NG2	DVH	−88.6	97.0	—	—	—	—	−866.5
SG	DVH	−152.4	49.0	—	—	—	—	−809.6
DV	DVP^b	−88.1 (Fig. 7a)	123.0 (Fig. 7b)	−381.3 (Fig. 7c)	154.7 (Fig. 7d)	—	—	−587.8 (Fig. 7e)
NP^c	DVP	−89.3	103.7	−448.4	7.4	—	—	−572.0
NP^d	DVP	−88.7	28.5	−405.4	153.3			−572.0
NG1	DVP	−88.2	*	−355.6	153.2	—	—	−496.9
NG2	DVP	−87.8	*	−349.1	117.1	—	—	−504.2
SG	DVP	−150.8	*	−508.6	29.6	−499.9	30.5	−507.2

---

In the case of the DVP approach, two barriers of 123.0 kJ mol⁻¹ and 154.7 kJ mol⁻¹ should be passed in order to chemisorb on DV (first barrier) and eventually convert the initial 5-8-5 rings to 5-7-7-5 ones (second barrier). Upon acetylene chemisorption on DV, the A₁A₂ bond length increases from 1.21 to 1.34 Å, which is characteristic of a C=C double bond. A further increase in the length of this bond to 1.49 Å occurs when acetylene becomes part of the graphene lattice. Interestingly, the resulting structure in this case is a partially hydrogenated SW defect (Fig. 7e). The main reason that justifies the respective barriers obtained in DVH and DVP mechanisms is the different initial distances of G₁G₂ (1.79 Å) and G₁G₃ (3.02 Å) atoms (Fig. 6a and 7a), leading to different stabilizing effects on under coordinated carbon carbons and, especially, making the absence of under coordinated carbons possible in DVH (Fig. 6c) unlike in the case of DVP (Fig. 7c).

Effect of heteroatom doping on the acetylene interaction with DV

Due to the key role of structural reconstruction on the interaction of carbon sources with DV, heteroatom doping seems to have a controlling effect on these interactions via affecting the reconstruction of DV upon interaction with acetylene. In other words, if dopants benefit from the expected functionality of the graphene-based material, structural reconstructions can be weakened or strengthened by dopants, depending on their positions on DV.

There are four distinct positions around DV for carbon substitution with nitrogen, whose influence on the interaction of carbon dimers with DV could not be neglected (Fig. 8). Before studying the carbon dimer interaction with doped DV structures, the total energy and stability of these four configurations were carefully calculated and compared (see the ESI† for details on N-doped defective structures).

Fig. 8 Schematic illustration of doped DVs in graphene. N_G1 and N_G2 are graphitic nitrogen-containing DV, N_P is pyridinic nitrogen-containing DV and S_G is sulfur-containing DV. In N_P and S_G, G₄ carbon is replaced by nitrogen or sulfur.

The doped defected graphene structures were labelled as Xyi. In which, ‘X’ is the symbol of the substituted atom, ‘y’ indicates the type of doping (pyridinic and graphitic) and ‘i’ is the number to indicate the different possibilities with the same ‘X’ and same ‘y’.

N_G1 is the most stable configuration for nitrogen doping around DV. Indeed, in this configuration two undercoordinated carbon atoms at the edge of DV are influenced symmetrically by an electron withdrawing effect of nitrogen, which subsequently strengthens the pseudo-bond between two undercoordinated carbons and makes the interaction of N_G1 with carbon dimers more difficult. In the case of N_G2, nitrogen has a non-symmetrical effect on the two mentioned carbons. On the other hand, pyridinic nitrogen is less unstable than undercoordinated carbon atoms, therefore, the reconstructed N–C length in the NP configuration is larger than the reconstructed C–C length and less stabilized than the undercoordinated carbon atom at the edge of DV, which facilitates the interaction of carbon dimers with NP. The N_G3 configuration seems to be the less stable and was not considered in this study. The main reason for the instability of N_G3, compared to N_G1 and N_G2, could be attributed to the different sizes of their corresponding rings, a 5-member ring in the former case and 8-member rings in the latter case.

Graphitic nitrogen doping such as in N_G1 and N_G2 (Fig. 8) strengthens the reconstruction by decreasing the under coordinated carbon–carbon distances, for example G₁G₂, from 1.79 Å in undoped DV to 1.69 and 1.71 Å in N_G1 and N_G2 respectively (Table 3). As a result, the barrier of DVH healing by acetylene increases from 58.0 kJ mol⁻¹ in the undoped structure to 104.2 kJ mol⁻¹ in N_G1 and 97.0 kJ mol⁻¹ in N_G2 (Table 2).

Table 3 Effect of doping on weakening or strengthening DV reconstruction. G₁, G₂, G₃ and G₄/N/S as in Fig. 8

GBM	G1G2 (Å)	G3 (G4/N/S) (Å)
DV	1.79	1.79
NG1	1.66	1.69
NG2	1.70	1.71
NP	1.91	2.36
SG	1.96	1.94

---

On the other hand, pyridinic nitrogen (N_P) weakens the reconstruction significantly, due to the larger stability of the pyridinic nitrogen compared to the original under coordinated carbon atom (G₄, Fig. 8) and subsequently lower interaction of pyridinic nitrogen compared to G₄ with G₃. In this case, the reconstructed G₃N_P length is 2.36 Å and the reconstructed G₁G₂ length is 1.91 Å (Table 3). Consequently in N_P, after acetylene chemisorption on the reconstructed G₁G₂, barriers of only 103.7 and 7.4 kJ mol⁻¹ should be passed in order to form the SW defect through the DVP mechanism, much lower than those in the un-doped DVP case (123.0 and 154.7 kJ mol⁻¹, Table 2). When acetylene fills DV of N_P through DVP, the pyridinic nitrogen becomes a graphitic nitrogen and the product contains a nitrogen doped pentagon ring which may be considered an active site for special reactions.

In the presence of graphenic sulfur (S_G) as another heteroatom dopant, the reconstructed G₁G₂ and G₃S_G lengths are 1.96 and 1.94 Å (Fig. 8 and Table 3). In addition, S_G is the most energetically favourable combination of sulfur atom and DV compared to the three other possible positions for doping sulfurs on DV while keeping the DV defect for interaction with acetylene. After acetylene chemisorption through DVP on G₁G₂, a barrier of 29.7 kJ mol⁻¹ should be passed in order to form the A₁G₃ bond. Then, another barrier of 30.5 kJ mol⁻¹ should be passed for forming the A₂S_G bond. This process is approximately reversible, due to the comparable energy barriers calculated for the reverse transformations. The reversible nature of this process is interesting to increase the lifetime of extremely reactive under coordinated carbons at the edge of sulfur-doped DV.

Conclusions

Understanding how to engineer active sites in defective graphene sheets is very important for the application of these materials in catalysis. DFT calculations indicate that the two extreme orientations for C₂-hydrocarbon alignment on a DV on graphene, DVH and DVP result in the conversion of the 5-8-5 rings to 6-6-6-6 and 5-7-7-5 rings, respectively.

There are two main bottlenecks for these transformations using ethylene as a carbon source: hydrogen transfer and DV reconstruction. By using acetylene instead of ethylene the two steps of hydrogen transfer are removed. Moreover, introducing pyridinic nitrogen to the edge of DV not only reduces the energy barrier for DVH healing by acetylene from 58 to 14 kJ mol⁻¹, but also reduces the energy barrier for DVP healing by acetylene from 123 and 154.7 kJ mol⁻¹ to 103.7 and 7.4 kJ mol⁻¹, making both DVH and DVP mechanisms possible, hence facilitating the formation (through DVP) of the doped SW defect. In the case of sulfur-doped DV, the 5-7-7-5 defect formation after acetylene chemisorption through DVP becomes a reversible process. The reversible nature of these reactions may be interesting to extend the lifetime of extremely reactive undercoordinated carbons at the edge of the sulfur-doped DV.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

PA, FS and SM thank the Iranian Ministry of Science, Research and Technology (MSRT) for funding. GS thanks Generalitat Valenciana (PROMETEO/2021/077) for financial support. PA and GS thank ASIC-UPV for the use of computational facilities.

Notes and references

1. J. He, A. Anouar, A. Primo and H. García, Nanomaterials, 2019, 9, 895.
2. S. Lee, W. K. Park, Y. Yoon, B. Baek, J. S. Yoo, S. B. Kwon, D. H. Kim, Y. J. Hong, B. K. Kang and D. H. Yoon, J. Mater. Sci. Eng. B, 2019, 242, 63–68.
3. L. Liu, M. Qing, Y. Wang and S. Chen, J. Mater. Sci. Technol., 2015, 31, 599–606.
4. M. Salehi, P. Bastani, L. Jamilpanah, A. Madani, S. M. Mohseni and B. Shokri, Sci. Rep., 2021, 11, 20334.
5. H. Huang, S. Chen, A. Wee and W. Chen, Graphene, Elsevier, 2014, pp. 177–198.
6. Z. Li, P. Wu, C. Wang, X. Fan, W. Zhang, X. Zhai, C. Zeng, Z. Li, J. Yang and J. Hou, ACS Nano, 2011, 5, 3385–3390.
7. M. Saeed, Y. Alshammari, S. A. Majeed and E. Al-Nasrallah, Molecules, 2020, 25, 3856.
8. Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. McGovern, B. Holland, M. Byrne and Y. K. Gun'Ko, Nat. Nanotechnol., 2008, 3, 563–568.
9. L. Chai, X.-j Cui, Y.-q Qi, N. Teng, X.-l Hou and T.-s Deng, New Carbon Mater., 2021, 36, 1179–1186.
10. S. Pei and H.-M. Cheng, Carbon, 2012, 50, 3210–3228.
11. V. Agarwal and P. B. Zetterlund, Chem. Eng. J., 2021, 405, 127018.
12. M. Latorre-Sánchez, A. Primo, P. Atienzar, A. Forneli and H. García, Small, 2015, 11, 970–975.
13. A. Primo, A. Forneli, A. Corma and H. García, ChemSusChem, 2012, 5, 2207–2214.
14. X. Kong, Y. Zhu, H. Lei, C. Wang, Y. Zhao, E. Huo, X. Lin, Q. Zhang, M. Qian and W. Mateo, Chem. Eng. J., 2020, 125808.
15. Z. Wang, D. Shen, C. Wu and S. Gu, Green Chem., 2018, 20, 5031–5057.
16. V. K. Das, Z. B. Shifrina and L. M. Bronstein, J. Mater. Chem. A, 2017, 5, 25131–25143.
17. E. E. Mathew and B. Manoj, Carbon Lett., 2021, 1–20.
18. J. Wang, R. Zhao, M. Yang, Z. Liu and Z. Liu, J. Chem. Phys., 2013, 138, 084701.
19. A. Eftekhari and H. Garcia, Mater. Today Chem., 2017, 4, 1–16.
20. G. Rajasekaran, P. Narayanan and A. Parashar, Crit. Rev. Solid State Mater. Sci., 2016, 41, 47–71.
21. K. R. Pyun and S. H. Ko, Mater. Today Energy, 2019, 12, 431–442.
22. Y. V. Skrypnyk and V. M. Loktev, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 085436.
23. A. Zandiatashbar, G.-H. Lee, S. J. An, S. Lee, N. Mathew, M. Terrones, T. Hayashi, C. R. Picu, J. Hone and N. Koratkar, Nat. Commun., 2014, 5, 3186.
24. S. K. Tiwari, R. K. Mishra, S. K. Ha and A. Huczko, ChemNanoMat, 2018, 4, 598–620.
25. L. Li, S. Reich and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 184109.
26. J. C. Meyer, C. Kisielowski, R. Erni, M. D. Rossell, M. F. Crommie and A. Zettl, Nano Lett., 2008, 8, 3582–3586.
27. A. Nascimento and R. Nunes, Nanotechnology, 2013, 24, 435707.
28. A. El-Barbary, R. Telling, C. Ewels, M. Heggie and P. Briddon, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 144107.
29. H. C. Schniepp, J.-L. Li, M. J. McAllister, H. Sai, M. Herrera-Alonso, D. H. Adamson, R. K. Prud'homme, R. Car, D. A. Saville and I. A. Aksay, J. Phys. Chem. B, 2006, 110, 8535–8539.
30. L. Liu, K. T. Rim, D. Eom, T. F. Heinz and G. W. Flynn, Nano Lett., 2008, 8, 1872–1878.
31. S. Naghdi, K. Y. Rhee and S. J. Park, Carbon, 2018, 127, 1–12.
32. J.-b Wang, Z. Ren, Y. Hou, X.-l Yan, P.-z Liu, H. Zhang, H.-x Zhang and J.-j Guo, New Carbon Mater., 2020, 35, 193–208.
33. G. Nandamuri, S. Roumimov and R. Solanki, Nanotechnology, 2010, 21, 145604.
34. M. Qi, Y. Zhou, F. Hu, X. Xu, W. Li, A. Li, J. Bai and Z. Ren, J. Phys. Chem. C, 2014, 118, 15054–15060.
35. C. Wang, B. Xiao and Y.-H. Ding, New J. Chem., 2013, 37, 640–645.
36. B. Xiao, X.-f Yu and Y.-h Ding, J. Mol. Model., 2014, 20, 2125.
37. S. Wang, W. Zhang, P. Huai, W. Gong and Z. Zhu, Chem. Phys. Lett., 2013, 567, 43–47.
38. J. Li and L. Kang, Int. J. Quantum Chem., 2021, 121, e26561.
39. G.-L. Chai, Z. Hou, D.-J. Shu, T. Ikeda and K. Terakura, J. Am. Chem. Soc., 2014, 136, 13629–13640.
40. S. Liu, Y. Zhang, B. Ge, F. Zheng, N. Zhang, M. Zuo, Y. Yang and Q. Chen, Adv. Mater., 2021, 33, 2103133.
41. D. Liu, Y. Tong, X. Yan, J. Liang and S. X. Dou, Batteries Supercaps, 2019, 2, 743–765.
42. L.-H. Zhang, Y. Shi, Y. Wang and N. R. Shiju, Adv. Sci., 2020, 7, 1902126.
43. H. Yin, X. Shi, C. He, M. Martinez-Canales, J. Li, C. J. Pickard, C. Tang, T. Ouyang, C. Zhang and J. Zhong, Phys. Rev. B, 2019, 99, 041405.
44. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, J. Phys.: Condens. Matter, 2009, 21, 395502.
45. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, J. Phys.: Condens. Matter, 2017, 29, 465901.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
47. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
48. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
49. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
50. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
51. H. Jónsson, G. Mills and K. W. Jacobsen, Classical and Quantum Dynamics in Condensed Phase Simulations, 1998, 385–404.

---

Footnote

† Electronic supplementary information (ESI) available: The effect of supercell size on defect formation energy and the criteria to distinguish between physisorption and chemisorption are included. An estimation of the entropic effects on the reaction free energies is presented. A geometric analysis is provided corresponding to all the studied reactions in Tables 1 and 2, as well as the corresponding energies in Tables S1–S13. Also, the energies attributed to these paths are discussed. To facilitate this discussion, Fig. 1 and Tables 1–3 are reproduced. See DOI: https://doi.org/10.1039/d2cp05233d

---