Solvent quality and solvent polarity in polypeptides

Abstract

Using molecular dynamics and thermodynamic integration, we report on the solvation process of seven polypeptides (GLY, ALA, ILE, ASN, LYS, ARG, GLU) in water and in cyclohexane. The polypeptides are selected to cover the full hydrophobic scale while varying their chain length from tri- to undeca-homopeptides, providing indications on possible non-additivity effects as well as the role of the peptide backbone in the overall stability of the polypeptides. The use of different solvents and different polypeptides allows us to investigate the relation between solvent quality – the capacity of a given solvent to fold/unfold a given biopolymer often described on a scale ranging from “good” to “poor”; and solvent polarity – related to the specific interactions of any solvent with respect to a reference solvent. Undeca-glycine is found to be the only polypeptide to have a stable collapse in water (polar solvent), with the other hydrophobic polypeptides displaying repeated folding and unfolding events in water, with polar polypeptides presenting even more complex behavior. By contrast, all polypeptides are found to keep an extended conformation in cyclohexane, irrespective of their polarity. All considered polypeptides are also found to have favorable solvation free energy independent of the solvent polarity and their intrinsic hydrophobicity, clearly highlighting the prominent stabilizing role of the peptide backbone – with the solvation process largely enthalpically dominated in polar polypeptides and partially entropically driven for hydrophobic polypeptides. Our study thus reveals the complexity of the solvation process of polypeptides defying the common view “like dissolves like”, with the solute polarity playing the most prominent role. The absence of mirror symmetry upon the inversion of polarities of both the solvent and the polypeptides is confirmed.

---

1 Introduction

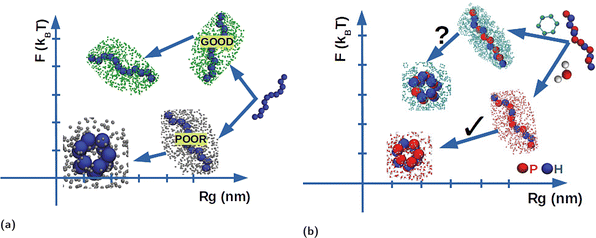
In polymer physics^1–4 the term poor solvent indicates that a synthetic polymer tends to collapse into a compact conformation because the effective intra-chain interactions occurring between the different monomers composing the polymer, overcome the monomer–solvent interactions. In the opposite limit of a good solvent, the polymer tends to remain in an extended conformation. This effect is pictorially represented in Fig. 1a in a plot of the free energy F/k_BT, in units of thermal energy k_BT, as a function of the mean radius of gyration R_g. In the case of a poor solvent, the polymer lowers its free energy by folding into a compact conformation, thus reducing R_g, whereas in the second case the free energy decreases but R_g remains large because the polymer is solvophobic. The distinction between good and bad solvent can be made more quantitative using familiar scaling arguments from polymer physics where R_g ∼ N^ν: where ν ≈ 3/5 for extended/swollen conformation and ν ≈ 1/3 for compact/globule conformation.^1,3–6 While this picture is very simple and handy, it clearly disregards the fact that it depends on the specific properties of the polymer as well as of the solvent. Hence solvent quality is used to identify the relative character of one solvent with respect to a reference one, in terms of the above picture. Thus one solvent can be a good solvent for one polymer and bad for another one, and this point becomes extremely important in the framework of biopolymers and biomolecules.⁷

Fig. 1 Cartoon description of the solvophobic effects in different environments in the plane free energy F (units of thermal energy k_BT), F/k_BT, with respect to gyration radius, R_g, of the polymer. Panel (a) is for a synthetic homopolymer which collapses into a globule in a “poor” solvent and remains extended in a “good” solvent. Panel (b) displays the question of whether a heteropolymer formed by hydrophobic (H) and polar (P) monomers assumed to be collapsing in water into a unique fold with preferential exposition of the polar residues P, collapses in a non-polar solvent such as cyclohexane (cC₆H₁₂) by reversing inside out its fold with H residues exposed to the solvent and P residues buried inside the fold.

The conformational freedom of biomolecules in general, and of proteins in particular, enables them to inter-convert between several states in solution, thereby adapting upon changing solvent environments, for example by changing from a polar to a non-polar solvent. The same flexibility allows them to perform various functions in vivo. However, even though water is undoubtedly the most-like biological milieu, stability is not necessarily compromised in non-polar solvents.^8,9 A protein can be regarded as a chain formed by a sequence of amino acids taken from 20 alphabet letters, half of which have hydrophobic (H) character, so they tend to avoid contact with water, whereas the other half are polar (P) so they are happy to stay in contact with water. Proteins in water fold reproducibly and reliably to achieve their unique native states driven by several concurring interactions, including the tendency to avoid contact with water, denoted as the hydrophobic effect, as indicated in Fig. 1b. Note that solvent polarity in fact refers to the polar character of a specific solvent as compared to water, that is taken as a reference scale for an optimal polar solvent, and this is clearly different from the definition of solvent quality defined earlier, albeit the two definitions are often interpreted as meaning the same thing. However, the presence of the hydrophobic residues might suggest a similar folding event occurring also in the non-aqueous milieu, such as for instance an organic solvent. In this case, it might happen that the “protein would turn inside out with its hydrophilic or polar residues inside and hydrophobic apolar residues outside”, as suggested by Wolynes sometime ago,⁸ and pictorially represented in Fig. 1b. To the best of our knowledge, no record of such events exist in the literature. In a conventional surfactant framework oil forms droplets in water and water forms droplets in oil. However, it has been recently shown¹⁰ that this “ mirror symmetry” is not respected using “unconventional” surfactants – where a hydrophobic head and polar tail do not form micelles in apolar solvents in the same way as conventional surfactants do in polar solvents such as water. Hence there is no “ mirror symmetry” in this more complex case, and the same appears to be true in proteins.^11,12 Likely, this is because this argument overlooks the character of the peptide bond, a feature that might turn the delicate balance provided by the amino acid properties.^7,13 In addition, the actual length and energy scales are different in the two cases: in water, the enthalpy gain in saturating hydrogen bonds as well as the entropy increase stemming from the additional free water molecules, has no counterpart in organic solvents where the van der Waals interactions are much weaker and the entropic gain significantly reduced.^10–12 Confirmation of this picture is the aim of the present study.

For a fully solvated analyte, the solvation free energy can be used as a good indicator of the overall stability of the studied system, in relation to the solvent considered, and we have already carried out a detailed analysis of the solvation free energy of each single amino acid side chain equivalent, both in water (H₂O) and cyclohexane (cC₆H₁₂), as the paradigmatic representative of an organic, apolar solvent.¹⁴ It was found that the transfer free energy from H₂O to cC₆H₁₂, that is the work necessary to bring one single amino acid side chain from one solvent to the other, was respecting the expected hydrophobic scale of the amino acids. Hence, hydrophobic amino acid side chains have decreasing free energy transfer, whereas polar amino acid side chains have increasing free energy, in agreement with experimental findings.¹⁵ In this analysis, however, the backbone part of each amino acid was removed and replaced by a single hydrogen atom – obtaining what is hereafter referred to as side chain amino acid equivalents, thus hindering the effect of the backbone part that it was already argued to play an important role.¹⁶ Experimentally the solubility of polypeptides in H₂O decreases as the length increases,¹³ so this dependence should also been taken into account. Both aspects will then be considered in the present study.

Polyglycine peptides (GLY_n), formed by n identical repeated residues, are a common model for the peptide units. Other polypeptides can be formed in the same way using amino acids with different polarities, as for instance those reported in Table 1. The interest in understanding the n dependence of the solvation free energy is twofold. On the one hand, it constitutes one of the key ingredients of the forces stabilizing protein folding.⁷ On the other hand, the solvation process is known to be significantly different above and below a critical size (of order of 1 nm), at least in water.¹⁷ For both these reasons, there were several studies in recent literature reporting several useful results.

Table 1 The correspondence between the seven amino acids with their tri- and uni-code nomenclature used in this work to build the homopeptides. See e.g. ref. 18

Character	Amino acid	Short name	Single letter
Hydrophobic	Glycine	GLY	G
Hydrophobic	Alanine	ALA	A
Hydrophobic	Isoleucine	ILE	I
Polar	Asparagine	ASN	N
Polar	Lysine	LYS	K
Polar	Arginine	ARG	R
Polar	Glutamic acid	GLU	E

---

Tomar et al.¹⁹ addressed the paradoxical difference between theory and experiments on the group-additivity of the solvation free energy in an osmolyte solution (water plus small organic cosolutes), and emphasized the importance of evaluating the transfer free energy from one solution to another.

Using calorimetric measurements of the solvation enthalpies of some dipeptide analogs, Avbelj and Baldwin²⁰ suggested that the principle of group additivity does not hold true for the interaction of the peptide group with H₂O. According to their results, the main reason of this breakdown is the strong electrostatic interactions between neighbouring NHCO units of peptides in H₂O.

In 2013, Kokubo et al.²¹ analysed the effect of flexibility on the solvation free energies of alanine peptides in H₂O. They found a linear dependence with respect to the peptide length n, for both electrostatics, van der Waals cavity-formation, and total solvation free energies.

In an attempt to provide a general view on the additivity character of the solvation free energy, Staritzbichler and collaborators²² used multiconfiguration thermodynamic integration, along with a generalized-born surface area solvation model to compute the solvation free energy of different polypeptides in the form of rigid helices of various length n, in H₂O and in chloroform (CHCl₃). They preferentially considered uncharged amino acids while tuning their backbones to fit an ideal helix conformation. Their results suggest the nonlinearity in the solvation free energy in the case of short (n ≤ 5) peptide chains, turning to linear for longer chains.

Hajari and van der Vegt¹⁶ performed a molecular simulation study on the temperature dependence of solvation free energy of both polar and hydrophobic tripeptides in H₂O. They found a significant deviation from linearity in the case of hydrophobic polypeptides and a nearly linear dependence for polar polypeptides. This latter result was ascribed to a near perfect enthalpy–entropy compensation, leading the overall solvation free energy to be almost unaltered by the peptide backbone. Contrariwise, no such compensation was found for hydrophobic tripeptides.

In their work, Konig et al.²³ addressed the extent to which the assumption of group additivity to the absolute solvation free energy can hold valid. In doing so, they made use of molecular dynamics-based free energy simulations to estimate the absolute solvation free energies for 15 N-acetyl-methylamide amino acids with neutral side chains. The authors have shown that values of solvation free energies of full amino acids based on group-additive approaches are systematically too negative while completely overestimating the hydrophobicity of glycine.

Work from the Montgomery Pettitt group²⁴ explored the solvation free energy of polyglycines of different length n, in pure H₂O and in osmolyte solutions – 2 M urea and 2 M trimethylamine N-oxide (TMAO). The solvation free energies were found to be linearly dependant on n and they identified the dependence on the specific interactions (van der Waals, electrostatics, etc.).

While all these studies prove to be rather useful, a coherent picture of the solvation process is still lacking. Motivated by this, in the present work we first analyze the poor/good paradigm of H₂O and cC₆H₁₂ on polypeptides of different length n, and different polarities (hydrophobic and polar), and then compute the corresponding solvation free energies, disentangling the enthalpic and entropic contributions.

The remaining part of the paper is organized as follows: in Section 2 we describe the underlying theory and the simulation methods used in this study. Section 3 then includes all results and Section 4 a summary of the results along with a discussion. ESI,† includes additional figures and tables relative to the results reported in the main text.

2 Theory and methods

2.1 Thermodynamic integration

The solvation free energy ΔG_sol can be defined as the difference between the free energy of a single analyte molecule in a specified solvent G_solvent and in a vacuum G_vacuum

ΔG_sol = G_solvent − G_vacuum (1)

If ΔG_sol < 0 (ΔG_sol > 0) the solvent is stabilizing (destabilizing) the molecule with respect to the vacuum. This concept can clearly be extended to the free energy transfer ΔΔG(S₁ → S₂) between two different solvents, S₁ and S₂,

ΔΔG(S₁ → S₂) = ΔG_S2 − ΔG_S1 (2)

where ΔG_S1 and ΔG_S2 are the solvation free energy for solvents S₁ and S₂, respectively.

From a numerical viewpoint, free energy differences can be conveniently computed using thermodynamic integration²⁵

where V(r,λ) is the potential energy of the system as a function of the coordinate vector r, and λ is a switching-on parameter allowing to go from state A to state B by changing its value from λ_A to λ_B. The average 〈…〉_λ in eqn (3) is the usual thermal average with potential V(r,λ). The λ interval [λ_A,λ_B] is partitioned into a grid of small intervals, molecular dynamics simulations are performed for each value of λ belonging to each interval, and the results are then integrated over all values of λ to obtain the final free energy difference.

Assuming a constant heat capacity, the temperature dependence of the solvation free energy can be written as

ΔG(T) = a + bT + cT ln T (4)

so thatwith very little dependence on the choice of the specific functional form.¹⁶ The enthalpy change can then be obtained from

ΔH(T) = ΔG(T) + TΔS(T) (6)

A numerical fit of the parameters a, b, and c appearing in eqn (4) based on the results of simulations at different temperatures, will provide the required expressions for the entropy (eqn (5)) and for the enthalpy (eqn (6)). Standard deviation can then be evaluated using error block analysis.¹⁶

We remark here that this is neither the unique nor the most efficient way to compute TΔS and ΔH. Indeed, Fogolari et al.^26,27 and Lai and Oostenbrink²⁸ looked for different ways to compute entropies and enthalpies directly, thus avoiding the use of the phenomenological expression given in eqn (4). However, this analysis is much more computationally demanding and it could not be afforded for the systematic investigation that we are presenting here. We further note that eqn (4) is known to hold true only in H₂O within the temperature range 270–330 K considered in the present study,¹⁶ and it also appears to work for single amino acid side chain equivalents in cC₆H₁₂.¹⁴

2.2 Numerical protocols

The amino acid building blocks for the polypeptides selected in this work span the full hydrophobic scale ranging from polar uncharged (ASN) to hydrophobic (GLY, ALA, ILE) through to charged moieties (LYS, ARG, GLU). Moreover, most of the latter were recently shown to preferentially populate the α-helical conformational space,²⁹ one of the major secondary structural motifs found in biopolymers. The initial structures for the polypeptides were prepared using the Avogadro tool (ver 1.2.0)³⁰ in their extended configurations with dihedral angles of (ϕ,ψ) = (180°,180°) with the N- and C-termini capped with the neutral acetate (ACE) and methylamine (NME), respectively. All the polypeptides were simulated in full atomistic detail by employing the GROMOS96 (54a7) force field³¹ that appears to be an optimal compromise between precision and computational cost when computing hydration enthalpies as tested against experimental data.^14,32,33 A summary of the amino acids used to build the homopeptides, along with their common names, and both their simplified three letter codification with the corresponding uni-letter nomenclature, is shown in Table 1 above.

It is worth stressing that in this work we have explicitly included charged residues, unlike previous work that avoided this case because of the tremendous effort needed to model them,²³ as the charged moieties require complex parameterization for the treatment of finite-range electrostatic interactions.^34,35 This endeavour represents a significant step forward even at the computational implementation level with respect to previous studies.

The simulations were performed in H₂O and cC₆H₁₂, as paradigmatic representatives of polar and hydrophobic solvents, and five polymers of length from tri- (n = 3) to undeca-peptides (n = 11) were considered. In all cases they were initially aligned along the z-axis as shown in ESI,† Fig. SI in a rectangular box, and subsequently solvated with the solvent. The box dimensions and the number of solvent molecules used are reported in Table 2. The simulations were performed with the Gromacs simulation package (series 2018, 2020 and 2021)³⁶ and all the solutes were modelled roughly at their physiological pH. Therefore, GLU was preferentially modelled in its conjugate base i.e. the singly-negative anion glutamate, whilst the carboxylic acid of ARG was deprotonated and the amino and guanidino groups protonated, leading to a singly-positive acid. Likewise, the carboxylic acid of LYS was deprotonated and both its α-amino and side chain lysyl groups protonated, resulting in a monocation. Accordingly, Na⁺ and Cl⁻ counterions were added to preserve the system's electroneutrality and achieve the physiological-like concentration of 0.15 M. As detailed in Section 2, free energy differences as given in eqn (3) have been computed from the fully coupled (λ = 0) to the fully uncoupled (λ = 1) system, by gradually switching off all non-steric interactions. A grid of Δλ = 0.05 has been used in all cases, resulting in 21 binning points. Altogether, the data discussed throughout this study are the result of approximately 10 290 individual runs, running up to nearly 103 μs, and thus it represents a large scale extensive computational endeavour.

Table 2 Simulation details including the unit box dimensions in nm³ and the number of solvent molecules used in the case of H₂O and cC₆H₁₂ for different polymer lengths. The table is meant to provide a general overview of the number of solvent molecules, as subtle differences may arrive due to the size of the solute upon changing from GLY to ARG towards LYS and ILE

n	3	5	7	9	11
Box (nm^3)	3 × 3 × 3.5	3 × 3 × 4	3 × 3 × 4.5	3 × 3 × 5	3 × 3 × 5.5
H2O	1007	1157	1251	1393	1517
cC6H12	181	210	218	241	262

---

The simulations described herein follow our previous protocol.¹⁴ However, unlike the case of single amino acid side chain equivalents, here the full atomistic polypeptide structures of different lengths have been considered, and the fully fledged thermodynamics integration has been carried out. Throughout the thermodynamics integration calculations, the polymers were kept restrained in a stretched conformation by applying a force at the two CA end-points of the polymer, as illustrated in the ESI,† Fig. SI. This maximizes the number of solute–solvent contacts and hence the solvation, thus allowing direct comparison between them.

Following preliminary equilibration steps in the canonical NVT and isobaric–isothermal NPT ensembles, most of the thermodynamic integrations were performed with a time step of 2 × 10⁻¹⁵ s, although in some cases stability tests suggested the use of time steps as low as 1 × 10⁻¹⁵ s.

In order to assess the enthalpic and entropic single contributions, a set of 7 different temperatures ranging from 270 K to 330 K were performed. In the case of the undeca-polypeptides, an additional set of simulations of various time-scales were performed under the same conditions as above, but the polymers were unrestrained, closely following a previous protocol.³⁷ These conventional simulations were performed at room temperature, 300 K, and the conformational freedom of the homopeptides enables them to explore the available phase space and thus adopt the most favourable conformation with respect to the solvent considered.

Standard probes such as the radius of gyration R¹_g, and the solvent accessible surface are (SASA)³⁸ were used to provide a quantitative assessment of the peptide behaviours in the considered solvents. It is important to highlight that while calculation of SASA in the folded state is unambiguously defined, the corresponding values in the unfolded conformation are not.³⁹

3 Results

3.1 Good and poor solvents

As a preliminary step, we have performed molecular dynamics simulations of polypeptides formed by 11 identical residues ranging from hydrophobic (GLY, ALA, ILE), to polar (ASN) and charged (LYS, ARG, GLU). In the following, we denote ASN11, ALA11, etc. polypeptides formed by 11 identical ASN, ALA, etc. Note that we are denoting them as “polypetides” even if it is not strictly correct for a number of residues ranging from 3 to 11, as considered here. We also included GLY as glycine has essentially no side chain (its side chain reduces to a hydrogen atom), and hence it represents a very convenient benchmark to compare. It has been argued that H₂O at room temperature is a poor solvent for GLY15 ⁴⁰ and more generally for protein backbones.⁷ We confirm this result here with GLY11. In contrast, we see that cC₆H₁₂ is a good solvent for the same chain, indicating the presence of preferential interactions between the backbone of GLY11 and cyclohexane molecules. Support to this interpretation stems from the present calculations as well as from the linear decrease of the solvation free energy as a function of the number of repeat units, as discussed further below.

We performed molecular dynamics of GLY11 and ALA11 in both H₂O and cC₆H₁₂ at room temperature (T = 300 K). In all cases the initial condition was taken to be a random swollen conformation. Self-assembly of GLY and ALA oligopeptides in water were previously studied by Pettit and collaborators^21,41 who observed a fast aggregation coherent with our results. Results for the other considered polypeptides can be found in the ESI.†

Fig. 2 reports the behavior of the three selected probes to the conformational state: the root-mean-square-deviation from the initial state (RMSD) (top panels (a) for water H₂O and (b) for cyclohexane cC₆H₁₂), the radius of gyration R_g (middle panels (c) for H₂O and (d) for cC₆H₁₂), and the solvent accessible surface area (SASA) (bottom panels (e) for H₂O and (f) for cC₆H₁₂). The inset highlights the significant drop in all three probes in the case of GLY11 in water (magenta solid line in (A)-(a), (c) and (e)) occurring within the first 1.5 nanoseconds from the initial extended conformation, followed by equilibration around these values. A much more unstable trajectory is followed by ALA11 in H₂O (orange line in panels (B)-(a), (c) and (e)), with repeat folding and unfolding events occurring during the entire trajectory. By contrast, in cyclohexane (panels (A) and (B)-(b), (d) and (f)), both GLY11 and ALA11 settle fast into an extended conformation, essentially equivalent to the initial conformation. Note that a more quantitative assessment on the difference between compact/globule and extended/swollen can be obtained by computing the ν exponent in R_g ∼ n^ν with ν ≈ 0.6 in the extended (Flory) regime and ν ≈ 0.33 in the compact/globule regime.^1,3–6 However, it should be emphasized that the above scaling is strictly valid in the n ≫ 1 limit (as is the case in polymer physics), so its application to small polypeptides like those treated in this paper, should be taken with great care. This is shown in ESI,† Fig. SII, where we find ν too small for the considered peptides, irrespective of their polarity.

Fig. 2 Initial (inset) and equilibrium probes of the conformational behaviour of GLY11 and ALA11 at the pre-production stages (NVT and NPT equilibration). (B) Panels (a and b): root-mean-square-deviation (RMSD) from the initial state in H₂O (a) and in cC₆H₁₂ (b). Panels (c and d): radius of gyration, R_g, in H₂O (c) and in cC₆H₁₂ (d). Panels (e and f): the solvent accessible surface area (SASA) in H₂O (e) and in cC₆H₁₂ (f). In all cases the inset (A) reports the few initial nanoseconds of the equilibration process. Results for GLY11 are displayed in magenta and for ALA11 in orange. The insets also report representative snapshots of GLY11 (magenta) and ALA11 (orange) both at the initial and final stages. In all cases, the initial conformation is a random coil.

All in all, the results for GLY11 in H₂O support past reports^13,42 that water is a poor solvent for polyglycine, whereas the results for GLY11 in cC₆H₁₂ are consistent with the presence of a long-lived metastable state for globular proteins in cC₆H₁₂.⁴³ The results are also in line with the idea⁷ that H₂O is a poor solvent for protein backbones, and that this is one of the main driving forces in the collapse of the chain to a globule-shaped structure, along with solvent entropy gain and the burial of the hydrophobic side chains.⁴² This is particularly effective in H₂O because of its small size (≈2.8 Å of diameter) and large number density (55.3 M under standard conditions). Cyclohexane has a size more than two times larger than H₂O with significantly smaller number density, and the solvent entropic gain is reduced accordingly.

The behavior of ALA11 in water, which displays an erratic sequence of folding and unfolding events for which no stable collapse is observed (see Fig. 2), is more surprising. ALA is usually classified as a hydrophobic amino acid (see Table 1), and hence conformational folding akin to GLY11 may be expected. However, ALA has a larger side chain that provides a larger steric hindrance that may hamper the collapse of the small peptides such as those considered here. In addition the energetic interactions of the two polypeptides with water is different. By contrast, the behaviour of the GLY11 and ALA11 is nearly identical in cC₆H₁₂, with both remaining extended throughout the full trajectory. This can be interpreted as cC₆H₁₂ being a good solvent for both, and it might provide one possible reason of the experimentally noted absence of a collapse of proteins in cC₆H₁₂, and more generally in any non-polar solvent.⁴³Table 3 summarizes all these results in a synoptic form where H₂O is referred to as a poor+ (i.e. with stable fold) solvent for GLY11 and as poor (no stable collapse) for ALA11. Likewise cC₆H₁₂ is referred to as a good+ solvent for both.

Table 3 Summary of the solvent properties in relation to the polymers (undeca-mer) considered here in H₂O and cC₆H₁₂. Good and poor are used to point out whether the solvent tends to promote the extension or the collapse of the solute, respectively. Furthermore, the sign + is an indication of either a fully extended or fully compact conformation, without any significant structural fluctuations that characterize those cases without the + sign

Polymers	GLY11	ALA11	ILE11	ASN11	LYS11	ARG11	GLU11
H2O	Poor+	Poor	Poor	Good	Good	Good	Poor
cC6H12	Good+	Good+	Good+	Poor+	Good	Poor	Good

---

For the remaining 5 considered polypeptides, the results for RMSD (top panel), the radius of gyration R_g (middle panel) and the SASA (bottom panel) for the full trajectory in H₂O (left) and in cC₆H₁₂ (right) are reported in ESI,† Fig. SIII, and confirm a rather complex and diverse behaviour. In H₂O, ILE11 (hydrophobic) displays an initial collapse followed by a fluctuating behaviour about a less compact conformation (black line left panel), whereas for ASN11 (polar, red line left panel) R_g remains mostly stable throughout the full trajectory following an initial drop, but with a final large fluctuation. Interestingly, in cC₆H₁₂, ILE11 remains extended (black line right panel) whereas ASN11 collapses (red line right panel). The other three polypeptides (LYS11, ARG11, and GLU11, polar because charged), display large fluctuations in H₂O (left panel), and remain rather extended in cC₆H₁₂ (right panel). All these findings are summarized in Table 3.

The results of these last three polypeptides (LYS11, ARG11, and GLU11) show complex behaviour that defies any simple description in terms of poor and good solvent. Of course, this was to be expected: each residue has its own characteristics that go beyond the operative description in terms of good and bad solvents, and sometimes this matters for this kind of calculation. For instance, isoleucine (ILE) is known to be a strong hydrophobic amino acid and the corresponding marked collapse of ILE11 occurs in H₂O with noticeable structural rearrangement in the course of the simulation, as depicted in the RMSD (top), R_g (middle) and SASA (bottom) plots in ESI,† Fig. SIII. Also, the corresponding absence of any collapse or structural rearrangement of ILE11 in cC₆H₁₂, could be ascribed to the stabilizing effect of cC₆H₁₂ in line with its hydrophobic character. However, the negatively charged GLU11 polypeptide in H₂O, adopts a U-like shape after a long equilibration, and subsequently collapses to a globule although with less compact shape. We surmise that the length and shape of the side chain arms are major factors prohibiting the proper collapse of GLU11 in H₂O. In cC₆H₁₂, after a short equilibration time a relatively steady and stable conformation is achieved, compatible with favourable solute–solvent interactions over the solvent entropy promoting the collapse.

Comparatively, ASN11 and ARG11 behave symmetrically, with H₂O acting as a good solvent whereas cC₆H₁₂ is a poor one. Indeed, ASN11 in H₂O seems to remain marginally extended and undergoes a number of noticeable conformational fluctuations as reported by the minor changes seen in its solvent accessible surface area plot and the root mean square deviation analysis, respectively. Transiently formed globular-like conformations are identified in the trajectory signalled by the significant decrease in the radius of gyration R_g reported.

In cC₆H₁₂, after a short equilibration period corresponding to the coil-to-globule adaptation, all RMSD, R_g and SASA level off and remain flat throughout the simulation timescale, implying favourable and stable ASN11–cC₆H₁₂ interactions. Furthermore, we monitored an increase in the number of intramolecular hydrogen bonds (see also further below) in ASN11 as shown in ESI,† Fig. SIV, a sign of increased compactness of the globular shape obtained. ARG11, albeit simulated on a shorter time span, displays behaviour in both H₂O and cC₆H₁₂ that mirrors that reported for ASN11. Again, as already mentioned for GLU11, the long arms of ARG11 side chains form a cage-like network around the backbone, thus restraining the degrees of freedom of the latter thereby shielding its proper collapse to a globular state. Meanwhile, in cC₆H₁₂ a fast structural reorganization of ARG11 is seen wherein the polymer's side chains are preferentially folded back inside towards the core, and the backbone is exposed to the bulk.

In summary, we observe the general tendency of undeca-polypeptide folding in water, and the absence of folding in cyclohexane; and conversely those folding in cyclohexane which do not fold in water. However, LYS11 fails to follow this general rule as it remains essentially extended in both H₂O and cC₆H₁₂, albeit with side chains more parallel to the backbone in the latter case, see Fig. 3. This behaviour might be ascribed to the steric hindrance of the long arms of the side chain densely packing around the relatively short undeca-homopeptide backbone, thus significantly reducing its conformational space, not allowing the proper collapse of the polymer within the simulated time considered here.

Fig. 3 Representative snapshots of the smallest R_g conformers i.e. the most collapsed conformations. On the left are the structures obtained in H₂O and on the right are those obtained in cC₆H₁₂. From top to bottom the corresponding structures are for GLY11, ALA11, ILE11, ASN11, LYS11, ARG11 and GLU11.

In principle, the relative stability of each polypeptide with respect to a specific solvent can also be quantified by direct calculation of the solvation free energy in both H₂O and cC₆H₁₂. This will be carried out in the next section. However, in interpreting a comparison with the data reported here, the differences in the flexibility conditions (fully flexible here, fully constrained in the solvation free energy calculation reported below), plays an important role as noted earlier.²¹

Fig. 3 reports snapshots of the most representative conformers in all considered cases, and Table 3 summarizes these results in a synoptic form.

Additional insight can be obtained by monitoring the evolution in the fractions of peptide–solvent and intra-peptide hydrogen bonds. Confining our attention to the initial equilibration stage over a few nanoseconds first (Fig. 4 (A)), we report the total number of inter-chain hydrogen bonds with H₂O for both GLY11 (black line in (A)-(a)) and ALA11 (black line in (A)-(b)). Correspondingly, the total number of intra-chain hydrogen bonds are also reported for GLY11 (red line in (A)-(a)) and for ALA11 (red line in (A)-(b)). For GLY11, the number of hydrogen bonds with water shows a fast drop (black line in (A)-(a)), consistent with the folding of GLY11 being further stabilized by an increase in the number of intra-chain hydrogen bonds (red line in (A)-(a)). This does not seem to be the case for ALA11 where the number of hydrogen bonds with water does not show any drop with time (black line in (A)-(b)) and the number of intra-chain hydrogen bonds remains essentially unchanged (red line in (A)-(b)). It is worth noting from Fig. 4 that on assuming an approximate average value of (20 kJ mol⁻¹) for each hydrogen bond, the typical total energy involved for approximately 30 bonds is of the order of 600 kJ mol⁻¹, which is comparable with the solvation free energy discussed in the next section. This confirms the fundamental role played by the hydrogen bonds in stabilizing the protein fold as discussed in detail in ref. 44.

Fig. 4 Top panel (A): Initial stage evolution of the number of hydrogen bonds for GLY11 ((A)-(a)) and ALA11 ((A)-(b)). Both inter- (H₂O–solute black line, (A)-(a) & (A)-(b)) and intra- (solute–solute in H₂O red line and cC₆H₁₂ blue line, (A)-(a) & (A)-(b)) molecular hydrogen bonds are plotted. Bottom panel (B): Long time evolution of the number of hydrogen bonds of GLY11 (black line) and ALA11 (red line). (B)-(a) Solute–H₂O hydrogen bonds; (B)-(b) histogram distribution of (B)-(a); (B)-(c) solute–solute hydrogen bonds in H₂O; (B)-(d) solute–solute hydrogen bonds in cC₆H₁₂.

At equilibrium, the above findings are confirmed. Fig. 4(a) and (c) in panel (B) report the fluctuations of the solute–water and solute–solute hydrogen bonds, respectively (black lines refer to GLY11 and red lines to ALA11). Note that the total number of hydrogen bonds with H₂O is of the order of 25 for both GLY11 and ALA11; whereas the total number of internal hydrogen bonds is stable in the order of 2.5 for GLY11 but is highly fluctuating between 0 and 2.5 in the case of ALA11 – clearly showing the lack of a stable fold for ALA11 in water.

Fig. 4(b) in panel (B) displays a histrogram of the distribution of the total number of hydrogen bonds for both GLY11 (black) and ALA11 (red) with water. They turn out to be nearly identical, as visible. In cC₆H₁₂ the behaviour is clearly different: Fig. 4(d) in panel (B) shows the fluctuation in the number of solute–solute hydrogen bonds in cC₆H₁₂ for GLY11 (black line) and ALA11 (red line). Here the total number of intra-chain hydrogen bonds is significantly higher for GLY11 (black line) than for ALA11 (red line), indicating a much more stable fold in the case of GLY11. When compared to H₂O, the total number of intra-chain hydrogen bonds for ALA11 is larger in H₂O than in cC₆H₁₂ (compare the red lines in Fig. 4(c) and (d)) in panel (B), so ALA11 is still less stable in cC₆H₁₂ than in H₂O.

In the ESI† we report the same quantities for ILE11, ASN11, LYS11, ARG11, and GLU11: ESI,† Fig. SIV(a) displays the total number of hydrogen bonds of ILE11 (black line), ASN11 (red line), LYS11 (green line), ARG11 (blue line), and GLU11 (magenta line) with H₂O. While a near constant trend is observed in all cases, the actual total number decreases from GLU11 (the largest) to ILE11 (the smallest), with ESI,† Fig. SIV(b) displaying the corresponding equilibrium distribution. The total number of solute–solute intra-chain hydrogen bonds, depicted in ESI,† Fig. SIV(c), also shows a constant trend with slightly variable absolute number. This number increases in the case of cC₆H₁₂, again due to the absence of an alternative provided by the solvent, and again decreases from GLU11 (the largest) to ILE11 (the smallest), thus confirming the stabilization effect of cC₆H₁₂ decreasing from the charged GLU11 to the hydrophobic ILE11.

3.2 Solvation free energy

In Section 3.1 we discuss how different polypeptides behave in solvents with different polarities. This analysis highlights that the definition of a ‘good’ and ‘poor’ solvent is not an absolute property but has to be related to the specificities of the polypeptides. For example, H₂O is a poor solvent for polyglycine, polyanaline, polyisoleucine and polyglutamic acid, but it is a good solvent for polyasparagine, polylysine and polyarginine. Conversely, cC₆H₁₂ is a poor solvent for polyasparagine and polyarginine, but it is a good solvent for polyglycine, polyalanine, polyisoleucine, and polylysine. In most cases these findings agree with our intuition and with the common view that “like dissolves like” but this is not always the case. For instance, polyglutamic acid collapses in H₂O and remains extended in cC₆H₁₂, whereas the reverse behavior would be expected on the basis of the charged nature of the glutamic acid GLU residue. An even more notable exception is provided by polylysine which shows no collapse in either cC₆H₁₂ or H₂O, in spite of the charged nature of the lysine residue.

In drafting these conclusions we must bear in mind two additional points. First, none of the investigated homo polypeptides are really hydrophobic, irrespective of the polarities of their residues. Indeed, we have shown that each of the considered polypeptides forms a number of hydrogen bonds with the solvent, ranging from 2–3 bonds per residue for ILE11 to more than 10 hydrogen bonds per residue for GLU11 (see ESI,† Fig. SIV(a)). This is also evident from the snapshot of the initial conformation that shows in all cases, significant hydrogen bonding with the solvent, as explicitly displayed in ESI,† Fig. SVI. Accordingly, none, with the exception of GLY11, is shown to have a stable fold in H₂O (see representative snapshots in Fig. 5), although clearly ILE11 has a stronger tendency to fold compared to GLU11. The second point that is worth stressing is that the difference between extended/swollen and compact/globule is well defined only for sufficiently longer polypeptides compared to those analyzed in the present work.

Fig. 5 Solvation free energy, ΔG_solv: (a) ΔG_w from vacuum to H₂O at 25 °C and (b) ΔG_c from vacuum to cC₆H₁₂. The polypeptides shown in the x-axis are representative of the full hydrophobic scale following previous work.¹⁴ Their lengths vary from tri- (n = 3) to undeca- (n = 11) polypeptides. Note that all plots are in the same scale.

Next, we turn our attention to the corresponding solvation free energies that can be computed via thermodynamic integration. As anticipated, the aims here are twofold. First, we would like to extend our previous calculation¹⁴ for a single amino acid side chain equivalent – a single amino acid where the backbone part of the amino acid has been replaced with a single hydrogen atom – to include the effect of the backbone as well as the dependence of the number n of included residues. Relevant questions here include the possible non-linear effects of the solvation free energy as a function of the number of repeated units, and whether there is a mirror symmetry by changing a highly polar solvent such as H₂O to an apolar organic solvent such as cC₆H₁₂. For instance, is the solvation free energy of (G)_n equal to n times the solvation free energy of a single amino acid (G)₁? And is this depending on the polarity properties of the amino acids and/or the polarity of the solvent? Both questions will be addressed in the present section.

A second issue of paramount importance is what is the main driving force to solvation. A conventional simple accepted picture is that solvation includes two different and competing processes: the entropically unfavourable creation of a cavity, and the enthalpically favourable attractive dispersion contributions arising from the introduction of the solute. Note that in water this picture is known to be affected above a critical solute size of 1 nm in view of the fact that sufficiently small solutes (smaller than 1 nm) do not affect the water hydrogen bond network.¹⁷

While we will not consider all 18 side chains studied by Dongmo Foumthuim et al.,¹⁴ our representative results will be sufficient to understand the emerging pattern.

Fig. 5 displays the solvation free energy for H₂O (Fig. 5a) and cC₆H₁₂ (Fig. 5b), at room temperature (25 °C) in both cases. All corresponding values can be found in ESI,† Tables SII and SIII. The ordering is according to the nominal character of the amino acid from hydrophobic (left) to polar (right). Glycine is listed first as the simplest case.

As visible in Fig. 5a all considered polypeptides display negative solvation free energy, indicating that in H₂O the onset of attractive energies originating upon the insertion of the polypeptides overwhelms the entropic cost of creating a cavity. The effect is more pronounced for polar and charged amino acids, with the ΔG decreasing with the increase of the number of identical amino acids n from 3 to 11 (i.e. the length of the peptide).

The same trend is observed for the solvation free energy in cC₆H₁₂, as reported in Fig. 5b. While in H₂O this behaviour is in marked contrast with that of single amino acid equivalents¹⁴ where the solvation free energy ΔG_w is found to be large and positive for hydrophobic amino acid side chain equivalents, and large and negative for polar ones,¹⁴ in accord with a similar computational study of tripeptides in water.¹⁶ In cC₆H₁₂, however, this behaviour is more intriguing. We note that both hydrophobic and polar peptides have negative solvation free energy, ΔG_c, in cC₆H₁₂, more negative for polar than for hydrophobic ones.¹⁴ A calculation of the transfer free energy ΔΔG_w>c from H₂O to cC₆H₁₂, however, restores our intuitive picture in terms of the relative stability.

Fig. 6 reports ΔΔG_w>c for polypeptides from H₂O to cC₆H₁₂ with the same arrangement and ordering of Fig. 5: hydrophobic (left) and polar (right), at different peptide lengths n. With the exclusion of asparagine (ASN), all ΔΔG_w>c are negative, significantly larger for polar than for hydrophobic polypeptides, although n = 3 is clearly an outlier for hydrophobic polypeptides, likely due to its small size. As anticipated, and previously alluded to in Fig. 2 and in ESI,† Table SI, all tripeptides (n = 3) have sizes smaller that 1 nm, which is known to be a critical value for solvation in water,¹⁷ whereas all peptides with n > 3 have sizes larger than this value. In this respect, the present results are complementary to those tripeptides reported in ref. 16.

Fig. 6 ΔΔG_w>c from H₂O to cC₆H₁₂ at 25 °C. Ordering is the same as in Fig. 5.

Consider GLY_n first (Fig. 6). Here ΔΔG_w>c is small and negative, indicating the stabilizing effect of cC₆H₁₂ compared to H₂O. This agrees with the calculations of Section 3.1 and confirms findings from previous studies.^21,40 However, the trend is not linear: ΔΔG_w>c increases from n = 3 to n = 7 and then decreases again for higher n = 9, 11. Polyalanine (ALA_n) and polyisoleucine (ILE_n) show a more regular increasing trend, whereas polyasparagine (ASN_n) switches from negative to positive ΔΔG_w>c as n increases. Polar and charged polypeptides, on the other hand, display a much more significantly negative ΔΔG_w>c with a monotonic increase with n, a result that defies our physical intuition, but is again in agreement with previous results on tripeptides.¹⁶

The emerging scenario is then that the stability of a (homo) polypeptide is mainly dictated by the polarity of the solute, with the polarity of the solvent playing a minor role.

3.3 Entropy–enthalpy compensation

Two remaining issues are left from the results. The first issue is whether any observed process is predominantly enthalpically or entropically driven, and this will be discussed in this section. This can be conveniently obtained by the analysis of the solvation free energy at different temperatures which allows us to separate out the entropy and the enthalpy contributions, as anticipated in Section 2. The second issue is discussed in Section 3.4.

As anticipated, the solvation free energy, ΔG, can be factorized in two terms. First, the creation of a cavity in the solvent to accommodate the solute. This process is clearly entropically unfavourable so TΔS < 0 (−TΔS > 0). However, attractive interactions may form upon inserting the solute in the cavity, thus leading to a favourable process with ΔH < 0. If the two processes happen to balance each other, then ΔG ≈ 0 and −TΔS = −ΔH, thus leading to a perfect anticorrelation in the −TΔS versus ΔH plane, known as “entropy–enthalpy compensation” with a slope = −1 (see ESI,† Fig. SVII). If the slope is >−1, then the system is entropically driven, conversely to enthalpically driven.

Fig. SVIII and SIX (ESI†) display the temperature dependence of ΔG_w in H₂O and ΔG_c in cC₆H₁₂, respectively. Both are increasing with temperature function as expected, since both TΔS_w and TΔS_c are entropically positive costs, irrespective of the solvent polarity in agreement with the results from the single amino acid side chain equivalents as well as past experimental results.¹⁴ Curvatures are, however, different depending of the specific solvent and also on the length n of the polypeptide, indicating a very complex patchwork of interactions that in water may also depend on the size of the polypeptide.¹⁷

In ref. 14, we reported this calculation for each single amino acid side chain equivalent. In H₂O, hydrophobic amino acid side chain equivalents were found to comply with the entropy–enthalpy compensation rule reasonably well, with a wide distribution of values along the line with slope ≈−1 in the −TΔS vs. ΔH plane, depending on the specificity of each single residue. Polar amino acid side chain equivalents showed instead a tendency to lump together around a specific region of this line, with the exception of ARG. In cC₆H₁₂ the tendency to lump similar state points was found to be even more pronounced for both polar and hydrophobic amino acids.¹⁴

The values of the slopes along with the intercept at origin and the corresponding correlation coefficients, are reported in ESI,† Table SVII for all considered polypeptides and for both H₂O and cC₆H₁₂. Interestingly, all slopes are found to be <1 indicating that all these solvation processes are largely enthalpically dominated.

Fig. 7 reports the results of this analysis, where the entropic part of the free energy −TΔS is plotted as a function of the enthalpic part ΔH. Each panel a–g, includes points computed at different lengths from n = 3 to n = 11 for all the considered polypeptides. In all cases, data for H₂O are in black, and those for cC₆H₁₂ are in red.

Fig. 7 Entropic contribution −TΔS of the solvation free energy ΔG as a function of the enthalpic counterpart ΔH in the case of H₂O and cC₆H₁₂ for different polymer lengths. The solvation data in H₂O are displayed in black and those in cC₆H₁₂ are plotted in red while the error bars represent the standard deviation. The subplots annotated from (a) to (g) correspond to each of the polypeptides used here: GLY, ALA, ILE, ASN, LYS, ARG, and GLU, respectively. Furthermore, the continuous lines represent the linear fit of the simulation data. Please note that different scales have been used in different cases.

Consider the GLY case first, see Fig. 7a. In H₂O (black), nearly all points G₃–G₁₁, lump very closely to one another along a line with slope approximately −1. By contrast, in cC₆H₁₂ (Fig. 7a red) there is very clear anti-correlation in the sense that ΔH decreases with increasing length n, with a corresponding increase of −TΔS. That is, a gain in enthalpy translates into a corresponding loss of entropy. This corresponds exactly to the entropy–enthalphy compensation usually found in H₂O (see e.g., ref. 11 and 12 this time in cC₆H₁₂ rather than in water, and it reflects the fact that cC₆H₁₂ is a good solvent for polyglycine whereas H₂O is poor one, in agreement with the results of Section 3.1. The cases of ALA (Fig. 7b) and ILE (Fig. 7c) are expected to follow a similar pattern on the basis of their hydrophobic character (Table 1), but they appear to present a more complex behaviour. In the case of ALA (Fig. 7b) a rather similar behaviour in H₂O (black) and cC₆H₁₂ (red) is found (note the two scales of Fig. 7a and b are nearly equivalent), suggesting similar behaviour for GLY and ALA. An additional notable feature of ALA in H₂O is the irregular dependence as a function of n, with n = 11 very different from all others, in line with the same trend displayed for ΔΔG_w>c (Fig. 6). ILE (Fig. 7c) also shows an entropy–enthalpy compensation for both H₂O and cC₆H₁₂, but with a much more linear dependence on n. Interestingly, ASN also displays a similar pattern (Fig. 7d) where for LYS (Fig. 7e), ARG (Fig. 7f), and GLU (Fig. 7f), a rather different trend is observed for H₂O and cC₆H₁₂, in all cases with a slope significantly smaller than −1, indicating a predominant enthalpic role. Here, we emphasize again that the assumed temperature dependence reported in eqn (4) is phenomenological and it might break down for some of the cases reported here, although it has been found to work rather well in past similar studies on single amino acid side chain equivalents both in H₂O ^14,16 and in cC₆H₁₂. More robust direct calculations are possible²⁸ but they are much more computationally demanding.

3.4 Chain length dependence of solvation free energy, ΔG: implication on additivity

The second point is related to the n dependence of ΔG in H₂O and in cC₆H₁₂ that was anticipated in Fig. 7. Here the relevant question is whether ΔG_n ∝ n (linear dependence on the length) or there exists non-linear effects due to the backbone, as observed in the case of tripeptides.¹⁶ Note that in water a marked change is expected when the hydrophobic solute size increases from below to above 1 nm because below 1 nm a cavity able to accommodate the solute can be created without affecting the hydrogen bond network¹⁷ and the tripeptides considered in ref. 16 were all smaller that 1 nm.

Fig. 8 reports our results for ΔG (black circles), and it includes the corresponding dependence of ΔH (blue triangles) and TΔS (magenta squares), in H₂O (panels (a)–(g)) and in cC₆H₁₂ (panels (h)–(n)). In all cases the solid lines represent a linear fit. Note that TΔS and ΔH both decrease as a function of n indicating enthalpic gain and entropic loss. Fig. 5 already suggested the linear dependence on n of both ΔG_w and ΔG_c for all considered polypeptides. This is indeed confirmed in Fig. 8 (black lines) but with different slopes: smaller for the hydrophobic polypeptides (GLY, ALA, ILE, top three row panels (a) to (c) for H₂O and (h) to (j) for cC₆H₁₂), as well as for ASN ((d) for H₂O and (k) for cC₆H₁₂); larger in all cases for the polar polypeptides (LYS, ARG, GLU) (lower four panels (e) to (g) in H₂O and (l) to (n) in cC₆H₁₂). Upon splitting by enthalpic and entropic terms, rather different contributions are found in the different cases: for GLY, ALA, ILE and ASN, the relative contributions of ΔH and TΔS appear to be comparable resulting in a weak increase of ΔG_w and ΔG_c as a function of n (Fig. 8a–d), in agreement with the findings of Fig. 7: in contrast, LYS, ARG, GLU have a much stronger n dependence stemming from ΔH, as is clearly visible in Fig. 8e–g, so its additivity is purely enthalpically driven. While this is clearly consistent with the different trends observed in the enthalpy–entropy plots of Fig. 7e–g, the very similar behaviour in H₂O and cC₆H₁₂ is rather surprising and will require further analysis which is planned in the future.

Fig. 8 Solvation free energy, enthalpy, and entropy (ΔG, ΔH, TΔS) changes with the polymer chain length n in H₂O and cC₆H₁₂ at 25 °C for each of the polypeptides considered in this work (GLY, ALA, ILE, ASN, LYS, ARG, GLU). The continuous lines connecting the points show the representative linear fitting. The data representing the hydration thermodynamics in H₂O are shown from (a) to (g), whilst those corresponding to cC₆H₁₂ are plotted from (h) to (n) for each of the polypeptides. Negative ΔG and ΔH represent an energetic gain upon solvation, whereas a negative TΔS represents an entropic loss, upon solvation.

Another related relevant issue concerns the relation with past results referring to the solvation free energy ΔG₁ for a single amino acid side chain equivalent,¹⁴ that is, a single amino acid with the backbone part replaced with a single hydrogen atom. We show this analysis in ESI,† Fig. SV where ΔG_n is plotted versus n × ΔG₁ both in H₂O and cC₆H₁₂ for all considered polypeptides, with the exception of GLY for which there is clearly no amino acid side chain equivalent since it does not have a proper side chain. The results highlight rather clearly the importance of the backbone, in particular for ALA and ILE for which a significant deviation from the naive expectation ΔG_n ∝ n(ΔG₁) is observed. Again, this is consistent with the relevant role of the backbone in the case of nominally hydrophobic polypeptides.

4 Conclusions

In this paper, we have addressed the issue of “good” and “poor” solvents in the framework of polypeptides of different polarities, both hydrophobic and polar, and including polyglycines as a reference point. Here the definition of good and poor solvent refers to the common view of “like dissolves like”: polar solutes dissolve in polar solvents and hydrophobic solutes dissolve in hydrophobic (apolar) solvents. Polar solvents have typically large dipole moments and high dielectric constants, a feature that can be easily rationalized by the fact that high dielectric constants favour the tendency to dissociate and hence form dipoles. A paradigmatic example of a polar solvent is water (dielectric constant ≈80), and hence polar solvents typically mix with water. As a representative example of a hydrophobic solvent, we have considered cyclohexane that has dielectric constant ≈2 and hence can be considered the opposite of water. Similar reasoning applies to solutes that can be classified as polar or hydrophobic based on the same rationale as the solvent. Hence good and poor solvents are to be defined with respect to a specific solute. A fully hydrophobic polypeptide is expected to collapse in water (water is a poor solvent), but it remains extended in cyclohexane (cyclohexane is a good solvent). Conversely, a fully polar polypeptide usually folds in a poor solvent such as cyclohexane, while remaining extended in a good solvent such as water. Hence, the solvent quality always requires the solvent polarity to be unambiguously defined. This is especially important for polypeptides as they are formed by an identical backbone, plus a sum of single side chains that provide their hydrophobic/polar character. While the polarity character is usually attributed to the side chains on the basis of their chemical characters, a much more robust indication is given by their solvation free energies in solvents with different polarities, and we have studied their properties in the present paper.

Our main findings can be summarized as follows.

(1) There is no general mirror symmetry between the behaviour of hydrophobic/polar polypeptides in water/cyclohexane, due to the presence of the backbone, as well as of the different energy scales involved. Hence hydrophobic polypeptides in water do not behave as polar peptides in cyclohexane, nor the other way around. Polyglycine is formed by n different residues having a single hydrogen atom as a side chain, and it is usually regarded as a rough model for the peptide backbone of a protein. We find that it collapses in water and it remains extended in cyclohexane, so water is a poor solvent for polyglycine (in line with past studies), and cyclohexane a good one. Accordingly, the solvation free energy in cyclohexane, ΔG_c, is negative and decreases approximately linearly with n residues. Interestingly, a similar trend is also found for the solvation free energy in water, ΔG_w, with the transfer free energy ΔΔG_w>c being negative and decreasing with the length of the polypeptide. Additional hydrophobic polypeptides, such as ALA and ILE, behave similarly to GLY, with some small differences. These results can be rationalized as follows: firstly, none of these polypeptides are really hydrophobic irrespective of the polarities of the single side chain. This is evident since they all form at least 2–3 hydrogen bonds per residue. Secondly, the solvation free energy is composed of an entropically unfavourable term associated with the creation of a cavity, and an enthalpic favourable term originating from the insertion of the polypeptides in the solvent. Our results indicate that the latter always dominate the former leading to negative solvation free energies.

(2) Polar polypeptides such as ASN_n, LYS_n, ARG_n, and GLU_n markedly deviate from the mirror symmetry. GLU_n collapses in water but not in cyclohexane, whereas both water and cyclohexane are good solvents for LYS_n. Accordingly, the transfer free energy ΔΔG_w>c from water to cyclohexane is found to be negative, with linearly decreasing n residues, and significantly more negative than the hydrophobic counterparts. LYS_n, ARG_n, and GLU_n are mostly enthalpically driven, whereas in ASN_n, as well as all the hydrophobic polypeptides, the driving force is a mixture of enthalpic and entropic contributions. These results suggest that the solvation process is mainly dominated by the polarity of the solute, with the solvent playing a minor role.

(3) For all hydrophobic polypeptides as well as for ANS_n, there is nearly a similar entropy–enthalpy compensation in both water and cyclohexane, whereas for the other polar polypeptides LYS_n, ARG_n, and GLU_n there is a marked difference. Combined with the previous point, this shows that ANS_n hardly belongs to the same class as LYS_n, ARG_n, and GLU_n, and more generally that the rough polar/hydrophobic division of the amino acids scale is not representative of the complexity of the interactions, and additional features (e.g. charge, size, etc.) should be taken into account. The peculiar properties of ASN_n reported throughout this study might also be related to its marked propensity together with aspartic acid (ASP) to populate loop regions in protein structures, and thus often have no defined secondary structure.²⁹

While the present work is focused specifically on the solvation process of polypeptides and its dependence on both the solvent and peptide polarities, a similar study has been tackled by the present authors for a specific synthetic polymer displaying a coil–helix transition, which will be presented elsewhere. Coupled with the present findings, the general scenario still presents some missing points requiring further study. One promising route that has already been addressed in past studies,²⁸ is the quantification of the individual entropic and enthalpic solute–solvent and solvent–solvent contributions, thus allowing a quantitative assessment on the exact putative cancellation of the solvent–solvent enthalpy and solvent–solvent entropy in water and not in cyclohexane. We are planning to explore this possibility in a future dedicated study. Altogether it is hoped that systematic analyses as those outlined above, will provide new insights on the nuances of solvation mechanisms in different solvents, a process which is ubiquitous in biological systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge the useful discussions and correspondence with Giuseppe Graziano, George Rose and Chris Oostenbrink, as well as networking support by COST Action CA17139. The use of the SCSCF multiprocessor cluster at the Università Ca' Foscari Venezia is gratefully acknowledged. We also acknowledge the CINECA projects HP10CGFUDT and HP10C1XOOJ for the availability of high performance computing resources through the ISCRA initiative. The work was supported by MIUR PRIN-COFIN2017 Soft Adaptive Networks grant 2017Z55KCW (A. G.).

Notes and references

1. P. Flory, Statistical mechanics of chain molecules, Interscience Publishers, 1969.
2. M. Doi and S. F. Edwards, The Theory of Polymer Dynamics (International Series of Monographs on Physics), Clarendon Press, 1988.
3. A. R. Khokhlov, A. Y. Grosberg and V. S. Pande, Statistical Physics of Macromolecules (Polymers and Complex Materials), American Institute of Physics, 1994th edn, 2002.
4. M. Rubinstein and R. H. Colby, Polymer Physics (Chemistry), Oxford University Press, 1st edn, 2003.
5. P. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1979.
6. S. M. Bhattacharjee, A. Giacometti and A. Maritan, J. Phys.: Condens. Matter, 2013, 25, 503101.
7. D. W. Bolen and G. D. Rose, Annu. Rev. Biochem., 2008, 77, 339–362.
8. P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 2426–2427.
9. T. Meyer, V. Gabelica, H. Grubmüller and M. Orozco, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 408–425.
10. M. Carrer, T. Skrbic, S. L. Bore, G. Milano, M. Cascella and A. Giacometti, J. Phys. Chem. B, 2020, 124, 6448–6458.
11. T. Hayashi, S. Yasuda, T. Škrbić, A. Giacometti and M. Kinoshita, J. Chem. Phys., 2017, 147, 125102.
12. T. Hayashi, M. Inoue, S. Yasuda, E. Petretto, T. Škrbić, A. Giacometti and M. Kinoshita, J. Chem. Phys., 2018, 149, 045105.
13. D. Karandur, K.-Y. Wong and B. M. Pettitt, J. Phys. Chem. B, 2014, 118, 9565–9572.
14. C. J. Dongmo Foumthuim, M. Carrer, M. Houvet, T. Škrbić, G. Graziano and A. Giacometti, Phys. Chem. Chem. Phys., 2020, 22, 25848–25858.
15. R. Wolfenden, C. A. Lewis, Y. Yuan and C. W. Carter, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7484–7488.
16. T. Hajari and N. F. A. van der Vegt, J. Chem. Phys., 2015, 142, 144502.
17. D. Chandler, Nature, 2005, 437, 640–647.
18. D. Voet and J. G. Voet, Biochemistry, John Wiley & Sons, 2010.
19. D. S. Tomar, D. Asthagiri and V. Weber, Biophys. J., 2013, 105, 1482–1490.
20. F. Avbelj and R. L. Baldwin, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 3137–3141.
21. H. Kokubo, R. C. Harris, D. Asthagiri and B. M. Pettitt, J. Phys. Chem. B, 2013, 117, 16428–16435.
22. R. Staritzbichler, W. Gu and V. Helms, J. Phys. Chem. B, 2005, 109, 19000–19007.
23. G. König, S. Bruckner and S. Boresch, Biophys. J., 2013, 104, 453–463.
24. C. Y. Hu, H. Kokubo, G. C. Lynch, D. W. Bolen and B. M. Pettitt, Protein Sci., 2010, 19, 1011–1022.
25. D. Frenkel and B. Smit, Understanding Molecular Simulation, Second Edition: From Algorithms to Applications (Computational Science Series, Vol 1), Academic Press, 2nd edn, 2001.
26. F. Fogolari, C. J. Dongmo Foumthuim, S. Fortuna, M. A. Soler, A. Corazza and G. Esposito, J. Chem. Theory Comput., 2016, 12, 1–8.
27. F. Fogolari, O. Maloku, C. J. Dongmo Foumthuim, A. Corazza and G. Esposito, J. Chem. Inf. Model., 2018, 58, 1319–1324.
28. B. Lai and C. Oostenbrink, Theor. Chem. Acc., 2012, 131, 1–13.
29. T. Škrbić, A. Maritan, A. Giacometti and J. R. Banavar, Protein Sci., 2021, 30, 818–829.
30. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17.
31. N. Schmid, A. P. Eichenberger, A. Choutko, S. Riniker, M. Winger, A. E. Mark and W. F. van Gunsteren, Eur. Biophys. J., 2011, 40, 843.
32. C. Oostenbrink, A. Villa, A. E. Mark and W. F. Van Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676.
33. A. Villa and A. Mark, J. Comput. Chem., 2002, 23, 548–553.
34. M. M. Reif, P. H. Hünenberger and C. Oostenbrink, J. Chem. Theory Comput., 2012, 8, 3705–3723.
35. M. R. Shirts, J. W. Pitera, W. C. Swope and V. S. Pande, J. Chem. Phys., 2003, 119, 5740–5761.
36. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
37. C. J. Dongmo Foumthuim, A. Corazza, R. Berni, G. Esposito and F. Fogolari, BioMed Res. Int., 2018, 2018, 1–14.
38. F. Eisenhaber, P. Lijnzaad, P. Argos, C. Sander and M. Scharf, J. Comput. Chem., 1995, 16, 273–284.
39. H. Gong and G. D. Rose, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 3321–3326.
40. H. T. Tran, A. Mao and R. V. Pappu, J. Am. Chem. Soc., 2008, 130, 7380–7392.
41. D. Karandur, R. C. Harris and B. M. Pettitt, Protein Sci., 2016, 25, 103–110.
42. A. Merlino, N. Pontillo and G. Graziano, Phys. Chem. Chem. Phys., 2017, 19, 751–756.
43. C. N. Pace, S. Trevino, E. Prabhakaran and J. M. Scholtz, Philos. Trans. R. Soc. London, Ser. B, 2004, 359, 1225–1235.
44. G. D. Rose, P. J. Fleming, J. R. Banavar and A. Maritan, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 16623–16633.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp05214h

---