Water model for hydrophobic cavities: structure and energy from quantum-chemical calculations

Abstract

This ab initio study aims to design a series of large water clusters having a hollow clathrate-like cage able to host hydrophobic solutes of various sizes. Starting from the (H₂O)_n (n = 18, 20, 24 and 28) hollow cages, water layers have been added in a stepwise manner in order to model the configuration of water molecules beyond the primary shell. The large (H₂O)₁₀₀, (H₂O)₁₂₀ and (H₂O)₁₄₀ clusters complete the hydrogen bonding network of the cage with optimal and regular tiling of the do-, tetra-decahedron and hexa-decahedron, respectively. This study is corroborated by an investigation of dense water clusters up to the (H₂O)₁₂₃ one, being highly consistent with experimental data on ice concerning the electronic and zero-point energies for aggregate formation at 0 K and enthalpy and entropy at 273 K. The cavity creation profoundly alters the orientation of water molecules compared with those found in dense clusters. Nevertheless, such a large reorganization is necessary to maximize the water–water attraction by making it similar to the one found in dense clusters. The cage formation is an endothermic process; however, the computed values are large compared with previous reports for hydrocarbon aqueous solutions. Larger clusters are required for a more fruitful comparison.

---

Introduction

Condensed phases of pure water show extraordinary properties due to the strength, directionality, and plasticity of intermolecular hydrogen bonding between neighbouring molecules.^1–7 There are nineteen ice structures known so far, as well as three families of amorphous ice, namely low-density, high-density and very-high-density.² Despite the phase diagram of the ice being very complex, the fixed positions of the molecules have allowed exhaustive characterization of the polymorphism. When the ice melts, the overall hydrogen bonding weakens by about 12%. However, the large residual part compacts the opened ice I_h structure, the volume reduces, and a sort of short-range tetrahedral order remains steady at around 4 °C. Because of the molecular thermal motion, hydrogen bonds (HBs) continuously break and re-form very quickly (an average lifetime of less than 1 ps), and the structure is unstable and changeable even at low temperatures. As the temperature increases, the analogies to ice reduce, the short-range order diminishes and dynamics become much faster. Despite the countless experimental and theoretical research studies,^8–13 an exhaustive understanding of microscopic processes is still far from being achieved. Under room conditions, it is commonly believed that water is a homogeneous solvent, in which each water molecule forms, on average, two strong donor and two strong acceptor bonds with a fluxional tetrahedral shape and a high degree of hydrogen bonding connectivity. The analysis of neutron diffraction data suggested a number of HBs per water molecule of 3.9,⁹ while ref. 10 and 11 suggested a lower value of 3.1, with a conspicuous amount of broken HBs. Recently, electron diffraction studies have challenged this view and a more structured three-dimensional network has been proposed with a higher coordination number (5 ± 0.7).¹² In line with these findings, X-ray diffraction measurements showed an O⋯O coordination number of 4.3 ± 0.2 and this value is independent of temperature.¹³

In many circumstances, water molecule networks appear to be heterogeneous and an equilibrium between two different microscopic domains or clusters with low-density-water and high-density-water has been proposed for supercooled water.^14–20 Some researchers have taken this idea to the extreme, also for ordinary water. This has ignited a wide debate within the scientific community.²¹ Much more important are the deviations from the homogeneous behaviour of liquid water when a solute is added. It is known that the strong electrostatic ion–water interaction causes a great reorganization of the solvent molecules close to the ions. Fortunately, in this case, there is a general agreement on the hydration shell shape and on the action mechanism.²²

Hydrophobic molecules or molecules with hydrophobic chains also perturb the water structure near solutes; however, many microscopic details are still unclear and a matter of debate.^23–28 Solubilisation of hydrophobic molecules is generally viewed as a two-step process.²⁹ The first step concerns the formation of an appropriate size cavity in the solvent to encapsulate the solute molecule. This process is thermodynamically unfavoured and depends on how many particles must be displaced, and the energy required is termed the cavitation energy. Therefore, there is a natural tendency of the solvent to minimize the cavity size. The second step involves the interaction between the solute and the solvent once the cavity is filled and, given that the solute cannot form HBs with water, the interaction is mainly of the van der Waals type. To minimize the loss of HBs during cage formation, the water molecules rearrange spatially assuming a tangential orientation around the hydrophobic surface and the overall shape may resemble those found in clathrate hydrates.^30–35 If the cage is not static, it fluctuates around some “optimal” configurations nonetheless.

In light of these ideas, a large number of clathrate-like structures have been recently proposed for the very first water shell around hydrocarbons and the side chain of aliphatic amino acids, obtaining a reasonable comparison with the available experimental and computational data.^36,37 Furthermore, the comparison of the calculated encapsulation enthalpies (cage–host interaction) and the experimental solution enthalpies obtained at 273.25 K is particularly intriguing.³⁷ At this temperature, the thermal motion is highly damped, and the water molecule configuration should not deviate much from the tangential orientation with respect to the solute surface. Qualitatively, the experimental and computational trends are similar although the latter are always more exothermic and the difference increases as the size of the solute increases. Because the hydrocarbon insertion occurs in the already formed cage and considering the reliability of quantum chemical calculations when predicting the hydrophobe–cage electronic interactions, the observed difference has been ascribed to the unfavourable water structure reorganization upon cage formation, which causes a weakening in solvent hydrogen bonding.^38–40

This research focuses on the description of solvent reorganization extending for two layers of water molecules around the clathrate cages, which might represent the first-order model of the solvent cavity. While doing that, quantum chemical methodologies have been adopted to scrutinize structures and energies of amorphous dense clusters and clusters with clathrate-like cages of various sizes and, in particular, the undecahedron (4²5⁸6¹), dodecahedron (5¹²), tetradecahedron (5¹²6²) and hexadecahedron (5¹²6⁴). Geometry optimizations of compact structures have been performed starting from numerous low-lying and global minima reported for water clusters^41–48 thus representing the most favourable conformations in terms of electronic energy or enthalpy. Clusters with the cage were constructed assuming a symmetrical water molecule distribution around the cage attempting to maximize the HB number and minimize geometrical strains. It will be shown that models with several layers of water molecules can be built around the core cage, achieving intriguing and reliable results. Furthermore, with the aim of analysing the effect of the second shell on host–guest electronic interactions and structures, we also analysed the inclusion of methane, ethane, propane and isobutane in these clusters, along with the appropriate cages.

Due to the presence of a large amount of energetically very close structures and the ease with which these interconvert, the static approach currently adopted to describe the compact water state and cavity formation may seem too simplistic, and only the methods that hold thermal motion are significant. On the other hand, the use of quantum mechanics methodologies, that is, the natural way to describe phenomena at the atomic level, allows us to obtain homogeneous information on the totality of the hydration phenomena overcoming the transferability limit of empirical potentials normally used in molecular dynamics or Monte Carlo simulations. Thus, the dynamic studies which make use of empirical potentials and static investigation which makes use of quantum chemical potential approaches seem to be complementary and independent tools to study hydration phenomena as recognized by various authors: “the attempts to capture properties of ice and water with special cluster models for parts of the (dynamical) hydrogen bonding network are not misguided”.⁴¹

Calculation methods

The geometries were optimized using the DFT/M06-2X electronic structure method,⁴⁹ employing the 6-31+G* basis set and including implicitly solvent effects.⁵⁰ In M06-2X computations, the grid mesh in integral evaluation was settled to the “Integral (UltraFineGrid)” option. Minima were characterized evaluating the Hessian matrix and the associated harmonic vibrational frequencies. Implicit solvent effects were modelled using the polarized continuum method (PCM) adopting a 78.36 dielectric constant for water as implemented in the Gaussian09 program.⁵¹

To improve energetics and to reduce the intermolecular basis set superposition error, the single point energy evaluation at the optimized geometries was performed using the more accurate aug-cc-pVTZ basis set. The electronic energies were corrected for zero-point vibrational and thermal energies to obtain enthalpy and entropy at 273 K ( and , respectively). To calculate the entropy, , the different contributions to the partition function were evaluated by using the standard expressions for an ideal gas in the canonical ensemble, the particle in a 3-dimensional box, the harmonic oscillator, and the rigid rotor approximations.

The reliability of present M06-2X based computations has been previously evaluated using extensive traditional ab initio MP2 (and in some cases MP4-SDQ) calculations with the 6-31+G* basis set for optimization/Hessian followed by the single point aug-cc-pVTZ energy. Thus, comparable molecular properties have been reported for numerous hydrocarbon filled cages³⁷ and hydrated complexes of alanine and dialanine at both M06-2X and MP2 levels.^52,53

Results and discussion

High density amorphous clusters

Among the simple units that water molecules can form, the five-membered ring is the one that best meets the energy and geometric requirements to optimize hydrogen bonding. However, since the pentagon is the basic unit to form fractals,⁵⁴ it cannot form a regular tiling without sacrificing a considerable amount of volume, so compact clusters will also have irregular shapes containing 4- and 6-membered rings. For this reason, there is no known simple way to find a global minimum-energy structure of water clusters, even for medium size aggregates (less than 60 water molecules). The complexity of the problem increases for larger clusters since the configuration number increases exponentially as the cluster size increases and, furthermore, there are very small changes in energy among the various configurations. For larger clusters (n ∼ 300), the lowest energy structures show an incipient crystallinity with the central core consisting of “ordered” six-membered rings, while the subsurface and surface (molecules with three HBs) are disordered.^47,48 The presence of an ordered core part makes easier to find the structure global minima and has allowed a reliable study on very large clusters.

In spite of these difficulties, the global minimum structures of medium size clusters have been searched by using empirical potential functions and developing several ad hoc methodologies to probe the configurational space.^41–47 Kazachenko and Thakkar^43,44 used a hybrid scheme, which employs a minima-hopping algorithm together with an evolutionary algorithm, for the optimization of HB topologies to obtain global minima of clusters up to 55 water molecules. Using a coarse-grained representation of the potential, Farrell and Wales⁴⁵ located putative lowest energy structures for N ≤ 55 using their basin-hopping algorithm. The two methodologies reported fairly similar structures ensuring that the geometries are indeed the true global minima. These algorithms could be used for larger water clusters but authors warn that final structures could be not the true global minima. Starting from the selected clusters derived from the crystal structures of various ices followed by the relaxation procedure applying their evolutionary algorithm, and then a single local optimization, Bandow and Hartke⁴⁶ tentatively explored water clusters up to 105 molecules. A combination of temperature dependent classical trajectories, hydrogen network topology improvement and rigid body diffusion Monte Carlo was used by Kazimirski and Buch to locate the low-energy TIP4P structures for large clusters (H₂O)_n with n = 48, 123, 293, 600 and 931.^47,48

All these data allowed for the systematic study of amorphous and compact structures of variable dimensions by means of quantum chemical calculations. In order to find the most stable water cluster conformations, several forms of selected (H₂O)_n (n ranges from 18 to 123) arrangements have been optimized using the M06-2X/6-31+G*/PCM level followed by a single point energy calculation using the aug-cc-pVTZ basis set. For each cluster, the most stable structure and energetic data are shown in Fig. 1 and Table 1, while the data of other low-lying structures are shown in Fig. S1–S4 and Tables S1 (ESI†).

Fig. 1 M06-2X/6-31+G*/PCM optimized structures of the global minimum water clusters. Hydrogen atoms have been omitted for clarity and the sticks represent the O–H bonds involved in hydrogen bonding. The full solvated molecules are indicated with blue oxygens.

Table 1 Average coordination number (c.n.) of water, interaction electronic energy and enthalpy per water molecule

	Label	c.n.	E int/n
(H2O)18 Pentagonal prism and cubes	18A	3.44	−11.62	−9.83
(H2O)20 Edge-sharing prisms	20A	3.40	−11.64	−9.90
(H2O)24 One internal molecule	24A	3.33	−11.87	−10.17
(H2O)28 Two internal molecules	28A	3.43	−12.10	−10.35
(H2O)34 Three internal molecules	34A	3.53	−12.18	−10.38
(H2O)35 Two internal molecules	35A	3.54	−12.23	−10.43
(H2O)45 Five internal molecules	45A	3.60	−12.40	−10.57
(H2O)52 Seven internal molecules	52A	3.54	−12.50	−10.72
(H2O)55 Nine internal molecules	55A	3.60	−12.53	−10.74
(H2O)123 33 internal molecules	123	3.67	−12.66	−10.81

---

The global minimum of the (H₂O)₁₈ cluster consists of one pentagonal prism and two cubes (Table 1 and Fig. 1). At 1.6 kcal mol⁻¹ above the global minimum, the edge-sharing pentagonal prism with two fused cubes and the irregular prism with two cubes are observed, while at 3.3 kcal mol⁻¹ the 3-stacked hexagonal prism is observed (Table S1 and Fig. S1, ESI†). The lowest minimum found for the (H₂O)₂₀ cluster consists of 3-edge-sharing pentagonal prisms, 20A. However, close in energy, we found the 2-face-sharing pentagonal prisms fused with a cube (20B) and the 3-face-sharing pentagonal prisms (3-stacked pentagonal prisms 20C, Table S1 and Fig. S1, ESI†).

These results agree with previous findings which suggest that for small clusters the most common rings are pentagons and squares, while hexagonal structures are energetically disadvantaged. As the size of the cluster increases, the energetically favoured geometries show one water molecule completely solvated by others. Thus, for the (H₂O)₂₄ cluster, three structures with one internal solvated water molecule have been found at low energy (24A, B and C) and the geometries resemble a water-centred cage complemented with a 4-, 5- or 6- membered ring (Table S1 and Fig. S1, ESI†). A structure with all surface molecules, i.e. the pentagonal prism/cube configuration, 24D, is located at 2 kcal mol⁻¹ above in energy.

As the cluster size increases, the number of internally solvated molecules increases. The most stable structures of (H₂O)₂₈, (H₂O)₃₄, (H₂O)₃₅, and (H₂O)₄₅ show 2, 3, 2, and 5 fully hydrated molecules, respectively, while structures with less internally solvated molecules lie at higher energies (Table S1 and Fig. S2 and S3, ESI†). Once the size exceeds 50 water molecules, fully solvated six-membered rings appear and branched hexagons (with 8 and 9 molecules) are found in the inner cores of the (H₂O)₅₂ and (H₂O)₅₅ clusters (Fig. 1 and Fig. S3, S4, ESI†). These structures take a spheroidal shape and the five- and six-membered rings become the most common.

For the (H₂O)₁₂₃ cluster, ten structures have been proposed by Kazimirski and Buch⁴⁷ as the possible candidate for the global minimum. The most stable structure has a nearly spherical shape with 33 internal molecules and only one molecule bicoordinate on the surface (Fig. 1 and Table 1); therefore, it should be close enough to the global minimum.

The computed electronic interaction energy and enthalpy at 273.15 K per molecule (E_int/n and 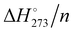) for the global minimum of the currently studied clusters are shown in Fig. 2 together with the energy values reported by Kazachenko and Thakkar⁴³ using five interaction potential energy models (TIP4P, AMOEBA, TIP4P-Ew, TIP4P/2005 and TTM2.1-F) for clusters up to (H₂O)₅₅. For the TIP4P potential, they reported some extrapolated interaction energies for n = 80, 100 and 123. Both E_int/n and show a monotonic increase of exoenergeticity for clusters up to n = 55 for which the global minimum is well established. (H₂O)₁₂₃ also shows an increment of the exoenergeticity (–0.1 kcal mol⁻¹). However, it is rather modest considering the cluster size variation, thus indicating that structures reported by Kazimirski and Buch are local minima rather than global minima. An estimation on the energy difference between these structures and the global minimum has been reported by Kazachenko and Thakkar extrapolating data on clusters up to n = 55.⁴³ Depending on the extrapolation technique, they reported a shift in the 0.1–0.5% range, i.e. 0.06–0.23 kcal mol⁻¹ on the E_int/n value. The shift is small but not negligible; however, the structures reported by Kazimirski and Buch for the (H₂O)₁₂₃ cluster are the best available in the literature and they are used here as a reference.

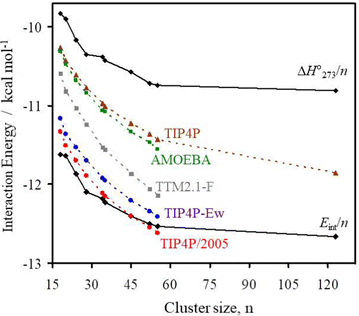Fig. 2 M06-2X/aug-cc-pVTZ/PCM interaction electronic energies and enthalpy per water molecule (E_int/n and , solid lines) of the global minimum clusters. Dashed lines are the interaction energies of the TIP4P (brown), AMOEBA (green), TTM2.1-F (grey), TIP4P-Ew (blue), and TIP4P/2005 (red) empirical potentials from ref. 43.

The M06-2X/PCM computed energy and enthalpy trends are similar to that obtained by Kazachenko and Thakkar with the five potentials;⁴³ however, the curve positions are rather different. The TIP4P/2005 curve almost overlaps with the present calculated E_int/n, while the TIP4P-Ew curve lies 0.1–0.2 kcal mol⁻¹ at higher energy. The TIP4P/2005 potential has been parametrized on a fit of the temperature of maximum density and the stability of several ice polymorphs.⁵⁵ Therefore, the similarity with the present motionless quantum chemical results appears plausible. The TTM2.1-F potential has been derived from high level electronic structure computations of small clusters⁵⁶ and should be close to current calculations, instead the TTM2.1-F curve lies 0.8 kcal mol⁻¹ higher in energy. The small size of clusters used in the TTM2.1-F parametrization produces strained HBs and few or no tetracoordinate water molecules. Instead, large clusters have tri- and four-coordinated molecules, and thus, the hydrogen bonding synergy increases enhancing the overall water–water interactions. The TIP4P and AMOEBA energies are close to each other, and they are the smallest in magnitude. The TIP4P potential was parametrized to obtain the enthalpy of liquid water at 300 K,⁵⁷ the zero-point energy and thermal effects are effectively included in the model potential and actually they are the closest to the values.

In terms of binding energy, it is clear that the various model potentials show differences that reflect the way in which they were generated. However, the global minima, found for each of the five potentials, have very similar shapes and comparable stability (Table S1, ESI†), i.e. the global minimum structures are barely influenced by the model potentials.^43,45

The accurate thermal measurements on the gas-phase water molecule assembly in the hypothetical I_h ice at 0 K indicate a release of −11.3 kcal mol⁻¹ of heat (Table 2).^58,59 This energy is mainly related to the electronic stabilization of molecules in the formation of ice (the well bottom of the ice lattice) and to a secondary contribution due to the change in the vibrational state of the molecules, the zero-point energy (ZPE), as clarified in the following:

Ice deposition energy = (E_int + ZPE_intermol + ΔZPE_intramol)/n

Table 2 Energies (kcal mol⁻¹) of the ice I_h relative to vapour and related quantities derived from the (H₂O)₅₅ and (H₂O)₁₂₃ clusters

	(H2O)55	(H2O)123	Experiments
a Ref. 58. b Ref. 59. c Ref. 60. d Ref. 63.
Ice deposition energy, 0 K	−9.78	−9.85	−11.3^a	−11.3^b
Interaction electronic energy	−12.53	−12.66	−13.4^a	−14.0^b
Intramolecular ZPE difference	−0.95	−0.94	−1.4^a	−1.2^b
Intermolecular ZPE	+3.69	+3.75	+3.5^a	+3.9^b
ZPE difference	+2.75	+2.81	+2.1^a	+2.7^b
Ice deposition enthalpy,	−10.74	−10.81	–12.2^c
(ice)	10.17	9.56	8.3^d
(gas)			44.4^d

---

The intermolecular ZPE arises from the “transformation” of rotational and translational motions into vibrations upon vapour molecules quenching in ice, while the intramolecular difference ZPE mainly comes from the perturbations of water molecule vibrational frequencies. These contributions were estimated using Einstein and Debye distributions for the intramolecular and intermolecular vibrations, respectively, and, depending on the experimental vibrational frequencies adopted, two sets of ZPE and electronic energy have been reported by Whalley^58,59 (Table 2). Although the structure and the mean coordination number of the molecules in the largest (H₂O)₅₅ and (H₂O)₁₂₃ clusters presently considered differ from those of the I_h ice, the energy comparison could be fruitful. Both experiments and computations reveal that the intramolecular and intermolecular ZPE contributions have opposite signs and partially cancel. Furthermore, the intramolecular energy mainly comes from the perturbations induced to the stretching modes (ν₁ and ν₃) while the contribution of the bending (ν₂) is rather small. The computed electronic energy is close enough to the experimental estimation and the difference (∼1 kcal mol⁻¹) could be related to both the limited size of the cluster and the presently adopted electronic structure method.

The sublimation enthalpy of the ice I_h between 0 and 273.16 K has been tabulated by Feistel and Wagner⁶⁰ and considering that the enthalpy of transition I_h ice to the amorphous ice is small (∼0.3 kcal mol⁻¹),⁶¹ it is possible to compare the experimental deposition enthalpy at 273 K with the present estimation (Table 2). Both the computation and experimental data show an increment of exothermicity (∼0.9 kcal mol⁻¹) upon increasing the temperature from 0 K to 273 K; thus, the statistical thermodynamic approach adopted here reproduces the thermal motion features occurring in the water deposition.

The absolute standard entropy at 273.15 K per molecule, , of the analysed amorphous clusters (Fig. 3) shows a progressive reduction as the size increases and for the (H₂O)₅₅ and (H₂O)₁₂₃ clusters it reaches 10.17 and 9.56 cal K⁻¹ mol⁻¹ values, respectively. As the number of molecules forming the cluster increases, the efficiency of the packing improves, the average coordination number of water molecules increases and the system tends towards a more ordered state with a low absolute entropy value. Considering that the entropy variation for the ice I_h transformation to low- or high-density amorphous ices is rather modest (0.24 and 0.5 cal K⁻¹ mol⁻¹),⁶² the computed for the (H₂O)₁₂₃ cluster can be compared with the experimental value obtained for the I_h ice 8.3 cal K⁻¹ mol⁻¹. This value has been estimated using the experimental 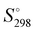and the heat capacity of the ice (9.08 and 9.1 cal K⁻¹ mol⁻¹, respectively)⁶³ by the following relationship

Fig. 3 M06-2X/6-31+G*/PCM absolute entropy per water molecule () of the global minimum clusters.

In spite of the simplicity of the statistical thermodynamic treatment and limitations of the cluster approach, the experiment and computation are numerically comparable 8.3 vs. 9.56 cal K⁻¹ mol⁻¹. To this end, it is also worth mentioning that the entropy of the single water molecule (44.4 cal K⁻¹ mol⁻¹) coincides exactly with the experimental value of gas at 273 K, 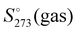, computed by the relationship

Not only does the proposed methodology allow for a reasonable estimation of the interaction energy, which is generally the most reliable thermodynamic parameter derived from quantum mechanical calculations, but also provides reliable data on the thermal motion effects in ice and entropy through standard statistical thermodynamic treatments.

Clusters with a cage

The clathrate-like cages, which have been proposed as idealized structures to host hydrophobic molecules, show that each water molecule forms three HBs, a number considerably lower than that found for the compact structures described above. However, they have n/2 dangling hydrogen atoms and n/2 dangling oxygen lone pairs that point toward the external side of the cage volume and can be involved in hydrogen bonding with successive water layers to reduce this energetic penalty. To this purpose, the evaluation of the second hydration shell around the (H₂O)_n (n = 18, 20, 24 and 28) cages was attempted in this section (Fig. 4–6). In the present analysis, the chosen hydrogen configurations of the (H₂O)₂₀ and (H₂O)₂₄ cages result in the C_i and C₃ symmetries, respectively.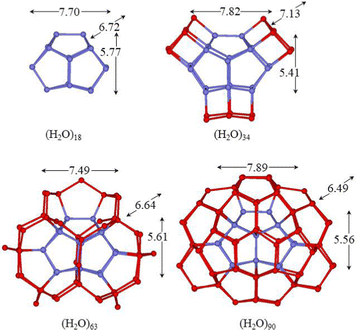

Fig. 4 M06-2X/6-31+G*/PCM optimized structures of the clusters with the hollow undecahedron (H₂O)₁₈ cage. Hydrogen atoms have been omitted for clarity and the sticks represent the O–H bonds.

Fig. 5 M06-2X/6-31+G*/PCM optimized structures of the clusters with the hollow dodecahedron (H₂O)₂₀ cage. Hydrogen atoms have been omitted for clarity and the sticks represent the O–H bonds.

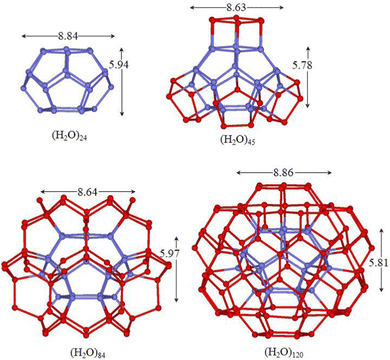Fig. 6 M06-2X/6-31+G*/PCM optimized structures of the clusters with the hollow tetradecahedron (H₂O)₂₄ cage. Hydrogen atoms have been omitted for clarity and the sticks represent the O–H bonds.

A first approach to construct the second shell around cages would be the use of automatic algorithms to find the global electronic energy minimum by fixing the core of the hollow cage and surrounding it with a discrete number of molecules. However, because of the high tendency of water molecules to agglomerate, this would not result in a symmetric distribution of water molecules around the cage; as one would expect, rather, it will result in the formation of structures in which a dense cluster develops on one side of the cage.⁶⁴ It is much more practical to use a heuristic approach by exploiting the symmetry of the cages to construct the second coordination sphere.

The simplest way to saturate a large part of the dangling HBs of the hollow cages consists of the capping distal square, pentagonal and hexagonal faces with the square, and pentagonal and hexagonal water rings, respectively. For the 4²5⁸6¹, 5¹², 5¹²6², and 5¹²6⁴ cages, this procedure results in the formation of the (H₂O)₃₄, (H₂O)₃₅, (H₂O)₄₅ and (H₂O)₅₂ clusters, with a roughly symmetric molecule distribution around the cages (Fig. 4–7). A considerable number of HBs are formed and a significant interaction energy gain per particle is obtained. Although the number of HBs is similar to that obtained for the related global minimum, these structures are less stable (Tables 1 and 2) because of the high deviations from tetrahedrality around oxygens that form square faces.

Fig. 7 M06-2X/6-31+G*/PCM optimized structures of the clusters with the hollow hexadecahedron (H₂O)₂₈ cage. Hydrogen atoms have been omitted for clarity and the sticks represent the O–H bonds.

A more useful way to construct a suitable second hydration shell is to devise a pentagonal ring on each of the edges of the cage, thus each dangling HBs of the cage is saturated with a water molecule and in turn they form a bridge. The spheroidal shape maximizes the cohesive force of the cluster and the second sphere exerts the symmetrical “pressure” on the cage surface. With this tessellation, the 4²5⁸6¹, 5¹², 5¹²6², and 5¹²6⁴ cages form the following clusters (H₂O)₆₃, (H₂O)₇₀, (H₂O)₈₄, and (H₂O)₉₈ (Fig. 4, 6 and 7), respectively. For the dodecahedron, the tessellation with pentagons is rather strained, and an HB breaks during the geometry optimization; thus, an extra water molecule is added to form a hexagon, giving rise to the (H₂O)₇₁ cluster (Fig. 5). The second sphere network is similar to that found around the cages of clathrate hydrates;⁶⁵ however, in these cases, some pentagons are replaced by hexagons. There are 2n tetracoordinate water molecules and (n + n_faces − 2) bicoordinate water molecules for all structures, but for (H₂O)₇₁, where the bicoordinate molecules are (n + n_faces − 1). The presence of a high number of bicoordinated water molecules implies a reduced stability of the clusters. In fact, an increase of E_int/n is observed compared to the previous proposed modelling (Table 3). In these clusters, the molecules are arranged in three concentric shells and for example in the (H₂O)₉₈ cluster they are roughly at 4.59, 7.34 and 8.59 Å from the centroid of the hexadecahedron. The average O⋯O⋯O hydrogen bond angles of bicoordinate molecules for the (H₂O)₆₃ and (H₂O)₇₁ clusters (116.4° and 114.0°, respectively) differ from the optimal value in the pentagon (107.7°), thus indicating a strain on tessellation. For the (H₂O)₈₄ and (H₂O)₉₈ clusters, the curvature of the cage decreases, and tessellation with pentagons can be achieved with very modest strain for both the tetradecahedron and hexadecahedron (the mean angles are 110.1° and 106.8°, respectively). This reflects the energy gain (E_int/n) as the size of the cage increases for this kind of clusters (Table 3).

Table 3 Average coordination number of water, distances between the cage centroid and oxygen atoms (Å), electronic interaction energy and enthalpy per water molecule and cavitation energies (kcal mol⁻¹)

	c.n.	Ocentr–O	E int/n		ΔEc	ΔHc
(H2O)18	3.00	3.69	−11.26	−9.64	6.4	3.4
(H2O)34	3.47	3.67	−11.89	−10.15	9.6	7.8
(H2O)63	3.14	3.61	−11.75	−10.09	50.9	41.7
(H2O)90	3.40	3.64	−12.25	−10.48	33.7	27.7
(H2O)20_Ci	3.00	3.87	−11.33	−9.70	6.2	3.0
(H2O)35	3.43	3.83	−11.96	−10.20	6.2	8.1
(H2O)71	3.13	3.79	−11.87	−10.20	50.5	40.4
(H2O)100_Ci	3.40	3.81	−12.46	−10.70	17.2	9.3
(H2O)24_C3	3.00	4.26	−11.38	−9.74	11.9	10.2
(H2O)45_C3	3.47	4.23	−12.10	−10.34	13.3	10.2
(H2O)84_C3	3.14	4.21	−11.96	−10.27	54.8	43.0
(H2O)120_C3	3.40	4.25	−12.41	−10.64	29.8	20.6
(H2O)28	3.00	4.61	−11.36	−9.74	20.6	17.3
(H2O)52	3.33	4.58	−12.11	−10.38	20.1	18.1
(H2O)98	3.14	4.59	−11.97	−10.26	64.6	51.8
(H2O)140	3.40	4.62	−12.41	−10.64	36.5	24.5

---

Another way to obtain appropriate layers of molecules around cages was proposed by Chaplin⁶⁶ two decades ago for the dodecahedron and successively extended to a large variety of cages.^1,67 In this tessellation, an appropriate number of a 14-molecule building block with a slightly flattened tetrahedral shape is arranged around the cage to form an extended and regular hydrogen bonding network. The number of 14-molecule units, required to make a hollow cage, is equal to the number of molecules present in the cage, thus leading to the formation of the (H₂O)₂₅₂, (H₂O)₂₈₀, (H₂O)₃₃₆ and (H₂O)₃₉₂ clusters for the 4²5⁸6¹, 5¹², 5¹²6², and 5¹²6⁴ cages, respectively. The size of these clusters makes the quantum mechanical study prohibitive. However, it is possible to remove the outermost shells maintaining a symmetric distribution of molecules around the cage without the formation of bicoordinate molecules on the surface. This type of water assembly has been extensively discussed by Müller et al. for the (H₂O)₂₈₀ cluster in which the depletion leads to the formation of the (H₂O)₁₀₀ cluster (Fig. 5).⁶⁸ Furthermore, this well-organized water arrangement has been characterized by X-ray diffraction in the cavity of a spherical polyoxomolybdate cluster of the type {(Mo)Mo₅}₁₂(spacer)₃₀.⁶⁹ In this cluster, the molecules are arranged in three concentric shells with radii of 3.84–4.04, 6.51–6.83 and 7.56–7.88 Å spanned by 20, 20, and 60 molecules, respectively. The core dodecahedron is linked to the external (H₂O)₆₀ rhombicosidodecahedron through the intermediate dodecahedral shell, in which each connects the molecules from three different pentagons of the third shell with one molecule of the central dodecahedron. The molecules of the core and the intermediate dodecahedrons realize the four-fold coordination, while the rhombicosidodecahedron surface molecules are tricoordinate; thus the average coordination number of HBs in the cluster is of 3.4. This type of structure can also be achieved for the 4²5⁸6¹, 5¹²6², and 5¹²6⁴ cages leading to the (H₂O)₉₀, (H₂O)₁₂₀ and (H₂O)₁₄₀ clusters, respectively, maintaining the same average coordination number of HBs of 3.4 per molecule (Fig. 4, 6 and 7).

For the (H₂O)₁₀₀ cage, various hydrogen bonding topologies have been considered and, among them, the structure with C_i symmetry proposed by Lenz and Ojamäe⁷⁰ was found to be the most stable, while that reported by Lobota and Goncharuk⁷¹ was found to be 7 kcal mol⁻¹ higher in energy. In the latter structure, the pentagons at the top and bottom of the cage (Fig. 1 in ref. 71) show all molecules in the double-acceptor, single-donor (AAD) energetically unfavourable configuration. Therefore, for the construction of the other clusters, it is appropriate to keep in mind that, for the tricoordinate molecules located on the cluster surface, it is necessary to alternate AAD and ADD hydrogen topologies as much as possible and to minimize the number of consecutive AAD or ADD in order to improve the hydrogen bonding cooperativity.⁴³

In the (H₂O)₁₀₀ cluster, the average distances of the three layers of molecules from the centroid of the dodecahedron are 3.81, 6.53 and 7.77 Å with a sharp distribution and they are quite close to the X-ray diffraction average values (3.94, 6.67 and 7.72 Å).⁶⁹ The average O⋯O separation between hydrogen bonded molecules of the core and intermediate dodecahedrons (2.72 Å) is slightly shorter than those of the intermediate and surface layers (2.77 Å). In the former, all molecules are in the optimal tetrahedral four-fold coordination, while in the latter also tricoordinate molecules are involved, emphasizing the importance of synergy in the HB strength. The mean O_cent–O distances of the core cage always decrease as the second coordination shell is formed; however, the reduction is small and never exceeded 0.07 Å. The reduction is mainly due to the three-fold to four-fold change in the hydrogen bonding state of molecules of the core cage, which strengthen HBs with the consequent reduction of O–H⋯O bond distances. The rhombicosidodecahedron surface is formed exclusively by the optimal five membered rings with mean O⋯O⋯O angles of about 108°, while the angles of the boat-hexamer that connect two pentamers show small deviations from the favourable value of the isolated (H₂O)₆-boat conformation (111.2° vs. 109.3°, respectively). Overall, (H₂O)₁₀₀ does not present any significant strain.

Similar arguments show that (H₂O)₁₂₀ and (H₂O)₁₄₀ do not present significant strain in O⋯O⋯O angles on the surface molecules; therefore, the tessellation proposed for the 5¹²6² and 5¹²6⁴ cages is satisfactory. For example, the angles of the pentagons and planar hexagons are about 107.9° and 120°, while the angle of the boat-hexagons is 110 ± 5°, all quite close to the values of isolated rings (107.7°, 120° and 109.3°, respectively). Because of the oblate spheroid shape, two sets of concentric oxygen layers are found for the (H₂O)₁₂₀ cluster (4.01, 6.75, 7.68 and 4.49, 7.23, 8.5 Å) while for the (H₂O)₁₄₀ cluster the three concentric spheres of oxygen are placed at about 4.6, 7.4, and 8.9 Å.

For the cluster (H₂O)₉₀, the small height of the core 4²5⁸6¹ cage (5.77 Å, Fig. 4) infers a high curvature to the cluster surface and the construction of successive water layers with the adopted scheme forms O⋯O⋯O angles of the boat-hexagons much larger (up to 139.1°) than the optimal value of 109.3°. This indicates a structural strain and the proposed tessellation is not adequate to wrap small cages. These structural features are reflected in the electronic interaction energy per molecule (Table 3); thus the cluster stability follows the order of

(H₂O)₁₀₀ > (H₂O)₁₂₀, ∼ (H₂O)₁₄₀ > (H₂O)₉₀.

Finally, it is worth noting that several studies reported significant molecular orientational preferences that extend up to 8 Å into the liquid.^72,73 For instance, the first methane hydration shell contains 19–20 water molecules, while the second shell contains ∼70 water molecules; thereafter, it is impossible to identify additional well-defined shells.⁷²

Cage formation energies

Energies of highly compact amorphous clusters and cage-clusters can be tentatively used to analyse the energetics of the cavitation process which occurs when a hydrophobe dissolves in water. For clusters up to 52 molecules, a direct comparison of the thermodynamic quantities of dense and cage-clusters is possible, while the absence of a reliable global minimum for compact clusters, formed by 63, 71, 84, 90, 98, 100, 120 and 140 water molecules, hampers it. The E_int/n and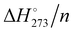 quantities obtained for the (H₂O)₅₅ global minimum and for (H₂O)₁₂₃, which is close to the global minimum, show a modest variation (Table 1). Therefore, data derived from these clusters can be taken as a reference to interpolate and extrapolate the thermodynamics of the global minima of unavailable compact clusters. To this purpose, the following linear equations were used:

E (hartree) = −76.4503350n + 0.019065

The formation of bare cages from the related global minimum requires about the same electronic energy (ΔE_c ∼ 6.3 kcal mol⁻¹, Table 3) for the (H₂O)₁₈ and (H₂O)₂₀ clusters, while it increases for larger clusters (11.9 and 20.6 kcal mol⁻¹ for n = 24 and 28, respectively). This trend reflects the significant loss of HBs as the size of the cage increases. The partial capping of the cages with pentagons and hexagons increases the energy and enthalpy required for the formation of the cages relative to the global minimum (Table 3). The cavitation energies show a huge increment when tessellation with pentagons and they reflect the low stability caused by the large number of bicoordinate molecules on the surface. In all cases, the larger tessellation reduces the electronic energy penalty in the cage formation, even though it remains rather high (Table 3). The ZPE correlates negatively with the electronic energy; thus, its inclusion reduces the energy penalty. The geometrical rearrangement of amorphous clusters to generate the 5¹², 5¹²6² and 5¹²6⁴ cages in the largest tessellation requires enthalpies of 9.3, 20.6, and 24.5 kcal mol⁻¹, respectively. These values are large compared with the solvent reorganization contribution to the enthalpy of small hydrocarbon solutions reported by Levy et al.³⁸ from Monte Carlo simulations at 298 K (CH₄ = 1.3, C₂H₆ = 2.3, and C₃H₈ = 3.3, kcal mol⁻¹, which have primary coordination numbers of 20.3, 23, and 27.3, respectively). The values of Levy et al.³⁸ are similar to the solvent reorganization enthalpy estimated as the difference between the experimental solution enthalpy and the computed encaging enthalpy (roughly 1, 2 and 4 kcal mol⁻¹ for the 5¹², 5¹²6² and 5¹²6⁴ cages, respectively).³⁷

Although the simplicity of the (H₂O)₁₀₀, (H₂O)₁₂₀ and (H₂O)₁₄₀ clusters are appealing in forming suitable shells for the 5¹², 5¹²6² and 5¹²6⁴ cages, the average water coordination number (3.40) is rather small if compared to that obtained for the (H₂O)₁₂₃ compact cluster (3.67) and an extra effort is needed to obtain more representative models. The first attempt involves the inclusion of an additional water layer, the (H₂O)₂₈₀, (H₂O)₃₃₆ and (H₂O)₃₉₂ clusters, for which the average water coordination number reaches 3.57. It is well known that although the reorganization energy of the solvent is small, the local structuring of the solvent requires a collective and longer-range reorientation to preserve hydrogen bonding;^72,73 thus a single water shell around the 5¹², 5¹²6² and 5¹²6⁴ cages is not enough to account for solvent reorganization. The second issue concerns the density. The (H₂O)₁₀₀, (H₂O)₁₂₀ and (H₂O)₁₄₀ structures in some way resemble those found in clathrate hydrates, because over each pentagonal and hexagonal faces there are hollow boxes with radii of ∼3.4 Å and ∼3.8 Å, respectively (Fig. 8). The radii of these boxes are 0.4 Å smaller than those found in the 5¹² and 5¹²6² cages; thus their density is greater than that found in the sI clathtrate hydrate. Also, liquid water presents a significant fraction of void volume. However, it is partitioned in very small cavities, less than 0.5 Å radius;⁷⁴ thus its density is greater than the analysed cage-clusters so far. Some energy gain could be obtained considering more compact structures over the surface of the 5¹², 5¹²6² and 5¹²6⁴ cages. Both topics are important; however, at present, their treatment is very complex and requires enormous computational efforts.

Fig. 8 Detailed features of the (H₂O)₁₂₀ cluster structure with the tetradecahedron 5¹²6² cage (blue). The red oxygens show the hollow boxes over pentagonal and hexagonal faces.

Clusters with filled cages

With the aim of analysing the effect of successive water layers on hydrocarbon enclathration, the cage of some bare and solvated clusters has been filled with methane, ethane, propane and isobutane. Some geometrical parameters and energetic results are reported in Table 4, while structures are shown in Fig. S5 and S6 (ESI†).

Table 4 M06-2X average distance between the cage centroid and oxygen atoms and cage centroid and alkane centroid (Å), electronic energy and enthalpy (kcal mol⁻¹) variations for alkane encapsulation

	Ocentr–O	Ocentr–Ccentr	ΔE
CH4@(H2O)18	3.67	0.19	−7.2	−5.1
CH4@(H2O)34	3.66	0.19	−7.9	−5.9
CH4@(H2O)63	3.59	0.12	−8.1	−6.3
CH4@(H2O)20	3.84	0.12	−6.7	−5.2
CH4@(H2O)35	3.82	0.10	−7.1	−5.7
CH4@(H2O)71	3.78	0.21	−7.7	−6.4
C2H6@(H2O)24	4.23	0.50	−8.2	−6.3
C2H6@(H2O)45	4.21	0.85	−9.6	−8.2
C3H8@(H2O)28	4.59	0.87	−10.0	−7.8
C3H8@(H2O)52	4.56	0.79	−10.6	−8.8
i-C4H10@(H2O)28	4.59	0.77	−13.9	−11.3
i-C4H10@(H2O)52	4.57	0.81	−14.1	−11.6

---

All the cages are slightly perturbed by the inclusion of the guest molecule and, due to the attractive host–guest van der Waals interactions, the (O)_centr⋯O distances undergo minor contractions (<0.03 Å) with respect to hollow cages (Tables 3 and 4). The methane is close to the oxygen centroid in both undecahedron and dodecahedron cage clusters, while ethane (in the tetradecahedron cages) and propane and isobutane (in the hexadecahedron) significantly displace from the oxygen–centroid of the cage (Table 4). Thus, to maximize van der Waals interactions, these hydrocarbons move toward one side of the internal wall of the cages. As far as the energetic trend, the most important aspect concerns the modest increase of the exothermicity as the second water molecule layer is included. The long-range attractive van der Waals interaction goes beyond the very first hydration shell, and for methane an energy gain of about 1 kcal mol⁻¹ (∼15% of overall interaction) is obtained for both the 4²5⁸6¹ and 5¹² cages. For ethane encapsulation, the increment in the interaction energy is rather noticeable (about 2 kcal mol⁻¹, ∼20%), while for propane and isobutane it is rather modest (∼10% and ∼2%, respectively). Propane and isobutane move toward one side of the internal wall of the 5¹²6⁴ cage (∼0.8 Å away from the O_centr) and probably they lose a large part of the favourable van der Waals interaction with the second water molecule layer. For instance, the optimal cage to host propane was predicted to be the smaller pentadecahedron, 5¹²6³, one.³⁷

The energy gain due to the second water layer on the overall solute–solvent interaction is modest; nevertheless, it is significant in the delicate balance between the enthalpy and entropy contributions to the Gibbs free energy associated with hydrophobic hydration phenomena.

Conclusions

In the current research, the cluster approach along with electronic structure methods has proven to be a fairly reliable, useful tool to study some aspects of condensed states of water and hydrophobic hydration phenomena. Thus, geometries and energies of high-density amorphous clusters and of clusters with a clathrate-like cage of various sizes have been computed using ab initio calculations.

The computed electronic and zero-point energies for the formation of the largest and dense (H₂O)₁₂₃ cluster (−12.7 and +2.8 kcal mol⁻¹ per molecule) agree well with those derived from accurate thermal measurements on the gas-phase water molecule assembly in the hypothetical I_h ice at 0 K (−14.0 and +2.7 kcal mol⁻¹). The molecular properties derived from electronic structure theory together with a simple statistical thermodynamic approach accurately reproduce the measured increment of exothermicity (−0.9 kcal mol⁻¹) in the deposition enthalpy of ice upon increasing the temperature from 0 K to 273 K. A favourable experiment/computation comparison is also obtained for the absolute standard entropy of clusters and ice at 273 K (8.3 vs. 9.56 cal K⁻¹ mol⁻¹ per molecule). These are important results for the water cluster modeling and offer a solid basis for further upscaling and for the computation capture of reliable data not experimentally derivable otherwise.

Some intuitive water layers around the (H₂O)_n (n = 18, 20, 24 and 28) hollow cages have been proposed to model, in a step-like manner, the configuration of water molecules beyond those constrained in the very first shell around hydrophobes. The large (H₂O)₁₀₀, (H₂O)₁₂₀ and (H₂O)₁₄₀ clusters present optimal and regular HB tiling around the do-, tetra- and hexa-decahedron hollow cages, respectively. The proposed tessellation could be extended to the tri-, penta-, and hepta-decahedron hollow cages with negligible structural strain. These clathrate-like structures are an ideal representation of how water molecules rearrange themselves as a result of hydrophobic solute restrictions. There are several studies that report the significant molecular orientational preferences that extend up to 8 Å into the liquid while for the methane the well-defined shell comprises ∼90 water molecules.^72,73

The energies of dense and cage clusters were used for a tentative estimation of solvent reorganization energy upon cavity formation. In agreement with the current view, cavity formation is an endothermic process; however, the computed values are quite large compared with the solvent reorganization contribution to the enthalpy of the solution of small hydrocarbons reported by Levy et al.⁴¹ from Monte Carlo simulations at 298 K. This shortcoming is probably due to the limited number of water molecules in the clusters with the cage, i.e. a much thicker water layer is needed to minimize the artefact due to the absence of bulk water beyond the water shell on the primary solvent sphere.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by Università di Catania. Open access funding was provided by Università degli Studi di Catania within the CRUI-CARE Agreement. I cordially thank Prof. Udo Buck and Dr Bernhard Bandow (Max-Planck-Institut Göttingen, Germany), and Prof. Sigurd Bauerecker (Technische Universität Braunschweig, Germany) for providing the Cartesian coordinates of structures reported in ref. 46–48.

References

1. M. F. Chaplin, https://water.lsbu.ac.uk/water/, 2022.
2. C. G. Salzmann, J. S. Loveday, A. Rosu-Finsen and C. L. Bull, Structure and nature of ice XIX, Nat. Commun., 2021, 12, 3162.
3. H. S. Frank and W.-Y. Wen, Structural aspects of ion-solvent interaction in aqueous solutions: A suggested picture of water structure, Discuss. Faraday Soc., 1957, 24, 133–140.
4. H. J. Bakker and J. L. Skinner, Vibrational spectroscopy as a probe of structure and dynamics in liquid water, Chem. Rev., 2010, 110, 1498–1517.
5. G. Hura, D. Russo, R. M. Glaeser, T. Head-Gordon, M. Krack and M. Parrinello, Water structure as a function of temperature from x-ray scattering experiments and ab initio molecular dynamics, Phys. Chem. Chem. Phys., 2003, 5, 1981–1991.
6. E. Brini, C. J. Fennell, M. Fernandez-Serra, B. Hribar-Lee, M. Luksič and K. A. Dill, How water's properties are encoded in its molecular structure and energies, Chem. Rev., 2017, 117, 12385–12414.
7. E. T. J. Nibbering and T. Elsaesser, Ultrafast vibrational dynamics of hydrogen bonds in the condensed phase, Chem. Rev., 2004, 104, 1887–1914.
8. A. K. Soper, The radial distribution functions of water and ice from 220 to 673 K and at pressures up to 400 MPa, Chem. Phys., 2000, 258, 121–137.
9. P. D. Fleming and J. H. Gibbs, An adaptation of the lattice gas to the water problem. II. Second-order approximation, J. Stat. Phys., 1974, 10, 351–378.
10. W. T. King and R. E. Barletta, Oxygen isotope fractionation in H₂O and the structure of liquid water, J. Chem. Phys., 1977, 67, 180–188.
11. A. Geiger, F. H. Stillinger and A. Rahman, Aspects of the percolation process for hydrogen-bond networks in water, J. Chem. Phys., 1979, 70, 4185–4193.
12. M. B. de Kock, S. Azim, G. H. Kassier and R. J. D. Miller, Determining the radial distribution function of water using electron scattering: A key to solution phase chemistry, J. Chem. Phys., 2020, 153, 194504.
13. L. B. Skinner, C. J. Benmore, J. C. Neuefeind and J. B. Parise, The structure of water around the compressibility minimum, J. Chem. Phys., 2014, 141, 214507.
14. V. Holten and M. A. Anisimov, Entropy-driven liquid–liquid separation in supercooled water, Sci. Rep., 2012, 2, 713.
15. Y. Liu, J. C. Palmer, A. Z. Panagiotopoulos and P. G. Debenedetti, Liquid-liquid transition in ST2 water, J. Chem. Phys., 2012, 137, 214505.
16. J. Russo and H. Tanaka, Understanding water's anomalies with locally favoured structures, Nat. Commun., 2014, 5, 3556.
17. P. H. Poole, F. Sciortino, U. Essmann and H. E. Stanley, Phase behaviour of metastable water, Nature, 1992, 360, 324–328.
18. G. A. Appignanesi, J. A. Rodriguez Friz and F. Sciortino, Evidence of a two-state picture for supercooled water and its connections with glassy dynamics, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 29, 305–310.
19. K. T. Wikfeldt, A. Nilsson and L. G. M. Pettersson, Spatially inhomogeneous bimodal inherent structure of simulated liquid water, Phys. Chem. Chem. Phys., 2011, 13, 19918–19924.
20. C. Huang, K. T. Wikfeldt, D. Nordlund, U. Bergmann, T. McQueen, J. Sellberg, L. G. M. Pettersson and A. Nilsson, Wide-angle X-ray diffraction and molecular dynamics study of medium-range order in ambient and hot water, Phys. Chem. Chem. Phys., 2011, 13, 19997–20007.
21. T. Head-Gordon and M. E. Johnson, Tetrahedral structure or chains for liquid water, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7973–7977.
22. Y. Marcus, Effect of Ions on the Structure of Water: Structure Making and Breaking, Chem. Rev., 2009, 109, 1346–1370.
23. P. Ball, Water is an active matrix of life for cell and molecular biology, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13327–13335.
24. D. Chandler, Interfaces and the driving force of hydrophobic assembly, Nature, 2005, 437, 640–647.
25. C. Tanford, The hydrophobic effect: Formation of micelles and biological membranes, Wiley-Interscience, New York, 2nd edn, 1980.
26. W. Blokzijl and J. B. F. N. Engberts, Hydrophobic effects. Opinions and facts, Angew. Chem., Int. Ed. Engl., 1993, 32, 1545–1579.
27. S. Höfinger and F. Zerbetto, Simple models for hydrophobic hydration, Chem. Soc. Rev., 2005, 34, 1012–1020.
28. H. S. Ashbaugh and L. R. Pratt, Scaled particle theory and the length scales of hydrophobicity, Rev. Mod. Phys., 2006, 78, 159–178.
29. G. Graziano, Contrasting the hydration thermodynamics of methane and methanol, Phys. Chem. Chem. Phys., 2019, 21, 21418–21430.
30. J.-L. Li, R. Car, C. Tang and N. S. Wingreen, Hydrophobic interaction and hydrogen-bond network for a methane pair in liquid water, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2626–2630.
31. M. Montagna, F. Sterpone and L. Guidoni, Structural and spectroscopic properties of water around small hydrophobic solutes, J. Phys. Chem. B, 2012, 116, 11695–11700.
32. N. Galamba, Water's Structure around hydrophobic solutes and the iceberg model, J. Phys. Chem. B, 2013, 117, 2153–2159.
33. R. L. Mancera, A. D. Buckingham and N. T. Skipper, The aggregation of methane in aqueous solution, J. Chem. Soc., Faraday Trans., 1997, 93, 2263–2267.
34. X. Wu, W. Lu, L. M. Streacker, H. S. Ashbaughand and D. Ben-Amotz, Methane hydration-shell structure and fragility, Angew. Chem., Int. Ed., 2018, 57, 15133–15137.
35. F. M. Floris, M. Selmi, A. Tani and J. Tomasi, Free energy and entropy for inserting cavities in water: Comparison of Monte Carlo simulation and scaled particle theory results, J. Chem. Phys., 1997, 107, 6353–6365.
36. G. Lanza and M. A. Chiacchio, The water molecule arrangement over the side chain of some aliphatic amino acids: A quantum chemical and bottom-up investigation, Int. J. Quantum Chem., 2020, 120, e26161.
37. G. Lanza and M. A. Chiacchio, On the size, shape and energetics of the hydration shell around alkanes, Phys. Chem. Chem. Phys., 2021, 23, 24852–24865.
38. E. Gallicchio, M. M. Kubo and R. M. Levy, Enthalpy-entropy and cavity decomposition of alkane hydration free energies: Numerical results and implications for theories of hydrophobic solvation, J. Phys. Chem. B, 2000, 104, 6271–6285.
39. T. Lazaridis, Solvent reorganization energy and entropy in hydrophobic hydration, J. Phys. Chem. B, 2000, 104, 4964–4979.
40. W. L. Jorgensen, J. Gao and C. Ravimohan, Monte Carlo simulations of alkanes in water: hydration numbers and the hydrophobic effect, J. Phys. Chem., 1985, 89, 3470–3473.
41. B. Hartke, Structural transitions in clusters, Angew. Chem., Int. Ed., 2002, 41, 1468–1487.
42. A. Rakshit, P. Bandyopadhyay, J. P. Heindel and S. S. Xantheas, Atlas of putative minima and low-lying energy networks of water clusters n = 3–25, J. Chem. Phys., 2019, 151, 214307.
43. S. Kazachenko and A. J. Thakkar, Water nanodroplets: Predictions of five model potentials, J. Chem. Phys., 2013, 138, 194302.
44. S. Kazachenko and A. J. Thakkar, Are there any magic numbers for water nanodroplets, (H₂O)_n, in the range 36 ≤ n ≤ 50?, Mol. Phys., 2010, 108, 2187–2193.
45. J. D. Farrell and D. J. Wales, Clusters of coarse-grained water molecules, J. Phys. Chem. A, 2014, 118, 7338–7348.
46. B. Bandow and B. Hartke, Larger water clusters with edges and corners on their way to ice: structural trends elucidated with an improved parallel evolutionary algorithm, J. Phys. Chem. A, 2006, 110, 5809–5822.
47. J. K. Kazimirski and V. Buch, Search for low energy structures of water clusters (H₂O)_n, n = 20–22, 48, 123, and 293, J. Phys. Chem. A, 2003, 107, 9762–9775.
48. V. Buch, S. Bauerecker, J. P. Devlin, U. Buck and J. K. Kazimirski, Solid water clusters in the size range of tens–thousands of H₂O: a combined computational/spectroscopic outlook, Int. Rev. Phys. Chem., 2004, 23, 375–433.
49. Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 Other Functionals, Theor. Chem. Acc., 2008, 120, 215–241.
50. J. Tomasi, B. Mennucci and R. Cammi, Quantum mechanical continuum solvation models, Chem. Rev., 2005, 105, 2999–3094.
51. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision A.02, Gaussian, Inc., Wallingford CT, 2010.
52. G. Lanza and M. A. Chiacchio, Ab initio MP2 and density functional theory computational study of AcAlaNH₂ peptide hydration: A bottom-up approach, ChemPhysChem, 2014, 15, 2785–2793.
53. G. Lanza and M. A. Chiacchio, Quantum mechanics approach to hydration energies and structures of alanine and dialanine, ChemPhysChem, 2017, 18, 1586–1596.
54. O. M. Becker and M. Karplus, The topology of multidimensional potential energy surfaces: Theory and application to peptide structure and kinetics, J. Chem. Phys., 1997, 106, 1495–1517.
55. J. L. F. Abascal and C. Vega, A general purpose model for the condensed phases of water: TIP4P/2005, J. Chem. Phys., 2005, 123, 234505.
56. C. J. Burnham and S. S. Xantheas, Development of transferable interaction models for water. IV. A flexible, all-atom polarizable potential (TTM2-F) based on geometry dependent charges derived from an ab initio monomer dipole moment surface, J. Chem. Phys., 2002, 116, 5115–5124.
57. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935.
58. E. Whalley, The difference in the intermolecular forces of H₂O and D₂O, Trans. Faraday Soc., 1957, 53, 1578–1585.
59. E. Whalley, Energies of the phases of ice at zero temperature and pressure, J. Chem. Phys., 1984, 81, 4087–4092.
60. R. Feistel and W. Wagner, Sublimation pressure and sublimation enthalpy of H₂O ice I_h between 0 and 273.16 K, Geochim. Cosmochim. Acta, 2007, 71, 36–45.
61. Y. P. Handa, O. Mishima and E. Whalley, High-density amorphous ice. III. Thermal properties, J. Chem. Phys., 1986, 84, 2766–2770.
62. E. Whalley, D. Klug and Y. Handa, Entropy of amorphous ice, Nature, 1989, 342, 782–783.
63. P. Atkins, J. de Paula and J. Keeler, Atkins’ Physical Chemistry, Oxford University Press, Oxford, UK, 11th edn, 2018.
64. J. M. Mullin and M. S. Gordon, Alanine: Then there was water, J. Phys. Chem. B, 2009, 113, 8657–8669.
65. Z. M. Aman and C. A. Koh, Interfacial phenomena in gas hydrate systems, Chem. Soc. Rev., 2016, 45, 1678–1690.
66. M. F. Chaplin, A proposal for the structuring of water, Biophys. Chem., 1999, 83, 211–221.
67. D. J. Anick, Polyhedral water clusters, I: Formal consequences of the ice rules, J. Mol. Struct., 2002, 587, 87–96.
68. A. Müller, E. Krickemeyer, H. Bögge, M. Schmidtmann, B. Botar and M. O. Talismanova, Drawing small cations into highly charged porous nanocontainers reveals “water” assembly and related interaction problems, Angew. Chem., Int. Ed., 2003, 42, 2085–2090.
69. A. Müller, H. Bögge and E. Diemann, Structure of a cavity-encapsulated nanodropof water, Inorg. Chem Commun., 2003, 52–53 and the related correction Inorg. Chem. Commun., 2003, 6, 329.
70. A. Lenz and L. Ojamäe, Computational studies of the stability of the (H₂O)₁₀₀ nanodrop, J. Mol. Struct., 2010, 944, 163–167.
71. O. Loboda and V. Goncharuk, Theoretical study on icosahedral water clusters, Chem. Phys. Lett., 2010, 484, 144–147.
72. G. Bolis and E. Clementi, Methane in Aqueous Solution at 300 K, Chem. Phys. Lett., 1981, 82, 147–152.
73. C. Y. Lee, J. A. McCammon and P. J. Rossky, The structure of liquid water at an extended hydrophobic surface, J. Chem. Phys., 1984, 80, 4448–4454.
74. G. Graziano, Water: cavity size distribution and hydrogen bonds, Chem. Phys. Lett., 2004, 396, 226–231.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S6 report the cluster structures and the tables report the Cartesian coordinates of all clusters presently analyzed. See DOI: https://doi.org/10.1039/d2cp05195h

---