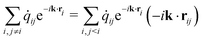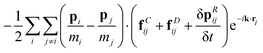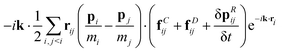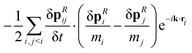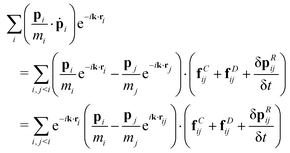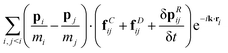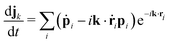Transport coefficients from Einstein–Helfand relations using standard and energy-conserving dissipative particle dynamics methods
Received
16th October 2022
, Accepted 24th March 2023
First published on 6th April 2023
Abstract
In this article we demonstrate that contrary to general belief, the standard Einstein–Helfand (EH) formulas are valid for the evaluation of transport coefficients of systems containing dissipative and random forces provided that for these mesoscopic systems: (i) the corresponding conservation laws are satisfied, and (ii) the transition probabilities satisfy detailed balance. Dissipative particle dynamics (DPD) and energy-conserving DPD methods (DPDE), for instance, are archetypical of such mesoscopic approaches satisfying these properties. To verify this statement, we have derived a mesoscopic heat flux form for the DPDE method, suitable for the calculation of the thermal conductivity from an EH expression. We have compared EH measurements against non-equilibrium simulation values for different scenarios, including many-body potentials, and have found excellent agreement in all cases. The expressions are valid notably for systems with density- and temperature-dependent potentials, such as the recently developed generalised DPDE method (GenDPDE) [Avalos et al., Phys. Chem. Chem. Phys., 2019, 21, 24891]. We thus demonstrate that traditional EH formulas in equilibrium simulations can be widely used to obtain transport coefficients, provided that the appropriate expression for the associated flux is used.
1 Introduction
Mesoscopic simulation is a constantly growing field for studying the behaviour of complex systems over time and length scales beyond the capabilities of atomistic and molecular simulations. The development of mesoscopic models inherently introduces a certain degree of coarse-graining, as a reduced number of degrees of freedom (DoF) are represented, which are derived from the total number of DoF present in the underlying physical system. Coarse-graining inevitably gives rise to dissipative and random interactions, due to the interplay between the resolved variables and the unresolved (smoothed-out) physical DoF. Among many others, Dissipative Particle Dynamics (DPD),1,2 and the variant to include heat transport through the energy-conserving DPD (DPDE) method,3–5 have become widespread tools for exploring the equilibrium and dynamic properties of fluids. Extensions have been proposed, which are targeted towards the description of more complex systems, together with increasing the transferability of the model parameters. These include density-dependent potentials in both DPD6,7 (MB-DPD) and DPDE (MB-DPDE),8–10 along with the introduction of density- and temperature-dependent potentials (GenDPDE),11,12 and even chemical reactions13 or interparticle mass transfer.14,15 Many other applications can be found in the literature.16–18 However, as it stands, GenDPDE is the most complete method, as the others can be derived from the latter as limiting cases.
Macroscopic transport coefficients (e.g., thermal conductivity, diffusion or shear viscosity) can be obtained from molecular simulations by applying equilibrium and non-equilibrium methods. Although non-equilibrium methods19 are relatively straightforward to implement, they often introduce complexity in the simulation setup, and are specific for the given property to be measured.20,21 In contrast, equilibrium methods allow all desired transport coefficients to be calculated in one single simulation with no special modification of the simulation setup. Particularly in classical molecular dynamics methods, the calculation of transport coefficients for systems in equilibrium can be performed by applying Green–Kubo (GK) relations,22,23 or alternatively Einstein–Helfand (EH) relations.24,25 Although GK and EH formulas are directly related,26 in practice EH relations are often preferred over GK formulas since they allow a larger degree of accuracy for the same computational cost. However, it has been argued that both GK and EH formulas present conceptual challenges when the dynamics of the system involves stochastic and dissipative forces, as occurs in DPD and its variants. The key argument is that such mesoscopic models do not follow Hamiltonian dynamics and their trajectories are not time-reversible. Addressing such systems, Ernst and Brito27 proposed modifications of the GK formulas for the calculation of transport coefficients in systems with random forces and (or) lack of time-reversal invariance. Jung and Schmid28 validated the expressions of Ernst and Brito through the evaluation of both the shear and bulk viscosities for isothermal DPD. More recently, Panoukidou et al.29 proposed an EH relation for the shear viscosity of a DPD polymer solution derived from the expressions of Ernst and Brito. Although some authors have applied the traditional GK and EH expressions to DPD with success,30 the apparent community opinion is that GK and EH methods are problematic when applied to DPD systems, and require specifically derived formulas, including complex formal expressions for the observables, which are cumbersome.
However, the validity of GK and EH relations only relies on the long wave-length and long-time behaviour of hydrodynamic modes, together with the Detailed Balance (DB) condition. These conditions stem from (i) the existence of mesoscopic conserved properties, inherited from the microscopic conservation laws, and (ii) the time-reversal invariance of the underlying microscopic system.31 Therefore, the time-reversibility of the mesoscopic equations of motion is not a necessary condition for the GK and EH formulas to be valid. Hence, if it is possible to deduce the GK and EH expressions by considering only the conservation laws and their associated macroscopic hydrodynamic behaviour,26 then they would be valid independent of the presence of dissipative and random forces (more generally dissipative and random fluxes) in the mesoscopic dynamics, provided that the mesoscopic properties are conserved and the random terms satisfy the appropriate Fluctuation-Dissipation Theorem (FDT). However, the important point is that the traditional expressions for quantities such as the microscopic heat flux or the stress tensor, need to be re-derived to properly include the effect of these dissipative and random contributions, which are not present in Hamiltonian systems.
In this work we focus on the application of the EH formulas to transport coefficients in GenDPDE. The conclusions drawn are therefore also valid for DPD, MB-DPD, DPDE, and MB-DPDE. We prove that the formal expressions traditionally used26 are applicable to this type of dissipative systems, provided that their dynamics satisfy the aforementioned conditions (i) and (ii), contrary to the present community consensus. However, the major novel contribution in this article is the mesoscopic expression for the heat flux to be used in the corresponding EH formula for thermal conductivity in DPDE, GenDPDE, and all possible related methods. The validity of our analysis is strongly supported by the comparison of our EH data against a collection of non-equilibrium results with different conditions, involving a wide range of densities, different values of the mesoscopic heat conduction parameter, and the presence of potential interactions between the particles.
For completeness, we have also compared our EH values for shear viscosity with non-equilibrium data existing in the literature,28 used as a benchmark, and also with other equilibrium approaches. We have found that, while our EH calculations are in excellent agreement, the EH formula obtained in ref. 29 produce results that systematically underestimate these benchmark non-equilibrium simulations. Although the latter are obtained from the GK expressions given in ref. 27, some correlations are missing in the derivation due to the non-symmetrical nature of the referred GK expression, which cannot straightforwardly be cast under an EH form. We have also carried out the evaluation of the shear viscosity from this GK expression of ref. 27. As found also in ref. 28, the values obtained are in better agreement with the reference ones, as well as with our EH calculations. The agreement is more striking as our approach and the one in ref. 27 stem from completely different starting points. Indeed, the detailed simulations for rather broad conditions conducted in this work show that despite their formal differences they produce only tiny numerical variations of the order of the statistical error in the measure, which suggests that they are equivalent. We provide in the manuscript the comparison between the different data, but leave the deeper questions for a separate analysis.
The article is organised as follows. In Section 2, we introduce the derivation of the EH formulas based on property conservation and DB for a generic property. The theoretical analysis also includes the description of the GenDPDE algorithm used in the derivation of its corresponding mesoscopic heat flux expression. In Section 3, we provide the simulation details for the equilibrium and the boundary-driven non-equilibrium simulations performed for validation. In Section 4, the results for the different situations studied are presented and discussed. Finally, Section 5 is devoted to a review of the main conclusions of this work.
2 Theoretical analysis
2.1 Einstein–Helfand formulas
The derivation of the expression for the diffusion coefficient of suspended particles by Einstein24 was the first example of a relation that provided a macroscopic coefficient in terms of the microscopic physical details. The method was based on the calculation of the mean square displacement of a suspended particle. This approach was later generalised by Helfand25 to other transport coefficients. Notably, Green–Kubo relations22,23 have the same objective, but use a different correlation function to establish the link between the macroscopic and the microscopic levels. In this section, we present the derivation of the EH relations for systems that satisfy conditions (i) and (ii). A complete description and derivation of general EH relations can be found in the basic monographs on liquid theory, notably in the book by Hansen and McDonald.26 Most of the considerations discussed here regarding the hydrodynamic limit and the calculation of transport coefficients in systems with periodic boundary conditions are also addressed in detail elsewhere.32
We begin the derivation of the general transport relations by considering a conserved property ai transported by the mesoscopic particles, i.e., GenDPDE type-particles in our case study. This property may be exchanged between mesoscopic particles due to the particle–particle interactions, thus its value is susceptible to changes with time. This quantity may simply be the numerical value of 1, associated with the invariability of the number of particles in the simulation, particle momenta pi, or particle energy εi. Given a conserved property, the associated field A(r,t) can be defined as
| | 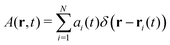 | (1) |
and the corresponding Fourier modes as
| | 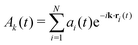 | (2) |
Given that
ai is a conserved quantity implies that

.
Conservation imposes that field A satisfies a balance equation, whose general form is given by
| |  | (3) |
where
JA is the macroscopic flux of
A. In the domain of validity of linear response,
33,34 which allows us to disregard advective terms, the fluxes are related to gradients of
A,
i.e.,
where
α is the associated transport coefficient and
JA,R is a random flux due to the thermal fluctuations. Here, since our intent is to be merely illustrative, we have only considered a single field with no coupling with other conserved fields, as occurs, for example, in the Ludwig–Soret effect.
34 For the general case, the reader is referred to the classical monographs on liquid theory and simulation.
26
Thus, in the hydrodynamic limit, the relaxation of the fluctuations of Ak in a system that is in overall thermal equilibrium satisfy
| |  | (5) |
with
| | | −ik·JAk → −αk2Ak − ik·JA,Rk | (6) |
However, from
eqn (2), we can also write the balance equation in terms of the microscopic variables
| |  | (7) |
where
ui ≡
ṙi, which is assumed to exist in the sense fixed by the dynamic integration algorithm, as we illustrate in Section 2.1.2. If
ai can be exchanged between particles, the equation of motion for
ai needs to be provided, which also determines
ȧi. It is important to realise that, despite its apparent form, the right-hand-side of
eqn (7) can be written as −
ik·
JAk in the hydrodynamic limit, which is a necessary consequence of the conserved nature of property
ai. Hence, the right-hand-side of
eqn (7) has to be formally identical to the macroscopic counterpart,
eqn (6).
Before proceeding further with the derivation, the properties of the random flux need to be specified. On the one hand, an equilibrium probability distribution for the variable Ak, namely Peq(Ak), can be derived from the underlying microscopic Hamiltonian system, according to the coarse-grain procedure. On the other hand, the dynamics of the transitions between states in equilibrium must satisfy DB, with a transition probability w(Ak(t) → Ak(t + dt)) consistent with eqn (5), together with eqn (6). The general expression for DB takes the form
| |  | (8) |
where

and
Ak =
Ak(
t) for the direct trajectory while

and

for the reverse trajectory. The sign
σ depends on whether the variable
A is even (
σ = +1) or odd (
σ = −1) under time reversibility. The transition probabilities can be derived from the stochastic dynamics of the field,
eqn (5) and (6),
i.e.,
| |  | (9) |
where the subscript
R indicates that the average is taken over the probability distribution of
JA,Rk. In Appendix A we show that from
eqn (8) and (9), it follows that the random flux has zero average
together with the corresponding FDT
| |  | (11) |
Here (*) represents the complex conjugate of the variable, which is necessary to maintain the translational invariance of the correlation function. Note that
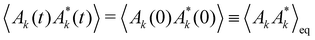
is the equilibrium equal-time correlation, which is independent of time, due to the time-translational invariance of the equilibrium properties.
2.1.1 Derivation of Einstein–Helfand relations.
Next, we derive the general EH relations. At the macroscopic level, eqn (5) and (6) can be integrated yielding| |  | (12) |
Hence, the following correlation function can be expanded as,| |  | (13) |
This expression produces three distinct terms: (i) the product of the two terms related to the initial condition Ak(0), (ii) the product of the terms related to the random flux JA,Rk, and (iii) the crossed terms involving the product of both. In the hydrodynamic limit, k → 0 prior to t → ∞, e−αk2t − 1 ≃ −αk2t → 0. Hence, the first of the three terms is of the order (−αk2t)2. The third term vanishes due to eqn (10) and the fact that the initial condition is not correlated to the random fluxes. Thus, we are left only with the second term, which gives| |  | (14) |
Therefore using eqn (11)| |  | (15) |
where the limit in the last line corresponds to the hydrodynamic limit k2t → 0. Thus, the last contribution, being linear in k2t, is the dominant contribution in the hydrodynamic limit. Therefore, the EH relation takes the form,| |  | (16) |
However, due to the fact that the real simulations are performed in systems of finite size, the true minimum value of kmin ∼ π/L, where L is the lateral size of the box. As a consequence, the direct use of the correlation 〈|Ak(t) − Ak(0)|2〉 ∝ k2 in a system with periodic boundary conditions, is not convenient due to such an explicit k-dependence.32,35,36 Instead, we can replace the displacement Ak(t) − Ak(0) by the time-integral of the right-hand-side of eqn (5). Thus, the explicit k-dependency is cancelled, leaving only the direction of the wavevector, and therefore| |  | (17) |
where ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) = k/k. The microscopic expression of JAk is to be used in eqn (17). Such an expression should be derived from the fact that
= k/k. The microscopic expression of JAk is to be used in eqn (17). Such an expression should be derived from the fact that  , in agreement with eqn (7). Under this form, one can consistently take the formal limit k → 0. The
, in agreement with eqn (7). Under this form, one can consistently take the formal limit k → 0. The ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) vectors are arbitrary as they merely indicate the wavevector direction of the relaxing plane wave whose relaxation is formally being studied.
vectors are arbitrary as they merely indicate the wavevector direction of the relaxing plane wave whose relaxation is formally being studied.
2.1.2 Self-diffusion as a simple example.
The self-diffusion of a single colloidal particle in a fluid is an example of a system with no Hamiltonian dynamics, where neither momentum nor energy are conserved. In this simple example, only the particle number is conserved, which from a macroscopic viewpoint, produces a diffusion-type hydrodynamic equation. Thus, this simple example can be considered as a direct application of the EH formula to non-Hamiltonian systems.
Let us assume that the dynamics of a colloidal particle is described by a classical Langevin equation of the form
| |  | (18) |
| | | r(t + δt) = r(t) + u(t)δt | (19) |
where
γ is the friction coefficient,
m is the particle mass, and δ
uR is a Wiener process that can be approximated for discrete times as
Γωδ
t1/2. The amplitude
Γ is given by the FDT as
where
kB is the Boltzmann constant and
T is the system temperature. In turn,
ω(
t) = (
Ωx(
t),
Ωy(
t),
Ωz(
t)) is a collection of normalised Gaussian random numbers satisfying 〈
Ωα〉 = 0 and
| |  | (21) |
where Greek letters represent Cartesian coordinates,
δ is the Kronecker delta, and
δtt′ is 1, if |
t −
t′| < δ
t and 0 otherwise. In this example, the only conserved field is the particle density, as the number of colloidal particles remains constant during the simulation. We thus identify the observable
Ak as the particle density
δ(
r −
r(
t)), which in Fourier space becomes
which implies that both
a = 1 and the equilibrium average 〈
A0A0〉
eq = 1. Next, we determine the particle flux
JAk from
eqn (7), yielding
Arbitrarily selecting
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif)
= (1, 0, 0) in
eqn (17), we obtain the well-known result for the diffusion coefficient
| |  | (24) |
Solving
eqn (18) with respect to time, inserting the result into
eqn (24) and integrating, we arrive at the well-known Stokes–Einstein result,
D =
kBT/
γ. Furthermore, note that
eqn (18) indicates that
u is discontinuous in the limit δ
t → 0. In turn,
r(
t) is a continuous function in the same limit, as follows from
eqn (19), although its derivative is not well defined. Therefore, the algorithm,
eqn (18) and (19), formulated in a discrete form, defines the meaning of the time-derivative operators used in the derivation,
i.e.,
| |  | (25) |
with no ambiguity.
2.2 GenDPDE: generalised energy-conserving dissipative particle dynamics
To obtain explicit expressions for the EH relations for DPD-related methods, we introduce the GenDPDE algorithm because the final expressions for the stress tensor and the heat flux density depend on the form and the parameters appearing in the model dynamics. In this section, we briefly present the GenDPDE method, because it is the most general method and embraces all other DPD-type models as special cases.
GenDPDE is the generalisation of DPDE3,4,37,38 to many-body density- and temperature-dependent interparticle potentials. GenDPDE is a particular type of DPD method that includes an internal energy term u as an additional property carried by the particle, along with the particle number (i.e., mass) and momentum. In this way, in addition to the conservation of particle number and total momentum, the system also conserves energy despite the presence of dissipative and random forces. In GenDPDE, associated with the particle internal energy u is the particle temperature, which is responsible for the heat exchanged with neighbouring particles due to their temperature differences. Therefore, with the GenDPDE framework, heat transport can be simulated. Fig. 1 depicts the transport processes present in GenDPDE.
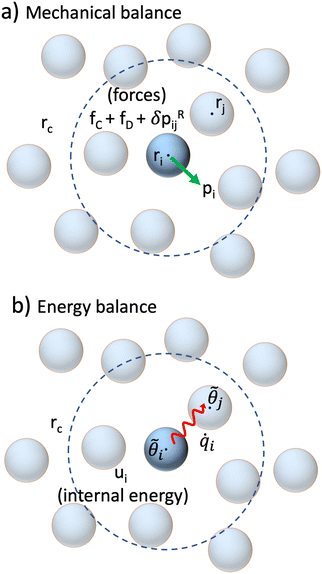 |
| | Fig. 1 Schematic of the GenDPDE simulation method. (a) Mechanical balance governed by eqn (26) and (27). (b) Energy balance governed by eqn (39). | |
In the GenDPDE algorithm, the mechanical DoF evolve according to the same dynamics as in standard DPD and DPDE,3,37,38i.e.,
| | 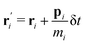 | (26) |
| | 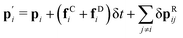 | (27) |
where prime and non-prime variables refer to the time
t + δ
t and
t, respectively, δ
t is the timestep, and
fCi and
fDi are the conservative and dissipative forces, respectively; δ
pRij is the random contribution to the momentum defined as proportional to a Wiener process. As such, one can define a timestep dependent random force as
| |  | (28) |
More importantly, note that the distinction between the different many-body variants lies in the specific form of the conservative force
fCi, which can be density-dependent (MB-DPD and MB-DPDE), density- and temperature-dependent potentials (GenDPDE), or contain merely pair potentials depending on the interparticle distance (DPD and DPDE). However with regards to the main thesis of this article, there is no need to specify the type of force involved, as
fCi can be left undefined in the expressions, being a completely general function satisfying only the action–reaction principle. Here for completeness and illustrative purposes, we provide the form of the conservative force used in the GenDPDE simulations, in which the definition of a local particle volume

related to the local particle number density
ni, is required. The
ni and

are related by
| |  | (29) |
where
rij =
ri −
rj. The weighting function
w(
rij) is a smooth monotonously decreasing function of the interparticle distance
rij = |
ri −
rj|, which is zero if
rij >
rc;
rc is the spherical cut-off distance. In GenDPDE, the reversible dynamics of the resolved mechanical DoF follows from the effective Hamiltonian
| |  | (30) |
In the absence of external, dissipative and random forces,
H is constant and equal to the total energy of the system
E. The
u depends on the particle volume

,
i.e., the local density
ni and on the particle bare temperature
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif)
.
11,12 The conservative force is thus
fCi = − ∂
ui/∂
ri|
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) i
i, which can be separated into pairwise contributions of the form
| | 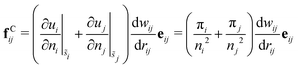 | (31) |
where
eij =
rij/
rij,

is the particle pressure, and d
wij/d
rij < 0. The subscript
![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) i
i emphasizes that the derivative is taken under adiabatic conditions (
i.e., no simultaneous heat transfer between particles occur while updating velocities and positions). The bare entropy is defined from the density of states

of the non-resolved DoF of the mesoscopic particle
| |  | (32) |
i.e.,
| |  | (33) |
relates the particle temperature to the thermodynamics of the non-resolved DoF of the mesoparticle.
†
Regarding the dissipative force, we assume the traditional pairwise additive form
| |  | (34) |
where
γ is the friction coefficient and
ω(
rij) is the weighting function, which is also a smooth uniformly decreasing function of the interparticle distance with range
rc.
The random contribution to the momentum, δpRij, satisfies the FDT3
| |  | (35) |
with δ
pRij = −δ
pRji and
| |  | (36) |
Here, the normalised Gaussian random numbers
ξij satisfy
| |  | (38) |
where the average is taken over the probability distribution of
ξij.
In addition to the momentum transfer, GenDPDE particles can exchange heat ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) i related to particle temperature differences. Given that Ė = 0 if the total energy is to be conserved, we define the variation of the particle internal energy. Following the standard procedure,11 the energy balance over a single timestep permits us to define the internal energy variation as
i related to particle temperature differences. Given that Ė = 0 if the total energy is to be conserved, we define the variation of the particle internal energy. Following the standard procedure,11 the energy balance over a single timestep permits us to define the internal energy variation as
| |  | (39) |
Note that the heat flow
![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) i
i has been included in the energy balance as an additional DoF involved in the particle energy change. It can be expressed as the summation over contributions from all the particle pairs, according to a mesoscopic analogue of Onsager's linear relationships between fluxes and forces,

, with
![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) ij
ij = −
![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) ji
ji. Then, we propose,
| |  | (40) |
where
κij =
κ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif)
(
rij),
κ is the particle thermal conductivity and
![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif)
(
rij) represents a weighting function analogous to the weighting function for the momentum interaction. The
![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif)
(
rij) is also limited to a given range
rc, but it does not need to be the same as for the momentum transport or the calculation of the local density. In turn, δ
uRij is the random heat exchanged between particles
i and
j during the time step δ
t, which is also proportional to a Wiener process. Here we define the time step-dependent random heat flux between two particles as

. To satisfy total energy conservation, we require that δ
uRij = −δ
uRji. The amplitude of the random heat exchange between particles is given by
| |  | (41) |
where the amplitude is fixed by the corresponding FDT, and
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ij
ij is the normalised Gaussian number for the heat exchange with properties:
| | 〈![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ij〉 = 0 ij〉 = 0 | (42) |
| | 〈![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ij ij![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) kl〉 = δikδjl − δilδjk kl〉 = δikδjl − δilδjk | (43) |
Note that the term  in eqn (39) is
in eqn (39) is 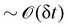 . The average of this term is non-zero, but exactly cancels the average of
. The average of this term is non-zero, but exactly cancels the average of 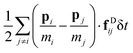 and therefore, the equilibrium average
and therefore, the equilibrium average 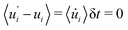 . If the balance is calculated from the continuous limit instead of the discrete algorithm, then this term could be easily overlooked. Moreover, if this expression is extracted from the Fokker–Plank equation, instead of this quadratic random term one obtains its equilibrium average,3,4 which only guarantees energy conservation in the mean but not at every timestep.
. If the balance is calculated from the continuous limit instead of the discrete algorithm, then this term could be easily overlooked. Moreover, if this expression is extracted from the Fokker–Plank equation, instead of this quadratic random term one obtains its equilibrium average,3,4 which only guarantees energy conservation in the mean but not at every timestep.
With regards to the other DPD-type methods, the dynamics described by the previous algorithm reduces to standard DPD or MB-DPD in the limit CV/kB → ∞, as this limit ensures constant θi ≃ T and the dynamics is thus isothermal. Here CV is the particle heat capacity, defined in the usual way from its internal thermodynamics, CV = ∂ui/∂![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i|V. Effectively in the canonical ensemble, energy fluctuations scale as 〈δE2〉 = kBCVT2. Thus, writing for the mesoparticle δE ≃ CV(T −
i|V. Effectively in the canonical ensemble, energy fluctuations scale as 〈δE2〉 = kBCVT2. Thus, writing for the mesoparticle δE ≃ CV(T − ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) ), we can infer that
), we can infer that  . Thus, the choice of a large heat capacity CV ≫ kB in the DPDE method makes its dynamics for the mechanical DoF identical to standard isothermal DPD. Furthermore, the mesoscopic expression for the heat flux can be used also in DPDE as well as in MB-DPDE, as the latter follows from the former if the internal energy per particle can be separated into two contributions, each depending on a single variable, according to the form,
. Thus, the choice of a large heat capacity CV ≫ kB in the DPDE method makes its dynamics for the mechanical DoF identical to standard isothermal DPD. Furthermore, the mesoscopic expression for the heat flux can be used also in DPDE as well as in MB-DPDE, as the latter follows from the former if the internal energy per particle can be separated into two contributions, each depending on a single variable, according to the form,
| |  | (44) |
2.3 Microscopic fluxes for viscosity and thermal conductivity
In this section, we derive the form of the stress tensor and the heat flux density for our mesoscopic model. The derived expressions are non-trivial and represent the cornerstone of the application of the EH relations to the calculation of the associated transport coefficients.
2.3.1 Einstein–Helfand relations for the thermal conductivity.
The relevant observable for the heat transport is the associated conserved quantity, i.e., the energy density. According to eqn (2), we get| |  | (45) |
To obtain the expression for the energy density flux, from eqn (7) and (5), the latter can be written as| |  | (46) |
In Appendix B, we expand this last expression to obtain,| |  | (47) |
where Jε ≡ Jεk→0 to simplify the notation. Eqn (47) is the main result of this article together with our demonstration that the EH formulas are also valid for conserved quantities in models with dissipative and random interactions.
In comparison with standard molecular dynamics, the heat flux density for the GenDPDE algorithm contains several additional contributions. Firstly, there is the work performed by the dissipative and random forces, which adds to the traditional work done by the conservative forces; the first term in eqn (47). Secondly, there is an additional quadratic term in the random forces, ∝fRij·δpRj, that appears due to the energy balance carried out for discrete times. Similar to other terms, this term is also  . Thirdly, there is the direct contribution to the heat transport due to the mesoscopic heat exchange between the particles, including the random heat exchange; the last two terms in eqn (47). The last term in eqn (47) corresponds to the advected energy with the motion of the particles. In comparison with standard molecular dynamics, here εi also contains the internal energy u in addition to the kinetic energy. Furthermore, the macroscopic advective transport of enthalpy needs to be separated from the total energy flux density,26i.e.,
. Thirdly, there is the direct contribution to the heat transport due to the mesoscopic heat exchange between the particles, including the random heat exchange; the last two terms in eqn (47). The last term in eqn (47) corresponds to the advected energy with the motion of the particles. In comparison with standard molecular dynamics, here εi also contains the internal energy u in addition to the kinetic energy. Furthermore, the macroscopic advective transport of enthalpy needs to be separated from the total energy flux density,26i.e.,
| |  | (48) |
where
j is the momentum density; therefore,
j/ρ is the velocity field. As remarked in ref.
26, if we choose the total momentum of the simulation box to be zero then the momentum density vanishes in the long-wavelength limit and this correction can be ignored. It is important to realise that the latter condition must be enforced in the simulations for the relation
Jq =
Jε to hold.
In eqn (17),  26 is obtained from the canonical ensemble, considered here to be the equilibrium distribution (see comments regarding the ensembles in ref. 19). Therefore, since macroscopically the hydrodynamic field Ak ≡ εk = ρcPTk, with
26 is obtained from the canonical ensemble, considered here to be the equilibrium distribution (see comments regarding the ensembles in ref. 19). Therefore, since macroscopically the hydrodynamic field Ak ≡ εk = ρcPTk, with
| |  | (49) |
then
α ≡
κ =
λ/(
ρcP);
cP is the heat capacity per unit mass,
ρ is the mass density, and
λ stands for the substance thermal conductivity. The EH expression,
eqn (17), thus takes the usual form
| |  | (50) |
although
Jq has the form derived in this article,
eqn (47). We can then choose either one component of
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif)
, or use an average over the three Cartesian coordinates to increase the statistics.
As no particular form of the conservative force is required in the derivation, the expression can be applied to the different variants of energy-conserving DPD methods including GenDPDE.
2.3.2 Einstein–Helfand relations for the shear viscosity.
The derivation of the relevant components of the stress tensor starts by identifying one of the three components of the momentum flux as the variable under scrutiny. Initially, let us write the observable in its vectorial form| |  | (51) |
From eqn (7), we evaluate the time-derivative of the observable along the same lines as for the heat flux density, and obtain| |  | (52) |
To study shear waves, the velocity field needs to be orthogonal to the wavevector ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) . We thus arbitrarily choose the x-component of the momentum in eqn (51) and the z-component of k. Thus,
. We thus arbitrarily choose the x-component of the momentum in eqn (51) and the z-component of k. Thus,| |  | (53) |
From eqn (53), it is evident that both the dissipative force and the random force need to be incorporated in the calculation of the stress since they contribute to the global momentum balance along with the conservative forces.
Hence, using the fact that macroscopically
| |  | (54) |
then
α ≡
ν =
η/
ρ, where
η is the shear viscosity coefficient. Moreover, as

we obtain from
eqn (17)| |  | (55) |
which is the standard expression for the viscosity found in the literature.
26
3 Simulation methods
3.1 Simulation details
For all the simulations performed in this work, the weighting function for the dynamic properties, such as the friction forces and interparticle heat transport, is given by| | 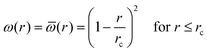 | (56) |
The weighting function to calculate the local density is normalised such that its volume integral is unity, i.e.,| |  | (57) |
In all cases, the weighting functions are zero for r > rc.
3.1.1 Thermal conductivity measurements.
We used an internally developed GenDPDE code, which is implemented in Fortran with OpenMP parallelisation, in all the simulations. The algorithm to update the position and momentum follows a velocity-Verlet integration scheme, while the energy is updated following a simple Euler form; see ref. 3, 5 and 38. For simplicity, we used the particle EoS given in eqn (44), in which the many-body potential u is independent of the particle temperature. All simulations were performed in reduced units, where rc is the unit of length, m is the unit of mass, and kBT is the unit of energy. Based on these choices then, the unit of time is given by  . The simulated systems contained N = 20
. The simulated systems contained N = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles in volume V. A cubic simulation box was used (see Fig. 2c) with periodic boundary conditions. The box volume was adjusted for each simulation to obtain overall particle densities
000 particles in volume V. A cubic simulation box was used (see Fig. 2c) with periodic boundary conditions. The box volume was adjusted for each simulation to obtain overall particle densities ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ≡ N/V = 4, 8, 16, and 32 with a timestep of δt = 0.001, 0.0005, 0.00005, and 0.00005, respectively. The timestep was adjusted to obtain satisfactory energy conservation from the integration of the equations of motion. The system is initialised by rescaling the particle kinetic energy to reach a temperature T = 1, prior to the constant energy simulation that is performed to obtain the data. This initialisation scheme implies that the dimensionless kinetic energy of the system is
≡ N/V = 4, 8, 16, and 32 with a timestep of δt = 0.001, 0.0005, 0.00005, and 0.00005, respectively. The timestep was adjusted to obtain satisfactory energy conservation from the integration of the equations of motion. The system is initialised by rescaling the particle kinetic energy to reach a temperature T = 1, prior to the constant energy simulation that is performed to obtain the data. This initialisation scheme implies that the dimensionless kinetic energy of the system is  , and simultaneously the average particle temperature
, and simultaneously the average particle temperature  . Note that, unlike the momentum integration, the mechanical energy term in the balance equation produces an energy drift, which increases with the size of the time step. Such a drift impairs long simulations with explicit algorithms. However, this drift can be avoided by absorbing the numerical error Δ in every timestep, which is proportional to kBT ∼ 1, into the particles' internal energy u, which causes an internal temperature variation of the order of Δ/(CVT) ≪ 1. Note that if the timestep is not properly chosen, differences between the kinetic temperature and the internal temperature averages may occur. The friction coefficient γ was set to 4.5, the heat capacity CV to 60, and the particle thermal conductivity κ to either 5 or 50 to test different heat transport regimes.
. Note that, unlike the momentum integration, the mechanical energy term in the balance equation produces an energy drift, which increases with the size of the time step. Such a drift impairs long simulations with explicit algorithms. However, this drift can be avoided by absorbing the numerical error Δ in every timestep, which is proportional to kBT ∼ 1, into the particles' internal energy u, which causes an internal temperature variation of the order of Δ/(CVT) ≪ 1. Note that if the timestep is not properly chosen, differences between the kinetic temperature and the internal temperature averages may occur. The friction coefficient γ was set to 4.5, the heat capacity CV to 60, and the particle thermal conductivity κ to either 5 or 50 to test different heat transport regimes.
 |
| | Fig. 2 GenDPDE simulation of thermal conductivity: (a) snapshot of the non-equilibrium simulation box for density 32 where the particle colour represents different particle temperatures, (b) final particle temperature gradient for a non-equilibrium simulation at density 32, red and blue shading represent hot and cold regions respectively, and (c) snapshot of the equilibrium simulation box for density 32, the particle colour represents different particle temperatures. | |
For the purposes of testing different conditions, we simulated: (a) systems with no conservative force, i.e., u(![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) ,n) = CV
,n) = CV![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) , cf.eqn (44), which is referred to as the ideal GenDPDE system, and (b) systems with a conservative force fC, obtained from a many-body force potential given by a quadratic well, i.e.,
, cf.eqn (44), which is referred to as the ideal GenDPDE system, and (b) systems with a conservative force fC, obtained from a many-body force potential given by a quadratic well, i.e.,
| |  | (58) |
n0 is a reference particle density, which eventually determines the pressure of the system. The parameter
β was set to 0.2 and the target density
n0 was set equal to the overall density of the system
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
for each case.
For the analysis of the EH relation, we used different time windows for every density, each sufficiently long so that the linear diffusive regime of the correlation
| |  | (59) |
is observed, and the linear regression can be applied. The slope of the regression directly yields the thermal conductivity.
Fig. 3 shows the typical results for the EH correlation for the viscosity measurements; the EH correlations for the thermal conductivity have the same appearance. The chosen correlation time steps,
ncorr, were 100
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000, 100
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000, 15
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000, and 1000, for
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
= 4, 8, 16, and 32, respectively. To increase statistical sampling, new overlapping time-series were created after
ncorr/10 time steps, while the total duration of each simulation was 10
7 time steps.
 |
| | Fig. 3 Einstein–Helfand correlation as a function of time and its linear regression at a density of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 3, which is used for the calculation of the viscosity; R(t) − R(0) represents = 3, which is used for the calculation of the viscosity; R(t) − R(0) represents  . . | |
3.1.2 Shear viscosity measurements.
For the viscosity measurements, we performed simulations under the conditions described in ref. 28. We used a standard DPD isothermal algorithm to match the exact same conditions of the benchmark simulations that will be discussed in the comparison. However, we also include values of shear viscosity obtained from GenDPDE simulations, with a large heat capacity (CV = 1000), to show the equivalence with isothermal DPD simulations under these conditions. As in the reference work, no potential forces between the particles were considered. The number of particles was set to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and different box volumes were chosen to obtain
000, and different box volumes were chosen to obtain ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 3, 4, 5, 6, 7, quoted in the benchmark reference, plus
= 3, 4, 5, 6, 7, quoted in the benchmark reference, plus ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 8, 16 and 32, which we have computed to extend the parameter range. The simulations were performed at T = 1, γ = 5 and δt = 0.01, for densities from 3 to 7, as in the benchmark, and δt = 0.005, 0.002 and 0.001 for densities 8, 16 and 32, respectively. Correlation windows of sizes ncorr = 2000, 1500, 1000, 1000, 1000, 1000, 1000 and 500 time steps were used for
= 8, 16 and 32, which we have computed to extend the parameter range. The simulations were performed at T = 1, γ = 5 and δt = 0.01, for densities from 3 to 7, as in the benchmark, and δt = 0.005, 0.002 and 0.001 for densities 8, 16 and 32, respectively. Correlation windows of sizes ncorr = 2000, 1500, 1000, 1000, 1000, 1000, 1000 and 500 time steps were used for ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 3, 4, 5, 6, 7, 8, 16 and 32, respectively. New time-series were created after 20 timesteps, while the total simulated time was 107 time steps.
= 3, 4, 5, 6, 7, 8, 16 and 32, respectively. New time-series were created after 20 timesteps, while the total simulated time was 107 time steps.
3.2 Thermal conductivity via non-equilibrium simulations
For comparison to the EH data, we also performed independent non-equilibrium simulations. The box was orthorhombic in the x-direction, where a thermal gradient is present. The box length in the x-direction Lx was three times larger than in the other two directions, i.e., Ly = Lz = Lx/3, and periodic boundary conditions were applied in all directions; for details see Fig. 2a. The non-equilibrium system contained a hot and a cold slab, whose mid-plane was located at x = Lx/4 and x = 3Lx/4, respectively. The width of the hot and the cold slabs was Lx/10 in the x-direction. We enforced heat flow in the system by artificially pumping heat from the internal energy of the particles located in the cold region into the internal energy of the particles located in the hot region, such that the total energy of the system is constant. This method corresponds to an extension of the PeX algorithm to GenDPDE systems.39,40 Using this approach, a heat flow rate ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) = 500 was sustained, such that when steady-state conditions were reached, a linear temperature gradient developed between the hot and cold slabs. The value of the externally imposed heat exchange rate was chosen to create a relatively small temperature gradient between the regions to avoid non-linearities due to variations in the local particle density, which may influence the thermal conductivity; see Fig. 2b.
= 500 was sustained, such that when steady-state conditions were reached, a linear temperature gradient developed between the hot and cold slabs. The value of the externally imposed heat exchange rate was chosen to create a relatively small temperature gradient between the regions to avoid non-linearities due to variations in the local particle density, which may influence the thermal conductivity; see Fig. 2b.
The values of the thermal conductivity coefficient λ from the non-equilibrium simulations were obtained from a direct application of Fourier's law
| | ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) = −λ∇T = −λ∇T | (60) |
For our non-equilibrium system with the hot and cold regions, we obtained the thermal conductivity from
| |  | (61) |
where
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif)
is the amount of heat transferred from the cold region to the hot region during a timestep, and
A is the cross-sectional area along the
yz-plane. Both were set
a priori in the simulation. The resulting temperature gradient was estimated from the ratio Δ
T/Δ
x obtained from the linear portion of the temperature profile that formed between the hot and cold regions in the
x-direction; see
Fig. 2b.
3.3 Shear viscosity via non-equilibrium simulations
Similarly to the simulations performed for the thermal conductivity, we also conducted independent non-equilibrium simulations for the shear viscosity. The box length in the x-direction Lx was two times larger than in the other two directions, i.e., Ly = Lz = Lx/2, and periodic boundary conditions were applied in all directions. The non-equilibrium shear viscosity was imposed using PeX method.39,40 To induce a velocity gradient we defined two narrow slabs in specific locations along the x-axis. We thus exchange the largest momentum in positive z-direction of the slab located at x = Lx/4, with the largest momentum in negative z-direction of the slab located at x = 3Lx/4. The width of both slabs was Δx = Lx/10. The timestep for the simulations is the same as in the corresponding equilibrium simulations described above. The values of the shear viscosity η are obtained from the relation:| |  | (62) |
were  is the induced velocity gradient between slabs, which we measured by a linear regression of the velocity profile in the central region. Πxz is the shear stress imposed due to the exchange in momentum between slabs that can be obtained as,
is the induced velocity gradient between slabs, which we measured by a linear regression of the velocity profile in the central region. Πxz is the shear stress imposed due to the exchange in momentum between slabs that can be obtained as,| | 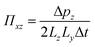 | (63) |
where Δpz is the accumulated momentum exchanged in a given, sufficiently long, time interval Δt, after the system reaches steady state. The stress is thus controlled by the frequency with which the momenta exchanges are introduced, nexc. LzLy is the cross-sectional area of the x-side of the box. The number 2 in the denominator is due to the duplication of the velocity gradient in the simulation setup.
4 Results and discussion
4.1 Benchmark results for the shear viscosity
Firstly, we verify that the classic EH formula given in eqn (55) with the stress tensor given in eqn (53) can be applied to obtain the viscosity. In Fig. 3, we represent the correlation function| | 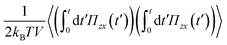 | (64) |
A linear regression for the linear portion of the correlation, after an initial non-diffusive regime, permits a value of the viscosity to be identified from its slope. We first compare our results using the EH relation of eqn (55) to the non-equilibrium data given by Jung and Schmidt,28 who considered a limited range of rather low densities ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 3, 4, 5, 6, and 7. In Fig. 4, we provide a comparison between our results and the non-equilibrium values of the viscosity from Fig. 5 of ref. 28, showing excellent agreement between both of them.
= 3, 4, 5, 6, and 7. In Fig. 4, we provide a comparison between our results and the non-equilibrium values of the viscosity from Fig. 5 of ref. 28, showing excellent agreement between both of them.
 |
| | Fig. 4 Comparison between values of the viscosity obtained from our proposed EH formula and non-equilibrium simulation results of Fig. 5 in ref. 28. Blue circles correspond to isothermal DPD simulations with γ = 5, T = 1, and the same time step as in the original reference, δt = 0.01. The errors are of the size of the symbols. Green triangles represent the values obtained from GenDPDE simulations with large heat capacity CV = 1000 and an interparticle thermal conductivity κ = 50. | |
Furthermore, to demonstrate that the EH formulas are applicable to very dissipative systems, we also evaluated the viscosity for larger densities, namely, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 4, 8, 16, and 32, which are presented in Fig. 5 together with our non-equilibrium simulations and the theoretical predictions,41
= 4, 8, 16, and 32, which are presented in Fig. 5 together with our non-equilibrium simulations and the theoretical predictions,41
| | 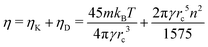 | (65) |
We see that the simulation results from the derived EH relation (
eqn (55)) are again in excellent agreement with the non-equilibrium results. Furthermore, the results are consistent and in rather good agreement with the theory in the large density limit. The discrepancies between theory and simulations have been addressed in ref.
42 and
43.
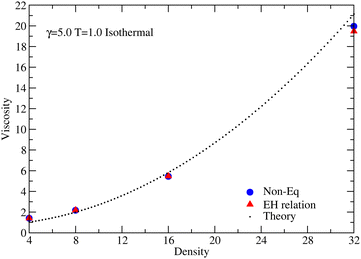 |
| | Fig. 5 Viscosity as a function of the system density. Red triangles represent the results obtained from equilibrium DPD simulations using our proposed EH relation, eqn (55). Blue circles represent the results obtained from non-equilibrium DPD simulations and the dotted black line represents predicted theoretical values. The simulations have been performed with γ = 5.0 under isothermal conditions at T = 1.0. The integration was performed with a timestep of δt = 0.01, 0.005, 0.002 and 0.001 for ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 4, 8, 16 and 32, respectively. The largest errors occur in the non-equilibrium simulations at density = 4, 8, 16 and 32, respectively. The largest errors occur in the non-equilibrium simulations at density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 32, (0.2 with the 68% confidence), which is of the size of the symbol. = 32, (0.2 with the 68% confidence), which is of the size of the symbol. | |
In Table 1 we present the results obtained from the approaches of the aforementioned authors, for comparison. Our approach is in excellent agreement with the non-equilibrium evaluation of the shear viscosity, which should be taken as the objective reference for the estimate of this transport coefficient, as it emulates the physical process. The estimates using the various formulas are very close to each other and within the error in the estimate of the non-equilibrium simulation. Only the data of column EH (a) slightly underestimate the value of the shear viscosity coefficient.
Table 1 Comparison of the various approaches to determine the shear viscosity. Non equilibrium values for densities from ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 3, 4, 5, 6, 7 are obtained from ref. 28, while for densities
= 3, 4, 5, 6, 7 are obtained from ref. 28, while for densities ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 8, 16, 32 are our own simulation data. (a) Values calculated from the EH formula in ref. 29, eqn. (2.14). The errors in the EH equations are evaluated from the error in the slope of the linear regression. (b) Values calculated using eqn (19) in ref. 27. The error is calculated from the fitting of the hydrodynamic part of the decay of the correlation to a function of the type y = Ae−btc, where A, b and c are adjustable parameters. Errors in the non-equilibrium simulations are entirely due to the linear regression used to determine the linear velocity gradient in the box
= 8, 16, 32 are our own simulation data. (a) Values calculated from the EH formula in ref. 29, eqn. (2.14). The errors in the EH equations are evaluated from the error in the slope of the linear regression. (b) Values calculated using eqn (19) in ref. 27. The error is calculated from the fitting of the hydrodynamic part of the decay of the correlation to a function of the type y = Ae−btc, where A, b and c are adjustable parameters. Errors in the non-equilibrium simulations are entirely due to the linear regression used to determine the linear velocity gradient in the box
| Density |
η
|
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
|
Non-equ. |
EH (eqn (55)) |
EH (a) |
GK (b) |
| 3 |
1.28 ± 0.01 |
1.2790 ± 0.0002 |
1.2360 ± 0.0002 |
1.286 ± 0.002 |
| 4 |
1.40 ± 0.01 |
1.4110 ± 0.0003 |
1.3730 ± 0.0003 |
1.418 ± 0.002 |
| 5 |
1.56 ± 0.01 |
1.5733 ± 0.0003 |
1.4940 ± 0.0003 |
1.543 ± 0.002 |
| 6 |
1.74 ± 0.01 |
1.7337 ± 0.0002 |
1.6720 ± 0.0002 |
1.731 ± 0.003 |
| 7 |
1.96 ± 0.01 |
1.9613 ± 0.0003 |
1.8740 ± 0.0003 |
1.989 ± 0.003 |
| 8 |
2.17 ± 0.01 |
2.1860 ± 0.0002 |
2.0840 ± 0.0002 |
2.169 ± 0.004 |
| 16 |
5.45 ± 0.02 |
5.4749 ± 0.0005 |
5.4400 ± 0.0005 |
5.434 ± 0.008 |
| 32 |
20.0 ± 0.2 |
19.479 ± 0.003 |
19.470 ± 0.003 |
19.68 ± 0.03 |
4.2 Results for the thermal conductivity
To assess the ability of eqn (50) with the heat flow density given in eqn (47) to evaluate the thermal conductivity, we simulated four densities ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 4, 8, 16, and 32 under equilibrium and non-equilibrium conditions. The thermal conductivity in non-equilibrium conditions was obtained as described in Section 3.1. In all cases, we also include the theoretical prediction derived from the superposition of the limit of interparticle heat transport dominance37 and the limit of kinetic transport dominance,44i.e.,
= 4, 8, 16, and 32 under equilibrium and non-equilibrium conditions. The thermal conductivity in non-equilibrium conditions was obtained as described in Section 3.1. In all cases, we also include the theoretical prediction derived from the superposition of the limit of interparticle heat transport dominance37 and the limit of kinetic transport dominance,44i.e.,| |  | (66) |
We explored three cases. First, we considered a system without conservative forces and a relatively large particle thermal conductivity κ, case A. This corresponds to the situation where the transport is dominated by the dissipative heat exchange between particles over kinetic transport; the latter controlled by either ballistic or even diffusive motion, which can be faster than the direct heat transport between particles, and which is a genuine effect of energy-conserving DPD methods. In the second case, case B, we further analysed the same system, but with lower values of κ. In both cases, the GenDPDE method studied the ideal DPDE fluid. Finally in the third case, case C, we explored the effect of the interparticle many-body conservative forces at moderate values of κ, corresponding to the model given in eqn (58).
For case A in Fig. 6, we plot the thermal conductivity λ as a function of the density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) for equilibrium and non-equilibrium simulations, which are compared with the theoretical prediction, for completeness. The simulations were carried out at T = 1 and with κ = 50, γ = 4.5, and CV = 60. The EH values and the non-equilibrium simulation results are in excellent agreement over the entire range of
for equilibrium and non-equilibrium simulations, which are compared with the theoretical prediction, for completeness. The simulations were carried out at T = 1 and with κ = 50, γ = 4.5, and CV = 60. The EH values and the non-equilibrium simulation results are in excellent agreement over the entire range of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) studied, supporting the correctness of the combination of eqn (50) and (47).
studied, supporting the correctness of the combination of eqn (50) and (47).
 |
| | Fig. 6 Thermal conductivity as a function of the density for values of the particle thermal conductivity κ = 50 and 5. The circles represent the results obtained from non-equilibrium DPDE simulations (red circles κ = 50 and blue circles κ = 5), the triangles from equilibrium DPDE simulations using our proposed EH relation (green triangles κ = 50 and grey triangles κ = 5), and the predicted theoretical value from mean-field approximation (dotted black line). | |
From the theoretical expression eqn (66), a naïve approach suggests that the system is dominated by the interparticle heat transport if the condition  , where the second equality is obtained after the values of the dimensionless constant parameters have been introduced. Therefore for case A, the crossover density is approximately
, where the second equality is obtained after the values of the dimensionless constant parameters have been introduced. Therefore for case A, the crossover density is approximately ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) c ≃ 10, which implies that most of the data are in the region dominated by the direct interparticle heat transport. In comparison with the theoretical prediction, the simulation values of λ are also in rather good agreement. There is a small deviation as we increase the density, which was previously noted in ref. 37.
c ≃ 10, which implies that most of the data are in the region dominated by the direct interparticle heat transport. In comparison with the theoretical prediction, the simulation values of λ are also in rather good agreement. There is a small deviation as we increase the density, which was previously noted in ref. 37.
Case B is explored by reducing the value of κ, but still in the absence of any conservative force. The simulations were performed at T = 1 and with κ = 5, γ = 4.5, and CV = 60. Under these conditions, case B describes a dominance of the kinetic regime as the crossover density is ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) c ∼ 30. In Fig. 6, we plot the thermal conductivity λ as a function of the density
c ∼ 30. In Fig. 6, we plot the thermal conductivity λ as a function of the density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) . Again, we observe that the equilibrium and non-equilibrium simulation results are in very good agreement over the entire range of
. Again, we observe that the equilibrium and non-equilibrium simulation results are in very good agreement over the entire range of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) studied. However, the theoretical prediction eqn (66) yields values significantly lower than the simulation values over the entire density range. The quantitative theoretical analysis of the thermal conductivity with respect to the different parameters will be presented elsewhere.
studied. However, the theoretical prediction eqn (66) yields values significantly lower than the simulation values over the entire density range. The quantitative theoretical analysis of the thermal conductivity with respect to the different parameters will be presented elsewhere.
Finally for case C, we also included the conservative many-body forces between the particles given by eqn (31), using eqn (58). In Fig. 7, we plot the thermal conductivity λ as a function of the density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) from equilibrium and non-equilibrium simulations. The GenDPDE simulations were carried out at T = 1, with κ = 5, γ = 4.5 and CV = 60, and with β = 0.2 and n0 =
from equilibrium and non-equilibrium simulations. The GenDPDE simulations were carried out at T = 1, with κ = 5, γ = 4.5 and CV = 60, and with β = 0.2 and n0 = ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) in eqn (58). From Fig. 7, we can observe that the equilibrium and non-equilibrium simulation results are again in very good agreement over the density range studied. With respect to the theoretical predictions, a disagreement is expected as the derivation of eqn (66) does not include any conservative force between the particles.
in eqn (58). From Fig. 7, we can observe that the equilibrium and non-equilibrium simulation results are again in very good agreement over the density range studied. With respect to the theoretical predictions, a disagreement is expected as the derivation of eqn (66) does not include any conservative force between the particles.
 |
| | Fig. 7 Thermal conductivity as a function of the density for a value of the particle thermal conductivity κ = 5, and with conservative forces that follow from eqn (58). The circles represent the results obtained from non-equilibrium simulations (blue circles), the triangles from equilibrium simulations using our proposed EH relation (grey triangles) and the predicted theoretical values from mean-field approximation (dotted black line). | |
5 Conclusions
In this work we have shown that the standard Einstein–Helfand relations for the calculation of transport coefficients in DPD-type algorithms are valid. The key element is that the appropriate expression for the conserved property flux for the mesoscopic model needs to be specifically determined. We have applied this perspective to derive, for the first time, the heat flux density for a general energy-conserving dissipative particle dynamics method (GenDPDE) from which the thermal conductivity has been evaluated. For the expression to be appropriate for any DPD-type algorithm, all that is required is for it to satisfy two conditions: that the transported property is conserved by the mesoscopic dynamics, and that the transition probabilities induced by the latter satisfy detailed balance. These two basic conditions are inherited from the underlying physical system, i.e., the conservation of the transported property and the time-reversibility of the physical trajectories at the microscopic level.
As verification of the correctness of the previous statements, we have evaluated the shear viscosity as well as the thermal conductivity from non-equilibrium simulations and compared them against the corresponding EH values, with excellent agreement found in all the cases considered. For both properties, we previously evaluated the corresponding expressions for the stress tensor and the heat flux density adequate for these dissipative systems, which include non-trivial contributions due to the dissipative and random terms. Therefore, the theoretical demonstration together with the simulation results support our claim that the standard equilibrium approach using EH correlations can be applied to dissipative models such as DPD-type algorithms.
With regards to the simulations, we have addressed a rather wide range of densities. The increase of the density results in an increase of the number of neighbours and the dissipative effects, which complicate the simulation analyses. The number of neighbours ranges from 17 at ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 4 to 134 at
= 4 to 134 at ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 32. Even in highly dissipative conditions like the latter, the EH formulas provide reliable accurate data. For the heat transport, we have studied two different regimes depending on whether the transport is dominated by advective or dissipative effects. We have analysed a third case with density-dependent potential interactions, which strongly influence the behaviour of the system. In all these cases the agreement is excellent, which we consider sound verification of our methodology. For completeness, we have also addressed the case of the shear viscosity. We have derived the expression for the stress tensor suitable for GenDPDE, and hence for all DPD-type methods that can be derived from it, which include the standard isothermal DPD method that was used as a benchmark in this work. The agreement between our data and the non-equilibrium simulations of Jung and Schmid,28 together with our non-equilibrium data for the extended density range, is also excellent. Note that in this last reference, non-equilibrium simulations were used to compare with different Green–Kubo expressions specifically obtained for DPD-type methods.27 The different equilibrium evaluations are given in Table 1 for comparison. Despite the different, possibly conflicting, theoretical perspectives from which these were obtained, the numerical differences are or the order of the error in the non-equilibrium simulation data. Only the data obtained from the EH formula derived from it in ref. 29 systematically deviates from the benchmark, we believe because some of the correlations present in the GK formula of ref. 27 were lost in its transformation to the EH counterpart proposed in the former. The analysis of the GK expressions of ref. 27 in comparison with the present EH relations is relevant, we prefer to leave this discussion for a more detailed study.
= 32. Even in highly dissipative conditions like the latter, the EH formulas provide reliable accurate data. For the heat transport, we have studied two different regimes depending on whether the transport is dominated by advective or dissipative effects. We have analysed a third case with density-dependent potential interactions, which strongly influence the behaviour of the system. In all these cases the agreement is excellent, which we consider sound verification of our methodology. For completeness, we have also addressed the case of the shear viscosity. We have derived the expression for the stress tensor suitable for GenDPDE, and hence for all DPD-type methods that can be derived from it, which include the standard isothermal DPD method that was used as a benchmark in this work. The agreement between our data and the non-equilibrium simulations of Jung and Schmid,28 together with our non-equilibrium data for the extended density range, is also excellent. Note that in this last reference, non-equilibrium simulations were used to compare with different Green–Kubo expressions specifically obtained for DPD-type methods.27 The different equilibrium evaluations are given in Table 1 for comparison. Despite the different, possibly conflicting, theoretical perspectives from which these were obtained, the numerical differences are or the order of the error in the non-equilibrium simulation data. Only the data obtained from the EH formula derived from it in ref. 29 systematically deviates from the benchmark, we believe because some of the correlations present in the GK formula of ref. 27 were lost in its transformation to the EH counterpart proposed in the former. The analysis of the GK expressions of ref. 27 in comparison with the present EH relations is relevant, we prefer to leave this discussion for a more detailed study.
The importance of EH expressions for the measurement of transport coefficients lies in the fact that a single simulation can provide the entire set of the transport coefficients with no modification of the simulation setup to include any particular boundary conditions, which are required in non-equilibrium simulations. Thus, for energy-conserving methods like GenDPDE, the thermal conductivity and the shear viscosity can be simultaneously calculated with significant economy of computational time and effort.
We believe that the approach proposed in this article will be essential for future applications of any mesoscopic model that falls under the scope of the two conditions required by the EH formulas to be valid. Finally, together with energy and momentum, further conserved properties and their corresponding transport coefficients can be handled in mesoscopic models by the same framework presented in this work.
Author contributions
DCM, ADM and JBA have contributed to the investigation, methodology, formal analysis, validation, visualisation and writing of the original draft. In addition, JBA has contributed to the conceptualisation and project management. ML, JPL and JKB have contributed to the formal analysis and editing of the original draft and finalising the manuscript.
Conflicts of interest
There are no conflicts to declare.
Appendices
A. Derivation of the properties of JARk
The derivation of the properties of JARk follows the methodology introduced in ref. 11 and 12. Due to the fact that eqn (5) induces a Markovian process linearly proportional to Ak, the random flux is Gaussian. Although it is a necessary condition for eqn (8) to be satisfied, we refer the reader to the classical works for a detailed demonstration.31,33,34 However, this assumption is not necessary if only the first and second moments of the random variable Ak need to be calculated, which indeed is our only requirement.
First, we consider eqn (8) and multiply both sides by 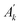 , followed by an integration over Ak and
, followed by an integration over Ak and  . The left-hand side corresponds to the direct trajectory and becomes
. The left-hand side corresponds to the direct trajectory and becomes
| | 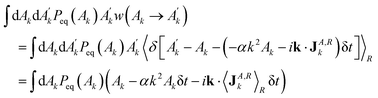 | (A1) |
For the reverse trajectory we have
| |  | (A2) |
The average is independent of whether the field belongs to the reverse or direct trajectory because the equilibrium average is only concerned with the state of the field, but not with the dynamics. Note that if
Ak is even, the zeroth-order term in δ
t vanishes. Thus in this case, because the flux should vanish in equilibrium, −
αk2〈
Ak〉
eq = 0. Hence, it follows that 〈
Ak〉
eq = 0 for
k ≠ 0. For an odd
Ak, instead 〈
Ak〉
eq = 0 due to the symmetry of the argument of the probability distribution.
31 Note that outside of the linear regime,
α may depend on
Ak and hence the previous statement would not be valid. Therefore in general,
| |  | (A3) |
from which we obtain
eqn (10).
Next, we again consider eqn (8), but we multiply both sides by  , followed by the same integration over Ak and
, followed by the same integration over Ak and  . For the direct trajectory we obtain
. For the direct trajectory we obtain
| |  | (A4) |
while, using the same transformations as for the first moment, the average over the reverse trajectory gives
| | 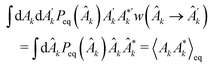 | (A5) |
Due to this result, the zeroth-order terms identically cancel. Moreover by construction, the random fluxes are not correlated with the state variables at the same time and 〈
JARk〉 = 0, thus we are left with the equality
| |  | (A6) |
Hence, realising that

is taken at the same instant of time, we can write the FDT in its final form as given in
eqn (11).
B. Derivation of the expression for the heat flux density in GenDPDE
The starting point for the derivation of the expression for the heat flux density in GenDPDE is the energy density field, which in Fourier space becomes| |  | (B1) |
The dynamics of the energy density field follows after time differentiation, i.e.,| |  | (B2) |
where we defined the particle total energy content εi = pi2/(2mi) + ui.
Due to the fact that there are many contributions, we separate the analysis into three contributions, corresponding to the three terms on the right-hand side of eqn (B2), which are addressed as sections in this Appendix.
B.1 Second term in eqn (B2).
The second term in eqn (B2) can be separated into four additional contributions, in view of eqn (39), which may be written as| | 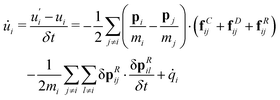 | (B3) |
On the right-hand side of eqn (39), we have the mechanical energy transport, which first includes the work done by all the forces acting on the particles, followed by a second-order random momenta contribution. The last term contains the contributions due to the direct heat flow between particles, including the random heat flow. We start with the analysis of this last contribution to the second term in eqn (B2) because its simpler form illustrates the technical procedure required to derive its contribution to the heat flux density, which later be applied to more complex terms.
B.1.1 Dissipative heat transport contributions.
Let us consider the term| | 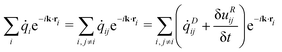 | (B4) |
in the hydrodynamic limit, i.e., krij → 0. Then, we separate the double summation into two similar contributions| |  | (B5) |
The order of the summation can be changed in the second term to get| |  | (B6) |
Next, we rename the dummy indices of the second term by exchanging their names.| |  | (B7) |
where we used ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) ji = −
ji = −![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) ij. The range of the particle–particle interaction rc is typically much smaller than the box size L. Thus, provided that rc ≪ L, we can proceed to take the hydrodynamic limit also for a finite system since, as kmin = 2π/L, kminrc ≪ 1. Then,
ij. The range of the particle–particle interaction rc is typically much smaller than the box size L. Thus, provided that rc ≪ L, we can proceed to take the hydrodynamic limit also for a finite system since, as kmin = 2π/L, kminrc ≪ 1. Then,| | 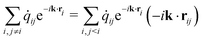 | (B8) |
Therefore, we can write the final contribution to the heat flux density as| |  | (B9) |
B.1.2 Mechanical energy transport.
Next, we substitute the first term of eqn (B3) into eqn (B2), where then the term to be investigated is| | 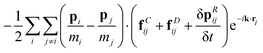 | (B10) |
As before, separating the summation over j into two sums, exchanging the indices, and using the symmetries of the summation arguments, this term can be written as| |  | (B11) |
Note that here the permutation of the particle indices has different parity as compared with the previous case. As a consequence, the expansion in terms of k·rij → 0 produces a zeroth order term plus a contribution proportional to k, which adds to the energy flux. The zeroth order term is| |  | (B12) |
In turn, the contribution to the flux becomes| | 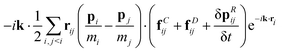 | (B13) |
B.1.3 Second-order random terms.
The last term to be analysed is the second term of eqn (B3), which again is cast into eqn (B2). Effectively, the quadratic random term contribution in eqn (39) leads to| |  | (B14) |
where we summed over the index l in the derivation of the right-hand side of this equation. Repeating the same algebraic transformations of the sums, and using the symmetries under permutation of the indices because the parity of the term is the same as in eqn (B18), we obtain analogous contributions. The zeroth order term is| | 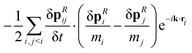 | (B15) |
while the contribution to the flux becomes| |  | (B16) |
B.2 First term in eqn (B2).
The first term in eqn (B2) can be expanded using the equation of motion, eqn (27), together with the discrete definition of the time derivative, which we write here again for clarity:| | 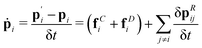 | (B17) |
Hence,| |  | (B18) |
Hence using the same approach as in Section B.1.1, the equivalent of eqn (B7) is| | 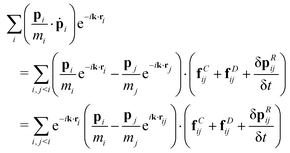 | (B19) |
The expansion in powers of k·rij yields two terms. The first term remains in the hydrodynamic limit, while the second term is a contribution to the energy flux. The first term becomes| | 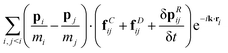 | (B20) |
while the second is| |  | (B21) |
B.3 Complete expression for the energy flux.
Gathering all terms together, eqn (B9), (B13), (B16) and (B21), and adding the last term of eqn (B2), we obtain| |  | (B22) |
Using the definitions of the random forces and heat flux, and writing ṙi = ui, we obtain| |  | (B23) |
The result in eqn (47) follows from again taking the hydrodynamic limit such that e−ik·ri → 1.
C. Derivation of the expression for the stress tensor in GenDPDE
The conserved field for the stress tensor in GenDPDE is the momentum flux density, which in terms of mesoscopic variables, can be written as| |  | (C1) |
The dynamics of the momentum flux is obtained after differentiation, i.e.,| | 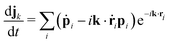 | (C2) |
The expression for ṗi is given in (B17). Hence,| |  | (C3) |
Analogous to the derivations in Section B.1.1, the double summations involving the forces can be expanded to obtain two terms. The zeroth order term is the total force on the system, which identically cancels because no external forces have been considered. The first order term gives the contribution to the stress tensor due to pairwise forces, which produces the result given in eqn (52),| |  | (C4) |
Acknowledgements
The authors would like to thank Prof. F. Schmid and Dr G. Jung for making their data available. Research performed by JBA and ADM was sponsored by the Army Research Office under Cooperative Agreement Number W911NF-20-2-0227 and Grant PID2021-122187NB-C33 funded by MCIN/AEI/10.13039/501100011033 and ERDF A way of making Europe. Research performed by ML was sponsored by the Army Research Office under Cooperative Agreement Number W911NF-20-2-0203. JKB and JPL acknowledge support in part for a grant of computer time from the DoD High Performance Computing Modernization Program at the Army, Navy, and Air Force Supercomputing Resource Centers.
Notes and references
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- P. Español and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef.
- J. B. Avalos and A. D. Mackie, Europhys. Lett., 1997, 40, 141–146 CrossRef CAS.
- P. Español, Europhys. Lett., 1997, 40, 631–636 CrossRef.
- M. Lísal, J. K. Brennan and J. B. Avalos, J. Chem. Phys., 2011, 135, 204105 CrossRef PubMed.
- I. Pagonabarraga and D. Frenkel, J. Chem. Phys., 2001, 115, 5015 CrossRef CAS.
- P. B. Warren, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 066702 CrossRef CAS PubMed.
- J. D. Moore, B. C. Barnes, S. Izvekov, M. Lísal, M. S. Sellers, D. E. Taylor and J. K. Brennan, J. Chem. Phys., 2016, 144, 104501 CrossRef PubMed.
- J. K. Brennan, M. Lisal, J. D. Moore, S. Izvekov, I. V. Schweigert and J. P. Larentzos, J. Phys. Chem. Lett., 2014, 5, 2144–2149 CrossRef CAS PubMed.
- J. P. Larentzos, J. M. Mansell, M. Lísal and J. K. Brennan, Mol. Phys., 2018, 116, 3271–3282 CrossRef CAS.
- J. B. Avalos, M. Lísal, J. P. Larentzos, A. D. Mackie and J. K. Brennan, Phys. Chem. Chem. Phys., 2019, 21, 24891–24911 RSC.
- J. B. Avalos, M. Lísal, J. P. Larentzos, A. D. Mackie and J. K. Brennan, Phys. Rev. E, 2021, 103, 062128 CrossRef PubMed.
- M. Lísal, J. P. Larentzos, J. B. Avalos, A. D. Mackie and J. K. Brennan, J. Chem. Theory Comput., 2022, 18, 2503–2512 CrossRef PubMed.
- J. B. Avalos, M. Lísal, J. P. Larentzos, A. Mackie and J. K. Brennan, J. Chem. Theory Comput., 2022, 18(12), 7639–7652 CrossRef CAS PubMed.
- M. Lísal, J. B. Avalos, J. P. Larentzos, A. Mackie and J. K. Brennan, J. Chem. Theory Comput., 2022, 18(12), 7653–7670 CrossRef PubMed.
- E. Moeendarbary, T. Y. Ng and M. Zangeneh, Int. J. Appl. Mech., 2009, 01, 737–763 CrossRef.
- P. Español and P. B. Warren, J. Chem. Phys., 2017, 146, 150901 CrossRef PubMed.
- K. P. Santo and A. V. Neimark, Adv. Colloid Interface Sci., 2021, 298, 102545 CrossRef CAS PubMed.
-
M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Cambridge, UK, 2017 Search PubMed.
- J. A. Backer, C. P. Lowe, H. C. J. Hoefsloot and P. D. Iedema, J. Chem. Phys., 2005, 122, 154503 CrossRef CAS PubMed.
- A. Boromand, S. Jamali and J. M. Maia, Comput. Phys. Commun., 2015, 196, 149–160 CrossRef CAS.
- M. S. Green, J. Chem. Phys., 1954, 22, 398–413 CrossRef CAS.
- R. Kubo, J. Phys. Soc. Jpn., 1957, 12, 570–586 CrossRef.
- A. Einstein, Ann. Phys., 1905, 322, 549–560 CrossRef.
- E. Helfand, Phys. Rev., 1960, 119, 1 CrossRef.
-
J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Elsevier, 2006 Search PubMed.
- M. H. Ernst and R. Brito, Europhys. Lett., 2006, 73, 183–189 CrossRef CAS.
- G. Jung and F. Schmid, J. Chem. Phys., 2016, 144, 204104 CrossRef PubMed.
- M. Panoukidou, C. R. Wand and P. Carbone, Soft Matter, 2021, 17, 8343–8353 RSC.
- N. Lauriello, J. Kondracki, A. Buffo, G. Boccardo, M. Bouaifi, M. Lsal and D. Marchisio, Phys. Fluids, 2021, 33, 073106 CrossRef CAS.
-
N. G. van Kampen, Stochastic Processes in Physics and Chemistry, North Holland, 1992 Search PubMed.
-
M. P. Allen, Computer Simulation in Chemical Physics. Proceedings of the NATO Advanced Study Institute on New Perspectives in Computer Simulation in Chemical Physics Alghero, Sardinia, Italy, September 14–24, 1992, Dordrecht, 1993, pp. 49–92.
- L. Onsager and S. Machlup, Phys. Rev., 1953, 91, 1505–1512 CrossRef CAS.
-
S. R. de Groot and P. Mazur, Non-equilibrium Thermodynamics, Dover Publications, Inc., 1984 Search PubMed.
- B. J. Alder, D. M. Gass and T. E. Wainwright, J. Chem. Phys., 1970, 53, 3813–3826 CrossRef CAS.
- J. J. Erpenbeck, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 6255–6266 CrossRef CAS PubMed.
- J. B. Avalos and A. D. Mackie, J. Chem. Phys., 1999, 111, 5267–5276 CrossRef CAS.
- A. D. Mackie, J. B. Avalos and V. Navas, Phys. Chem. Chem. Phys., 1999, 1, 2039–2049 RSC.
- F. Müller-Plathe, J. Chem. Phys., 1997, 106, 6082–6085 CrossRef.
- C. Nieto-Draghi and J. B. Avalos, Mol. Phys., 2003, 101, 2303–2307 CrossRef CAS.
- C. A. Marsh, G. Backx and M. H. Ernst, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1997, 56, 1676–1691 CrossRef CAS.
- A. J. Masters and P. B. Warren, Europhys. Lett., 1999, 48, 1–7 CrossRef CAS.
- G. T. Evans, J. Chem. Phys., 1999, 110, 1338–1342 CrossRef CAS.
- F. A. Soleymani, M. Ripoll, G. Gompper and D. A. Fedosov, J. Chem. Phys., 2020, 152, 064112 CrossRef CAS PubMed.
Footnote |
| † In previous works we have used the so-called dressed entropy to define the adiabatic conditions,11,12 since our control variable was s (see the definition of control variable in ref. 12). Throughout this article, we consider that the control variable is the internal energy u, which corresponds to the use of bare variables instead of the dressed variables. Choosing one or the other is a matter of convenience, as the physical behaviour is independent of the choice, once the model has been established. |
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
M.
Lísal
a,
M.
Lísal
 bc,
J. P.
Larentzos
d,
J. K.
Brennan
d,
A. D.
Mackie
bc,
J. P.
Larentzos
d,
J. K.
Brennan
d,
A. D.
Mackie
 a and
J. Bonet
Avalos
a and
J. Bonet
Avalos
 *a
*a
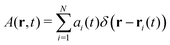
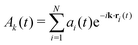
 .
.




 and Ak = Ak(t) for the direct trajectory while
and Ak = Ak(t) for the direct trajectory while  and
and  for the reverse trajectory. The sign σ depends on whether the variable A is even (σ = +1) or odd (σ = −1) under time reversibility. The transition probabilities can be derived from the stochastic dynamics of the field, eqn (5) and (6), i.e.,
for the reverse trajectory. The sign σ depends on whether the variable A is even (σ = +1) or odd (σ = −1) under time reversibility. The transition probabilities can be derived from the stochastic dynamics of the field, eqn (5) and (6), i.e.,

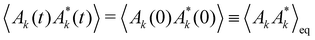 is the equilibrium equal-time correlation, which is independent of time, due to the time-translational invariance of the equilibrium properties.
is the equilibrium equal-time correlation, which is independent of time, due to the time-translational invariance of the equilibrium properties.






![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) = k/k. The microscopic expression of JAk is to be used in eqn (17). Such an expression should be derived from the fact that
= k/k. The microscopic expression of JAk is to be used in eqn (17). Such an expression should be derived from the fact that  , in agreement with eqn (7). Under this form, one can consistently take the formal limit k → 0. The
, in agreement with eqn (7). Under this form, one can consistently take the formal limit k → 0. The ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) vectors are arbitrary as they merely indicate the wavevector direction of the relaxing plane wave whose relaxation is formally being studied.
vectors are arbitrary as they merely indicate the wavevector direction of the relaxing plane wave whose relaxation is formally being studied.


![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) = (1, 0, 0) in eqn (17), we obtain the well-known result for the diffusion coefficient
= (1, 0, 0) in eqn (17), we obtain the well-known result for the diffusion coefficient


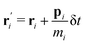
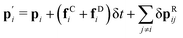

 related to the local particle number density ni, is required. The ni and
related to the local particle number density ni, is required. The ni and  are related by
are related by

 , i.e., the local density ni and on the particle bare temperature
, i.e., the local density ni and on the particle bare temperature ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) .11,12 The conservative force is thus fCi = − ∂ui/∂ri|
.11,12 The conservative force is thus fCi = − ∂ui/∂ri|![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) i, which can be separated into pairwise contributions of the form
i, which can be separated into pairwise contributions of the form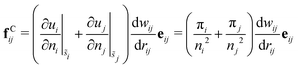
 is the particle pressure, and dwij/drij < 0. The subscript
is the particle pressure, and dwij/drij < 0. The subscript ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) i emphasizes that the derivative is taken under adiabatic conditions (i.e., no simultaneous heat transfer between particles occur while updating velocities and positions). The bare entropy is defined from the density of states
i emphasizes that the derivative is taken under adiabatic conditions (i.e., no simultaneous heat transfer between particles occur while updating velocities and positions). The bare entropy is defined from the density of states  of the non-resolved DoF of the mesoscopic particle
of the non-resolved DoF of the mesoscopic particle





![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) i related to particle temperature differences. Given that Ė = 0 if the total energy is to be conserved, we define the variation of the particle internal energy. Following the standard procedure,11 the energy balance over a single timestep permits us to define the internal energy variation as
i related to particle temperature differences. Given that Ė = 0 if the total energy is to be conserved, we define the variation of the particle internal energy. Following the standard procedure,11 the energy balance over a single timestep permits us to define the internal energy variation as
![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) i has been included in the energy balance as an additional DoF involved in the particle energy change. It can be expressed as the summation over contributions from all the particle pairs, according to a mesoscopic analogue of Onsager's linear relationships between fluxes and forces,
i has been included in the energy balance as an additional DoF involved in the particle energy change. It can be expressed as the summation over contributions from all the particle pairs, according to a mesoscopic analogue of Onsager's linear relationships between fluxes and forces,  , with
, with ![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) ij = −
ij = −![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) ji. Then, we propose,
ji. Then, we propose,
![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) (rij), κ is the particle thermal conductivity and
(rij), κ is the particle thermal conductivity and ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) (rij) represents a weighting function analogous to the weighting function for the momentum interaction. The
(rij) represents a weighting function analogous to the weighting function for the momentum interaction. The ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) (rij) is also limited to a given range rc, but it does not need to be the same as for the momentum transport or the calculation of the local density. In turn, δuRij is the random heat exchanged between particles i and j during the time step δt, which is also proportional to a Wiener process. Here we define the time step-dependent random heat flux between two particles as
(rij) is also limited to a given range rc, but it does not need to be the same as for the momentum transport or the calculation of the local density. In turn, δuRij is the random heat exchanged between particles i and j during the time step δt, which is also proportional to a Wiener process. Here we define the time step-dependent random heat flux between two particles as  . To satisfy total energy conservation, we require that δuRij = −δuRji. The amplitude of the random heat exchange between particles is given by
. To satisfy total energy conservation, we require that δuRij = −δuRji. The amplitude of the random heat exchange between particles is given by
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ij is the normalised Gaussian number for the heat exchange with properties:
ij is the normalised Gaussian number for the heat exchange with properties:![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ij〉 = 0
ij〉 = 0![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ij
ij![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) kl〉 = δikδjl − δilδjk
kl〉 = δikδjl − δilδjk in eqn (39) is
in eqn (39) is  . The average of this term is non-zero, but exactly cancels the average of
. The average of this term is non-zero, but exactly cancels the average of 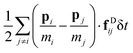 and therefore, the equilibrium average
and therefore, the equilibrium average 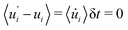 . If the balance is calculated from the continuous limit instead of the discrete algorithm, then this term could be easily overlooked. Moreover, if this expression is extracted from the Fokker–Plank equation, instead of this quadratic random term one obtains its equilibrium average,3,4 which only guarantees energy conservation in the mean but not at every timestep.
. If the balance is calculated from the continuous limit instead of the discrete algorithm, then this term could be easily overlooked. Moreover, if this expression is extracted from the Fokker–Plank equation, instead of this quadratic random term one obtains its equilibrium average,3,4 which only guarantees energy conservation in the mean but not at every timestep.![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) i|V. Effectively in the canonical ensemble, energy fluctuations scale as 〈δE2〉 = kBCVT2. Thus, writing for the mesoparticle δE ≃ CV(T −
i|V. Effectively in the canonical ensemble, energy fluctuations scale as 〈δE2〉 = kBCVT2. Thus, writing for the mesoparticle δE ≃ CV(T − ![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) ), we can infer that
), we can infer that  . Thus, the choice of a large heat capacity CV ≫ kB in the DPDE method makes its dynamics for the mechanical DoF identical to standard isothermal DPD. Furthermore, the mesoscopic expression for the heat flux can be used also in DPDE as well as in MB-DPDE, as the latter follows from the former if the internal energy per particle can be separated into two contributions, each depending on a single variable, according to the form,
. Thus, the choice of a large heat capacity CV ≫ kB in the DPDE method makes its dynamics for the mechanical DoF identical to standard isothermal DPD. Furthermore, the mesoscopic expression for the heat flux can be used also in DPDE as well as in MB-DPDE, as the latter follows from the former if the internal energy per particle can be separated into two contributions, each depending on a single variable, according to the form,



 . Thirdly, there is the direct contribution to the heat transport due to the mesoscopic heat exchange between the particles, including the random heat exchange; the last two terms in eqn (47). The last term in eqn (47) corresponds to the advected energy with the motion of the particles. In comparison with standard molecular dynamics, here εi also contains the internal energy u in addition to the kinetic energy. Furthermore, the macroscopic advective transport of enthalpy needs to be separated from the total energy flux density,26i.e.,
. Thirdly, there is the direct contribution to the heat transport due to the mesoscopic heat exchange between the particles, including the random heat exchange; the last two terms in eqn (47). The last term in eqn (47) corresponds to the advected energy with the motion of the particles. In comparison with standard molecular dynamics, here εi also contains the internal energy u in addition to the kinetic energy. Furthermore, the macroscopic advective transport of enthalpy needs to be separated from the total energy flux density,26i.e.,
 26 is obtained from the canonical ensemble, considered here to be the equilibrium distribution (see comments regarding the ensembles in ref. 19). Therefore, since macroscopically the hydrodynamic field Ak ≡ εk = ρcPTk, with
26 is obtained from the canonical ensemble, considered here to be the equilibrium distribution (see comments regarding the ensembles in ref. 19). Therefore, since macroscopically the hydrodynamic field Ak ≡ εk = ρcPTk, with

![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) , or use an average over the three Cartesian coordinates to increase the statistics.
, or use an average over the three Cartesian coordinates to increase the statistics.


![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) . We thus arbitrarily choose the x-component of the momentum in eqn (51) and the z-component of k. Thus,
. We thus arbitrarily choose the x-component of the momentum in eqn (51) and the z-component of k. Thus,

 we obtain from eqn (17)
we obtain from eqn (17)
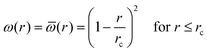

 . The simulated systems contained N = 20
. The simulated systems contained N = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles in volume V. A cubic simulation box was used (see Fig. 2c) with periodic boundary conditions. The box volume was adjusted for each simulation to obtain overall particle densities
000 particles in volume V. A cubic simulation box was used (see Fig. 2c) with periodic boundary conditions. The box volume was adjusted for each simulation to obtain overall particle densities ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ≡ N/V = 4, 8, 16, and 32 with a timestep of δt = 0.001, 0.0005, 0.00005, and 0.00005, respectively. The timestep was adjusted to obtain satisfactory energy conservation from the integration of the equations of motion. The system is initialised by rescaling the particle kinetic energy to reach a temperature T = 1, prior to the constant energy simulation that is performed to obtain the data. This initialisation scheme implies that the dimensionless kinetic energy of the system is
≡ N/V = 4, 8, 16, and 32 with a timestep of δt = 0.001, 0.0005, 0.00005, and 0.00005, respectively. The timestep was adjusted to obtain satisfactory energy conservation from the integration of the equations of motion. The system is initialised by rescaling the particle kinetic energy to reach a temperature T = 1, prior to the constant energy simulation that is performed to obtain the data. This initialisation scheme implies that the dimensionless kinetic energy of the system is  , and simultaneously the average particle temperature
, and simultaneously the average particle temperature  . Note that, unlike the momentum integration, the mechanical energy term in the balance equation produces an energy drift, which increases with the size of the time step. Such a drift impairs long simulations with explicit algorithms. However, this drift can be avoided by absorbing the numerical error Δ in every timestep, which is proportional to kBT ∼ 1, into the particles' internal energy u, which causes an internal temperature variation of the order of Δ/(CVT) ≪ 1. Note that if the timestep is not properly chosen, differences between the kinetic temperature and the internal temperature averages may occur. The friction coefficient γ was set to 4.5, the heat capacity CV to 60, and the particle thermal conductivity κ to either 5 or 50 to test different heat transport regimes.
. Note that, unlike the momentum integration, the mechanical energy term in the balance equation produces an energy drift, which increases with the size of the time step. Such a drift impairs long simulations with explicit algorithms. However, this drift can be avoided by absorbing the numerical error Δ in every timestep, which is proportional to kBT ∼ 1, into the particles' internal energy u, which causes an internal temperature variation of the order of Δ/(CVT) ≪ 1. Note that if the timestep is not properly chosen, differences between the kinetic temperature and the internal temperature averages may occur. The friction coefficient γ was set to 4.5, the heat capacity CV to 60, and the particle thermal conductivity κ to either 5 or 50 to test different heat transport regimes.
![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) ,n) = CV
,n) = CV![[small theta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e123.gif) , cf.eqn (44), which is referred to as the ideal GenDPDE system, and (b) systems with a conservative force fC, obtained from a many-body force potential given by a quadratic well, i.e.,
, cf.eqn (44), which is referred to as the ideal GenDPDE system, and (b) systems with a conservative force fC, obtained from a many-body force potential given by a quadratic well, i.e.,
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) for each case.
for each case.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 100
000, 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 15
000, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and 1000, for
000, and 1000, for ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 4, 8, 16, and 32, respectively. To increase statistical sampling, new overlapping time-series were created after ncorr/10 time steps, while the total duration of each simulation was 107 time steps.
= 4, 8, 16, and 32, respectively. To increase statistical sampling, new overlapping time-series were created after ncorr/10 time steps, while the total duration of each simulation was 107 time steps.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and different box volumes were chosen to obtain
000, and different box volumes were chosen to obtain ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 3, 4, 5, 6, 7, quoted in the benchmark reference, plus
= 3, 4, 5, 6, 7, quoted in the benchmark reference, plus ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 8, 16 and 32, which we have computed to extend the parameter range. The simulations were performed at T = 1, γ = 5 and δt = 0.01, for densities from 3 to 7, as in the benchmark, and δt = 0.005, 0.002 and 0.001 for densities 8, 16 and 32, respectively. Correlation windows of sizes ncorr = 2000, 1500, 1000, 1000, 1000, 1000, 1000 and 500 time steps were used for
= 8, 16 and 32, which we have computed to extend the parameter range. The simulations were performed at T = 1, γ = 5 and δt = 0.01, for densities from 3 to 7, as in the benchmark, and δt = 0.005, 0.002 and 0.001 for densities 8, 16 and 32, respectively. Correlation windows of sizes ncorr = 2000, 1500, 1000, 1000, 1000, 1000, 1000 and 500 time steps were used for ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 3, 4, 5, 6, 7, 8, 16 and 32, respectively. New time-series were created after 20 timesteps, while the total simulated time was 107 time steps.
= 3, 4, 5, 6, 7, 8, 16 and 32, respectively. New time-series were created after 20 timesteps, while the total simulated time was 107 time steps.
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) = 500 was sustained, such that when steady-state conditions were reached, a linear temperature gradient developed between the hot and cold slabs. The value of the externally imposed heat exchange rate was chosen to create a relatively small temperature gradient between the regions to avoid non-linearities due to variations in the local particle density, which may influence the thermal conductivity; see Fig. 2b.
= 500 was sustained, such that when steady-state conditions were reached, a linear temperature gradient developed between the hot and cold slabs. The value of the externally imposed heat exchange rate was chosen to create a relatively small temperature gradient between the regions to avoid non-linearities due to variations in the local particle density, which may influence the thermal conductivity; see Fig. 2b.
![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) = −λ∇T
= −λ∇T
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) is the amount of heat transferred from the cold region to the hot region during a timestep, and A is the cross-sectional area along the yz-plane. Both were set a priori in the simulation. The resulting temperature gradient was estimated from the ratio ΔT/Δx obtained from the linear portion of the temperature profile that formed between the hot and cold regions in the x-direction; see Fig. 2b.
is the amount of heat transferred from the cold region to the hot region during a timestep, and A is the cross-sectional area along the yz-plane. Both were set a priori in the simulation. The resulting temperature gradient was estimated from the ratio ΔT/Δx obtained from the linear portion of the temperature profile that formed between the hot and cold regions in the x-direction; see Fig. 2b.

 is the induced velocity gradient between slabs, which we measured by a linear regression of the velocity profile in the central region. Πxz is the shear stress imposed due to the exchange in momentum between slabs that can be obtained as,
is the induced velocity gradient between slabs, which we measured by a linear regression of the velocity profile in the central region. Πxz is the shear stress imposed due to the exchange in momentum between slabs that can be obtained as,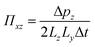
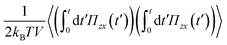
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 3, 4, 5, 6, and 7. In Fig. 4, we provide a comparison between our results and the non-equilibrium values of the viscosity from Fig. 5 of ref. 28, showing excellent agreement between both of them.
= 3, 4, 5, 6, and 7. In Fig. 4, we provide a comparison between our results and the non-equilibrium values of the viscosity from Fig. 5 of ref. 28, showing excellent agreement between both of them.

![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 4, 8, 16, and 32, which are presented in Fig. 5 together with our non-equilibrium simulations and the theoretical predictions,41
= 4, 8, 16, and 32, which are presented in Fig. 5 together with our non-equilibrium simulations and the theoretical predictions,41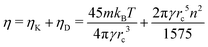

![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 4, 8, 16 and 32, respectively. The largest errors occur in the non-equilibrium simulations at density
= 4, 8, 16 and 32, respectively. The largest errors occur in the non-equilibrium simulations at density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 32, (0.2 with the 68% confidence), which is of the size of the symbol.
= 32, (0.2 with the 68% confidence), which is of the size of the symbol.![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 3, 4, 5, 6, 7 are obtained from ref. 28, while for densities
= 3, 4, 5, 6, 7 are obtained from ref. 28, while for densities ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 8, 16, 32 are our own simulation data. (a) Values calculated from the EH formula in ref. 29, eqn. (2.14). The errors in the EH equations are evaluated from the error in the slope of the linear regression. (b) Values calculated using eqn (19) in ref. 27. The error is calculated from the fitting of the hydrodynamic part of the decay of the correlation to a function of the type y = Ae−btc, where A, b and c are adjustable parameters. Errors in the non-equilibrium simulations are entirely due to the linear regression used to determine the linear velocity gradient in the box
= 8, 16, 32 are our own simulation data. (a) Values calculated from the EH formula in ref. 29, eqn. (2.14). The errors in the EH equations are evaluated from the error in the slope of the linear regression. (b) Values calculated using eqn (19) in ref. 27. The error is calculated from the fitting of the hydrodynamic part of the decay of the correlation to a function of the type y = Ae−btc, where A, b and c are adjustable parameters. Errors in the non-equilibrium simulations are entirely due to the linear regression used to determine the linear velocity gradient in the box
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 4, 8, 16, and 32 under equilibrium and non-equilibrium conditions. The thermal conductivity in non-equilibrium conditions was obtained as described in Section 3.1. In all cases, we also include the theoretical prediction derived from the superposition of the limit of interparticle heat transport dominance37 and the limit of kinetic transport dominance,44i.e.,
= 4, 8, 16, and 32 under equilibrium and non-equilibrium conditions. The thermal conductivity in non-equilibrium conditions was obtained as described in Section 3.1. In all cases, we also include the theoretical prediction derived from the superposition of the limit of interparticle heat transport dominance37 and the limit of kinetic transport dominance,44i.e.,
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) for equilibrium and non-equilibrium simulations, which are compared with the theoretical prediction, for completeness. The simulations were carried out at T = 1 and with κ = 50, γ = 4.5, and CV = 60. The EH values and the non-equilibrium simulation results are in excellent agreement over the entire range of
for equilibrium and non-equilibrium simulations, which are compared with the theoretical prediction, for completeness. The simulations were carried out at T = 1 and with κ = 50, γ = 4.5, and CV = 60. The EH values and the non-equilibrium simulation results are in excellent agreement over the entire range of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) studied, supporting the correctness of the combination of eqn (50) and (47).
studied, supporting the correctness of the combination of eqn (50) and (47). , where the second equality is obtained after the values of the dimensionless constant parameters have been introduced. Therefore for case A, the crossover density is approximately
, where the second equality is obtained after the values of the dimensionless constant parameters have been introduced. Therefore for case A, the crossover density is approximately ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) c ≃ 10, which implies that most of the data are in the region dominated by the direct interparticle heat transport. In comparison with the theoretical prediction, the simulation values of λ are also in rather good agreement. There is a small deviation as we increase the density, which was previously noted in ref. 37.
c ≃ 10, which implies that most of the data are in the region dominated by the direct interparticle heat transport. In comparison with the theoretical prediction, the simulation values of λ are also in rather good agreement. There is a small deviation as we increase the density, which was previously noted in ref. 37.![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) c ∼ 30. In Fig. 6, we plot the thermal conductivity λ as a function of the density
c ∼ 30. In Fig. 6, we plot the thermal conductivity λ as a function of the density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) . Again, we observe that the equilibrium and non-equilibrium simulation results are in very good agreement over the entire range of
. Again, we observe that the equilibrium and non-equilibrium simulation results are in very good agreement over the entire range of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) studied. However, the theoretical prediction eqn (66) yields values significantly lower than the simulation values over the entire density range. The quantitative theoretical analysis of the thermal conductivity with respect to the different parameters will be presented elsewhere.
studied. However, the theoretical prediction eqn (66) yields values significantly lower than the simulation values over the entire density range. The quantitative theoretical analysis of the thermal conductivity with respect to the different parameters will be presented elsewhere.![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) from equilibrium and non-equilibrium simulations. The GenDPDE simulations were carried out at T = 1, with κ = 5, γ = 4.5 and CV = 60, and with β = 0.2 and n0 =
from equilibrium and non-equilibrium simulations. The GenDPDE simulations were carried out at T = 1, with κ = 5, γ = 4.5 and CV = 60, and with β = 0.2 and n0 = ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) in eqn (58). From Fig. 7, we can observe that the equilibrium and non-equilibrium simulation results are again in very good agreement over the density range studied. With respect to the theoretical predictions, a disagreement is expected as the derivation of eqn (66) does not include any conservative force between the particles.
in eqn (58). From Fig. 7, we can observe that the equilibrium and non-equilibrium simulation results are again in very good agreement over the density range studied. With respect to the theoretical predictions, a disagreement is expected as the derivation of eqn (66) does not include any conservative force between the particles.
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 4 to 134 at
= 4 to 134 at ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 32. Even in highly dissipative conditions like the latter, the EH formulas provide reliable accurate data. For the heat transport, we have studied two different regimes depending on whether the transport is dominated by advective or dissipative effects. We have analysed a third case with density-dependent potential interactions, which strongly influence the behaviour of the system. In all these cases the agreement is excellent, which we consider sound verification of our methodology. For completeness, we have also addressed the case of the shear viscosity. We have derived the expression for the stress tensor suitable for GenDPDE, and hence for all DPD-type methods that can be derived from it, which include the standard isothermal DPD method that was used as a benchmark in this work. The agreement between our data and the non-equilibrium simulations of Jung and Schmid,28 together with our non-equilibrium data for the extended density range, is also excellent. Note that in this last reference, non-equilibrium simulations were used to compare with different Green–Kubo expressions specifically obtained for DPD-type methods.27 The different equilibrium evaluations are given in Table 1 for comparison. Despite the different, possibly conflicting, theoretical perspectives from which these were obtained, the numerical differences are or the order of the error in the non-equilibrium simulation data. Only the data obtained from the EH formula derived from it in ref. 29 systematically deviates from the benchmark, we believe because some of the correlations present in the GK formula of ref. 27 were lost in its transformation to the EH counterpart proposed in the former. The analysis of the GK expressions of ref. 27 in comparison with the present EH relations is relevant, we prefer to leave this discussion for a more detailed study.
= 32. Even in highly dissipative conditions like the latter, the EH formulas provide reliable accurate data. For the heat transport, we have studied two different regimes depending on whether the transport is dominated by advective or dissipative effects. We have analysed a third case with density-dependent potential interactions, which strongly influence the behaviour of the system. In all these cases the agreement is excellent, which we consider sound verification of our methodology. For completeness, we have also addressed the case of the shear viscosity. We have derived the expression for the stress tensor suitable for GenDPDE, and hence for all DPD-type methods that can be derived from it, which include the standard isothermal DPD method that was used as a benchmark in this work. The agreement between our data and the non-equilibrium simulations of Jung and Schmid,28 together with our non-equilibrium data for the extended density range, is also excellent. Note that in this last reference, non-equilibrium simulations were used to compare with different Green–Kubo expressions specifically obtained for DPD-type methods.27 The different equilibrium evaluations are given in Table 1 for comparison. Despite the different, possibly conflicting, theoretical perspectives from which these were obtained, the numerical differences are or the order of the error in the non-equilibrium simulation data. Only the data obtained from the EH formula derived from it in ref. 29 systematically deviates from the benchmark, we believe because some of the correlations present in the GK formula of ref. 27 were lost in its transformation to the EH counterpart proposed in the former. The analysis of the GK expressions of ref. 27 in comparison with the present EH relations is relevant, we prefer to leave this discussion for a more detailed study.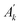 , followed by an integration over Ak and
, followed by an integration over Ak and  . The left-hand side corresponds to the direct trajectory and becomes
. The left-hand side corresponds to the direct trajectory and becomes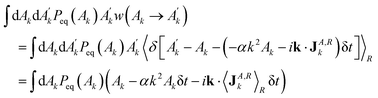


 , followed by the same integration over Ak and
, followed by the same integration over Ak and  . For the direct trajectory we obtain
. For the direct trajectory we obtain

 is taken at the same instant of time, we can write the FDT in its final form as given in eqn (11).
is taken at the same instant of time, we can write the FDT in its final form as given in eqn (11).


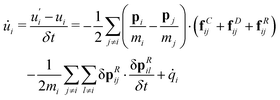
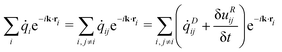



![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) ji = −
ji = −![[q with combining dot above]](https://www.rsc.org/images/entities/i_char_0071_0307.gif) ij. The range of the particle–particle interaction rc is typically much smaller than the box size L. Thus, provided that rc ≪ L, we can proceed to take the hydrodynamic limit also for a finite system since, as kmin = 2π/L, kminrc ≪ 1. Then,
ij. The range of the particle–particle interaction rc is typically much smaller than the box size L. Thus, provided that rc ≪ L, we can proceed to take the hydrodynamic limit also for a finite system since, as kmin = 2π/L, kminrc ≪ 1. Then,