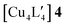Open Access Article
Open Access ArticleA theoretical study of M–M′ polar-covalent bonding in heterobimetallic multinuclear organometallic complexes of monovalent group 11 metal centres†‡
Hassan
Rabaâ
 *ac,
Dage
Sundholm
*ac,
Dage
Sundholm
 *b and
Mohammad A.
Omary
*c
*b and
Mohammad A.
Omary
*c
aDepartment of Chemistry, Ibn Tofail University, ESCTM, P.O. Box 133, 14000, Kenitra, Morocco. E-mail: hrabaa@yahoo.com
bDepartment of Chemistry, Faculty of Science, FI-00014, University of Helsinki, P.O. Box 55, A. I. Virtasen aukio 1, Finland
cDepartment of Chemistry, University of North Texas, P.O. Box 305070, Denton, TX 76203, USA
First published on 8th February 2023
Abstract
Complexes with closed-shell (d10–d10) interactions have been studied for their interesting luminescence properties in organic light-emitting diode (OLED) devices. The present computational study aims at understanding the chemical bonding/interactions in a series of molecules with unusually short metal–metal bond distances between monovalent coinage-metal (d10–d10) centres. The investigated molecules include pentanuclear  complexes with M or M′ = Cu(I), Ag(I), or Au(I) and Mes = 2,4,6-Me3C6H2. In such complexes, the M–M′ distances are up to 50–100 pm shorter than typical metallophilic bonds in homometallic analogues. Characterization and analysis of the chemical bond strength was performed using ab initio methods, density functional theory methods including a semi-empirical treatment of dispersion interactions (DFT-D3) and semi-empirical calculations at the extended Hückel theory (EHT) level. Population analysis suggests that hybridization occurs by mixing the (n + 1)s and (n + 1)p orbitals of M with the (nd) orbitals of M′. The orbital mixing plays a pivotal role in the polydentated polar-covalency/dative M–M′ bonds that distinguish this bonding from the weaker metallophilic interactions.
complexes with M or M′ = Cu(I), Ag(I), or Au(I) and Mes = 2,4,6-Me3C6H2. In such complexes, the M–M′ distances are up to 50–100 pm shorter than typical metallophilic bonds in homometallic analogues. Characterization and analysis of the chemical bond strength was performed using ab initio methods, density functional theory methods including a semi-empirical treatment of dispersion interactions (DFT-D3) and semi-empirical calculations at the extended Hückel theory (EHT) level. Population analysis suggests that hybridization occurs by mixing the (n + 1)s and (n + 1)p orbitals of M with the (nd) orbitals of M′. The orbital mixing plays a pivotal role in the polydentated polar-covalency/dative M–M′ bonds that distinguish this bonding from the weaker metallophilic interactions.
Introduction
The strength of the aurophilicity or metallophilicity in multinuclear complexes has been discussed in many previous articles.1–14 Although several heterometallic complexes exhibit suitable optoelectronic properties there are fewer examples of coinage-metal containing molecules with short M–M′ bonds. Molecules with closed-shell (d10–d10)2–7,13 interactions have also been studied for their interesting luminescence properties in organic light emitting diode (OLED) devices.8–13 Omary et al. reported an approximately order-of-magnitude higher binding energy for the M–M′ bond by comparing the relative strengths of closed-shell M–M interactions – all of which were pertaining to intermolecular M–M′ bonding phenomena.6,7 Gambarotta, and co-workers12 reported an early synthesis of a ligand-supported pentameric structure of an arylcopper ([CuMes]5), 1, exhibiting a μ2-C1-atom (i.e., the carbanionic C-atom in the 1-position) as a single-atom bridging mode for two adjacent metal atoms in each phenyl ring; see Fig. 1. This arrangement leads to a remarkably – short ligand assisted – Cu(I)–Cu(I) bond distance of 2.437–2.469 Å−1.12 | ||
| Fig. 1 The molecular structure of the [Cu(μCl-Mes]5 complex 1. Copper, carbon, and hydrogen atoms are designated by red, grey, and white spheres, respectively. | ||
Numerous theoretical studies supporting (d10–d10) closed-shell interactions and (d10–d10) metallophilic interactions have been performed at various levels of theory, including those that account for relativistic and correlation effects to properly describe van der Waals-type interactions8,14–27 such as the metallophilic attraction.16 This generalized concept as well as the historically precedent aurophilicity are best described as a correlative dispersion phenomenon, enhanced by induction. Later, the significant role of electron correlation in this type of closed-shell/closed-shell interaction was pointed out by Pyykkö et al.16–21 who have also mentioned the importance of relativistic effects on the Au(I)–Au(I) aurophilic bonding (d10–d10) in closed-shell molecules such as [Au(PH3)Cl]2.14–17 In these calculations, no M–M interaction was observed with the Hartree-Fock (HF) treatment, whereas at the second-order Møller–Plesset (MP2) level, which includes electron correlation, relativistic calculations yield a deep potential minimum at an Au(I)–Au(I) equilibrium distance of 2.657 Å 19. On the other hand, extended Hückel theory (EHT)37–40 calculations carried out by Mehrotra and Hoffmann23–25 suggested the importance of the mixing of empty bonding combinations of the 4s/4p atomic orbitals (AOs) into the occupied 3d-block. Hoffmann et al. drew similar conclusions from qualitative EHT studies of the molecular orbitals (MO) of [Au2(S2PH2)2]2, which is a simpler binuclear model Au(I) compound with intramolecular/ligand-assisted d10–d10 interactions than those in 1.23–25 The partial bonding due to Cu(I)–Cu(I) cuprophilic interactions could then be accounted for through-metal (4s0 4p0/3d10) mixing.
We have an ongoing effort27 to study mixed coinage-metal compounds and have provided evidence for the quasi-covalent metallophilicity of the internuclear/ligand-unassisted M–M′ bonding in [Cu(PH3)Cl][Au(PH3)Cl] analogues of Pyykkö's complexes. Herein we focus on the aforementioned experimental/computational Gambarotta/Hoffmann's [CunAu5−n(μC1-Mes)5] complexes (starting with n = 3 in this first theoretical investigation en route to ongoing experimental/computational efforts with other n values and M–M′ combinations). Distinct from previous efforts by members of this research team, the parent M–M system being emulated is Cu–Cu instead of Au–Au. Hence, this allows for a higher chance of uncovering new M–M′ species whereby theory predicts experiment in terms of shorter M–M′ distances, but not necessarily larger dissociation energies, given the much shorter covalent radius of Cu(I) than Au(I) as reflected in the respective parent compounds. Indeed, some of the results obtained have attained both shorter distances and higher bonding energies in both the MM′ heterometallic and the MM or M′M′ homometallic clusters, which are guiding ongoing experiments.
Here, we also show that the hybridization, which was suggested by Hoffmann, plays an important role for the M–M′ interaction, whereas the metallophilic interaction plays a smaller role because it contributes significantly less than hybridization to the bonding when the M–M′ distance is short, and the bonding is strong. We have here carried out calculations at the DFT and MP2 levels to investigate the short genuine M–M′ quasi-covalent metallophilic bonds and to estimate the M–M′ bonding energy in pentanuclear  and the related analogous tetranuclear
and the related analogous tetranuclear  organometallic complexes (and the opposite nuclearity thereof to assess the thermodynamic/kinetic factors affecting the experimental nuclearity for each). The nature of the interaction between the closed-shell Cu(I)–Cu(I), Ag(I)–Cu(I) or Au(I)–Cu(I) atoms at such short distances and the role of the d10–d10 bonding have been studied for complexes containing the three coinage metals.
organometallic complexes (and the opposite nuclearity thereof to assess the thermodynamic/kinetic factors affecting the experimental nuclearity for each). The nature of the interaction between the closed-shell Cu(I)–Cu(I), Ag(I)–Cu(I) or Au(I)–Cu(I) atoms at such short distances and the role of the d10–d10 bonding have been studied for complexes containing the three coinage metals.
Computational details
The d10–d10 closed-shell attraction is analysed at the density functional theory (DFT)28,29 and ab initio30,31 levels using the Gaussian and Turbomole packages.32 The molecular structures and the thermodynamic properties of the studied cluster models were calculated at the density functional theory (DFT) level using the TPSS functional33 and the def2-TZVP basis sets.34 The Au basis set considers 19 electrons (5s25p65d106s1) while 60 core electrons are replaced by an effective core potential (ECP). The Ag basis set also considers 19 electrons (4s24p64d105s1) while 28 core electrons are replaced by the ECP. The Cu basis set is an all-electron basis set. At the DFT level, the van der Waals interaction was considered by using the D3(BJ) semi-empirical dispersion correction.35 The CACAO 98 package36 was used for constructing the extended Hückel molecular orbital (EHMO) diagrams37–40 and for performing the natural bond orbital (NBO) and overlap population analyses. It was also used for calculating the atomic charges and binding energies. The potential energy surface (PES) for [Cu3Au2(Mes5)] 3 was calculated to determine how the equilibrium distances depend on the employed levels of theory, HF,41 MP2,42 and TPSS-D3(BJ).43,44 The neutral molecules studied herein exhibit a genuine closed-shell d10 electronic configuration in the singlet ground state, justifying use of single-reference methods. Binding energies were calculated by subtracting the energies of the five metal atomic cations and five ligand molecular anions from the total energy of each neutral cluster molecule. Calculations of analogous tetranuclear clusters with the same and different ligands have been performed to assess whether the pentanuclear clusters herein are kinetic or thermodynamic reaction products. The optimized molecular structures together with additional computational details are deposited in the ESI‡ document.Results and discussion
The most relevant bond distances and angles in the optimized molecular structures are compared in Table 1 to the experimental values for the [CuMes]5 complex 1 shown in Fig. 1. The calculated Cu(I)–Cu(I) distances of 2.417Å are close to the sum of the atom radius of Cu of 2.556 Å. The calculated Cu(I)–Cu(I) bond is only 0.037 Å shorter than the experimental value.12 At the MP2 level, we obtain a longer Cu(I)–Cu(I) distance of 2.670 Å that is shorter than the sum of the van der Waals radii of 2.80 Å.36 The experimental M–C–M angle is 75.2° as compared to the calculated value of 74.1°. complexes (L = mesityl) calculated at the TPSS/def2-TZVP level (columns 2–4). Values obtained in the TPSS-D3(BJ)/def2-TZVP calculations are given in parentheses. Values calculated at the HF level are reported in column 5 and available experimental data for Cu5L5 are given in column 6
complexes (L = mesityl) calculated at the TPSS/def2-TZVP level (columns 2–4). Values obtained in the TPSS-D3(BJ)/def2-TZVP calculations are given in parentheses. Values calculated at the HF level are reported in column 5 and available experimental data for Cu5L5 are given in column 6
| [Cu5L5] 1 | [Cu3Au2L5] 2 | [Cu3Ag2L5] 3 | [Cu5L5] 1 (HF) | [Cu5L5] 1 exp.12 | |
|---|---|---|---|---|---|
| M–M′ (Å) | 2.587 (2.581) | 2.577 (2.544) | |||
| M–M (Å) | 2.435 (2.402) | 2.417 (2.412) | 2.437 (2.396) | 2.810 (2.756) | 2.454 |
| M′–C (Å) | 2.145 (2.135) | 2.247 (2.219) | 2.112 (2.102) | ||
| M–C (Å) | 2.004 (1.978) | 2.007 (2.042) | 1.994 (1.968) | 2.031 | |
| M–C–M (°) | 74.6 (74.1) | 74.2 (73.9) | 77.2 (75.12) | 82.5 (81.9) | 75.2 |
| M–C–M′ (°) | 76.5 (75.6) | 74.7 (69.9) | |||
| E tot (H) | −9951.91 | −6942.207 | −6964.627 | 6923.18 |
The DFT-optimized molecular structure of [Cu3Au2(Mes5)] 2 shown in Fig. 2 has short Cu–Au distances of 2.587 Å (see Table 1) suggesting that there is a strong (d10–d10) interaction between the Cu(I) and Au(I) ions. The elongation in the Cu–Au and Cu–Ag distances for models 2 or 3 as compared to the Cu–Cu distance for model 1 is similar or even smaller than the ∼12 and ∼20 pm larger covalent radii of Au(I) and Ag(I) as compared to the one of Cu(I), respectively.46
 | ||
| Fig. 2 The DFT optimized molecular structure of [Cu3Au2(Mes5)], 2. The Au, Cu, C, and H atoms are coloured in yellow, orange, grey, and light grey, respectively. | ||
The EHT calculations yield the short M–M′ distances that result in a large overlap of the d orbitals of 0.125 in 1 and 0.102 in 2, suggesting that there is strong spd mixing in the bonding as previously reported by Hoffmann et al.23–25 Molecular structure optimization was also carried out at the MP2 level yielding an Au(I)–Cu(I) distance of 2.720 Å, which is also 0.24 Å shorter than the sum of the van der Waals radii. The M–C–M′ angle obtained at the MP2 level is 76.2°.
The calculated binding energy of [Cu5(Mes5)] is 256 kcal mol−1, which was obtained in an energy decomposition analysis (EDA) at the TPSS level with unrelaxed fragments. This corresponds to a binding energy of 51 kcal mol−1 for the Cu(I)–Cu(I) bond in [Cu5(Mes5)]. The EDA calculation on [Cu3Au2(Mes5)] yields a binding energy of 251 kcal mol−1 suggesting that the strength of the Au(I)–Cu(I) bond is 50 kcal mol−1. Allowing structural relaxation of the fragments leads to a slightly smaller binding energy of 201 kcal mol−1 for both [Cu3Au2(Mes5)] and [Cu5(Mes5)], which is 40 kcal mol−1 per metal–metal bond. Calculating the binding energies of [Cu5(Mes5)] and [Cu3Au2(Mes5)] at the MP2 level yielded slightly larger values of 335 kcal mol−1 and 337 kcal mol−1, respectively, which correspond to binding energies of about 67 kcal mol−1 for both the Cu(I)–Cu(I) and the Au(I)–Cu(I) bond.
Calculations on a model compound with only one Cu–Au bond and without the large mesityl ligands yielded an Au(I)–Cu(I) binding energy of 15.4 kcal mol−1 and a bond length of 2.87 Å. The binding energy of the model compound is 18.7 kcal mol−1 at the coupled-cluster singles and doubles level with a Cu–Au distance that is 25 pm longer than that obtained at the TPSS level. The model compound represents a system with a metallophilic interaction, whereas the polydentate bonding of the metals in the pentamers leads to short metal–metal distances and strong metal–metal bonds.
The bond strengths of the Cu(I)–Cu(I) and Au(I)–Cu(I) bonds are significantly larger than metallophilic interactions suggesting that the Au(I)–Cu(I) bond in 2 has a significant contribution of a polar-covalent bond (nd10 (M) → (n + 1)s/p (M′) as opposed to nd10–n′d10). The population analysis on 2 yielded the following occupations for Cu and Au orbitals: 3d9.78, 4s0.51, 4p0.23 and 5d9.65, 6s0.86, 6p0.25, respectively, demonstrating significant spd hybridization/mixing in the M–M′ bonding.
Similar calculations on [Cu3Ag2(Mes5)] yielded a short Ag(I)–Cu(I) distance of 2.58 Å (see Table 1). The EDA calculations at the TPSS/def2-TZVP level yielded a binding energy of 241 kcal mol−1 for [Cu3Ag2(Mes5)], which corresponds to a bond strength of 47 kcal mol−1 for the Ag(I)–Cu(I) bond. The EDA calculation suggests that it might also be possible to synthesize [Cu3Ag2(Mes5)]. For 3, we obtained the following shell occupations for Cu and Ag: 3d9.77, 4s0.49, 4p0.25 and 4d9.83, 5s0.53, 5p0.31, respectively. At the DFT-D3 level, the calculations yielded slightly shorter M–M′ and M–C bond lengths as compared to the bond distances obtained in the DFT calculations without the D3 correction (see Table 1). The atomic charges calculated from the charge density are 0.06/0.05e for the Au/Cu atoms in 2 and are 0.01/−0.07e for Cu/Ag atoms in 3. The metals are practically neutral at the DFT level. Further details are in Table S3 (ESI‡), which suggests the general bond strength order Ag–Cu > Au–Cu > Cu–Cu due to the reduction of Pauli repulsion in that order.
An alternative organometallic cluster with a silicon-containing ligand is shown in Fig. 3. It has attained a tetranuclear structure instead of the pentanuclear geometry. The resulting molecule is  , where L′ = Me3SiCH2 in a μ2-CH2 carbanionic C-atom bridging mode, and was obtained experimentally by Jarvis et al.45 We computationally examine the analogous mixed-metal tetranuclear
, where L′ = Me3SiCH2 in a μ2-CH2 carbanionic C-atom bridging mode, and was obtained experimentally by Jarvis et al.45 We computationally examine the analogous mixed-metal tetranuclear  clusters,
clusters, 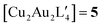 and
and  . Table 2 contains some geometric parameters of the coordination sphere plus the Si–CH2 bond in the two mixed-metal clusters and in the parent
. Table 2 contains some geometric parameters of the coordination sphere plus the Si–CH2 bond in the two mixed-metal clusters and in the parent  complex, which are compared to the available experimental data. The calculated M–M′ distances and bond angles in Table 2 agree qualitatively to those in Table 1 and to the experimental Cu–Cu distance in 4. That is, the elongation in the Cu–Au or Cu–Ag distance values in Table 2 for molecule 5 or molecule 6 as compared to the Cu–Cu distance in molecule 4 is similar or smaller than the ∼12 and 20 pm elongation in Au(I) and Ag(I) covalent radii with respect to the one of Cu(I), respectively.46 The calculations on the
complex, which are compared to the available experimental data. The calculated M–M′ distances and bond angles in Table 2 agree qualitatively to those in Table 1 and to the experimental Cu–Cu distance in 4. That is, the elongation in the Cu–Au or Cu–Ag distance values in Table 2 for molecule 5 or molecule 6 as compared to the Cu–Cu distance in molecule 4 is similar or smaller than the ∼12 and 20 pm elongation in Au(I) and Ag(I) covalent radii with respect to the one of Cu(I), respectively.46 The calculations on the  and
and  clusters suggest that stronger metal–metal bonding could be anticipated in the MM′ containing clusters as compared to the homometallic Cu clusters. However, the present calculations yielded almost identical binding energies of the metal–metal bonds, regardless of whether they are Cu(I)–Cu(I), Ag(I)–Cu(I) or Au(I)–Cu(I) bonds.
clusters suggest that stronger metal–metal bonding could be anticipated in the MM′ containing clusters as compared to the homometallic Cu clusters. However, the present calculations yielded almost identical binding energies of the metal–metal bonds, regardless of whether they are Cu(I)–Cu(I), Ag(I)–Cu(I) or Au(I)–Cu(I) bonds.
 | ||
Fig. 3 The experimental molecular structure of the tetranuclear cluster,  (4, top), and a proposed mixed-metal analogue, (4, top), and a proposed mixed-metal analogue,  (5, bottom). (5, bottom). | ||
 and
and  complexes (L′ = Me3SiCH2) calculated at the TPSS/def2-TZVP level (columns 2–4) are compared to the HF values (column 5) and to the available experimental data for [Cu4L4] (column 6)
complexes (L′ = Me3SiCH2) calculated at the TPSS/def2-TZVP level (columns 2–4) are compared to the HF values (column 5) and to the available experimental data for [Cu4L4] (column 6)
| (HF) | (exp.)45 | ||||
|---|---|---|---|---|---|
| Si–CH2 | 1.891 | 1.892 | 1.861 | 1.851 | |
| M–M′ | 2.544 | 2.575 | |||
| M–M | 2.369 | 2.383 | 2. 384 | 2.810 | 2.417 |
| M′–C | 2.371 | 2.171 | 2.574 | 2.112 | 2.417 |
| M–C | 2.011 | 2.121 | 2.240 | 2.001 | |
| M–C–M | 71.5 | 72.3 | 71.2 | 82.5 | 73.8 |
| M–C–M′ | 73.4 | 71.8 |
We have investigated the effect of an alternative nuclearity in both [Cu5L5] and  clusters, the structural parameters of which are reported in Tables S1 and S2 of the ESI.‡ We have calculated the total energy at the TPSS/def2-TZVP and MP2/def2-TZVP levels for [Cu5L5] where L = mesityl and have compared the energy to the one for [Cu4L4]. Comparison of the energy contribution from each CuL moiety shows that [Cu5L5] is slightly stabilized with respect to [Cu4L4] by the additional van der Waals interaction energy between the ligands. The pentamer is, therefore, obtained in the synthesis likely due to the combination of this small thermodynamic stabilization also with the possibly that it is the kinetic product. The
clusters, the structural parameters of which are reported in Tables S1 and S2 of the ESI.‡ We have calculated the total energy at the TPSS/def2-TZVP and MP2/def2-TZVP levels for [Cu5L5] where L = mesityl and have compared the energy to the one for [Cu4L4]. Comparison of the energy contribution from each CuL moiety shows that [Cu5L5] is slightly stabilized with respect to [Cu4L4] by the additional van der Waals interaction energy between the ligands. The pentamer is, therefore, obtained in the synthesis likely due to the combination of this small thermodynamic stabilization also with the possibly that it is the kinetic product. The  cluster, on the other hand, was obtained in a previous experimental study as a tetranuclear complex instead of the pentanuclear one,45 possibly due to the larger Si-containing organometallic trimethylsilylmethyl ligand that would add strain to an alternative planar-pentanuclear cluster as that of the mesityl system. Another reason why the tetramer is obtained in the synthesis might be the smaller dispersion interaction between the trimethylsilylmethyl groups than between the mesityl groups. One of the present authors has engaged in related work on cyclic non-organometallic multinuclear pyrazolate complexes,47 which have shown a similar dependence on the steric effect of the ligand on the nuclearity of trinuclear vs. tetranuclear reaction products, akin to what we predict for the two organometallic systems studied here.
cluster, on the other hand, was obtained in a previous experimental study as a tetranuclear complex instead of the pentanuclear one,45 possibly due to the larger Si-containing organometallic trimethylsilylmethyl ligand that would add strain to an alternative planar-pentanuclear cluster as that of the mesityl system. Another reason why the tetramer is obtained in the synthesis might be the smaller dispersion interaction between the trimethylsilylmethyl groups than between the mesityl groups. One of the present authors has engaged in related work on cyclic non-organometallic multinuclear pyrazolate complexes,47 which have shown a similar dependence on the steric effect of the ligand on the nuclearity of trinuclear vs. tetranuclear reaction products, akin to what we predict for the two organometallic systems studied here.
We also assessed the isomerisation energy of the [Cu3Au2L5] complex. The total energy of the [Cu3Au2L5] complex without any Au–Au bonds is 3 kcal mol−1 lower than the energy of the [Cu3Au2L5] complex with one Au–Au bond. Therefore, we have not investigated the other possible MM′ isomers with M′–M′ bonds. An exhaustive theoretical study of all possible isomers is not needed at this stage when experimental studies are still missing.
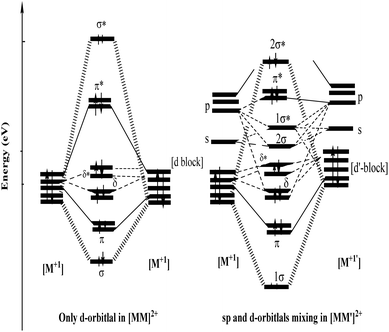
The EHT calculations predict that the heterometallic complexes have an overlap population of ∼0.1, leading to a d–s/d–p mixing of the M and M′ atomic orbitals. The amount of mixing from the empty (n + 1)s and (n + 1)p orbitals with the orbitals of the closed (n)d shell depends on the length of the Cu(I)–Au(I) bond. The orbital mixing in 2 occurs between the 6s/6p orbitals of Au(I) with the 3d orbitals of Cu(I) instead of the 4s/4p orbitals of Cu(I) with the 5d orbitals of Au(I), as concluded by Galassi et al. in the study of such systems and claimed Au(I)–Cu(I) polar-covalent bonding.7
The extended Hückel molecular orbital (EHMO) diagram of the hypothetical [M2]2+ and [MM′]2+ complexes without or with significant spd mixing is shown in Fig. 4. The analysis reveals large differences in terms of the σ and σ* bond character of [M2]2+ and [MM′]2+. Since the energy levels of M and M′ are different, the (n)d/(n + 1)s/p interaction is also different, showing a wide gap between the σ and σ* orbitals, which is seen on the right-hand side of the MO diagram in Fig. 4.
In the absence of the (n + 1)s/p hybridization of the (n)d orbitals (see the left-hand side of the MO diagram in Fig. 4), only the repulsion between the closed-shell d orbitals persists. At shorter M–M′ distances, the empty s and p orbitals contribute to the bonding, primarily via hybridization of the dz2 and pz orbitals, which introduces partial σ-bonding with polar-covalent character to the M–M′ bond. The 4s and 4p orbitals on Cu(I) stabilize the bonding and antibonding combination of the Au 5d orbitals, leading to stronger Cu–Au interactions for the dxy and dx2−y2 orbitals in the xy plane.
The question of metallophilic or covalent M–M′ bonding was investigated in a simplified [Cu3Au2(Me5)] model using methyl groups instead of mesityl groups. We determined the equilibrium distance (Re) at the HF and TPSS/D3(BJ)/def2-TZVP levels of theory, i.e., without and with electron correlation included.
The HF calculations yielded a minimum at 2.65 Å, showing a short M–M′ bond. At the TPSS-D3 level, we obtained a shorter equilibrium distance of 2.46 Å. While the shorter Cu–Au distance and a deeper potential well are expected at the TPSS-D3 level than in the HF calculations, a potential energy scan yielded an unmistakable potential well at the HF level, which represents strong evidence for the polar-covalent character of the Au(I)–Cu(I) bonding. This is in contrast to the non-covalent metallophilic bonding behaviour whereby this same kind of approach used by Pyykkö and co-workers had attained a significant potential well only when electron correlation was considered, which is usually done by performing MP2 calculations that then yield a potential well, whereas a non-bonding curve is obtained at the HF level.16–22 However, note that the electrostatic attraction and the small ligand bite size also contribute to the total binding energy. This situation may necessitate future investigations of the breakdown of the relative interaction strength of various attractive/repulsive forces by studying other species that are less sensitive to coulombic M–L attraction, which is necessary to avoid interference with the concomitant variations in the potential energy surface of the M–M′ interaction.
To assess the contribution of dispersion into the total cluster stabilization and geometry, we have done full optimization at the TPSS and TPSS-D3(BJ) levels. Optimization at the TPSS-D3(BJ) level leads to distortions of the orientation of the ligands due to van der Waals interactions between the mesityl groups. Such distortions do not occur in the solid state.
In conclusion, optimization of the molecular structures of the studied pentanuclear  complexes yielded M–M′ distances that are much shorter than the M–M′ distances of molecules with metallophilic interactions, which are dominated by van der Waals interactions and strengthened by relativistic effects. Orbital analysis and EHT calculations show that the s, p and d orbitals form hybrid orbitals that contribute to the bond between the metals. The role of hybridization is verified by performing calculations at the Hartree–Fock (HF) level. The HF calculations that do not consider electron correlations and van der Waals interactions also yielded a bound complex implying that a chemical bond with shared electrons is to some extent formed. The hybridization is stronger between metals with different electronegativities suggesting that it might be possible to synthesize mixed coinage metal complexes. The binding energy of the M–M′ bond is 40–50 kcal mol−1. The Cu–Au interaction energy and the equilibrium distance calculated for [Cu3Au2(Mes5)] complexes by using different levels of theory showed a deep minimum at a short M–M′ distance.
complexes yielded M–M′ distances that are much shorter than the M–M′ distances of molecules with metallophilic interactions, which are dominated by van der Waals interactions and strengthened by relativistic effects. Orbital analysis and EHT calculations show that the s, p and d orbitals form hybrid orbitals that contribute to the bond between the metals. The role of hybridization is verified by performing calculations at the Hartree–Fock (HF) level. The HF calculations that do not consider electron correlations and van der Waals interactions also yielded a bound complex implying that a chemical bond with shared electrons is to some extent formed. The hybridization is stronger between metals with different electronegativities suggesting that it might be possible to synthesize mixed coinage metal complexes. The binding energy of the M–M′ bond is 40–50 kcal mol−1. The Cu–Au interaction energy and the equilibrium distance calculated for [Cu3Au2(Mes5)] complexes by using different levels of theory showed a deep minimum at a short M–M′ distance.
Conflicts of interest
There are no conflicts to declare.Note added after first publication
This version of the article replaces the previous one to correct an error in the title.Appendix
In the EHT calculations, the parameters used for carbon, hydrogen, and copper were: Hss = −11.4 eV, Hpp = −6.06 eV, Hdd = −14.0 eV, ζ4s = 2.2, ζ4p = 2.2, (ζd1 = 5.95, ζd2 = 2.3), c1 = 0.5933, c2 = 0.5744. For gold, we used Hss = −10.92 eV, Hpp = −5.55 eV, Hdd = −15.07 eV, ζ6s = 2.6002 ζ6p = 2.584, (ζd1 = 6.613, ζd2 = 2.794), c1 = 0.6442, c2 = 0.5356. For silver, we used Hss = Hpp = −6.06 eV, Hdd = −14.0 eV, ζ4s = 1.850, ζ4p = 1.30, (ζd1 = 3.91, ζd2 = 1.54), c1 = 0.824, c2 = 0.329.Acknowledgements
HR acknowledges funding from the U.S. Department of State's Bureau of Educational and Cultural Affairs as well as from the HPC-Europa3 project (INFRAIA-2016-1-730897). HR also thanks Prof. P. Pyykkö for useful discussions. This work has been supported by the Academy of Finland through project 340583. MAO acknowledges the Welch Foundation (B-1542) and the National Science Foundation (CHE-1413641) for supporting his group's contribution in this work. Computational resources from the Center for Advanced Scientific Computing and Modelling (CASCaM), at the University of North Texas and from the CSC – IT Center for Science, partially supported by the National Science Foundation (CHE-1531468), are acknowledged.Notes and references
- F. A. Cotton, X. Feng, M. Matusz and R. Poli, J. Am. Chem. Soc., 1988, 110, 7077–7083 CrossRef
.
- A. Muñoz-Castro and R. Guajardo Maturana, J. Phys. Chem. C, 2014, 118, 21185–21191 CrossRef
.
- W. Schneider, A. Bauer and H. Schmidbaur, Organometallics, 1996, 15, 5445–5446 CrossRef CAS
.
- C. A. Murillo, Comments Inorg. Chem., 2015, 35, 39–58 CrossRef CAS
.
- J. P. Collman and R. Boulatov, Angew. Chem., Int. Ed., 2002, 41, 3948–3961 CrossRef CAS PubMed
.
- M. Brooke, O. Kortney, M. Melançon and M. A. Omary, Comments Inorg. Chem., 2018, 38, 1–35 CrossRef
.
- R. Galassi, M. M. Ghimire, B. M. Otten, S. Ricci, R. N. McDougald, R. M. Almotawa, D. Alhmoud, J. F. Ivy, A.-M.-M. Rawashdeh, V. N. Nesterov, E. W. Reinheimer, L. M. Daniels, A. Burini and M. A. Omary, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 5042–5051 CrossRef PubMed
.
- R. Galassi, M. A. Rawashdeh-Omary, H. V. R. Dias and M. A. Omary, Comments Inorg. Chem., 2019, 39, 287–348 CrossRef CAS
.
- E. Cerrada, M. Contel, A. D. Valencia, M. Laguna, T. Gelbrich and M. B. A. Hursthouse, Angew. Chem., Int. Ed., 2000, 13, 2353–2356 CrossRef
.
- A. Balch, J. K. Nagle, D. E. Oram and P. E. Reedy, J. Am. Chem. Soc., 1988, 110, 454–462 CrossRef CAS
.
- J. Zheng, Z. Lu, K. Wu, G.-H. Ning and D. Li, Chem. Rev., 2020, 120, 9675–9742 CrossRef CAS PubMed
.
- S. Gambarotta, C. Floriani, A. Chiesi-Villa and C. Guastini, J. Chem. Soc., Chem. Commun., 1983, 1156–1158 RSC
.
- E. M. Meyer, S. Gambarotta, C. Floriani, A. Chiesi-Villa and C. Guastini, Organometallics, 1989, 8, 1067–1079 CrossRef CAS
.
- M. H. Whangbo and R. Hoffmann, J. Am. Chem. Soc., 1978, 100, 6093–6098 CrossRef CAS
.
- J. H. Ammeter, H.-B. Bürgi, J. C. Thibeault and R. Hoffmann, J. Am. Chem. Soc., 1978, 100, 3686–3692 CrossRef CAS
.
- P. Pyykkö, J. Li and N. Runeberg, Chem. Phys. Lett., 1994, 218, 133–138 CrossRef
.
- P. Pyykkö, Chem. Rev., 1997, 97, 597–636 CrossRef PubMed
.
- P. Pyykkö and Y. Zhao, Angew. Chem., 1991, 103, 604–605 CrossRef
.
- P. Pyykkö, X.-G. Xiong and J. Li, Faraday Discuss., 2011, 152, 169–178 RSC
.
- P. Pyykkö, Chem. Soc. Rev., 2008, 37, 1967–1997 RSC
.
- P. Pyykkö and M. Atsumi, Chem. – Eur. J., 2009, 15, 186–197 CrossRef PubMed
.
- S. Riedel, P. Pyykkö, R. A. Mata and H. J. Werner, Chem. Phys. Lett., 2005, 405, 148–152 CrossRef CAS
.
- R. Hoffmann and P. Hofmann, J. Am. Chem. Soc., 1976, 98, 598–604 CrossRef CAS
.
- P. K. Mehrotra and R. Hoffmann, Inorg. Chem., 1978, 17, 2187–2189 CrossRef CAS
.
- A. Dedieu and R. Hoffmann, J. Am. Chem. Soc., 1978, 100, 2074–2079 CrossRef CAS
.
- F. M. Siu, N. L. Ma and C. W. Tsang, J. Chem. Phys., 2001, 114, 7046–7051 CrossRef
.
-
(a) Z. Lu, B. Chilukuri, C. Yang, A.-M. Rawashdeh, R. K. K. Arvapally, S. Tekarli, X. Wang, C. Cardenas, T. R. Cundari and M. A. Omary, Chem. Sci., 2020, 11, 11179–11188 RSC
; (b) H. Rabaa, A. Rawashdeh and M. Omary, unpublished results on [Cu(PH3)Cl][Au(PH3)Cl] analogues of Pyykkö's complexes Unpublished work.
- J. Beck and J. Strähle, Angew. Chem., Int. Ed. Engl., 1985, 24, 409–410 CrossRef
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed
.
- W. J. Stevens, M. Krauss, H. Basch and P. G. Jasien, Can. J. Chem., 1992, 70, 612–630 CrossRef CAS
.
- H. L. Schmider and A. D. Becke, J. Chem. Phys., 1998, 108, 9624–9631 CrossRef CAS
.
-
M. J. Frisch, et al., Gaussian 03, Gaussian, Inc., Pittsburgh PA, 2003 (Gaussian) Search PubMed
; F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 4, 91–100 Search PubMed
(Turbomole).
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- S. Grimme, J. Antony, S. Ehrlich and H. A. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
-
E. Wiberg, A. F. Holleman and N. Wiberg, Lehrbuch der Anorganischen Chemie, Auflage, W. de Gruyter, Berlin, 2007, 102 Search PubMed
.
- C. Mealli, A. Ienco and D. M. Prosperio, Package CACAO98. 1997.
- R. Hoffmann, J. Chem. Phys., 1963, 39, 1397–1412 CrossRef CAS
.
- R. Hoffmann and W. N. Lipscomb, J. Chem. Phys., 1962, 36, 2179–2189 CrossRef CAS
.
- R. Hoffmann and W. N. Lipscomb, J. Chem. Phys., 1962, 37, 2872–2883 CrossRef CAS
.
- V. A. Fock, Z. Phys., 1930, 61, 126–148 CrossRef
.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef
.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed
.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed
.
- J. A. J. Jarvis, B. T. Kilbourn and R. Pearce, J. Chem. Soc., Chem. Commun., 1973, 475–476 RSC
.
- A. Bayler, A. Schier, G. A. Bowmaker and H. Schmidbaur, J. Am. Chem. Soc., 1996, 118, 7006–7007 CrossRef CAS
.
- H. V. R. Dias, H. V. K. Diyabalanage, M. M. Ghimire, J. M. Hudson, D. Parasar, C. S. Palehepitiya Gamage, S. Li and M. A. Omary, Dalton Trans., 2019, 48, 14979–14983 RSC
.
Footnotes |
| † Dedicated to Roald Hoffmann, Professor Emeritus at Cornell University (USA). |
| ‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04774h |
| This journal is © the Owner Societies 2023 |