Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accurate quantum-chemical fragmentation calculations for ion–water clusters with the density-based many-body expansion†
Stefanie
Schürmann
 ,
Johannes R.
Vornweg
,
Johannes R.
Vornweg
 ,
Mario
Wolter
,
Mario
Wolter
 and
Christoph R.
Jacob
and
Christoph R.
Jacob
 *
*
Technische Universität Braunschweig, Institute of Physical and Theoretical Chemistry, Gaußstraße 17, 38106 Braunschweig, Germany. E-mail: c.jacob@tu-braunschweig.de
First published on 29th November 2022
Abstract
The many-body expansion (MBE) provides an attractive fragmentation method for the efficient quantum-chemical treatment of molecular clusters. However, its convergence with the many-body order is generally slow for molecular clusters that exhibit large intermolecular polarization effects. Ion–water clusters are thus a particularly challenging test case for quantum-chemical fragmentation methods based on the MBE. Here, we assess the accuracy of both the conventional, energy-based MBE and the recently developed density-based MBE [Schmitt-Monreal and Jacob, Int. J. Quantum Chem., 2020, 120, e26228] for ion–water clusters. As test cases, we consider hydrated Ca2+, F−, OH−, and H3O+, and compare both total interaction energies and the relative interaction energies of different structural isomers. We show that an embedded density-based two-body expansion yields highly accurate results compared to supermolecular calculations. Already at the two-body level, the density-based MBE clearly outperforms a conventional, energy-based embedded three-body expansion. We compare different embedding schemes and find that a relaxed frozen-density embedding potential yields the most accurate results. This opens the door to accurate and efficient quantum-chemical calculations for large ion–water clusters as well as condensed-phase systems.
1 Introduction
Water plays an essential role in chemistry and is a prerequisite for life as we know it.1 Its exceptional properties have puzzled scientists for generations, and many fundamental questions concerning the properties of water are still unresolved (see, e.g., ref. 2–5 and references therein). Many chemical and most biological processes crucially depend on water as a solvent,6 and solvent effects intricately determine both the structure7–9 and spectroscopic properties10 of solvated molecular systems. In turn, solutes change the structure and properties of liquid water by influencing water–water interactions.11–13For studying these interactions at the molecular level, clusters of water as well as ion–water clusters present ideal model systems.14,15 In the past decades, such clusters have been investigated both spectroscopically (see, e.g., ref. 16–20) and computationally (for reviews, see, e.g., ref. 21 and 22). Despite increasing computational resources as well as methodological advances, the accurate, yet sufficiently efficient quantum-chemical treatment of large molecular clusters remains a challenging task.
Fragmentation methods,23–27 which partition such clusters into their molecular constituents, offer an attractive approach for overcoming this bottleneck. The most straightforward realization of such a fragmentation method is the well-known many-body expansion (MBE) (see, e.g., ref. 28–30), which approaches the total interaction energy of a molecular cluster as a sum of n-mer (dimer, trimer, tetramer etc.) interaction energy contributions. If the MBE can be truncated at a sufficiently low order, it provides a low-scaling and highly parallelizable computational approach for the accurate quantum-chemical treatment of molecular clusters. Generally, a truncation at second order (i.e., a two-body expansion) would be highly desirable. In addition, the MBE provides the basis for the development of accurate force-field models, in particular for water31–34 and ion–water systems.35–37
Ion–water clusters present a particularly challenging test case for the MBE.14,21,33,38–40 There have been numerous computational studies of ion–water clusters that employ a MBE (for recent examples, see ref. 35, 36 and 39–41). Because of the large polarization effects, three-body and four-body effects generally play an important role and the conventional MBE cannot be truncated at low order. To some degree, this can be alleviated with more general fragmentation schemes based on overlapping fragments.42,43
Recently, starting from the observation that a MBE of the electron density converges faster than a MBE for the total energy, our research group developed a density-based MBE (db-MBE).44 Instead of expanding the total density, the db-MBE is based on an expansion of the total electron density of a molecular cluster in terms of electron densities of embedded monomers, dimers, trimers etc. This expansion can then be used to obtain a density-based correction to the total energy. We could show that such a db-MBE can capture many-body polarization effects in water clusters already with a two-body expansion and that accurate total and relative energies can be obtained with a density-based two-body expansion.45 Here, we set out to explore the db-MBE for ion–water clusters, which present an even more challenging test case. We will particularly consider the importance of self-consistent embedding for the fragment calculations, which can be expected to be more important in ion–water clusters.
2 Computational methodology
2.1 (Embedded) many-body expansion
To treat a cluster consisting of N molecular fragments with the help of the MBE, instead of doing a quantum-chemical calculation for the full system, calculations are performed for the N monomers, the N(N − 1)/2 dimers that can be formed from them, and possibly also for trimers, tetramers, etc. A property of interest P is then calculated for each of the monomers, P(1)I, for each dimer, P(2)IJ, for each trimer P(3)IJK and so on. Here, the superscript indicates the size of the considered subsystem and the subscript lists the monomers included in it.The corresponding property Ptot of the full cluster is then approximated as,29,30
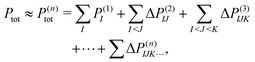 | (1) |
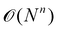 . Usually, one aims at truncating the MBE at low order (ideally, already at second order), while the exact, supermolecular result is recovered by construction for n = N.
. Usually, one aims at truncating the MBE at low order (ideally, already at second order), while the exact, supermolecular result is recovered by construction for n = N.
In the simplest case, the calculations of P(1)I, P(2)IJ, P(3)IJK, … are performed for the isolated active subsystem without considering the remaining fragments (isolated MBE). To accelerate the convergence of the MBE, the effect of the remaining fragments on the active monomer, dimer, trimer etc. can be approximated by means of a suitable embedding potential47–50 (embedded MBE). Here, we consider different local embedding potentials v(IJ⋯)emb(r), where the superscript indicates the fragments included in the active subsystem. Note that the inclusion of an embedding potential does not change the scaling of the computational effort of the MBE.
First, we consider a purely electrostatic point-charge (PC) embedding potential,
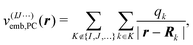 | (2) |
Second, we consider a more sophisticated embedding potential depending on the electron densities ρK(r′) of the fragments in the environment, i.e., the embedding potential of frozen-density embedding (FDE) theory,51,52
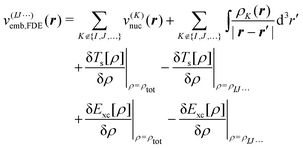 | (3) |
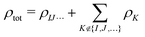 . This embedding potential includes the full electrostatic nuclear and electronic Coulomb potentials of the monomers in the environment as well as non-classical contributions due to the exchange–correlation and kinetic energy, which are evaluated using approximate functionals. For obtaining the electron densities of the fragments in the environment, the simplest variant is the use of those obtained in calculations for the isolated monomers. Since for ion–water clusters large polarization effects can be expected, we also iteratively updated all embedded monomer densities using freeze-and-thaw (ft) cycles. While the calculation of the relaxed monomer densities comes with some computational effort, this only needs to be done at the level of the monomers, i.e., the scaling of the computational effort remains unchanged.
. This embedding potential includes the full electrostatic nuclear and electronic Coulomb potentials of the monomers in the environment as well as non-classical contributions due to the exchange–correlation and kinetic energy, which are evaluated using approximate functionals. For obtaining the electron densities of the fragments in the environment, the simplest variant is the use of those obtained in calculations for the isolated monomers. Since for ion–water clusters large polarization effects can be expected, we also iteratively updated all embedded monomer densities using freeze-and-thaw (ft) cycles. While the calculation of the relaxed monomer densities comes with some computational effort, this only needs to be done at the level of the monomers, i.e., the scaling of the computational effort remains unchanged.
We will refer to these different variants of the MBE by the following acronyms: ‘iso’ is used for the isolated MBE, ‘PC’ refers to the embedded MBE using point-charge embedding, ‘FDE’ indicates that an embedded MBE with a frozen-density embedding potential based on the unrelaxed frozen densities of the isolated monomers has been used, whereas ‘FDE-ft’ denotes the use of a frozen-density embedding potential based on relaxed monomer densities optimized self-consistently in freeze-and-thaw cycles.
2.2 Energy-based many-body expansion
Conventionally, the MBE is performed for the total energy of the system, which is approximated as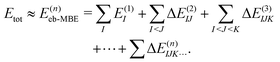 | (4) |
Here, the energies E(1)I, E(2)IJ, E(3)IJK,… are obtained from single-point calculations for the monomers, dimers, trimers, etc. In case of an embedded MBE, it is important to ensure that these energies refer to the active subsystem only and that they do not include the interaction with the environment, i.e., the interaction energy
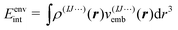 | (5) |
2.3 Density-based many-body expansion
Similarly, the total electron density can be approximated using the MBE as,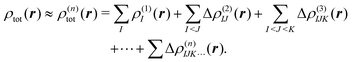 | (6) |
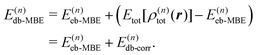 | (7) |
| Etot[ρ] = Ts[ρ] + Vnuc[ρ] + J[ρ] + Exc[ρ] + ENN | (8) |
The density-based energy correction E(n)db-corr in eqn (7) is a functional of the monomer, dimer, trimer etc. densities that is given by
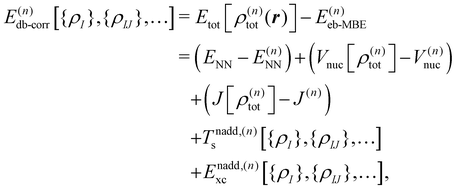 | (9) |
| Tnadd,(n)s[{ρI},{ρIJ},…] = Ts[ρ(n)tot] − T(n)s | (10) |
| Enadd,(n)xc[{ρI},{ρIJ},…] = Exc[ρ(n)tot] − E(n)xc, | (11) |
The first three terms in the above density-based energy correction E(n)db-corr correct the electrostatic interaction energies such that they correspond to the full n-body electron density. Note that for the nuclear–nuclear repulsion energy, a correction only appears at first order. The nonadditive kinetic and exchange–correlation energies account for non-classical interactions. In the spirit of subsystem-DFT,52 these contributions are evaluated using approximate, semi-local density functionals. For further details on the evaluation of the different terms in eqn (9), we refer to ref. 44 and 45.
We note that the calculation of the density-based energy correction is only done once after the individual subsystem calculations required in the MBE. Therefore, the scaling of the computational effort with cluster size is the same for the eb-MBE(n) and the db-MBE(n), even though in the latter case the need for calculating the subsystem electron densities increases the prefactor.44,45
2.4 Computational details
All quantum-chemical calculations have been performed using DFT with the Amsterdam Density-Functional (ADF) engine of the Amsterdam Modeling Suite (AMS)55,56 with the PBE0 hybrid functional57–59 and a triple-zeta plus polarization (TZP) basis set of Slater-type orbitals.60 A Becke integration grid of “good” accuracy61 and the numerical accuracy setting “good” have been used throughout. All total energies have been obtained with ADF's total energy implementation.62For the point-charge embedded MBEs we used TIP3P63 point charges (qH = +0.417 and qO = −0.834) for the environment water molecules. For the Ca2+ and F−, point charges were set to +2 and –1, respectively. For the hydroxide ion, we selected partial charges of qH = +0.183 and qO = −1.183,64 and for the H3O+ ion we chose qH = +0.524 and qO = −0.571.65 For the frozen-density embedded MBEs we employed ADF's implementation of FDE66 with the PW91k nonadditive kinetic-energy functional67 and the PBE57 functional for the nonadditive xc contributions. In the case of the FDE-ft embedded MBEs, three freeze-and-thaw-cycles were performed using monomer subsystems, and the resulting relaxed monomer electron densities were then used to assemble the frozen density in the subsequent calculations of the monomer, dimer, etc. subsystems.
The eb-MBE and db-MBE have been implemented in the PyADF scripting framework,68,69 which was used for all calculations presented in this work. PyADF includes a PyEmbed module, which provides a stand-alone implementation of the subsystem DFT embedding potential and interaction energy terms. For the nonadditive xc and kinetic energy contributions, it makes use of the XCFun library.70,71 Here, we employed the PW91k kinetic-energy functional67 and the PBE57 xc functional for the nonadditive energy contributions. The electrostatic interaction energies are evaluated by PyEmbed using numerical integration as described in ref. 44. The most recent version of PyADF, which can be used for reproducing all calculations presented here, is available at ref. 69.
All figures have been generated using Matplotlib72 and Seaborn.73 A data set containing coordinates of all considered molecular structures, PyADF input scripts for executing the eb-MBE and db-MBE calculations, raw data from all eb-MBE and db-MBE calculations as well as Jupyter notebooks for data analysis and for generating all tables and figures contained in this article are available at ref. 74.
3 Results and discussion
To assess the accuracy of the db-MBE for ion–water clusters, we will consider different test cases in the following. First, we investigate the absolute error in the total interaction energies of Ca2+–water clusters of increasing size (see Section 3.1). Second, we evaluate the accuracy of the relative energies of different structural isomers of selected F−–water clusters (see Section 3.2), OH−–water clusters (see Section 3.3), and H3O+–water clusters (see Section 3.4). In each case, the ion (Ca2+, F−, OH−, or H3O+) is treated as a separate, charged fragment in the MBE. For the H3O+–water clusters, the additional proton is assigned to the closest water molecule to form the H3O+ ion.For all clusters, we perform calculations using the eb-MBE of second and third order [eb-MBE(2) and eb-MBE(3)] and using the db-MBE of first, second, and third order [db-MBE(1), db-MBE(2), db-MBE(3)]. As reference, a supermolecular calculation of the full cluster is used. In all cases, we calculate interaction energies, 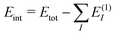 , i.e., the difference between the total energy of the cluster and the energies of the monomers. This also holds for relative interaction energies, which do not include the contribution that is due to changes in the monomer geometries (see the discussion in ref. 45). As explained above, we compare different embedding schemes in the MBE calculations, namely using the isolated subsystems (no embedding, labelled “iso”), point-charge embedding (labelled “PC”), and frozen-density embedding both with the unrelaxed frozen densities of the isolated environment molecules (labelled “FDE”) and with a relaxed frozen environment density updated in freeze-and-thaw cycles (labelled “FDE-ft”).
, i.e., the difference between the total energy of the cluster and the energies of the monomers. This also holds for relative interaction energies, which do not include the contribution that is due to changes in the monomer geometries (see the discussion in ref. 45). As explained above, we compare different embedding schemes in the MBE calculations, namely using the isolated subsystems (no embedding, labelled “iso”), point-charge embedding (labelled “PC”), and frozen-density embedding both with the unrelaxed frozen densities of the isolated environment molecules (labelled “FDE”) and with a relaxed frozen environment density updated in freeze-and-thaw cycles (labelled “FDE-ft”).
For comparison, we recall some of our earlier results from ref. 45, in which we benchmarked the accuracy of the db-MBE for neat water clusters. For the total interaction energies of water clusters of increasing size (up to 55 water molecules), we found that the absolute error of the MBEs increases linearly with the number of water molecules. For the isolated eb-MBE(2), it amounts to about 10 kJ mol−1 per water molecule (for B3LYP/DZP). This error is reduced to ca. 6 kJ mol−1 when using point-charge or frozen-density embedding. The db-MBE(1) provides an accuracy that is comparable to the eb-MBE(2), and with the second-order db-MBE(2) the error per water molecule is reduced to ca. 2 kJ mol−1, i.e., well below the threshold of chemical accuracy (1 kcal mol−1) for the interaction energy per fragment.
For the relative energies of selected isomers of water clusters of different size, we found that the eb-MBE(2) and even the eb-MBE(3) fail to reproduce the ordering of the isomers and/or their energy differences, even if point-charge or frozen-density embedding is used. In contrast, the embedded db-MBE(2) generally reproduces both the energy ordering of the considered isomers and their energy differences correctly. Across the test set of water cluster isomers investigated in ref. 45, the mean and the maximum errors in the relative interaction energies amount to only 0.13 kJ mol−1 and 0.32 kJ mol−1 per fragment, respectively.
While we found that the use of a suitable embedding potential generally leads to a clear improvement compared to the corresponding isolated MBEs, for water clusters we noticed that the difference between point-charge and frozen-density embedding is rather small. Therefore, the use of freeze-and-thaw cycles (FDE-ft) was not considered previously and is investigated here for the first time.
3.1 Ca2+(H2O)N (N = 3,…,20)
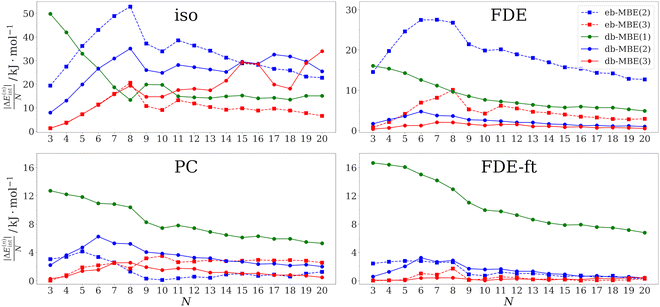
As a first test case, we examine hydrated calcium ions in Ca2+–water clusters containing three to twenty water molecules. The structures of these clusters have been taken from ref. 75. This system has been used recently by Veccham et al. to assess the accuracy of an embedded many-body expansion.76 Up to eight water molecules, these are directly coordinated to the calcium ion, while for larger clusters, a second solvation shell starts to build.The errors in the total interaction energy per water molecule for the different MBEs in combination with different embedding schemes are plotted in Fig. 1 as a function of cluster size. The corresponding mean and maximum errors across all considered cluster sizes are listed in Table 1.
| eb-MBE(n) | db-MBE(n) | |||||
|---|---|---|---|---|---|---|
| n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | ||
| Mean | Iso | 33.01 | 9.73 | 20.43 | 26.00 | 17.78 |
| PC | 1.42 | 2.42 | 8.23 | 3.43 | 1.26 | |
| FDE | 18.93 | 4.51 | 8.57 | 2.22 | 1.08 | |
| FDE-ft | 1.36 | 0.34 | 10.71 | 1.38 | 0.23 | |
| Max | iso | 52.85 | 20.55 | 49.80 | 35.07 | 33.95 |
| PC | 4.13 | 3.49 | 12.71 | 6.23 | 2.54 | |
| FDE | 27.48 | 10.07 | 16.04 | 4.69 | 2.01 | |
| FDE-ft | 2.79 | 1.71 | 16.64 | 3.24 | 0.44 | |
For the isolated eb-MBE(2), the error per water molecule increases up to eight water molecules, where it reaches its maximum of 53 kJ mol−1. For larger clusters, it decreases and drops to 23 kJ mol−1 for the largest considered cluster with 20 water molecules. Over all clusters, the mean error per water molecule amounts to 33 kJ mol−1. These results are very similar to those reported in ref. 76 for the same molecular structures, but with a different xc functional and basis set. When going to a three-body expansion with the isolated eb-MBE(3), the trend remains similar, but the errors are reduced by a factor of 2–3. Still, the mean and maximum errors remain substantial and amount to 10 kJ mol−1 and 21 kJ mol−1 per water molecule, respectively.
The accuracy of the eb-MBE(2) improves when it is combined with an embedding potential in the subsystem calculations. With point-charge embedding (using TIP3P charges for the water molecules), the mean and maximum errors drop to only 1.4 kJ mol−1 and 4.1 kJ mol−1 per water molecule, respectively. These errors are already below the threshold of chemical accuracy for the interaction energy per water molecule. With an unrelaxed FDE embedding potential, the errors are larger and the mean and maximum errors amount to 19 kJ mol−1 and 27 kJ mol−1 per water molecule, respectively. These errors are comparable to those found in ref. 76 for a point-charge embedded eb-MBE(2) using point charges determined from the electrostatic potential of isolated water molecules. In contrast, TIP3P point charges already account for the mutual polarization of water molecules in the condensed phase. The fact that the accuracy of electrostatically embedded eb-MBEs shows a strong dependence on the choice of embedding charges is well established in the literature.76–78 Accounting for the mutual polarization of the molecules within the cluster by using a FDE-ft embedding potential based on a relaxed frozen density that was obtained in freeze-and-thaw cycles reduces the mean and maximum errors of the eb-MBE(2) to 1.4 kJ mol−1 and 2.8 kJ mol−1 per water molecule, which is slightly lower than for TIP3P point-charge embedding. Importantly, in contrast to point-charge embedding, FDE-ft does not rely on any parametrization.
When going from the eb-MBE(2) to the eb-MBE(3), the errors are generally reduced. An exception is point-charge embedding, which indicates that the very low error for the point-charge embedded eb-MBE(2) might be partly accidental. For FDE-ft embedding, the agreement of the eb-MBE(3) with the supermolecular reference becomes almost perfect, with a mean error of only 0.34 kJ mol−1 per water molecule.
For the isolated db-MBEs, the errors are reduced compared to the isolated eb-MBE(2), but remain rather large. Thus, while for water clusters already the isolated db-MBE(2) could reduce the error per fragment below the threshold of chemical accuracy,45 for ion–water clusters the use of a suitable embedding potential is essential. As soon as some embedding potential is included, the accuracy of the db-MBE improves. For the db-MBE(1), which only requires calculations for the monomers, the mean error amounts to ca. 8–11 kJ mol−1 per water molecule. With the db-MBE(2), the mean errors drop below 4 kJ mol−1 per water molecule with all three embedding schemes. Remarkably, this is also the case with the unrelaxed FDE embedding, which led to substantially larger errors in the case of the eb-MBE(2). The relaxed FDE-ft embedding scheme results in the most accurate db-MBE(2) interaction energies, with a mean and maximum error of only 2.2 kJ mol−1 and 3.2 kJ mol−1 per water molecule, respectively.
Finally, the embedded three-body db-MBE(3) reduces the errors even further, and results in mean and maximum errors of 1.2 kJ mol−1 and 2.5 kJ mol−1 per water molecule, respectively, for point-charge embedding, and of 0.23 kJ mol−1 and 0.44 kJ mol−1 per water molecule, respectively, for relaxed FDE-ft embedding. In all cases, this is a substantial improvement both compared to the corresponding eb-MBE(3) and db-MBE(2).
Overall, we find that for Ca2+–water clusters, the accuracy of the embedded db-MBE(2) previously observed for neat water clusters45 is retained and the mean error in the total interaction energies per water molecule remains below the threshold of chemical accuracy. With relaxed FDE-ft embedding, it is significantly below this threshold. For the Ca2+–water clusters the proper inclusion of an embedding potential is crucial, and the best results are obtained with the parameter-free, relaxed FDE-ft embedding potential. However, we note that for the clusters considered here, excellent results can already be obtained with the eb-MBE(2), as long as suitable point-charge embedding or a relaxed FDE-ft embedding potential is included.
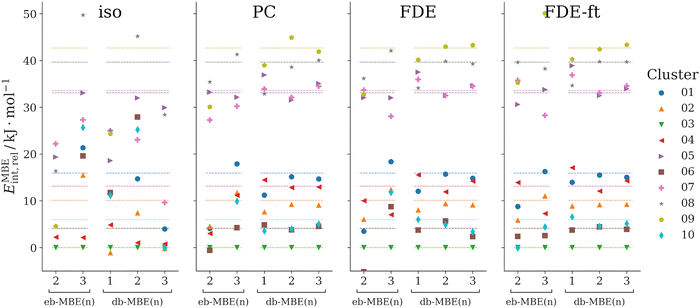
3.2 F−(H2O)10
As a second test case, we consider clusters of a fluoride anion with ten water molecules, F−(H2O)10. Here, we compare ten structural isomers, whose structures have been taken from ref. 42. These structures had been generated using molecular dynamics simulations and were used earlier as a test case for a MBE with overlapping fragments. The labels used for the different isomers correspond to those used previously in ref. 42.Here, we consider the relative interaction energies of the different isomers,
| Eisomeriint,rel = Eisomeriint,tot − Eisomer03int,tot, | (12) |
| eb-MBE(n) | db-MBE(n) | |||||
|---|---|---|---|---|---|---|
| n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | ||
| Mean, total | Iso | 158.16 | 128.21 | 122.93 | 172.02 | 81.51 |
| PC | 65.46 | 48.00 | 2.64 | 8.18 | 3.37 | |
| FDE | 78.79 | 51.47 | 3.23 | 6.12 | 4.33 | |
| FDE-ft | 42.75 | 29.39 | 5.82 | 0.59 | 0.81 | |
| Mean, relative | Iso | 25.01 | 10.99 | 12.95 | 10.26 | 14.47 |
| PC | 8.00 | 3.35 | 2.91 | 1.19 | 0.88 | |
| FDE | 6.74 | 4.75 | 2.62 | 0.78 | 1.22 | |
| FDE-ft | 3.55 | 2.80 | 2.74 | 0.63 | 0.72 | |
| Max, total | Iso | 174.44 | 147.39 | 139.66 | 192.09 | 100.95 |
| PC | 74.73 | 60.80 | 6.85 | 11.04 | 4.59 | |
| FDE | 89.97 | 51.47 | 7.72 | 7.98 | 6.64 | |
| FDE-ft | 47.55 | 37.47 | 11.07 | 1.25 | 1.63 | |
| Max, relative | Iso | 38.78 | 25.61 | 28.12 | 23.75 | 27.79 |
| PC | 16.45 | 14.54 | 6.79 | 2.23 | 2.01 | |
| FDE | 17.25 | 12.39 | 5.51 | 1.57 | 2.60 | |
| FDE-ft | 7.43 | 7.43 | 5.81 | 1.42 | 1.13 | |
First, we notice that neither the eb-MBE(2) nor the eb-MBE(3) are able to provide the correct energetic ordering of the isomers. While the energy-based three-body expansion improves compared to the two-body expansion, it still misorders multiple isomers and produces significant errors for energy differences between isomers. This holds for all considered embedding schemes. Comparing the different embedding schemes, the isolated eb-MBE(3) performs worst (mean and maximum errors in relative energies of 11 kJ mol−1 and 26 kJ mol−1, respectively), whereas the smallest errors are obtained with the relaxed FDE-ft embedding potential (mean and maximum errors in relative energies of 2.8 kJ mol−1 and 7.8 kJ mol−1, respectively).
Without the inclusion of an embedding potential, the isolated db-MBE does not provide useful results for the relative energies. However, if an embedding potential is included, already the one-body db-MBE(1) leads to a significant improvement compared to the eb-MBE(2) and eb-MBE(3). It groups the isomers correctly into a lower energy group (isomers 01, 02, 03, 04, 06, and 10) and a higher energy group (isomers 05, 07, 08, and 09), even though the ordering within these groups is not fully correct. This is remarkable, given that the db-MBE(1) uses only calculations for the embedded monomers.
With the embedded db-MBE(2), the relative energies are further improved. The energetic ordering of the isomers is mostly correct, except for some close-lying isomers (e.g., isomers 06 and 10, isomers 05 and 07) and some remaining deviations in the energy differences between isomers. For the db-MBE(2) relative energies, all three embedding schemes perform comparably well. The most accurate results are found for the relaxed FDE-ft embedding potential with a mean error of 0.6 kJ mol−1 and a maximum error of 1.4 kJ mol−1 in the relative energies. The db-MBE(3) further improves the energy differences between isomers slightly. With FDE-ft embedding, the mean and maximum errors in relative energies amount to 0.7 kJ mol−1 and 1.1 kJ mol−1.
Altogether, already the embedded db-MBE(2) clearly improves compared to the eb-MBE(2) and eb-MBE(3), which both do not provide sufficient accuracy for the relative interaction energies. The db-MBE(2) is able to reproduce the ordering of the isomers as well as their relative energies accurately. Previously, such an accuracy for this test case was only reached with an eb-MBE based on larger, overlapping fragments.42 It is noteworthy that with FDE-ft embedding, excellent agreement is also reached for the total interaction energies, for which the mean and maximum errors are as low as 0.6 kJ mol−1 and 1.3 kJ mol−1, respectively.
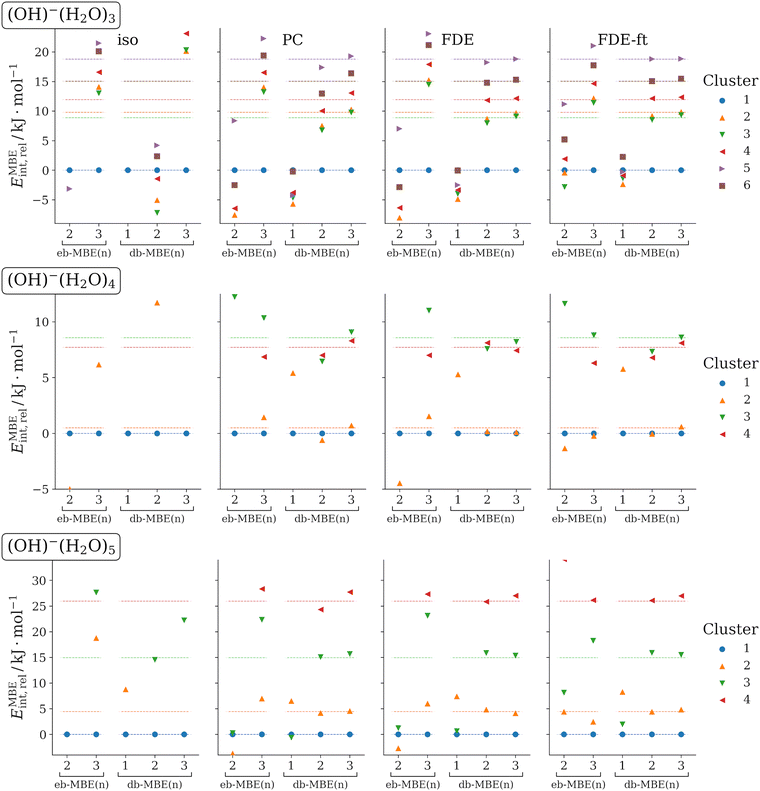
3.3 OH−(H2O)N (N = 3, 4, 5)
As another test case, we consider clusters of a hydroxide anion with three, four, and five water molecules. For each cluster size, different low-energy structural isomers are considered. The structures of these clusters have been taken from ref. 35, in which Egan and Paesani analyzed many-body effects in these systems using high-level coupled-cluster calculations. They found that in OH−(H2O)5, three-body effects amount to up to 60 kJ mol−1, four-body effects to up to 8 kJ mol−1, and five-body effects still contribute up to 2 kJ mol−1. The lowest-energy clusters of each size were also used as test case in ref. 76. At the DFT level, errors of ca. 140 kJ mol−1 were found for OH−(H2O)5 with an isolated eb-MBE(2), which could be reduced to ca. 21 kJ mol−1 by combining the eb-MBE(2) with a sophisticated quantum-embedding scheme.The relative interaction energies of the different isomers for each cluster size that are calculated with the eb-MBEs and the db-MBEs are compared to the supermolecular reference values in Fig. 3. The mean and maximum errors in the total and in the relative interaction energies are given in Table 3. These refer to all considered clusters (the lowest-energy isomer is excluded for the relative interaction energies) and are not normalized to the cluster size.
| eb-MBE(n) | db-MBE(n) | |||||
|---|---|---|---|---|---|---|
| n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | ||
| Mean, total | Iso | 68.82 | 14.68 | 168.08 | 55.18 | 33.44 |
| PC | 34.80 | 3.80 | 24.01 | 3.80 | 1.63 | |
| FDE | 40.76 | 4.35 | 22.58 | 3.04 | 1.66 | |
| FDE-ft | 13.56 | 1.29 | 18.23 | 1.34 | 0.28 | |
| Mean, relative | Iso | 24.84 | 7.55 | 35.79 | 17.57 | 16.91 |
| PC | 13.74 | 3.34 | 14.39 | 1.44 | 0.74 | |
| FDE | 14.83 | 3.88 | 14.24 | 0.55 | 0.33 | |
| FDE-ft | 7.82 | 1.85 | 12.44 | 0.46 | 0.34 | |
| Max, total | Iso | 114.89 | 31.27 | 233.05 | 104.62 | 87.41 |
| PC | 52.07 | 9.92 | 51.30 | 6.47 | 3.72 | |
| FDE | 61.77 | 4.35 | 49.26 | 4.70 | 3.39 | |
| FDE-ft | 21.65 | 3.82 | 40.70 | 2.30 | 0.95 | |
| Max, relative | Iso | 45.45 | 14.29 | 75.10 | 37.62 | 34.72 |
| PC | 26.92 | 7.37 | 32.64 | 2.27 | 1.76 | |
| FDE | 30.21 | 3.88 | 32.33 | 1.09 | 1.05 | |
| FDE-ft | 16.67 | 3.29 | 27.84 | 1.26 | 1.00 | |
As for the previous test cases, it is obvious from Fig. 3 that the use of a suitable embedding potential is essential for ion–water clusters. For the isolated eb-MBEs and db-MBEs, rather large errors are found. The embedded MBEs generally show much better performance. When comparing the mean and maximum errors in Table 3, we notice that point-charge embedding and unrelaxed FDE show comparable errors, with generally slightly better accuracy for unrelaxed FDE. In all cases, the most accurate results are obtained with the relaxed FDE-ft embedding potential, for which the mean and maximum errors are lower than for PC and FDE by at least a factor of two.
However, the embedded eb-MBE(2) is not able to reproduce the correct ordering of the isomers at all. For the most accurate FDE-ft embedding, the mean and maximum errors in the relative interaction energies still amount to 8 kJ mol−1 and 17 kJ mol−1, respectively. The embedded eb-MBE(3) improves and results in the correct ordering of the isomers in most cases, but it still shows significant errors in the energy differences, with mean and maximum errors in the relative energies of 1.9 kJ mol−1 and 3.3 kJ mol−1, respectively, for FDE-ft embedding.
The embedded db-MBE(1) performs worse than for the fluoride–water clusters in the previous section, and largely underestimates the energy differences between the structural isomers. In contrast, the embedded db-MBE(2) results in the correct energetic ordering of the structural isomers and yields rather accurate energy differences. With FDE-ft embedding, the mean and maximum errors in the relative energies are reduced to 0.46 kJ mol−1 and 1.3 kJ mol−1, respectively. The embedded db-MBE(3) slightly improves upon this and reduces these errors to 0.34 kJ mol−1 and 1.0 kJ mol−1, respectively.
Again, we note that the excellent accuracy of the db-MBE(2) and db-MBE(3) does not only hold for the relative interaction energies, but also the corresponding total interaction energies turn out to be highly accurate, with maximum errors of only 2.30 kJ mol−1 and 0.95 kJ mol−1, respectively, for the density-based two-body and three-body expansions.
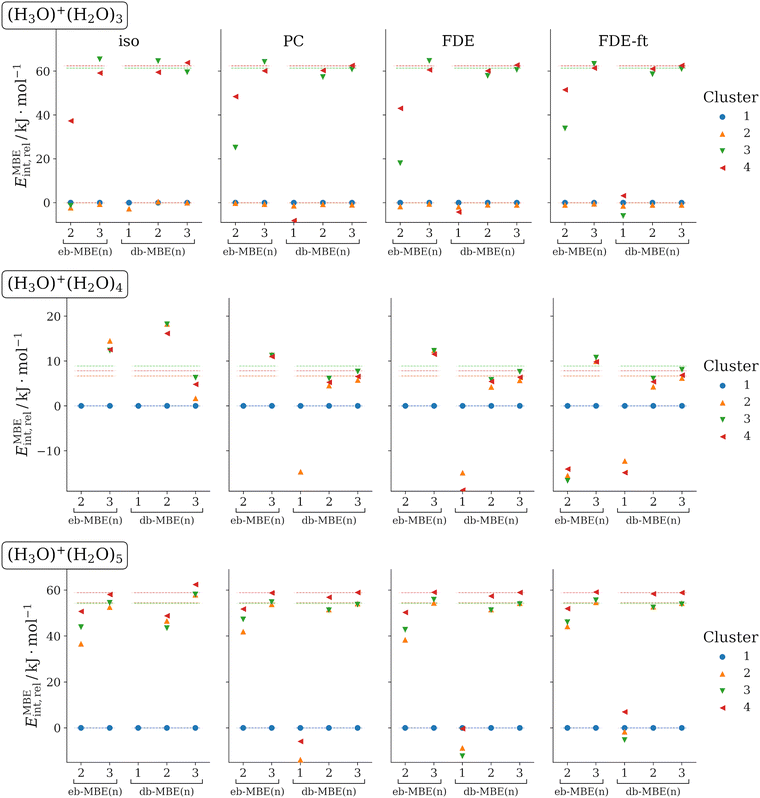
3.4 H3O+(H2O)N (N = 3, 4, 5)
As last test case, we examine protonated water clusters with four to six water molecules. Again, for each cluster size different structural isomers are considered. The structures have been taken from ref. 36. For applying the MBE, these clusters are partitioned into one H3O+ cation and N water molecules. We note that some isomers contain a Zundel ion, H5O2+, as a substructure, which is nevertheless partitioned into an H3O+ cation and a water molecule. Previously, it was found that with an isolated eb-MBE, three-body contributions amount to up to 40 kJ mol−1, four-body contributions can be as large as 5.5 kJ mol−1, whereas five-body contributions become negligible.36The relative interaction energies obtained with eb-MBEs and db-MBEs in combination with different embedding schemes are visualized in Fig. 4 and compared to the supermolecular reference data. Mean and maximum errors in the total and relative interaction energies are summarized in Table 4.
| eb-MBE(n) | db-MBE(n) | |||||
|---|---|---|---|---|---|---|
| n = 2 | n = 3 | n = 1 | n = 2 | n = 3 | ||
| Mean, total | Iso | 31.50 | 3.18 | 196.92 | 10.80 | 1.21 |
| PC | 19.12 | 2.10 | 73.78 | 1.20 | 0.49 | |
| FDE | 23.90 | 2.07 | 67.65 | 1.45 | 0.51 | |
| FDE-ft | 13.01 | 1.38 | 61.64 | 1.46 | 0.35 | |
| Mean, relative | Iso | 33.83 | 2.96 | 88.95 | 7.16 | 2.80 |
| PC | 18.70 | 1.90 | 49.66 | 2.48 | 0.68 | |
| FDE | 24.15 | 2.25 | 46.70 | 2.43 | 0.72 | |
| FDE-ft | 14.95 | 1.37 | 41.12 | 1.87 | 0.50 | |
| Max, total | Iso | 57.94 | 5.56 | 289.57 | 20.70 | 3.62 |
| PC | 34.92 | 3.77 | 127.00 | 2.71 | 0.97 | |
| FDE | 41.57 | 2.07 | 117.89 | 2.60 | 0.93 | |
| FDE-ft | 24.33 | 2.50 | 106.13 | 2.73 | 0.73 | |
| Max, relative | Iso | 65.80 | 7.79 | 150.79 | 11.56 | 5.00 |
| PC | 36.32 | 4.77 | 82.45 | 4.03 | 1.32 | |
| FDE | 44.14 | 2.25 | 77.34 | 3.55 | 1.50 | |
| FDE-ft | 27.59 | 3.26 | 67.49 | 2.83 | 1.01 | |
Overall, the results confirm the picture obtained in the previous sections. The eb-MBE(2) is not able to reproduce the energetic ordering of the structural isomers correctly. In contrast, the db-MBE(2) yields highly accurate results when combined with a suitable embedding scheme. For the most accurate relaxed FDE-ft embedding, the mean and maximum errors in the relative energies amount to only 1.9 kJ mol−1 and 2.8 kJ mol−1, respectively. A similar error is reached for the total interaction energies with mean and maximum errors of 1.5 kJ mol−1 and 2.7 kJ mol−1, respectively. These errors of the db-MBE(2) are slightly lower than those found for the more expensive eb-MBE(3).
4 Conclusions
In this work, we have evaluated the accuracy of the eb-MBE and of the db-MBE recently developed in our research group for ion–water clusters. With the conventional eb-MBE, the errors in the total and relative interaction energies of these systems are significantly larger than for neat water clusters, mainly because of the large polarization effects that are induced by the ion. Thus, ion–water clusters present a very challenging test case for the db-MBE. To avoid the steep scaling of the computational effort with cluster size that plagues higher-order MBEs, our goal is to achieve sufficient accuracy already with a two-body expansion.Our results show that the two-body db-MBE(2) is able to provide highly accurate relative and total interaction energies for all test cases considered here. The remaining errors are comparable to those found earlier for neat water clusters45. Thus, the density-based many-body expansion is able to capture the large polarization effects in these systems already at the level of a two-body expansion. With the conventional eb-MBE, a three-body or even a four-body expansion is required to achieve a similar accuracy.
The db-MBE achieves this by performing the MBE not in terms of the energy, but by expanding the electron density and by applying a density-functional to evaluate a density-based correction to the total energy of the eb-MBE. This MBE of the electron density accounts for the interactions among the polarized electron densities that only appear at higher orders in the conventional eb-MBE44. Because at any given order, the eb-MBE and the db-MBE rely on the same quantum-chemical calculations for subsystems, the scaling of their computational effort with cluster size remains comparable. Therefore, accounting for many-body polarization effects already in the db-MBE(2) instead of requiring a higher-order eb-MBE reduces the overall computational effort for large systems and thus pushes the limit of the system sizes that can be treated accurately and efficiently. Further strategies for reducing the computational cost that have been established for the eb-MBE, such as distance-based screening of higher-order contributions,43,47 are also applicable for the db-MBE and will be explored in our future work.
For ion–water clusters, the use of a suitable embedding potential within the MBE subsystem calculations turns out to be essential. Here, we compared the use of a point-charge embedding potential (with parametrized partial charges) as well as frozen-density embedding with the unrelaxed monomer frozen densities (FDE) and with monomer densities relaxed in freeze-and-thaw cycles (FDE-ft). While we notice that for the db-MBE the resulting energies are less sensitive to the choice of the embedding potential than for the eb-MBE, we still find that in all cases, FDE-ft embedding leads to the most accurate results. Thus, we recommend to use FDE-ft embedding, which does not rely on any parametrization, in future applications of the db-MBE to systems with large polarization effects.
While we only performed DFT calculations in the present study, the db-MBE can be combined with other quantum-chemical methods, in particular with accurate wavefunction-based methods. As the number of monomer and dimer calculations required for the db-MBE(2) scales only quadratically with the number of fragments while retaining excellent accuracy, it might allow us to overcome the scaling bottleneck of accurate wavefunction-based quantum chemistry. This will enable the efficient, yet accurate treatment of large ion–water clusters and possibly also of condensed-phase systems with the db-MBE(2).
Data availability
Data for this paper, including xyz files of all considered molecular structures, PyADF input scripts for executing the eb-MBE and db-MBE calculations, csv files containing the raw data from all eb-MBE and db-MBE calculations as well as Jupyter notebooks for data analysis and for generating all tables and figures contained in this article, are available at Zenodo at https://doi.org/10.5281/zenodo.7113146.Author contributions
Stefanie Schürmann: Investigation (lead), software (equal), data curation (equal), visualization (lead), writing – original draft (equal), writing – review and editing (equal). Johannes R. Vornweg: software (equal), supervision (supporting), visualization (supporting), writing – review and editing (equal). Mario Wolter: conceptualization (supporting), supervision (lead), visualization (supporting), writing – review and editing (equal). Christoph R. Jacob: conceptualization (lead), data curation (equal), writing – original draft (equal), writing – review and editing (lead).Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding from the Deutsche Forschungsgemeinschaft for the development of PyADF (Project Suresoft, JA 2329/7-1) is gratefully acknowledged. We thank Daniel Schmitt-Monreal for originally developing the code for preparing Fig. 2–4.Notes and references
- E. Brini, C. J. Fennell, M. Fernandez-Serra, B. Hribar-Lee, M. Lukšič and K. A. Dill, How Water's Properties Are Encoded in Its Molecular Structure and Energies, Chem. Rev., 2017, 117, 12385–12414 CrossRef CAS PubMed.
- M. D. Fayer, Dynamics of Water Interacting with Interfaces, Molecules, and Ions, Acc. Chem. Res., 2012, 45, 3–14 CrossRef CAS PubMed.
- A. Hassanali, F. Giberti, J. Cuny, T. D. Kühne and M. Parrinello, Proton transfer through the water gossamer, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 13723–13728 CrossRef CAS PubMed.
- M. Ceriotti, J. Cuny, M. Parrinello and D. E. Manolopoulos, Nuclear quantum effects and hydrogen bond fluctuations in water, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15591–15596 CrossRef CAS PubMed.
- L. G. M. Pettersson, R. H. Henchman and A. Nilsson, Water—The Most Anomalous Liquid, Chem. Rev., 2016, 116, 7459–7462 CrossRef CAS PubMed.
- M. Havenith, Solvation Science: A New Interdisciplinary Field, Angew. Chem., Int. Ed., 2016, 55, 1218–1219 CrossRef CAS PubMed.
- S. Ebbinghaus, S. J. Kim, M. Heyden, X. Yu, U. Heugen, M. Gruebele, D. M. Leitner and M. Havenith, An extended dynamical hydration shell around proteins, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20749–20752 CrossRef CAS PubMed.
- M.-C. Bellissent-Funel, A. Hassanali, M. Havenith, R. Henchman, P. Pohl, F. Sterpone, D. van der Spoel, Y. Xu and A. E. Garcia, Water Determines the Structure and Dynamics of Proteins, Chem. Rev., 2016, 116, 7673–7697 CrossRef CAS PubMed.
- S. S. Ribeiro, N. Samanta, S. Ebbinghaus and J. C. Marcos, The synergic effect of water and biomolecules in intracellular phase separation, Nat. Rev. Chem., 2019, 3, 552–561 CrossRef CAS.
- T. Giovannini, F. Egidi and C. Cappelli, Molecular spectroscopy of aqueous solutions: a theoretical perspective, Chem. Soc. Rev., 2020, 49, 5664–5677 RSC.
- B. Hribar, N. T. Southall, V. Vlachy and K. A. Dill, How Ions Affect the Structure of Water, J. Am. Chem. Soc., 2002, 124, 12302–12311 CrossRef CAS.
- Y. Marcus, Effect of Ions on the Structure of Water: Structure Making and Breaking, Chem. Rev., 2009, 109, 1346–1370 CrossRef CAS.
- P. Lo Nostro and B. W. Ninham, Hofmeister Phenomena: An Update on Ion Specificity in Biology, Chem. Rev., 2012, 112, 2286–2322 CrossRef CAS.
- S. S. Xantheas, Cooperativity and hydrogen bonding network in water clusters, Chem. Phys., 2000, 258, 225–231 CrossRef CAS.
- R. Ludwig, Water: From Clusters to the Bulk, Angew. Chem., Int. Ed., 2001, 40, 1808–1827 CrossRef CAS.
- J. W. Shin, N. I. Hammer, E. G. Diken, M. A. Johnson, R. S. Walters, T. D. Jaeger, M. A. Duncan, R. A. Christie and K. D. Jordan, Infrared Signature of Structures Associated with the H+(H2O)n (n = 6 to 27) Clusters, Science, 2004, 304, 1137–1140 CrossRef CAS PubMed.
- M. Miyazaki, A. Fujii, T. Ebata and N. Mikami, Infrared Spectroscopic Evidence for Protonated Water Clusters Forming Nanoscale Cages, Science, 2004, 304, 1134–1137 CrossRef CAS PubMed.
- N. Yang, C. H. Duong, P. J. Kelleher, A. B. McCoy and M. A. Johnson, Deconstructing water's diffuse OH stretching vibrational spectrum with cold clusters, Science, 2019, 364, 275–278 CrossRef CAS PubMed.
- S. Mitra, N. Yang, L. M. McCaslin, R. B. Gerber and M. A. Johnson, Size-Dependent Onset of Nitric Acid Dissociation in Cs+⋅(HNO3)(H2O)n=0-11 Clusters at 20 K, J. Phys. Chem. Lett., 2021, 12, 3335–3342 CrossRef CAS PubMed.
- H. J. Zeng and M. A. Johnson, Demystifying the Diffuse Vibrational Spectrum of Aqueous Protons Through Cold Cluster Spectroscopy, Annu. Rev. Phys. Chem., 2021, 72, 667–691 CrossRef CAS PubMed.
- S. R. Gadre, S. D. Yeole and N. Sahu, Quantum Chemical Investigations on Molecular Clusters, Chem. Rev., 2014, 114, 12132–12173 CrossRef CAS PubMed.
- J. C. Howard and G. S. Tschumper, Wavefunction methods for the accurate characterization of water clusters, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 199–224 CAS.
- G. J. O. Beran and K. Nanda, Predicting Organic Crystal Lattice Energies with Chemical Accuracy, J. Phys. Chem. Lett., 2010, 1, 3480–3487 CrossRef.
- M. S. Gordon, D. G. Fedorov, S. R. Pruitt and L. V. Slipchenko, Fragmentation Methods: A Route to Accurate Calculations on Large Systems, Chem. Rev., 2012, 112, 632–672 CrossRef PubMed.
- K. Raghavachari and A. Saha, Accurate Composite and Fragment-Based Quantum Chemical Models for Large Molecules, Chem. Rev., 2015, 115, 5643–5677 CrossRef.
- Fragmentation: Toward Accurate Calculations on Complex Molecular Systems, ed. M. S. Gordon, Wiley, Hoboken, NJ, 1st edn, 2017 Search PubMed.
- G. J. O. Beran, Modeling Polymorphic Molecular Crystals with Electronic Structure Theory, Chem. Rev., 2016, 116, 5567–5613 CrossRef PubMed.
- J. Cui, H. Liu and K. D. Jordan, Theoretical Characterization of the (H2O)21 Cluster: Application of an n-body Decomposition Procedure, J. Phys. Chem. B, 2006, 110, 18872–18878 CrossRef PubMed.
- R. M. Richard, K. U. Lao and J. M. Herbert, Understanding the many-body expansion for large systems. I. Precision considerations, J. Chem. Phys., 2014, 141, 014108 CrossRef PubMed.
- J. M. Herbert, Fantasy versus reality in fragment-based quantum chemistry, J. Chem. Phys., 2019, 151, 170901 CrossRef PubMed.
- Y. Wang and J. M. Bowman, Towards an ab initio flexible potential for water, and post-harmonic quantum vibrational analysis of water clusters, Chem. Phys. Lett., 2010, 491, 1–10 CrossRef CAS.
- Y. Wang, X. Huang, B. C. Shepler, B. J. Braams and J. M. Bowman, Flexible, ab initio potential, and dipole moment surfaces for water. I. Tests and applications for clusters up to the 22-mer, J. Chem. Phys., 2011, 134, 094509 CrossRef PubMed.
- G. A. Cisneros, K. T. Wikfeldt, L. Ojamäe, J. Lu, Y. Xu, H. Torabifard, A. P. Bartók, G. Csányi, V. Molinero and F. Paesani, Modeling Molecular Interactions in Water: From Pairwise to Many-Body Potential Energy Functions, Chem. Rev., 2016, 116, 7501–7528 CrossRef CAS PubMed.
- E. Lambros, S. Dasgupta, E. Palos, S. Swee, J. Hu and F. Paesani, General Many-Body Framework for Data-Driven Potentials with Arbitrary Quantum Mechanical Accuracy: Water as a Case Study, J. Chem. Theory Comput., 2021, 17, 5635–5650 CrossRef CAS.
- C. K. Egan and F. Paesani, Assessing Many-Body Effects of Water Self-Ions. I: OH(H2O)n Clusters, J. Chem. Theory Comput., 2018, 14, 1982–1997 CrossRef CAS PubMed.
- C. K. Egan and F. Paesani, Assessing Many-Body Effects of Water Self-Ions. II: H3O+(H2O)n Clusters, J. Chem. Theory Comput., 2019, 15, 4816–4833 CrossRef CAS PubMed.
- Y. Zhai, A. Caruso, S. Gao and F. Paesani, Active learning of many-body configuration space: application to the Cs+–water MB-nrg potential energy function as a case study, J. Chem. Phys., 2020, 152, 144103 CrossRef PubMed.
- C. H. Pham, S. K. Reddy, K. Chen, C. Knight and F. Paesani, Many-Body Interactions in Ice, J. Chem. Theory Comput., 2017, 13, 1778–1784 CrossRef PubMed.
- J. P. Heindel and S. S. Xantheas, The Many-Body Expansion for Aqueous Systems Revisited: II. Alkali Metal and Halide Ion–Water Interactions, J. Chem. Theory Comput., 2021, 17, 2200–2216 CrossRef PubMed.
- K. M. Herman, J. P. Heindel and S. S. Xantheas, The many-body expansion for aqueous systems revisited: III. Hofmeister ion–water interactions, Phys. Chem. Chem. Phys., 2021, 23, 11196–11210 RSC.
- H. R. Leverentz and D. G. Truhlar, Electrostatically Embedded Many-Body Approximation for Systems of Water, Ammonia, and Sulfuric Acid and the Dependence of Its Performance on Embedding Charges, J. Chem. Theory Comput., 2009, 5, 1573–1584 CrossRef PubMed.
- R. M. Richard and J. M. Herbert, A generalized many-body expansion and a unified view of fragment-based methods in electronic structure theory, J. Chem. Phys., 2012, 137, 064113 CrossRef PubMed.
- J. Liu, L.-W. Qi, J. Z. H. Zhang and X. He, Fragment Quantum Mechanical Method for Large-Sized Ion–Water Clusters, J. Chem. Theory Comput., 2017, 13, 2021–2034 CrossRef CAS PubMed.
- D. Schmitt-Monreal and Ch. R. Jacob, Frozen-density embedding-based many-body expansions, Int. J. Quantum Chem., 2020, 120, e26228 CrossRef CAS.
- D. Schmitt-Monreal and Ch. R. Jacob, Density-Based Many-Body Expansion as an Efficient and Accurate Quantum-Chemical Fragmentation Method: Application to Water Clusters, J. Chem. Theory Comput., 2021, 17, 4144–4156 CrossRef CAS PubMed.
- I. G. Kaplan, R. Santamaria and O. Novaro, Non-additive forces in atomic clusters, Mol. Phys., 1995, 84, 105–114 CrossRef CAS.
- E. E. Dahlke and D. G. Truhlar, Electrostatically Embedded Many-Body Expansion for Large Systems, with Applications to Water Clusters, J. Chem. Theory Comput., 2007, 3, 46–53 CrossRef CAS PubMed.
- E. E. Dahlke and D. G. Truhlar, Electrostatically Embedded Many-Body Expansion for Simulations, J. Chem. Theory Comput., 2008, 4, 1–6 CrossRef CAS PubMed.
- P. J. Bygrave, N. L. Allan and F. R. Manby, The embedded many-body expansion for energetics of molecular crystals, J. Chem. Phys., 2012, 137, 164102 CrossRef CAS PubMed.
- S. Wen and G. J. O. Beran, Accurate Molecular Crystal Lattice Energies from a Fragment QM/MM Approach with On-the-Fly Ab Initio Force Field Parametrization, J. Chem. Theory Comput., 2011, 7, 3733–3742 CrossRef CAS.
- T. A. Wesolowski and A. Warshel, Frozen Density Functional Approach for ab Initio Calculations of Solvated Molecules, J. Phys. Chem., 1993, 97, 8050–8053 CrossRef CAS.
- C. R. Jacob and J. Neugebauer, Subsystem density-functional theory, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 325–362 CAS.
- S. Humbel, S. Sieber and K. Morokuma, The IMOMO method: Integration of different levels of molecular orbital approximations for geometry optimization of large systems: Test for n-butane conformation and SN2 reaction: RCl + Cl−, J. Chem. Phys., 1996, 105, 1959–1967 CrossRef CAS.
- L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, The ONIOM Method and Its Applications, Chem. Rev., 2015, 115, 5678–5796 CrossRef PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef.
- Software for Chemistry and Materials, Amsterdam, AMS, Amsterdam Modelling Suite, Version 2021.201, 2021, http://www.scm.com.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef PubMed.
- M. Ernzerhof and G. E. Scuseria, Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef.
- E. Van Lenthe and E. J. Baerends, Optimized Slater-type basis sets for the elements 1-118, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- M. Franchini, P. H. T. Philipsen and L. Visscher, The Becke Fuzzy Cells Integration Scheme in the Amsterdam Density Functional Program Suite, J. Comput. Chem., 2013, 34, 1819–1827 CrossRef CAS PubMed.
- A. W. Götz, S. M. Beyhan and L. Visscher, Performance of Kinetic Energy Functionals for Interaction Energies in a Subsystem Formulation of Density Functional Theory, J. Chem. Theory Comput., 2009, 5, 3161–3174 CrossRef.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- M. W. Lee and M. Meuwly, Hydration free energies of cyanide and hydroxide ions from molecular dynamics simulations with accurate force fields, Phys. Chem. Chem. Phys., 2013, 15, 20303–20312 RSC.
- U. C. Singh, F. K. Brown, P. A. Bash and P. A. Kollman, An approach to the application of free energy perturbation methods using molecular dynamics: applications to the transformations of methanol → ethane, oxonium → ammonium, glycine → alanine, and alanine → phenylalanine in aqueous solution and to H3O+ (H2O)3 → NH4+ (H2O)3 in the gas phase, J. Am. Chem. Soc., 1987, 109, 1607–1614 CrossRef CAS.
- C. R. Jacob, J. Neugebauer and L. Visscher, A flexible implementation of frozen-density embedding for use in multilevel simulations, J. Comput. Chem., 2008, 29, 1011–1018 CrossRef CAS PubMed.
- A. Lembarki and H. Chermette, Obtaining a gradient-corrected kinetic-energy functional from the Perdew-Wang exchange functional, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 50, 5328–5331 CrossRef CAS PubMed.
- C. R. Jacob, S. M. Beyhan, R. E. Bulo, A. S. P. Gomes, A. W. Götz, K. Kiewisch, J. Sikkema and L. Visscher, PyADF—A scripting framework for multiscale quantum chemistry, J. Comput. Chem., 2011, 32, 2328–2338 CrossRef CAS PubMed.
- C. R. Jacob, T. Bergmann, S. M. Beyhan, J. Brüggemann, R. E. Bulo, M. Chekmeneva, T. Dresselhaus, A. S. P. Gomes, A. W. Goetz, M. Handzlik, K. Kiewisch, M. Klammler, L. Ridder, J. Sikkema, L. Visscher, J. Vornweg and M. Wolter, PyADF Version 1.1, 2022 DOI:10.5281/zenodo.7025692, URL: https://github.com/chjacob-tubs/pyadf-releases/tree/v1.1.
- U. Ekström, L. Visscher, R. Bast, A. J. Thorvaldsen and K. Ruud, Arbitrary-Order Density Functional Response Theory from Automatic Differentiation, J. Chem. Theory Comput., 2010, 6, 1971–1980 CrossRef PubMed.
- U. Ekström, R. Bast, R. Di Remigio, Ch. R. Jacob, S. Reine, J. Juselius, E. Rebolini, A. S. P. Gomes, S. R. Jensen, S. Reimann, A. Borgoo, D. H. Friese, L. Frediani, M. Iliaš, Y. Victorovich and J. Furness, XCFun: Exchange-Correlation functionals with arbitrary order derivatives, Version 2.2.1, 2020 DOI:10.5281/zenodo.4269992, URL: https://github.com/dftlibs/xcfun/tree/v2.1.1.
- Matplotlib Version 3.4.2, 2021 DOI:10.5281/zenodo.4743323, URL: https://matplotlib.org.
- M. L. Waskom, seaborn: statistical data visualization, J. Open Source Software, 2021, 6, 3021 CrossRef.
- S. Schürmann, J. R. Vornweg, M. Wolter and Ch. R. Jacob, Data Set: “Accurate quantum-chemical fragmentation calculations for ion–water clusters with the density-based many-body expansion”, Zenodo, 2022 DOI:10.5281/zenodo.7113146.
- B. S. González, J. Hernández-Rojas and D. J. Wales, Global minima and energetics of Li+(H2O)n and Ca2+(H2O)n clusters for n ≤ 20, Chem. Phys. Lett., 2005, 412, 23–28 CrossRef.
- S. P. Veccham, J. Lee and M. Head-Gordon, Making many-body interactions nearly pairwise additive: The polarized many-body expansion approach, J. Chem. Phys., 2019, 151, 194101 CrossRef PubMed.
- R. M. Richard, K. U. Lao and J. M. Herbert, Aiming for Benchmark Accuracy with the Many-Body Expansion, Acc. Chem. Res., 2014, 47, 2828–2836 CrossRef CAS PubMed.
- K. U. Lao, K.-Y. Liu, R. M. Richard and J. M. Herbert, Understanding the many-body expansion for large systems. II. Accuracy considerations, J. Chem. Phys., 2016, 144, 164105 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tables listing additional raw data, in particular total and relative interaction energies, for all considered clusters. See DOI: https://doi.org/10.1039/d2cp04539g |
| This journal is © the Owner Societies 2023 |