Defective graphene/SiGe heterostructures as anodes of Li-ion batteries: a first-principles calculation study

Abstract

Two-dimensional silicon-based material siligene (SiGe) has a low diffusion barrier and high theoretical specific capacity, but the conductivity drops sharply after being fully lithiated. To improve their electrical conductivity, the three heterostructures (SV-G/S, DV-G/S, and SW-G/S) formed with defective graphene and SiGe were proposed and the feasibility of them as anode materials was analyzed systematically. Based on density functional theory, the structural properties of defective graphene/SiGe heterostructures (Def-G/S), the adsorption and diffusion behaviours of Li, the voltage and theoretical capacity, and electrical conductivity during the lithiation process were investigated. The results show that defective graphene can form a stable heterostructure with SiGe and the heterostructure with defects can accommodate more Li atoms. The good adsorption and low diffusion energy barrier ensure the capacity, cycling, and safety performance of Def-G/S as anode materials. Moreover, Def-G/S significantly improves the conductivity of pristine 2D SiGe after full lithiation. These excellent properties indicate that Def-G/S has great potential as an anode material for Li-ion batteries.

---

1. Introduction

Silicon (Si) is expected to replace graphite as the anode material for next-generation lithium-ion batteries (LIBs) due to its extremely high theoretical specific capacity (4200 mA h g⁻¹).^1–3 However, Si undergoes a large volume change (>300%) during the charging/discharging process, causing pulverization, delamination of the active materials, and unstable solid electrolyte interfacial film (SEI), which further leads to the capacity decay and short cycle life.^4,5 To solve this problem, it is imperative to propose new materials as the anode of LIBs.

Two-dimensional (2D) materials have been considered novel anode materials for LIBs because of their large surface area,⁶ small volume change,^7,8 and lower diffusion barrier.^9,10 Among them, the two-dimensional material silicene has many excellent properties as an anode material. The first-principles calculation results show that it is metallic, the properties of which are better than the semiconductor properties of silicon. The specific capacity of 954 mA h g⁻¹ is more than twice that of graphite (372 mA h g⁻¹), and diffusion energy barrier of 0.23 eV¹¹ is less than 0.58 eV¹² of bulk silicon. Although silicene shows great potential as an anode material for LIBs, the mixed sp²–sp³ hybridization makes the free-standing form of silicene unstable.^13,14 However, chemical compounds that consist of Si and other elements can effectively improve the structural stability, for example, g-SiC₂, g-SiC₃ (g denotes graphitic),¹⁵ Si₂BN,¹⁶ Si₃N¹⁷ and Si₃C.¹⁸

Recently, Jiang et al.¹⁹ studied 2D SiGe as an anode material. 2D SiGe has an electronic structure similar to graphene, and due to the different hydrogenation capabilities of Si and Ge, its electronic structure can be tuned by controlling the coverage of hydrogen. At the same time, the stable structure, low diffusion barrier (∼0.35 eV), and theoretical specific capacity (532.13 mA h g⁻¹) make it a promising anode material for LIBs. However, upon full lithiation, the electronic conductivity of 2D SiGe drops drastically, which affects the cycle and rate performance of the electrode.^15,20

On one hand, density functional theory (DFT) calculations show that compounding a graphene layer on a 2D material with poor electrical conductivity to form a heterostructure can effectively improve the electrical conductivity of the material. Liu et al.²¹ combined phosphorene and graphene to form a P/G heterostructure, significantly improving the electrical conductivity of pristine phosphorene. Shin et al.²² used a single-layer SnS₂ and graphene to form a heterostructure as a sodium ion electrode material. This structure effectively improved the electrical conductivity of single-layer SnS₂. On the other hand, heterostructures have been successfully synthesized by experimental methods such as chemical vapor deposition (CVD),²³ mechanical transfer technique,²⁴ combining vapour transport deposition and a hydrothermal method,²⁵ combining a simple solvothermal reaction and subsequent post-treatment,²⁶etc. Moreover, 2D bilayer structures can be modified by defect engineering.^27,28 In particular, by employing modern techniques such as electron beam irradiation,²⁹ ozone exposure,³⁰ plasma and chemical treatments,³¹ and laser illumination,³² controlled point defects can be created to fabricate practical devices. Therefore, from the view of experiment and theoretical calculations, the conductivity of 2D SiGe can be improved by forming a heterostructure between graphene and 2D SiGe.

Based on the above consideration, in this paper, the feasibility of a new type of heterostructure as an anode material for LIBs is analyzed from the perspective of theoretical calculations. First, the stability of Gra/SiGe is studied, and according to the stability analysis results, three kinds of common defective graphene (single-vacancy defect (SV), double-vacancy defect (DV) and Stone–Wales (SW) defect graphene³³) and SiGe are proposed to form a heterostructure (SV-G/S, DV-G/S and SW-G/S, collectively known as Def-G/S) as an anode material for LIBs. Then, Def-G/S heterostructures were systematically studied. Their structural stability, Li adsorption and diffusion properties, electrode voltage, theoretical specific capacity, and electrical conductivity were analyzed. The results show that the Def-G/S has good electronic conductivity before and throughout the lithiation process and great potential as anode materials. This work sheds light on the influence of defects on the electrochemical properties of Gra/SiGe heterostructure electrode materials and points out a promising research strategy for battery researchers to design high-performance heterostructure materials.

2. Computational methods

All calculations are performed with the VASP package based on DFT. The relevant calculation results were proceeded using the VAPKIT software package.³⁴ The generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof (PBE) form is used to solve Kohn–Sham equations by the exchange-correlation functional. The van der Waals interaction is based on Grimme's DFT-D2 approach.³⁵ An energy cut-off of 500 eV was applied for the expansion of plane waves. To avoid the imaginary interaction between two free sides, a vacuum space (20 Å) was added to all structures. The k-point grid was 3 × 3 × 1 for self-consistent calculations. Denser grids (9 × 9 × 1) were used for the electronic density of states (DOS) calculations. The convergence criteria for energy are less than 10⁻⁴ eV and the force converged to 0.01 eV Å⁻¹. According to previous research and our tests, this convergence criteria is acceptable.³⁶

To study the strength of binding between the perfect graphene and 2D SiGe, the binding energy (E_b)^37,38 is defined by

E_b = E_het − E_Gra − E_SiGe (1)

where E_het, E_Gra, and E_SiGe are the total energy of the Gra/SiGe heterostructure, graphene, and 2D SiGe, respectively (the graphene and 2D SiGe monolayers in a vacuum, respectively).

The Li adsorption energy (E_ads) is evaluated with

where E_het-Li, E_het, E_Li, and n are the total energy of lithiated Def-G/S, Def-G/S, the isolated Li atom in a vacuum, and the number of Li atoms. The charge density difference Δρ is defined as

Δρ = ρ_het-Li − ρ_het − ρ_Li (3)

where ρ_het-Li and ρ_het are the charge density of the adsorbed system and pristine Def-G/S, respectively and ρ_Li is the charge density of the isolated Li atom. The open circuit voltage (OCV) is expressed using^18,36where E_het-n1Li and E_het-n2Li are the total energies of Def-G/S adsorbed with n₁, n₂ Li atoms, and μ is the chemical potential of metallic Li (the energy per Li atom in the bulk). The theoretical specific capacity can be obtained fromwhere n_max is the maximum number of inserted Li atoms, F is the Faraday constant and M is the relative molecular mass of Def-G/S. The diffusion energy barrier of Li was calculated by the climbing image nudged elastic band (CI-NEB) method.³⁹

3. Results and discussion

3.1 Structural properties

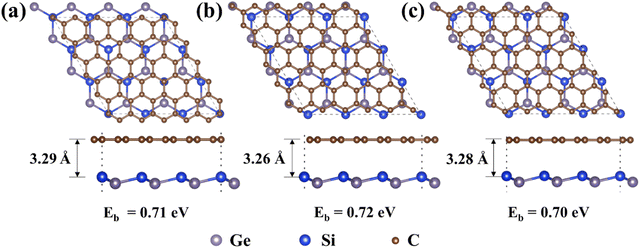
The lattice constant of optimized 2D SiGe and graphene is 3.93 Å and 2.46 Å, respectively, which is consistent with the previous results.^19,40 The Gra/SiGe heterostructure was constructed by using a 3 × 3 × 1 supercell of SiGe and a 5 × 5 × 1 supercell of graphene, along with a lattice mismatch of 1.3%. Based on the symmetry, we consider three heterostructure configurations as shown in Fig. 1a–c. However, the binding energy of Gra/SiGe heterostructures is 0.71 eV, 0.72 eV and 0.70 eV, respectively, which indicates that the Gra/SiGe is energetically unstable and difficult to be synthesized experimentally.^37,41

Fig. 1 (a–c) Three different stacking structures of Gra/SiGe.

The original properties of the structure can be changed by introducing defects.⁴² Therefore, we propose three kinds of graphene with common defects (SV (Fig. 2b), DV (Fig. S4b, ESI†), and SW (Fig. S5b, ESI†)) to form a heterostructure with SiGe (Fig. 2a), which are named SV-G/S, DV-G/S, and SW-G/S, collectively named Def-G/S. The results show that the binding energy of the three kinds of Def-G/S is negative (Fig. S1–S3, ESI†), which indicates that the heterostructures with defective graphene become energetically favorable compared with the heterostructure with original graphene.

Fig. 2 (a) Top and side views of the structure of 2D SiGe. (b) Top and side views of the structure of graphene with SV defects. (c) Top and (d) side views of the structure of SV-G/S. (e) Free energy as a function of MD time at a temperature of 300 K for SV-G/S.

According to different stacking patterns, there are 13 different configurations of SV-G/S, 14 different configurations of DV-G/S, and 14 different configurations of SW-G/S (Fig. S1–S3, ESI†), and the most stable structure of each heterogeneous structure is shown in Fig. 2c, d and Fig. S4c, d and S5c, d (ESI†), respectively. Their binding energy is estimated to be −2.32 eV, −1.81 eV, and −0.89 eV, respectively, which indicates that the formation of the heterogeneous structure is an exothermic reaction, thereby having good structural stability. It is noted that SV-G/S and DV-G/S have lower binding energy, which is because of the proximity of carbon atoms around the defect point to SiGe and even the bonding of carbon atoms to silicon atoms, resulting in stronger bonding of defective graphene with SiGe (Fig. 2d and Fig. S4d, ESI†). However, SW-G/S does not appear the bond between SiGe and defective graphene (Fig. S5d, ESI†), therefore it has higher binding energy. Furthermore, thermal stability is extremely important for electrode materials. The Def-G/S at a temperature of 300 K for 6 ps was simulated by the ab initio molecular dynamics method (AIMD). As shown in Fig. 2e and Fig. S4e, and S5e (ESI†), it can be found that the energy of Def-G/S quickly reaches equilibrium (<0.3 ps), and then slightly fluctuates around the equilibrium value. This reveals that the three Def-G/S heterostructures have good thermodynamic stability.

3.2 Li adsorption and diffusion properties

During lithiation, when the interaction energy between Li and the electrode material is higher than the cohesive energy of Li metal, the intercalation potential is lower than 0 V (vs. Li/Li+), which will promote the growth of Li dendrites,^15,43 thereby affecting the capacity, cycling, and safety performance of LIBs.⁴⁴ Therefore, it is necessary to explore the adsorption properties of Li in Def-G/S. First, we verified the rationality of our calculations by studying the adsorption of Li on the best adsorption position of SiGe, namely, the center of the hexagonal ring. The calculated adsorption energy is −2.67 eV, while the one in the reference is −0.85 eV.¹⁹ This is because, in the adsorption energy formula, the energy values for Li are different. We take the energy of Li atoms as the energy of an isolated Li atom in a vacuum, while the reference takes the energy per metal atom in Li bulk. The difference between them is the Li cohesive energy value (−1.87 eV), and the error is only 1.6%,¹⁵ which demonstrates that our calculation is reasonable.

To study the adsorption of Li in the Def-G/S heterostructure, three cases were considered: (1) Li atom adsorbed on the top of Def-G/S (Li/Gra/SiGe), (2) Li atom embedded in the middle of Def-G/S (Gra/Li/SiGe), and (3) Li atom adsorbed on the bottom of Def-G/S (Gra/SiGe/Li). Considering the similarity of the three heterostructures, we take the Li adsorption on SV-G/S as an example (Fig. 3a and b). Due to the high asymmetry of Def-G/S, we calculated the adsorption energy for each possible adsorption site for Li/Gra/SiGe, Gra/Li/SiGe, and Gra/SiGe/Li, respectively (Table S1, ESI†), and took the average value of Li adsorption at the same interface (Table 1).¹⁴ It can be seen that the average adsorption energy of Li in Def-G/S is lower than the cohesive energy of Li (−1.87 eV), indicating that Li can be stably adsorbed on Def-G/S, ensuring the capacity, safety, and cycling performance of LIBs. In addition, for Gra/Li/SiGe and Gra/SiGe/Li cases, the adsorption energy is lower than that on the pristine 2D SiGe (−2.67 eV), indicating that the formation of the heterostructure enhances the Li adsorption capacity. The adsorption energy of Li in the Def-G/S interlayer is the lowest, followed by the bottom of Def-G/S, and the highest on the top, which implies that Li intercalates the middle of Def-G/S first during the charging process.

Fig. 3 (a) Top and (b) side views of adsorption sites for one Li adsorbed at the top, middle, and bottom of the optimized SV-G/S heterostructure. Charge density difference distribution for one single Li adsorbed at the (c) top, (d) middle, and (e) bottom of the SV-G/S heterostructure (H_T, H_I, and H_L denote the Li adsorption on the top, middle, and bottom of SV-G/S, respectively.) (The red/yellow regions represent electron depletion/accumulation with an isosurface value of 0.0007 e Å⁻³.)

Table 1 Average adsorption energy (E_ad) of Li adsorbed on the top, middle, and bottom of Def-G/S

System	E ad (eV)
	SV-G/S	DV-G/S	SW-G/S
Li/Gra/SiGe	−2.56	−2.51	−2.27
Gra/Li/SiGe	−3.57	−3.57	−3.34
Gra/SiGe/Li	−3.18	−3.13	−2.91

---

To further explore the Li adsorption properties of Def-G/S, we performed charge density difference calculations and Bader charge analysis. Taking the Li adsorption on SV-G/S as an example, the results are shown in Fig. 3c–e and Table 2 (the average charge transfer in the other two cases is shown in Tables S2 and S3, ESI†). When Li is adsorbed on the top of SV-G/S, the charges are transferred from Li to the graphene layer (Fig. 3c), and the average charge transfer amount is 0.74|e|, indicating that Li and C form an ionic bond.⁴⁵ When Li is adsorbed in the middle of SV-G/S, the charges are transferred to the upper graphene layer and the lower layer SiGe, respectively (Fig. 3d), and the average transfer amount is 0.42|e|, showing a certain covalent bond property. When Li is adsorbed on the bottom of SV-G/S, similar to Li adsorption on the graphene of SV-G/S, the charges are transferred from Li and C to the SiGe (Fig. 3e and Table 2), and the average transfer amounts of Li and C are 0.40|e| and 0.62|e|, respectively, indicating that the ionic bond between Li and C is weakened.

Table 2 Average charge transfer of Li(ΔQ_Li), top (ΔQ_Gra), and bottom (ΔQ_SiGe) in SV-G/S, and the positive/negative ΔQ denotes the loss/gain of electrons

System	ΔQLi	ΔQSiGe	ΔQGra
Li/Gra/SiGe	+0.74	−1.47	+0.74
Gra/Li/SiGe	+0.42	−1.07	+0.65
Gra/SiGe/Li	+0.40	−1.01	+0.62

---

If the Li diffusion energy barrier is larger than the charge voltage (∼3.6 eV), then Li will not be able to migrate freely in the electrode material, which affects the electrochemical performance of the material.⁴⁶ First, the diffusion barrier of Li on SiGe was calculated, and the obtained result was 0.34 eV, which is consistent with the literature (0.35 eV).¹⁹ Subsequently, we investigated the diffusion of Li in Def-G/S, and the energy barriers and Li diffusion paths are shown in Fig. 4a–f, respectively. It can be seen that the diffusion barriers of Li in the middle (Fig. 4b) and the bottom (Fig. 4c) of Def-G/S are between 0.35 and 0.37 eV, which is very close to the Li atom diffusion on pristine 2D SiGe (0.34 eV). This demonstrates that the heterostructure formation produces a slight inhibitory effect on the diffusivity of Li on the SiGe surface in Def-G/S. However, the diffusion energy barriers of Li on the top of Def-G/S (Fig. 4a) are quite different. The diffusion energy barriers of Li on the top of SV-G/S and DV-G/S are 0.53 and 0.50 eV, respectively, while the diffusion barrier in SW-G/S is 0.26 eV. Fan et al.⁴⁷ calculated the diffusion barriers of Li diffusion on SV, DV and SW defective graphene to be 0.31, 0.24, and 0.17 eV, respectively, but Hardikar et al.⁴⁸ obtained results of 0.49, 0.35, and 0.13 eV. This shows that the diffusion energy barrier value of Li in the above-mentioned several kinds of defective graphene is controversial, but the changing trend of our results is consistent. We believe that the higher diffusion barrier is due to the formation of the heterostructure, which turns pristine flat graphene into curved graphene (Fig. 3c–e), resulting in the inhibition of Li diffusion. In conclusion, compared to Li atom diffusion on pristine 2D SiGe and defective graphene, Li atom diffusion on Def-G/S is more difficult. And Li atom diffuses faster on the middle and bottom of Def-G/S than on the top. While for the top of Def-G/S, Li atom diffusion on SW-G/S is easier than SV-G/S and DV-G/S.

Fig. 4 Energy barrier profile of Li at (a) top (b) middle and (c) bottom of the Def-G/S heterostructure. Diffusion pathways: Li diffusion on the top of (d) SV-G/S, (e) DV-G/S, and (f) SW-G/S.

3.3 Voltage and theoretical capacity

The high theoretical specific capacity of electrode materials is extremely important to improve the energy density of batteries. Hence, the open circuit voltage (OCV) and theoretical capacity were calculated. The results show that Li can be fully adsorbed in the middle and on the bottom of Def-G/S, but when Li is adsorbed on the top of Def-G/S, only one Li atom can be adsorbed, and the adsorption site is the defect site of each defective graphene. As shown in Fig. 5a–c, the OCV of SV-G/S, DV-G/S, and SW-G/S showed a steep drop when Li is adsorbed on the top (Li = 19), from 1.07 V down to 0.38 V, 0.97 V to 0.13 V, and 1.10 V to 0.18 V, respectively. If additional Li is adsorbed, the OCV of Def-G/S drops sharply below 0, indicating that the Li intercalation reaction will not proceed.¹⁶ Furthermore, the adsorption energy as a function of Li density profile can also support this conclusion. As shown in Fig. S6 (ESI†), the adsorption energies of the three Def-G/S increased slowly when the Li content is from 1 to 18. The adsorption energy increased sharply when the 19th Li was adsorbed. But when the 20th Li is reached, the adsorption energy is higher than the cohesive energy, which is consistent with the above conclusion. However, for the graphene/silicene heterostructure, Li can only be adsorbed in the middle of the graphene/silicene heterostructure and on the surface of silicene, but will not be adsorbed on the surface of graphene.¹⁴ Through comparative analysis, we believe that the heterostructure with defects can enhance the lithium storage capacity, which is consistent with the study by Tanwar et al.⁴⁹ According to formula 5, the theoretical specific capacities of the three kinds of Def-G/S are 340.90 mA h g⁻¹, 343.66 mA h g⁻¹, and 338.18 mA h g⁻¹, respectively. In addition, their OCVs between 0 and 2 V ensure that the electrode can work normally.⁵⁰

Fig. 5 The OCV of (a) SV-G/S (b) DV-G/S and (c) SW-G/S as a function of specific capacity.

Graphene-containing 2D heterostructures have been extensively studied in recent years, and we compare the lithium storage capacity of Def-G/S with other graphene-containing 2D heterostructures. Compared with P/G (485 mA h g⁻¹),²¹ and silicene/G (487 mA h g⁻¹),¹⁴ the theoretical specific capacity of Def-G/S is less than 100 mA h g⁻¹, which we speculate is due to the larger Ge molecular mass. But compared with those of other heterostructures, such as Ti₂C(OH)₂/G (196 mA h g⁻¹),⁵¹ Sc₂(OH)₂/G (228 mA h g⁻¹), Sc₂CO₂/G (230 mA h g⁻¹), V₂C(OH)₂/G (232 mA h g⁻¹),⁵²etc., the theoretical specific capacity of Def-G/S is as much as 100 mA h g⁻¹ higher than them. Interestingly, compared with that of the traditional graphite anode, the capacity of Def-G/S is very close to it (372 mA h g⁻¹). However, it is worth noting that graphite is composed of multi-layer graphene. We speculate that in the case of multi-layer stacking of Def-G/S materials, the defective graphene layers in Def-G/S can be filled with Li on both the upper and lower sides. Thereby, a higher theoretical capacity is obtained, exceeding that of graphite, but this requires further research to verify.

In general, compared with other graphene-containing heterostructures and graphite, the theoretical specific capacity of Def-G/S shows good theoretical specific capacity, which can meet the capacity requirements of LIBs.

3.4 Electronic conductivity

After 2D SiGe is fully adsorbed with lithium ions, the conductivity of the whole system decreases.¹⁹ To explore whether Def-G/S can improve the electronic conductivity of SiGe, we calculated the DOS of SiGe and three Def-G/S heterostructures and analyzed the change in the electronic conductivity of the system with the increase of lithiation. The results are shown in Fig. 6 and Table 3. The SiGe and SW-G/S show semimetallic characteristics with a band gap of 0 eV, but the DOS of SV-G/S and DV-G/S at the Fermi level is 10.73 and 5.46 states eV⁻¹. That is, the SV-G/S and DV-G/S already have enough electronic conductivity as the anode material for LIBs before lithiation. When they are absorbed with one layer of Li ions (Li = 9), the DOS of SiGe at the Fermi level suddenly increases from 0 to 17.01 states eV⁻¹. But for Def-G/S, compared with their initial state, the DOS of DV-G/S and SW-G/S at the Fermi level increases while that of the SV-G/S decreases. When they are absorbed with two layers of Li ions (Li = 18), SiGe reaches a fully lithiated state. The DOS of SiGe at the Fermi level suddenly drops to 0 with a wide band gap, which is undesirable for application in LIBs. Interestingly, the DOS of Def-G/S at the Fermi level also drops compared with that when one layer of Li ions was adsorbed. The reason is the enhanced repulsion between lithiated Def-G/S and Li. Finally, when Def-G/S reaches a fully lithiated state (Li = 19), the DOS at the Fermi level of SV-G/S, DV-G/S and SW-G/S increases to 16.07, 21.42 and 20.66 states eV⁻¹, indicating that the conductivity of the fully lithiated system has been further improved.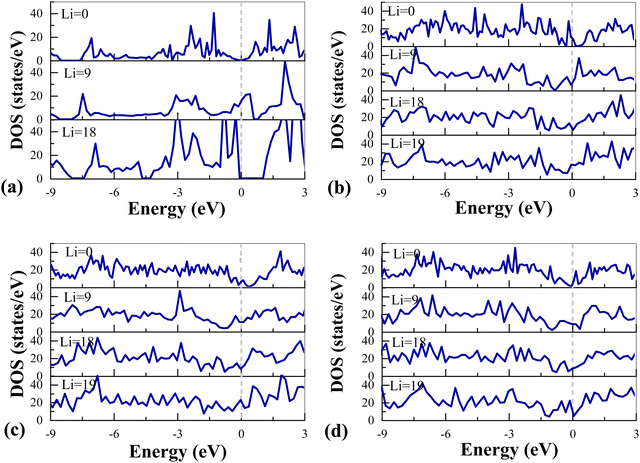

Fig. 6 DOS of (a) SiGe, (b) SV-G/S, (c) DV-G/S, and (d) SW-G/S with different Li concentrations. The Fermi level is set to be 0 eV.

Table 3 The DOS at the Fermi level of SiGe and three Def-G/S heterostructures as the lithiation degree

System	Li numbers	DOS (states eV^−1)
SiGe	0	0
	9	17.01
	18	0
SV-G/S	0	10.73
	9	6.39
	18	5.79
	19	16.07
DV-G/S	0	5.46
	9	9.46
	18	6.74
	19	21.42
SW-G/S	0	0.00
	9	7.75
	18	4.08
	19	20.66

---

Based on the above analysis, compared with the wide band gap near the Fermi level after SiGe is fully adsorbed with Li ions, although Def-G/S has fluctuations in DOS at the Fermi level during the lithiation process, the DOS at the Fermi level is improved after they are fully adsorbed with Li ions. This indicates that Def-G/S shows good and fluctuating electronic conductivity throughout the lithiation process compared to pristine 2D SiGe and meets the requirements of being used as anode materials for LIBs.

4. Conclusions

Based on the DFT method, the feasibility of Def-G/S as anode materials for LIBs is systematically studied. The results reveal that Gra/SiGe is unstable, but Def-G/S has good structural stability and can accommodate more Li at the defective site. Li exhibits excellent adsorption and diffusion properties in Def-G/S. During the lithiation process of Def-S/G, Li is preferentially adsorbed in the middle of Def-G/S. The diffusion barrier of Li in Def-S/G is superior to that in bulk silicon (<0.53 eV) and Li has the lowest diffusion barrier (∼0.25 eV) on the top of SW-G/S. The theoretical capacities of 340.90 mA h g⁻¹, 343.66 mA h g⁻¹, and 338.18 mA h g⁻¹ were obtained for SV-G/S, DV-G/S, and SW-G/S, respectively, which were lower than those of pristine 2D SiGe, but compared with those of other heterostructures constructed with graphene, the theoretical capacity of Def-G/S is higher. In addition, the OCV between 0.48 and 1.38 V ensures the proper functioning of the Def-G/S anode. Finally, the Def-G/S shows good electronic conductivity before and throughout the lithiation process, which improves the poor electrical conductivity of the original SiGe after full lithiation.

The research in this paper provides a theoretical basis for the design of new silicon-based electrode materials and a useful reference for the study of heterostructures with defects as an electrode material. At present, the research of heterostructures as electrodes of LIBs is mostly composed of two perfect structures without defects and there are relatively few studies on heterostructures with defects. We believe that heterostructures with defects can exhibit better properties, but further research is needed.

Author contributions

Jun Song: investigation, resources, methodology, writing – original draft, and funding acquisition. Mingjie Jiang: investigation, resources, and writing – original draft. Chi Wan: investigation, formal analysis, and writing – original draft. Huijie Li: investigation, resources, and writing – original draft. Qi Zhang: methodology, writing – review & editing, and funding acquisition. Yuhui Chen: conceptualization, and writing – review & editing. Xuehong Wu: conceptualization, methodology and writing – review & editing. Xuemei Yin: conceptualization, methodology and writing – review & editing. Juanfang Liu: methodology, writing – review & editing, and funding acquisition.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China under Grant No. 51906229, 51906230, 51776027, the Key Scientific Research Project of the University of Henan Province of China under Grant No. 21B470013 and the Science and Technology Research Project of Henan Province of China under Grant No. 212102210235. This work was performed in part at the School of Energy and Power Engineering, Chongqing University. Jun Song and all authors appreciate the support from the Key Laboratory of Low-grade Energy Utilization Technologies and Systems (Chongqing University), Ministry of Education of China.

References

1. X. Su, Q. Wu, J. Li, X. Xiao, A. Lott, W. Lu, B. W. Sheldon and J. Wu, Adv. Energy Mater., 2014, 4, 1300882.
2. C. X. J. Song, Q. Zhang, Y. H. Chen, X. Q. Zhang, G. S. Zhang and R. L. Zhang, Chem. Ind. Eng. Prog., 2021, 40, 3664–3678.
3. C. K. Chan, H. Peng, G. Liu, K. McIlwrath, X. F. Zhang, R. A. Huggins and Y. Cui, Nat. Nanotechnol., 2008, 3, 31–35.
4. F. Tang, Y. Tan, T. Jiang and Y. Zhou, J. Mater. Sci., 2022, 57, 2803–2812.
5. H. Wu and Y. Cui, Nano Today, 2012, 7, 414–429.
6. H. Jia, X. Li, J. Song, X. Zhang, L. Luo, Y. He, B. Li, Y. Cai, S. Hu, X. Xiao, C. Wang, K. M. Rosso, R. Yi, R. Patel and J.-G. Zhang, Nat. Commun., 2020, 11, 1474.
7. J. Deng, J. Z. Liu and N. V. Medhekar, RSC Adv., 2013, 3, 20338–20344.
8. Y.-H. Guo, J.-X. Cao and B. Xu, Chin. Phys. B, 2016, 25, 017101.
9. Q. Xu, J.-Y. Li, J.-K. Sun, Y.-X. Yin, L.-J. Wan and Y.-G. Guo, Adv. Energy Mater., 2017, 7, 1601481.
10. T. Yoon, T. Bok, C. Kim, Y. Na, S. Park and K. S. Kim, ACS Nano, 2017, 11, 4808–4815.
11. G. A. Tritsaris, E. Kaxiras, S. Meng and E. Wang, Nano Lett., 2013, 13, 2258–2263.
12. W. Wan, Q. Zhang, Y. Cui and E. Wang, J. Phys.: Condens. Matter, 2010, 22, 415501.
13. J. Zhao, H. Liu, Z. Yu, R. Quhe, S. Zhou, Y. Wang, C. C. Liu, H. Zhong, N. Han, J. Lu, Y. Yao and K. Wu, Prog. Mater. Sci., 2016, 83, 24–151.
14. L. Shi, T. S. Zhao, A. Xu and J. B. Xu, J. Mater. Chem. A, 2016, 4, 16377–16382.
15. X. Lv, W. Wei, B. Huang and Y. Dai, J. Mater. Chem. A, 2019, 7, 2165–2171.
16. V. Shukla, R. B. Araujo, N. K. Jena and R. Ahuja, Nano Energy, 2017, 41, 251–260.
17. H. Li, J. Hou and D. Jiang, J. Electron. Mater., 2020, 49, 4180–4185.
18. Y. Wang and Y. Li, J. Mater. Chem. A, 2020, 8, 4274–4282.
19. A. Sannyal, Y. Ahn and J. Jang, Comput. Mater. Sci., 2019, 165, 121–128.
20. T. Yu, Z. Zhao, L. Liu, S. Zhang, H. Xu and G. Yang, J. Am. Chem. Soc., 2018, 140, 5962–5968.
21. G.-C. Guo, D. Wang, X.-L. Wei, Q. Zhang, H. Liu, W.-M. Lau and L.-M. Liu, J. Phys. Chem. Lett., 2015, 6, 5002–5008.
22. A. Samad, M. Noor-A-Alam and Y.-H. Shin, J. Mater. Chem. A, 2016, 4, 14316–14323.
23. Z. Liu, L. Song, S. Zhao, J. Huang, L. Ma, J. Zhang, J. Lou and P. M. Ajayan, Nano Lett., 2011, 11, 2032–2037.
24. C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim, K. L. Shepard and J. Hone, Nat. Nanotechnol., 2010, 5, 722–726.
25. Y. Li, S. Yu, T. Yuan, M. Yan and Y. Jiang, J. Power Sources, 2015, 282, 1–8.
26. H. Ye, H. Li, F. Jiang, J. Yin and H. Zhu, Electrochim. Acta, 2018, 266, 170–177.
27. J. Jiang, T. Xu, J. Lu, L. Sun and Z. Ni, Research, 2019, 2019, 4641739.
28. J. S. Park, S. Kim, Z. Xie and A. Walsh, Nat. Rev. Mater., 2018, 3, 194–210.
29. X. U. Tao, K. B. Yin, L. T. Sun and N. P. Center, Chin. Sci. Bull., 2017, 62(25), 2919–2930.
30. Y. Wu, H. Tao, S. Su, H. Yue, H. Li, Z. Zhang, Z. Ni and X. Chen, Sci. Rep., 2017, 7, 46583.
31. Z. Hu, Z. Wu, C. Han, J. He, Z. Ni and W. Chen, Chem. Soc. Rev., 2018, 47, 3100–3128.
32. J. Lu, J. Wu, A. Carvalho, A. Ziletti, H. Liu, J. Tan, Y. Chen, A. H. Castro Neto, B. Özyilmaz and C. H. Sow, ACS Nano, 2015, 9, 10411–10421.
33. Y. Bahari, B. Mortazavi, A. Rajabpour, X. Zhuang and T. Rabczuk, Energy Storage Mater., 2021, 35, 203–282.
34. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
35. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
36. L. Shi, T. Zhao, A. Xu and J. Xu, Science Bulletin, 2016, 61, 1138–1144.
37. X. He, A. Tang, Y. Li, Y. Zhang, W. Chen and S. Huang, Appl. Surf. Sci., 2021, 563, 150269.
38. T. Wang, S. Zhang, L. Yin, C. Li, C. Xia, Y. An and S. Wei, J. Phys.: Condens. Matter, 2020, 32, 355502.
39. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
40. H. Zhou, M. Zhao, X. Zhang, W. Dong, X. Wang, H. Bu and A. Wang, J. Phys.: Condens. Matter, 2013, 25, 395501.
41. B. Liu, T. Gao, P. Liao, Y. Wen, M. Yao, S. Shi and W. Zhang, Phys. Chem. Chem. Phys., 2021, 23, 18784–18793.
42. D. Datta, J. Li, N. Koratkar and V. B. Shenoy, Carbon, 2014, 80, 305–310.
43. H. Wang, M. Wu, X. Lei, Z. Tian, B. Xu, K. Huang and C. Ouyang, Nano Energy, 2018, 49, 67–76.
44. J. Huang, H.-J. Chen, M.-S. Wu, G. Liu, C.-Y. Ouyang and B. Xu, Chin. Phys. Lett., 2013, 30, 017103.
45. F. Zhou, N. Liao, M. Zhang and W. Xue, Appl. Surf. Sci., 2019, 463, 610–615.
46. J.-L. Zang and Y.-P. Zhao, Composites, Part B, 2012, 43, 76–82.
47. X. Fan, W. T. Zheng and J.-L. Kuo, ACS Appl. Mater. Interfaces, 2012, 4, 2432–2438.
48. R. P. Hardikar, D. Das, S. S. Han, K.-R. Lee and A. K. Singh, Phys. Chem. Chem. Phys., 2014, 16, 16502–16508.
49. K. Tanwar, X. Tan, S. C. Smith and Y. I. Chen, J. Phys. Chem. C, 2021, 125, 23597–23603.
50. Q. Zhang, C. Tang, W. Zhu and C. Cheng, J. Phys. Chem. C, 2018, 122, 22838–22848.
51. Y.-T. Du, X. Kan, F. Yang, L.-Y. Gan and U. Schwingenschlögl, ACS Appl. Mater. Interfaces, 2018, 10, 32867–32873.
52. Y. Aierken, C. Sevik, O. Gülseren, F. M. Peeters and D. Çakır, J. Mater. Chem. A, 2018, 6, 2337–2345.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04040a

---