Theoretical investigations of positron affinities and their structure-dependent properties of carbon dioxide clusters (CO2)n (n = 1–5)†
Miku
Furushima
 a,
Makito
Takagi
a,
Daisuke
Yoshida
a,
Makito
Takagi
a,
Daisuke
Yoshida
 ab,
Yukiumi
Kita
a,
Tomomi
Shimazaki
ab,
Yukiumi
Kita
a,
Tomomi
Shimazaki
 a and
Masanori
Tachikawa
a and
Masanori
Tachikawa
 *a
*a
aQuantum Chemistry Division, Yokohama City University, Seto 22-2, Kanazawa-ku, Yokohama 236-0027, Kanagawa, Japan. E-mail: tachi@yokohama-cu.ac.jp
bNishina Center for Accelerator-Based Science, RIKEN, Hirosawa 2-1, Wako 351-0198, Japan
First published on 29th November 2022
Abstract
Although positron binding to van der Waals intermolecularly bonded clusters of non-polar carbon dioxide (CO2) molecules was experimentally suggested, the positron binding feature has been poorly understood. We investigated positron affinities (PAs) by means of multi-component configuration interaction calculations for various structures of (CO2)n (n = 1–5) obtained by the single-component artificial force induced reaction (SC-AFIR) method. Our calculations showed that CO2 monomers do not bind a positron, whereas positron affinities for clusters tend to increase with an increase in the cluster size. Our regression analyses for determining PAs with electrostatic and structural properties of conformations revealed a significant conformer effect due to which structural characteristics such as flatness may have a strong influence on PA for loosely bound positronic complexes of (CO2)n.
1 Introduction
A positron is an anti-particle of an electron and they pair-annihilate by emitting γ-rays after collision.1 This property has been applied in the technique for analyzing vacancies in solids,2 surface electronic structures,3 mass analyses of molecules in the gas-phase,4etc. For further application of positron annihilation in materials science, it is important to understand the interaction of a positron with various sizes of materials involving molecules, molecular clusters, and their conformations.Both experimental and theoretical studies have revealed the existence of positronic complexes with various atoms and molecules. Experimentally, the technique of positron irradiation and electron–positron annihilation γ-ray detection developed by Surko et al. has shown the existence of complexes for about 90 kinds of polyatomic molecules.5–10 Also, positron binding energies (positron affinity; PA) for these positron–molecule complexes were measured from the observed annihilation spectra. They presented effective regression models for PA with the magnitude of dipole moment μ and polarizability α.9 Theoretically, systematic studies of ab initio predicted PAs also suggested such a chemical trend of dipole moments for amino acids,11–13 fluorinated benzene molecules,14etc. On the other hand, in a case study of positron binding to a carbon disulfide (CS2) dimer, vibrational enhancement of PAs was revealed, where the positron binding mechanism was partially attributed to its dependence on polarizability increased by particular vibrational motions.15
Meanwhile, the dependence of PAs on conformations is theoretically predicted in case studies involving large alkanes,16 1-chlorohexane, and propyl formate conformations.17 In these studies, large values of both μ and α are not very effective in increasing PA,17 and in contrast, there is a case in which the positron binding energies are strongly dependent on spatial extents of the rotational isomers.16
According to experimental data,18 typical small molecules, such as nitrogen (N2), carbon dioxide (CO2) and water (H2O), do not have positive PAs. On the other hand, there is an experimental observation for the positron annihilation lifetime on CO2 in the gas-phase by Charlton et al.19 They claimed that their data show evidence of positron binding to CO2 clusters under their experimental conditions with gas pressure being higher than that in the experiments by Surko et al.18 The results of ab initio theoretical calculations by Koyanagi et al.20 also supported the fact that positrons do not bind to unimolecular CO2, at least. It is considered to be due to the small polarizability and small polarity relative to organic species with positive positron affinities, in terms of the regression model by Danielson et al.9 In the experiment by Charlton et al., however, the cluster size was not identified so it is an indirect evidence and other models related to a monomer collision to a positron–monomer complex were mentioned by Gribakin et al.5 For the verification of these experimental results and understanding their positron binding features, it is necessary to unveil positron binding mechanisms to cluster systems formed with van der Waals (vdW) intermolecular bonds.
In order to figure out positron binding features on CO2 clusters, it is necessary to comprehensively understand the chemical properties to characterize the positronic properties, which depend on cluster sizes and structures. Recently, a technique for generating molecular clusters by a pulsed supersonic slit-jet expansion method has been developed,21 and infrared/Raman spectroscopy,22,23 mass analysis,24 photoelectron spectroscopy,25etc. give us basic information such as vibrational properties and mass-to-charge ratios of CO2 clusters. It is, however, difficult to identify geometrical structures of molecular clusters in detail only by these spectroscopic measurements, and it becomes possible to determine their stabilities and to figure out their conformational properties by combining spectroscopic measurements with theoretical investigations.
There are several methods to theoretically determine cluster structures, such as the Monte Carlo approach (MCA),26 molecular tailoring approach (MTA),27–29 and genetic algorithm (GA).30,31 Regarding CO2, MTA and GA were applied for (CO2)n with n up to 20.29,31 The single-component artificial force induced reaction (SC-AFIR) method32,33 is also thought to be a useful and powerful algorithm for systematic and comprehensive research on structures, being key points on reaction pathways.34
For the calculation of positron binding features, several methods have been developed. For atoms and molecules with up to four atoms, the stochastic variational method (SVM),35–37 explicitly correlated Gaussian (ECG) method,38,39 quantum Monte Carlo (QMC) method,40–42 full configuration interaction (FCI) method,43etc. were applied for accurate calculations of positron and positronium binding energies. These methods, however, demand high calculation cost. For the calculations of PAs and annihilation rates of various sizes of organic molecules15,44,45 with several carbon atoms, a multi-component molecular orbital (MC_MO) method with Hartree–Fock (HF) treatment and truncated configuration interaction (CI) treatment was applied. Considering the computing capability today, MC_MO truncated CI is appropriate for our purpose of unveiling positron binding to arbitrary size of CO2 clusters.
In this study, we investigate the PAs of CO2 molecules/clusters with focus on both the electrostatic properties and structural characteristics. First, we performed systematic searches for the equilibrium structures of (CO2)n clusters by using the SC-AFIR method with accurate quantum chemical calculations. Second, we systematically calculated PAs based on the MC_MO method with CI treatment and analyzed cluster-specific positron binding abilities. We will discuss the positron binding mechanism associated with electrostatic properties and structural properties.
2 Methodology
2.1 Structure search
For (CO2)n with n = 1 and 2, structure optimizations were carried out in the usual manner starting from several initial structures. For CO2 molecules, we used a linear D∞h structure and for (CO2)2, we used a “slipped parallel” structure,31,46 also known as “shifted parallel”28.For searching the complex structures for (CO2)n with n = 3–5, we applied the SC-AFIR method. The SC-AFIR method can be used to perform systematic structure search on a potential energy surface by pushing (or pulling apart) the systematically defined fragment pairs. In this study, the CO2 molecules were pushed (or pulled apart) by applying an artificial force to induce structural deformations. In this work, we performed stochastic search for lower energy structures.
In this stochastic search starting from a randomly generated structure, the calculation is terminated if the recent P AFIR paths do not update the lowest M structures. The numbers of P and M were set to 10N and 3N where N is the number of atoms. The model collision parameter γ was set to 100 kJ mol−1. In addition, during the search, to avoid dissociation of the cluster, weak forces were applied between CO2 molecules with γ = 5 kJ mol−1.
To reduce the computational cost, the searches were performed at a rough calculation level and after that the obtained structures were reoptimized with higher level calculation. During the search the spin-restricted wave function referenced density functional method with the hybrid functional of Becke three-parameter Lee–Yang–Parr (B3LYP)47,48 with Grimme dispersion correction49 (D3) with the 6-31+G(d) basis set (B3LYP-D3/6-31+G(d)) was adopted. Subsequently, those candidate structures were reoptimized to obtain more accurate local minimum structures using second-order Møller-Plesset perturbation (MP2) theory with the augmented correlation-consistent polarized valence double zeta basis set (aug-cc-pVDZ). In these procedures, GRRM 1750–52 was employed for the SC-AFIR algorithm and Gaussian 1653 was employed for computations of both total energies and energy gradients.
2.2 PA calculation
The positron affinity (PA) is defined as a decrease in the total energy due to the positron attachment, viz,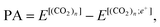 | (1) |
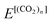 and
and  are the total energies of (CO2)n without/with a positron, respectively. The total energies of parent systems were calculated by the HF method, while the total energies of positronic complexes were calculated by the MC_MO CI method with the configuration interactions arising from the single electronic, single positronic, and both single electronic–single positronic excitations, taking into account the important electron–positron correlation effect.54
are the total energies of (CO2)n without/with a positron, respectively. The total energies of parent systems were calculated by the HF method, while the total energies of positronic complexes were calculated by the MC_MO CI method with the configuration interactions arising from the single electronic, single positronic, and both single electronic–single positronic excitations, taking into account the important electron–positron correlation effect.54
An electronic basis set combining the 6-31+G(d) basis set and [1s1p1d] Gaussian type functions was employed. The latter basis function centers are located at the center of mass and exponents for s-, p-, and d-type functions were set to 0.1, 0.1, and 0.01, respectively. For the positronic basis set, [6s6p3d2f1g] Gaussian type functions were employed. These function centers are located at the center of mass and the exponent values {ai} were determined in an even-tempered scheme, ai+1 = c × ai, where 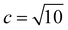 and the first term
and the first term  ,
, 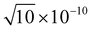 , 1 × 10−8,
, 1 × 10−8, 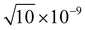 , 1 × 10−6 for s-, p-, d-, and f, and g-type functions, respectively. Calculations of
, 1 × 10−6 for s-, p-, d-, and f, and g-type functions, respectively. Calculations of  and
and 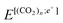 were performed using the FVOPT program.54
were performed using the FVOPT program.54
2.3 Electrostatic and structural properties
In this paper, we introduced the electrostatic properties of parent systems such as magnitudes of the permanent dipole moment μ and the traceless quadrupole moment Q, and dipole polarizability α. We also introduced the structural properties of roughly approximated flatness F and surface area S. They are used as descriptors of regression analyses later.The values of μ and α were calculated at the ab initio level similar to the total energy calculation of the parent system  using Gaussian 16.53 The value of Q at the center of mass was calculated at the same level using GAMESS.55
using Gaussian 16.53 The value of Q at the center of mass was calculated at the same level using GAMESS.55
To quantify the structural properties, the nuclear structure of a molecule or a cluster was approximated to be an ellipsoid. Then, flatness F and surface area S can be introduced. An ellipsoid is expressed with semi-axes of l, m, and s (l ≥ m ≥ s) as follows
 | (2) |
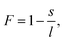 | (3) |
 | (4) |
3 Results and discussion
3.1 Cluster structure search
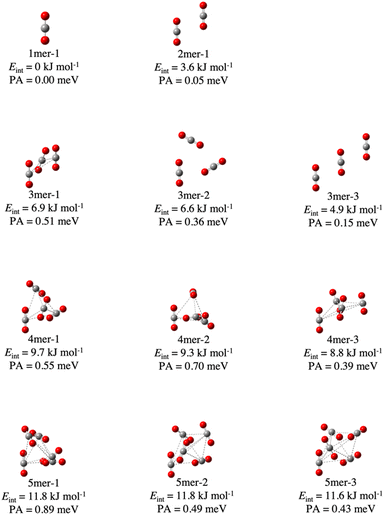
We obtained 40 structures for molecules/clusters (CO2)n with n = 1–5. All the optimized structures and their numerical data are shown in Fig. S1 and Table S1 in ESI,† respectively. PAs for all the structures were calculated. First, we will discuss the obtained structures.The obtained three lowest-energy structures for n = 3–5 and CO2 molecules, and the (CO2)2 cluster are shown in Fig. 1. Hereafter, the n-mer with the mth lowest energy will be denoted as “n-mer-m.” The interaction energy per molecule Eint and the PA value are also labeled for each system and summarized in Table S2 in ESI.† The energies Eint for the obtained CO2 clusters are in the range of 4–12 kJ mol−1, which are reasonable values for vdW intermolecular bonding clusters. CO2 clusters can take various types of structures such as the tetrahedral (4mer-1) and the plane-type (4mer-6) ones. The linear symmetry of a CO2 molecule is almost unchanged even with formation of these (CO2)n clusters with n = 2–5.
In the case of (CO2)3 clusters, we obtained three conformations including the previously reported two structures; 3mer-1 with a “Z-trimer” structure29 (also referred to as the “twisted barrel-shaped structure”31) and 3mer-2 with a “cyclic trimer31 or a “planar cyclic structure”.29 To the best of our knowledge, 3mer-3 has never been reported, yet. Since the total energy differences between these conformations are very small, these competitive conformations will be important for thermal properties such as positron binding features.
Similarly, we found ten conformations of (CO2)4 and twenty five conformations of (CO2)5, including previously reported structures: a “trigonal pyramidal geometry”29 or “tetrahedral structure”31 or “trigonal pyramidal”57 (4mer-1), a “square geometry”29 (4mer-6), and a “trigonal bipyramid geometry”29 or “trigonal bipyramidal”31 (5mer-1). Energy differences between conformations for (CO2)4 and (CO2)5 are less than 4.8 kJ mol-1 and 13.0 kJ mol−1, respectively, which are comparable to those for (CO2)3. Therefore, it may be possible to experimentally detect these structures. Note that the tetramer “IVB”29 was not obtained in our search, because this structure cannot be verified as an equilibrium structure at our calculation level of B3LYP-D3/6-31+G(d). This structure is composed of a CO2 molecule perpendicular to a planar cyclic trimer. Besides, this structure includes a “T-shaped” CO2 dimer, on which whether this structure is stable or not is under debate; the stationary state of the “T-shaped” dimer was predicted to be the equilibrium state in both MPWB1K/6-31++G(2d)29 and ωB97X-D/6-311++G(d,p)31 calculations, while it was predicted to be a saddle point in MP2/[5s4p2d] calculation.58 The topic of whether this structure is an equilibrium structure or a saddle point is beyond the scope of our study.
In this study, we also obtained various new conformations with three-dimensional and two-dimensional structures unreported so far. A part of them slipped parallel like conformations with a planar symmetry are shown in Fig. 2. The total energies of these tetramers and pentamers are only 16.0–16.4 and 28.0–29.0 kJ mol−1 lying higher than those of the most stable structures (4mer-1 and 5mer-1), respectively. We should mention that in these slipped parallel like structures, arbitrary adjacent two CO2 molecules have the structures almost similar to that of “slipped parallel” dimers (the dimer unit). Reflecting this, the interaction energy per cluster is roughly equal to the sum of the interaction energies of the dimer units. Consequently, they may be important under the condition of gas-phase.
 | ||
| Fig. 2 Slipped parallel like new conformations of (CO2)ns found in this study. The name, interaction energy per molecule Eint, and PA are shown in the labels. | ||
3.2 Positron binding features
We calculated PAs of all the obtained 40 structures of (CO2)n as shown in Fig. 1 and 2 in the main text and Fig. S1 in ESI.† Also, PAs are summarized in Table S2 in ESI.† The calculated PAs are shown as functions of the number of constituent CO2 molecules of a cluster, n, in Fig. 3. The PA of a monomer is predicted to be 0.00 meV and this value means that a CO2 molecule does not bind a positron. This result is consistent with the previous calculations by Koyanagi et al.20 For the clusters, PAs of (CO2)2, (CO2)3, (CO2)4 and (CO2)5 are 0.05 meV, 0.15–0.51 meV, 0.02–0.61 meV and 0.43–1.51 meV, respectively. We also evaluated thermal averages of PAs with the Boltzmann factor at temperature T = 300 K as an indicator of PA dependent on n. These values are shown by red crosses in Fig. 3. Thermal averages of PAs increase with the increase in n. For n = 3–5, PAs vary with cluster conformations, where the most stable structure (in black open circle) does not have the largest PA. This PA dependency on the conformations is further discussed in Section 3.3.We show the positron density distribution for 5mer-22, which has the largest PA of 1.51 meV in the present calculations as shown in Fig. 4. These isosurfaces show that the positronic wave function is quite diffusing. The diffuseness of the positronic wavefunction has been predicted from the small PA (<2 meV) and a theoretical study in a previous report.59 The trend of our result is consistent with those of other weak positronic compounds. Also, other CO2 clusters may have more delocalized positronic wave functions.
Considering the delocalized positronic distribution enclosing the clusters, the nuclear configurations may affect the positron binding feature. The positron binding mechanism is discussed by regression analyses with respect to structures and PAs in the next section.
3.3 Linear regression analyses of PA properties
To find out the factors effective in increasing PAs of CO2 clusters, we performed linear regression analyses using some electrostatic and structural properties of the parent clusters. These properties and PA are summarized in Table S2 in ESI.† First, we examined contributions of the magnitude of the dipole moment μ (in Debye) and polarizability α (in Bohr3), which have been frequently employed as explanatory variables (descriptors) in linear regression for various molecules.11–14 This regression model referred to as μ–α model yielded a determination coefficient (R2) of 0.45, which indicates that it is an insufficient regression model (see Fig. S2 in ESI† for details). Second, we examined a μ–Q–α model containing descriptors μ, α, and the magnitude of the quadrupole moment Q (in Buckingham), at the center of mass, which is the third term of the multipole expansion of electrostatic potential next to the second term, μ. The result is shown in Fig. 5(a), where the calculated PA is shown as a function of the fitted PA. The linear regression equation for PA (in meV) is| PAreg = –0.55 + 0.48μ + 0.020Q + 0.015α, | (5) |
In the previous subsections, we reported that CO2 molecules can take various types of cluster structures such as the tetrahedral and the plane-type ones. The positron binding properties on CO2 clusters may be influenced by differences between these cluster structures, especially for the structures in Fig. 2. In order to take the influence of structural properties into consideration, we further employed additional simple descriptors to represent cluster structures for the multiple regression: the flatness F and surface area S. This μ–Q–α-struct model shows R2 = 0.58, which is actually improved compared to that of the μ–Q–α model. The calculated PA as a function of fitted PA in the μ–Q–α-struct model is summarized in Fig. 5(b). The linear function for PA (in meV) of the μ–Q–α-struct model is represented as
| PAreg = −0.10 + 0.79μ + 0.028Q + 0.0082α − 0.49F + 0.0024S, | (6) |
To confirm the validity of the μ–Q–α-struct model, we evaluated the Akaike information criterion (AIC).60 In linear regression analysis, the model performance, which is measured using the correlation coefficient and the determination coefficient R2, is inevitably improved as the explanatory variables increase. The AIC metric is frequently employed to compare the performances of models with different numbers of explanatory variables, where models with lower AIC values are considered to be superior. The present μ–Q–α-struct model shows a better AIC metric of 12.4, compared with 16.5 for the μ–Q–α model and 17.1 for the μ–α model. Thus, from AIC analysis, we confirmed that the conformational effect plays important roles in positron binding to CO2 clusters.
It is well known that the conformer effect plays essential roles in molecular clusters and condensed systems, and leads to interesting physical and chemical features.61,62 In this paper, we obtained that the structure affects the positron binding properties of CO2 molecular cluster systems, using simple descriptors such as flatness F and the surface area S. It is a future research target to explore and construct more reasonable regression models for positron binding properties for clusters with other descriptors. Additionally, the relation found by us between PA and surface areas is similar to the experimental results for solid materials. That is, several solid materials bind a positron on the surface rather than in bulk.63 We hope that universality of the phenomena we obtained would be confirmed, which would result in progress of cluster chemistry.
4 Conclusions
We systematically searched for the cluster structures of (CO2)n with n = 1–5 and calculated their PAs. By applying the SC-AFIR method, we found many structures for n = 3–5, with many already reported structures and newly obtained structures such as planar slipped parallel like ones. The PA of a CO2 monomer is predicted to be 0.00 meV, while PAs of the clusters increase to the values in the range of 0.02 to 1.51 meV. These loosely bound positronic wave functions are strongly delocalized. We analyzed the dependence of PA on the cluster sizes and conformations by linear regression analyses using electrostatic and structural properties. We obtained that the regression model with the magnitude of dipole moments, quadrupole moments, and dipole polarizability yields R2 = 0.49, indicating significant correlation but low linearity. We further obtained that structural properties such as flatness and surface areas are likely to become effective parameters, which are competitive to above electrostatic properties.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partly supported by the Grants-in-Aid for Scientific Research (KAKENHI) from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) (grant no. 18H01945 and 21H00026 for M. Tachikawa, grant no. 18K05041 and 21K04983 for Y. Kita, and grant no. 22K05038 for T. Shimazaki.). The computations were partly performed using the resources provided by the Research Center for Computational Science (RCCS), Okazaki, Japan (project: 22-IMS-C009). This work partly used computational resources through the HPCI System Research Project (Project ID: hp220061).Notes and references
- P. A. M. Dirac, Quantised singularities in the electromagnetic field, Proc. R. Soc. London, Ser. A, 1931, 133, 60–72, DOI:10.1098/rspa.1931.0130.
- F. Tuomisto and I. Makkonen, Defect identification in semiconductors with positron annihilation: Experiment and theory, Rev. Mod. Phys., 2013, 85, 1583–1631, DOI:10.1103/RevModPhys.85.1583.
- K. O. Jensen and A. Weiss, Theoretical study of the application of positron-induced Auger-electron spectroscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 3928–3936, DOI:10.1103/PhysRevB.41.3928.
- L. D. Jr Hulett, D. L. Donohue, J. Xu, T. A. Lewis, S. A. McLuckey and G. L. Glish, Mass spectrometry studies of the ionization of organic molecules by low-energy positron, Chem. Phys. Lett., 1993, 216(1–2), 236–240, DOI:10.1016/0009-2614(93)E1231-5.
- G. F. Gribakin, J. A. Young and C. M. Surko, Positron-molecule interactions: Resonant attachment, annihilation, and bound states, Rev. Mod. Phys., 2010, 82, 2557–2607, DOI:10.1103/RevModPhys.82.2557.
- S. J. Gilbert, L. D. Barnes, J. P. Sullivan and C. M. Surko, Vibrational-Resonance Enhancement of Positron Annihilation in Molecules, Phys. Rev. Lett., 2002, 88, 043201, DOI:10.1103/PhysRevLett.88.043201.
- J. R. Danielson, J. A. Young and C. M. Surko, Dependence of positronmolecule binding energies on molecular properties, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 235203, DOI:10.1088/0953-4075/42/23/235203.
- J. R. Danielson, J. J. Gosselin and C. M. Surko, Dipole enhancement of positron binding to molecules, Phys. Rev. Lett., 2010, 104, 233201, DOI:10.1103/PhysRevLett.104.233201.
- J. R. Danielson, A. C. L. Jones, J. J. Gosselin, M. R. Natisin and C. M. Surko, Interplay between permanent dipole moments and polarizability in positron-molecule binding, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 022709, DOI:10.1103/PhysRevA.85.022709.
- J. R. Danielson, A. C. L. Jones, M. R. Natisin and C. M. Surko, Comparisons of positron and electron binding to molecules, Phys. Rev. Lett., 2012, 109, 113201, DOI:10.1103/PhysRevLett.109.113201.
- M. Ozaki, D. Yoshida, Y. Kita, T. Shimazaki and M. Tachikawa, Positron Binding and Annihilation Properties of Amino Acid Systems, ACS Omega, 2021, 6(44), 29449–29458, DOI:10.1021/acsomega.1c03409 . PMID: 34778617.
- J. A. Charry, J. Romero, M. T. do Nascimento Varella and A. Reyes, Calculation of positron binding energies of amino acids with the any-particle molecular-orbital approach, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 052709, DOI:10.1103/PhysRevA.89.052709.
- K. Koyanagi, Y. Kita and M. Tachikawa, Systematic theoretical investigation of a positron binding to amino acid molecules using the ab initio multi-component molecular orbital approach., Eur. Phys. J. D, 2012, 66(5), 121, DOI:10.1140/epjd/e2012-20638-y.
- K. Ono, T. Oyamada, Y. Kita and M. Tachikawa, Theoretical analysis of the binding of a positron and pair-annihilation in fluorinated benzene molecules, Eur. Phys. J. D, 2020, 74(5), 89, DOI:10.1140/epjd/e2020-100538-3.
- M. Furushima, D. Yoshida, Y. Kita, T. Shimazaki and M. Tachikawa, Theoretical investigation of the enhancement of positron affinity by the vibration and dimerization of non-polar carbon disulfide, Phys. Chem. Chem. Phys., 2021, 23, 21512–21520, 10.1039/D1CP02808A.
- A. R. Swann and G. F. Gribakin, Effect of molecular constitution and conformation on positron binding and annihilation in alkanes, J. Chem. Phys., 2020, 153(18), 184311, DOI:10.1063/5.0028071.
- Y. Sugiura, H. Suzuki, T. Otomo, T. Miyazaki, T. Takayanagi and M. Tachikawa, Positron–electron correlation-polarization potential model for positron binding in polyatomic molecules, J. Comput. Chem., 2020, 41(17), 1576–1585, DOI:10.1002/jcc.26200.
- J. A. Young and C. M. Surko, Feshbach-resonance-mediated positronannihilation in small molecules, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 032702, DOI:10.1103/PhysRevA.78.032702.
- M. G. Colucci, D. P. van der Werf and M. Charlton, The temperature and density dependence of positron annihilation in CO2 and SF6, J. Phys. B: At. Mol. Opt. Phys., 2011, 44(17), 175204, DOI:10.1088/0953-4075/44/17/175204.
- K. Koyanagi, Y. Kita and M. Tachikawa, Vibrational enhancement of positron affinities for nonpolar carbon dioxide and carbon disulfide molecules: Multi-component molecular orbital study for vibrational excited states, Int. J. Quantum Chem., 2013, 113(3), 382–385, DOI:10.1002/qua.24111.
- M. V. Johnston, Supersonic jet expansions in analytical spectroscopy, TrAC, Trends Anal. Chem., 1984, 3(2), 58–61 CrossRef CAS . Available from: https://www.sciencedirect.com/science/article/pii/0165993684870557.
- J. N. Oliaee, M. Dehghany, N. Moazzen-Ahmadi and A. R. W. McKellar, Spectroscopic identification of carbon dioxide clusters: (CO2)6 to (CO2)13, Phys. Chem. Chem. Phys., 2011, 13, 1297–1300, 10.1039/C0CP02311F.
- B. Maté, G. Tejeda and S. Montero, Raman spectroscopy of supersonic jets of CO2: Density, condensation, and translational, rotational, and vibrational temperatures, J. Chem. Phys., 1998, 108(7), 2676–2685, DOI:10.1063/1.475660.
- C. E. Klots and R. N. Compton, Electron attachment to carbon dioxide clusters in a supersonic beam, J. Chem. Phys., 1977, 67(4), 1779–1780, DOI:10.1063/1.435044.
- T. Hatamoto, M. Matsumoto, X. J. Liu, K. Ueda, M. Hoshino and K. Nakagawa, et al., Vibrationally resolved C and O 1s photoelectron spectra of carbon dioxide, J. Electron Spectros. Relat. Phenomena., 2007, 155(1), 54–57 CrossRef CAS . Scattering, Coincidence and Absorption Studies of Molecules. Available from: https://www.sciencedirect.com/science/article/pii/S0368204806001198.
- S. Shanker and P. Bandyopadhyay, Monte Carlo Temperature Basin Paving with Effective Fragment Potential: An Efficient and Fast Method for Finding Low-Energy Structures of Water Clusters (H2O)20 and (H2O)25, J. Phys. Chem. A, 2011, 115(42), 11866–11875, DOI:10.1021/jp2073864 . PMID: 21928813.
- S. D. Yeole and S. R. Gadre, Molecular cluster building algorithm: Electrostatic guidelines and molecular tailoring approach, J. Chem. Phys., 2011, 134(8), 084111, DOI:10.1063/1.3556819.
- S. D. Yeole, N. Sahu and S. R. Gadre, Structures, energetics and vibrational spectra of CO2 clusters through molecular tailoring and cluster building algorithm, Phys. Chem. Chem. Phys., 2012, 14, 7718–7723, 10.1039/C2CP23761J.
- K. V. Jovan Jose and S. R. Gadre, An ab initio investigation on (CO2)n and CO2(Ar)m clusters: Geometries and IR spectra, J. Chem. Phys., 2008, 128(12), 124310, DOI:10.1063/1.2838202.
- S. G. Neogi and P. Chaudhury, Structure and spectroscopy of water-fluoride microclusters: A combined genetic algorithm and DFT-based study, J. Comput. Chem., 2012, 33(6), 629–639, DOI:10.1002/jcc.21994.
- N. S. Ganguly, S. Talukder and P. Chaudhury, Structural and spectroscopic studies of carbon dioxide clusters: a combined genetic algorithm and DFT based study, Struct. Chem., 2014, 25, 909–918, DOI:10.1007/s11224-013-0360-8.
- S. Maeda, T. Taketsugu and K. Morokuma, Exploring transition state structures for intramolecular pathways by the artificial force induced reaction method, J. Comput. Chem., 2014, 35(2), 166–173, DOI:10.1002/jcc.23481.
- S. Maeda, Y. Harabuchi, M. Takagi, T. Taketsugu and K. Morokuma, Artificial Force Induced Reaction (AFIR) Method for Exploring Quantum Chemical Potential Energy Surfaces, Chem. Rec., 2016, 16(5), 2232–2248, DOI:10.1002/tcr.201600043.
- S. Maeda and Y. Harabuchi, On Benchmarking of Automated Methods for Performing Exhaustive Reaction Path Search, J. Chem. Theory Comput., 2019, 15(4), 2111–2115, DOI:10.1021/acs.jctc.8b01182 . PMID: 30860828.
- J. Mitroy and G. G. Ryzhikh, Improved binding energies for LiPs, e+Be, NaPs and e+Mg, J. Phys. B: At., Mol. Opt. Phys., 2001, 34(10), 2001–2007, DOI:10.1088/0953-4075/34/10/313.
- J. Mitroy, M. W. J. Bromley and G. G. Ryzhikh, Positron and positronium binding to atoms, J. Phys. B: At., Mol. Opt. Phys., 2002, 35(13), R81–R116, DOI:10.1088/0953-4075/35/13/201.
- J. Mitroy, Energy and expectation values of the PsH system, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 054502, DOI:10.1103/PhysRevA.73.054502.
- J. Mitroy, S. Bubin, W. Horiuchi, Y. Suzuki, L. Adamowicz and W. Cencek, Theory and application of explicitly correlated Gaussians, Rev. Mod. Phys., 2013, 85, 693–749, DOI:10.1103/RevModPhys.85.693.
- S. Bubin and L. Adamowicz, Nonrelativistic variational calculations of the positronium molecule and the positronium hydride, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 052502, DOI:10.1103/PhysRevA.74.052502.
- Y. Kita, R. Maezono, M. Tachikawa, M. D. Towler and R. J. Needs, Ab initio quantum Monte Carlo study of the binding of a positron to alkali-metal hydrides, J. Chem. Phys., 2011, 135(5), 054108, DOI:10.1063/1.3620151.
- Y. Yamada, Y. Kita and M. Tachikawa, Theoretical prediction of the binding of a positron to a formaldehyde molecule using a first-principles calculation, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 062711, DOI:10.1103/PhysRevA.89.062711.
- D. Bressanini, Positron chemistry by quantum Monte Carlo. II. Ground-state of positron-polar molecule complexes, J. Chem. Phys., 1998, 109(5), 1716–1720, DOI:10.1063/1.476745.
- M. Tachikawa, Simultaneous optimization of Gaussian type function exponents for electron and positron with full-CI wavefunction—application to ground and excited states of positronic compounds with multi-component molecular orbital approach, Chem. Phys. Lett., 2001, 350(3–4), 269–276, DOI:10.1016/S0009-2614(01)01286-6.
- M. Tachikawa, Y. Kita and R. J. Buenker, Bound states of the positron with nitrile species with a configuration interaction multicomponent molecular orbital approach, Phys. Chem. Chem. Phys., 2011, 13, 2701–2705, 10.1039/C0CP01650K.
- M. Tachikawa, Y. Kita and R. J. Buenker, Bound states of positron with simple carbonyl and aldehyde species with configuration interaction multi-component molecular orbital and local vibrational approaches, New J. Phys., 2012, 14(3), 035004, DOI:10.1088/1367-2630/14/3/035004.
- R. Bukowski, J. Sadlej, B. Jeziorski, P. Jankowski, K. Szalewicz and S. A. Kucharski, et al., Intermolecular potential of carbon dioxide dimer from symmetry-adapted perturbation theory, J. Chem. Phys., 1999, 110(8), 3785–3803, DOI:10.1063/1.479108.
- A. D. Becke, A new mixing of Hartree–Fock and local density functional theories, J. Chem. Phys., 1993, 98(2), 1372–1377, DOI:10.1063/1.464304.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789, DOI:10.1103/PhysRevB.37.785.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104, DOI:10.1063/1.3382344.
- S. Maeda, Y. Harabuchi, Y. Sumiya, M. Takagi, K. Suzuki, M. Hatanaka, Y. Osada, T. Taketsugu, K. MorokumaK. Ohno, GRRM17, http://iqce.jp/GRRM/index_e.shtml (accessed date 25/5, 2022).
- S. Maeda, K. Ohno and K. Morokuma, Systematic exploration of the mechanism of chemical reactions: the global reaction route mapping (GRRM) strategy using the ADDF and AFIR methods., Phys. Chem. Chem. Phys., 2013, 15, 3683–3701, 10.1039/C3CP44063J.
- S. Maeda, Y. Harabuchi, M. Takagi, K. Saita, K. Suzuki and T. Ichino, et al., Implementation and performance of the artificial force induced reaction method in the GRRM17 program, J. Comput. Chem., 2017, 39(4), 233–250, DOI:10.1002/jcc.25106.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, et al., Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- M. Tachikawa, K. Mori, K. Suzuki and K. Iguchi, Full variational molecular orbital method: Application to the positronmolecule complexes, Int. J. Quantum Chem., 1998, 70, 491–501, DOI:10.1002/(SICI)1097-461X(1998)70:3<491::AID-QUA5>3.0.CO;2-P.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva and J. E. Deustua, et al., Recent developments in the general atomic and molecular electronic structure system, J. Chem. Phys., 2020, 152(15), 154102, DOI:10.1063/5.0005188.
- E. Lutwak, D. Yang and G. Zhang, A new ellipsoid associated with convex bodies, Duke Math. J., 2000, 104(3), 375–390, DOI:10.1215/S0012-7094-00-10432-2.
- H. Takeuchi, Geometry Optimization of Carbon Dioxide Clusters (CO2)n for 4 ≤ n ≤ 40, J. Phys. Chem. A, 2008, 112(33), 7492–7497, DOI:10.1021/jp802872p . PMID: 18665573.
- R. Eggenberger, S. Gerber and H. Huber, The carbon dioxide dimer, Mol. Phys., 1991, 72(2), 433–439, DOI:10.1080/00268979100100341.
- G. F. Gribakin and C. M. R. Lee, Positron annihilation in molecules by capture into vibrational Feshbach resonances of infraredactive modes, Phys. Rev. Lett., 2006, 97, 193201, DOI:10.1103/PhysRevLett.97.193201.
- D. G. Brooks, Akaike Information Criterion Statistics, Technometrics, 1989, 31(2), 270–271, DOI:10.1080/00401706.1989.10488538.
- G. M. Pastor, P. Stampfli and K. H. Bennemann, On the transition from van der Waals- to metallic bonding in Hg-clusters as a function of cluster size, Phys. Scr., 1988, 38(4), 623–626, DOI:10.1088/0031-8949/38/4/022.
- B. W. van de Waal, Calculated ground-state structures of 13-molecule clusters of carbon dioxide, methane, benzene, cyclohexane, and naphthalene, J. Chem. Phys., 1983, 79(8), 3948–3961, DOI:10.1063/1.446263.
- P. J. Schultz and K. G. Lynn, Interaction of positron beams with surfaces, thin films, and interfaces, Rev. Mod. Phys., 1988, 60(3), 701–781, DOI:10.1103/RevModPhys.60.701.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03788b |
| This journal is © the Owner Societies 2023 |