Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational NMR of the iron pyrazolylborate complexes [Tp2Fe]+ and Tp2Fe including solvation and spin-crossover effects†
Ari
Pyykkönen
 and
Juha
Vaara
and
Juha
Vaara
 *
*
NMR Research Unit, University of Oulu, P.O. Box 3000, Oulu FIN-90014, Finland. E-mail: ari.pyykkonen@oulu.fi; juha.vaara@iki.fi
First published on 27th December 2022
Abstract
Transition metal complexes have important roles in many biological processes as well as applications in fields such as pharmacy, chemistry and materials science. Paramagnetic nuclear magnetic resonance (pNMR) is a valuable tool in understanding such molecules, and theoretical computations are often advantageous or even necessary in the assignment of experimental pNMR signals. We have employed density functional theory (DFT) and the domain-based local pair natural orbital coupled-cluster method with single and double excitations (DLPNO-CCSD), as well as a number of model improvements, to determine the critical hyperfine part of the chemical shifts of the iron pyrazolylborate complexes [Tp2Fe]+ and Tp2Fe using a modern version of the Kurland–McGarvey theory, which is based on parameterising the hyperfine, electronic Zeeman and zero-field splitting interactions via the parameters of the electron paramagnetic resonance Hamiltonian. In the doublet [Tp2Fe]+ system, the calculations suggest a re-assignment of the 13C signal shifts. Consideration of solvent via the conductor-like polarisable continuum model (C-PCM) versus explicit solvent molecules reveals C-PCM alone to be insufficient in capturing the most important solvation effects. Tp2Fe exhibits a spin-crossover effect between a high-spin quintet (S = 2) and a low-spin singlet (S = 0) state, and its recorded temperature dependence can only be reproduced theoretically by accounting for the thermal Boltzmann distribution of the open-shell excited state and the closed-shell ground-state occupations. In these two cases, DLPNO-CCSD is found, in calculating the hyperfine couplings, to be a viable alternative to DFT, the demonstrated shortcomings of which have been a significant issue in the development of computational pNMR.
1 Introduction
Nuclear magnetic resonance (NMR) of open-shell, paramagnetic compounds (pNMR) has become increasingly important in the fields of biochemistry and materials science.1–5 Theoretical determination of the NMR chemical shifts via electronic structure methods can aid in the assignment and interpretation of experimental spectra,6 and sometimes reveal a need for re-assignment of experimental spectra.7,8 The classic Kurland–McGarvey theory of paramagnetic shielding9 expresses the hyperfine part of the shielding tensor in terms of the electron paramagnetic resonance (EPR) parameters of the ground multiplet of 2S + 1 electronic states, where S is the effective electron spin. In modern quantum-chemical implementations10–12 of this theory, one requires the ability to reliably compute the g-tensor, the zero-field splitting (ZFS, D, in S > 1/2 systems with more than one unpaired electron) and the hyperfine couplings (HFC, A) of the system.Transition metal ions such as Fe(II) and Fe(III) play important roles in a number of biological processes and have many applications in pharmacy.13 Iron systems have also received attention as cost-effective and environmentally friendly catalysts in chemistry and materials science.14 The present work focuses on the calculation of NMR chemical shifts in isolated paramagnetic iron complexes. Some modern computational pNMR work on iron systems has been previously published.15–18 Mondal and Kaupp15,16 computed pNMR chemical shifts of solid-state iron systems as part of studies on a series of lithium-ion battery cathode materials. Martin and Autschbach17 performed Kohn–Sham (KS) density functional theory (DFT) pNMR calculations on a set of paramagnetic organometallic complexes to investigate the roles of the KS delocalisation error, Gaussian-type versus Slater-type basis sets, relativistic effects, and ZFS. Our earlier work18 focused on computational pNMR predictions of a series of transition metal pyrazolylborate complexes, including iron systems. In this work, we study the iron pyrazolylborate complexes [Tp2Fe(III)]+ and Tp2Fe(II) encountered in our previous work18 more rigorously, exploring various computational methods for calculating their EPR parameters. An image of this type of molecule is shown in Fig. 1. With the former, spin doublet (S = 1/2) complex, we are particularly interested in whether model improvements such as more accurate g-tensor and ZFS calculations, or consideration of solvation effects can explain the observed discrepancy between theory and experiment for carbon shifts, which contrasted with the otherwise generally good theoretical results in the rest of the investigated series of metal complexes.18 The latter complex is a spin-crossover compound, for which different computational fitting methods are explored in this work. In addition to our earlier work,18 these systems were studied experimentally by Feher,19 whose measurements are compared to presently, as well as previously.
Some metal complexes exhibit behaviour in which their spin state changes due to an external stimulus, such as temperature, pressure or light, usually involving conversion between low-spin and high-spin configurations.20 This so-called spin-crossover was first observed by Cambi and Szegö21 in 1931, and it has various potential applications in, e.g., molecular electronics, data storage and display devices.22,23 The phenomenon is commonly seen in first-row transition metal complexes with d4 to d7 electron configuration and octahedral ligand geometry. One system displaying spin-crossover is Tp2Fe(II), shown in Fig. 1, which switches between a diamagnetic singlet (S = 0) state and a paramagnetic quintet (S = 2) state. Recently, the spin-state energetics of manganese spin-crossover complexes have been studied computationally by ab initio methods by Drosou, Mitsopoulou and Pantazis,24 who found complete active-space self-consistent field (CASSCF)/n-electron valence-state perturbation theory (NEVPT2) calculations unable to accurately describe the spin-state energies of their systems. This suggests that the CASSCF/NEVPT2 method we routinely use for the EPR property calculations of relevance to pNMR shifts may not be well-suited for the determination of energetics. The authors recommend, instead, DLPNO-CCSD(T) for energy calculations, which has also been utilised earlier by Flöser et al.25 Iron spin-crossover compounds, including Tp2Fe, have been studied several times in the past.26–30 Recent papers also report investigations of spin-crossover systems and particularly their applications.31–36 Adjacent to the topic, related spin equilibrium systems have been studied computationally using DFT and Boltzmann statistics by Ke et al.37,38 with the high-spin and low-spin configurations arising from two distinct paramagnetic centers. In this work, we examine the significance of the spin-crossover effect in predicting the pNMR chemical shifts in an isolated Tp2Fe(II) molecule, and how different computational fitting methods for handling its equilibrium state succeed in reproducing the experimental results.18,19
Section 2 gives a brief overview of the theory behind paramagnetic NMR computations including the spin-crossover effect. Section 3 describes the details of the specific computational methods adopted in this work. Section 4.1 discusses the iron complex [Tp2Fe(III)]+ and the various computational methods for prediction its NMR chemical shifts, whereas Section 4.2 focuses on the spin-crossover compound Tp2Fe(II) and ways of handling its equilibrium state computationally.
2 Theoretical background
The present theoretical prediction of NMR chemical shifts of paramagnetic systems is based on the Kurland–McGarvey theory9 in its modern form,10–12 in which magnetic interactions are parameterised in the ground multiplet by EPR parameters: HFCs, ZFS and the g-tensor. The resulting expression for the Cartesian ετ-component of the pNMR shielding tensor for nucleus K is | (1) |
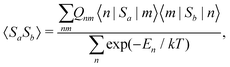 | (2) |
 | (3) |
 | (4) |
| δK = σref − σK,iso. | (5) |
The spin-crossover system Tp2Fe undergoes rapid spin interconversion near room temperature between a low-spin, S = 0 electronic ground state and a high-spin, S = 2 excited state. The populations of these states follow the Boltzmann distribution, with the probability of state i being
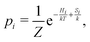 | (6) |
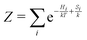 is the partition function. The (2S + 1)-fold degeneracy of the electronic states is included implicitly through the entropy term
is the partition function. The (2S + 1)-fold degeneracy of the electronic states is included implicitly through the entropy term  in the exponent. In order to calculate the NMR chemical shift of the equilibrium state, the enthalpy (energy) gap ΔH = H2 − H0 and the entropy gap ΔS = S2 − S0 must be determined, and the NMR shieldings of both the high-spin and low-spin states must be computed.
in the exponent. In order to calculate the NMR chemical shift of the equilibrium state, the enthalpy (energy) gap ΔH = H2 − H0 and the entropy gap ΔS = S2 − S0 must be determined, and the NMR shieldings of both the high-spin and low-spin states must be computed.
3 Computational methods
3.1 Geometry
Throughout the present discussion, unless otherwise specified, geometry optimisations were carried out with the TURBOMOLE programme42 using unrestricted Kohn–Sham (UKS) DFT and the PBE0 functional43 with 25% exact Hartree–Fock exchange energy (the PBE-25 notation is later used synonymously). Dispersion effects were accounted for with the DFT-D3 BJ dispersion correction.44,45 Relativistic effects were approximated by placing the Stuttgart-type scalar relativistic effective core potential ECP10MDF46 on the metal center, along with a corresponding 6s5p3d2f1g/8s7p6d2f1g (contracted/uncontracted notation) valence basis set.47 The def2-TZVP basis set48 was employed for ligand atoms. Coordinates for the optimised structures are provided in the ESI† (Tables S1–S6 and Fig. S1–S4).3.2 g- and ZFS tensors
The “standard method” adopted previously49,50 for computing the EPR parameters necessary to determine the NMR shieldings has been successfully applied to a number of isolated molecules in previous works.7,8,18 It involves calculating the g-tensor and ZFS at the CASSCF51/NEVPT252–54 level of theory. The basic NEVPT2 calculation for the g-tensor and ZFS uses a state-average (SA) cas(n,5) CASSCF wavefunction that correlates n d-electrons of the metal center in the five metal 3d-orbitals. The Douglas–Kroll–Hess (DKH2)55,56 approximation has been used in this context since ref. 50 to account for scalar relativistic effects in the optimisation of the SA-CASSCF states, and quasidegenerate perturbation theory (QDPT)57,58 is utilised to incorporate spin–orbit effects using the picture-changed spin–orbit operator. Only the spin–orbit contribution to the ZFS is included, since the spin–spin contribution can be assumed to be small, e.g., as we demonstrated in our earlier work.18 This calculation is carried out with the ORCA software.59,60 A locally dense basis set is used, in which the DKH-def2-TZVP basis set61 is placed on the metal center and atoms directly bonded to it, and a the smaller DKH-def2-SVP basis set is placed on the more distant ligand atoms.3.3 HFC tensors
The DFT-based, fully relativistic four-component matrix Dirac–Kohn–Sham (mDKS) method62,63 was mainly used to evaluate the hyperfine couplings. HFC calculations require polarisation of the core electrons in order to obtain reasonable results; for this reason unrestricted DFT (UKS) is necessary as, e.g., restricted open-shell DFT does not allow core spin polarisation. The mDKS calculation of hyperfine couplings is performed with the ReSpect program package64 using mostly the PBE0 functional with 25% exact exchange, which again has been the “standard choice” for such calculations since the work in ref. 50. Both scalar relativistic and spin–orbit effects are considered variationally within this method. The decontracted Dyall-VTZ basis set65 is placed on the metal atom, and a decontracted DKH-def2-TZVP basis set on the ligand atoms. This is the large wavefunction component basis set, and the small-component basis is generated by kinetic balance.3.4 Orbital shielding
The orbital shielding term, which is often less critical than the hyperfine term, is calculated at the UKS/PBE0 level of theory employing the Gaussian software66 and the DKH-def2-TZVP basis set. The NMR shieldings of the diamagnetic, closed-shell reference compounds, TMS for 1H and 13C, BF3 (O(C2H5)2) for 11B, and CH3NO2 for 14N, are computed at the restricted Kohn–Sham (RKS)/DKH-def2-TZVP level with the same functional as used in the corresponding HFC calculation. The reference shieldings are provided in Table S7 in the ESI.† In the present work, the computation of the diamagnetic (S = 0) low-spin state of Tp2Fe follows the same formula.3.5 Model improvements
In this work, four distinct modifications to the standard method are tested:(1) The CASSCF active space in the NEVPT2 calculation of the g-tensor and ZFS is expanded from cas(n,5) to cas(n,12) by including two occupied metal–ligand bonding orbitals and five empty metal 4d-orbitals.
(2) Solvation effects67 are included in the HFC computations through the conductor-like polarisable continuum model C-PCM,68 approximating electrostatic solute–solvent interactions. Importantly, non-electrostatic effects such as hydrogen bonding are not represented by the C-PCM model. Additional calculations with explicit solvent molecules are performed for [Tp2Fe]+ for comparison. An image of the [Tp2Fe]+ structure with twelve acetone molecules is shown in Fig. S3 in the ESI.† Furthermore, the presence of the [PF6]− counterion is considered for [Tp2Fe]+.
(3) The amount of exact Hartree–Fock exchange energy in the mDKS DFT hybrid functional in HFC calculations is varied (0%, 25%, 40% and 100%).
(4) The HFCs are calculated using the domain-based local pair natural orbital coupled-cluster method with single and double excitations (DLPNO-CCSD) employing lambda equations for unrelaxed coupled-cluster density,69 now implemented in ORCA. This is an approximation to CCSD that scales nearly linearly with system size but achieves good accuracy, recovering almost all of the CCSD correlation energy. However, similar to CCSD, it is a single-reference method, which may prove limiting with systems that have strong multireference character. This method has recently been applied with good results to HFC computations in pNMR by Jaworski and Hedin.70
3.6 Spin-crossover
The equilibrium-state NMR chemical shifts of the spin-crossover system Tp2Fe are expressed as Boltzmann averages between the high-spin S = 2 state and the low-spin S = 0 state by fitting the enthalpy gap ΔH and the entropy gap ΔS to experimental NMR data. The sum of squared errors is minimised to find optimal values for ΔH and ΔS. The available experimental data, reported by Feher,18,19 cover 1H, 13C, 11B and 14N chemical shifts, each at one temperature (excluding the N2 center) and the NMR temperature series of all four 1H nuclei from 290 K to 455 K. The fitting is performed in three different ways.(1) Global fit to the 1H temperature series of all four protons, resulting in two fitting parameters ΔH(H) and ΔS(H).
(2) Individual fits to each of the four 1H temperature series with each equivalent group assigned its own fitting parameter, resulting in eight fitting parameters ΔH(H3), ΔH(H4), ΔH(H5), ΔH(BH), ΔS(H3), ΔS(H4), ΔS(H5) and ΔS(BH). For nuclei other than protons, the average values ΔHavg and ΔSavg are used.
(3) Global fit to all experimental data including the 1H temperature series, as well as 13C, 11B and 14N shifts, resulting in two fitting parameters ΔH(all) and ΔS(all).
4 Results
4.1 Doublet iron complex [Tp2Fe]+
The measurement and computational temperatures with this molecule were 305 K (1H), 300 K (13C) and 298 K (11B and 14N). The full set of results is tabulated in Table S8 in the ESI,† and a computational 1H temperature series is displayed in Fig. S5 (ESI†).| H3 | H4 | H5 | BH | |
|---|---|---|---|---|
| Exptl18,19 | −52.9 | −13.2 | −8.2 | 39.4 |
| cas(5,5) | −51.3 | −10.0 | −2.0 | 41.5 |
| cas(9,12) | −50.9 | −9.4 | 0.3 | 42.0 |
| C3 | C4 | C5 | B | |
|---|---|---|---|---|
| Exptl18,19 | 2.5 | 175.8 | 19.6 | 95.2 |
| cas(5,5) | 34.7 | −3.6 | 93.7 | 91.2 |
| cas(9,12) | 34.6 | 2.5 | 91.6 | 92.5 |
In stark contrast to computed proton and boron shifts, there is a severe discrepancy in carbon shifts, as was discussed previously.18 The potential causes are elaborated on in Section 4.1.5.
Expanding the active space from cas(5,5) to cas(9,12) in CASSCF/NEVPT2 calculations has a noteworthy impact on the g-tensor (Table 2), especially visible in the g11 eigenvalue, and comparable to the differences between the base CASSCF and the NEVPT2 calculation based on it. It is seen that the improved level of theory does not translate into a notable effect on NMR shieldings, which demonstrates their insensitivity to the quality of the g-tensor due to the relatively small range of variation of the g-tensor components compared to the HFC. The improvement of the g-tensor calculations has no meaningful impact on the question of agreement between theory and experiment, or signal shift assignment in this molecule.
| System/level of theory | S | D (cm−1) | E/D | g 11 | g 22 | g 33 | g iso |
|---|---|---|---|---|---|---|---|
| a Doublet systems have no ZFS. b High-spin multiplet. | |||||||
| [Tp2Fe]+a | 1/2 | ||||||
| cas(5,5), CASSCF | 0.074 | 0.897 | 4.594 | 1.855 | |||
| cas(5,5), NEVPT2 | 0.507 | 0.990 | 4.378 | 1.958 | |||
| cas(9,12), CASSCF | 0.225 | 0.880 | 4.289 | 1.798 | |||
| cas(9,12), NEVPT2 | 0.340 | 0.871 | 4.290 | 1.834 | |||
| Tp2Feb | 2 | ||||||
| cas(6,5), CASSCF | 9.68 | 0.0089 | 1.994 | 2.140 | 2.143 | 2.092 | |
| cas(6,5), NEVPT2 | 8.69 | 0.0088 | 1.996 | 2.111 | 2.113 | 2.074 | |
| cas(10,12), CASSCF | 8.44 | 0.0088 | 1.995 | 2.120 | 2.122 | 2.079 | |
| cas(10,12), NEVPT2 | 8.25 | 0.0086 | 1.997 | 2.106 | 2.108 | 2.070 | |
| HFC level of theory | H3 | H4 | H5 | BH |
|---|---|---|---|---|
| a Acetone-d6 (ε = 20.7). b COSMO-optimised geometry used in HFC calculation. | ||||
| Exptl18,19 | −52.9 | −13.2 | −8.2 | 39.4 |
| mDKS in vacuo | −50.9 | −9.4 | 0.3 | 42.0 |
| DKH in vacuo | −43.9 | −9.1 | −2.6 | 36.6 |
| DKH + counterion [PF6]− | −41.9 | −11.5 | −3.7 | 34.4 |
| DKH + solvent (C-PCM)a | −44.3 | −8.9 | −2.5 | 36.6 |
| DKH + solvent (C-PCM)ab | −43.8 | −9.3 | −2.3 | 36.4 |
| DKH + 12 acetones | −41.8 | −7.9 | −4.7 | 34.6 |
| HFC level of theory | C3 | C4 | C5 | B |
|---|---|---|---|---|
| a Chloroform (ε = 4.81). b Dichloromethane (ε = 8.93). c Acetone-d6 (ε = 20.7). d COSMO-optimised geometry used in HFC calculation. | ||||
| Exptl18,19 | 2.5 | 175.8 | 19.6 | 95.2 |
| mDKS in vacuo | 34.6 | 2.5 | 91.6 | 92.5 |
| DKH in vacuo | 61.2 | 2.9 | 88.5 | 78.5 |
| DKH + counterion [PF6]− | 58.2 | 8.5 | 96.4 | 74.1 |
| DKH + solvent (C-PCM) | 61.7a | 4.3a | 89.9a | 78.9b |
| DKH + solvent (C-PCM)c | 60.3 | 2.5 | 89.0 | 78.9 |
| DKH + solvent (C-PCM)cd | 70.3 | 3.8 | 102.3 | 78.5 |
| DKH + 12 acetones | 68.1 | −2.0 | 106.0 | 75.1 |
Calculations with the presence of twelve explicit acetone molecules in the hyperfine computations have been included to illustrate the difference to the C-PCM continuum solvation model. This structure was optimised using the PBE functional to reduce the computational cost. For carbon and boron, an additional C-PCM calculation using acetone as solvent is shown for valid comparison between the different computational methods.
The scalar relativistic DKH versus fully relativistic mDKS hyperfine calculations are in greater contrast for this molecule than solvent effects are to in vacuo computations, with differences of several ppm for hydrogen, over 26 ppm for C3 and 14 ppm for boron. For H3 and B, mDKS is clearly in better agreement with experiment, while for H5, DKH is closer to measurements.
The C-PCM model results in very small deviations from the non-solvated DKH model, of no more than 1 ppm even for carbon. Non-specific electrostatic effects approximated by the C-PCM model thus appear to be unimportant for this system. In contrast, moving to an explicit solvation model has a notably larger impact of a couple ppm for hydrogen, and up to 17 ppm for carbons C3 and C5. Therefore, in this case, the continuum solvation model is not sufficient to capture the most important solvent effects. If inclusion of the solvent is desired, a more accurate model is necessary. In some cases, such as H5, explicit solvation improves compatibility with experiment, whereas in others compatibility is worsened. In the latter cases, the non-solvated calculations likely again benefit from error cancellation.
Furthermore, a calculation in which HFCs were computed using a COSMO-optimised geometry is included for completeness. The impact on proton and boron chemical shifts is small, with results changing by less than 1 ppm. For carbon, we see somewhat more substantial changes of the order of 10 ppm for C3 and C5. For these nuclei, the discrepancies between the C-PCM model and explicit solvation are alleviated, suggesting that the exact geometry may have some importance, although such an alleviation is not consistent across all the other nuclei.
Finally, hyperfine couplings have been calculated otherwise in vacuo but in the presence of the counterion [PF6]− used in the measurements. The counterion changes chemical shifts roughly by 2 ppm for hydrogen, and by a few ppm for carbon and boron. The effect is stronger than that of the C-PCM model, although explicit solvation by 12 solvent molecules remains overall more impactful. In calculations requiring great accuracy, including the counterion effect may be meaningful.
Overall, computations underestimate the proton H3, H4 and H5 shifts across the board, and solvent considerations provide no systematic improvement.
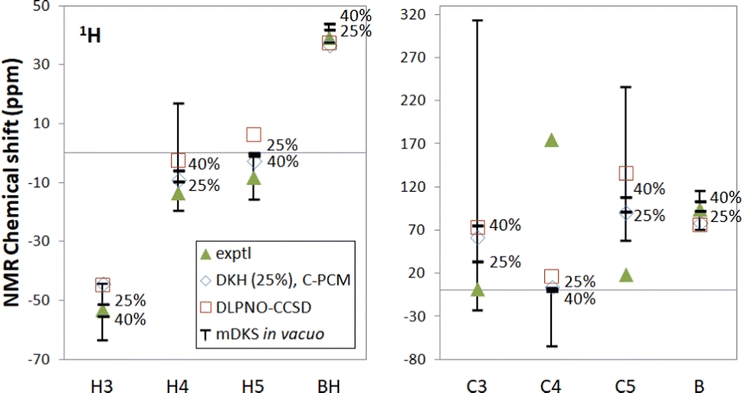 | ||
| Fig. 2 Experimental18,19 and computational NMR chemical shifts for [Tp2Fe]+. Bars indicate the range of in vacuo mDKS results for hyperfine coupling tensors obtained with hybrid, PBE0-based exchange–correlation functionals with different exact exchange admixtures (0%, 25%, 40% and 100%). | ||
With the functional PBE-100 with 100% exact exchange it should be noted that spin contamination in hyperfine DFT calculations may be significant and may distort results, although DFT computations at the DKH level do not indicate major spin contamination for either [Tp2Fe]+ or Tp2Fe based on deviation from the theoretical expectation value 〈S2〉. Here the full 0–100% range has been included for illustrative purposes, but of greater practical interest is the 25–40% range.
The mDKS results with varying proportions of exact exchange cover a range of up to 40 ppm for hydrogen and up to 300 ppm for carbon, although PBE-25 and PBE-40 are closer together. This kind of large range of results constitutes a major problem with employing DFT in the computation of HFCs, since the amount of exact exchange is based on empirical considerations – there is no theoretical justification for, e.g., choosing PBE-25 over the 40% exact exchange admixture. The latter was pragmatically recommended by Kaupp et al.63
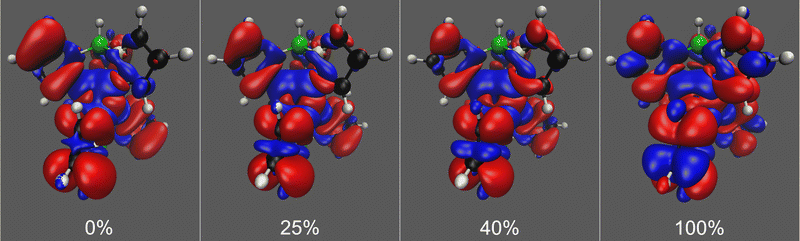
Pure DFT functionals are known to overestimate the covalent character of ligand–metal bonding especially for open-shell metal complexes with large ligand contact shifts, causing spin density to extend too far from the paramagnetic metal center to the ligand atoms.71,72 This spin delocalisation error can be reduced by hybrid functionals containing exact Hartree–Fock exchange energy. Conversely, however, an overly localised electronic structure may underestimate the covalent nature of metal–ligand interactions and likewise lead to an unrealistic picture of the electronic structure. In addition, hybrid functionals containing a high admixture of exact exchange tend to overestimate valence-shell spin polarisation, which may lead to significant spin contamination.73 On the other hand, hybrid functionals are also needed to satisfactorily capture core–shell spin polarisation, which is important in the computation of core properties such as hyperfine couplings. We see the expected trend in spin delocalisation in Fig. 3, where we have plotted the spin density isosurfaces of [Tp2Fe]+ at the UKS/DKH level of theory with 0%, 25%, 40% and 100% exact exchange. Increasing the exact exchange admixture causes positive spin density isosurfaces to slightly shrink, indicating decreasing spin delocalisation. Simultaneously, the negative spin density isosurfaces clearly increase, possibly reflecting growing spin polarisation and eventual spin contamination problems.
In our computed NMR chemical shift results, 25% or 40% exact exchange typically reproduce experimental shifts better than 0% or 100%. This is in line with the expectation that a mid-range portion of exact exchange should provide a more balanced description of spin delocalisation and spin polarisation effects for a global hybrid functional than either of the two extremes.
DLPNO-CCSD produces overall slightly worse shifts in comparison to PBE-25 or PBE-40 for this system. Only the BH signal is reproduced better by DLPNO-CCSD. In this comparison one must bear in mind that other factors, e.g., the presently omitted rovibrational effects70 may disfavour the ab initio data in this case. The fact that the DLPNO-CCSD data are quasirelativistic, as opposed to the fully relativistic nature of the DFT data, also contributes to the differences.
Another plausible explanation is in contributions from a low-lying excited state 601.1 cm−1 above the ground state, possessing the same doublet multiplicity as in the ground state multiplet, predicted by cas(5,5)/NEVPT2 calculations in our earlier work.18 Our newest cas(9,12)/NEVPT2 computations predict the excited doublet 538.8 cm−1 above the ground state (see below). This explanation was speculated upon in ref. 18 by very approximate calculations based on a fitting procedure to obtain hypothetical NMR shieldings for the excited state and Boltzmann-weighted thermal occupations of the ground and excited multiplets. The possibility was further explored in the present work by estimating the NMR shieldings of the excited doublet and fitting a thermal equilibrium of the ground and excited doublets to experimental data. An improved agreement with experiment was not achieved, however, possibly due to the inadequacy of the employed approximations. See the section “Excited state of [Tp2Fe]+” in the ESI† for more details. A more likely explanation is that a re-assignment of the experimental 13C signals is appropriate. In particular, both DFT and DLPNO-CCSD calculations seem to support re-assignment.
The physical contributions to the nuclear shieldings of [Tp2Fe]+ in the ground doublet state, following an explanation of the various terms in Table S11 in the ESI,† have been included in Table S12 (and correspondingly for the excited quintet of Tp2Fe in Table S13, ESI†). Across the series of calculations, the shieldings in [Tp2Fe]+ are dominated by the contact and pseudocontact terms (1 and 9 in the numbering of the table), with smaller contributions by the “con,3” term number 6. The prominence of the pseudocontact and “con,3” terms arises from the significant g-tensor anisotropy of the system.
4.2 Spin-crossover compound Tp2Fe
Measurements and calculations were carried out at the temperatures 290 K (1H), 305 K (13C) and 298 K (11B and 14N). In addition, a temperature series from 290 K to 455 K has been recorded for the proton shifts. The full set of results is tabulated in Tables S14 and S15 in the ESI.†It should be noted that our results correspond to the equilibrium between the S = 0 ground and S = 2 excited multiplets. The possibility of an excited triplet (S = 1) multiplet receiving significant thermal occupation in addition to the ground singlet and excited quintet was considered, but ruled out on the basis that the triplet was found computationally to lie far higher above the ground state than the quintet (see Section 4.2.7).
| H3 | H4 | H5 | BH | |
|---|---|---|---|---|
| Exptl18,19 | 13.0 | 12.9 | 8.1 | −2.7 |
| cas(6,5) | 15.3 | 15.5 | 9.1 | −2.0 |
| cas(10,12) | 15.1 | 15.5 | 9.2 | −1.8 |
| C3 | C4 | C5 | B | N1 | |
|---|---|---|---|---|---|
| Exptl18,19 | 266 | 168 | 229 | −26.4 | −126 |
| cas(6,5) | 341.3 | 231.9 | 332.5 | −37.5 | −143.9 |
| cas(10,12) | 342.4 | 232.8 | 333.9 | −37.0 | −143.4 |
As the NMR results suggest, the g-tensor in the high-spin (S = 2) state is only a little changed by the cas(6,5) to cas(10,12) expansion (Table 2), unlike in the case of [Tp2Fe]+. Likewise, the ZFS D-parameters produced by the two active spaces are quite similar at the NEVPT2 level, although at the CASSCF level a somewhat larger change is seen. The ZFS of commonly occurring magnitude has previously been reported to have negligible impact on NMR shifts at ambient temperatures – its importance is significant at very low temperatures and in cases where pseudocontact mechanisms are dominant in the total shift.12,17,49 The ZFS and the g-tensor determine the magnetic susceptibility,74,75 which can be used to formulate pseudocontact shifts.1
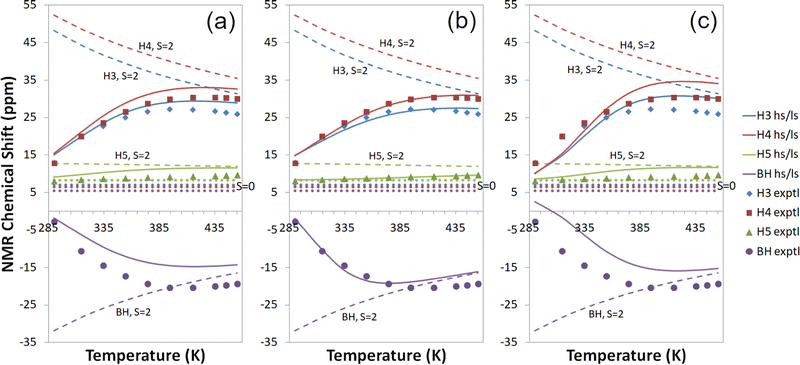 | ||
| Fig. 4 Experimental18,19 and computational 1H temperature series for Tp2Fe at the cas(10,12) + NEVPT2/mDKS/PBE0 level with (a) a global fit to 1H temperature series (b) individual proton fits to 1H temperature series and (c) a global fit to all experimental data. Dashed lines: S = 2 state; dotted lines: S = 0 state; solid lines: high-spin/low-spin equilibrium state. Symbols indicate experimental data. | ||
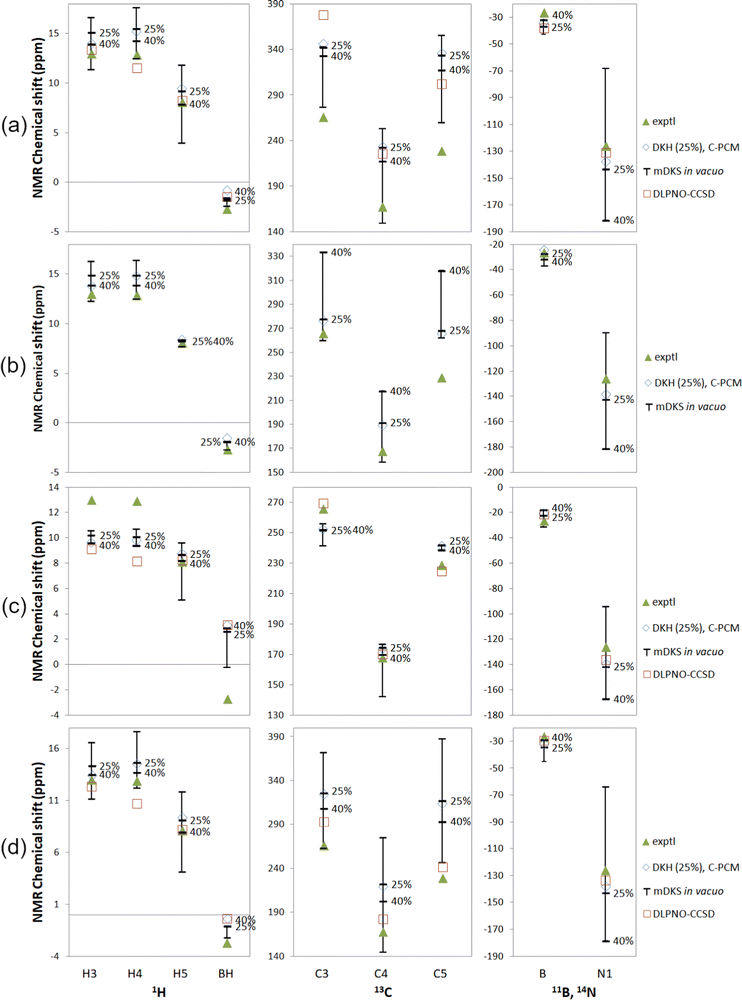 | ||
| Fig. 5 Experimental18,19 and computational NMR chemical shifts for Tp2Fe with (a) a global fit to 1H temperature series, (b) proton fits to individual 1H temperature series, (c) a global fit to all experimental data and (d) experimental ΔH and ΔS (ref. 18). Bars indicate the range of in vacuo mDKS results for hyperfine coupling tensors obtained with hybrid, PBE0-based exchange–correlation functionals with different exact exchange admixtures. Temperature for 1H: 290 K; 13C: 305 K; 11B and 14N: 298 K. | ||
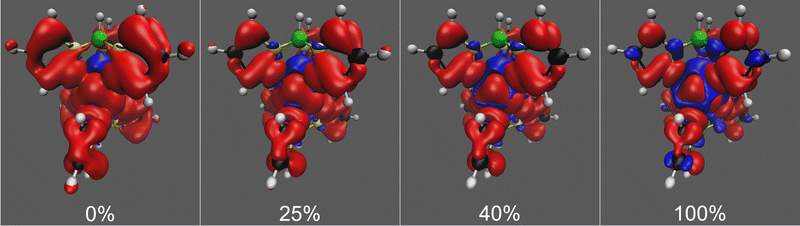
In the spin density isosurface plots as a function of exact exchange for the high-spin (S = 2) state of Tp2Fe in Fig. 6, we see more clearly the same trends regarding spin delocalisation as in the case of [Tp2Fe]+. Here, however, the positive spin density extends much further from the metal center than the negative, with a more balanced distribution appearing only with 100% exact exchange. This is explained by the lack, in this d6 system, of vacant spin-up acceptor 3d orbitals on the metal center, causing an unbalanced ligand–metal back-bonding, similarly to what was discussed by Pritchard and Autschbach71 in the cases of Cr(acac)3 and Fe(acac)3. In contrast, the d5 system [Tp2Fe]+ has two empty metal 3d orbitals, which allows a more balanced ligand–metal back-bonding as shown by the spin density plots of that system (Fig. 3).
The physical contributions to the nuclear shieldings for the high-spin (S = 2) state of Tp2Fe are listed in Table S13 in the ESI.† We have reported these at the temperature of 455 K, where the high-spin state is the primary contributor to the equilibrium state. In all calculations, we see the most significant contributions arising from the contact, dipolar and pseudocontact terms 1, 2 and 9 (see ESI† for numbering). The latter two are a consequence of the appreciable ZFS (D-parameter of around 9 cm−1) and g-tensor anisotropy, respectively. In 13C shieldings, the contact term dominates despite notable additional contributions by the “con,3” term 6, which originates from an isotropic g-shift and contact hyperfine coupling.
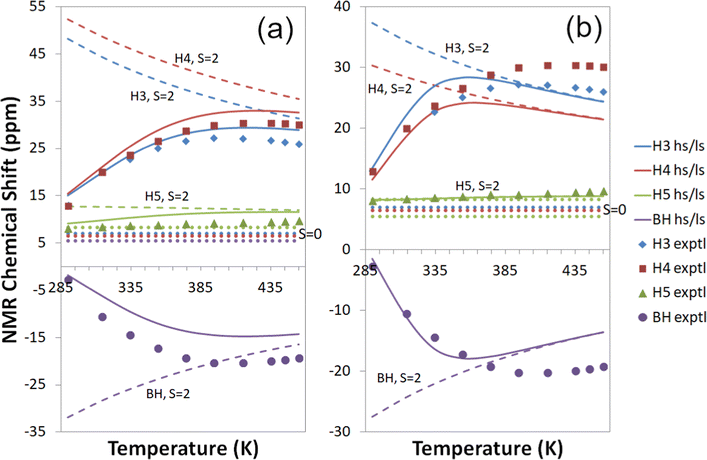 | ||
| Fig. 7 Experimental18,19 and computational 1H temperature series for Tp2Fe with a global fit to 1H temperature series (a) at the cas(10,12) + NEVPT2/mDKS/PBE0 level and (b) at the cas(10,12) + NEVPT2/DLPNO-CCSD level. Dashed lines: S = 2 state; dotted lines: S = 0 state; solid lines: high-spin/low-spin equilibrium state. Symbols indicate experimental data. | ||
In, instead, fitting individual equivalent groups of protons to 1H temperature series (Fig. 5(b)), we see a narrower range of DFT results with varying exact exchange for hydrogen, but not for other nuclei, as expected due to the proton-focused fitting method. In the cases of C3 and C5, the computations performed for HFCs at the PBE-25 and PBE-40 levels yield NMR shifts nearly at the opposite ends of the range of DFT results. The experimental data point at C5 again falls rather far outside the range of computational results. In this case, the obtained DLPNO-CCSD fitting parameters were dependent on the initial values of the fitting algorithm, and no meaningful shifts could be obtained. These results have therefore been omitted in Tables S14 and S15 in the ESI† as well as Fig. 5.
In the individual proton fits to 1H temperature series, the fitted average ΔH and ΔS fall in roughly the same range of 20–30 kJ mol−1 and 40–90 J K−1 mol−1, respectively, as in the global 1H temperature series fit (Table S14, ESI†).
By fitting computational parameters globally to all experimental data, i.e. besides the 1H temperature series, also the 13C, 11B and 14N signal shift measurements (Fig. 5(c)), we get the best agreement with experiment for carbon shifts, but at the expense of worse performance for proton shifts. This is a natural outcome, since we now move away from a proton-focused fitting technique and take experimental carbon results into account as well. DLPNO-CCSD is again overall competitive with DFT. DFT produces clearly better results only for H4.
With this all-data fit, ΔH and ΔS become larger than with the other two fitting methods, with typical ranges of 30–40 kJ mol−1 and 100–120 J K−1 mol−1, respectively (Table S14, ESI†), although again it should be remembered that here the experimental data is not necessarily of the greatest accuracy. The DLPNO-CCSD fit again stands as an outlier with ΔH of 63.2 kJ mol−1 and ΔS of 196.5 J K−1 mol−1.
Finally, the NMR shifts of Tp2Fe have been thermally averaged without a fitting procedure, by using the experimental values of ΔH and ΔS from ref. 18, in Fig. 5(d). Here we, again, see a quite large range of the mDKS results as a function of exact exchange admixture. Agreement with experiment is overall comparable to the 1H temperature series fit (a). DLPNO-CCSD is better than or comparable with DFT for most nuclei, with the exceptions of H4 and BH. The NMR shifts have additionally been calculated using the experimental ΔH and ΔS of ref. 26 (Fig. S6 in the ESI†). With these alternative parameters, agreement with experiment is notably worse in most cases, particularly for the 13C shifts.
The proton temperature series calculated with each of the three fitting methods are shown side by side in Fig. 4. The best agreement with measurements is gained with individual proton fits (b), though this also results in weaker performance for other nuclei. A global fit to all experimental data (c) yields the poorest 1H temperature series in comparison to experiment but reproduces carbon shifts better, as mentioned before. Fitting globally to the proton temperature series (a) produces an overall good agreement with experiment as an intermediate form between (b) and (c). All in all, each of the three fitting methods is quite well suited for qualitatively understanding NMR shifts, and the choice of the method can be guided by the availability of experimental data and the primary information targeted.
It is clear that CASSCF yields very poor energies in all cases, with energy gaps ΔH = H2 − H0 of the wrong sign, implying S = 2 ground state, on the order of around −200 kJ mol−1 compared to the experimental values of 16.1 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 or 24 kJ mol−1.18 Introducing dynamic electron correlation via NEVPT2 significantly improves the results, with the calculation based on a cas(10,12) wavefunction with the SVP/QZVPP basis set yielding an energy gap of 13.1 kJ mol−1, approaching the range of experimental results. The best results are obtained with DLPNO-CCSD(T), giving a result of 14.6 kJ mol−1 with the SVP/QZVPP basis set. The choice of basis set is clearly significant, as enlarging it around the metal center from triple-zeta to quadruple-zeta is required at the cas(10,12) + NEVPT2 and DLPNO-CCSD(T) levels to obtain an energy gap of the correct sign. Overall, DLPNO-CCSD(T) performs better than NEVPT2, although the agreement with experiment (ref. 18 and 26) cannot be considered quantitative. Ref. 24 found CASSCF to be a poor method for calculating energy gaps in their spin-crossover molecules even with a NEVPT2 correction, preferring DLPNO-CCSD(T). Our findings are largely in line with this, although we get a fairly satisfactory NEVPT2 result with the larger cas(10,12) CASSCF active space.
26 or 24 kJ mol−1.18 Introducing dynamic electron correlation via NEVPT2 significantly improves the results, with the calculation based on a cas(10,12) wavefunction with the SVP/QZVPP basis set yielding an energy gap of 13.1 kJ mol−1, approaching the range of experimental results. The best results are obtained with DLPNO-CCSD(T), giving a result of 14.6 kJ mol−1 with the SVP/QZVPP basis set. The choice of basis set is clearly significant, as enlarging it around the metal center from triple-zeta to quadruple-zeta is required at the cas(10,12) + NEVPT2 and DLPNO-CCSD(T) levels to obtain an energy gap of the correct sign. Overall, DLPNO-CCSD(T) performs better than NEVPT2, although the agreement with experiment (ref. 18 and 26) cannot be considered quantitative. Ref. 24 found CASSCF to be a poor method for calculating energy gaps in their spin-crossover molecules even with a NEVPT2 correction, preferring DLPNO-CCSD(T). Our findings are largely in line with this, although we get a fairly satisfactory NEVPT2 result with the larger cas(10,12) CASSCF active space.
In addition, the entropy gap from the harmonic vibrational frequencies was computed with TURBOMOLE at room temperature (298 K) and normal pressure (0.1 MPa) to be ΔSvib = S2,vib − S0,vib = 73.9 J K−1 mol−1, while the electronic contribution arising from the five-fold degenerate quintet is 13.4 J K−1 mol−1.76 The sum of these contributions is 87.3 J K−1 mol−1, which is somewhat higher than the experimental result in ref. 18, but consistent with the higher end of the range of our fitted results.
At the DLPNO-CCSD(T0) level of theory, with a locally dense def2-SVP/def2/QZVPP basis set, the lowest triplet multiplet was computed to be 93.0 kJ mol−1 above the ground state, compared to 14.6 kJ mol−1 for the quintet. NEVPT2 based on a cas(10,12) wavefunction yields a similar result (Table S16, ESI†). The difference is considerable enough that the triplet is not expected to have significant thermal occupation, which justifies its omission from the present consideration of the thermal equilibrium.
5 Conclusions
We have conducted a study of the challenging iron complexes [Tp2Fe]+ and Tp2Fe, with attention paid to the computational factors influencing 13C signal assignment in the former and the spin-crossover behavior of the latter compound. The impact of a number of model improvements and computational modifications to the “standard method” of pNMR calculations have been considered: more accurate g-tensor and ZFS calculations by expanding the CASSCF active space, solvation effects via the implicit C-PCM method and, for [Tp2Fe]+, explicit solvent molecules, use of the ab initio DLPNO-CCSD method to compute HFCs, as well as DFT calculation of HFCs with different proportions of exact exchange.Of interest has especially been the discrepancy between theory and measurements of carbon shifts in [Tp2Fe]+. For the spin-crossover compound Tp2Fe, three fitting methods for the Boltzmann averaging between the diamagnetic ground state and the thermally occupied quintet excited state have been employed, the fitting parameters being the enthalpy and entropy gaps between the spin states: a global fit to 1H temperature series, individual proton fits to 1H temperature series, and global fit to all 1H, 13C, 11B and 14N experimental data.
Expanding the CASSCF active space from five to twelve active orbitals in the g-tensor and ZFS calculations has little effect on the NMR shieldings of the [Tp2Fe]+ and Tp2Fe systems due to the relatively small range of variation of the g-tensor components and the negligible impact of the ZFS at ambient temperatures. This does not appear to be a promising way to improve the accuracy of paramagnetic NMR calculations except in some special cases.
Comparison between C-PCM and explicit solvent calculations for [Tp2Fe]+ reveals that the continuum solvation model is not sufficient to account for the important solvent effects in this system. Non-electrostatic effects that cannot be reproduced by continuum solvation evidently play a significant role. In accurate calculations accounting for solvent contributions, a more complex model is therefore needed.
A major issue with using DFT in the computation of hyperfine couplings is the resulting wide range of NMR shifts with different proportions of exact exchange. Even though it is possible to tune the exact exchange to improve computational results for certain nuclei or systems, no theoretical argument can be made for why, e.g., 25% should be preferred over 40%. The ab initio DLPNO-CCSD method was explored as a possible alternative, and the results seem promising, overall producing shifts comparable with DFT, albeit with significantly greater demands on computational resources.
The disagreement between theoretical and experimental 13C NMR shifts of the [Tp2Fe]+ system encountered previously18 has been reviewed in the present work. The assignment of measured signal shifts appears to be the most likely cause despite the lack of support by linewidth data. However, the theoretical results are not fully satisfactory even with re-assignment and consideration of explicit solvation or counterion effects. Still, the fact that both DFT and DLPNO-CCSD calculations support re-assignment strengthens this point of view. A low-lying excited state is another candidate, which was tentatively supported by earlier rough calculations. We could not verify this in the present slightly more advanced, but still very approximate calculations of the contributions of the excited multiplet. There is currently no practical way to reliably compute the excited-state contributions.
With the spin-crossover system Tp2Fe, of note is the observation that the paramagnetic quintet state alone cannot reproduce a qualitatively correct temperature behavior of the NMR chemical shifts – the singlet state occupation must be taken into account to obtain reasonable results at the lower end of the temperature range, including room temperature. All three fitting techniques used produce results qualitatively in line with signal shift measurements, although which data is used in the fitting procedure results in better or worse compatibility with experiment for different groups of nuclei.
Author contributions
A. Pyykkönen was responsible for data curation, general investigation, visualisation of methods and results, and writing of the original draft; J. Vaara supervised the entire work. Both authors contributed together to conceptualisation of the project and reviewing/editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. Dr Frank H. Köhler (Munich) for useful discussions and comments. We are also thankful for the suggestions of one of the anonymous reviewers of the first submitted version of this paper. This work was funded by the Academy of Finland (project no. 331008), the University of Oulu (Kvantum Institute) and the Finnish Cultural Foundation. Computational resources were provided by the CSC – IT Center for Science (Espoo, Finland) and the Finnish Grid and Cloud Infrastructure project (persistent identifier urn:nbn:fi:research-infras-2016072533).Notes and references
- I. Bertini, C. Luchinat and G. Parigi, Solution NMR of Paramagnetic Molecules, Elsevier, Amsterdam, 2001 Search PubMed.
- C. P. Grey and N. Dupré, Chem. Rev., 2004, 104, 4493–4512 CrossRef.
- M. Kaupp and F. H. Köhler, Coord. Chem. Rev., 2009, 253, 2376–2386 CrossRef.
- P. H. Keizers and M. Ubbink, Prog. Nucl. Magn. Reson. Spectrosc., 2011, 58, 88–96 CrossRef.
- A. J. Pell, G. Pintacuda and C. P. Grey, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271 CrossRef.
- M. Kaupp, M. Bühl and V. G. Malkin, Calculation of NMR and EPR Parameters: Theory and Applications, Wiley-VCH, Weinheim, 2004 Search PubMed.
- A. B. A. Andersen, A. Pyykkönen, H. J. Aa. Jensen, V. McKee, J. Vaara and U. G. Nielsen, Phys. Chem. Chem. Phys., 2020, 22, 8048–8059 RSC.
- S. A. Rouf, V. B. Jakobsen, J. Mareš, N. D. Jensen, C. J. McKenzie, J. Vaara and U. G. Nielsen, Solid State Nucl. Magn. Reson., 2017, 87, 29–37 CrossRef PubMed.
- R. J. Kurland and B. R. McGarvey, J. Magn. Reson., 1970, 2, 286–301 Search PubMed.
- W. Van den Heuvel and A. Soncini, J. Chem. Phys., 2013, 138, 054113 CrossRef PubMed.
- B. Martin and J. Autschbach, J. Chem. Phys., 2015, 142, 054108 CrossRef PubMed.
- J. Vaara, S. A. Rouf and J. Mareš, J. Chem. Theory Comput., 2015, 11, 4840–4849 CrossRef.
- Metal Ions in Biological Systems, ed. H. Sigel, Dekker, Basel, 1982, vol. 14 Search PubMed.
- D. Lopez-Tejedor, R. Benavente and J. M. Palomo, Catal. Sci. Technol., 2018, 8, 1754–1776 RSC.
- A. Mondal and M. Kaupp, J. Phys. Chem. C, 2019, 123, 8387–8405 CrossRef.
- A. Mondal and M. Kaupp, J. Phys. Chem. Lett., 2018, 9, 1480–1484 CrossRef.
- B. Martin and J. Autschbach, Phys. Chem. Chem. Phys., 2016, 18, 21051–21068 RSC.
- A. Pyykkönen, R. Feher, F. H. Köhler and J. Vaara, Inorg. Chem., 2020, 59, 9294–9307 CrossRef.
- R. Feher, Dissertation, Technische Universität München, 1996.
- P. Gütlich and H. Goodwin, in Spin Crossover in Transition Metal Compounds I, ed. P. Gütlich and H. A. Goodwin, Springer-Verlag Berlin, Heidelberger Platz 3, D 14197 Berlin, Germany, 2004, vol. 233 of Topics in Current Chemistry-Series, pp. 1–47 Search PubMed.
- L. Cambi and L. Szegö, Ber. Dtsch. Chem. Ges. (A and B Series), 1931, 64, 2591–2598 CrossRef.
- J.-F. Létard, P. Guionneau and L. Goux-Capes, Towards Spin Crossover Applications, Spin Crossover in Transition Metal Compounds III. Topics in Current Chemistry, Springer, Berlin, Heidelberg, 2004, vol. 235 Search PubMed.
- K. S. Kumar and M. Ruben, Angew. Chem., Int. Ed., 2021, 60, 7502–7521 CrossRef.
- M. Drosou, C. A. Mitsopoulou and D. A. Pantazis, Polyhedron, 2021, 208, 115399 CrossRef.
- B. M. Flöser, Y. Guo, C. Riplinger, F. Tuczek and F. Neese, J. Chem. Theory Comput., 2020, 16, 2224–2235 CrossRef PubMed.
- J. P. Jesson, S. Trofimenko and D. R. Eaton, J. Am. Chem. Soc., 1967, 89, 3158–3164 CrossRef CAS.
- J. P. Jesson, J. F. Weiher and S. Trofimenko, J. Chem. Phys., 1968, 48, 2058–2066 CrossRef CAS.
- B. Hutchinson, L. Daniels, E. Henderson, P. Neill, G. J. Long and L. W. Becker, J. Chem. Soc., Chem. Commun., 1979, 1003–1004 RSC.
- F. Grandjean, G. J. Long, B. B. Hutchinson, L. Ohlhausen, P. Neill and J. D. Holcomb, Inorg. Chem., 1989, 28, 4406–4414 CrossRef.
- L. Salmon, G. Molnár, S. Cobo, P. Oulié, M. Etienne, T. Mahfoud, P. Demont, A. Eguchi, H. Watanabe, K. Tanaka and A. Bousseksou, New J. Chem., 2009, 33, 1283–1289 RSC.
- A. A. Pavlov, G. L. Denisov, M. A. Kiskin, Y. V. Nelyubina and V. V. Novikov, Inorg. Chem., 2017, 56, 14759–14762 CrossRef PubMed.
- F. Milocco, F. de Vries, I. M. A. Bartels, R. W. A. Havenith, J. Cirera, S. Demeshko, F. Meyer and E. Otten, J. Am. Chem. Soc., 2020, 142, 20170–20181 CrossRef PubMed.
- J. Huang, R. Xie, Y. Hu, S. Lei and Q. Li, Chem. Phys. Lett., 2020, 758, 137925 CrossRef.
- J. Villalva, A. Develioglu, N. Montenegro, R. Sánchez-de Armas, A. Gamonal, M. Gaarcia, M. Ruiz-González, J. S. Costa, C. Calzado, E. Pérez and E. Burzuri, Nat. Commun., 2021, 12, 1578 CrossRef PubMed.
- S. K. Karuppannan, A. Martín-Rodríguez, E. Ruiz, P. Harding, D. J. Harding, X. Yu, A. Tadich, B. Cowie, D. Qi and C. A. Nijhuis, Chem. Sci., 2021, 12, 2381–2388 RSC.
- H. Zhang, C. Niu, J. Zhang, L. Zou, Z. Zeng and X. Wang, Phys. Chem. Chem. Phys., 2021, 23, 9679–9685 RSC.
- Z. Ke, L. E. Jamieson, D. M. Dawson, S. E. Ashbrook and M. Bühl, Solid State Nucl. Magn. Reson., 2019, 101, 31–37 CrossRef CAS PubMed.
- Z. Ke, D. M. Dawson, S. E. Ashbrook and M. Bühl, Origin of temperature dependence of 13C pNMR shifts for copper paddlewheel metal-organic frameworks, 2021, poster, Center for Magnetic Resonance Day, University of St. Andrews, Scotland, June 3rd (2021) Search PubMed.
- W. Van den Heuvel and A. Soncini, Phys. Rev. Lett., 2012, 109, 073001 CrossRef.
- F. Gendron, K. Sharkas and J. Autschbach, J. Phys. Chem. Lett., 2015, 6, 2183–2188 CrossRef CAS PubMed.
- F. Gendron and J. Autschbach, J. Chem. Theory Comput., 2016, 12, 5309–5321 CrossRef CAS PubMed.
- TURBOMOLE V7.2 2017, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS.
- J. M. L. Martin and A. Sundermann, J. Chem. Phys., 2001, 114, 3408–3420 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. A. Rouf, J. Mareš and J. Vaara, J. Chem. Theory Comput., 2015, 11, 1683–1691 CrossRef CAS PubMed.
- S. A. Rouf, J. Mareš and J. Vaara, J. Chem. Theory Comput., 2017, 13, 3731–3745 CrossRef CAS.
- B. Roos, Chem. Phys. Lett., 1972, 15, 153–159 CrossRef.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 CAS.
- B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748 CrossRef CAS PubMed.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2006, 125, 024103 CrossRef PubMed.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2013, 138, 104113 CrossRef.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- E. Malkin, M. Repiský, S. Komorovský, P. Mach, O. L. Malkina and V. G. Malkin, J. Chem. Phys., 2011, 134, 044111 CrossRef.
- S. Gohr, P. Hrobárik, M. Repiský, S. Komorovský, K. Ruud and M. Kaupp, J. Phys. Chem. A, 2015, 119, 12892–12905 CrossRef.
- ReSpect, version 5.1.0 Relativistic Spectroscopy DFT program of authors M. Repisky, S. Komorovsky, V. G. Malkin, O. L. Malkina, M. Kaupp, K. Ruud, with contributions from R. Bast, U. Ekstrom, M. Kadek, S. Knecht, L. Konecny, E. Malkin, I. Malkin-Ondik, 2019, (see http://www.respectprogram.org).
- K. G. Dyall and A. S. P. Gomes, unpublished, Available from the Dirac web site, http://dirac.chem.sdu.dk/basisarchives/dyall/.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2019 Search PubMed.
- J. Novotný, M. Sojka, S. Komorovsky, N. Marek and R. Marek, J. Am. Chem. Soc., 2016, 138, 8432–8445 CrossRef.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- A. Jaworski and N. Hedin, Phys. Chem. Chem. Phys., 2022, 24, 15230–15244 RSC.
- B. Pritchard and J. Autschbach, Inorg. Chem., 2012, 51, 8340–8351 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Science, 2008, 321, 792–794 CrossRef CAS.
- C. J. Schattenberg, T. M. Maier and M. Kaupp, J. Chem. Theory Comput., 2018, 14, 5653–5672 CrossRef CAS.
- L. Benda, J. Mareš, E. Ravera, G. Parigi, C. Luchinat, M. Kaupp and J. Vaara, Angew. Chem., Int. Ed., 2016, 55, 14713–14717 CrossRef CAS.
- L. Lang, E. Ravera, G. Parigi, C. Luchinat and F. Neese, J. Phys. Chem. Lett., 2020, 11, 8735–8744 CrossRef CAS PubMed.
- G. Privault, J.-Y. Mevellec, M. Lorenc, B. Humbert, E. Janod, N. Daro, G. Chastanet, A. Subedi and E. Collet, Cryst. Growth Des., 2022, 22, 5100–5109 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03721a |
| This journal is © the Owner Societies 2023 |