Simulation of solid-state phase transition in DL-methionine

Abstract

Solid-to-solid polymorphic transitions are a common phenomenon in organic crystals. The different interactions that play a role in these transitions are however far from understood. In this computational study, we aim to quantify the interactions that play a role in these transitions using the α ↔ β phase transition of DL-methionine as a model system. DL-Methionine has a layered structure and its phase transition occurs via shifting of the bilayers parallel to the b and c lattice vectors and the rotation of the side chains, which mostly affects the layers along the c lattice vector. We obtained two “order parameters” to describe the changes along b and c, respectively and that can be used to quantify the phase transition in terms of its thermodynamic parameters. The potential energy landscape is an interplay between van der Waals energy and configurational energy, where α is stabilized by configurational energy and destabilized by van der Waals energy as compared to β. The entropic contribution to the free energy difference between α and β is found to be in good agreement with experiments and completely dominated by configurational entropy.

---

1 Introduction

Materials are often produced in their crystalline form for many different industries including the production of pharmaceuticals, dyes, pigments, food, and explosives.^1–4 Many molecular materials show polymorphism, which is the ability of a substance to exist in more than one crystalline structure. This is typically undesired since polymorphic forms of the same compound can differ in physical, thermodynamic, spectroscopic, kinetic, surface, mechanical, and chemical properties.⁵ Moreover, for the stability of the production process, compounds with only one easily accessible polymorphic form are favored.

Different polymorphic forms can appear through recrystallization and through a solid-to-solid transition between two forms. The latter can be triggered by changes in physical conditions and is the topic of the current paper. Here, we study the racemic amino acid methionine. DL-Methionine (DL-MET) has two polymorphic forms of which the crystal structures are resolved: α and β,⁶ which have an enantiotropic relation. In an enantiotropic system, the free energy curves of the two polymorphic forms cross at a temperature below the melting temperature and transitions between the two polymorphs occur reversibly.⁷ The structural difference between the two forms involves both a packing difference as well as a difference in the torsional angle of the aliphatic tail as indicated in Fig. 1. In general, the phase transitions are classified as first order if the first derivatives of the free energy (volume, enthalpy, and entropy) are discontinuous and second-order if the discontinuity starts from second derivatives.⁸ Within this classification, the second-order phase transitions occur at infinite length scales. Because of this Mnyukh strongly refused the existence of second-order phase transitions. He stated that all solid-state phase transitions are first-order and proceed via a nucleation-and-growth mechanism in a molecule-by-molecule fashion.⁹ However, Mnyukh's theory fails to explain more complex phenomena in molecular crystals such as a cooperative mechanism that creates a first nucleus, and the transition occurs in a more ‘zip’-like fashion.¹⁰

Fig. 1 The phase transition between α and β polymorphs. The shifts are displayed in (a, b) and (a, c) projections, and the torsional rotations are most visible in the (a, c) projection. L-MET is indicated in blue (absolute configuration S) and D-MET is in pink.

The cooperative transitions characterize salient materials or the so-called “jumping crystals”. In such systems, molecular motions are induced by stimuli such as a temperature gradient, magnetic field, and mechanical force.^11–13 Jumping crystals convert the external perturbations to mechanical force, accompanied by instantaneous changes in the unit cell parameters.¹¹ These crystals have potential applications in fabricating actuators, sensors, motors, biomimetic materials, and memory devices.^13–20 Although the mechanism behind the thermosalient and mechanosalient phenomenon is not fully understood, its application is gradually increasing.

The study of solid-state phase transition in racemates of aliphatic amino acids is interesting in this context. These amphiphilic molecules all show very similar crystal packings,^21–26 where the polar heads form strong two-dimensional (2D) bilayers, which weakly interact with each other through van der Waals interactions between the aliphatic chains. They exhibit enantiotropic phase transitions by relative shifts of the bilayers, sometimes accompanied by conformational changes in the side chains. In a previous experimental study, we showed that phase transitions in racemic aliphatic amino acid crystals that involve only shifts likely proceed through a cooperative mechanism. Instead, the transitions that involve a large conformational change have a more-traditional nucleation-and-growth mechanism.²⁷DL-2-Amino-4-(methylthio)butanoic acid (DL-methionine, DL-MET) is of an intermediate type: the transition involves shifts in two directions and the conformational change is at the last torsion, which is only a minor conformational change. On the mechanism of the phase transition in DL-MET, a study by Shi et al.²⁸ shows that different pathways are possible depending on the density of the defect sites. The samples with no or low density of defects follow a one-step cooperative pathway. In this case, the bilayers displace within the van der Waals interconnections while the hydrogen bonds stay intact. The other mechanism occurs in crystals with a high density of defect sites. Initially, a large fraction of the crystal transforms via the first cooperative mechanism. The remaining part continues via a nucleation-and-growth mechanism through breakage and reformation of the hydrogen bonds at defect sites. The focus of the present paper is on the first mechanism or the phase transition in a crystal without defects.

Computational studies complement our empirical understanding of the properties of polymorphs and the polymorphic phase transitions in planar crystals. In the literature, there are interesting examples of both types such as designing a virtual tensile test to predict the mechanical properties of 4-bromophenyl 4-bromobenzoate polymorphs²⁹ and studying the impact of heat-induced polymorphic transformation on the sensitivity, energy, and safety characteristics of FOX-7 as an energetic material.³⁰ In this research, we aim to understand the mechanism of the phase transition in DL-MET using computer simulations. So far, the phase transitions studied in amino acids proceed via either conformational or packing transformations,^31,32 whereas, both types are involved in the DL-MET phase transition. Computer simulations can reveal unique details about the phase transition mechanisms. However, it is often impossible to directly simulate the phase transition using molecular dynamics (MD) simulations, due to the gap between experimental and simulation timescales. Many enhanced sampling methods have been developed to resolve the sampling and time scale problems. In this study, we benefit from the following methods. Steered molecular dynamics (SMD),^33–35 path-metadynamics (path-MTD),³⁶ and umbrella sampling.^37,38 All these methods facilitate the dynamics of the system and bias it to visit new states. Furthermore, the path-MTD and umbrella sampling methods enable us to calculate the free energy of the system with respect to its reaction coordinates and therefore to obtain the free energy landscape.

2 Collective variables that describe the structures of α and β-DL-methionine

The first attempt to describe polymorphism in DL-MET was performed by Mathieson in 1952.⁶ In subsequent studies, the α-DL-MET, β-DL-MET polymorphs, and their phase transition were studied at various temperatures. According to some literature references, also a γ-DL-MET polymorph exists.^39–43 However, observations made by Smets et al. did not suggest this.⁴⁴ In particular, they obtained the γ form with the C2 symmetry and compared it with the low-temperature β form with the C2/c symmetry, which did not indicate any difference in the conformational and molecular arrangement. The present paper will focus on the β to α phase transition. This transition is found to occur upon heating. The onset temperature for this process is at 324 to 325 K and the transition is complete at 373 K. However, the α to β transition is not fully reversible, as only 75% of the sample transforms to β during cooling (from 293 K to 138 K).

Table 1 gives the crystallographic unit cell information of both forms. On the right-hand side, α is shown in the P2₁/a setting and β in the I2/a setting to allow for easy comparison between the two forms. The most prominent change is seen in the monoclinic angle, which increases by 4.1% for the α → β transition.

Table 1 The lattice parameters of α-DL-MET and β-DL-MET in two different settings for each polymorphic form⁴⁴

Polymorph	α-Form	β-Form	α-Form	β-Form
Temperature (K)	340	320	340	320
Space group	P21/c	C2/c	P21/a	I2/a
a (Å)	16.811	31.774	9.886	9.8939
b (Å)	4.7281	4.6969	4.7281	4.6969
c (Å)	9.886	9.8939	16.811	33.0764
β (°)	101.951	91.224	101.951	106.177
Z/Z′	4/1	8/1	4/1	8/1

---

Simulation methods that enhance the dynamics by applying a bias potential require that the phase transition is described by so-called collective variables (CVs). These CVs indicate the similarity of a given structure, defined by its (x, y, z)-coordinates and the size and shape of the simulation box, to the two reference structures, in this case, the α and β polymorphic forms. Ideally, the CVs reflect the reaction coordinates for the phase transition.

Fig. 1 shows two different projections for both forms. The molecules in the center are colored to indicate their chirality pattern. The packing transformations occur through shifts in the plane of the bilayers. These shifts occur parallel to the b and c lattice vectors, between the bilayers with the hydrophobic interactions. The molecules inside a bilayer are arranged with alternating patterns of D and L enantiomers. During the α → β transition, the chirality pattern between the bilayers changes in both the (a, b) and the (a, c) planes. As is indicated by the color coding in Fig. 1, molecules with different handiness face each other in the (a, b) plane for the α form. This changes to D facing D and L facing L for the β form. The reverse occurs in the (a, c) plane ((D–D and L–L) changes to (D–L)). The conformational transformations occur via the rotation of the C–C–S–C torsions. This dihedral change is most visible in the (a, c) projection.

Our simulation cells have two replications in a direction, which gives two bilayers. Including more bilayers will always lead to more CVs and is further, not straightforward since shifts in one bilayer will affect its neighboring two-bilayer positioning. With the current setup, this is only one bilayer (and its periodic image). As well, the restriction in the multiplicity of the transition paths is mainly influenced by the number of bilayers and the continuous shifting of bilayers through alternative α and β states. We have already reduced the number of these alternative pathways by including two bilayers in the simulation cell and simulating the phase transition between the polymorphic states reached via the minimum shifting along “b” and “c” vectors. In total, we have six CVs describing this system. Two, d¹_b and d²_b, account for the shifts in the two bilayers along b, similarly, two, d¹_c and d²_c, describe the shifts along c, and finally, two, t_α and t_β, that give the fraction of molecules in either the α or β dihedral configuration. Since a full six-dimensional space is too large to explore, we have further combined these six CVs into two CVs: one for the (a, b) projection, d_b, which describes the shift of the bilayers along b, and one for the (a, c) projection, s that includes both shifts along c and a dihedral angle change. For both CVs, the equilibrium value for α is near 0 and near 1 for β. We refer to the ESI† section S1 for a detailed explanation of the construction of the initial six CVs and the further reduction into d_b and s.

3 Computational methods

3.1 Force field

The crystallographic information file (CIF) of DL-methionine is obtained for α-DL-MET, in the P2₁/c setting. The β state is always obtained from the simulated phase transition. Thus the lattice parameters of both polymorphs are directly comparable. For the experimental structures, the same comparison is made using P2₁/a and I2/a settings in Table 1. The simulation box contains 2 × 8 × 4 replicas of the α-DL-MET unit cell. Periodic boundary conditions are applied in all directions. The MD simulations are performed with the LAMMPS⁴⁵ package and the collective variable calculations and the additional bias is performed by the PLUMED^36,46–49 interfaced with LAMMPS. The simulation results are visualized by the VMD program.^50–57 The Antechamber package is used to generate the Amberff15ipq force field parameters and charges for DL-MET.^58–61 The long-range interactions are calculated using Ewald summation with a relative accuracy of 10⁻⁶.⁶² The Lennard-Jones interactions are calculated with a cutoff value of 10 A. The time integration is performed using the Nose–Hoover method in the isothermal–isobaric (NPT) ensemble.⁶³ Thermostat and barostat parameters are set to 40 and 400 fs, respectively. The α and β structures are thermalized in two steps. First, we carry out a 50 ps simulation with an increasing temperature from 100 K to a target temperature of 250 K or 300 K to release any initial potential energy of the system starting from the experimental structure. Then in a second step, the system is further equilibrated at the target temperature for 100 ps. The simulation cell is allowed to fully relax and no symmetry constraints are imposed on the system.

Fig. 2 plots the vibrational density of states at 250 K for the α and β forms in the thick blue and orange lines, respectively. These are obtained from the mass-weighted velocity-autocorrelation functions. The thin lines of the same colors give the Raman spectra of both forms and are reproduced from ref. 64. The agreement between the calculated vibrational density of states and the experimental spectrum in terms of peak position indicates the accuracy of the force field. The calculations do not include activities of the vibrational states to obtain a proper Raman spectrum and the vibrational density of states both including Raman and infrared active modes. Overall, there is a good agreement between the calculated spectra and the experimental spectra which gives confidence in the force field that is used. Especially, since this force field is not optimized to reproduce spectra. There are three areas with a marked difference between the calculated spectra and the Raman spectra. At low frequencies, the calculated spectra have several features between 200 and 400 cm⁻¹ whereas these are at much lower intensities in the Raman. Infrared spectra, shown in dotted lines, do however show intensities at these frequencies. Please notice that although the infrared spectra have been recorded in absorption, we have plotted them here as a positive feature for easy comparison. Other differences appear around 1600–1800⁻¹ and above 3200 cm⁻¹. These features are all attributed to vibrations in either the amino- or the acid group. Especially the features above 3200 cm⁻¹ can be attributed to an incomplete description of the hydrogen bond. Indeed, the Amberff15ipq force field is known to have problems with the zwitterionic character. However, we do not think this is a problem, since the hydrogen-bonded layer remains unaffected during the transition and is rather far away “from the action”. Indeed, some of the experimentally observed differences between the α and β spectra are reproduced by calculations: (i) the weakening of the feature around 280 cm⁻¹ and the increase of a feature around 200 cm⁻¹, which are both assigned to torsion involving S and a neighboring C atom, (ii) the shift from 710 to 720 cm⁻¹ of the S–C stretch mode, and (iii) the changes in the large bands around 1000–1100 cm⁻¹ due to different CH_x groups, which change environments upon dihedral changes.

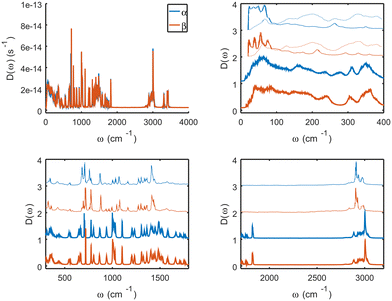Fig. 2 Mass-weighted vibrational density of states for the α and β form calculated at 250 K. This is compared to Raman spectra of thin lines and infrared spectra for the low frequencies in dotted lines. The experimental spectra are reproduced from https://doi.org/10.1002/bbpc.19860900520.

3.2 Steered molecular dynamics

Once the system is properly equilibrated, an external force is applied to the system via d_b and s to enforce the phase transition. In SMD, a moving restraint is added to each CV (d_b and s) that forces the system to gradually change its value from in the α state (often 0) to its value in the β state (often 1).^33–35 Here, we mainly used these SMD simulations to confirm that the CVs correctly describe the phase transition and to determine their interdependence. Both the force constant κ of the bias and the transition time were varied. The interdependence is tested by changing the order by which the CVs are forced to change. In several instances, a second CV is observed to change upon steering another CV and vice versa. In this way, d_b was found to change rather independently from d_c and the CVs describing the torsional changes, whereas the latter two are clearly inter dependable, we come back to the dependence of the CVs at a later point. This can be explained since changes in d_b can be mostly observed in the (a, b) projection, whereas the d_c and the torsional changes are most visible in (a, c). Because of this interdependence, shifts d_c1 and d_c2 and torsional fractions t_α and t_β are combined into one path CV.

3.3 2D umbrella sampling simulations

A 2D free energy surface of the transition is obtained by umbrella sampling.^37,38 The idea behind umbrella sampling is to run a series of MD simulations in which a known harmonic bias is added, which forces the system to sample around a particular point along the transition path. Different points are chosen, referred to as different windows and finally, the histograms of the individual runs are combined to compute the free energy curve of the transition using the weighted histogram analysis method. Here both d_b and s are varied independently, yielding a 2D free energy surface. Harmonic potentials with κ = 1000 kcal mol⁻¹ for d_b and 6000 kcal mol⁻¹ for s are used. We observed that the simulation cell gets easily disrupted when it is quickly forced to go to the required value of d_b and s. At the beginning of each window, the system is first equilibrated at this location with restraints on the inner torsions and on z, the deviation from the path CV. After an initial equilibration of 100 ps, these constraints are released and only the window constraints on d_b and s remain and the sampling starts. The inner torsions and z typically remain close to the restrained value and the crystal structure appears to remain intact during the transition. If these restraints are not enforced during the window equilibration part, the strong initial bias force from the harmonic restraints distorts the structure and the final free energy profile shows strong hysteresis with much higher barriers. The simulations start with the equilibrated α structure as described above. The windows are sampled starting from d_b = 0 and s = −0.05 and incrementing s by 0.1 until s = 1.05 is reached. Next, s is further sampled in a reverse direction (s = 1.0 to s = 0.0 with increment −0.1). This procedure is repeated for d_b = 0.1 until d_b = 1.0 is reached.

3.4 Generation of the path collective variable

The final umbrella sampling runs are performed on a converged path CV, PCV, which contains d¹_c, d²_c, t_α, and t_β. The progress along the path is measured by s. The values of d¹_c, d²_c, t_α, and t_β at s = 0 are 0.0, 0.0, 0.5, and 0.1 respectively. At s = 1, they are 0.5, −0.5, 0.1, and 0.5, respectively. The path is initially estimated as a linear change in all four CVs with s. This is however allowed to change as the simulations progress. For this, we run the umbrella sampling routine as described above twice: once where the PCV is allowed to change and the second time with a fixed path. In the first iteration, the final estimate of the path in the previous simulation is used as input for the subsequent simulation. The sampled points in this iteration are only used to converge the PCV and not for estimating the free energy. Only the sampled points in the second iteration are used for the weighted histogram method to obtain a 2D free energy surface and other 2D surfaces.

3.5 Weighted histogram analysis method

The free energy is calculated using the weighted histogram analysis method (WHAM).⁶⁵ In our setting, we use 2D-WHAM, which employs self-consistent equationsandto obtain the unbiased probability (〈ρ(ξ₁, ξ₂)〉) per bin, and the free energy constants (F_i), which correct the free energy difference between successive windows. The n_i〈ρ(ξ₁, ξ₂)〉_(i) is the number of times each bin is sampled and n_j is the number of times each window is sampled. The ω_j(ξ₁, ξ₂) is the bias energy that the sampled conformation feels in its own bin and window. The 〈ρ(ξ₁, ξ₂)〉 obtained after self-consistency is converted to free energy using

E = −k_BT log(〈ρ(ξ₁, ξ₂)〉). (3)

By having F_i we can now calculate the time series of any properties (T_i,j) of the system viaThe δX_i,j is 1 for the points corresponding to the bins , and 0 otherwise.⁶⁶

4 Results and discussion

4.1 Energy and free energy contributions to the transition

Fig. 3 shows the free energy surface and several energy surfaces as a function of collective variables s and d_b at 250 K. The free energy is directly obtained from the 2D-WHAM method, whereas the total potential energy and the potential energy contributions are obtained by applying eqn (4). The energies shown in Fig. 3 are per unit cell. The white areas appearing on the edges are not sampled because of their high free energy and are skipped since they are out of the transition path. The free energy surface clearly shows two minima: one at (s, d_b) = (0.2, 0) and one around (s, d_b) = (1, 1). The first corresponds to the α phase and the latter to the β phase. The minimum of the α phase is not at s = 0, which would correspond to a fully ordered system with all molecules in the dominant α torsional angle, but rather at a slightly elevated s. Visual inspection of the structure at this point shows that a small fraction of the C–C–S–C torsions is in the β conformation and s = 0.2 hence corresponding to a disordered structure. The minimum of the β phase is at s = 1, which corresponds to a fully ordered structure. Indeed experimental X-ray studies show that the α form has a slight disorder of 5% at 340 K whereas β does not.^67,68 In Fig. 5 for the structures at s = 0.2, a disorder of 4% on average is found in one bilayer whereas the other bilayer has 50% of both orientations. For both layers, a dynamic disorder is found where individual molecules change conformations in time. In one layer the experimental disorder is very well reproduced, whereas in the other it is not. This might be due to the limited system size of two bilayers where transitions in one bilayer might constrain transitions in the other bilayer. Both minima are very similar in terms of free energy. At this temperature, the β form should be more stable, but a difference in free energy cannot be observed within the energy resolution of the method.

Fig. 3 Free energy (FE) surface and potential energy surfaces as a function of the CVs s and d_b at T = 250 K. Several contributions to the total potential energy (E_PE) are shown: van der Waals energy (E_VdW), dihedral energy (E_dih), and Coulomb energy (E_Coul). Energies are in kcal mol⁻¹, divided by the number of unit cells in the simulation cell (Z = 4). The minimum energy routes are specified on the FE surface. The white areas appearing on the edges are not sampled because of their high free energy and they disappear at higher temperatures in Fig. 4b and c.

The free energy surface further shows that the system cannot move completely independently in both directions: shifts in the layers along b result in the destabilization of the system unless also changes occur in the perpendicular direction. The opposite is also true. In general two transition paths can be envisioned, as we have indicated in Fig. 3FE to guide the eye, each with a barrier of roughly 4 kcal mol⁻¹, which avoids the higher barrier region around (0.7, 0.5). For each path, the part along d_b is more even with lower barriers compared to the changes along s. The graphs show the system can change d_b and s independently for a limited range, following either of two pathways. This is to avoid the high free energy regions around (0, 1) and (1, 0). The completely independent movement would have resulted in intermediate states at these locations. Variable s has a highly reduced dimensionality since it depends on both the torsions and shifts along c. The main concern about the reduction of CVs is an erroneous estimate of free energy if the applied CVs do not correctly describe the order parameters for the phase transition. If this is the case, it will appear as a hysteresis effect as a function of the CV. For this reason, we have sampled the 2D free energy surface both by increasing and decreasing s. Inspection of d¹_c, d²_c, t_α, and t_β as a function of s shows a rather smooth transition for all CVs, that is equal in both directions and at all values of d_b. We are hence confident that the description of our system by only the variables d_b and s is justified.

Our transition without defects corresponds with the first mechanism in ref. 28. They experimentally found a barrier of 366.7 kJ mol⁻¹ for unmilled samples. This can be converted to an E_b/R = 44 100 K. We find a barrier of E_b/R = 1500 K per unit cell at 350 K. This would mean that crystal parts of 30 unit cells can transform cooperatively. This is roughly half of our simulation cell size.

To gain more insight into the relatively large free energy barrier as compared to the transition free energy difference, the potential energy is calculated as a function of the collective variables s and d_b as well as different components of the potential energy. All contributions are shifted such that the lowest energy is 0 and the color gradients cover the same range in all panels for easy comparison. The potential energy graphs are not as smooth as the free energy, which is mainly due to the Coulomb interaction. The graphs show that the α polymorph is stabilized via the dihedral interactions, and to a lesser extent via the Coulomb interactions. The β form however is stabilized by the van der Waals interactions. The role of the Coulomb interaction is rather small. The β dihedral configuration is less stable than the α configuration, but this is compensated by less steric hindrance. The van der Waals surface also shows that the dihedral configuration determines to an important extent which shifting orientation along b is stable. Since s contains both shifts along c and the dihedral configuration it is less straightforward to conclude whether this is also the case for shifts along c. Table 2 gives the absolute non-bonded and dihedral energies. It shows that the Coulomb energy is dominant in an absolute sense to stabilize the two forms, although it does not contribute strongly to the energy difference as indicated in Fig. 3. The van der Waals energy has a contribution to the energy difference that is twice as large as the dihedral contribution.

Table 2 The absolute non-bonded interactions for the α (s, d_b = 0.2, 0) and β (s, d_b = 1, 1). The energies are divided by the number of the unit cells in the simulation cell (Z = 4)

Polymorph	Energies (kcal mol^−1)
	E VdW	E dih	E Coul
α	−34.0	−36.7	−65
β	−36.6	−35.4	−64.5

---

4.2 Temperature dependence

Fig. 4 shows similar 2D free energy surfaces for three different temperatures: 250, 300, and 350 K. The surface for 250 K is the same as the one plotted in Fig. 3. Let us consider the free energy at 300 K, which is close to the experimental transition temperature of 315 K.²⁷ Again no distinction can be made between the two forms in terms of free energy. Smets et al.²⁷ determined the experimental enthalpy and entropy difference between the two forms at the transition temperature. This corresponds to ΔH_trs = 0.26 ± 0.02 kcal mol⁻¹ and ΔS_trs = 0.79 ± 0.08 cal mol⁻¹ K⁻¹. This leads to Gibbs free energy differences of 0.062, 0.023, and −0.016 kcal mol⁻¹ at 250, 300, and 350 K, respectively, if we assume that the enthalpy and entropy differences do not change with temperature. The Helmholtz free energy differences are −0.019, −0.058, and −0.098 kcal mol⁻¹, respectively. Fig. 4 plots the Helmholtz free energy and we can indeed see that the method does not allow us to resolve these differences. The driving force for the transition is hence rather small compared to the barrier for the transition. Indeed experimentally a hysteresis of 18 K was observed, which is rather large.

Fig. 4 Free energy surfaces as a function of the collective variables s and d_b at a) T = 250 K, b) T = 300 K, and c) T = 350 K. A similar setup as in Fig. 3 is used.

Although the relative stability between the two forms does not significantly change with temperature, other changes can be observed. The α stable minimum shifts towards higher values of s with temperature. As mentioned earlier, this corresponds to structures with a higher fraction of disorder. The following section discusses the role of configurational entropy in more detail. Another difference that can be observed is that the stable area in CV space becomes larger with temperature. Although the free energy barrier height does not really change, its width becomes more narrow. At 300 and 350 K, the large barrier around (0.7, 0.5) has disappeared or is reduced. This allows for more transition channels at a higher temperature.

4.3 Entropy

In enantiotropic systems, like the current DL-methionine system, entropy plays a critical role, since it is typically the TΔS contribution to the free energy that is responsible for the change in the relative stability between the enantiotropic forms. Comparing the free energy and potential energy panels in Fig. 3 indicates the importance of this contribution. It appears to be rather small as the two panels are similar in scale along the transition path. This seems to contradict the previous statement that entropy is critically important in driving the transition of an enantiotropic system. However, as mentioned above, the driving force for the transition for this particular system is very small resulting in a large hysteresis of the transition. Typically, a large driving force makes the barrier strongly temperature dependent, such that the barrier toward the stable form will vanish at some point. This is both upon heating and upon cooling. The small driving force for the current system results in a very constant barrier with temperature, and a strong overheating or undercooling is required to lower the barrier.

We will consider the entropic contribution in more detail. The total entropy of a system consists of a configurational component (S_conf) and a vibrational component (S_vib). The configurational entropy arises due to the different configurations in a disordered system. As mentioned earlier, the α form is slightly disordered whereas the β form is a fully ordered form and the latter has hence no S_conf contribution. This contribution can be expressed as

S_conf = −k_B ln p. (5)

where p is the probability to be in the majority configuration (either α or β states) and hence ranges from 0.5 for a fully disordered system to 1 for a fully ordered system. This probability can be directly linked to t_α or t_β through

p = max(t_α, t_β). (6)

To obtain S_conf as a function of s, the p is calculated for all visited configurations, and the corresponding S_conf is averaged for the windows as a function of s. The results are plotted in Fig. 5 where the dotted lines indicate the s values corresponding to both forms. Fig. 5 shows that the –TΔS_conf contribution to the free energy at 250 K is −0.10 kcal mol⁻¹, in favor of the α polymorphic form due to its higher disorder. The transition goes via a disordered structure, which is favorable in terms of configurational entropy and leads to a lowering of the free energy barrier by 0.12 kcal mol⁻¹ for the α form at 250 K. This lowering of the barrier becomes more important at higher temperatures, as seen in Fig. 4. The configurational entropy component is most likely also responsible for the shift in s value of the α stable configuration with the temperature, visible in Fig. 4.

Fig. 5 Configurational entropy versus s at 250 K. The two dotted lines indicate the s values corresponding to the α and β forms.

The vibrational component to the entropy can be calculated from the mass-weighted vibrational density of states as presented in Fig. 2 following the method of Galimberti and Sauer.⁶⁹ To obtain the entropy difference between the two forms, we integrate the spectrum over the full range. This leads to an entropic contribution of −T(S_vib(α) − S_vib(β)) = −1.1 × 10⁻⁴ kcal mol⁻¹ at 250 K, which is negligible. Excluding the bands above 1650 cm⁻¹ which have a large contribution due to the hydrogen-bonded layer, only makes the effect smaller. We can hence conclude that the entropic contribution is mainly due to the configurational entropy of −0.10 kcal mol⁻¹ at 250 K. This is remarkably close to the experimentally obtained entropic contribution of −0.20 kcal mol⁻¹.

5 Discussion and conclusion

The presented molecular dynamics simulation revealed in detail the different contributions responsible for the α ↔ β phase transition in DL-MET. The enhanced sampling methods, allowed us to obtain a free energy profile that is directly linked to the atomic movement during the phase transition. The temperature-dependent stability is an interplay between steric hindrance, dihedral stabilization, and entropic effects. The transition itself is not only triggered by different thermodynamic stability between the two forms that create a driving force for the transition but is also kinetically triggered by a narrowing of the free energy barrier with temperature because of the configurational disorder during the transition. The critical barrier height is however not lowered, because the rate-limiting step is most likely the shift of the layers along the b and c crystallographic axes. Initial inspection of the structure and the transition indicated that the movement along b and along c is mainly independent. This is however only to a limited extent; the FE indicates that small shifts in either direction-of roughly half the required distance for the full transition-can be done by inducing movement in the perpendicular direction. Full shifts, however, require changes in the perpendicular direction as well, due to steric hindrance. With these different contributions in mind, we can try to understand the differences and similarities between other phase transitions in similar materials. Obvious examples are racemic aliphatic amino acids, like DL-norleucine (DL-NLE)³² and DL-heptanoic acid.⁷⁰

The α ↔ β transition in DL-norleucine (DL-NLE) involves two shifts in perpendicular directions, without configurational changes. Norleucine is very similar to methionine, where the S is replaced by a CH₂ group and the packing of DL-norleucine is very similar to the packing of DL-methionine. The configuration of DL-NLE is similar to that in the β form of DL-MET. Molecular dynamics simulations of β DL-NLE have shown that shifts along b occur spontaneously.^32,71 This corresponds to shifts along b in DL-MET. Together with the shifts along b, small shifts in the perpendicular direction are also observed. The calculations of the energy barriers for transition suggested that fluctuation plays a role in lowering the barrier. This was however without a full free energy analysis as is done in the present paper. The MD results for DL-NLE however suggest an additional intermediate free energy well around (0.8, 0.2) which is not present in DL-MET. Overall, the energies involved in the transition for DL-NLE are much smaller than for DL-MET, this is likely because the transition does not include a conformational change (ΔE_dih = 0) and because of missing sulfur interaction. For DL-MET, this intermediate well is not present at (0.8, 0.2). Looking at Fig. 3, it appears that the dihedral change during the DL-MET transition destabilizes an intermediate around (0.8, 0.2) and favors the transition to α, purely based on the dihedral energy.

DL-Heptanoic acid has an additional CH₂ group and has five different polymorphic forms.⁷⁰ In terms of structures, intermediate structures that are not stable for DL-MET are now obtained as well. Comparing the different DL-HEP and DL-MET structures, form I of DL-HEP appears to be a highly disordered α form, form II a slightly disordered β form, form III appears similar to β, and form IV has α packing in both planes but β conformation. Form V is very disordered and hence not so easily comparable to DL-MET. We have schematically placed these forms in the CV space that we have set up for DL-MET as can be seen in Fig. S2.† The four DL-HEP forms remain in the low free energy regions for DL-MET. Although no simulation data is available for this system, we can speculate that the overall less steric hindrance because of the replacement of S for CH₂–CH₂ results in weaker van der Waals interactions. On the other hand, the additional chain length allows for more configurational entropy.

Author contributions

Conceptualization: SG, HC; methodology: SG, BE, HC; software: SG, BE, HC; validation: SG, HC; formal analysis: SG, HC; investigation: SG; writing-original draft: SG, HC; visualization: SG; writing-review and editing: SG, BE, HC; supervision: BE, HC; project administration: HC; resources and data curation: SG, HC.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by Institute for Molecules and Materials (IMM), Radboud University. We would also like to thank our colleagues from the Theoretical and Computational Chemistry group at Radboud University and also from Van't Hoff Institute for Molecular Sciences at the University of Amsterdam for the useful discussions and feedback.

Notes and references

1. D. Chistyakov and G. Sergeev, Pharmaceutics, 2020, 12, 34.
2. J. Bernstein, Polymorphism in Molecular Crystals, Oxford University Press, 2007.
3. H. Hondoh and S. Ueno, Prog. Cryst. Growth Charact. Mater., 2016, 62, 398–399.
4. L. M. Luong, M. M. Olmstead and A. L. Balch, Chem. Commun., 2020, 11, 11705–11713.
5. H. Wang, Q. Pan, Q. Wu, X. Zhang, Y. Huang, A. Lushington, Q. Li and X. Sun, J. Mater. Chem. A, 2017, 5, 4576–4582.
6. A. McL Mathieson, Acta Crystallogr., 1952, 5, 332–341.
7. K. Kawakami, J. Pharm. Sci., 2007, 96, 982–989.
8. P. Ehrenfest, Proc. K. Ned. Akad. Wet., 1933, 153–157.
9. Y. Mnyukh, arXiv, 2011, preprint, arXiv:1110.1654,  DOI:10.5923/j.ajcmp.20130304.01.
10. C. Brandel, Y. Cartigny, N. Couvrat, M. E. S. Eusebio, J. Canotilho, S. Petit and G. Coquerel, Chem. Mater., 2015, 27, 6360–6373.
11. S. C. Sahoo, S. B. Sinha, M. Kiran, U. Ramamurty, A. F. Dericioglu, C. M. Reddy and P. Naumov, J. Am. Chem. Soc., 2013, 135, 13843–13850.
12. P. Naumov, S. Chizhik, M. K. Panda, N. K. Nath and E. Boldyreva, Chem. Rev., 2015, 115, 12440–12490.
13. D. P. Karothu, J. Weston, I. T. Desta and P. Naumov, J. Am. Chem. Soc., 2016, 138, 13298–13306.
14. L. Lan, L. Li, Q. Di, X. Yang, X. Liu, P. Naumov and H. Zhang, Adv. Mater., 2022, 34, 2200471.
15. Q. Di, L. Li, X. Miao, L. Lan, X. Yu, B. Liu, Y. Yi, P. Naumov and H. Zhang, Nat. Commun., 2022, 13, 5280.
16. L. Lan, X. Yang, B. Tang, X. Yu, X. Liu, L. Li, P. Naumov and H. Zhang, Angew. Chem., Int. Ed., 2022, 61, e202200196.
17. X. Yang, L. Lan, L. Li, X. Liu, P. Naumov and H. Zhang, Nat. Commun., 2022, 13, 2322.
18. R. Costil, M. Holzheimer, S. Crespi, N. A. Simeth and B. L. Feringa, Chem. Rev., 2021, 121, 13213–13237.
19. F. Tong, D. Kitagawa, I. Bushnak, R. O. Al-Kaysi and C. J. Bardeen, Angew. Chem., Int. Ed., 2021, 60, 2414–2423.
20. S. Ghosh and M. K. Mishra, Cryst. Growth Des., 2021, 21, 2566–2580.
21. C. H. Görbitz, F. Alebachew and V. Petříček, J. Phys. Chem. B, 2012, 116, 10715–10721.
22. P. Ren, D. Reichert, Q. He, L. Zhang and H. Tang, J. Phys. Chem. B, 2011, 115, 2814–2823.
23. C. H. Görbitz, J. Phys. Chem. B, 2011, 115, 2447–2453.
24. S. Coles, T. Gelbrich, U. Griesser, M. Hursthouse, M. Pitak and T. Threlfall, Cryst. Growth Des., 2009, 9, 4610–4612.
25. M. Smets, S. Brugman, E. Van Eck, J. Van Den Ende, H. Meekes and H. Cuppen, Cryst. Growth Des., 2015, 15, 5157–5167.
26. C. H. Görbitz, J. C. Paulsen and J. Borgersen, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2015, 71, o398–o399.
27. M. Smets, E. Kalkman, A. Krieger, P. Tinnemans, H. Meekes, E. Vlieg and H. Cuppen, IUCrJ, 2020, 7, 331–341.
28. G. Shi, S. Li, P. Shi, J. Gong, M. Zhang and W. Tang, IUCrJ, 2021, 8, 584–594.
29. A. E. Masunov, M. Wiratmo, A. A. Dyakov, Y. V. Matveychuk and E. V. Bartashevich, Cryst. Growth Des., 2020, 20, 6093–6100.
30. R. Bu, W. Xie and C. Zhang, J. Phys. Chem. C, 2019, 123, 16014–16022.
31. H. M. Cuppen, M. M. Smets, A. M. Krieger, J. A. van den Ende, H. Meekes, E. R. van Eck and C. H. Gorbitz, Cryst. Growth Des., 2019, 19, 1709–1719.
32. J. A. van den Ende, M. M. Smets, D. T. de Jong, S. J. Brugman, B. Ensing, P. T. Tinnemans, H. Meekes and H. M. Cuppen, Faraday Discuss., 2015, 179, 421–436.
33. H. Grubmüller, B. Heymann and P. Tavan, Science, 1996, 271, 997–999.
34. S. Izrailev, S. Stepaniants, B. Isralewitz, D. Kosztin, H. Lu, F. Molnar, W. Wriggers and K. Schulten, Computational molecular dynamics: challenges, methods, ideas, Springer, 1999, pp. 39–65.
35. J. Gore, F. Ritort and C. Bustamante, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 12564–12569.
36. G. D. Leines and B. Ensing, Phys. Rev. Lett., 2012, 109, 020601.
37. C. Bartels and M. Karplus, J. Phys. Chem. B, 1998, 102, 865–880.
38. G. Torrie and J. Valleau, J. Comput. Phys., 1977, 23, 187–199.
39. M. Matsuoka, M. Yamanobe, N. Tezuka, H. Takiyama and H. Ishii, J. Cryst. Growth, 1999, 198, 1299–1306.
40. M. Yamanobe, H. Takiyama and M. Matsuoka, J. Cryst. Growth, 2002, 237, 2221–2226.
41. M. Yamanobe-Hada, A. Ito and H. Shindo, J. Cryst. Growth, 2005, 275, e1739–e1743.
42. L. Wantha and A. E. Flood, J. Cryst. Growth, 2013, 362, 66–70.
43. L. Wantha and A. E. Flood, Chem. Eng. Technol., 2013, 36, 1313–1319.
44. M. Smets, S. Brugman, E. Van Eck, P. Tinnemans, H. Meekes and H. Cuppen, CrystEngComm, 2016, 18, 9363–9373.
45. https://lammps.sandia.gov/cite.html .
46. M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci and R. A. Broglia, et al. , Comput. Phys. Commun., 2009, 180, 1961–1972.
47. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
48. A. Pérez de Alba Ortíz, A. Tiwari, R. C. Puthenkalathil and B. Ensing, J. Chem. Phys., 2018, 149, 072320.
49. M. Bonomi, G. Bussi, C. Camilloni, G. A. Tribello, P. Banaš, A. Barducci, M. Bernetti, P. G. Bolhuis, S. Bottaro and D. Branduardi, et al. , Nat. Methods, 2019, 16, 670–673.
50. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
51. J. Stone, MSc thesis, Computer Science Department, University of Missouri-Rolla, 1998.
52. J. Stone, J. Gullingsrud, P. Grayson and K. Schulten, 2001 ACM Symposium on Interactive 3D Graphics, New York, 2001, pp. 191–194.
53. J. Eargle, D. Wright and Z. Luthey-Schulten, Bioinformatics, 2006, 22, 504–506.
54. D. Frishman and P. Argos, Proteins: Struct., Funct., Genet., 1995, 23, 566–579.
55. A. Varshney, F. P. Brooks and W. V. Wright, IEEE Comput. Graph. Appl., 1994, 14, 19–25.
56. M. Sanner, A. Olsen and J.-C. Spehner, Proceedings of the 11th ACM Symposium on Computational Geometry, New York, 1995, pp. C6–C7.
57. R. Sharma, M. Zeller, V. I. Pavlovic, T. S. Huang, Z. Lo, S. Chu, Y. Zhao, J. C. Phillips and K. Schulten, IEEE Computer Graphics and Applications, 2000, 20, 29–37.
58. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
59. C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280.
60. M. K. Gilson, H. S. Gilson and M. J. Potter, J. Chem. Inf. Comput. Sci., 2003, 43, 1982–1997.
61. K. T. Debiec, D. S. Cerutti, L. R. Baker, A. M. Gronenborn, D. A. Case and L. T. Chong, J. Chem. Theory Comput., 2016, 12, 3926–3947.
62. P. J. in't Veld, A. E. Ismail and G. S. Grest, J. Chem. Phys., 2007, 127, 144711.
63. H. A. Posch, W. G. Hoover and F. J. Vesely, Phys. Rev. A, 1986, 33, 4253.
64. A. Grunenberg and D. Bougeard, Berichte der Bunsengesellschaft für physikalische Chemie, 1986, 90, 485–492.
65. B. Roux, Comput. Phys. Commun., 1995, 91, 275–282.
66. A. Grossfield, The Weighted Histogram Analysis Method, 2003, https://dasher.wustl.edu/alan/wham_talk.pdf.
67. C. H. Görbitz, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2014, 70, 341–343.
68. C. H. Görbitz, L. Qi, N. T. K. Mai and H. Kristiansen, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2014, 70, 337–340.
69. D. R. Galimberti and J. Sauer, J. Chem. Theory Comput., 2021, 17, 5849–5862.
70. M. M. Smets, M. B. Pitak, J. Cadden, V. R. Kip, G. A. De Wijs, E. R. Van Eck, P. Tinnemans, H. Meekes, E. Vlieg and S. J. Coles, et al. , Cryst. Growth Des., 2018, 18, 242–252.
71. M. Harding, B. Kariuki, L. Williams and J. Anwar, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 1059–1062.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ce00227f

---