L-Glutamic acid crystals of pure α form and uniform size distribution from continuous non-seeded reaction crystallization in slug flow

Abstract

Desired goals of crystal synthesis include high crystal quality (e.g., pure solid forms and uniform size distribution) and high process efficiency and reproducibility. A simple reactor/crystallizer has been designed based on slug flow, for continuous generation of high-quality L-glutamic acid crystals (model compound), from solution reaction of monosodium glutamate and sulfuric acid. Multiple average crystal sizes can be consistently achieved (e.g., from 19 μm to 37 μm), while maintaining the uniformity in both α-crystalline form and the crystal size distribution, by adjusting the supersaturation (stoichiometric reactant concentrations) with proper residence time. The whole reaction/crystallization process takes less than 15 minutes at room temperature, without requiring external seeding nor mechanical stirring blades.

---

1. Introduction

Continuous crystallization from solution reaction has received increased attention from both academia and industry,^1–10 towards synthesizing crystals of good qualities (e.g., pure polymorphic form,¹¹ uniform size and shape), with high reproducibility and process efficiency. One important model compound is the amino acid L-glutamic acid (LGA),¹ with an annual global demand¹² of 4 million tons by 2023. Besides as a non-essential nutrient, LGA is used widely in protein biosynthesis, and as an excitatory neurotransmitter for the central nervous system.¹³ LGA has two conformational polymorphic forms with different typical crystal shapes (Fig. S1†), the metastable α-form of prismatic shapes,¹⁴ and the stable β-form of needle or flower shapes.¹⁵ α-Form crystals are preferred in LGA manufacturing, as their prismatic shape is easier for post-synthesis separation, powder tapping, with less water retention and gelatinization.^16,17

Much progress has been made towards manufacturing pure α-form LGA crystals (Table 1),^18–26 almost all based on gradual addition of the acid reactant (sulfuric or hydrochloric acid) to the other reactant (monosodium glutamate, MSG), in tank/flask reactors under vigorous stirring. It is not clear whether these tanks are the only feasible reactor/crystallizer configuration, and whether the semi-batch mode (e.g., reactant addition to a stirred-tank reactor over extended time)²⁷ is the only feasible operation mode. In addition, the size distribution of product LGA crystals are typically wide, even with advanced strategies, such as tuning the acid addition rate,^18,19,21,22 agitation intensity,^19,22,25 and supersaturations,^20,22–24 and applying additives¹⁹ or ultrasonication.²⁴ Similarly, wide size distributions of product crystals from stirred tank crystallizers have been demonstrated with other molecules and/or other types of crystallizations.^28–43

Table 1 Representative studies on reactive crystallization of L-glutamic acid

Main reactants and concentrations	Supersaturation S^a or ΔC as reported	Agitation speed (rpm)	Reaction time (min)	Crystal form, shape	Crystal size range (μm)	Mean size (um)	Effective factors	Ref.
a The supersaturation values (S and ΔC) listed here are as defined and/or reported in individual reference papers. For example, S = Ci/C*, ΔC = Cm − C*, where Ci is the “initial” LGA concentration, calculated from the starting/initial reactant concentrations, assuming both reactants at stoichiometry fully convert to product LGA before any crystallization occurs;^25Cm is measured concentration of LGA during reaction crystallization; and C* is the solubility of α-form (e.g., ref. 19 and 26) or β-form (e.g., ref. 15) LGA in water.
0.6 M MSG, 0.6 M HCl	N/A	250	80	α, prism	100–300	150	Rate of acid addition	18
1.2 M MSG, 0.6 M HCl			158
0.86 M MSG, 1 M H2SO4, 0.01 M L-phe	S = 2.6 (45 °C)	500	120	α, prism	N/A	232.4	Addition rate of acid, reaction temperature, agitation rate, and additive (L-phe) concentration	19
0.86 M MSG, 1 M H2SO4, 0.02 M L-phe	S = 4 (35 °C)	600				139.2
0.86 M MSG, 1 M H2SO4, 0.05 M L-phe	S = 5.3 (25 °C)	400				131.7
	S = 2.6 (45 °C)	600				196.1
0.86 M MSG, 1 M H2SO4, 0.01 M L-phe	S = 4 (35 °C)	400				230.1
0.86 M MSG, 1 M H2SO4, 0.02 M L-phe	S = 5.3 (25 °C)	500				120.9
	S = 2.6 (45 °C)	400				252.1
0.86 M MSG, 1 M H2SO4, 0.05 M L-phe	S = 4 (35 °C)	500				104.6
0.86 M MSG, 1 M H2SO4, 0.01 M L-phe	S = 5.3 (25 °C)	600				119
1.5 M MSG, 1.5 M H2SO4	ΔC = 0.3 M	167	8.5	β, flake	N/A	37.08	ΔC control based on added reagent mass	20
	ΔC = 0.5 M		4.6			34.03
	ΔC = 0.7 M		14.7			37.14
	ΔC = 0.9 M		2.5	83% β, flake		35.47
	ΔC = 1 M		26.7	99% β, flake		34.52
	ΔC = 1 M		11.3	84% β, flake		67.73
	ΔC = 1 M		4.6	63% β, flake		51.42
	ΔC = 1.1 M		5	39% β, flake		74.88
0.75 M MSG, 1.5 M HCl	S = 8	250	43	α, prism	0–500	240	Acid choice and acid addition rate	21
		500			0–275	125
		250	21	α/trace β, prism	0–600	240
		500		α, prism	0–300	125
0.75 M MSG, 0.75 M H2SO4		250	43	α, prism	0–500	210
		500			0–300	125
		250	21	α, prism	0–600	210
		500			0–300	125
0.75 M MSG, 0.75 M H2SO4	ΔC = 0.3 M	250	40	α prism	0–700	312	Reactant concentration, mixing, and feeding positions	22
		500			0–500	185
0.75 M MSG, 0.75 M H2SO4	ΔC = 0.35 M	250	40	α, prism	0–600	303
	ΔC = 0.3 M	500			0–400	197
1.5 M MSG (25 °C), 1.5 M H2SO4, (10 °C)	ΔC = 1 M	—	23	α, prism	0.5–100	62	Ultrasound and ΔC	24
			23	α, prism	0.5–100	55	Ultrasound and ΔC
	ΔC = 0.7 M		33	95% β, flake	0.5–100	49	Seeding and ΔC
1.5 M MSG (25 °C),1.5 M H2SO4 (10 °C)	S = 17.1 (ΔC = 0.9 M)	—	28	25% α, prism	NA	NA	Supersaturation control	23
	S = 18.9 (ΔC = 1 M)		21	43% α, prism
	S = 20.6 (ΔC = 1.1 M)		30	70% α prism
MSG, H2SO4	S = 4	—	From few seconds for S = 22 to 2 hours for S = 4	α, prism	NA	NA	Mechanical stirring	25
				4% α, prism
	S = 8			α, prism
				6% α, prism
	S = 13			97% α, prism
				8% α, prism
	S = 17			96% β, spherulites
	S = 22			96% β, spherulites
0.5 M HCl, 0.5 M H2SO4	S = 1.94	250	50	100% α, prism	100–300	200	Size of seeds	26
					200–400	300
					300–600	450

---

This article evaluates a simple alternative reactor/crystallizer design based on self-mixed slug flow,^{28–31,39,40,43,46–49} instead of mechanical stirrers. The slug flow process is designed, towards continuous generation of uniformly sized pure α-form L-glutamic acid crystals, with minimal aggregation. The effect of LGA supersaturation (reactant concentrations) on the average product crystal size is also evaluated.

2. Experimental methods

2.1 Materials and chemicals

The two main reactants in eqn (1), monosodium glutamate (MSG, ≥98%) and sulfuric acid (H₂SO₄, ≥99.99%), were purchased from Sigma Aldrich. All chemicals were used as received without further treatment. All the stock solutions were prepared with deionized water.

2MSG(aq) + H₂SO₄(aq) → 2LGA(s) + Na₂SO₄(aq) (1)

2.2 Reactive crystallization in stirred-tank and slug-flow reactors

For each experiment, stock solutions for both reactants were prepared into concentrations in Table 2, with 18 mL total volume of the MSG stock solutions, and 12 mL of the acid H₂SO₄ solutions. In this way, when reactant addition is complete, the total molar ratio between the two reactants is 2 : 1 (MSG : acid), based on the stoichiometry in eqn (1).²⁵ As the two reactants mix and react, LGA is generated in solution, then gets supersaturated. The supersaturation value (S) in Table 2 is calculated²¹ as the ratio between the maximal possible solution concentration of LGA throughout the whole process and the α-form LGA solubility (9.225 g LGA per kg water at the experiment temperature 20 °C, Fig. S1a†).⁴⁴ The maximal possible LGA concentration (C_i as in Table 1) is calculated from the starting/initial reactant concentrations, assuming both reactants at stoichiometry fully convert to product LGA before any crystallization occurs.²⁵ All reactions were carried out at room temperature (20 °C), and repeated twice. Crystallization of LGA occurs from supersaturated solution, then the slurry containing crystals were immediately collected, and poured onto a Buchner funnel under vacuum for filtration. The filter for the funnel is a hydrophilic membrane filter (MF-Millipore™, 47 mm diameter) with 0.22 μm pore size. After filtration, the crystals on top of the filter were dried overnight at 50 °C, before characterization.

Table 2 Experimental conditions for room-temperature reactive crystallization of L-glutamic acid in stirred-tank reactors (semi-batch mode) or slug flow reactors

Experiment ID	MSG stock solution concentration (M)	H2SO4 stock solution concentration (M)	Supersaturation	Crystallizer configuration and mode	Reaction residence time (minute)
B1_1/2	0.47	0.35	4.5	Stirred tank – semi-batch mode (dropwise addition of reactant H2SO4)	12.3
B2_1/2	0.5	0.38	4.8		12.3
B3_1/2	0.55	0.41	5.3		12.3
B4_1/2	0.6	0.45	5.7		12.3
B5_1/2	0.7	0.53	6.7		5.4
B6_1/2	0.8	0.60	7.7		5.4
S1_1/2	0.47	0.35	4.5	Tubular slug flow – continuous mode (Fig. 1)	12.3
S2_1/2	0.5	0.38	4.8		12.3
S3_1/2	0.55	0.41	5.3		12.3
S4_1/2	0.6	0.45	5.7		12.3
S5_1/2	0.7	0.53	6.7		5.4
S6_1/2	0.8	0.60	7.7		5.4

---

For stirred-tank experiments, 18 mL of MSG stock solution was placed in a 50 ml round-bottom flask under stirring using a magnetic stirring bar at 300 rpm. Then a total volume of 12 mL acid H₂SO₄ stock solution was pipetted dropwise over ∼5 minutes into the stirred flask. The reaction residence time for tank reactors here is the time between the addition of the first acid droplet to the stirred tank/flask, and the termination of the whole experiment. And this reaction residence time can be directly adjusted by terminating experiment (slurry collection and filtration).

The slug flow reactor was designed as in Fig. 1. Filtered air and MSG stock in a syringe was transferred to a T-mixer to continuously generate stable MSG solution slugs, by a peristaltic pump at 13 ml min⁻¹ and a syringe pump at 2 ml min⁻¹ (Model# NE 4000, New Era Pump Systems), respectively. Then sulfuric acid solution in a syringe were injected at 1 ml min⁻¹ into each MSG solution slug, through a capillary tube (1/16′′ ID), by another syringe pump (Model# NE 4000, New Era Pump Systems). Downstream of the injection point, the slugs containing mixture of two reactants, with a total molar ratio of 2 : 1 (MSG : acid) based on the stoichiometry, continue to flow inside the silicone tubing (Masterflex transfer tubing, platinum-cured silicone, 1/8′′ ID × 1/4′′ OD, 3.1 mm inner diameter), while LGA gets supersaturated and crystallized. The time that each mixture slug stays in the tubular reactor/crystallizer (from injection point to exit) is the reaction residence time for slug flow, as reported in Table 2. The reaction residence time in slug flow can be directly adjusted with the tubing length. The slurry slugs can then be collected at the exit for vacuum-filtration. To generate more crystal mass for XRD analysis, the slurry slugs can be collected in a 10 mL round-bottom flask under stirring (300 rpm) for short time (50 seconds) before filtration.

Fig. 1 Schematic diagram of the slug flow reactor/crystallizer for LGA reactive crystallization, with video snapshots of reactant acid injection to slug (bottom left), and the slug flow reactor packed in coil (bottom right).

2.3 Crystal characterization

The crystal size and morphology were characterized using microscope images. Individual slurry slugs directly from the slug flow crystallizer were placed in covered glass slides, with images taken in a compound microscope (Amscope ME520TA) with polarizers and an MU-90 camera. The sizes of all crystals from representative microscope images were quantified using the AmScope software, such as in Fig. S1b.† The crystal size statistics, such as the average, standard deviation (SD), and coefficient of variation (CV), were quantified using basic functions in Microsoft Excel.

The crystalline form of product crystals (after filtration and drying as in section 2.2) were characterized based on X-ray powder diffraction (XRD), using Rigaku MiniFlexII X-ray Diffractometer with a Cu Kα radiation source. The XRD data was collected at a voltage of 30 kV, current of 15 mA, and a wavelength of 1.5406 Å. Besides from XRD, the solid and crystalline forms of product crystals were further confirmed with differential scanning calorimetry (DSC, Q1000, TA Instrument), in the temperature range of 40 to 220 °C with a heating ramp of 10 °C per minute.

3. Results and discussion

3.1 Improve the size uniformity of α-form LGA crystals from stirred tanks using slug flow

As in Table 1, pure α-form LGA crystals can be generated at proper supersaturations, from gradual addition of one reactant acid to the stirred-tank reactor/crystallizer (semi-batch mode, Fig. 2 and S2†). However, aggregation and tiny crystals exist in product crystals, widening the crystal size distribution (CSD), such as in Fig. 2 and from literature values^18–24 (e.g., crystal size range of 10–600 um). The situation of crystal aggregation and wide CSD does not improve by changing the operational mode to the batch mode (from combining all reactants at once to the stirred tank). These tiny crystals likely come from attrition/breakage from the stirrers, and/or wide residence time distribution of crystallization.⁴⁵ When the reactant acid is gradually added to the stirred tank, new crystals are generated over the whole addition time (e.g., minutes in this study or even hours in Table 1), while existing crystals in the tank continue to grow, leading to a wide distribution of residence time among all crystals within the stirred tank for each experiment.

Fig. 2 Representative microscope images of LGA crystals (Table 3), from reactive crystallization in a stirred tank at a supersaturation of a) 4.5, b) 4.8, c) 5.3, d) 5.7, e) 6.7, and f) 7.7. Two images at two different sampling locations (top & bottom of flask) were shown for each condition, with experimental details in Table 2. The residence time is 12.3 minutes for (a–c), and 5.4 minutes for (d and e). Microscope images of the corresponding repeat experiments are shown in Fig. S2.†

Here we evaluate a non-tank-based reactor with spatial uniformity of reaction and crystallization, towards uniformly sized metastable α-form crystals. The reactor is designed based on slug flow, as demonstrated for improved crystal size uniformity in reaction crystallization (molecules other than LGA^30–35,39) and cooling crystallization.^46–49 Uniformly sized slugs are continuously generated from combining solution and gas streams at proper flow rates. These slugs (solution or slurry) serve as series of individual milli-fluidic reactors/crystallizers of uniform volumes, towards spatially uniform reaction environment. Mixing of these slugs is achieved by intrinsic recirculation,⁴⁶ rather than external mixing blades, thus the chance of mechanical attrition is low. Compared to product crystals from stirred tanks at similar supersaturations (Fig. 2 and S2†), the crystals from slug flow (Fig. 3 and S3†) are more uniform in size (smaller coefficient of variations in Table 3), with much fewer aggregation, and fewer tiny crystals. The much less aggregation is likely due to reduced number of small crystals (Fig. 2 and 3). In slug flow, all reactants are added only once, thus all crystals have very similar growth time thus similar sizes (without some crystals much smaller than others) if the process was tuned well. With proper residence time (Table 2), slug flow completely eliminates aggregation for low supersaturations, and keeps aggregation level low at high supersaturations when the probability of aggregation is higher. These aggregation from slug flow can be reversed (disassembled) back to individual crystals (Fig. S4†), upon brief (50 seconds) stirring of slurry slugs collected in a tank. In contrast, had the same reactant solutions started in a stirred tank (instead of slug flow), the same brief post-crystallization stirring would not be able to break aggregates back to individual crystals (from experimental observation).

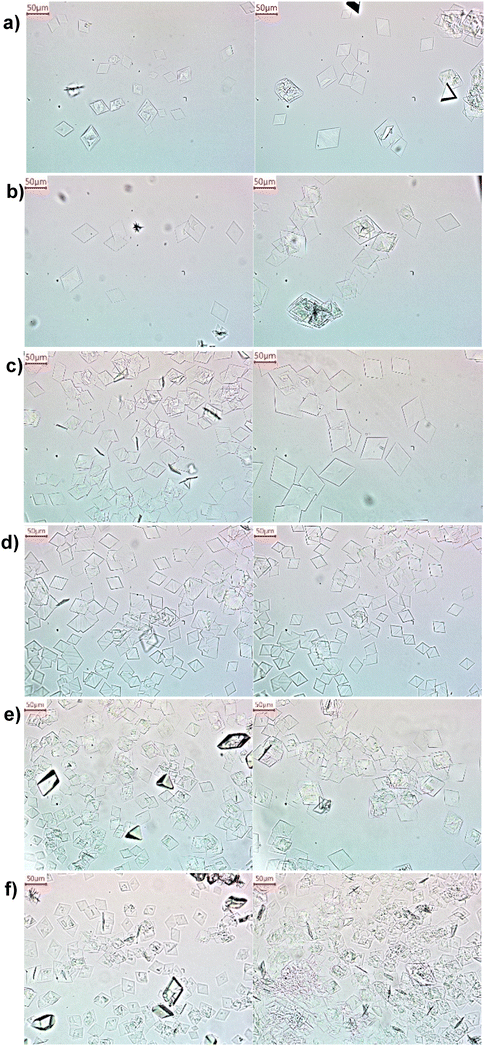Fig. 3 Representative microscope images of α-form LGA crystals (confirmed with XRD data in Fig. S6†), from reactive crystallization in slug flow at an initial supersaturation of a) 4.5, b) 4.8, c) 5.3, d) 5.7, e) 6.7 and f) 7.7. Two images were shown for each condition, with experimental details in Table 2. The residence time in slug flow is 12.3 minutes for (a–d), and 5.4 minutes for (e and f). Microscope images of the corresponding repeat experiments are shown in Fig. S3.†

Table 3 Crystal product statistics from reactive crystallization in a stirred-tank reactor/crystallizer (semi-batch mode). For each experiment in Table 2, 2 sample droplets of 20 μl each has been collected from (top & bottom of) the 50 mL round bottom flask. The crystal size refers to the longest dimension, as in Fig. S1b.† Crystal product statistics from reactive crystallization in a slug flow reactor/crystallizer (Fig. 1). For each slug flow experiment in Table 2, 2 sample slugs of 25 μl each has been collected

Experiment ID	Figure #	Crystal form	Crystal morphology and aggregation situation	Total number of crystals measured	Average crystal size in sample (μm)	Standard deviation (μm)	Coefficient of variation (CV)
a
B1_1	2a	α-Form	Prismatic, evident aggregation	127	18.71	12.52	0.67
B1_2	S2a†			296	11.33	11.14	0.98
B2_1	2b			77	19.14	13.44	0.70
B2_2	S2b†			85	13.97	12.25	0.88
B3_1	2c			134	18.58	13.98	0.75
B3_2	S2c†			119	18.49	13.45	0.73
B4_1	2d			139	20.05	13.65	0.68
B4_2	S2d†			101	16.66	11.63	0.70
B5_1	2e			147	20.16	11.71	0.58
B5_2	S2e†			172	20.45	11.67	0.57
B6_1	2f			146	16.10	12.67	0.79
B6_2	S2f†			130	21.07	15.33	0.73

---

b
S1_1	3a	α-Form	Prismatic, minimal aggregation	42	37.20	7.69	0.21
S1_2	S3a†			32	36.67	4.30	0.12
S2_1	3b			23	35.68	4.19	0.12
S2_2	S3b†			34	35.95	4.66	0.13
S3_1	3c			96	34.92	4.99	0.14
S3_2	S3c†			59	33.94	8.93	0.26
S4_1	3d			175	30.81	4.44	0.14
S4_2	S3d†			165	28.99	4.82	0.17
S5_1	3e			125	28.40	5.17	0.18
S5_2	S3e†			93	27.29	3.12	0.11
S6_1	3f		Prismatic, aggregation	64	21.56	3.37	0.16
S6_2	S3f†			121	18.64	4.91	0.26

---

While all existing studies that generate α-form crystals (Table 1) require mechanical stirring over the whole residence time (5 minutes or longer), Fig. S5 and S6† (XRD and DSC data) show that using slug flow can replace most of mechanical stirring, while still generating α-form crystals with proper residence time (Table 2). The brief remaining stirring (less than 1 minute) after slug flow can also serve to allow more growth time and more solid mass for XRD measurement, without changing the crystalline form (Fig. S8†). Fig. S8† shows that the thermodynamically metastable β-form is kinetically stable (zero conversion to α-form) for at least 5 minutes under stirring, thus existing α-form (measured after slug flow and brief stirring of less than 1 minute) is 100% from slug flow, not from any potential β-form conversion. If the residence time of slug flow is long, such as longer than 12 minutes listed in Table 2 for a starting supersaturation of 7.3, some portion of β-form crystals could appear (data not shown), likely due to increased probability of liquid-aided form conversion from the metastable α-form crystals (much larger than the critical nuclei size in classical nucleation theory⁵⁰). As a side comment, existing evidence does not exclude the possibility that the solids nucleated in slug flow (mass too small for XRD measurement) were in mixed forms, but pure α-form product crystals (Fig. 3) were collected after proper residence time (minutes) in slug flow. If those nuclei were not in pure α-form, then one likely reason for the pure product is the relatively faster growth kinetics of the α-form than the β-form,⁵¹ so only α-nuclei gets to grow to a stable or evident size (above the critical nuclei size in classical nucleation theory⁵⁰), while β-nuclei dissolves before reaches critical nuclei size.⁵⁰

3.2 Generate crystals of pure α-form and narrow size distribution at multiple crystal sizes using slug flow

As discussed in section 3.1, the spatially uniform reaction environment in small-volume slugs, together with suppressing secondary nucleation and/or mechanical attrition, can facilitate narrowing the product crystal size distribution. Here the slug flow with intrinsic recirculation has been designed for more uniform spatial distribution of crystals in good-quality slugs. Specifically, uniform-size slugs were generated with an aspect ratio ∼1 (Fig. 1), as shown from prior studies.⁴⁶ Even at high solute concentrations (e.g., larger than 0.4 M), the slug quality remains good, without any slug breakage nor combination nor solid drop-off during the whole process. Specifically for LGA crystals, the density is around 1.548 g cm⁻³,¹⁷ which is not too much higher than the aqueous solution. And the microscope images of slurry slugs right afterwards (Fig. 3) show crystal size uniformity, and indicate the slug flow here can handle the gravity effect to some extent while maintaining the good quality of crystal size uniformity.

Here for simplicity, the LGA supersaturation (or reactant concentrations at the stoichiometric ratio of 2 : 1 for MSG : H₂SO₄) and reasonable residence time is chosen as the lumped handle (process variable) to adjust crystal size within each slug. For all LGA supersaturations tested (4.5–7.7), the product crystal CSD from slug flow (Table 3 and Fig. 4) is much narrower than from a stirred tank, with the batch mode (Fig. S7†) or even with the semi-batch mode (gradual addition, Fig. 2). From experiment observation, gravity could widen crystal size distribution in flask/tank crystallizers, as larger crystals can sediment to the bottom and accumulate, unless very high stirring rate is applied which often comes with higher chance of attrition or crystal breakage.

Fig. 4 Cumulative distribution of LGA product crystals on a volume basis (labelled as Q₃), from different supersaturations (colors) in a slug flow reactor/crystallizer (dashed line) and a stirred-tank reactor (solid line). A zoom-in of the cumulative distribution is presented for S = 5.7 for detailed comparison. Crystals sampled from the same experiments are combined for size distribution statistics (Table 3a and b). The experiment ID refers to in Table 2, e.g., “S” refers to slug flow, “B” refers to semi-batch.

From Table 3b and Fig. 3 and 5, as the supersaturation value increases from 4.5 to 7.7 in slug flow, the average crystal size monotonically decreases from 37 μm to 19 μm, while maintaining a narrow size distribution, as indicated from the steep slope in the cumulative size distribution in Fig. 4. There is no such clear trend of crystal size in stirred tank (Table 3), likely due to a wider CSD and higher aggregation. The narrow CSD from slug flow, together with the monotonic change of crystal size with respect to supersaturation, facilitates size tuning, as in Fig. 5. The total residence time (starting from solution) can also be further reduced at higher supersaturation, such as 5.4 minutes for a supersaturation value of 6.7, compared to 12.3 minutes for a supersaturation value within the range of 4.5–5.7. As a side comment, the concentration of one reactant H₂SO₄ also directly affects pH of the reaction mixture, thus the protonated state (and effective concentration) of the other reactant MSG. This effect/interaction between two reactants is interesting and complex, but could be a good topic of future study.

Fig. 5 Average sizes of the pure α-form LGA crystals produced at different supersaturations from a) a semi-batch stirred-tank reactor/crystallizer and b) a slug flow reactor/crystallizer. The experiments conditions are detailed in Table 2, e.g., “S” refers to slug flow, “B” refers to semi-batch, N = 1–6, and “_” refers to duplicates. The error bar shows the standard deviation of product crystal size for each experiment, as in Table 3a and b.

4. Conclusion

A simple reaction crystallization process has been designed based on slug flow, for continuous generation of pure α-form L-glutamic acid crystals with uniform sizes and minimal aggregation. The process and product crystal quality is reproducible, without requiring external seeding, by implementing in situ nucleation in slug flow, and suppressing undesired secondary nucleation.⁴⁶ Starting from solution, the total reaction/crystallization process takes less than 15 minutes at room temperature. While all current studies that generate α-form crystal require mechanical stirring over the whole residence time, this study uses slug flow with intrinsic recirculation⁴³ to replace most/all of blade stirring, and improves the crystal size uniformity.

The slug flow reactor/crystallizer also allows tuning the average crystal size with the LGA supersaturation (stoichiometric reactant concentrations), at reasonable residence time. Specifically, the average crystal size increases monotonically from 19 to 37 μm, while maintaining a narrow size distribution, when the supersaturation is reduced from 7.7 to 4.5. At each condition, the size variability from slug flow is smaller than from a stirred tank in the semi-batch mode (the current best reactor and mode for LGA crystals manufacturing). As the slug flow process is designed not based on a specific reaction nor concentration, but on general physical chemical principles (liquid volume segmentation for enhanced heat and mass transfer), it is potentially useful: (1) for improving the spatial uniformity of LGA reaction crystallization at other concentration combinations, allowing evaluating interactions between these concentrations with reduced variability and/or morphology tuning; and (2) for forming uniformly-sized crystals from other reactions besides LGA, allowing synthesizing and manufacturing other useful materials.^28,30,39,52

Author contributions

The manuscript was written through contributions of both authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Virginia Commonwealth University is acknowledged for financial support.

References

1. M. A. McDonald, H. Salami, P. R. Harris, C. E. Lagerman, X. Yang, A. S. Bommarius, M. A. Grover and R. W. Rousseau, React. Chem. Eng., 2021, 6, 364–400.
2. T. C. Farmer, S. K. Schiebel, B. F. Chmelka and M. F. Doherty, Cryst. Growth Des., 2018, 18, 4306–4319.
3. M. Jiang and R. D. Braatz, CrystEngComm, 2019, 21, 3534–3551.
4. V. V. Banakar, S. S. Sabnis, P. R. Gogate, A. Raha and Saurabh, Chem. Eng. Res. Des., 2022, 182, 273–289.
5. J. Orehek, D. Teslić and B. Likozar, Org. Process Res. Dev., 2021, 25, 16–42.
6. Y. Ma, S. Wu, E. G. J. Macaringue, T. Zhang, J. Gong and J. Wang, Org. Process Res. Dev., 2020, 24, 1785–1801.
7. B. Wood, K. P. Girard, C. S. Polster and D. M. Croker, Org. Process Res. Dev., 2019, 23, 122–144.
8. M. O. Besenhard, P. Neugebauer, O. Scheibelhofer and J. G. Khinast, Cryst. Growth Des., 2017, 17, 6432–6444.
9. S. R. Perumalla, C. Wang, Y. Guo, L. Shi and C. C. Sun, CrystEngComm, 2019, 21, 2089–2096.
10. J. A. Oliva, K. Pal, A. Barton, P. Firth and Z. K. Nagy, Chem. Eng. J., 2018, 351, 498–505.
11. S. Aitipamula, R. Banerjee, A. K. Bansal, K. Biradha, M. L. Cheney, A. R. Choudhury, G. R. Desiraju, A. G. Dikundwar, R. Dubey, N. Duggirala, P. P. Ghogale, S. Ghosh, P. K. Goswami, N. R. Goud, R. R. K. R. Jetti, P. Karpinski, P. Kaushik, D. Kumar, V. Kumar, B. Moulton, A. Mukherjee, G. Mukherjee, A. S. Myerson, V. Puri, A. Ramanan, T. Rajamannar, C. M. Reddy, N. Rodriguez-Hornedo, R. D. Rogers, T. N. G. Row, P. Sanphui, N. Shan, G. Shete, A. Singh, C. C. Sun, J. A. Swift, R. Thaimattam, T. S. Thakur, R. Kumar Thaper, S. P. Thomas, S. Tothadi, V. R. Vangala, N. Variankaval, P. Vishweshwar, D. R. Weyna and M. J. Zaworotko, Cryst. Growth Des., 2012, 12, 2147–2152.
12. H. M. R. Özüdoğru, M. Nieder-Heitmann, K. F. Haigh and J. F. Görgens, Ind. Crops Prod., 2019, 133, 259–268.
13. M. Can, S. Demirci, A. K. Sunol and N. Sahiner, Microporous Mesoporous Mater., 2020, 309, 110533.
14. T. D. Turner, N. Dawson, M. Edwards, J. H. Pickering, R. B. Hammond, R. Docherty and K. J. Roberts, Cryst. Growth Des., 2022, 22, 3042–3059.
15. T. T. H. Trinh, P. I. Schodder, B. Demmert and A. T. Nguyen, Chem. Eng. Res. Des., 2021, 169, 176–188.
16. T. D. Turner, P. Gajjar, I. S. Fragkopoulos, J. Carr, T. T. H. Nguyen, D. Hooper, F. Clarke, N. Dawson, P. J. Withers and K. J. Roberts, Cryst. Growth Des., 2020, 20, 4252–4263.
17. M. T. Ruggiero, J. Sibik, J. A. Zeitler and T. M. Korter, J. Phys. Chem. A, 2016, 120, 7490–7495.
18. A. Borissova, Y. Jammoal, K. H. Javed, X. Lai, T. Mahmud, R. Penchev, K. J. Roberts and W. Wood, Cryst. Growth Des., 2005, 5, 845–854.
19. H. L. Lee, C. L. Yang and T. Lee, CrystEngComm, 2022, 24, 7176–7192.
20. H. Alatalo, H. Hatakka, J. Kohonen, S. Reinikainen and M. Louhi-kultanen, AIChE J., 2009, 56, 2063–2076.
21. U. Ojaniemi, J. Puranen, M. Manninen, E. Gorshkova and M. Louhi-Kultanen, Chem. Eng. Sci., 2018, 178, 167–182.
22. H. M. Alatalo, H. Hatakka, J. Kohonen, R. Satu-pia Pia and M. Louhi-Kultanen, Chem. Eng. Technol., 2009, 33, 3466–3475.
23. H. M. Alatalo, H. Hatakka, M. Louhi-Kultanen, J. Kohonen and S. P. Reinikainen, Chem. Eng. Technol., 2010, 33, 743–750.
24. H. Hatakka, H. Alatalo, M. Louhi-Kultanen, I. Lassila and E. Hæggström, Chem. Eng. Technol., 2010, 33, 751–756.
25. C. P. M. Roelands, J. H. Ter Horst, H. J. M. Kramer and P. J. Jansens, AIChE J., 2007, 53, 354–362.
26. J. Schöll, C. Lindenberg, L. Vicum, J. Brozio and M. Mazzotti, Faraday Discuss., 2007, 136, 247.
27. H. S. Fogler, Elements of Chemical Reaction Engineering, Prentice Hall, 5th edn, 2016.
28. C. X. Zhao, L. He, S. Z. Qiao and A. P. J. Middelberg, Chem. Eng. Sci., 2011, 66, 1463–1479.
29. P. Moschou, M. H. J. M. De Croon, J. Van Der Schaaf and J. C. Schouten, Rev. Chem. Eng., 2014, 30, 127–138.
30. R. Vacassy, J. Lemaître, H. Hofmann and J. H. Gerlings, AIChE J., 2000, 46, 1241–1252.
31. P. Neugebauer and J. G. Khinast, Cryst. Growth Des., 2015, 15, 1089–1095.
32. S. Guillemet-Fritsch, M. Aoun-Habbache, J. Sarrias, A. Rousset, N. Jongen, M. Donnet, P. Bowen and J. Lemaître, Solid State Ionics, 2004, 171, 135–140.
33. T. Yonemoto, M. Kubo, T. Doi and T. Tadaki, Chem. Eng. Res. Des., 1997, 75, 413–419.
34. A. Testino, F. Pilger, M. A. Lucchini, J. E. Q. Quinsaat, C. Stähli and P. Bowen, Molecules, 2015, 20, 10566–10581.
35. K. Robertson, P.-B. Flandrin, A. R. Klapwijk and C. C. Wilson, Cryst. Growth Des., 2016, 16, 4759–4764.
36. G. H. Albuquerque and G. S. Herman, Cryst. Growth Des., 2017, 17, 156–162.
37. K.-J. Kim, R. P. Oleksak, E. B. Hostetler, D. A. Peterson, P. Chandran, D. M. Schut, B. K. Paul, G. S. Herman and C.-H. Chang, Cryst. Growth Des., 2014, 14, 5349–5355.
38. L. Yu, Y. Pan, C. Wang and L. Zhang, Chem. Eng. J., 2013, 219, 78–85.
39. A. M. Nightingale and J. C. Demello, Adv. Mater., 2013, 25, 1813–1821.
40. C. J. Gerdts, V. Tereshko, M. K. Yadav, I. Dementieva, F. Collart, A. Joachimiak, R. C. Stevens, P. Kuhn, A. Kossiakoff and R. F. Ismagilov, Angew. Chem., Int. Ed., 2006, 45, 8156–8160.
41. Handbook of Industrial Crystallization, ed. A. S. Myerson, D. Erdemir and A. Y. Lee, Cambridge University Press, 2019.
42. M. Abolhasani, A. Oskooei, A. Klinkova, E. Kumacheva and A. Günther, Lab Chip, 2014, 14, 2309–2318.
43. M. Abolhasani, C. W. Coley, L. Xie, O. Chen, M. G. Bawendi and K. F. Jensen, Chem. Mater., 2015, 27, 6131–6138.
44. Y. Tahri, E. Gagnière, E. Chabanon, T. Bounahmidi and D. Mangin, J. Cryst. Growth, 2016, 435, 98–104.
45. M. Brunsteiner, A. G. Jones, F. Pratola, S. L. Price and S. J. R. Simons, Cryst. Growth Des., 2005, 5, 3–16.
46. M. Jiang, Z. Zhu, E. Jimenez, C. D. Papageorgiou, J. Waetzig, A. Hardy, M. Langston and R. D. Braatz, Cryst. Growth Des., 2014, 14, 851–860.
47. M. Mou and M. Jiang, J. Pharm. Innov., 2020, 15, 281–294.
48. M. Jiang and R. D. Braatz, Chem. Eng. Technol., 2018, 41, 143–148.
49. M. Mou, H. Li, B.-S. Yang and M. Jiang, Crystals, 2019, 9, 38–40.
50. D. Kashchiev, J. Chem. Phys., 2006, 125, 014502.
51. Y. Tahri, E. Gagnière, E. Chabanon, T. Bounahmidi, Z. Kožíšek, N. Candoni, S. Veesler, M. Boukerche and D. Mangin, Cryst. Growth Des., 2019, 19, 3329–3337.
52. M. Mou, A. Patel, S. Mallick, B. P. Thapaliya, M. P. Paranthaman, J. H. Mugumya, M. L. Rasche, R. B. Gupta, S. Saleh, S. Kothe, E. Baral, G. P. Pandey, H. Lopez and M. Jiang, ACS Omega, 2022, 7, 42408–42417.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ce01528e

---