Open Access Article
Open Access ArticleDeep-UV optical properties of KDP-family crystals: a comprehensive characterization
Zijian
Cui
 *,
Mingying
Sun
*,
De'an
Liu
and
Jianqiang
Zhu
*,
Mingying
Sun
*,
De'an
Liu
and
Jianqiang
Zhu
Key Laboratory of High Power Laser and Physics, Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai 201800, China. E-mail: cuizijian@siom.ac.cn; sunmy@siom.ac.cn
First published on 23rd November 2022
Abstract
As a class of widely used optical materials, KH2PO4 (KDP)-family crystals play an important role in the generation of infrared, visible, UV, and deep-UV lasers, but their deep-UV optical characteristics have been lacking in systematic research. Aiming at the typical KDP-family nonlinear crystals, including NH4H2PO4, KDP, K(H1−xDx)2PO4 (partially deuterated KDP), and KD2PO4 crystals, we systematically investigated their transmittance, cut-off edge, band-gap energy, linear absorption, and nonlinear two-photon absorption (TPA) properties in the deep-UV spectral region. By using a vacuum-UV spectrophotometer, the UV absolute transmittances were measured in the range of 160–290 nm. Based on the measured results, the UV cut-off edges of these crystals were obtained and band-gap energies were calculated. By using an Nd:YLF picosecond laser (1053 nm, 9 ps, 10 Hz), the fourth and fifth harmonics (263.2 and 210.5 nm) were generated respectively via a LiB3O5 crystal and two β-BaB2O4 crystals. The anisotropic linear absorption and nonlinear TPA coefficients of the above KDP-family crystals were obtained in detail from intensity-dependent transmittance measurements at 263.2 and 210.5 nm with ordinary and extraordinary polarization states. This comprehensive investigation of the deep-UV optical properties of commonly used KDP-family optical materials and the obtained new data can provide an important parameter basis for crystal growth with higher optical purity, deep-UV laser generation, and applications.
1 Introduction
KDP-family crystals represented by NH4H2PO4 (ADP), KH2PO4 (KDP), and KD2PO4 (DKDP) are a class of optical materials with a long history and excellent performances, and have been widely used in many important optical functional devices.1–4 One of the most typical applications is that KDP and DKDP crystals are commonly used as electro-optic switches and modulators to control or modulate laser radiation due to their large electro-optical coefficients.4,5 In the field of nonlinear optics, because of adequate nonlinear optical coefficients and high laser damage thresholds,6–12 as shown in Table 1, KDP-family crystals are the key materials in frequency converters, which can achieve the second-, third-, and fourth-harmonic generation of lasers near 1 μm.13,14 In addition, KDP-family crystals also have a remarkable feature where their growth sizes exceed that of any other water-soluble crystals,2,4,15 which makes them indispensable materials for obtaining high-energy and high-power lasers in large laser facilities such as the National Ignition Facility, the LMJ facility, and the ShenGuang facility.16–18 Owing to a series of significant advantages and improvements in the growth process, the application fields of KDP-family crystals are continuously expanded. Particularly in recent years, the research on temporal compression of high-power laser pulses, Cherenkov radiation, and high-energy deep-UV laser radiation generation based on KDP-family crystals has attracted a lot of attention.19–23| λ (nm) | Pulse width (ns) | Beam diameter | Damage test | Damage threshold (J cm−2) |
|---|---|---|---|---|
| 1064 | 1.1 | 30 μm | — | 11.7–12.3 (a/b)11 |
| 19.5–23 (c)11 | ||||
| 3 | — | — | 348 | |
| 3 | 0.9–1.9 mm | 600-on-1 | 24–349 | |
| 10 | 1 mm | N-on-1 | 647 | |
| 11 | 320 μm | 1-on-1 | 4910 | |
| 532 | 1 | 30 μm | — | 6–13.5 (a/b)11 |
| 12–20 (c)11 | ||||
| 3 | — | — | 208 | |
| 11 | 220 μm | 1-on-1 | 2210 | |
| R-on-1 | 2910 | |||
| 355 | 0.85 | 30 μm | — | 4.3–4.8 (a/b)11 |
| 4.8–5.3 (c)11 | ||||
| 3 | 287 μm | — | 8.7212 | |
| — | — | 128 | ||
| 0.9–1.9 mm | 600-on-1 | 15–209 | ||
| 10 | 1 mm | N-on-1 | 28.67 | |
| 11 | 450 μm | 1-on-1 | 1810 | |
| 266 | 3 | — | — | 38 |
The methods of growing KDP-family crystals mainly include the traditional temperature cooling technique and the “point seed” rapid growth technique.2,12,24–26 The traditional technique is to slowly reduce the solution temperature to obtain the driving force for crystal growth. This technique has the advantages of large pyramidal face growth, high optical homogeneity, and high damage threshold, but its disadvantages are that it requires a large cross-section seed crystal, slow growth speed, and long growth cycles. The rapid growth technique can increase the growth rate of KDP-family crystals by an order of magnitude, and the preparation of a point seed crystal is easy. However, there are two main problems with the rapid growth technique.26 First, the growth solution needs to maintain high stability, and second, compared with the traditional technique, the optical qualities of the crystals obtained by the rapid growth technique are decreased, such as an increase of internal light scattering and UV absorption, a decrease of optical homogeneity, and a reduction of laser damage threshold. At present, by studying the properties of KDP-family crystals under different growth conditions (including raw materials, growth methods, seed orientation, and deuterium content), the optimal growth process has been determined and large-aperture and high-quality KDP-family crystals have been successfully obtained by both the traditional method and rapid growth method.12,27–29 Single crystal optical devices with a size of >400 mm can be fabricated. Meanwhile, a series of Fe3+, Zn2+, and borax additive doped KDP crystals were grown, and the influence of doping on the optical properties of the crystal, such as transmissivity, nonlinear optical properties, laser-induced damage threshold, Raman spectrum, and second-harmonic generation, was also studied.30–32
To better apply KDP-family crystals, it is important to accurately obtain material parameters in the deep-UV spectral region to systematically understand their optical characteristics. Presently, although the partial deep-UV optical properties of a few crystals in the KDP-family have been reported in some studies,23,33–42 these results are fragmentary. There is still a lack of systematic data on the material optical properties of KDP-family crystals in the deep-UV waveband near 200 nm, especially the deep- and vacuum-UV transmittance, linear absorption, and nonlinear two-photon absorption (TPA) of the crystals with different deuterium contents. In addition, for deep-UV lasers with different polarization states, it is also crucial to reveal the polarization dependence of the absorption loss in KDP-family crystals for their applications in nonlinear optics. To the best of our knowledge, the measurement of quite a few parameters is still lacking, which cannot provide comprehensive information on the linear absorption coefficient and nonlinear TPA of KDP-family crystals. Therefore, it is necessary to deeply investigate the optical properties of these materials in the deep-UV waveband.
Here, we systematically characterized the optical properties of commonly used KDP-family nonlinear crystals in the deep-UV spectrum range, including the UV transmittance, cut-off edge, band-gap energy, linear absorption, and nonlinear TPA coefficients. Four uncoated crystal samples of ADP, KDP, 70% deuterated KDP, and DKDP (deuterium content >98%) were prepared (110 cut), and they were all grown using traditional technology. The crystal samples are shown in Fig. 1. In this work, the anisotropic linear absorption and nonlinear TPA coefficients of each crystal sample were measured in detail at two typical deep-UV wavelengths of 263.2 and 210.5 nm, including two polarization states of ordinary and extraordinary light (o light and e light). In addition, for the measurement of the TPA coefficient, we used a CCD camera to measure the transverse profile of the beam instead of the traditional method of assuming the spatial profile distribution of the laser intensity, thereby more accurately reconstructing the three-dimensional laser intensity distribution to achieve precise measurement.
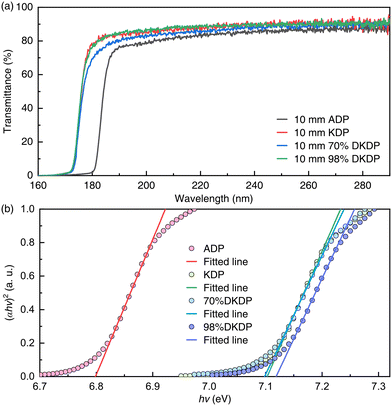
2 UV transmittance and band-gap energy
By using a vacuum-UV (VUV) spectrophotometer (Metrolux ML6500, Germany, operation pressure: <3 × 10−3 Pa, wavelength ranges with double lamps: 115 to 230 nm and 160 to 320 nm), we measured the UV absolute transmittances of the KDP-family crystal samples in the spectral region of 160–290 nm (0.2 nm step), as shown in Fig. 2(a). Their UV cut-off wavelengths, which are defined by the “0” transmittance level, are shown in Table 2. Compared with the KDP, 70% deuterated KDP, and DKDP crystals, the ADP crystal has longer UV cut-off edges, which means that it has a smaller band-gap energy (Eg). It can also be seen that the KDP, 70% deuterated KDP, and DKDP crystals have similar UV cut-off wavelengths, while the overall UV transmittances of the 70% deuterated KDP crystal are slightly lower than those of the KDP and DKDP crystals. The main reason is that there may be more impurities in the 70% deuterated KDP crystal than in the KDP and DKDP crystals. For crystals grown in aqueous solutions, such as KDP-family crystals, the presence of growth defects (including intrinsic point defects, scattering particles, and impurity ions) can cause rather strong absorptions in the UV waveband.40,43–54 Typical intrinsic point defects in KDP-family crystals include Hi, VP, VK, and VN. Particularly, the V5−P defect is regarded as one of the most destructive intrinsic point defects in the KDP crystal, which could introduce a strong defect state in the band gap of KDP and cause extra optical absorption at 310–620 nm.49,50 For the scattering particles in KDP-family crystals, they can significantly reduce the optical quality of the crystal,51,52 and the scattering particles can cause light loss in the whole transmission wavebands of the crystals. During the growth of KDP-family crystals, the metal ions in solution, such as Fe3+ [peak absorption wavelength (PAW) <290 nm], Al3+ (PAW 266 nm), Cr3+ (PAW 358 & 270 nm), and Pb2+ (PAW <230 nm), can significantly enhance the absorption of the UV waveband, and the absorption is closely related to the concentration of metallic absorption impurities.53–56 The higher the concentration, the lower the UV transmittance. Hence, for the KDP crystal, especially the one obtained by the rapid growth method, its prismatic part has higher UV absorption than the pyramidal part because of the charge states of the (100) and (101) planes, and trivalent metals (including Al3+, Fe3+, Cr3+) are mostly incorporated in the prismatic sector.56 In addition, the absorption loss is also closely related to the orientation (or polarization), and the results show that at the same ion concentration, the absorption along the z-direction is always greater than that along the type-II phase-matching direction.30,57In Table 2, the measured UV cut-off edges were slightly different from the results reported in the literature. The first reason is that the thicknesses of the crystal samples are different.33,34 What's more, as mentioned above, for KDP-family crystals, metal ion impurities have a significant effect on UV transmittance. Therefore, the crystal samples grown by different processes in the literature will lead to diverse measured results.
Since the band-gap of a material describes the energy required to excite an electron from the valence band to the conduction band and can be used to predict the photophysical and photochemical properties of materials, accurate determination of the band-gap energy is very important. In 1966, Tauc proposed a method to estimate the band-gap energy by using optical absorption spectra, and after further development, it has become a common method to calculate the band-gap energy.58
The Tauc method shows that the energy-dependent absorption coefficient α can be expressed by the following equation:
| (ahv)1/n = A(hv − Eg) | (1) |
Based on the measured results of the UV transmittance, we calculated the band-gap energies of the ADP, KDP, 70% deuterated KDP, and DKDP crystals using the Tauc method. The results are shown in Fig. 2(b) and Table 2. The measured UV cut-off edges and band-gap energies revealed an almost perfect agreement with the reported data. It is worth noting that for the DKDP crystals with different deuterium contents, their UV cut-off edges and band-gap energies are almost identical. Therefore, it can be reasonably concluded that the deuterium content almost does not affect these properties.
3 Measurement of linear absorption and nonlinear TPA coefficients
3.1 Experimental setup
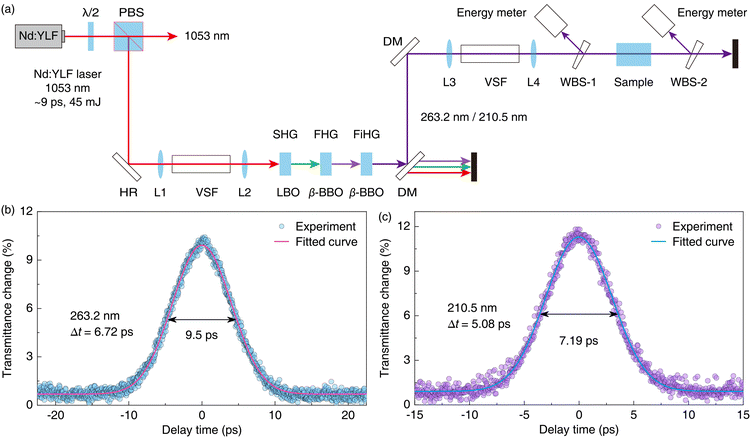
To measure the linear absorption and nonlinear TPA coefficients, an Nd:YLF laser (1053 nm, 10 Hz) with a pulse duration of ∼9 ps (FWHM) and maximum output energy of 45 mJ was used as the fundamental laser source (ω1). The transverse profile is a circular spot with a diameter of 4.3 mm defined as the measurement of 10% of the peak irradiance point. To generate a deep-UV laser of 263.2 and 210.5 nm, a 4.5 mm-thick LiB3O5 (LBO) crystal (θ = 90°, φ = 11°, type-I phase matching) was used to generate the second harmonic (ω2), then a β-BaB3O4 (β-BBO) crystal (θ = 48.4°, φ = 0°, type-I phase matching) with a thickness of 1.2 mm was used to generate the fourth harmonic (ω4), and finally, a β-BBO crystal (θ = 52.1°, φ = 0°, type-I phase matching) with a thickness of 0.8 mm was used to generate the fifth harmonic (ω5). The surfaces of each crystal were coated with anti-reflection films at the corresponding wavelengths.A schematic diagram of the experimental setup is shown in Fig. 3(a). The temperature of the LBO crystal was always controlled at 55 °C, and the two β-BBO crystals were at room temperature. To obtain laser pulses with high spectral purity, both the generated fourth and fifth harmonics were separated from other wavelength lasers using two dichroic mirrors. The whole experiment involved four laser radiations with different wavelengths, which were 1053, 526.5, 263.2, and 210.5 nm, respectively. The pulse durations of the generated fourth and fifth harmonics were measured using TPA pump–probe experiments, and the measured results are 6.72 and 5.08 ps (FWHM), respectively, as shown in Fig. 3(b) and (c).
The polarization direction of the fundamental wave output from the laser was perpendicular to the horizontal plane, and the polarization directions of the obtained fourth and fifth harmonics were perpendicular and parallel to the horizontal plane, respectively. Due to the strict limitation of the phase matching, the laser radiations obtained by frequency conversion have a good polarization degree, and the polarizations of the fourth and fifth harmonics measured with a Gran prism were better than 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
In the measurement of absorption coefficients, two wedged beam splitters (WBSs, wedge angle: 5 degrees) were used to sample the deep-UV laser energy. Since the MgF2 crystal has a high transmittance and a very weak TPA effect in the deep-UV spectral region,59 MgF2 was employed for the material of the WBSs. In addition, to minimize the influence of sampling materials on the results in the measurement process, the reflection scheme of the back surface was adopted to characterize the incident laser energy before the sample, while the laser energy output from the sample was measured by the reflection scheme of the front surface. For the measurement of laser energy, two energy meters (PE9-ES-C, OPHIR, Israel) with the same model were used and calibrated with each other. To reduce the impact of energy fluctuation on the measurement results, 30 pulse energies were measured and averaged each time in the follow-up experiments.
To ensure the accuracy of the measurement results, we firstly calibrated the sampling rates of WBS-1 and WBS-2 at different incident energies, and the results are shown in Fig. 4. It can be seen from the measured results that there is little change in the sampling rate of the WBSs at different laser energies, which means that each sampling rate can be regarded as a constant in this experiment. At the wavelengths of 263.2 and 210.5 nm, the sampling rates of WBS-1 are 3.213% and 1.796%, respectively, and those of WBS-2 are 3.129% and 2.181%, respectively. The fluctuations of the fourth and fifth harmonic energy sampling rate were less than 0.05% and 2%, respectively, and they were mainly caused by the fluctuation of laser energy during the measurement process and the measurement deviation of the energy meter at different wavelengths and energy levels.
 | ||
| Fig. 4 Sampling rates of (a) WBS-1 and (b) WBS-2 at different incident energies at the wavelengths of 263.2 and 210.5 nm. | ||
3.2 Linear absorption coefficients
For the deep-UV laser, numerous optical materials show a strong nonlinear TPA effect in a high-peak-power regime. Therefore, the measurement of the linear absorption coefficients of materials in the deep-UV region needs to use a laser with low peak power to ensure that the nonlinear absorption is far weaker than the linear absorption. In this part of the experiment, the peak intensities of the incident lasers (both 263.2 and 210.5 nm) were controlled below 100 MW cm−2. For the beam normally incident to the crystal sample, the surface reflection R, linear transmittance TL, and linear absorption coefficient of the crystal sample can be described as:40,60 | (2) |
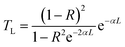 | (3) |
 | (4) |
| Crystal | Length | Orientation | Polarization | n @ 263.2 nm | n @ 210.5 nm |
|---|---|---|---|---|---|
| ADP | 10 mm | θ = 90°, ϕ = 45° | o | 1.5813264 | 1.6314394 |
| e | 1.5275895 | 1.5715802 | |||
| KDP | 10 mm | θ = 90°, ϕ = 45° | o | 1.5609935 | 1.6061728 |
| e | 1.5113071 | 1.5499245 | |||
| 70% DKDP | 10 mm | θ = 90°, ϕ = 45° | o | 1.5570717 | 1.6055643 |
| e | 1.5091906 | 1.5472657 | |||
| DKDP | 10 mm | θ = 90°, ϕ = 45° | o | 1.5555002 | 1.6053208 |
| e | 1.5083431 | 1.5462008 |
As the laser intensity gradually increases from zero, the low-intensity transmittances of o light and e light in the ADP, KDP, 70% deuterated KDP, and DKDP crystal samples were measured in detail, and the results are shown in Fig. 5. For the whole transmittances of the ADP, KDP, 70% deuterated KDP, and DKDP crystal samples at 263.2 nm, it can be seen that the measured transmittances have good consistency, which indicates that the nonlinear absorption effect is very weak in this measurement process. However, at the wavelength of 210.5 nm, the transmittances decrease slightly with the increase of energy, especially when the peak intensity is greater than 10 MW cm−2. This means that the nonlinear absorption effect has begun to appear. Therefore, the measured data with a peak intensity of less than 10 MW cm−2 were used to calculate the linear absorption coefficients. According to the parameters of the crystal samples, low-intensity transmittances, and eqn (2)–(4), the linear absorption coefficients of the crystal samples were obtained from numerical calculations, and the results are listed in Table 4.
 | ||
| Fig. 5 Low-intensity transmittances of ADP, KDP, 70% deuterated KDP, and DKDP crystal samples at (a)–(d) 263.2 and (e)–(h) 210.5 nm. | ||
| Crystal | Polarization | α @ 263.2 nm (cm−1) | α @ 210.5 nm (cm−1) | ||
|---|---|---|---|---|---|
| Experiment | Literature | Experiment | Literature | ||
| ADP | o | 0.0916 | — | 0.357 | — |
| e | 0.0674 | 0.07, 0.03534,38,39 | 0.310 | — | |
| KDP | o | 0.0452 | — | 0.158 | 0.2, 0.3134,40 |
| e | 0.0314 | 0.01–0.2, 0.03, 0.2734,40 | 0.131 | ||
| 70% DKDP | o | 0.0535 | 0.083941 | 0.183 | — |
| e | 0.0454 | 0.067141 | 0.152 | — | |
| DKDP | o | 0.0525 | — | 0.163 | — |
| e | 0.0330 | 0.03538,39 | 0.125 | — | |
Since the employed laser has high stability and the linear absorption coefficient is only determined by the laser energy and independent of the peak power, the measurement error mainly arises from the energy measurement and the calculation of surface reflection loss. According to the deviation of the energy detector (2–5%) and the accuracy (<1%) of the refractive index, the measurement error is estimated to be less than 6%. In Table 4, we also listed the reported data of the linear absorption coefficient as far as possible. Compared with them, it can be seen that the results measured in this work are in good agreement with some published data, but there are also obvious differences with several data. An important reason is that the materials used by different research groups to characterize UV optical properties, their growth processes, and the experimental conditions are different. A number of fragmentary reported results make it difficult to form a complete and unified conclusion.
3.3 Nonlinear TPA coefficients
For the determination of the TPA coefficient, accurately measuring the intensity-dependent energy transmittance and reconstructing the three-dimensional distribution of laser intensity are two critical procedures. To measure the energy transmittances at different intensities, a high-intensity and intensity-tunable laser source is required. Generally, the output energy of the laser can be changed by adjusting the delay between the signal light and the xenon lamp or laser diode pump. However, the transverse distribution of the output beam will also be changed obviously in this way, which is unfavorable to the reconstruction of the laser intensity distribution, thus affecting the accuracy of TPA coefficient results. Therefore, the output energy from the Nd:YLF laser was set to 15 mJ during the whole measurement process, and the energy tuning was controlled via the half-wave plate and polarization beam splitter to ensure that the pulse duration, temporal waveform, and spatial distribution of the output laser have a good consistency.To reconstruct the laser intensity distribution, a common method is to use an approximate function to establish a mathematical description based on the measurement results of the laser beam. Essentially, this is only an approximation, especially the description of the spatial profile. This is not the best way to determine the TPA coefficient because it is extremely dependent on the intensity distribution. In fact, based on the high stability laser, it is a more straightforward and practical method that directly uses the measured data of the beam spatial profile to reconstruct the complete three-dimensional intensity information of the laser. Therefore, the transverse profile measured using a CCD camera was used here instead of the traditional method to reconstruct the laser intensity distribution more accurately and truly.
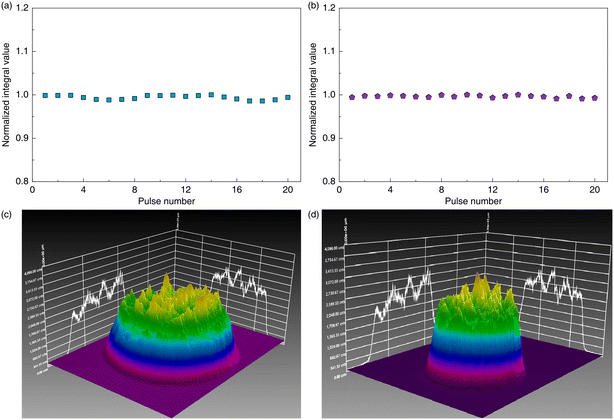
Experimentally, the spatial profiles of the fourth and fifth harmonics were measured. The number of effective pixels and the pixel spacing of the CCD camera are 1928 × 1448 and 3.69 μm, respectively. 20 sets of spatial profile data were measured both at 263.2 and 210.5 nm, and they were normalized by dividing by the respective maximum values. The normalized intensity distributions are numerically integrated, and the integration results are shown in Fig. 6(a) and (b). According to the integration values, it can be seen that the transverse distributions of the beams at the two wavelengths have a good consistency. The final intensity distributions of the 263.2 and 210.5 nm lasers are shown in Fig. 6(c) and (d), and they were used to reconstruct the three-dimensional intensity distribution and calculate the TPA coefficient.
Based on the measured temporal and transverse spatial distribution of the pulse, a normalized intensity distribution of laser radiation was established, and the true 3D intensity distribution of the beam can thus be reconstructed according to the measured energy. Considering both linear absorption and nonlinear TPA absorption, for the laser pulse propagating along the z direction, the change of intensity I with propagation can be expressed as:40,63
 | (5) |
For a beam with a temporal Gaussian intensity profile, its three-dimensional intensity distribution Iin(x, y, t) and the intensity-dependent transmittance TNL through the crystal sample can be described as:
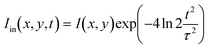 | (6) |
 | (7) |
The maximum energy of the second harmonic generated by using an LBO crystal was 11.1 mJ, and the corresponding conversion efficiency is 74%. Subsequently, β-BBO crystals were used to generate the fourth and fifth harmonics with maximum energies of 6.3 and 4.2 mJ, respectively, and the conversion efficiency was 42% and 28%, respectively. The accessible ranges of intensities at 263.2 and 210.5 nm in the collimated beam were up to 6.2 and 5.3 GW cm−2, respectively. The measured intensity-dependent transmittances of the ADP, KDP, 70% deuterated KDP, and DKDP crystal samples at 263.2 and 210.5 nm are shown in Fig. 7. According to eqn (6) and (7), we numerically fitted the experimental data by varying the value of the TPA coefficient, and the final results are listed in Table 5. In this experiment, the errors of the pulse duration determination (350–500 fs) and energy calibration (2–5%) were the main factors that contributed to the absolute error (<15%) in the TPA coefficient determination. Deep-UV laser sources have key applications in numerous fields including laser physics, plasma experiments, and industrial processing, and TPA is an important loss mechanism that affects the generation and propagation of high-intensity deep-UV laser radiation. However, as the key materials to obtain deep-UV laser sources, reports on the TPA coefficients of KDP-family crystals are fragmentary presently. Hence, the TPA coefficients systematically presented in Table 5 have great practical significance for understanding the generation, propagation, loss characteristics, and applications of deep-UV lasers in KDP-family materials.
| Crystal | Polarization | β @ 263.2 nm (cm/GW) | β @ 210.5 nm (cm/GW) | ||
|---|---|---|---|---|---|
| Experiment | Literature | Experiment | Literature | ||
| ADP | o | 0.37 | 0.25, 0.24, 0.11, 0.0623,35,38,39 | 1.67 | 1.223 |
| e | 0.26 | 1.54 | |||
| KDP | o | 0.25 | 0.27, 0.2635,40 | 1.59 | 1.36, 0.640,42 |
| e | 0.13 | 1.45 | |||
| 70% DKDP | o | 0.23 | 0.3241 | 1.56 | — |
| e | 0.10 | 0.1741 | 1.43 | — | |
| DKDP | o | 0.21 | 0.027, 0.0238,39 | 1.57 | — |
| e | 0.09 | 1.42 | — | ||
3.4 Discussion
Based on the results of the above optical characterization, it can be found that the KDP-family crystals are a class of optical materials with excellent performances in the deep-UV band, which makes them have important application potential in the generation of deep-UV laser sources. Especially the KDP and deuterated KDP crystals, compared with the ADP crystal, they not only have higher transmittance, shorter UV cut-off edge, and larger band-gap energy but also have weaker linear absorption and nonlinear TPA effects, which means that they have lower energy loss. And it can be further seen that the linear and nonlinear absorption effects at the wavelength of 210.5 nm are more obvious than those at 263.2 nm because the photon energy is higher and closer to the UV cut-off edge of the crystal. In addition, the measured results show that the e-light loss in the KDP-family crystals is generally lower than that of o light in the deep-UV region, whether linear absorption or nonlinear absorption. The results presented in the UV waveband are similar to those reported in the literature in the visible waveband.30,57 And, for the KDP crystals with different deuterium contents, there is no significant difference in these UV optical characteristics, which indicates that the deuterium content does not significantly enhance or weaken these properties. These parameters fully show that large-aperture KDP-family crystals are especially suitable for obtaining high-energy deep-UV lasers.4 Conclusion
We have systematically investigated the deep-UV absolute transmittances, cut-off edges, band-gap energies, linear absorption, and nonlinear TPA coefficients of a series of commonly used KDP-family crystals, including ADP, KDP, 70% deuterated KDP, and DKDP. Especially at the typical deep-UV wavelengths of 263.2 and 210.5 nm, the anisotropic linear and nonlinear absorption coefficients of the materials in the case of different polarization states were measured comprehensively. The results show that the KDP-family crystals have short UV cut-off edges, especially the KDP and deuterated KDP crystals, and their UV cut-off edges are close to 170 nm. In terms of absorption losses, both the linear absorption coefficients (0.0674–0.0916 cm−1 @ 263.2 nm and 0.31–0.357 cm−1 @ 210.5 nm) and TPA coefficients (0.26–0.37 cm/GW @ 263.2 nm and 1.54–1.67 cm/GW @ 210.5 nm) of the ADP crystal are higher than those of KDP and deuterated KDP crystals (0.0314–0.0535 cm−1 @ 263.2 nm, 0.125–0.183 cm−1 @ 210.5 nm, 0.09–0.25 cm/GW @ 263.2 nm, and 1.42–1.59 cm/GW @ 210.5 nm). For the KDP crystals with different deuterium contents, their UV cut-off edges, band-gap energies, and absorption coefficients are not significantly different. Since the KDP-family crystals have unparalleled large-scale growth characteristics of other water-soluble crystals, and the refractive index can be controlled by doping deuterium, these unique advantages endow the KDP-family crystals with broad application prospects in the fields of high-energy deep-UV laser generation, deep-UV optical devices, plasma experiments, and advanced scientific instruments. The obtained new optical data and conclusions in this work can provide key technical references for the growth and application in the deep-UV waveband of KDP-family crystals.Author contributions
Zijian Cui: conceptualization, methodology, investigation, and writing – original draft; Mingying Sun: investigation, validation, and resources; De'an Liu: project administration and writing – review & editing; Jianqiang Zhu: supervision and writing – review & editing. All authors have approved the final version of the manuscript.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The authors wish to thank Prof. Weili Zhang, Dr. Hu Wang, and Dr. Duanyang Chen from the Shanghai Institute of Optics and Fine Mechanics, CAS for the helpful discussion. This work was supported by the National Natural Science Foundation of China (Grants No. 12004404, No. 61975218, and No. 62105344); the Shanghai Sailing Program (Grant No. 18YF1425900); the “Strategic Priority Research Program” of the Chinese Academy of Sciences (Grant No. XDA25020202); and the Youth Innovation Promotion Association CAS (Grant No. 2018282).Notes and references
- D. Eimerl, Ferroelectrics, 1987, 72, 95–139 CrossRef CAS.
- N. Zaitseva and L. Carman, Prog. Cryst. Growth Charact. Mater., 2001, 43, 1–118 CrossRef CAS.
- M. Anis, S. Hussaini, M. Baig, M. I. Anis and E. E. S. Massoud, J. Mater. Sci.: Mater. Electron., 2021, 32, 23206–23214 CrossRef CAS.
- L. Rashkovich, KDP-Family Single Crystals, CRC Press, 1991 Search PubMed.
- I. P. Kaminow, Phys. Rev. Lett., 1961, 6, 528–530 CrossRef CAS.
- I. Shoji, T. Kondo, A. Kitamoto, M. Shirane and R. Ito, J. Opt. Soc. Am. B, 1997, 14, 2268–2294 CrossRef CAS.
- K. E. Montgomery and F. P. Milanovich, J. Appl. Phys., 1990, 68, 3979–3982 CrossRef CAS.
- F. Rainer, L. J. Atherton, J. H. Campbell, F. P. D. Marco, M. R. Kozlowski, A. J. Morgan and M. C. Staggs, Laser-Induced Damage in Optical Materials, 1992, pp. 116–127 Search PubMed.
- F. Rainer, L. J. Atherton and J. J. D. Yoreo, 24th Annual Boulder Damage Symposium Proceedings – Laser-Induced Damage in Optical Materials, 1993, pp. 46–58 CAS.
- J. Y. Natoli, J. Capoulade, H. Piombini and B. Bertussi, Laser-Induced Damage in Optical Materials, 2007, p. 672016 Search PubMed.
- H. Yoshida, T. Jitsuno, H. Fujita, M. Nakatsuka, M. Yoshimura, T. Sasaki and K. Yoshida, Appl. Phys. B., 2000, 70, 195–201 CrossRef CAS.
- D. Chen, B. Wang, H. Wang, X. Zhu, Z. Xu, Y. Zhao, S. Wang, K. Ni, L. Zheng, H. Zhang, H. Qi and J. Shao, High Power Laser Sci. Eng., 2020, 8, e6 CrossRef.
- Z. Cui, D. Liu, M. Sun, J. Miao and J. Zhu, J. Opt. Soc. Am. B, 2016, 33, 525–534 CrossRef CAS.
- Z. Cui, D. Liu, J. Miao, A. Yang and J. Zhu, Phys. Rev. Lett., 2017, 118, 043901 CrossRef PubMed.
- H. Tu, Y. Zhao, Y. Yue, F. Fan and Z. Hu, CrystEngComm, 2015, 17, 6669–6673 RSC.
- P. A. Baisden, L. J. Atherton, R. A. Hawley, T. A. Land, J. A. Menapace, P. E. Miller, M. J. Runkel, M. L. Spaeth, C. J. Stolz, T. I. Suratwala, P. J. Wegner and L. L. Wong, Fusion Sci. Technol., 2016, 69, 295–351 CrossRef.
- C. Cavailler, N. Fleurot, T. Lonjaret and J.-M. Di-Nicola, Plasma Phys. Controlled Fusion, 2004, 46, B135–B141 CrossRef.
- J. Zhu, J. Zhu, X. Li, B. Zhu, W. Ma, X. Lu, W. Fan, Z. Liu, S. Zhou, G. Xu, G. Zhang, X. Xie, L. Yang, J. Wang, X. Ouyang, L. Wang, D. Li, P. Yang, Q. Fan, M. Sun, C. Liu, D. Liu, Y. Zhang, H. Tao, M. Sun, P. Zhu, B. Wang, Z. Jiao, L. Ren, D. Liu, X. Jiao, H. Huang and Z. Lin, High Power Laser Sci. Eng., 2018, 6, e55 CrossRef.
- A. Shaykin, V. Ginzburg, I. Yakovlev, A. Kochetkov, A. Kuzmin, S. Mironov, I. Shaikin, S. Stukachev, V. Lozhkarev and A. Prokhorov, et al. , High Power Laser Sci. Eng., 2021, 9, e54 CrossRef CAS.
- S. Y. Mironov, I. B. Mukhin, V. V. Lozhkarev, A. K. Potemkin, M. A. Martyanov, I. V. Kuzmin and E. A. Khazanov, Appl. Opt., 2022, 61, 6033–6037 CrossRef CAS PubMed.
- Y. Guan, F. Wang, Y. Yang, D. Wang, X. Zhang, Q. Yuan, D. Hu, X. Deng, H. Ren, Y. Zheng and X. Chen, Chin. Opt. Lett., 2021, 19, 031901 CrossRef.
- Z. Cui, L. Han, C. Wang, M. Sun, D. Liu and J. Zhu, Opt. Lett., 2022, 47, 2947–2950 CrossRef CAS PubMed.
- I. A. Begishev, G. Brent, S. Carey, R. Chapman, I. A. Kulagin, M. H. Romanofsky, M. J. Shoup, J. D. Zuegel and J. Bromage, Opt. Express, 2021, 29, 1879–1889 CrossRef CAS PubMed.
- T. Sasaki and A. Yokotani, J. Cryst. Growth, 1990, 99, 820–826 CrossRef CAS.
- N. Zaitseva, J. Atherton, R. Rozsa, L. Carman, I. Smolsky, M. Runkel, R. Ryon and L. James, J. Cryst. Growth, 1999, 197, 911–920 CrossRef CAS.
- G. Dhanaraj, K. Byrappa, V. Prasad and M. Dudley, Springer Handbook of Crystal Growth, Springer Science & Business Media, 2010 Search PubMed.
- M. Xu, L. Zhang, F. Liu, S. Wang, Y. Lian, F. Wang, Z. Wang, X. Xu, X. Sun and S. Sun, Cryst. Res. Technol., 2018, 53, 1700298 CrossRef.
- L. Zhang, S. Wang, H. Liu, L. Xu, X. Li, X. Sun and B. Wang, Rengong Jingti Xuebao, 2021, 50, 724–731 Search PubMed.
- M. Xu, B. Liu, L. Zhang, H. Ren, Q. Gu, X. Sun, S. Wang and X. Xu, Light: Sci. Appl., 2022, 11, 1–15 CrossRef.
- D. Wang, T. Li, S. Wang, J. Wang, Z. Wang, J. Ding, W. Li, C. Shen, G. Liu and P. Huang, CrystEngComm, 2016, 18, 9292–9298 RSC.
- L. Zhang, S. Wang, H. Yang, W. Cheng, H. Liu, X. Li, B. Wang, S. Wang and Y. Li, Opt. Laser Technol., 2022, 156, 108538 CrossRef CAS.
- V. T. Phan, K. D. Nguyen, D. T. Nguyen, T. V. A. Le, T. V. V. Nguyen and H. V. T. Le, Opt. Mater., 2022, 124, 112014 CrossRef CAS.
- W. L. Smith, Appl. Opt., 1977, 16, 1798–1798 CrossRef CAS.
- D. N. Nikogosyan, Nonlinear Optical Crystals: A Complete Survey, Springer Science & Business Media, 2005 Search PubMed.
- P. Liu, W. L. Smith, H. Lotem, J. H. Bechtel, N. Bloembergen and R. S. Adhav, Phys. Rev. B: Solid State, 1978, 17, 4620–4632 CrossRef CAS.
- C. S. Liu, N. Kioussis, S. G. Demos and H. B. Radousky, Phys. Rev. Lett., 2003, 91, 015505 CrossRef CAS PubMed.
- A. Dyan, G. Duchateau, S. Eslava, J. L. Stehle, D. Damiani and H. Piombini, J. Mod. Opt., 2009, 56, 27–31 CrossRef CAS.
- J. Reintjes and R. Eckardt, IEEE J. Quantum Electron., 1977, 13, 791–795 CrossRef.
- J. Reintjes and R. C. Eckardt, Appl. Phys. Lett., 1977, 30, 91–93 CrossRef CAS.
- A. Dubietis, G. Tamošauskas, A. Varanavičius and G. Valiulis, Appl. Opt., 2000, 39, 2437–2440 CrossRef CAS PubMed.
- X. Chai, Q. Zhu, B. Feng, F. Li, X. Feng, F. Wang, W. Han and L. Wang, Opt. Mater., 2017, 64, 262–267 CrossRef CAS.
- G. G. Gurzadyan and R. K. Ispiryan, Appl. Phys. Lett., 1991, 59, 630–631 CrossRef CAS.
- M. Anis, G. G. Muley, M. D. Shirsat and S. S. Hussaini, Cryst. Res. Technol., 2015, 50, 372–378 CrossRef CAS.
- M. Anis, D. A. Hakeem and G. G. Muley, Results Phys., 2016, 6, 645–650 CrossRef.
- M. Anis, G. G. Muley, M. I. Baig, S. S. Hussaini and M. D. Shirsat, Mater. Res. Innovations, 2017, 21, 439–446 CrossRef CAS.
- M. I. Baig, M. Anis and G. G. Muley, Opt. Mater., 2017, 72, 1–7 CrossRef CAS.
- M. Anis, M. Shkir, S. AlFaify, M. I. Baig, A. M. Alshehri and H. Algarni, Mater. Chem. Phys., 2020, 246, 122809 CrossRef CAS.
- D. Damiani, H. Piombini and D. Plessis, Laser-Induced Damage in Optical Materials, 2005, pp. 540–549 Search PubMed.
- T. Sui, L. Wei, Y. Lian, M. Xu, L. Zhang, Y. Li, X. Zhao, X. Xu and X. Sun, CrystEngComm, 2020, 22, 1962–1969 RSC.
- W. Ding, J. Cheng, L. Zhao, Z. Wang, H. Yang, Z. Liu, Q. Xu, J. Wang, F. Geng and M. Chen, Nanoscale, 2022, 14, 10041–10050 RSC.
- L. Ye, Z. Li, G. Su, X. Zhuang and G. Zheng, Opt. Commun., 2007, 275, 399–403 CrossRef CAS.
- K. Wang, C. Fang, J. Zhang, X. Sun, S. Wang, Q. Gu, X. Zhao and B. Wang, J. Cryst. Growth, 2006, 287, 478–482 CrossRef CAS.
- C. D. Marshall, J. A. Speth, L. D. DeLoach and S. A. Payne, Solid State Lasers for Application to Inertial Confinement Fusion: Second Annual International Conference, 1997, pp. 343–363 Search PubMed.
- N. Zaitseva, L. Carman, I. Smolsky, R. Torres and M. Yan, J. Cryst. Growth, 1999, 204, 512–524 CrossRef CAS.
- M. Pommiès, D. Damiani, B. Bertussi, J. Capoulade, H. Piombini, J. Y. Natoli and H. Mathis, Opt. Commun., 2006, 267, 154–161 CrossRef.
- M. Pommiès, D. Damiani, X. Le Borgne, C. Dujardin, A. Surmin, J. C. Birolleau, F. Pilon, B. Bertussi and H. Piombini, Opt. Commun., 2007, 275, 372–378 CrossRef.
- L. Xu, C. Lu, S. Wang, P. Huang, H. Liu, L. Zhang, X. Li, B. Wang and D. Wang, CrystEngComm, 2020, 22, 5338–5344 RSC.
- P. Makuła, M. Pacia and W. Macyk, J. Phys. Chem. Lett., 2018, 9, 6814–6817 CrossRef.
- S. Patankar, S. T. Yang, J. D. Moody, G. F. Swadling, A. C. Erlandson, A. J. Bayramian, D. Barker, P. Datte, R. L. Acree, B. Pepmeier, R. E. Madden, M. R. Borden and J. S. Ross, Appl. Opt., 2017, 56, 8309–8312 CrossRef CAS PubMed.
- C. H. Huang, G. Zhang, Z. Q. Chen, X. J. Huang and H. Y. Shen, Opt. Laser Technol., 2002, 34, 209–211 CrossRef CAS.
- G. Ghosh and G. Bhar, IEEE J. Quantum Electron., 1982, 18, 143–145 CrossRef.
- V. V. Lozhkarev, G. I. Freidman, V. N. Ginzburg, E. A. Khazanov, O. V. Palashov, A. M. Sergeev and I. V. Yakovlev, Laser Phys., 2005, 15, 1319–1333 CAS.
- M. Rumi and J. W. Perry, Adv. Opt. Photonics, 2010, 2, 451–518 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |