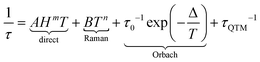Isotopic enrichment in lanthanide coordination complexes: contribution to single-molecule magnets and spin qudit insights

Abstract

Lanthanide Single-Molecule Magnets (SMMs) fascinate the scientific community due to their plethora of potential applications ranging from data storage to spintronic devices and quantum computing. This review article proposes a comprehensive description of the influence of the nuclear spin, i.e. hyperfine interaction, on the magnetic properties of lanthanide SMMs and on quantum information processing of qudit. This influence is analysed for non-Kramers and Kramers lanthanide SMMs as well as for the electronic distribution of the electron in 4f orbitals i.e. oblate and prolate ions. Then the role of magnetic interactions in isotopically enriched polynuclear Dy(III) SMMs is discussed. Finally the possible effect of superhyperfine interaction due to the nuclear spin of elements originating from the surrounding of the lanthanide centre is analyzed. The effect of nuclear spin on the dynamics of the lanthanide SMMs is demonstrated using different techniques such as magnetometry, muon spectroscopy (μ-SR), and Mössbauer and Resonance Vibrational Spectroscopies.

---

Fabrice Pointillart

Fabrice Pointillart obtained his PhD in physics and chemistry of materials from Pierre et Marie Curie University in 2005, supervised by Prof. Cyrille Train and Prof. Michel Verdaguer. After postdoctoral research at the University of Florence with Prof. Roberta Sessoli he joined the University of Rennes in 2007, as a CNRS researcher. He has been awarded the CNRS Bronze Medal (2014) and Young researcher Coordination Chemistry Division (2017). His current research interests are focused on multifunctional molecular materials based on lanthanides combining magnetic and (chir)optical properties for the observation of single molecule magnet behaviour, magneto-chiral dichroism and circularly polarized luminescence.

Kevin Bernot

Kevin Bernot received his PhD in Inorganic Chemistry in 2007 under the supervision of Prof. O. Guillou (INSA Rennes, France) and Prof. A. Caneschi (University of Florence, Italy) working on lanthanide-radical systems. After a post-doc under the supervision of Prof R. Sessoli dedicated to single-crystal magnetometry he joined INSA Rennes in 2008. His research activities focus on lanthanides coordination chemistry for the design of molecules, material and devices with luminescent and/or magnetic properties. He has been a full professor at INSA-Rennes since 2021.

Boris Le Guennic

Boris Le Guennic received his PhD in Chemistry from the University of Rennes in 2002. He then successively moved to the Universities of Erlangen, Buffalo, and Bonn for postdoctoral stays in the groups of Profs. Jochen Autschbach and Markus Reiher. In 2005, he was appointed as a CNRS researcher at ENS de Lyon (France). In 2011, he moved to the Chemical Sciences Institute of Rennes (University of Rennes, France) where he is currently a Senior CNRS researcher. He has been the head of the Inorganic Theoretical Chemistry Team since 2018. His research is devoted mainly to the application of quantum chemical methodologies for the interpretation of magnetic and (chir-)optical properties in transition metal and f-element complexes, with a particular emphasis on lanthanide-based Single Molecule Magnets.

Olivier Cador

The research activities of Olivier Cador started in 1994 in Bordeaux (France). From its beginnings he contributed to the development of molecular magnetism under different aspects. He mainly focused on the studies of the magnetic properties of systems with various dimensionalities, from nanoparticles to isolated molecules which show quantum behaviours, and finally to magnets with atypical behaviours. Since he was recruited by the University de Rennes 1 in 2003 its research studies have oriented toward multifunctional molecular-based materials. He oriented part of its activities on Single-Molecule Magnets (SMMs); more particularly those based on lanthanides. He has been a full Professor at Université de Rennes since 2017.

---

1. Introduction

Frederick Soddy forged the term ‘isotope’ about 110 years ago and he received the Nobel prize of chemistry a few years later (1921) for his pioneering research in this field. Historically, the concepts of isotope and radioactivity have been intimately linked because for a given chemical element a large number of nuclides (isotopes) are radioactive and disintegrate. There are thousands of nuclides, natural and artificially produced, but only about 1000 with half-lives longer than one hour and only about 250 are observationally stable. There exist plenty of applications for radioactive nuclides (dating, nuclear power plants, nuclear medicine, tracers, markers, sterilization…) and they all use disintegration processes.^1–5 Stable isotopes are mostly used for identification since natural isotopic abundances are fixed for each element. The masses of the nuclei are then the key factors used to identify the different isotopes, including isotope fractionation of light elements. Indeed, for light elements, variations in the mass number even of one unit affect significantly the mass of an atom and then its inertia. For heavier elements, this fractionation becomes less obvious due to smaller variations in the mass number.^6,7

As far as the electronic properties are concerned, such as conductivity and/or magnetism, few efforts have involved isotopic effects.^8–11 Substitution of ¹²C by ¹³C changes the ordering temperature of superconductors while replacing ¹⁶O with ¹⁸O shifts the ferromagnetic Curie temperature by 20 K, from 210 K down to 190 K, respectively.^12–21 Nevertheless, all these results are related to mass effects through electron–phonon interactions. When chemists go down the periodic table this mass number effect becomes less obvious but variation of the number of neutrons changes nuclear spins which can be coupled to the electrons through hyperfine coupling. EPR spectroscopy intensively uses hyperfine (or super-hyperfine) coupling to characterize species with single electrons^22,23 regardless of the metal centred or organic radicals. Historically, isotopes in molecular magnetism^24–31 have never really been discussed because it was commonly considered that the contribution of nuclear spins to the global magnetism is negligible when single electrons are present.

Molecular magnetism developed principally around the concept of molecular magnets which is, strictly speaking, an electronic property that allows a chemical object to retain magnetic memory in a zero external field (magnetic remanence). The first molecular magnets were based on the concept of magnetic ordering, and therefore on interactions between electronic magnetic moments that propagate in a 3D array.^32,33 In the last thirty years the so-called Single-Molecule Magnets (SMMs) have emerged.³⁴ Their specificity is to be able to store magnetic information at the molecular level thanks to axial magnetic anisotropy that hampers microscopic magnetization to flip freely between two opposite orientations. In this prolific field of research lanthanide-based complexes have the lead because they present the largest axial magnetic anisotropy and a wide variety of coordination polyhedron geometry.³⁵ Magnetic anisotropy is monitored by the height of the energy barrier and the magnetic moment needs to jump to flip its orientation with a barrier height of about a few thousands of wavenumbers.^36–38 This barrier can also be crossed through Quantum Tunnelling of Magnetization (QTM). This of course weakens the memory since it offers a possibility for the magnetic moment to relax rapidly from one side to the other but, at the same time, it gives an opportunity to deal with quantum mechanics. There are several origins of QTM but all of them are related to the admixture of quantum states that are on both sides of the energy barrier. Hyperfine coupling is one of them^39,40 and at this stage one should look at the periodic table of (stable) isotopes, their nuclear spins and how such atoms have been used to produce SMMs. All the SMMs (in zero field) to date are made of 3d transition metal ions or lanthanides at the exception, to the best of our knowledge, of one Uranium-based complex.⁴¹ Most of the 3d-based zero-field SMMs are based on polynuclear complexes in which superexchange interactions take place. These interactions are orders of magnitude stronger than hyperfine coupling and therefore tend to dilute its effect. In order to avoid perturbation of the electronic system by exchange (or superexchange) interaction one should focus on SMMs based on single ions (the so-called Single-Ion Magnets even if the terminology can be a subject of debate). From a 3d ion point of view, only iron–based^42,43 and cobalt-based^44–46 zero-field SIM are known. Since natural cobalt is monoisotopic (100% ⁵⁹Co) all the experimental data will correspond to the nuclear spin I = 7/2. This allowed the investigation of ⁵⁹Co based-complexes by NMR showing the effect of magnetic nuclei on electronic effects as well as how the isotopic enrichment on the ligands affected the ligand field.⁴⁷ For iron the situation is opposite since natural iron is dominated by nuclear spin free isotopes (91.7% ⁵⁶Fe and 5.8% ⁵⁴Fe) and only 2.1% of the nuclear spin active (I = 1/2) ⁵⁷Fe. Then, in principle, one should be able to compare SMMs based on ⁵⁷Fe with the ones based on ⁵⁶Fe. This has been done on a polymetallic species and this pioneering work demonstrated that in the quantum regime the presence (or the absence) of nuclear spin at metal sites significantly modifies the relaxation of the magnetic moment of the molecule.^48–51 Probably, the small number of mononuclear SMMs based on 3d ions limits the efforts on the effects of the isotopic enrichment on magnetic properties.^42–46

The first reason why lanthanide ions are the best elements to investigate the effects of isotopic enrichment on the magnetic properties of mononuclear SMMs is the number of candidates that can be drafted. Even if we restrain ourselves to mononuclear species at oxidation number +3 that operate as a magnet in the absence of any external static field one can end with hundreds of chemical edifices in both coordination and organometallic chemistry. The second reason is that the lanthanide series offers more choice since obviously 14 ions are concerned and also because a simple look at a periodic table of stable isotopes is more coloured on the lanthanide line than on the 3d line. Table 1 lists the 14 stable lanthanide elements with the most abundant isotopes. Promethium apart, five elements are constituted of only one stable isotope (La, Pr, Tb, Ho and Tm) but all with nuclear spins different from zero. These elements can be used to probe hyperfine interaction from one single nucleus without any further isotopic separation. However, since the oxidation number +3 is by far the most stable there is no hyperfine coupling for La(III) since it is diamagnetic and, interestingly, the four others are non Kramers ions. One must consider that Lu(III) enters in the same category as La(III) with no single electrons. Eu(III) multiplet ground state (4f⁶, ⁷F₀) is also diamagnetic but because orbital and spin moments compensate each other's. Ce(III) is made of two different isotopes but both are nuclear spin free with no hyperfine coupling as well. With Gd it is possible to tune the nuclear spin between 0 and 3/2 but Gd(III) is a spin pure ion with no orbital contribution and therefore with no magnetic anisotropy.

Table 1 List of the 14 stable lanthanide elements with the mass numbers of the most stable isotopes. Their natural abundance is given in brackets with nuclear spin values.⁵²

Element	Kramers/Non-Kramers^a	Z	A = mass number, in brackets the natural abundance and the nuclear spin number for A^b
a Trivalent ions. b Nuclear spin abundance rounded to the %.
La	—	57	A = 139 (100%, I = 7/2)
Ce	K	58	A = 140 (89%, I = 0), 142 (11%, I = 0)
Pr	NK	59	A = 141 (100%, I = 5/2)
Nd	K	60	A = 142 (27%, I = 0), A = 143 (12%, I = 7/2), A = 144 (24%, I = 0), A = 145 (8%, I = 7/2), A = 146 (17%, I = 0), A = 148 (6%, I = 0), A = 150 (6%, I = 0)
Sm	K	62	A = 144 (3%, I = 0), A = 147 (15%, I = 7/2), A = 148 (11%, I = 0), A = 149 (14%, I = 7/2), A = 150 (7%, I = 0), A = 152 (27%, I = 0), A = 154 (23%, I = 0),
Eu	NK	63	A = 151 (48%, I = 5/2), 153 (52%, I = 5/2),
Gd	K	64	A = 154 (2%, I = 0), A = 155 (15%, I = 3/2), A = 156 (21%, I = 0), A = 157 (16%, I = 3/2), A = 158 (25%, I = 0), A = 160 (22%, I = 0),
Tb	NK	65	A = 159 (100%, I = 3/2)
Dy	K	66	A = 160 (2%, I = 0), A = 161 (19%, I = 5/2), A = 162 (25%, I = 0), A = 163 (25%, I = 5/2), A = 164 (28%, I = 0),
Ho	NK	67	A = 165 (100%, I = 7/2)
Er	K	68	A = 164 (2%, I = 0), A = 166 (33%, I = 0), A = 167 (23%, I = 7/2), A = 168 (27%, I = 0), A = 170 (15%, I = 0),
Tm	NK	69	A = 169 (100%, I = 1/2)
Yb	K	70	A = 170 (3%, I = 0), A = 171 (14%, I = 1/2), A = 172 (22%, I = 0), A = 173 (16%, I = 5/2), A = 174 (32%, I = 0), A = 176 (13%, I = 0),
Lu	—	71	A = 175 (97%, I = 7/2), A = 176 (3%, I = 7)

---

This element is therefore out of the launch window of zero-field mononuclear SMMs. In the end, five Ln(III) elements possess an electronic magnetic moment with substantial magnetic anisotropy and stable isotopes with various nuclear spins: Nd, Sm, Dy, Er and Yb. These five elements are Kramers ions as far as the oxidation number +3 is retained. In the next sections we will survey the recent works dealing with isotopic features of SMMs without being exhaustive but focusing on key examples. We will target Kramers and non-Kramers ions, ligand's nuclei isotopic substitution and finally address the perspective of isotopologues for qudits applications.

2. Slow relaxation of magnetic moment as a signature of single-molecule magnet

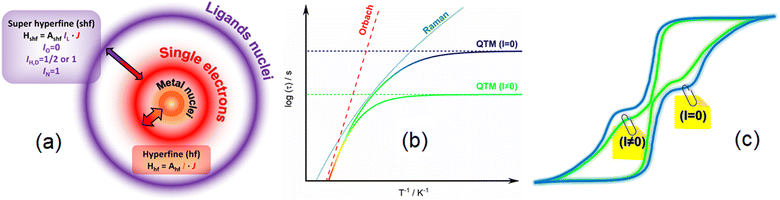
By definition a magnet operates in the absence of an external stimulus and so, in a zero external static field. The opening of the magnetic hysteresis loop at zero field is the ultimate signature of the magnetic memory with the magnetic moment that can be oriented in two opposite directions. However, even if the terminology “permanent magnet” is widely employed one should keep in mind that the magnetic memory depends on time scale and temperature scale. This memory effect disappears at very long time scales and so cannot be viewed as a static property but more in a dynamic perspective. In this dynamic framework, the time it takes for the magnetic moment to align parallel to the external field corresponds to the relaxation time. Magnetometry in an alternating magnetic field provides an experimental tool that gives access to this kind of relaxation time in a relatively large time window: in the absence of relaxation the magnetization is in-phase and follows instantaneously the oscillation of the external field, while in the presence of relaxation processes the magnetization is delayed and an out-of-phase component appears. There are basically four different processes that govern the relaxation time τ of the magnetic moments in matter that depend on temperature (T) and external magnetic field (H).⁵³

In the previous equation the first three terms involve coupling between spin and phonons and are temperature dependent while the last term is temperature independent and refers to the tunnelling of the magnetization between two opposite directions of the magnetic moment. The direct process implies the application of an external static field and does not operate in zero field. The thermal variations of the relaxation time in a zero external dc field is represented on Scheme 1b with the separated contribution of Raman, Orbach and QTM terms. The fastest process wins and so, QTM takes the lead at the lowest temperature and Orbach at the highest, and eventually Raman in an intermediate regime. Since hyperfine coupling between nuclear spins and electronic spins contributes to QTM we differentiated on Scheme 1b contributions from a hypothetic nuclear spin free system with I = 0 (slow) or I ≠ 0 (fast). At this stage it is important to mention that the coupling between spin and nuclei can occur through hyperfine coupling but also through superhyperfine coupling with the nuclei of ligands (Scheme 1a) for which selection of isotopes is also possible. The application of an external static field suppresses the possibility for the magnetic moment to tunnel through the barrier so the relaxation becomes much slower in this field. This creates butterfly shaped hysteresis curves (Scheme 1c) with an opening at the origin that can be modulated by playing with isotopes.

Scheme 1 (a) Scheme of the hyperfine interaction (hf) between the metal nuclei (I, orange) and the single electrons and super-hyperfine interaction (shf) between the single electrons and the ligands nuclei (I_L, purple). (b) Thermal variation of the relaxation time with representation of the three main relaxation mechanisms: Orbach (red), Raman (turquoise blue) and QTM for I = 0 (blue) and I ≠ 0 (green). (c) Scheme of hysteresis loops for two isotopologues with I = 0 (blue) and I ≠ 0 (green).

3. Hyperfine interactions influence slow magnetic relaxation

3.1. Naturally pure isotopic non-Kramers lanthanide SMM

3.1.1. Terbium element. Terbium has a 100% natural abundance of ¹⁵⁹Tb, that possesses a nuclear spin of I = 3/2. In other words, any coordination complex made from this metal ion can be described as an isotopically pure compound.

The first magnetic investigation of the nuclear spin effect was performed in 2005 by W. Wernsdorfer and colleagues⁵⁴ on the bis(phthalocyaninato)terbium anion [Pc₂Tb]⁻ (1) (Pc = dianion of phthalocyanine) deeply explored for its remarkable SMM properties some years before.^55–57 The latter coordination complex displayed magnetic relaxation occurring through the thermally activated Orbach process above 25 K.^58,59 Clear evidence of QTM was highlighted on a diluted sample of 1 in an Y(III) diamagnetic isomorphous matrix (1@Y) to cancel the intermolecular dipolar interactions.⁶⁰ This investigation was possible thanks to magnetic hysteresis measurements at very low temperature (0.04 K) using the micro-SQUID technique (SQUID = Superconducting QUantum Interference Device)^61,62 with the magnetic field aligned parallel to the easy axis of magnetization by the transverse field method.⁶³ The QTM in 1@Y resulted in a staircase-like structure of the hysteresis loop and was attributed to the interaction between the electronic spin (4f⁸, J = 6) and the nuclear spin (I = 3/2). Thus, the Zeeman diagram for the eight ∣J_z〉∣I_z〉 states created from the combination of the J_z = ±6 doublets and I = 3/2 quartets gave level intersections at 13 different magnetic-field positions which are all observed in the experimental hysteresis loop. The 13 step positions were reproduced by using A_hf = 0.0173 cm⁻¹ and P = 0.010 cm⁻¹ where A_hf is the constant of the hyperfine interaction (A_hfJI) and P is the constant of the nuclear quadrupole interaction term (P{I_z² − 1/3I(I + 1)}).

3.1.2. Holmium element. As for Terbium, Holmium has a 100% natural abundance of ¹⁶⁵Ho, that possesses a nuclear spin of I = 7/2. Concomitantly to the magnetic investigation of 1@Y, the same authors studied the Ho(III) analogue (2@Y).⁶⁴ The conclusions are identical to 1@Y, namely that the resonant quantum tunnelling between entangled states of the electronic (J_z = ±5) and nuclear spin (I = 7/2) systems is responsible for the quantum process. More than a decade later, M.-L. Tong and colleagues investigated another non-Kramers Ho(III) mononuclear SMM of formula [Ho(CyPh₂PO)₂(H₂O)₅](I)₃·2(CyPh₂PO)·H₂O·EtOH (Cy = cyclohexyl) (3) (Fig. 1a).³⁹ The high SMM performance of 3 was attributed to the D_5h symmetry of the pentagonal-bipyramidal geometry of the Ho(III) coordination sphere leading to the suppression of the QTM in zero applied magnetic field, mainly attributed to the hyperfine interactions. These hyperfine interactions between the J = 8 electronic spin and the I = 7/2 nuclear spin of ¹⁶⁵Ho were detected by the occurrence of multiple peaks in the field dependence of the relaxation time using alternating-current (AC) susceptibility measurements (Fig. 1b) as well as the steps on the hysteresis loops (Fig. 1c and d).

Fig. 1 (a) Representation of the molecule of 3. Iodine anion, free oxophosphine and solvent molecules of crystallization are omitted for clarity. Ho: light green, P: orange, O: red, C: grey, H: white. (b) Zeeman energy diagram (green lines) and field dependence of the relaxation time determined by AC measurements at 8 K for 3 (blue) and 3@Y (red). Grey circles represent the avoided level crossing due to the hyperfine interactions. Inset: Zoom view at zero field for the lowest doublet with (green) and without (purple) hyperfine interactions. (c) Normalized magnetic hysteresis loops for a single crystal of 3. (d) Derivatives of the hysteresis loops with predicted magnetic field positions of the avoided level crossings (black dashed lines). Adapted with permission from ref. 39. Copyright 2017, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.

In 2021, M.-L. Tong and colleagues reported a 3d4f heterobimetallic SMM of formula HoNi₅(quinha)₅F₂(dfpy)₁₀](ClO₄)·2EtOH (4) where H₂quinha = quinaldichydroxamic acid and dfpy = 3,5-difluoropyridine.⁶⁵ The Ho(III) is surrounded by the metallacrown and two axial fluoride ions leading to a similar D_5h pentagonal-bipyramidal geometry than in 3. 4 displayed slow magnetic relaxation with a record energy barrier of 577 cm⁻¹ for a Ho(III) based SMM. The introduction of the [15-MCNi-5] metallacrown induced incoherent QTM with field dependent oscillation of the barrier height and of the relaxation time. This field dependence was attributed to the joint effect of the hyperfine interactions at the Ho(III) ion and the exchange coupling with surrounding Ni(II) ions. This phenomenon is promising for the manipulation of memory spin qubits.

Hyperfine interactions have also been studied for single atom magnets (SAMs). Especially Holmium SAMs have been deposited on the MgO(100) surface.⁶⁶ When adsorbed on this surface, holmium atoms have a J = 8 ground state manifold which is split by the crystal field created by the on-top oxygen adsorption site.⁶⁷ X-ray magnetic circular dichroism (XMCD) allowed the measurement of long-lived magnetization lifetimes. Nevertheless, the zero-field stability of Ho on the MgO surface required the use of antiferromagnetic spin-polarized scanning tunnelling microscopy (SP-STM).⁶⁷ This stability allowed identification of the ground state J_z = ±8 and the existence of avoided level crossings that couple the positive and negative spin manifolds and allow transitions via Landau–Zener tunnelling.

The magnetic investigations at very low temperature of single atom and single ion magnets involving Tb(III) and Ho(III) non-Kramers ions, demonstrated that the non-zero nuclear spin provides significant hyperfine interaction. In the case of non-Kramer ions, the hyperfine interaction participates to cancel the QTM at zero field while it provokes avoided level crossings leading to field-induced QTM. Finally, the Zeeman diagram can be established if the following three components are considered: crystal field, hyperfine interaction and nuclear quadrupole interaction.

3.2. Isotopically enriched Kramers lanthanide SMM

3.2.1. Mononuclear dysprosium-SMM. All other lanthanides likely to give rise to SMM behaviour are found with an isotopic composition with various nuclear spin values. Indeed, for Dysprosium, seven stable isotopes can be found with I = 5/2 for ¹⁶¹Dy (18.91%) and ¹⁶³Dy (24.90%) while the five other isotopes ¹⁵⁶Dy (0.06%), ¹⁵⁸Dy (0.01%), ¹⁶⁰Dy (2.34%), ¹⁶²Dy (25.51%) and ¹⁶⁴Dy (28.18%) have an I = 0 (see Table 1). It is worth noticing that the Dy(III) ion possesses an oblate electronic distribution. The influence of the I value i.e. the presence or not of hyperfine interaction on the magnetic dynamics of a Dy(III) SMM was investigated by us in 2015 on a mononuclear complex of formula [Dy(tta)₃(L¹)]·C₆H₁₄ (5) (tta⁻ = 2-thenoyltrifluoroacetonate and L¹ = 4,5-bis(propylthio)-tetrathiafulvalene-2-(2-pyridyl)benzimidazole methyl-2pyridine) (Fig. 2a).⁶⁸ After magnetic dilution in an Y(III) diamagnetic isomorphous matrix to cancel the dipolar interactions, isotopic enrichments in ¹⁶¹Dy (¹⁶¹5@Y) and ¹⁶⁴Dy (¹⁶⁴5@Y) were realized. The natural isotope displayed magnetic relaxation through a combination of Orbach and QTM processes.⁶⁹ The latter process comes from mixing of the |J_z = ±15/2〉 and |J_z = ± 13/2〉 components in the frame of the crystal field theory by combination of the different Stevens operators acting in low symmetry.²² Then the hyperfine coupling H_hf = A_hfIJ allows the coupling between electronic and nuclear spins giving rise to QTM^40,64 due to the mixing of |J_z = ±15/2〉 and |J_z = ±13/2〉 through the transverse component. The ac susceptibility investigation highlighted that ¹⁶⁴5@Y relaxed about 10 times slower than ¹⁶¹5@Y at 2 K due to the decreasing efficiency of QTM by cancellation of hyperfine interaction while the relaxation times are not changed in the Orbach regime (T > 10 K) (Fig. 2b). A few years later, the relaxation time of the magnetization of the pure isotopic SMM ¹⁶¹5 and ¹⁶⁴5 was probed using muon spin spectroscopy (μ-SR, Fig. 2d).⁷¹

Fig. 2 (a) Representation of the molecule of 5, n-hexane molecule of crystallization is omitted for clarity. (b) Thermal variation of the relaxation time of the magnetization for 5 (black dots), ¹⁶¹5 (blue dots), ¹⁶²5 (orange dots), ¹⁶³5 (green dots), ¹⁶⁴5 (red dots), ¹⁶¹5@Y (blue circles), ¹⁶²5@Y (orange circles), ¹⁶³5@Y (green circles) and ¹⁶⁴5@Y (red circles) in a zero applied magnetic field in the temperature range of 2–15 K. Full lines are a guide for the eyes. (c) The normalized magnetic hysteresis loop at 0.46 K and a sweep rate of 16 Oe s⁻¹ for ¹⁶²5 (orange line) and ¹⁶³5 (green line). In the inset is a zoomed view of the origin. Adapted from ref. 69–72. (d) Thermal variation of the relaxation times extracted from ac susceptibility (full symbols) and μSR (empty symbols) for ¹⁶¹5 (red) and ¹⁶⁴5 (blue).

This study showed that the trend seen using standard magnetometry is confirmed via a local probe technique that captures fine details of the spin dynamics.

A step forward in the hyperfine interaction effect on SMM magnetic dynamics was achieved with the highlighting of the hyperfine constant (A_hf) effect. Indeed, the study of the two pure isotopes ¹⁶¹5@Y and ¹⁶³5@Y both with I = 5/2 but with different A_hf values demonstrated that ¹⁶¹5@Y relaxed four times slower than ¹⁶³5@Y because A_hf for ¹⁶¹5 < A_hf¹⁶³5.⁷² The consequences of hyperfine interactions on the magnetic relaxation are visible on the hysteresis loops measured at 0.46 K with a magnetic bistability in zero-magnetic field for the nuclear spin free ¹⁶²5@Y compound while the hysteresis loop is closed for ¹⁶³5@Y (Fig. 2c). One could also observe a staircase-like structure of the hysteresis loop for ¹⁶³5@Y because the hyperfine interactions provoke avoided level crossings leading to field-induced QTM.

This hyperfine interaction effect on dynamics of SMM was also confirmed on a different molecular system involving the same Dy(tta)₃ unit associated with a different TTF-based ligand (4,5-bis(methylthio)-tetrathiafulvalene-2-(benzothiazole-2pyridine)).⁷³

Finally, the two nuclear spin isomers of the magnetically diluted Dy(III) analogue of 1 were studied in case of the tetraethyl ammonium salt.⁷⁴ While both Et₄N[¹⁶³Dy@YPc₂] (¹⁶³6@Y) and Et₄N[¹⁶³Dy@YPc₂] (¹⁶⁴6@Y) displayed slow magnetic relaxation, the nuclear spin free ¹⁶⁴6@Y is designed for SMM applications whereas ¹⁶³6@Y could be used as a multilevel nuclear spin qubit (called qudit with d = 6) for quantum information processing (see part 4 of this review).

In 2019, the isotopic enrichment of lanthanide SMMs allowed us to suggest the existence of another phenomenon at the origin of fast relaxation of the magnetization at zero applied magnetic field.⁷⁵ The three SMMs of formula [Dy(^tBuO)Cl(THF)₅][BPh₄] (7),⁷⁶ [K(18-crown-6-ether)(THF)₂][Dy(BIPM)₂] (8)⁷⁷ (BIPM = C{PPh₂NSiMe₃}₂) and [Dy(Cp^ttt)₂][B(C₆F₅)₄] (9) (Cp^ttt = C₅H₂^tBu₃-1,2,4)³⁷ were selected because of their high energy barrier. The hysteresis loops of the natural isotope samples, magnetically diluted samples and ¹⁶⁴Dy isotope and diluted samples were measured and compared showing that neither dipolar interactions nor hyperfine interaction are solely responsible for the QTM at zero field. The authors demonstrated that the vibrational modes that most impact the first Dy(III) coordination sphere, are active at energies which follow the trend 7 < 8 < 9. These energies can be correlated with the coercive field values of the complexes. Therefore, the authors suggested that molecular vibrations could be at the origin of the fast relaxation of the magnetization at zero field through a so-called “vibrational QTM”.

The same year, the possibility of synthesizing pure isotope lanthanide SMM opens the way to the use of spectroscopies such as Synchrotron Mössbauer Spectroscopy (SMS). Local moments and spin-relaxation dynamics were already determined in iron-containing SMMs using ⁵⁷Fe Mössbauer spectroscopy^78–81 but this technique has not yet been used to investigate the magnetic properties of lanthanide SMMs. V. Schünemann, A. K. Powell and colleagues carried out ¹⁶¹Dy time-domain SMS using ¹⁶¹Dy nucleus and hyperfine interaction as a probe for the dysprosium magnetization.⁸² Thus the authors were able to determine the magnetic hyperfine field of the isotopologue [¹⁶¹Dy(Cy₃PO)₂(H₂O)₅]Br₃·2(Cy₃PO)·2H₂O·2EtOH (10) (Cy₃PO = tricyclohexylphosphine oxide)⁸³ with a value of 582.3(5) T which is significantly larger than that of the free-ion Dy(III) with M_J = ±15/2 as the ground state.^84–86 The difference was attributed to the Fermi contact between the s and 4f electrons of the Dy(III) ion which is influenced by the coordinating Cy₃PO and H₂O ligands.

The previously described work of N. Chilton and colleagues⁷⁵ suggested that the SMM performances limitation could be due to the fast relaxation at zero applied magnetic field due to molecular vibrations. Thus, a probe of such vibrations is required to investigate their role in the magnetic relaxation. In this context, the incorporation of a Mössbauer active nucleus such as ¹⁶¹Dy allowed the detection of vibrational properties of a material using the Nuclear Resonance Vibrational Spectroscopy (NRVS) also referring to Nuclear Inelastic Scattering (NIS) or Nuclear Resonant Inelastic X-ray Scattering (NRIXS).^87–89 NRVS detects all the vibrational modes that include a Dy displacement⁹⁰ and it was applied to compound 10.⁹¹ Extraction of the vibration modes gave some vibration with significant intensity at the energies corresponding to the electronic transitions leading to the conclusion that no relaxation process occurred involving electronic transitions in resonance with molecular vibrations with dysprosium displacements.

3.2.2. Dinuclear dysprosium-SMM and 3d4f heterobimetallic SMMs. The first isotopic enrichment on a polynuclear lanthanide SMM was achieved in 2018 by some of us on the dinuclear complex [Dy(tta)₃(PyNO)]₂ (11) (PyNO = pyridine-N-oxide).⁹² The natural isotopologue of 11 behaves as a SMM with an opening of the hysteresis loop at 0.46 K highlighting an S-shape sign of significant antiferromagnetic (AF) interaction between the two Dy(III) ions. The overall Dy–Dy magnetic interaction J is close to −3 cm⁻¹ with a main dipolar component. 11 was isotopically enriched with the nuclear spin free ¹⁶⁴Dy and I = 5/2 ¹⁶¹Dy isotopes. As anticipated, this did not significantly change the opening of the hysteresis loops because the Dy–Dy AF interaction is several orders of magnitude stronger than the hyperfine interaction. A second isotopic enrichment for a dinuclear Dy(III)-based SMM of formula [(Dy(tmhd)₃)₂(bpym)2]⁹³ (12) (tmhd = tri(tetramethylheptanedionato), bpym = bipyrimidine) (Fig. 3a) and its magnetic investigation were achieved soon after.⁹⁴ The dinuclear SMM ¹⁶⁴12 showed an S-shape opening hysteresis loop with a remnant magnetization (Fig. 3b) greater than the one for ¹⁶³12 (Fig. 3c). This trend was confirmed by ac magnetic measurements. The slower magnetic relaxation at 0 Oe for ¹⁶⁴12 than ¹⁶³12 was ascribed to the I = 0 for the former compared to I = 5/2 for the latter.

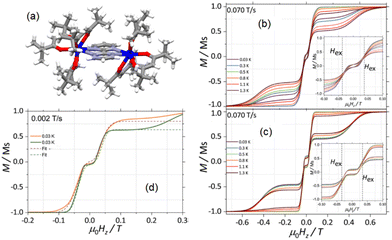Fig. 3 (a) X-ray structure on the single crystal for 12. Field dependence of the magnetization for ¹⁶³12 (b) and ¹⁶⁴12 (c) in the temperature range of 0.03–1.3 K at a field sweep rate of 0.070 T s⁻¹. In the insets: zoomed-in view of the origin region. (d) Fits of the magnetization curves of ¹⁶³12 (orange) and ¹⁶⁴12 (green). Adapted from ref. 94.

These observations are in contradiction with what was observed with the dinuclear compound 11. Nevertheless, it is worth noticing that the AF interaction in 12 is about four times weaker than in 11. A similar tunnelling rate was determined in both isotopologues by fitting the hysteresis loops (Fig. 3d) confirming that the QTM is not solely responsible for the magnetic relaxation of the isotopologues. For the first time in the study of the hyperfine coupling effect on the magnetic relaxation of a SMM, the authors proposed an explanation for the difference of opening of the hysteresis loop in an applied magnetic field. They proposed that the splitting of the larger spectrum of hyperfine state for ¹⁶³12 due to the splitting of I = 5/2 in eight states under the hyperfine coupling⁹⁴ allows a better coupling to acoustic phonons. In other words, the efficiency of the under-barrier relaxation process such as the direct relaxation process is increased due to the modulation of the electric field of the magnetic ion through phonons^22,95,96 leading to a reduced hysteresis loop for ¹⁶³12 than for ¹⁶⁴12 (Fig. 3d).

Previously, the nuclear spin driven QTM phenomena was studied using a theoretical model for both terbium and dysprosium dinuclear complexes i.e. quadruple-decker phthalocyanine complexes without isotopic enrichment.⁹⁷ The authors demonstrated that under zero applied magnetic field, the f–f dipolar interactions supressed the QTMs while at 1000 Oe they enhanced the nuclear spin driven QTM leading to faster magnetic relaxation for dinuclear rather than mononuclear complexes.

The last Dy(III)-based system investigated by isotopic enrichment is a 3d4f heterobimetallic complex in which the Dy(III) centre is associated with a diamagnetic Zn(II) both coordinated to a Schiff base ligand (L² = N,N′-bis(3-methoxysalicylidene)phenylene-1,2-diamine). This compound of formula [Zn₂(L²)₂DyCl₃]·2H₂O (13) highlighted good SMM performances thanks to the polarization of the phenoxido oxygen atoms and favouring axial distribution of the electron distribution.^98–101

The magnetic dynamics of the isotopically enriched compounds ¹⁶³13, 13 and ¹⁶²13 were studied (Fig. 4a) as well as the magnetic hysteresis loops for magnetically diluted analogues ¹⁶³13@Y, 13@Y and ¹⁶²13@Y (Fig. 4b).¹⁰² The investigation of the thermal dependence of the relaxation time of the magnetization under zero applied magnetic field demonstrated that the nuclear spin free isotopologue (¹⁶²13) relaxed slightly slower than ¹⁶³13 with the natural compound relaxing with a relaxation time at 2 K in between those of the two pure isotopes as already observed for isotopic enrichment of pure mononuclear lanthanide compounds.^69,72 The isotopic enrichment effect was also visible under an applied dc field on the opening of the hysteresis loops for magnetically diluted samples (Fig. 4b). Indeed, the opening of the hysteresis loop for ¹⁶²13@Y is wider than for the natural element which is itself wider than for ¹⁶³13@Y. This behaviour was attributed to the possible interaction between the M_J sublevels and the matrix as proposed by M. Ruben and colleagues⁹³ in the previously related example of this review. It is worth noticing that this explanation could be applied to compound 5 for which the effect of the isotopic enrichment on the opening of the hysteresis loop under applied magnetic field was also observed.

Fig. 4 (a) Temperature dependence of the magnetic relaxation time for ¹⁶²13 (red), 13 (black) and ¹⁶³13 (blue). Full and dashed lines are the best fitted curves and separated Raman (purple), Orbach (green) and QTM (colour of the compound) contributions, respectively. (b) Normalized magnetic hysteresis loops at 0.5 K at a sweep rate of 16 Oe s⁻¹ for ¹⁶²13@Y (orange), 13@Y (grey) and ¹⁶³13@Y (light blue). Insets: Zoomed-in view of the origin region. Adapted from ref. 102.

3.2.3. Mononuclear ytterbium-SMM. Examples of Yb(III) based-SMMs are quite rare and in almost all cases slow magnetic relaxation is observed under an applied dc field because of the existence of efficient QTM.¹⁰³ In order to know if slow magnetic relaxation could be observed in a zero applied magnetic field for an ytterbium complex, some of us realized both magnetic dilution and isotopic enrichment of the Yb(III) analogue of compound 5 ([Yb(tta)₃(L¹)]·C₆H₁₄ (14)).¹⁰⁴ It is worth noticing that the Yb(III) ion has a prolate electronic distribution. The two diluted isotopologues ¹⁷³14@Y (¹⁷³Yb, I = 5/2) and ¹⁷⁴14@Y (¹⁷⁴Yb, I = 0) as well as the natural one (14@Y) were prepared and the ac magnetic susceptibility measurements highlighted slow magnetic relaxation of the magnetization in a zero applied dc field. The thermal variation of the relaxation time of the magnetization for the three compounds (Fig. 5) allowed us to conclude that the magnetic relaxation happened through a combination of Orbach and Raman as well as QTM for ¹⁷³14@Y and 14@Y while no QTM was detected for the diluted nuclear spin free ¹⁷⁴14@Y. In other words, this work demonstrated that the strategy to enhance magnetic properties through isotopic enrichment of oblate dysprosium SMMs can be extended to prolate Yb(III) analogues. Indeed, the suppression of the QTM by isotopic enrichment led to a relaxation speed on the order of 100 times slower for ¹⁷⁴14@Y than for ¹⁷³14@Y.

Fig. 5 Thermal variation of the magnetic relaxation time for the three isotopologues ¹⁷³14@Y (blue), 14@Y (black) and ¹⁷⁴14@Y (red) in a zero applied magnetic field and temperature range 2–6 K. Full and dashed lines are the best-fitted curves and separated Orbach (green), Raman (orange) and QTM (colour of the compounds) contributions, respectively. Reprinted with permission from ref. 104. Copyright 2021, American Chemical Society.

3.2.4. Mononuclear erbium-SMM. One of the most used prolate lanthanide ions to design SMMs with great success is probably the Er(III) ion.^105–111 This element is constituted of six stable isotopes mainly with I = 0 (¹⁶²Er, ¹⁶⁴Er, ¹⁶⁶Er, ¹⁶⁸Er and ¹⁷⁰Er) and one nuclear spin active isotope (¹⁶⁷Er, I = 7/2). The first isotopic enrichment on a lanthanide SMM was investigated on the Na₉[Er(W₅O₁₈)₂]·yH₂O (15·yH₂O) by F. Luis and colleagues (Fig. 6a).¹¹² They demonstrated that the QTM (T < 4 K) is affected by the isotopic enrichment since the ¹⁶⁷15 relaxed 5 times slower than the natural 15. Nevertheless this trend is in contradiction with what was predicted for spin–phonon processes^113–116 and what was observed for the nuclear spin active isotopic enrichment for oblate Dy(III) and prolate Yb(III) ions (see paragraphs 2.2.1 to 2.2.3).

Fig. 6 (a) The molecular structure of 15·yH₂O, sodium and water inorganic network was omitted for clarity. (b) Thermal dependence of the relaxation time of the magnetization for Na₉[Er_xY_1−x(W₅O₁₈)₂]·yH₂O in a zero applied magnetic field. Adapted from ref. 112.

The authors hypothesized that the collective emission of a single phonon by many spins could play a decisive role in the explanation of the observed trend.¹¹⁷ These observations were confirmed when some of us studied the solvato-modulation of the magnetic bistability in 15·yH₂O (y ranges from 35 to 6).¹¹⁸ The nuclear spin-free ¹⁶⁶15·35H₂O was also studied showing that it relaxes faster than the nuclear spin active ¹⁶⁷15·35H₂O following the opposite trend observed by F. Luis and colleagues. In both papers, a considerable broadening of the out of phase component of the magnetic susceptibility in the quantum tunnelling regime was observed, a sign of the coexistence of multiple spin–lattice relaxation processes associated to the splitting of the ground state doublet M_J = ±13/2 into 2I + 1 states (I = 7/2) due to the hyperfine interaction. It is worth noticing that an isotopic enrichment investigation was realized only on this system and nowadays no definitive explanations have been given.

3.3. “Super-hyperfine interactions” influence on slow magnetic relaxation

We have discussed the hyperfine coupling between the electronic and nuclear spins of the lanthanide centre has been discussed in isotopically enriched SMMs as well as its effect on the slow magnetic relaxation in zero applied magnetic field (QTM) and applied magnetic field (direct processes) for mono-, bi- and heterobi–nuclear complexes involving oblate Dy(III) ion and prolate Yb(III) and Er(III) ions. Nevertheless, the interaction between the electronic spins of the metal and the nuclear spins of the first coordination sphere (super-hyperfine interaction) could have also a significant influence on the magnetic dynamic of the SMM. This effect was demonstrated in 2000 on the well-known Fe₈ cluster by performing a partial deuteration (^DFe₈) and by comparing the relaxation rates.⁴⁸ It is only very recently that similar investigation was carried out for a lanthanide SMM.¹¹⁹ The mononuclear Ho(III) SMM 3 was partially deuterated by replacing the five equatorial H₂O coordinated molecules with five D₂O (^D3). The authors demonstrated that the difference in the nuclear spin value for protium (I = 1/2) and deuterium (I = 1) and the presence of significant super-hyperfine interaction allowed the formation of super-hyperfine electronic energy spectra which differ for 3 and ^D3 leading to sizeable differences in their magnetic relaxation rates (Fig. 7).

Fig. 7 Thermal dependence of the magnetic relaxation time for 3 (blue) and ^D3 (red). Reprinted with permission from ref. 119. Copyright 2021, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.

4. Future development of isotopologues

In the last few years, the role of the hyperfine interaction was investigated in spin Qubits and Qudits. In this context, M. Ruben, W. Wernsdorfer and colleagues reviewed how the first mononuclear lanthanide SMM ((TbPc₂)⁻, 1) can be a molecular nuclear spin qudit (d = 4) which displays all the requirements to perform quantum operations i.e. isolation, initialization, read out, long coherence times and manipulations.¹²⁰

Another mononuclear field-induced SMM namely Yb(trensal) (Fig. 8a) (H₃trensal = 2,2′,2′′-tris(salicylideneimino)trimethylamine) (16) was studied for its potential applications in quantum information processing.¹²¹ The dilution of 16 in a diamagnetic isomorphous Lu(III) matrix (16@Lu) allowed the observation of a Hahn echo by oriented single-crystal echo-detected field-swept (EDFS) X-band pulsed EPR experiment.¹²² The phase memory time and the spin–lattice relaxation time were found to be independent from the isotopes because of the applied magnetic field used for the EDFS pulsed EPR experiment leading to magnetic relaxation through Raman-like processes and not through the electron nuclear spins coupling. Transient nutation experiments highlighted more than 70 Rabi oscillations of the spin echo (Fig. 8b) proving that this molecular system could be used as an electronic Qubit (S_eff = 1/2). Soon after, 16@Lu was isotopically enriched in a nuclear spin active ¹⁷³Yb isotope (I = 5/2) (¹⁷³16@Lu).¹²³ NMR measurements concluded that ¹⁷³16@Lu molecules behave as a nuclear qudit (I = 5/2, d = 6) coupled to an electronic qubit (S_eff = 1/2). Strong hyperfine interaction and long coherence times are key parameters to rapidly and coherently manipulate the nuclear qudit. ¹⁷³16@Lu can encode a qubit thanks to its nuclear qudit with embedded basic quantum error correction (Fig. 8c).

Fig. 8 (a) Molecular structure of 16. (b) Echo intensity at selected field positions (left) and its corresponding Fourier transforms (right). (c) Encoding of a qubit protected from amplitude shift errors in the nuclear levels of ¹⁷³16@Lu. Reprinted with permission from ref. 121. Copyright 2016, American Chemical Society and from ref. 122. Copyright 2018, American Chemical Society.

Finally, W. Wernsdorfer and M. Ruben¹²⁴ proposed the elaboration of multinuclear lanthanide metal complexes to reach the aim of scalability of the available Hilbert space which is expressed by the qudit-dimension. Indeed, the indirect coupling between the multiple nuclear spin units via their electron spins and bridging ligands will exponentially extend the Hilbert space available for Quantum Information Processing.

5. Conclusion and outlook

This feature article summarized the studies dealing with the isotopic enrichments in lanthanide single-molecule magnets and their effects on physical properties such as slow magnetic relaxation, magnetic memories or spin qudits behaviour. This overview covered Kramers and non-Kramers lanthanide SMMs with oblate and prolate electronic distributions for both mononuclear and polynuclear complexes.

Some key points can be taken away considering the advances reviewed herein:

1. Pure nuclear spin active (I ≠ 0) Tb(III) and Ho(III) based SMMs allowed the observation of interactions between electronic and nuclear spins (hyperfine coupling) and determination of the hyperfine interaction constant (A_hf).

2. Dynamics study of two ¹⁶¹Dy and ¹⁶⁴Dy SMM isotopologues demonstrated the effect of hyperfine coupling on QTM and magnetic bistability at 0 Oe while the thermally activated relaxation processes (Raman and Orbach) were not affected. The magnetic bistability at H ≠ 0 was also altered due to the coupling between I and the acoustic phonons. Not only has the nuclear spin value had an influence on the QTM but also the hyperfine coupling constant.

3. The isotopic enrichment combined with magnetic dilution made it possible to highlight the existence of another phenomenon at the origin of fast magnetic relaxation at 0 Oe called vibrational QTM induced by molecular vibrations.

4. Extrapolations of isotopic enrichment to polynuclear complexes demonstrated that an effect on slow magnetic relaxation can be observed in the case of magnetic interaction of a magnitude weaker than the hyperfine interactions.

5. Isotopic enrichment for prolate Yb(III)-based SMMs led to a similar trend on slow magnetic relaxation time than for Dy(III)-based SMMs while studies on Er(III)-based SMM concluded an opposite trend.

6. Isotopic enrichment of the coordinated ligands (for example H₂O vs. D₂O) could have an influence on the slow magnetic relaxation. The origin could be attributed to the effect of the changing mass on molecular vibrations or/and to superhyperfine interactions. However the process is not fully understood at this time.

7. Two SMMs isotopologues can find potential applications for magnetic memory or multi-level nuclear spin qudits depending if they are nuclear spin active or not, respectively.

The field of isotopic enrichment in lanthanide SMMs has been growing for less than 10 years, however, it already demonstrated that pure isotopes of SMMs could have potential applications in high-density storage with nuclear spin-free SMMs. Indeed, such SMMs have reduced QTM efficiency and they permitted to highlight current limitations of SMM performances because of the fast magnetic relaxation through molecular vibrations. The latter might be managed by designing specific molecular systems. Additionally, the isotopic enrichment of SMMs, especially pure nuclear spin active isotopologues, opened the route to potential applications in Quantum Information Processing because the electronic qubit can be coupled to nuclear qudit. The topic of isotopic enrichment of lanthanide SMMs is a perfect example of the need for both chemists and physicists to work hand in hand.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Université de Rennes, CNRS, and the European Commission through the ERC-CoG 725184 MULTIPROSMM (project n. 725184).

Notes and references

1. E. Maxwell, Phys. Rev., 1950, 78, 477.
2. R. Blinc, J. Phys. Chem. Solids, 1960, 13, 204–211.
3. N. W. Ashcroft and M. Cyrot, Europhys. Lett., 1993, 23, 605–608.
4. A. Greco and R. Zeyher, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 1296–1302.
5. C. C. Tong and K. C. Hwang, J. Phys. Chem. C, 2007, 111, 3490–3494.
6. T. Kosone, C. Kachi-Terajima, C. Kanadani, T. Saito and T. Kitazawa, Chem. Lett., 2008, 37, 754–755.
7. K. Hosoya, T. Kitazawa, M. Takahashi, M. Takeda, J. F. Meunier, G. Molnar and A. Bousseksou, Phys. Chem. Chem. Phys., 2003, 5, 1682–1688.
8. T. W. Ebbesen, J. S. Tsai, K. Tanigaki, J. Tabuchi, Y. Shimakawa, Y. Kubo, I. Hirosawa and J. Mizuki, Nature, 1992, 355, 620–622.
9. J. P. Franck, I. Isaac, W. Chen, J. Chrzanowski and J. C. Irwin, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 5189.
10. M. S. Fuhrer, K. Cherrey, A. Zettl, M. L. Cohen and V. H. Crespi, Phys. Rev. Lett., 1999, 83, 404.
11. G.-M. Zhao, K. Conder, H. Keller and K. A. Müller, Nature, 1996, 381, 676–678.
12. S. Cantekin, D. W. R. Balkenende, M. M. J. Smulders, A. R. A. Palmans and E. W. Meijer, Nat. Chem., 2011, 3, 42–46.
13. A. Shengelaya, G. M. Zhao, C. M. Aegerter, K. Conder, I. M. Savic and H. Keller, Phys. Rev. Lett., 1999, 83, 5142–5145.
14. P. W. Fowler and W. T. Raynes, Mol. Phys., 1981, 43, 65–82.
15. M. H. Rummeli, M. Loffler, C. Kramberger, F. Simon, F. Fulop, O. Jost, R. Schonfelder, A. Gruneis, T. Gemming, W. Pompe, B. Buchner and T. Pichler, J. Phys. Chem. C, 2007, 111, 4094–4098.
16. R. Watanabe, H. Ishiyama, G. Maruta and S. Takeda, Polyhedron, 2005, 24, 2599–2606.
17. R. H. Liu, T. Wu, G. Wu, H. Chen, X. F. Wang, Y. L. Xie, J. J. Ying, Y. J. Yan, Q. J. Li, B. C. Shi, W. S. Chu, Z. Y. Wu and X. H. Chen, Nature, 2009, 459, 64–67.
18. K. A. Muller, Z. Phys. B: Condens. Matter, 1990, 80, 193–201.
19. D. D. Lawrie, J. P. Franck and C. T. Lin, Phys. C, 1998, 297, 59–63.
20. R. Ofer, G. Bazalitsky, A. Kanigel, A. Keren, A. Auerbach, J. S. Lord and A. Amato, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 220508R.
21. R. Giraud, W. Wernsdorfer, A. M. Tkachuk, D. Mailly and B. Barbara, Phys. Rev. Lett., 2001, 87, 5.
22. A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of transition Ions, Clarendon Press, Oxford, 1970.
23. J. A. Weil and J. R. Bolton, Electron Paramagnetic Resonance: Elementary Theory and Practical Applications, John Wiley & Sons, Inc, 2006.
24. T. Kubo, T. Goto, T. Koshiba, K. Takeda and K. Awaga, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 224425.
25. T. Kubo, A. Nagano, T. Goto, K. Takeda and K. Awaga, J. Magn. Magn. Mater., 2004, 272, E727–E729.
26. T. Kubo, T. Koshiba, T. Goto, A. Oyamada, Y. Fujii, K. Takeda and K. Awaga, Physica B, 2001, 294, 310–313.
27. R. M. Achey, P. L. Kuhns, A. P. Reyes, W. G. Moulton and N. S. Dalal, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 064420.
28. R. Blinc, B. Zalar, A. Gregorovic, D. Arcon, Z. Kutnjak, C. Filipic, A. Levstik, R. M. Achey and N. S. Dalal, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 094401.
29. A. G. Harter, N. E. Chakov, B. Roberts, R. Achey, A. Reyes, P. Kuhns, G. Christou and N. S. Dalal, Inorg. Chem., 2005, 44, 2122–2124.
30. J. Dolinsek, D. Arcon, R. Blinc, P. Vonlanthen, J. L. Gavilano, H. R. Ott, R. M. Achey and N. S. Dalal, Europhys. Lett., 1998, 42, 691–694.
31. H. Kohlmann, F. Werner, K. Yvon, G. Hilscher, M. Reissner and G. J. Cuello, Chem. – Eur. J., 2007, 13, 4178–4186.
32. S. Turner, O. Kahn and L. Rabardel, J. Am. Chem. Soc., 1996, 118, 6428–6432.
33. J. S. Miller, J. C. Calabrese, A. J. Epstein, R. W. Bigelow, J. H. Zhang and W. M. Reiff, J. Chem. Soc., Chem. Commun., 1986, 1026–1028.
34. R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143.
35. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148.
36. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449.
37. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
38. C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202.
39. Y.-C. Chen, J.-L. Liu, W. Wernsdorfer, D. Liu, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Angew. Chem., Int. Ed., 2017, 56, 4996–5000.
40. N. Ishikawa, M. Sugita and W. Wernsdorfer, Angew. Chem., Int. Ed., 2005, 44, 2931–2935.
41. J. D. Rinehart and J. R. Long, J. Am. Chem. Soc., 2009, 131, 12558–12559.
42. S. Mossin, B. L. Tran, D. Adhikari, M. Pink, F. W. Heinemann, J. Sutter, R. K. Szilagyi, K. Meyer and D. J. Mindiola, J. Am. Chem. Soc., 2012, 134, 13651–13661.
43. J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581.
44. X.-N. Yao, J.-Z. Du, Y.-Q. Zhang, X.-B. Leng, M.-W. Yang, S.-D. Jiang, Z.-X. Wang, Z.-W. Ouyang, L. Deng, B.-W. Wang and S. Gao, J. Am. Chem. Soc., 2017, 139, 373–380.
45. J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732–20734.
46. M. S. Fataftah, J. M. Zadrozny, D. M. Rogers and D. E. Freedman, Inorg. Chem., 2014, 53, 10716–10721.
47. T. M. Ozvat, A. K. Rappé and J. M. Zadrozny, Inorg. Chem., 2022, 61, 778–785.
48. W. Wernsdorfer, A. Caneschi, R. Sessoli, D. Gatteschi, A. Cornia, V. Villar and C. Paulsen, Phys. Rev. Lett., 2000, 84, 2765.
49. M. Evangelisti, F. Luis, F. L. Mettes, R. Sessoli and L. J. de Jongh, Phys. Rev. Lett., 2005, 95, 227206.
50. Y. Furukawa, S. Kawakami, K. Aizawa, K. Kumagai and F. Borsa, Polyhedron, 2003, 22, 2277–2279.
51. Y. Furukawa, Y. Hatanaka, K. Kumagai, S. H. Baek and F. Borsa, in Low Temperature Physics, Pts a and B, ed. Y. Takano, S. P. Hershfield, P. J. Hirschfeld and A. M. Goldman, Amer Inst Physics, Melville, 2006, vol. 850, pp. 1147–1148.
52. J. Meija, T. B. Coplen, M. Berglund, W. A. Brand, P. D. Bièvre, M. Gröning, N. E. Holden, J. Irrgeher, R. D. Loss, T. Walczyk and T. Prohaska, Pure Appl. Chem., 2016, 88, 293–306.
53. S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669.
54. N. Ishikawa, M. Sugita and W. Wernsdorfer, Angew. Chem., Int. Ed., 2005, 44, 2931–2935.
55. A. De Cian, M. Moussavi, J. Fischer and R. Weiss, Inorg. Chem., 1985, 24, 3162–3167.
56. H. Konami, M. Hatano and A. Tajiri, Chem. Phys. Lett., 1989, 160, 163.
57. N. Ishikawa, M. Sugita, T. Okubo, N. Tanaka, T. Iino and Y. Kaizu, Inorg. Chem., 2003, 42, 2440.
58. N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695.
59. N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Phys. Chem. B, 2004, 108, 11265.
60. F. Habib, P.-H. Lin, J. Long, I. Korobkov, W. Wernsdorfer and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 8830–8833.
61. W. Wernsdorfer, Adv. Chem. Phys., 2001, 118, 99.
62. W. Wernsdorfer, Supercond. Sci. Technol., 2009, 22, 064013.
63. W. Wernsdorfer, N. E. Chakov and G. Christou, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 132413.
64. N. Ishikawa, M. Sugita and W. Wernsdorfer, J. Am. Chem. Soc., 2005, 127, 3650–3651.
65. S.-G. Wu, Z.-Y. Ruan, G.-Z. Huang, J.-Y. Zheng, V. Vieru, G. Taran, J. Wang, Y.-C. Chen, J.-L. Liu, L. T. A. Ho, L. F. Chibotaru, W. Wernsdorfer, X.-M. Chen and M.-L. Tong, Chem, 2021, 7, 982–992.
66. F. Donati, S. Rusponi, S. Stepanow, C. Wäckerlin, A. Singha, L. Persichetti, R. Baltic, K. Diller, F. Patthey, E. Fernandes, J. Dreiser, Z. Sljivancanin, K. Kummer, C. Nistor, P. Gambardella and H. Brune, Science, 2016, 352, 318–321.
67. E. Fernandes, F. Donati, F. Patthey, S. Stavric, Z. Sljivancanin and H. Brune, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 045419.
68. P. R. Forrester, F. Patthey, E. Fernandes, D. P. Sblendorio, H. Brune and F. D. Natterer, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 100, 180405.
69. F. Pointillart, K. Bernot, S. Golhen, B. Le Guennic, T. Guizouarn, L. Ouahab and O. Cador, Angew. Chem., Int. Ed., 2015, 54, 1504–1507.
70. T. T. da Cunha, J. Jung, M.-E. Boulon, G. Campo, F. Pointillart, C. L. M. Pereira, B. Le Guennic, O. Cador, K. Bernot, F. Pineider, S. Golhen and L. Ouahab, J. Am. Chem. Soc., 2013, 135, 16332–16335.
71. L. Tesi, Z. Salman, I. Cimatti, F. Pointillart, K. Bernot, M. Mannini and R. Sessoli, Chem. Commun., 2018, 54, 7826.
72. J. Flores Gonzalez, F. Pointillart and O. Cador, Inorg. Chem. Front., 2019, 6, 1081–1085.
73. Y. Kishi, F. Pointillart, B. Lefeuvre, F. Riobé, B. Le Guennic, S. Golhen, O. Cador, O. Maury, H. Fujiwara and L. Ouahab, Chem. Commun., 2017, 53, 3575–3578.
74. E. Moreno-Pineda, M. Damjanovic, O. Fuhr, W. Wernsdorfer and M. Ruben, Angew. Chem., Int. Ed., 2017, 56, 9915–9919.
75. F. Ortu, D. Reta, Y.-S. Ding, C. A. P. Goodwin, M. P. Gregson, E. J. L. McInnes, R. E. P. Winpenny, Y.-Z. Zheng, S. T. Liddle, D. P. Mills and N. F. Chilton, Dalton Trans., 2019, 48, 8541–8545.
76. J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450.
77. M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, Chem. Sci., 2016, 7, 155–165.
78. S. F. M. Schmidt, C. Koo, V. Mereacre, J. Park, D. W. Heermann, V. Kataev, C. E. Anson, D. Prodius, G. Novitchi, R. Klingeler and A. K. Powell, Inorg. Chem., 2017, 56, 4796.
79. A. Cini, M. Mannini, F. Totti, M. Fittipaldi, G. Spina, A. Chumakov, R. Rgffer, A. Cornia and R. Sessoli, Nat. Commun., 2018, 9, 480.
80. V. Mereacre, A. Baniodeh, C. E. Anson and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 15335–15337.
81. J. M. Zadrozny, D. J. Xiao, J. R. Long, M. Atanasov, F. Neese, F. Grandjean and G. J. Long, Inorg. Chem., 2013, 52, 13123–13131.
82. L. Scherthan, S. F. M. Schmidt, H. Auerbach, T. Hochdörffer, J. A. Wolny, W. Bi, J. Zhao, M. Y. Hu, T. Toellner, E. E. Alp, D. E. Brown, C. E. Anson, A. K. Powell and V. Schünemann, Angew. Chem., Int. Ed., 2019, 58, 3444–3449.
83. Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837.
84. J. P. Evans, G. A. Stewart, J. M. Cadogan, W. D. Hutchison, E. E. Mitchell and J. E. Downes, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 54431.
85. W. D. Hutchison, G. A. Stewart, J. M. Cadogan, A. Princep, R. Stewart and D. H. Ryan, AIP Adv., 2017, 7, 055702.
86. P. C. M. Gubbens, A. M. van der Kraan and K. H. J. Buschow, Hyperfine Interact., 1988, 40, 389.
87. M. Seto, Y. Yoda, S. Kikuta, X. W. Zhang and M. Ando, Phys. Rev. Lett., 1995, 74, 3828–3831.
88. W. Sturhahn, T. S. Toellner, E. E. Alp, X. Zhang, M. Ando, Y. Yoda, S. Kikuta, M. Seto, C. W. Kimball and B. Dabrowski, Phys. Rev. Lett., 1995, 74, 3832.
89. E. Gerdau and H. DeWaard, Hyperfine Interact., 1999, 123, 0.
90. R. Rchlsberger, Nuclear Condensed Matter Physics with Synchrotron Radiation, Springer STMP 208, Berlin Heidelberg, 2004.
91. L. Scherthan, R. F. Pfleger, H. Auerbach, T. Hochdörffer, J. A. Wolny, W. Bi, J. Zhao, M. Y. Hu, E. E. Alp, C. E. Anson, R. Diller, A. K. Powell and V. Schünemann, Angew. Chem., Int. Ed., 2020, 59, 8818–8822.
92. G. Huang, X. Yi, J. Jung, O. Guillou, O. Cador, F. Pointillart, B. Le Guennic and K. Bernot, Eur. J. Inorg. Chem., 2018, 326–332.
93. W. Yu, F. Schramm, E. Moreno-Pineda, Y. Lan, O. Fuhr, J. Chen, H. Isshiki, W. Wernsdorfer, W. Wulfhekel and M. Ruben, Beilstein J. Nanotechnol., 2016, 7, 126–137.
94. E. Moreno-Pineda, G. Taran, W. Werndorfer and M. Ruben, Chem. Sci., 2019, 10, 5138–5145.
95. M. Ganzhorn, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Nat. Nanotechnol., 2013, 8, 165–169.
96. M. Ganzhorn, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Nat. Commun., 2016, 7, 11443.
97. T. Fukuda, K. Matsumura and N. Ishikawa, J. Phys. Chem. A, 2013, 117, 10447–10454.
98. J. Long, R. Vallat, R. A. S. Ferreira, L. D. Carlos, F. A. Almeida Paz, Y. Guari and J. Larionova, Chem. Commun., 2012, 48, 9974–9976.
99. A. Upadhyay, S. K. Singh, C. Das, R. Mondol, S. K. Langley, K. S. Murray, G. Rajaraman and M. Shanmugam, Chem. Commun., 2014, 50, 8838–8841.
100. A. Upadhyay, C. Das, S. Vaidya, S. K. Singh, T. Gupta, R. Mondol, S. K. Langley, K. S. Murray, G. Rajaraman and M. Shanmugam, Chem. – Eur. J., 2017, 23, 4903–4916.
101. W.-B. Sun, P.-F. Yan, S.-D. Jiang, B.-W. Wang, Y.-Q. Zhang, H.-F. Li, P. Chen, Z.-M. Wang and S. Gao, Chem. Sci., 2016, 7, 684–691.
102. J. Flores Gonzalez, B. Lefeuvre, B. Degraeve, O. Cador and F. Pointillart, Dalton Trans., 2021, 50, 11466–11471.
103. F. Pointillart, O. Cador, B. Le Guennic and L. Ouahab, Coord. Chem. Rev., 2017, 346, 150–175.
104. J. Flores Gonzalez, H. Douib, B. Le Guennic, F. Pointillart and O. Cador, Inorg. Chem., 2021, 60, 540–544.
105. S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733.
106. K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952–17957.
107. L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., 2014, 53, 4413–4417 ( Angew. Chem. , 2014 , 126 , 4502–4506 ).
108. P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484–4487.
109. A. J. Brown, D. Pinkowicz, M. R. Saber and K. R. Dunbar, Angew. Chem., Int. Ed., 2015, 54, 5864–5868 ( Angew. Chem. , 2015 , 127 , 5962–5966 ).
110. M. A. AlDamen, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, C. Martí-Gastaldo, F. Luis and O. Montero, Inorg. Chem., 2009, 48, 3467–3479.
111. M. A. AlDamen, J. M. Clemente-Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874–8875.
112. F. Luis, M. J. Martinez-Perez, O. Montero, E. Coronado, S. Cardonna-Serra, C. Marti-Gastaldo, J. M. Clemente-Juan, J. Sesé, D. Drung and T. Schurig, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 060403.
113. R. de and L. Kronig, Physica, 1939, 6, 240.
114. J. H. Van Vleck, Phys. Rev., 1940, 57, 426.
115. R. Orbach, Proc. R. Soc. London, 1961, A264, 458.
116. G. H. Larson and C. D. Jeffries, Phys. Rev. B: Condens. Matter Mater. Phys., 1966, 145, 311.
117. H. N. V. Temperley, Proc. Cambridge Philos. Soc., 1939, 35, 256.
118. J. Flores Gonzalez, V. Montigaud, V. Dorcet, K. Bernot, B. Le Guennic, F. Pointillart and O. Cador, Chem. – Eur. J., 2021, 27, 10160–10169.
119. Y. Liu, L. T. A. Ho, G.-Z. Huang, Y.-C. Chen, L. Ungur, J.-L. Liu and M.-L. Tong, Angew. Chem., Int. Ed., 2021, 60, 27282–27287.
120. E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513.
121. K. S. Pedersen, J. Dreiser, H. Weihe, R. Sibille, H. V. Johannesen, M. A. Sorensen, B. E. Nielsen, M. Sigrist, H. Mutka, S. Rols, J. Bendix and S. Piligkos, Inorg. Chem., 2015, 54, 7600–7606.
122. K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804.
123. R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. S. Pedersen, R. De Renzi, S. Piligkos and S. Carreta, J. Am. Chem. Soc., 2018, 140, 9814–9818.
124. W. Wernsdorfer and M. Ruben, Adv. Mater., 2019, 31, 1806687.

---