Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Augmentation of FTIR spectral datasets using Wasserstein generative adversarial networks for cancer liquid biopsies†
Rose G.
McHardy
ab,
Georgios
Antoniou
b,
Justin J. A.
Conn
b,
Matthew J.
Baker
bc and
David S.
Palmer
 *ab
*ab
aDepartment of Pure and Applied Chemistry, Thomas Graham Building, 295 Cathedral Street, University of Strathclyde, Glasgow, G1 1XL, UK. E-mail: david.palmer@dxcover.com
bDxcover Ltd, Royal College Building, 204 George Street, Glasgow, G1 1XW, UK
cSchool of Medicine, Faculty of Clinical and Biomedical Sciences, University of Central Lancashire, Preston, PR1 2HE, UK
First published on 6th July 2023
Abstract
Over recent years, deep learning (DL) has become more widely used within the field of cancer diagnostics. However, DL often requires large training datasets to prevent overfitting, which can be difficult and expensive to acquire. Data augmentation is a method that can be used to generate new data points to train DL models. In this study, we use attenuated total reflectance Fourier-transform infrared (ATR-FTIR) spectra of patient dried serum samples and compare non-generative data augmentation methods to Wasserstein generative adversarial networks (WGANs) in their ability to improve the performance of a convolutional neural network (CNN) to differentiate between pancreatic cancer and non-cancer samples in a total cohort of 625 patients. The results show that WGAN augmented spectra improve CNN performance more than non-generative augmented spectra. When compared with a model that utilised no augmented spectra, adding WGAN augmented spectra to a CNN with the same architecture and same parameters, increased the area under the receiver operating characteristic curve (AUC) from 0.661 to 0.757, presenting a 15% increase in diagnostic performance. In a separate test on a colorectal cancer dataset, data augmentation using a WGAN led to an increase in AUC from 0.905 to 0.955. This demonstrates the impact data augmentation can have on DL performance for cancer diagnosis when the amount of real data available for model training is limited.
1 Introduction
Cancer is the second most frequent cause of deaths worldwide, with the probability of five-year overall survival for all primary cancer sites being 68%, yet this number varies greatly depending on the cancer site in question.1,2 One of the primary reasons for this is late-stage diagnosis, predominantly caused by the non-specific nature of early-stage cancer symptoms.When diagnosed at an early stage, survival rates are substantially higher. If the cancer is caught during the early stages (stage I–II), the average mortality rate for primary cancers sits at 27%, when compared with the vast increase for cancers detected at stage IV leading to a mortality rate of 82%. This demonstrates that early diagnosis is important to the treatment of cancer.1
Current screening diagnosis routes for patients in at-risk populations include a mammography for breast cancer,3 Pap smear for cervical cancer,4 low-dose computed tomography for lung cancer,5 endoscopic ultrasound for pancreatic cancer,6 and colonoscopy for colorectal cancer.7 Although many of these methods have been deemed effective, they are often expensive, and in some cases invasive.8 There is therefore an urgent need for a more convenient method for earlier diagnosis for many cancers.
Liquid biopsies are a cost-effective method of utilising a wide variety of substances, both tumor and non-tumor derived, to detect various cancer types, particularly at the early stages.9 Most commonly, circulating-tumor DNA (ctDNA) is a key marker used to detect cancer within the blood stream. The analysis of ctDNA has shown promise in the detection of various cancer types and is the primary biomarker type used by the current liquid biopsy platforms.10 However, the success of detecting ctDNA is limited to the monitoring of advanced stage cancers; the levels of ctDNA during the early stages are often too low to be detected.8
One method that has developed over recent years is the use of vibrational spectroscopy as the basis of the liquid biopsy in order to capture multiple tumor and non-tumor derived biomarkers within one measurement.11–13 It has the benefits of being rapid and low-cost, and can be used to analyse multiple different biofluids.14 Vibrational spectroscopic methods such as Raman and infrared (IR) spectroscopy have previously demonstrated their potential uses within cancer detection.14,15 In particular, attenuated total reflection Fourier-transform infrared (ATR-FTIR) has shown great promise for early cancer detection.16–18 Brennan et al.19 reported a sensitivity and specificity of 0.81 and 0.80, respectively, for the diagnosis of brain tumours in a prospectively collected clinical dataset of dried serum samples. For pancreatic cancer in particular, Sala et al.20 were able to utilise ATR-FTIR analysis of dried serum samples and machine learning to achieve an area under the receiver operating characteristic (ROC) curve (AUC) of 0.95 when classifying between pancreatic cancer and healthy samples (n = 200), and an AUC of 0.83 when classifying between pancreatic cancer and samples from patients presenting as symptomatic of pancreatic cancer but subsequently diagnosed as non-cancerous (n = 70). This example used machine learning methods common in the field of chemometrics, namely partial least squares (PLS) and random forest (RF).
With continuous hardware developments, more interest is being directed at the use of deep learning, particularly within cancer diagnostics.21 However, despite the general success of deep learning over the recent years, the main obstacle researchers face in the healthcare field is data availability.22 Although the volume of data needed for deep learning is present within electronic health records, healthcare data is often limited in quality due to data sparsity, variability, and privacy policies.22 Deep learning models, such as convolutional neural networks (CNNs), require large volumes of data in order to achieve maximum performance as they have many parameters; small datasets can lead to non-generalisable models that overfit and perform poorly on unseen data.
A solution to reaching the dataset sizes required for deep learning is data augmentation.23 Data augmentation is a method to artificially increase the size of a dataset with the aim to improve the performance of a predictive model. It can be particularly useful when larger datasets are either not available or if it would be particularly laborious to generate more samples.
Data augmentation can be broadly split into two categories: non-generative and generative methods. Non-generative methods create new data from the original data using some well-defined transformations. For example, for image augmentation, this can be in the form of geometric or colour transformations. Generative methods use neural networks to generate data artificially without directly using the original dataset other than for model training.
Non-generative methods of data augmentation have been used successfully within image classification using relatively simple and computationally inexpensive methods, as demonstrated by Taylor et al.24 who were able to use geometric and photometric transformations to generate new images to train a CNN and increase their classification accuracy from 0.48 to 0.62. Similar data augmentation methods have also been used within cancer diagnostics. Hao et al.25 used various techniques such as rotation, flipping, and cropping of magnetic resonance images to diagnose prostate cancer, increasing the AUC of the CNN from 0.80 to 0.85. Non-generative methods have also been used for spectral data, in particular infrared (IR) data.26,27 Bjerrum et al.26 in particular were able to decrease the root mean squared error from 4.01 mg to 1.80 mg by changing the offset and slope of spectra to generate more synthetic samples.
Over recent years, more complex forms of data augmentation have begun to surface, such as generative adversarial networks (GANs).28 GANs comprise two neural networks: a discriminator and a generator. The generator is tasked with generating new data based on the training set of available real data, and the discriminator is tasked with becoming an expert in determining whether a sample is real or simulated. These components work adversarially to generate the most realistic augmented data possible. GANs have great potential for data augmentation applications, but are substantially more computationally expensive when compared with non-generative methods.
In particular, GANs have shown their use within cancer diagnostics. Al-Dhabyani et al.29 utilised GANs to generate ultrasound images for the diagnosis of breast cancer, increasing their diagnostic accuracy from 84% to 96%.
As well as image-based data, GANs have been used previously with infrared (IR) spectra also. Wickramaratne et al.30 were able to use GANs with IR spectra to classify a subject's task as either a left finger tap, right finger tap, or a foot tap. They were able to increase the AUC from 0.79 to 0.98. Despite their benefits, GANs persistently suffer from problems with vanishing gradients, which can lead to a halt in generator learning, and mode collapse, in which the generator continuously generates similar data points that have been found to trick the discriminator.31 One solution to eliminate these issues are Wasserstein GANs (WGANs).32 The more stable WGANs have already shown their use for deep learning models trained on spectral data. Nagasawa et al.33 utilised WGANs to augment near IR spectra to classify motor tasks. They were able to increase their classification accuracy from 0.4 to 0.7, demonstrating the potential use of WGANs with spectra data for other applications. Zhao et al.34 also utilised WGANs with IR spectra with multiple traditional and deep learning models. In all cases, adding WGAN augmented spectra considerably increased the classification accuracy.
In this study, we aim to demonstrate the benefits of using data augmentation within spectral liquid biopsies to diagnose pancreatic cancer. Previous studies have been carried out that have used data augmentation and imaging data to diagnose pancreatic cancer, but none as of yet related to spectral data.35–37
Firstly, we will use non-generative data augmentation methods, including adding noise to spectra and averaging spectra, to create new data points, which can be found in section 3.6. Secondly, we will then optimise a WGAN network structure to simulate pancreatic cancer and non-cancer spectra, which can be found in section 4.1.
Thirdly, we will compare non-generative and WGAN augmentation methods during CNN model training, which can be found in section 4.2. We show that when we compare a CNN containing no augmented spectra, a CNN trained with WGAN augmented spectra has a better overall performance for diagnosing pancreatic cancer. We also use a separate colorectal cancer dataset to demonstrate that the method is disease and dataset invariant.
2 Theory
2.1 GANs
A GAN generates augmented data by utilising two neural networks known as the discriminator D and the generator G.28 The overall network is trained by optimising the value function adversarially; the discriminator is trained to minimise and the generator is trained to maximise the value function. That is, the minmax objective is defined as: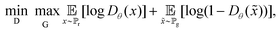 | (1) |
![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) is the expected value,
is the expected value, ![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) r is the real data probability distribution,
r is the real data probability distribution, ![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) g is the generated data probability distribution,
g is the generated data probability distribution, ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = Gw(z), where z is the latent variable, θ are the discriminator weights, w are the generator weights, and x is the real training data.
= Gw(z), where z is the latent variable, θ are the discriminator weights, w are the generator weights, and x is the real training data.
GAN training occurs by continuously updating the discriminator weights, θ, before updating the generator weights, w, to minimise the Jensen–Shannon divergence, which measures the similarity between two probability distributions.38 One of the main issues however with GANs is vanishing gradients, which is caused by an optimised discriminator that cannot provide enough information for generator training to progress. This is often caused by the Jensen–Shannon divergence not being continuous with respect to w when probability distribution domains do not overlap. GANs also are known to experience mode collapse, where the generator continuously outputs similar data points which successfully fool the discriminator.28
2.2 WGANs
The problems with vanishing gradients and mode collapse experienced by GANs motivated the development of WGANs.31 For the former problem, a WGAN minimises the Wasserstein distance, which instead looks at the distance between two probability distributions, instead of the Jensen–Shannon divergence. It aims to prevents vanishing gradients as the Wasserstein distance is continuous with respect to w. In addition, to prevent mode collapse, instead of a discriminator, which classifies data as either real or fake, WGANs use a critic, which instead provides a “realness score” to the data. Where a GAN discriminator can learn very quickly the difference between real and fake samples, the gradient also quickly vanishes during optimisation. A WGAN critic can instead be optimised while maintaining a gradient.31The minmax objective for a WGAN is instead defined as:
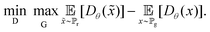 | (2) |
Originally, Arjovsky et al.31 used a Lipschitz constraint on the gradient functions to ensure a maximum gradient. This was enforced on the critic by clipping its weights to lie within an interval [−c, c], where c is the real number representing the weight clipping parameter, to allow faster training by constraining the critic gradient. However, it was further proposed by Gulrajani et al.32 that this was a problematic method of training the critic. Without careful tuning of the weight clipping parameter, the critic can experience exploding or vanishing gradients; if c is too large, then the critic will never train optimally, too small and it will cause vanishing gradients. Therefore, Gulrajani et al.32 changed the value function for WGANs to include a gradient penalty term (WGAN-GP) which thus leads to the minmax objective being defined as:
 | (3) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) is defined as:32
is defined as:32![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) = εx + (1 − ε) = εx + (1 − ε)![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , , | (4) |
A WGAN-GP can be extended by imposing conditions based on some additional information, y, to obtain a conditional WGAN-GP (CWGAN-GP).39 In this study, y corresponds to the class label of the spectra. This results in the following minmax objective:
 | (5) |
In the present paper, we will be utilising a CWGAN-GP for generating synthetic FTIR spectra.
3 Materials and methods
3.1 Patient samples
All patient serum samples were sourced from biobanks. Cancer samples were gathered from the Wellcome Trust Clinical Research Facility at the Western General Hospital, Edinburgh, the Emergency Medicine Research Group (EMERGE) at the Edinburgh Royal Infirmary, The Beatson West of Scotland Cancer Centre in Glasgow, the University of Swansea, Manchester Cancer Research Centre, and Tissue Solutions Glasgow. All cancer samples were collected from patients with a confirmed pancreatic cancer diagnosis according to the data collection methods of specified biobanks. Samples were collected before surgical resection or the start of other anti-cancer therapies. The non-cancer group was comprised of both asymptomatic controls and patients with symptomology aligned with a possible cancer diagnosis.Blood samples were obtained with venipuncture using serum collection tubes; S-Monovette Z Gel (Sarstedt, Germany) and Vacutainer SST/SST II (BD, USA), and anonymized. Serum was extracted via centrifugation and stored in a −80 °C freezer. Non-identifiable clinical and demographic data were obtained in-line with each biobank's data control procedures.
Ethical approval for this study was granted by Lothian REC(15/ES/0094), Preston Brain Tumour North-West (BTNW) Application #1108, Beatson West of Scotland Cancer Centre (MREC 10/S0704/18), and the Integrated Research Application System, IRAS, (ID #238735) from Health Research Authority (HRA) and University of Strathclyde Ethics Committee (UEC 17/81). All participants consented to inclusion in the study.
3.2 Patient sample analysis
In this study, the serum samples were stored at −80 °C until the date of analysis; samples were allowed to thaw for up to 30 minutes at room temperature (18–25 °C) and inverted three times to ensure mixing and thawing before use. Each patient sample was prepared for analysis by pipetting 3 μL of serum onto each of the three sample wells of the Dxcover® Sample Slide (Dxcover® Ltd, UK).16,40 Prepared slides were placed in a drying unit incubator (Thermo Scientific™ Heratherm™, USA) at 35 °C for 1 hour, to control the dehydration process of the serum droplets. Each dried sample slide was then inserted into the Dxcover® Autosampler (Dxcover® Ltd, UK) to be prepared for spectra collection. In this study, a PerkinElmer® Spectrum Two™ FTIR spectrometer (PerkinElmer® Inc., USA) was used to generate the spectral data (16 co-added scans at 4 cm−1 resolution with 1 cm−1 data spacing). A total of three spectra were collected for each sample well, resulting in nine replicates per patient, then submitted to the diagnostic algorithm to generate the disease prediction. Patient samples were reported as cancer positive or negative according to the diagnostic algorithm results.3.3 Dataset
For this study, a full dataset comprising of 625 patients was compiled: 166 pancreatic cancer and 459 non-cancer patients. From this dataset, a subset of 100 patients (50 cancer and 50 non-cancer) were set aside to use as a modelling set. This subset was age, sex, and stage matched to the full dataset and will be hence labelled the 100-patient dataset. The patient metadata of the 100-patient dataset can be seen in Table 1.| C | NC | Total | ||
|---|---|---|---|---|
| Age, years | Mean | 64 | 56 | 60 |
| Min–max | 40–83 | 20–80 | 20–83 | |
| Sex, n (%) | Female | 25 (50) | 30 (60) | 55 (55) |
| Male | 25 (50) | 20 (40) | 45 (45) | |
| Cancer stage, n (%) | I | 2 (4) | — | 2 (2) |
| II | 20 (40) | — | 20 (20) | |
| III | 22 (44) | — | 22 (22) | |
| IV | 6 (12) | — | 6 (6) | |
The remainder of the dataset will be labelled the 525 patient dataset and comprised 116 pancreatic cancer and 409 non-cancer patients. The patient metadata of the full dataset and the 525-patient dataset can be found in Tables S1 and S2† respectively.
3.4 Spectral pre-processing
Raw FTIR spectra cover 4000–450 cm−1 of the frequency domain. For this study, raw spectra were first cut to 3700–1000 cm−1 as wavenumbers outside of this region are highly susceptible to noise, and do not contribute useful diagnostic information. Following this, an extended multiplicative signal correction (EMSC) was applied to the spectra, up to and including second-order correction terms.41 This was followed by the removal of the silent region (2700–1800 cm−1).3.5 CNNs
CNNs were built using Keras v2.8.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 for R v4.1.2
42 for R v4.1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43 with Tensorflow v2.8.0
43 with Tensorflow v2.8.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 as the computation back end. The final chosen model consisted of two consecutive units each of which comprised a one-dimensional convolutional layer (with 10 filters and a kernel size of 5) with a rectified linear activation, batch normalization, and a max-pooling layer with a pool size of 2. The output from the final convolutional unit was flattened and fed into dense layers, with 0.1 and 0.2 dropout respectively and a rectified linear activation. The output was two dense neurons with a softmax activation. The loss function was categorical cross entropy and training was done with the RMSprop optimizer.45 All CNN model training was carried out using the ARCHIE-WeST High Performance Computing Centre based at the University of Strathclyde, with each CNN model being trained using 10 Lenovo SD530 CPU cores with model training lasting on average 12 hours per model.
44 as the computation back end. The final chosen model consisted of two consecutive units each of which comprised a one-dimensional convolutional layer (with 10 filters and a kernel size of 5) with a rectified linear activation, batch normalization, and a max-pooling layer with a pool size of 2. The output from the final convolutional unit was flattened and fed into dense layers, with 0.1 and 0.2 dropout respectively and a rectified linear activation. The output was two dense neurons with a softmax activation. The loss function was categorical cross entropy and training was done with the RMSprop optimizer.45 All CNN model training was carried out using the ARCHIE-WeST High Performance Computing Centre based at the University of Strathclyde, with each CNN model being trained using 10 Lenovo SD530 CPU cores with model training lasting on average 12 hours per model.
The architecture for the CNN models used in this study can be seen in Fig. 1.
3.6 Non-generative augmentation
All non-generative data augmentation was performed on the 525 patient dataset. Spectra were augmented by using the spectra collected for a single patient. As augmentation was isolated to each patient, the label of the newly generated spectra could be assumed to be the patient label. The effect of the various non-generative augmentation methods can be seen in Fig. 2. For each of the non-generative methods, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 spectra were created: 5000 pancreatic cancer and 5000 non-cancer spectra. The volume of augmented spectra added during the model training is described further in Tables 3 and 4. The routines used for the non-generative augmentations are described in the next three subsections.
000 spectra were created: 5000 pancreatic cancer and 5000 non-cancer spectra. The volume of augmented spectra added during the model training is described further in Tables 3 and 4. The routines used for the non-generative augmentations are described in the next three subsections.
Fig. 2 shows randomly adding noise to spectra within varying levels of standard deviations. It was determined as part of initial investigations that adding one standard deviation of noise was sufficient.
3.7 WGAN architecture
The first step to generate spectra using WGANs was to optimise the structure of the WGAN network. This involved optimising the structure of the generator and the critic networks.While maintaining a fixed generator architecture (generator architecture was determined as part of initial investigations), the critic architecture was optimised. The tested architectures included varying the number of hidden layers from 1 to 3 and the corresponding hidden units from 256 to 2048. A general trend was observed that increasing the number of units within each dense layer improved the distribution of the generated spectra. However, with an increase in the number of dense layers, while the distribution of generated spectra improved, the level of noise within the generated spectra also increased.
As the distribution of generated spectra improved with the increase in the number of dense layers and the number of units within those layers, the choice was made to use three dense layers in the critic. All results from WGAN architecture optimisation can be found in Fig. S1–6.†Table 2 describes the final network structure for each of the layers in the critic and generator.
| Layer | Critic | Generator |
|---|---|---|
| Input | 1802 × 2 | 100 × 2 |
| Hidden | Units = 2048 layer norm. | Units = 256 batch norm. Dropout = 0.3 |
| Hidden | Units = 1024 layer norm. | Units = 512 batch norm. Dropout = 0.3 |
| Hidden | Units = 512 layer norm. | Units = 1024 batch norm. Dropout = 0.3 |
| Output | 1 | 1802 × 2 |
Input to the critic consisted of FTIR spectral data from patient serum analysis. The dimension of the latent space was 100, and a latent variable formed by randomly sampling from a normal distribution N(0, 1) with a dimension of 100 was used as the input to the generator. The generator network included batch normalisation after each hidden layer. Layer normalisation was used for the critic because batch normalisation is incompatible with the gradient penalty.32 Dropout (0.3) was also added after each hidden layer in the generator to further prevent mode collapse.
A leaky rectified linear unit (ReLU) was used as the activation function for the hidden layers in both the critic and the generator.
The weights of the critic and generator were updated using the Adam optimizer, with the parameter values for Adam being α = 0.0001, β1 = 0, and β2 = 0.9. The critic weights were also updated 5 times in the space of the generator weights being updated once. These are the optimal values determined by Gulrajani et al.32
The WGAN training was set to run for a maximum of 6000 epochs, with early-stopping applied using parametric functions measuring absolute noise in the wavenumber region 3500–3000 cm−1. These parameters measure the relative height of peaks and troughs in the region to determine satisfactory spectral quality. The patience for early stopping was set to 600 epochs. All WGAN models were developed with Python v3.9.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46 using Tensorflow v2.9.1.44 All WGAN training was carried out using the ARCHIE-WeST High Performance Computing Centre based at the University of Strathclyde, with WGAN training utilising 10 NVidia A100 GPU cores housed in Lenovo SR670 servers and optimisation lasting on average 4 hours. GPU computation was done using CUDA version 11.2.
46 using Tensorflow v2.9.1.44 All WGAN training was carried out using the ARCHIE-WeST High Performance Computing Centre based at the University of Strathclyde, with WGAN training utilising 10 NVidia A100 GPU cores housed in Lenovo SR670 servers and optimisation lasting on average 4 hours. GPU computation was done using CUDA version 11.2.
3.8 Model validation
CNN models were developed to identify the cancerous signature from a labelled patient cohort and then predict the presence of cancer in an unknown population. A nested cross-validation (CV) strategy was used to develop the model, in which the inner CV was used to tune the model hyper-parameters, and the outer CV provided a robust test of model performance. In this approach, for the outer CV, patients were randomly split into training and test sets with a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 split, repeated 51 times. Model hyper-parameters were tuned to optimize the area under the ROC curve during the inner 5-fold CV on the training set (70%). The trained model was used to make predictions from the spectra in the test set (30%). Training and test sets were stratified by patient ID, and therefore spectra from individual patients were not allowed to be present in both the training and test sets for a given resample. To ensure that the CNN training was not tuning the model towards the augmented spectra, any augmented spectra were removed from the validation set used for model tuning and early stopping prior to training. The by-spectrum AUCs obtained for each of the 51 outer CV iterations were aggregated, and the mean and standard deviation of the resulting classification metrics were computed.
30 split, repeated 51 times. Model hyper-parameters were tuned to optimize the area under the ROC curve during the inner 5-fold CV on the training set (70%). The trained model was used to make predictions from the spectra in the test set (30%). Training and test sets were stratified by patient ID, and therefore spectra from individual patients were not allowed to be present in both the training and test sets for a given resample. To ensure that the CNN training was not tuning the model towards the augmented spectra, any augmented spectra were removed from the validation set used for model tuning and early stopping prior to training. The by-spectrum AUCs obtained for each of the 51 outer CV iterations were aggregated, and the mean and standard deviation of the resulting classification metrics were computed.
4 Results and discussion
4.1 WGAN generated spectra
The optimised WGAN was trained on the 525 patient dataset and used to generate 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 spectra to use as input for the subsequent WGAN augmented CNN models; 5000 pancreatic cancer and 5000 non-cancer spectra.
000 spectra to use as input for the subsequent WGAN augmented CNN models; 5000 pancreatic cancer and 5000 non-cancer spectra.
Although the WGAN worked well in generating fake spectra that contained the correct general spectral features, the spectra produced were also excessively noisy. This could be rectified by continuing to optimise the WGAN architecture until this noise level was reduced. However, the computational resources required to do this would be vast, and the same reduction in noise could be achieved using smoothing. Therefore, a Savitzky–Golay filter with a window of 21 was used to smooth the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generated spectra to remove this noise. Fig. 3 shows a real spectrum used to train the WGAN, a WGAN-generated spectrum, and that generated spectrum after smoothing.
000 generated spectra to remove this noise. Fig. 3 shows a real spectrum used to train the WGAN, a WGAN-generated spectrum, and that generated spectrum after smoothing.
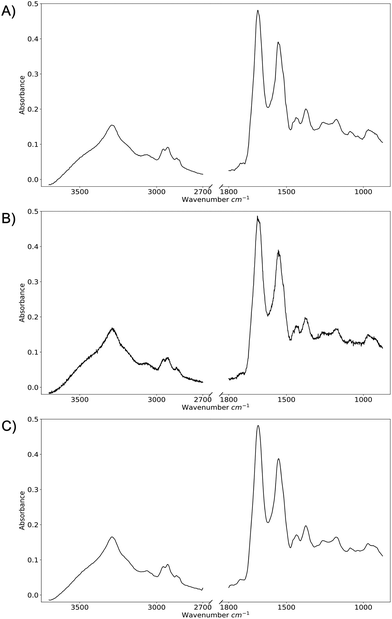 | ||
| Fig. 3 (A) Real spectrum, (B) WGAN-generated spectrum, and (C) WGAN-generated spectrum after smoothing. | ||
4.2 Comparison of traditional augmentation and WGANs
A CNN model was trained and tested using nested cross-validation on the 100-patient dataset. Nested cross-validation prevents data leakage by blinding the model to the test data during training, and it reduces sample bias by providing classification statistics as averages over multiple repeat experiments (in which training and test sets are selected at random based on patient ID). To assess the effect of data augmentation, the nested CV experiment was repeated using different generative and non-generative augmentation methods, with other factors kept constant. Since only the training sets were augmented, the mean classification statistics for the test sets were used to compare different methods.Although nested cross-validation is a data efficient and rigorous method to train ML models, it requires retraining the CNN model on 255 different training sets in every run (51 training sets in outer CV × 5 training sets in inner CV). Since nested CV had to be repeated 22 times (5 quantities of augmented data for each of 4 augmentation methods, plus two baseline models), that equates to 5610 training sets. This presents a practical problem since retraining the WGAN model on each training set would be computationally expensive and difficult to monitor. Therefore, in the first experiments, data augmentation was carried out using a WGAN pre-trained on the 525-patient dataset. To provide a like-for-like comparison, the non-generative augmented spectra were also obtained from the 525-patient dataset, and a second benchmark model was evaluated in which the 525-patient dataset was added to each training set during nested cross-validation (further experiments in which the CNN and WGAN were trained on the same training sets are described below). All models are compared via the by-spectrum AUCs in Table 3.
| Augmentation | No. of spectra added | No. of training spectra | AUC |
|---|---|---|---|
| No augmentation | 630 | 0.668 | |
| Augmentation with real spectra | 4725 | 5355 | 0.748 |
| Random noise | 500 | 1130 | 0.721 |
| 1000 | 1630 | 0.746 | |
| 2000 | 2630 | 0.748 | |
| 5000 | 5630 | 0.743 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 630 |
0.753 | |
| Mean bootstrap sample | 500 | 1130 | 0.745 |
| 1000 | 1630 | 0.753 | |
| 2000 | 2630 | 0.759 | |
| 5000 | 5630 | 0.730 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 630 |
0.757 | |
| Splice spectra | 500 | 1130 | 0.708 |
| 1000 | 1630 | 0.751 | |
| 2000 | 2630 | 0.749 | |
| 5000 | 5630 | 0.737 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 630 |
0.749 | |
| WGAN augmentation | 500 | 1130 | 0.771 |
| 1000 | 1630 | 0.768 | |
| 2000 | 2630 | 0.770 | |
| 5000 | 5630 | 0.781 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 630 |
0.757 | |
Table 3 shows that data augmentation leads to an improvement in model performance in all cases. Furthermore, the CNNs that utilize the WGAN-augmented spectra during training perform better than those that use augmented spectra from non-generative methods. The model highlighted in bold, that is the CNN that adds 5000 WGAN-augmented spectra at each training step, shows a statistically significant improvement (using a Student's t-test) from the second benchmark model in which real spectra from the 525-patient dataset are used for data augmentation.
Although Table 3 shows evidence of model improvement from data augmentation, the imbalance between the augmented training set and the unaugmented validation set used for early stopping seemed to have a detrimental effect on model training. For example, adding 5000 augmented spectra led to 5405 spectra in the training set and only 99 spectra in the early-stopping set during 5-fold cross validation. A small validation set might cause inaccurate hyperparameter selection or underfitting.
Therefore, CNN models were re-run, this time with a fixed amount of data added to the early stopping sets. To provide a like-for-like comparison between different augmentation methods, each early stopping set was augmented with the same 4725 real spectra from the 525-patient dataset. This meant that for each resample, the training set would contain 5405 spectra (consisting of the 100-patient dataset split for training and generated spectra) and the validation set would contain 4824 spectra (consisting of the 100-patient dataset split for validation and the 525-patient dataset), balancing the ratio. The results for these models is shown in Table 4.
| Augmentation | No. of spectra added | No. of training samples | AUC |
|---|---|---|---|
| No augmentation | 630 | 0.668 | |
| Augmentation with real spectra | 4725 | 5355 | 0.748 |
| Random noise | 500 | 1130 | 0.729 |
| 1000 | 1630 | 0.734 | |
| 2000 | 2630 | 0.735 | |
| 5000 | 5630 | 0.750 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 630 |
0.737 | |
| Mean bootstrap sample | 500 | 1130 | 0.740 |
| 1000 | 1630 | 0.736 | |
| 2000 | 2630 | 0.751 | |
| 5000 | 5630 | 0.733 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 630 |
0.738 | |
| Splice spectra | 500 | 1130 | 0.711 |
| 1000 | 1630 | 0.741 | |
| 2000 | 2630 | 0.730 | |
| 5000 | 5630 | 0.728 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 630 |
0.730 | |
| WGAN augmentation | 500 | 1130 | 0.779 |
| 1000 | 1630 | 0.800 | |
| 2000 | 2630 | 0.768 | |
| 5000 | 5630 | 0.787 | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 630 |
0.765 | |
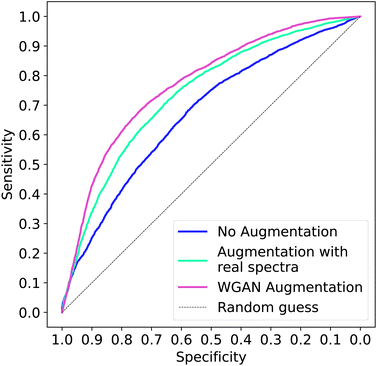
Table 4 shows that two more of the WGAN augmented models present a statistical improvement on the by-spectrum AUC produced by the benchmark model, with one model achieving an AUC of 0.800. This improvement due to data augmentation is evident in the comparison of the mean ROC curves in Fig. 4. Mean ROC curves were obtained by averaging sensitivity and specificity for a fixed threshold across 51 models. There is still the same trend as previously in which WGAN-augmented spectra seem to have more benefit than the non-generative methods.
An unexpected result apparent in Tables 3 and 4 is the lack of correlation between the number of generated spectra added during training and the resultant AUC. It was assumed that including more data during model training would result in improved model performance. However, this study shows that this is not the case. This might suggest that, even though adding more data is expanding the training set, the generated data is limited in the new information it can add to model learning. This explain the non-linear relationship between data volume and model performance.
To simulate the model being used in a real-life scenario, when the CNN and WGAN would more likely be trained on the same training set, two CNN models were trained on the full 525 patient dataset, one augmented with 1000 WGAN generated spectra and one without. Both CNN models were then used to predict the 100 patient dataset. The improvement in AUC from 0.661 to 0.757, as reported in Table 5, is a clear demonstration of the benefit of data augmentation using the WGAN.
| Model | AUC |
|---|---|
| Train: 525-patient dataset test: 100-patient dataset | 0.661 |
| Train: 525-patient dataset and augmented spectra test: 100-patient dataset | 0.757 |
The previous results demonstrate the successful use of WGANs to improve the AUC of the pancreatic dataset. To further demonstrate the benefit of WGAN augmentation on other datasets, a separate dataset comprising of colorectal cancer patients (N = 200) and non-cancer patients (N = 459) in which FTIR spectra had been measured from dried serum samples was used. These samples are covered by the Ethical Approval quoted in section 3.1. In a similar method to the pancreatic dataset, a subset of 100 samples were set aside to use as an external test set, leaving 559 samples to be used for WGAN training. The subsets of the data were age and sex matched to the full dataset. The patient metadata of the full colorectal dataset, the 559-patient dataset, and the 100-patient dataset can be found in Tables S3–5† respectively. The same architecture used previously was first trained on this 559-patient dataset and then used to predict the 100-patient dataset. This result was then used to compare a CNN trained on the 559-patient dataset alongside 1000 WGAN-augmented spectra to predict the 100-patient dataset. These by-spectrum AUCs are shown in Table 6.
| Model | AUC |
|---|---|
| Train: 559 patient dataset test: 100 colorectal | 0.905 |
| Train: 559 patient dataset and augmented spectra test: 100 colorectal | 0.955 |
The increase in the test set AUC after the addition of WGAN augmented spectra for a differing dataset further demonstrates the benefit of data augmentation and its use across different cancer datasets.
These results show for the first time the benefit of data augmentation for model training within spectroscopic liquid biopsy cancer diagnostics. The results follow the trend demonstrated by Wickramaratne et al.30 who demonstrated that data augmentation using GANs can improve model performance, as well as Nagasawa et al.33 who showed similar results with WGAN generated spectra. However, our study, to the best of our knowledge, is the first to compare the performance of various data augmentation methods using multiple independent resamples to reduce bias that can occur from particular train/test splits. This method has enabled a like-for-like comparison between non-generative augmentation and WGAN generated spectra.
5 Conclusions
This study determines overall that adding WGAN-augmented spectra at each resample improves model performance. It can also be demonstrated that using WGAN augmented spectra has a more beneficial impact when compared to non-generative augmentation methods.One hypothesis that was made before the study began was that as more augmented data was added, the CNN performance was expected to increase. However, this was not the case. This could demonstrate a particular downfall of data augmentation: the quality of information it adds to a model. Although it was somewhat expected that WGAN augmentation would outperform non-generative augmentation as it doesn't just change aspects of the data, but actually learns from the real data, there is still a limit to the information it can learn and create. It seems to be that augmentation simply adds complexity to the dataset helping to regularise the model, hence the non-linear relationship between the number of augmented data points added and model performance.
Further work would include obtaining an external test set of patients from a different location to the training set. This would have the added benefit of providing spectra that were also analysed at a different time, further validating the model's performance as a potential method for clinical use. The methods described could also be applied to other cancer types, particularly rarer types where there are naturally fewer samples available for analysis.
Author contributions
Conceptualization: DSP, MJB. Data curation: RGMcH. Formal analysis: RGMcH, GA. Funding acquisition: DSP, MJB. Investigation: RGMcH, GA. Methodology: RGMcH, GA. Project administration: DSP, MJB. Resources: MJB, DSP, JJAC. Software: GA, DSP, RGMcH, JJAC. Supervision: DSP, MJB. Validation: RGMcH, GA. Visualization: RGMcH. Writing – original draft: RGMcH. Writing – review & editing: GA, DSP, RGMcH, JJAC.Conflicts of interest
DSP and MJB are Directors of Dxcover Ltd, a company developing spectroscopic liquid biopsies for diagnosing cancers. RGMcH, GA, and JJAC are employees of Dxcover Ltd.Acknowledgements
The authors thank the ARCHIE-WeST High Performance Computing Centre (https://www.archie-west.ac.uk/) for computational resources. RGMcH and DSP thank the University of Strathclyde and Dxover Ltd for PhD funding for RGMcH.References
- R. L. Siegel, K. D. Miller, H. E. Fuchs and A. Jemal, CA-Cancer J. Clin., 2022, 72, 7–33 CrossRef PubMed.
- E. Hubbell, C. A. Clarke, A. M. Aravanis and C. D. Berg, Cancer Epidemiol., Biomarkers Prev., 2021, 30, 460–468 CrossRef CAS PubMed.
- A. Bleyer and H. G. Welch, N. Engl. J. Med., 2012, 367, 1998–2005 CrossRef CAS PubMed.
- A. C. Perkins and E. N. Skinner, N. C. Med. J., 2016, 77, 420–422 Search PubMed.
- K. L. Huang, S. Y. Wang, W. C. Lu, Y. H. Chang, J. Su and Y. T. Lu, BMC Pulm. Med., 2019, 19, 126 CrossRef PubMed.
- V. Tonini and M. Zanni, World J. Gastroenterol., 2022, 28, 4235–4248 CrossRef CAS PubMed.
- R. Nishihara, K. Wu, P. Lochhead, T. Morikawa, X. Liao, Z. R. Qian, K. Inamura, S. A. Kim, A. Kuchiba, M. Yamauchi, Y. Inamura, W. C. Willett, B. A. Rosner, C. S. Fuchs, E. Giovannucci, S. Ogino and A. T. Chan, N. Engl. J. Med., 2013, 369, 1095 CrossRef CAS PubMed.
- D. Crosby, S. Bhatia, K. M. Brindle, L. M. Coussens, C. Dive, M. Emberton, S. Esener, R. C. Fitzgerald, S. S. Gambhir, P. Kuhn, T. R. Rebbeck and S. Balasubramanian, Science, 2022, 375, eaay9040 CrossRef CAS PubMed.
- E. Lianidou and K. Pantel, Genes, Chromosomes Cancer, 2019, 58, 219–232 CrossRef CAS PubMed.
- M. Malla, J. M. Loree, P. M. Kasi and A. R. Parikh, J. Clin. Oncol., 2022, 40, 2846–2857 CrossRef CAS PubMed.
- S. Connal, J. M. Cameron, A. Sala, P. M. Brennan, D. S. Palmer, J. D. Palmer, H. Perlow and M. J. Baker, J. Transl. Med., 2023, 21, 118 CrossRef PubMed.
- A. Sala, J. M. Cameron, C. A. Jenkins, H. Barr, L. Christie, J. J. A. Conn, T. R. J. Evans, D. A. Harris, D. S. Palmer, C. Rinaldi, A. G. Theakstone and M. J. Baker, Cancers, 2022, 14, 3048 CrossRef CAS PubMed.
- J. M. Cameron, C. Rinaldi, H. J. Butler, M. G. Hegarty, P. M. Brennan, M. D. Jenkinson, K. Syed, K. M. Ashton, T. P. Dawson, D. S. Palmer and M. J. Baker, Cancers, 2020, 12, 1710 CrossRef CAS PubMed.
- A. Sala, A. J. Anderson, P. M. Brennan, H. J. Butler, J. M. Cameron, M. D. Jenkinson, C. Rinaldi, A. G. Theakstone and M. J. Baker, Cancer Lett., 2020, 477, 122–130 CrossRef CAS PubMed.
- M. Paraskevaidi, M. J. Baker, H. J. Butler, H. J. Byrne, T. P. V. Chakkumpulakkal, L. Christie, S. Crean, P. Gardner, C. Gassner, S. G. Kazarian, K. Kochan, M. Kyrgiou, K. G. M. Lima, P. L. Martin-Hirsch, E. Paraskevaidis, S. Pebotuwa, J. A. Adegoke, A. Sala, M. Santos, J. Sulé-Suso, G. Tyagi, M. Walsh and B. Wood, Appl. Spectrosc. Rev., 2021, 56, 804–868 CrossRef CAS.
- H. J. Butler, P. M. Brennan, J. M. Cameron, D. Finlayson, M. G. Hegarty, M. D. Jenkinson, D. S. Palmer, B. R. Smith and M. J. Baker, Nat. Commun., 2019, 10, 4501 CrossRef PubMed.
- A. G. Theakstone, P. M. Brennan, M. D. Jenkinson, S. J. Mills, K. Syed, C. Rinaldi, Y. Xu, R. Goodacre, H. J. Butler, D. S. Palmer, B. R. Smith and M. J. Baker, Cancers, 2021, 13, 3851 CrossRef CAS PubMed.
- J. M. Cameron, P. M. Brennan, G. Antoniou, H. J. Butler, L. Christie, J. J. A. Conn, T. Curran, E. Gray, M. G. Hegarty, M. D. Jenkinson, D. Orringer, D. S. Palmer, A. Sala, B. R. Smith and M. J. Baker, Neuro-Oncol. Adv., 2022, 4, vdac024 CrossRef PubMed.
- P. M. Brennan, H. J. Butler, L. Christie, M. G. Hegarty, M. D. Jenkinson, C. Keerie, J. Norrie, R. O’Brien, D. S. Palmer, B. R. Smith and M. J. Baker, Brain Commun., 2021, 3, fcab056 CrossRef PubMed.
- A. Sala, J. M. Cameron, C. A. Jenkins, H. Barr, L. Christie, J. J. A. Conn, T. R. J. Evans, D. A. Harris, D. S. Palmer, C. Rinaldi, A. G. Theakstone and M. J. Baker, Cancers, 2022, 14, 3048–3061 CrossRef CAS PubMed.
- G. Antoniou, J. J. A. Conn, B. R. Smith, P. M. Brennan, M. J. Baker and D. S. Palmer, Analyst, 2023, 148, 1770–1776 RSC.
- D. Chen, S. Liu, P. Kingsbury, S. Sohn, C. B. Storlie, E. B. Habermann, J. M. Naessens, D. W. Larson and H. Liu, npj Digital Med., 2019, 2, 43 CrossRef PubMed.
- S. I. Nikolenko, Synthetic Data for Deep Learning, Springer Cham, 2021 Search PubMed.
- L. Taylor and G. Nitschke, Improving Deep Learning using Generic Data Augmentation, 2017, 1–6 Search PubMed.
- R. Hao, K. Namdar, L. Liu, M. A. Haider and F. Khalvati, J. Digital Imaging, 2021, 34, 862–876 CrossRef PubMed.
- E. J. Bjerrum, M. Glahder and T. Skov, Data Augmentation of Spectral Data for Convolutional Neural Network (CNN) Based Deep Chemometrics, 2017, 1–10 CAS.
- U. Blazhko, V. Shapaval, V. Kovalev and A. Kohler, Chemom. Intell. Lab. Syst., 2021, 215, 104367–104376 CrossRef CAS.
- I. J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, Adv. Neural Inf. Process. Syst., 2014, 2672–2680 Search PubMed.
- W. Al-Dhabyani, M. Gomaa, H. Khaled and A. Fahmy, Int. J. Adv. Comput. Sci. Appl., 2019, 10, 618–627 Search PubMed.
- S. D. Wickramaratne and S. Mahmud, Front. Big Data, 2021, 4, 659146 CrossRef PubMed.
- M. Arjovsky, S. Chintala and L. Bottou, 34th International Conference on Machine Learning, 2017, vol. 70, pp. 214–223.
- I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin and A. Courville, Adv. Neural Inf. Process. Syst., 2017, 5767–5777 Search PubMed.
- T. Nagasawa, T. Sato, I. Nambu and Y. Wada, J. Neural Eng., 2020, 17, 016068–016078 CrossRef PubMed.
- Y. Zhao, S. Tian and Y. Xing, Spectroscopy, 2021, 4, 28–40 Search PubMed.
- X. Gao and X. Wang, Diagn. Interv. Imaging, 2020, 101, 91–100 CrossRef CAS PubMed.
- K. Si, Y. Xue, X. Yu, X. Zhu, Q. Li, W. Gong, T. Liang and S. Duan, Theranostics, 2021, 11, 1982–1990 CrossRef PubMed.
- K. Liu, T. Wu, P. Chen, Y. M. Tsai, H. Roth, M. Wu, W. Liao and W. Wang, Lancet, 2020, 2, e303–e313 Search PubMed.
- J. Lin, IEEE Trans. Inf. Theory, 1991, 37, 145–151 CrossRef.
- M. Zheng, T. Li, R. Zhu, Y. Tang, M. Tang, L. Lin and Z. Ma, Inf. Sci., 2020, 512, 1009–1023 CrossRef.
- M. J. Baker, M. Hegarty, H. J. Butler and D. Palmer, Infra-red spectroscopy system, US11215553B2, 2022.
- H. Martens and E. Stark, J. Pharm. Biomed. Anal., 1991, 9, 625–635 CrossRef CAS PubMed.
- F. Chollet, J. Allaire, et al., R Interface to Keras, 2017, https://github.com/rstudio/keras Search PubMed.
- R Core Team, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, 2022 Search PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015, https://www.tensorflow.org/, Software available from tensorflow.org Search PubMed.
- I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT Press, 2016 Search PubMed.
- G. Van Rossum and F. L. Drake, Python 3 Reference Manual, CreateSpace, Scotts Valley, CA, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3an00669g |
| This journal is © The Royal Society of Chemistry 2023 |