Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Recurrent neural networks for time domain modelling of FTIR spectra: application to brain tumour detection†
Georgios
Antoniou
a,
Justin J. A.
Conn
a,
Benjamin R.
Smith
a,
Paul M.
Brennan
 b,
Matthew J.
Baker
ac and
David S.
Palmer
b,
Matthew J.
Baker
ac and
David S.
Palmer
 *ad
*ad
aDxcover Limited, Suite RC534, Royal College Building, 204 George Street, Glasgow G1 1XW, UK
bTranslational Neurosurgery, Centre for Clinical Brain Sciences, University of Edinburgh, Midlothian, Edinburgh EH4 2XU, UK
cSchool of Medicine, Faculty of Clinical and Biomedical Sciences, University of Central Lancashire, Preston PR1 2HE, UK
dDepartment of Pure and Applied Chemistry, University of Strathclyde, Glasgow G1 1XL, UK. E-mail: david.palmer@strath.ac.uk
First published on 24th March 2023
Abstract
Attenuated total reflectance (ATR)-Fourier transform infrared (FTIR) spectroscopy alongside machine learning (ML) techniques is an emerging approach for the early detection of brain cancer in clinical practice. A crucial step in the acquisition of an IR spectrum is the transformation of the time domain signal from the biological sample to a frequency domain spectrum via a discrete Fourier transform. Further pre-processing of the spectrum is typically applied to reduce non-biological sample variance, and thus to improve subsequent analysis. However, the Fourier transformation is often assumed to be essential even though modelling of time domain data is common in other fields. We apply an inverse Fourier transform to frequency domain data to map these to the time domain. We use the transformed data to develop deep learning models utilising Recurrent Neural Networks (RNNs) to differentiate between brain cancer and control in a cohort of 1438 patients. The best performing model achieves a mean (cross-validated score) area under the receiver operating characteristic (ROC) curve (AUC) of 0.97 with sensitivity of 0.91 and specificity of 0.91. This is better than the optimal model trained on frequency domain data which achieves an AUC of 0.93 with sensitivity of 0.85 and specificity of 0.85. A dataset comprising 385 patient samples which were prospectively collected in the clinic is used to test a model defined with the best performing configuration and fit to the time domain. Its classification accuracy is found to be comparable to the gold-standard for this dataset demonstrating that RNNs can accurately classify disease states using spectroscopic data represented in the time domain.
1 Introduction
Today, cancer ranks as one of the leading causes of death worldwide. According to Globocan 2020‡ an estimated 19.3 million new cancer cases and about 10 million cancer deaths have been reported across the world only in 2020. In particular, cancers of the brain and the central nervous system account for about 1.6% of all new cases and 2.5% of all new deaths, posing significant diagnostic challenges. Associated symptoms are frequently generic (e.g., headache) which can thus lead to misdiagnoses1 or detection at an advanced stage.2,3In a series of retrospective4–7 and prospective8–10 studies, a liquid biopsy approach based on the combination of FTIR spectroscopy and machine learning has been proposed to address the issue of early detection of brain cancer. The Dxcover® Brain Cancer liquid biopsy test bears the advantage of being simple, label free, non-invasive, and non-destructive showing great potential as a triage tool in the current diagnostic pathways. In the first prospective clinical study9 established at the Western General Hospital Edinburgh (NHS Lothian) to test this technology, blood samples from 385 patients (cf., cohort B in Section 2.1) were collected and subsequently analysed. A diagnostic model was used to predict the disease status of the samples achieving 81% sensitivity and 80% specificity. The development of the technology along with interim results for this study were published in an article by Butler et al.8 More recently10 this technology was further clinically validated in a larger prospective study comprising samples from 603 patients. The diagnostic model was tuned for either high sensitivity (96% sensitivity with 45% specificity) and high specificity (90% specificity with 47% sensitivity) demonstrating that this liquid biopsy test can be a versatile tool that fits into the requirements of diverse diagnostic pathways and healthcare systems.
Deep learning techniques have been employed for various types of spectral analysis including Raman spectroscopy,11 spectral imaging12 and FTIR vibrational spectroscopy.13 Convolutional Neural Networks (CNNs) in particular (see Schmidhuber14 and references therein), which have emerged in computer vision, can provide a powerful alternative to traditional machine learning algorithms for these tasks mainly for their ability to extract spectral and local spatial patterns. Examples of CNN architectures developed in this context include DeepSpectra15 and SpectraVGG16 which are based on the inception and VGG architectures respectively. It is important to note however that the effectiveness of deep learning methods scales with dataset size17 and in general they tend to under-perform when compared to tree-based (e.g., Random Forest) or boosting (e.g., eXtreme Gradient Boosting) methods for modelling tabular data.18
In this work we build on our previous diagnostic research4–10 to classify spectroscopic data obtained from blood serum of patients with differing brain cancer types and non-cancer patients. Our motivation for this study is twofold.
Firstly, we question the necessity of the Fourier transformation in the process of obtaining an IR spectrum for ML analysis. Despite algorithmic optimisations (e.g., fast Fourier transform), this discrete transformation is time consuming and may result in an efficiency bottleneck when performing the analysis on many samples (see Griffiths and de Haseth19 and references therein for a comprehensive efficiency comparison of discrete Fourier transform algorithms). Additionally, the accuracy of the resulting IR spectrum also depends on the phase correction and apodisation steps,20,21 involved from the transformation of an interferogram to a spectrum. We attempt to answer this question indirectly (rather than based on interferogram data) by applying an inverse Fourier transform on the IR spectra. Thus we utilise a powerful family of deep learning algorithms, namely RNNs which are designed for processing sequential data (such as time series) by maintaining a state of the underlying data structure. The performance of the best performing model is compared against that of our gold-standard model (previously published in Brennan et al.9) on the same patient cohort but on standard FTIR spectra.
Secondly, we perform a search over various deep learning architectures incorporating RNN blocks in order to identify suitable algorithms for modelling spectroscopic data. The corresponding architectures comprise CNN and LSTM22 (long-short-term-memory) layers and are used to define models on data in the time and frequency domain. We show that models built on time domain perform better over models trained on the original frequency domain data, thus providing evidence for the suitability of RNN algorithms in the modelling of time domain, potentially extending to a range of applications related to chemometric analyses including but not limited to healthcare, food testing and pharmaceutics.
2 Methods
2.1 Datasets
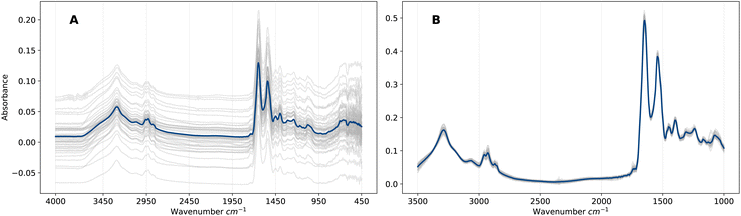
Patient serum samples were analysed using the Dxcover® Brain Cancer liquid biopsy.8,9 In this process, serum is appropriately prepared and pipetted onto three sample wells of the Dxcover® Sample Slides which consist of a SIRE8 (Silicon Internal Reflection Element) in a plastic holder. A total of three FTIR spectra for each sample well are subsequently measured from the dried sample slides. For more information on the sample preparation and spectral collection methodologies we refer to Butler et al.8We considered two datasets comprising ATR-FTIR spectra measured from serum samples of two distinct patient cohorts A and B, where cohort A consists of 1438 retrospectively collected biobank samples and cohort B of 385 prospectively collected samples (see Brennan et al.9 for details on cohort B). Table 1 summarises the distributions of the two classes for each cohort. The non-cancer group of cohort A consists of samples obtained from healthy controls, while the non-cancer group of cohort B consists of samples obtained from symptomatic patients referred for brain imaging from primary care with suspected brain tumour in the clinic. Symptoms recorded for cohort B as part of the original clinical study are presented in Table S6.† Additional information on both cohorts such as age, sex and disease breakdown are presented in Tables S1–S4.†
| Cohort | Non-cancer | Cancer |
|---|---|---|
| A | 438 | 1000 |
| B | 318 | 67 |
A small number of spectra from cohort A that failed quality tests (e.g., due to noise) were removed. Overall, 12448 and 3465 spectra were used for subsequent analysis corresponding to cohorts A and B respectively. In what follows, we will refer to spectral datasets from cohorts A, B as datasets A and B respectively. The precise stratification of the number of spectra per sample can be found in Table S5.†
2.2 Spectral pre-processing
A spectrum can be represented as an n-dimensional vector| x = (xi1,…,xin), i1 > … > in, |
A sequence of two pre-processing steps was applied to raw frequency domain spectra. Firstly, they were cut to the wavenumber region 3500–1000 cm−1, which contains significant features of molecular vibrations relevant for disease classification, as seen in previous studies.23,24 Subsequently, an Extended Multiplicative Signal Correction25 (EMSC) was applied to the spectra.§
EMSC is a non-linear least-squares regression on the vector representation of the reference spectrum r, and thus the transformation applied to vector x is uniquely defined by the pair (r, x). Overall, the EMSC transformation aligns all spectra to the reference, which removes artefacts (e.g., baseline effects) that would otherwise introduce noise into the ML analysis. The effect on the spectra is evident in Fig. 1 in which the raw and pre-processed spectra are compared. We will refer to this representation of pre-processed frequency domain spectra as F. Although EMSC is a common pre-processing step in the field of IR spectroscopy, the optimal spectral pre-processing method is often problem, dataset and algorithm specific.26
By applying an inverse discrete Fourier transform to the FR and F representations we define the representations TR and T, respectively. That is, TR denotes data in the time domain which have not been pre-processed in neither frequency or time domain, while T denotes data in the time domain which have first been pre-processed as described above in the frequency domain and then mapped to the time domain via an inverse Fourier transform. A diagrammatic representation of the data representations and the corresponding transformations can be found in Fig. S1.† It is important to note that TR is not equivalent to the interferogram representation of the signal as generated by the spectrometer, since additional steps are required to obtain a spectrum from an interferogram, including taking the modulus of the complex Fourier coefficients for each vibrational frequency and performing phase correction.20
2.3 Statistical design
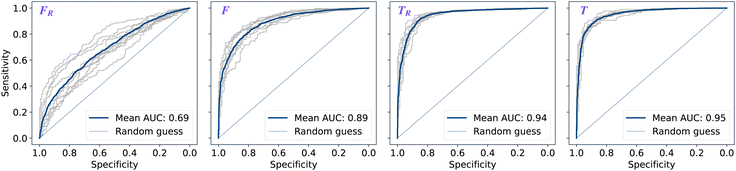
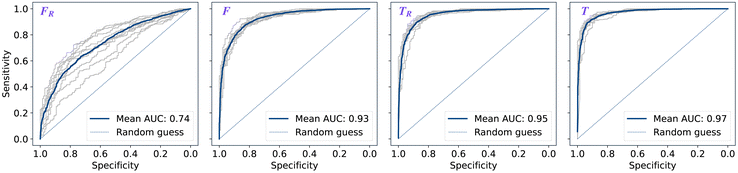
The ML models were trained and validated using nested cross-validation to ensure ML models were blind to test sets during training. The full dataset was split into training α100% and testing (1 − α)100%, 0 ≤ α ≤ 1 sets based on patient ID so that all spectra from a single patient were in the same subset. Early stopping was utilised based on a validation set defined as 20% of the training data, where binary cross-entropy (BCE) loss was monitored to avoid overfitting to the training data. For each split of the data into training, validation and testing sets, the mean and standard deviation of the features were computed from the training data and subsequently used to apply a centering and scaling transformation¶ to all groups. Subsequently, the minority class (non-cancer in dataset A) was over-sampled to balance the classes in the training set. The prediction for each patient was taken as the maximum vote of the predictions for all spectra for that patient; ties were broken at random since they occurred so infrequently as to have no discernible effect on the results. Note that all results are reported on a by-patient basis.Dataset A was used to perform ML analysis over the various architectures and data types. Models were trained with the methodology described above and with α = 0.7. To reduce sampling bias in the train-test split, all classification metrics for this part (see Table 2) were reported as means for 10 independent experiments using different training and test set splits; 10 iterations were found to be sufficient to converge the estimate of the AUC to a mean of about 0.02 standard deviations. Subsequently, the best performing model architecture and dataset representation were utilised to train a single model (α = 1) over the whole dataset A which was used to predict dataset B.
| Architecture | Representation | AUC | Sensitivity | Specificity |
|---|---|---|---|---|
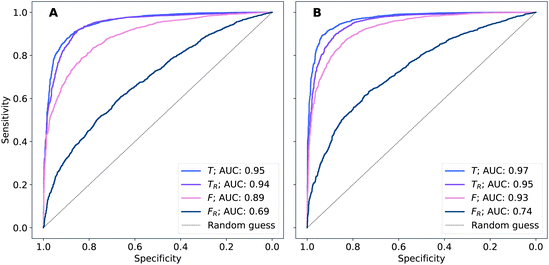
| ConvBNMaxP-L-MLP | F R | 0.685 ± 0.057 | 0.630 ± 0.048 | 0.630 ± 0.048 |
| F | 0.892 ± 0.024 | 0.811 ± 0.026 | 0.811 ± 0.026 | |
| T R | 0.945 ± 0.009 | 0.882 ± 0.013 | 0.882 ± 0.013 | |
| T | 0.952 ± 0.007 | 0.887 ± 0.012 | 0.888 ± 0.011 | |
| ConvBNMaxP2-L-MLP | F R | 0.734 ± 0.060 | 0.670 ± 0.056 | 0.670 ± 0.057 |
| F | 0.928 ± 0.012 | 0.853 ± 0.015 | 0.853 ± 0.015 | |
| T R | 0.954 ± 0.008 | 0.886 ± 0.019 | 0.886 ± 0.019 | |
| T | 0.969 ± 0.006 | 0.912 ± 0.011 | 0.912 ± 0.012 | |
Due to availability of computational resources, model hyperparameters were tuned in a standalone experiment by a grid search to optimise AUC computed on a by-spectrum basis from 5-fold cross-validation. The best hyperparameters were subsequently used to fit the model on the full (70%) training dataset and make predictions of the test set for each independent experiment as described above.
2.4 Deep learning
Neural networks were trained using TensorFlow27 (v2.8.0) in R28 (v4.1.2). All models were built using PRFFECT – an in-house R code that has previously been published.29 Several deep learning architectures were tested comprising three general structures: (i) convolution blocks ConvBMaxP – comprising a 1D convolutional layer into a batch normalisation layer into a max pooling layer; (ii) an RNN layer X – comprising either a LSTM (L), a bidirectional LSTM layer (BL), or a gated recurrent unit30 (G); (iii) a MLP block – comprising one dense layer followed by a dropout layer. Tanh/sigmoid activation functions were applied to the L, BL and G layers. Relu/sigmoid activation functions were applied to the convolutional and dense layers. Initial testing showed that BL layers did not result in any significant improvement in performance despite being more computationally expensive to train than L layers. Additionally, L layers were preferred over G layers due to increased representational power. Model hyperparameters were optimised with the grid search described in the previous section, however no exhaustive search was performed across all dimensions of the hyperparameter space. In particular, the following hyperparameters and values were optimised for each architecture: L/G dropout rate (0, 0.2, 0.4), L/G units (16, 32) and dense layer hidden units (8, 32). The kernel size, number of filters and pool size of the convolution block were fixed to 7, 64 and 3 respectively, while the recurrent dropout of the L/G layers was set to 0, following an initial analysis. The maximum number of epochs was fixed to 200 and early stopping was implemented with patience 10. Batch size was fixed to 32. Model weights were updated minimising regularised BCE loss function using the Adam31 optimiser with default parameters except for the learning rate which was set to 10−4. Below, ConvBMaxPβ-X-MLP denotes the general architecture, where β = 1, 2 is the number of times the block is repeated.3 Results & discussion
3.1 Cohort A
The performance of models was evaluated using AUC reported as an average across 10 independent experiments. Additionally, sensitivity and specificity were computed for each model at a threshold (balance point) such that the absolute difference of these statistics attains it's minimum value. These results are summarised in Table 2. Fig. 2–4 show ROC curves for RNN models for all data representations. In particular, ROC curves for each individual experiment as well as the mean ROC curve for model types ConvBNMaxP-L-MLP, and ConvBNMaxP2-L-MLP are presented in Fig. 2 and 3 respectively. Mean ROC curves were obtained by averaging sensitivity and specificity for a fixed threshold across 10 models. Mean ROC curves are presented in Fig. 4 for each data representation and RNN model.Overall, a sequence of two ConvBMaxP blocks in the model architecture leads to higher classification scores across all data representations, with larger differences being observed for the representations F and FR. Models trained in the frequency domain are unstable with higher bias and variance, which results in inferior performances and larger test set errors, which can be seen from Table 2 and Fig. 2 and 3. It is clear from this analysis that when neural network architectures comprise RNN blocks it is necessary to map spectra to the time domain prior to further analysis.
Additionally, it is interesting to note from Table 2 that spectral pre-processing has a larger effect on the performance of models in frequency domain (FRvs. F), rather than in time domain (TRvs. T). This is likely due to the fact that most variance in the raw frequency domain spectra (see Fig. 1A) is explained by baseline offset which is mapped under the Fourier transform to a Dirac delta function (up to proportionality) in the time domain. Thus, it is expected that the performances of models on TR and T are comparable. Moreover, the results for raw time domain data were better than those for pre-processed frequency domain or raw frequency domain data. Model performance between raw and pre-processed frequency domain data is thought to be heavily dependent on the properties of the dataset used rather than being a systematic observation (see e.g. Blazhko et al.16 and references therein).
3.2 Cohort B
The best performing (based on AUC) combination of architecture and data representation in modelling dataset A, that is ConvBNMaxP2-L-MLP in the T representation, were used to train a new model on the full dataset A. The hyperparameters of this model were: kernel size 7, pool size 3, number of filters 64 for both ConvBNMaxP blocks; L dropout rate 0.4 (recurrent dropout set to 0), L units 32, and dropout rate 0.4.This model was subsequently used to predict the disease status of dataset B. This is a stringent test of the model because the prospectively collected data in B comes from a different patient cohort than the retrospectively collected biobank data in A. Moreover, dataset B includes non-cancer samples taken from patients with suspected brain tumour based on assessment of their symptoms in primary care rather than healthy patients, and has a lower prevalence of cancer patients (17% compared to 70%). The predictions result in a by-patient AUC of 0.84, and 0.78 for both sensitivity and specificity. The baseline model (gold-standard) for this dataset was reported in Brennan et al.9 and was obtained by performing an extensive search to identify optimal combination of spectral pre-processing, classifier algorithm and corresponding hyperparameters, achieving a by-patient AUC of 0.86 (see Fig. 3 in Brennan et al.9) with 0.81 sensitivity and 0.80 specificity.
Our results show that RNN model defined in the time domain representation provides comparable performance to the gold-standard model for this dataset. It is interesting that this is achieved without an extensive optimisation of the neural network architecture and corresponding hyperparameters.
4 Conclusions
We investigated the use of RNN algorithms for modelling spectral data. Our main motivation for this study was to understand the effect of the Fourier transform used to obtain FTIR spectra in the development of deep learning models. As a first step we interrogated various deep learning architectures incorporating RNN blocks from which we identified a set of suitable candidates, namely ConvBNMaxPβ-L-MLP, β = 1, 2. These were subsequently used to model four different representations of spectral data measured from cohort A: the original raw FTIR spectra, EMSC pre-processed spectra, and their corresponding Fourier transformed data.We showed that these networks benefit significantly when trained in the time domain representations regardless of whether pre-processing to the spectra is applied. The best model was used to predict an external spectral dataset which was obtained from a prospective patient cohort comprising patients diagnosed with differing brain tumours as well non-cancer symptomatic patients.9 The performance of this model was found to be comparable to the gold-standard classification results for this dataset reported by Brennan et al.9 We note that our results may be further improved with more optimisation of the NN architecture and hyperparameters, by increasing the size of the training dataset, as well as utilising data augmentation techniques to combat model overfitting. The approach presented in this paper has the potential to be extended to a variety of FTIR chemometric applications spanning a number of fields; from healthcare to bio-processing, to food testing and pharmaceutics. On the question of necessity of the Fourier Transform prior to the ML analysis, we recognise that we have not performed the study on interferogram data directly, as they were not available to us at the time, however we plan to address this in the near future.
Author contributions
Conceptualisation: GA, JJAC and DSP. Methodology: GA, JJAC, BRS, MJB and DSP. Investigation: GA and DSP. Software: GA, JJAC, BRS and DSP. Formal analysis: GA and DSP. Resources: PMB, MJB and DSP. Data curation: GA, JJAC, BRS, PMB and DSP. Visualisation: GA. Project administration: DSP. Supervision: MJB and DSP. Writing – original draft: GA and DSP. Writing – review & editing: GA, JJAC, BRS, MJB and DSP.Conflicts of interest
MJB, DSP are directors and GA, JJAC, BRS are employees of Dxcover Ltd. PMB is an employee of the University of Edinburgh, receives payment for consultancy work he undertakes with Dxcover Ltd.Acknowledgements
The authors would like to thank the Wellcome Trust Clinical Research Facility at the Western General Hospital, Edinburgh, as well as the Edinburgh Clinical Trials Unit (ECTU) and Emergency Medicine Research Group (EMERGE) at the Edinburgh Royal Infirmary for their contributions to patient recruitment. Most importantly, the authors would like to thank the patients for their involvement in this study, without whom this study would not have been possible.Notes and references
- F. Walter, C. Penfold and A. Joannides, Br. J. Gen. Pract., 2019, 69(681), e224–e235 CrossRef PubMed.
- Q. Ostrom, L. Bauchet, F. Davis, J. Fisher, C. Langer, M. Pekmezci, J. Schwartzbaum, M. Turner, K. Walsh, M. Wrensch and J. Barnholtz-Sloan, Neuro-Oncology, 2014, 16(7), 896–913 CrossRef CAS PubMed.
- M. Ozawa, P. Brennan, K. Zienius, K. Kurian, W. Hollingworth, D. Weller, W. Hamilton, R. Grant and Y. Ben-Shlomo, Fam. Pract., 2018, 35(5), 551–558 CrossRef PubMed.
- J. Hands, P. Abel, K. Ashton, T. Dawson, C. Davis, R. Lea, A. McIntosh and M. Baker, Anal. Bioanal. Chem., 2013, 405, 7347–7355 CrossRef CAS PubMed.
- J. Hands, P. Abel, K. Ashton, A. Brodbelt, C. Davis, T. Dawson, R. Lea, C. Walker and M. Baker, J. Biophotonics, 2014, 7, 189–199 CrossRef CAS PubMed.
- J. Hands, G. Clemens, K. Ashton, A. Brodbelt, C. Davis, T. Dawson, M. Jenkinson, R. Lea, C. Walker and M. Baker, J. Neurooncol., 2016, 127, 463–472 CrossRef PubMed.
- B. Smith, K. Ashton, A. Brodbelt, T. Dawson, M. Jenkinson, N. Hunt, D. Palmer and M. Baker, Analyst, 2016, 141, 3668–3678 RSC.
- H. Butler, P. Brennan, J. Cameron, D. Finlayson, M. G. Hegarty, M. Jenkinson, D. Palmer, B. Smith and M. Baker, Nat. Commun., 2019, 10, 4501 CrossRef PubMed.
- P. Brennan, H. Butler, C. Loren, M. Hegarty, M. Jenkinson, C. Keerie, J. Norrie, R. O'Brien, D. Palmer, B. Smith and M. Baker, Brain Commun., 2021, 3, 33–42 Search PubMed.
- J. Cameron, P. Brennan, G. Antoniou, H. Butler, L. Christie, J. Conn, T. Curran, E. Gray, M. Hegarty, M. Jenkinson, D. Orringer, D. Palmer, A. Sala, B. Smith and M. Baker, Neuro-Oncol. Adv., 2022, 4, 1 Search PubMed.
- R. Luo, J. Popp and T. Bocklitz, Analytica, 2022, 3, 287–301 CrossRef.
- L. Huang, R. Luo, X. Liu and X. Hao, Light: Sci. Appl., 2022, 11, 61 CrossRef CAS PubMed.
- J. Acquarelli, T. van Laarhoven, J. Gerretzen, T. N. Tran, L. M. Buydens and E. Marchiori, Anal. Chim. Acta, 2017, 954, 22–31 CrossRef CAS PubMed.
- J. Schmidhuber, Neural Networks, 2015, 61, 85–117 CrossRef PubMed.
- X. Zhang, T. Lin, J. Xu, X. Luo and Y. Ying, Anal. Chim. Acta, 2019, 1058, 48–57 CrossRef CAS PubMed.
- U. Blazhko, V. Shapaval, V. Kovalev and A. Kohler, Chemom. Intell. Lab. Syst., 2021, 215, 104367 CrossRef CAS.
- N. Thompson, K. Greenewald, K. Lee and G. Manso, arXiv 2022, preprint, DOI:10.48550/arXiv.2007.05558.
- V. Borisov, T. Leemann, K. Seßler, J. Haug, M. Pawelczyk and G. Kasneci, IEEE Trans. Neural Netw. Learn. Syst., 2022, 1–21, DOI:10.1109/TNNLS.2022.3229161.
- P. R. Griffiths and J. A. de Haseth, in Fourier Transform Infrared Spectroscopy, Wiley, New Jersey, 2nd edn, 2007, ch. 4, p. 85 Search PubMed.
- P. R. Griffiths and J. A. de Haseth, in Fourier Transform Infrared Spectroscopy, Wiley, New Jersey, 2nd edn, 2007, ch. 4, pp. 85–88 Search PubMed.
- A. Ben-David and A. Ifarraguerri, Appl. Opt., 2002, 41, 1181–1189 CrossRef PubMed.
- S. Hochreiter and J. Schmidhuber, Neural Comput., 1997, 9, 1735–1780 CrossRef CAS PubMed.
- J. Cameron, J. Conn, C. Rinaldi, A. Sala, P. Brennan, M. Jenkinson, H. Caldwell, G. Cinque, K. Syed, H. Butler, M. Hegarty, D. Palmer and M. Baker, Cancers, 2020, 12, 3682 CrossRef CAS PubMed.
- J. Cameron, C. Rinaldi, H. Butler, M. Hegarty, P. Brennan, M. Jenkinson, K. Syed, K. Ashton, T. Dawson, D. Palmer and M. Baker, Cancers, 2020, 12, 1710 CrossRef CAS PubMed.
- H. Martens and E. Stark, J. Pharm. Biomed. Anal., 1991, 9, 625–635 CrossRef CAS PubMed.
- H. Butler, B. Smith, R. Fritzsch, P. Radhakrishnan, D. Palmer and M. Baker, Analyst, 2018, 143, 6121–6134 RSC.
- J. Allaire, D. Eddelbuettel, N. Golding and Y. Tang, tensorflow: R Interface to TensorFlow, 2016 Search PubMed.
- R Core Team, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, 2022 Search PubMed.
- B. Smith, D. Palmer and M. Baker, Chemom. Intell. Lab. Syst., 2018, 172, 33–42 CrossRef CAS.
- K. Cho, B. van Merriënboer, D. Bahdanau and Y. Bengio, Proceedings of SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation, 2014, pp. 103–111.
- D. Kingma and J. Ba, arXiv 2017, preprint, DOI:10.48550/arXiv.1412.6980.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2an02041f |
| ‡ https://gco.iarc.fr |
| § Up to and including second-order correction terms. |
¶ Defined as 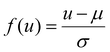 , where μ, σ denote the mean and standard deviation of the feature u, as estimated from the training set. , where μ, σ denote the mean and standard deviation of the feature u, as estimated from the training set. |
| This journal is © The Royal Society of Chemistry 2023 |