Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Conical shell illumination incorporating a moving aperture for depth-resolved high-energy X-ray diffraction
Daniel
Spence
a,
Anthony
Dicken
a,
David
Downes
a,
Keith
Rogers
b and
Paul
Evans
 *a
*a
aImaging Science Group, Rosalind Franklin Building, Clifton, Nottingham Trent University, Nottingham, UK. E-mail: paul.evans@ntu.ac.uk
bCranfield Forensic Institute, Cranfield University, Shrivenham, Swindon, UK
First published on 16th January 2023
Abstract
In many applications, the main limitation of X-ray absorption methods is that the signals measured are a function of the attenuation coefficient, which tells us almost nothing about the chemical or crystallographic nature of objects under inspection. To calculate fundamental crystallographic parameters requires the measurement of diffracted photons from a sample. Standard laboratory diffraction methods have been refined for well over a century and provide ‘gold standard’ structural models for well-prepared samples and single crystals but have little applicability for thick heterogeneous samples as demanded by many screening applications. We present a new high-energy X-ray diffraction probe, which in comparison with previous depth-resolving hollow beam techniques, requires a single beam, point detector and a simple swept aperture to resolve sample signatures at unknown locations within an inspection space. We perform Monte Carlo simulations to support experiments on both single- and multiple-material localisation and identification. The new probe is configured and tested using low-cost commercial components to provide a rapid and cost-effective solution for applications including explosives detection, process control and diagnostics.
Introduction
X-ray diffraction (XRD) techniques for probing molecular structures within heterogeneous objects can be greatly beneficial to fields including explosives detection systems,1–3 food quality and safety,4 combinatorial screening,5 bone quality,6–8 and cancer diagnostics.9 The versatility of X-rays as a non-destructive ‘molecular’ probe stems from their relatively short wavelength of the order of 10−10 m.10 Probing photons can interact with the sample's molecular structure to produce coherently scattered (signal) photons, which can escape from the sample without energy loss. The knowledge of both the energy and trajectory of such photons enables the calculation of material characterisation information. This process is the basis of crystallography and powder diffraction.11 However, while X-ray diffraction (XRD) offers perhaps the most specific method of material phase identification it remains restricted to the laboratory. For example, although some microbeam systems are air-cooled, most standard laboratory diffractometers usually require water cooling as thermionic X-ray generation is <1% efficient. However, the relatively low energy of the interrogating photons e.g., Cu Kα radiation ∼8 keV results in near-surface specimen depths of around a fraction of a mm. Thus, while the standard method has been refined for well over a century and provides ‘gold standard’ structural resolution for well-prepared samples and single crystals it has little applicability for thick heterogeneous samples. The evaluation of extended regions of interest along the probing direction requires at least an order of magnitude increase in photon energies for many screening applications. For example, the detection of concealed explosives in aviation luggage screening usually requires ∼140 keV photons. In addition, a practical probe would require resolving explosives at unknown positions along the beam in the presence of ‘cluttering’ materials both of which individually would confound a standard approach.Recent developments in XRD-based, spatially resolved materials identification techniques often require collimation into narrow pencil, or fan beams and can require either extended measurement times,12 or powerful X-ray sources,13 to ensure sufficient photon statistics for material identification. Rapid material identification by energy-dispersive XRD is possible at 48 mAs to 0.4 mAs but at the expense of spatial resolution.14 In addition, tomographic XRD implementation strategies have been investigated including 3DXRD,15 TEDDI,16,17 XDi,18 SICSI,13 and XRD-CT,19–23 and all have been individually adapted to their proposed applications.
Focal construct technology (FCT) is a technique, which uses an annular beam of radiation and has been designed to improve such shortcomings.24–26 When an annular beam is incident normally on a semi- or polycrystalline material, Debye cones with well-understood energy and angular relationships11 are produced from each point of intersection within an annular gauge volume. These Debye cones overlap downstream in the imaging chain resulting in significantly increased scattered signal intensity.24 FCT has been shown to deal favourably with non-ideal samples such as those exhibiting large grain size, preferred orientation (or texture),27 and liquid samples,28 that only exhibit short-range order. New incarnations of the FCT technique designed to work in an energy-dispersive mode (ED-FCT),27,29 using a polychromatic X-ray beam and energy-resolving point detector exhibit advantages over angular-dispersive FCT (AD-FCT),30–32 in terms of measurement time reduction, although with some trade-off against d-spacing resolution. In summary, prior FCT methods without collimation or modulation of the diffraction signal require the position of the sample in the beam is known to calculate structural parameters such as d-spacings. Although, AD-FCT tomography overcomes this limitation it requires raster scanning a sample through the beam and a spatially resolving detector to measure the diffracted flux.33
Depth-resolved ED-FCT has recently been developed by using a two-dimensional pixelated energy-resolving detector, receiving scattered flux from the sample via a ∼2 mm pinhole between the sample and detector. The pinhole acts as a 2θ selector to provide information about the spatial origin of coherently scattered photons incident on the detector.34 Alternatively, an energy-resolving point detector can replace the pinhole. In which case, to determine 2θ, the sample must be scanned through a dual configuration of shell beams,35 each configured with a central detector. To recap, the former approach requires an expensive pixelated detection surface, while the latter requires 2× point detectors together with dual beam optics and a sample scanning mechanism.
Here we investigate a novel X-ray diffraction system, which combines the advantages of both the ‘pinhole’ and ‘dual beam’ ED-FCT approaches by combining a single interrogating beam and point detector i.e., without the requirement for pixelated detectors or dual beams/optics and sample translation. Instead, objects under inspection are illuminated with a similar polychromatic annular X-ray beam but with a much wider circular XRD collection aperture, ∼10 mm diameter optically coupled to an energy-resolving single-pixel detector. Depth information is recovered by translating the aperture along the symmetry axis of the system, providing a cumulative interrogation of a three-dimensional object, along one axis (z).
We perform Monte Carlo simulations to support experiments on both single- and multiple-material localisation and identification.36
The method described in this work uses commercial, off-the-shelf, low-cost components and has the potential to significantly enhance performance in areas such as security and industrial process control where cost-effective solutions are an important factor.
Experimental section
Materials
In this work we attempt to identify signature diffraction patterns of sucrose (C12H22O11), calcite (CaCO3) and calcium hydroxide (Ca(OH)2). All materials are crystalline powders contained within sealed plastic cylindrical containers, with diameter, 2Rs = 90 mm and depth, t = 15 mm.Instrumentation
We perform experiments and simulations, which are analogous to our swept-aperture concept, see Fig. 1, by implementing discrete increments of the aperture position along the z-axis.A polychromatic Hamamatsu point X-ray source, operating at 130 kV, 300 μA illuminates a bespoke tungsten optic, which transmits a conical shell of primary X-rays with a mean half-opening angle ϕavg = 3.92° and beam divergence Δϕ = 0.05°, as described in detail elsewhere.27 At some distance downstream of the X-ray source is an Amptek XR-100T-CdTe energy-resolving detector module with a 3 mm diameter detection surface. The detector is placed at zd = 690 mm at the origin of the x − y plane. Energy resolution of the detector is ∼850 eV with a total energy range of 1–130 keV.
Where the primary X-ray cone intersects a material with long-range order, placed between the X-ray source and detector, photons are diffracted under the satisfaction of Bragg's condition. The diffraction angle for a subset of these photons enables them to be received on the detector at zd and are measured by photon counting.
A circular aperture of radius, ra = 4.5 mm, rests initially in a position between the X-ray source and the detector, downstream of the inspection region of interest. The aperture transmits only scattered photons generated at the intersection of the primary X-ray cone from a potential conical volume element in space defined by the lines-of-sight of the extrema of the two-dimensional detector, through the aperture, see Fig. 2. As the aperture is translated along the z-axis, towards the detector, the specimen volume increases for relatively thick samples. For example, at some point a cumulative scatter signal is received at the detector from the entire intersection volume for z ≤ zmax, as determined by the aperture dimensions and relative position during the translation.
Depth information is recovered by evaluating the additional photons transmitted through the aperture (and reaching the detector) with each increment in its position, za relative to the previous position, za − Δza whereΔza is small. This is analogous to a continuously moving aperture where Δza = zaΔt, and za is the translation velocity of the aperture along the z-axis. With each new aperture position, the detector observes an additional contribution to the total diffraction signal, which can be assigned to some additional specimen/intersection region in space.
Considering the two-dimensional y − z plane of the system represented in Fig. 1 (at x = 0), there are multiple intersection points (ZL, ZB, ZT, ZR) between the cone of primary X-rays and lines-of-sight of the extrema of the detector. The detector lines-of-sight are limited by the aperture dimensions and position, illustrated in Fig. 2.
For a given aperture increment, za → za + Δza the detector receives additional diffracted photons originating within the additional intersection of the “two volumes”. There exists some central position, zC which the detector can be said to observe for a given aperture window za → za + Δza. The locations of these intersection points are:
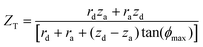 | (1a) |
 | (1b) |
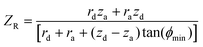 | (1c) |
 | (1d) |
We find that  , which indicates that beam divergence is negligible in this system when considering the range of z-space observed by the detector for a given aperture position. The central position of the observation range can be assumed to be the mid-point between ZR and ZL
, which indicates that beam divergence is negligible in this system when considering the range of z-space observed by the detector for a given aperture position. The central position of the observation range can be assumed to be the mid-point between ZR and ZL
 | (2) |
The aperture radius, ra and the detector half-width, rd are both fixed, as is the down-stream detector location zd. The uncertainty in sample position is:
 | (3) |
Within the range of ZC observable in the above geometry, the presence of materials with long-range order will generate coherent scattering (diffraction) in the form of overlapping polychromatic Debye cones,27 impinging on the detector. If the one-dimensional spatial density (along the z-axis) of each diffracting object is described by a Gaussian profile, the total diffracted photon count observed at the detector can be modelled as a linear sum of the integrals of these Gaussian profiles; each term in the sum corresponding to an individual sample, Sn at position zs,n. This Linear Sum of Gaussian Integrals (LSGI) model uses, as the integral of a Gaussian function, the error function. A constant term cs,0 is included to account for system noise and miscellaneous scattering from the system upstream of the minimum interrogation volume.
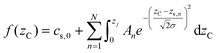 | (4a) |
 | (4b) |
The LSGI model's primary parameters are the set of zs,n indicating the presence of diffracted photons from the nth object entering the line-of-sight of the detector. To extract the contributing Gaussian profiles observed during the aperture sweep, we take the first derivative the LSGI fit.
 | (5) |
The centres of the contributory Gaussians are identified by zero-crossing points in the second derivative of the LSGI fit. Having obtained estimates for the location of each diffracting material in z-space, one can calculate the appropriate 2θn and material d-spacing values for corresponding photons arriving at the centre of the energy-resolving detector.
 | (6a) |
And from Bragg's condition.
 | (6b) |
Here, 2θn is the diffraction angle; ϕavg is the average half-opening angle of the primary beam;  is the wavelength of diffracted photons observed at energy E; h is Planck's constant and c is the speed of light in a vacuum.
is the wavelength of diffracted photons observed at energy E; h is Planck's constant and c is the speed of light in a vacuum.
Monte Carlo simulations
To support the experimental work, we simulate the response of an energy-resolved X-ray detector under similar-geometry, swept-aperture conditions to those described in previous sections.Two systems are investigated; (i) a single sample with depth, t = 15 mm comprised of sucrose (C12H22O11), located at 220 mm from the X-ray source, and (ii) a series of two t = 15 mm samples, calcium hydroxide (Ca(OH)2) and calcite (CaCO3), the former being positioned at 160 mm from the source and the latter at 280 mm from the source.
For all simulations, the aperture is initially at za = 350 mm and increases to 680 mm in steps of Δza = 1 mm. Taking a 0.1 s exposure time per aperture position, the total equivalent continuous sweep duration would be ∼33 s and a sweep velocity of 10 mm s−1.
Annular beam experiments
An annular beam is realized with a geometry as in Fig. 1 and 2 such that zD = 690 mm, ϕmin = 3.87° and ϕmax = 3.97°.In the first set of experiments (i) we replicate the simulation of sucrose (C12H22O11) contained in cylindrical plastic containers with sample depth t = 15 mm. The sucrose sample is placed at ∼220 ± 10 mm from the X-ray source. A second set of experiments (ii) replicates the simulation of t = 15 mm calcium hydroxide (Ca(OH)2) and t = 15 mm calcite (CaCO3). The powder samples are placed at ∼160 ± 10 mm and ∼280 ± 10 mm, respectively.
In both sets of experiments, single- and multi-sample, the aperture is initially at za = 350 mm and increases to 680 mm in steps of Δza = 1 mm. The photon collection time at each aperture position is either 0.1 or 0.02 seconds, producing total equivalent sweep durations of ∼33 s and 6.6 s respectively, with corresponding aperture sweep velocities of 10 mm s−1 or 50 mm s−1.
Spatial sampling
In both simulation and experiment, we sample at regular intervals in za, collecting photons for a period of 0.1 seconds or 0.02 seconds. This is analogous to a constant aperture sweep velocity of 10 mm s−1 or 50 mm s−1, respectively. Additionally, there is a non-linear relationship between za and zC, leading to a non-linear sampling of z-space, weighted towards low z. The equivalent continuously swept aperture would be translated at a constant velocity, ża with acceleration za = 0. To sample z-space at regular intervals would require translation of the aperture with ża = ża(za) i.e., non-zero acceleration.The sampling rate is determined by the aperture translation interval, or the equivalent aperture sweep velocity in a continuously translated system. By increasing either, the aperture translation interval or sweep velocity we can sample z-space more sparsely and therefore reduce measurement times. The effect of this sparse sampling is discussed with reference to experiment measurements.
Results and discussion
Monte Carlo simulation
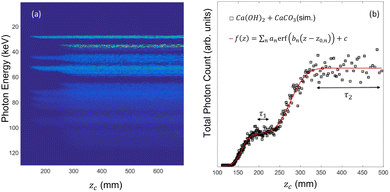
A single t = 15 mm region of sucrose (C12H22O11) is simulated in the beam path of the annular source described above. Fig. 3 illustrates the energy-resolved intensity measurements at the detector as the aperture sweep enables an increasingly large intersection volume (and solid angle) from which diffracted photons may be detected.The energy spectrum at each aperture position is integrated (see Fig. 3(b)), revealing a step-like function of aperture position, with a zero-value baseline (instrument noise is not simulated). The rising-edge feature is due to the increasing specimen volume interrogated as afforded by the moving aperture. The response plateau occurs when the maximum specimen thickness remains visible to the detector. A more precise assessment of the sample location requires application of the model in eqn 4(a) and 4(b) to the integrated detector intensity (Fig. 3(b)). The location of sucrose, predicted at the maximum of eqn (5), is calculated as 225 ± 38 mm from the X-ray source. The ‘true’ spatial range of sucrose in this simulation is 220–235 mm.
In Fig. 4 we reconstruct the diffractogram (with reference standard for comparison) of the object located at 220–235 mm by integration of the detector intensity within each energy bin collected along the plateau region of Fig. 3(b), i.e., zC > 350 mm.
 | ||
| Fig. 4 Reconstruction of simulated diffractogram of the C12H22O11 sample investigated in Fig. 3. Sample location is 225–235 mm from the X-ray source with approximate corresponding diffraction angle, 2θ = 5.8°. | ||
Next, we simulate the presence of multiple crystalline samples; calcium hydroxide (Ca(OH)2) and calcite (CaCO3), each with t = 15 mm and separated by a centre-to-centre distance of 220 mm along the z-axis. The energy-resolved and energy-integrated detector intensities are shown in Fig. 5.
The presence of two crystalline objects in the conical beam path results in a series of step changes in total photon count at the detector and plateau regions. The first plateau, τ1 includes photons from the object closest to the source (as with the previous single sucrose example) however the second plateau, τ2 now includes diffracted photons from both the first and second objects. To isolate the second object, we subtract the integrated detector signal from the first plateau, weighted to account for sampling frequency within the respective plateaus, from the second.
The first derivative of the LSGI fit now indicates that there are two Gaussian profiles along the z-axis centred at 161 ± 26 mm and 282 ± 45 mm. The simulated locations are set at 160–175 mm and 280–295 mm, respectively. Reconstructed diffractogram and reference standards are illustrated in Fig. 6.
 | ||
| Fig. 6 Reconstruction of simulated diffractograms of the (a) Ca(OH)2 and (b) CaCO3 samples investigated in Fig. 5. Sample locations are (a) ∼161 mm from the X-ray source with approximate corresponding diffraction angle, 2θ = 5.1° and (b) ∼282 mm from the X-ray source with approximate corresponding diffraction angle, 2θ = 6.6°. | ||
Swept aperture experiments
A single, t = 15 mm sucrose sample is illuminated by the annular source as described. Fig. 7 shows the energy-resolved and energy-integrated detector signal during the translation of the aperture. In contrast to simulation, there is now the presence of a non-zero baseline to the energy-integrated total photon count in Fig. 7(b) arising from system noise. The baseline is compensated by the constant term in the LSGI model cs,0.The first derivative of the LSGI model predicts a sample location zs,n = 229 ± 38 mm or zs,n = 228 ± 38 mm for the ża = 10 mm s−1 or 50 mm s−1, respectively. The corresponding diffractogram reconstruction is illustrated in Fig. 8.
 | ||
| Fig. 8 Reconstruction of experiment diffractogram of the C12H22O11 sample investigated in Fig. 7, with aperture velocities of 10 mm s−1 (black, solid) and 50 mm s−1 (blue, dashed). Predicted sample location is ∼229 mm from the X-ray source. | ||
Next, sequential, t = 15 mm regions of Ca(OH)2 and CaCO3 are illuminated by the annular X-ray source. Fig. 9 shows the energy-resolved and energy-integrated detector signal during translation of the aperture.
Two sample responses are indicated in the integrated detector intensity profile. The first derivative of the LSGI model correspondingly predicts two mean sample locations of the 15 mm thick samples; the first sample Ca(OH)2 is likely located at zs,1 = 160 ± 25 mm or 159 ± 25 mm for the ża = 10 mm s−1 and 50 mm s−1 sweeps. The second sample CaCO3 is predicted at zs,n = 302 ± 47 mm or zs,n = 304 ± 47 mm, where the latter (worst case) reconstructed diffractogram is illustrated in Fig. 10.
 | ||
| Fig. 10 Reconstruction of experiment diffractogram of the CaCO3 sample investigated in Fig. 9. Predicted sample location ∼ 302 mm with approximate corresponding diffraction angle, 2θ = 6.6°. | ||
Conclusion
The swept aperture ED-FCT technique can identify multiple object locations along the depth axis and provide material composition information. Measurement times for inspection of an extended Δz = 400 mm region of interest are ∼40 s and ∼8 s, corresponding to X-ray exposures of 12 mAs and 2.4 mAs respectively, depending on the aperture translation speed.This technique requires collecting spectra from sufficient ‘empty’ z-space before the region of interest. This is because a model fitted to an incomplete step i.e., without a ‘baseline plateau’ can introduce additional uncertainty in the calculation 2θ for a sample. In practice, this occurrence is accommodated by defining appropriate near and far limits to the inspection region.
In general, most background scatter in a real security luggage screening scenario arises from low density, amorphous materials. As such this scatter has a relatively low magnitude and thus, we fully expect the approach to be applicable even when the volume contains potentially confounding materials. The depth resolution of the probe will certainly help exclude confounding scatter from above and below the target region within the limits of the probe's depth resolution. Where there can be scattering from crystalline ‘clutter’ then this may be resolved following similar protocols found within the diffractionists’ armoury for accommodating mixed phase materials.37 Also, it is unlikely that any probe technology would circumvent ‘dark alarms’ as these are due to insufficient X-ray penetration of dense or masked target areas. Thus, for a luggage screening application we recommended a brighter source of around 180 kV, 3 mA in comparison to the one used in our experiments. This would provide increased penetration, in line with current industry practice, and around 20 times the amount of signal photons to improve photon statistics. The depth resolution can be improved by employing a smaller diameter ‘point’ detector.
For a security application that only requires a phase identification, no refinement of the data is required although conventional match indices could be applied. For more detailed analysis beyond simple phase, the data could be refined against a structural model,38 but the unique geometry would result in specific and non-conventional parameter forms of, for example, Lorentz and absorption corrections.
The compact probe architecture uses cost-effective point detector technology and is scalable in both X-ray energy and inspection space. Potential applications include false alarm resolution in security luggage screening, process control and medical diagnostics.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was funded by The Royal Society and The Wolfson Foundation RSWF\R1\180012; The Department of Homeland Security (DHS), Science and Technology Directorate, Homeland Security Advanced Research Projects Agency, Explosives Division through the Advanced X-ray Material Discrimination Program (HSHQDC-15-CB0036); and the Engineering and Physical Sciences Research Council EP/T034238/1.References
- S. Singh and M. Singh, Signal Process., 2003, 83(1), 31–55 CrossRef.
- G. Harding and A. Harding, 8 - X-ray Diffraction Imaging for Explosives Detection, in Counterterrorist Detection Techniques of Explosives, ed. J. Yinon, Elsevier Netherlands, 1st edn, 2007, pp. 199–235 Search PubMed.
- J. A. Greenberg and J. Carpenter, 9 - X-ray diffraction for explosives detection, in Counterterrorist Detection Techniques of Explosives, ed. A. Kagan and J. C. Oxley, Elsevier Science, 2nd edn, 2022, pp. 315–338 Search PubMed.
- S. R. Purohit, L. E. Jayachandran, A. S. Raj, D. Nayak and P. S. Rao, 22 - X-ray diffraction for food quality evaluation, in Evaluation Technologies for Food Quality, ed. J. Zhong and X. Wang, Elsevier Woodhead, 2019, 579–594 Search PubMed.
- B. B. He, 11-Combinatorial Screening, in Two-Dimensional X-Ray Diffraction, Wiley, USA, 2009, pp. 351–368 Search PubMed.
- A. J. Dicken, J. P. O. Evans, K. D. Rogers, N. Stone, C. Greenwood, S. X. Godber, D. Prokopiou, J. G. Clement, D. Lyburn, R. M. Martin and P. Zioupos, Phys. Med. Biol., 2015, 60, 5803–5812 CrossRef CAS PubMed.
- C. Greenwood, K. Rogers, M. Wilson, I. Lyburn, P. Evans and D. Prokopiou, Developing focal construct technology for in vivo diagnosis of osteoporosis, J. Phys.: Conf. Ser., 2019, 1151, 012020 CrossRef CAS , IOP Publishing.
- A. J. Dicken, J. P. O. Evans, K. D. Rogers, N. Stone, C. Greenwood, S. X. Godber, J. G. Clement, I. D. Lyburn, R. M. Martin and P. Zioupos, Sci. Rep., 2016, 6, 29011 CrossRef CAS PubMed.
- A. R. Round, S. J. Wilkinson, C. J. Hall, K. D. Rogers, O. Glatter, T. Wess and I. O. Ellis, Phys. Med. Biol., 2005, 50, 4159–4168 CrossRef CAS PubMed.
- W. C. Rontgen, Nature, 1896, 53(1369), 274–277 Search PubMed.
- W. Bragg, Nature, 1912, 90, 410 CrossRef.
- I. Drakos, P. Kenny, T. Fearn and R. Speller, Crime Sci., 2017, 6(1), 1 CrossRef.
- J. A. Greenberg, M. Hassan, K. Krishnamurthy and D. Brady, Analyst, 2014, 139, 709–713 RSC.
- D. O'Flynn, C. Crews, I. Drakos, C. Christodoulou, M. D. Wilson, M. C. Veale and R. Speller, J. Phys. D: Appl. Phys., 2016, 49(17), 175304 CrossRef.
- S. F. Nielsen, E. M. Lauridsen, D. J. Jensen and H. F. Poulsen, J. Mater. Sci. Eng. A, 2001, 319–321, 179–181 CrossRef.
- R. J. Cernik, K. H. Khor and C. Hansson, J. R. Soc., Interface, 2008, 5(21), 477–481 CrossRef CAS PubMed.
- O. Lazzari, S. Jacques, T. Sochi and P. Barnes, Analyst, 2009, 134, 1802–1807 RSC.
- K. Wells and D. A. Bradley, Appl. Radiat. Isot., 2012, 70(8), 1729–1746 CrossRef CAS PubMed.
- A. Vamvakeros, S. D. M. Jacques, M. Di Michiel, P. Senecal, V. Middelkoop, R. J. Cernik and A. M. Beale, J. Appl. Crystallogr., 2016, 49, 485–496 CrossRef CAS PubMed.
- R. Warr, E. Ametova, R. J. Cernik, G. Fardell, S. Handschuh, J. S. Jørgensen, E. Papoutsellis, E. Pasca and P. J. Withers, Sci. Rep., 2021, 11, 20818 CrossRef CAS PubMed.
- C. K. Egan, S. D. M. Jacques, M. D. Wilson, M. C. Veale, P. Seller, A. M. Beale, R. A. D. Pattrick, P. J. Withers and R. J. Cernik, Sci. Rep., 2015, 5, 15979 CrossRef CAS PubMed.
- G. Artioli, T. Cerulli, G. Cruciani, M. C. Dalconi, G. Ferrari, M. Parisatto, A. Rack and R. Tucoulou, Anal. Bioanal. Chem., 2010, 397, 2131–2136 CrossRef CAS PubMed.
- E. Possenti, C. Conti, G. D. Gatta, N. Marinoni, M. Merlini, M. Realini, G. B. M. Vaughan and C. Colombo, iScience, 2022, 25(10), 105112 CrossRef CAS PubMed.
- P. Evans, K. Rogers, J. Chan, J. Rogers and A. Dicken, Appl. Phys. Lett., 2010, 97, 204101 CrossRef.
- K. Rogers, P. Evans, J. Rogers, J. Chan and A. Dicken, J. Appl. Crystallogr., 2010, 43(2), 264–268 CrossRef CAS.
- K. Rogers and P. Evans, X-ray diffraction and focal construct technology, in X-Ray Diffraction Imaging: Technology and Applications, ed. J. Greenberg, Taylor and Francis Group, 2019, 165–188 Search PubMed.
- A. Dicken, J. P. O. Evans, K. D. Rogers, C. Greenwood, S. X. Godber, D. Prokopiou, N. Stone, J. G. Clement, I. Lyburn, R. M. Martin and P. Zioupos, Opt. Express, 2015, 23(10), 13443–13454 CrossRef CAS PubMed.
- D. Prokopiou, K. Rogers, P. Evans, S. Godber and A. Dicken, Appl. Radiat. Isot., 2013, 77, 160–165 CrossRef CAS PubMed.
- F. Li, Z. Liu, T. Sun, B. Jiang and Y. Zhu, J. Chem. Phys., 2016, 144, 104201 CrossRef PubMed.
- X. H. Chen, B. Li, T. Xue and J. Li, Rev. Sci. Instrum., 2020, 91, 083908 CrossRef CAS PubMed.
- D. Prokopiou, J. McGovern, G. Davies, S. Godber, P. Evans, A. Dicken and K. Rogers, J. Appl. Crystallogr., 2020, 53(4), 1073–1079 CrossRef CAS PubMed.
- A. Dicken, A. Shevchuk, K. Rogers, S. Godber and P. Evans, Opt. Express, 2015, 23(5), 6304–6312 CrossRef CAS PubMed.
- P. Evans, K. Rogers, A. Dicken, S. Godber and D. Prokopiou, Opt. Express, 2014, 22(10), 11930–11944 CrossRef CAS PubMed.
- A. Dicken, J. P. O. Evans, K. D. Rogers, D. Prokopiou, S. X. Godber and M. Wilson, Opt. Express, 2017, 25(18), 21321–21328 CrossRef CAS PubMed.
- A. Dicken, D. Spence, K. Rogers, D. Prokopiou and P. Evans, Analyst, 2018, 143(20), 4849–4853 RSC.
- E. B. Knudsen, A. Prodi, J. Baltser, M. Thomsen, P. K. Willendrup, M. Sanchez del Rio, C. Ferrero, E. Farhi, K. Haldrup, A. Vickery, R. Feidenhans'l, K. Mortensen, M. M. Nielsen, H. F. Poulsen, S. Schmidt and K. Lefmann, J. Appl. Crystallogr., 2013, 46(3), 679–696 CrossRef.
- R. F. Karlak and D. S. Burnett, Anal. Chem., 1966, 38(12), 1741–1745 CrossRef CAS PubMed.
- L. B. McCusker, R. B. Von Dreele, D. E. Cox, D. Louër and P. Scardi, J. Appl. Crystallogr., 1999, 32(1), 36–50 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |