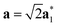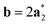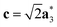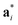Open Access Article
Open Access ArticleUnderstanding the structure-band gap relationship in SrZrS3 at elevated temperatures: a detailed NPT MD study†
Namrata
Jaykhedkar
 ab,
Roman
Bystrický
ac,
Milan
Sýkora
*a and
Tomáš
Bučko
ab,
Roman
Bystrický
ac,
Milan
Sýkora
*a and
Tomáš
Bučko
 *bc
*bc
aLaboratory for Advanced Materials, Faculty of Natural Sciences, Comenius University, Ilkovičova 6, 842 15 Bratislava, Slovakia. E-mail: sykoram@uniba.sk
bDepartment of Physical and Theoretical Chemistry, Faculty of Natural Sciences, Comenius University in Bratislava, Ilkovičova 6, 842 15 Bratislava, Slovakia. E-mail: tomas.bucko@uniba.sk
cInstitute of Inorganic Chemistry, Slovak Academy of Sciences, Dúbravská Cesta 9, 845 36, Bratislava, Slovakia
First published on 8th August 2022
Abstract
Thermal effects on the structure, bulk modulus (B0), and electronic band gap (Eg) of the needle-like (NL) (NH4CdCl3 structure type) and distorted perovskite (DP) (GdFeO3 structure type) phases of SrZrS3 were investigated over the temperature range 300–1200 K by means of ab initio molecular dynamics in an NPT ensemble, accelerated by adaptive machine learning. An anisotropic thermal expansion of a distinctly different quality was observed for the two phases. While all lattice vectors of the NL phase expand monotonously with T, the thermal behavior of the DP phase is more complex, with two vectors (b and c) monotonously expanding and one (a) contracting after an initial expansion. We show that the thermally-induced structural changes in the DP phase are a consequence of proximity of the cubic phase (C), into which it transforms quasi-continuously upon heating. A linear decrease of B0 with T (from 45.9 GPa to 33.6 GPa for NL and from 66.8 GPa to 48.5 GPa for DP) is predicted. Since the temperature dependent Eg values are determined as the NPT ensemble averages, both the lattice expansion and the electron–phonon coupling effects are naturally taken into account in our simulations. We found that the Eg for NL is nearly constant, while that for DP decreases by as much as ∼0.5 eV within the studied temperature range. The latter is shown to be almost exclusively due to a very large atomic displacement contribution resulting from the proximity of the parent C phase, with the Eg ∼ 0.8 eV lower than that of the DP phase.
1 Introduction
Over the past decade, there has been a great deal of interest in the materials from the Hybrid Organic–Inorganic Perovskites (HOIPs) family due to their favourable properties for the use in photovoltaics and other optoelectronic applications.1–7 Although the HOIPs show a great potential, their broader commercial exploitation has so far been hindered by a limited thermal and chemical stability and a toxicity associated with the presence of lead in their structure.8,9 Recently, it has been proposed that ternary chalcogenides (TCs) with the general formula ABX3 (where A and B are metals and X is S or Se), especially with the perovskite crystal structure, may be an appealing alternative, thanks to the electronic properties analogous to HOIPs, and a broad variety of possible chemical compositions that can be chosen to avoid the use of lead or other toxic metals.10–12 It has also been shown that the experimentally prepared TCs exhibit good chemical properties and a high thermal stability.9,13–16From the perspective of practical applications of TCs in optoelectronics, it is important to understand how they are affected by various thermodynamic conditions. In this regard, previous studies focused mainly on the pressure dependence of the band gap (Eg). In their experimental work, Gross et al.17 found that Eg of BaZrS3 decreases with pressure, at the average rate of ∼−0.015 eV GPa−1, over the 0 to 8.9 GPa range. A modest monotonous decrease of Eg with pressure was reported for several TCs in recent theoretical studies.18,19 One of the pre-requirements for effective exploitation of new materials in applications is an understanding of how their electronic properties vary with temperature. In many materials, variations in temperature over a practically relevant range can induce structural distortions and even phase transitions which may cause significant and abrupt changes in the material's physical and electronic properties, such as lattice parameters, electronic band gap, electrical conductivity and many others. An understanding of the temperature dependent behavior is also important for identifying appropriate experimental conditions for preparation of materials with desired electronic properties. While temperature dependent effects have been observed and systematically studied in ternary halogenides and oxides, such as CsPbBr3,20 CH3NH3PbI3,21 CH3NH3PbBr3,20 or SrTiO3,22 similar studies have been lacking in case of TCs.
In this work, our goal is to partially address this deficiency by performing a theoretical investigation of the finite temperature properties (including the band gap) of a representative TC material, SrZrS3. Our choice of the material is motivated by the fact that SrZrS3 is one of the few TCs that have been experimentally prepared in two crystal phases, both stable at ambient conditions:13,15,23–26 type NH4CdCl3 (also known as needle-like (NL) phase) and type GdFeO3 (also known as distorted perovskite (DP) phase). At ambient conditions the two phases differ substantially in their Eg (1.53 eV (NL) vs. 2.13 (DP))15,23 and absorption properties. In their theoretical study of 18 TCs, Sun et al.23 have shown that the materials in the DP phase have better absorption properties than the NL phase. It has been suggested in experimental work of Niu et al.15 that although the band gaps of BaZrS3 or SrZrS3 in DP phase are suboptimal, their excellent optical properties still qualify them as suitable candidates for solar cell materials and a similar conclusion was made also in a recent experimental and theoretical work of Nishigaki et al.27 Here we systematically investigate temperature-induced changes in the structure of both phases in the temperature range of 300–1200 K, and the effect of these structural changes on the electronic structure, particularly Eg. We find that, while the structural and electronic changes are relatively small for the NL phase, they are quite substantial for the DP phase, with the band gap shifting closer to the optimal photovoltaic range when temperature is increased. Based on our analysis, we expect similar effects to be observed also for other TCs. Our results indicate that more systematic investigations and screening of temperature dependent properties of TCs are likely to provide important insights in the search for the most promising candidate materials for photovoltaics and other optoelectronics applications.
The most popular approach to study Eg dependence on T by ab initio computer simulations is the Allen–Heine–Cardona (AHC) method,28,29 successfully applied to the pristine and the oxygen-vacant cubic LaCrO3−δ,30 CH3NH3PbI3,31 or SrTiO322 and other materials. The AHC method, however, suffers from several important limitations, such as the neglect of lattice thermal expansion contribution, or the use of rigid ion approximation in calculating the one-electron eigenvalues associated with the atomic displacement. The latter problem can be eliminated by Monte Carlo sampling of the quantum harmonic oscillations, which can be realized also as a ‘one-shot’ calculation, if a sufficiently large supercell is used, as recently proposed by Zacharias and Giustino.32 As shown by Karsai et al.,33 this method can be combined with the quasi-harmonic approximation34 (QHA) to account also for the lattice thermal expansion, which was found to be crucial for accurate predictions of the temperature dependence of Eg for diamond. Unfortunately, the QHA is not reliable for materials with highly anharmonic modes, especially if high temperature properties are of interest. An uncompromising solution to this problem is the use of molecular dynamics in an NPT ensemble (NPT MD), which allows a consistent treatment of lattice thermal expansion and electron–phonon effects within one simulation protocol. Until recently, the computational time needed to obtain well converged results from NPT MD was impractically large compared to the more approximate approaches such as QHA. With the recent development of the machine learning force field (MLFF), implemented in VASP 6.3,35,36 however, ab initio-quality NPT MD became feasible for routine applications, with the CPU cost comparable to the QHA. Among the advantages of this method is that the training configurations are chosen automatically and on-the-fly during a training ab initio MD run based on the similarity with other training configurations and the quality of predictions of energies, forces, and stress tensor components. A well-trained MLFF provides ab initio quality results at a fraction of time of an explicit ab initio calculation, enabling thus improvements in sampling quality via performing longer MD simulations. The MLFF approach can be used to study many important physical properties including the entropy-driven hcp–bcc phase transition of zirconia,37 the heat transport properties of ZrO2 at ambient pressure,38 or the hydration free energies of oxygen atoms and hydroxyl groups adsorbed on the Pt surfaces in water.39 Inspired by a successful use of this approach in the investigation of temperature-stimulated phase transitions of hybrid perovskite materials MAPbI3 and CsPbI3,40 we employ it here to explore thermal effects on the structure and band gap of the NL and DP phases of a prominent TC material SrZrS3.
This paper is organized as follows: the methodology used in this work is described in Section 2, reference zero-temperature results are discussed in Section 3.1, thermal effects on the structure and electronic band gap are analyzed in Sections 3.2 and 3.3, respectively, and summary of the most important results is provided in Section 4.
2 Methods and materials
2.1 Computational methods
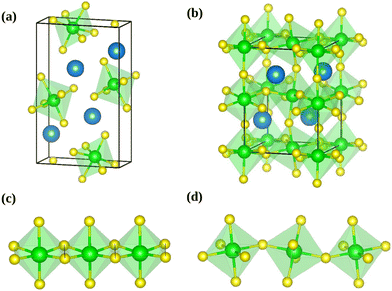
The calculations were performed using the periodic density-functional theory (DFT) code Vienna Ab-initio Simulation Package (VASP).35,36 The Kohn-Sham equations were solved variationally in a plane-wave basis set with the maximal kinetic energy of 400 eV using the projector-augmented-wave (PAW) method of Blöchl,41 as adapted by Kresse and Joubert.42 Unless stated otherwise, the Perdew, Burke, and Ernzerhof (PBE) exchange–correlation functional in the generalized gradient approximation proposed by Perdew et al.43 was used. The convergence criterion for the electronic self-consistency cycle, measured by the change in the total energy between successive iterations, was set to 10−6 eV per cell.Just like other perovskites, SrZrS3 forms lower symmetry variants of its parent cubic phase at the ambient conditions. The low temperature NL phase transforms into the DP phase at ∼1250 K.13 Although the NL phase is thermodynamically stable at room temperature, the DP structure can also be prepared as a long-lived metastable phase. Both types of crystals are orthorhombic, belonging to the Pnma space group. The experimentally determined geometries of conventional unit cells (Fig. 1) are compiled in Table 1. The optimizations of NL and DP structures were carried out for conventional unit cells using an external optimizer Gadget.44 In the relaxed structures, all forces acting on the atoms were below 5 × 10−3 eV Å−1. The grids of 4 × 8 × 2 and 4 × 4 × 4 k-points were used to sample the Brillouin zone for relaxations of NL and DP, respectively.
| a (Å) | b (Å) | c (Å) | V (Å3) | B 0 (GPa) | |
|---|---|---|---|---|---|
| NL phase | |||||
| Exp.13 | 8.525 | 3.826 | 13.925 | 454.1 | — |
| Exp.15 | 8.504 | 3.820 | 13.917 | 452.1 | — |
| DFT (this work) | 8.649 | 3.840 | 14.015 | 465.4 | 50.3 |
| DP phase | |||||
| Exp.13 | 7.108 | 9.772 | 6.741 | 468.2 | — |
| Exp.16 | 7.103 | 9.758 | 6.731 | 466.5 | — |
| DFT (ref. 18) | 7.147 | 9.843 | 6.804 | 478.7 | |
| DFT (this work) | 7.169 | 9.829 | 6.787 | 478.2 | 69.7 |
| C phase | |||||
| DFT (ref. 18) | 5.016 | 126.2 | 73.5 | ||
| DFT (this work) | 5.007 (7.082) | (10.015) | (7.082) | 125.6 (502.3) | 73.3 |
Molecular dynamics (MD) simulations were performed in an NPT ensemble at zero pressure and temperatures of 300 K, 600 K, 900 K, 1200 K and 1500 K. The simulation temperature was controlled by Langevin thermostat with a friction coefficient of 2 ps−1 for all atoms. The pressure was controlled by a Parrinello–Rahman barostat,45,46 whereby a mass of 2 amu and a friction coefficient of 10 ps−1 were used for the lattice degrees of freedom. The equations of motion of the ions were integrated using the velocity Verlet algorithm,47 with a time step of 3 fs. Supercells consisting of 2 × 4 × 1 and 2 × 2 × 2 multiples of conventional unit cells (both containing 160 atoms) were used in the MD simulations of NL and DP phases, respectively. This choice was made to account for the most essential atomic motions and to keep the crystal structures close to the cubic shape, allowing the use of the same computational settings in all simulations. As demonstrated in Section SII (ESI†), further increase in the size of the supercells does not lead to significant variations in the lattice parameters or radial distribution functions of the predicted structures. Consistently with the setting used in relaxations, the k-points grid was set to 2 × 2 × 2 in all MD simulations.
To accelerate our computationally demanding MD simulations, the machine learned force field (MLFF) recently implemented in VASP 6.335,36 was employed. The MLFF uses descriptors based on Gaussian representation of atomic distribution36,48 and predicts the target properties – energies, forces and stress tensor components – via Bayesian linear regression. Consequently, the quality of predictions can be measured by Bayesian error estimator.35,49 Importantly, the training configurations are chosen automatically and on-the-fly during an MD run, based on the similarity with other training configurations. This strategy ensures that new training configurations are added whenever an unexplored part of the configuration space is visited. In our calculations, a separate training procedure for each phase and temperature was executed with the initial Bayesian error threshold of 0.01 eV Å−1. The training typically consisted of 2 × 104 MD steps but the actual number of DFT calculations was much lower (150 to 600, depending on the temperature) and hence the training procedure was relatively fast. Once the training procedure was completed, a production run of length of ∼3 ns was performed at the MLFF level and the corresponding data were used to determine the observables. The use of MLFF allowed for enormous CPU time savings compared to a direct DFT (time needed to complete one MD step decreased from 1.6 CPU-hours to only 0.069 CPU-hours) while maintaining the ab initio quality of simulations, as discussed in more detail in Section SI (ESI†).
Upon performing the MD simulations, the equilibration period was determined using statistical Mann–Kendall tests,50 applied to averages and variances of all measured quantities. Upon discarding the data corresponding to the equilibration period, the remaining data (production period) exhibited no statistically significant trend and were used to calculate the ensemble averages. The standard error for computed properties was determined using the blocking method.51 The statistical uncertainty was predicted by assuming the confidence interval of 95% (i.e., the quantile of 1.96 was used). The basic observables such as the structural parameters or band gap values were computed as simple averages over the NPT ensemble. Linear and volume expansion coefficients were calculated via
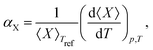 | (1) |
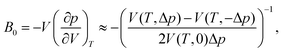 | (2) |
Drawings of structures presented in this work were created using the program VESTA.52
2.2 Experimental methods
3 Results and discussion
3.1 Static calculations
Before discussing the finite-temperature properties of SrZrS3 (vide infra), it is useful to explore the structure, energetics, elastic and electronic properties of this material by means of static calculations. Since the results presented here correspond to a classical zero temperature thermodynamic limit, they will serve as a reference for the discussion of finite-T properties.The energy versus volume dependence was obtained in a series of constant volume relaxations performed for each phase, which was subsequently fitted to Murnaghan equation of state53 to determine the ground state volume and bulk modulus. The ground state geometry was then obtained in a relaxation with the cell volume fixed at the ground state value. Finally, the band structure calculation was performed for the relaxed ground state structure.
The computed ground state quantities are compiled in Table 1. As it can be seen from the presented data, the relative errors with respect to the experimental values13,15 are within 1.7% for the lattice constants and within 2.9% for the cell volume. We notice, however, that our calculations systematically overestimate the structural parameters. Since the experimental measurements were conducted at a finite temperature (298 K for both the NL and DP phases), it can be expected that the actual relative error should increase further when the finite temperature effects are taken into account. We hypothesize that this small systematic overestimation of the lattice parameters is due to an incorrect treatment of long-range London dispersion interactions, which is a well-known shortcoming of (semi-)local density function approximations.54 Although several different correction schemes are currently available to alleviate this problem,55–61 a dedicated theoretical study would be necessary to identify the method that works best for the system at hand. We emphasize, however, that the systematic error remains very small (within 2%) even when the thermal effects are taken into account, as we discuss in Section 3.2. Hence, the choice of the simulation method in this study is justified.
Although the energies of the ground state structures of the NL and DP phases are very similar, the former is slightly more stable at 0 K with the energy difference being only 2 meV f.u.−1. The lower ground state energy of the NL phase is consistent with the experimental observation that this phase is stable at the temperatures below 1250 K, while DP is thermodynamically preferred at higher T.13
The computed values of the bulk modulus suggest that the NL phase is more compressible than the DP phase. This is a direct consequence of the atomic arrangement in the NL phase, which lacks the rigid three dimensional covalent network of octahedra, present in the DP phase (Fig. 1).
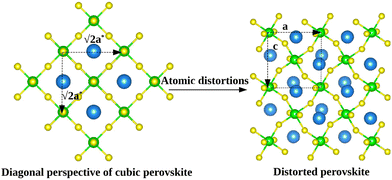
As it will be discussed in more detail in Section 3.2, it is crucial for understanding of the thermal behavior of the DP phase that its structure has its origin in the undistorted cubic (C) phase. The transformation is a result of symmetry lowering distortions (thus the name ‘distorted perovskite’), as shown schematically in Fig. 2. Thus, one can represent the C phase in the setting of DP by choosing the lattice vectors of the former as follows: 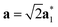 ,
, 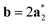 , and
, and 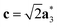 , where
, where 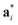 represents a lattice vector of a primitive cell of C. By comparing the cell geometries of the DP and C phases given in Table 1 one can see that, due to the distortions, the values of c and b are shortened by 4.2% and 1.9% respectively while a is elongated by 1.1% and the cell volume is reduced by 4.8%. In terms of energy, the symmetry breaking of the cubic structure into the DP phase results in stabilization by as much as 705 meV f.u.−1. Counter-intuitively, the C phase with lower density is predicted to be slightly less compressible than the more condensed DP phase, as evident from the computed values of bulk modulus (B0) shown in Table 1. Importantly, vibrational analysis of the unperturbed cubic phase reveals that the C phase is unstable at low T, as indicated by the presence of several vibrational modes with imaginary frequencies in the center of Brillouin zone (see Table S4 (ESI†)). Consistently with this conclusion, there are currently no experimental reports of the preparation of the SrZrS3 in the cubic phase.
represents a lattice vector of a primitive cell of C. By comparing the cell geometries of the DP and C phases given in Table 1 one can see that, due to the distortions, the values of c and b are shortened by 4.2% and 1.9% respectively while a is elongated by 1.1% and the cell volume is reduced by 4.8%. In terms of energy, the symmetry breaking of the cubic structure into the DP phase results in stabilization by as much as 705 meV f.u.−1. Counter-intuitively, the C phase with lower density is predicted to be slightly less compressible than the more condensed DP phase, as evident from the computed values of bulk modulus (B0) shown in Table 1. Importantly, vibrational analysis of the unperturbed cubic phase reveals that the C phase is unstable at low T, as indicated by the presence of several vibrational modes with imaginary frequencies in the center of Brillouin zone (see Table S4 (ESI†)). Consistently with this conclusion, there are currently no experimental reports of the preparation of the SrZrS3 in the cubic phase.
The three phases of SrZrS3 discussed here exhibit distinctly different band gaps (Eg). Using the PBE functional, we predict the values of 0.61 eV, 1.23 eV and 0.47 eV for NL, DP, and C respectively. We note that the the band gap of NL and DP is direct,18,23 at the Γ point of the Brillouin zone (BZ), while that of C is indirect (see Fig. S7 and S8 (ESI†)).18 The latter emerges as a difference between the conduction band value in the center (Γ point) and valence band at the edge (point R) of BZ defined for the primitive cell of C. Therefore, the zone folding62,63 due to the use of the DP setting for the C lattice remaps the maximum of the valence band onto the Γ point (Fig. S8 (ESI†)) and the band gap becomes direct. It is evident from the comparison with the available experimental data15 that the PBE functional underestimates the measured values ((1.53 eV (NL), 2.05–2.13 eV (DP))) by ∼0.9 eV for both phases. As reported previously,23 this error can be significantly reduced by using the HSE06 functional.64–66 Indeed, the band gaps computed at the HSE06 level (1.40 eV (NL), 2.04 eV (DP) and 1.21 eV (C)) are in a reasonable agreement with the experimental reference. We also note that the PBE and HSE06 results obtained in this work are in a very good agreement with previous theoretical reports.18,23 Finally, we remark that we neglected the thermal effects in the simulations presented so far – as we shall show in Section 3.3, these are small at T = 300 K, the temperature at which the experimental measurements were conducted.15
3.2 Thermal effects on crystal structure
In order to study the finite temperature effects on the structure of SrZrS3, ab initio NPT MD simulations accelerated by MLFF35,36 were performed, as described in Section 2.1. To this end, two series of independent MD runs, one initialized from the NL and the other from the DP structure, were executed for the temperatures of 300 K, 600 K, 900 K, 1200 K, and 1500 K (only DP). The simulation settings related to the electronic structure calculations used to train the MLFF were consistent with those used in the static calculations discussed in Section 3.1.The finite temperature values of structural parameters for the NL and DP phases are listed in Table 2. Plots with the thermal variations of parameters are shown in Fig. S3 and S4 (ESI†). As can be seen from the data, our calculations overestimate somewhat the cell sizes at room temperature. The overestimation is approximately isotropic and similar in magnitude for both stable phases. Nevertheless, the agreement with the experiment is reasonable (within 2.0% for the lengths of lattice vectors and within 4.3% for the cell volumes).
| T (K) | a (Å) | b (Å) | c (Å) | V (Å3) | B 0 (GPa) |
|---|---|---|---|---|---|
| NL phase | |||||
| 0 | 8.649 | 3.840 | 14.015 | 465.4 | 50.3 |
| 300 | 8.674 | 3.858 | 14.098 | 471.7 | 45.9 |
| 600 | 8.713 | 3.878 | 14.185 | 479.3 | 42.1 |
| 900 | 8.758 | 3.901 | 14.277 | 487.7 | 37.8 |
| 1200 | 8.815 | 3.926 | 14.372 | 497.2 | 33.6 |
| DP phase | |||||
| 0 | 7.169 | 9.829 | 6.787 | 478.2 | 69.7 |
| 300 | 7.177 | 9.868 | 6.827 | 483.5 | 66.8 |
| 600 | 7.182 | 9.915 | 6.876 | 489.7 | 60.4 |
| 900 | 7.182 | 9.973 | 6.936 | 496.7 | 54.3 |
| 1200 | 7.150 | 10.037 | 7.033 | 504.5 | 48.5 |
| (Pseudo-)C phase | |||||
| 0 | 5.007 (7.082) | (10.015 | (7.082)) | 125.6 (502.3) | 73.3 |
| 1200 | 5.017 (7.099) | (10.031) | (7.098) | 126.3 (505.2) | 48.5 |
| 1500 | 5.505 (7.142) | (10.103) | (7.143) | 128.8 (515.2) | 42.9 |
Across the temperature range examined here, the thermal effects cause smooth but anisotropic expansion of the NL and DP lattices. We note that NL is known to transform to DP at 1250 K.13 However, this first order phase transition is associated with re-connection of covalent Zr–S bonds, which is an activated process that, due to the time scale problem, can not be effectively studied by straightforward MD simulations used here. As shown in Fig. 3, the lattices of both phases differ in their thermal behavior. In NL, the linear thermal expansion coefficients for all three lattice vectors increase monotonously with T and eventually converge to approximately the same value at 1200 K (Fig. 3), i.e., the lattice expansion becomes virtually isotropic at this point. In the DP, in contrast, the differences in α increase with T, whereby the coefficient for the lattice vector a monotonously decreases and even becomes negative at T > 750 K. Hence, although the coefficients αb and αc are significantly larger at T > 500 K in the case of DP than in the case of NL, the volume expansion of the NL lattice is actually larger over the entire temperature range examined here (Fig. 3).
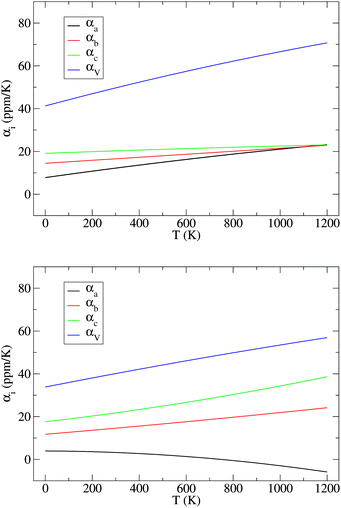 | ||
| Fig. 3 Variation of linear (αa, αb, and αc) and isotropic (αV) thermal expansion coefficients in the NL (top) and DP (bottom) phases of SrZrS3 with temperature. | ||
The key observation to explain the behavior of DP is that it converts quasi-continuously into undistorted cubic structure upon heating: the lattice parameters a and c become identical while the lattice constant b approaches the value of 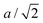 . This interpretation is also supported by the results of our in-house temperature-dependent X-ray diffraction measurements (Fig. 4) although a high enough temperature needed to observe the cubic phase was, due to the sample oxidation, not reached. As demonstrated earlier, the deformation of the unperturbed cubic structure yielding the DP phase involves a significant shortening of c (4%), a relatively small contraction along b (2.3%) but a slight expansion of a (1.5%). The reverse structural changes occur at high temperatures when the DP phase is transformed into the (pseudo-) C phase. Hence, the observed changes in the expansion coefficients, especially at high temperatures, are a direct consequence of the formation of the cubic phase.
. This interpretation is also supported by the results of our in-house temperature-dependent X-ray diffraction measurements (Fig. 4) although a high enough temperature needed to observe the cubic phase was, due to the sample oxidation, not reached. As demonstrated earlier, the deformation of the unperturbed cubic structure yielding the DP phase involves a significant shortening of c (4%), a relatively small contraction along b (2.3%) but a slight expansion of a (1.5%). The reverse structural changes occur at high temperatures when the DP phase is transformed into the (pseudo-) C phase. Hence, the observed changes in the expansion coefficients, especially at high temperatures, are a direct consequence of the formation of the cubic phase.
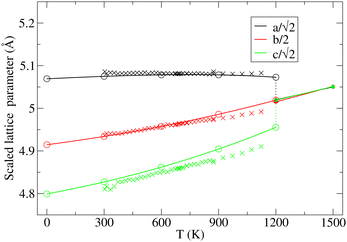 | ||
Fig. 4 Variation in the average lengths of scaled lattice vectors 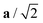 , b/2, and , b/2, and 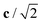 of DP/C phase of SrZrS3 with temperature. Circle and cross symbols represent the theoretical and experimental results, respectively. To facilitate a clearer comparison with theory, which tends to slightly overestimate the lengths of the lattice vectors (see. Table 1), all experimental data points were shifted by a constant value of 0.05 Å. Note that, according to the theoretical predictions, DP and C coexist at 1200 K. At T = 1500 K, conversion of DP to C is complete and therefore all three values of scaled lattice parameters coincide. of DP/C phase of SrZrS3 with temperature. Circle and cross symbols represent the theoretical and experimental results, respectively. To facilitate a clearer comparison with theory, which tends to slightly overestimate the lengths of the lattice vectors (see. Table 1), all experimental data points were shifted by a constant value of 0.05 Å. Note that, according to the theoretical predictions, DP and C coexist at 1200 K. At T = 1500 K, conversion of DP to C is complete and therefore all three values of scaled lattice parameters coincide. | ||
At T = 1200 K, the cell volume of DP phase is only slightly larger than that of the relaxed structure of the phase C (Table 2). Also the kinetic energy 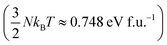 is now higher than the potential energy difference between the relaxed C and DP structures (0.705 eV f.u.−1), making the DP to C transition feasible. By monitoring the values of lattice parameters a and c (see Fig. S9 (ESI†)), multiple abrupt switching events between the DP and C phases are observed, suggesting that both phases are close to coexistence (although the C phase already prevails). Hence, although temperature increase facilitates a seemingly gradual conversion from DP to C, the phase transition is still of the first order. The DP to C transformation is virtually complete at 1500 K as is evident from the values of lattice constants in Table 2 and inspection of the atomic positions and lattice parameters averaged over all MD-generated configurations (Fig. S10 (ESI†)).
is now higher than the potential energy difference between the relaxed C and DP structures (0.705 eV f.u.−1), making the DP to C transition feasible. By monitoring the values of lattice parameters a and c (see Fig. S9 (ESI†)), multiple abrupt switching events between the DP and C phases are observed, suggesting that both phases are close to coexistence (although the C phase already prevails). Hence, although temperature increase facilitates a seemingly gradual conversion from DP to C, the phase transition is still of the first order. The DP to C transformation is virtually complete at 1500 K as is evident from the values of lattice constants in Table 2 and inspection of the atomic positions and lattice parameters averaged over all MD-generated configurations (Fig. S10 (ESI†)).
A useful insight into the temperature-induced changes in internal structure can be gained from an analysis of partial radial distribution functions (RDF) for the Zr–S pairs (Fig. 5). The positions of the first peaks on the RDF, corresponding to the nearest neighbor distance, are 2.59 Å (NL) and 2.56 Å (DP), which are to be compared with the experimentally reported average bond lengths of 2.57 Å (NL) and 2.55 Å (DP).13 Regardless of the SrZrS3 phase, the position of this RDF peak gradually shifts to smaller values with increase in T, reaching the value of 2.53 Å at 1200 K. The RDFs evaluated separately for the DP and the C phases at 1200 K are virtually identical (see Fig. S11 (ESI†)), indicating that the local structure of both phases is very similar at these conditions. The latter is also the reason why multiple phase transitions have been observed within our MD run (vide supra). Also, this result shows that the internal structure is not yet fully transformed into the C phase (cf. RDF for 1500 K), as one could incorrectly assume based on the lattice geometry (Table 2). The gradual shift of the peak maximum towards lower values (2.51 Å) continues all the way to 1500 K, where the C phase formation is virtually complete.
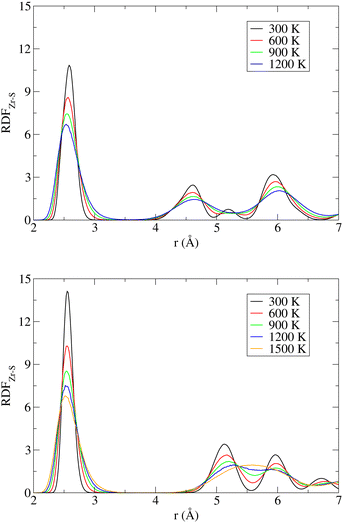 | ||
| Fig. 5 Radial distribution function for the Zr–S pairs (RDFZr–S) in the NL (top) and DP/C (bottom) phases of SrZrS3 at various temperatures. | ||
The likelihood of a temporary Zr–S bond breaking increases with T, which is evident from the increase in the RDF amplitude in the region r ≤ 3.0 Å. This effect is more pronounced in the NL than in the DP/C (at 1200 K, for instance, the RDF amplitude at r = 3.0 Å reaches the values of 0.75 and 0.55 for the NL and the DP/C, respectively). As mentioned above, the Zr–S re-connection is a prerequisite for the NL to DP phase transition to take place. Hence, although the phase transition did not spontaneously occur within our simulations, the increased likelihood of the Zr–S bonds breaking can be viewed as a sign of proximity to such a process.
In the case of the NL, a gradual disappearance of the RDF peak at r ≈ 5.2 Å, representing the inter-chain non-bonding Zr–S distance, is observed. This is caused by a temperature induced deformation of the chain of edge-sharing octahedra (see Fig. S12 (ESI†)). In the case of the RDF evaluated for simulations initialized from the DP phase, a gradual transition from the DP to the C phase is observed, which is evident from the reduction of separation between the two initially well-resolved next-nearest neighbour peaks located at r ≈ 5.1 Å and ∼6.0 Å that are being progressively replaced by one broad band centered at r ≈ 5.6 Å representing the next-nearest Zr–S distance in a perfect cubic structure.
The values of the isothermal bulk modulus, determined as described in Section 2.1, are presented in Table 2. The results indicate that the NL phase is less compressible than the DP phase at all temperatures considered, whereby the difference in the B0 is 15–21 GPa. As expected, bulk modulus decreases approximately linearly with T and the DP to C phase transition seem to have only a modest effect on the B0vs. T dependence.
3.3 Thermal effects on electronic band gaps
The results and conclusions reached in the previous section motivate an important question: How do the temperature-induced structural changes affect the electronic properties of SrZrS3? To address this question, electronic band gap values for all relevant phases were calculated as ensemble averages at each temperature. For this purpose, we made use of the configurations generated in long MD runs used to analyze the T-dependent structure (see Section 3.2) out of which we randomly selected a representative set of 200 configurations. For each of the selected configurations, a single point electronic structure calculation has been performed at the DFT level. Finally, the band gap observables for each T were obtained as arithmetic averages over the representative set members. As discussed in Section 3.1, the NL and DP phases have a direct band gap at the Γ point of the BZ while the indirect band gap found in C appears as a direct gap at Γ when the DP setting is used in calculations (Fig. S8 (ESI†)). Since the integral multiples of conventional NL and DP cells were used in our MD calculations, we were able to determine the band gap conveniently as a difference between the Γ point values of the lowest conduction and highest valence bands. The Eg distributions determined for each T are shown in Fig. S13 (ESI†). The resulting averages of Eg exhibit a very small statistical uncertainty (within 0.002 eV).The resulting T-dependences of the band gaps of NL, DP and C phases are shown in Fig. 6. The NL and DP phases exhibit a distinctly different behavior: while Eg of the former is virtually constant over the entire temperature range (no finite T value deviates from the zero T value by more than 0.05 eV), the band gap of the latter monotonously and steeply decreases with T, whereby the difference between the values determined for 1200 K and 0 K is as large as 0.45 eV. The values of Eg computed for DP and C at 1200 K, at which both phases coexist, differ only by ∼0.05 eV.
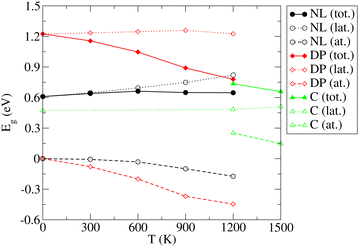 | ||
| Fig. 6 Variation of the band gap (Eg) of the NL, DP, and C phases of SrZrS3 with temperature. Lattice (lat.) and atomic displacement (at.) contributions to the total (tot.) values are shown. | ||
Traditionally, the T dependence of band gap is thought to be a result of two contributions, the lattice expansion (Eg,lat.) and the atomic displacements (or electron–phonon interaction, Eg,at.).67 Our approach allows us to separate these two terms. To identify the Eg,lat. term, the band gap is computed for a set of relaxed structures with cell geometries set to those predicted (as ensemble averages) by the NPT MD simulations presented in Section 3.2. Since the relaxation procedure ensures that the net forces acting on each atom vanish, the atoms in these relaxed structures sit in their optimal unperturbed positions. Consequently, the band gap dependence on volume includes the cell expansion contribution only, while the atomic displacement contribution vanishes. The latter dependence is therefore identified as Eg,lat.(V) = Eg(V). Because the ensemble averaged cell geometry is fixed by temperature, the T-dependence of the Eg,lat. term is obtained as Eg,lat.(T) = Eg,lat.(V(T)). Finally, the atomic displacement contribution is determined trivially via Eg,at. = Eg − Eg,lat.. As shown in Fig. 6, the lattice contribution is always positive but differs in magnitude for different phases. For NL, Eg,lat. increases monotoneously with T and ranges between 0.61 eV (0 K) and 0.82 eV (1200 K). In contrast, Eg,lat. determined for the DP and C phases, is nearly constant over the entire T range considered here (variations within 0.04 eV). The atomic displacement contributions for the NL and DP phases are negative and decrease monotoneously with T (by up to −0.17 eV (NL) and −0.45 eV (DP) at 1200 K). In the C phase, Eg,at. becomes positive and decreases with T such that at 1500 K, where the C phase is fully formed, the atomic displacement contribution to the band gap is only 0.15 eV.
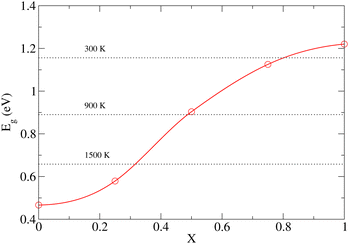
To demonstrate that the very large atomic displacement contribution to the band gap of DP phase is indeed a consequence of proximity to the parent C phase, we computed Eg values for a series of structures created by interpolation of relaxed C and DP structures as follows:
| qX = q0 + X(q1 − q0), | (3) |
As already discussed in Section 3.1, the PBE functional used throughout this work strongly underestimates the values of Eg for the NL and DP phases. Therefore, it is important to confirm that the conclusions regarding the dependence of Eg on temperature discussed above are correct. In particular, we wish to test if the predicted trends remain the same upon replacing the PBE functional by the HSE06 method, which is known to yield accurate predictions for the chalcogenide perovskite compounds23 and which significantly improves the Eg predictions in static calculations (see Section 3.1). Unfortunately, the HSE06 calculations are about 80-times more time-consuming than those performed at the PBE level, rendering the recalculation of Eg for all configurations, used to draw ensemble averages in our finite T simulations, impractical. We note, however, that the HSE06 and PBE values of Eg are strongly linearly correlated (see Fig. S14–S16 (ESI†)). We therefore devised an efficient computational scheme, in which we performed only 20–40 explicit Eg calculations at the HSE06 level for each temperature. We then set up a linear regression model and used it to predict the HSE06 Eg values for all 200 configurations used in the PBE calculations to determine the ensemble average. The calculated HSE06 and PBE ensemble averages of Eg are compared in Fig. 8 (the corresponding numerical values are presented in Table S5 (ESI†)). As expected, the HSE06 band gaps are larger by 0.5–0.8 eV compared to the PBE counterparts. Importantly, however, both methods predict very similar overall trends. We conclude therefore that although the PBE underestimates the absolute values of the band gaps systematically, it is still quite reliable in predicting the thermal dependence of Eg. Finally, comparing the band gaps obtained at the HSE06 level for 0 K (1.40 (NL), 2.04 (DP)) and 300 K (1.36 eV (NL), 1.96 eV (DP)) with the experiment conducted at ambient conditions (1.53 eV (NL), 2.05-2.13 eV (DP)),15 we observe that the systematic error of the HSE06 functional is ∼0.1 eV when thermal effects are taken into account and hence the agreement with the experiment remains reasonably good. As discussed in the literature,23 further improvements can be achieved by inclusion of relativistic spin–orbit coupling effects and improved treatment of many-body electronic problem (e.g., via Green's function (GW) methods). This is, however, beyond the scope of the present work.
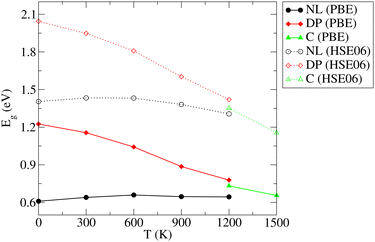 | ||
| Fig. 8 Comparison of the PBE and HSE06 predictions of the variation of electronic band gap (Eg) of the needle-like (NL), distorted perovskite (DP), and cubic (C) phases of SrZrS3 with temperature. | ||
4 Conclusions
Ab initio based molecular dynamics simulations in an NPT ensemble were performed to investigate properties of the NL and DP phases of SrZrS3 in the temperature range between 300 K and 1200 K. Compared to a straightforward ab intio MD, the use of the adaptive machine learning scheme implemented35,36 in VASP allowed us to extend the simulation times from few tens of picoseconds to nanoseconds improving thus the sampling quality greatly. The structural changes occurring in the NL phase upon heating are relatively modest and include an anisotropic but monotonous lattice expansion. The changes are much more dramatic in the DP phase, as the evolution of both the lattice geometry and the internal structure is strongly affected by the proximity of the cubic phase. Although the temperature induced process of conversion of DP to C is seemingly continuous, abrupt changes in the lattice parameters were detected at 1200 K, when both phases co-exist. The transition is complete at 1500 K.The isothermal bulk modulus, computed from the cell volume fluctuations, was found to decrease linearly with T, with the slope of 0.014 GPa K−1 and 0.020 GPa K−1 for NL and DP, respectively.
The finite temperature effect on the band gap of SrZrS3 was investigated. Since we determined Eg as an observable in NPT MD, our approach describes both the lattice expansion and atomic displacement (electron–phonon coupling) contributions to the thermal dependence of the band gap. The calculated PBE band gaps for the NL phase were found to be virtually temperature independent in the 300–1200 K range. In contrast, the Eg of the DP phase was found to decrease monotonously with T, whereby the value obtained for 1200 K is 0.45 eV lower than that obtained for 300 K. The analysis revealed that the observed Eg decrease is almost exclusively due to the large atomic displacements which are, in turn, a consequence of the proximity of the DP phase to the parent C phase, with the band gap lower by ∼0.8 eV. The important observation is that the temperature causes a gradual conversion of the DP phase into the C phase which is linked to the Eg reduction. Our results show that this process starts well below the temperatures at which the C phase becomes stable (see Fig. 8). The results obtained by the PBE simulations were validated by additional calculations using the HSE06 functional, which yields band gap values that are in a much better agreement with the experiment. Since the Egvs. T trends obtained by the two methods are nearly identical, it is concluded that the use of a less CPU intense PBE functional is justified in the future finite-T analysis of the electronic structure in materials similar to SrZrS3.
To be suitable for application in photovoltaics, the material electronic band gap should fall within the range of 0.9–1.6 eV.68 In case of SrZrS3 the calculated band gap for NL is about 1.4 eV,23 which is within the desired range. However, according to Sun et al.,23 the onset of the optical absorption in NL phase is significantly higher than its band gap and therefore this phase of the material is not suitable for application in photovoltaics. Our results show that the NL phase exhibits a very modest dependence of its structure and band gap on temperature. On the other hand, the band gap of DP phase of the SrZrS3 was theoretically predicted to be about 2.0 eV,23i.e., above the optimal photovoltaic range. However, our study reveals that, thanks to the interesting dynamic response being a consequence of proximity to the cubic phase, the band gap of this phase moves closer to the optimum range with increasing temperature. Since the phase transition from the DP to cubic is quite steady and progressive, the decrease in the band gap is significant, but not abrupt. We anticipate that in closer inspection similar behavior will be observed in for other TCs provided that: (i) there is a significant difference between the band gaps of DP and C phase and (ii) the C phase is less stable than the DP phase, but still energetically accessible. Our exploratory static results suggest that number of sulfides and selenides meet these requirements (see Fig. S17 and Table S6 (ESI†)). Moreover, judging from smaller energy differences between the DP and C phases found for some compounds, some of the TCs are likely to transform to the cubic phase at much lower temperatures than the DP phase of the SrZrS3, with the effect on the band gap being even more dramatic. These deeper insights into the structure-band gap relationship in TCs are essential for identifying the materials with the optimal properties for photovoltaics and other applications. We hope this work will stimulate further studies in this direction.
Author contributions
Namrata Jaykhedkar: investigation, visualization, writing-original draft preparation. Roman Bystrický: investigation, writing-reviewing and editing. Milan Sýkora: conceptualization, funding acquisition, project administration, writing-reviewing and editing. Tomáš Bučko: conceptualization, investigation, formal analysis, visualization, writing-original draft preparation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the European Union's Horizon 2020 research and innovation programme under grant agreement No. 810701 and by the Slovak Research and Development Agency under grant agreement No. APVV-19-0410. NJ and TB gratefully acknowledge the use of HPC facility by PRACE (Partnership for Advanced Computing in Europe) within the programme DECI-16 and of the supercomputing infrastructure of Computing Center of the Slovak Academy of Sciences acquired in projects ITMS 26230120002 and 26210120002 supported by the Research and Development Operational Program funded by the ERDF. The use of the high performance computing facilities CLARA@UNIBA.SK at Comenius University in Bratislava, services and staff expertise of Centre for Information Technology is acknowledged. TB is thankful to Dr Ryosuke Jinnouchi and Dr Ferenc Karsai for introducing him the MLFF method.References
- J. Berry, T. Buonassisi, D. A. Egger, G. Hodes, L. Kronik, Y.-L. Loo, I. Lubomirsky, S. R. Marder, Y. Mastai, J. S. Miller, D. B. Mitzi, Y. Paz, A. M. Rappe, I. Riess, B. Rybtchinski, O. Stafsudd, V. Stevanovic, M. F. Toney, D. Zitoun, A. Kahn, D. Ginley and D. Cahen, Adv. Mater., 2015, 27, 5102–5112 CrossRef CAS PubMed.
- D. A. Egger, A. M. Rappe and L. Kronik, Acc. Chem. Res., 2016, 49, 573–581 CrossRef CAS PubMed.
- H. J. Snaith, Nat. Mater., 2018, 17, 372–376 CrossRef CAS PubMed.
- S.-T. Ha, R. Su, J. Xing, Q. Zhang and Q. Xiong, Chem. Sci., 2017, 8, 2522–2536 RSC.
- N.-G. Park, J. Phys. Chem. Lett., 2013, 4, 2423–2429 CrossRef CAS.
- F. Chiarella, A. Zappettini, F. Licci, I. Borriello, G. Cantele, D. Ninno, A. Cassinese and R. Vaglio, Phys. Rev. B, 2008, 77, 045129 CrossRef.
- B. Kshirsagar, N. Jaykhedkar, K. Jain, S. Kishor, V. Shah, L. M. Ramaniah and S. Tiwari, J. Phys. Chem. C, 2021, 125, 2592–2606 CrossRef CAS.
- D. B. Straus, S. Guo, A. M. Abeykoon and R. J. Cava, J. Adv. Mater., 2020, 32, 2001069 CrossRef CAS PubMed.
- T. Gupta, D. Ghoshal, A. Yoshimura, S. Basu, P. K. Chow, A. S. Lakhnot, J. Pandey, J. M. Warrender, H. Efstathiadis, A. Soni, E. Osei-Agyemang, G. Balasubramanian, S. Zhang, S.-F. Shi, T.-M. Lu, V. Meunier and N. Koratkar, Adv. Funct. Mater., 2020, 30, 2001387 CrossRef CAS.
- K. V. Sopiha, C. Comparotto, J. A. Márquez and J. J. S. Scragg, Adv. Opt. Mater., 2021, 2101704 Search PubMed.
- D. Tiwari, O. S. Hutter and G. Longo, J. Phys. Energy, 2021, 3, 034010 CrossRef CAS.
- A. Swarnkar, W. J. Mir, R. Chakraborty, M. Jagadeeswararao, T. Sheikh and A. Nag, Chem. Mater., 2019, 31, 565–575 CrossRef CAS.
- C.-S. Lee, K. Kleinke and H. Kleinke, Solid State Sci., 2005, 7, 1049–1054 CrossRef CAS.
- S. Perera, H. Hui, C. Zhao, H. Xue, F. Sun, C. Deng, N. Gross, C. Milleville, X. Xu, D. F. Watson, B. Weinstein, Y.-Y. Sun, S. Zhang and H. Zeng, Nano Energy, 2016, 22, 129–135 CrossRef CAS.
- S. Niu, H. Huyan, Y. Liu, M. Yeung, K. Ye, L. Blankemeier, T. Orvis, D. Sarkar, D. J. Singh, R. Kapadia and J. Ravichandran, Adv. Mater., 2017, 29, 1604733 CrossRef PubMed.
- S. Niu, J. Milam-Guerrero, Y. Zhou, K. Ye, B. Zhao, B. C. Melot and J. Ravichandran, J. Mater. Res., 2018, 33, 4135–4143 CrossRef CAS.
- N. Gross, Y.-Y. Sun, S. Perera, H. Hui, X. Wei, S. Zhang, H. Zeng and B. A. Weinstein, Phys. Rev. Appl., 2017, 8, 044014 CrossRef.
- M. Oumertem, D. Maouche, S. Berri, N. Bouarissa, D. P. Rai, R. Khenata and M. Ibrir, J. Comput. Electron., 2019, 18, 415–427 CrossRef CAS.
- A. Majumdar, A. A. Adeleke, S. Chakraborty and R. Ahuja, J. Mater. Chem. C, 2020, 8, 16392–16403 RSC.
- G. Mannino, I. Deretzis, E. Smecca, A. La Magna, A. Alberti, D. Ceratti and D. Cahen, J. Phys. Chem. Lett., 2020, 11, 2490–2496 CrossRef CAS PubMed.
- C. Quarti, E. Mosconi, J. M. Ball, V. D'Innocenzo, C. Tao, S. Pathak, H. J. Snaith, A. Petrozza and F. De Angelis, Energy Environ. Sci., 2016, 9, 155–163 RSC.
- Y.-N. Wu, W. A. Saidi, J. K. Wuenschell, T. Tadano, P. Ohodnicki, B. Chorpening and Y. Duan, J. Phys. Chem. Lett., 2020, 11, 2518–2523 CrossRef CAS PubMed.
- Y.-Y. Sun, M. L. Agiorgousis, P. Zhang and S. Zhang, Nano Lett., 2015, 15, 581–585 CrossRef CAS PubMed.
- A. Clearfield, Acta Crystallogr., 1963, 16, 135–142 CrossRef CAS.
- R. Lelieveld and D. J. W. IJdo, Acta. Crystallogr. B., 1980, 36, 2223–2226 CrossRef.
- H. Igwebuike, E. Ntsoenzok and N. Dzade, Materials, 2020, 13, 978 CrossRef PubMed.
- Y. Nishigaki, T. Nagai, M. Nishiwaki, T. Aizawa, M. Kozawa, K. Hanzawa, Y. Kato, H. Sai, H. Hiramatsu, H. Hosono and H. Fujiwara, Sol. RRL, 2020, 4, 1900555 CrossRef CAS.
- P. B. Allen and V. Heine, J. Phys. C: Solid State Phys., 1976, 9, 2305–2312 CrossRef CAS.
- P. B. Allen and M. Cardona, Phys. Rev. B, 1981, 23, 1495–1505 CrossRef CAS.
- J. Park, W. Saidi, J. Wuenschell, B. Howard, B. Chorpening and Y. Duan, ACS Appl. Mater. Interfaces, 2021, 13(15), 17717–17725 CrossRef CAS PubMed.
- W. A. Saidi, S. Poncé and B. Monserrat, J. Phys. Chem. Lett., 2016, 7, 5247–5252 CrossRef CAS PubMed.
- M. Zacharias and F. Giustino, Phys. Rev. B, 2016, 94, 075125 CrossRef.
- F. Karsai, M. Engel, E. Flage-Larsen and G. Kresse, New J. Phys., 2018, 20, 123008 CrossRef CAS.
- S. Baroni, P. Giannozzi and E. Isaev, in Density-Functional Perturbation Theory for Quasi-Harmonic Calculations, ed. R. Wentzcovitch and L. Stixrude, 2010, vol. 71, pp. 39–57 Search PubMed.
- R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 014105 CrossRef CAS.
- R. Jinnouchi, F. Karsai, C. Verdi, R. Asahi and G. Kresse, J. Chem. Phys., 2020, 152, 234102 CrossRef CAS PubMed.
- P. Liu, C. Verdi, F. Karsai and G. Kresse, Phys. Rev. B, 2022, 105, L060102 CrossRef CAS.
- C. Verdi, F. Karsai, P. Liu, R. Jinnouchi and G. Kresse, npj Comput. Mater., 2021, 7, 156 CrossRef CAS.
- R. Jinnouchi, F. Karsai, C. Verdi and G. Kresse, J. Chem. Phys., 2021, 154, 094107 CrossRef CAS PubMed.
- R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701 CrossRef CAS PubMed.
- P. Blöchl, Phys. Rev. B, 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- T. Bucko, J. Hafner and J. G. Angyan, J. Chem. Phys., 2005, 122, 124508 CrossRef PubMed.
- M. Parrinello and A. Rahman, Phys. Rev. Lett., 1980, 45, 1196–1199 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding molecular simulation: From algorithms to applications, Academic Press, San Diego, 2002, pp. 74–77 Search PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- C. M. Bishop, Pattern Recognition and Machine Learning, Springer, 2006 Search PubMed.
- S. K. Schiferl and D. C. Wallace, J. Chem. Phys., 1985, 83, 5203–5209 CrossRef CAS.
- H. Flyvbjerg and H. Petersen, J. Chem. Phys., 1989, 91, 461–466 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- F. D. Murnaghan, P. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247 CrossRef CAS PubMed.
- J. F. Dobson, K. McLennan, A. Rubio, J. Wang, T. Gould, H. M. Le and B. P. Dinte, Aust. J. Chem., 2001, 54, 513–527 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- T. Bučko, S. Lebègue, J. Hafner and J. Ángyán, J. Chem. Theory Comput., 2013, 9, 4293–4299 CrossRef PubMed.
- T. Bučko, S. Lebègue, J. G. Ángyán and J. Hafner, J. Chem. Phys., 2014, 141, 034114 CrossRef PubMed.
- A. Ambrosetti, A. M. Reilly, R. A. DiStasio and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed.
- T. Gould, S. Lebègue, J. G. Ángyán and T. Bučko, J. Chem. Theory Comput., 2016, 12, 5920–5930 CrossRef CAS PubMed.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Harcourt College Publisher, 1976, pp. 151–174 Search PubMed.
- C. Kittel, Introduction to Solid State Physics, Wiley, 2004, pp. 223–254 Search PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- J. Paier, R. Hirschl, M. Marsman and G. Kresse, J. Chem. Phys., 2005, 122, 234102 CrossRef PubMed.
- Y. Varshni, Physica, 1967, 34, 149–154 CrossRef CAS.
- M.-G. Ju, J. Dai, L. Ma and X. C. Zeng, Adv. Energy Mater., 2017, 7, 1700216 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2tc02253b |
| This journal is © The Royal Society of Chemistry 2022 |