Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of the nanoparticle size on thermometric properties of a single-band ratiometric luminescent thermometer in NaYF4:Nd3+†
K. Trejgis *a,
K. Ledwa
*a,
K. Ledwa a,
Leipeng Lib and
L. Marciniak
a,
Leipeng Lib and
L. Marciniak *a
*a
aInstitute of Low Temperature and Structure Research, Polish Academy of Sciences, Okolna 2, 50-422 Wroclaw, Poland. E-mail: k.trejgis@intibs.pl; l.marciniak@intibs.pl
bHebei Key Laboratory of Optic-electronic Information and Materials, College of Physics Science and Technology, Hebei University, Baoding 071002, China
First published on 26th January 2022
Abstract
Due to the fact that temperature is one of the key physical quantities determining the occurrence of physical phenomena, chemical reactions or biological processes, one of the important issues to be solved is the precise determination of temperature. In order to achieve this even under demanding conditions, a lot of attention has recently been focused on methods of remote temperature readout, especially on luminescence thermometry. One of the recent and very interesting methods, the so-called single-band ratiometric luminescence thermometry, is based on the phenomenon of absorption from an excited state and allows for temperature determination based on thermally induced changes in the intensity of a single emission band under two excitation conditions, i.e., by absorption from the ground state and from the excited state. However, the complexity of the latter process in particular requires a number of studies leading to an understanding of the factors affecting the excited level occupancy, which will enable the development of highly sensitive luminescent thermometers based on this method. One of the important aspects is to investigate the influence of the size of the material and the associated occurrence of surface effects, as considered in this work. NaYF4:2%Nd3+ nanocrystals with grain sizes varying from 15 nm to 200 nm were analyzed. A regular trend of widening the useful temperature range with increasing nanocrystallite size was observed. Very high relative sensitivities were obtained, which in the nanocrystals of the largest size analyzed were as high as 19.1% K−1 at 198 K.
Introduction
Luminescence thermometry is a remote temperature readout method based on thermally induced changes in the spectroscopic parameters of a given phosphor.1–9 Due to its several advantages, it has attracted the attention of many researchers over the past years. One of such features is a remote operating mode, which enables temperature readout even in severe conditions that prevail for instance in high-temperature smelting furnaces or in case of rotating elements of equipment without disturbing them or stopping the machine.10–12 So far, for remote temperature sensing, the thermovision method has been mainly used, however, it suffers from some limitations, which include the possibility of imaging the temperature of only the first object encountered in the optical path and the dependence of the outcomes on a predetermined value of the camera input parameter, which is the emissivity.13 An erroneous estimation of the emissivity can result in a temperature misalignment that can reach several hundred degrees. Therefore, luminescence thermometry can be an accurate alternative to thermovision cameras, which, owing to the possibility of imaging not only the surface but also deeper layers, in addition to applications in the field of technology, can also be suitable for applications in biomedicine, e.g. in cancer therapy.14–16 In luminescence thermometry aimed at biological applications, the most suitable optically active ions are Nd3+, which is due to several factors. First of all, Nd3+ ions exhibit the ability to both be excited and to emit in the near-infrared (NIR) region,17,18 which covers the region of biological optical windows.19–25 This is highly desirable because in such a spectral region, light absorption and scattering by cells and tissues are minimized, so that the depth of penetration of the radiation beams can be deeper and the reliability of the results improved. Furthermore, the 808 nm excitation line, which is one of the most suitable wavelengths for Nd3+ ions excitation, is about 20 times less absorbed by the tissues compared to the 980 nm beam frequently used for excitation of up-conversion emission (used to excite Yb3+ ions).26 Hence, the risk of side effects due to overheating of tissues during phosphor excitation is minimized.As shown recently, unique configuration of the energy level diagram of Nd3+ ions, including energy difference between ground 4I9/2 and first excited 4I11/2 states of around 2000 cm−1, and the possibility of the occurrence of cross-relaxation process, makes them perfect candidate for the single band ratiometric (SBR) approach of luminescence thermometry.9,27–34 Temperature determination by this method is based on the analysis of the intensity ratio of a single emission band being excited by two wavelengths, where one of them is matched to the conventionally used ground state absorption (GSA) and the other to the excited state absorption (ESA). This approach was developed to overcome the limitations of the conventional dual-band ratiometric thermometry, in which the modulation of the emission spectra shape by the dispersive dependence of the extinction of the medium surrounding the phosphor leads to unreliable temperature readout (in the SBR shape of the emission band in modified in the same way regardless of the excitation wavelength used). The intensity of the ESA-excited luminescence depends on many factors. If only the thermal factor is considered, according to Boltzmann's distribution it would be proportional to the energy distance between the ground and the excited multiplet states.35 However, the population of an excited level from which the ESA process occurs is affected by many other factors in addition to the thermal energy supplied to the system. One of the factors influencing the occupancy of the 4I11/2 level from which absorption occurs is the interionic interactions through the cross-relaxation (CR) pathway.36–38 The energy match between pairs of 4F3/2–4I15/2 and 4I9/2–4I15/2 levels makes {4F3/2; 4I9/2} → {4I15/2; 4I15/2} cross-relaxation very probable. This process occurs particularly efficiently for high concentrations of dopant ions, however, although it is beneficial for the ESA process, on the other hand, it leads to the quenching of the Nd3+ emission intensity. Furthermore, as a result of efficient nonradiative depopulation of excited states for heavily Nd3+ ion doped nanomaterials, light to heat conversion can occur, which may further quench the emission intensity and reduce the reliability of measurements.39,40 Therefore, it is necessary to optimize a dopant ion concentration that balances those two effects. Moreover, one of the key drivers affecting the occupation of the excited level is the probability of nonradiative transitions, which depends heavily on the energy of the host phonons and the quenching associated with the surface of the phosphor.
Recently, the critical role of surface processes on the ESA process probability and thus on the thermometric parameters of SBR thermometers, such as relative sensitivity, temperature resolution, and useful temperature range, has been highlighted using YAG:Nd3+ as an example. Unfortunately those studies were limited only to three types of samples of drastically varying sizes, i.e., nanocrystals, microcrystals, and ceramics.29 The main insight coming from this research is that the growing ratio of ions on the surface of the phosphor relative to those in the volume part, observed with decreasing particle size, makes the luminescence more sensitive to the interactions with functional groups of the medium or with ligands attached to the nanocrystal surface.41 The interactions at the surface of the structure can strongly contribute to the depopulation of the excited 4I11/2 level of Nd3+ ions, since the energy difference of less than 2000 cm−1 occurring between the 4I9/2 and 4I11/2 states can be effectively overcome by at least one vibrational mod of the OH− groups.
For biomedical applications, the size of thermometers must be within the nanometer scale, so the consideration of the impact of size and surface effects on the thermometric properties of SBR luminescent thermometers should be very carefully investigated and evaluated. Therefore, in this work, the detailed studies of the influence of the particle size on the thermometric properties of the Nd3+ based luminescent thermometer operating in the SBR mode are presented. Since the probability of nonradiative depopulation of the excited states is affected by the host phonons, the studies presented here were conducted on the low-phonon host material, namely NaYF4:2%Nd3+ nanocrystals with sizes ranging from 10 to 200 nm.
Experimental
Materials preparation
The materials were synthesized by thermal decomposition method in boiling oleic acid and octadecene acting as solvents.42Neodymium(III) acetate hydrate ((CH3CO2)3Nd·3H2O with 99.9% purity), yttrium(III) acetate hydrate ((CH3CO2)3Y·3H2O with 99.9% purity), gadolinium(III) acetate hydrate ((CH3CO2)3Gd·3H2O with 99.9% purity), ammonium fluoride (NH4F of 98% purity), acetic acid (CH3CO2H of 99% purity), oleic acid (CH3(CH2)7CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH2)7COOH of 90% purity) and 1-octadecene (CH3(CH2)15CH
CH(CH2)7COOH of 90% purity) and 1-octadecene (CH3(CH2)15CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 with 90% purity) were purchased from Sigma Aldrich. Sodium hydroxide (NaOH with 99.8% purity), ethanol (C2H5OH, 96% pure p.a.), methanol (CH3OH, 99.8%), n-hexane (C6H14, pure p.a.) and chloroform (CHCl3, 98.5%) were purchased from POCH S.A. (Poland). All of the chemical reagents were used as received without future purification.
CH2 with 90% purity) were purchased from Sigma Aldrich. Sodium hydroxide (NaOH with 99.8% purity), ethanol (C2H5OH, 96% pure p.a.), methanol (CH3OH, 99.8%), n-hexane (C6H14, pure p.a.) and chloroform (CHCl3, 98.5%) were purchased from POCH S.A. (Poland). All of the chemical reagents were used as received without future purification.
The synthesis was performed for 1.50 mmol of final product. Depending on the dopant ion concentration, appropriate amounts of neodymium acetate and either yttrium acetate or gadolinium acetate depending on the matrix synthesized (NaYF4, NaGdF4) were placed in a 250 mL three-neck round-bottom flask along with 22.5 mL of octadecene and 9 mL of oleic acid. The solution was then magnetically stirred and heated slowly to 140 °C under vacuum conditions and further stirred at this temperature for 30 min to form Y(oleate)3 and to remove residual water and oxygen. At the same time, 0.22222 g (6 mmol) of ammonium fluoride and 0.14999 g (3.75 mmol) of sodium hydroxide were weighed into another vessel and 10 mL of methanol was added and magnetically stirred together. In the next step the temperature of oleates was reduced to 50 °C and the atmosphere was changed from vacuum to a gentle flow of nitrogen. When the temperature of the solution reached 50 °C, the methanol solution of NaOH and NH4F was added quickly to the flask through the side neck and stirred under these conditions for 30 minutes. After this time, the temperature was increased to 85 °C and the conditions were changed to vacuum to completely evaporate the methanol from the reaction mixture. After the methanol evaporation the reaction temperature was increased to 300 °C as quickly as possible and maintained at this temperature for 60 minutes under the nitrogen flow. The final transparent solution was then cooled to room temperature. The NPs were precipitated by addition of ethanol and isolated by centrifugation at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 10 min. For purification, the resulting pellet was dispersed in a minimal amount of n-hexane and again precipitated with excess ethanol. The UCNPs were isolated by centrifugation at 14000 rpm for 10 min. The final product stabilized with OA ligands was dispersed in 3.75 cm3 of chloroform (CHCl3).
000 rpm for 10 min. For purification, the resulting pellet was dispersed in a minimal amount of n-hexane and again precipitated with excess ethanol. The UCNPs were isolated by centrifugation at 14000 rpm for 10 min. The final product stabilized with OA ligands was dispersed in 3.75 cm3 of chloroform (CHCl3).
Samples for spectroscopic measurements were prepared by dropping 0.75 μL onto a glass slide and evaporating the chloroform.
Characterization
Powder diffraction data were obtained using a PANalyticalX’Pert Pro diffractometer equipped with an Anton Paar TCU 1000 N Temperature Control Unit using Ni-filtered Cu Kα radiation (V = 40 kV, I = 30 mA). Transmission electron microscope (TEM) images were performed with the Philips CM-20 SuperTwin transmission electron microscope, operating at 160 kV. A drop of the suspension was put on a copper microscope grid covered with carbon. Before the measurement, the sample was dried and purified in a H2/O2 plasma cleaner for 1 min. The hydrodynamic size of nanoparticles was determined by dynamic light scattering (DLS) conducted by Malvern ZetaSizer Nano ZS90 at room temperature in quartz cuvette using chloroform as a dispersant. The excitation spectra and luminescence decay profiles were measured using the FLS1000 Fluorescence Spectrometer from Edinburgh Instruments equipped with 450 W Xenon lamp and μFlash lamp as an excitation sources and R5509-72 photomultiplier tube from Hamamatsu in nitrogen-flow cooled housing as a detector. To carry out the temperature measurement, the temperature of the sample was controlled using a THMS 600 heating–cooling stage from Linkam (0.1 °C temperature stability and 0.1 °C set point resolution). The emission spectra were measured using the 808 nm and 1060 nm excitation lines from laser diodes (LD) and a Silver-Nova Super Range TEC Spectrometer from Stellarnet (1 nm spectral resolution) as a detector.Results and discussion
Although there are two known polymorphs of the NaYF4 structure, i.e., crystallographic α-cubic and β-hexagonal phases, for single-band ratiometric thermometry applications, tetrafluorides crystallizing into a β-polymorph are more suitable. This is due to the fact that interionic interactions via cross-relaxation which have a beneficial impact on the intensity of ESA induced luminescence are at least an order of magnitude stronger in the hexagonal phase than in its cubic counterpart and that much more efficient luminescence is observed in the hexagonal phase,43,44 which is one of the crucial requirements of luminescence thermometry. In the crystallographic structure of β-phase of the NaYF4, an ordered arrangement of F− ions, which neighbor two cationic positions can be found. One of them is completely filled with Y3+ ions while the other has a mixed occupancy with Na+ and Y3+ ions (Fig. 1a). The NaYF4 host adopts the P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) symmetry group45 and the unit cell parameters in the hexagonal phase take the values a = b = 5.96 Å and c = 3.53 Å. X-Ray diffraction patterns of β-NaYF4:2%Nd3+ nanocrystals are presented in Fig. 1b. The diffraction reflections of synthesized materials correlate well with the reference pattern ICDS 04-011-3581, which confirms that the phase purity of samples was not affected by particles size. Nevertheless, one can see the broadening of the Bragg reflections relative to the standard pattern, which is due to the small size of the nanocrystallites.46–48
symmetry group45 and the unit cell parameters in the hexagonal phase take the values a = b = 5.96 Å and c = 3.53 Å. X-Ray diffraction patterns of β-NaYF4:2%Nd3+ nanocrystals are presented in Fig. 1b. The diffraction reflections of synthesized materials correlate well with the reference pattern ICDS 04-011-3581, which confirms that the phase purity of samples was not affected by particles size. Nevertheless, one can see the broadening of the Bragg reflections relative to the standard pattern, which is due to the small size of the nanocrystallites.46–48
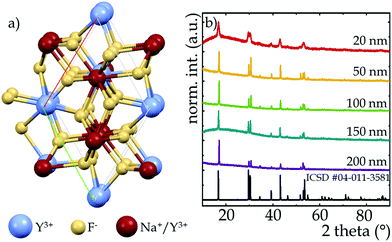 | ||
| Fig. 1 Visualization of Na+ and Y3+ sites in the hexagonal NaYF4 structure (a); X-ray diffraction patterns of NaYF4:2%Nd3+ nanocrystals with different sizes (b). | ||
The size modifications were made by changing the ratio of NH4F to RE3+ ions. As shown by Qiyue et al.,42 the concentration of F− can control the nucleation rate,49 so that the size of NaYF4 nanoparticles can be effectively controlled by changing the NH4F amount. For the stoichiometric F−/RE3+ ratio, tiny nanoparticle sizes on the order of 20 nm were obtained, however, by reducing the amount of NH4F from 4 mmoles (stoichiometric) to 2 mmoles, i.e., causing a shortage of F− ions relative to RE3+ ions, the size of the nanocrystals increased up to 200 nm. However, changes in nanocrystal size due to changes in F− ion concentration do not occur linearly but exponentially (see Fig. S1, ESI†). Size alterations induced by changes in the NH4F/RE3+ ratio were confirmed by TEM images (Fig. 2) and the corresponding hydrodynamic size distributions determined from DLS measurements (Fig. S2, ESI†). The morphological studies proved that the average sizes of the nanocrystals were 15, 60, 100, 150 and 200 nm for the NH4F/RE3+ ratios equal 4, 3, 2.5, 2.25, 2, respectively (Fig. 2). Furthermore, it showed that non-aggregated nanocrystals were obtained, however, the greater the F− ions deficiency, the wider the size distribution was recorded.
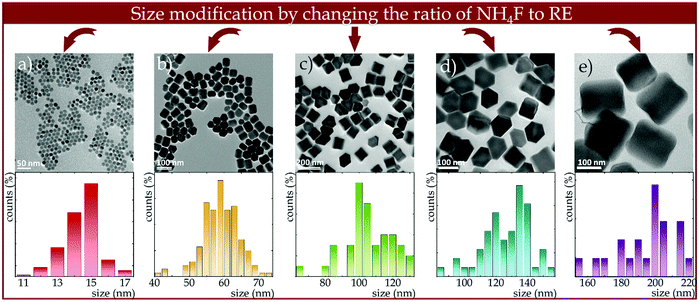 | ||
| Fig. 2 Effect of changing the NH4F to RE3+ ratio on NaYF4:2%Nd3+ nanocrystals size and morphology and corresponding size distributions determined from TEM images using Feret's method. | ||
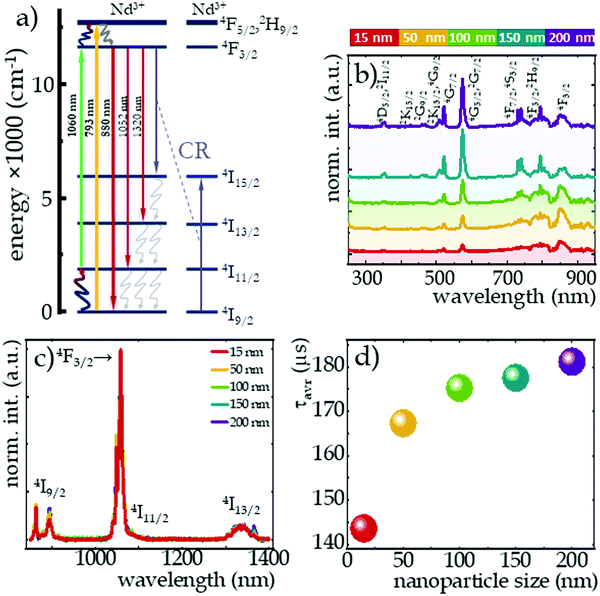
The spectroscopic properties of all the synthesized materials were investigated. As presented in the simplified energy level diagram of Nd3+ ions (Fig. 3a), two wavelengths were used to excite the NaYF4:2%Nd3+ nanocrystals. Both wavelengths were selected so that the excitation of the nanocrystals occurred in the near-infrared region. One of them is the GSA-matched 793 nm wavelength, which allows 4I9/2 → 4F5/2, 2H9/2 electron transfer traced by immediate nonradiative relaxation to the 4F3/2 level and the other is the ESA-matched 1060 nm wavelength, which results in electron transfer from the excited 4I11/2 state to the 4F3/2 level. Although in general probability of the absorption from the ground state exceeds ESA, with a sufficiently large filling of the 4I11/2 excited level, this second type of excitation can also occur. Several mechanisms may contribute to the population of this level, such as: (1) {4F3/2; 4I9/2} → {4I15/2; 4I15/2} cross-relaxation followed by a nonradiative transition to the 4I11/2 state (purplish and gray wavy arrows, respectively, in Fig. 3a); (2) as a result of 4F3/2 → 4I11/2 emission transitions, which are characterized by a nearly 60% branching ratio; or (3) by thermalization of the excited level with electrons from the ground state according to the Boltzmann distribution (navy blue-red wavy arrow). On the other hand, the 4I11/2 state may be also depopulated by the surface-related quenching processes. This is due to the small energy distance between the 4I11/2 and 4I9/2 levels, which is smaller than e.g. one vibrational mod of the OH− groups of water or COOH of the surface ligands. It is also worth noting that the increase of the particle size leads to the increase of the crystallinity of the particles. Surface-related nonradiative quenching caused by structural defects associated with the modified coordination of surface ions and by quenchers attached to the nanoparticle surface, is particularly highlighted in nanosized phosphors.41 An increase in the intensity of the excitation bands monitored at 1058 nm with growing size of the nanocrystals was noted (Fig. 3b). This is presumably due to an increase with nanocrystal size in the ratio of ions present in the volume relative to those located on the nanocrystal surface, so that surface-related quenching effects are attenuated. Furthermore, the ratio of the intensity of the excitation band at 350 nm (4I9/2 → 4D5/2, 2I11/2) to the band at 580 nm (4I9/2 → 4G5/2, 2G7/2) was observed to be size dependent (Fig. S3, ESI†). Its value increased with increasing nanocrystal size from 0.043 in 15 nm nanocrystals to 0.133 in 200 nm nanocrystals. It may indicate a change in the symmetry of the crystal field acting on Nd3+ ions. Although the largest absorption cross section is evident for the band at 580 nm associated with the 4I9/2 → 4G3/2, 2G7/2 transition, as mentioned above, the 793 nm wavelength associated with the 4I9/2 → 4F5/2, 2H9/2 transition was used to provide excitation in the NIR region. As can be seen in Fig. 3c, independently on the excitation wavelength used three main emission bands, associated with the radiative depopulation of the 4F3/2 state can be observed in the emission spectra at 880 nm (4F3/2 → 4F9/2), 1058 nm (4F3/2 → 4F11/2) and 1335 nm (4F3/2 → 4F13/2). In addition, the effect of size on the intensity of individual components of the emission band at 880 nm associated with electronic transitions from R1 and R2 of the Stark sublevels to the Stark Z1 sublevel of the 4I9/2 state was noted (Fig. S4a, ESI†). The intensity of the short-wavelength component decreases with size, which can be explained in terms of the self-filtering effect. When the size of the particle increases, the average optical path that the photons emitted by the Nd3+ ions must travel is longer, and thus the probability of its reabsorption is higher. An effect of nanocrystals size changes was also noted in subtle changes in the kinetics of the excited 4F3/2 level measured at 123 K (Fig. S5, ESI†). Due to the nonexponential behavior of the decay curves, the average decay times (according to eqn (S1) and Fig. S6, ESI†) were determined. As shown in Fig. 3d, with decreasing size of nanoparticles, a gentle reduction in decay times from τavr = 181 μs for 200 nm nanoparticles to 144 μs recorded in 15 nm NaYF4:2%Nd3+ was evident (see Table S1, ESI†). This may be a confirmation of the stronger surface-related luminescence quenching when the smaller the size of the structure analyzed.
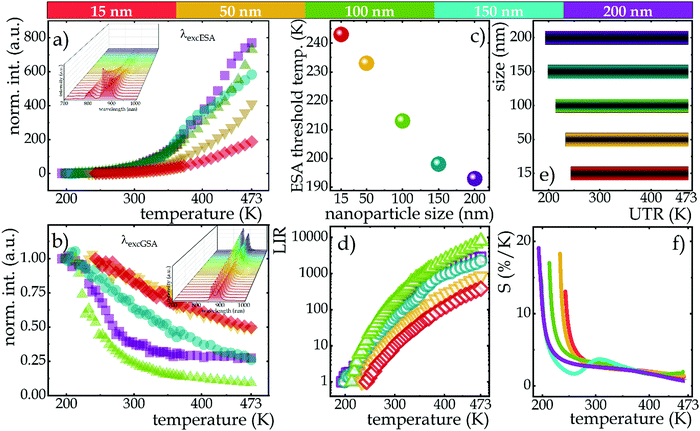
The influence of temperature on the emission intensity of Nd3+ ions and thermometric parameters of the SBR-based luminescence thermometer is shown in Fig. 4. The clearly opposite direction of thermally induced changes in luminescence intensity of 4F3/2 → 4I9/2 emission band at 862 nm upon excitation of ESA versus GSA has been evidenced (Fig. 4a and b for ESA and GSA, respectively). A qualitative comparison between nanocrystals of different sizes is provided by the integral emission intensities under ESA (Fig. 4a) and GSA (Fig. 4b) excitations. As expected, at low temperatures the occupancy of the 4I11/2 level was negligibly small and ESA-excited luminescence was not observed, however, beyond a certain threshold temperature the process occurred and an intense emission band was visible at high temperatures. The threshold temperature for which the process occurred shifted toward lower temperatures as the size of the nanocrystals increased (Fig. 4c). This is due to the fact that the smaller the nanocrystals, the stronger the surface-related quenching interactions that cause depopulation of the 4I11/2 state. In smaller sized nanocrystals, the number of ions on the surface may dominate over that in the bulk part, thus stronger surface-related quenching is noted. Consequently, the smaller the nanocrystals, the higher the thermal energy which competes with the depopulation processes must be delivered to the system to effectively populate the level from which the ESA process occurs. Regardless of size, the trend of change was similar for all nanocrystals, but the rate of change increased with the size. That is, at 473 K, a 200-fold increase in the intensity of ESA-excited luminescence relative to the initial intensity was seen in 20 nm nanocrystals, while a 4-fold enhancement of this effect, and thus an 800-fold increase in intensity relative to the initial, was recorded for 200 nm nanocrystals. Depending on the size, surface effects may have different impact on the nonradiative depopulation of the excited level, resulting in weaker intensities in the smaller nanocrystals. It is worth noting here that at high temperatures, two additional bands were visible in the emission spectrum at 800 nm (above 288 K) and 750 nm (above 400 K), which are due to the thermalization of the higher 4F5/2, 2H9/2 and 4F7/2, 4S3/2 levels and their radiative depopulation to the 4I9/2 level (inset on Fig. 4a). In the case of GSA-excited luminescence, the intensity of the same 4F3/2 → 4I9/2 band manifests a gradual decrease at elevated temperatures, however, no clear size trend of the changes was observed. The observed decrease in intensity is the result of multiphonon relaxation. However, in this case the energy difference between emitting 4F3/2 state and the next lower-laying 4I15/2 state, equals around 6000 cm−1, thus resulting in significantly lower efficiency of the nonradiative depopulation process related to the surface effects.
This opposite nature of the emission intensity variation with excitation wavelength is a great basis for developing a strongly temperature-dependent LIR parameter, according to the following formula:
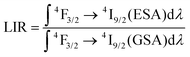 | (1) |
The ability of SBR-based luminescent thermometers can be quantified by the relative sensitivity to temperature changes. This is a standardized parameter, determined as follows:
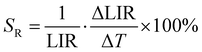 | (2) |
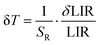 | (3) |
Conclusions
In this paper, the effect of size changes in nanometer-scale on the thermometric properties of single-band ratiometric luminescent thermometers based on NaYF4:2%Nd3+ nanocrystals was analyzed. Five sizes of NaYF4:2%Nd3+ nanoparticles in the range from 20 to 200 nm were analyzed. Thermometric studies were performed using two excitation wavelengths matching absorption from the ground state (λEXC = 793 nm) and from the excited state (λEXC = 1060 nm) in order to investigate the suitability of analyzed materials for single-band ratiometric luminescence thermometry. The emission intensity of the band at 880 nm associated with the 4F3/2 → 4I9/2 electronic transition upon the mentioned excitation wavelengths was used to determine the temperature remotely. Due to the divergent effects of two different physical processes, i.e. the thermal population of the excited 4I11/2 state and the nonradiative multiphonon quenching of the 4F3/2 level, two opposite trends were observed on the thermally induced intensity changes depending on the excitation wavelength. As a consequence of nonradiative multiphonon quenching, a decrease in the intensity of GSA-excited luminescence was observed, while the thermal population of the 4I11/2 state resulted in a strong and dynamic increase in the intensity of ESA-excited luminescence. The determined temperature-dependent LIR parameter showed very pronounced changes with increasing temperature and the trend was similar regardless of nanocrystals size, however, the rate of change already depended on it. The least pronounced increase in LIR value at 473 K relative to the initial value was observed in the smallest nanocrystals analyzed, which is due to the existence of a higher number of ions affected by the surface-related quenching of the 4I11/2 state population, which is due to the fact that the smaller the nanocrystals are, the higher the ratio of ions on the surface to those in the volume. Moreover, for smaller nanocrystals the threshold temperature for which the ESA process occurs is shifted towards higher temperatures. Consequently, the smaller the nanocrystals, the narrower the useful temperature range was observed. Furthermore, although the size of the nanocrystals affected the probability of ESA and the UTR, it does not critically affect the sensitivity values over a wide temperature range from 273 to 473 K. The high relative sensitivities are also reflected in terms of temperature resolutions that at temperatures above 273 K reach values of 0.1–0.2 K. Therefore, although a significant effect of crucially changing size at the nanoparticle–microparticle-ceramic scale has been previously demonstrated, no drastic changes in the values of thermometric parameters such as relative sensitivity or temperature resolution were observed for changes at the nanometer scale. Consequently, SBR-based luminescent thermometers can be successfully applied without fear that size reduction, e.g. due to possible ion release, could generate some falsification of results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by National Science Center Poland (NCN) under project no. UMO-2019/33/N/ST5/00011.References
- M. Dramicanin, Luminescence Thermometry: Methods, Materials and Applications, Woodhead Publishing, Elsevier, 2018 Search PubMed
.
- L. D. Carlos and F. Palacio, Thermometry at the Nanoscale, Nanoscience & Nanotechnology Series, The Royal Society of Chemistry, 2016 10.1039/9781782622031
.
- C. D. S. Brites, A. Millán and L. D. Carlos, Lanthanides in Luminescent Thermometry, Handbook on the Physics and Chemistry of Rare Earths, 2016, vol. 49, pp. 339–427 DOI:10.1016/bs.hpcre.2016.03.005
.
- M. D. Dramićanin, Trends in Luminescence Thermometry, J. Appl. Phys., 2020, 128(4), 40902, DOI:10.1063/5.0014825
.
- C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millán, V. S. Amaral, F. Palacio and L. D. Carlos, Thermometry at the Nanoscale, Nanoscale, 2012, 4(16), 4799, 10.1039/c2nr30663h
.
- D. Jaque and F. Vetrone, Luminescence Nanothermometry, Nanoscale, 2012, 4(15), 4301, 10.1039/c2nr30764b
.
- A. Bednarkiewicz, L. Marciniak, L. D. Carlos and D. Jaque, Standardizing Luminescence Nanothermometry for Biomedical Applications, Nanoscale, 2020, 12(27), 14405–14421, 10.1039/d0nr03568h
.
- J. Zhou, B. del Rosal, D. Jaque, S. Uchiyama and D. Jin, Advances and Challenges for Fluorescence Nanothermometry, Nat. Methods, 2020, 1, 967–980, DOI:10.1038/s41592-020-0957-y
.
- A. Bednarkiewicz, J. Drabik, K. Trejgis, D. Jaque, E. Ximendes and L. Marciniak, Luminescence Based Temperature Bio-Imaging: Status, Challenges, and Perspectives, Appl. Phys. Rev., 2021, 8(011317), 1–55, DOI:10.1063/5.0030295
.
- A. H. Khalid, K. Kontis and H. Z. Behtash, Phosphor Thermometry in Gas Turbines: Consideration Factors, Proc. Inst. Mech. Eng., Part G, 2010, 224(7), 745–755, DOI:10.1243/09544100JAERO560
.
- S. W. Allison and G. T. Gillies, Remote Thermometry with Thermographic Phosphors: Instrumentation and Applications, Rev. Sci. Instrum., 1997, 68(7), 2615–2650, DOI:10.1063/1.1148174
.
- O. Yarimaga, S. Lee, D. Y. Ham, J. M. Choi, S. G. Kwon, M. Im, S. Kim, J. M. Kim and Y. K. Choi, Thermofluorescent Conjugated Polymer Sensors for Nano- and Microscale Temperature Monitoring, Macromol. Chem. Phys., 2011, 212(12), 1211–1220, DOI:10.1002/macp.201100099
.
- S. Yakunin, B. M. Benin, Y. Shynkarenko, O. Nazarenko, M. I. Bodnarchuk, D. N. Dirin, C. Hofer, S. Cattaneo and M. V. Kovalenko, High-Resolution Remote Thermometry and Thermography Using Luminescent Low-Dimensional Tin-Halide Perovskites, Nat. Mater., 2019, 18(8), 846–852, DOI:10.1038/s41563-019-0416-2
.
- M. P. Melancon, M. Zhou and C. Li, Cancer Theranostics with Near-Infrared Light-Activatable Multimodal Nanoparticles, Acc. Chem. Res., 2011, 44(10), 947–956, DOI:10.1021/ar200022e
.
- H. D. A. Santos, E. C. Ximendes, M. Iglesias-de la Cruz, C. del, I. Chaves-Coira, B. del Rosal, C. Jacinto, L. Monge, I. Rubia-Rodríguez, D. Ortega, S. Mateos, J. GarcíaSolé, D. Jaque and N. Fernández, In Vivo Early Tumor Detection and Diagnosis by Infrared Luminescence Transient Nanothermometry, Adv. Funct. Mater., 2018, 28(43), 1803924, DOI:10.1002/adfm.201803924
.
- Y. Shen, H. D. A. Santos, E. C. Ximendes, J. Lifante, A. Sanz-Portilla, L. Monge, N. Fernández, I. Chaves-Coira, C. Jacinto, C. D. S. Brites, L. D. Carlos, A. Benayas, M. C. Iglesias-de la Cruz and D. Jaque, Ag2S Nanoheaters with Multiparameter Sensing for Reliable Thermal Feedback during In Vivo Tumor Therapy, Adv. Funct. Mater., 2020, 2002730, DOI:10.1002/adfm.202002730
.
- K. Prorok, M. Pawlyta, W. Strek and A. Bednarkiewicz, Energy Migration Up-Conversion of Tb3+ in Yb3+ and Nd3+ Codoped Active-Core/Active-Shell Colloidal Nanoparticles, ACS Chem. Mater., 2016, 28, 2295–2300, DOI:10.1021/acs.chemmater.6b00353
.
- M. Pedroni, P. Cortelletti, I. Xochilt, N. Pinna, P. Canton, M. Quintanilla, F. Vetrone and A. Speghini, Colloidal Nanothermometers Based on Neodymium Doped Alkaline-Earth Fluorides in the First and Second Biological Windows, Sens. Actuators, B, 2017, 250, 147–155, DOI:10.1016/j.snb.2017.04.160
.
- L. Marciniak, A. Bednarkiewicz, D. Kowalska and W. Strek, A New Generation of Highly Sensitive Luminescent Thermometers Operating in the Optical Window of Biological Tissues, J. Mater. Chem. C, 2016, 4(24), 5559–5563, 10.1039/C6TC01484D
.
- C. Matuszewska, K. Elzbieciak-Piecka and L. Marciniak, Transition Metal Ion-Based Nanocrystalline Luminescent Thermometry in SrTiO3:Ni2+,Er3+ Nanocrystals Operating in the Second Optical Window of Biological Tissues, J. Phys. Chem. C, 2019, 123(30), 18646–18653, DOI:10.1021/acs.jpcc.9b04002
.
- A. D. Lozano-gorrín, U. R. Rodríguez-mendoza, V. Venkatramu and V. Monteseguro, Lanthanide-Doped Y3Ga5O12 Garnets for Nanoheating and Nanothermometry in the First Biological Window, Opt. Mater., 2018, 84(March), 46–51, DOI:10.1016/j.optmat.2018.06.043
.
- A. M. Smith, M. C. Mancini and S. Nie, Second Window for in Vivo Imaging, NIH, 2010, 4(11), 710–711, DOI:10.1038/nnano.2009.326.Second
.
- A. Nexha, J. J. Carvajal, M. C. Pujol, F. Díaz and M. Aguiló, Lanthanide Doped Luminescence Nanothermometers in the Biological Windows: Strategies and Applications, Nanoscale, 2021, 13(17), 7913–7987, 10.1039/d0nr09150b
.
- E. Hemmer, A. Benayas, F. Légaré and F. Vetrone, Exploiting the Biological Windows: Current Perspectives on Fluorescent Bioprobes Emitting above 1000 Nm, Nanoscale Horiz., 2016, 168–184, 10.1039/c5nh00073d
.
- A. Zhang, Z. Sun, M. Jia, G. Liu, F. Lin and Z. Fu, Simultaneous Luminescence in I, II and III Biological Windows Realized by Using the Energy Transfer of Yb3+ → Er3 +/Ho3+ → Cr3+, Chem. Eng. J., 2019, 365, 400–404, DOI:10.1016/j.cej.2019.02.061
.
- C. Altavilla, Upconverting Nanomaterials Perspectives, Synthesis and Applications, 2017, ch. 6 Search PubMed
.
- K. Trejgis, A. Bednarkiewicz and Ł. Marciniak, Engineering Excited State Absorption Based Nanothermometry for Temperature Sensing and Imaging, Nanoscale, 2020, 12, 4667–4675, 10.1039/C9NR09740F
.
- K. Trejgis, K. Maciejewska, A. Bednarkiewicz and L. Marciniak, Near-Infrared-to-Near-Infrared Excited-State Absorption in LaPO4:Nd3+ Nanoparticles for Luminescent Nanothermometry, ACS Appl. Nano Mater., 2020, 3(5), 4818–4825, DOI:10.1021/acsanm.0c00853
.
- K. Trejgis, F. Tian, J. Li, A. Bednarkiewicz and L. Marciniak, The Role of Surface Related Quenching in the Single Band Ratiometric Approach Based on Excited State Absorption Processes in Nd3+ Doped Phosphors, Mater. Res. Bull., 2021, 139(February), 111288, DOI:10.1016/j.materresbull.2021.111288
.
- J. Drabik, R. Kowalski and L. Marciniak, Enhancement of the Sensitivity of Single Band Ratiometric Luminescent Nanothermometers Based on Tb3+ Ions through Activation of the Cross Relaxation Process, Sci. Rep., 2020, 10(1), 11190, DOI:10.1038/s41598-020-68145-5
.
- J. Drabik, R. Lisiecki and L. Marciniak, Optimization of the Thermometric Performance of Single Band Ratiometric Luminescent Thermometer Based on Tb3+ Luminescence by the Enhancement of Thermal Quenching of GSA-Excited Luminescence in TZPN Glass, J. Alloys Compd., 2021, 858(157690), 1–7, DOI:10.1016/j.jallcom.2020.157690
.
- J. Drabik, R. Kowalski and L. Marciniak, Enhancement of the Sensitivity of Single Band Ratiometric Luminescent Nanothermometers Based on Tb3+ Ions through Activation of the Cross Relaxation Process, Sci. Rep., 2020, 10(1), 11190, DOI:10.1038/s41598-020-68145-5
.
- J. Drabik and L. Marciniak, KLaP4O12:Tb3+ Nanocrystals for Luminescent Thermometry in a Single-Band-Ratiometric Approach, ACS Appl. Nano Mater., 2020, 3(4), 3798–3806, DOI:10.1021/acsanm.0c00485
.
- J. Drabik and L. Marciniak, Excited State Absorption for Ratiometric Thermal Imaging, ACS Appl. Mater. Interfaces, 2021, 13(1), 1261–1269, DOI:10.1021/acsami.0c18570
.
- M. Suta and A. Meijerink, A Theoretical Framework for Ratiometric Single Ion Luminescent Thermometers—Thermodynamic and Kinetic Guidelines for Optimized Performance, Adv. Theory Simul., 2020, 3(2000176), 1–32, DOI:10.1002/adts.202000176
.
- F. Auzel, Multiphonon Processes, Cross-Relaxation and UP-Conversion in Ion-Activated Solids, Exemplified By Minilaser Materials, in Radiationless Processes, ed. B. DiBartolo, Plenum Press, New York and London, 1980 DOI:10.1007/978-1-4613-3174-2
.
- B. P. Petreski, P. M. Farrell and S. F. Collins, Cross-Relaxation in Praseodymium-Doped Fluorozirconate Glass, 1996, vol. 132 Search PubMed
.
- J. Ganem, J. Crawford, P. Schmidt, N. W. Jenkins and S. R. Bowman, Thulium Cross-Relaxation in a Low Phonon Energy Crystalline Host, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(24), 1–15, DOI:10.1103/PhysRevB.66.245101
.
- D. Wawrzynczyk, A. Bednarkiewicz, M. Nyk, W. Strek and M. Samoc, Neodymium(III) Doped Fluoride Nanoparticles as Non-Contact Optical Temperature Sensors, Nanoscale, 2012, 4(22), 6959–6961, 10.1039/c2nr32203j
.
- L. Marciniak, A. Pilch, S. Arabasz, D. Jin and A. Bednarkiewicz, Heterogeneously Nd3+ Doped Single Nanoparticles for NIR-Induced Heat Conversion, Luminescence, and Thermometry, Nanoscale, 2017, 9(24), 8288–8297, 10.1039/c7nr02630g
.
- F. T. Rabouw, P. T. Prins, P. Villanueva-Delgado, M. Castelijns, R. G. Geitenbeek and A. Meijerink, Quenching Pathways in NaYF4:Er3+,Yb3+ Upconversion Nanocrystals, ACS Nano, 2018, 12(5), 4812–4823, DOI:10.1021/acsnano.8b01545
.
- D. Li, Q. Shao, Y. Dong and J. Jiang, Phase-, Shape- and Size-Controlled Synthesis of NaYF4:Yb3 +,Er3+ Nanoparticles Using Rare-Earth Acetate Precursors, J. Rare Earths, 2014, 32(11), 1032–1036, DOI:10.1016/S1002-0721(14)60179-4
.
- M. Banski, A. Podhorodecki and J. Misiewicz, NaYF4 Nanocrystals with TOPO Ligands: Synthesis-Dependent Structural and Luminescent Properties, Phys. Chem. Chem. Phys., 2013, 15(44), 19232–19241, 10.1039/c3cp52865k
.
- G. S. Yi and G. M. Chow, Synthesis of Hexagonal-Phase NaYF4:Yb,Er and NaYF4:Yb,Tm Nanocrystals with Efficient up-Conversion Fluorescence, Adv. Funct. Mater., 2006, 16(18), 2324–2329, DOI:10.1002/adfm.200600053
.
- M. Karbowiak, J. Cichos and C. Rudowicz, Spectroscopic Determination of Site Symmetry and Space Group in Lanthanide-Doped Crystals: Resolving Intricate Symmetry Aspects for β-NaLnF4, Polyhedron, 2016, 105, 42–48, DOI:10.1016/j.poly.2015.11.044
.
- P. Scardi, M. Ermrich, A. Fitch, E. Wen Huang, R. Jardin, R. Kuzel, A. Leineweber, A. Cuevas Mendoza, S. T. Misture, L. Rebuffi and C. Schimpf, Size-Strain Separation in Diffraction Line Profile Analysis, J. Appl. Crystallogr., 2018, 51, 831–843, DOI:10.1107/S1600576718005411
.
- J. I. Langford and A. J. C. Wilson, Scherrer after Sixty Years: A Survey and Some New Results in the Determination of Crystallite Size, J. Appl. Crystallogr., 1978, 11, 102–113 CrossRef CAS
.
- D. Balzar, N. Audebrand, M. R. Daymond, A. Fitch, A. Hewat, J. I. Langford, A. le Bail, D. Louer, O. Masson, C. N. McCowan, N. C. Popa, P. W. Stephens and B. H. Toby, Size – Strain Line-Broadening Analysis of the Ceria Round-Robin Sampl, J. Appl. Crystallogr., 2004, 37, 911–924, DOI:10.1107/S0021889804022551
.
- C. Liu, H. Wang, X. Li and D. Chen, Monodisperse, Size-Tunable and Highly Efficient β-NaYF 4:Yb,Er(Tm) up-Conversion Luminescent Nanospheres: Controllable Synthesis and Their Surface Modifications, J. Mater. Chem., 2009, 19(21), 3546–3553, 10.1039/b820254k
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc06069d |
| This journal is © The Royal Society of Chemistry 2022 |