Mechanical, thermal transport, electronic and photocatalytic properties of penta-PdPS, -PdPSe and -PdPTe monolayers explored by first-principles calculations

Abstract

In two of the latest experimental advances in the field of two-dimensional (2D) materials, penta-PdPS and -PdPSe layered materials have been fabricated. Inspired by these accomplishments, herein first-principles calculations are employed to explore the direction-dependent key physical properties of the PdPX (X = S, Se, Te) monolayers. Our results indicate that the PdPS, PdPSe, and PdPTe monolayers are indirect semiconductors, with HSE06 band gaps of 2.13, 1.89, and 1.37 eV, respectively. Optical calculations reveal that the first absorption peaks of these novel monolayers along the in-plane polarizations are located in the visible range of light. Moreover, it is predicted that the PdPSe monolayer yields suitable valence and conduction band edge positions for visible-light-driven water splitting reactions. Our results confirm the decline of elastic modulus, tensile strength, phonons’ group velocity, and lattice thermal conductivity with the increase of the atomic weight of chalcogen atoms in PdPX nanosheets. It is furthermore shown that these novel 2D systems exhibit anisotropic mechanical, optical, and heat conduction properties. The obtained first-principles results provide a comprehensive vision about the critical physical properties of the PdPX (X = S, Se, Te) nanosheets and highlight their prospect for nanoelectronics, optoelectronics, and energy conversion applications.

---

1. Introduction

In the ongoing process of prediction and experimental realization of 2D semiconductors beyond the gapless semimetallic graphene,^1–3 most recently Li et al.⁴ succeeded in the fabrication of low-symmetry and puckered pentagonal phosphochalcogenide (penta-PdPSe) layered structures. They employed a combined high-temperature solid-state reaction and mechanical exfoliation technique to fabricate penta-PdPSe. They found that this novel 2D system exhibits a moderate electron mobility and angle-dependent electronic and optoelectronic properties. This experimental advance is expected to also facilitate the synthesis of PdPS and PdPTe nanosheets. In fact, most recently, Wang et al.⁵ fabricated penta-PdPS structures with highly appealing optical properties. In this work, our goal is to examine the stability of the PdPS, PdPSe, and PdPTe monolayers with the pentagonal lattice and explore their intrinsic physical properties. For this purpose, density functional theory (DFT) calculations are employed to examine the dynamical stability and mechanical, electronic, optical, and phononic thermal conduction properties of the PdPS, PdPSe, and PdPTe monolayers. The lattice thermal conductivity is examined by the full-iterative solutions of the Boltzmann transport equation, accelerated by machine learning interatomic potentials. The transport properties are particularly investigated along the two different in-plane directions in order to examine the anisotropicity in the transport properties. The obtained first-principles results provide a comprehensive vision on stability and angle-dependent physical properties of PdPS, PdPSe, and PdPTe nanosheets and highlight their prospect to design next-generation angle-dependent optoelectronic and energy conversion nanodevices.

2. Computational methods

First-principles density functional theory (DFT) calculations are performed by employing the Vienna Ab initio Simulation Package.^6,7 The generalized gradient approximation (GGA) is employed with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional. The plane wave and self-consistent loop cutoff energies are defined as 400 and 10⁻⁶ eV, respectively. To obtain the geometry optimized and stress-free structures, atomic positions and lattice sizes are altered using conjugate gradient algorithm until Hellman–Feynman forces drop below 0.002 eV Å⁻¹⁸ with 15 × 15 × 1 Monkhorst–Pack⁹K-point grid. Periodic boundary conditions are considered in all directions with around 16 Å vacuum distance in order to avoid interactions with systems’ images along with the nanosheets’ thickness. The electronic band structures are analyzed by employing PBE/GGA and HSE06 hybrid¹⁰ functional. A dense k-point grid of 12 × 12 × 1 Γ-centered Monkhorst–Pack is set to evaluate electronic properties. In the evaluation of optical properties with random phase approximation approach and HSE06 functional, a denser k-point mesh size of 24 × 24 × 1 is adjusted. For more details about calculations of optical properties refer to the ESI† document.

Density functional perturbation theory (DFPT) calculations are conducted using the VASP package over 3 × 3 × 1 supercells to acquire phonon dispersions and harmonic force constants utilizing the PHONOPY code.¹¹ Moment tensor potentials (MTPs)¹² are trained as an accurate class of machine learning interatomic potentials to interpolate the interatomic forces,¹³ utilizing the MLIP package.¹⁴ The datasets for the MTPs training are acquired by conducting ab initio molecular dynamics (AIMD) simulations with a time step of 1 fs over supercells consisting of 48 atoms using a 2 × 2 × 1 a Monkhorst–Pack K-point grid. For evaluating the 2nd and 3rd order interatomic force constants, two AIMD calculations are conducted within the NVT ensemble, first, from 10 to 100 K and second, from 100 to 1000 K, each for 1000 time steps. For the efficient training of the MTPs, original AIMD trajectories are with equal steps subsampled and around 660 configurations are selected to train MTPs. Phonon dispersions on the basis of trained MTPs are obtained using the PHONOPY code, as elaborately discussed in our previous work.¹³ Anharmonic 3rd order interatomic force constants are obtained over the same supercells as those employed for harmonic force constant calculations by considering the interactions with eights nearest neighbors. This is equivalent with single-step force calculations over 1152 structures with 192 atoms for a single-layer penta-PdPX lattice, which can be obtained within a negligible time with the MTP-based method and is otherwise computationally extensively demanding with the standard DFT method. The ShengBTE¹⁵ package is employed to conduct the full iterative solution of the Boltzmann transport equation (BTE) with force constant inputs, as discussed in our previous study.¹⁶ In these calculations, isotope scattering is considered to predict the phononic thermal conductivity of naturally occurring samples.

3. Results and discussions

We first study the structural properties and bonding mechanism of the PdPS, PdPSe, and PdPTe monolayers. As the representative structure, in Fig. 1 the geometry-optimized lattice of the PdPSe monolayer along with isosurface and section maps of electron localization function (ELF)¹⁷ are illustrated. These 2D systems exhibit orthorhombic configurations in which each Pd atom is in a square-planar coordination, surrounded by two chalcogen and two phosphorus atoms and forming a pentagonal structure over the surface. In order to investigate the anisotropicity in the transport response of the PdPX monolayers, two different directions of x and y are considered as distinguished in Fig. 1. The lattice constants of stress-free PdPS, PdPSe and the PdPTe monolayers along the x (y) directions are predicted to be 5.69 (5.72), 5.84 (5.90) and 6.07(6.17) Å, respectively, which reveals that despite different bonding configurations, they show close lattice values along the two different planar directions. The stress-free PdPX lattices are included in the ESI† document. As expected, with the increase in the atomic weight of chalcogen atoms in these systems, the lattice constants slightly increase. As the representative lattice which exhibits the general features of these 2D systems, in the side views of Fig. 1 the ELF isosurface corresponding to the value of 0.7 and the ELF section in the P–P–Se plane of the PdPSe monolayer are also plotted. ELF is a spatial function between 0 to 1, and the ELF values close to unity reveal strong covalent interaction or lone pair electrons, whereas lower ELF values represent weaker ionic, metallic, or van der Waals interactions. From the Fig. 1 ELF results the existence of lone pairs is visible around chalcogen atoms. Generally, high electron localization is clear around P and the chalcogen atoms, whereas Pd atoms are almost free of electron localization. From the section and isosurface results, it is clear that ELF values around the center of X–P and P–P bonds are larger than 0.7, indicating the formation of covalent bonding. Because of the higher electronegativity of S and Se atoms than Pd and P, they tend to attract electrons from their neighboring atoms, and according to our Bader¹⁸ charge analysis, they gain around 0.51 and 0.23 e in the PdPS and PdPSe monolayers, respectively. In contrast, in the PdPTe lattice, Te atoms, due to their slightly lower electronegativity than Pd and P, are found to transfer around 0.17 e according to Bader charge analysis.

Fig. 1 Top and side views of the PdPSe monolayer along with the electron localization function (ELF) presented in the side views. ELF isosurface value is set to 0.7.

After investigating the structural properties of the PdPX (X = S, Se, Te) monolayers, we next study their mechanical response. In Fig. 2, the uniaxial true stress–strain responses of the PdPX monolayers along the x and y directions are compared. The predicted stress–strain relations are uniaxial and such that during the deformation, the structure is under stress only along the loading direction and is stress-free along the two other perpendicular directions of the loading. Since nanosheets can freely move along their thickness direction, upon the geometry minimization, the system's stress component normal to the sheet naturally reaches a negligible value. Therefore in the conducted DFT simulations, the simulation cell size along the other in-plane perpendicular direction of the loading (either x or y) is adjusted to satisfy the negligible stress condition after the geometry minimization. It should also be noted that the stress values are calculated at every strain by considering the real volume of the deformed monolayers. In this regard, the area of the monolayers can be easily obtained using the periodic simulation cell sizes along the planar direction. To calculate the area, the effective thickness at every step is calculated as the normal distance between boundary chalcogen atoms plus their effective van der Waals diameter (vdW). For example, the thickness of the PdPS and PdPSe monolayers according to experimental measurements are 6.65¹⁹ and 6.9⁴ Å, respectively. According to the obtained geometry optimized lattices, the normal distances between X–X atoms in the aforementioned systems are 4.19 and 4.41 Å, respectively, which are equivalent with effective vdW diameters of 2.46 and 2.49 Å, for S and Se atoms in these systems, respectively, to satisfy the corresponding monolayers’ thickness. In a consistent way, a thickness of 7.3 Å is estimated for the stress-free PdPTe monolayer. According to DFT-based stress–strain relations, the elastic modulus of the PdPS, PdPSe, and PdPTe monolayers along the y (x) directions are predicted to be 262 (205), 218 (152), and 181(115) GPa, respectively. Moreover, the Poisson's ratio values of the PdPS, PdPSe, and PdPTe monolayers for the loading along the y (x) directions are found to be 0.14 (0.18), 0.13 (0.19), and 0.12(0.19), respectively. It is thus revealed that during the deformation, these systems tend to contract more along the width for the uniaxial loading along the x direction than the y direction. The ultimate tensile strength of the PdPS, PdPSe, and the PdPTe monolayers along the y (x) directions are predicted to be 22.0(16.7), 19.6 (14.7), and 15.7 (12.8) GPa, respectively. These results reveal that these nanosheets are remarkably stronger along the y direction than the x direction, and they thus show anisotropic mechanical characteristics. Moreover, these results also confirm a clear decline of the elastic modulus and tensile strength in PdPX nanosheets with the increase in the atomic weight of chalcogen atoms. To better understand the anisotropic mechanical response of these nanosheets, in Fig. 2 the deformed PdPS monolayer at strain levels after the tensile strength points are plotted for the both considered loading directions. It appears that for the loading along the x direction, the failure occurs along the Pd–S bond, those constructing the over surface pentagonal atomic configurations. In fact, for the loading along this direction, only the Pd–S bonds are oriented along the loading direction and yield dominant contribution to the load bearing. In contrast, for the loading along the y direction, both the Pd–S and P–S bonds are oriented along the loading and engage in the load transfer, resulting in a higher strength. It can be seen that the Pd–X bonds play a dominant role in the tensile strength and rigidity of these nanosheets. In addition, the anisotropic mechanical responses can be attributed to the pentagonal atomic arrangement that results in more bonds engagements in the load carrying along the y direction than the other planar counterpart.

Fig. 2 (a–c) True uniaxial stress–strain relations of the PdPX (X = S, Se, Te) monolayers elongated along the y and x directions. (e and f) Present the stress-free and deformed PdPS monolayers at strain level of 0.2 for the loading along the x and y directions, respectively.

We next study the electronic properties of the PdPX (X = S, Se, Te) monolayers. To probe the electronic properties of the free-standing PdPS, PdPSe, and PdPTe monolayers, the band structures and the projected density of states (PDOS) of these systems are calculated within HSE06 approach, as illustrated in Fig. 3. The obtained electronic band structure for the PdPS monolayer reveals a semiconducting behavior and the indirect band gap of 2.13 eV, in which both the valence band maximum (VBM) and conduction band minimum (CBM) lie between the C and Y points. The indirect band gap is predicted to be 1.89 and 1.37 eV for the PdPSe and PdPTe monolayers, respectively, with the VBM appearing along the C–Y wave vector while the CBM locates along Y–Γ. Our estimated band gap of the PdPSe monolayer is in a good agreement with results in the original experimental study by Li et al.⁴ The calculation of the PDOS indicates that the d orbital from Pd yields the main contribution to form the CBM and VBM of all PdPX monolayers, with a weak hybridization of X p states resulting in the Mott insulator. In order to uncover the capabilities of these novel monolayers for photocatalytic water splitting, the valence band (VB) and conduction band (CB) edge positions of these systems have been calculated using HSE06 and shown in Fig. 4. It can be seen that the VB and CB edge positions generally shift to lower potential energy with the increase in the atomic number of the S, Se, and Te elements. These results show that the PdPSe monolayer possesses suitable band edge positions that correctly bracket the water redox potentials for visible-light-driven overall water splitting reactions. In contrast, the PdPS monolayer is predicted to be a good candidate only for the water oxidation and O₂ evolution, and the PdPTe nanosheet can be used only for the hydrogen evolution. These findings however do not guarantee the effectiveness of these novel 2D systems for the efficient photocatalytic water splitting, but may hopefully guide further studies to more elaborately examine this aspect.

Fig. 3 Band structure and partial electronic density of states PDOS of (a) PdPS, (b) PdPSe, and (c) PdPTe monolayers. The dashed black lines indicate the Fermi energy.

Fig. 4 Calculated conduction (green color) and valence band (purple color) edge positions for PdPS, PdPSe, and PdPTe monolayers with respect to vacuum level. The dashed black lines indicate the water stability limits for hydrogen and oxygen evolution. The absolute potential of the standard hydrogen electrode was taken as 4.44 eV at a pH = 0.

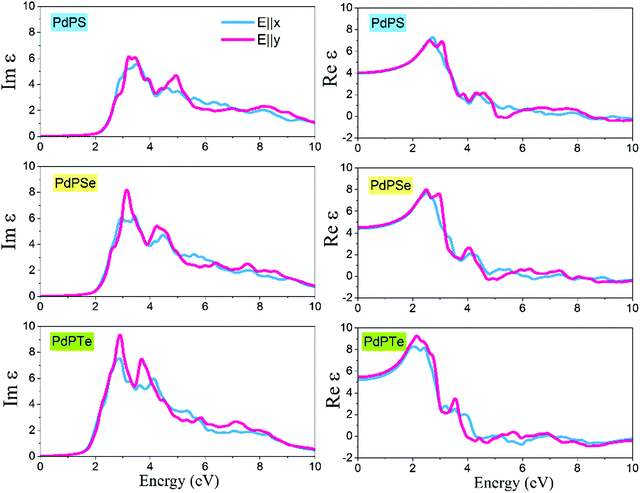
We next discuss the optical response of the PdPS, PdPSe, and PdPTe monolayers using the RPA method constructed over HSE06 results. Because of the asymmetric geometry along the x- and y-axes, the optical spectra of these structures are also found to be anisotropic for light polarization along the in-plane directions. Hence, the optical properties for both the x- and y-polarized direction (E||x and E||y) are reported. The optical properties of these 2D materials along the light polarization perpendicular to the plane are ignored because of the huge depolarization effect.²⁰ The imaginary and real parts of the dielectric function (Im ε and Re ε) of these 2D monolayers for the in-plane polarized directions versus photon energy are calculated, and the obtained results are illustrated in Fig. 5. The absorption edges of Im ε occur at the energy of ∼2.0, 1.80, and 1.40 eV along the in-plane direction for the PdPS, PdPSe, and PdPTe monolayer sheets, respectively, which are in the visible range. The values of the static dielectric constant (the values of Re ε at zero energy) for the novel PdPS, PdPSe, and PdPTe monolayers were measured to be ∼4.1, 4.6, and 5.5 along E||x and 4.0, 4.4, and 5.2 along E||y, respectively. These results indicate that by decreasing the electronic band gap in these 2D structures, the static dielectric constant increases.

Fig. 5 Imaginary and real parts of the dielectric function as a function of photon energy for the PdPS, PdPSe, and PdPTe monolayers predicted using the RPA + HSE06 approach to the in-plane (x- and y-polarized) incident light.

The absorption coefficient α for these novel 2D systems along in-plane polarization as a function of photon energy and wavelength is plotted in Fig. 6. The absorption edge of α for the PdPS monolayer occurs at a wavelength of ∼550 nm along the x- and y-axes, while the corresponding absorption edge for the PdPSe and PdPTe monolayers shifts to the longer wavelengths (red shift), occurring at wavelength of 600 and 700 nm, respectively. In general, contrary to the indirect band gap nature of the studied novel 2D materials, the high absorption coefficients in the visible range of light are attained (∼10⁵ cm⁻¹) for the PdPX monolayers, which are higher than the typical absorption coefficient value for direct-gap semiconductors²¹ and comparable to those of organic perovskite solar cells.^22,23 These results indicate that the PdPX monolayers possess significant light-harvesting capabilities for the solar spectrum in the UV-visible range (300–700 nm) of light. Moreover, the results of anisotropic optical properties along the in-plane directions suggest that they exhibit attractive prospects for the design of novel electronic and optical nanodevices that exploit their anisotropic properties, such as polarization-sensitive photodetectors.

Fig. 6 Optical absorption spectra as a function of (a) energy (b) and wavelength in the UV-visible range (300–700 nm) of light for the PdPS, PdPSe, and PdPTe monolayers to the in-plane (x- and y-polarized) incident light.

We finally explore the phononic properties of the PdPS, PdPSe, and PdPTe monolayers. In this regard, firstly the phonon dispersion relations of the PdPX monolayers obtained by DFPT and MTP-based methods along highly symmetrical points of the first Brillouin zone are investigated, as compared in Fig. 7. All the considered lattices show three acoustic modes starting from the Γ point, consistent with other 2D structures. Near the Γ point, the out-of-plane acoustic modes (ZA) show quadratic relation for all the three considered monolayers, whereas the remaining two acoustic modes show linear dispersions.²⁴ Predicted phonon dispersions by both methods reveal that acoustic and optical modes are free of imaginary frequencies, which confirm the dynamical stability of the PdPS, PdPSe, and PdPTe monolayers. Moreover, the comparison between DFPT and MTP-based results confirm the remarkable accuracy of the developed classical models in reproducing the phonon dispersion relations. As it is noticeable, the MTP model yields an excellent accuracy in describing the acoustic modes, which are usually the main heat carriers in semiconductors. Similarly to the conducted analysis of mechanical and electronic properties, it is visible that the general features of phonon dispersion relations in these 2D systems are also very identical. As a useful preliminary finding, it nonetheless appears that with the increase in the weight of chalcogen atoms, dispersion of phonon modes in the entire frequency range shrink, which is also conspicuous for the case of ZA acoustic mode. As it is clear, two and three rather large gaps appear in the phonon dispersions of the PdPSe and PdPTe monolayers, respectively. The narrower dispersions of phonon bands suggest the suppression of their group velocity, which generally can lead to a lower thermal conductivity.

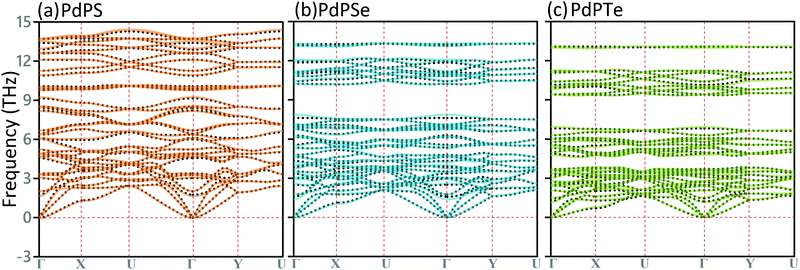Fig. 7 Phonon dispersion relations of the PdPS, PdPSe, and PdPTe monolayers predicted by the DFPT and MTP methods, respectively, illustrated by continuous and dotted lines.

We now study the predicted lattice thermal conductivity of the PdPS, PdPSe, and PdPTe monolayers along the two planar directions as a function of temperature, as illustrated in Fig. 8. In these results, the thickness of the PdPS, PdPSe, and PdPTe monolayers are assumed to be 6.65,¹⁹ 6.9⁴ and 7.3 Å, respectively. The phononic thermal conductivity of the PdPS, PdPSe, and PdPTe monolayers with taking into account the isotope scattering at 300 K along the y (x) directions, are predicted to be 72 (60), 65(44), and 33 (23) W mK⁻¹, respectively. As expected, with the increase in the weight of chalcogen atoms, the lattice thermal conductivity decreases, which is also consistent with the classical theory that materials with a lower elastic modulus show a lower thermal conductivity. Normally the lattice thermal conductivity follows a ∼T^−λ trend with temperature (T), in which λ is the temperature power factor and usually takes a value close to unity. The temperature power factors of 1.05, 1.03, and 1.01 are predicted for the PdPS, PdPSe, and PdPTe monolayers, respectively, which are close to 1 and reveal that the phonon–phonon interactions in these systems follow the same trend of conventional materials. The corresponding power factor for graphene, MoS₂, F-diamane and CrC₂N₄ monolayers has been predicted to be 1.32,²⁵ 1.02,²⁶ 1.16²⁷ and 1.35,²⁵ respectively. For the PdPS, PdPSe, and PdPTe monolayers at 300 K, it is found that acoustic modes count for 86(88), 86(89), and 82(87)% of the overall thermal conductivity along the x (y) directions, respectively. This is an expectable finding because these modes generally show wider dispersions and lower intersection with other bands, and consequently showing higher group velocities and lifetimes, respectively, both resulting in facilitated thermal transport. In accordance with our results for mechanical properties, these lattices also show anisotropic thermal transport. As discussed earlier and from the basic structural understanding of these lattices, along the y direction more bonds are oriented along the load and heat transfer. From the phonon dispersions, it is also clear that acoustic mode shows wider dispersion and consequently higher group velocity along the y direction (Γ–Y path) than along the x direction (Γ–X path).

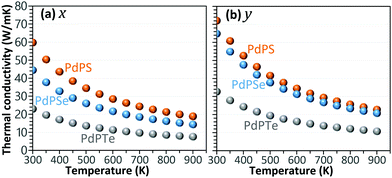Fig. 8 Predicted lattice thermal conductivity of the PdPS, PdPSe, and PdPTe monolayers as a function of temperature along the (a) x and (b) y directions.

In Fig. 9 the phonons’ group velocity and lifetime of the PdPS, PdPSe, and PdPTe monolayers are compared. As expected and shown in Fig. 9a, with the increase in the weight of chalcogen because of the induced narrower dispersions of phonon modes and lower elasticity of the PdPX monolayers, the phonons’ group velocities are also suppressed. The maximum phonon group velocity in the PdPS, PdPSe, and PdPTe monolayers are predicted to be 6.91, 5.84, and 5.17 km s⁻¹, respectively, which are by around three-folds lower than that of the graphene. For the phonons’ lifetime illustrated in Fig. 9b, however, the suppressing effect of chalcogen atoms is found to be much weaker than those for the group velocity. As it is clear, while the scattering rates for phonons are relatively close for different systems, the corresponding group velocities decrease noticeably with the increase in the weight of chalcogen atoms, resulting in a lower thermal conductivity. Our results reveal that the PdPX monolayers show moderate lattice thermal conductivity values, which suggests that with the application of these semiconductors in nanoelectronics, the thermal management issues can be facilitated. The PdPTe nanosheet at high temperatures nonetheless shows a rather low thermal conductivity, which along with its semiconducting nature might be useful for thermoelectric applications, which requires a further investigation.

Fig. 9 (a) phonons’ group velocity and (b) lifetime of PdPS, PdPSe, and PdPTe monolayers.

4. Concluding remarks

Motivated by the latest reports concerning the synthesis of 2D penta-PdPS⁵ and penta-PdPSe,⁴ herein extensive first-principles investigations are conducted to explore the physical properties of the PdPX (X = S, Se, Te) monolayers. It is shown that the considered monolayers are dynamically and mechanically stable. Moreover, it is found that the PdPS, PdPSe, and PdPTe monolayers are indirect semiconductors with band gaps of 2.13, 1.89, and 1.37 eV, respectively, according to the HSE06 calculations. The evaluation of the VB and CB edge positions confirms that these 2D structures possess suitable band edge positions for photocatalytic water splitting reactions. The linear photon energy-dependent dielectric functions of the considered materials are investigated using the RPA + HSE06 approach. The optical analysis indicates that the optical spectra for these materials are anisotropic to the in-plane incident light. It is also found that the first absorption peaks of single-layer PdPX along the in-plane polarizations are located in the visible range of light. These results show that these novel 2D materials can be promising for angle-dependent optoelectronic devices such as polarization-sensitive photodetectors and photocatalytic applications. The obtained results clearly confirm the decrease of elastic modulus, tensile strength, phonons’ group velocity, and lattice thermal conductivity with the increase in the atomic weight of chalcogen atoms in the PdPX nanosheets. The underlying mechanisms resulting in the anisotropic mechanical and heat conduction properties of these nanosheets are also investigated. Acquired results reveal that PdPX nanosheet generally show moderate thermal conductivities. The obtained results provide an extensive vision concerning the critical direct-dependent physical properties of PdPX (X = S, Se, Te) semiconductors, confirm their good mechanical and heat transport properties and highlight their application prospect in optoelectronics and energy conversion systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

B. M. and X. Z. appreciate the funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy within the Cluster of Excellence PhoenixD (EXC 2122, Project ID 390833453). B. M. and T. R. are thankful to the VEGAS cluster at Bauhaus University of Weimar for providing the computational resources. B. M. also thanks Dr Chernenko for the support of this study. A. V. S. is supported by the Russian Science Foundation (Grant No 18-13-00479, https://rscf.ru/project/18-13-00479/).

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric field effect in atomically thin carbon films., Science, 2004, 306, 666–669,  DOI:10.1126/science.1102896.
2. A. K. Geim and K. S. Novoselov, The rise of graphene, Nat. Mater., 2007, 6, 183–191,  DOI:10.1038/nmat1849.
3. A. H. Castro Neto, N. M. R. Peres, K. S. Novoselov, A. K. Geim and F. Guinea, The electronic properties of graphene, Rev. Mod. Phys., 2009, 81, 109–162,  DOI:10.1103/RevModPhys.81.109.
4. P. Li, J. Zhang, C. Zhu, W. Shen, C. Hu, W. Fu, L. Yan, L. Zhou, L. Zheng, H. Lei, Z. Liu, W. Zhao, P. Gao, P. Yu and G. Yang, Penta-PdPSe: A New 2D Pentagonal Material with Highly In-Plane Optical, Electronic, and Optoelectronic Anisotropy, Adv. Mater., 2021, 33, 2102541,  DOI:10.1002/adma.202102541.
5. X. Wang, T. Xiong, K. Zhao, Z. Zhou, K. Xin, H.-X. Deng, J. Kang, J. Yang, Y.-Y. Liu and Z. Wei, Polarimetric Image Sensor and Fermi Level Shifting Induced Multi-Channel Transition Based on Two-dimensional PdPS, Adv. Mater., 2021, 2107206,  DOI:10.1002/adma.202107206.
6. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186,  DOI:10.1103/PhysRevB.54.11169.
7. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
8. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561,  DOI:10.1103/PhysRevB.47.558.
9. H. Monkhorst and J. Pack, Special points for Brillouin zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192,  DOI:10.1103/PhysRevB.13.5188.
10. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125, 224106,  DOI:10.1063/1.2404663.
11. A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5,  DOI:10.1016/j.scriptamat.2015.07.021.
12. A. V. Shapeev, Moment tensor potentials: A class of systematically improvable interatomic potentials, Multiscale Model. Simul., 2016, 14, 1153–1173,  DOI:10.1137/15M1054183.
13. B. Mortazavi, I. S. Novikov, E. V. Podryabinkin, S. Roche, T. Rabczuk, A. V. Shapeev and X. Zhuang, Exploring phononic properties of two-dimensional materials using machine learning interatomic potentials, Appl, Mater. Today, 2020, 20, 100685,  DOI:10.1016/j.apmt.2020.100685.
14. A. S. Ivan Novikov and K. Gubaev, Evgeny Podryabinkin, The MLIP package: Moment Tensor Potentials with MPI and Active Learning, Mach. Learn, Sci. Technol., 2021, 2, 025002,  DOI:10.1088/2632-2153/abc9fe.
15. W. Li, J. Carrete, N. A. Katcho and N. Mingo, ShengBTE: A solver of the Boltzmann transport equation for phonons, Comput. Phys. Commun., 2014, 185, 1747–1758,  DOI:10.1016/j.cpc.2014.02.015.
16. B. Mortazavi, E. V. Podryabinkin, I. S. Novikov, T. Rabczuk, X. Zhuang and A. V. Shapeev, Accelerating first-principles estimation of thermal conductivity by machine-learning interatomic potentials: A MTP/ShengBTE solution, Comput. Phys. Commun., 2021, 258, 107583,  DOI:10.1016/j.cpc.2020.107583.
17. B. Silvi and A. Savin, Classification of Chemical-Bonds Based on Topological Analysis of Electron Localization Functions, Nature, 1994, 371, 683–686,  DOI:10.1038/371683a0.
18. G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360,  DOI:10.1016/j.commatsci.2005.04.010.
19. T. A. Bither, P. C. Donohue and H. S. Young, Palladium and platinum phosphochalcogenides—Synthesis and properties, J. Solid State Chem., 1971, 3, 300–307,  DOI:10.1016/0022-4596(71)90043-0.
20. M. Shahrokhi, Quasi-particle energies and optical excitations of ZnS monolayer honeycomb structure, Appl. Surf. Sci., 2016, 390, 377–384,  DOI:10.1016/j.apsusc.2016.08.055.
21. M. Shahrokhi, P. Raybaud and T. Le Bahers, On the understanding of the optoelectronic properties of S-doped MoO₃ and O-doped MoS₂ bulk systems: a DFT perspective, J. Mater. Chem. C, 2020, 8, 9064–9074,  10.1039/D0TC02066D.
22. N. J. Jeon, J. H. Noh, Y. C. Kim, W. S. Yang, S. Ryu and S. Il Seok, Solvent engineering for high-performance inorganic–organic hybrid perovskite solar cells, Nat. Mater., 2014, 13, 897–903,  DOI:10.1038/nmat4014.
23. M. Shirayama, H. Kadowaki, T. Miyadera, T. Sugita, M. Tamakoshi, M. Kato, T. Fujiseki, D. Murata, S. Hara, T. N. Murakami, S. Fujimoto, M. Chikamatsu and H. Fujiwara, Optical Transitions in Hybrid Perovskite Solar Cells: Ellipsometry, Density Functional Theory, and Quantum Efficiency Analyses for ${\mathrm{CH}}_{3}{\mathrm{NH}}_{3}{\mathrm{PbI}}_{3}$, Phys. Rev. Appl., 2016, 5, 14012,  DOI:10.1103/PhysRevApplied.5.014012.
24. H. Chang, H. Wang, K.-K. Song, M. Zhong, L.-B. Shi and P. Qian, Origin of phonon-limited mobility in two-dimensional metal dichalcogenides, J. Phys.: Condens. Matter, 2022, 34, 13003,  DOI:10.1088/1361-648x/ac29e1.
25. L. Lindsay, W. Li, J. Carrete, N. Mingo, D. A. Broido and T. L. Reinecke, Phonon thermal transport in strained and unstrained graphene from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 155426,  DOI:10.1103/PhysRevB.89.155426.
26. B. Peng, Z. Ning, H. Zhang, H. Shao, Y. Xu, G. Ni and H. Zhu, Beyond Perturbation: Role of Vacancy-Induced Localized Phonon States in Thermal Transport of Monolayer MoS₂, J. Phys. Chem. C, 2016, 120, 29324–29331,  DOI:10.1021/acs.jpcc.6b10812.
27. M. Raeisi, B. Mortazavi, E. V. Podryabinkin, F. Shojaei, X. Zhuang and A. V. Shapeev, High thermal conductivity in semiconducting Janus and non-Janus diamanes, Carbon, 2020, 167, 51–61,  DOI:10.1016/j.carbon.2020.06.007.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc05297g

---