 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the effect of lattice polarisability on the electrochemical properties of lithium tetrahaloaluminates, LiAlX4 (X = Cl, Br, I)†
Nicolás
Flores-González
 a,
Martí
López
a,
Martí
López
 b,
Nicolò
Minafra
c,
Jan
Bohnenberger
e,
Francesc
Viñes
b,
Nicolò
Minafra
c,
Jan
Bohnenberger
e,
Francesc
Viñes
 b,
Svemir
Rudić
b,
Svemir
Rudić
 d,
Ingo
Krossing
e,
Wolfgang G.
Zeier
d,
Ingo
Krossing
e,
Wolfgang G.
Zeier
 c,
Francesc
Illas
c,
Francesc
Illas
 b and
Duncan H.
Gregory
b and
Duncan H.
Gregory
 *a
*a
aWestCHEM, School of Chemistry, University of Glasgow, Joseph Black Building, Glasgow G12 8QQ, UK. E-mail: Duncan.Gregory@Glasgow.ac.uk
bDepartament de Ciència de Materials i Química Física & Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, C/Martí i Franquès 1, 08028 Barcelona, Spain
cInstitute for Inorganic and Analytical Chemistry, University of Münster, Correnstr. 39, 48149, Germany
dISIS Pulsed Neutron and Muon Source, STFC Rutherford Appleton Laboratory, Didcot, Oxfordshire OX11 0QX, UK
eInstitut für Anorganische und Analytische Chemie and Freiburger Materialforschungszentrum (FMF), Universität Freiburg, Albertstr. 21, 79104 Freiburg, Germany
First published on 1st June 2022
Abstract
Establishing links between the structure and physical properties of solid-state ionic conductors contributes not only to a rationale of their fundamental nature, but also provides design principles to accelerate the discovery of new materials. Lithium ion conduction in complex halides is not well-elucidated and so the interplay between lattice dynamics, electronic structure, and electrochemical properties in such halides has been explored in the isostructural family of lithium tetrahaloaluminates LiAlX4 (X = Cl, Br, I). Using a combination of experimental methods (diffuse reflectance UV-Vis spectroscopy, pulse-echo speed of sound measurements, Raman spectroscopy, inelastic neutron scattering) and periodic Density Functional Theory (DFT) based calculations, we demonstrate that softer lattices (quantified in terms of Debye frequencies or Li-phonon band centres as a function of X) provide lower activation energies for Li+ migration. However, the relationship between polarisability and Li+ conductivity is not straightforward. In line with expectations emergent from the Meyer–Neldel rule, the activation energy for Li+ hopping, Ea, and the pre-exponential terms collated as σ0 in the Arrenhius equation for activated conductivity, correlate. It is also evident that the electrochemical oxidative potential limit correlates with the X− phonon band centre in the Vibrational Density of States (VDOS) and that the Electrochemical stability Window (EW) and optical band gap are interlinked, as expected.
Introduction
Inorganic solid-state electrolytes (SSEs) can be employed in a number of emerging technologies ranging from solid oxide fuel cells to solid-state batteries.1 In particular, the replacement of flammable liquid electrolytes in conventional Li-ion batteries (LIBs) with solid-state analogues could not only improve their safety and longevity, but also enable higher energy density cells (using Li–metal anodes and high-voltage cathodes) in all-solid batteries (SSBs).2 During the past four decades, a vast amount of lithium SSEs have been studied. Among them, sulfide-based materials have shown the highest ionic conductivities at room temperature, e.g. Li9.54Si1.74P1.44S11.47Cl0.3 (σ = 25 mS cm−1 for a sintered pellet of 90% density),3 however their narrow electrochemical windows (e.g. 1.7–2.4 and 1.1–2.8 V vs. Li+/Li for the thio-LISICON Li10GeP2S12 and the argyrodite Li6PS5Cl, respectively)4,5 and limited chemical stability have prevented their large-scale commercialization.4 Among the alternatives, lithium ternary halides, LiAlX4 (X = halogen),6 LixScCl3+x,7 Li2Sc2/3Cl4,8 Li2InxSc2/3−xCl4,9 Li2ZrCl6,10 Li3MIIIX6 (MIII = Sc, Y, In, La, Ho, Er; X = halogen)11–17 and Li3−xM1−xZrxCl6 (MIII = Y, Er),18 are raising interest with appreciable ionic conductivity at room temperature, low activation energies for Li+ migration and wide electrochemical windows (e.g. 1.75–4.25 and 0.62–4.21 V vs. Li+/Li for Li2ZrCl6 and Li3YCl6, respectively).14,19 Despite the fact that most of the ternary halides described above react with water or are highly hygroscopic/deliquescent, recent reports have demonstrated notable exceptions in Li3InCl6 and Li2ZrCl6.15,19 While the former chloride will convert to Li3InCl6·2H2O when exposed to a humid atmosphere (which can be easily dehydrated by heating under vacuum), the latter showed no signs of moisture uptake nor conductivity degradation after exposure to an atmosphere with 5% relative humidity. Furthermore, it has been shown that the intrinsic instability of halide SSEs against Li can be overcome by using a InLi alloy or by protecting the electrolyte with a Li7P3S11 layer.11,19Generally, it can be demonstrated that the ionic conductivity of an electrolyte is given by:20
 | (1) |
 | (2) |
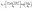 | (3) |
The activation energy for migration, Ea, depends on the conduction mechanism. For a temperature-independent mobile-ion site occupancy Ea = ΔHm; for Schottky defects Ea = ΔHm + 1/2ΔHS; and for Frenkel defects Ea = ΔHm + 1/2ΔHF (ΔHS and ΔHF are the enthalpies of formation of Schottky and Frenkel defects, respectively). Steered by eqn (1), design principles and descriptors have been presented in the literature for significant cationic conductivity to occur in a solid. These are typically: (i) a large carrier concentration; (ii) empty and occupied sites with similar potential energies, with a low activation barrier for direct ion hopping between them (via channels to allow long range transport, neglecting high-energy transition states); (iii) structural disorder in the cation (or anion) sublattice (as appropriate); (iv) anion (cation) sublattices with bcc-like frameworks (as opposed to ccp or hcp frameworks) to allow cations (anions) to migrate via interconnected tetrahedral sites with equivalent energies; and (v) a highly polarisable anion framework (in a cation conductor).1,22–26 Besides the structural considerations (i–iv), the role of lattice polarisability embodied in (v) (as the underlying cause of lattice softness) and its effect on ionic transport has attracted renewed scrutiny recently.27,28 It has been hypothesised that increasing the polarisability of anions within isostructural cation conductors (where the conductions pathways do not change significantly) would decrease the activation energy for cation migration. This is based on the idea that decreasing the bond strength between the mobile cation and the anion sublattice (by increasing bond polarity), should lower the migration barrier (since less energy is needed to jump from a stable lattice site). However, research shows that increasing the lattice softness can also decrease the Arrhenius pre-exponential factor (σ0) by decreasing the corresponding attempt frequency (ν0), i.e. reducing the probability for a Li+ ion to jump to a neighbouring site, and the entropy of migration (ΔSm) (eqn (1)).29,30 These effects will have a competing impact on the ionic conductivity and establishing which might dominate in any given system remains to be determined in the majority of cases. In terms of the quantification of lattice softness, Zeier, Muy and co-workers demonstrated that both acoustic modes (probed by speed of sound measurements) and phonon band centres (as determined by inelastic neutron scattering and density functional theory calculations), may be used as descriptors for the softness of the lattice.31 However, such studies remain narrow in focus, dealing only with a few families of Li+ conductors, including argyrodites Li6PS5X (X = Cl, Br, I),27 LISICON materials derived from Li3PO4,32 and NASICON-type Li1−3xGaxZr2(PO4)3.30
Since very little is known about the influence of anion sublattice polarisability on the properties of ternary lithium halides,13 we focused on the isostructural family of lithium tetrahaloaluminates LiAlX4 (X = Cl, Br, I), using a combination of experimental (DR-UV-Vis, PE-SoS, Raman, and INS) and periodic Density Functional Theory (DFT) based calculations to establish connections between electronic structure, lattice dynamics and electrochemical/transport data to piece together the appropriate composition–structure–property relationships.
Experimental
Synthesis of LiAlX4
LiCl (Sigma Aldrich, ≥99.99%), AlCl3 (Sigma Aldrich, anhydrous, 99.999%), LiBr (Alfa Aesar, anhydrous, 99.995%), AlBr3 (Sigma Aldrich, anhydrous, 99.999%), LiI (Sigma Aldrich, anhydrous, 99.99%) and AlI3 (Sigma Aldrich, anhydrous, 99.999%) were used as starting materials without further purification. Because of the air and/or moisture sensitivity of the starting materials and the final products, all manipulations were carried out in a continuously purified, Ar-filled (BOC, 99.998%) glove box (MBraun LABstar, O2 ≤ 5 ppm, H2O ≤ 0.5 ppm). A total of ca. 0.5 g of the starting materials were weighed out in the desired molar ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and added to a stainless-steel grinding jar containing ten stainless steel balls (10 mm diameter), each of which weighed ca. 4 g (giving a Ball-to-Powder Ratio (BPR) of 80
1) and added to a stainless-steel grinding jar containing ten stainless steel balls (10 mm diameter), each of which weighed ca. 4 g (giving a Ball-to-Powder Ratio (BPR) of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The grinding jar was sealed under Ar in the glove box before transfer to the ball mill. Ball milling was conducted in a planetary ball mill (Retsch PM100) in 5 minute milling periods (reverse rotation at 450 rpm, 300 rpm and 200 rpm for X = Cl, Br and I, respectively), followed by 5 minute rest periods for durations of 3 h (X = Cl) or 6 h (X = Br, I).6
1). The grinding jar was sealed under Ar in the glove box before transfer to the ball mill. Ball milling was conducted in a planetary ball mill (Retsch PM100) in 5 minute milling periods (reverse rotation at 450 rpm, 300 rpm and 200 rpm for X = Cl, Br and I, respectively), followed by 5 minute rest periods for durations of 3 h (X = Cl) or 6 h (X = Br, I).6
Characterisation
Powder X-ray diffraction
Powder X-ray Diffraction (PXD) measurements were conducted to confirm the identity and purity of mechanochemically-synthesised lithium haloaluminates. PXD data were recorded at room temperature with a Bruker D8 Advance diffractometer in transmission geometry using Cu Kα radiation (1.54184 Å) with a slit size of 2.0 mm. The moisture/air-sensitive samples were loaded inside glass capillaries (0.5 or 0.7 mm internal diameter), sealed with vacuum grease inside an Ar-filled glovebox, and subsequently flame-sealed outside the glovebox. The aligned capillaries were continuously rotated throughout the analysis and scanned over 5 ≤ 2θ/° ≤110 ranges (0.0167 step size, 14–15 h). Collected PXD patterns, as compared to reference data,6 are presented in the ESI (Fig. S1†) and showed the formation of the desired products without evident impurities.Electrochemical impedance spectroscopy
Electrical conductivities were measured by AC Electrochemical Impedance Spectroscopy (EIS) using isostatically pressed pellets (325 MPa, measured densities were 88, 84 and 80% of the crystallographically determined values for X = Cl, Br, I, respectively), which were subsequently coated via thermal evaporation with thin gold (200 nm) electrodes. Electrochemical impedance analysis was conducted in the temperature range of −40 to 60 °C using a SP300 impedance analyser (Biologic) at frequencies from 7 MHz to 50 mHz with an amplitude of 10 mV. The total ionic conductivities were obtained by fitting the spectra with an equivalent circuit consisting of one (X = Cl) or two (X = Br, I) parallel Constant Phase Element (CPE)/resistor in series with a CPE representing the behaviour of the electrolyte and blocking electrodes, respectively (ESI, Table S8†).6Raman spectroscopy
Raman spectra were recorded at room temperature with a Bruker VERTEX 70 spectrometer equipped with a Bruker RAM II module (1064 nm laser) with a nitrogen-cooled Ge detector. The samples were contained in sealed soda-lime glass Pasteur pipettes and measured over a region of 4000–50 cm−1 with a resolution of 4 cm−1.Inelastic neutron scattering
The experimental Vibrational phonon Density of States (VDOS) for each halide was determined from Inelastic Neutron Scattering (INS) data measured using the TOSCA33 spectrometer at the ISIS neutron and muon source at the Rutherford Appleton Laboratory in Oxfordshire. Samples (ca. 1.5 g) were loaded into aluminium cans and sealed with an indium wire gasket inside an Ar-filled glovebox. INS spectra were recorded at 10 K. Since the non-halide elements in LiAlX4 have small coherent neutron scattering cross sections, samples were scanned for a duration of 2000 μA h (corresponding to ∼12 h of exposure). The empty aluminium cans were measured in identical conditions and these recorded data were subtracted from the sample spectra. INS data were analysed using the Mantid34 open source software.Pulse-echo speed of sounds measurements
Pulse-Echo Speed of Sound (PE-SoS) measurements were performed on consolidated discs using an Epoch 600 instrument (Olympus) with 5 MHz transducers for longitudinal and transverse speeds of sound. Measurements were conducted on isostatically pressed pellets (325 MPa) under N2 atmosphere (O2 < 40 ppm). In order to prevent side reactions of the couplant and sample, pellets were coated with a thin layer (ca. 200 nm) of gold via thermal evaporation prior to the measurements. The extraction of the Debye frequencies from PE-SoS data was performed as described in detail previously.27,28Diffuse reflectance (DR) UV-Vis spectroscopy
Since the materials in this work are air- and/or moisture-sensitive, airtight cells were used for all samples in UV-Vis experiments in order to measure reliable optical bandgap values. Sample powders were spread on the BaSO4 powder standard inside an Ar- or N2-filled glovebox. DR spectra were recorded using a Shimadzu, UV-2600 UV-Vis spectrophotometer within a wavelength range of 190–1300 nm.Computational details
Corresponding calculations were performed in the framework of DFT within the Generalised Gradient Approximation (GGA), using the Perdew–Burke–Ernzerhof (PBE)35 exchange–correlation functional as implemented in the Vienna Ab Initio Simulation Package (VASP).36,37 In these calculations, the valence electron density was expanded using a plane-wave basis set with kinetic energy cut-offs of 650, 550, and 500 eV for LiAlCl4, LiAlBr4 and LiAlI4, respectively. Energy convergence tests revealed negligible energy variations if the plane-waves basis set was enlarged further. The effect of the core electrons on the valence region was evaluated by the Projector Augmented Wave (PAW) method described by Blöchl and implemented by Kresse and Joubert.38,39 For each of the structures, the necessary numerical integrations in reciprocal space were realised using a Γ-centred Monkhorst–Pack mesh of special k-points, with a grid size optimised until convergence below 10−3 eV was achieved (6 × 6 × 3 for each of the halides).40 The LiAlX4 structures displayed in Fig. 1 were modelled using a monoclinic unit cell (space group P21/c, no. 14), and fixing the lattice parameters of the unit cells to the experimental values obtained from Rietveld refinement against Powder X-ray Diffraction (PXD) data at room temperature.6 The atomic positions were optimised using a conjugate-gradient algorithm. The structural optimization of atomic positions within the experimental unit cell was continued until the forces acting on all atoms were smaller than 10−3 eV Å−1. The threshold convergence for the electronic energy was set to 10−5 eV. A Gaussian smearing with a smearing width of 0.2 eV was used to enhance the convergence, although the final total energies were always extrapolated to 0 K. All calculations were performed in a non-spin-polarised formalism. | ||
| Fig. 1 Optimised (DFT/PBE) crystal structures of LiAlCl4 (P21/c) projected along the b-axis as visualised with VESTA41 showing: (a) a polyhedral representation of the extended structure and (b) the linkage between an LiCl6 octahedron and neighbouring AlCl4 tetrahedra. Li, Al, and Cl atoms are represented by pink, blue, and green spheres, respectively. | ||
Calculations to predict the phonon spectra were performed by the supercell approach. Real-space force constants of supercells were calculated employing Density Functional Perturbation Theory (DFPT) as implemented in VASP. Phonon frequencies and irreducible representations were calculated from the force constants using the PHONOPY code.42 For LiAlX4, force constants were computed from a 2 × 2 × 1 supercell expansion with the same k-point sampling for all X. Raman spectra were computed from the above phonon calculations and the respective macroscopic dielectric tensors using the Finite Displacement (FD) method as implemented in VASP.43,44 Since the Raman active frequency values calculated by these methods are generally underestimated compared to the corresponding experimental frequencies,45 the former were scaled-up by a factor of 1.02 as suggested by Kesharwani et al.46 The average vibrational frequency, ωav, of the given compound, which is the phonon frequency weighted by the Vibrational Density of States (VDOS), was estimated using eqn (4) and is denoted here as the phonon band centre, representing the average phonon energy:32
 | (4) |
The phonon band centre can be viewed as the centroid of the VDOS. By replacing VDOS(ω) by the total VDOS or by one of the atom-projected VDOS (for instance, the Li-projected VDOS), one can obtain the total phonon band centre or the individual atom phonon band centre (i.e. lithium in this case), respectively.
Results and discussion
Electronic structure
A good SSE must possess, among other properties, a high ionic conductivity and low electronic conductivity, i.e. it should be an electronic insulator (with a wide band gap). In this work, electronic structure calculations were conducted to predict and analyse the band gap energies (Eg) in LiAlX4 (X = Cl, Br, I), which have been shown to correlate with the electrochemical oxidative stability of SSEs, and to study the nature of interaction between Li+ and complex [AlX4]− ions.47 However, it is important to underscore that although a large band gap is a necessary criterion, it alone cannot guarantee the compatibility of a SSE with a high-voltage cathode (which is determined by the SSE oxidation potential).48 This is because the band edges of the SSE must be positioned relative to those of the cathode so as to prevent electron transfer to the latter.49,50 The DFT calculations, carried out by single-point calculations with the PBE-optimized structure show that each of the LiAlX4 materials exhibits a wide indirect band gap along the Γ → Z direction, with values of 5.61, 4.36, and 3.44 eV for X = Cl, Br, and I, respectively (see Fig. 2a; ESI, S2 and S3†). Nevertheless, it should be noted that direct transitions at Γ point are just ∼0.03 eV higher than the indirect ones. Since both transitions are very similar in energy, it is expected that the experimental optical behaviour will be dominated by the direct transition since such transitions are not phonon-assisted and thus have a greater probability to occur. It also worth noting that the PBE functional is known to underestimate the band gap and, hence, the values above can be considered as the lower bounds. As expected, the contribution to the covalency of the bonding between Li+ and the complex [AlX4]− anions increases from Cl < Br < I, which is characterised by a decrease (in absolute values) in the anion p-band centres with respect to the mid-gap (Fig. 2b; ESI, S4†).47 The covalency of the bonds was found to correlate with the oxidative potential limit (as determined from Linear Sweep Voltammetry; LSV.6 ESI, Fig. S19†). This correlation is consistent with the observation that the measured oxidative potential increases with the band gap width (see Fig. 4a; ESI, S5†).47 At this point it is also worth noting the consistency between the oxidative potential limits for both solid LiAlCl4 and LiAlBr4 (4.4 V and 3.4 V vs. Li+/Li, respectively)6 and the corresponding [AlCl4]− and [AlBr4]− anions (onsets ca. 4.4 V and 3.5 V vs. Li+/Li, respectively) in liquid electrolytes (1 M EC/DMC 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1).51 Since the metals remain the same in each halide, i.e. Li and Al, then the band gap will be dependent only on the position of the halide anion valence p-band edges. Diffuse Reflectance UV-Vis spectroscopy (DR-UV-Vis) measurements were performed to obtain experimental values for the optical band gaps, allowing us to make comparisons with our calculated data. The DR-UV-Vis spectra of the three lithium tetrahaloaluminates (ESI, Fig. S6†) show that these materials have absorption edges located in the near- and mid-UV regions. Tauc plots to fit allowed direct transitions to the data yielded measured band gaps of 5.15, 4.01 and 3.01 eV for X = Cl, Br, and I, respectively (Fig. 2c; ESI, S7†), in relatively good agreement with the computed values (despite using a GGA functional) and confirming the premise that all three lithium tetrahaloaluminates are electronic insulators. The electrochemical windows for LiAlX4 have been previously calculated in the literature for X = Cl and Br yielding values of 2.8 V and 2.1 V (vs. Li+/Li, respectively).52 If these computed values are plotted against the measured optical band gaps (ESI, Fig. S8†) then following the assumption that the two quantities are related linearly, one can extrapolate to predict an Electrochemical stability Window (EW) of approximately 1.4 V vs. Li+/Li for LiAlI4.
1).51 Since the metals remain the same in each halide, i.e. Li and Al, then the band gap will be dependent only on the position of the halide anion valence p-band edges. Diffuse Reflectance UV-Vis spectroscopy (DR-UV-Vis) measurements were performed to obtain experimental values for the optical band gaps, allowing us to make comparisons with our calculated data. The DR-UV-Vis spectra of the three lithium tetrahaloaluminates (ESI, Fig. S6†) show that these materials have absorption edges located in the near- and mid-UV regions. Tauc plots to fit allowed direct transitions to the data yielded measured band gaps of 5.15, 4.01 and 3.01 eV for X = Cl, Br, and I, respectively (Fig. 2c; ESI, S7†), in relatively good agreement with the computed values (despite using a GGA functional) and confirming the premise that all three lithium tetrahaloaluminates are electronic insulators. The electrochemical windows for LiAlX4 have been previously calculated in the literature for X = Cl and Br yielding values of 2.8 V and 2.1 V (vs. Li+/Li, respectively).52 If these computed values are plotted against the measured optical band gaps (ESI, Fig. S8†) then following the assumption that the two quantities are related linearly, one can extrapolate to predict an Electrochemical stability Window (EW) of approximately 1.4 V vs. Li+/Li for LiAlI4.
Vibrational density of states
Recent work has demonstrated the correlation between lattice dynamics, as manifested by the phonon band centre (eqn (4)), with select and important properties of ionic conductors such as the enthalpy of migration and the electrochemical oxidative stability.32 Experimentally, the VDOS can be obtained via INS measurements. Since the neutron scattering lengths and, hence, coherent cross sections are different for different elements, the VDOS derived from simulations need to be neutron-weighted before valid comparisons between computed and measured VDOS can be made.53Fig. 3 shows the computed phonon dispersions and neutron-weighted zero-temperature harmonic VDOS, respectively, for LiAlCl4 (results for the bromide and iodide analogues are shown in the ESI, Fig. S9 and 10†). | ||
| Fig. 4 (a) Correlation between the measured oxidative potential limit (from Linear Sweep Voltammetry; LSV)6 and the measured direct optical band gap (from DR-UV-Vis data) of LiAlX4 (X = Cl, Br, I) materials. The dotted line corresponds to a linear fit (R2 = 1.00). (b) Correlation between Li+ migration activation energies as measured via7Li solid state NMR54 (solid circles) and electrochemical impedance spectroscopy (EIS) techniques6,55 (open circles) and the computed (DFPT/PBE) Li phonon band centre (ωLi) for LiAlX4 (X = Cl, Br, I). The dotted black line corresponds to a linear fit to the EIS data (R2 = 0.885). (c) Correlation between the oxidative potential limit (as measured by LSV6) and the computed (DFPT/PBE) anion phonon band centre (ωX) for LiAlX4 (X = Cl, Br, I). The dotted line corresponds to a linear fit (R2 = 0.974). | ||
INS spectra were measured at 10 K as an experimental verification of the calculated VDOS results and to assess the accuracy of the phonon calculations. This was an important test since the latter form a key component towards understanding the structure–property relationships in LiAlX4 materials. It was found that the experimental spectrum at 10 K and computed VDOS (0 K) are in close qualitative agreement. It is noticeable that the spectral resolution achieved for LiAlBr4 and LiAlI4 decreased significantly as compared to the chloride due to the lower neutron scattering cross sections of both Br (5.9 barn) and I (3.81 barn) vs. Cl (16.8 barn). In all cases, the systems were found to be vibrationally, i.e. dynamically, stable. Substitution of lighter halides for heavier equivalents in isostructural LiAlX4 led to a significant softening of the Li-projected VDOS, which can be quantified as a decrease in the average vibrational frequency, ωLi. The ωLi values for the haloaluminates each lie in the 20–30 meV range (ESI, Table S1†). This softening and corresponding decrease in ωLi can be rationalised by the weaker coulombic (less ionic) interactions between Li+ and the respective complex [AlX4]− ions as Cl is replaced by more polarisable Br and I. There is, therefore, a direct correlation between the Li phonon band centre and the anion-p band centres in the respective electronic DOS. (ESI, Fig. S11†). The softening of the Li-projected VDOS also correlates with a decrease in the measured activation energies (Fig. 4b), as previously reported for different families of Li+ and Na+ ionic conductors.31,32,47 The above observations support the hypothesis that softer lattices allow larger displacement amplitudes (u) of the mobile ion (Li+), which are associated with low phonon frequencies (ωE) in the Einstein model:
 | (5) |
Raman spectra
Raman spectra were measured for the LiAlX4 materials for comparison with the INS spectra and information regarding the vibrational modes of complex anionic species such as [AlX4]− can be readily found in the literature; however, these data correspond to the gas phase species rather than solid state compounds and do not consider the myriad of ionic interactions in a crystalline system.51,54 Corresponding calculations for solid-state systems can therefore make an important contribution to the understanding and unbiased assignment of the experimental spectra, especially as new materials are synthesised. LiAlX4 (X = Cl, Br, I) crystallize in monoclinic space group P21/c (C2h5) with twenty-four atoms per unit cell. Therefore, seventy-two phonon modes of vibration are expected (three acoustic and sixty-nine optical modes).According to a nuclear site analysis (see ESI†),56 the optical modes at the Γ point are as follows:
| Γoptic = 18Ag (R) + 17Au (IR) + 18Bg (R) + 16Bu (IR), |
 | ||
| Fig. 5 Computationally simulated (DFT/FD/PBE; black line) vs. experimentally observed (blue line) Raman spectra for LiAlCl4 (λlaser = 1064 nm). | ||
Generally, there is good agreement between the measured and calculated Raman spectra within the harmonic approximation. However, the assignment of the vibrational modes to the experimental data is not always straightforward, since some of the observed bands appear as a convolution of two individual modes, e.g. the experimentally observed bands at 499, 406, and 343 cm−1 for LiAlCl4, LiAlBr4 and LiAlI4, respectively, are a convolution of Bg and Ag modes. It is worth noting that Raman active vibrations that might have been attributed to starting materials in the synthesis process such as AlX3 were not present in the respective experimental Raman spectra (ESI, Fig. S16†). This supports evidence from diffraction (ESI, Fig. S1†) and the findings from previous thermal analysis to confirm the efficacy of the mechanochemical synthesis in yielding high purity final products.6 The relevant Raman spectra for the respective AlX3 materials are also included in the ESI for reference in Fig. S17 and Table S7.†
Correlation between lattice dynamics and ionic transport: the Meyer–Neldel rule
Fig. 6a shows the correlation between the two proposed descriptors to quantify the effect of lattice dynamics on the ionic transport, i.e. the Debye frequency (νD, as obtained from PE-SoS measurements; ESI, Fig. S18†) and the Li phonon band centre (ωLi, taken from the DFPT/PBE calculations). As can be seen, the respective νD and ωLi values lie within the same approximate frequency range, with a relationship of νD ∼ 0.5ωLi in LiAlCl4, for example. Despite the fact that the extracted Li phonon band centres are obtained under the zero-temperature harmonic approach, which present inherent limitations as recently highlighted by Cazorla and co-workers,29 one would at least expect the trend among the halides to remain true at room temperature due to the isostructural nature of the LiAlX4 compounds. | ||
| Fig. 6 (a) Correlation between the extracted Debye frequencies from PE-SoS measurements and the computed (DFPT/PBE) Li phonon band centres for LiAlX4 materials (X = Cl, Br, I). The dotted line corresponds to a linear fit (R2 = 0.898); (b) correlation between the extracted Debye frequencies (from PE-SoS measurements) and the extracted pre-factors and activation energies (from EIS measurement) in LiAlX4 materials (X = Cl, Br, I).6 The dotted lines correspond to linear fits (blue, R2 = 0.987) (black, R2 = 0.981). (c) Natural logarithm of the Arrhenius pre-factor vs. the respective activation energies obtained from EIS measurements for LiAlX4 materials (X = Cl, Br, I). The dotted line corresponds to the linear fit provided by applying the Meyer–Neldel rule (R2 = 0.922). | ||
Traditionally, it is usually expected that a highly polarisable anion framework is required to achieve high ionic conductivity in the solid state.22 A common interpretation of this statement is that replacing harder anions (e.g. O2−) with softer equivalents (e.g. S2−) within the same structural family (where similar conduction mechanisms would be inferred to prevail), would increase the ionic conductivity (σ) via a decrease in Ea, the activation energy for the migration of the mobile cation (eqn (2)). However, there is no such straightforward relationship between σ and Ea for the haloaluminates, since the room temperature ionic conductivity first slightly increases but then subsequently decreases when switching from X = Cl through Br to I. The implication is that the role of the pre-exponential term across the halide series is by no means insignificant and similar behaviour has been reported previously for lithium argyrodites27 and sodium thiophosphates.28 At the root of this apparent non-compliance by the haloaluminates is that both σ0 and Ea in eqn (2) decrease simultaneously when the anion becomes more polarizable (quantified in terms of either νD or ωLi as shown in Fig. 6b, for example). Thus, there is an optimum value of the pre-exponential and exponential factors that maximises σ, a phenomenon first described by Meyer and Neldel in their study of carrier transport in semiconductor oxides.57 By taking the expression of the pre-exponential factor (eqn (3)), it can be seen that, since γ (geometric factor), c (carrier density), Z (charge number of the mobile ion), and e (the elementary charge) are inferred to be constant in LiAlX4, the above equation leaves only three variables, i.e. the attempt frequency (ν0), jump distance (a0), and the entropy of migration (ΔSm). Under the assumption that ν0 ≈ νD, the decrease in ν0 it is not enough in itself to explain the decrease in σ0 (Fig. 6b) with halide, X. This relationship must be predominantly governed by ΔSm (since the jump distance between adjacent sites, a0, increases from Cl through Br to I, as the lattice parameters increase).6,30,58 According to the Meyer–Neldel rule (MNR; also known as the compensation rule), there is a linear relationship between ln(σ0) and Ea in the form of
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ0 = αEa + β, σ0 = αEa + β, | (6) |
 | (7) |
Based on eqn (7), Gao et al.59 highlighted that the relationship between σ and Ea depends on the sign of (1/Δ0 − 1/kBT) at a given temperature. For example, for materials where Δ0 > kBT (labelled as type 1), decreasing Ea would lead to a higher σ. Conversely, if Δ0 < kBT, increasing Ea would lead to a higher σ (type 2). On the other hand, for materials where Δ0 ∼ kBT, σ is not sensitive to changes in Ea (type 3). A similar behaviour has been derived for proton conductors, where the relationship between σ and Ea depends on the sign of (1/Tiso − 1/T), where Tiso is termed the isokinetic temperature.60 Although the fit across the halide series deviates from linearity (Fig. 6c, R2 = 0.922) one can obtain a tentative value for Δ0 of 19(5) meV, which lies within the energy scale of the Li-phonon band centres obtained from DFT (Fig. 4b, ESI Table S6†). Based on the value of Δ0, it is not surprising that σRT remains in the range 0.012–0.033 mS cm−1 despite the decrease in Ea when switching from X = Cl through Br to I, since kBT ∼ 26 meV at 298 K. The above results support the idea that the Meyer–Neldel energy can be explained by the Multi-Excitation Entropy (MEE) proposed by Yelon et al.61 Within this framework, for any thermally activated process, the activation entropy (ΔSm in eqn (1)) is proportional to the Ea by taking Δ0 as the average energy of the phonons in the system. ΔSm arises from the multiplicity of microstates, from a statistical mechanics point of view, associated with the absorption of excitations, i.e. phonons, needed to overcome a migration barrier Ea.58 In this regard, our results verify that the interplay between σ and Ea depends on the relative magnitude of Δ0 and kBT, and that Δ0 can be linked to the average energy of the phonons, i.e. ωLi, in ionic conductors that obey the Meyer–Neldel rule.58,59
Conclusions
In this work we studied the effect of lattice polarisability on the ionic conductivity and the electrochemical oxidative stability of lithium tetrahaloaluminates, based on lattice dynamics and electronic structure considerations. Our results demonstrate that the activation energy for Li+ diffusion in LiAlX4 (X = Cl, Br, I) correlates with the two proposed descriptors that quantify the overall lattice vibrations in solids, i.e. the Debye frequency and the Li-phonon band centre, and that both quantities lie within the same approximate frequency range. We also show that the oxidative potential limit correlates with the X− phonon band centre, and that the EW and optical band gap are interlinked, which points to the possibility of estimating the upper limit of the EW by DR-UV-Vis. Nevertheless, that ωLi and ωX are obtained from calculations rather than by experiment, places limitations on an interpretation of lattice dynamics from INS data. Furthermore, for materials containing elements with low neutron scattering cross sections, long scans are essential to achieve good spectral resolution. In addition, further experimental and computational tools are needed in order to determine migration entropies in SSEs accurately. Finally, our data show that softer lattices provide lower activation energies for Li+ migration in isostructural compounds (where the conduction pathways are known not to change significantly). However, this work illustrates once again that an improvement in ionic conductivity does not automatically follow since Ea and σ0 correlate in line with expectations emergent from the Meyer–Neldel rule. Preliminary results indicate that the anion sublattice polarisability could be tuned even further by judicious substitution and the results of these studies will be communicated in due course.Conflicts of interest
There are no conflicts to declareAcknowledgements
The authors acknowledge the Advanced Human Capital Program of the National Commission for Scientific and Technological Research (CONICYT/Becas Chile/No. 72170338) for a PhD scholarship for N. F. G., the Royal Society of Chemistry for a Researcher Mobility Grant No. RM1602-2758 and the EPSRC for associated funding under grant EP/N001982/1. The authors also thank the UK Science and Technology Facilities Council (STFC) for the award of neutron beamtime on TOSCA spectrometer at the ISIS Facility via the direct access route. N. M. and W. Z. are grateful for support by the Deutsche Forschungsgemeinschaft (DFG)under grant number ZE 1010/4-1. M. L., F. V., and F. I. thank the Spanish MCIN/AEI/10.13039/501100011033 funded RTI2018-095460 B-I00 and María de Maeztu MDM-2017-0767 grants, including funding from European Union and, in part, by and COST Action CA18234. Finally, M. L. thanks Universitat de Barcelona for an APIF predoctoral contract.References
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1, 16141 CrossRef.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- F. Han, Y. Zhu, X. He, Y. Mo and C. Wang, Adv. Energy Mater., 2016, 6, 1501590 CrossRef.
- C. Zheng, J. Zhang, Y. Xia, H. Huang, Y. Gan, C. Liang, X. He, X. Tao and W. Zhang, Small, 2021, 17, 2101326 CrossRef CAS PubMed.
- N. Flores-González, N. Minafra, G. Dewald, H. Reardon, R. I. Smith, S. Adams, W. G. Zeier and D. H. Gregory, ACS Mater. Lett., 2021, 3, 652–657 CrossRef PubMed.
- J. Liang, X. Li, S. Wang, K. R. Adair, W. Li, Y. Zhao, C. Wang, Y. Hu, L. Zhang, S. Zhao, S. Lu, H. Huang, R. Li, Y. Mo and X. Sun, J. Am. Chem. Soc., 2020, 142, 7012–7022 CrossRef CAS PubMed.
- L. Zhou, C. Y. Kwok, A. Shyamsunder, Q. Zhang, X. Wu and L. F. Nazar, Energy Environ. Sci., 2020, 13, 2056–2063 RSC.
- L. Zhou, T.-T. Zuo, C. Y. Kwok, S. Y. Kim, A. Assoud, Q. Zhang, J. Janek and L. F. Nazar, Nat. Energy, 2022, 7, 83–93 CrossRef CAS.
- H. Kwak, D. Han, J. Lyoo, J. Park, S. H. Jung, Y. Han, G. Kwon, H. Kim, S.-T. Hong, K.-W. Nam and Y. S. Jung, Adv. Energy Mater., 2021, 11, 2003190 CrossRef CAS.
- T. Asano, A. Sakai, S. Ouchi, M. Sakaida, A. Miyazaki and S. Hasegawa, Adv. Mater., 2018, 30, 1803075 CrossRef PubMed.
- R. Schlem, S. Muy, N. Prinz, A. Banik, Y. Shao-Horn, M. Zobel and W. G. Zeier, Adv. Energy Mater., 2020, 10, 1903719 CrossRef CAS.
- R. Schlem, T. Bernges, C. Li, M. A. Kraft, N. Minafra and W. G. Zeier, ACS Appl. Energy Mater., 2020, 3, 3684–3691 CrossRef CAS.
- S. Wang, Q. Bai, A. M. Nolan, Y. Liu, S. Gong, Q. Sun and Y. Mo, Angew. Chem., Int. Ed., 2019, 58, 8039–8043 CrossRef CAS PubMed.
- X. Li, J. Liang, N. Chen, J. Luo, K. R. Adair, C. Wang, M. N. Banis, T.-K. Sham, L. Zhang, S. Zhao, S. Lu, H. Huang, R. Li and X. Sun, Angew. Chem., Int. Ed., 2019, 58, 16427–16432 CrossRef CAS PubMed.
- Z. Xu, X. Chen, K. Liu, R. Chen, X. Zeng and H. Zhu, Chem. Mater., 2019, 31, 7425–7433 CrossRef CAS.
- Y. Liu, S. Wang, A. M. Nolan, C. Ling and Y. Mo, Adv. Energy Mater., 2020, 10, 2002356 CrossRef CAS.
- K.-H. Park, K. Kaup, A. Assoud, Q. Zhang, X. Wu and L. F. Nazar, ACS Energy Lett., 2020, 5, 533–539 CrossRef CAS.
- K. Wang, Q. Ren, Z. Gu, C. Duan, J. Wang, F. Zhu, Y. Fu, J. Hao, J. Zhu, L. He, C.-W. Wang, Y. Lu, J. Ma and C. Ma, Nat. Commun., 2021, 12, 4410 CrossRef CAS PubMed.
- S. Ohno, A. Banik, G. F. Dewald, M. A. Kraft, T. Krauskopf, N. Minafra, P. Till, M. Weiss and W. G. Zeier, Prog. Energy, 2020, 2, 022001 CrossRef.
- J. B. Goodenough, in Solid State Electrochemistry, ed. P. G. Bruce, Cambridge University Press, Cambridge, 1994, p. 55 Search PubMed.
- A. R. West, Solid State Chemistry and its Applications, Wiley, 2014 Search PubMed.
- P. P. Kumar and S. Yashonath, J. Chem. Sci., 2006, 118, 135–154 CrossRef CAS.
- Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier, M. Armand and L. Chen, Energy Environ. Sci., 2018, 11, 1945–1976 RSC.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS PubMed.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031 CrossRef CAS PubMed.
- M. A. Kraft, S. P. Culver, M. Calderon, F. Böcher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918 CrossRef CAS PubMed.
- T. Krauskopf, C. Pompe, M. A. Kraft and W. G. Zeier, Chem. Mater., 2017, 29, 8859–8869 CrossRef CAS.
- A. K. Sagotra, D. Chu and C. Cazorla, Phys. Rev. Mat., 2019, 3, 035405 CAS.
- S. Duan, C. Huang, M. Liu, Z. Cao, X. Tian, S. Hou, J. Li, B. Huang and H. Jin, J. Mat. Chem. A, 2021, 9, 7817–7825 RSC.
- T. Krauskopf, S. Muy, S. P. Culver, S. Ohno, O. Delaire, Y. Shao-Horn and W. G. Zeier, J. Am. Chem. Soc., 2018, 140, 14464–14473 CrossRef CAS PubMed.
- S. Muy, J. C. Bachman, L. Giordano, H.-H. Chang, D. L. Abernathy, D. Bansal, O. Delaire, S. Hori, R. Kanno, F. Maglia, S. Lupart, P. Lamp and Y. Shao-Horn, Energy Environ. Sci., 2018, 11, 850–859 RSC.
- R. S. Pinna, M. Zanetti, S. Rudić, S. F. Parker, J. Armstrong, S. P. Waller, D. Zacek, C. Smith, S. M. Harrison, G. Gorini and F. Fernandez-Alonso, J. Phys. Conf. Ser., 2018, 1021, 012029 CrossRef.
- J. Taylor, O. Arnold, J. Bilheaux, A. Buts, S. Campbell, M. Doucet, N. Draper, R. Fowler, M. Gigg, V. Lynch, A. Markvardsen, K. Palmen, P. Parker, P. Peterson, S. Ren, M. Reuter, A. Savici, R. Taylor, R. Tolchenov, R. Whitley, W. Zhou and J. Zikovsky, presented in part at the APS March Meeting Abstracts, February 01, 2012 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- A. Togo and I. Tanaka, Scripta Mater., 2015, 108, 1–5 CrossRef CAS.
- D. Porezag and M. R. Pederson, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 7830–7836 CrossRef CAS PubMed.
- A. Fonari and S. Stauffer, 2013, https://github.com/raman-sc/VASP/.
- P. Vajeeston, P. Ravindran and H. Fjellvåg, J. Phys. Chem. A, 2011, 115, 10708–10719 CrossRef CAS PubMed.
- M. K. Kesharwani, B. Brauer and J. M. L. Martin, J. Phys. Chem. A, 2015, 119, 1701–1714 CrossRef CAS PubMed.
- S. Muy, J. Voss, R. Schlem, R. Koerver, S. J. Sedlmaier, F. Maglia, P. Lamp, W. G. Zeier and Y. Shao-Horn, iScience, 2019, 16, 270–282 CrossRef CAS PubMed.
- T. K. Schwietert, V. A. Arszelewska, C. Wang, C. Yu, A. Vasileiadis, N. J. J. de Klerk, J. Hageman, T. Hupfer, I. Kerkamm, Y. Xu, E. van der Maas, E. M. Kelder, S. Ganapathy and M. Wagemaker, Nat. Mater., 2020, 19, 428–435 CrossRef CAS PubMed.
- P. Peljo and H. H. Girault, Energy Environ. Sci., 2018, 11, 2306–2309 RSC.
- T. Thompson, S. Yu, L. Williams, R. D. Schmidt, R. Garcia-Mendez, J. Wolfenstine, J. L. Allen, E. Kioupakis, D. J. Siegel and J. Sakamoto, ACS Energy Lett., 2017, 2, 462–468 CrossRef CAS.
- F. Scholz, W. Unkrig, P. Eiden, M. A. Schmidt, A. Garsuch and I. Krossing, Eur. J. Inorg. Chem., 2015, 2015, 3128–3138 CrossRef CAS.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Chem. Mater., 2016, 28, 266–273 CrossRef CAS.
- D. Bansal, J. Hong, C. W. Li, A. F. May, W. Porter, M. Y. Hu, D. L. Abernathy and O. Delaire, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 054307 CrossRef.
- K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Two Volume Set, Wiley, 2008 Search PubMed.
- K. Yamada, M. Kinoshita, K. Hosokawa and T. Okuda, Bull. Chem. Soc. Jpn., 1993, 66, 1317–1322 CrossRef CAS.
- D. L. Rousseau, R. P. Bauman and S. P. S. Porto, J. Raman Spectrosc., 1981, 10, 253–290 CrossRef CAS.
- W. Meyer and H. Neldel, Z. Tech. Phys., 1937, 12, 588–593 Search PubMed.
- S. Muy, R. Schlem, Y. Shao-Horn and W. G. Zeier, Adv. Energy Mater., 2021, 11, 2002787 CrossRef CAS.
- Y. Gao, N. Li, Y. Wu, W. Yang and S.-H. Bo, Adv. Energy Mater., 2021, 11, 2100325 CrossRef CAS.
- P. Du, N. Li, X. Ling, Z. Fan, A. Braun, W. Yang, Q. Chen and A. Yelon, Adv. Energy Mater., 2022, 12, 2102939 CrossRef CAS.
- A. Yelon, B. Movaghar and H. M. Branz, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 12244–12250 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ta02821b |
| This journal is © The Royal Society of Chemistry 2022 |


