Improving the thermoelectric performance of ZrNi(In,Sb)-based double half-Heusler compounds

Abstract

The complexity of crystal structures plays an intriguing role in manipulating properties in thermoelectrics, spintronics, and batteries. In comparison to the widely studied ternary half-Heusler thermoelectric compounds, quaternary double half-Heusler compounds are promising due to their intrinsically low lattice thermal conductivities (κ_L). However, they have been much less investigated due to the limited material availability. In this study, we report a new double half-Heusler compound based on ZrNi(In,Sb). Upon tuning the ratio of In/Sb from 0.5/0.5 to 0.4/0.6 and reducing the nominal concentrations of Zr and Ni by 10%, we greatly reduce the intensities of the impurity-phase peaks in the diffraction patterns. An even better phase purity, in combination with an optimized power factor, is realized by substituting Co at the Ni sites. Further alloying Hf at the Zr sites enhances the point defect scattering of phonons, which yielded a minimum κ_L of ∼1.8 W m⁻¹ K⁻¹ and a maximum zT of ∼0.5 for Zr_0.7Hf_0.2Ni_0.65Co_0.25In_0.4Sb_0.6 at 973 K. Our work thus confirms the intrinsically low κ_L of ZrNi(In,Sb) double half-Heusler compounds and indicates their promising applications upon further improving their electrical transport properties.

---

1 Introduction

Exotic or even anomalous physical phenomena are often observed in materials by designing complex crystal structures, such as enhancing the mechanical properties with multiple elements alloyed in high-entropy alloys¹ and facilitating the diffusion of lithium ions with the desired atom site occupancies in battery materials.² Therefore, it is imaginable that similarly amazing electrical and thermal transport properties can be achieved in robust materials with the designed complex crystal structures to enable a tailored manipulation of the transport mechanism of carriers.³

Thermoelectric (TE) technology is a promising sustainable solution to alleviate the energy crisis and environmental pollution.⁴ The performance of TE materials is determined by the coupled electrical and thermal transport, as manifested in the expression of the figure-of-merit, zT, given by zT = S²ρ⁻¹(κ_ele + κ_L)⁻¹T, where S, ρ, κ_ele, κ_L, and T are the Seebeck coefficient, the resistivity, the electrical thermal conductivity, the lattice thermal conductivity and the absolute temperature, respectively.⁵ Thus, good TE materials require high power factors (PF = S²ρ⁻¹) as well as low total thermal conductivity to realize high zT.⁶ However, optimizing the zT is challenging due to the intercorrelation of the transport parameters (S, ρ, and κ_ele), such as via the carrier concentration.⁷ To realize effective decoupling, tremendous efforts are devoted, which can generally be categorized into two approaches.⁸ One is to maximize the PF by optimizing the carrier concentration via doping or band engineering,⁹ while another one targets seeking materials or processes to minimize the thermal conductivity.¹⁰

As a prominent TE material candidate in the moderate temperature region, half-Heusler (HH) compounds have attracted significant attention due to their low cost, high thermal stability, and mechanical robustness, as well as their excellent electrical properties.¹¹ The bandgap of HH compounds varies from 0.1 to 3.7 eV based on the composition.¹¹ The valence electron count (VEC) per unit cell has been confirmed to play a critical role in the transport properties.¹² A slight variation from the 18 VEC (i.e., through doping) will optimize the PF, and the high PF is marked as the unique advantage of HH compounds.¹³ For instance, an ultrahigh PF value of ∼10.6 mW m⁻¹ K⁻² has been achieved in Ti-doped NbFeSb, and a record output power density of ∼22 W cm⁻² is obtained in a single-leg TE device.¹⁴ In another example, Zhu et al. reported an outstanding zT of ∼1.5 at 923 K for p-type HH in a Sn-doped ZrCoBi alloy with a high PF (3.7 mW m⁻¹ K⁻² at 823 K).¹⁵ Despite the excellent electronic performance, in comparison with other classic thermoelectric materials (e.g. Bi₂Te₃-, PbTe- and Cu₂Se-based TE materials),^13,16,17 the intrinsically large κ_L of HH compounds impedes their further zT improvement. Because of their innately low thermal conductivity, the nominal 19-electron half-Heusler compounds,¹⁸ or defective half-Heusler compounds,¹⁹ have recently been identified as attractive TE material options for HH compounds. As a result, the primary objective of discovery in the TE discipline is to create novel HH alloys with low κ_L yet strong electrical characteristics.

The complexity of a primitive unit cell is a key factor to reduce the κ_L of HH compounds. Anand et al.²⁰ compared the phonon frequency dependence of calculated cumulative κ_L of ternary (TiCoSb) and quaternary (Ti₂FeNiSb₂) HH compounds. A κ_L reduction of ∼50% as found for Ti₂FeNiSb₂ occurred in the high energy range of the phonons. In comparison to TiCoSb, a lower group velocity and a higher scattering rate of Ti₂FeNiSb₂ have been found, which indicates that quaternary HH compounds with more complex crystal structures would in general have lower κ_L than the traditional ternary HH compounds. Hence, HH systems are promising candidates for designing complex crystal structures to suppress the κ_L. Anand et al. predicted a total number of 713 possible ternary, defect-free HH compounds, of which 487 have been fully explored.²⁰ However, quaternary double HH compounds, based on the same calculations, have been rarely investigated, with only TiFe_1−xNi_xSb being successfully synthesized.²¹ The lowest κ_L of 2.5 W m⁻¹ K⁻¹ at 973 K has been achieved in TiFe_0.6Ni_0.4Sb while still reaching a high PF (∼1.5 mW m⁻¹ K²), indicating that enhancing the complexity of a primitive unit cell for HH alloys can dramatically suppress the κ_L.²¹ Thus, quaternary HH compounds have huge potential to enable the discovery of further new highly performing TE materials due to the huge unexplored phase space of ∼7719 quaternary HH compounds.²⁰

In this study, a new n-type double HH compound based on ZrNi(In,Sb) is realized (Fig. 1(a)). Starting from ZrNiIn_0.5Sb_0.5, we find obvious impurity peaks besides the main HH phase by X-ray powder diffraction (XRD). The intensity of the impurity peaks is substantially reduced after tuning the composition by changing the nominal In/Sb ratio to 0.4/0.6. Lowering the nominal amount of Zr and Ni by 10% improves this impurity phase reduction. Further substituting Co at the Ni sites not only tunes the carrier concentrations to realize an almost doubled peak PF from 1.08 to 2.03 mW m⁻¹ K² at 973 K in Zr_0.9Ni_0.65Co_0.25In_0.4Sb_0.6 but also further removes the impurity phase completely according to the detection limit of the diffractometer. Additionally, we further suppressed the κ_L from 2.10 to 1.81 W m⁻¹ K⁻¹ at 973 K by alloying a small amount of Hf to partially substitute Zr on the respective sites, which is comparable with other HH materials that have shown minimized κ_L (Fig. 1(b)). As a result of simultaneously optimizing the electrical properties and suppressing the κ_L, the final zT values were enhanced by 336% from 0.11 to 0.48 at 973 K in a compound with the composition of Zr_0.7Hf_0.2Ni_0.65Co_0.25In_0.4Sb_0.6 (Fig. 1(c)), demonstrating the great potential of ZrNi(In,Sb) HH compounds for intermediate- and high-temperature energy conversion.

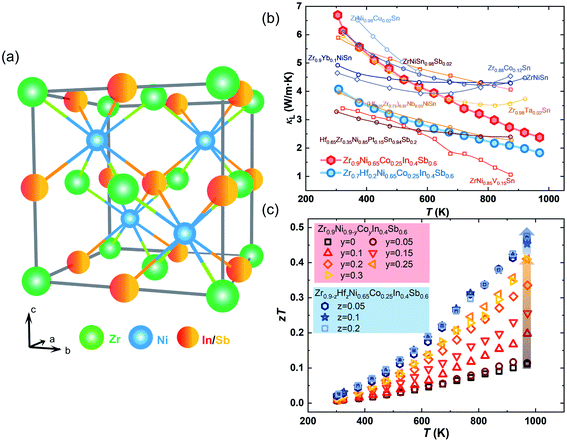Fig. 1 (a) Unit cell of the crystal structure of ZrNi(In,Sb) double HH compounds (space group F4̄3m). (b) Comparison of temperature-dependent κ_L among other low κ_L HH systems. (c) Temperature-dependent zT values of ZrNi(In,Sb) double HH compounds.^2,38–41,42

2 Experimental

2.1 Materials synthesis

The samples with nominal compositions of ZrNiIn_xSb_1−x (x = 0.4–0.6), Zr_0.9Ni_0.9−yCo_yIn_0.4Sb_0.6 (y = 0–0.3) and Zr_0.9−zHf_zNi_0.65Co_0.25In_0.4Sb_0.6 (z = 0.05–0.2) are prepared by arc melting, ball milling, and hot-pressing processes. The stoichiometrically weighed raw materials (Zr sponges, 99.2%; Ni granules, 99.98%; In granules, 99.9%; Sb shots, 99.8%; Hf sponges, 99.9%; Co powder, 99.9%) were melted three times in an Ar-protected chamber to form homogeneous ingots. Subsequently, the ingots were loaded into an Ar-filled stainless steel jar and ball milled for 4 h in a SPEX 8000D machine. The ball-milled powders were pressed into pellets by spark plasma sintering (AGUS-PECS SPS-210Gx) at 1173 K for 5 minutes under vacuum with a uniaxial pressure of 50 MPa.

2.2 Phase identification and microstructure characterization

X-ray powder diffraction (XRD) measurements for bulk samples were performed using a Bruker D8 with a Co source in the Bragg–Brentano mode to examine the phase purity and crystal structure of the samples. For the Rietveld analysis, the powders were prepared as flat samples, where powder less than the tip of a spatula was glued on acetate foil. The sample was inserted into a Stoe Stadi P powder diffractometer equipped with a Mo source and a Ge(111) monochromator that yield a single wavelength of 0.7093 Å. The position sensitive detector was a Mythen 1K from Dectris. The samples were measured in the range of 10° ≤ 2θ ≤ 60° in the transmission mode. The recorded data were analyzed according to the Rietveld method²² with the program package Fullprof/WinPlotR.²³ With the profile function nPr = 7 for the structure model refinement, the isotropic temperature factors (B_iso) and the asymmetry parameters Asy1 and Asy2 were refined. An instrumental resolution function was deduced from the NIST 640d silicon standard. All data were used as measured. For the main HH phase, the ZrCoSb structure model with the space group F4̄3m of Romaka et al.²⁴ was adopted to carry out investigation on the compounds. The fractured surface of the samples was analyzed by field emission scanning electron microscopy (Sigma300-ZEISS FESEM). Inductively coupled plasma-optical emission spectrometry (ICP-OES) measurements were conducted with an iCAP 6500 Duo View (Thermo Fisher Scientific) after aqueous acidic digestion.

2.3 Thermoelectric measurement

Both sides of the obtained pellets were polished after spark plasma sintering (AGUS-PECS SPS-210Gx), and the thermoelectric properties were directly quantified afterward. The temperature-dependent Seebeck coefficient (S) and electrical resistivity (ρ) were measured by the standard four-probe method (LSR-3, Linseis). The temperature-dependent thermal diffusivity (λ) was evaluated by a laser flash method in a helium atmosphere (LFA 1000, Linseis). The density (ρ) of the samples was measured by the Archimedes method, and the heat capacity (C_p) was calculated using the Dulong–Petit law. The thermal conductivity (κ_tot) was calculated according to the relationship κ_tot = λρC_p. The carrier concentration and Hall mobility were determined from 10 K to 300 K with Hall measurements in the van-der-Pauw geometry with a physical property measurement system (9 T LOT Dynacool system).

3 Results and discussion

3.1 Phase identification and purification

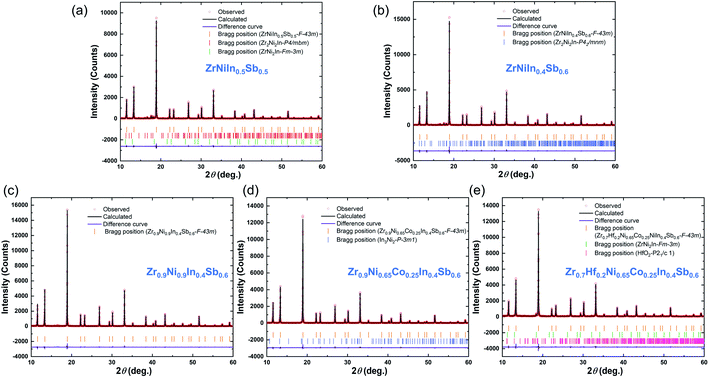
The bulk XRD patterns of all the samples of ZrNi(In,Sb) double HH are shown in Fig. S1.† Compared with the crystal structure of ZrCoSb,²⁴ the main reflections of all the samples correspond well with the MgAgAs-type with the space group F4̄3m (No. 216). In the starting compound, ZrNiIn_0.5Sb_0.5, we also find multiple impurities with the main reflections indexed as Zr₂Ni₂In and ZrNi₂In. The impurities vary in concentration upon changing the ratio of In/Sb. For example, with an In/Sb ratio of 0.6/0.4, the main reflection intensity of Zr₂Ni₂In (at 2θ ∼ 49° with Co Kα radiation) is significantly enhanced. In contrast, the ZrNi₂In reflection almost vanishes with an In/Sb ratio of 0.4/0.6. Furthermore, since other impurities are intermetallics of Zr–Ni in ZrNiIn_0.4Sb_0.6, we modified the composition by reducing the nominal concentrations of Zr and Ni by 10%. This way, only a small fraction of an In-based impurity remains in the sample with the nominal composition Zr_0.9Ni_0.9In_0.4Sb_0.6. Moreover, we substituted Co for Ni, forming Zr_0.9Ni_0.9−yCo_yIn_0.4Sb_0.6 (y = 0–0.3). Interestingly, we found that the remaining In-based impurity almost disappears with higher concentrations of Co (y = 0.25 and 0.3). Nevertheless, by substituting Hf at Zr sites to form Zr_0.9−zHf_zNi_0.65Co_0.25In_0.4Sb_0.6, the slight impurity reflection of In-based impurity reappears with low intensity, and the second phase of impurity becomes more prominent with increased Hf content (Fig. S1(c)†). All of these experimental observations suggest that ZrNiIn_xSb_1−x-based compounds exhibit the HH crystal structure, although most end up with slight impurities. The phase-evolvement dynamics of the studied system remain unclear and could be rather complex due to its multi-element nature. It may originate from the composition-dependent state of equilibrium, or simply from the multi-step processing under partially harsh conditions. For example, In and Sb have much higher vapor pressure compared to Zr and Ni, so the reduced nominal concentration of Zr and Ni in improving the phase purity may simply be because it compensates for the losses of In and Sb during the arc melting process. A more detailed analysis demands further study in the future.

Subsequently, to evaluate the lattice parameters and phase contents, Rietveld analyses based on the XRD results were performed for four specimens with the nominal compositions of ZrNiIn_0.5Sb_0.5, ZrNiIn_0.4Sb_0.6, Zr_0.9Ni_0.9In_0.4Sb_0.6, Zr_0.9Ni_0.65Co_0.25In_0.4Sb_0.6, and Zr_0.7Hf_0.2Ni_0.65Co_0.25In_0.4Sb_0.6 as shown in Fig. 2, and the detailed information can be found in Table S1.†

Fig. 2 Results of the Rietveld analyses for compounds with the nominal compositions (a) ZrNiIn_0.5Sb_0.5, (b) ZrNiIn_0.4Sb_0.6, (c) Zr_0.9Ni_0.9In_0.4Sb_0.6, (d) Zr_0.9Ni_0.65Co_0.25In_0.4Sb_0.6, and (e) Zr_0.7Hf_0.2Ni_0.65Co_0.25In_0.4Sb_0.6.

For the Rietveld analyses, the structural model of Romaka et al.²⁴ was adopted for the previously discussed elements. The resulting structural model fits the X-ray powder diffraction patterns to a great extent and with a phase content > 93 wt% to almost 99 wt% depending on the total amount of minor phases. Here, the specimen with the nominal composition ZrNiIn_0.5Sb_0.5 has the highest percentage of ∼7 wt% and ∼1 to 2 wt% for all other compounds. The evaluated sizes of the lattice parameter a result in the following order of the compounds: ZrNiIn_0.4Sb_0.6 > ZrNiIn_0.5Sb_0.5 > Zr_0.9Ni_0.9In_0.4Sb_0.6 > Zr_0.9Ni_0.65Co_0.25In_0.4Sb_0.6 > Zr_0.7Hf_0.2Ni_0.65Co_0.25In_0.4Sb_0.6 reflecting the different concentrations of substituent elements and their respective radii. As Sb has a smaller radius than Zr, Ni, and Co, reduced lattice parameters are expected, and the lattice parameters of the individual compounds therewith follow their composition obtained by the ICP-OES analyses shown in Table S2.† We find that while the concentrations of other elements agree well with the nominal one, In always displays certain deficiencies that may originate from the losses during the arc melting. Additionally, increased Sb and Ni/Co concentrations are found, whereas the In concentration decreased. Both may lead to the resulting lattice parameter order. The occupancy has not been included in this consideration as these results need further investigation to explain them plausibly. Fig. 3 illustrates the fracture surface obtained by SEM (scanning electron microscopy) for the compounds ZrNiIn_xSb_1−x (x = 0.4–0.6). The grain boundaries on this scale become less defined with decreasing In content, as displayed in Fig. 3(b) and (c). Additionally, the average grain size values of ZrNiIn_xSb_1−x are similar based on statistics but still show a slightly increasing trend with lower In content. This behavior may be attributed to the distinct response to the current-assisted sintering process, as will be discussed soon since the Sb-rich compound is more conductive than the In-rich one. It is worth noting that the increasing trend of grain size is more visible, while the electrical resistivities increased in Co-doped samples. As shown in Fig. S2,† the clear grain boundaries can be observed, and the grain size significantly increased with increased Co doping content (Fig. S2(h)†). Additionally, grain sizes above 1 μm appeared and were distributed uniformly – marked with the red circles – when the Co-doped content reached 0.3 (Fig. S2†).

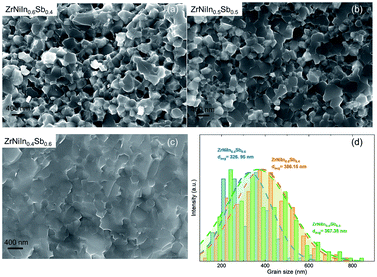Fig. 3 The fracture surfaces obtained by SEM for (a) ZrNiIn_0.6Sb_0.4, (b) ZrNiIn_0.5Sb_0.5 and (c) ZrNiIn_0.4Sb_0.6, and the distribution of the (d) grain size for the above composition.

3.2 Electrical transport properties

As is known, HH compounds involve p-type/n-type transport with a valence electron count (VEC) less and more than 18, respectively. As displayed in Fig. 4(a), the Seebeck coefficients exhibit an increasing trend upon heating. All samples show a strong n-type conductor behavior even with x = 0.6 that nominally has a VEC of 17.8. This finding is related to the loss of In, as documented by the ICP-OES results. The temperature-dependent ρ of ZrNiIn_xSb_1−x (x = 0.4–0.6) are given in Fig. 4(b). All ρ of the investigated samples increase for the measured temperature range pointing to degenerated or metal-like behaviors. A lower Sb content increases the value of ρ from 1.27 μΩ m to 2.33 μΩ m at 300 K. The nominal deficiency of Zr/Ni has little influence on ρ, suggesting that the effect of a second phase on the electrical properties is negligible for such a heavily doped conductor. Finally, a maximum PF of ∼1.8 mW m⁻¹ K² is obtained for ZrNiSb_0.5In_0.5. However, Zr_0.9Ni_0.9Sb_0.6In_0.4 exhibits relatively low impurities, which is the reason it was selected for subsequent optimizations.

Fig. 4 Temperature dependence of S (a and d), ρ (b and e) and PF (c and f) for ZrNi(In,Sb) double HH compounds.

Considering the low electrical resistivity and the Seebeck coefficient, it is desirable to reduce the carrier concentration to optimize the power factor, which is realized by substituting Co for Ni. As illustrated in Fig. 4(d) and (e), both the electrical resistivity and the Seebeck coefficient of Zr_0.9Ni_0.9−yCo_yIn_0.4Sb_0.6 (y = 0–0.3) are linearly dependent on the temperature in the degenerated nature. The value of ρ increases monotonically from 2.35 to 12.57 μΩ m with the doping level of Co at 973 K (Fig. 4(e)). Correspondingly, the S also increases three times from −51.3 to −151.1 μV K⁻¹ at 973 K (Fig. 4(d)), implying that the Co doping could effectively tune the electrical properties. Benefiting from the huge increase of S, the PF displays ∼100% enhancement from 1.07 to 2.04 mW m⁻¹ K² for the composition of y = 0.25 (Fig. 4(f)).

The variation in the electrical properties can be understood from the results of the carrier concentration (n) and the Hall mobility (μ). Fig. 5(a) and (b) show the Hall measurement results in the range of 10–300 K. The n values of all the samples are found in the range of 10²¹ cm⁻³ and are weakly dependent on the temperature. As shown in Fig. 5(a), the ZrNiIn_0.5Sb_0.5 sample has the lowest Hall concentration (n_H) among the ZrNiIn_1−xSb_x samples in the temperature range of 10–300 K. The Hall concentration was found to increase by either increasing the In/Sb ratio to 0.6/0.4 or decreasing it to 0.4/0.6. Whereas the increased n_H stems from an increased VEC in the Sb-rich composition (nominally the VECs are 18 for ZrNiIn_0.5Sb_0.5, and 18.2 for ZrNiIn_0.4Sb_0.6), it has more complex origins in the In-rich composition because of the much higher concentration of impurities (Fig. S1(a)†). Interestingly, the carrier concentration changes little by decreasing the nominal concentrations of both Zr and Ni by 10% from ZrNiIn_0.4Sb_0.6 to Zr_0.9Ni_0.9In_0.4Sb_0.6. The Co-substituted composition, Zr_0.9Ni_0.65Co_0.25In_0.4Sb_0.6, displays a further reduced n to ∼2 × 10²¹ cm⁻³, thus explaining its higher power factor in Fig. 4(f). Additionally, Fig. 5(a) shows that the substitution of Hf on the Zr site doesn't influence the n_H significantly due to the isovalent nature of Zr and Hf, as well as the lanthanide-contraction of Hf as has been discussed by Liu et al.²⁵ Accordingly, the electrical properties do not change significantly upon Hf substitution, as shown in Fig. S3.†

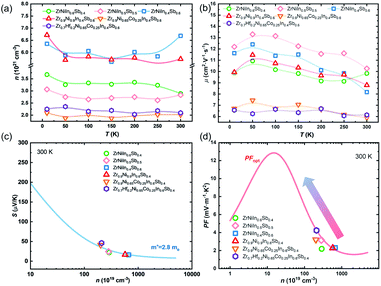Fig. 5 (a) Temperature dependence of n; (b) μ and (c) n dependence of |S| at 300 K ; (d) optimum PF at 300 K for the ZrNi(In,Sb) double HH compounds.

On the other hand, the μ values for all the Co-free samples are similar, typically ranging from 14 to 10 cm² V⁻¹ s⁻¹. The substitution of Co in Zr_0.9Ni_0.65Co_0.25In_0.4Sb_0.6 yields a reduction in the mobility by nearly ∼40%, probably due to the enhanced electron scattering through alloying. Based on the Hall measurement and electrical measurement results, we plotted the carrier-concentration as a function of the absolute Seebeck coefficient in Fig. 5(c) together with the calculations to evaluate the DOS effective mass m*, using the single parabolic band (SPB) model,²⁶ which is estimated to be 2.8m_e and similar to the ZrNiSn-based compounds.^27–29 This approach is reasonable since the band edges mainly constitute the d-orbitals from the transition metals (Zr and Ni), so the modification at the most electronegative sites (In/Sb or Sn) is not expected to change the effective mass drastically. Fig. 5(d) shows the n-dependent optimum PF of ZrNi(In,Sb) samples at 300 K following an SPB model,²⁶ together with our experimental results. Clearly, there is great potential to further improve the power factor by further reducing the carrier concentration. However, this idea is not realized by increasing the Co concentration to y = 0.3, as shown in Fig. 4, which might originate from an enhanced alloy scattering when the Co amount exceeds a certain limit. Therefore, other approaches are sought to further enhance the thermoelectric performance, which will be introduced later.

3.3 Thermal transport properties

Fig. 6(a) plots the temperature-dependent total thermal conductivity κ_tot of the ZrNiIn_xSb_1−x-based HH compounds. The κ_tot of the ZrNiIn_xSb_1−x compound decreases weakly with increased temperature and In/Sb ratio. For example, the κ_tot decreases from 9.90 W m⁻¹ K⁻¹ in ZrNiIn_0.4Sb_0.6 to 7.65 W m⁻¹ K⁻¹ at 973 K in ZrNiIn_0.6Sb_0.4. Fig. 6(b) shows the κ_L, as obtained by subtracting the electronic component κ_e using the Wiedemann–Franz law, κ_e = LσT, where L is the Lorenz number determined by the formula L = 1.5 + exp(−|S|/116) (Fig. S4(a)†).³⁰κ_L shows a decrease from 2.22 W m⁻¹ K⁻¹ to 0.98 W m⁻¹ K⁻¹ at 973 K with a shrinking In/Sb ratio. Apparently, κ_e dominates the heat conduction, suggesting the importance of reducing the carrier concentration for a lower κ_tot. Additionally, the introduced deficiencies of Zr and Ni further suppress the κ_L to ∼0.4 W m⁻¹ K⁻¹ at 973 K, which is even lower than the theoretical Cahill minimum κ_L (∼0.7 W m⁻¹ K⁻¹ for ZrNiSn). Admittedly, such an extremely low κ_L may originate from an overestimated κ_e due to the inaccurate evaluation of the Lorenz number for such a complex system. Nevertheless, these results do confirm the low-κ_L nature of the double HH compounds ZrNi(In,Sb), which has been rarely realized in ternary half-Heusler compounds. Glassbrenner and Slack suggested that the κ_L follows the T⁻¹ relationship if only the Umklapp scattering process above the Debye temperature is considered.³¹ The curves in Fig. 6(b) indicate that such a T⁻¹ relationship is roughly followed except for ZrNiIn_0.6Sb_0.4, implying that the phonon scattering is dominated by the phonon–phonon interaction. The κ_L ∼ T^−0.67 relationship of ZrNiIn_0.6Sb_0.4 implies other dominant phonon scattering mechanisms such as point defects or impurities.³² Furthermore, we compare in Fig. 6(c) our κ_L with other double half-Heusler compounds based on theoretical calculations and experimentally discovered TiFe_1−xNi_xSb at 300 K. The κ_L of ZrNi(In,Sb) is found to be comparable with TiFe_1−xNi_xSb, and much lower than the values as predicted by theoretical calculations (e.g., 13.60 W m⁻¹ K⁻¹ for ZrNiIn_0.5Sb_0.5).²⁰ We thus demonstrate the great potential of ZrNi(In,Sb) as a low-κ_L platform to realize subsequent improvement of zT.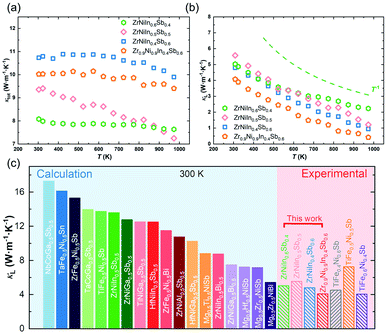

Fig. 6 Temperature dependence of (a) κ_tot and κ_L (b) for ZrNiIn_xSb_1−x, and (c) the comparison of κ_L of the calculated/experimental double HH alloys at 300 K.²⁰

Subsequently, we investigated the dependence of the thermal transport properties on the Co and Hf substitutions. In parallel, the temperature-dependent κ_tot and κ_L of Zr_0.9Ni_0.9−yCo_yIn_0.4Sb_0.6 and Zr_0.9−zHf_zNi_0.65Co_0.25In_0.4Sb_0.6 compounds are presented in Fig. 7. For Zr_0.9Ni_0.9−yCo_yIn_0.4Sb_0.6, while κ_tot is suppressed by increasing the Co content (Fig. 7(a)), κ_L displays an inverse trend (Fig. 7(b)). Thus, the reduction of κ_e is very important to overcompensate the rebound of κ_L. Furthermore, the increased κ_L with respect to the increased Co content is counter-intuitive, since heavier alloying usually scatters phonons more strongly. The Rietveld analysis (Table S1†) suggested that the half-Heusler phase has a phase content of ∼98.6 mass% for the Zr_0.9Ni_0.65Co_0.25In_0.4Sb_0.6 sample; therefore, the impurity phases should contribute negligibly to the varied lattice thermal conductivity. Furthermore, we observe a trend of grain enlargement with more Co following the SEM results (Fig. S2†), which could be partially accountable for the enhanced κ_L. The mechanism of such a grain-enlargement is not well understood, but it has been widely reported for half-Heusler materials that, under the same preparation conditions, a lower electrical resistivity usually yields a small grain size.^33,34 This is probably due to less Joule heating produced during sintering. In addition, our group recently revealed that a higher doping level will induce, spontaneously, a stronger charge-compensation effect in the half-Heusler compounds by producing charged point defects to counteract the extrinsic doping.³⁴ This effect is widely appreciated in tuning the electronic transport, but it can also significantly intensify the phononic scattering. The substitution of Co at the Ni sites reduces the carrier concentration/doping level, thus reducing the formation of charged point defects that are against the extrinsic doping. Admittedly, considering the complex multiple-elemental nature and the formation of impurities, it is very challenging to quantify the point defect through refinement based on a Mo anode. Diffraction patterns with higher quality are necessary such as those obtained by synchrotron or even neutron radiation. These will be subject to future studies.

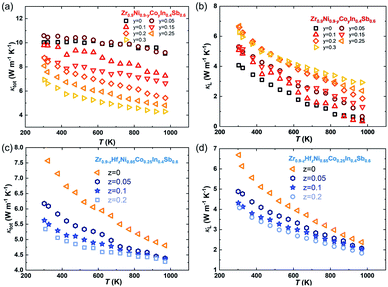Fig. 7 Temperature dependence of κ_tot (a and c) and κ_L (b and d) for the Co-doped and Hf-doped ZrNiIn_xSb_1−x based HH alloy samples.

For Zr_0.9−zHf_zNi_0.65Co_0.25In_0.4Sb_0.6 samples, the κ_tot gradually decreases as the Hf content increases, while there is only a negligible difference of κ_e (Fig. S4(c)†). Hence, the decrease of κ_tot is related to a stronger mass fluctuation induced by higher Hf contents. In particular, the lowest κ_L of Zr_0.7Hf_0.2Ni_0.65Co_0.25In_0.4Sb_0.6 is ∼4.1 W m⁻¹ K⁻¹ at room temperature and ∼1.81 W m⁻¹ K⁻¹ at 973 K as given in Fig. 7(d). Finally, the zT values increase from ∼0.1 to ∼0.4 at 973 K with a tuned carrier concentration by Co-doping and are further improved to ∼0.5 at 973 K with suppressed lattice thermal conductivity realized in the compound with the nominal stoichiometry Zr_0.7Hf_0.2Ni_0.65Co_0.25In_0.4Sb_0.6 as shown in Fig. 1(c). Additionally, the optimum zT of the newly discovered ZrNi(In,Sb) compounds is comparable with that of other double HH systems^21,35–37 (Fig. S5†), demonstrating that ZrNi(In,Sb) compounds enrich the HH families and can potentially be applied in electricity generation.

4 Conclusion

In this work, we proposed and examined the thermoelectric properties of new double HH ZrNi(In,Sb) compounds. We also demonstrated how the phase purity evolves by controlling the In/Sb ratio and the nominal content of Zr and Ni, doping the Ni sites with Co, and substituting Hf for Zr. The interrelated TE parameters are partially decoupled, through which simultaneously optimized electronic and phononic properties could be realized. A reduced κ_L ∼ 1.8 W m⁻¹ K⁻¹ and a peak zT ∼ 0.5 are obtained for the compound with a nominal stoichiometry of Zr_0.7Hf_0.2Ni_0.65Co_0.25In_0.4Sb_0.6 at 973 K. These findings reveal the role of Co doping in improving the PF via tuning the charge carrier concentration and the role of Hf in suppressing κ_L by enhancing the point defect-related phonon scattering. The enhanced TE performance indicated the effectiveness of this strategy and suggests its potential for further enhancement, which may help enrich HH families and discover novel materials.

Author contributions

S. H., A. B., and R. H. designed the research; A. B., P. Y., and S. H. prepared the samples; S. H. and A. B. performed the microstructure characterization studies; S. H., A. B., and R. H. measured the thermoelectrical properties; S. H. conducted the Hall measurement, and X. Z. analyzed the data; L. G. conducted the powder XRD and Rietveld analysis; S. H., A. B., R. H., and K. N. prepared the manuscript, and all the authors commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by Deutsche Forschungsgemeinschaft (DFG), Project Number 453261231. A. B. acknowledges the Alexander von Humboldt Foundation for the Postdoctoral Research Fellowship funding. P. Y. acknowledges the financial support from the strategic project at IFW Dresden on “Wireless sensor devices for high temperature applications”.

Notes and references

1. S. Zhou, T. Mei, X. Wang and Y. Qian, Nanoscale, 2018, 10, 17435–17455.
2. D. B. Miracle and O. N. Senkov, Acta Mater., 2017, 122, 448–511.
3. C. A. Cox, E. S. Toberer, A. A. Levchenko, S. R. Brown, G. J. Snyder, A. Navrotsky and S. M. Kauzlarich, Chem. Mater., 2009, 21, 1354–1360.
4. A. Bahrami, G. Schierning and K. Nielsch, Adv. Energy Mater., 2020, 10(19), 1904159.
5. S. He, Y. Li, L. Liu, Y. Jiang, J. Feng, W. Zhu, J. Zhang, Z. Dong, Y. Deng, J. Luo, W. Zhang and G. Chen, Sci. Adv., 2020, 6, eaaz8423.
6. S. He, S. Lehmann, A. Bahrami and K. Nielsch, Adv. Energy Mater., 2021, 11, 2101877.
7. X. Qi, J. Chen, K. Guo, S. He, J. Yang, Z. Li, J. Xing, J. Hu, H. Luo, W. Zhang and J. Luo, Chem. Eng. J., 2019, 374, 494–501.
8. S. He, J. Yang, A. Bahrami, X. Zhang, R. He, M. Hantusch, S. Lehmann and K. Nielsch, ACS Appl. Energy Mater., 2022, 5, 4041–4046.
9. L. You, Z. Li, Q. Ma, S. He, Q. Zhang, F. Wang, G. Wu, Q. Li, P. Luo, J. Zhang and J. Luo, Research, 2020, 2020, 1–8.
10. S. He, Y. Yang, Z. Li, J. Zhang, C. Wang, W. Zhang and J. Luo, Sci. China Mater., 2021, 64, 1751–1760.
11. S. Chen and Z. Ren, Mater. Today, 2013, 16, 387–395.
12. T. Fang, K. Xia, P. Nan, B. Ge, X. Zhao and T. Zhu, Mater. Today Phys., 2020, 13, 100200.
13. C. Fu, T. Zhu, Y. Pei, H. Xie, H. Wang, G. J. Snyder, Y. Liu, Y. Liu and X. Zhao, Adv. Energy Mater., 2014, 4, 1400600.
14. R. He, D. Kraemer, J. Mao, L. Zeng, Q. Jie, Y. Lan, C. Li, J. Shuai, H. S. Kim, Y. Liu, D. Broido, C.-W. Chu, G. Chen and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13576–13581.
15. H. Zhu, R. He, J. Mao, Q. Zhu, C. Li, J. Sun, W. Ren, Y. Wang, Z. Liu, Z. Tang, A. Sotnikov, Z. Wang, D. Broido, D. J. Singh, G. Chen, K. Nielsch and Z. Ren, Nat. Commun., 2018, 9, 1–9.
16. J.-F. Li and J. Liu, Phys. Status Solidi, 2006, 203, 3768–3773.
17. F. Kong, J. Bai, Y. Zhao, Y. Liu, J. Shi, Z. Wang and R. Xiong, Appl. Phys. Lett., 2019, 115, 203901.
18. K. Xia, P. Nan, S. Tan, Y. Wang, B. Ge, W. Zhang, S. Anand, X. Zhao, G. J. Snyder and T. Zhu, Energy Environ. Sci., 2019, 12, 1568–1574.
19. K. Xia, Y. Liu, S. Anand, G. J. Snyder, J. Xin, J. Yu, X. Zhao and T. Zhu, Adv. Funct. Mater., 2018, 28, 1705845.
20. S. Anand, M. Wood, Y. Xia, C. Wolverton and G. J. Snyder, Joule, 2019, 3, 1226–1238.
21. Z. Liu, S. Guo, Y. Wu, J. Mao, Q. Zhu, H. Zhu, Y. Pei, J. Sui, Y. Zhang and Z. Ren, Adv. Funct. Mater., 2019, 29, 1905044.
22. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
23. T. Roisnel and J. Rodríquez-Carvajal, Mater. Sci. Forum, 2001, 378–381, 118–123.
24. V. V. Romaka, L. Romaka, P. Rogl, Y. Stadnyk, N. Melnychenko, R. Korzh, Z. Duriagina and A. Horyn, J. Alloys Compd., 2014, 585, 448–454.
25. Y. Liu, C. Fu, K. Xia, J. Yu, X. Zhao, H. Pan, C. Felser and T. Zhu, Adv. Mater., 2018, 30, 1800881.
26. J. Zhu, X. Zhang, M. Guo, J. Li, J. Hu, S. Cai, W. Cai, Y. Zhang and J. Sui, npj Comput. Mater., 2021, 7, 116.
27. A. Bahrami, P. Ying, U. Wolff, N. P. Rodríguez, G. Schierning, K. Nielsch and R. He, ACS Appl. Mater. Interfaces, 2021, 13, 38561–38568.
28. C. Fu, M. Yao, X. Chen, L. Z. Maulana, X. Li, J. Yang, K. Imasato, F. Zhu, G. Li, G. Auffermann, U. Burkhardt, W. Schnelle, J. Zhou, T. Zhu, X. Zhao, M. Shi, M. Dressel, A. V. Pronin, G. J. Snyder and C. Felser, Adv. Sci., 2020, 7, 1902409.
29. C. Yu, H. Xie, C. Fu, T. Zhu and X. Zhao, J. Mater. Res., 2012, 27, 2457–2465.
30. S. He, A. Bahrami, X. Zhang, I. G. Martínez, S. Lehmann and K. Nielsch, Adv. Mater. Technol., 2021, 2100953.
31. C. J. Glassbrenner and G. A. Slack, Phys. Rev., 1964, 134, A1058–A1069.
32. W. Ren, H. Zhu, Q. Zhu, U. Saparamadu, R. He, Z. Liu, J. Mao, C. Wang, K. Nielsch, Z. Wang and Z. Ren, Adv. Sci., 2018, 5, 1800278.
33. H. Zhu, R. He, J. Mao, Q. Zhu, C. Li, J. Sun, W. Ren, Y. Wang, Z. Liu, Z. Tang, A. Sotnikov, Z. Wang, D. Broido, D. J. Singh, G. Chen, K. Nielsch and Z. Ren, Nat. Commun., 2018, 9, 2497.
34. R. He, T. Zhu, Y. Wang, U. Wolff, J.-C. Jaud, A. Sotnikov, P. Potapov, D. Wolf, P. Ying, M. Wood, Z. Liu, L. Feng, N. P. Rodriguez, G. J. Snyder, J. C. Grossman, K. Nielsch and G. Schierning, Energy Environ. Sci., 2020, 13, 5165–5176.
35. A. Karati, S. Ghosh, R. C. Mallik, R. Shabadi, B. S. Murty and U. V. Varadaraju, J. Mater. Eng. Perform., 2022, 31, 305–317.
36. R. Hasan, T. Park, S. Kim, H.-S. Kim, S. Jo and K. H. Lee, Advanced Energy and Sustainability Research, 2022, 2100206.
37. Q. Wang, X. Li, C. Chen, W. Xue, X. Xie, F. Cao, J. Sui, Y. Wang, X. Liu and Q. Zhang, Phys. Status Solidi, 2020, 217, 2000096.
38. H. Xie, H. Wang, C. Fu, Y. Liu, G. J. Snyder, X. Zhao and T. Zhu, Sci. Rep., 2014, 4, 1–6.
39. B. Gong, Y. Li, F. Liu, J. Zhu, X. Wang, W. Ao, C. Zhang, J. Li, H. Xie and T. Zhu, ACS Appl. Mater. Interfaces, 2019, 11, 13397–13404.
40. N. S. Chauhan, S. Bathula, A. Vishwakarma, R. Bhardwaj, B. Gahtori, A. Kumar and A. Dhar, ACS Appl. Energy Mater., 2018, 1, 757–764.
41. X. Yang, Z. Jiang, J. Li, H. Kang, D. Liu, F. Yang, Z. Chen, E. Guo, X. Jiang and T. Wang, Nano Energy, 2020, 78, 105372.
42. S. Katsuyama, H. Matsushima and M. Ito, J. Alloys Compd., 2004, 385, 232–237.

---

Footnotes

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ta02413f

‡ These authors contributed equally to this work.

---