Data mining for predicting gas diffusivity in zeolitic-imidazolate frameworks (ZIFs)

Abstract

Molecular sieving is based on mobility differences of species under extreme confinement, i.e. within pores of molecular dimensions. The pore properties of a material determine its separation efficiency, while pore network engineering provides a way to optimize the sieving performance. Unlike rigid and structurally limited carbon and zeolite molecular sieves, metal organic frameworks (MOFs) offer flexible networks with unlimited pore tailoring possibilities, by using different linkers, functional groups and metals/clusters. Nevertheless, knowledge-based pore optimization towards highly selective materials is hampered by the complex relationship between structural modifications and molecular diffusivity. Machine learning (ML) approaches can elucidate this correlation, but pertinent research in MOFs has so far focused solely on sorption properties. Herein, we report the first ML-assisted work towards understanding how the replacement of basic MOF building units affects the pore structure and consequently the molecular diffusivity. The ML approach developed is general; the work is however focused on zeolitic-imidazolate frameworks (ZIFs) with SOD topology. Since there is no database of relevant ZIF variations, we constructed a new ensemble of 72 existing and new ZIFs through systematic sub-unit replacement, developed a force-field for each of these structures and performed molecular dynamics (MD) simulations on fully flexible systems to calculate framework properties and the diffusivity of different molecules (ranging from helium to n-butane). Based on this new database, a predictive multi-step ML model was developed and trained. The model can rapidly and efficiently estimate the diffusivity of molecules in any possible ZIF structure with SOD topology by using readily accessible input information.

---

Nanoporous metal–organic frameworks (MOFs) can be engineered at the molecular level^1–11 and are thus, in theory, ideal platforms for developing novel molecular sieving materials tailored for any gas separation application. In sieving systems and particularly in membranes made of crystalline, ultra-microporous solids with narrow pores or pore windows (<5 Å), the overall selectivity is mainly governed by diffusivity,^12,13 which for a specific species is determined by the molecular level characteristics of the pore network. For a given topology, careful selection of coordination sub-units (e.g., metals or clusters and linkers in MOFs) coupled with additional subtle linker functionalization can in principle accurately tune the shape and size of pores or pore windows and/or modify the framework flexibility leading to extremely high mobility differences even for very similar molecules. However, up to now this strategy is practically inapplicable as there is a major scientific gap; the correlation between modifications in flexible frameworks and the diffusivity of a species is extremely complex, almost impossible to address experimentally and thus remains largely unresolved. Computational material screenings and high-throughput simulations,^14–17 as well as Machine Learning (ML)-assisted investigations^18–20 could be of great help; so far, however, the focus has been mainly on gas adsorptivity or simplified diffusivity simulations based on the assumption of rigid frameworks that can greatly compromise the validity of computations, as recently shown by Yang and Sholl.²¹ Diffusivity investigations in non-rigid pore networks constitute a far more challenging simulation task, where framework flexibility creates a complex interplay between possible material modifications and the resulting mobility of gases in the pores. ML-assisted computations on gas diffusion in MOFs have not been reported, and this is apparent by the total lack of references on diffusion in relevant review papers.^22–27

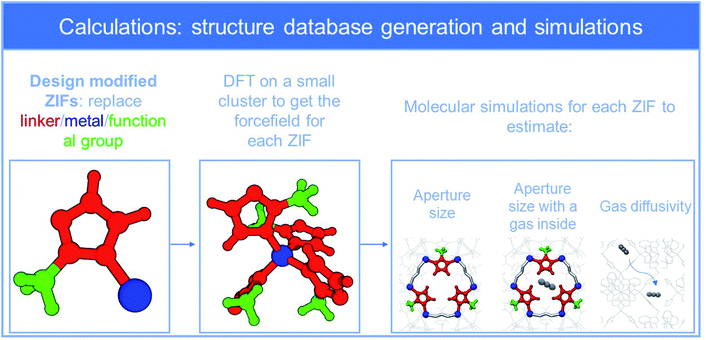
In this work, we present for the first time a data mining strategy assisted by ML for predicting the diffusivity of species in flexible crystalline nanoporous materials. Unlike conventional ML approaches in which databases of existing MOF (e.g., CoRE) are screened in order to identify the best performing structures (e.g., in terms of adsorption capacity) our aim is to develop a tool that can predict the diffusivity of a molecule upon any possible structural alteration. This tool may then be used for the design and synthesis of new MOFs by directing the synthesis efforts towards meaningful structures. Zeolitic-imidazolate frameworks (ZIFs),^28,29 a sub-family of MOFs and in particular ZIF-8 analogues were chosen as a case study for three reasons: firstly, due to their unique flexible structure and swinging/gate opening effect they have been widely investigated for several membrane-based gas separation processes;³⁰ secondly, there are indications that some modifications may indeed lead to highly selective materials, but a clear modification–diffusivity correlation has yet to be understood;^1,30–34 finally, ZIF-8 analogues exhibit a distinct structural characteristic, which is the aperture connecting the framework cages, that seems to control diffusivity,^33,35–38 and subsequently the material performance. However, contrary to MOFs, an adequately extended database of ZIF-8 type structures that can support a big data analysis, is unavailable. In this respect, a new structural dataset was created. The set comprises 72 chemically robust ZIF variants with SOD topology (ZIF-8 type) that were developed after systematic replacement of the linker, metal and/or functional group. It should be mentioned that in order to isolate and study the impact of building units' modifications on diffusivity, we chose to work on one topology only. In fact, topology variations would severely obscure our findings as this is an additional factor,^20,39 which can greatly affect the aperture size as well as the network connectivity and therefore the diffusion of penetrants.^33,40 The design of new variants was driven from the insight gained from our recent works^41–45 regarding the impact of modifications on the aperture which bridges the cages (Fig. 1). In brief, bulkier linkers decrease the aperture,^43,44 while its size and rigidity depend on the ionic radius of the metal.⁴² On the other hand, the functional group's impact on aperture is not fully understood. Information on the building units of each ZIF of the dataset is reported in ESI (ESI_1‡), along with refences to existing ZIFs that incorporate some of these units.

Fig. 1 (a) Profile view of the aperture bridging two cages in ZIF-8 and (b) front-view of the aperture. The multicolor sketch depicts the ZIF-8 building unit and its sub-units.

Force field parameters, such as charges, and bond length, angle and torsional parameters, for each of the 72 ZIF structures were developed through elaborate density functional theory (DFT) calculations. In a second step, the force fields were employed in fully flexible molecular dynamics (MD) simulations in order to calculate for each framework the sizes of aperture and “stretched” aperture, i.e., the aperture when a penetrant molecule of He, H₂, O₂, CO₂, N₂, CH₄, C₂H₄, C₂H₆, C₃H₆, C₃H₈, i-C₄H₁₀ and n-C₄H₁₀ lies in its center (results are provided as ESI_2‡). The third step was the deduction of diffusivity of each of these penetrants in all ZIFs, by means of dynamically corrected transition state theory (dc-TST), through simulations that accounted for the flexibility of the frameworks. DFT, MD and dc-TST simulation details are given in ESI_1,‡ while all force field parameters are tabulated in ESI_3.‡Fig. 2 summarizes the workflow of our computations. At this point, it is worth noting that five (5) out of the 72 ZIFs of our dataset have been synthesized, and used to validate our computational approach, by comparing simulations with experiments for ZIF structural characteristics and properties such as gas sorption, diffusivity, and permeability in these ZIFs.^{41,42,44,46,47}

Fig. 2 Workflow: generation of ZIFs database and computations.

Overall, the new ZIF database, which can be found in ESI_2,‡ sums up to 712 entries (ZIF-penetrant-aperture-stretched aperture and diffusivity). Fig. S1‡ shows the resulting distribution of aperture sizes and diffusivities in our dataset, proving that the modification scheme adopted spans throughout the range of interest. In general, more than 2000 ZIFs based on SOD topology can be designed (see Table S3‡) by using different metals, linkers, and functional groups and this can increase dramatically if combinations (e.g., two different metals) are employed. The 72 ZIFs of our study focus on a part of the available structural landscape; the structures considered however, cover sufficiently the most important range of apertures and diffusivities. Indeed, diffusion through apertures beyond the largest one employed (CdIF-1: 3.92 Å) is quite unrestricted and thus the separation potential for all gas pairs under investigation is poor, while apertures below the smallest one (Be-ZIF-7-8-I: 1.96 Å) will result to diffusivities that are extremely low for any practical application.

Based on the dc-TST results (details provided in ESI_2‡) it is evident that diffusivities and their ratios can vary by several orders of magnitude in different ZIFs, after minute aperture changes; for example, the ratio D_CO2/D_CH4 for ZIF-8 is approx. 9, which is increased to 3 × 10³ by replacing one out of three mIm linkers with bIm (ZIF-7-8), causing a 15% decrease of the aperture size. An additional modification in the framework, by replacing the Zn²⁺ metal with Be²⁺ decreases the aperture by 13%, leading to a D_CO2/D_CH4 substantial enhancement from 3 × 10³ to 6.43 × 10⁹. Likewise, the replacement of Zn²⁺ with Co²⁺ or Cu²⁺ in ZIF-8 reduces the aperture diameter by just 0.03% or 0.06%, but D_propylene/D_propane increases by 30% or 85% respectively, shifting the structure from just satisfactory to top performing.⁴⁸ Beyond this aperture size – diffusivity relationship, a closer look at the dataset (see ESI_2‡) reveals a rather extreme complexity at several levels. For instance, bulkier linkers decrease the aperture diameter while simultaneously increase its flexibility, resulting in higher diffusivities than expected in several cases (e.g., bIm vs. mIm). In addition, some combinations of metals and linkers give unexpected results; Zn²⁺ replacement by Co²⁺ is expected to decrease the aperture, but in some cases the reverse happens (e.g., F-ZIF-7-8 vs. Co-F-ZIF-7-8; Br-ZIF-7-8 vs. Co-Br-ZIF-7-8). Likewise, Cd, has the largest ionic radius and is thus expected to produce the largest apertures, but this is not the case (e.g., Cd-I-ZIF-7-8 vs. Mn-I-ZIF-7-8). Moreover, the impact of the functional group on the aperture size/flexibility is largely unclear. Overall, it seems that a rather obscure “dynamic” penetrant/framework interaction controls molecular mobility. The above show that correlating structural changes with gas mobility is a multivariant and extremely complex problem that cannot be deconvoluted by simplistic structure–diffusion relationships.⁴⁸

A possible way to address such highly complicated relationships is to employ artificial intelligence (AI) approaches and in this respect an ML model was trained to predict the logarithm of diffusivity of the various penetrants in ZIFs (details in the Computational Methodology of ESI_1‡). The training set is based on the newly developed ZIF database and comprises simulation deduced values (aperture sizes, stretched aperture sizes and penetrant diffusivities), as well as physically meaningful numerical descriptors of the ZIF building units and the gases (Tables 1 and S8‡). The ML model predictive performance is shown in Fig. 3(a).

Table 1 Descriptors for ZIF modifications and penetrants

		Features
a Lennard–Jones parameters.
		Ionic radius of metal
		Length
		Mass
		σ and ε^a of aperture atoms (see ESI)
		Length
		Mass
Penetrant (diffusing molecule)		Mass van der Waals diameter
		Kinetic diameter
		Acentric factor

---

Fig. 3 (a) Performance of the ML model for diffusivity prediction and (b) dominant descriptors on the model.

The trained model exhibits a satisfying efficiency all over the diffusivity scale range, with an average performance of R² = 0.96 and explained variance EV = 0.96. Additionally, feature importance analysis was performed and revealed the descriptors that govern our model (Fig. 3(b)). Among the various gas features, van der Waals diameter (gas_vdW) is the most prominent, while aperture size proves to be the dominant ZIF descriptor. Surprisingly, the stretched aperture does not affect the model performance. It should be emphasized at this point that except aperture sizes (normal and stretched), the descriptors are readily available physical properties. Stretched aperture seems to be unimportant and could thus be omitted but the very important aperture size requires elaborate DFT and MD calculations on fully flexible crystals hampering the generic, facile use of the ML model (e.g., for ZIF sub-units and penetrants not included in our dataset).

Based on the above, a two-step ML strategy could prove applicable: a first model, M1, may be trained on ZIF physical descriptors (Table 1) in order to predict the aperture sizes of ZIF variants. Then, a second model (M2) can be trained to predict the diffusivity of a penetrant in a ZIF, by using the penetrant descriptors (Table 1) and the predicted ZIF aperture as well as the rest of the ZIF descriptors of M1. The overall procedure is summarized schematically in Fig. 4.

Fig. 4 Description of the two-step ML model and its performance.

The comparison of the predicted aperture sizes of M1 with the actual (simulation) ones (Fig. 4) yields R² = 0.90 and EV = 0.91, highlighting an overly satisfying predictive potential. M2 predicts the log(D) of any gas with R² = 0.93 and EV = 0.93, which is a surprisingly high performance especially when considering that it is based only on readily available physical properties and the M1 predicted aperture size. In fact, by comparing the performances of the first model (Fig. 3) and the two-step model, it becomes evident that only a small amount of information is lost by using the M1 predicted aperture sizes (instead of the MD calculated ones). Additionally, based on the importance ranking of descriptors, a much simpler M2 model (M2_simple), was trained only on the most prominent descriptors for ZIFs (predicted aperture size from M1) and the gases (vdW diameter). The M2_simple model (Fig. 4) has R² = 0.86 and EV = 0.85, which is considered quite impressive, given the simplicity of the input required versus the complexity of the task.

In conclusion, since an adequate ensemble of pre-synthesized or pre-designed ZIF-8 variants was not available we have built 72 new SOD structures by varying both the organic and the metal sections of the framework. Instead of adopting the conventional approach of using a common force-field across all the ZIF variants, we performed accurate DFT calculations specifically for each structure. The force-fields developed were used for MD and dc-TST simulations in fully flexible crystals. The results (apertures and diffusivities) were for the first time considered collectively for the training of predictive ML models, that account for the interplay between the structure modifications and the diffusion of penetrants.

Most ML-related works employ descriptors (such as pore diameters, free volume and gravimetric/volumetric surface areas) that need prior knowledge of the full unit cell representation of the frameworks under study, as well as descriptors that are extracted (e.g., potential energy surfaces) by computations on the unit cell.^49–52 In our case, the use of similar descriptors or even elaborate DFT-based descriptors (e.g. charges, bond length/bond angle parameter) is by all means possible and actually leads to improved predictive power (data not presented). Nevertheless, the utilization of simple and mainly readily available input information such as the mass and size of the basic building units, was chosen in order to make the ML routines easy to employ: a researcher can consider a new functionalization of ZIF-8, bypass the multiple computational steps (ZIF cluster construction, DFT calculations, unit cell construction and MD, dc-TST simulations) and directly obtain a good estimation of the diffusivity of different penetrants (and thus the structure's selectivity potential) through a simple two-step ML model.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 894585 (SmartDeZign). This publication was made possible in part by NPRP grant number 12S-0209-190064 from the Qatar National Research Fund (a member of Qatar Foundation). The statements made herein are solely the responsibility of the authors. We are grateful to the High-Performance Computing Center of Texas A&M University at Qatar for generous resource allocation.

References

1. H. Lyu, Z. Ji, S. Wuttke and O. M. Yaghi, Digital Reticular Chemistry, Chem, 2020, 6, 2219–2241.
2. R. Banerjee, H. Furukawa, D. Britt, C. Knobler, M. O'Keeffe and O. M. Yaghi, Control of Pore Size and Functionality in Isoreticular Zeolitic Imidazolate Frameworks and Their Carbon Dioxide Selective Capture Properties, J. Am. Chem. Soc., 2009, 131, 3875–3877.
3. B. Yuan, J. Wang, Y. Chen, X. Wu, H. Luo and S. Deng, Unprecedented Performance of N-Doped Activated Hydrothermal Carbon towards C2H6/CH4, CO2/CH4, and CO2/H2 Separation, J. Mater. Chem. A, 2016, 4, 2263–2276.
4. J. Sánchez-Laínez, A. Veiga, B. Zornoza Encabo, S. Rodríguez-Gómez Balestra, S. Hamad, A. R. Ruiz-Salvador, S. Calero, C. Téllez Ariso and J. Coronas, Tuning the Separation Properties of Zeolitic Imidazolate Framework Core-Shell Structures via Post-Synthetic Modification, J. Mater. Chem. A, 2017, 5, 25601–25608.
5. B. Tam and O. Yazaydin, Design of Electric Field Controlled Molecular Gates Mounted on Metal-Organic Frameworks, J. Mater. Chem. A, 2017, 5, 8690–8696.
6. C. L. Hobday, T. D. Bennett, D. Fairen-Jimenez, A. J. Graham, C. A. Morrison, D. R. Allan, T. Düren and S. A. Moggach, Tuning the Swing Effect by Chemical Functionalization of Zeolitic Imidazolate Frameworks, J. Am. Chem. Soc., 2018, 140, 382–387.
7. S. Kuyuldar, D. T. Genna and C. Burda, On the Potential for Nanoscale Metal-Organic Frameworks for Energy Applications, J. Mater. Chem. A, 2019, 7, 21545–21576.
8. Y. Ye, Z. Ma, R. B. Lin, R. Krishna, W. Zhou, Q. Lin, Z. Zhang, S. Xiang and B. Chen, Pore Space Partition within a Metal-Organic Framework for Highly Efficient C 2 H 2/CO 2 Separation, J. Am. Chem. Soc., 2019, 141, 4130–4136.
9. Q. Hou, Y. Wu, S. Zhou, Y. Wei, J. Caro and H. Wang, Ultra-Tuning of the Aperture Size in Stiffened ZIF-8_Cm Frameworks with Mixed-Linker Strategy for Enhanced CO2/CH4 Separation, Angew. Chem., Int. Ed., 2019, 58, 327–331.
10. X. Wang, Z. Niu, A. M. Al-Enizi, A. Nafady, Y. Wu, B. Aguila, G. Verma, L. Wojtas, Y. S. Chen, Z. Li and S. Ma, Pore Environment Engineering in Metal-Organic Frameworks for Efficient Ethane/Ethylene Separation, J. Mater. Chem. A, 2019, 7, 13585–13590.
11. J. Wang, Y. Zhang, P. Zhang, J. Hu, R. B. Lin, Q. Deng, Z. Zeng, H. Xing, S. Deng and B. Chen, Optimizing Pore Space for Flexible-Robust Metal-Organic Framework to Boost Trace Acetylene Removal, J. Am. Chem. Soc., 2020, 142, 9744–9751.
12. W. J. Koros and C. Zhang, Materials for Next-Generation Molecularly Selective Synthetic Membranes, Nat. Mater., 2017, 16, 289–297.
13. R. Krishna, Methodologies for Screening and Selection of Crystalline Microporous Materials in Mixture Separations, Sep. Purif. Technol., 2018, 194, 281–300.
14. Z. Qiao, C. Peng, J. Zhou and J. Jiang, High-Throughput Computational Screening of 137953 Metal-Organic Frameworks for Membrane Separation of a CO2/N2/CH4mixture, J. Mater. Chem. A, 2016, 4, 15904–15912.
15. C. Altintas, G. Avci, H. Daglar, E. Gulcay, I. Erucar and S. Keskin, Computer Simulations of 4240 MOF Membranes for H2/CH4 Separations: Insights into Structure-Performance Relations, J. Mater. Chem. A, 2018, 6, 5836–5847.
16. C. Altintas, G. Avci, H. Daglar, A. Nemati Vesali Azar, I. Erucar, S. Velioglu and S. Keskin, An Extensive Comparative Analysis of Two MOF Databases: High-Throughput Screening of Computation-Ready MOFs for CH4 and H2 Adsorption, J. Mater. Chem. A, 2019, 7, 9593–9608.
17. S. Keskin, Screening for Selectivity, Nat. Energy, 2020, 5, 8–9.
18. G. S. Fanourgakis, K. Gkagkas, E. Tylianakis and G. E. Froudakis, A Universal Machine Learning Algorithm for Large-Scale Screening of Materials, J. Am. Chem. Soc., 2020, 142, 3814–3822.
19. R. M. Giappa, E. Tylianakis, M. Di Gennaro, K. Gkagkas and G. E. Froudakis, A Combination of Multi-Scale Calculations with Machine Learning for Investigating Hydrogen Storage in Metal Organic Frameworks, Int. J. Hydrogen Energy, 2021, 46, 27612–27621.
20. Y. Yan, Z. Shi, H. Li, L. Li, X. Yang, S. Li, H. Liang and Z. Qiao, Machine Learning and In-Silico Screening of Metal–Organic Frameworks for O2/N2 Dynamic Adsorption and Separation, Chem. Eng. J., 2022, 427, 131604.
21. Y. Yang and D. S. Sholl, A Systematic Examination of the Impacts of MOF Flexibility on Intracrystalline Molecular Diffusivities, J. Mater. Chem. A, 2022, 10, 4242–4253.
22. Z. Shi, W. Yang, X. Deng, C. Cai, Y. Yan, H. Liang, Z. Liu and Z. Qiao, Machine-Learning-Assisted High-Throughput Computational Screening of High Performance Metal-Organic Frameworks, Mol. Syst. Des. Eng., 2020, 5, 725–742.
23. H. Wang, Y. Ji and Y. Li, Simulation and Design of Energy Materials Accelerated by Machine Learning, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, 1–18.
24. S. M. Moosavi, K. M. Jablonka and B. Smit, The Role of Machine Learning in the Understanding and Design of Materials, J. Am. Chem. Soc., 2020, 142, 20273–20287.
25. C. Altintas, O. F. Altundal, S. Keskin and R. Yildirim, Machine Learning Meets with Metal Organic Frameworks for Gas Storage and Separation, J. Chem. Inf. Model., 2021, 61, 2131–2146.
26. B. C. Bukowski, F. J. Keil, P. I. Ravikovitch, G. Sastre, R. Q. Snurr and M. O. Coppens, Connecting Theory and Simulation with Experiment for the Study of Diffusion in Nanoporous Solids, Adsorption, 2021, 27, 683–760.
27. A. S. Rosen, J. M. Notestein and R. Q. Snurr, Realizing the Data-Driven, Computational Discovery of Metal-Organic Framework Catalysts, Curr. Opin. Chem. Eng., 2022, 35, 100760.
28. R. Banerjee, A. Phan, B. Wang, C. Knobler, H. Furukawa, M. O'Keeffe and O. M. Yaghi, High-Throughput Synthesis of Zeolitic Imidazolate Frameworks and Application to CO2 Capture, Science, 2008, 319, 939–943.
29. M. R. Abdul Hamid, T. C. Shean Yaw, M. Z. Mohd Tohir, W. A. Wan Abdul Karim Ghani, P. D. Sutrisna and H. K. Jeong, Zeolitic Imidazolate Framework Membranes for Gas Separations: Current State-of-the-Art, Challenges, and Opportunities, J. Ind. Eng. Chem., 2021, 98, 17–41.
30. H. K. Jeong, Metal–Organic Framework Membranes: Unprecedented Opportunities for Gas Separations, AIChE J., 2021, 67, 1–8.
31. C. Zhang and W. J. Koros, Zeolitic Imidazolate Framework-Enabled Membranes: Challenges and Opportunities, J. Phys. Chem. Lett., 2015, 6, 3841–3849.
32. K. Adil, Y. Belmabkhout, R. S. Pillai, A. Cadiau, P. M. Bhatt, A. H. Assen, G. Maurin and M. Eddaoudi, Gas/Vapour Separation Using Ultra-Microporous Metal–Organic Frameworks: Insights into the Structure/Separation Relationship, Chem. Soc. Rev., 2017, 46, 3402–3430.
33. C. Han, Y. Yang and D. S. Sholl, Quantitatively Predicting Impact of Structural Flexibility on Molecular Diffusion in Small Pore Metal-Organic Frameworks-A Molecular Dynamics Study of Hypothetical ZIF-8 Polymorphs, J. Phys. Chem. C, 2020, 124, 20203–20212.
34. Y. Ban, M. Zhao and W. Yang, Metal-Organic Framework-Based CO2 Capture: From Precise Material Design to High-Efficiency Membranes, Front. Chem. Sci. Eng., 2020, 14, 188–215.
35. R. J. Verploegh, S. Nair and D. S. Sholl, Temperature and Loading-Dependent Diffusion of Light Hydrocarbons in ZIF-8 as Predicted Through Fully Flexible Molecular Simulations, J. Am. Chem. Soc., 2015, 137, 15760–15771.
36. K. Eum, K. C. Jayachandrababu, F. Rashidi, K. Zhang, J. Leisen, S. Graham, R. P. Lively, R. R. Chance, D. S. Sholl, C. W. Jones and S. Nair, Highly Tunable Molecular Sieving and Adsorption Properties of Mixed-Linker Zeolitic Imidazolate Frameworks, J. Am. Chem. Soc., 2015, 137, 4191–4197.
37. H. An, K. Yong Cho, S. Yu, K. Chul Kim, J. Ho Shin, K. Jin Nam, J. Hoon Park and J. Suk Lee, Triple-Ligand Zeolitic Imidazolate Frameworks for Highly CO2 Selective Mixed Matrix Membranes, Chem. Eng. J., 2021, 133606.
38. M. R. Abdul Hamid, Y. Qian, R. Wei, Z. Li, Y. Pan, Z. Lai and H. K. Jeong, Polycrystalline Metal-Organic Framework (MOF) Membranes for Molecular Separations: Engineering Prospects and Challenges, J. Membr. Sci., 2021, 640, 119802.
39. B. C. Bukowski and R. Q. Snurr, Topology-Dependent Alkane Diffusion in Zirconium Metal-Organic Frameworks, ACS Appl. Mater. Interfaces, 2020, 12, 56049–56059.
40. J. Yang, Y. B. Zhang, Q. Liu, C. A. Trickett, E. Gutiérrez-Puebla, M. Á. Monge, H. Cong, A. Aldossary, H. Deng and O. M. Yaghi, Principles of Designing Extra-Large Pore Openings and Cages in Zeolitic Imidazolate Frameworks, J. Am. Chem. Soc., 2017, 139, 6448–6455.
41. P. Krokidas, M. Castier and I. G. Economou, Computational Study of ZIF-8 and ZIF-67 Performance for Separation of Gas Mixtures, J. Phys. Chem. C, 2017, 121, 17999–18011.
42. P. Krokidas, S. Moncho, E. N. Brothers, M. Castier and I. G. Economou, Tailoring the Gas Separation Efficiency of Metal Organic Framework ZIF-8 through Metal Substitution: A Computational Study, Phys. Chem. Chem. Phys., 2018, 20, 4879–4892.
43. P. Krokidas, S. Moncho, E. N. Brothers, M. Castier, H. K. Jeong and I. G. Economou, On the Efficient Separation of Gas Mixtures with the Mixed-Linker Zeolitic-Imidazolate Framework-7-8, ACS Appl. Mater. Interfaces, 2018, 10, 39631–39644.
44. P. Krokidas, S. Moncho, E. N. Brothers and I. G. Economou, Defining New Limits in Gas Separations Using Modified ZIF Systems, ACS Appl. Mater. Interfaces, 2020, 12, 20536–20547.
45. F. Hillman, M. R. A. Hamid, P. Krokidas, S. Moncho, E. N. Brothers, I. G. Economou and H. K. Jeong, Delayed Linker Addition (DLA) Synthesis for Hybrid SOD ZIFs with Unsubstituted Imidazolate Linkers for Propylene/Propane and n-Butane/i-Butane Separations, Angew. Chem., Int. Ed., 2021, 133, 10191–10199.
46. P. Krokidas, M. Castier, S. Moncho, E. Brothers and I. G. Economou, Molecular Simulation Studies of the Diffusion of Methane, Ethane, Propane, and Propylene in ZIF-8, J. Phys. Chem. C, 2015, 119, 27028–27037.
47. P. Krokidas, M. Castier, S. Moncho, D. N. Sredojevic, E. N. Brothers, H. T. Kwon, H. K. Jeong, J. S. Lee and I. G. Economou, ZIF-67 Framework: A Promising New Candidate for Propylene/Propane Separation. Experimental Data and Molecular Simulations, J. Phys. Chem. C, 2016, 120, 8116–8124.
48. H. T. Kwon, H. K. Jeong, A. S. Lee, H. S. An and J. S. Lee, Heteroepitaxially Grown Zeolitic Imidazolate Framework Membranes with Unprecedented Propylene/Propane Separation Performances, J. Am. Chem. Soc., 2015, 137, 12304–12311.
49. B. J. Bucior, N. S. Bobbitt, T. Islamoglu, S. Goswami, A. Gopalan, T. Yildirim, O. K. Farha, N. Bagheri and R. Q. Snurr, Energy-Based Descriptors to Rapidly Predict Hydrogen Storage in Metal-Organic Frameworks, Mol. Syst. Des. Eng., 2019, 4, 162–174.
50. P. Halder and J. K. Singh, High-Throughput Screening of Metal-Organic Frameworks for Ethane-Ethylene Separation Using the Machine Learning Technique, Energy Fuel., 2020, 34, 14591–14597.
51. E. H. Cho, X. Deng, C. Zou and L. C. Lin, Machine Learning-Aided Computational Study of Metal-Organic Frameworks for Sour Gas Sweetening, J. Phys. Chem. C, 2020, 124, 27580–27591.
52. H. Liang, K. Jiang, T. A. Yan and G. H. Chen, XGBoost: An Optimal Machine Learning Model with Just Structural Features to Discover MOF Adsorbents of Xe/Kr, ACS Omega, 2021, 6, 9066–9076.

---

Footnotes

† The data set and force field terms for each ZIF structure are also available in the Zenodo repository (https://doi.org/10.5281/zenodo.6342588 and https://doi.org/10.5281/zenodo.6389957).

‡ Electronic supplementary information (ESI) available: Information on the building units used to produce the ZIF structures of our database and relevant tables, force field description and DFT details, simulation and machine learning methods, estimation of the linkers and functional groups size, computational tools, and software data set and force field terms for each ZIF structure. See https://doi.org/10.1039/d2ta02624d

---