Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structure–property correlation in oxide-ion and proton conductors for clean energy applications: recent experimental and computational advancements
Mauro
Coduri
 a,
Maths
Karlsson
a,
Maths
Karlsson
 b and
Lorenzo
Malavasi
b and
Lorenzo
Malavasi
 *a
*a
aDepartment of Chemistry, University of Pavia, Viale Taramelli 12, 27100 Pavia, Italy. E-mail: lorenzo.malavasi@unipv.it; Tel: +39 382 987921
bDepartment of Chemistry and Chemical Engineering, Chalmers University of Technology, 412 96 Gothenburg, Sweden
First published on 15th February 2022
Abstract
In the last decade, the field of oxide-ion and proton conductors continued to trigger a significant amount of basic research aimed at improving the properties and the comprehension of actual materials, as well as at discovering novel phases. This need comes from the current and future urgent requests of changing our energy management towards cleaner solutions such as solid oxide fuel cells. In this review article, we highlight the most recent advancements in this exciting field by putting particular emphasis on the structure–property correlations in oxide-ion and proton conductors both from an experimental and a computational perspective. Special focus is laid on developments in the area of operando and in situ spectroscopy, machine learning and high-throughput approaches to accelerate the discovery of new and advanced materials.
Introduction
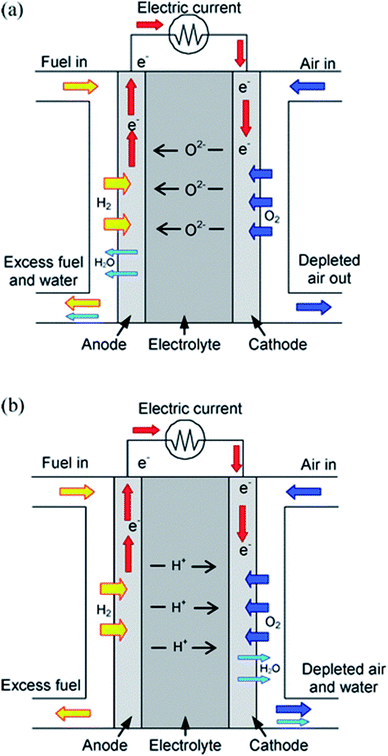
Starting from the Paris Agreement signed in 2015, 195 countries agreed to keep global warming below 2 °C, an ambitious goal requiring a strong decarbonization of the actual energy system. One of the core activities to achieve this goal is to promote a large-scale energy transition towards clean, low-carbon systems. As a matter of fact, very recently, several countries worldwide announced hydrogen roadmaps in order to afford this energy transition with the hope of achieving more than 20% of the final energy demand by 2050. In this respect, fuel cell technology becomes a major player of this challenging and exciting novel scenario for both transportation and stationary power generation.1Among the different kinds of fuel cells designed and optimized during these last decades, Solid Oxide Fuel Cells (SOFCs) have the potential to be one of the cleanest and most energy-efficient technologies for the direct conversion of hydrogen into electricity.2 The basic design of a SOFC includes anode and cathode electrodes, whose chambers are electrically connected, sandwiching a dense layer made of an ion conductor. State-of-the-art SOFCs generally encompass an oxide-ion conductor as the electrolyte, with Yttria Stabilized Zirconia (YSZ) being the reference material in terms of stability and performance, with optimal working temperatures between 700 and 1000 °C.3 On the other hand, the requirement of reducing the operation temperature of SOFCs below 600 °C to improve thermal compatibility of the component materials, thermal cycle capability and reducing the fabrication and materials costs by using metallic interconnectors in the SOFC stack cell, triggered, since the '80s, a significant research on devices including a proton-conducting electrolyte, with acceptor-doped cerates and zirconates, namely BaCeO3 and SrZrO3, as state-of-the-art proton conductors.3 The schematic operation of a SOFC according to the nature of the electrolyte, i.e. oxide-ion or proton conductor, is shown in Fig. 1.
In 2010 one of the authors of the present work reported an extensive review about the known oxide-ion and proton conducting electrolyte materials with a focus on their structural and mechanistic features.3 In these last ten years, materials chemistry research has aimed at discovering and developing novel and more efficient electrolyte materials, as well as at achieving a deeper microscopic understanding of the working mechanisms underlying ion conductivity in these materials, and hence, considerable advancements in the wider field of solid state ionics. The strong motivation to this continuous research efforts is, among others, to provide more efficient ion conductors displaying good performance at lower temperatures with respect to the actual ones, together with the need of gathering the required level of fundamental understanding of structure–property correlations in ion conductors generally. Such a motivation has pushed the level of the experimental study of the microscopic phenomena occurring in ion conductors to unprecedented levels making significant use also of operando and in situ approaches.4 Finally, the need of discovering novel materials brought materials informatics into the field of ion conductors with the aim of accelerating materials discovery.5,6
In the present Review, we focus our attention on the advancements of the last decade in the field of oxide-ion and proton conductors, encompassing materials discovery, characterization tools, and computational modelling, thus providing a critical update with respect to the state-of-the-art presented ten years ago, with particular emphasis to structure–property correlations, defect chemistry and property tuning strategies.3 The reader is referred to previous works for more traditional ion conductors for SOFCs.3,7,8
Recent advances in oxide-ion conductors
While several oxide-ion conductors have now found practical applications and are currently employed as electrolytes in SOFCs, the need of reducing operation temperatures, mitigating electronic conductivity, and improving chemical stability resulted in the discovery of some novel compositions of structural families possessing good performance with still significant space left for future research and further improvement. In this section we highlight the most recent findings in terms of novel materials/compositions concerning oxide-ion conductors. Due to the significant number of advancements in this research area, the section has been organized by collecting the different materials as a function of their structural family.ABO3 perovskites
Materials with the perovskite crystal structure displaying excellent oxide-ion conductivity are known since the '90s, in particular the doped lanthanum gallate, LaGaO3, family.9,10 One of the most exciting novel classes of ion conductors, based on the ferroelectric perovskite Na0.5Bi0.5TiO3 (NBT), has been reported in 2014 by Sinclair and co-workers.11 NBT has been for long time known as a lead-free piezoelectric material but, with a proper modulation of the material stoichiometry, it is possible to switch from an electronic to a nearly pure oxide-ion conductivity.11,12 The mechanism promoting such a transition in the transport properties of undoped NBT is based on the presence of a low Bi deficiency (which in uncontrolled synthetic procedure occurs incidentally due to the high volatility of Bi2O3) generating oxygen vacancies according to | (1) |
Since the increase of Bi-deficiency cannot be used, according to eqn (1), to further improve ion conductivity by oxygen vacancies creation as a consequence of the formation of significant amounts of secondary phases, defect chemistry has been exploited to tune the transport properties of NBT.14 It has been observed that, in general, NBT can accommodate low acceptor doping levels, mainly due to the formation of secondary phases, in analogy with Bi-deficient NBT. Several acceptor dopants have been explored, both considering the perovskite A-site to replace Bi3+ (with K+, Ca2+, Sr2+, and Ba2+) and B-site to replace Ti4+(Mg2+, Zn2+, Sc3+, Al3+, and Ga3+).14 Electrical measurements confirmed the best enhancement of bulk conductivity, oxide-ion transport numbers (up to 0.98) and oxygen diffusion coefficients for 1% Mg-doped and 2% Sr-doped NB0.49T, according to the following defect chemistry reactions:
 | (2) |
 | (3) |
The Arrhenius plot of bulk conductivity, σb, for undoped and acceptor-doped NBT ceramics is reported in Fig. 2a, where the dotted line represents the upper limit of bulk conductivity based on the oxygen-vacancy diffusion coefficient predicted for NBT with an oxygen deficiency of 0.025, calculated from the Nernst–Einstein equation.15
Possible reasons proposed for this limited enhancement of bulk conductivity by acceptor-doping in NBT are the low solid solubility of acceptor dopants (typically <2 at%) and trapping of oxygen vacancies especially by B-site acceptor dopants, which decreases the mobility of charge carriers.14Fig. 2a shows also a change in activation energy, Ea, from ∼0.4 eV above 300 °C to ∼0.9 eV below 300 °C for undoped and acceptor-doped NBTs. To date, no clear evidence of the origin of this phenomenon is available.
 | ||
| Fig. 2 (a) Arrhenius plot of bulk conductivity, σb, for undoped and acceptor-doped NBT ceramics. The dash-dot line represents the upper limit of σb based on the oxygen-vacancy diffusion coefficient, see text. Reprinted with permission from ref. 12. Copyright (2017) The Royal Society of Chemistry; (b) crystal structure of NdBaInO4 viewed along the c-axis (left) and b-axis (right). The solid lines represent the unit cell. Reprinted with permission from ref. 21. Copyright (2014) American Chemical Society; (c) Arrhenius plots of oxide-ion conductivities σion of BaGd0.9Ca0.1InO3.95, BaNdInO4, Ba1.1Nd0.9InO3.95, BaNd0.9Sr0.1InO3.95 and SrYbInO4. Reprinted with permission from ref. 23. Copyright (2020) The Royal Society of Chemistry; (d) difference bond valence sum maps for an oxide ion in NdBaInO4 at 1000 °C viewed along the c-axis (left side) and b-axis (right side). Red arrows show the possible diffusion paths of oxide ions. Reprinted with permission from ref. 21. Copyright (2014) American Chemical Society. | ||
Computational modelling of ion migration in NBT was used to infer a detailed microscopic picture of the diffusion behavior.16 Atomistic simulations confirmed that appreciable diffusivity is only exhibited by oxide ions, with cation not showing diffusion on the timescale and temperature range of the simulations.16 The analysis of different diffusion pathways in the cubic structure of NBT, revealed that the lower activation energy for oxide-ion migration, ΔEmig, is observed for the jump from a TiO2 layer to a BiO+ layer (0.11 eV) in the (100)-ordered structure, following curved routes in analogy with other perovskite oxides.16–18 Finally, while it appears that much research has been carried out on doping strategies to tune the ionic conductivity of NBT, there is still a lack of fundamental structural characterization in particular at the local scale. An early paper (before the evidence of ion conductivity) investigated the local structure of NBT by Transmission Electron Microscopy (TEM).19 This detailed work evidenced a complex cation distribution with the co-existence of chemical (Bi/Na) and displacive (octahedral tilting and cation displacements) disorder at RT, proposing that NBT consists of nanoscale domains with peculiar tilting extending over few perovskite cells.19 Moreover, the HRTEM allowed to explain the average monoclinic distortion observed by XRD and put in prominence the presence of cation displacements showing a substantial disorder along specific crystallographic directions which are at the origin of the observed diffuse scattering.19 A more recent paper tried to address such a point by collecting total scattering data coupled to reverse Monte Carlo modelling suggesting that A-site cation vacancies form large inactive spaces for oxide-ion conductivity and that materials without such vacancies could deliver much higher oxide-ion conductivity.20
Layered perovskites
A novel class of perovskite-related oxide-ion conductors was reported in 2014 by Fujii and co-workers who devised a layered structure based on the AA′BO4 general formula but showing an ordering of the A/A′ cations.21 The prototype system is the NdBaInO4 monoclinic compound consisting of Nd–O and (Nd2/8Ba6/8InO3) units with the structure (space group P21/c) depicted in Fig. 2b, as determined by synchrotron XRD and neutron diffraction (ND).21 In this crystal structure the InO6 octahedron is surrounded by the eight cations (two Nd and six Ba) giving the (A,A′)BO3 perovskite unit with the characteristic and novel feature of the edge of the B-site octahedron facing the A–O unit, differently from previously known AA′BO4 perovskite-related layered structures having the apical oxygen atoms of the perovskite unit facing the A–O unit.21 It is interesting to observe that the basic, elegant, idea which resulted in such discovery comes from an evaluation of the relative size of the A and A′ cations. In most of the AA′BO4 structures, the A and A′ cations have similar ionic radii leading to a random occupation of the crystallographic sites. On the other hand, Fujii and co-workers, explored the possible ordering of the two cations, anticipating an increase of oxide-ion conductivity, by selecting ions with significantly different size, thus resulting in the ordering reported in Fig. 2b and in the observed high ionic conductivity.22The Arrhenius plot of total conductivity of NdBaInO4, prepared by solid state reaction at 1400 °C starting from a mixture of BaCO3, In2O3, and Nd2O3, is reported in Fig. 2c, with total and ionic conductivities (measured in air) at 850 °C of σtotal = 5.3 × 10−4 S cm−1 and σion = 3.1 × 10−5 S cm−1, respectively. P(O2) independent conductivity was observed in the range from 3.2 × 10−11 to 3.0 × 10−19 atm, showing therefore a quite wide range of pure oxide-ion conductivity.21,23 Out of this range NdBaInO4 is a mixed oxide-ion and electron–hole conductor. The oxide-ion migration pathway was determined by the bond valence method at 1000 °C by using ND data. The possible diffusion paths were found to be two-dimensional and mainly involving two of the four oxygen sites (O3 and O4) connected to each other along both b- and c-axes. A sketch of the migration path devised from difference bond valence sum maps is shown in Fig. 2d.21 While the oxygen sites are fully occupied, according to the ND refinement, it is possible that minor oxygen vacancy defects are present as a consequence of slight uncontrolled cation non-stoichiometry during sample preparation.
Acceptor-doping has been used as the main strategy to improve the ion conductivity of NdBaInO4. Yang and co-workers reported a detailed experimental and computational investigation of Ca2+, Sr2+, and Ba2+ doping on the Nd3+ site of the layered perovskite NdBaInO4.24 Among these dopants, Ca2+ was found to be the most favorable one, as confirmed also by the lowest defect energy formation (0.76 eV) thus creating oxygen vacancies according to the following equation:
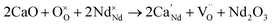 | (4) |
Already a small amount (5%) of Ca-doping can enhance the total conductivity by ∼2 orders of magnitude, while a further increase of Ca-content to x = 0.1 and 0.2 in Nd1−xCaxBaInO4−0.5x, led to a relatively smaller increase of conductivity, reaching, for x = 0.2, an oxide-ion conductivity of ∼3 × 10−4 to 1.3 × 10−3 S cm−1 within 600–800 °C with an activation energy of ∼0.70 eV.24 Static lattice and molecular dynamics simulations presented in ref. 23 indicate 2D oxygen vacancy migration in acceptor-doped NdBaInO4 where the bridging O1 and the terminal O3 and O4 sites are involved.24 Other compositions resulting in an improvement of about 1 order of magnitude of σion are Nd0.9Ba1.1InO3.95 and Nd0.9BaSr0.1InO3.95, with the existence of oxygen vacancies experimentally confirmed by single-crystal XRD and ND.25,26
Other NdBaInO4-related materials with general formula RBaInO4 (R = Sm, Ho, Y, Er, and Yb) have attracted attention in virtue of their oxide-ion conductivity and, among these phases, GdBaInO4 was found to be not isostructural to NdBaInO4 but displaying an orthorhombic crystal structure of the Ba2Y2CuPtO8 type consisting of InO5 square pyramids, InO6 octahedra, GdO7 polyhedra (monocapped trigonal prisms) and Ba cations.23 Oxide-ion conductivity of Ca-doped (10%) GdBaInO4 was comparable to that of monoclinic materials of this family with a bulk conductivity of Gd0.9Ca0.1BaInO3.95 equal to 1.3 × 10−3 S cm−1 at 700 °C and P(O2) = 10−4 atm in the electrolyte domain.23 The Arrhenius plot of some selected members of the RBaInO4 layered perovskite family of oxide-ion conductors is reported in Fig. 2c.23
The last relevant recent advancement in the field of oxide-ion conductors refers to the first evidence of such kind of conductivity in a Dion–Jacobson (DJ) type oxide reported in 2020 by the Yashima group.27 The DJ phase is an A′/A cation-ordered layered perovskite with a general formula of A′ [An−1BnO3n+1] (A′ = Cs, Rb, Li, H, Ag; A = La, Ca, Sr, Bi; and B = Ti, Nb, Ta, etc.), where n denotes the number of the BO6 octahedral layers, and the A′ cation separates the An−1BnO3n+1 perovskite-like layers.28,29 In the original paper reporting oxide-ion conductivity in a DJ oxide, the authors explored 69 phases using crystallographic data and the bond-valence method leading to the identification that the CsBi2Ti2NbO10 composition is one of the most performing based on the calculated energy barrier for the oxide-ion migration.27 CsBi2Ti2NbO10 crystallizes in the orthorhombic Ima2 structure and undergoes a first order phase transition towards a tetragonal P4/mmm structure around 800 K with a lattice volume change at the structural transition of about −0.042(5)%.27 The orthorhombic and tetragonal crystal structures of CsBi2Ti2NbO10−x are depicted in Fig. 3a. Bulk (σb) and grain boundary (σgb) electrical conductivity are reported in Fig. 3b showing a step rise at the phase transition with a significant increase of conductivity which has been correlated to a reduction of the oxygen content above 800 K up to x = 0.2 in CsBi2Ti2NbO10−x and therefore to an increase of oxygen vacancies. Interestingly, the tion remains close to 1 up to 1173 K under air/O2 atmosphere and the total DC electrical conductivity (σtot) at 973![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K is almost independent of the oxygen partial pressure P(O2) between P(O2) = 2.0 × 10−22 and 1
K is almost independent of the oxygen partial pressure P(O2) between P(O2) = 2.0 × 10−22 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) atm.27
atm.27
 | ||
| Fig. 3 (a) Crystal structures of orthorhombic (space group: Ima2, left panel) and tetragonal (973 K, space group: P4/mmm, right panel) CsBi2Ti2NbO10−x; (b) bulk electrical conductivity σb and grain boundary conductivity σgb of CsBi2Ti2NbO10−δ in dry air on heating; (c) a part of the structure and corresponding BVEL (d) showing the O1–O2 and O1–O1 oxide-ion diffusion paths. Blue and red-dotted lines with arrows denote the possible O1–O2 and O1–O1 diffusion pathways of oxide ion, respectively. Reprinted with permission from ref. 27. Copyright (2020) Nature Publisher. | ||
Concerning the origin of the high oxide-ion conductivity in CsBi2Ti2NbO10−x, it was found, by Rietveld refinement of ND data at 973 K of the tetragonal structure, that isotropic atomic displacement parameters of the equatorial oxygen atom, O1, and apical oxygen, O2, in the oxide-ion conducting inner perovskite layer (see Fig. 3a) were much higher than those of the equatorial O3 and apical O4 atoms in the outer perovskite layers.27 Moreover, by analyzing the anisotropic displacement parameters together with the use of the maximum-entropy method (MEM) and bond-valence-based energy landscapes (BVELs), a two-dimensional (2D) oxide-ion diffusion pathway was proposed.27 In more detail, the novel concept of large bottlenecks for oxide-ion by the large size of Cs+ and Bi3+ displacement was proposed to explain the migration in CsBi2Ti2NbO10−x, leading to the possible O1–O2 and O1–O1 diffusion pathways shown in Fig. 3c. For more details, the reader is referred to ref. 26.
The presence of a structural phase transition in CsBi2Ti2NbO10−x makes it unsuitable for practical applications and, very recently, Zhang and co-workers discovered the DJ-type oxide-ion conductor CsLa2Ti2NbO10−δ that does not show any transition in the temperature range from 297 to 1073 K.30 Ion transport properties evidenced oxide-ions as major charge carrier in CsLa2Ti2NbO10−δ while ion conductivity is lower with respect to CsBi2Ti2NbO10−x, possibly as a consequence of the reduced amount of oxygen vacancies due to oxygen under-stoichiometry. However, being this the first example of a DJ-type oxide-ion conductor without phase transitions, it is expected that cation doping and/or modification of the chemical composition will increase the conductivity performance.30
Hexagonal perovskite structural family
Conventional perovskites exhibit a 3D arrangement of corner-sharing octahedra but when the size mismatch between the two cations of the perovskite is large enough, the lattice strain can be reduced by allowing adjacent octahedra to share faces rather than corners. This is equivalent to considering the hexagonal stacking of AO3 layers (green planes in Fig. 4a) with the B-site cations sandwiched between the layers. Conversely, a cubic stacking would impose corner-sharing octahedra (Fig. 4b). Hexagonal (h) and cubic (c) stacking can alternate giving rise to many different perovskite structures. The conversion from cubic to hexagonal stacking in perovskites is detailed in ref. 31; examples of compounds with mixed stacking are given in ref. 32. | ||
| Fig. 4 Example of (a) hexagonal and (b) cubic stacking of BO6 octahedra of a general ABO3 perovskite, with the AO3 layers displayed in green; (c) Arrhenius plot of the bulk ionic conductivity of Ba3NbMoO8.5 (x = 0) and Ba3Nb0.9V0.1MoO8.5 (x = 0.1) with activation energies reported in eV. Reprinted with permission from ref. 37. Copyright (2020) American Chemical Society. Crystallographic structure and layer stacking of (d) 9R, (e) palmierite and BNMO (f). Adapted from ref. 39. | ||
In 2016, Fop et al. discovered that Ba3NbMoO8.5 (BNMO) displays similar bulk ionic conductivity to Gd-doped ceria, slightly higher than that of conventional Y2O3-stabilized zirconia at 500 °C.33 BNMO is the first hexagonal perovskite exhibiting important oxide ion conductivity, with 97–99% oxide ionic component to the total conductivity in O2 and 90–94% in 5% H2 in Ar. Oxide-ion conductivity is observed in a wide pO2 range, from 10−20 to 1 atm at 600 °C.33 The substitution of W for Mo avoids the insurgence of electronic conduction under a reducing atmosphere, ascribed to the facile reduction of Mo6+.34 Though the bulk conductivity of Ba3NbWO8.5 (BNWO) is one order of magnitude lower than that of the Mo analogous at 450 °C, it converges at higher temperatures.35 In addition, the total concentration of oxide ions can be tuned by adjusting the relative amount of Nb and Mo species. However, the temperature behavior is similar to that of a W-rich compound and no improvement was achieved.36 The partial substitution of V for Nb (∼10%) increases the bulk ion conductivity in BNMO by even an order of magnitude;37 however, full replacement of V for Nb in BVMO has a detrimental effect.38 The comparison of the bulk conductivities of BNMO and Ba3Nb0.9V0.1MoO8.5 is reported in Fig. 4c.37
BNMO has the intermediate stoichiometry (A3B2O8.5) between two reference structures, i.e. palmierite (A3B2O8) and 9R (A3B3O9).32 The term 9R stands for a rhombohedral (R) system with a periodicity of 9 layers (Fig. 4d). It is composed of trimers of face-sharing BO6 octahedra (chh units) connected through corner-sharing, repeated three times within a unit cell (chh)3. Instead, the B ions in palmierite form layers of isolated tetrahedra alternating to layers of vacant octahedra (Fig. 4e). BNMO has the same amount of B cations as palmierite, so that only two polyhedra in the trimers are actually occupied, thus favoring important cation disorder. Given that the oxygen population is intermediate between those of 9R and palmierite, Fop et al.33 proposed a hybrid structural model between the two reference structures, with the cations facing onto the cubic layers (c′) coordinated either tetrahedrally or octahedrally to oxygen. This hybrid model was later optimized by single crystal XRD, which revealed the off-centering of the partially vacant B2 cation lying in the central octahedron of the trimer (Fig. 4f).40
The main structural consequence of chemical doping concerns the relative population of tetrahedral and octahedral units. At RT, the substitution of W for Mo increases the population of octahedral units,34,41,42 while replacing Nb with V has the opposite effect.37 Moving towards oxygen-deficient systems, the oxygen vacancies induced by increasing the fraction of Nb at the expense of Mo in BNMO form preferentially on tetrahedral sites, thus increasing the relative fraction of octahedral units.36
An important aspect of the RT structure of BNMO is the O ion distribution within the cubic layer. Since the O sites of octahedral units are shared with the nearby polyhedra, each octahedron imposes octahedral coordination on its three neighbors, leading to an ideally, and unlikely, infinite layer of octahedra. As the simultaneous occupation of the two oxygen sites would lead to unreliable too short O–O distances, the presence of tetrahedral units introduces structural defects. In this context, Auckett et al.40 proposed the occurrence of distorted 5-fold coordinated B1 sites at the interface between octahedral and tetrahedral units. A neutron pair distribution function (PDF) study reported that at RT ∼ 45% of B1 sites are 5-fold coordinated.43 On the other hand, the more the octahedral units, the more the vacant B1 cations, which would act as a buffer between different polyhedra.44 This view is proposed by another PDF study, which suggests the local formation of tetrahedral-rich nanodomains, embedded in a matrix where the main coordination is octahedral.44 This is consistent with an early High-Resolution Transmission Electron Microscopy (HRTEM) investigation, which revealed the order of palmierite regions within the cubic layer.45 The two models can be reconciled by considering that intermediate coordination could occur at the interface of the domains.
The high temperature structural evolution was investigated first in ref. 46 to make a correlation with the conductivity behavior. The increase of temperature induces a progressive structural rearrangement, involving two main effects: (i) redistribution of the cations between the B1 and B2 sites, and (ii) transformation of octahedral into tetrahedral units. In this context, Chambers et al. revealed that the above changes occur via a first order reconstructive phase transition between 150 and 350 °C, likely driven by the disordering of the oxygen substructure.43,44 Concerning the distribution of oxygen ions, the conversion of part of octahedral unit into tetrahedral sites is systematically observed in the high temperature phase as revealed by synchrotron and ND data, as well as by the direct analysis of neutron PDF.35,36,41,44,46,47 This effect is even more apparent for compounds with large amount of octahedral units at room temperature, such as those rich in W and V. Interestingly, it was found that bulk ion conductivity scales systematically with the fraction of tetrahedral units.35,36,41,46 For example, BNWO shows a limited bulk ion conductivity at low temperature, which increases at high temperature to converge to the values observed for BNMO.35 Consequently, it has been proposed that oxygen ion conduction occurs via a concerted exchange between occupied and vacant oxygen sites, with the tetrahedral units being more flexible, thus providing low energy transition paths for oxygen diffusion. On the other hand, based on BVEL, Auckett et al. proposed that the observed increase in tetrahedral units induced by temperature could be interpreted as a dynamic effect, as a consequence of the O ion mobility, rather than a static occupation of tetrahedral O sites.40 They found that oxide-ion conductivity occurs predominantly within the ab plane, with some possible connectivity of the migration pathways along the c-axis. In this context, Yashima et al. proposed that conductivity is two-dimensional, showing sinusoidal diffusion pathways in the (010) plane due to the repulsion between B1 and the O ions in tetrahedral units.47 Fop et al. delved into the BVEL analysis, estimating the energy barriers related to the different migration processes.37 They reported that in BNMO-based hexagonal perovskites the O diffusion in the ab plane is clearly favored with respect to migration along c. Concerning the in-plane diffusion, two main energy barriers were identified: (i) E1, related to the ion exchange between O ions in tetrahedral and octahedral units, whose magnitude decreases by increasing the fraction of flexible tetrahedral units; (ii) E2, related to the out-of-plane relaxation of O ions during the exchange between the two O sites. The combination of the two effects correctly described the evolution of the activation energy as a function of the V content in Ba3Nb1−xVxMoO8.5.37 Moving instead from BNMO to BNWO, E1 increases dramatically, likely because of the lower fraction of tetrahedral units. In this respect, Auckett et al.48 suggested that it is the energy difference between the two O sites that drive the occupancies observed experimentally, not the opposite. Gilane et al. applied BVEL to Ba3VWO8.5 (BVWO), which exhibits ordered vacancies on the B2 site.38 The energy barriers are similar to those of BNMO. However, BVWO showed much lower bulk conductivity than BNMO and BNWO. The reason is ascribed to the missing connectivity between O sites along the c axis, due to the vacant B2 sites. It turned out that while bulk conductivity in BVWO is limited to the ab plane, it is three dimensional for BNMO and BNWO. Therefore, even the cation distribution plays a major role defining the magnitude of ion conductivity.
The promising transport properties found in BNMO-related materials inspired the search for new hexagonal perovskites with similar cation and anion disordered environments. In this framework, in 2020 remarkable oxygen ion and proton conduction was reported in Ba7Nb4MoO20 (B7NMO).49 The oxygen ion bulk conductivity of B7NMO is considerably higher than that of yttria-stabilized zirconia and comparable to La0.8Sr0.2Ga0.83Mg0.17O2.815 (LSGM), with oxide-ion transport number >0.99 under both air/O2 and air/5% H2 (in Ar). The electrolytic domain of B7NMO extends between ∼10−18 and 1 atm at 600 °C. In addition, the bulk conductivity in humid air (4.0 mS cm−1 at 510 °C) is in the same order of magnitude of both Y-doped barium cerate and zirconate.
B7NMO has similar structure characteristics as BNMO (Fig. 5a). It is a cation-deficient 7H hexagonal perovskite (hhcchhc′) formed by an intergrowth of palmierite-like (hc′h) and 12R perovskite blocks (hcch).50 It is composed of two sets of face-sharing trimers of octahedra, alternated by a layer of corner-sharing octahedra. This corresponds to the alternation of two hexagonal and two cubic layers (hhcc), typical of the 12R structure. The 12R-like block is followed by an oxygen-deficient palmierite-like layer (c′). Whereas in BNMO two different metal sites occupy the trimers, in B7NMO the three B sites are independent. The site located far away from the c′ layer (B3) has full occupancy, while the other two sites are only partially occupied. All oxygen sites are fully occupied except those on the c′ layer. Again, depending on which site is occupied, either tetrahedral or octahedral units form, leading to different local geometries. In addition, similarly to BNMO, the increase of temperature induces a structural rearrangement, forming more tetrahedral units and changing the relative occupation of B sites. In the case of B7NBO, however, full conversion of octahedral into tetrahedral units is observed above 300 °C, thus providing favorable and more dynamic environments for oxygen migration with respect to the BNMO family, which conserves a significant number of octahedral units at high temperature. This phase transition is closely related to an increase in proton conductivity which is discussed later in this review. The effect of hydration on the crystallographic structure has been deepened via in situ ND under controlled hydration with deuterated water.51 Dry B7NMO exhibits most of O vacancies on the O2 – octahedral site – within the palmierite c′ layer. In addition, the B2 site is fully vacant, leading to an ordered cationic arrangement along the c axis. Ab initio molecular dynamics (AIMD) simulations at 1000 K revealed that oxygen ion diffusion occurs mostly within the c′ layers (Fig. 5b). BVSE confirmed the lowest bond-valence site energy connectivity along the palmierite-like layers (Fig. 5c). In addition, being the octahedral site empty at high temperature, the cooperative diffusion mechanism proposed for BNMO is prevented for dry B7NMO, implying a curved conduction pathway instead.51
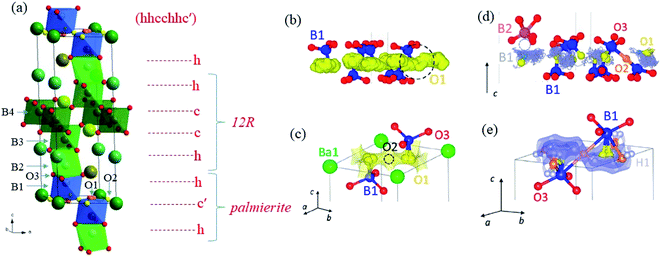 | ||
| Fig. 5 (a) Crystallographic structure and layer stacking of B7NMO. (b) Oxide ion trajectory plot for dry Ba7Nb4MoO20 obtained by AIMD simulations at 1100 K. The black dashed circle highlights hopping between adjacent O1 sites. (c) Bond-valence site energy map showing the oxide-ion conduction pathway formed by the lowest energy connecting isosurfaces for an O2− ion along the palmierite-like layer in dry B7MNO. Isosurface levels are drawn at <0.4 eV over the global minimum. (d) Proton trajectory plots for hydrated Ba7Nb4MoO20·0.5H2O obtained by AIMD simulations. A proton in proximity of an empty M1 site (indicated by the gray dotted circle) does not undergo any hopping for the duration of the simulation. (e) BVSE map calculated for a test H+ ion for hydrated Ba7Nb4MoO20 showing connectivity along the palmierite-like layer (isosurface levels <0.15 eV). Adapted with permission from ref. 50. Copyright 2021 American Chemical Society. | ||
Water absorption occurs via the hydration of oxygen vacancies within the vacant octahedral (O2) sites, with the formation of protonic defects. The mechanism of proton migration, derived by AIMD, involves the rotational diffusion of the protons around the tetrahedral and octahedral O positions, followed by hopping onto an H site on an adjacent B1 center (Fig. 5d). When the B1 site is vacant, the migration energy barrier of the proton is increased significantly, thus trapping the proton close to the vacant B1 site. The proton trapping is likely at the origin of the unusual increase of proton conductivity observed on increasing temperature. BVSE confirmed that the proton migration pathway as well resides along the palmierite-like layers (Fig. 5e).
A further enhancement of ion conduction has been obtained in 2021 by increasing the relative amount of Mo6+ for Nb5+ in B7NMO.52 The charge mismatch is compensated by the formation of interstitial O ions forming Ba7Nb3.9Mo1.1O20.05. Again, the O ions in excess occupy octahedral sites in the palmierite-like c′ layer; though Ba7Nb3.9Mo1.1O20.05 shows the same interstitialcy diffusion mechanism as BNMO, which is different than undoped B7NMO.51
The limited amount of O2 sites hinders the water uptake, limiting proton conduction, thus making oxide-ion the dominant charge carrier. Electronic conductivity was observed only in the P(O2) range of 6 × 10−24 to 4 × 10−26 atm at 900 °C while the ion transport number is 1.00 between 700 and 900 °C. The bulk conductivity at 300 °C (nearly 1 mS cm−1) is the highest ever recorded at such a low temperature (Fig. 6a and b). The origin of such a performance lies in the oxide-ion diffusional pathway between the tetrahedral and interstitial octahedral units within the palmierite-like cubic layer, favoured by the large amount of interstitial oxygen ions. The energy barriers for oxide-ion migration within the ab plane (0.19 eV) is much lower than that along the c axis (1.54 eV), thus leading to a mostly 2D oxide-ion diffusion. These results highlight the high potential of the hexagonal perovskite related oxides, driving research towards the implementation of chemical species that favor the formation of low coordination polyhedra in the conducting planes.
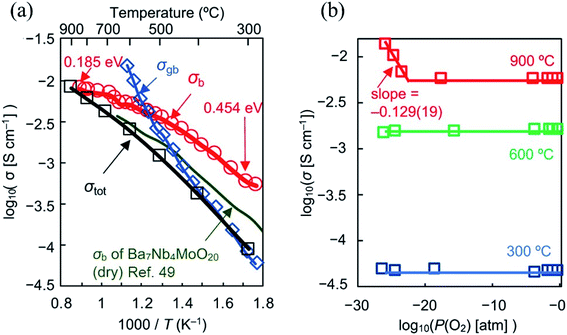 | ||
Fig. 6 (a) Arrhenius plots of bulk conductivity σb, grain-boundary conductivity σgb and DC σtot of Ba7Nb3.9Mo1.1O20.05 in dry air. Activation energy for σb of Ba7Nb3.9Mo1.1O20.05 decreases with temperature from 0.454 to 0.185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV as shown by the red numbers in panel c. Green line represents σb of Ba7Nb4MoO20 reported by Fop et al. in ref. 49; (b) oxygen partial pressure P(O2) dependence of σtot of Ba7Nb3.9Mo1.1O20.05. Reprinted with permission from ref. 52. Copyright 2021 Nature Publishing Group. eV as shown by the red numbers in panel c. Green line represents σb of Ba7Nb4MoO20 reported by Fop et al. in ref. 49; (b) oxygen partial pressure P(O2) dependence of σtot of Ba7Nb3.9Mo1.1O20.05. Reprinted with permission from ref. 52. Copyright 2021 Nature Publishing Group. | ||
Table 1 summarizing the compositions, crystal structure, conductivity and transport numbers of all the oxide-ion conductors discussed in the previous section is shown below, while Fig. 7 reports an Arrhenius plot summarizing the oxide-ion conductors considered in this review compared to YSZ.
| Composition | Structure type | Conductivity (S cm−1)/temperature | Transport number/temperature | Ref. |
|---|---|---|---|---|
| Na0.5Bi0.49TiO2.985 | Perovskite | 1.42 × 10−3/500 °C | 0.93/600 °C | 11 |
| Na0.5Bi0.49Ti0.98Mg0.02O2.965 | Perovskite | 4.06 × 10−3/500 °C | 0.98/600 °C | 11 |
| Na0.5Bi0.49Ti0.98Sr0.02O2.965 | Perovskite | 5.13 × 10−3/500 °C | 0.96/600 °C | 13 |
| NdBaInO4 | Perovskite derivative | 5.13 × 10−3/850 °C | <0.04 | 20 |
| Nd0.8Ca0.2BaInO3.9 | Perovskite derivative | 1.35 × 10−3/800 °C | 0.25/700 °C | 22 |
| Gd0.9Ca0.1BaInO3.95 | Perovskite derivative | 1.3 × 10−3 S cm−1/700 °C | — | 23 |
| CsBi2Ti2NbO10−δ | Dion–Jacobson cation-ordered layered perovskite | 1.3 × 10−3/800 | 1.00–0.98/600–900 °C | 27 |
| Ba3NbMoO8.5 | Hexagonal perovskite | 2.2 × 10−3 S cm−1/600 °C | 0.97–0.99/450–600 °C air/O2 | 33 |
| 0.90–0.94/450–600 °C air/5% H2 in Ar | ||||
| Ba3NbWO8.5 | Hexagonal perovskite | 1.7 × 10−3 S cm−1/600 °C | — | 34 |
| Ba3Nb0.9V0.1MoNbO8.5 | Hexagonal perovskite | 1.01 × 10−2 S cm−1/600 °C | — | 37 |
| Ba7Nb4MoO20 | Hexagonal perovskite | 1.9 × 10−3 S cm−1/510 °C (dry) | >0.99/500–800 °C air and air/5% H2 in Ar | 49 |
| 4.0 × 10−3 S cm−1/510 °C (air + H2O) | ||||
| Ba7Nb3.9Mo1.1O20.05 | Hexagonal perovskite | 5.8 × 10−4 S cm−1/310 °C | ≥0.99/600–900 °C air/O2 | 52 |
| 0.98/600 °C air/5% N2 in H2 |
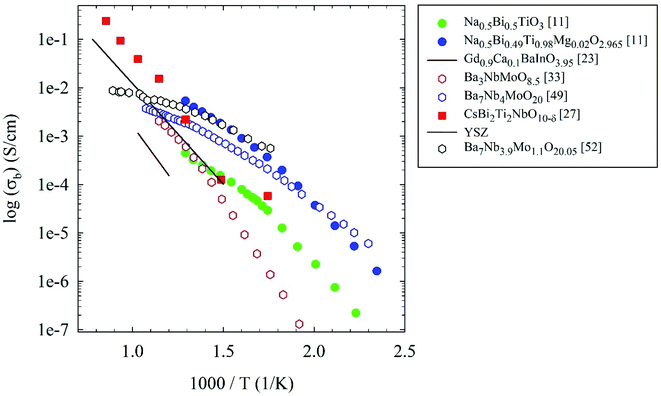 | ||
| Fig. 7 Arrhenius plots of bulk conductivity of the oxide-ion conductors considered in the present review. For details see the main text. | ||
Recent advances in proton conductors
The reduction of fuel cells' operating temperatures can be obtained by replacing the oxide-ion conducting electrolyte with a proton conductor. Thanks to the lower activation energy of proton migration with respect to oxide-ions, protonic ceramic fuel cells (PCFCs) offer appealing potential for high-performance at lower temperatures. The field of proton conducting electrolytes has been since long time dominated by perovskite oxide materials such as acceptor doped AMO3 (A = Sr, Ba, M = Zr, Ce, etc.), where the key mechanism of water incorporation is mediated by the presence of oxygen vacancies.3,53–56 Despite their good conductivities, the high grain boundary resistance and fabrication difficulties, related to the refractory nature of perovskite materials, have to date limited the real application of PCFCs. This couples also to the lack of ad hoc cathode materials engineered for proton conducting electrolytes which is a very active field of investigation for PCFCs.57–59Coming to the recent advancements on proton electrolytes, fewer results have been reported in the last decade with respect to oxide-ion conductors. One of the main reasons for this may be related to the mechanism of proton conductivity. In the previously mentioned perovskite oxides, protons are incorporated in the electrolyte through the oxygen vacancies created by acceptor doping through the following mechanism:
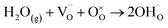 | (5) |
Such a mechanism is found in several other proton conducting oxides which share in most cases the problems of sintering and fabrication of suitable dense electrolytes. On the other hand, materials incorporating intrinsic protons such as solid acids based on titanates and niobates, for example H2Ti3O7 and HPb2Nb3O10·nH2O have relatively low ionic conductivities and operational temperature range.60,61
In the search for possible novel proton conductors, Lan and co-workers explored intercalation materials widely used as cathode in lithium batteries, where Li+ shows fast anisotropic diffusion in the structure channels.62 Starting from this evidence, the authors modified the known materials such as LiCoO2, LiFeO2, and LiNiO2 in order to promote proton migration and suppress the electronic conductivity. As a result, the single phase materials with the following formula LixAl0.5Co0.5O2 with x < 1.0 have been prepared and reported for possible proton conductivity.62 The presence of lithium deficiency is expected to be beneficial for the incorporation of hydrogen at high temperature leading to the LixHyAl0.5Co0.5O2 material. A sketch of the proposed mechanism for proton insertion in layered LixAl0.5Co0.5O2 is shown in Fig. 8a.
 | ||
| Fig. 8 (a) Diagram for insertion of protons in the LixAl0.5Co0.5O2 in presence of hydrogen. Red sphere, Li+ ions; blue sphere, H+ ions. Reprinted with permission from ref. 62. Copyright (2014) Wiley; (b) ionic conductivities for LSZG at different temperatures determined from impedance data at high frequencies: (a) Li ion conductivity as measured using a Ag/LSZG/Ag symmetrical cell in air, (b) H+ conductivity as measured in a Ni/LSZG/Ni symmetrical cell in 4% H2/Ar + 5% H2O with 0.4 V DC voltage bias, and (c) oxygen ion conductivity of GDC electrolyte in a LSCF/GDC/LSCF cell in air; (c) proton transport trajectories from ab initio molecular dynamics simulations. H+ = light magenta trajectories, purple tetrahedra are GeO4, large green spheres are Li+, and small red spheres are O2−. Reprinted with permission from ref. 68. Copyright (2017) American Chemical Society; (d) schematic diagram of SOFC with samarium nickelate (SNO) perovskite electrolyte and its operation mechanism. Spontaneous hydrogen incorporation creates a strongly correlated insulating layer and suppresses the electronic current. Reprinted with permission from ref. 72. Copyright (2016) Elsevier Publisher. | ||
The material with nominal formula LiAl0.5Co0.5O2 belongs to the trigonal system (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, a = 2.8016(7) Å, c = 14.1631(34) Å), with cobalt and aluminum ions sharing, randomly, the (0, 0, 1/2) sites, and thermal analysis did not evidence any phase transition up to 1000 °C.62 To test the performance of the material, LiAl0.5Co0.5O2 was used as the electrolyte for a H2/air fuel cell using silver as both the anode and cathode as well as current collector. Such cell exhibited good performance between 475 and 575 °C. At 525 °C, the maximum current density and power density were 698 mA cm−2 and 173 mW cm−2 respectively, while the thickness of the electrolyte was 0.79 mm.62 Moreover, a proton conductivity of 0.1 S cm−1 was observed at 500 °C for LiAl0.5Co0.5O2 with a measured OCV at 525 °C of 1.022 V. The overall results indicate that LiAl0.5Co0.5O2 is almost a pure H+ or O2− or mixed H+/O2− ionic conductor under H2/air fuel cell operating conditions with a negligible electronic conductivity.62 This report of protonic conductivity in LiAl0.5Co0.5O2 layered oxide did not prompt a significant amount of further work in order to optimize this electrolyte, while similar oxides have found interesting applications as triple conducting (oxide-ion, proton and electron) cathodes in low-temperature SOFC in the presence of a conventional proton conducting electrolyte.63–67
m, a = 2.8016(7) Å, c = 14.1631(34) Å), with cobalt and aluminum ions sharing, randomly, the (0, 0, 1/2) sites, and thermal analysis did not evidence any phase transition up to 1000 °C.62 To test the performance of the material, LiAl0.5Co0.5O2 was used as the electrolyte for a H2/air fuel cell using silver as both the anode and cathode as well as current collector. Such cell exhibited good performance between 475 and 575 °C. At 525 °C, the maximum current density and power density were 698 mA cm−2 and 173 mW cm−2 respectively, while the thickness of the electrolyte was 0.79 mm.62 Moreover, a proton conductivity of 0.1 S cm−1 was observed at 500 °C for LiAl0.5Co0.5O2 with a measured OCV at 525 °C of 1.022 V. The overall results indicate that LiAl0.5Co0.5O2 is almost a pure H+ or O2− or mixed H+/O2− ionic conductor under H2/air fuel cell operating conditions with a negligible electronic conductivity.62 This report of protonic conductivity in LiAl0.5Co0.5O2 layered oxide did not prompt a significant amount of further work in order to optimize this electrolyte, while similar oxides have found interesting applications as triple conducting (oxide-ion, proton and electron) cathodes in low-temperature SOFC in the presence of a conventional proton conducting electrolyte.63–67
On the same line of trying to make use of Li+ conductors to promote proton diffusion, Wei and co-workers applied this approach on the class of lithium super ionic conductor (LISICON) materials.68 In particular, Sr-doped Li13.9Sr0.1Zn(GeO4)4 (LSZG) was tested as a possible proton conductor by fully replacing Li+ ions by H+ ions through ion exchange.68 Under testing condition of pristine LSZG with different gases, including 4% H2/Ar + 5% H2O in a symmetrical cell (Ni/LSZG/Ni) a high protonic conductivity of 0.039 S cm−1 at 600 °C was measured.68 To further verify the proton conductivity of LSZG, all the mobile Li+ ions were replaced with protons by using acetic acid ion exchange improving the proton conductivity to about 0.048 S cm−1 at 600 °C. Finally, proton conduction in LSZG was also measured by manufacturing a full cell with a configuration of Ni/LSZG/LSCF. Fig. 8b shows the conductivity of the LSZG electrolyte as measured under different conditions (see figure caption for details) at a cell voltage of 0.7 V. When tested under SOFC operation conditions, the LSZG electrolyte displayed proton conductivity of 0.034 S cm−1 at 600 °C which is two times higher than GDC.68Ab initio molecular dynamics simulations at 600, 700, 800 and 900 K were used to elucidate the possible mechanism for H+ migration. It was assumed that protons moved through the same sites actually used by lithium in LISICON materials, and that a facile Li+/H+ ion exchange may occur when lithium ions are placed in nonframework sites.68 As a result, the most probable migration path for protons involves the interstitial space, as shown in Fig. 8c, thanks to the presence of Li+ vacancies. The estimated diffusion coefficient in the LSZG system is above 6 × 10−5 cm2 s−1, while in Y-doped BaZrO3 at the same temperature, both simulation and experiments show a value close to 10−5 cm2 s−1.68–70
A completely new approach in the design of proton electrolytes has been proposed by Zhou and co-workers by employing strongly correlated perovskites, such as SmNiO3, which are electronic conductors in the temperature range of low-temperature (300–500 °C) fuel cells.71 The authors discovered that under exposure to hydrogen, such as in the environment of a SOFC, electrons are doped into SmNiO3via spontaneous hydrogenation and the valence of nickel is reduced to Ni2+ through the following reaction:
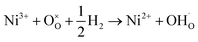 | (6) |
Such a mechanism leads to a suppression of the electronic transport by the Hubbard intra-orbital electron–electron Coulomb interaction which is defined as filling-controlled Mott transition, allowing the use of hydrogenated SmNiO3 as an electrolyte.71 This is a quite remarkable result since it also implies that the concentration of protons in the perovskite is not limited by the number of oxygen vacancies as in traditional acceptor-doped materials (see eqn (5)). A schematic diagram of a SOFC operating with SmNiO3 (SNO) is shown in Fig. 8d, where H–SNO refers to the hydrogenated compound.72 Under operating conditions, when the hydrogen fuel is introduced at the anode, hydrogen molecules dissociate into protons and donate electrons to Ni3+ in SmNiO3 at the triple phase boundaries. The hydrogenation process creates an electrically insulating H–SNO on the anode side and, once this insulating layer is formed, as long as hydrogen fuel is supplied, protons can continue to diffuse under the chemical potential gradient, while the electron transport through H–SNO directly to the cathode is strongly suppressed by carrier localization. As a result, electrons are forced to pass through the external circuit and generate electrical power.71 The performance of micro-fabricated SOFCs employing H–SNO are comparable to the best-performing proton conducting fuel cells with a power output reaching a maximum value of 225 mW cm−2 at 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. Also the highest OCV achieved (1.03
°C. Also the highest OCV achieved (1.03![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V) is very close to the Nernst potential (∼1.07
V) is very close to the Nernst potential (∼1.07![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V), indicating an ionic transference number close to 1.71 A thorough X-ray Absorption Spectroscopy (XAS) investigation in ref. 71, probing the Ni-L edge of SNO and H–SNO (both in situ and ex situ), confirmed the high proton concentration not only at the surface but also through the thickness of the SNO film. Such results have been confirmed on SNO epitaxial thin films grown by pulsed laser deposition reporting a high ionic conductivity of 0.030 S cm−1 at 773 K and a small activation energy of 0.23 eV at 473–573 K.73 As in the previous case of layered materials, no significant further development of this interesting result has been provided to date, possibly due to the difficulty in incorporating such exotic electrolyte into optimized devices as well as for the availability of suitable electrodes for real applications.
V), indicating an ionic transference number close to 1.71 A thorough X-ray Absorption Spectroscopy (XAS) investigation in ref. 71, probing the Ni-L edge of SNO and H–SNO (both in situ and ex situ), confirmed the high proton concentration not only at the surface but also through the thickness of the SNO film. Such results have been confirmed on SNO epitaxial thin films grown by pulsed laser deposition reporting a high ionic conductivity of 0.030 S cm−1 at 773 K and a small activation energy of 0.23 eV at 473–573 K.73 As in the previous case of layered materials, no significant further development of this interesting result has been provided to date, possibly due to the difficulty in incorporating such exotic electrolyte into optimized devices as well as for the availability of suitable electrodes for real applications.
Very recently, a novel strategy, in addition to acceptor doping, has been proposed to increase the hydration of brownmillerite-type structure by Kawamori and co-workers.74 Hydrated Ba2Sc2O5 has been previously reported in form of nanosized powder prepared by means of low-temperature techniques.75 During this process, the naturally present oxygen vacancies of the brownmillerite structure are consumed and a perovskite-type structure, namely BaScO2(OH), is obtained. However, previous approaches did not allow to obtain dense pellets and fully hydrated phases. The novel strategy proposed in ref. 75 makes use of high-pressure synthesis, starting from Ba(OH)2·H2O and Sc2O3, by using a multianvil apparatus under 8 GPa at 1200 °C for 8 hours, followed by pressure quenching. The actual amount of protons in the obtained samples, as determined by thermogravimetry, was around 8.3 mass%, achieving the BaSc0.67O(OH)2 composition. This proton concentration is about 10 times higher than that of conventional perovskite-type proton conductors such as acceptor-doped BaZrO3. This approach allowed to achieve an electrical conductivity of about 10−2 S cm−1 at 450–500 °C. Clearly, this method of improving the proton concentration in perovskite-related materials, can be hardly thought to be scalable, requiring the use of high-pressure apparatus. However, the evidence of a novel charge compensation mechanism for proton-conducting oxides may open a new technological route to increase their ionic conductivity.
Further enhancement of ionic conductivity in traditional perovskite proton conductors has been achieved by heavily doping barium zirconate with Sc.76 This dopant was choosen because of a lower proton–dopant association energy with respect, for example, to Y. Improvement of conductivity by increasing the acceptor doping level in BaZrO3 often results in low densities and resistive grain boundaries. However, Hyodo and co-workers were able to introduce up to 60 wt% of Sc in BaZrO3 by chemical solution and sintering at 1600 °C, providing dense pellets of a single-phase cubic perovskite material.76 Importantly, this high doping level resulted in a proton concentration close to 0.55 mol per formula unit leading to a total proton conductivity, reflecting both the bulk and grain boundary resistivities in the polycrystalline pellet, exceeding 0.01 S cm−1 between 396 and 534 °C under a water partial pressure of 0.02 atm.76 Finally, this composition resulted also to be stable against CO2 as determined by an accelerated test at 400 °C. Clearly this work highlights some further potential of cerates and zirconates event though the well-known high temperature sintering issues still represent a practical problem to be overcome.
Another interesting strategy to promote proton conductivity has been recently proposed by Lee and co-workers.77 The authors prepared A-site deficient hydrated CaTiO3 by directly replacing the lattice oxygens  with hydroxide (OH−) through a solvothermal process. This approach resulted to be tenfold more effective in the sample hydration with respect to traditional acceptor-doping strategy of creating and filling oxygen vacancies. The final stoichiometry of a sample prepared by this solvothermal route was determined to be Ca0.92TiO2.84(OH)0.16.77 This sample, with respect to a common sample prepared by solid state chemistry, showed a remarkable increase in the bulk conductivity below 300 °C reaching a value of 3.4 × 10−5 S cm−1 at 200 °C being comparable to the benchmark conductivity values obtained for barium zirconate/cerate and disordered hexagonal perovskite in the same temperature regime.54,78 Above 350 °C an electronic contribution to conductivity has been found in mildly reducing atmosphere. This strategy to enhance the proton conductivity in a traditional perovskite oxide should trigger further experimental work in other related materials to try going beyond the limits imposed by the conventional aliovalent doping approaches.
with hydroxide (OH−) through a solvothermal process. This approach resulted to be tenfold more effective in the sample hydration with respect to traditional acceptor-doping strategy of creating and filling oxygen vacancies. The final stoichiometry of a sample prepared by this solvothermal route was determined to be Ca0.92TiO2.84(OH)0.16.77 This sample, with respect to a common sample prepared by solid state chemistry, showed a remarkable increase in the bulk conductivity below 300 °C reaching a value of 3.4 × 10−5 S cm−1 at 200 °C being comparable to the benchmark conductivity values obtained for barium zirconate/cerate and disordered hexagonal perovskite in the same temperature regime.54,78 Above 350 °C an electronic contribution to conductivity has been found in mildly reducing atmosphere. This strategy to enhance the proton conductivity in a traditional perovskite oxide should trigger further experimental work in other related materials to try going beyond the limits imposed by the conventional aliovalent doping approaches.
Interestingly, two structural types discussed above as potential oxide-ion conductors, have been also investigated for their proton conductivity.78 As a matter of fact, the first report of high proton conductivity in a hexagonal perovskite was reported in 2020 by Fop and co-workers.49 In the previous section we already highlighted the oxide-ion conductivity of B7NBO. Concerning the proton conductivity, the authors observed a decrease in activation energy above 300 °C, simultaneous to the structural reorganization, which is more apparent working in humid atmosphere. Conductivity measurements revealed that the proton transport number increases steeply, reaching ∼0.81 at 525 °C. Indeed, the structural rearrangement of the oxygen/vacancy distribution facilitates the water uptake. BNMO, on the contrary, contains a larger concentration of octahedral units and uptakes water only to a lesser extent. This is not enough to promote significant proton conduction; still it does induce structural distortions. This is likely the reason for discrepancies in structural parameters observed in different studies on the same compounds of the BNMO family, or even within the same work.43 The mechanism of proton conductivity has been discussed above in connection with the oxide-ion migration path, being the two closely related to the structural features of B7NBO.
Proton conducting hexagonal perovskite-related oxides of general formula Ba5M2Al2ZrO13 (M = Gd, Dy, Ho, Er, Tm, Yb, Lu, In) have been reported as well in 2020 (few months after the discovery of B7NBO). This family of compounds adopts a structure which consists of triple-layer cubic perovskite blocks that are separated by an intrinsically oxygen-deficient hexagonal BaO (h′) layer.79 The Ba5Er2Al2ZrO13 member of this family showed a total conductivity higher than 10−3 S cm−1 between 300 and 1200 °C, with proton transport number close to 1 (>0.99) from 300 to 600 °C (see Fig. 9a).79 From a mechanistic point of view, the crystal structure of Ba5Er2Al2ZrO13 possesses the oxygen-deficient h′ layers, yielding a large number of oxygen vacancies without any acceptor doping. The authors suggest that water is incorporated in the h′ layers leading to the formation of proton carriers as follows:
 | (7) |
 | ||
| Fig. 9 (a) Arrhenius plots of the total electrical conductivity of Ba5Er2Al2ZrO13·xH2O in dry and wet (water vapor pressure P(H2O) = 0.017 atm) air in the cooling process; (b) crystal structure of Ba5Er2Al2ZrO13.23H0.46 refined using neutron-diffraction data at 18 °C. Green, pink, blue, gray, light red, dark red and red ellipsoids, and red and black spheres represent Ba, Er, Zr, Al, O1, O2, O3, O4, and H atoms, respectively. Thermal ellipsoids are drawn at the 95% probability level. Reprinted with permission from ref. 79. Copyright (2020) American Chemical Society; (c) Arrhenius plot of bulk conductivity of a BNC20 sample under dry and wet N2. Reprinted with permission from ref. 80. Copyright (2021) American Chemical Society. | ||
A sketch of the hexagonal lattice (P63/mmc) of protonated Ba5Er2Al2ZrO13, with highlighted water incorporation layers, is shown in Fig. 9b.79 According to ND analysis, the protons are mainly located on the O3 sites of the structure (Fig. 9b) and the final refinement of a fully protonated sample gave the composition of Ba5Er2Al2ZrO13.23H0.46.79 These recent evidences of high proton conductivity in a hexagonal perovskite-related structures by Fop and Murakami, suggest that other possible compositions within this structural type could be good proton conductors.49,79
The other material which has been already discussed as an oxide-ion conductor, which can be also a potential proton conductor, is the layered perovskite NdBaInO4. In particular, through Ca-doping according to eqn (4) the number of oxygen vacancies increases resulting in an improvement of electrical conductivity in dry air, as reported above.24 These oxygen vacancies can be possible water incorporation sites according to eqn (5). This has been verified by Zhou and co-workers by measuring electrical conductivity in wet-air on Nd0.9BaCa0.1InO3.95 and Nd0.8BaCa0.2InO3.9 compositions.80 In particular for the latter, both the total conductivity, and the bulk conductivity, were enhanced in wet atmosphere over a large temperature range (250–750 °C) compared with those measured in dry atmosphere (see for example Fig. 9c), particularly in N2 environment.80 The proton conductivity was estimated by subtraction of total conductivity in wet N2 and the total conductivity in dry N2, giving, in the temperature range from 250 to 475 °C, a transport number of protons from 0.41 to 0.57.80 The result reported is not unexpected since most of the oxide ion conductors having intrinsic oxygen vacancies are suitable materials for water incorporation according to eqn (2). On the other hand, this composition also showed a poor chemical stability when being exposed to the humid environment for a long period of time. While this specific material will not see any significant application due to the issue reported, it will be of interest to pursue a deep investigation of related layered perovskites to improve their stability and proton conductivity.
Table 2 summarizes the essential data of the novel proton conductors discussed above, while Fig. 10 reports the Arrhenius plot of the most significant novel proton conductors.
| Composition | Structure type | Conductivity (S cm−1)/temperature | Transport number/temperature | Ref. |
|---|---|---|---|---|
| LiAl0.5Co0.5O2 | Layered | 0.10/500 °C | 0.3–0.71/500–625 °C | 62 |
| Li13.9Sr0.1Zn(GeO4)4 | LISICON-type | 0.034/600 °C | — | 68 |
| SmNiO3 | Perovskite | 0.030/500 °C | ∼1/600 °C | 71 |
| BaSc0.67O(OH)2 | Perovskite | 0.01/500 °C | — | 74 |
| BaZr0.4Sc0.6O2.7 | Perovskite | 0.01/400 °C | ∼1/600 °C | 76 |
| Ba5Er2Al2ZrO13 | Hexagonal perovskite | 10−3/300–1200 °C | ∼1/300–600 °C | 79 |
| Nd0.8BaCa0.2InO3.9 | Perovskite derivative | 1.3 × 10−4/500 °C | 0.41–0.57/250–475 °C | 80 |
| Ba7NbMo4O20 | Hexagonal perovskite | 4.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3/510 10−3/510![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C °C |
0.81/525![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C °C |
49 |
| Ca0.92TiO2.84(OH)0.16 | Perovskite | 10−6/300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C °C |
— | 77 |
 | ||
| Fig. 10 Arrhenius plots of the bulk electrical conductivity of novel proton conductors discussed in the present review. See main text for details. | ||
Combined in situ structure–property correlation studies
As highlighted in the previous sections, despite remarkable progress, a too low ionic conductivity under typical operating conditions continues to be a limiting factor for the use of the currently available solid-state proton- and oxide-ion conductors as electrolytic membranes in practical devices. The discovery and optimization of new, better, materials depend on a deep understanding of the relationship between structure and macroscopic ion conductivity. Such a development, in turn, depends on careful characterization of the structure and dynamical properties of the material. Of specific concern here, electrolyte materials are, in devices in actual operation, exposed to rather extreme conditions of high electrical currents, high temperature, gas pressure, and oxidizing/reducing atmospheres etc., which may affect significantly the structural and dynamical properties of the material. Hence, the characterization of crystallographic, electrochemical, and thermodynamical properties should be preferably performed simultaneously in situ. By doing so, not only the inherent uncertainty that comes from correlating data from separate measurements is avoided, but it becomes possible to understand and predict the behavior of the material under realistic operating conditions.In situ studies of materials are by nature demanding and often require the development of specialized and complex sample environments. A particular progress in this regard has been seen in relation to materials characterization techniques based on synchrotron X-ray and neutron scattering. This is because synchrotron X-ray and neutron techniques are featured by several unique benefits for enabling in situ studies of materials. On the one hand, synchrotron X-rays interact with the electron clouds of the atoms with the strength of the interaction following a systematic dependence on atomic number. With respect to small-scale laboratory X-ray sources, the higher flux offered by synchrotron X-ray sources translates into a higher spatial and temporal resolution, which open up for time resolved studies. On the other hand, neutrons interact with atomic nuclei and while the strength of the interaction is particularly strong for hydrogen, and reasonably so for oxygen, meaning that proton and oxide-ion conductors are well suited for neutron studies, the interaction is for many elements somewhat weak. This means that the neutrons can penetrate large and complex pieces of sample environment, which is a clear advantage in the design of in situ experiments, while still being sensitive to hydrogen and oxygen in a material. In addition, neutron methods offer the potential to access information of both structure and dynamics, through the momentum and energy transferred in the scattering event, respectively. Quasielastic neutron scattering (QENS) and ND are complementary tools in this matter. QENS allows determining the self-dynamics of protons by profiting from the large incoherent neutron scattering cross section of hydrogen, while ND is suitable for determining crystal structures, oxygen non-stoichiometry, and proton positions with high precision. These capabilities make neutron techniques unique for investigating structure and dynamics in proton and oxide-ion conductors.
In the following of this section, we summarize recent advances in our understanding of structure–property correlations of proton and oxide-ion conductors, with a particular emphasis on advances that have been possible thanks to the development of new capabilities for in situ neutron and synchrotron X-ray studies. Rather than providing a complete account for all the excellent work done in this field, our aim is to highlight the broad scope and unique information that can be obtained from such studies, as well as to point out perspectives for future in situ studies in this field. Key fundamental aspects that are addressed include structural changes upon dehydration/hydration, bulk vs. (thin) film phenomena, and proton and oxide-ion dynamics.
Oxide-ion conducting oxides
Liu et al., reported on a combined in situ ND and impedance spectroscopy study to investigate the precise correlation between crystal structure and electrical properties of the La2Mo2O9 oxide-ion conductor.86 The combined analysis of structural and electrical data revealed that the unit cell volume undergoes a large increase at around 580 °C due to a structural phase transition from a low-temperature monoclinic structure to a high-temperature cubic structure, which correlates with a rise in bulk conductivity (Fig. 11a), suggesting that an open crystal structure is favorable for fast oxygen transport. In more detail, the phase transition upon increasing temperature is accompanied with a change of the distribution of oxygen defects, from long-range order to dynamic, short-range order in the cubic phase, featured with higher oxide-ion mobility.87,88
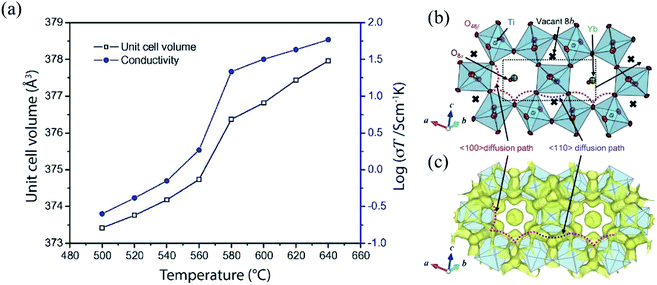 | ||
| Fig. 11 (a) The correlation between the unit cell volume and the bulk conductivity of La2Mo2O9. Adapted from ref. 86. Copyright (2011) Elsevier Publisher. (b) A part of the refined crystal structure and (c) equidensity surface of the MEM neutron scattering length density distribution of Yb2Ti2O7 at 1173 K at 0.002 fm Å−3. Reprinted with permission from ref. 90. Copyright (2018) JCS-Japan. | ||
In this regard, Fujishiro et al. reported on XRD and in situ convergent-beam electron diffraction (CBED) at room temperature and 700 °C, on BaFe0.9In0.1O3−δ.89 The combined analyses of XRD and CBED data showed contrasting results in that the XRD data indicated an ideal perovskite structure (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), whereas the CBED data indicated a deviation from such a structure, possibly featured by partial ordering and/or clustering of oxide-on vacancies. CBED measurements at elevated temperatures revealed the transformation to an ideal perovskite structure with oxide-ion vacancies randomly distributed. Crucially, the change in crystal symmetry happened along a sudden decrease in the activation energy for oxide-ion conduction at 600 °C. Furthermore, Uno et al. applied ND with Rietveld analysis and the maximum-entropy method (MEM) to study the oxide-ion diffusion paths in Yb2Ti2O7.90 The combined technique of in situ ND and the MEM allowed to obtain reliable data on the neutron scattering length density distribution of the crystal structure of Yb2Ti2O7. In effect, this allowed the unravelling of two kinds of oxide-ion diffusion paths, along the 〈110〉 and 〈100〉 direction, respectively, cf.Fig. 11b, again showcasing a strong relationship between crystal structure, oxide-ion ordering, and oxide-ion mobility. Other examples or recent in situ works of oxide-ion conductors are the investigation of oxygen uptake/release of YPrO3+δ (0 ≤ δ ≤ 0.5) under oxidizing and reducing atmosphere and as a function of temperature, and the phase diagram of Sc(2−x)VxO3+δ (0 ≤ δ ≤ 2.00).91,92
m), whereas the CBED data indicated a deviation from such a structure, possibly featured by partial ordering and/or clustering of oxide-on vacancies. CBED measurements at elevated temperatures revealed the transformation to an ideal perovskite structure with oxide-ion vacancies randomly distributed. Crucially, the change in crystal symmetry happened along a sudden decrease in the activation energy for oxide-ion conduction at 600 °C. Furthermore, Uno et al. applied ND with Rietveld analysis and the maximum-entropy method (MEM) to study the oxide-ion diffusion paths in Yb2Ti2O7.90 The combined technique of in situ ND and the MEM allowed to obtain reliable data on the neutron scattering length density distribution of the crystal structure of Yb2Ti2O7. In effect, this allowed the unravelling of two kinds of oxide-ion diffusion paths, along the 〈110〉 and 〈100〉 direction, respectively, cf.Fig. 11b, again showcasing a strong relationship between crystal structure, oxide-ion ordering, and oxide-ion mobility. Other examples or recent in situ works of oxide-ion conductors are the investigation of oxygen uptake/release of YPrO3+δ (0 ≤ δ ≤ 0.5) under oxidizing and reducing atmosphere and as a function of temperature, and the phase diagram of Sc(2−x)VxO3+δ (0 ≤ δ ≤ 2.00).91,92
A crucial challenge regarding QENS studies of oxide-ion dynamics is that the oxide-ion is an almost purely coherent scatterer of neutrons, which, in comparison to proton conductors, makes the QENS analysis far more complex. Consequently, whereas several QENS experiments on oxide-ion conductors have noted the appearance of QENS it has been difficult to model it. Instead, several neutron spectroscopy studies of oxide-ion conductors focused on the determination of the generalized density of states (GDOS), to validate computer simulations, but the insight into the actual oxide-ion diffusion then comes indirectly from simulations rather than directly by analyzing the QENS data. However, recently Wind et al. showed that it is indeed possible to extract quantitative information about the oxide-ion dynamics by applying a modified version of a jump-diffusion model previously reserved for the analysis of QENS data of purely incoherent scatterers.95 More specifically, by using the archetypical oxide-ion conductor δ-Bi2O3 as a model system for QENS analysis, it was shown that the oxide-ion diffusion is isotropic (liquid-like), with a weighted average of all possible jumps with the δ-Bi2O3 unit cell of 3.33 Å (Fig. 12). In a subsequent study, the validity of the new approach was as well confirmed on a study on the type II transition metal-doped variants, i.e. Bi22W5O48, Bi22Nb5O45.5, and Bi22W2.5Nb2.5O46.75, which indicated that the oxide-ions diffuse almost exclusively within fluorite-type regions via an isotropic, liquid-like mechanism. These studies thus represent a new, very useful, methodological development for QENS studies of oxide-ion conducting materials.96 Nevertheless, the indirect information about oxide-ion dynamics by structural probes, such as diffraction methods, is often highly complementary and indispensable for the development of a thorough understanding of the oxide-ion transport in these types of materials. As a very recent example in this regard, we have the combined neutron total scattering and computer simulation study by Marlton et al., on the pyrochlore/defect-fluorite Y2Sn2−xZrxO7, which analyzed the relationship between anion sub-lattice disorder and Frenkel defects facilitating oxide-ion transport.99
 | ||
| Fig. 12 Locally relaxed average crystal structure of δ-Bi2O3, where the purple spheres represent Bi atoms and the red tetrahedra represent disordered O positions. Black arrows indicate possible oxygen jumps in 〈100〉, 〈110〉, and 〈111〉 directions. Adapted from ref. 95. | ||
The increased performances of modern QENS instruments in terms of incident flux and detection efficiency as well as access to longer diffusion time scales up to nanoseconds, has only recently opened to the possibility of investigating the diffusion mechanism of oxygen ions conductors. The QENS technique combined with DFT calculations has been recently applied to investigate the oxide ion dynamics on a nanosecond timescale in the fast ion conductor La2Mo2O9 (LAMOX). This work represents the observation of oxygen dynamics by neutron scattering on the longest timescales reported to date. The analysis of the Q dependence of the QENS signal provided a conductivity timescale in agreement with macroscopic measurements. More importantly, the authors were able, by combining simulation with QENS data, to provide a solid oxide-diffusion pathway in this complex material consisting of variable MoOx coordination spheres.97 A similar approach was also used to directly observe oxide ion dynamics in bismuth vanadate with formula Bi0.913V0.087O1.587 by the same authors of the previous work.98 The main results in this case was the observation of the presence of two processes contributing to the oxide ion dynamics in Bi0.913V0.087O1.587: the long-range diffusive movement of oxide ions through the Bi–O sublattice, and a localized motion of oxygen atoms within the VOx groups of the bismuth vanadate.98 This last process does not directly contribute to the long-range conduction but facilitates the movement of oxygen atoms into and out of the VOx groups and, owing to the flexible coordination requirements of the V5+ cation, allows the VO4 groups to accept additional oxygens atoms from the Bi–O sublattice. The ability of achieving this atomic-level comprehension of the ion dynamics in oxide ion conductors pave the way to propose design principles for chemical modifications of oxide ion conductors to further improve their properties.
Proton conducting oxides
The initial work in this regard was done by Kinyanjui et al., who used in situ ND methods at the ISIS Neutron Source in U.K. to investigate the structural response of hydration and dehydration of the archetypical proton conductor BaZr0.5In0.5O2.75.110 By the use of a custom-made sample environment for in situ hydration/dehydration, not only did the authors reveal a, non-obvious, increase in the lattice parameters upon hydration, but also the co-existence of a two-phase region, containing one hydrated and one non-hydrated phase in the temperature range of ≈573–873 K (Fig. 13a). Subsequent in situ measurements of the ionic conductivity of a pre-deuterated BaZr0.5In0.5O2.75 sample, using the same sample environment as developed by Engin et al., showed there is a strict relationship between the ionic conductivity and change in deuterium content (Fig. 13b).111
 | ||
Fig. 13 (a) Variation of the lattice parameter as a function of temperature as the sample was exposed to dry or wet argon atmosphere. The following symbols overlap in the whole temperature range: ○, △, ▽. The open symbols correspond to the non-deuterated phase while the filled symbols correspond to the deuterated phase; (b) variation of the ionic conductivity, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ, of a pre-deuterated BaZr0.5In0.5O2.75 sample as a function of temperature under dry Ar gas. Reprinted with permission from ref. 110. Copyright (2012) Elsevier Publisher; (c) evolution of the lattice parameters with temperature, during dehydration, for BaTi1−xScxO3−δ (x = 0.50), and BaTi1−xScxO3−δ (x = 0.70) (d). The dotted line shows the modelled evolution of the hydrated material solely by thermal expansion. The modelled curves of chemical expansion are shown by the solid lines, with the respective oxygen vacancy size in the legend. Reprinted with permission from ref. 117. Copyright (2018) Elsevier Publisher. σ, of a pre-deuterated BaZr0.5In0.5O2.75 sample as a function of temperature under dry Ar gas. Reprinted with permission from ref. 110. Copyright (2012) Elsevier Publisher; (c) evolution of the lattice parameters with temperature, during dehydration, for BaTi1−xScxO3−δ (x = 0.50), and BaTi1−xScxO3−δ (x = 0.70) (d). The dotted line shows the modelled evolution of the hydrated material solely by thermal expansion. The modelled curves of chemical expansion are shown by the solid lines, with the respective oxygen vacancy size in the legend. Reprinted with permission from ref. 117. Copyright (2018) Elsevier Publisher. | ||
Other relevant in situ neutron diffraction works on conventional proton conductors were carried out on zirconates/cerates by various authors, both in dry and wet atmospheres, accessing in this way the structural dependence on hydration, phase stability, and detailed correlation with crystal structure.112–114 Further works exploiting the same approach, to which the readers are referred, analyzed the in situ behavior, among others, of lanthanum tungstate, niobates, and hexagonal perovskite derivatives.37,115,116
Torino et al., reported on ND studies combined with simultaneous thermogravimetric analysis on hydrated samples of the BaTi1−xScxO3−δ (x = 0.5 and 0.7) proton conductors.117 The combined analyses of structural and thermogravimetric data allowed to correlate the dehydration properties with the structural response, where, for example, the Sc dopant level was found to impact strongly on the evolution of the lattice parameter during hydration. For BaTi1−xScxO3−δ (x = 0.5), the thermal expansion upon heating compensates for the contraction caused by dehydration and associated oxygen vacancy formation, leading to a plateau region for the unit cell parameter, whereas for BaTi1−xScxO3−δ (x = 0.7) the lattice parameter decreases systematically upon dehydration suggesting that chemical expansion associated with hydration is larger for the more heavily Sc doped system (Fig. 13c and d). Furthermore, Mazzei et al., investigated the structure and dehydration properties of epitaxial thin films of the proton conductor BaZr0.53In0.47O3−δH0.47−2δ, using X-ray and neutron reflectivity, as well as nuclear reaction analysis, with the latter two techniques being employed for the first time on a proton conducting oxide.118 A key result was the observation of an uneven proton concentration depth profile, with a near-surface layer that dehydrates somewhat differently from the bulk of the film.118 Besides being of considerable fundamental interest, this new insight into the hydration/dehydration properties of Ba{Zr,Ti}O3 based proton conductors is of relevance for the development of SOFCs in actual operations that need to be periodically taken into and out of service (i.e. hydrated and dehydrated), especially since hydration-induced thermal expansion may lead to mechanical stability issues such as micro-fissures in the electrolyte and/or delamination at the electrolyte/electrode interface.
Experimentally, the role of O–H vibrational dynamics in relation to proton diffusion was studied in a hydrogen-containing single crystal sample of KTaO3, using time-resolved infrared (IR) absorption spectroscopy.120 One of the key findings evolving from this study was that the excitation of the O–H stretch mode decays into a lower-energy O–Ta–O bending motion that was shown to enhance the rate of proton transfer between neighboring oxygen atoms by as much as 7 orders of magnitude. A subsequent study on a hydrogen-containing single crystal sample of rutile TiO2 showed that the O–H stretch mode decays into an assist O–H bend motion, leading to an increase of proton transfer events by 9 orders of magnitude.121 As opposed to KTaO3, however, the huge enhancement in proton transfer rate in TiO2 could be explained by quantum-mechanical tunnelling rather than classical “over-the-barrier” hopping.121 Accordingly, these pioneering results demonstrate that the physics underpinning proton motion may have a strong structural dependence and, furthermore, are extremely exciting since they suggest that IR stimulus of O–H stretch modes may work as an effective mean to enhance proton conductivity without heating the sample. In this context, we also note the recent work on Y-doped BaCeO3 and BaZrO3, by using a multi-technique approach encompassing pressure dependent synchrotron XRD, pressure dependent Raman spectroscopy, ND, QENS, electronic structure and nudged elastic band simulations, indicating that the proton transfer process is coupled to low-frequency lattice phonons.122–124 In more detail, the proton dynamics data were interpreted in terms of a cooperative motion, meaning that one proton influences the motion of another nearby proton, thus leading to a rather complex mechanism in the case of significant proton concentrations.124
Regarding the proton transfer and O–H reorientational processes, these can be probed with QENS. In agreement with the first QENS studies of proton conducting oxides (see ref. 119 and references therein), recent works on acceptor doped BaZrO3 based compounds have established that these localized proton motions are characterized by a relaxation time of some picoseconds.125 However, in contrast to earlier studies, Noferini et al. showed that the observed QENS signal is not due to a well-defined process characterized by a unique activation energy but to a distribution of activation energies due to many different local proton sites present.125,126 The situation of several different localized proton motions contributing to the overall QENS signal is in agreement with the results obtained from recent neutron spin-echo measurements, as well as with many structural studies that point towards pronounced local structural distortions even in perovskites featuring low dopant and proton concentrations.109,127,128 This illustrates the importance of using local structural probes in combination with dynamical techniques like QENS to reveal the nature of proton dynamics that is sensitive to local proton coordination environments.
Regarding the actual long-range, translational, diffusion of protons, which occurs as a series of proton transfers and O–H rotational motions, there is a fair agreement in the literature amongst QENS studies of various proton conducting perovskites that the proton transfer occurs as jumps between neighbouring oxygen ions, which are separated by a distance of approximately 3 Å.119 The activation energy for proton transport as obtained by QENS mostly falls into the range of 0.04–0.2 eV, which is lower than the activation energy for proton conductivity as derived from impedance spectroscopy (typically, >0.4 eV).70 In an effort to scrutinize the reason for this mismatch in activation energies, Chen et al. developed an impedance spectroscopy insert for a QENS spectrometer at the Paul-Scherrer Institute in Switzerland and performed in situ variable temperature QENS and impedance spectroscopy on a hydrated sample of BaCe0.8Y0.2O3−δ.129 The combined analysis of QENS and impedance spectroscopy data still showed on different activation energies for the proton diffusion measured by the two different techniques. This result points toward the presence of potential energy features on a length-scale longer than that probed with QENS techniques (≈1–20 Å) that affect the macroscopic proton conductivity. This is in agreement with a recent structural and dynamical study of BaCe0.4Zr0.4Y0.2O3−δ, using QENS, and simultaneous synchrotron XRD and impedance spectroscopy, which, in addition, revealed a strong correlation between the proton conductivity and the lattice parameter.130
Possibly, the higher activation energy observed on the macroscopic length-scale is a result of trapping of the protons at the dopant sites. Such a picture was initially proposed by Hempelmann et al. on the basis of QENS data on SrCe0.95Yb0.05O2.975 and has since found support from various experimental and computational studies on similar materials.131–135 However, a recent QENS study by Noferini et al. of BaZr1−xMxO3−x/2 with M = Sc and Y for x = 0.1 and M = In for x = 0.1, 0.2, and 0.25 using the high-resolution neutron backscattering technique does not point toward such a trapping behaviour.136 Furthermore, a recent first-principles calculations study on the archetypical proton conductor BaZr0.8Y0.2O2.9, as well as a combined inelastic neutron scattering (INS) and first-principles calculations study of BaZr0.5In0.5O2.75 showed that the dopants preferentially migrate along percolation paths of dopant ions throughout the perovskite lattice (Fig. 14c).137,138 That is, the proton does not need to detrap when moving throughout the lattice. In addition, a recent theoretical study on BaZr0.8Y0.2O2.9 showed that in this case, with a typical dopant level of 20%, the protons interact with each other.139 These proton–proton interactions have two competitive effects on the proton diffusivity, i.e. the negative effect of carrier blocking and the positive effect of trap filling.
Clearly, the nature of the local structure complicates the description about the proton conduction mechanism and a consensus regarding the link between proton conductivity and atomic-scale structure and dynamics is yet to be reached. In this endeavor, not only might QENS measurements at higher temperatures distinguish the trapping event from the wide range of processes observed in recent QENS studies, but systematic investigations of the proton dynamics for materials featuring different local structures are likely to elucidate the role of dopant atoms on proton transport properties in these types of materials. In this context, a recent study on BaZr1−xMxO3−x/2 with M = In and Sc, and x = 0.1 and 0.5, using INS, IR and Raman spectroscopy, and first-principles computer simulations points toward a rather peculiar dependence between the type and concentration of dopant atoms and the local coordination of protons, as it is found to be similar for BaZr1−xScxO3−x/2 with x = 0.1 and 0.5 and BaZr1−xInxO3−x/2 with x = 0.1, whereas for BaZr1−xInxO3−x/2 with x = 0.5 additional proton sites, likely featuring different proton transport behavior, seem to be present.
Materials informatics applied to oxide-ion and proton conductors
As highlighted in the above sections, there is a continuous need of designing and realizing materials with optimal and tailored properties, and this argument holds for the whole field of clean energy materials for renewable and sustainable energy technologies. One strategy which is becoming increasingly popular and effective is the application of computational methods to accelerate materials design through a rapid and comprehensive prediction of materials stability and properties. To date, the number of theoretically predicted materials in computational materials property databases is comparable to the number of experimental entries in crystallographic database.140 A comprehensive overview of the current status and future perspectives on “materials by design” can be found in the 2019 roadmap, including various contributions from the computational techniques to the high-throughput (HT) combinatorial methods, applied to various energy relevant technologies.140 In this section we will provide some examples of the application of these methods to accelerate the discovery of oxide-ion and proton conductors while the reader is referred to ref. 140 and references therein for a more detailed discussion. Overall, a key central theme of materials informatics is the need for HT computational techniques to be coupled to a vast database of experimental results as the foundation for the materials by design paradigm with the final aim of exploiting the synthesis and manufacturing processes for new materials. This concept is summarized in the following (Fig. 15).140 Of significance for the current research on materials design, is the need of more detailed experimental data coming from in situ studies which, coupled to computational methods, can profoundly accelerate the discovery and development of new materials. | ||
| Fig. 15 Schematic of the materials by design approach. Reprinted with permission from ref. 140 (2019) IOP Science Publisher. | ||
The use of computational methods to accelerate materials discovery through HT approaches has been recently applied to several functional materials such as thermoelectrics, multifunctional alloys, catalysts, functional ceramics, optoelectronic semiconductors, and, Li-ion battery components (electrodes and electrolytes).141–151
Concerning oxide-ion and proton conductors, the available examples of the application of HT computational approach to develop new materials are still scarce. The reasons for this partly rely on the availability of large experimental datasets which, for oxide-ion conductors, for example, requires to have ion-conduction libraries with accurately measured conductivities. In this respect, however, we should mention that large databases are appearing in the current literature as the one by Zhang and co-workers including crystal structure information, ion migration channel connectivity information, and 3D channel map for ≈29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Li-, Na-, K-, Ag-, Cu-, Mg-, Zn-, Ca-, Al-, O-, and F-containing inorganic compounds.152
000 Li-, Na-, K-, Ag-, Cu-, Mg-, Zn-, Ca-, Al-, O-, and F-containing inorganic compounds.152
In addition, it is important to be able to identify the phase of each library quickly, which in turn requires the use of HT structural methods such as synchrotron XRD. Finally, it is important to develop a HT system for measuring physical properties that is suitable for the targeted functional materials, which in the present case is the impedance response of the materials.6 A way of accelerating the availability of experimental data to be coupled to the computational methods has been recently proposed by Matsubara and co-workers for bismuth-based oxides by using a HT conductivity measurements system.6 The development of such a HT experimental approach will for sure speed up the future computational materials screening with improved reliability. As a matter of fact, the same authors further expanded their approach in this direction by a combinatorial scheme that combines materials informatics technique to define a chemical search space with HT synthesis and evaluation.153
Fig. 16 summarizes the scheme proposed in ref. 153 for discovering new ion conductors in the Ca–(Nb,Ta)–Bi–O system. A virtual screening based on the proposed machine learning (ML) model ranks materials in the inorganic crystal structure database (ICSD) that are expected to be superior oxide-ion conductors. The model also predicts elemental combinations with a similarity metric to narrow the practical search space for subsequent combinatorial synthesis. The HT evaluation is introduced to increase the total throughput of experimental screening.153
 | ||
| Fig. 16 Scheme of materials discovery proposed in ref. 153. The film libraries are prepared with an automatic pipetting system. Their crystal phases are identified via HT synchrotron XRD analysis. The conductivity and thermal stability of the compounds are evaluated with the HT conductivity measurement system. Reprinted with permission from ref. 153 (2020) Nature Publisher. | ||
The approach used to design novel oxide-ion conductors started with the definition of 92 hand-crafted, general crystal structure descriptors (e.g., polyhedral distortion, radial distribution function, etc.) related to ion conductivity. The ML model was built by including experimental oxide-ion conductivities as training data and devising a strategy based on local structure similarity to compensate for the insufficient number of experimental data. More details on the method used can be found in ref. 153. Through this approach a number of possible candidates with good ionic conductivities were identified by the authors and selected for the combinatorial chemistry experiments, including HT methods for XRD and conductivity measurements, previously devised by the same authors.6 Overall, the chemical space studied in the six-by-six combinatorial libraries, was expressed as [Cax(Nb1−yTay)1−x]1−zBizOδ (0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0.1 ≤ z ≤ 0.8), where the bismuth content (z) in each library was fixed, and the Ca (x) and Ta (y) contents within each library were varied. The materials informatics algorithm developed together with HT experimental study of the library materials allowed the authors to discover novel oxide-ion conductors in the Ca–(Nb,Ta)–Bi–O system that exhibited high conductivity and durability.153
As mentioned above, one of the main limitations in the application of ML methods to ion conductors to identify potential candidates, from hundreds of thousands of compounds in a database as a first-pass screening, is related to the fact that “materials data are not big data”.154 As already used in ref. 153, some further descriptors – related to ion conductivity – can be employed to compensate for the relatively low number of experimental training data. Recently, such an approach has been further extended by Kajita and co-workers through the use of virtual-screening process via ensemble-based machine learning with one handcrafted and two generic descriptors to maximize the inference ability even using a small training dataset.154 A sketch of the ensemble-scope descriptor used in ref. 154 is reported in Fig. 17 below.
 | ||
| Fig. 17 The scheme is composed of three independent machine learning models for the oxygen-ion conductivity (σ) as the target property. The first model employs a knowledge-based handcrafted descriptor, the second descriptor is smooth overlap of atomic positions (SOAP), which calculates a metric between compounds with respect to the atomic geometry and electronic negativity, and the third descriptor encodes the BVS voxel data, which approximate the oxygen-ion transportation path into a fixed-length array that is suitable for the three-dimensional convolutional neural networks (3D-CNN) model. Reprinted with permission from ref. 154 (2020) Nature Publisher. | ||
As hand-crafted descriptor the authors used atomic properties, bond valence sum (BVS) and porosity properties as elements of the descriptor generated from the crystal structures where, for example, the ion number density is calculated from the atomic positions. The second descriptor was the alchemically extended SOAP (smooth overlap of atomic positions) generated from the atomic geometries of a unit cell as the input data. Essentially, this descriptor provides a similarity metric of two local atomic environments with overlapping atomic-neighbor densities and electronegativities.155 Finally, the third descriptor used is the R3DVS which made use of BVS voxel data as the field feature.
By using this ensemble-scope learning approach including only 29 training dataset, the authors performed the virtual screening of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 oxides recorded in the inorganic crystal structure database.154 By excluding, for example, materials containing hydrogen which are prone to degradation at high temperatures, the authors chose 18 oxides with a predicted conductivity higher than 10−4 S cm−1 and synthesized and characterized their ionic conductivity. Among these 18 candidates, eight oxides, EuGe2KO6, Ca3Fe2Ge3O12, BaCu2Ge2O7, and DyAlO3, and four bismuth oxides were found as oxygen-ion conductors and are reported in Fig. 18, together with the calculated and experimental oxide-ion conductivities at 700 °C.
384 oxides recorded in the inorganic crystal structure database.154 By excluding, for example, materials containing hydrogen which are prone to degradation at high temperatures, the authors chose 18 oxides with a predicted conductivity higher than 10−4 S cm−1 and synthesized and characterized their ionic conductivity. Among these 18 candidates, eight oxides, EuGe2KO6, Ca3Fe2Ge3O12, BaCu2Ge2O7, and DyAlO3, and four bismuth oxides were found as oxygen-ion conductors and are reported in Fig. 18, together with the calculated and experimental oxide-ion conductivities at 700 °C.
 | ||
Fig. 18 (a) Graphics of the unit cells of the host materials of oxygen-ion conductors; (b) experimental and predicted values for the oxygen-ion conductivities σ at 700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. Reprinted with permission from ref. 154 (2020) Nature Publisher. °C. Reprinted with permission from ref. 154 (2020) Nature Publisher. | ||
While the approach proposed in ref. 154 still requires to be improved, for example, regarding the defect chemistry and doping strategies in the identified stoichiometric compounds, which are often the key source of ion conductivity, the concept of ensemble-scope descriptor learning provided a significant advance in virtual screening, in particular for its efficient search capability using only a few tens of training datasets.154
Lee and co-workers performed a first-principles screening on 90 types of garnet-type oxides (A3B2C3O12) to consider their potential as oxygen ion conductors based on the recent computation work on Ca3Fe2Ge3O12 which indicated this composition as a possible novel conductor characterized by an oxygen interstitial (Oi) diffusion mechanism.156,157 In detail, the authors generated 90 combinations of A3B2C3O12 with typical valences of cations A, B, and C of 2+, 3+, and 4+, respectively, to search for energetically and dynamically stable garnet-type oxides with low Emig for the Oi on the migration path. With this approach, they were able to identify 14 stable oxides with Emig < 0.5 eV. Among them, Cd3Sc2Ge3O12, Ca3Y2Ge3O12, Ca3In2Ge3O12, and Ca3Ga2Ge3O12 are expected to form the Oi at 1000 K by extrinsic doping with donor dopants with a σO similar to that of the reference level of ∼10−2 S cm−1 of YSZ at 1000 K.157
A very recent paper by Priya and Aluru applied ML tools for the design and discovery of ABO3-type perovskite oxides for various energy applications, using over 7000 data points from the literature.158 In particular, the authors were interested in building a statistical learning model to search for solid oxide perovskites by using total conductivities as input experimental data, and classifying the materials based on the nature of the major carriers. The screening of the composition space of the perovskite oxides was based on the nominal charge states of the A and B sites, namely AO + BO2 and A2O3 + B2O3 perovskites. The important chemical features from the ML regressor model turned out to be the minimum electronegativity and the average ionic radius of B-site ions, while for the classifier model they were minimum atomic mass of B-site ions and minimum formation energy of B-site oxides.158 By using these chemical features the authors screened 7230 known perovskites and correlated such parameters to the nature of the conductivity (proton, oxygen, mixed protonic/electronic, mixed oxide/electronic, mixed protonic/oxide, and electronic conductors), showing the important features of their ML model. This approach allowed them to further screen stable pure and doped perovskites at different temperatures and atmospheres (dry/wet; H2, O2, and air) and predict their conductivities both in terms of nature and values. For stoichiometric perovskite oxides, for example, among good candidates already partially experimentally investigated in the past, EuNbO3 and EuSnO3 with conductivities two orders of magnitude higher than the zirconates, are scarcely known, together with InLaO3, GdCeO3, and EuNdO3 which are predicted to be proton conducting.158 Some novel possible candidates have been also identified as oxide-ion conductors, such as ScGaO3, which has a total conductivity that is two orders of magnitude higher compared to the more commonly known LSGM and, to date, has not yet been studied. Many other perovskites resulted to be mixed conductors which may be of interest for the development of cathode materials.
The ML model was, as mentioned, also used to screen the A- and B-site doped chemistries with a nominal 5% doping to avoid clustering.158 The result of this screening showed that B-site doping increases the total conductivity for each of the charge carrier type, identifying over 4000 proton conductors with conductivities above the well-known BZY as well as over 300 candidates for oxide-ion conduction above the well-known ceria nanocomposites for intermediate to low temperature applications.158 A summary of the all screened stable perovskites as a function of the major carrier type is reported in Fig. 19.
 | ||
| Fig. 19 Screened stable perovskites classified according to the different charge carriers. Different colored symbols indicate different classes of perovskites: red solid symbols are pure type I (AO + BO2) perovskites, blue are type II (A2O3 + B2O3) perovskites, yellow are the A-site doped type I perovskites, green are A-site doped type II, purple are the B-site doped type I, and gray are the B-site doped type II perovskites. Type I are doped with M2O3 and type II are doped with MO type oxides. The top candidate for each class has been labeled. The conductivity of BZY at 400 °C is shown by a black line for reference. Reprinted with permission from ref. 158 (2021) Nature Publisher. | ||
As can be seen from Fig. 19, the ML approach used in ref. 139 to screen 1793 undoped and 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832 A and B-site doped perovskites for high conductivities, and by classifying them for majority charge carrier type, allowed the authors to predict some potential candidates with purely proton or oxide-ion conductors. In addition to this, the ML model used was further validated by predicting the conductivities of compounds not present in the training set thus confirming that such an approach, computationally inexpensive, is an effective mean to guide the material design and further experimental work.
832 A and B-site doped perovskites for high conductivities, and by classifying them for majority charge carrier type, allowed the authors to predict some potential candidates with purely proton or oxide-ion conductors. In addition to this, the ML model used was further validated by predicting the conductivities of compounds not present in the training set thus confirming that such an approach, computationally inexpensive, is an effective mean to guide the material design and further experimental work.
The accelerated search for novel proton-conducting oxides has been object of a study by Wisesa and co-workers by a HT DFT-based computational search to identify structure types that are likely to have high proton mobility.159 The approach in this work was mostly related to the structure types rather than individual compounds with the assumption that the ion arrangement in the unit cell represents the key ingredient in determining the ionic conductivity of a material. Details on the computational methodology employed by the authors can be found in ref. 159. The training structures used were 52, and the potential model developed allowed to nicely predict the average migration energies and correlate them to the various structure types investigated (cubic perovskite, hexagonal perovskite, elpasolite, and spinel).159 The authors further applied the model to predict the activation energies for proton diffusion in all 1946 test structures, representing 41 different structure types with at least 20 oxide materials per type. Through this approach, four structure types, namely CrVO4, calcite, zircon, and NaMn7O12, had the lowest average activation energies. Interestingly, CrVO4 structure type with orthorhombic lattice resulted to have a very low predicted average migration energy (more than 0.1 eV below that of the next-best structure type) suggesting exceptionally high proton mobility with a predicted Grotthuss-type mechanism. 29 materials with the CrVO4 structure type were further investigated by the authors with particular interest in defining the proton migration path. It turned out that one-, two-, and three-dimensional diffusion should occur readily, with migration energies close to those in cubic perovskites, but with a likely two-dimensional diffusion path. Finally, calculations showed that acceptor-doped CrVO4-structured materials are capable of hosting competitively high concentrations of protons without creating an unacceptably large thermodynamic driving force for decomposition.159 Most of the materials predicted to be good proton conductors in this study have not yet been synthesized and characterized.
The most recent and accurate work dealing with the accelerated discovery of proton-conducting perovskite oxides is due to Hyodo and co-workers.160 In this study, data-driven structure–property maps for hydration, that capture its physicochemical fundamentals for exploring new proton-conducting oxides, was constructed. In particular, the data set was built by performing thermogravimetry measurements of 22 perovskite compounds to obtain reliable proton concentrations for different chemical compositions, temperatures, and water partial pressures.160 These results, together with data from literature, were used to train the model. The prediction was then performed for 8613 hypothetical compounds AB1−xB′xO3−δ, which consists of 78 different hosts for a variety of A, B, and B′ cations, with a step size of 0.05 in x (0.05 ≤ x ≤ 0.45), at 11 temperatures between 20 and 1000 °C, for a total of nearly 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data points. Such results were used to construct structure–property maps for hydration in the chemical space and the descriptor spaces (more details in ref. 160). This approach allowed the authors to report a novel proton-conducting oxide, namely SrSn0.8Sc0.2O3−δ, which was not previously recognized for proton incorporation or conduction.160 This work represents a significant improvement in the machine learning approach to discover proton-conducting oxide since it allows, for the first time, a quantitative prediction capability of proton concentration against temperature and chemical compositions. This has been possible, in particular, by including the physicochemical phenomenon of hydration and considering all the well-known structural and chemical factors correlated to this phenomenon in the learning model.
000 data points. Such results were used to construct structure–property maps for hydration in the chemical space and the descriptor spaces (more details in ref. 160). This approach allowed the authors to report a novel proton-conducting oxide, namely SrSn0.8Sc0.2O3−δ, which was not previously recognized for proton incorporation or conduction.160 This work represents a significant improvement in the machine learning approach to discover proton-conducting oxide since it allows, for the first time, a quantitative prediction capability of proton concentration against temperature and chemical compositions. This has been possible, in particular, by including the physicochemical phenomenon of hydration and considering all the well-known structural and chemical factors correlated to this phenomenon in the learning model.
We conclude this section by highlighting that the increasing integration and importance of machine learning in chemical science has been recently discussed in terms of best practices for the community to make models as much as possible reliable, repeatable, and reproducible.161 Such guidelines include a critical discussion of the data sources, data cleaning and curation, data representation, model choice, model training and validation, and code and reproducibility. The efforts are aimed at maintaining high digital standards in the use of machine learning particularly now that such an approach, with grate potential and power, is progressively becoming central in the chemistry field.161
Outlook and future perspectives
In the near future, the worldwide society will face an unprecedented energy revolution with a progressive transition towards cleaner and more sustainable sources to afford the serious environmental concerns related to anthropogenic climate changes. In this respect, SOFC devices, together with other technological solutions, can provide a strong push in this direction. While SOFCs are already commercialized since years, the need of further development to improve their sustainability and reduce their – limited – environmental impact, also in terms of the presence of critical raw materials, still requires much research. A central part of this effort, as for many other fields, is centered around the discovery of new materials with enhanced performance, the optimization of the existing ones, and the acquisition of a deep understanding of structure–property correlation. In this respect, in the present Review, we highlighted the most recent and exciting results about oxide-ion and proton conductor electrolytes, which constitute the key component of a SOFC. It is clear that in the last ten years, the period essentially covered by this Review, there has been a continuous basic material science research directed not only towards material discovery but also to the acquisition of a deep understanding of the structure–property correlation and on the mechanisms behind the ion migration, directly correlated to the material performance.It is exciting to see how the current research on oxide-ion conductors also developed original approaches to discover new materials. The Na0.5Bi0.5TiO3 perovskite is a fascinating example where, through a consolidated defect chemistry strategy, its conduction properties can be switched from electronic to purely ionic achieving optimal oxide-ion conductivity. Possibly, such strategy, could be further extended to other perovskites sharing similar basic features.11 Together with traditional structural families, novel classes of oxide-ion conductors have been reported, such as the layered AA′BO4 perovskite-related family and the DJ cation-ordered layered perovskites with general formula A′ [An−1BnO3n+1], both showing ordering of the A/A′ cations.21,27 Through cation replacement and acceptor doping strategies these novel materials could achieve purely ionic conductivities comparable to state-of-the-art oxide-ion conductors. This also is true for the rich new family of hexagonal perovskites first reported in 2016 with the Ba3NbMoO8.5 composition displaying similar bulk ionic conductivity to Gd-doped ceria.33 Starting from this result, the number of novel related compositions has grown significantly in the last 5 years up to the very recent oxide-ion and proton conductor Ba7Nb4MoO20.49 For sure, the rich materials chemistry allowed by hexagonal perovskites, both in terms of crystal structure modulation and doping strategies, will assure the advent of a rich number of optimized and novel compositions in the next years.
Together with material discovery, fundamental research of structure–property correlations in proton and oxide-ion conductors will continue to play a critical role for the development of design criteria for new, more efficient, materials. An interesting trend in recent work relates to the correlation between vibrational dynamics and ion conduction. In this regard, the combined analyses of recent experimental and theoretical data established that the proton conduction mechanism depends strongly on the vibrational dynamics of the material, but the correlation between local structure and dynamics and macroscopic proton conductivity is still unclear for these materials. Studies of ion conduction under the condition of mode-selective vibrational excitation may provide new insight into this matter.120,121,123,124 Another interesting trend in recent work relates to the application of a modified version of the Chudley–Elliott jump diffusion model to account for coherent scattering in QENS studies of solid oxide-ion conductors. In the future, this approach may be extended to systems featuring mixed coherent–incoherent scatterers, such as mixed proton-oxide-ion conducting systems.95,96 For the specific application of proton conducting oxides in SOFCs, one would use a film (<1 μm) of the proton conductor sandwiched between the electrodes. Differently from powder samples, such films represent a confined state and, furthermore, can be textured, strained, and exhibit varying degrees of crystallinity, which may affect significantly the proton conducting properties. Investigations of the dynamics in thin film ionic conductors is therefore an exciting avenue of research. In view of the increased flux that will be provided at future neutron sources, capabilities for surface sensitive QENS are now being envisaged.162 At present, such studies are not feasible, but if a robust technique for studies of surface/interface dynamics can be developed, this would allow for studies of dynamics at interfacial hydrated layers, such as in nanostructured yttria-doped zirconia, or dynamics in thin films, and could even provide insight into SOFCs electrode reactions if carried out in situ.163
The search of novel oxide-ion and proton conductors is still pivotal for the development of SOFC technology. Traditional experimental approaches have provided the results highlighted in this Review, but it is clear that this process should be accelerated. In this respect, in the last years, the emergence of HT machine learning-based methods have become central in many fields of materials chemistry.140 Concerning oxide-ion and proton conductors, few examples are available to date. A possible reason for this limited number of results is related to the availability of adequate and consistent training data set for the modelling. Some limitations can be partially overcome by including hand-crafted descriptors based on structural properties when, for example, conductivity data or other functional properties are missing.154 Despite these limitations, the results achieved so far are extremely encouraging having succeeded in predicting novel oxide-ion and proton conductors, and we may anticipate that machine learning will progressively extend its impact also in this field of materials chemistry.
To conclude, the overview presented in this Review, covering the last 10 years advancements in structure–property correlation and material discovery of oxide-ion and proton conductors, confirmed the vitality of this field of materials science. The advent of advanced computational and experimental tools in the hands of the researchers pave the way for the future design of advanced materials capable of matching the technological requirements of the forthcoming energy economy transition.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
MK is grateful for financial support from the Swedish Energy Agency (grant no. 48712-1) and the Swedish Research Council (grant no. 2016-06958). LM acknowledge the support from RSE SpA.References
- I. Staffell, D. Scamman, A. Velazquez Abad, P. Balcombe, P. E. Dodds, P. Ekins, N. Shah and K. R. Ward, Energy Environ. Sci., 2019, 12, 463–491 RSC.
- T. A. Adams, J. Nease, D. Tucker and P. I. Barton, Ind. Eng. Chem. Res., 2013, 52, 3089–3111 CrossRef CAS.
- L. Malavasi, C. A. J. Fisher and M. S. Islam, Chem. Soc. Rev., 2010, 39, 4370–4387 RSC.
- L. Malavasi, Structural Characterization Techniques Advances and Applications in Clean Energy, New York, 2016 Search PubMed.
- D. P. Tabor, L. M. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberla, J. H. Montoya, S. Dwaraknath, M. Aykol, C. Ortiz, H. Tribukait, C. Amador-Bedolla, C. J. Brabec, B. Maruyama, K. A. Persson and A. Aspuru-Guzik, Nat. Rev. Mater., 2018, 3, 5–20 CrossRef CAS.
- M. Matsubara, A. Suzumura, S. Tajima and R. Asahi, ACS Comb. Sci., 2019, 21, 400–407 CrossRef CAS PubMed.
- J. A. Kilner, Solid State Ionics, 2000, 129, 13–23 CrossRef CAS.
- M. Yashima, J. Ceram. Soc. Jpn., 2009, 117, 1055–1059 CrossRef CAS.
- T. Ishihara, H. Matsuda and Y. Takita, J. Am. Chem. Soc., 1994, 116, 3801–3803 CrossRef CAS.
- K. Huang, R. Tichy, J. B. Goodenough and C. Milliken, J. Am. Ceram. Soc., 1998, 81, 2581–2585 CrossRef CAS.
- M. Li, M. J. Pietrowski, R. A. De Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2014, 13, 31–35 CrossRef CAS PubMed.
- F. Yang, M. Li, L. Li, P. Wu, E. Pradal-Velázque and D. C. Sinclair, J. Mater. Chem. A, 2017, 5, 21658–21662 RSC.
- F. Yang, P. Wu and D. C. Sinclair, Solid State Ionics, 2017, 299, 38–45 CrossRef CAS.
- F. Yang, M. Li, L. Li, P. Wu, E. Pradal-Velázquez and D. C. Sinclair, J. Mater. Chem. A, 2018, 6, 5243–5254 RSC.
- R. A. De Souza, Adv. Funct. Mater., 2015, 25, 6326–6342 CrossRef CAS.
- H. Zhang, H. H. AmrRamadan and R. A. De Souza, J. Mater. Chem. A, 2018, 6, 9116–9123 RSC.
- M. Cherry, M. S. Islam and C. R. A. Catlow, J. Solid State Chem., 1995, 118, 125–132 CrossRef CAS.
- M. Saiful Islam, J. Mater. Chem., 2000, 10, 1027–1038 RSC.
- I. Levin and I. M. Reaney, Adv. Funct. Mater., 2012, 22, 3445–3452 CrossRef CAS.
- N. Kitamura, N. Hayashi, N. Ishida and Y. Idemoto, Chem. Lett., 2019, 48, 1398–1401 CrossRef CAS.
- K. Fujii, Y. Esaki, K. Omoto, M. Yashima, A. Hoshikawa, T. Ishigaki and J. R. Hester, Chem. Mater., 2014, 26, 2488–2491 CrossRef CAS.
- K. Fujii and M. Yashima, J. Ceram. Soc. Jpn., 2018, 126, 852–859 CrossRef CAS.
- H. Yaguchi, K. Fujii and M. Yashima, J. Mater. Chem. A, 2020, 8, 8638–8647 RSC.
- X. Yang, S. Liu, F. Lu, J. Xu and X. Kuang, J. Phys. Chem. C, 2016, 120, 6416–6426 CrossRef CAS.
- M. Shiraiwa, K. Fujii, Y. Esaki, S. J. Kim, S. Lee and M. Yashima, J. Electrochem. Soc., 2017, 164, F1392 CrossRef CAS.
- K. Fujii, M. Shiraiwa, Y. Esaki, M. Yashima, S. J. Kim and S. Lee, J. Mater. Chem. A, 2015, 3, 11985–11990 RSC.
- W. Zhang, K. Fujii, E. Niwa, M. Hagihala, T. Kamiyama and M. Yashima, Nat. Commun., 2020, 11, 1224 CrossRef CAS PubMed.
- M. Dion, M. Ganne and M. Tournoux, Mater. Res. Bull., 1981, 16, 1429–1435 CrossRef CAS.
- A. J. Jacobson, J. W. Johnson and J. T. Lewandowski, Inorg. Chem., 1985, 24, 3727–3729 CrossRef CAS.
- W. Zhang, K. Fujii, T. Ishiyama, H. Kandabashi and M. Yashima, J. Mater. Chem. A, 2020, 8, 25085–25093 RSC.
- L. Katz and R. Ward, Inorg. Chem., 1964, 3, 7 Search PubMed.
- J. Darriet and M. A. Subramanianb, J. Mater. Chem., 1995, 5, 10 RSC.
- S. Fop, J. M. S. Skakle, A. C. McLaughlin, P. A. Connor, J. T. S. Irvine, R. I. Smith and E. J. Wildman, J. Am. Chem. Soc., 2016, 138, 16764–16769 CrossRef CAS PubMed.
- K. S. McCombie, E. J. Wildman, S. Fop, R. I. Smith, J. M. S. Skakle and A. C. Mclaughlin, J. Mater. Chem. A, 2018, 6, 5290–5295 RSC.
- K. S. McCombie, E. J. Wildman, C. Ritter, R. I. Smith, J. M. S. Skakle and A. C. Mclaughlin, Inorg. Chem., 2018, 57, 11942–11947 CrossRef CAS PubMed.
- S. Fop, E. J. Wildman, J. M. S. Skakle, C. Ritter and A. C. Mclaughlin, Inorg. Chem., 2017, 56, 10505–10512 CrossRef CAS PubMed.
- S. Fop, K. McCombie, R. I. Smith and A. C. Mclaughlin, Chem. Mater., 2020, 32, 4724–4733 CrossRef CAS.
- A. Gilane, S. Fop, F. Sher, R. I. Smith and A. C. Mclaughlin, J. Mater. Chem. A, 2020, 8, 16506–16514 RSC.
- S. Fop, K. S. McCombie, E. J. Wildman, J. M. S. Skakle and A. C. Mclaughlin, Chem. Commun., 2019, 55, 2127–2137 RSC.
- J. E. Auckett, K. L. Milton and I. R. Evans, Chem. Mater., 2019, 31, 1715–1719 CrossRef CAS.
- A. Bernasconi, C. Tealdi and L. Malavasi, Inorg. Chem., 2018, 57, 6746–6752 CrossRef CAS PubMed.
- A. Bernasconi, C. Tealdi, M. Mühlbauer and L. Malavasi, J. Solid State Chem., 2018, 258, 628–633 CrossRef CAS.
- M. S. Chambers, K. S. McCombie, J. E. Auckett, A. C. McLaughlin, J. T. S. Irvine, P. A. Chater, J. S. O. Evans and I. R. Evans, J. Mater. Chem. A, 2019, 7, 25503–25510 RSC.
- M. Coduri, A. Bernasconi, H. E. Fischer and L. Malavasi, J. Mater. Chem. A, 2020, 8, 21227–21240 RSC.
- E. García-González, M. Parras and J. M. González-Calbet, Chem. Mater., 1998, 10, 1576–1581 CrossRef.
- S. Fop, E. J. Wildman, J. T. S. Irvine, P. A. Connor, J. M. S. Skakle, C. Ritter and A. C. Mclaughlin, Chem. Mater., 2017, 29, 4146–4152 CrossRef CAS.
- M. Yashima, T. Tsujiguchi, K. Fujii, E. Niwa, S. Nishioka, J. R. Hester and K. Maeda, J. Mater. Chem. A, 2019, 7, 13910–13916 RSC.
- J. E. Auckett, M. J. Gutmann and I. R. Evans, Inorg. Chem., 2020, 59, 14245–14250 CrossRef CAS PubMed.
- S. Fop, K. S. McCombie, E. J. Wildman, J. M. S. Skakle, J. T. S. Irvine, P. A. Connor, C. Savaniu, C. Ritter and A. C. Mclaughlin, Nat. Mater., 2020, 19, 752–757 CrossRef CAS PubMed.
- E. García-González, M. Parras and J. M. González-Calbet, Chem. Mater., 1999, 11, 433–437 CrossRef.
- S. Fop, J. A. Dawson, A. D. Fortes, C. Ritter and A. C. McLaughlin, Chem. Mater., 2021, 33, 4651–4660 CrossRef CAS.
- M. Yashima, T. Tsujiguchi, Y. Sakuda, Y. Yasui, Y. Zhou, K. Fujii, S. Torii, T. Kamiyama and S. J. Skinner, Nat. Commun., 2021, 12, 556 CrossRef CAS PubMed.
- S. Li and J. T. S. Irvine, Solid State Ionics, 2021, 361, 115571 CrossRef CAS.
- E. Fabbri, D. Pergolesi and E. Traversa, Chem. Soc. Rev., 2010, 39, 4355 RSC.
- N. Kochetova, I. Animitsa, D. Medvedev, A. Demin and P. Tsiakaras, RSC Adv., 2016, 6, 73222–73268 RSC.
- C. Duan, J. Huang, N. Sullivan and R. O'Hayre, Appl. Phys. Rev., 2020, 7, 011314 CAS.
- M. Shang, J. Tong and R. O'Hayre, RSC Adv., 2013, 3, 15769–15775 RSC.
- J. Tong, W. Yang, B. Zhu and R. Cai, J. Membr. Sci., 2002, 203, 175–189 CrossRef CAS.
- C. Duan, J. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Science, 2015, 349, 1321–1326 CrossRef CAS PubMed.
- D. J. D. Corcoran, D. P. Tunstall and J. T. S. Irvine, Solid State Ionics, 2000, 136–137, 297–303 CrossRef CAS.
- C. E. Tambelli, J. P. Donoso, C. J. Magon, A. C. D. Ângelo, A. O. Florentino and M. J. Saeki, Solid State Ionics, 2000, 136–137, 243–247 CrossRef CAS.
- R. Lan and S. Tao, Adv. Energy Mater., 2014, 4, 1301683 CrossRef.
- L. Fan and P.-C. Su, J. Power Sources, 2016, 306, 369–377 CrossRef CAS.
- Y. Meng, W. Zhang, Z. He, C. Liu, J. Gao, M. Akbar, R. Guo, S. Zhou, Y. Ji, X. Wang and Y. Yang, Int. J. Hydrogen Energy, 2021, 46, 9874–9881 CrossRef CAS.
- D. Xie, K. Li, J. Yang, D. Yan, L. Jia, B. Chi, J. Pu and J. Li, Int. J. Hydrogen Energy, 2021, 46, 10007–10014 CrossRef CAS.
- S. Rauf, B. Zhu, M. A. K. Yousaf Shah, Z. Tayyab, S. Attique, N. Ali, N. Mushtaq, B. Wang, C. Yang, M. I. Asghar and P. D. Lund, ACS Appl. Mater. Interfaces, 2020, 12, 35071–35080 CrossRef CAS PubMed.
- G. Chen, W. Sun, Y. Luo, H. Liu, S. Geng, K. Yu and G. Liu, Int. J. Hydrogen Energy, 2018, 43, 417–425 CrossRef CAS.
- T. Wei, L. A. Zhang, Y. Chen, P. Yang and M. Liu, Chem. Mater., 2017, 29, 1490–1495 CrossRef CAS.
- M. Karlsson, D. Engberg, M. E. Björketun, A. Matic, G. Wahnström, P. G. Sundell, P. Berastegui, I. Ahmed, P. Falus, B. Farago, L. Börjesson and S. Eriksson, Chem. Mater., 2010, 22, 740–742 CrossRef CAS.
- K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359 CrossRef CAS.
- Y. Zhou, X. Guan, H. Zhou, K. Ramadoss, S. Adam, H. Liu, S. Lee, J. Shi, M. Tsuchiya, D. D. Fong and S. Ramanathan, Nature, 2016, 534, 231–234 CrossRef CAS PubMed.
- Y. Zhou, S. Ramanathan and S. Ramanathan, Fuel Cell. Bull., 2016, 2016, 14 CrossRef.
- X. Xu, C. Liu, J. Ma, A. J. Jacobson, C. Nan and C. Chen, J. Materiomics, 2019, 5, 247–251 CrossRef.
- H. Kawamori, I. Oikawa and H. Takamura, Chem. Mater., 2021, 33, 5935–5942 CrossRef CAS.
- R. B. Cervera, S. Miyoshi, Y. Oyama, Y. E. Elammari, T. Yagi and S. Yamaguchi, Chem. Mater., 2013, 25, 1483–1489 CrossRef CAS.
- J. Hyodo, K. Kitabayashi, K. Hoshino, Y. Okuyama and Y. Yamazaki, Adv. Energy Mater., 2020, 10, 2000213 CrossRef CAS.
- J. G. Lee, A. B. Naden, C. D. Savaniu, P. A. Connor, J. L. Payne, J. M. Skelton, A. S. Gibbs, J. Hui, S. C. Parker and J. T. S. Irvine, Adv. Energy Mater., 2021, 11, 2103234 CrossRef CAS.
- S. Fop, J. Mater. Chem. A, 2021, 9, 18836–18856 RSC.
- T. Murakami, J. R. Hester and M. Yashima, J. Am. Chem. Soc., 2020, 142, 11653–11657 CrossRef CAS PubMed.
- Y. Zhou, M. Shiraiwa, M. Nagao, K. Fujii, I. Tanaka, M. Yashima, L. Baque, J. F. Basbus, L. V. Mogni and S. J. Skinner, Chem. Mater., 2021, 33, 2139–2146 CrossRef CAS PubMed.
- F. S. da Silva and T. M. de Souza, Int. J. Hydrogen Energy, 2017, 42, 26020–26036 CrossRef CAS.
- J. Wind, R. A. Mole, D. Yu, M. Avdeev and C. D. Ling, Chem. Mater., 2018, 30, 4949–4958 CrossRef CAS.
- C. A. Fuller, Q. Berrod, B. Frick, M. R. Johnson, M. Avdeev, J. S. O. Evans and I. R. Evans, Chem. Mater., 2020, 32, 4347–4357 CrossRef CAS.
- M. S. Chambers, P. A. Chater, I. R. Evans and J. S. O. Evans, Inorg. Chem., 2019, 58, 14853–14862 CrossRef CAS PubMed.
- M. Ceretti, G. Agostini, M. Brunelli, S. Corallini, G. Perversi, G. Cuello, A. Marsicano and W. Paulus, Inorg. Chem., 2020, 59, 9434–9442 CrossRef CAS PubMed.
- J. Liu, S. Hull, I. Ahmed and S. J. Skinner, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 539–543 CrossRef CAS.
- I. R. Evans, J. A. K. Howard and J. S. O. Evans, Chem. Mater., 2005, 17, 4074–4077 CrossRef CAS.
- L. Malavasi, H. Kim, S. J. L. Billinge, T. Proffen, C. Tealdi and G. Flor, J. Am. Chem. Soc., 2007, 129, 6903–6907 CrossRef CAS PubMed.
- F. Fujishiro, C. Sasaoka, Y. Shibata, K. Tsuda and T. Hashimoto, J. Am. Ceram. Soc., 2019, 102, 4427–4430 CrossRef CAS.
- W. Uno, K. Fujii, E. Niwa, S. Torii, P. Miao, T. Kamiyama and M. Yashima, J. Ceram. Soc. Jpn., 2018, 126, 341–345 CrossRef CAS.
- J. A. Lussier, K. M. Szkop, A. Z. Sharma, C. R. Wiebe and M. Bieringer, Inorg. Chem., 2016, 55, 2381–2389 CrossRef CAS PubMed.
- J. A. Lussier, F. J. Simon, P. S. Whitfield, K. Singh, V. Thangadurai and M. Bieringer, Inorg. Chem., 2018, 57, 5607–5614 CrossRef CAS PubMed.
- D. M. Halat, R. Dervişoğlu, G. Kim, M. T. Dunstan, F. Blanc, D. S. Middlemiss and C. P. Grey, J. Am. Chem. Soc., 2016, 138, 11958–11969 CrossRef CAS PubMed.
- L. Holmes, L. Peng, I. Heinmaa, L. A. O'Dell, M. E. Smith, R.-N. Vannier and C. P. Grey, Chem. Mater., 2008, 20, 3638–3648 CrossRef CAS.
- J. Wind, R. A. Mole, D. Yu and C. D. Ling, Chem. Mater., 2017, 29, 7408–7415 CrossRef CAS.
- J. Wind, R. A. Mole and C. D. Ling, J. Phys. Chem. C, 2019, 123, 15877–15884 CrossRef CAS.
- J. R. Peet, C. A. Fuller, B. Frick, M. Zbiri, A. Piovano, M. R. Johnson and I. R. Evans, Chem. Mater., 2017, 29, 3020–3028 CrossRef CAS.
- J. R. Peet, C. A. Fuller, B. Frick, M. M. Koza, M. R. Johnson, A. Piovano and I. R. Evans, J. Am. Chem. Soc., 2019, 141, 9989–9997 CrossRef CAS PubMed.
- F. P. Marlton, Z. Zhang, Y. Zhang, T. E. Proffen, C. D. Ling and B. J. Kennedy, Chem. Mater., 2021, 33, 1407–1415 CrossRef CAS.
- K. D. Kreuer, Solid State Ionics, 1997, 97, 1–15 CrossRef CAS.
- K. D. Kreuer, Solid State Ionics, 1999, 125, 285–302 CrossRef CAS.
- K. D. Kreuer, S. Adams, W. Münch, A. Fuchs, U. Klock and J. Maier, Solid State Ionics, 2001, 145, 295–306 CrossRef CAS.
- I. Ahmed, S.-G. Eriksson, E. Ahlberg, C. S. Knee, P. Berastegui, L.-G. Johansson, H. Rundlöf, M. Karlsson, A. Matic, L. Börjesson and D. Engberg, Solid State Ionics, 2006, 177, 1395–1403 CrossRef CAS.
- I. Ahmed, S.-G. Eriksson, E. Ahlberg, C. S. Knee, H. Götlind, L.-G. Johansson, M. Karlsson, A. Matic and L. Börjesson, Solid State Ionics, 2007, 178, 515–520 CrossRef CAS.
- I. Ahmed, M. Karlsson, S.-G. Eriksson, E. Ahlberg, C. S. Knee, K. Larsson, A. K. Azad, A. Matic and L. Börjesson, J. Am. Ceram. Soc., 2008, 91, 3039–3044 CrossRef CAS.
- A. Longo, F. Giannici, A. Balerna, C. Ingrao, F. Deganello and A. Martorana, Chem. Mater., 2006, 18, 5782–5788 CrossRef CAS.
- E. Fabbri, D. Pergolesi, S. Licoccia and E. Traversa, Solid State Ionics, 2010, 181, 1043–1051 CrossRef CAS.
- D. Han, Y. Nose, K. Shinoda and T. Uda, Solid State Ionics, 2012, 213, 2–7 CrossRef CAS.
- D. Noferini, M. M. Koza, P. Fouquet, G. J. Nilsen, M. C. Kemei, S. M. H. Rahman, M. Maccarini, S. Eriksson and M. Karlsson, J. Phys. Chem. C, 2016, 120, 13963–13969 CrossRef CAS.
- F. G. Kinyanjui, S. T. Norberg, I. Ahmed, S. G. Eriksson and S. Hull, Solid State Ionics, 2012, 225, 312–316 CrossRef CAS.
- T. E. Engin, A. V. Powell, R. Haynes, M. A. H. Chowdhury, C. M. Goodway, R. Done, O. Kirichek and S. Hull, Rev. Sci. Instrum., 2008, 79, 095104 CrossRef CAS PubMed.
- A. K. Eriksson Andersson, S. M. Selbach, T. Grande and C. S. Knee, Dalton Trans., 2015, 44, 10834–10846 RSC.
- L. Malavasi, C. Ritter and G. Chiodelli, Chem. Mater., 2008, 20, 2343–2351 CrossRef CAS.
- L. Malavasi, C. Tealdi, C. Ritter, V. Pomjakushin, F. Gozzo and Y. Diaz-Fernandez, Chem. Mater., 2011, 23, 1323–1330 CrossRef CAS.
- A. Magrasó, C. H. Hervoches, I. Ahmed, S. Hull, J. Nordström, A. W. B. Skilbred and R. Haugsrud, J. Mater. Chem. A, 2013, 1, 3774–3782 RSC.
- L. Malavasi, C. Ritter and G. Chiodelli, J. Alloys Compd., 2009, 475, L42–L45 CrossRef CAS.
- N. Torino, P. F. Henry, C. S. Knee, S. K. Callear, R. I. Smith, S. M. H. Rahman and S. G. Eriksson, Solid State Ionics, 2018, 324, 233–240 CrossRef CAS.
- L. Mazzei, M. Wolff, D. Pergolesi, J. A. Dura, L. Börjesson, P. Gutfreund, M. Bettinelli, T. Lippert and M. Karlsson, J. Phys. Chem. C, 2016, 120, 28415–28422 CrossRef CAS.
- M. Karlsson, Phys. Chem. Chem. Phys., 2015, 17, 26–38 RSC.
- E. J. Spahr, L. Wen, M. Stavola, L. A. Boatner, L. C. Feldman, N. H. Tolk and G. Lüpke, Phys. Rev. Lett., 2010, 104, 205901 CrossRef CAS PubMed.
- E. J. Spahr, L. Wen, M. Stavola, L. A. Boatner, L. C. Feldman, N. H. Tolk and G. Lüpke, Phys. Rev. Lett., 2009, 102, 075506 CrossRef CAS PubMed.
- Q. Chen, T.-W. Huang, M. Baldini, A. Hushur, V. Pomjakushin, S. Clark, W. L. Mao, M. H. Manghnani, A. Braun and T. Graule, J. Phys. Chem. C, 2011, 115, 24021–24027 CrossRef CAS.
- A. Braun and Q. Chen, Nat. Commun., 2017, 8, 15830 CrossRef CAS PubMed.
- P. Du, Q. Chen, Z. Fan, H. Pan, F. G. Haibach, M. A. Gomez and A. Braun, Commun. Phys., 2020, 3, 200 CrossRef CAS.
- D. Noferini, M. M. Koza, S. M. H. Rahman, Z. Evenson, G. J. Nilsen, S. Eriksson, A. R. Wildes and M. Karlsson, Phys. Chem. Chem. Phys., 2018, 20, 13697–13704 RSC.
- D. Noferini, M. M. Koza and M. Karlsson, J. Phys. Chem. C, 2017, 121, 7088–7093 CrossRef CAS.
- M. Karlsson, A. Matic, C. S. Knee, I. Ahmed, S. G. Eriksson and L. Börjesson, Chem. Mater., 2008, 20, 3480–3486 CrossRef CAS.
- M. Karlsson, I. Ahmed, A. Matic and S. G. Eriksson, Solid State Ionics, 2010, 181, 126–129 CrossRef CAS.
- Q. Chen, J. Banyte, X. Zhang, J. P. Embs and A. Braun, Solid State Ionics, 2013, 252, 2–6 CrossRef CAS.
- J. F. Basbus, M. D. Arce, F. R. Napolitano, H. E. Troiani, J. A. Alonso, M. E. Saleta, M. A. González, G. J. Cuello, M. T. Fernández-Díaz, M. P. Sainz, N. Bonanos, C. E. Jimenez, L. Giebeler, S. J. A. Figueroa, A. Caneiro, A. C. Serquis and L. V. Mogni, ACS Appl. Energy Mater., 2020, 3, 2881–2892 CrossRef CAS.
- T. Matzke, U. Stimming, C. Karmonik, M. Soetratmo, R. Hempelmann and F. Güthoff, Solid State Ionics, 1996, 86–88, 621–628 CrossRef CAS.
- B. Groß, C. Beck, F. Meyer, T. Krajewski, R. Hempelmann and H. Altgeld, Solid State Ionics, 2001, 145, 325–331 CrossRef.
- R. Hempehnann, C. Karmonik, T. Matzke, M. Cappadonia, U. Stimming, T. Springer and M. A. Adams, Solid State Ionics, 1995, 77, 152–156 CrossRef.
- R. Hempelmann, M. Soetratmo, O. Hartmann and R. Wäppling, Solid State Ionics, 1998, 107, 269–280 CrossRef CAS.
- Y. Yamazaki, F. Blanc, Y. Okuyama, L. Buannic, J. C. Lucio-Vega, C. P. Grey and S. M. Haile, Nat. Mater., 2013, 12, 647–651 CrossRef CAS PubMed.
- D. Noferini, B. Frick, M. M. Koza and M. Karlsson, J. Mater. Chem. A, 2018, 6, 7538–7546 RSC.
- K. Toyoura, W. Meng, D. Han and T. Uda, J. Mater. Chem. A, 2018, 6, 22721–22730 RSC.
- L. Mazzei, A. Perrichon, A. Mancini, G. Wahnström, L. Malavasi, S. F. Parker, L. Börjesson and M. Karlsson, J. Mater. Chem. A, 2019, 7, 7360–7372 RSC.
- K. Toyoura, T. Fujii, N. Hatada, D. Han and T. Uda, J. Phys. Chem. C, 2019, 123, 26823–26830 CrossRef CAS.
- K. Alberi, M. B. Nardelli, A. Zakutayev, L. Mitas, S. Curtarolo, A. Jain, M. Fornari, N. Marzari, I. Takeuchi, M. L. Green, M. Kanatzidis, M. F. Toney, S. Butenko, B. Meredig, S. Lany, U. Kattner, A. Davydov, E. S. Toberer, V. Stevanovic, A. Walsh, N.-G. Park, A. Aspuru-Guzik, D. P. Tabor, J. Nelson, J. Murphy, A. Setlur, J. Gregoire, H. Li, R. Xiao, A. Ludwig, L. W. Martin, A. M. Rappe, S.-H. Wei and J. Perkins, J. Phys. D: Appl. Phys., 2018, 52, 013001 CrossRef PubMed.
- P. Gorai, V. Stevanović and E. S. Toberer, Nat. Rev. Mater., 2017, 2, 17053 CrossRef CAS.
- R. Xiao, H. Li and L. Chen, Sci. Rep., 2015, 5, 14227 CrossRef CAS PubMed.
- G. Hautier, A. Jain, H. Chen, C. Moore, S. P. Ong and G. Ceder, J. Mater. Chem., 2011, 21, 17147–17153 RSC.
- X. Wang, R. Xiao, H. Li and L. Chen, Phys. Rev. Lett., 2017, 118, 195901 CrossRef PubMed.
- O. N. Senkov, J. D. Miller, D. B. Miracle and C. Woodward, Nat. Commun., 2015, 6, 6529 CrossRef CAS PubMed.
- C. C. Fischer, K. J. Tibbetts, D. Morgan and G. Ceder, Nat. Mater., 2006, 5, 641–646 CrossRef CAS PubMed.
- S. Ding, Y. Liu, Y. Li, Z. Liu, S. Sohn, F. J. Walker and J. Schroers, Nat. Mater., 2014, 13, 494–500 CrossRef CAS PubMed.
- Y. J. Li, A. Savan, A. Kostka, H. S. Stein and A. Ludwig, Mater. Horiz., 2018, 5, 86–92 RSC.
- W. Chen, J. George, J. B. Varley, G.-M. Rignanese and G. Hautier, npj Comput. Mater., 2019, 5, 72 CrossRef.
- H. Hafiz, A. I. Khair, H. Choi, A. Mueen, A. Bansil, S. Eidenbenz, J. Wills, J.-X. Zhu, A. V. Balatsky and T. Ahmed, npj Comput. Mater., 2018, 4, 63 CrossRef.
- S. Luo, T. Li, X. Wang, M. Faizan and L. Zhang, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1489 CAS.
- L. Zhang, B. He, Q. Zhao, Z. Zou, S. Chi, P. Mi, A. Ye, Y. Li, D. Wang, M. Avdeev, S. Adams and S. Shi, Adv. Funct. Mater., 2020, 30, 2003087 CrossRef CAS.
- M. Matsubara, A. Suzumura, N. Ohba and R. Asahi, Commun. Mater., 2020, 1, 5 CrossRef.
- S. Kajita, N. Ohba, A. Suzumura, S. Tajima and R. Asahi, NPG Asia Mater., 2020, 12, 31 CrossRef.
- S. De, A. P. Bartók, G. Csányi and M. Ceriotti, Phys. Chem. Chem. Phys., 2016, 18, 13754–13769 RSC.
- J. Lee, N. Ohba and R. Asahi, Sci. Rep., 2019, 9, 2593 CrossRef PubMed.
- J. Lee, N. Ohba and R. Asahi, Chem. Mater., 2020, 32, 1358–1370 CrossRef CAS.
- P. Priya and N. R. Aluru, npj Comput. Mater., 2021, 7, 90 CrossRef CAS.
- P. Wisesa, C. Li, C. Wang and T. Mueller, RSC Adv., 2019, 9, 31999–32009 RSC.
- J. Hyodo, K. Tsujikawa, M. Shiga, Y. Okuyama and Y. Yamazaki, ACS Energy Lett., 2021, 6, 2985–2992 CrossRef CAS.
- N. Artrith, K. T. Butler, F.-X. Coudert, S. Han, O. Isayev, A. Jain and A. Walsh, Nat. Chem., 2021, 13, 505–508 CrossRef CAS PubMed.
- M. Wolff, A. Devishvili, J. A. Dura, F. A. Adlmann, B. Kitchen, G. K. Pálsson, H. Palonen, B. B. Maranville, C. F. Majkrzak and B. P. Toperverg, Phys. Rev. Lett., 2019, 123, 016101 CrossRef CAS PubMed.
- S. Miyoshi, Y. Akao, N. Kuwata, J. Kawamura, Y. Oyama, T. Yagi and S. Yamaguchi, Chem. Mater., 2014, 26, 5194–5200 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |