Are you using the right probe molecules for assessing the textural properties of metal–organic frameworks?†
Timur
Islamoglu‡
 a,
Karam B.
Idrees‡
a,
Karam B.
Idrees‡
 a,
Florencia A.
Son
a,
Florencia A.
Son
 a,
Zhijie
Chen
a,
Zhijie
Chen
 a,
Seung-Joon
Lee
a,
Peng
Li
a,
Seung-Joon
Lee
a,
Peng
Li
 b and
Omar K.
Farha
b and
Omar K.
Farha
 *a
*a
aDepartment of Chemistry and International Institute for Nanotechnology, Northwestern University, 2145 Sheridan Road, Evanston, Illinois 60208, USA. E-mail: o-farha@northwestern.edu
bShanghai Key Laboratory of Molecular Catalysis and Innovative Materials, Department of Chemistry, Fudan University, 2005 Songhu Road, Shanghai 200438, China
First published on 13th December 2021
Abstract
Textural properties—such as the surface area, pore size distribution, and pore volume—are at the forefront of characterization for porous materials. Therefore, it is essential to accurately and reproducibly report a material's textural properties as they could ultimately dictate its applicability. This work aims to provide insightful and comprehensive studies of textural properties for a set of metal–organic frameworks (MOFs), a class of porous materials, using various gases to equip researchers in the field with a helpful guide and reference. We selected a series of nine MOFs with different surface areas, pore sizes, shapes, and chemical environments to represent a wide range of materials. We probed the textural properties of these MOFs using traditional and distinctive gases: N2, Kr and O2 at 77 K, Ar at 87 K, and CO2 at 195 and 273 K. With regard to surface area, we discuss the validity and challenges associated with the current BET method, the importance of utilizing the Rouquerol et al. consistency criteria to ensure accuracy and reproducibility, and the recommended gas probes for certain materials. For pore size distribution, we discuss the efficacy of each probe for determining the pore sizes within a porous material relative to the calculated distribution from its crystal structure, the limitations of current computational kernels used to calculate pore size distributions, and the need for advanced kernels to envelope the diversity of porous materials. Finally, for pore volume, we discuss the use of the Gurvich rule to obtain the total pore volume in comparison with calculated values from crystal structures and its consistency as a metric for porous materials. Ultimately, we hope that this article will aid researchers in characterizing the textural properties of porous materials and encourage the development of new kernels capable of encompassing the complexity of MOFs and other porous materials.
Introduction
Porous materials have gained significant interest from both academic and industrial researchers owing to their accessible internal surfaces, which provide unparalleled advantages.1 Specifically, microporous materials can offer surface areas that are orders of magnitude higher than those of non-porous counterparts, including nano-sized non-porous particles that typically require more challenging syntheses. While porous materials were initially recognized for their applicability in adsorption-based separations, their potential uses were quickly expanded to offer promising solutions to challenges faced in fields ranging from single site catalysis to drug delivery.2–4 Owing to advancements in synthetic and characterization techniques, researchers have gained a deeper understanding of structure–property relationships in porous materials. Textural properties—such as surface area, pore size, and pore shape—have a decisive role in determining the performance of a material for a given application. For example, microporous materials (pore sizes <2 nm) are promising for the separation of small gases, while mesoporous materials (2 nm < pore size < 50 nm) have been instrumental as catalysts/supports or carriers for large molecules.3 Driven by both the curiosity and need for porous materials with predictable surface areas, pore sizes, and pore shapes, metal–organic frameworks (MOFs), atomically precise hybrid porous materials, were discovered.5–8 The last two decades witnessed a significant development in the design and synthesis of MOFs.9 Thanks to the wide variety of building units—metal nodes and organic struts—researchers can design MOFs with desired properties, and thousands of structures have already been reported in The Cambridge Crystallographic Data Centre, despite the relatively young age of the field.10 Although we can gain a deeper understanding of MOFs from the crystal structures obtained from single crystals, the powder form is often needed for implementation of these materials to solve real life challenges.11 This implies that the assessment of MOFs towards an application is highly dependent on the properties of bulk material. Therefore, the accurate characterization of the textural properties of bulk MOF powders is crucial.Many experimental techniques have been developed for characterizing porous materials, including gas/vapor sorption at various temperatures,12,13 X-ray and neutron scattering,14 electron microscopy,15 mercury adsorption,16 and nuclear magnetic resonance spectroscopy.17 While each method has its own advantages and limitations, the adsorption of inert gases at temperatures below their critical points is the most commonly implemented method for porosity characterization, including the surface area, pore size distribution, and pore volume.18–21 Importantly, all this information can be obtained from a single sorption isotherm data set. Adsorption is the process where free molecules (adsorbate) change to a less mobile state after being attached to a surface (adsorbent). The relationship between the amount adsorbed and the equilibrium pressure of the adsorbate at a constant temperature is referred to as the adsorption isotherm. Prior to conducting adsorption measurements, the guest molecules inside the pores have to be removed while maintaining the material's structural integrity, typically performed under vacuum and mild heat (i.e. 100 °C). In the case that a porous material undergoes structural changes (reversible or irreversible) during the removal of guest molecules, we recommend using a supercritical carbon dioxide dryer for the removal of guest molecules. This topic has been reviewed recently and will not be discussed herein; therefore, we refer readers to the recent reviews on the topic.22,23
Since the first systematic measurements of nitrogen isotherms at 77 K, gas sorption studies have been indispensable for characterizing the textural properties of porous materials.24,25 Although we can directly measure the amount of gas adsorbed gravimetrically using highly sensitive microbalances, the manometric method is more commonly used due to ease of instrument design for high-throughput analysis, which results in a more cost-effective analyzer. In manometric instruments, the change in pressure is measured after the gas is dosed and equilibrium is reached.26 Subsequently, the change in pressure is used for calculating the amount of gas adsorbed and the isotherms are reported as the volume of gas adsorbed (at standard temperature and pressure) per gram of adsorbent. The full isotherm profile is comprised of two curves: adsorption and desorption branch. After the desired adsorption pressure is achieved, often the saturation pressure of adsorbate at the analysis temperature, desorption, the reverse process, is started where the adsorbate is withdrawn gradually until the equilibrium is achieved at a predetermined pressure. With modern commercial instruments, researchers can measure gas and vapor sorption isotherms of different porous materials reproducibly at various temperatures and low pressures (up to 1 bar) for structural characterization, and high pressures (typically up to 100 bar) for gas storage applications. Fully automated instruments equipped with turbopumps can achieve very low pressures, allowing for the collection of high-resolution adsorption data of up to seven orders of magnitude relative pressure range.
Typically, the first step in the interpretation of an isotherm is the determination of its isotherm type, which provides substantial information about the textural properties of the material. The IUPAC report released in 2015 summarizes all the isotherm types in detail.27 Here, we will only describe the isotherm types commonly observed in MOFs. Previously,28 nitrogen isotherms of all microporous materials were classified as Type I; however, the most recent IUPAC report introduced Type I(a) and Type I(b) isotherms based on the sizes of micropores present (Fig. 1). With this updated report,27 isotherms for ultramicroporous (i.e. pore width <1 nm) materials are classified as Type I(a), where there is a steep increase in gas uptake at very low pressures followed by a plateau parallel to the pressure axis. On the other hand, isotherms observed with materials containing wider micropores (i.e. pore widths of 1–2 nm) are classified as Type I(b), where there is a steep uptake at low pressure followed by a shallower increase in gas uptake, resulting in a rounded isotherm shape as opposed to almost perfectly cornered isotherm shape observed in Type I(a). The isotherms of porous materials containing mesopores are classified as Type IV, where the condensation of the gas in the pores is observed after the initial multilayer adsorption in the mesopores and is subsequently followed by a plateau parallel to the pressure axis. Materials with pore widths larger than 4 nm exhibit a hysteresis in desorption branch of their isotherms,29,30 while materials with pore widths smaller than 4 nm show a nearly perfect overlap of adsorption and desorption branch of isotherms. These isotherms are classified as Type IV(a) and Type IV(b), respectively. It is worth noting that many mesoporous MOFs also contains micropores and, therefore, show a combination of Type I and Type IV isotherms. A specific range or full range of isotherms (explained below) is used for deriving surface area, pore size distribution, and pore volume of materials.
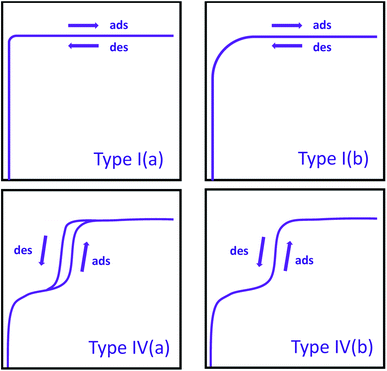 | ||
| Fig. 1 IUPAC classification of commonly observed isotherms in MOFs. Ads = adsorption; des = desorption. | ||
While nitrogen isotherms at 77 K is the most commonly used method for assessing the textural properties of MOFs, isotherms collected at 77 K for O2 and Kr, 87 K for Ar, and 195 K for CO2 can also be used to derive this information.31 Due to the different physicochemical properties of these probe molecules (Table 1) and the influence on isotherm shape that the chemical and physical properties of MOFs impart, we were motivated to investigate the different probes to characterize the textural properties of selected MOFs with distinct properties (Fig. 2).
| Probe | Cross-sectional area (nm2) | Molecular weight (g mol−1) | Kinetic diameter (Å) | Critical temperature (K) | Benefits |
|---|---|---|---|---|---|
| N2 (77 K) | 0.162 | 28.01 | 3.64 | 126.2 | Affordable and most commonly used |
| O2 (77 K) | 0.143 | 32.00 | 3.46 | 154.6 | Lower quadrupole moment compared to N2 |
| Ar (87 K) | 0.143 | 39.95 | 3.40 | 150.8 | No quadrupole moment, consistent orientation, and faster equilibration compared to N2 |
| CO2 (195 K/273 K) | 0.142 | 44.01 | 3.30 | 304.2 | Small kinetic diameter and fast equilibration |
| Kr (77 K/87 K) | 0.210 | 83.80 | 3.60 | 209.3 | High sensitivity towards low surface area materials |
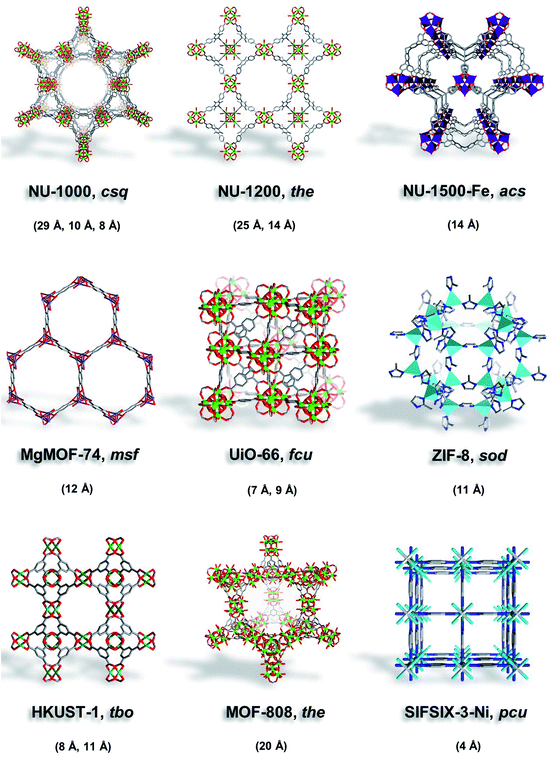 | ||
| Fig. 2 Illustrations of MOFs studied here (NU-1000, NU-1200, NU-1500-Fe, MgMOF-74, UiO-66, ZIF-8, HKUST-1, MOF-808, and SIFSIX-3-Ni) with their corresponding topology and pore size. | ||
Here, we selected MOFs that contain ultramicropores (UiO-66, SIFSIX-3-Ni), micropores (MgMOF-74, HKUST-1, NU-1500), micropores/mesopores (NU-1200, NU-1000), and MOF-808 with ∼20 Å can be considered on the borderline. Moreover, we selected MOFs with open metal sites to assess the effect of strongly polarizing sites on different probe molecules. NU-1000 (csq) is a Zr-based MOF assembled from 8-connected Zr6 clusters and pyrene-based linkers (1,3,6,8-tetrakis(p-benzoate)pyrene) to form a framework with mesoporous hexagonal channels (∼29 Å) and two microporous channels (∼8 and ∼12 Å).32,33 NU-1200 (the) is a Zr-based MOF assembled from 8-connected Zr6 clusters and tribenzoic-based linkers (4,4′,4′′-(2,4,6-trimethylbenzene-1,3,5-triyl) tribenzoic acid) yielding mesoporous channels (∼25 Å) and microporous cages (∼14 Å).34 Fe-NU-1500 (acs) is an Fe-based MOF composed of trinuclear Fe3+ clusters and hexacarboxylic acid triptycene-based linkers (H6PET) with hexagonal channels (∼14 Å).35 MgMOF-74 (msf) is a Mg-based MOF composed of divalent Mg2+ cations and dicarboxylic acid linkers (2,5-dihydroxybenzene-1,4-dicarboxylic acid) that form hexagonal channels (∼12 Å).36 UiO-66 (fcu) is a Zr-based MOF assembled from 12-connected Zr6 clusters and dicarboxylic acid linkers (1,4-benzenedicarboxylic acid) to form octahedral cavities (∼9 Å) and tetrahedral cavities (∼7 Å).37 ZIF-8 (sod) is a Zn-based MOF comprised of tetrahedral Zn2+ cations and imidazolate linkers (2-methylimidazole) to form cages (∼11 Å) with flexible pore apertures.38,39 HKUST-1 (tbo) is a Cu-based MOF assembled from dimeric copper paddlewheels and tricarboxylic acid linkers (1,3,5-benzenetricarboxylic acid) to form microporous cavities (∼8, 11 Å).40 MOF-808 (the) is assembled from 6-connected Zr6 clusters and tricarboxylic acid linkers (1,3,5-benzenetricarboxylic acid), forming large spherical cavities (∼20 Å) and small tetrahedral cavities.41 SIFSIX-3-Ni (pcu) is a Ni-based MOF comprised of Ni(pyrazine)22+ cations connected by SiF62− anions to form 1-dimensional channels (∼4 Å).42
The purpose of this report is to provide the isotherms with commonly used probe molecules of the selected MOFs with different properties to highlight the merits and limitations of each system when reporting the expected properties from the crystal structures of these MOFs. The isotherms for all gases were measured successively using the same MOF powder in the analysis tube to minimize any error in determining the mass of the sample, or any possible variations due to the activation of MOFs. Therefore, the differences observed with the selected probe molecules on surface areas, pore size distributions, and pore volumes of the MOFs can be attributed to the nature of the probe molecule at the analysis temperature, rather than non-systematical experimental errors. Here, we do not suggest settings for the data collection software as this would apply to only one particular brand that was used for this study. Instead, we highlight the general criteria that researchers should pay attention to when setting up their analyses. In the following sections, we discuss the details of how surface area, pore size distribution, and pore volume are calculated from the isotherms followed by a thorough analysis of each probe molecule for its ability to report these textural properties.
Surface area
Specific surface area, or the area of surface per unit mass of material, is one of the most important values used in the characterization of porous materials. It is also used as a metric for non-porous materials to compare the external surface areas of different materials. Therefore, there is a growing interest in accurately determining of the specific surface areas of solid materials both computationally and experimentally. Computationally, surface areas can be calculated geometrically, where a probe molecule of a certain size (commonly the size of a dinitrogen molecule) is rolled across the total accessible surface.43 Experimentally, the isotherms of gases measured at temperatures lower than the critical temperature of adsorbates are utilized for evaluating the surface area of the various materials.44 The Langmuir model was initially introduced to describe adsorption processes and derive the specific surface area based on a given isotherm.45,46 However, the integral assumptions of this model were too simplistic to fully describe adsorption in porous materials. Specifically, the assumption that adsorption of gas molecules only occurs on the solid surface as a single layer (monolayer adsorption) leads to the overestimation of surface area as multilayer adsorption occurs in porous materials far more often than monolayer adsorption. The multilayer adsorption model; an extension of the Langmuir model that was described by Brunauer, Emmett and Teller (BET); received significant attention since its inception in 1938, because it produces more reliable surface areas, especially with materials that have large pores allowing multilayer adsorption.47 Through BET theory, it became evident that the plateau in a Type I isotherm does not necessarily correspond to the completing of monolayer coverage, but it could also imply the completion of pore filling in materials that have large pores allowing multilayer packing of adsorbates.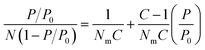 | (1) |
The BET equation (eqn (1)) is the most commonly accepted and applied method. In this method, the adsorption isotherm is converted to a BET plot: [(P/P0)/N (1 − P/P0)] vs. P/P0, where N is the amount of gas adsorbed, P is pressure, and P0 is saturation pressure of the gas at the analysis temperature. N is the amount of gas adsorbed at corresponding P/P0 and Nm is the amount of gas adsorbed to achieve an apparent monolayer coverage. C is the dimensionless BET constant that relates to the enthalpy of the adsorption of the probe molecule on the surface. Previously, it was a common practice to assume that monolayer surface coverage occurs in the range 0.05 < P/P0 < 0.3; however, many studies have shown that monolayer coverage can occur at much lower relative pressures.48,49 This is commonly observed in microporous MOFs where monolayer coverage can be achieved at P/P0 <0.05. Despite the efficacy of the BET model in describing adsorption processes through multilayer coverage, inconsistencies in its applications to derive the specific surface areas remained as multiple regions on the BET plot often times resulted in a linear correlation. The presence of multiple “seemingly” viable regions for BET analysis can lead to variations in the BET area based on user's discretion, making it difficult to replicate and compare results across different laboratories.50 Consequently, Rouquerol et al. proposed a set of consistency criteria to eliminate/minimize the error in determining the amount adsorbed for monolayer coverage which is used for deriving the BET area.51 The criteria suggested by Rouquerol et al. are:
(1) Select the relative pressure range where N (1 − P/P0) continuously increases together with P/P0.
(2) BET constant, C, should be positive.
(3) The monolayer loading, Nm, calculated from BET equation should correspond to a relative pressure from the isotherm that is located within the relative pressure range selected for BET analysis.
(4) The relative pressure corresponding to the monolayer capacity calculated from BET eqn (1/(√C + 1)) should be similar equal within 20% tolerance.
After the most reasonable monolayer coverage capacity is calculated from the BET equation, then the BET area can be calculated using the molecular cross-sectional area of the probe molecule. As an example, Fig. 3 shows the BET plot of UiO-66 from nitrogen isotherms, along with the other parameters calculated when considering the consistency criteria. While the first two criteria have been widely practiced by researchers, the last two criteria have commonly been overlooked. However, there are many reports demonstrating the importance of applying the full set of criteria, particularly if hierarchical pore structures are present in the structure where pore filling and monolayer coverage of different pores can happen at different relative pressures.52 It is also important to note that commercial software for data reduction typically do not provide options to check the last two criteria, and this is, most likely, the main reason why they are not as frequently practiced. While we recommend researchers to implement Rouquerol et al. consistency criteria to obtain more reliable BET areas of their materials, we also encourage the instrument manufacturers to implement these rules into their software so that they are readily available to researchers. Additionally, we encourage researchers to report BET plots as well as the parameters derived from them so that readers can benefit from the data when comparing the results obtained for the following studies. Importantly, the surface area obtained for a microporous material or a hierarchical material that is predominantly microporous should not be received as an absolute probe accessible surface area, but rather as an “apparent surface area” or a “BET area”.27 This is due to the challenge associated with distinguishing the monolayer coverage versus pore filling in these materials. Also, researchers should take caution and not use the terms “surface area” and “porosity” interchangeably, as porosity is the ratio of the total pore volume to the apparent volume of a crystal while the surface area refers to total surface measured by a given method.
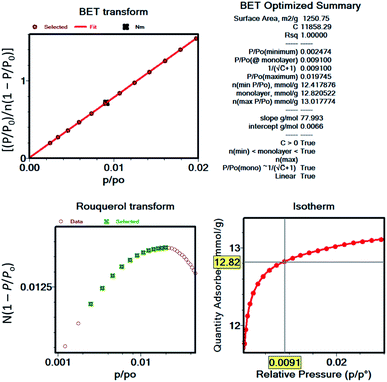 | ||
| Fig. 3 BET plot and related parameters for UiO-66 nitrogen isotherm as an example for demonstration of Rouquerol et al. consistency criteria. | ||
Herein, to further confirm the valid selection of pressure regions for BET analysis in addition to the consistency criteria, we also explored the implementation of excess sorption work (ESW) method. The ESW method was proposed in the late 1990s as an alternative method for determining the monolayer coverage, based on the idea that the excess surface work will minimize at the maximum of adsorbate–adsorbate and adsorbate–adsorbent interaction, which is defined as the monolayer capacity.53 This method considers the thermodynamic properties of the adsorbate in converting the adsorption isotherm into the ESW function with respect to loading. This is especially useful if multiple regions can satisfy the consistency criteria for BET area calculations.54 This method, in combination with BET (ESW + BET), could provide a uniform and reliable way to report BET areas within the field by eliminating the ambiguity in region selection. Furthermore, the monolayer capacity can be found at the local minimum of the ESW function (eqn (2)).
ϕ = nRT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(x) ln(x) | (2) |
In this study, we calculated the BET areas for MOFs from isotherms collected at 77 K for N2, O2, and Kr, 87 K for Ar, and 195 K for CO2 by utilizing Rouquerol et al. consistency criteria (Fig. 5). By fulfilling the consistency criteria, we also note the difference in relative pressure region selected for the BET area using varying probes and MOFs.
Pore size distribution
Pore size refers to the distance between two opposite walls of the pore and is commonly referred to as the pore diameter for cylindrical pores and the pore width for slit-shaped pores. Pore size distribution (PSD) is the relative abundance of each of pore size within a porous material. Contrary to surface area, the determination of PSD requires the full isotherm starting from the lowest relative pressure achievable on the instrument (i.e. P/P0 ∼10−7) to obtain a comprehensive profile. Since ultramicropores are filled at very low relative partial pressures, data collection must occur on an instrument with a turbo pump to reach those low pressures. The accurate determination of P/P0 is crucial for the reliability of the obtained results; therefore, it is recommended to record the P0 at each pressure point by a dedicated analysis tube. Importantly, special care must be taken for data points at very low relative pressures to ensure full equilibration has been achieved since non-equilibrated data can cause the underestimation of uptake and/or a shift in the relative pressure region. Typically, an equilibration interval of ∼20 seconds is sufficient to achieve full equilibration at low pressures in nitrogen or argon isotherms at cryogenic temperatures with micro/mesoporous materials. However, if the size of the adsorbate is close to the pore size of the adsorbent, researchers should consider longer equilibration times. Additionally, the real time pressure data can help researchers to determine if the equilibration has been achieved or not for a given data point in an isotherm.55 The experimental isotherms are then fitted to theoretical models (kernels), commonly based on density functional theory (DFT), to obtain the PSD curve.56 It is critical to point out that the DFT models are generated based on certain assumptions, such as pore shape (i.e. cylindrical, spherical, slit) or surface heterogeneity (i.e. metal-oxide, carbon, hybrid). Therefore, researchers should evaluate the resulting kernel fitting to the experimental isotherm to achieve the most reliable data for PSD.57 For example, MOFs with pores resembling ordered channels or cylinders with both ends open, such as MgMOF-74, would be better suited for a cylindrical pore model. On the other hand, pores between parallel plates are often characterized using a slit pore model. Owing to the exceptionally tunable platform offered by MOFs, due to diversity of metal-nodes and organic linkers and their unique combinations, a large variety of pore shapes and sizes as small as molecular dimensions of probe molecules (<0.4 nm) up to ∼10 nm pores have been reported in MOFs.42,58,59 While there are microporous MOFs exhibiting Type I isotherms and mesoporous MOFs with Type IV isotherms, a significant fraction of MOFs are hierarchical, containing micropores and mesopores, resulting in isotherms featuring multiple steps at different relative pressures.60–62 Notably, synthetic conditions can be controlled to introduce structural defects on MOF crystallites, which can result in macropores making the MOF crystallite a hierarchically porous structure.63 While gas probes cannot detect the full range of macropores, the pore sizes up to ∼100 nm can be detected with gas adsorption isotherms at cryogenic temperatures.27 Despite the exponential increase in the number of the MOF structures reported annually, the field is still, unfortunately, missing models to capture unique pore sizes and shapes offered by MOFs that have not been seen in other porous materials. Our recent report illustrated that the practicality of developing hybrid models for MOFs that allowed us to detect the micropores in an isoreticular series of Zr-based MOFs.64 Here, we utilized the DFT models available for N2 at 77 K, Ar at 87 K, and O2 at 77 K isotherms (Table S6†) and compared the pore size distributions obtained from these isotherms to the values obtained from Zeo++, a computational tool to calculate the pore sizes from crystal structures.65 Beyond isotherms collected at cryogenic temperatures, CO2 isotherms at 273 K are also often used to characterize microporous samples.66 Therefore, we have also measured CO2 isotherms at 273 K and compared the micropore sizes obtained to values obtained from other probe molecules.Pore volume
Pore volume is another crucial piece of information that can be easily obtained from the gas/vapor isotherms collected at temperatures where the adsorbate condenses at P/P0 ∼1, known as the unity, or below. While there are a variety of methods available for obtaining pore volume from the isotherms, including DFT models used for PSD,67 the Gurvich rule is the most commonly used to obtain the total pore volume of porous materials.68,69 The Gurvich rule utilizes the amount of gas adsorbed at P/P0 ∼1 and assumes that the density of the confined liquid in the pores is the same as the density of the adsorbate at the same temperature. Pore filling in microporous materials showing Type I isotherms occur at much lower relative pressures (i.e. <P/P0 = 0.05) followed by a plateau. Therefore, the calculation of pore volume at relative pressures much lower than the unity should result in similar pore volume values. In contrast, for mesoporous materials, the multilayer adsorption results in capillary condensation, where the adsorbate condenses into a liquid-like phase at pressures less than the saturation pressure at a given temperature. Therefore, data points at a relative pressure range after the capillary condensation has occurred needs to be collected to obtain the total pore volume.Isotherms of materials with small particle sizes (i.e. particle size <500 nm) may possess a steep uptake at relative pressures close to unity, which can be ascribed to the capillary condensation of the adsorbate in the disordered interparticle voids.70 Therefore, pore volume from these isotherms should be calculated using the uptake at earlier relative pressures before the condensation occurs in interparticle voids, i.e. P/P0 ∼0.85. Importantly, the condensation of the adsorbate in the interparticle voids (macropores) often results in no hysteresis, while the condensation in large mesopores (pore width >4 nm) results in a hysteresis in the isotherm which can be helpful in determining the nature of the condensation.27
The total pore volume is often used as a metric for researchers to confirm the porosity that they were able to access compared to theoretical values or an experimental value from literature. This is because the BET areas are often reported as numbers without reporting the BET plot and the relative pressure region utilized for calculation. As previously mentioned, the BET areas obtained are very sensitive to the relative pressure region used; therefore, BET plots should be reported along with the BET areas. Here, we utilized the Gurvich rule for obtaining the total pore volumes from the isotherms collected at cryogenic temperatures where the adsorbate condenses in the pores. The total pore volumes are compared to the values obtained from Zeo++. The total pore volumes are not calculated for CO2 isotherms at 273 K since the CO2 does not condense at 273 K and 1 bar, and, therefore, it does not result in a liquid-like CO2 density within the pores.
Isotherms of inert gases
Nitrogen
Nitrogen gas is frequently used as a probe molecule to obtain BET area, pore size distribution, and pore volume of porous materials.12 This is in part due to the relatively low costs of liquid nitrogen (77 K temperature bath) and ultra-high purity nitrogen gas (adsorptive). However, the relatively large quadrupole moment of nitrogen gas makes it vulnerable to heterogeneous surfaces containing exposed polar surface sites such as heteroatoms and/or open-metal sites, where selective adsorption of nitrogen gas has been anticipated.27 Nevertheless, the applicability of nitrogen gas as probe molecule to obtain critical information about the textural properties of porous materials has been widely accepted. Therefore, we began by collecting the nitrogen sorption isotherms of all MOFs in our study (Fig. 4). The archetypal MOFs studied here have previously been characterized by nitrogen isotherms and powder X-ray diffraction (PXRD); comparison to literature reports permitted us to confirm the structural purity and high crystallinity of the MOFs.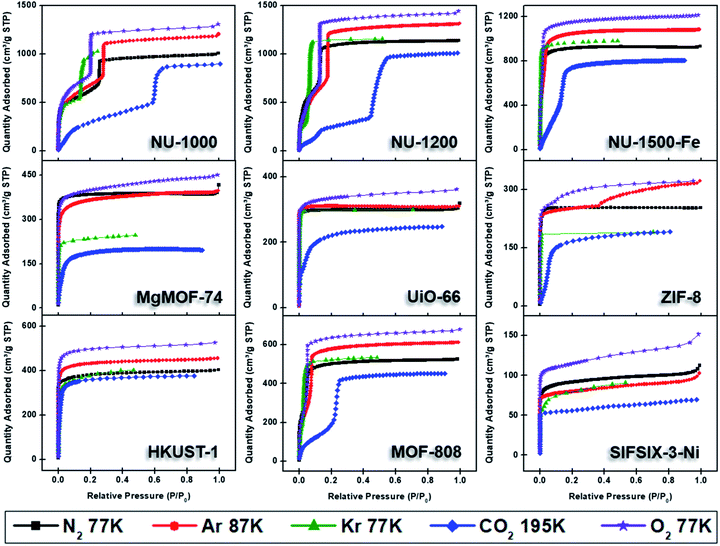 | ||
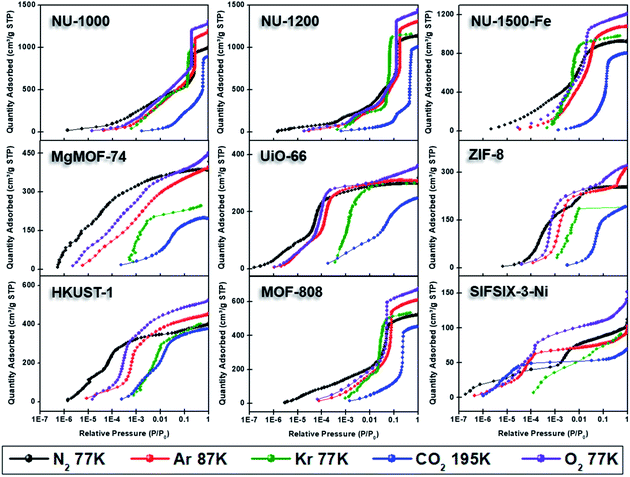
| Fig. 4 Adsorption isotherms of NU-1000, NU-1200, NU-1500-Fe, MgMOF-74, UiO-66, ZIF-8, HKUST-1, MOF-808, and SIFSIX-3-Ni using N2 (77 K), Ar (87 K), Kr (77 K), CO2 (195 K), and O2 (77 K). | ||
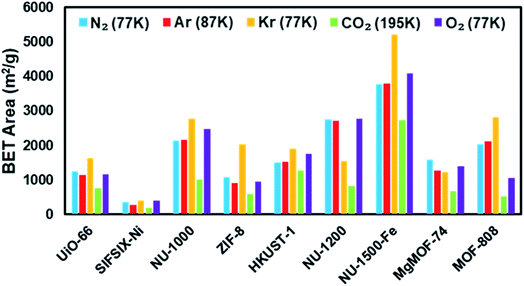
Fig. 4 shows the nitrogen isotherms of MOFs collected at 77 K. MOFs with pore sizes of ∼1 nm ZIF-8, UiO-66 and MgMOF-74 show Type I(a) nitrogen isotherms. While SIFSIX-3-Ni also has narrow pores, its nitrogen isotherm is closer to Type I(b) classification which can be ascribed to significant amount of nitrogen uptake on the external surfaces of the crystallites. The isotherms of NU-1000 and NU-1200 showed a second steep uptake at higher partial pressures due to the presence of mesopores where the condensation occurs, resulting in Type IV(b) isotherms. Despite the fact that MOF-808 and NU-1500 do not contain mesopores, their large micropores are filled at higher partial pressures compared to other MOFs, with narrow micropores resulting in a noticeable second step in their isotherms. Importantly, the partial pressures where the pore filling occurs are significantly lower than the MOFs with mesopores. Next, we calculated the BET area of the MOFs studied here. BET areas were obtained using the four consistency criteria described by Rouquerol et al. which we described in a previous section. Additionally, we applied excess sorption work (ESW) method to evaluate the accuracy of the monolayer capacity determination with MOFs selected for this study. ESW is especially helpful when there are multiple pressure ranges that can satisfy the consistency criteria. It was previously assumed that monolayer surface coverage occurs in the range 0.05 <P/P0 <0.3, so this region is commonly used for BET area calculations. However, it is now well-documented that monolayer coverage with nitrogen gas at 77 K can occur at much lower relative pressures. For example, all MOFs studied here show monolayer coverage at partial pressures lower than even the staring pressure range described above, and the partial pressure range is even lower for the materials with narrower micropores. The BET areas reported here still may not report the actual surface area due to the above-mentioned challenges with nitrogen isotherms at 77 K. Nevertheless, since nitrogen gas is the most commonly available and used probe molecule in literature, the results from the other probes will be compared to those obtained from nitrogen isotherms. We hope that this will help readers reevaluate their needs for alternative probe molecules in addition to nitrogen gas. BET areas (m2 g−1) of NU-1000 (2135), NU-1200 (2760), Fe-NU-1500 (3770), MgMOF-74 (1580), UiO-66 (1250), ZIF-8 (1075), HKUST-1 (1500), MOF-808 (2040) and SIFSIX-3-Ni (355) are tabulated in Table 2 and Fig. S5–S49† along with other parameters. Materials with large micropores can accommodate multi-layers of adsorbate molecules and pore filling can occur in a narrow pressure range. In these cases, ESW can be helpful for determining the monolayer coverage loading.
| MOF/probe | BET areas (m2 g−1) | ||||
|---|---|---|---|---|---|
| N2 (77 K) | Ar (87 K) | Kr (77 K) | CO2 (195 K) | O2 (77 K) | |
| UiO-66 | 1250 | 1145 | 1640 | 765 | 1170 |
| SIFSIX-3-Ni | 355 | 275 | 390 | 195 | 395 |
| NU-1000 | 2135 | 2160 | 2770 | 1020 | 2480 |
| ZIF-8 | 1075 | 900 | 2035 | 580 | 955 |
| HKUST-1 | 1500 | 1530 | 1905 | 1275 | 1765 |
| NU-1200 | 2760 | 2715 | 1535 | 830 | 2785 |
| Fe-NU-1500 | 3770 | 3785 | 5220 | 2740 | 4090 |
| MgMOF-74 | 1580 | 1260 | 1220 | 665 | 1390 |
| MOF-808 | 2040 | 2110 | 2825 | 530 | 1050 |
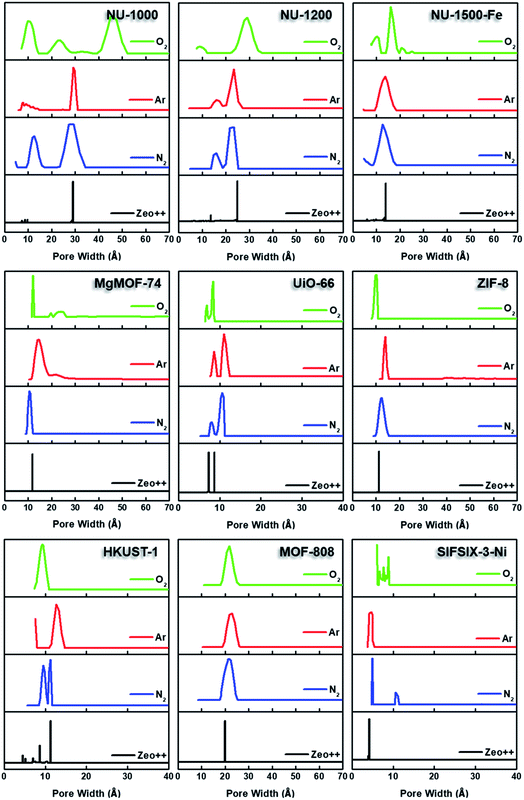
By converting the pressure axes of nitrogen isotherms to a logarithmic scale, it becomes clear that micropore filling in all MOFs starts at extremely low partial pressures (i.e. P/P0 <10−6) compared to the isotherms of other probe molecules, and the difference can be a few orders of magnitude for ultramicroporous MOFs (i.e. UiO-66 and SIFSIX-3-Ni). The diffusion rate of nitrogen at 77 K, especially into the ultramicropores, is slow in this low-pressure range. Additionally, the relatively high quadrupole moment of dinitrogen molecule makes it vulnerable to heterogeneous surface sites, which can affect the orientation of nitrogen molecules on the surface and/or can block the entrance of narrow pores. These concerns raise the question of whether or not a fully equilibrated nitrogen isotherm at 77 K can been achieved for materials with ultramicroporosity, which ultimately affects the pore size distribution and BET area calculated from these isotherms. Nevertheless, pore size distributions (PSD) obtained from nitrogen isotherms were mostly in line with the PSDs predicted by Zeo++ (Fig. 7 and Table 3). The pore size determined from nitrogen isotherm of MgMOF-74 agreed surprisingly well with the PSD estimated from Zeo++, despite the open metal sites present. On the other hand, the pore sizes of UiO-66 (ca. 8.1 and 10.6 Å) were slightly overestimated by nitrogen isotherms, while two distinct pores are clearly visible. Some studies reporting the PSD of UiO-66 only show a single pore centered around 10 Å, which can be attributed to the lack of low-pressure data in the isotherms to capture the gradual filling of smaller tetrahedral pore in UiO-66. The pore size of SIFSIX-3-Ni, on the other hand, is significantly overestimated despite the presence of low-pressure data indicating the issues of nitrogen isotherms for estimating the pore size distribution of MOFs with ultramicropores, especially if the pore dimensions are close to the molecular dimensions of nitrogen gas. PSD of NU-1200 shows a reasonable agreement with values obtained from Zeo++. In contrast, NU-1500 shows a single pore representing the large 1D channel pore while the narrower micropore between the adjacent metal nodes along c-axis was not captured. Of note, the PSD of MOF-808 with nitrogen and other probe molecules studied here does not show the presence of the small pore which can be ascribed to the narrow opening <3.2 Å of the cage preventing the access of the all probe molecules studied here. The large pore of MOF-808 was calculated to be ∼20 Å, which is in agreement with the size estimated from other probe molecules and Zeo++.
| MOF | Pore size distribution (Angstrom) | |||
|---|---|---|---|---|
| N2 (77 K) | Ar (87 K) | O2 (77 K) | Zeo++ | |
| UiO-66 | 8.1, 10.6 | 8.6, 11.0 | 6.9, 8.4 | 7.3, 8.7 |
| SIFSIX-Ni | 5.0 | 4.7 | 6.1 | 4.2 |
| NU-1000 | 12.7, 29.5 | 7.8, 9.1, 11.9, 29.1 | 10.3, 22.7, 45.1 | 7.8, 8.7, 9.7, 29.1 |
| ZIF-8 | 12.4 | 14.0 | 10.1 | 11.3 |
| HKUST-1 | 9.5, 11.3 | 12.7 | 9.3 | 4.5, 5.2, 8.6, 11.3 |
| NU-1200 | 15.9, 23.4 | 15.9, 23.3 | 9.1, 29.2 | 13.6, 24.9 |
| NU-1500-Fe | 12.7 | 13.7 | 16.1 | 13.9 |
| MgMOF-74 | 10.6 | 14.0 | 12.0 | 11.8 |
| MOF-808 | 21.7 | 21.8 | 21.7 | 19.9 |
We have also calculated the pore volumes of the MOFs studied here from the isotherm using Gurvich rule, which assumes that the density of the bulk liquid is the same as the density of the condensed liquid in the pores for a given temperature. Table 4 summarizes the total pore volumes of MOFs studied here obtained from the isotherms of different probe molecules.
| MOF | Pore volumes (cm3 g−1) | |||||
|---|---|---|---|---|---|---|
| N2 (77 K) | Ar (87 K) | Kr (77 K) | CO2 (195 K) | O2 (77 K) | Zeo++ | |
| UiO-66 | 0.47 | 0.39 | 0.40 | 0.39 | 0.43 | 0.44 |
| SIFSIX-Ni | 0.17 | 0.13 | 0.12 | 0.11 | 0.17 | 0.18 |
| NU-1000 | 1.56 | 1.51 | 1.37 | 1.39 | 1.55 | 1.62 |
| ZIF-8 | 0.39 | 0.40 | 0.26 | 0.30 | 0.38 | 0.55 |
| HKUST-1 | 0.62 | 0.58 | 0.54 | 0.59 | 0.62 | 0.66 |
| NU-1200 | 1.76 | 1.68 | 1.54 | 1.57 | 1.71 | 1.72 |
| Fe-NU-1500 | 1.44 | 1.38 | 1.31 | 1.25 | 1.44 | 1.41 |
| MgMOF-74 | 0.61 | 0.51 | 0.33 | 0.31 | 0.54 | 0.70 |
| MOF-808 | 0.81 | 0.78 | 0.72 | 0.70 | 0.81 | 0.94 |
While alternative probe molecules can address some limitations of nitrogen isotherms (discussed below), we recommend users to increase the equilibration time for data acquisition, especially for low-relative pressure region to obtain a more accurate isotherm. We also recommend considering other probe molecules when analyzing ultramicroporous samples.
Argon
Argon gas is monoatomic with no quadrupole moment and is less polarizable compared to diatomic nitrogen gas. While the higher analysis temperature (87 K) makes it less sensitive to surface heterogeneity,71 the slightly smaller kinetic dimeter of argon (3.4 Å) compared to diatomic N2 molecule (3.6 Å) and higher relative pressure pore filling is advantageous for determining a reliable BET area and PSD of ultramicroporous materials. Therefore, argon has been recommended by IUPAC as the alternative probe molecule for characterizing the textural properties of porous materials with narrow micropores and/or exposed polar surface sites.27 Argon gas at 77 K is ∼6.5 K below the bulk triple point temperature, so the state of the argon complicates the identification of gradual surface coverage and pore filling pressures. Therefore, argon isotherms are recommended to be collected at 87 K, which necessitates the use of liquid argon or a cryo-cooler. The added cost of maintaining the 87 K bath can be considered the chief reason why argon isotherms are less preferred, despite the reported advantages over nitrogen isotherms.We collected argon isotherms of all MOFs in our study at 87 K (Fig. 4). As mentioned above, argon fills the pores at higher partial pressures. Therefore, higher relative pressure region in argon isotherms, compared to nitrogen isotherms, satisfied the consistency criteria for BET area calculations. Importantly, the pressure region where BET areas were calculated are still much lower in relative pressure compared to P/P0 of 0.05–0.3 region. In general, BET areas obtained from argon isotherms are in line with BET areas obtained from nitrogen isotherms, except for MOFs with narrow pores or a high density of open metal sites, such as MgMOF-74, SIFSIF-3-Ni, UiO-66, and ZIF-8. In the case of MgMOF-74 the BET area estimated from argon isotherm is ∼20% lower compared to nitrogen isotherm. This may be due to the open metal sites interacting with nitrogen molecules and effecting their orientation on the surface, and thereby the cross-sectional area of nitrogen gas, resulting in overestimation of the BET area. This is also clear from the BET constant (C) which is nearly 7 times larger from nitrogen isotherm. Therefore, the nitrogen isotherm of MgMOF-74 can be classified as Type I(a) with a sharp plateau after micropore filling occurs, while argon isotherm with shallower increase in uptake with increasing pressure can be classified as Type I(b). The open metal sites of HKUST-1 did not result in an overestimation of BET area with nitrogen isotherm, despite its higher BET constant, highlighting the importance of the effect of topology and/or the density of open metal sites on the observed results. In contrast, SIFSIX-3-Ni does not contain open metal sites. However, due to the ultramicropores (∼3.6 Å) present in SIFSIX-3-Ni, argon gas is a better probe for this particular MOF, as argon has a considerably smaller kinetic diameter compared to nitrogen gas (3.40 vs. 3.64 Å). The narrow micropores of UiO-66 resulted in a smaller, but noticeable, difference (∼10%) in BET area from nitrogen and argon isotherms suggesting a superior diffusion and equilibration of argon gas. Despite MOF-808 having comparable BET areas with nitrogen and argon isotherms, ESW plot of nitrogen isotherm show two distinct minima and first minima results in ∼60% smaller BET area. On the other hand, the argon isotherm showed only one clear minima, and monolayer coverage obtained from that minima agrees well with the value obtained from BET equation. A recent study on carbon nanotubes (CNT) showed that a CNT containing pores of ∼17 Å showed a BET area that is significantly overestimated.54 This is due to overlapping of the pore filling region with the monolayer coverage region of the larger pores. In the case of CNT, applying ESW method resulted in identifying the correct monolayer coverage area. The overlapping of monolayer coverage and pore-filling area appears also in other materials with large micropores or narrow mesopores, which shows steep uptake due condensation in the pore near P/P0 of 0.05 with nitrogen gas at 77 K. With argon, this relative pressure region is shifted to nearly P/P0 of 0.1, which could be the reason of observing only one minimum in ESW plot. Therefore, we recommend validating the experimental BET areas with calculated geometric surface areas when large micropores or narrow mesopores are present in materials.
Semi-logarithmic isotherms in Fig. 6 show that the pore filling in all argon isotherms occurs at higher relative pressure regions compared to nitrogen isotherms. The difference in relative pressures becomes more significant if the MOF possesses open metal sites, such as MgMOF-74 and HKUST-1, highlighting the advantage of using argon for these kinds of materials. While there are pronounced differences in pore filling pressures for micropore containing MOFs, such as UiO-66, the difference is less distinct with MOFs containing larger pores, such as NU-1000 and NU-1200. The pore filling occurs at very low relative pressures (i.e. P/P0 <10−6) even with argon for the isotherms of SIFSIX-3-Ni due to its very narrow pore size that is close to the size of argon molecule. This shows that argon is more sensitive to the pore size rather than the heterogeneity of the surface at 87 K. Therefore, one needs to be careful about characterizing ultramicroporous materials with argon and should consider allowing longer equilibration times to obtain more reliable isotherms. The PSDs derived from argon isotherms are shown in Fig. 7. Importantly, here we used a recently developed DFT kernel for MOFs (hybrid materials) for calculating PSDs.64 In general, PSDs calculated from argon isotherms agree with the pore widths estimated with Zeo++. This is especially noticeable for the PSD of NU-1000, where narrow micropores corresponding to the space between the nodes of different layers is present, while they are not observed in the PSD from its nitrogen isotherm. Surprisingly, the PSD obtained from argon isotherms slightly overestimates the PSD of MgMOF-74 (Table 2 and Fig. 7). Similarly, the PSD of UiO-66 is also slightly overestimated, despite the accurate representation of two distinct pore types. It is worth noting that the PSD results also depend on the kernel selected and the resulting fitting of the experimental isotherms. By applying the recently developed DFT kernel, we found that this model shows reasonable predictions for argon isotherms of MOFs with large micropores or mesopores, while overestimating pore sizes of MOFs with micropores in general. The PSD calculated from the argon isotherm of SIFSIF-3-Ni showed a better estimation of PSD compared to the value obtained from nitrogen isotherm. The pore centered around 12 Å in PSD of SIFSIX-3-Ni from nitrogen isotherm is not present in PSD from argon isotherm highlighting the advantage of argon isotherm for this MOF.
Pore volumes calculated using Gurvich rule, generally agree well with the values obtained from nitrogen isotherms, except MgMOF-74, UiO-66, and SIFSIX-3-Ni. The higher pore volume obtained from nitrogen isotherms in those MOFs can be ascribed to the presence of open metal sites or ultramicropores, where a truly equilibrated isotherms may not be achieved.
In general, the textural properties obtained from nitrogen and argon isotherms are in agreement; however, we recommend using argon for materials with a high density of open metal sites or if ultramicropores are present. With such materials, we recommend using elongated equilibration times (∼30 s) to allow sufficient diffusion and equilibration even with argon isotherms.
Carbon dioxide
While nitrogen and argon are the most commonly utilized inert probe gases for attaining the textural properties of porous materials, carbon dioxide is also heavily used and has certain advantages over nitrogen and argon gases.72 Specifically, CO2 has a smaller kinetic diameter than either of them (Table 1) allowing for the characterization of ultramicroporous materials.30 Additionally, CO2 isotherms for characterization of textural properties are collected at 195 K or 273 K, temperatures at which the diffusion of the gas into the pores, especially into the ultramicropores, are significantly faster compared to 77 or 87 K. Furthermore, at 77 or 87 K, the rotation of the linkers are more restricted compared to the temperatures of CO2 isotherms resulting in more rigid structures, where entries to narrow pores might be blocked.73,74 All combined, this allows carbon dioxide to enter the pores that argon and/or nitrogen cannot access or access with very slow diffusion. Therefore, CO2 can provide a significant advantage especially when <7 Å pores are present in the material. Another advantage of the CO2 over Ar isotherm is the analysis temperature maintenance. 195 K can be achieved with a dry ice/acetone bath and 273 K can be achieved with an ice/water bath, while 87 K requires liquid argon which may not be easily accessible to all researchers. A disadvantage of CO2, however, is that there are no kernels to derive PSD from CO2 collected at 195 K on the MicroActive software from Micromeritics we used for this study. Despite this, the BET area and pore volume can be easily calculated from these isotherms. There are kernels utilizing DFT for calculating PSD from CO2 isotherms collected at 273 K. It is important to note that data reduction of isotherms of any probe molecules requires accurate determination of saturation pressure (P0). For gases condensing at analysis temperature, this is typically measured in a separate cell with a dedicated pressure transducer. However, CO2 does not condense at 273 K and 1 bar; therefore, the analysis is performed by measuring only the absolute pressure of the analysis cell and converted to partial pressures by using the saturation pressure of CO2 at 273 K (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 Torr). Due to such high saturation pressure, the relative pressure range needed for the ultramicropore analysis can be achieved at moderate absolute pressure ranges. For the same reason, the highest achievable P/P0 on standard instruments is ∼0.03, where large micropores or mesopores will not be filled; therefore, this method fails to probe the sizes of pores larger than ∼1 nm, unless data points at above 1 bar is collected. Since CO2 does not condense at 273 K the total pore volume of materials with large micropores or mesopores cannot be obtained with this method.
200 Torr). Due to such high saturation pressure, the relative pressure range needed for the ultramicropore analysis can be achieved at moderate absolute pressure ranges. For the same reason, the highest achievable P/P0 on standard instruments is ∼0.03, where large micropores or mesopores will not be filled; therefore, this method fails to probe the sizes of pores larger than ∼1 nm, unless data points at above 1 bar is collected. Since CO2 does not condense at 273 K the total pore volume of materials with large micropores or mesopores cannot be obtained with this method.
Here, we collected CO2 isotherms of MOFs at both 195 and 273 K. The isotherms from 195 K were used for BET area and pore volume determination, while 273 K isotherms were utilized for PSD analysis in addition to the BET area. Fig. 4 shows 195 K CO2 isotherms overlaid along with isotherms of other probe molecules at cryogenic temperatures. While CO2 fills both micropores and mesopores at much higher partial pressures, this difference is in the orders of magnitudes in the case of micropores (Fig. 6). Importantly, pore filling of larger pores at higher relative pressures result in Type IV isotherms for materials that do not possess mesopores such as MOF-808 and Fe-NU-1500. While UiO-66 shows a Type I(a) isotherm with other probe molecules, it shows a Type I(b) isotherm with CO2 gas at 195 K. As mentioned earlier, CO2 isotherm at 195 K is typically considered when there is no uptake of nitrogen at 77 K or argon at 87 K. Researcher should take extra caution when analyzing CO2 isotherms at 195 K, especially if the structure is unknown, as the steps in the isotherm can easily be ascribed to the presence of mesopores. On the other hand, MOFs can show structural phase change upon adsorption of guest molecules and the partial pressure, where this change occurs can change based on some factors such as temperature, guest molecule, structure of MOF, etc.75 These kind of structural changes or rotational dynamic of linkers can also result in steps in the isotherms at high partial pressures; however, these are typically followed by a hysteresis. Therefore, desorption isotherms should be collected as well to understand the nature of the observed steps, particularly if the structure is unknown or amorphous.
BET areas calculated from CO2 isotherms collected at 195 K are tabulated in Table 2. For almost all MOFs, BET areas from isotherms collected at 195 K are underestimated significantly compared to those calculated from nitrogen isotherms, especially for MOFs with larger pores: MOF-808 (∼75%), NU-1200 (∼70%) and NU-1000 (∼50%). To our surprise, BET areas of SIFSIX-3-Ni and MgMOF-74 are also significantly underestimated. For SIFSIX-3-Ni, the region that satisfies the Rouquerol criteria is also at extremely low pressures (P/P0 for Nm ∼0.002). On the other hand, HKUST-1 showed a reasonable BET area compared to the area obtained from N2 isotherm. BET areas calculated from CO2 isotherms at 273 K also showed underestimated values (Fig. S5–S49†). As mentioned earlier, at 273 K, P/P0 of only ∼0.03 is achievable and this pressure range is low for monolayer coverage given the weaker CO2–surface interaction at 273 K. SIFSIX-3-Ni is an exception here as the extremely narrow pore size along with polar functional groups pointing into the pores facilitates CO2 uptake at 273 K, reaching the saturation limit even at low pressures.76 Therefore, the BET area obtained from the isotherm at 273 K has reasonable agreement with the areas calculated from nitrogen isotherm. Despite the strong interaction of CO2 with MgMOF-74 at 273 K, resulting in uptake capacity reaching the capacity obtained at 195 K, BET area from this isotherm significantly underestimates the surface area. We have also calculated the PSD from isotherms collected at 273 K using the NLDFT kernel. PSD of SIFSIX-3-Ni shows a single peak centered at 3.6 Å agreeing well with the pore size of the MOF. The PSD of UiO-66 showed two peaks centered at 5.7 Å and 8.4 Å, which corresponds to the pores of tetrahedral and octahedral cages, respectively. PSD of other MOFs that do not contain ultramicropores, such as NU-1000 and NU-1200, also show similar PSD profiles (Fig. S50†). Therefore, one needs to be careful of analyzing the pore size distribution of MOFs with 273 K CO2 isotherms. Extra care should be taken if the structure is unknown or the material is amorphous. Research on developing new kernels to account for the surface heterogeneity on MOFs would be extremely valuable to obtain better information about the PSD of MOF using CO2 isotherms.
Pore volumes calculated using Gurvich rule follows a similar trend as BET areas, where there is significant underestimation with CO2 isotherms. We recommend users to collect isotherms of nitrogen or argon at 77 or 87 K, respectively, if available, to obtain more representative information about the textural properties of their materials. The observation of Type IV isotherms when using CO2 as the probe should not be ascribed to the presence of mesopores, as we observed Type IV isotherms for MOFs that are not mesoporous such as Fe-NU-1500. Additionally, users should measure the temperature of the bath if a dry ice/acetone bath is used several times during the measurement and at the end of the measurement to ensure a constant temperature has been maintained throughout the analysis, unless a cryocooler has been employed. An acetone/dry ice bath will result in an inaccurate bath temperature if excess acetone has been employed, with higher bath temperatures resulting in significantly less uptake of CO2.
Krypton
While N2, Ar, and CO2 can report the surface area of highly porous materials, besides the limitations mentioned above, they are less reliable for analyzing materials with low surface areas (i.e. surface area <5 m2 g−1).27 This complication arises due to the way that the adsorbed quantity of the gas is determined with commercial instruments, where the remaining gas amount in the tube after equilibration is reached is subtracted from the initial amount of gas dosed. The amount of gas adsorbed in materials with low surface is much smaller compared to materials with high surface area. Therefore, the amount of gas in the tube after equilibrium is achieved becomes significant compared to the gas adsorbed, especially with increasing pressure, leading to errors in determining the adsorbed amount of gas. With N2, Ar, and CO2 isotherms this often leads to decreasing uptake with increasing relative pressure, which does not have a physical meaning and is a clear indication of the smaller adsorbed gas amount compared to the equilibrated gas in the analysis tube. It is important to note that the adsorbed amount corresponds to the absolute amount, not the specific amount which is often normalized by the mass of the adsorbent. Therefore, using a small quantity of a material with high surface area can still yield similar problems. This is often a challenge for determining the surface area of thin films prepared with porous materials, where only a small amount (ca. <5 mg) is deposited on the film.77 In this case, a bigger quantity of material needs to be used for analysis, which may not be possible for all materials. For instance, there is increasing body of research for developing radioactive MOFs, where the quantity of MOFs produced are intentionally kept at low milligram scales.78,79 Additionally, increasing the mass of the adsorbent also has a limitation due to the size of analysis tubes. While using glass rods to reduce the empty space in analysis tubes can help, it still does not provide an absolute solution. To this end, krypton (Kr) isotherms at 77 K provides a unique solution due to the much lower P0 of Kr (2.5 Torr) at 77 K compared to N2 gas (760 Torr). Since the pressure is proportional to the amount of gas present, there is about 300 times more N2 gas (760/2.5 = 304) in the empty tube space at a given relative pressure. Reducing the amount of gas in the free space of the tube by a factor of more than 300 significantly reduces the error in determining the adsorbed amount in the pores of materials with low surface area and/or materials with low quantities, resulting in more reproducible and meaningful isotherms with Kr at 77 K. Therefore, more reliable surface areas can be obtained for these materials. However, Kr at 77 K is below its triple point; therefore, the thermodynamic state of the adsorbed layer is not well defined, similar to Ar at 77 K.Herein, we collected Kr isotherms at 77 K for all MOFs. We collected the isotherms only up to P/P0 of ∼0.5, where the pore filling is complete. Consistent with its low saturation pressure, the relative pressures at which Kr condensation in the mesopores of NU-1200 and NU-1000 occurred were lowest for Kr compared to other probe molecules. In contrast, micropore filling started at higher relative pressures compared to N2 and Ar, but at lower relative pressures compared to CO2 isotherms at 195 K. Again, these are the relative pressures, and absolute pressures for Kr isotherms are much smaller due to smaller vapor pressure at the analysis temperature. Importantly, the shallower increases in N2 and Ar isotherms, due to multilayer adsorption, is much sharper in Kr isotherms, suggesting stronger interactions between adsorbed layers. For example, the gradual pore filling occurring in NU-1200 is completed at P/P0 ∼0.12 for N2 and ∼0.18 for Ar isotherms, while it is completed at P/P0 ∼0.08 with Kr, resulting in a much steeper uptake. Therefore, the pore filling pressures of micropore and mesopore are more distinct. However, this narrow relative pressure range for pore filling can result in pore contamination, where it is challenging to distinguish between monolayer coverage and pore filling. Despite the satisfaction of the all four consistency criteria with the pressure region selected, the BET area of NU-1200 from Kr isotherm is nearly the half of what is obtained from N2 or Ar isotherms. Importantly, ESW method also resulted in a surface area very close to the value obtained from BET method. While the pressure regions selected for analyzing BET areas of all MOFs satisfied all four consistency criteria, we could not find an appropriate relative pressure region for ZIF-8, which is evident from the estimated BET area that is twice the value obtained from both N2 and Ar (Table 2).39 That being said, BET areas for other MOFs were also overestimated (25–45%) compared to the areas obtained from N2 and Ar isotherms. Therefore, one must be careful about analyzing the surface area with Kr isotherms due to overestimation of the surface area despite utilization of consistency criteria.
Pore volume can be easily calculated using the Gurvich rule. Despite significant over estimation of BET areas with Kr isotherms, the pore volumes calculated using Gurvich rule showed more consistent values compared to Ar isotherms with the exception of MgMOF-74. The pore volume of MgMOF-74 with Kr isotherm is about 35% lower compared to Ar isotherm, which might be ascribed to the strongly polarizing open Mg sites.
Oxygen
While Ar isotherms have been recommended by IUPAC for analysis of materials with ultramicropores and/or heterogeneous surfaces, collecting Ar isotherms at 87 K might be cost-prohibitive for many researchers due to the high cost of UHP argon gas and liquid argon. A recent report showed that O2 isotherms at 77 K can be used as a more economical replacement and shows quantitative agreement with Ar isotherm at 87 K for PSD analysis of porous carbons.80 O2 isotherms offers advantages over N2 isotherms due to the smaller quadrupole moment of O2 (Table 1), which makes is less susceptible to the heterogeneous surfaces, i.e. metal sites in MOFs. Additionally, the P0 of O2 is also much smaller (155 Torr) compared to N2. This means there is about 5 times less O2 molecules compared to N2 in the free space when equilibrium achieved at a given pressure. As described above, low P0 of a sorbent provides advantage for determining the amount of adsorbed gas with higher accuracy. It is important noting that P0 of O2 is still significantly high compared to Kr, which has about 300 times less gas in the free space compared to N2 at 77 K.Here, we collected O2 isotherms of MOFs at 77 K to calculate BET areas, PSD, and pore volumes. It is important noting that O2can dissolve in pump oil and catch on fire. Therefore, for the diaphragm vacuum pump, we recommend using either a dry pump or an oil pump that runs with non-flammable oil. BET areas obtained from O2 isotherms are, in general, within 10% of the range of BET areas obtained from Ar isotherms at 87 K (Table 2). We were able to identify relative pressure regions that satisfy the consistency criteria for all MOFs, except NU-1200 and MOF-808 (Table S3†), where R2 of BET fitting was below 0.9975 and monolayer coverage uptake was not achieved in the selected partial pressure range. Surprisingly, the BET area of NU-1200 is still in very good agreement with the area obtained from N2 and Ar isotherms. On the other hand, BET area of MOF-808 obtained from O2 isotherm is nearly half of the value obtained from N2 or Ar isotherms, highlighting the importance of consistency criteria. BET areas of NU-1000 and HKUST-1 also show about 15% higher BET areas compared to Ar isotherms, despite calculating the BET areas from a partial pressure range that satisfies all four consistency criteria.
Micropore filling for O2 isotherms starts at higher relative pressure compared to N2, but lower compared to Ar at their respective analysis temperatures. Filling of mesopores, on the other hand, occurs at lower relative pressures. Importantly, steps in the N2 and Ar isotherms of NU-1200 were not as pronounced in Kr isotherm due to the completion of pore filling at a narrower pressure range. However, the O2 isotherm of NU-1200 still shows all of the steps clearly, despite completion of pore filling at a narrower pressure range. We have also utilized a recently reported DFT model for calculating PSD using O2 isotherms at 77 K (Fig. 7 and Table 2).80 Although this model agreed well with the Ar model to calculate the PSD of porous carbon, there were some large discrepancies in the case of MOFs. For example, the largest pore in NU-1000 is ∼29.1 Å, which is determined from crystal structure, and PSD calculated from isotherms of Ar and N2 corroborated this value. However, PSD determined from O2 isotherm resulted in a pore size of 45.1 Å, which is nearly 50% larger compared to the actual value. Similarly, the mesopore of NU-1200 is also overestimated, but to a lesser extent compared to the mesopore of NU-1000. Surprisingly, the PSD of UiO-66 has a good agreement with the PSD predicted from Zeo++, and it has even a better agreement with crystal structure data that of obtained from N2 or Ar isotherms. Similarly, MgMOF-74 showed very reasonable agreement, despite having open metal sites. The PSD of ZIF-8 and Fe-NU-1500 is closer to the predicted value with O2 compared to other probe molecules. Importantly, NU-1500 showed a smaller pore near 10 Å, which can be ascribed to the pore between the nodes, and this pore was not present in the PSD from other probe molecules. MOF-808 shows consistent pore sizes with all probe molecules and agrees well with the value obtained from Zeo++. HKUST-1, however, shows only one type of pore which can be attributed to the largest cage, while the smaller cage is present with the PSD obtained from N2 isotherm. SIFSIX-3-Ni exhibits pores much larger than the actual pore size, highlighting the importance of using Ar for ultramicroporous samples. Pore volumes calculated from oxygen isotherms were in reasonable agreement with the values obtained from Ar isotherms, except SIFSIX-3-Ni, which can be ascribed to the ultramicropores with a diameter close to the kinetic dimeter of oxygen gas.
In general, O2 isotherms yield comparable surface areas, PSDs, and pore volumes compared to N2 or Ar, besides the aforementioned exceptions. PSD obtained from O2 isotherms predicted the middle range micropores in good agreement with the expected value. However, the sizes of ultramicropores close to the size oxygen or large mesopores are overestimated significantly. We recommend using N2 or Ar probe molecules when available given the potential safety hazard associated with collecting O2 isotherms.
Conclusions
In conclusion, we have outlined some crucial textural properties (surface area, pore size distribution, and pore volume) of MOFs that can be obtained from gas adsorption isotherms. For this purpose, we selected a total of nine archetypical MOFs with different properties (high/moderate/low surface area, ultramicro/micro/mesoporous, open metal sites), and collected the isotherms of N2, Kr and O2 at 77 K, Ar at 87 K and CO2 at 195 and 273 K. We have compared the BET area, pore size distribution, and pore volume obtained from these isotherms and outlined the advantages and disadvantages of each gas molecules.While the validity of the BET method for determining the surface areas of MOFs has been widely accepted and confirmed via computational studies, there are cases where it has limitations to determine the amount of gas needed for monolayer surface coverage, even upon utilizing Rouquerol et al. consistency criteria. Therefore, it is suggested to refer the surface area obtained for microporous materials as “BET area” rather than the absolute surface area. Although N2 gas isotherms at 77 K is the most commonly utilized method for determining the textural properties of MOFs, the large quadrupole moment of N2 results in an overestimation of BET area for MOFs with open metal sites or for ultramicroporous MOFs. The latter is due to the limited diffusion of N2 gas in those very narrow micropores at 77 K, making it challenging to obtain fully equilibrated isotherms. For ultramicroporous materials, we recommend using longer equilibrium times to obtain fully equilibrated isotherms, especially for low pressure points, even for Ar isotherms. Kr isotherms at 77 K resulted in significant overestimation of BET areas for almost all MOFs compared to other probe molecules. Therefore, we recommend researchers to keep this in mind when reporting BET areas from Kr isotherms, particularly for materials with unknown/amorphous structures. CO2 isotherms at 195 K resulted in significant underestimation of BET areas for all MOFs studied here. Importantly, CO2 isotherms at 195 K resulted in Type IV isotherms for some microporous materials; therefore, the steps in these isotherms should not be ascribed to the presence of mesopores. BET areas obtained from O2 isotherms were mostly in line with BET areas obtained from Ar isotherms. However, O2 isotherms of MOF-808 did not have a pressure region which satisfied all 4 consistency criteria. The BET area for MOF-808 calculated from the O2 isotherm was significantly lower than the BET area calculated from the Ar isotherm, highlighting the importance of satisfying all 4 consistency criteria for BET method.
For PSD calculations, the full isotherm range is utilized and the collection of high-resolution adsorption data, especially for low pressure region, is crucial. For example, UiO-66 has a microporous material with octahedral cages (∼9 Å) and tetrahedral cages (∼7 Å). However, reports sometimes depict the PSD of UiO-66 as having only a single pore centered ∼10 Å due to the lack of data points at low-pressure ranges, which is often a result of using instruments with only a diaphragm pump. Therefore, we recommend users to utilize instruments with turbopumps to obtain high resolution data at low pressures for a more reliable PSD profile. PSD plots obtained from N2 isotherms are mostly in line with PSDs expected from crystal structures; however, ultramicroporous MOFs and MOFs with open-metal sites showed additional peaks in PSD or overestimated the pore sizes. Ar isotherms in these cases were capable of reporting pore sizes that are closer to the expected values. Pore size distributions calculated from O2 isotherms at 77 K were in good agreement with the expected pores for MOFs with midrange micropores; however, it significantly overestimated the pore sizes of MOFs with mesopores or ultramicropores. We highly recommend instrument manufacturers to improve the kernels for different kind of materials, as MOFs offer unique pore structures that are not observed in other porous materials. Pore volumes calculated using Gurvich rule showed reasonable values among the different probe gases we tested here.
Given that the same MOF samples were used for collecting gas isotherms with all the probes using the same instrument, the observed differences among different probe molecules can be ascribed to the inherit property of the gas molecules at analysis temperatures, rather than the activation and/or handling of particular MOF samples. Therefore, researchers can use the results from this study to evaluate their needs for obtaining the isotherms of different gases, in particular with less accessible gases. We hope that this tutorial article will aid researchers that work with porous materials, particularly those who study MOFs.
Conflicts of interest
OKF has a financial interest in the start-up company NuMat Technologies, which is seeking to commercialize metal–organic frameworks.Acknowledgements
The authors gratefully acknowledge the financial support from the Defense Threat Reduction Agency (HDTRA1-18-1-0003, HDTRA1-19-1-0007, HDTRA1-19-1-0010); Army Research Office (W911NF1910340); U.S. Department of Energy's Office of Energy Efficiency and Renewable Energy (EERE) under award no. DE-EE0008816; the U.S. Department of Energy (DOE) Office of Science, Basic Energy Sciences Program for Separation (DE-FG02-08ER15967); the Inorganometallic Catalyst Design Center, an EFRC funded by the DOE, Office of Science, Basic Energy Sciences (DE-SC0012702). F.A.S. is supported by the Department of Defense (DoD) through the National Defense Science & Engineering Graduate (NDSEG) Fellowship Program. This work made use of the IMSERC X-RAY facility at Northwestern University, which has received support from the Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF ECCS-2025633), and Northwestern University. F. A. S. also gratefully acknowledges support from the Ryan Fellowship and the International Institute for Nanotechnology at Northwestern University.References
- M. E. Davis, Nature, 2002, 417, 813–821 CrossRef CAS PubMed.
- A. G. Slater and A. I. Cooper, Science, 2015, 348, aaa8075 CrossRef PubMed.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- M.-H. Sun, S.-Z. Huang, L.-H. Chen, Y. Li, X.-Y. Yang, Z.-Y. Yuan and B.-L. Su, Chem. Soc. Rev., 2016, 45, 3479–3563 RSC.
- H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276–279 CrossRef CAS.
- S. Kitagawa, R. Kitaura and S.-I. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375 CrossRef CAS PubMed.
- G. Férey, C. Mellot-Draznieks, C. Serre, F. Millange, J. Dutour, S. Surblé and I. Margiolaki, Science, 2005, 309, 2040–2042 CrossRef.
- R. Robson, Dalton Trans., 2008, 5113–5131, 10.1039/B805617J.
- Z. Chen, M. C. Wasson, R. J. Drout, L. Robison, K. B. Idrees, J. G. Knapp, F. A. Son, X. Zhang, W. Hierse, C. Kuhn, S. Marx, B. Hernandez and O. K. Farha, Faraday Discuss., 2021, 225, 9–69 RSC.
- P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. P. Maloney, P. A. Wood, S. C. Ward and D. Fairen-Jimenez, Chem. Mater., 2017, 29, 2618–2625 CrossRef CAS.
- K. Ma, K. B. Idrees, F. A. Son, R. Maldonado, M. C. Wasson, X. Zhang, X. Wang, E. Shehayeb, A. Merhi, B. R. Kaafarani, T. Islamoglu, J. H. Xin and O. K. Farha, Chem. Mater., 2020, 32, 7120–7140 CrossRef CAS.
- K. S. W. Sing, Adv. Colloid Interface Sci., 1998, 76–77, 3–11 CrossRef CAS.
- I. Senkovska, K. A. Cychosz, P. Llewellyn, M. Thommes and S. Kaskel, in The Chemistry of Metal–Organic Frameworks, 2016, pp. 575–605, DOI:10.1002/9783527693078.ch19.
- N. Hu, N. Borkar, D. Kohls and D. W. Schaefer, J. Membr. Sci., 2011, 379, 138–145 CrossRef CAS.
- M. W. Anderson, T. Ohsuna, Y. Sakamoto, Z. Liu, A. Carlsson and O. Terasaki, Chem. Commun., 2004, 907–916, 10.1039/B313208K.
- H. Giesche, Part. Part. Syst. Charact., 2006, 23, 9–19 CrossRef.
- J. P. Butler, R. W. Mair, D. Hoffmann, M. I. Hrovat, R. A. Rogers, G. P. Topulos, R. L. Walsworth and S. Patz, J. Phys.: Condens. Matter, 2002, 14, L297–L304 CrossRef CAS PubMed.
- J. Moellmer, E. B. Celer, R. Luebke, A. J. Cairns, R. Staudt, M. Eddaoudi and M. Thommes, Microporous Mesoporous Mater., 2010, 129, 345–353 CrossRef CAS.
- S. Dantas and A. V. Neimark, ACS Appl. Mater. Interfaces, 2020, 12, 15595–15605 CrossRef CAS PubMed.
- S. Dantas, L. Sarkisov and A. V. Neimark, J. Am. Chem. Soc., 2019, 141, 8397–8401 CrossRef CAS PubMed.
- T. Düren, Y.-S. Bae and R. Q. Snurr, Chem. Soc. Rev., 2009, 38, 1237–1247 RSC.
- J. E. Mondloch, O. Karagiaridi, O. K. Farha and J. T. Hupp, CrystEngComm, 2013, 15, 9258–9264 RSC.
- X. Zhang, Z. Chen, X. Liu, S. L. Hanna, X. Wang, R. Taheri-Ledari, A. Maleki, P. Li and O. K. Farha, Chem. Soc. Rev., 2020, 49, 7406–7427 RSC.
- S. Brunauer and P. Emmett, J. Am. Chem. Soc., 1935, 57, 1754–1755 CrossRef CAS.
- P. H. Emmett and S. Brunauer, J. Am. Chem. Soc., 1937, 59, 1553–1564 CrossRef CAS.
- S. Lowell, J. E. Shields, M. A. Thomas and M. Thommes, in Characterization of Porous Solids and Powders: Surface Area, Pore Size and Density, Springer Netherlands, Dordrecht, 2004, pp. 242–259, DOI:10.1007/978-1-4020-2303-3_14.
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. Sing, Pure Appl. Chem., 2015, 87, 1051–1069 CAS.
- J. Rouquerol, D. Avnir, C. Fairbridge, D. Everett, J. Haynes, N. Pernicone, J. Ramsay, K. Sing and K. Unger, Pure Appl. Chem., 1994, 66, 1739–1758 CAS.
- K. S. W. Sing and R. T. Williams, Adsorpt. Sci. Technol., 2004, 22, 773–782 CrossRef CAS.
- K. A. Cychosz and M. Thommes, Engineering, 2018, 4, 559–566 CrossRef CAS.
- J. Rouquerol, F. Rouquerol, P. Llewellyn, G. Maurin and K. S. Sing, Adsorption by powders and porous solids: principles, methodology and applications, Academic press, 2013 Search PubMed.
- T. Islamoglu, K.-i. Otake, P. Li, C. T. Buru, A. W. Peters, I. Akpinar, S. J. Garibay and O. K. Farha, CrystEngComm, 2018, 20, 5913–5918 RSC.
- J. E. Mondloch, W. Bury, D. Fairen-Jimenez, S. Kwon, E. J. DeMarco, M. H. Weston, A. A. Sarjeant, S. T. Nguyen, P. C. Stair and R. Q. Snurr, J. Am. Chem. Soc., 2013, 135, 10294–10297 CrossRef CAS PubMed.
- T.-F. Liu, N. A. Vermeulen, A. J. Howarth, P. Li, A. A. Sarjeant, J. T. Hupp and O. K. Farha, Eur. J. Inorg. Chem., 2016, 2016, 4349–4352 CrossRef CAS.
- Z. Chen, P. Li, X. Zhang, P. Li, M. C. Wasson, T. Islamoglu, J. F. Stoddart and O. K. Farha, J. Am. Chem. Soc., 2019, 141, 2900–2905 CrossRef CAS PubMed.
- D. Britt, H. Furukawa, B. Wang, T. G. Glover and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20637–20640 CrossRef CAS PubMed.
- J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850–13851 CrossRef PubMed.
- K. S. Park, Z. Ni, A. P. Côté, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10191 CrossRef CAS.
- Despite the gate-opening mechanism reported in ZIF-8, it is included in the current study to increase the diversity of the MOFs studied here and compare the effect with different probe molecules. However, care should be taken when studying the textural properties of materials that undergo significant structural changes upon gas adsorption as these changes cannot be accounted by the adsorption theories. For ZIF-8 case, the difference in the geometric surface areas of both forms are calculated to be less than 3% D. Fairen-Jimenez, et al. , J. Am. Chem. Soc., 2011, 133, 8900 CrossRef CAS PubMed.
- S. S.-Y. Chui, S. M.-F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150 CrossRef CAS PubMed.
- H. Furukawa, F. Gandara, Y.-B. Zhang, J. Jiang, W. L. Queen, M. R. Hudson and O. M. Yaghi, J. Am. Chem. Soc., 2014, 136, 4369–4381 CrossRef CAS PubMed.
- S. Subramanian and M. J. Zaworotko, Angew. Chem., Int. Ed., 1995, 34, 2127–2129 CrossRef CAS.
- T. Düren, F. Millange, G. Férey, K. S. Walton and R. Q. Snurr, J. Phys. Chem. C, 2007, 111, 15350–15356 CrossRef.
- K. S. W. Sing, Colloids Surf., 1989, 38, 113–124 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361–1403 CrossRef CAS.
- H. Swenson and N. P. Stadie, Langmuir, 2019, 35, 5409–5426 CrossRef CAS PubMed.
- S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319 CrossRef CAS.
- K. S. Walton and R. Q. Snurr, J. Am. Chem. Soc., 2007, 129, 8552–8556 CrossRef CAS PubMed.
- D. A. Gómez-Gualdrón, P. Z. Moghadam, J. T. Hupp, O. K. Farha and R. Q. Snurr, J. Am. Chem. Soc., 2016, 138, 215–224 CrossRef PubMed.
- J. Osterrieth, J. Rampersad, D. G. Madden, N. Rampal, L. Skoric, B. Connolly, M. Allendorf, V. Stavila, R. Ameloot and J. Marreiros, ChemRxiv, 2021 DOI:10.26434/chemrxiv.14291644.v2.
- J. Rouquerol, P. Llewellyn and F. Rouquerol, Stud. Surf. Sci. Catal., 2007, 160, 1016 CrossRef.
- Z. Chen, P. Li, R. Anderson, X. Wang, X. Zhang, L. Robison, L. R. Redfern, S. Moribe, T. Islamoglu, D. A. Gómez-Gualdrón, T. Yildirim, J. F. Stoddart and O. K. Farha, Science, 2020, 368, 297–303 CrossRef CAS PubMed.
- J. Adolphs and M. J. Setzer, J. Colloid Interface Sci., 1998, 207, 349–354 CrossRef CAS PubMed.
- P. Sinha, A. Datar, C. Jeong, X. Deng, Y. G. Chung and L.-C. Lin, J. Phys. Chem. C, 2019, 123, 20195–20209 CrossRef CAS.
- F. A. Son, B. C. Bukowski, T. Islamoglu, R. Q. Snurr and O. K. Farha, Chem. Mater., 2021 DOI:10.1021/acs.chemmater.1c02462.
- J. Landers, G. Y. Gor and A. V. Neimark, Colloids Surf., A, 2013, 437, 3–32 CrossRef CAS.
- T. Roussel, J. Jagiello, R. J. M. Pellenq, M. Thommes and C. Bichara, Mol. Simul., 2006, 32, 551–555 CrossRef CAS.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472 CrossRef CAS PubMed.
- H. Deng, S. Grunder, K. E. Cordova, C. Valente, H. Furukawa, M. Hmadeh, F. Gándara, A. C. Whalley, Z. Liu, S. Asahina, H. Kazumori, M. O'Keeffe, O. Terasaki, J. F. Stoddart and O. M. Yaghi, Science, 2012, 336, 1018–1023 CrossRef CAS PubMed.
- D. Liu, D. Zou, H. Zhu and J. Zhang, Small, 2018, 14, 1801454 CrossRef PubMed.
- I. Senkovska and S. Kaskel, Chem. Commun., 2014, 50, 7089–7098 RSC.
- W. Xuan, C. Zhu, Y. Liu and Y. Cui, Chem. Soc. Rev., 2012, 41, 1677–1695 RSC.
- Y.-n. Wu, F. Li, W. Zhu, J. Cui, C.-a. Tao, C. Lin, P. M. Hannam and G. Li, Angew. Chem., Int. Ed., 2011, 50, 12518–12522 CrossRef CAS PubMed.
- P. Li, Q. Chen, T. C. Wang, N. A. Vermeulen, B. L. Mehdi, A. Dohnalkova, N. D. Browning, D. Shen, R. Anderson and D. A. Gómez-Gualdrón, Chem, 2018, 4, 1022–1034 CAS.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- D. Lozano-Castelló, D. Cazorla-Amorós and A. Linares-Solano, Carbon, 2004, 42, 1233–1242 CrossRef.
- M. Occelli, J. Olivier, J. Perdigon-Melon and A. Auroux, Langmuir, 2002, 18, 9816–9823 CrossRef CAS.
- S. J. Gregg, K. S. W. Sing and K. S. Sing, Adsorption, Surface Area, and Porosity, Academic Press, 1967 Search PubMed.
- D. Ongari, P. G. Boyd, S. Barthel, M. Witman, M. Haranczyk and B. Smit, Langmuir, 2017, 33, 14529–14538 CrossRef CAS PubMed.
- M. B. Majewski, H. Noh, T. Islamoglu and O. K. Farha, J. Mater. Chem. A, 2018, 6, 7338–7350 RSC.
- S. Lowell, J. E. Shields, M. A. Thomas and M. Thommes, Characterization of porous solids and powders: surface area, pore size and density, Springer Science & Business Media, 2012 Search PubMed.
- M. Thommes, C. Morlay, R. Ahmad and J. P. Joly, Adsorption, 2011, 17, 653 CrossRef CAS.
- A. Gonzalez-Nelson, F.-X. Coudert and M. A. van der Veen, Nanomaterials, 2019, 9, 330 CrossRef CAS PubMed.
- F. Moreau, D. I. Kolokolov, A. G. Stepanov, T. L. Easun, A. Dailly, W. Lewis, A. J. Blake, H. Nowell, M. J. Lennox, E. Besley, S. Yang and M. Schröder, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3056–3061 CrossRef CAS PubMed.
- A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096 RSC.
- O. Shekhah, Y. Belmabkhout, K. Adil, P. M. Bhatt, A. J. Cairns and M. Eddaoudi, Chem. Commun., 2015, 51, 13595–13598 RSC.
- A. Betard and R. A. Fischer, Chem. Rev., 2012, 112, 1055–1083 CrossRef CAS PubMed.
- E. A. Dolgopolova, A. M. Rice and N. B. Shustova, Chem. Commun., 2018, 54, 6472–6483 RSC.
- A. M. Hastings, D. Ray, W. Jeong, L. Gagliardi, O. K. Farha and A. E. Hixon, J. Am. Chem. Soc., 2020, 142, 9363–9371 CrossRef CAS PubMed.
- J. Jagiello and J. Kenvin, J. Colloid Interface Sci., 2019, 542, 151–158 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Materials synthesis and characterization, experimental PXRD patterns, adsorption–desorption isotherms, BET transform, Rouquerol transform and BET summary for representative MOFs, pore size distribution analysis for CO2 isotherms at 273 K, ESW plots, BET + ESW analysis. See DOI: 10.1039/d1ta08021k |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |