Open Access Article
Open Access ArticleSpectroscopic ellipsometry as a route to thermodynamic characterization†‡
Ronald P.
White
 a,
Dragos
Buculei
b,
Alexia M. J. M.
Beale
b,
Ilias
Goovaerts§
b,
Joseph L.
Keddie
a,
Dragos
Buculei
b,
Alexia M. J. M.
Beale
b,
Ilias
Goovaerts§
b,
Joseph L.
Keddie
 *b and
Jane E. G.
Lipson
*b and
Jane E. G.
Lipson
 *a
*a
aDepartment of Chemistry, Dartmouth College, Hanover, New Hampshire 03755, USA. E-mail: jane.e.g.lipson@dartmouth.edu
bDepartment of Physics, University of Surrey, Guildford, Surrey, GU2 7XH, UK. E-mail: j.keddie@surrey.ac.uk
First published on 18th August 2022
Abstract
Strategies for synthesizing molecularly designed materials are expanding, but methods for their thermodynamic characterization are not. This shortfall presents a challenge to the goal of connecting local molecular structure with material properties and response. Fundamental thermodynamic quantities, including the thermal expansion coefficient, α, can serve as powerful inputs to models, yielding insight and predictive power for phenomena ranging from miscibility to dynamic relaxation. However, the usual routes for thermodynamic characterization often require a significant sample size (e.g. one gram), or challenging experimental set-ups (e.g. mercury as a confining fluid), or both. Here, we apply spectroscopic ellipsometry, which is an optical technique for thin film analysis, to obtain thermodynamic data. We clarify issues in the scientific literature concerning the connection between ellipsometric and volumetric thermal expansion coefficients for substances in both the glass and melt states. We analyze temperature-dependent data derived using both ellipsometry and macro-scale dilatometric techniques for ten different polymers. We find superb correlation between the α values obtained via the two techniques, after considering the effects of mechanical confinement by the substrate for a glassy thin film. We show how the ellipsometric α can serve as input to the locally correlated lattice theory to yield predictions for the percent free volume in each polymer as a function of temperature. We find that the ellipsometric α at the glass transition temperature, Tg, is not only material dependent, but it is linearly correlated with Tg itself. Spectroscopic ellipsometry, which requires only very small quantities of sample and is straightforward to perform, will significantly expand the range of systems for which thermodynamic properties can be characterized. It will thus advance our ability to use theory and modeling to predict the miscibility and dynamic relaxation of new materials. As such, ellipsometry will be able to underpin materials synthesis and property design.
1. Introduction
Thermodynamic data are necessary for the modelling of material phenomena, including miscibility and dynamic relaxation. One essential parameter is the volumetric thermal expansivity (αV). When a substance is subjected to an isobaric temperature shift, it will equilibrate by changing its volume. The fractional volume change with temperature defines αV. Typically, αV is obtained via the gold standard method of pressurized dilatometry, which collects accurate pressure–volume–temperature (PVT) data.1–3If a substance is in the form of a thin film on a substrate, volume changes with increasing temperature are not easily measured; changes in the thickness are more easily quantified. For instance, ellipsometry is a non-invasive optical technique4 that measures film thicknesses with sub-nm accuracy. It has been used to measure the thermal expansivity in the direction normal to the substrate, αN. Here, we are interested in the relationship between αN and αV, and whether the connection between the two depends on the state (solid or liquid). As we describe below, there is inconsistent understanding of how an αN value (derived from ellipsometry) relates to the familiar, well-defined αV and to the one-dimensional linear expansivity. In this paper, we use new extensive experimental data to confirm the relationships explicitly for both the melt and glass states.
A key motivation of our research arises because important aspects of a material's dynamic, thermodynamic, and mechanical behavior can be correlated with αV using models such as theory-based equations of state (EOS).5–12 For a three-parameter EOS, a complete characterization requires an αV value together with the compressibility, κ, and a single value of specific volume. However, as we demonstrate in this work, useful correlations can be made using αV values alone. In our previous work using the EOS derived from the Locally Correlated Lattice (LCL) model, we were able to predict and compare the free volume (Vfree) that exists in a range of melt and glassy materials.13Vfree is the amount of space a solid or liquid has in excess of its limiting state at close molecular packing. It is strongly connected to both the material's thermodynamic behavior (one example being its compatibility, or miscibility, with other components),14,15 and to its dynamic properties,16,17 including viscosity, diffusion, segmental relaxation times, and ultimately the glass transition temperature, Tg. Thus, thermodynamic characterization powerfully unlocks an understanding of a wide range of properties.
Although αV (obtained via PVT measurements) is essential, in most laboratories, αN (e.g. via ellipsometry) is far more accessible. While carefully applied volume dilatometry can also yield atmospheric V(T) data,18 many substances, such as polymers, can be challenging to work with, and hence data availability is limited. Pressurized or ambient volume dilatometry requires confining fluids, commonly mercury. If mercury is avoided by the use of another type of confining fluid, then the PVT behavior of that fluid must be accurately known, and further, there must be no uptake of that particular fluid into the sample.3 With gas pycnometers, uptake of He into the sample is a similar concern in some cases (e.g. fluorocarbon polymers).1 Other methods to obtain ambient density, such as weighing bottles and hydrostatic weighing techniques, can be complicated by sample viscosities that are too high (former) or too low (latter).1,2 Further, most of these approaches have the disadvantage of requiring a relatively large sample size,1–3,18 typically 1 to 2 g, compared to <1 mg for a thin film for ellipsometry. Deuterium-labelled molecules19 and some novel materials are synthesized in small (<1 g) quantities. Synthetic efforts continue to expand the range of interesting polymers and copolymers, with the goal of optimizing properties for desired applications. Currently, aside from perhaps standard thermal analysis, many new materials have not been thermodynamically characterized at all. This objective would be significantly advanced by the ability to determine volumetric thermal expansion coefficients using the more readily available measurements of αNvia ellipsometry. The resulting expanded data set would lead to a better understanding of how to link molecular structure to properties and function.
We note that a comparison between volumetric and ellipsometric data is only relevant when the films are thick enough that the behavior can be considered bulk-like. There is substantial evidence, including in the ellipsometry studies of Singh et al.,20 and the X-ray reflectivity work of Miyazaki et al.,21 that for film thicknesses of at least 100 nm, αN becomes independent of thickness. In the work reported here, the mean thickness of the samples is ca. 450 nm, which is well into the bulk regime.
In this work we present experimental evidence, with appropriate data analysis, that shows ellipsometry can be a convenient and accessible route to fundamental thermodynamic characterization. We focus on polymers, but the methods and theory apply to any optically-transparent amorphous substance. An outline of the remainder of the paper is as follows. In Section 2, we define the relevant quantities, and provide physical background on the expected quantitative relationships between the measured expansivities, αN and αV. In Section 3, we verify these relationships as we present results and discussion that covers our ellipsometry measurements and analysis performed on 10 different polymers, including a comparison with corresponding results from PVT data. Following that, we use the αN values from these ellipsometry experiments to characterize and compare the free volume of all of the polymers by application of the LCL EOS. We present a summary in Section 4 and provide experimental details in Section 5.
2. Theoretical background
Using ellipsometry measurements of the height, h, of a thin film as a function of temperature, T, leads to results for the expansivity αN = (1/h)dh/dT, where N indicates that the expansion is in the direction normal to the substrate. However, αN is not the same quantity as the material's coefficient of linear expansion, αL = (1/L)dL/dT which characterizes expansion in the length, L, in a single direction when the conditions are isotropic and unconstrained. In other words, αL is defined for the situation in which the material is allowed to expand freely in all three directions and therefore (for an isotropic material) αL = αV/3, where αV = (1/V)dV/dT is the familiar volumetric thermal expansion coefficient of the bulk material.22 (Maintaining simplicity in notation, it is understood in the present context that αN, αL, and αV are all defined by derivatives taken at a constant ambient pressure.)In ellipsometry experiments, the material being analyzed, here a polymer film, adheres to a substrate that remains essentially at a fixed area, A, because the coefficient of thermal expansion for any typical substrate, e.g. Si, is two orders of magnitude lower than for polymers.23 Consequently, expansion is only possible in the direction normal to the substrate, i.e. only the film height, h, changes. See Fig. 1. When a polymer film is in the melt state, we make an important assumption that its behavior should be analogous to that of a liquid expanding inside a piston of fixed area. For such a case, with a constant A, we expect the following relationship:
 | (1) |
 | ||
| Fig. 1 How a thin film expands with increasing T when constrained by a non-expanding substrate. It is assumed here that there is no slipping at the interface. | ||
In contrast to the melt case, a polymer in a solid or glassy state cannot expand in just a single direction without accruing internal elastic stress. Thus, as temperature increases, a glassy sample will achieve a final volume that is less than the equilibrium volume of the free sample at that temperature. In this case, one should expect that αN < αV. The elastic model proposed by Wallace et al.25 (below) predicts this trend analytically. Additionally, in the ESI,† we walk the reader through a simple thought experiment that can illustrate this inequality in a more pictorial way.
For the case of an isotropic solid or a glass, αN can be connected to αV through the Poisson ratio, υ, which is the negative of the ratio of the lateral strain to the longitudinal strain.26 Based on this concept, the elastic model of Wallace et al.25 gives the following:
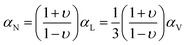 | (2) |
For the case of the melt, eqn (2) will reduce to the eqn (1) result, αN = αV, because the Poisson's ratio logically must become υ = 0.5; tabulated values for the Poisson ratio are typically quoted for the glassy state. Note that υ = 0.5 is sometimes associated with the system being mechanically “incompressible” (with P fixed). However, a liquid or melt is certainly compressible (e.g. via a pressure change), and in this case the value of 0.5 simply represents the reality that, upon constant pressure compression in one direction, an unrestricted liquid will expand in the other directions so as to retain its original volume.
Several examples in the literature exhibit some confusion – or at least a lack of consensus – in using ellipsometry data to determine thermal expansion coefficients. A recent review article27 implied that αN from ellipsometry (treated as a linear expansion coefficient, αL) should equal αV/3 and did not describe quantitatively the effects of mechanical confinement. Somewhat less directly, reported measurements28 have been implicitly connected to the linear expansion coefficient by the choice of notation, but with no relation to the given αV. There have also been several instances29–35 where the intent is to equate αN for the glass directly with αV; the mechanical confinement effect leading to the αN < αV prediction of the Wallace et al. elastic model is not considered. There are other examples36,37 that apparently apply the Wallace et al. model without changing υ to 0.5 at temperatures above Tg; such an approach leads to predicted αV values for the melt that will be larger by roughly 50%.
In summary, according to the simple model picture summarized in this section, αN, calculated by monitoring film thickness changes in a carefully executed ellipsometry experiment on a melt sample constrained by a non-expanding substrate should give the same result as αV, extracted from experimental PVT data collected on a corresponding unrestricted melt sample. However, for a glass, one should expect αN < αV. While the implications for the analysis of melt and glass data (eqn (1) and (2)) have been accepted and applied by multiple researchers, there nevertheless exists some significant confusion in the literature. This paper is the first to provide a substantive test of the model result, which we accomplish through careful analysis of ten different polymers. This level of scrutiny, verifying the relationship between αV and αN in the melt (eqn (1)) and in the glass (eqn (2)), is essential for promoting spectroscopic ellipsometry as a viable route to the data needed for EOS modeling, as will be demonstrated.
3. Results and discussion
Table 1 shows the polymer names and acronyms for the ten investigated polymers, as well as their molecular weights, Tg, and references to experimental PVT data to which we will compare our expansivity results obtained via ellipsometry. The systems cover a range of polymer chemistries and include one copolymer. Spectroscopic ellipsometry data were collected on thin films of these polymers supported on an Si substrate (with αL = 2.6 × 10−6 °C−1),23 deposited from solution via spin-coating (see Materials and methods). The films had a mean thickness of about 450 nm (all ≥150 nm). At these thickness values, we expect the relative contribution of the interfacial regions (e.g. α-relaxation times vary within ∼5 nm of an interface38,39) to be negligibly small compared to the amount of more bulk-like material in the film.| Acronym | Chemical name | M w (g mol−1) | T g (°C) | Ref. for PVT data |
|---|---|---|---|---|
| a The molecular weight (Mw) values tabulated here correspond to the samples studied here via ellipsometry. Literature sources for PVT data and Tg values correspond to different samples. b The Tg literature values are from the compilation in Table 1 of ref. 13. The Tg values apparent from the present ellipsometry measurements (for those polymers with Tg > room temperature) are within 5 °C of these values. c The PCHMA melt data points shown were regenerated from the published fit to the Tait equation of state (parameters available in ref. 12 and 40); given the accuracy of the Tait equation these values are equivalent to the actual measured data. Data for the PCHMA glass are from ref. 41. d The original data set contains PVT data for P ≥ 10 MPa; by fitting the LCL equation of state to this set we have predicted V(T) data points at P = 1 atm, which are expected to be very accurate. See ESI. | ||||
| PS | Polystyrene | 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
100 | 1 |
| PMMA | Poly(methyl methacrylate) | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
105 | 1 |
| PCHMA | Poly(cyclohexyl methyl methacrylate) | 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
104 | 40 and 41 |
| PVME | Poly(vinyl methyl ether) | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 070 |
−31 | 42 |
| PVAc | Poly(vinyl acetate) | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
32 | 1 |
| PαMS | Poly(α-methyl styrene) | 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
168 | 43 |
| PBMA | Poly(butyl methacrylate) | 182![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
20 | 1 |
| PEMA | Poly(ethyl methacrylate) | 340![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
63 | 1 |
| PSAN | Poly(styrene-co-acrylonitrile) (75%/25%) | 165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
107 | 1 |
| TMPC | Tetramethyl bisphenolA polycarbonate | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
196 | 44 |
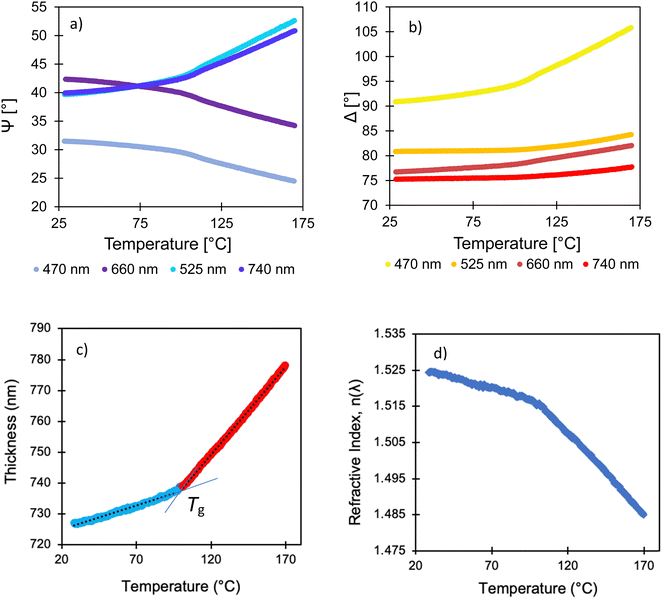
By analyzing the reflection of polarized light from a sample, ellipsometry measures – as a function of wavelength – two parameters: Ψ (related to the change in the amplitude of light) and Δ (related to its change in phase). There are two primary methods reported in the literature for using ellipsometry to determine αN values in thin films. In a dynamic scan,28,35,45,46 the temperature is increased at a constant heating rate while ellipsometry data are collected continuously. In a step-wise scan,20,24,30,34 the temperature is raised in increments, and data are collected at fixed temperatures. The data collection rate in a dynamic scan usually must be faster than in a step-wise scan. Typically, only a few wavelengths are used in the analysis, but fast spectroscopic scans over a wide spectrum are possible with modern instruments.46,47 Hereafter, we will compare the results obtained via dynamic scans and step-wise scans for PCHMA thin films, as an example.
Dynamic data are presented in Fig. 2(a and b) showing results obtained with four wavelengths measured as the temperature was raised at a constant rate of 2.5 °C min−1. The ellipsometry parameters change (increasing or decreasing) in approximate direct proportion to the change in the thickness (Δh) and refractive index (Δn).45 Following a quick glance at these data, two linear regions are apparent, corresponding to the glass in the lower temperature region and the melt state in the higher region. These data were analyzed using commercial software to obtain h and refractive index (n) of the PCHMA film as a function of temperature, as is shown in Fig. 2(c and d). The thickness increases weakly with temperature in the low temperature region, which is attributed to the glass. Similarly, there is a weaker dependence of n on temperature in this region.
The dynamic scans are very effective in identifying the temperature above which the thermal expansivity increases, which is used to define the Tg. For the purposes of illustration, our data analysis uses the room-temperature value of the complex refractive index as a function of wavelength, ñ(λ), for the silicon substrate, across the wide range of temperatures. (Here, ñ = n + ik, where k is the extinction coefficient.) This model is chosen frequently in the literature.28,32,35,45,48 Although neglecting the temperature dependence of ñ(λ) is not expected to affect the values obtained for the inflection point, and hence the Tg, it has a pronounced effect on the value of αN obtained. For this reason, dynamic scans are not suited for the determination of αN, unless the data analysis explicitly considers the changing ñ(λ) in the substrate.20,46,47 This point has been made previously by Kahle et al.46 In the analysis presented hereafter, we will show quantitatively the implications of using the fixed ñ(λ) model.
Continuing the example of PCHMA, we next present in Fig. 3(a) representative spectra obtained from a thin film at two different temperatures in a step-wise scan. The best-fits to the spectra were made by using ñ(λ) for Si at the corresponding temperatures. See Fig. S2 in ESI† for example data. The results of this analysis for a PCHMA thin film across the entire range of temperatures are shown in Fig. 3(b and c). Analysis of the h(T) obtained αN to be 1.86 (±0.07) × 10−4 °C−1 in the temperature range from 30 to 95 °C (attributed to the glass) and αN = 5.49 (±0.03) × 10−4 °C−1 from 100 to 180 °C (attributed to the melt). These values differ substantially from what were found using the dynamic analysis (reported in the caption for Fig. 2(c)). The difference between the two methods can be explained by the fact that the analysis of the step-wise data uses a different ñ(λ) for the Si substrate at each temperature, which is more difficult to include analytically in the dynamic modeling when the temperature is constantly changing during the measurement. Note that some commercial software does not offer ñ(T) in the analysis of dynamic data, which has resulted in some poor published results.
To provide a comparison of the models, the same ellipsometry spectra used to construct Fig. 3 were re-analyzed without considering the temperature dependence of ñ(λ) for the Si substrate. (See Fig. S3 and the comparison of αN values in Table S1 of the ESI.†) With inaccurate values for ñ(λ) of Si, the values of αN are noticeably higher. This same pattern was found in the experiments on other polymers reported in Table S1 (ESI†).
Moreover, we note that in a dynamic scan both T and h are changing during the course of a measurement (“on the fly”), naturally leading to uncertainty in both, which will be greatest when heating rates are fast and spectral acquisition is slow. The dynamic scan performed in Fig. 2 measured ψ and Δ at only four wavelengths (λ), and hence n(λ) was determined by fitting to four measurements (as described in the Methods), rather than across the entire spectrum, as was the case for the step-wise scans. (Data could have been collected at more wavelengths, but then the time of data acquisition would be greater, and the measurement would be made over a greater temperature interval, thereby adding uncertainty to T.) There is thus greater uncertainty in the n (and h) values obtained by the dynamic scan method, which explains the lack of agreement of values for PCHMA when comparing data in Fig. 2d and 3c.
Given these findings, all of the results presented hereafter will use measurements from step-wise temperature scans analyzed using temperature-dependent values of ñ(λ) for the substrate.
We aim to develop a robust method for measuring αN using ellipsometry, and to compare the results with αV from PVT data. We continue here to use PCHMA as an example to demonstrate a few of the finer points in calculating the α values. To calculate αN = (1/h)(dh/dT) (eqn (1)), one could evaluate the slope dh/dT over a chosen linear region and then divide it by the initial h value, or preferably, by the mean h value over that region. The selection of the particular value of h (or equivalently, the associated reference temperature that defines it) will have an impact on the value of αN, e.g. by about 2 or 3%. In the literature, there are examples of using an initial thickness at an arbitrary reference temperature35,45,47 and other examples using the mean thickness value for the temperature range.29 A more convenient approach is illustrated in Fig. 4(a),49 where we plot the natural log of h vs. T; here the slope will correspond directly to αN.
 | ||
| Fig. 4 Comparison of ellipsometry and PVT data for PCHMA. Experimental measurements of the temperature dependence of (a) the natural logarithm of h from Fig. 3b and (b) the natural logarithm of volume (taken from the literature40,41). (All data correspond to P = 1 atm.) The regions over which the linear best fits were taken are show by the red (melt) and blue (glass) symbols; the slope of each line gives the α value. Note that for consistency the regimes of the linear fits of the ellipsometry and PVT data are selected to cover matching T ranges. | ||
To draw the best comparison with PVT measurements, we have been careful to match the temperature ranges of the data used in both methods, because for some polymer melts the α value depends on temperature. (In these cases, typically, α will gradually increase with increasing T.) In deciding on the temperature range, it is important to avoid points that cross the glass transition temperature. Further, for PEMA and PBMA, we avoid choosing a temperature range that could lead to possible changes in partial melt crystallinity; the latter can be detected via calorimetry and have been discussed previously in Walsh et al.50 Finally, we excluded any ellipsometry data in the high T extreme of the range that show evidence of developing negative curvature in h vs. T. Pronounced negative curvature of h (or V) against T on an ambient pressure isobar would not be typical of standard single-phase expansion. Such a reversal in h(T) dependence might be caused by significant sample changes, for example, in the degree of partial crystallinity (e.g. ref. 50) or decomposition. Using this set of practical guidelines, we identified a viable T range for each set of ellipsometry data, and then (data availability allowing) have taken the same range from the PVT data. For completeness, the temperature ranges for all polymers are summarized in Tables 2 and 3.
| Polymer | Ellipsometry αN × 104 (°C−1) | PVT α V × 104 (°C−1) | α N /α V | Ellipsometry T range (°C) | PVT T range (°C) |
|---|---|---|---|---|---|
| a For PS, PCHMA, and PBMA, the αN value is the average from five separate trials and three separate trials in the case of PSAN; the αN result for all other polymers is from a single trial. b There was a negative curvature in h(T) for TPMC in the melt state at higher temperatures. Hence, only a narrow range of temperature could be used to estimate the αN for TMPC, and the results for this polymer melt are less reliable than for the others. | |||||
| PSa | 5.88 ± 0.29 | 5.87 | 1.002 | 100–165 | 100–170 |
| PMMA | 5.33 ± 0.38 | 5.97 | 0.893 | 115–180 | 121–179 |
| PCHMAa | 5.69 ± 0.12 | 6.03 | 0.943 | 105–160 | 103–163 |
| PVME | 6.39 ± 0.45 | 6.70 | 0.954 | 50–100 | 44–110 |
| PVAc | 6.85 ± 0.48 | 7.02 | 0.976 | 55–105 | 54–103 |
| PαMS | 5.05 ± 0.36 | 5.26 | 0.960 | 165–225 | 190–209 |
| PBMAa | 6.50 ± 0.26 | 6.21 | 1.047 | 40–100 | 43–101 |
| PEMA | 5.51 ± 0.39 | 6.01 | 0.917 | 70–110 | 70–112 |
| PSANa | 5.43 ± 0.11 | 5.69 | 0.954 | 105–170 | 110–170 |
| TMPCb | 8.20 ± 0.58 | 7.69 | 1.066 | 180–205 | 218–242 |
| Polymer | Ellipsometry αN × 104 (°C−1) | PVT α V × 104 (°C−1) | α N /α V | Ellipsometry T range (°C) | PVT T range (°C) |
|---|---|---|---|---|---|
| a Results were not obtained for three of the polymers (PVAc, PBMA, and PVME) in their glassy states because of their lower Tg values. Our ellipsometry stage does not cool below standard room temperature. b The αN value is the mean from five separate trials for PS, four separate trials for PCHMA, and three separate trials for PSAN; the αN result for all other polymers is from a single trial. | |||||
| PSb | 1.68 ± 0.14 | 2.46 | 0.681 | 40–90 | 40–91 |
| PMMA | 2.33 ± 0.45 | 2.65 | 0.879 | 40–105 | 40–101 |
| PCHMAb | 1.84 ± 0.10 | 3.27 | 0.562 | 40–85 | 40–85 |
| PαMS | 1.47 ± 0.28 | 2.14 | 0.687 | 120–160 | 120–160 |
| PEMA | 2.01 ± 0.38 | 2.33 | 0.863 | 40–45 | 30–38 |
| PSANb | 1.50 ± 0.26 | 2.08 | 0.712 | 30–95 | 30–90 |
| TMPC | 1.34 ± 0.26 | 1.60 | 0.838 | 100–175 | 103–177 |
Continuing with our example of PCHMA in Fig. 4(b), we show PVT data plotted as ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V over the relevant range in T (P = 1 atm). This is analogous to the ellipsometry ln
V over the relevant range in T (P = 1 atm). This is analogous to the ellipsometry ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h vs. T plot in panel (a). Both the PVT and ellipsometry data show a regime corresponding to the melt and another regime corresponding to the glass. (Tg occurs around 100 °C.) As discussed in the guidelines above, the figure shows how matching data ranges were selected for the determination of α, and how the corresponding linear fits of ln
h vs. T plot in panel (a). Both the PVT and ellipsometry data show a regime corresponding to the melt and another regime corresponding to the glass. (Tg occurs around 100 °C.) As discussed in the guidelines above, the figure shows how matching data ranges were selected for the determination of α, and how the corresponding linear fits of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h vs. T for the ellipsometry experiments and ln
h vs. T for the ellipsometry experiments and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V vs. T for the PVT measurements are obtained for both the melt and glass regimes. The ellipsometry results for this particular replicate PCHMA sample (more on replicate trials below) thus yield αN = 5.63 (±0.03) × 10−4 °C−1 for the melt and αN = 1.83 (±0.07) × 10−4 °C−1 for the glass, while the PVT measurements show corresponding results of αV = 6.03 × 10−4 °C−1 for the melt and αV = 3.27 × 10−4 °C−1 for the glass.
V vs. T for the PVT measurements are obtained for both the melt and glass regimes. The ellipsometry results for this particular replicate PCHMA sample (more on replicate trials below) thus yield αN = 5.63 (±0.03) × 10−4 °C−1 for the melt and αN = 1.83 (±0.07) × 10−4 °C−1 for the glass, while the PVT measurements show corresponding results of αV = 6.03 × 10−4 °C−1 for the melt and αV = 3.27 × 10−4 °C−1 for the glass.
For the case of the melt, it is important to note that the αN value for PCHMA thin films is in good agreement with its PVT-derived αV. This general agreement is evident from the summary of our results from a survey of ten different polymers in Table 2. The corresponding results for the polymers in their glassy states are summarized in Table 3. These tables report uncertainties for the αN values, which are estimated from random errors obtained from the analysis of replicates. Five independent measurements were made for three of the polymers (PCHMA, PS and PBMA), and three independent measurements for PSAN. For these polymers, the αN listed in Table 2 corresponds to the mean of the replicates, and we take the standard error in the mean to define the random error. The four polymer sets showed an average standard deviation of 7.1%, which led to an average standard error of 3.3% in the value of their mean αN. Using PBMA as example, the standard error of the mean was found to be 4.0% whereas the linear fitting error of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h vs. T was less than 0.1%. The random error likewise dominated the analysis for PCHMA and PS. Given the average standard deviation of 7.1% found for the αN of the four sets of replicates, we then applied this percentage error to estimate the error in αN for the remaining six polymers in Table 2, which have only a single measurement.
h vs. T was less than 0.1%. The random error likewise dominated the analysis for PCHMA and PS. Given the average standard deviation of 7.1% found for the αN of the four sets of replicates, we then applied this percentage error to estimate the error in αN for the remaining six polymers in Table 2, which have only a single measurement.
For polymers in their melt states (Table 2), we compare the αN and αV values by plotting them in Fig. 5(a). The best-fit slope (forcing a zero intercept) of 0.977 falls very close to the value for a perfect diagonal, illustrating excellent agreement between the two methods. There is one partial outlier, TMPC, for which the melt analysis is considered less reliable than the others. This is because the onset of a negative curvature in h(T) began at approximately 20 °C above the Tg. Consequently, data points over a very narrow T range were used in approximating the TMPC melt expansivity. Keeping or disregarding this approximated result will not change our overall conclusions.
 | ||
| Fig. 5 (a) Correlation of αN (obtained from ellipsometry) and αV (derived from literature PVT data) for (a) polymer melts and (b) polymer glasses. The line on each is a linear fit (with intercept forced through the origin). The fit in (a) includes consideration of the TMPC values (outlier in the upper right) which is derived from very limited data (see footnote in Table 2). The error bars represent the standard error in the mean for four polymers with replicate measurements or otherwise the mean standard deviations. The gradient is 0.98 for the melts, and 0.72 for glasses. | ||
Our result that αN ≈ αV for the melt supports our previously noted physical assumption, where a film maintaining a fixed mass on a substrate with a constant area expands only in the normal direction such that, if it is a melt, it can reach the expected volume for any T (without accruing stress) much like a fluid in a piston. More broadly, the data reported here, on a large set of polymers, with multiple replicates, demonstrates the feasibility of using ellipsometry experiments to approximate PVT properties.
We next consider results for the polymers in their glassy state. The data in Table 3 clearly show that the αN from ellipsometry for the glass is systematically lower than the corresponding αV from PVT measurements. In Fig. 5(b) the αN values are plotted against αV, and the line of best fit reveals that the αN for the glass falls short of the αV by an average factor of αN/αV = 0.72. Note that here we report this fitted slope because it is informative in average assessment, however, we should not expect, for the polymers in their glassy forms, that αNvs. αV, should form a perfect point-by-point linear relationship because glassy polymers do not all have the same Poisson ratios and hence the conversion factor in eqn (2) will change (more below).
The results for multiple polymers shown in the plot of Fig. 5(b) support the prediction of the Wallace et al. elastic model (eqn (2)) and the physical picture presented in the Theoretical Background, that, at least qualitatively, there is a significant difference between the αN and αV for a polymer glass. As for the melt, a glassy film is expected to be restricted to thermal expansion only in the normal direction. However, unlike a melt, a glass cannot expand solely in one direction without accruing an elastic stress, and so the observed αN is lower than the PVT-based αV.
We can further analyze the results in terms of the Wallace et al. model. Since eqn (2) proposes the relationship between αN and αV using the Poisson ratio, we therefore use our measured αN and αV values to back-calculate a value for υ that would be “implied” by the model. The results are tabulated in Table 4. Notice that for the polymer glasses we obtain an average implied Poisson ratio of 0.38 ± 0.03, which is in fairly good agreement with typical values of υ for polymer glasses. For instance, PS has a literature value of 0.33,51 and PMMA has a value of 0.40.52 Though the predictions may not always be quantitative, the elastic picture provides a sensible way to understand, at least qualitatively, why the polymer glasses are the systems for which αN is noticeably less than αV.
| Polymer | υ melt | υ glass |
|---|---|---|
| PS | 0.50 | 0.34 |
| PMMA | 0.46 | 0.45 |
| PCHMA | 0.48 | 0.26 |
| PVME | 0.48 | — |
| PVAc | 0.49 | — |
| PαMS | 0.49 | 0.35 |
| PBMA | 0.52 | — |
| PEMA | 0.47 | 0.44 |
| PSAN | 0.48 | 0.37 |
| TMPC | 0.52 | 0.43 |
| Mean | 0.49 ± 0.01 | 0.38 ± 0.03 |
As discussed in the assumptions described in the Theoretical Background, we expect polymer melts to expand without accruing elastic stress. In this limit the elastic model must reduce to give αN = αV, which follows from eqn (2) whenever υ = 0.5, which is the expected value for a liquid. The results of our back-calculations using eqn (2) for the polymer melts, presented in Table 4, show an average implied Poisson ratio of 0.49 ± 0.01, which equals 0.5 within uncertainty. The implied value of υ for TMPC in the melt state is >0.5, which is physically unrealistic. However, as already noted, our measurement of αN is less reliable for this polymer.
We now present some examples of how the present ellipsometry results can be used for thermodynamic characterization and analysis, an endeavor that would have normally required PVT data. In particular, we analyze and compare the free volume content of the polymer melts using the LCL EOS.13
In our work, free volume, Vfree, is defined as a quantity that depends on thermodynamic properties only, as follows
| Vfree = V − Vhc | (3) |
The LCL model has three molecular parameters, and solving uniquely for all of them requires, at a minimum, three single experimental quantities: αV, the compressibility (κ), and a specific volume value measured at some particular given (T, P). (A complete PVT data set would of course effectively contain all of this information and such data sets are commonly used to characterize the LCL model.) Relevant to the application here, we emphasize that if we are interested only in properties at ambient pressure, then the requirements lessen, and we can do without κ. Going further, if our goal is only to predict the fractional free volume Vfree/V, rather than absolute values of Vfree itself, then we only need an experimental value for α, and do not even require the specific volume. Further, α values lead directly to one of the key LCL characteristic parameters, viz. the non-bonded nearest-neighbor interaction energy operating between segments, ε. We have shown in previous work15 that both ε and the polymer Vfree are very strongly correlated with α. Thus, we can proceed using αN values determined from ellipsometry for the polymer melts where we have shown that we can now approximate that αV = αN.
In Table 5 we summarize modeling results for the polymer melts; details on these calculations are provided in the ESI.† The table lists the αN values determined via ellipsometry and the resulting fitted values of the characteristic LCL energetic parameter, ε. The right-hand columns in Table 5 list predictions for the percent free volume (%Vfree = 100 × Vfree/V) of each polymer compared all at a single common temperature (T = 125 °C, and P = 1 atm), and, compared when at each polymer's corresponding Tg. The free volume present in a material is intimately connected with its coefficient of thermal expansion. For example, the table shows that when they are compared at a common temperature, the higher the α, the higher is the %Vfree.
| Polymer | T g (°C) | α N × 104a (°C−1) | LCL |ε| (J mol−1) | LCL %Vfree at 125 °C | LCL %Vfree at Tg |
|---|---|---|---|---|---|
| a See Tables 2 and 3 for details on Tg and αN values. | |||||
| PS | 100 | 5.88 | 2119 | 12.38 | 11.12 |
| PMMA | 105 | 5.33 | 2223 | 11.44 | 10.51 |
| PCHMA | 104 | 5.69 | 2154 | 12.05 | 11.02 |
| PVME | −31 | 6.39 | 2037 | 13.22 | 6.01 |
| PVAc | 32 | 6.85 | 1972 | 13.96 | 9.02 |
| PαMS | 168 | 5.05 | 2283 | 10.96 | 12.97 |
| PBMA | 20 | 6.50 | 2021 | 13.40 | 8.15 |
| PEMA | 63 | 5.51 | 2187 | 11.75 | 8.92 |
| PSAN | 107 | 5.43 | 2204 | 11.61 | 10.75 |
| TMPC | 196 | 8.20 | 1816 | 16.05 | 21.33 |
As reflected in eqn (3), the system volume increases with T, therefore so must the free volume. In Fig. 6b we plot the temperature dependence of the percent free volume, %Vfree(T), at ambient pressure for each of the polymer melts. Over a T span of about 200 °C, the %Vfree of a polymer melt changes by about 10%. This may not seem like a large amount, however, small changes – even a fraction of a percent – can be important in determining both the dynamic response of a polymer, e.g. its segmental relaxation times near Tg,16,17 and its thermodynamic behavior, e.g. its miscibility with other components in blends.14,15
Fig. 6b also shows that the curve for any one polymer will not cross that of another, so the ranking between polymers persists over the entire temperature range. Comparing polymers among our set, we see that PVAc has the highest %Vfree, followed by PBMA and PVME; at the other end we have PαMS, with the lowermost value.
Related to this, PαMS has the highest Tg, whereas PVAc, PBMA, and PVME have the lowest Tgs among the set. We have noted in previous work13 that, comparing polymers at any single temperature, those with the lowest free volume have a tendency, on average, to be the ones with the highest Tg value and vice versa. The glass transition is a kinetic event where a material's molecular level dynamics slow down to the point that they are effectively slower than the practical experimental observation time scale. A polymer that tends to have more free space at any given T will tend to require less cooperativity for segmental motion, leading to lower activation barriers compared to other polymers. This serves to delay the glassy dynamic slowdown as T is further decreased. The connection between Vfree, cooperativity, and activation energy is discussed in detail in ref. 16 and 17.
In addition to comparing polymers at a common temperature, it is also very revealing to examine the trend in %Vfree across the series when calculated at each polymer's corresponding experimental T = Tg. In Fig. 6b, these %Vfree(T = Tg) values are marked as the large points, one on each polymer's %Vfree(T) curve. (Note the portion of any curve at temperatures below the experimental Tg would thus correspond to the theoretical extrapolation of the equilibrium melt.) These points, determined by applying our LCL model through ellipsometric characterization of each polymer, show the same striking linear trend we uncovered in earlier work13 for a large set of 50 polymers via analysis of their PVT data. Here, both the slope and intercept of the best-fit line drawn through the points are in excellent agreement with those of the line found from that previous PVT-based analysis, e.g. the slopes are 0.034 °C−1 and 0.033 °C−1 respectively.
Note that, while this is a strong correlation, it will not be “exact” because the glass transition temperatures themselves are not exact. The kinetic nature of the transition is reflected in the fact that the observed Tg point depends on the experimental timescale of observation (i.e. the heating or cooling rate), and on the experimental technique. It is common for reported Tg values to vary by ±5 °C (or more). However, this is still reproducible enough for our purposes. The range of system Tg values considered here spans hundreds of degrees; if one were to hypothetically alter each of the values randomly by ±5 °C, it would only have a small effect on the slope of the correlation line; none of the main conclusions would be affected.
The physical significance of the %Vfree(T = Tg) vs. T = Tg correlation line in Fig. 6 is that it marks the boundary between the melt regime (above) and glass regime (below). In other words, following along any particular melt's %Vfree(T) curve from high T as T decreases, the curve will intersect this boundary, and that intersection temperature is where, on average, the LCL theory predicts the polymer will become glassy. For a more complete description of the melt/glass boundary, see the discussion of Fig. 3 in ref. 13. In addition, we note explicitly that the correlation line in Fig. 6 demonstrates that the %free volume of a polymer at its Tg varies considerably, depending on its nature. This is counter to the historical view of free volume at Tg having a universal constant value, based on models55–57 that incorrectly assumed that polymer dynamics follow the Doolittle equation.58
T
g is an interesting quantity, a thermodynamic signature that reflects one aspect of dynamic response. The results above, i.e. that Vfree is not simply a constant at Tg, but rather carries with it a T-dependence, demonstrate that free volume plays an important role in dynamics but is not the only important variable. We have used our model for dynamic relaxation of melt materials and shown for many systems that segmental relaxation times (τ) follow a general form ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ ∼ f(T) × (1/Vfree).16,17 In other words, independent contributions to dynamics, both from temperature and specific volume, are important in understanding this material response. This form also reflects our discovery that the volume-dependent contribution is most effectively and analytically captured by using the free volume, not the total volume. Thus, we have found an essential role for Vfree, which can only be independently evaluated using thermodynamic information. Some alternative approaches can only operate by extracting Vfree values from dynamic data, however, that precludes using the results to understand dynamic response, since such a route would be circular. With the view that Vfree results can be illuminating for deeper understanding of both thermodynamic and dynamic properties, in this work we have extended this characterization route to the convenient ellipsometry approach.
τ ∼ f(T) × (1/Vfree).16,17 In other words, independent contributions to dynamics, both from temperature and specific volume, are important in understanding this material response. This form also reflects our discovery that the volume-dependent contribution is most effectively and analytically captured by using the free volume, not the total volume. Thus, we have found an essential role for Vfree, which can only be independently evaluated using thermodynamic information. Some alternative approaches can only operate by extracting Vfree values from dynamic data, however, that precludes using the results to understand dynamic response, since such a route would be circular. With the view that Vfree results can be illuminating for deeper understanding of both thermodynamic and dynamic properties, in this work we have extended this characterization route to the convenient ellipsometry approach.
4. Summary and conclusions
This work advances the soft matter community's ability to link material dynamic phenomena with thermodynamic data. Firstly, we have demonstrated spectroscopic ellipsometry as an ideal method to obtain vital thermodynamic information via the analysis of a material in the form of a thin film. Secondly, we combined the new results with thermodynamic analysis using the Locally Correlated Lattice (LCL) model to calculate the temperature dependence of the percent free volume, which is a quantity that has been used to explain trends in both miscibility and local dynamic relaxation, among other behavior.13,15,17 This is the first application of ellipsometry to find %Vfree(T) in this way.Ellipsometry offers distinct advantages over other techniques. In contrast to many dilatometric approaches, only a very small quantity of material is required for analysis, such as a thin film over a square centimeter (having a mass <0.1 mg). In experiments using bespoke deuterium-labelled molecules, often only small quantities are available.49 In contrast to other thin film analysis techniques, such as neutron or X-ray reflectivity,21,25 ellipsometry is often readily available within a laboratory and relatively inexpensive.
Our ellipsometric characterization of ten different polymer films on a substrate with a low thermal expansion coefficient demonstrates conclusively that the measurement of αN in the melt state is equal to the corresponding αV. However, in the glass state, a value of the Poisson ratio of the glass is needed to recover αV from a measurement of αNvia ellipsometry. Our new data strengthen previous LCL observations that the percentage of free volume at the Tg varies between 5% and 12%, depending on the particular polymer, and increases linearly with the Tg itself.
Ellipsometry has been used widely in the literature for decades to characterize solids and liquids. However, this work is the first to provide comprehensive and conclusive data testing the relationship between αN and αV for both the glass and melt states and thereafter obtaining the percent free volume as a function of temperature. Until now, the full usefulness of ellipsometry had not been exploited. Our research has thereby opened up the possibility of reliable essential thermodynamic characterization using this commonly available, straightforward technique, even when there is a small quantity of sample. We envisage that our methods will in the future underpin molecular design and synthesis to achieve target properties.
5. Materials and methods
5.1 Materials
The polymers, which are listed in Table 1, were obtained from either Sigma-Aldrich (Gillingham, Dorset, UK) or Polymer Laboratories (Church Stretton, Shropshire, UK). Laboratory reagent-grade, anhydrous toluene with low sulfur (Sigma-Aldrich) was used as the solvent to prepare solutions (typically 5 wt%). The only exception is that tetrahydrofuran (Sigma-Aldrich) was used as the solvent for PSAN. No unexpected or unusually high safety hazards were encountered. Pieces of single-side polished silicon (100) wafers (PI-KEM Tamworth, UK) were used as the substrate. Wafers were cut into pieces with typical dimensions of 2 cm × 2 cm.5.2 Sample preparation
The Si substrates were placed into a UV ozone cleaner (Bioforce Nanosciences, Inc.) for 15 min to remove any organic contaminants. Thin films were spin-cast onto the substrates from 0.5 mL of the polymer solutions using a photoresist spinner (PWM32 Series, Headway Research, Garland, Texas, USA). Samples were spun at 2000 rotations per min for 30 s. The thin films were then annealed in a vacuum oven (Technico) at 50 °C above the specific polymer's literature value for its Tg (Table 1) to remove residual solvent and to allow structural relaxation. Films were then cooled naturally while still under vacuum at a rate of approximately 0.25 °C min−1.5.3 Spectroscopic ellipsometry measurements
Ellipsometry analyzes the change in the state of the polarization of light upon reflection from interfaces. In our experiments, the thickness and refractive index of films were determined as a function of temperature using a variable-angle spectroscopic ellipsometer (V-VASE, J. A. Woollam Co., Lincoln, NE, USA). The films were secured to a vertical heating stage (HS-190) that was controlled via software (WVASE, J. A. Woollam Co.). A thermally-insulated cover (HTC-100 HeatCell) was placed over the vertical heating stage to stabilize and maintain the temperature of the sample holder. The cover has two ports on either side to allow light into and out of the sample cell, which contained the ambient atmosphere. Light from a 75 W Xe lamp passes through a linear polarizer before reflecting from the sample.Two different ellipsometry techniques were used: dynamic scans and step-wise scans. In a dynamic scan, four wavelengths of light (in the range between 400 nm and 800 nm) were selected. Data (consisting of ψ, Δ pairs) were collected over time consecutively at each of these wavelengths using an angle-of-incidence of 70° (measured from the normal to the plane of the substrate) as the sample was heated at a constant rate of 2.5 °C min−1.
In a step-wise scan, the temperature of the thin film was increased from room temperature in 5 °C increments using a heating rate of 2.5 °C min−1. The sample was allowed to equilibrate for 30 s before a spectroscopic scan commenced. Spectroscopic ellipsometry spectra were obtained at each temperature over the visible wavelength range from 400 nm to 800 nm, in increments of 10 nm, at an incident angle of 70°.
5.4 Ellipsometry data analysis
To determine a thin film's h and n at each temperature, a model was fit to the data using commercial software (WVASE). The model for the analysis, which is presented in Table 6, consisted of a substrate, thermal oxide layer (SiO2), and a polymer film layer. Complex refractive index values, ñ(λ) for the Si for a given temperature were obtained from the WVASE software. Preliminary ellipsometry measurements on uncoated Si wafers found that the mean thickness of the native oxide layer was 2.5 nm. This value was used in all of the models. The model used the refractive index values of thermal oxide obtained by Herzinger et al.59| Layer in the model | Varied parameters |
|---|---|
| 1. Polymer film | Cauchy parameters (A, B); h(T); thickness non-uniformity |
| 2. Thermal silicon dioxide layer (SiO2) | None |
| 3. Silicon substrate | Refractive index (n, k) |
The refractive index of the polymer layer was modelled using a Cauchy equation of the form:
 | (4) |
Author contributions
R. P. W.: conceptualization, formal analysis, methodology, visualization, writing original draft; D. B.: methodology, investigation, visualization, writing original draft; A. M. J. M. Beale: investigation; I. G.: investigation; J. L. K.: conceptualization, funding acquisition, supervision, writing – reviewing and editing; J. E. G. Lipson: conceptualization, funding acquisition, supervision, writing – reviewing and editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We benefitted from numerous useful discussions with Prof. Dame J. S. Higgins and Prof. J. T. Cabral (Imperial College). We thank Dr A. Gajewicz-Jaromin (University of Surrey) for technical support and Dr W. Sharratt (Imperial College) for providing the PCHMA and TMPC. Acknowledgment is made to the donors of The American Chemical Society Petroleum Research Fund for partial support of this research. J. E. G. L. and R. P. W. gratefully acknowledge the financial support provided by the National Science Foundation DMR-2006504.References
-
P. Zoller and D. Walsh, Standard Pressure-Volume-Temperature Data for Polymers, Technomic Pub Co., Lancaster, PA, 1995 Search PubMed
.
- J. E. Mckinney and M. Goldstein,
PVT Relationships for Liquid and Glassy Poly(Vinyl Acetate), J. Res. Natl. Bur. Stand., Sect. A, 1974, A78(3), 331–353, DOI:10.6028/jres.078A.018
.
- Y. Meng, P. Bernazzani, P. A. O’Connell, G. B. McKenna and S. L. Simon, A New Pressurizable Dilatometer for Measuring the Time-Dependent Bulk Modulus and Pressure-Volume-Temperature Properties of Polymeric Materials, Rev. Sci. Instrum., 2009, 80(5), 053903, DOI:10.1063/1.3122964
.
-
H. Fujiwara, Spectroscopic Ellipsometry: Principles and Applications, Wiley: Chichester, England; Hoboken, NJ, 1st edn, 2007 Search PubMed
.
- P. J. Flory, R. A. Orwoll and A. Vrij, Statistical Thermodynamics of Chain Molecule Liquids. I. Equation of State for Normal Paraffin Hydrocarbons, J. Am. Chem. Soc., 1964, 86(17), 3507, DOI:10.1021/ja01071a023
.
- R. Simha and T. Somcynsky, On Statistical Thermodynamics of Spherical and Chain Molecule Fluids, Macromolecules, 1969, 2(4), 342, DOI:10.1021/ma60010a005
.
- I. C. Sanchez and R. H. Lacombe, Elementary Molecular Theory of Classical Fluids - Pure Fluids, J. Phys. Chem., 1976, 80(21), 2352–2362, DOI:10.1021/j100562a008
.
- J. Dudowicz, K. F. Freed and W. G. Madden, Role of Molecular-Structure on the Thermodynamic Properties of Melts, Blends, and Concentrated Polymer-Solutions - Comparison of Monte-Carlo Simulations with the Cluster Theory for the Lattice Model, Macromolecules, 1990, 23(22), 4803–4819, DOI:10.1021/ma00224a009
.
- W. G. Chapman, K. E. Gubbins, G. Jackson and M. Radosz, Saft - Equation-Of-State Solution Model for Associating Fluids, Fluid Phase Equilib., 1989, 52, 31–38, DOI:10.1016/0378-3812(89)80308-5
.
- G. Sadowski, Modeling of Polymer Phase Equilibria Using Equations of State, Adv. Polym. Sci., 2011, 238, 389–418, DOI:10.1007/12_2010_94
.
- G. T. Dee and D. J. Walsh, Equations of State for Polymer Liquids, Macromolecules, 1988, 21(3), 811–815, DOI:10.1021/ma00181a043
.
- P. A. Rodgers, Pressure Volume Temperature Relationships for Polymeric Liquids - a Review of Equations of State and Their Characteristic Parameters for 56 Polymers, J. Appl. Polym. Sci., 1993, 48(6), 1061–1080, DOI:10.1002/app.1993.070480613
.
- R. P. White and J. E. G. Lipson, Polymer Free Volume and Its Connection to the Glass Transition, Macromolecules, 2016, 49(11), 3987–4007, DOI:10.1021/acs.macromol.6b00215
.
- R. P. White, J. E. G. Lipson and J. S. Higgins, How Pure Components Control Polymer Blend Miscibility, Macromolecules, 2012, 45(21), 8861–8871, DOI:10.1021/ma3018124
.
- R. P. White and J. E. G. Lipson, Free Volume, Cohesive Energy Density, and Internal Pressure as Predictors of Polymer Miscibility, Macromolecules, 2014, 47(12), 3959–3968, DOI:10.1021/ma5005474
.
- R. P. White and J. E. G. Lipson, The Cooperative Free Volume Rate Model for Segmental Dynamics: Application to Glass-Forming Liquids and Connections with the Density Scaling Approach, Eur. Phys. J. E: Soft Matter Biol. Phys., 2019, 42(8), 100, DOI:10.1140/epje/i2019-11862-3
.
- R. P. White and J. E. G. Lipson, A Simple New Way To Account for Free Volume in Glassy Dynamics: Model-Free Estimation of the Close-Packed Volume from PVT Data, J. Phys. Chem. B, 2021, 125(16), 4221–4231, DOI:10.1021/acs.jpcb.1c01620
.
- P. Badrinarayanan, W. Zheng, Q. Li and S. L. Simon, The Glass Transition Temperature versus the Fictive Temperature, J. Non-Cryst. Solids, 2007, 353(26), 2603–2612, DOI:10.1016/j.jnoncrysol.2007.04.025
.
-
J. S. Higgins and H. C. Benoît, Polymers and Neutron Scattering, Clarendon Press: Oxford, 1997 Search PubMed
.
- L. Singh, P. J. Ludovice and C. L. Henderson, Influence of Molecular Weight and Film Thickness on the Glass Transition Temperature and Coefficient of Thermal Expansion of Supported Ultrathin Polymer Films, Thin Solid Films, 2004, 449(1–2), 231–241, DOI:10.1016/S0040-6090(03)01353-1
.
- T. Miyazaki, K. Nishida and T. Kanaya, Thermal Expansion Behavior of Ultrathin Polymer Films Supported on Silicon Substrate, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69(6), 061803, DOI:10.1103/PhysRevE.69.061803
.
-
M. de Podesta, Understanding the Properties of Matter, CRC Press, London, 2nd edn, 2020 DOI:10.1201/9781315274751
.
-
CRC Handbook of Chemistry and Physics, ed. J. Rumble, CRC Press, Boca Raton London New York, 101st edn, 2020 Search PubMed
.
- G. Beaucage, R. Composto and R. Stein, Ellipsometric Study of the Glass-Transition and Thermal-Expansion Coefficients of Thin Polymer-Films, J. Polym. Sci., Part B: Polym. Phys., 1993, 31(3), 319–326, DOI:10.1002/polb.1993.090310310
.
- W. Wallace, J. Vanzanten and W. Wu, Influence of an Impenetrable Interface on a Polymer Glass-Transition Temperature, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52(4), R3329–R3332, DOI:10.1103/PhysRevE.52.R3329
.
- G. N. Greaves, Poisson's Ratio Over Two Centuries: Challenging Hypotheses, Notes Rec. R. Soc., 2013, 67(1), 37–58, DOI:10.1098/rsnr.2012.0021
.
- B. Hajduk, H. Bednarski and B. Trzebicka, Temperature-Dependent Spectroscopic Ellipsometry of Thin Polymer Films, J. Phys. Chem. B, 2020, 124(16), 3229–3251, DOI:10.1021/acs.jpcb.9b11863
.
- H. Lee, H. Ahn, S. Naidu, B. S. Seong, D. Y. Ryu, D. M. Trombly and V. Ganesan, Glass Transition Behavior of PS Films on Grafted PS Substrates, Macromolecules, 2010, 43(23), 9892–9898, DOI:10.1021/ma101743u
.
- M. M. Mok, J. Kim, S. R. Marrou and J. M. Torkelson, Ellipsometry Measurements of Glass Transition Breadth in Bulk Films of Random, Block, and Gradient Copolymers, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 31(3), 239–252, DOI:10.1140/epje/i2010-10569-3
.
- Y. Grohens, M. Brogly, C. Labbe, M. O. David and J. Schultz, Glass Transition of Stereoregular Poly(Methyl Methacrylate) at Interfaces, Langmuir, 1998, 14(11), 2929–2932, DOI:10.1021/la971397w
.
- R. Seemann, K. Jacobs, K. Landfester and S. Herminghaus, Freezing of Polymer Thin Films and Surfaces: The Small Molecular Weight Puzzle, J. Polym. Sci., Part B: Polym. Phys., 2006, 44(20), 2968–2979, DOI:10.1002/polb.20920
.
- C. Zhang, M. Davies and K. Karan, Probing Interfacial Interactions of Nafion Ionomer: Thermal Expansion of Nafion Thin Films on Substrates of Different Hydrophilicity/Hydrophobicity, J. Polym. Sci., Part B: Polym. Phys., 2019, 57(6), 343–352, DOI:10.1002/polb.24792
.
- G. Vignaud, M. S. Chebil, J. K. Bal, N. Delorme, T. Beuvier, Y. Grohens and A. Gibaud, Densification and Depression in Glass Transition Temperature in Polystyrene Thin Films, Langmuir, 2014, 30(39), 11599–11608, DOI:10.1021/la501639z
.
- M. Y. Efremov, S. S. Soofi, A. V. Kiyanova, C. J. Munoz, P. Burgardt, F. Cerrina and P. F. Nealey, Vacuum Ellipsometry as a Method for Probing Glass Transition in Thin Polymer Films, Rev. Sci. Instrum., 2008, 79(4), 043903, DOI:10.1063/1.2901601
.
- S. Kim, S. A. Hewlett, C. B. Roth and J. M. Torkelson, Confinement Effects on Glass Transition Temperature, Transition Breadth, and Expansivity: Comparison of Ellipsometry and Fluorescence Measurements on Polystyrene Films, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 30(1), 83–92, DOI:10.1140/epje/i2009-10510-y
.
- K. Fukao and Y. Miyamoto, Glass Transitions and Dynamics in Thin Polymer Films: Dielectric Relaxation of Thin Films of Polystyrene, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 61(2), 1743–1754, DOI:10.1103/PhysRevE.61.1743
.
- M. Mizuno, K. Nakamura, T. Konishi and K. Fukao, Glass Transition and Thermal Expansivity in Silica-Polystyrene Nanocomposites, J. Non-Cryst. Solids, 2011, 357(2), 594–597, DOI:10.1016/j.jnoncrysol.2010.06.061
.
- K. Paeng, S. F. Swallen and M. D. Ediger, Direct Measurement of Molecular Motion in Freestanding Polystyrene Thin Films, J. Am. Chem. Soc., 2011, 133(22), 8444–8447, DOI:10.1021/ja2022834
.
- A. Debot, R. P. White, J. E. G. Lipson and S. Napolitano, Experimental Test of the Cooperative Free Volume Rate Model under 1D Confinement: The Interplay of Free Volume, Temperature, and Polymer Film Thickness in Driving Segmental Mobility, ACS Macro Lett., 2019, 8(1), 41–45, DOI:10.1021/acsmacrolett.8b00844
.
- O. Olabisi and R. Simha, Pressure-Volume-Temperature Studies of Amorphous and Crystallizable Polymers. 1. Experimental, Macromolecules, 1975, 8(2), 206–210, DOI:10.1021/ma60044a022
.
- P. S. Wilson and R. Simha, Thermal-Expansion of Amorphous Polymers at Atmospheric-Pressure. 1. Experimental, Macromolecules, 1973, 6(6), 902–908, DOI:10.1021/ma60036a022
.
- T. Ougizawa, G. T. Dee and D. J. Walsh, Pressure Volume Temperature Properties and Equations of State in Polymer Blends - Characteristic Parameters in Polystyrene Poly(Vinyl Methyl-Ether) Mixtures, Macromolecules, 1991, 24(13), 3834–3837, DOI:10.1021/ma00013a015
.
- T. A. Callaghan and D. R. Paul, Interaction Energies for Blends of Poly(Methyl Methacrylate), Polystyrene, and Poly(Alpha-Methylstyrene) by the Critical Molecular-Weight Method, Macromolecules, 1993, 26(10), 2439–2450, DOI:10.1021/ma00062a008
.
- C. K. Kim and D. R. Paul, Interaction Parameters for Blends Containing Polycarbonates. 1. Tetramethyl Bisphenol-a Polycarbonate Polystyrene, Polymer, 1992, 33(8), 1630–1639, DOI:10.1016/0032-3861(92)91059-B
.
- S. Kawana and R. a L. Jones, Character of the Glass Transition in Thin Supported Polymer Films, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63(2), 021501, DOI:10.1103/PhysRevE.63.021501
.
- O. Kahle, U. Wielsch, H. Metzner, J. Bauer, C. Uhlig and C. Zawatzki, Glass Transition Temperature and Thermal Expansion Behaviour of Polymer Films Investigated by Variable Temperature Spectroscopic Ellipsometry, Thin Solid Films, 1998, 313, 803–807, DOI:10.1016/S0040-6090(97)00999-1
.
- E. C. Glor, G. V. Angrand and Z. Fakhraai, Exploring the Broadening and the Existence of Two Glass Transitions Due to Competing Interfacial Effects in Thin, Supported Polymer Films, J. Chem. Phys., 2017, 146(20), 203330, DOI:10.1063/1.4979944
.
- J. Q. Pham and P. F. Green, The Glass Transition of Thin Film Polymer/Polymer Blends: Interfacial Interactions and Confinement, J. Chem. Phys., 2002, 116(13), 5801–5806, DOI:10.1063/1.1456035
.
- R. P. White, Y. Aoki, J. S. Higgins, J. L. Keddie, J. E. G. Lipson and J. T. Cabral, Thermodynamics of Model PaMSAN/DPMMA Blend: A Combined Study by SANS, Ellipsometry, and Locally Correlated Lattice (LCL) Theory, Macromolecules, 2020, 53(16), 7084–7095, DOI:10.1021/acs.macromol.0c00706
.
- D. Walsh, T. Ougizawa, W. Tuminello and K. Gardner, Pressure Volume Temperature Properties of Polymethacrylates - Anomalous Behavior in the Melt, Polymer, 1992, 33(22), 4793–4797, DOI:10.1016/0032-3861(92)90694-R
.
-
L. E. Nielsen, Mechanical Properties of Polymers, Reinhold: New York, 1962 Search PubMed
.
-
D. W. van Krevelen and K. te Nijenhuis, Properties of Polymers: Their Correlation with Chemical Structure; Their Numerical Estimation and Prediction from Additive Group Contributions, Elsevier Science, Amsterdam, 4th edn, 2009 Search PubMed
.
- R. P. White and J. E. G. Lipson, Explaining the T,V-Dependent Dynamics of Glass Forming Liquids: The Cooperative Free Volume Model Tested against New Simulation Results, J. Chem. Phys., 2017, 147(18), 184503, DOI:10.1063/1.5001714
.
- R. P. White and J. E. G. Lipson, Pressure-Dependent Dynamics of Polymer Melts from Arrhenius to Non-Arrhenius: The Cooperative Free Volume Rate Equation Tested against Simulation Data, Macromolecules, 2018, 51(13), 4896–4909 CrossRef CAS
.
- M. L. Williams, R. F. Landel and J. D. Ferry, Mechanical Properties of Substances of High Molecular Weight. 19. the Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-Forming Liquids, J. Am. Chem. Soc., 1955, 77(14), 3701–3707, DOI:10.1021/ja01619a008
.
-
J. D. Ferry, Viscoelastic Properties of Polymers, Wiley: New York, 2nd edn, 1970 Search PubMed
.
- M. H. Cohen and D. Turnbull, Molecular Transport in Liquids and Glasses, J. Chem. Phys., 1959, 31(5), 1164–1169, DOI:10.1063/1.1730566
.
- A. K. Doolittle, Studies in Newtonian Flow. 2. the Dependence of the Viscosity of Liquids on Free-Space, J. Appl. Phys., 1951, 22(12), 1471–1475, DOI:10.1063/1.1699894
.
- C. M. Herzinger, B. Johs, W. A. McGahan, J. A. Woollam and W. Paulson, Ellipsometric Determination of Optical Constants for Silicon and Thermally Grown Silicon Dioxide via a Multi-Sample, Multi-Wavelength, Multi-Angle Investigation, J. Appl. Phys., 1998, 83(6), 3323–3336, DOI:10.1063/1.367101
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00959e |
| ‡ Original data can be obtained from https://doi.org/10.6084/m9.figshare.19165358 |
| § Present address: Laboratoire d’Astrophysique de Marseille, 38 Rue Frédéric Joliot Curie, 13013 Marseille, France. |
| This journal is © The Royal Society of Chemistry 2022 |