Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Model biomolecular condensates have heterogeneous structure quantitatively dependent on the interaction profile of their constituent macromolecules†
Julian C.
Shillcock
 *a,
Clément
Lagisquet
*a,
Clément
Lagisquet
 b,
Jérémy
Alexandre‡
c,
Laurent
Vuillon
b,
Jérémy
Alexandre‡
c,
Laurent
Vuillon
 *b and
John H.
Ipsen
*b and
John H.
Ipsen
 d
d
aBlue Brain Project and Laboratory of Molecular and Chemical Biology of Neurodegeneration, Ecole Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland. E-mail: julian.shillcock@epfl.ch
bLAMA, Univ. Savoie Mont Blanc, CNRS, LAMA, 73376 Le Bourget du Lac, France. E-mail: laurent.vuillon@univ-smb.fr
cBrain Mind Institute, Ecole Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland
dDept. of Physics, Chemistry and Pharmacy, University of Southern Denmark, Campusvej 55, DK-5230 Odense M, Denmark
First published on 25th August 2022
Abstract
Biomolecular condensates play numerous roles in cells by selectively concentrating client proteins while excluding others. These functions are likely to be sensitive to the spatial organization of the scaffold proteins forming the condensate. We use coarse-grained molecular simulations to show that model intrinsically-disordered proteins phase separate into a heterogeneous, structured fluid characterized by a well-defined length scale. The proteins are modelled as semi-flexible polymers with punctate, multifunctional binding sites in good solvent conditions. Their dense phase is highly solvated with a spatial structure that is more sensitive to the separation of the binding sites than their affinity. We introduce graph theoretic measures to quantify their heterogeneity, and find that it increases with increasing binding site number, and exhibits multi-timescale dynamics. The model proteins also swell on passing from the dilute solution to the dense phase. The simulations predict that the structure of the dense phase is modulated by the location and affinity of binding sites distant from the termini of the proteins, while sites near the termini more strongly affect its phase behaviour. The relations uncovered between the arrangement of weak interaction sites on disordered proteins and the material properties of their dense phase can be experimentally tested to give insight into the biophysical properties, pathological effects, and rational design of biomolecular condensates.
Introduction
The phase separation of intrinsically-disordered proteins (IDP) into biomolecular condensates has taken centre stage in cellular physiology.1 Biomolecular condensates (BC) appear in numerous locations in cells where they carry out many biochemical functions.2,3 They modulate enzymatic activity,4–7 a function that has been reproduced with rationally designed peptides,8–10 modulate buffer protein concentration,11 reduce noise in gene expression,12 and regulate cell migration.13 Phase separation of IDPs is crucial for the healthy functioning of neuronal synapses in the presynaptic axon14,15 and postsynaptic dendrite.16,17 However, dysfunctional phase separation underlies many pathological processes. Many neurodegenerative diseases involve aberrant phase transitions of IDPs,18 and interfering with such transitions presages new routes for therapeutic advances in neurology.19 Viral replication occurs within phase-separated inclusion bodies,20 and proteins responsible for packing the RNA of SARS-Cov2 also undergo phase separation.21 These processes depend on the ease with which enzymes and reactants can diffuse, fluctuate, and interact within BCs.22,23 A better understanding of how the molecular architecture of scaffold IDPs influences the material properties of BCs would help elucidate the physical mechanisms underlying their functions and guide the identification of targets for drugs,24 opening up new approaches to attack cancer and other diseases.25–28Although many biomolecular condensates are fluid,29 they do not behave as simple liquids.30,31 A slow transition from the fluid phase to a rigid, fibrillous phase has been observed in vivo and in vitro for IDPs including Huntingtin,32,33 FUS,34,35 and alpha synuclein.18 Chromatin has been shown to undergo phase separation in vitro,36 and to be mechanically restructured in a process that depends on its viscoelastic properties.37,38 Such experiments show that recapitulating the dynamics of condensates does not require the complex environment of a living cell.23 It has been conjectured that reversible phase separation is indicative of cellular health while irreversible rigidification of BCs marks a cell's transition into disease states.29 Empirically classifying biomolecular condensates on a spectrum from fluid (healthy) to rigid (disease) motivates us to learn how their material properties arise from their constituent IDPs.39–41 But although an enormous amount of experimental data is accessible in online databases,42–44via web-based interfaces (https://mlos.leloir.org.ar),45 there is no mechanistic understanding of how IDP molecular architecture controls the structure of their dense phase.
Computational modelling has been extensively used to connect molecular details such as multivalency and hydrophobicity to IDP phase behaviour in model systems.46–49 Exquisite detail on residue–residue interactions50 and the conformational dynamics of IDPs within condensates is revealed by Atomistic Molecular dynamics (aaMD) simulations,23,51 but these are limited to near-molecular system sizes and short times. Coarse-grained simulation techniques simplify the atomic details of proteins in order to simulate thousands of molecules.52–57 A minimal model of the phase separation of multivalent proteins is the patchy particle scheme in which proteins are treated as spheres with attractive sites on their surface.58,59 These models, however, ignore conformational fluctuations that may be important for flexible proteins. Other coarse-grained models represent an IDP as a linear polymer of monomers (or beads) held together by bonds (or springs), thereby retaining translational and conformational degrees of freedom of the IDPs whilst simplifying their enthalpic interactions to increase the accessible length and time scales. A bead represents one or more amino acids and the models differ chiefly in which molecular details are kept.39,46,47,52,55,60,61 Recent reviews describe how modeling is able to reveal physical principles underlying phase separation of IDPs.31,53,62,63
In this work, we go beyond establishing the phase boundaries of a model IDP in aqueous solution, and quantitatively study its dense phase. An IDP is represented as a semi-flexible polymer with multiple, punctate, attractive sites immersed in a good solvent.4,64 Our results are thus distinct from previous applications of similar stickers and spacers models, in which the polymers are in a poor solvent and possess a large fraction of hydrophobic monomers.39,40,47,65,66 Although motivated by the study of IDPs, our model is also applicable to the phase separation of uncharged, associative polymers.67 We use the coarse-grained simulation technique of dissipative particle dynamics,68,69 which is suitable for simulating (uncharged) IDPs because of their polymeric nature and transient, weak interactions.70 We find that the dense phase has a low (∼mM) internal concentration and approximately 70% solvent by volume, both results in good agreement with experiments on the uncharged IDP FUS.35,71 The IDPs form a structured fluid network in which their binding sites transiently meet at junctions. The molecules typically fluctuate between multiple junctions, which causes them to swell compared to their conformations in the dilute phase, an effect also observed in other recent studies.39,61,72 The length scale between the junctions is much larger than the monomer size, and varies more strongly with the binding site separation than with their affinity. It is reminiscent of the diffraction peaks observed in SANS experiments on the dense phase of the multivalent nucleolar protein NPM1.73 The spatial heterogeneity is revealed further using graph theoretic measures,74,75 which have been applied to metabolic networks,76 allosteric pathways,77 and the importance of residue mutations in proteins.78 We map the junctions to the nodes of a graph, and place edges between nodes spanned by at least one polymer. The local clustering coefficient quantifies the crowding of polymers around the nodes.79,80 Thirdly, the dense phase evolves on multiple timescales, indicating a complex internal dynamics of the IDPs.23 Finally, our model predicts that the location of attractive domains on IDPs is important for their phase separation. When the binding sites at the polymer endcaps are disabled, the dense phase dissolves.
Methods
Dissipative particle dynamics simulation technique
We use the dissipative particle dynamics simulation technique (DPD) to study the phase behaviour of a series of model IDPs. The source code for the simulations is available on Github.81 DPD is a coarse-grained, explicit-solvent simulation technique invented to study the hydrodynamic behaviour of complex fluids.68,69 It has since been applied to many soft matter systems including amphiphilic membranes,82–84 vesicle fusion,85,86 and domain formation in vesicles,87 among many others.88 It is highly suited to simulations of (uncharged) IDPs because the interactions are weak, and it has been shown that polymers in DPD exhibit self-avoiding walk scaling.89 DPD is able to follow the evolution of fluid systems over large length and time scales by grouping atoms or atomic groups into beads, and replacing complex, interatomic potentials by effective forces that are softer and short-ranged. This reduces the number of degrees of freedom being integrated, and allows a larger integration time step in the equations of motion.Beads in DPD have mass m and interact via three non-bonded interactions that are soft, short-ranged (vanish beyond a fixed length-scale d0), pairwise additive, and conserve linear momentum. A conservative force gives each bead an identity such as hydrophilic or hydrophobic:
FCij = aij(1 − rij/d0)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij, ij, | (1) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij is the unit vector directed from bead j to bead i. The other two non-bonded forces constitute a thermostat that ensures the equilibrium states of the simulation are Boltzmann distributed.69 The dissipative force is:
ij is the unit vector directed from bead j to bead i. The other two non-bonded forces constitute a thermostat that ensures the equilibrium states of the simulation are Boltzmann distributed.69 The dissipative force is:FDij = −γij(1 − rij/d0)2(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij·vij)· ij·vij)·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) ij, ij, | (2) |
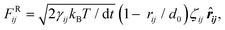 | (3) |
 is required in the random force so that the discretized form of the Langevin equation is well defined.69
is required in the random force so that the discretized form of the Langevin equation is well defined.69
Molecules are constructed by tying beads together using Hookean springs with potential energy:
| U2(i, i + 1) = (1/2)k2(rii+1 − l0)2, | (4) |
| U3(i − 1, i, i + 1) = k3(1 − cos(φ − φ0)), | (5) |
 ) for all bead pairs, and Hookean spring potential parameters (in units of kBT/d02 and d0 respectively). Note that E represents the endcap beads and F the internal binding site beads for computational and visualisation purposes, but these bead types have identical interactions except when one or the other is turned off as described in the text. NA = not applicable. A three-body bending potential is applied to adjacent triples of backbone beads (BBB) with parameters k3 = 5kBT and φ0 = 0
) for all bead pairs, and Hookean spring potential parameters (in units of kBT/d02 and d0 respectively). Note that E represents the endcap beads and F the internal binding site beads for computational and visualisation purposes, but these bead types have identical interactions except when one or the other is turned off as described in the text. NA = not applicable. A three-body bending potential is applied to adjacent triples of backbone beads (BBB) with parameters k3 = 5kBT and φ0 = 0
| Bead pairs | a ij | γ ij | k 2 | l 0 |
|---|---|---|---|---|
| WW, WE, WF | 25 | 4.5 | NA | NA |
| WB | 23 | 4.5 | NA | NA |
| BB, BE, BF | 25 | 4.5 | 128 | 0.5 |
| EE, EF, FF | Varies | 4.5 | 128 | 0.5 |
An IDP is represented as a linear polymer of hydrophilic backbone beads (B) with short segments of hydrophilic sticky beads regularly interspersed between them (Fig. 1). This is motivated by the observation that many IDPs have multiple attractive, aromatic residues (such as tyrosine) uniformly distributed throughout their disordered regions.90,91 Each binding site segment contains 4 beads of type F (type E for the endcaps) that adopt approximately spherical binding sites, and that prefer interacting with each other to the solvent or backbone beads. As is true for all coarse-grained simulation techniques, there is no direct relation between the DPD conservative force parameter aij between bead types i, j and atomic or molecular forces. The energy scale can be fixed by comparing an experimental force or work with the simulated value in a relevant process. But in the absence of this information, the conservative parameters for the sticky bead types E, F are set so that they prefer to interact with each other than with the solvent and backbone beads. Namely, we set aEW = aFW = aEB = aFB = aWW and aEE = aFF = aEF < aEW. Then this attraction is quantified by the dimensionless parameter ε = (aEW − aEE)/aEW. A value of ε = 0 means there is no net attraction between the sticky sites as they have the same interaction with each other as with the solvent beads. Increasing ε to 1 leads to effectively irreversible binding between the sticky beads on the timescale of the simulations. Bead types E and F have identical interactions except when one or other is disabled to represent disabling a binding site. Backbone beads are green, endcaps are red, and internal binding sites are yellow. They are coloured differently for visual distinctness only. The backbone beads are slightly more hydrophilic than binding sites to ensure they remain solvated in the dense phase. The solvent is represented by a single bead W and is invisible in all snapshots/movies for clarity.
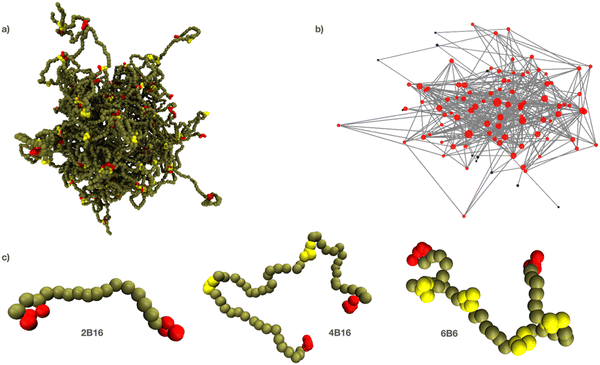
The number, location and affinity of the binding sites are the main parameters of the model. We use the nomenclature nBm (or nIm) to identify the structure of a polymer in the text, where n is the total number of binding sites (internal plus endcaps), and m is the number of backbone beads between adjacent binding sites (referred to as the gap between binding sites.) The letter B indicates that endcaps are present in the polymer and the letter I indicates that only internal binding sites are present. Selected binding sites can be turned on or off thereby changing the effective separation of the remaining active sites in a manner analogous to PTMs on a protein revealing/occluding specific interaction motifs. A typical phase separated droplet is shown in Fig. 1a together with its equivalent graph in Fig. 1b, which is further discussed in Section E. We refer to the dense phase equivalently as a droplet, network, or simply the dense phase. Three examples of polymers with different numbers of binding sites are shown in Fig. 1c.
Simulations take place in a cubical box of size (48d0)3 unless otherwise noted, and the system temperature is kBT = 1. A given number NIDP of IDPs are randomly distributed throughout the simulation box together with NW water particles to the constant density ρd03 = 3. Polymer concentrations are specified as the number fraction of IDPs, which is NIDP/(NIDP + NW). The system is evolved by integrating Newton's laws of motion for all beads for at least 3 million time steps. The integration step size is 0.02τ, where 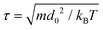 is the DPD timescale. The first million steps are discarded to allow the system to equilibrate, and ensemble averages are constructed by sampling from the remaining time. Because we are interested in equilibrium properties, we do not try to characterize the time-scale more precisely. One simulation of this system (3 million steps) requires 20 cpu days on a single core of a 4.5 GHz Ryzen Threadripper 3970X machine. Further details of the DPD technique are given in the literature.69,88
is the DPD timescale. The first million steps are discarded to allow the system to equilibrate, and ensemble averages are constructed by sampling from the remaining time. Because we are interested in equilibrium properties, we do not try to characterize the time-scale more precisely. One simulation of this system (3 million steps) requires 20 cpu days on a single core of a 4.5 GHz Ryzen Threadripper 3970X machine. Further details of the DPD technique are given in the literature.69,88
Results
A Dense phase concentration is modulated by binding site separation and affinity
We first explore how the phase behaviour of the model IDPs depends on the number and strength (or affinity) of their binding sites. The IDPs are hydrophilic, so the only direct attractive force between them arises from the interaction between these sites. They represent short residue motifs with weak, uncharged, attractive interactions.4,64 The strength of the attraction is represented by the dimensionless parameter ε. The value ε = 0 corresponds to no attraction and increasing ε towards 1 creates a stronger attraction between binding site beads (see Methods).Although representing an IDP as a semi-flexible polymer with discrete binding sites is a great simplification, the resulting model still possesses a large parameter space. At a minimum, the polymer length, bending stiffness, concentration, and the number, location and affinity of the binding sites must be specified. After a preliminary exploration, we focused on B48 polymers with 6 binding sites separated by 6, 8, or 10 backbone beads (referred to hereafter as 6B6, 6B8, 6B10 respectively). The top row of Fig. 2 shows the dense phase of 6B6 polymers for three values of the affinity decreasing from left to right. The droplet shows little visible change in cohesion over this range. By contrast, the bottom row shows that a droplet composed of 6B10 polymers begins to dissolve for the same change in affinity. The stability of the dense phase is clearly sensitive to the affinity and separation of the binding sites: more widely-separated binding sites require a higher affinity to drive their phase separation.
We establish a correspondence between the simulated droplets and experiments by calculating the concentration of the dense phase. Although it is difficult to measure the volume of arbitrarily-shaped droplets, their fluidity usually results in their being approximately spherical (cp. Fig. 2), which enables their volume to be estimated from their radius of gyration. This is obtained from the coordinates of the polymers’ binding site beads under the assumption (verified by visual inspection of snapshots) that they are uniformly distributed throughout the droplet's volume.
In equilibrium, the dense phase concentration C is:
 | (6) |
A common target for experimental investigation is the RNA-binding protein Fused in Sarcoma (FUS) that is implicated in the neurodegenerative disease ALS.92 The low complexity, N-terminal domain of FUS (FUS-LC, residues 1–163) is enriched in three polar amino acids (Q, S, Y), has only two charged residues (D), and around one quarter hydrophobic residues (mainly G and P) and none of the most hydrophobic residues (I, F, L, M V). FUS-LC phase separates into fluid droplets34 with a high viscosity.35 It makes multiple, transient, weak interactions within the dense phase indicating that it has little or no secondary structure.70,93 The near absence of charge and secondary structure make it suitable for coarse-grained simulations.
We do not attempt to map the specific residue sequence of FUS-LC onto the coarse-grained polymers in our model. Instead, we assign an effective attraction to the punctate binding sites along the polymers thereby allowing a variety of arrangements of binding sites to be mapped onto the experimental FUS-LC system. Next, we choose the level of coarse-graining to connect the simulated IDPs with the FUS-LC protein. The DPD length scale d0 is fixed by equating the experimentally derived radius of gyration of FUS-LC with the value obtained from a simulation of a single polymer in the dilute phase: 〈Rg〉d0 = RFUS-LCg. Fig. S9 in the ESI† shows the radius of gyration of each IDP studied obtained from independent simulations of a single polymer in dilute solution. It is evident that the model IDPs exhibit the conformational fluctuations of a self-avoiding walk for all the binding site affinities and polymer lengths studied.
Tomasso et al.,94 and Marsh and Forman-Kay95 have empirically fit the hydrodynamic radius Rh of a wide range of uncharged IDPs with the formula:
| Rh = (0.217 nm)N0.509, | (7) |
 and Dünweg et al. further established that the corresponding relation for a self-avoiding walk is
and Dünweg et al. further established that the corresponding relation for a self-avoiding walk is  . It is interesting to note that these relations imply that a polymer's hydrodynamic radius is smaller than its radius of gyration, which is the opposite of a uniformly-dense sphere, for which the relationship is
. It is interesting to note that these relations imply that a polymer's hydrodynamic radius is smaller than its radius of gyration, which is the opposite of a uniformly-dense sphere, for which the relationship is  . This implies that a fluctuating polymer in the dilute phase diffuses faster than a sphere with the same radius of gyration.
. This implies that a fluctuating polymer in the dilute phase diffuses faster than a sphere with the same radius of gyration.
FUS-LC contains 163 residues and its hydrodynamic radius is predicted to be 2.9 nm from eqn (2). Its radius of gyration is Rg = 4.36 nm using the relation for ideal chains or 4.61 nm for a SAW. The value of d0 is then fixed by: 〈Rg〉d0 = RFUS-LCg = 4.61 nm. Combining all the numerical factors together with 1000/0.6 to convert the concentration from polymers per nm3 into mM in eqn (1) allows the dense phase concentration to be determined from the formula 4.06〈N〉/(〈Rdropg〉/〈Rg〉)3 [mM], where we have adopted the SAW model for the polymer. The quantities in angle brackets are obtained by sampling from the equilibrated stage of the simulation. If the polymers are regarded as ideal chains instead of self-avoiding walks the numerical constant 4.06 changes to 4.8, corresponding to an increase in concentration of about 18% independent of the droplet size, which does not change our results significantly.
We find that the dense phase concentration lies in the range 1–15 mM for all systems with 4, 5, or 6 binding sites separated by 4–10 backbone beads, and for affinities between ε = 0.76–0.84 (Tables S3 and S4, ESI†) These values are in excellent agreement with recent experiments that find the dense phase concentration to be 2 mM for full length FUS,71 and 7 mM70 and 27.8 mM35 for FUS-LC. We also show in Section S6 of the ESI† that the dense phase contains 65–70% water by volume (Fig. S15, ESI†), a result also in good agreement with experiment.35
B The spatial structure of the dense phase varies with binding site separation
We next determine how the spatial organisation of the model IDPs depends on the affinity and location of their binding sites. Close examination of Fig. 2 shows that the binding sites (yellow for internal and red for endcaps) meet at junctions within the condensed phase that are separated by solvent-filled voids (Movies M1–M5 show the equilibrium fluctuations of droplets composed of 6B6 and 6B10 polymers with affinities ε = 0.84, 0.74, 0.68, ESI†). The distribution of binding sites at these junctions is highly heterogeneous. We quantify this observation by counting the number of binding sites on each junction (the junction mass) and measure the distance between them (the junction separation). Fig. 3 shows how these observables vary over a wide range of the total polymer concentration. Because the droplet is a fluid, there is a continuous exchange of polymers between it and the surrounding dilute phase, whose rate depends on the binding site affinity. For this analysis, we identify the dense phase with the Largest Equilibrium Network (LEN), which is defined as the largest set of polymers that are connected into a network by at least two binding sites. This excludes polymers in the dilute phase and those dangling off the droplet by a single binding site.The top row of Fig. 3 shows how properties of the dense phase of polymers 6Bm, m = 6, 8, 10, vary with the total concentration and binding site affinity in the standard simulation box (48d0)3. The dense phase grows linearly with concentration (Panel 3a), a result that holds even for the lowest affinity and largest spacing (ε = 0.76, 10 beads, dotted black curve) for which more polymers remain in the dilute phase. The mean junction separation, shown in panel 3b, increases when the binding sites are farther apart on the polymers, which is intuitively expected. But it is largely independent of the affinity, apart from a small divergence (less than the size of a single bead) for the 6B10 polymers, which suggests that the network is loosened by decreasing affinity (cp. bottom row of Fig. 2). This result implies that the porosity of a biomolecular condensate is insensitive to small changes in the strength of the interactions between the constituent IDPs but increases with increasing separation of their binding domains (cp. the top row of Fig. 2). Panel 3c shows that the mean junction mass increases systematically (albeit slowly) with increasing binding site affinity and decreasing separation. Combined with panel 3b, we find that increasing the binding site affinity while keeping their separation unchanged does not change the mean separation of connected junctions in the dense phase, but packs more polymers between them.
We have verified that the dense phase is in equilibrium with the surrounding dilute phase by two methods. It is clear from panels 3b and c that the junction separation and mass are independent of the total polymer concentration in the range studied, which supports the droplets being in thermodynamic equilibrium. We also simulated systems in a larger box (64d0)3 to confirm that the dense phase structure is independent of the simulation box size. Because the larger simulations are extremely time consuming, requiring 16 cpu days per million time-steps, we have only compared two affinities (ε = 0.76, 0.84) and two separations (6, 10). Panel 3d shows the fraction of polymers in the droplet in both system sizes is independent of the box size even for weak affinities (dashed curves) for which 10–30% of the polymers remain in the dilute phase over this concentration range. Similarly, panels 3e and f show that the mean junction separation and mass are independent of the box size and total concentration for all binding site affinities and spacings studied. Note that the droplets in the larger simulation box have been simulated at three lower concentrations than those in the smaller box. These concentrations are chosen so that there are the same number of polymers in the larger box as for the first three concentrations in the smaller box. It is clear that while the structural properties of the droplets are the same (panels 3e and f),panel 3d shows that polymers migrate from the dense to the dilute phase when a well-formed droplet in the smaller box is simulated in the larger box, further supporting the equilibrium state of the system. Comparing the first data points of the dashed-blue/circle and yellow/square curves shows that while ∼70% of the polymers are in the dense phase in the smaller box, this falls to about 25% of the (same number of) polymers in the larger box. (Section S4 and Fig. S10 of the ESI† provide further supporting data.)
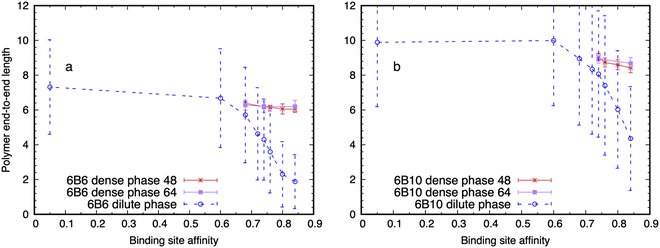
We find that the model IDPs adopt more extended conformations when they move from the dilute to the dense phase. This apparently counter-intuitive result is also seen in Monte Carlo simulations from the Wingreen61 and Pappu72 groups. Fig. 4 shows that a single polymer of types 6B6 and 6B10 in the dilute phase becomes increasingly compact on raising the affinity of its binding sites (dashed blue curve) because it can lower its free energy by making self-bonds with its multiple binding sites. But when its mean end-to-end length (Lee) drops below the value it would adopt in the dense phase, the latter becomes the equilibrium state. The transition occurs at a higher affinity for 6B10 polymers than for 6B6 polymers because the longer spacers require a higher binding enthalpy before the dense phase becomes stable. The large error bars in the dilute phase reflect the large conformational fluctuations of the single polymer (cp. Movie M7, ESI†). By contrast, the red (box size 48) and purple (box size 64) curves in Fig. 4 show that the mean Lee of the polymers in the dense phase is largely independent of affinity for 6B6 polymers but shows a small decrease for 6B10 polymers with increasing affinity (cp. Fig. 3b). (They also show that the results are independent of the system size.) The smaller error bars reflect the more extended conformational ensemble of the polymers in the dense phase (cp. Movie M8, ESI†). This result is supported by the observation that IDPs in the dense phase rarely span the same junctions more than once, which would imply binding to themselves (cp. Fig. S8, ESI†). Table S1 (ESI†) shows that 16% of 6B6 polymers in the dense phase span a pair of junctions twice, and only 1.6% three times.
The heterogeneous distribution of polymers within the dense phase raises the question of whether its structure changes on passing from its surface deeper into its core.72 We have examined the junction properties in two regions: those polymers closer to the droplet's centre of mass than a distance equal to its radius of gyration, and those polymers outside this distance. Because the polymers are extended objects, the two sets are not easily distinguished. We have varied the radius that distinguishes the two sets to check that the results are not overly-sensitive to the value chosen, and the results are stable, albeit not highly precise. Table S2 (ESI†) shows the junction separation and mass for 6B6 and 6B10 polymers with affinities ε = 0.84, 0.74. The junction separation varies little between the regions, but the junction mass drops by as much as a factor of two for junctions nearer the surface, the effect decreasing for longer spacers and weaker affinity. This result is intuitively expected as more than half the space around those junctions is solvent. It implies the mass of polymers around the junctions has a positive gradient moving deeper into the droplet.
The results of this section demonstrate that the model IDPs phase separate into an heterogeneously-structured fluid in thermodynamic equilibrium with the surrounding dilute phase for a range of combinations of the location and affinity of their binding sites. This supports our comparing the properties of the ∼50 nm diameter simulated droplets with those of much larger experimental BCs. It also suggests that the cell can tolerate some variation in the strength of IDP interactions without greatly modifying the stability and spatial structure of their dense phase.
C The dense phase has long-range spatial structure
The mean values of observables in Fig. 3 do not reveal their spatial variation throughout the dense phase. The radial distribution function (RDF) of the binding sites gives more complete information. The RDF is the probability of finding two entities at a given separation in space. The RDF of the endcaps and internal binding sites for polymers of types 6B10 and 6B6 are shown in Fig. 5 for strong and weak values of affinity (ε = 0.84, 0.76), where these terms are used qualitatively to describe the cases shown in the left and middle columns of Fig. 2. The dense phase possesses spatial structure out to length scales 3d0–8d0 far beyond the monomer size d0. The peak near the origin counts binding sites present at the same junction, and is uninteresting. The first interesting peak in the RDF quantifies the separation of junctions that are spanned by polymers. Notably, it does not shift significantly when the binding site affinity is reduced, but increases as expected when their separation is increased. The second peak also moves to larger distances but the peaks are less pronounced for the weaker affinity than the stronger. The near coincidence of the peak heights for the solid and dashed curves of the same colour shows that the mean junction separation shown in Fig. 3 is an average over junctions formed by endcaps and internal binding sites. The peak heights are proportional to the number of binding sites (4 internal and 2 endcaps), so dashed curves are always above the solid curves for the same affinity and spacing.D Dense phase properties are modified by the active binding site distribution
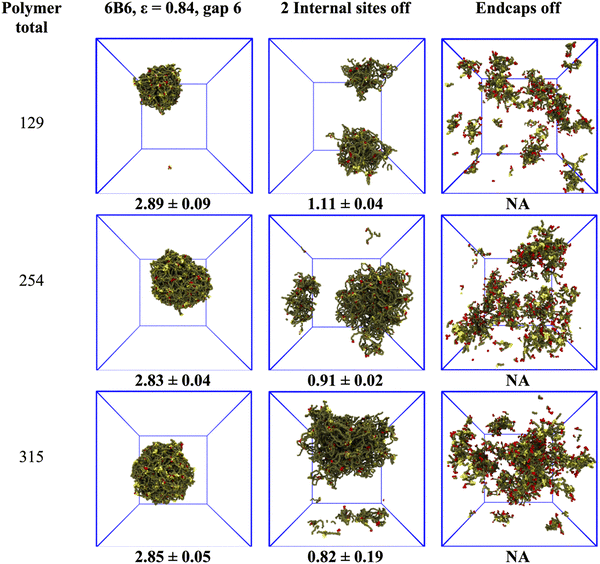
The previous section showed that the structure of the model biomolecular condensate responds to variations in the polymer binding site separation and affinity. This raises the question of what the consequences are for the condensate of disabling one or more sites. We performed independent simulations of 6B6 polymers with an affinity of ε = 0.84, over a range of concentrations, for the three cases in which all sites are active, the two internal sites adjacent to the endcaps are deactivated, or the endcaps are deactivated. We note here that each binding site on the coarse-grained IDPs represents a number of amino acids, not a single residue. Disabling the endcap corresponds to replacing all attractive residues (e.g., tyrosine) by polar ones (e.g., serine) in a segment of several residues (see Methods).Turning off internal binding sites/endcaps in the simulations is accomplished by setting their conservative self-interactions/cross-interactions equal to their interaction with the water beads, which sets their affinity ε = 0. Note that the binding site beads are still present in the polymer, so its length is unaltered. Fig. 6 shows typical droplets for these cases, and the dense phase concentration (mean and standard deviation of 4 runs) is below the snapshots. The first column shows that the droplet has a concentration of ∼3 mM independent of the total polymer concentration when all 6 binding sites are active. The droplet swells but remains phase separated when two internal sites are turned off and its concentration drops by a factor of 2–3 (middle column). Note that the concentration calculation is not affected by the dense phase crossing the periodic boundaries of the simulation box. But the concentration of a non-spherical droplet is not easily measured, and the value at the bottom of the middle column is included for completeness only. The final column shows that the dense phase disintegrates into hairy micelles or a box-spanning network with no sharp boundaries when the endcaps are disabled, even though the polymers still have 4 active binding sites.
We quantify the change in the droplet structure when two internal sites are disabled in Fig. 7 for polymers with three different separations (6B10, 6B8, 6B6) and fixed affinity ε = 0.84. Panel a shows that the network size changes little for the three cases, indicating that the polymers with fewer binding sites still phase separate into stable droplets. The mean junction separation, shown in panel b, increases systematically by a factor that also increases with the binding site separation, reaching almost a factor of two when the binding sites are separated by 10 backbone beads. Concomitantly, the mean junction mass, in panel c, decreases by an amount that is largest for the smallest binding site separation of 6 beads. We cannot measure dense phase properties when the endcaps are disabled because the remnant “networks” are too small to yield meaningful results.
 | ||
| Fig. 7 The structure of the dense phase of polymers with 6 binding sites and affinity ε = 0.84 (solid curves) changes when two inner sites are disabled (dashed curves). Arrows indicate the shift in the property. The binding site separation is colour coded – 6B10 (black), 6B8 (red), and 6B6 (yellow). (a) The dense phase contains (almost) all polymers for all separations and (internal) binding site states. The mean junction separation (b) increases, and the mean junction mass (c) decreases when the two sites are disabled. Snapshots corresponding to the solid and dashed yellow curves are seen in the left and centre columns in Fig. 6. The legend applies to all. | ||
Although results are shown for a single affinity (ε = 0.84), we expect from Fig. 3 that disabling internal sites for other affinities would be similar unless the combination of binding site separation and affinity were such as to render the droplet already close to the phase boundary, e.g., 6B10 with ε = 0.76. Comparing Fig. 3 and 7 shows that droplet's characteristic length scale is more sensitive to the spacing of the binding sites than their affinity, while the junction mass is sensitive to both.
E Clustering coefficient of the dense phase reveals a heterogeneous mass distribution
Although the model BC is an equilibrium thermodynamic phase, there is considerable variability in the spatial distribution of the mass. Fig. 5 shows that the dense phase has a structure that extends far beyond the monomer size and is not smeared out over time in spite of its fluidity. The regulation of biochemical reactions has been identified as a key function of BCs, and the spatial organisation of scaffold proteins within a BC should be expected to influence the diffusion and reactivity of client molecules.3,98 Previous simulations of telechelic polymers has shown that the distribution of the number of polymers that bind at junctions throughout the dense phase is broad.49 In this section we quantify the spatial heterogeneity of the dense phase using measures from graph theory.The dense phase is mapped to a graph by identifying a node with each junction where polymer binding sites meet, and connecting two nodes by an edge when the corresponding junctions are spanned by at least one polymer. For the purpose of constructing the graph, an edge is assigned to two nodes if two adjacent binding sites on a polymer connect two junctions. Only polymers with at least two binding sites connecting them to the dense phase are included in the graph to avoid skewing its properties with polymers that dangle off into the dilute phase. The graph is recalculated each time the simulation is sampled to generate a time series of graphs that represent the droplet's state from which equilibrium values of observables can be calculated.
All properties of the graph we use are calculated from its adjacency matrix Aij. This is the square matrix whose dimension is equal to the number of nodes in the graph, and whose elements Aij = 1, if the nodes i, j are connected by an edge, and 0 if not. Diagonal elements are zero because we ignore self-loops, which represent polymers multiply bound to the same junction. The number of neighbours of a node i, referred to as its degree, is the sum  of the elements in row i.
of the elements in row i.
From the matrix Aij we construct the local clustering coefficient that measures the mutual connectivity of the nodes connected to a given node.79,80,99 It is defined as the ratio of the number of linked pairwise neighbours of a node to the maximal possible number of linked pairwise neighbours averaged over all the nodes of the graph. The clustering coefficient Ci of node i is:
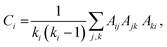 | (8) |
Fig. 8a shows that the CC of networks of polymers with multiple binding sites of affinity ε = 0.84 increases linearly with binding site number until it starts to saturate at six sites. The CC is 2–3 times larger than the value for a network of telechelic polymers (2B48) with a similar backbone length, and much greater than for a random graph (see Section S2 in the ESI† for the definition of the random graph). This indicates that multisite polymers form highly-connected junctions. The variance of the CC, indicated by its vertical extent, reinforces the evidence of the radial distribution function in Fig. 5 that the local network density is heterogeneous. Because of the large parameter space of polymers with multiple binding sites, we have not calculated the CC for all combinations of their number and affinity. Section S5 of the ESI† shows further data on the CC of the networks. For telechelic polymers, the CC increases approximately linearly with the binding site affinity (Fig. S12, ESI†). And for multisite polymers, the CC is independent of network size, and decreases with increasing binding site separation (Fig. S13 and S14, ESI†). We find that that both the number, separation, and affinity of the binding sites influence the clustering coefficient.
The wCC in Fig. 8b shows that the average connectivity of junctions increases sharply with increasing binding sites per polymer and its variance increases, particularly for polymers with 5 and 6 sites. Polymers with multiple binding sites form regions with a high local connection density as well as regions with a low density. These results are averaged over samples taken from simulations of 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 timesteps (after discarding 106 steps) indicating that they persist in equilibrium. We point out here that the wCC is calculated for each node i in the graph and normalized by dividing by the quantity ki (ki − 1), which is the maximum number of triangles the node could make, and then averaged over all nodes. The number of triangles a node actually makes is usually much smaller than this maximum (cp. Fig. 8a), which is why the ordinate of Fig. 8b is not large. But its vertical extent reflects the large variation in the number of polymers spanning the junctions. The wCC of the random graph is not shown because it has edges that span the whole graph, which renders it not comparable to locally-connected droplets. Although moving internal binding sites closer together along the IDPs systematically reduces the separation of the junctions in the BC (cp. Fig. 3b) and increases the mass distribution (cp. Fig. 3c), the dense phase remains highly heterogeneous.
000 timesteps (after discarding 106 steps) indicating that they persist in equilibrium. We point out here that the wCC is calculated for each node i in the graph and normalized by dividing by the quantity ki (ki − 1), which is the maximum number of triangles the node could make, and then averaged over all nodes. The number of triangles a node actually makes is usually much smaller than this maximum (cp. Fig. 8a), which is why the ordinate of Fig. 8b is not large. But its vertical extent reflects the large variation in the number of polymers spanning the junctions. The wCC of the random graph is not shown because it has edges that span the whole graph, which renders it not comparable to locally-connected droplets. Although moving internal binding sites closer together along the IDPs systematically reduces the separation of the junctions in the BC (cp. Fig. 3b) and increases the mass distribution (cp. Fig. 3c), the dense phase remains highly heterogeneous.
We hypothesize that a cell may regulate the structure of a BC via post-translational modifications to scaffold proteins that occlude or expose interaction sites. To explore the prediction of our model in this case, we have compared the CC for the networks composed of 6B6 polymers with all six sites active and when two internal binding sites are disabled. These correspond to the networks shown in the middle column of Fig. 6. Fig. 9 shows that the CC for the network is independent of concentration for the four points A–D and decreases when two internal binding sites are disabled (cp. “A” and “A two off”, etc.) but the dense phase is still heterogeneous.
F Binding site affinity and spacing influence dense phase fluidity
Many biomolecular condensates are in the fluid phase, and loss of fluidity has been proposed as a sign of pathology.29 In this section, we demonstrate that the dense phase of the model IDPs is fluid, and quantify how its internal dynamics depends on the binding site number and affinity.A common experimental demonstration of condensate fluidity is to follow the spontaneous fusion of two distinct droplets into a single, spherical droplet on contact.34,101 The same phenomenon is observed in our system. Fig. 10 shows two droplets fusing, each of which is composed of 763 telechelic 2B8 polymers with an endcap affinity ε = 0.76. On encountering each other by diffusion, they merge and eventually form a single, spherical droplet. Movie M6 (ESI†) shows the full evolution of the fusion event.
The fusion of two droplets is a non-equilibrium process, but equilibrium droplets are not static. Polymers diffuse and exchange between the droplet and the dilute phase in an affinity-dependent manner. Polymer dynamics in the dense phase may intuitively be separated into the diffusion of the whole polymer, as measured by its (relatively slow) centre of mass (CM) motion, and (relatively fast) conformational fluctuations by which it can bind/unbind to/from other polymers. The latter processes occur even if the polymer's CM is on average stationary. We introduce a new observable f(τ), which we call the network fluidity, that is defined on the droplet's equivalent graph to display the conformational dynamics of the dense phase:
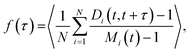 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time steps) this is not reflected in the fluidity measure. It would appear if the sampling rate were increased.
000 time steps) this is not reflected in the fluidity measure. It would appear if the sampling rate were increased.
The function f(τ) measures the number of descendent nodes into which each node splits during a time interval τ, averaged over the whole graph and normalized so that if a node is its own descendent it contributes 0, and if it totally splits up it contributes 1. It is similar to the auto-correlation function of the number of binding sites present on a node with the important difference that it tracks not only the number of binding sites per node but also their identity: if a binding site leaves a node and a different one joins, the fluidity measure reflects this even though the number of binding sites on the node has not changed. We introduce this definition because binding sites fluctuating between nodes represents a motion that will likely impact the behaviour of other molecules within it, e.g., by permitting the diffusion of objects larger than the mean junction separation because the network can rearrange around them.
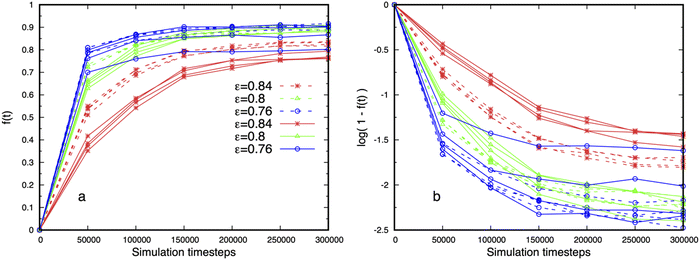
Adding more binding sites might be expected to reduce the dense phase fluidity, but this is not observed. Fig. 11 shows that droplets with multiple binding sites are more fluid than telechelic polymers with the same affinity ε = 0.84 (cp. Fig. S11, ESI†), and exhibit fluctuations on shorter timescales. Fig. 11a shows that the dynamics, as measured by the fluidity f (τ), slows down with increasing affinity as intuitively expected, but that the fast motion of the polymers is reduced with increasing binding site separation for stronger affinities (dashed 6B6 curves are above solid 6B10 curves). We attribute this effect to the increasing difficulty of the binding sites on a fluctuating polymer to move to a nearby junction as their separation along the polymer backbone increases (cp. junction separation in Fig. 3). Fig. 11b shows that the fluidity of droplets containing multi-binding site polymers cannot be described by single exponential decay for any of the affinities studied. Their internal dynamics therefore possesses at least two distinct time-scales. The splitting of the curves for 6B10 polymers with the lowest affinity at different concentrations reflects the small size and instability of the dense phase.
Finally, the independence of the fluidity on the total polymer concentration, and therefore on the droplet size, seen in Fig. 11 further supports the claim that the droplets are in equilibrium. Snapshots of droplets corresponding to Fig. 11 for the affinities ε = 0.8, 0.76 are shown in the left and middle images in Fig. 2, and quantitative measures of their structure in Fig. 3 and 5.
Discussion
We have shown that model IDPs with attractive binding sites phase separate into a dense phase in equilibrium with a dilute phase in the absence of a solvophobic repulsion. The dense phase is a dynamic network, in which the binding sites reversibly assemble at junctions (or nodes), and resembles associative polymer systems.102–104 When the model IDPs are mapped to the FUS low complexity domain, the dense phase has a concentration in the range 2–12 mM, and an aqueous volume fraction in the range 60–70% in good agreement with experiments.35 The junction distribution (or porosity) in the dense phase is spatially heterogeneous with a characteristic length-scale that is much larger than the size of the monomers (Fig. 5). This length-scale is selected by the contour length between binding sites on the IDPs, and is more sensitive to their separation than to their affinity (Fig. 3).We believe our results cannot be satisfactorily explained within Flory–Huggins (FH) theory,96 which is widely used to construct and interpret simulation studies of IDP phase behaviour.39,40,47,65,105 FH theory assigns all monomers in a polymer an energetic interaction with the solvent that is quantified by a parameter χ (for heteropolymers this is an effective parameter). When χ is negative (good solvent conditions), the entropy of mixing combines with the favourable solvation energy to keep the single-phase mixture stable. Phase separation only occurs in FH theory when the monomers are solvophobic (large positive χ parameter or bad solvent conditions).40,47 However, although the model IDPs are in good solvent conditions they are able to phase separate.
Tomasso et al.94 present data for a wide range of IDPs in dilute solution showing that they have the conformational fluctuations typical of polymers in a theta or good solvent in that their hydrodynamic radius scales with their monomer number according to eqn (7). Such IDPs cannot phase separate without additional attractive forces. A simple example is provided by telechelic polymers whose endcaps have an attractive self-interaction while both endcaps and backbone are solvophilic.102 Theory106,107 and computer simulations49,108–111 show that telechelic polymers phase separate into a reversible, heterogeneous physical gel.96 The presence of multiple binding sites on the IDPs here extends the range of affinity and molecular weight for which phase separation is observed, a robustness that may be important for cellular control of BCs with a varied composition.
We have explored this model of IDPs as polymers in good solvent conditions to understand those that do not contain a majority of hydrophobic residues (e.g., FUS-LC is almost uncharged and has only ∼25% hydrophobic residues). Our model is also applicable to the phase separation of uncharged, hydrophilic polymers possessing punctate sticky sites, and its extension to multicomponent systems is obvious.102,106,107,112 The observed dense phase has long-ranged, heterogeneous spatial structure (out to 10 monomer diameters) revealed by the radial distribution function of the binding sites (Fig. 5). We may contrast this with the results of Statt et al. who simulate IDPs as amphiphilic polymers composed of at least 60% hydrophobic beads using coarse-grained Molecular dynamics simulations.40 The radial distribution function of their dense phase shows no structure beyond 2–3 bead diameters indicating an homogeneous dense phase.
Perhaps surprisingly, we find that the IDPs are stretched in the dense phase. This swelling has been observed in other simulation techniques, suggesting it is a robust, emergent property.39,61,72 Weiner et al.61 found that the increase in conformational entropy of an IDP on moving into the dense phase was a crucial driver of phase separation. While an IDP in dilute phase must double back to gain binding enthalpy, it can bind to multiple junctions in the dense phase without looping, thereby gaining binding enthalpy and increasing its conformational entropy, Our results support their hypothesis that IDPs phase separate once their typical conformations in the dense phase are more extended than in the dilute phase (Fig. 4). We also find that they rarely span the same junctions more than once, which would imply binding to themselves (Table S1, ESI†).
Intriguingly, Weiner et al. observe that phase separation is weakened when there are many conformations of the single polymer whose intramolecular bonds stabilize the dilute phase.61 By contrast, we find that the dense phase forms when the probability of compact conformations of the single polymers increases (Fig. 4). The difference may originate in the backbone bending stiffness of k3 = 5kBT we impose on the polymers, while Weiner et al. have freely-jointed chain polymers. Conformational fluctuations on a short scale are substantially reduced in our model. We observed in a previous publication that telechelic polymers with zero bending stiffness found it hard to aggregate, and we included the bending stiffness in that and the present work to obviate this.49 This effect was also seen by Chatteraj et al. in Langevin dynamics simulations of surface-grafted polymers.113
We also observe that the distribution of IDPs in the dense phase changes with their distance from the surface. Although the junction spacing is insensitive to their location, the mean number of IDPs that bind to the junctions is reduced for junctions near the surface. This makes intuitive sense because those junctions are largely surrounded by solvent. This may affect the rate at which new molecules diffuse into the dense phase, and potentially also modify their conformational fluctuations at the surface of the condensate leading to an enhanced probability of their misfolding into amyloid shapes as observed recently.114 We point out here that a depth-dependent variation in the characteristic IDP conformations is also seen by Farag et al. in their Monte Carlo simulations of a similar stickers and spacers model of IDPs.46,72
We next explored how phase separation is affected by disabling a fraction of the binding sites (Fig. 6). A clear difference is found when sites distant from the polymer endcaps are disabled (dense phase swells and its concentration drops) compared to sites at the endcaps (dense phase dissolves.) Extrapolating our results to experimental IDPs, we predict that disabling interaction domains near their termini, by mutation or posttranslational modification, will destabilise the dense phase. But disabling domains within the IDPs is likely only to modulate the dense phase concentration. It is worth noting here that PTMs often cluster at the termini of IDPs. For example, FUS contains multiple PTM sites in its N-terminal prion-like domain (PLD) that are phosphorylated under stress conditions and reduce its tendency to undergo phase separation.115 Phosphomimetic alterations of the PLD also influence the transition of FUS granules into pathological solid phases, while leaving the dynamics in the fluid stress granules unaltered.116 The conformational flexibility of IDPs makes these terminal PTM sites easily accessible to diffusing species in the cytoplasm suggesting that regulation by diffusing kinases and phosphatases may be important for the function of FUS. Our results suggest that the reaction and diffusion of client proteins inside biomolecular condensates could by modulated by turning on or off appropriate interaction domains on their scaffold proteins, thereby modifying its porosity. It is instructive to compare these results to recent Monte Carlo simulations of Rana et al. whose model has a similar level of coarse-graining.66 An IDP is represented in their work as a sequence of (hydrophobic) sticker beads interspersed with (hydrophilic) spacer beads, in which at least 40% of the polymer sequence must be hydrophobic in order to observe phase separation. Rana et al. also find that the phase behaviour of their model is sensitive to the identity of the terminal beads, but their system changes from phase separated to aggregated clusters under the change of identity whereas we predict the dense phase should dissolve.
The simulated BCs maintain an heterogeneous junction mass distribution over time despite being a fluid, a result we first observed for the dense phase of telechelic polymers.49 We have quantified the magnitude of this inhomogeneity by measuring how the binding sites are distributed in the dense phase. By mapping the junctions to nodes of a graph, we used the clustering coefficient (CC) to measure the connectivity of the network and the weighted CC (wCC) for the junction mass distribution. Both the CC and the variance of the wCC (averaged over the dense phase) increase strongly with increasing binding site number, indicating a more heterogeneous, although still fluid phase (Fig. 8). It appears that the connectedness of the binding sites within the polymers, their backbone stiffness, and slow transport through the dense phase prevents all junctions from maintaining the same number of binding sites. Farag et al. also measured the clustering coefficient of the condensate in their Monte Carlo simulation model.72 But a detailed comparison of the two results is not simple. They mapped the IDP molecules to the nodes of a graph and placed edges between molecules that bind to each other, and found the resulting CC indicative of a small-world network. However, their graph combines the multiple binding sites of each IDP in one node of the graph, thereby losing their spatial separation. By contrast, we map the spatially-distributed junctions in the condensate to nodes and measure the resulting CC of the junctions. Each IDP can be represented by several nodes in this graph, because its binding sites can be on different junctions, and their spatial separation is preserved. This allows us to reveal the heterogeneous junction mass distribution and its dependence on binding site number (Fig. 8), affinity and separation (Fig. S13 and S14, ESI†). We find that the CC of the junctions is much larger than that of a random graph with the same number of nodes. We believe that further study is needed to resolve the question of the small-world nature of the connectedness in biomolecular condensates.
Fluid FUS-LC droplets have been observed to undergo an irreversible transition to a rigid fibrous state over several hours in vitro,34,117 and passive rheology experiments show that BCs undergo ageing and exhibit glassy behaviour.118 Condensates with material properties that range from liquid to solid have physiological roles in healthy cells,119 but can also facilitate pathological amyloid formation.31 Alpha synuclein (aSyn) fibrillisation is preceded by phase separation into dense fluid droplets, but the individual aSyn molecules are more rigid than in the dilute phase.120 The complexity of the electrostatic and hydrophobic domains in aSyn suggest that more complex forces are important in this case. On the other hand, small molecule drugs that harden biomolecular condensates can prevent RNA virus replication and provide novel therapeutic possibilities.121 We have constructed a novel measure (eqn (9)) to quantify the dynamics of polymer fluctuations within the dense phase, It reflects both the reversible binding/unbinding and diffusion of the IDPs, and shows that they exhibit multi-exponential decay in which both fast and slow relaxation processes are important (Fig. 11). The relaxation dynamics we find is independent of IDP concentration and not accompanied by stiffening of the network structure in the presence of more (weak) internal binding sites. The dense phase fluidity decreases with increasing affinity, but is reduced when the binding sites are more widely spaced. This supports the conjecture that biomolecular condensate structure can be tuned by switching on or off suitably located attractive residues, e.g., by posttranslational modification.115,122
Conclusions
The formation of biomolecular condensates via liquid–liquid phase separation (LLPS) of proteins has become a new paradigm within which to explain a wide range of phenomena in cellular physiology and pathology. But little solid information relating their material properties to their constituent IDPs is available, except for the primary sequence of the participating IDPs and the fact that under appropriate conditions they phase separate. Nevertheless, we can conclude based on the data that the widely-invoked explanation of LLPS based on the Flory-Huggins (FH) theory of polymer solutions fails for some IDPs, since they display good solvent properties in cytosol buffer conditions. Our work predicts that (uncharged, hydrophilic) IDPs with discrete attractive residues can phase separate into a heterogeneous dense phase that is stabilized by their ability to make multiple, fluctuating contacts. The IDPs swell on entering the dense phase, an effect seen in other simulation techniques, suggesting it is a robust, emergent property of weakly-interacting IDPs.61,72 The propensity of the dense phase to favour extended molecular conformations may explain observations that biomolecular condensates are protective against Aβ-42 misfolding into amyloid conformations.123 And its lower surface density might allow newly-adsorbed IDPs to sample more compact conformations, which may be relevant to experiments showing that formation of amyloid fibrils of hnRNPA12 is promoted at the boundary of condensates.114 The density variation in the condensate could also be important for segregating enzyme activity to distinct regions of BCs.98 We highlight some concrete suggestions for experimental testing of our predictions, and generalize our analysis to other fields.Although the model IDP binding sites do not represent specific residue–residue interactions, our finding that the dense phase structure is sensitive to their relative positions is interesting in the light of experimental observations that post-translational modification sites are often clustered along the disordered termini of IDPs.115 Our first prediction is that location and separation of interaction domains on phase-separating IDPs are key parameters for BC structure, but their precise affinity is not. We also find that the model IDPs can phase separate with binding endcaps in the absence of some internal binding sites, while the opposite does not hold. This could be experimentally tested by generating mutant IDPs, such as FUS, with segments of inert residues at the termini and observing their phase behaviour. A second prediction is that varying the spacing between attractive domains in IDPs modulates the heterogeneity of the dense phase. Small Angle Neutron Scattering (SANS) in conjunction with specific deuteration and contrast variation techniques is a promising tool to determine if the predicted scaling holds for experimental BCs.
Many IDPs possess multiple PTMs that can be modified by diffusing kinase/phosphatase species. A cell may use the action of these enzymes to adjust the separation and/or affinity of attractive residues.122 Steps towards computationally predicting how PTMs affect BC structure and dynamics have already been taken.124 Because enzyme diffusion would respond to changes in the heterogeneity of the condensate, this provides a level of feedback to regulate biochemical reactions or control condensate formation/dissolution.61 We have shown that the dense phase dynamics slows down on increasing the attraction between IDPs, and our third plea for experimental testing is to hasten measurements of dynamic properties of engineered BC phases. Fluorescence recovery after photobleaching could be used to test our prediction of the dependence of BC fluidity on binding domain strength.125 Single-particle tracking experiments that follow the diffusion of variously-sized fluorescent probes, or quantum dots, within the BC would probe the predicted porous nature of BCs.
Time-varying graphs are common in many fields, and the graph fluidity measure we introduce could be applied to bioinformatics networks, such as genome association in dynamic complex traits,126 metabolic networks,76 and be combined with molecular dynamics simulations of large flexible proteins to explore their allosteric properties.77,78 It may also be useful for studying the evolution of social networks,127,128 the emergence of a power-law distribution for the node degree and the process of rumour spreading,129,130 as well as transport and mobility networks, which typically involve shortest-path and trajectory prediction on time-varying graphs.131,132
In conclusion, our results connect the heterogeneous structure, material properties, and dynamics of model biomolecular condensates to the distribution of binding sites on their constituent IDPs. These relations may guide experimentalists in the design of synthetic BCs with tunable properties.133–135 Combined with the ability to modify the residue sequence of IDPs,64 and online tools to predict the effects of point mutations on local disorder and hydropathy of IDPs,136 this will undoubtedly reveal more fascinating mysteries in cellular use of BCs,137 and further our understanding of their pathological transitions in disease.138
Author contributions
J. C. Shillcock, conceptualization, methodology, software, validation, formal analysis, data curation, visualization, writing – original draft, writing – review and editing; C. Lagisquet, software, validation, data curation, visualization, writing – review and editing; J. Alexandre, software, validation, formal analysis, writing – review and editing. L. Vuillon, software, validation, formal analysis, resources, writing – review and editing, Funding acquisition, project administration. J. H. Ipsen, conceptualization, methodology, resources, writing – review and editing, project administration.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This study was supported by funding to the Blue Brain Project, a research centre of the École polytechnique fédérale de Lausanne (EPFL), from the Swiss government's ETH Board of the Swiss Federal Institutes of Technology, and the 80PRIME MITI CNRS programme. The authors gratefully acknowledge computer time provided by the Blue Brain Project and Swiss National Supercomputing Centre and the Abacus 2.0 Supercomputing cluster at the University of Southern Denmark. The Dissipative Particle Dynamics simulation source code used in this work is available on GitHub.81 Custom python code written for the data analysis includes algorithms from the open-source libraries scikit-learn (https://scikit-learn.org/stable/) and networkx (https://networkx.org). The graph analysis code is available on GitHub (https://github.com/clagis/droplets). The authors express their gratitude to M. Brochut and E. Chénais who wrote the analysis code for ref. 49, which was also used here, and to W. Pezeshkian for scripts to generate VMD format files. Snapshots and movies of simulated networks were produced using the open-source VMD software from the University of Illinois Urbana Champaign (http://www.ks.uiuc.edu/Research/vmd).139References
- J. Z. Zhang, S. Mehta and J. Zhang, Liquid–liquid phase separation: a principal organizer of the cell's biochemical activity architecture, Trends Pharmacol. Sci., 2021, 42(10), 845–856 CrossRef CAS PubMed.
- A. S. Holehouse and R. V. Pappu, Functional Implications of Intracellular Phase Transitions, Biochemistry, 2018, 57, 2415–2423 CrossRef CAS PubMed.
- A. S. Lyon, W. B. Peeples and M. K. Rosen, A framework for understanding the functions of biomolecular condensates across scales, Nat. Rev. Mol. Cell Biol., 2021, 22(3), 215–235 CrossRef CAS PubMed.
- S. F. Banani, H. O. Lee, A. A. Hyman and M. K. Rosen, Biomolecular Condensates: Organizers of Cellular Biochemistry, Nat. Rev. Mol. Cell Biol., 2017, 18, 285–298 CrossRef CAS PubMed.
- W. Stroberg and S. Schnell, Do Cellular Condensates Accelerate Biochemical Reactions? Lessons from Microdroplet Chemistry, Biophys. J., 2018, 115, 3–8 CrossRef CAS PubMed.
- E. Seif, J. J. Kang, C. Sasseville, O. Senkovich, A. Kaltashov and E. L. Boulier, et al., Phase separation by the polyhomeotic sterile alpha motif compartmentalizes Polycomb Group proteins and enhances their activity, Nat. Commun., 2020, 11, 5609 CrossRef CAS PubMed.
- Y. Zhang, G. J. Narlikar and T. G. Kutateladze, Enzymatic Reactions inside Biological Condensates, J. Mol. Biol., 2021, 433(12), 166624 CrossRef CAS PubMed.
- B. Saha, A. Chatterjee, A. Reja and D. Das, Condensates of short peptides and ATP for the temporal regulation of cytochrome c activity, Chem. Commun., 2019, 55, 14194–14197 RSC.
- M. Dzuricky, B. A. Rogers, A. Shahid, P. S. Cremer and A. Chilkoti, De novo engineering of intracellular condensates using artificial disordered proteins, Nat. Chem., 2020, 12(9), 814–825 CrossRef CAS PubMed.
- M. Heidenreich, J. M. Georgeson, E. Locatelli, L. Rovigatti, S. K. Nandi and A. Steinberg, et al., Designer protein assemblies with tunable phase diagrams in living cells, Nat. Chem. Biol., 2020, 16, 939–945 CrossRef CAS PubMed.
- D. Deviri and S. A. Safran, Physical theory of biological noise buffering by multicomponent phase separation, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(25), e2100099118 CrossRef CAS PubMed.
- A. Klosin, F. Oltsch, T. Harmon, A. Honigmann, F. Jülicher and A. A. Hyman, et al., Phase separation provides a mechanism to reduce noise in cells, Science, 2020, 367(6476), 464–468 CrossRef CAS PubMed.
- I. de Curtis, Biomolecular Condensates at the Front: Cell Migration Meets Phase Separation, Trends Cell Biol., 2021, 31(3), 145–148 CrossRef CAS PubMed.
- D. Milovanovic, Y. Wu, X. Bian and P. D. Camilli, A Liquid Phase of Synapsin and Lipid Vesicles, Science, 2018, 361, 604–607 CrossRef CAS PubMed.
- C. Hoffmann, R. Sansevrino, G. Morabito, C. Logan, R. M. Vabulas and A. Ulusoy, et al., Synapsin Condensates Recruit alpha-Synuclein, J. Mol. Biol., 2021, 433(12), 166961 CrossRef CAS PubMed.
- M. Zeng, X. Chen, D. Guan, J. Xu, H. Wu and P. Tong, et al., Reconstituted Postsynaptic Density as a Molecular Patform for Understanding Synapse Formation and Plasticity, Cell, 2018, 174, 1172–1187 CrossRef CAS PubMed.
- X. Wu, Q. Cai, Z. Feng and M. Zhang, Liquid–Liquid Phase Separation in Neuronal Development and Synaptic Signaling, Dev. Cell, 2020, 55(1), 18–29 CrossRef CAS PubMed.
- S. Ray, N. Singh, S. Pandey, R. Kumar, L. Gadhe and D. Datta, et al., Liquid–liquid phase separation and liquid-to-solid transition mediate alpha-synuclein amyloid fibril containing hydrogel formation, bioRxiv Preprint, 2019, 1–40 Search PubMed.
- N. B. Nedelsky and J. P. Taylor, Bridging biophysics and neurology: aberrant phase transitions in neurodegenerative disease, Nat. Rev. Neurol., 2019, 15(5), 272–286 CrossRef PubMed.
- Y. Zhou, J. M. Su, C. E. Samuel and D. Ma, Measles Virus Forms Inclusion Bodies with Properties of Liquid Organelles, J. Virol., 2019, 93(21), e00948–19 CrossRef CAS PubMed.
- I. Seim, C. A. Roden and A. S. Gladfelter, Role of spatial patterning of N-protein interactions in SARS-CoV-2 genome packaging, Biophys. J., 2021, 120(14), 2771–2784 CrossRef CAS PubMed.
- J. Söding, D. Zwicker, S. Sohrabi-Jahromi, M. Boehning and J. Kirschbaum, Mechanisms for Active Regulation of Biomolecular Condensates, Trends Cell Biol., 2020, 30(1), 4–14 CrossRef PubMed.
- A. Abyzov, M. Blackledge and M. Zweckstetter, Conformational Dynamics of Intrinsically Disordered Proteins Regulate Biomolecular Condensate Chemistry, Chem. Rev., 2022, 122, 6719–6748 CrossRef CAS PubMed.
- M. Biesaga, M. Frigolé-Vivas and X. Salvatella, Intrinsically disordered proteins and biomolecular condensates as drug targets, Curr. Opin. Chem. Biol., 2021, 62, 90–100 CrossRef CAS PubMed.
- S. Spanni, M. Tereshchenko, G. J. Mastromarco, S. J. Ihn and H. O. Lee, Biomolecular condensates in neurodegeneration and cancer, Traffic, 2019, 20, 890–911 CrossRef PubMed.
- S. Jiang, J. B. Fagman, C. Chen, S. Alberti and B. Liu, Protein phase separation and its role in tumorigenesis, eLife, 2020, 9, e60264 CrossRef CAS PubMed.
- D. Cai, Z. Liu and J. Lippincott-Schwartz, Biomolecular Condensates and Their Links to Cancer Progression, Trends Biochem. Sci., 2021, 46(7), 535–549 CrossRef CAS PubMed.
- K. Taniue and N. Akimitsu, Aberrant phase separation and cancer, FEBS J., 2021, 289, 17–39 CrossRef PubMed.
- S. Alberti and A. A. Hyman, Are Aberrant Phase Transitions a Driver of Cellular Aging?, BioEssays, 2016, 38, 959–968 CrossRef CAS PubMed.
- J. D. Schmit, J. J. Bouchard, E. W. Martin and T. Mittag, Protein Network Structure Enables Switching between Liquid and Gel States, J. Am. Chem. Soc., 2020, 142(2), 874–883 CrossRef CAS PubMed.
- S. Ranganathan and E. Shakhnovich, The physics of liquid-to-solid transitions in multi-domain protein condensates, Biophys. J., 2022 DOI:10.1016/j.bpj.2022.06.013.
- T. R. Peskett, F. Rau, J. O’Driscoll, R. Patani, A. R. Lowe and H. R. Saibil, A Liquid To Solid Phase Transition Underlying Pathological Huntingtin Exon1 Aggregation, Mol. Cell, 2018, 70, 588–601 CrossRef CAS PubMed.
- N. Riguet, A.-L. Mahul-Mellier, N. Maharjan, J. Burtscher, M. Croisier and G. Knott, et al., Nuclear and cytoplasmic huntingtin inclusions exhibit distinct biochemical composition, interactome and ultrastructural properties, Nat. Commun., 2021, 12(1), 6579 CrossRef CAS PubMed.
- A. Patel, H. O. Lee, L. Jawerth, S. Maharana, M. Jahnel and M. Y. Hein, et al., A Liquid-to-Solid Phase Transition of the ALS Protein FUS Accelerated By Disease Mutation, Cell, 2015, 162, 1066–1077 CrossRef CAS PubMed.
- A. C. Murthy, G. L. Dignon, Y. Kan, G. H. Zerze, S. H. Parekh and J. Mittal, et al., Molecular Interactions Underlying Liquid–Liquid Phase Separation of the FUS Low-Complexity Domain, Nat. Struct. Mol. Biol., 2019, 26, 637–648 CrossRef CAS PubMed.
- B. A. Gibson, L. K. Doolittle, M. W. G. Schneider, L. E. Jensen, N. Gamarra and L. Henry, et al., Organization of Chromatin by intrinsic and Regulated Phase Separation, Cell, 2019, 179, 470–484 CrossRef CAS PubMed.
- Y. Shin, Y.-C. Chang, D. S. W. Lee, J. Berry, D. W. Sanders and P. Ronceray, et al., Liquid Nuclear Condensates Mechanically Sense and Restructure the Genome, Cell, 2018, 175, 1481–1491 CrossRef CAS PubMed.
- M. Mir, W. Bickmore, E. E. M. Furlong and G. Narlika, Chromatin topology, condensates and gene regulation: shifting paradigms or just a phase?, Development, 2019, 146(19), dev182766 CrossRef CAS PubMed.
- G. L. Dignon, W. Zheng, Y. C. Kim, R. B. Best and J. Mittal, Sequence Determinants of Protein Phase Behavior from a Coarse-Grained Model, PLoS Comput. Biol., 2018, 14, e1005941 CrossRef PubMed.
- A. Statt, H. Casademunt, C. P. Brangwynne and A. Z. Panagiotopoulos, Model for disordered proteins with strongly sequence-dependent liquid phase behaviour, J. Chem. Phys., 2020, 152, 075101 CrossRef CAS PubMed.
- B. Wang, L. Zhang, T. Dai, Z. Qin, H. Lu and L. Zhang, et al., Liquid–liquid phase separation in human health and diseases, Signal Transduction Targeted Ther., 2021, 6(1), 290 CrossRef PubMed.
- V. N. Uversky, Intrinsically Disordered Proteins and Their Mysterious (Meta)Physics, Front. Phys., 2019, 7, 10 CrossRef.
- I. Peran and T. Mittag, Molecular structure in biomolecular condensates, Curr. Opin. Struct. Biol., 2020, 60, 17–26 CrossRef CAS PubMed.
- K. Bhandari, M. A. Cotten, J. Kim, M. K. Rosen and J. D. Schmit, Structure–Function Properties in Disordered Condensates. The, J. Phys. Chem. B, 2021, 125(1), 467–476 CrossRef CAS PubMed.
- F. Orti, A. M. Navarro, A. Rabinovich, S. J. Wodak and C. Marino-Buslje, Insight into membraneless organelles and their associated proteins: Drivers, Clients and Regulators, Comput. Struct. Biotechnol. J., 2021, 19, 3964–3977 CrossRef CAS PubMed.
- J.-M. Choi, F. Dar and R. Pappu, LASSI: A lattice model for simulating phase transitions of multivalent proteins, PLoS Comput. Biol., 2019, 15, e1007028 CrossRef CAS PubMed.
- T. S. Harmon, A. S. Holehouse, M. K. Rosen and R. V. Pappu, Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins, eLife, 2017, 6, e30294 CrossRef PubMed.
- H. Jafarinia, E. Van der Giessen and P. R. Onck, Phase Separation of Toxic Dipeptide Repeat Proteins Related to C9orf72 ALS/FTD, Biophys. J., 2020, 119, 843–851 CrossRef CAS PubMed.
- J. C. Shillcock, M. Brochut, E. Chénais and J. H. Ipsen, Phase behaviour and structure of a model biomolecular condensate, Soft Matter, 2020, 16(27), 6413–6423 RSC.
- M. Paloni, R. Bailly, L. Ciandrini and A. Barducci, Unraveling Molecular Interactions in Liquid–Liquid Phase Separation of Disordered Proteins by Atomistic Simulations, J. Phys. Chem. B, 2020, 124, 9009–9016 CrossRef CAS PubMed.
- W. Zheng, G. L. Dignon, N. Jovic, X. Xu, R. M. Regy and N. L. Fawzi, et al., Molecular Details of Protein Condensates Probed by Microsecond Long Atomistic Simulations, J. Phys. Chem. B, 2020, 124, 11671–11679 CrossRef CAS PubMed.
- G. L. Dignon, W. Zheng and J. Mittal, Simulation methods for liquid–liquid phase separation of disorded proteins. Curr Op, Chem. Eng., 2019, 23, 92–98 Search PubMed.
- A. E. Hafner, J. Krausser and A. Saric, Minimal coarse-grained models for molecular self-organisation in biology, Curr. Opin. Struct. Biol., 2019, 58, 43–52 CrossRef CAS PubMed.
- J. A. Joseph, A. Reinhardt, A. Aguirre, P. Y. Chew, K. O. Russell and J. R. Espinosa, et al., Physics-driven coarse-grained model for biomolecular phase separation with near-quantitative accuracy. Nature Computational, Science, 2021, 1(11), 732–743 Search PubMed.
- Z. Benayad, S. von Bülow, L. S. Stelzl and G. Hummer, Simulation of FUS Protein Condensates with an Adapted Coarse-Grained Model, J. Chem. Theory Comput., 2021, 17, 525–537 CrossRef CAS PubMed.
- K. J. Bari and D. D. Prakashchand, Fundamental Challenges and Outlook in Simulating Liquid–Liquid Phase Separation of Intrinsically Disordered Proteins, J. Phys. Chem. Lett., 2021, 12(6), 1644–1656 CrossRef CAS PubMed.
- M. Tsanai, W. J. M. Frederix Pim, C. F. E. Schroer, P. C. T. Souza and S. J. Marrink, Coacervate formation studied by explicit solvent coarse-grain molecular dynamics with the Martini model, Chem. Sci., 2021, 12(24), 8521–8530 RSC.
- J. A. Joseph, J. R. Espinosa, I. Sanchez-Burgos, A. Garaizar, D. Frenkel and R. Collepardo-Guevara, Thermodynamics and kinetics of phase separation of protein-RNA mixtures by a minimal model, Biophys. J., 2021, 120(7), 1219–1230 CrossRef CAS PubMed.
- S. Ranganathan and E. Shakhnovich, Effect of RNA on Morphology and Dynamics of Membraneless Organelles. The, J. Phys. Chem. B, 2021, 125(19), 5035–5044 CrossRef CAS PubMed.
- G. Tesei, K. Schulze Thea, R. Crehuet and K. Lindorff-Larsen, Accurate model of liquid–liquid phase behavior of intrinsically disordered proteins from optimization of single-chain properties, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(44), e2111696118 CrossRef CAS PubMed.
- B. G. Weiner, A. G. T. Pyo, Y. Meir and N. S. Wingreen, Motif-pattern dependence of biomolecular phase separation driven by specific interactions, PLoS Comput. Biol., 2022, 17(12), e1009748 CrossRef PubMed.
- K. M. Ruff, R. V. Pappu and A. S. Holehouse, Conformational Preferences and Phase Behaviour of Intrinsically Disordered Low Complexity Sequences: Insights from Multiscale Simulations, Curr. Opin. Struct. Biol., 2019, 56, 1–10 CrossRef CAS PubMed.
- J.-M. Choi, A. S. Holehouse and R. V. Pappu, Physical Principles Underlying the Complex Biology of Intracellular Phase Transitions, Annu. Rev. Biophys., 2020, 49(1), 107–133 CrossRef CAS PubMed.
- J. Wang, J.-M. Choi, A. S. Holehouse, H. O. Lee, X. Zhang and M. Jahnel, et al., A Molecular Grammar Governing the Driving Forces for Phase Separation of Prion-like RNA Binding Proteins, Cell, 2018, 174(3), 688–699.e16 CrossRef CAS PubMed.
- T. S. Harmon, A. S. Holehouse and R. V. Pappu, Differential Solvation of Intrinsically Disordered Linkers Drives the Formation of Spatially Organised Droplets in Ternary Systems of Linear Multivalent Proteins, New J. Phys., 2018, 20, 045002 CrossRef.
- U. Rana, C. P. Brangwynne and A. Z. Panagiotopoulos, Phase separation vs. aggregation behavior for model disordered proteins, J. Chem. Phys., 2021, 155(12), 125101 CrossRef CAS PubMed.
- Z. Zhang, Q. Chen and R. H. Colby, Dynamics of associative polymers, Soft Matter, 2018, 14(16), 2961–2977 RSC.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- R. D. Groot and P. B. Warren, Dissipative Particle Dynamics: Bridging the Gap Between Atomistic and Mesoscopic Simulations, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- K. A. Burke, A. M. Janke, C. L. Rhine and N. L. Fawzi, Residue-by-Residue View of In Vitro FUS Granules that Bind the C-Terminal Domain of RNA Polymerase II, Mol. Cell, 2015, 60, 231–241 CrossRef CAS PubMed.
- J. Ahlers, E. M. Adams, V. Bader, S. Pezzotti, K. F. Winklhofer and J. Tatzelt, et al., The key role of solvent in condensation: Mapping water in liquid–liquid phase-separated FUS, Biophys. J., 2021, 120(7), 1266–1275 CrossRef CAS PubMed.
- M. Farag, S. R. Cohen, W. M. Borcherds, A. Bremer, T. Mittag and R. V. Pappu, Condensates of disordered proteins have small-world network structures and interfaces defined by expanded conformations, bioRxiv, 2022 DOI:10.1101/2022.05.21.492916.
- D. M. Mitrea, J. A. Cika, C. S. Guy, D. Ban, P. R. Banerjee and C. B. Stanley, et al., Nucleophosmin integrates within the nucleolus via multi-modal interactions with proteins displaying R-rich linear motifs and rRNA, eLife, 2016, 5, e13571 CrossRef PubMed.
- A.-L. Barabási, Network Science, Cambridge University Press, 2016 Search PubMed.
- M. E. J. Newman, The Structure and Function of Complex Networks, SIAM Rev., 2003, 45(2), 167–256 CrossRef.
- J. Laniau, C. Frioux, J. Nicolas, C. Baroukh, M. P. Cortes and J. Got, et al., Combining graph and flux-based structures to decipher phenotypic essential metabolites within metabolic networks, PeerJ, 2017, 5, e3860 CrossRef PubMed.
- A. Gheeraert, L. Pacini, V. S. Batista, L. Vuillon, C. Lesieur and I. Rivalta, Exploring Allosteric Pathways of a V-Type Enzyme with Dynamical Perturbation Networks, J. Phys. Chem. B, 2019, 123(16), 3452–3461 CrossRef CAS PubMed.
- R. Dorantes-Gilardi, L. Bourgeat, L. Pacini, L. Vuillon and C. Lesieur, In proteins, the structural responses of a position to mutation rely on the Goldilocks principle: not too many links, not too few, Phys. Chem. Chem. Phys., 2018, 20(39), 25399–25410 RSC.
- D. J. Watts and S. H. Strogatz, Collective dynamics of 'small-world' networks, Nature, 1998, 393(6684), 440–442 CrossRef CAS PubMed.
- J. Saramäki, M. Kivelä, J.-P. Onnela, K. Kaski and J. Kertész, Generalizations of the clustering coefficient to weighted complex networks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75(2), 027105 CrossRef PubMed.
- J. C. Shillcock, OSPREY-DPD. Open Source Polymer Research Engine - Dissipative Particle Dynamics, 2020, https://github.com/Osprey-DPD/osprey-dpd.
- J. Shillcock and R. Lipowsky, Equilibrium structure and lateral stress distribution of amphiphilic bilayers from dissipative particle dynamics simulations, J. Chem. Phys., 2002, 117(10), 5048–5061 CrossRef CAS.
- M. Venturoli, M. M. Sperotto, M. Kranenburg and B. Smit, Mesoscopic Models of Biological Membranes, Phys. Rep., 2006, 437, 1–54 CrossRef CAS.
- V. Ortiz, S. Nielsen, D. Discher, M. Klein, R. Lipowsky and J. Shillcock, Dissipative particle dynamics simulations of polymersomes, J. Phys. Chem. B, 2005, 109(37), 17708–17714 CrossRef CAS PubMed.
- A. Grafmueller, J. Shillcock and R. Lipowsky, The Fusion of Membranes and Vesicles: Pathway and Energy Barriers from Dissipative Particle Dynamics, Biophys. J., 2009, 96(7), 2658–2675 CrossRef CAS PubMed.
- R. Lipowsky, M. Brinkmann, R. Dimova, C. Haluska and J. Kierfeld, Shillcock J. Wetting, budding, and fusion—morphological transitions of soft surfaces, J. Phys.: Condens. Matter, 2005, 17(31), S2885–S2902 CrossRef CAS.
- M. Laradji and P. B. Sunil Kumar, Domain growth, budding, and fission in phase-separating self-assembled fluid bilayers, J. Chem. Phys., 2005, 123(22), 224902 CrossRef PubMed.
- P. Espagnol and P. B. Warren, Perspective: Dissipative Particle Dynamics, J. Chem. Phys., 2017, 146, 150901 CrossRef PubMed.
- J. M. Ilnytskyi and Y. Holovatch, How does the scaling for the polymer chain in the dissipative particle dynamics hold?, Condens. Matter Phys., 2007, 10, 539–551 CrossRef.
- A. S. Holehouse, G. M. Ginell, D. Griffith and E. Böke, Clustering of Aromatic Residues in Prion-like Domains Can Tune the Formation, State, and Organization of Biomolecular Condensates, Biochemistry, 2021, 60(47), 3566–3581 CrossRef CAS PubMed.
- W. Martin Erik, S. Holehouse Alex, I. Peran, M. Farag, J. J. Incicco and A. Bremer, et al., Valence and patterning of aromatic residues determine the phase behavior of prion-like domains, Science, 2020, 367(6478), 694–699 CrossRef CAS PubMed.
- C. Chen, X. Ding, N. Akram, S. Xue and S.-Z. Luo, Fused in Sarcoma: Properties, Self-Assembly and Correlation with Neurodegenerative Diseases, Molecules, 2019, 24, 1622–1639 CrossRef CAS PubMed.
- A. C. Murthy, W. S. Tang, N. Jovic, A. M. Janke, D. H. Seo and T. M. Perdikari, et al., Molecular interactions contributing to FUS SYGQ LC-RGG phase separation and co-partitioning with RNA polymerase II heptads, Nat. Struct. Mol. Biol., 2021, 28(11), 923–935 CrossRef CAS PubMed.
- M. E. Tomasso, M. J. Tarver, D. Devarajan and S. T. Whitten, Hydrodynamic radii of Intrinsically Disordered Proteins Determined from Experimental Polyproline II Propensities, PLoS Comput. Biol., 2015, 12, 1–22 Search PubMed.
- J. A. Marsh and J. D. Forman-Kay, Sequence Determinants of Compaction in Intrinsically Disordered Proteins, Biophys. J., 2010, 98, 2383–2390 CrossRef CAS PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics. New York: Oxford University Press, 2003 Search PubMed.
- B. Dünweg, D. Reith, M. Steinhauser and K. Kremer, Corrections to scaling in the hydrodynamic properties of dilute polymer solutions, J. Chem. Phys., 2002, 117(2), 914–924 CrossRef.
- B. G. O'Flynn and T. Mittag, The role of liquid–liquid phase separation in regulating enzyme activity, Curr. Opin. Cell Biol., 2021, 69, 70–79 CrossRef PubMed.
- Y. Wang, E. Ghumare, R. Vandenberghe and P. Dupont, Comparison of Different Generalizations of Clustering Coefficient and Local Efficiency for Weighted Undirected Graphs, Neural Comput., 2017, 29(2), 313–331 CrossRef PubMed.
- J.-P. Onnela, J. Saramäki, J. Kertész and K. Kaski, Intensity and coherence of motifs in weighted complex networks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71(6), 065103 CrossRef PubMed.
- S. Elbaum-Garfinkle, Y. Kim, K. Szczepaniak, C. C.-H. Chen, C. R. Eckmann and S. Myong, et al., The disordered P granule protein LAF-1 drives phase separation into droplets with tunable viscosity and dynamics, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(23), 7189 CrossRef CAS PubMed.
- M. Rubinstein and A. V. Dobrynin, Solutions of Associative Polymers, TRIP, 1997, 5, 181–186 CAS.
- T. A. Witten, Structured Fluids, Phys. Today, 1990, 43(7), 21–28 CrossRef.
- M. Rubinstein and A. V. Dobrynin, Solutions of Associative Polymers, Trends Polym. Sci., 1997, 5(6), 181–186 CAS.
- C. P. Brangwynne, P. Tompa and R. V. Pappu, Polymer Physics of Intracellular Phase Transitions, Nat. Phys., 2015, 11, 899–904 Search PubMed.
- A. Zilman, T. Tlusty and S. A. Safran, Entropic networks in colloidal, polymeric and amphiphilic systems, J. Phys.: Condens. Matter, 2002, 15(1), S57–S64 CrossRef.
- J. Dudowicz and K. F. Freed, Lattice cluster theory of associating polymers. I. Solutions of linear telechelic polymer chains, J. Chem. Phys., 2012, 136(6), 064902 CrossRef PubMed.
- A. V. Dobrynin, Phase Diagram of Solutions of Associative Polymers, Macromolecules, 2004, 37(10), 3881–3893 CrossRef CAS.
- J. Bergsma, F. A. M. Leermakers, J. M. Kleijn and J. van der Gucht, A Hybrid Monte Carlo Self-Consistent Field Model of Physical Gels of Telechelic Polymers, J. Chem. Theory Comput., 2018, 14(12), 6532–6543 CrossRef CAS PubMed.
- N. Arai, Structural Analysis of Telechelic Polymer Solution Using Dissipative Particle Dynamics Simulations, Mol. Sim., 2015, 41, 996–1001 CrossRef CAS.
- C. Manassero, G. Raos and G. Allegra, Structure of Model Telechelic Polymer Melts by Computer Simulation, J. Macromol. Sci., Part B: Phys., 2005, 44, 855–871 CrossRef CAS.
- A. S. Holehouse and R. V. Pappu, Collapse Transitions of Proteins and the Interplay Among Backbone, Sidechain, and Solvent Interactions, Annu. Rev. Biophys., 2018, 47, 19–39 CrossRef CAS PubMed.
- A. Chatteraj, M. Youngstrom and L. M. Loew, The Interplay of Structural and Cellular Biophysics Controls Clustering of Multivalent Molecules, Biophys. J., 2019, 116, 560–572 CrossRef PubMed.
- M. Linsenmeier, L. Faltova, U. C. Palmiero, C. Seiffert, A. M. Küffner and D. Pinotsi, et al., The interface of condensates of the hnRNPA1 low complexity domain promotes formation of amyloid fibrils, bioRxiv, 2022 DOI:10.1101/2022.05.23.493075.
- A. Bratek-Skicki, R. Pancsa, B. Meszaros, J. Van Lindt and P. Tompa, A guide to regulation of the formation of biomolecular condensates, FEBS J., 2020, 287(10), 1924–1935 CrossRef CAS PubMed.
- I. Owen, S. Rhoades, D. Yee, H. Wyne, K. Gery and I. Hannula, et al., The prion-like domain of Fused in Sarcoma is phosphorylated by multiple kinases affecting liquid– and solid–liquid phase transitions, Mol. Biol. Cell, 2020, 31, 2522–2536 CrossRef CAS PubMed.
- T. Murakami, S. Qamar, J. Q. Lin, G. S. K. Schierle, E. Rees and A. Miyashita, et al., ALS/FTD Mutation-Induced Phase Transition of FUS Liquid Droplets and Reversible Hydrogels into Irreversible Hydrogels Impairs RNP Granule Function, Neuron, 2015, 88, 678–690 CrossRef CAS PubMed.
- L. Jawerth, E. Fischer-Friedrich, S. Saha, J. Wang, T. Franzmann and X. Zhang, et al., Protein condensates as aging Maxwell fluids, Science, 2020, 370(6522), 1317–1323 CrossRef CAS PubMed.
- J. B. Woodruff, A. A. Hyman and E. Boke, Organization and Function of Non-dynamic Biomolecular Condensates, Trends Biochem. Sci., 2018, 43(2), 81–94 CrossRef CAS PubMed.
- S. Ray, N. Singh, R. Kumar, K. Patel, S. Pandey and D. Datta, et al., Synuclein aggregation nucleates through liquid–liquid phase separation, Nat. Chem., 2020, 12(8), 705–716 CrossRef CAS PubMed.
- J. Risso-Ballester, M. Galloux, J. Cao, R. Le Goffic, F. Hontonnou and A. Jobart-Malfait, et al., A condensate-hardening drug blocks RSV replication in vivo, Nature, 2021, 595, 596–599 CrossRef CAS PubMed.
- M. Hofweber and D. Dormann, Friend or foe—Post-translational modifications as regulators of phase separation and RNP granule dynamics, J. Biol. Chem., 2019, 294(18), 7137–7150 CrossRef CAS PubMed.
- A. M. Küffner, M. Linsenmeier, F. Grigolato, M. Prodan, R. Zuccarini and U. Capasso Palmiero, et al., Sequestration within biomolecular condensates inhibits Aβ-42 amyloid formation, Chem. Sci., 2021, 12(12), 4373–4382 RSC.
- T. M. Perdikari, N. Jovic, G. L. Dignon, Y. C. Kim, N. L. Fawzi and J. Mittal, A predictive coarse-grained model for position-specific effects of post-translational modifications, Biophys. J., 2021, 120(7), 1187–1197 CrossRef CAS PubMed.
- N. O. Taylor, M. T. Wei, H. A. Stone and C. P. Brangwynne, Quantifying Dynamics in Phase-Separated Condensates Using Fluorescence Recovery after Photobleaching, Biophys. J., 2019, 117(7), 1285–1300 CrossRef CAS PubMed.
- M. Marchetti-Bowick, J. Yin, J. A. Howrylak and E. P. Xing, A time-varying group sparse additive model for genome-wide association studies of dynamic complex traits, Bioinformatics, 2016, 32(19), 2903–2910 CrossRef CAS PubMed.
- M. Latapy, T. Viard and C. Magnien, Stream graphs and link streams for the modeling of interactions over time, Soc. Netw. Anal. Min., 2018, 8(1), 61 CrossRef.
- M. Latapy, L. Tabourier and T. Armoux, Predicting interactions between Individuals with structural and dynamical information, Journal of Interdisciplinary Methodologies and Issues in Sciences, 2019, 5, 1–26 Search PubMed.
- X. Qiu, L. Zhao, J. Wang, X. Wang and Q. Wang, Effects of time-dependent diffusion behaviors on the rumor spreading in social networks, Phys. Lett. A, 2016, 380(24), 2054–2063 CrossRef CAS.
- A. Moinet and M. Starnini, Pastor-Satorras R. Burstiness and Aging in Social Temporal Networks, Phys. Rev. Lett., 2015, 114(10), 108701 CrossRef PubMed.
- A. Idri, M. Oukarfi, A. Boulmakoul, K. Zeitouni and A. Masri, A new time-dependent shortest path algorithm for multimodal transportation network, Proc. Comput. Sci., 2017, 109, 692–697 CrossRef.
- H. Girase, H. Gang, S. Malla, J. Li, A. Kanehara and K. Mangalam, et al., LOKI: Long Term and Key Intentions for Trajectory Prediction, IEEE/CVF International Conference on Computer Vision, 11–17 October 2021, Online 2021, pp. 9803–9812.
- D. Bracha, M. T. Walls and C. P. Brangwynne, Probing and engineering liquid-phase organelles, Nat. Biotechnol., 2019, 37(12), 1435–1445 CrossRef CAS PubMed.
- S. Elbaum-Garfinkle and R. W. Kriwacki, Phase Separation in Biology & Disease: The next chapter, J. Mol. Biol., 2021, 433(12), 166990 CrossRef CAS PubMed.
- R. L. Hastings and S. Boeynaems, Designer Condensates: A Toolkit for the Biomolecular Architect, J. Mol. Biol., 2021, 433(12), 166837 CrossRef CAS PubMed.
- R. Lohia, M. Hansen and G. Brannigan, Contiguously hydrophobic sequences are functionally significant throughout the human exome, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2116267119 CrossRef CAS PubMed.
- M. V. Garabedian, W. Wang, J. B. Dabdoub, M. Tong, R. M. Caldwell and W. Benman, et al., Designer membraneless organelles sequester native factors for control of cell behavior, Nat. Chem. Biol., 2021, 17, 998–1007 CrossRef CAS PubMed.
- J. Wheeler R, Therapeutics - how to treat phase separation-associated diseases, Emerging Top. Life Sci., 2020, 4, 331–342 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD - Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Technical details of the graph theoretic measures used, supporting results for condensed networks of polymers with a range of backbone lengths and endcap affinities; data showing that the dense phase concentration is independent of the system size, and that it is highly solvated. Movies of the networks under different conditions are also provided. Movie M1: Equilibrium fluctuations of 315 polymers of type 6B6 with ε = 0.84. Movie M2: Equilibrium fluctuations of 309 polymers of type 6B10 with ε = 0.84. Movie M3: Equilibrium fluctuations of 315 polymers of type 6B6 with ε = 0.74. Movie M4: Equilibrium fluctuations of 190 polymers of type 6B10 with ε = 0.74. Movie M5: Equilibrium fluctuations of 254 polymers of type 6B6 with ε = 0.68. Movie M6: Fusion of droplets each containing 763 polymers of type 2B8 with ε = 0.76. Movie M7: Single polymer of type 6B6 (left) and 6B10 (right) with ε = 0.84 in solvent. Movie M8: Droplet of 316 polymers of type 6B6 and ε = 0.84 with two coloured to follow their fluctuations in the dense phase. See DOI: https://doi.org/10.1039/d2sm00387b |
| ‡ Current address: Aktiia SA, Rue du Bassin 8a, 2000 Neuchâtel, Switzerland. |
| This journal is © The Royal Society of Chemistry 2022 |