DOI:
10.1039/D2SM00731B
(Paper)
Soft Matter, 2022,
18, 6582-6591
Force-driven active dynamics of thin nanorods in unentangled polymer melts†
Received
2nd June 2022
, Accepted 6th August 2022
First published on 8th August 2022
Abstract
Recent advances in the functional material and biomedical applications of nanorods call for a fundamental understanding of the active motion of nanorods in a viscoelastic medium. Molecular dynamics simulations are performed to investigate a model system consisting of force-driven active thin nanorods in a melt of unentangled polymers. The activeness of a thin nanorod arises from a constant external force applied uniformly along the rod. The simulations demonstrate that the active force overcomes the randomness of the diffusive motion and results in a ballistic motion along the direction of the applied force at long timescales. The constant speed of the force-driven ballistic motion is determined by the balance of the active force and the friction from the coupling of the nanorod with the polymer viscosity. The friction coefficient, which is computed as the ratio of the active force and the speed, decreases as the active force increases. The origin of the reduction in the friction coefficient is the high speed that allows the nanorod to renew its local environment faster than the relaxation time of melt chains. A scaling theory is developed to quantify the dependence of the friction coefficient on the strength of the active force. The simulations also demonstrate that the force-driven ballistic motion suppresses the rotational diffusion of the rod and cuts off the de-correlation of the rod axis with time. On the scaling level, the long-time trajectory of a force-driven active nanorod piercing through unentangled polymers may be described as a stretched array of “active blobs”, where the short-time random-walk trajectory within an active blob is unperturbed by the active force.
1 Introduction
The dynamics of nanorods in a viscoelastic medium are critical to many applications of nanorods. The fabrication and processing of nanorod-containing polymer composites, which possess tunable mechanical,1–4 optical,5–7 and electrical8–12 properties, are affected by the dynamics of nanorods. The uses of nanorods as diagnostic probes in bio-imaging13–16 and as drug delivery vehicles in bio-medicine17–26 rely on the dynamics of nanorods in a complex environment of biological molecules.27 With thermal agitation, the dynamics of nanorods are passive and coupled with the viscoelasticity of surrounding molecules, exhibiting the random nature of Brownian motion.28–32 Going beyond the randomness of passive dynamics, the active dynamics of nanorods may be induced either by an external field such as a magnetic field,18,33 an electric field,34 near-infrared light18 and ultra sound20,23 or by a chemistry-based mechanism of self-propulsion.17,35–39 A fundamental understanding of the active motion of nanorods in a viscoelastic medium will benefit further advances in the material and biomedical applications of nanorods.
The passive dynamics of thin nanorods in viscoelastic polymers are characterized by a length-scale- and shape-dependent breakdown of the Stokes-Einstein relation in the continuum theory.40 The diffusion coefficients for different modes of the nanorod dynamics, including the translational motion along and normal to the rod axis, the overall translational motion, and the rotational motion of the rod axis, are all related to the bulk viscosity of surrounding molecules in the Stokes–Einstein relation.41,42 Nevertheless, recent experiments28,29 and computer simulations30,31,43 have revealed the coupling of a nanorod only to a fraction of the bulk viscosity, indicating the breakdown of the Stokes–Einstein relation. Molecular dynamics simulations of monomerically thin nanorods in unentangled polymer melts43 have shown the anisotropy in the translational diffusion along and normal to the rod axis. The parallel diffusion in the body frame of the thin nanorod is coupled to the local viscosity on the monomer length scale, which is independent of the rod length l. The coupling to the local monomeric viscosity reflects a full screening of the hydrodynamic interactions. By contrast, the normal diffusion is coupled with an effective viscosity that depends on l with respect to the polymer chain size, corresponding to unscreened hydrodynamic interactions. The same effective viscosity for the normal diffusion also dictates the rotational diffusion of the rod axis. For the overall translational diffusion in the lab frame, the effective viscosity corresponds to a partial screening of the hydrodynamic interactions, as both the parallel and normal components contribute to the overall diffusion.
Activeness is anticipated to alter the interplay between the nanorods and the viscoelasticity of the surrounding medium, as the ballistic motion induced by the activeness has been shown to enhance the mobility of nanoscale objects in experiments27 and computer simulations.44,45 To investigate the active dynamics of nanorods in a viscoelastic medium, we perform molecular dynamics simulations and scaling analysis of a model system consisting of force-driven active thin nanorods in a melt of unentangled polymers. The thickness of the nanorod is comparable to the monomer size, and the aspect ratio of the nanorod is ≥4. The unentangled polymer chains represent a viscoelastic medium with internal chain relaxation dynamics. The activeness of a thin nanorod is introduced by applying an active force uniformly along the initial rod axis, which facilitates the arrival of the steady state in the simulations. We find that the active force overcomes the randomness of the diffusive motion and results in a ballistic motion of the thin nanorod along the force direction at long timescales. The constant speed of the force-driven ballistic motion is determined by the balance of the active force and the friction from the coupling of the nanorod with the polymer melt. The friction coefficient decreases as the strength of the active force increases. We determine the origin of the reduction in the friction coefficient is the fact that the high speed renews the local environment of the nanorod faster than the relaxation time of polymer chains. We develop a scaling theory that successfully describes the dependence of the friction coefficient on the strength of the active force as well as the onset of the reduction in the friction coefficient in the simulations. We also find that the active force suppresses the rotational diffusion of the rod and cuts off the de-correlation of the rod axis with time.
2 Models and methods
We simulate the polymers using the canonical bead-spring model.46–48 Monomers of size σ and mass m interact via the Lennard-Jones (LJ) potential with an interaction strength ε, cut-off distance rc = 2.5σ, and unit time 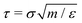 . Polymer chains of N monomers each are connected by the finitely extensible nonlinear elastic (FENE) bonds. We simulate the thin nanorods as rigid bodies made of beads identical to the monomers. To create a thin nanorod of length l, l/σ beads are placed along a straight line with regular spacing σ and grouped into a rigid body. The interaction between a bead of a nanorod and a surrounding monomer is the weakly attractive LJ potential with rc = 2.5σ, which promotes the dispersion of nanorods in the melt. The interaction between two beads from two different nanorods is the purely repulsive LJ potential with rc = 21/6σ, which prevents the aggregation of the nanorods.
. Polymer chains of N monomers each are connected by the finitely extensible nonlinear elastic (FENE) bonds. We simulate the thin nanorods as rigid bodies made of beads identical to the monomers. To create a thin nanorod of length l, l/σ beads are placed along a straight line with regular spacing σ and grouped into a rigid body. The interaction between a bead of a nanorod and a surrounding monomer is the weakly attractive LJ potential with rc = 2.5σ, which promotes the dispersion of nanorods in the melt. The interaction between two beads from two different nanorods is the purely repulsive LJ potential with rc = 21/6σ, which prevents the aggregation of the nanorods.
Nanorods and polymers were placed in a cubic box with side length L and periodic boundary conditions in all three directions. Each sample was equilibrated at temperature T = 1.0ε/kB and pressure P = 0. The equilibration was performed with a Nosé–Hoover thermostat/barostat applied to the polymer chains. A Nosé–Hoover thermostat was applied to both the translational and rotational degrees of freedom of the rigid nanorods. The characteristic damping time of the thermostat was 10τ, and that of the barostat was 100τ. The equilibration run lasted for a time that is much longer than the diffusion time of the polymer chains. There are two sets of simulation samples. In one set, the polymer chain length N = 16, and the rod length l = 4σ, 8σ, 16σ, and 32σ. In the other set, N = 64, while l = 4σ, and 8σ. The first set corresponds to l comparable to and larger than the root-mean-squared end-to-end size of the polymer chain, R = 4.7σ. The second set corresponds to l < R = 10.1σ. In all samples, the number of nanorods is Nr = 27, while the number of polymer chains Nc varies. Multiple nanorods are simulated simultaneously for a better statistical average of the dynamics data. As shown in Table 1, the volume fraction of the nanorods ϕr = Nrlσ2/L3 is less than 0.07%, and the volume fraction of the excluded volume ϕexl = Nrl2σ/L3 is less than 2.1% in all samples. Recently, it has been shown that the organization of nanorods in polymer nanocomposites depends on the details of the nanorod model.49,50 For the specific models of nanorods and polymers used here and the low volume fraction of nanorods in the simulations, we have confirmed that the nanorods are well dispersed without any aggregation in all samples.43 Additionally, because of the low volume fraction of nanorods in the simulations and the lack of a theory for the long-range correlation of nanorod pairs, we do not attempt to quantify and correct for the effects of any long-range pair correlation on the dynamics of individual nanorods.
Table 1 Parameters for the simulations of force-driven active thin nanorods in unentangled polymer melts
| Chain length N |
Num. of chains Nc |
Box size L (σ) |
Nanorod length l (σ) |
Num. of rods Nr |
Vol. fraction ϕr (%) |
Excluded vol. fraction ϕexl (%) |
| 16 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818 818 |
110.5 |
4 |
27 |
0.008 |
0.032 |
| 16 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818 818 |
110.5 |
8 |
27 |
0.016 |
0.128 |
| 16 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818 818 |
110.5 |
16 |
27 |
0.032 |
0.512 |
| 16 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818 818 |
110.5 |
32 |
27 |
0.064 |
2.048 |
| 32 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 909 909 |
110.2 |
4 |
27 |
0.032 |
0.516 |
| 32 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 909 909 |
110.2 |
8 |
27 |
0.065 |
2.065 |
The dynamics of nanorods in polymer melts were simulated at a fixed volume and a constant temperature T = 1.0ε/kB. The temperature of polymer chains was controlled using a Nosé–Hoover thermostat with a characteristic damping time of 10τ. The activeness of a nanorod was modeled by applying a constant active force along the initial rod axis such that the driven motion of the nanorod along the active force direction is commensurate with the preferential thermal diffusion of the nanorod along the rod axis,43 facilitating the arrival of the steady state in the simulations. The active force is uniformly distributed along the rod with each bead subjecting to an active force fa0u(0), where u(0) is the unit vector along the initial rod axis. Fig. 1 illustrates a force-driven active thin nanorod in an unentangled polymer melt. fa0 varied from 0 to 2.0ε/σ. To enable the activeness, no thermostat was applied to the thin nanorods. The time step for integrating the equations of motion was 0.01τ. The net linear momentum and net angular momentum of the polymer melt were zeroed after each step of integration, so there was no drift or rotation of the melt. All simulations were performed using the LAMMPS simulation package.51,52
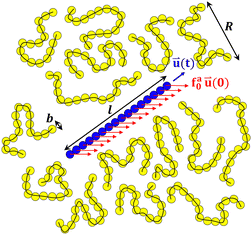 |
| | Fig. 1 Schematic illustration of a force-driven active thin nanorod (a rigid body of blue spheres) in a melt of unentangled polymers (yellow spheres connected by black lines). The monomer size b, rod length l, and melt chain size R are indicated. The active force is applied uniformly along the rod with a magnitude of fa0 per monomer length. The active force is along the initial rod axis with unit vector ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (0), while the orientation of the rod axis changes over time with a time-dependent unit vector (0), while the orientation of the rod axis changes over time with a time-dependent unit vector ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (t). (t). | |
3 Results and discussion
Representative trajectories for the dynamics of active nanorods in the simulations are shown in Fig. 2. The dynamics of an active nanorod is quantified by the mean-square displacement (MSD) 〈Δr2(t)〉 = 〈[![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) com(t) −
com(t) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) com(0)]2〉 of the center of mass of the nanorod as a function of time t in the polymer melts. Fig. 3 shows 〈Δr2(t)〉 for the nanorods of l = 32σ in the polymers of N = 16 with increasing fa0. 〈Δr2(t)〉 for t < 10τ and 10τ ≤ t ≤ 104τ are computed separately. Depending on the strength of the active force, the production run for MSD in the time window 10τ < t < 104τ lasted from 4 × 104τ to 6 × 105τ. Coordinates were dumped every 10τ. For the earlier time window 0.01τ < t < 10τ, the production run lasted for 100τ, and coordinates were dumped every 0.01τ in all cases. In the calculations of MSD, the average was taken over different nanorods and different time periods of the same length in the steady state.
com(0)]2〉 of the center of mass of the nanorod as a function of time t in the polymer melts. Fig. 3 shows 〈Δr2(t)〉 for the nanorods of l = 32σ in the polymers of N = 16 with increasing fa0. 〈Δr2(t)〉 for t < 10τ and 10τ ≤ t ≤ 104τ are computed separately. Depending on the strength of the active force, the production run for MSD in the time window 10τ < t < 104τ lasted from 4 × 104τ to 6 × 105τ. Coordinates were dumped every 10τ. For the earlier time window 0.01τ < t < 10τ, the production run lasted for 100τ, and coordinates were dumped every 0.01τ in all cases. In the calculations of MSD, the average was taken over different nanorods and different time periods of the same length in the steady state.
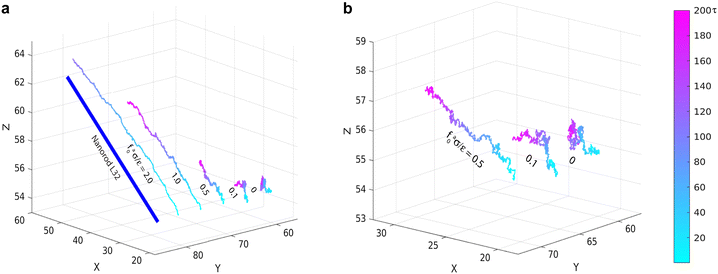 |
| | Fig. 2 (a) Molecular dynamics trajectories of force-driven active thin nanorods of length l = 32σ in polymer melts of chain length N = 16 at indicated magnitudes of active force. Three trajectories in (a) are enlarged and shown in (b). For the trajectory at the strongest active force fa0 = 2ε/σ, only the part comparable to the rod length is shown. | |
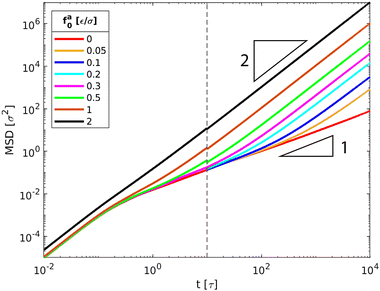 |
| | Fig. 3 MSD〈Δr2(t)〉 of the force-driven active thin nanorods with length l = 32σ and indicated active force per monomer fa0 in a melt of polymer chains with N = 16 monomers per chain. fa0 = 0 corresponds to the passive dynamics of thin nanorods with no activeness. Dashed line indicates t = 10τ that separates two independent computations of MSDs for t < 10τ and 10 ≤ t ≤ 104τ. | |
The scenario with fa0 = 0 corresponds to the passive dynamics of nanorods. The corresponding MSD exhibits a crossover from the initial thermal ballistic motion with α = d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log〈Δr2(t)〉/d
log〈Δr2(t)〉/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t = 2 to the sub-diffusive motion with α < 1 at intermediate timescales and eventually to the terminal diffusion with α = 1, in agreement with the previous simulation result.43 For fa0 > 0, the MSD is characterized by the new force-driven ballistic regime with α = 2 at long timescales. The overlap of the MSD for the active nanorods prior to the force-driven ballistic regime with the MSD for the passive dynamics of nanorods indicates that the active force is not sufficiently strong such that the nanorod dynamics are dictated by the thermal motion at short timescales. With increasing fa0, the force-driven ballistic regime begins at a shorter time. Eventually, for the largest fa0 = 2ε/σ, the force-driven ballistic regime covers the entire range of timescales explored in the simulations.
t = 2 to the sub-diffusive motion with α < 1 at intermediate timescales and eventually to the terminal diffusion with α = 1, in agreement with the previous simulation result.43 For fa0 > 0, the MSD is characterized by the new force-driven ballistic regime with α = 2 at long timescales. The overlap of the MSD for the active nanorods prior to the force-driven ballistic regime with the MSD for the passive dynamics of nanorods indicates that the active force is not sufficiently strong such that the nanorod dynamics are dictated by the thermal motion at short timescales. With increasing fa0, the force-driven ballistic regime begins at a shorter time. Eventually, for the largest fa0 = 2ε/σ, the force-driven ballistic regime covers the entire range of timescales explored in the simulations.
For the simulation samples in Fig. 3, we further decomposed the overall MSD into two components that are parallel and normal to the direction of the applied force, respectively. Note that the direction of the force, which is aligned with the initial rod axis, is fixed in the lab frame. The results from the decomposition are presented as ESI.† The parallel component is almost identical to the overall MSD in the force-driven ballistic regime, indicating the force-driven ballistic motion is along the force direction. The normal component exhibits rich time-dependent features that need further study, but its contribution to the overall MSD in the force-driven ballistic regime is very minor. See ESI† for a more detailed discussion.
In all cases, the force-driven ballistic motion is quantified by a constant speed va, which is computed from the long-time value of 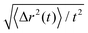 . The increase of va with increasing fa0 for the samples in Fig. 3 is shown in Fig. 4. va for fa0 = 2ε/σ is slightly above the thermal speed of the nanorod with 32 beads of mass m, which is
. The increase of va with increasing fa0 for the samples in Fig. 3 is shown in Fig. 4. va for fa0 = 2ε/σ is slightly above the thermal speed of the nanorod with 32 beads of mass m, which is 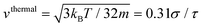 . va > vthermal indicates that the ballistic motion dominates the thermal motion at all timescales, as the displacement vat from the active motion is sufficiently large that it surpasses the displacement vthermalt from the undamped thermal ballistic motion. The increase of va with increasing fa0 can also be observed in the representative trajectories of active nanorods in Fig. 2, where the displacement over the same time of 200τ increases with increasing fa0.
. va > vthermal indicates that the ballistic motion dominates the thermal motion at all timescales, as the displacement vat from the active motion is sufficiently large that it surpasses the displacement vthermalt from the undamped thermal ballistic motion. The increase of va with increasing fa0 can also be observed in the representative trajectories of active nanorods in Fig. 2, where the displacement over the same time of 200τ increases with increasing fa0.
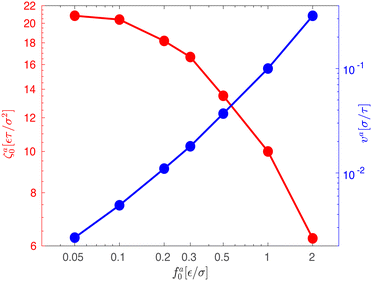 |
| | Fig. 4 The speed va for the force-driven ballistic motion (right axis) and the monomeric friction coefficient ζa0 = fa0/va (left axis) as functions of the active force per monomer fa0 for the same systems in Fig. 3. | |
As the speed va increases with the strength of the active force, the friction coefficient for the force-driven ballistic motion of an active nanorod decreases. In the force-driven ballistic regime, there is a balance between the active force fa0(l/σ) and the frictional force ζava, where ζa is the friction coefficient. From fa0(l/σ) = ζava, the monomeric friction coefficient ζa0 = ζa/(l/σ) = fa0/va. The dependence of ζa0 on fa0 for the simulation samples in Fig. 3 is shown in Fig. 4. In the limit of vanishing fa0, ζa0 approaches a plateau that corresponds to the passive dynamics of the nanorod, for which the monomeric friction coefficient is ζ0 = 22.5ετ/σ2.43 As fa0 increases, ζa0 deviates from ζ0 and decreases as the force-driven ballistic motion dominates over the thermal motion at decreasing timescale.
To understand the dynamics of an active nanorod in unentangled polymers, we develop a scaling theory. Consider a nanorod of length l and thickness comparable to the Kuhn monomer size b in a polymer melt. Each polymer consists of N monomers, and the polymer chains are unentangled. The active force along the initial rod axis is fa0 per monomer. Refer to Fig. 1 for a schematic illustration of the force-driven nanorod in polymer chains.
We first review the scaling description of the passive dynamics of the nanorods with fa0 = 0 in unentangled polymers. The nanorod in diffusion experiences an effective viscosity ηeff that is comparable to the geometric mean of the viscosity η0 on the monomer length scale and the maximum viscosity ηmax that the rod can experience. The scaling relation ηeff ≈ (η0ηmax)1/2 corresponds to a partial screening of the hydrodynamic interactions in the coupling between the nanorod and the melt. Note that if ηeff ≈ η0 and ηeff ≈ ηmax, there is a full screening and no screening of the hydrodynamic interactions beyond the monomer length scale, respectively. When l is larger than the average size R ≈ N1/2b of the melt chain in the random-walk conformation, ηmax for unscreened hydrodynamic interactions is comparable to the melt viscosity ηmelt ≈ η0N. However, when l < R, ηmax is instead only comparable to the viscosity ηg ≈ η0g ≈ η0(l2/b2) of local chain segments, which contain g monomers in each segment and have an average chain size g1/2b ≈ l.
A length-scale dependent ηeff has been used to describe the diffusion of spherical nanoparticles in various polymer systems,40,53–57 and it is consistent with the length-scale dependent nanoparticle dynamics in alternative theoretical approach.58–60 For nanorods, the rule of geometric mean reflects the additional effects of the anisotropic particle shape on ηeff. While the diffusion along the rod axis is determined by the monomeric viscosity η0, the diffusion normal to the rod axis is determined by ηmax. Such a difference between the parallel and normal components with respect to the rod axis, i.e., in the body frame, has been shown by the recent simulations on the diffusion of nanorods.43 The rule of geometric mean composites the viscosity for the diffusion parallel and normal to the rod axis to obtain ηeff for the diffusion in the lab frame. The rule was first used by Aponte-Rivera and Rubinstein61 in the scaling theory for the dynamical coupling in oppositely charged polyelectrolytes, where ηeff for the polyanion correlation segments is the geometric mean of the values for the full screening and no screening of the hydrodynamic interactions. Note that in the theoretical description throughout the paper, ≈ indicates the equation is on the scaling level with an order-of-unity coefficient dropped.
The friction coefficient for the passive dynamics of a nanorod ζ ≈ ηeffl, and the diffusion coefficient D = kBT/ζ, according to the Stokes law and Einstein relation, respectively. As a result, the MSD is 〈Δr2(t)〉 ≈ Dt ≈ (kBT/ηeffl)t in the terminal diffusive regime. If l ≥ R, the time scale τd at which the terminal diffusion begins is comparable to the relaxation time of the melt τmelt. Using the N-dependence of the relaxation time in the Rouse dynamics model,41τmelt ≈ τ0N2, where τ0 is the monomeric time scale. If l < R, τd is comparable to the Rouse time of the g-monomer segments, τg ≈ τ0g2 < τmelt.
For a force-driven active nanorod, the friction coefficient ζa is comparable to ζ in the limit of vanishing fa0, as shown by the simulation result in Fig. 4. The force-driven ballistic motion of an active nanorod with a small speed va begins at a time scale τaballistic > τd, where the motion of a passive nanorod with fa0 = 0 is already in the terminal diffusive regime. The ballistic motion with τaballistic > τd renews the local environment of the nanorod sufficiently slow such that the relaxation dynamics that determine the thermal diffusion of the passive nanorod is complete. As a result, the same friction that affects the thermal diffusion resists the force-driven ballistic motion, i.e., ζa ≈ ζ. An example of this scenario in the simulations is the active dynamics with the smallest fa0 = 0.05ε/σ in Fig. 3.
The reduction of ζa with respect to ζ results from the strong activeness that makes the force-driven ballistic motion begins at τaballistic < τd. The ballistic motion with τaballistic < τd renews the local environment of the nanorod at a rate that only allows the relaxation dynamics of chain segments with ga monomers each to be complete, i.e.
| | | τaballistic ≈ τag ≈ τ0(ga)2 | (1) |
where the monomeric time scale
| | 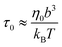 | (2) |
The MSD of a force-driven active nanorod at
τaballistic is comparable to the MSD of a passive nanorod at
τag. For
t >
τaballistic ≈
τag, the MSD due to the force-driven ballistic motion is above the MSD for the passive thermal motion, allowing the active nanorod to escape the effects of the relaxation dynamics of chain segments longer than
ga. As a result, for the force-driven active nanorod, the maximum viscosity corresponding to unscreened hydrodynamic interactions is
The effective viscosity using the rule of geometric mean is
| | | ηaeff ≈ (η0ηamax)1/2 ≈ η0(ga)1/2 | (4) |
The friction coefficient is
which is smaller than
ζ for the passive dynamics. A typical example of this scenario is the active dynamics with
fa0 = 0.3
ε/
σ in
Fig. 3.
For a large fa0 that makes τaballistic ≈ τag < τd, we calculate the friction coefficient ζa of a force-driven active nanorod by matching the MSDs for the active and passive motion at τaballistic ≈ τag. The constant speed of the force-driven ballistic motion
| | 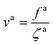 | (6) |
where
| | 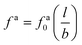 | (7) |
The MSD for the ballistic motion at
t ≈
τaballistic ≈
τag is
| | | 〈Δr2(τag)〉aballistic ≈ (vaτag)2 | (8) |
The MSD for the passive thermal motion at
t ≈
τag is
| | 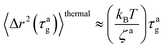 | (9) |
where
kBT/
ζa is the diffusion coefficient. From 〈Δ
r2(
τag)〉
aballistic ≈ 〈Δ
r2(
τag)〉
thermal, we obtain the number of monomers per segment for the chain segments that affect the force-driven ballistic motion of the nanorod is
| | 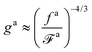 | (10) |
where
| | 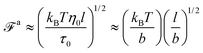 | (11) |
As a result, the effective viscosity for the force-driven active nanorod is
| | 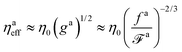 | (12) |
The corresponding friction coefficient is
| | 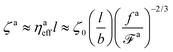 | (13) |
where the monomeric friction coefficient for the passive dynamics
Finally, the friction coefficient per monomer for the force-driven active nanorod is
| | 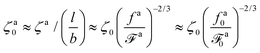 | (15) |
where
| | 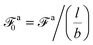 | (16) |
Matching the two MSDs at τag corresponds to the work performed by the active force fa at a speed va over a time of τag is comparable to the thermal energy kBT, i.e.,
which one can verify using
eqn (1), (6), (10), (11), (13), and (14). Therefore,
τag is the time scale above which the energy from the active force outcompetes the thermal energy
kBT. Recall that Einstein relation
D =
kBT/
ζ shows the diffusion coefficient for the passive dynamics is dictated by the thermal energy
kBT. Therefore,
wa >
kBT for
t >
τag is consistent with the fact that the long-time ballistic motion of the force-driven nanorod is not affected by the thermal agitation. Likewise, the force
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) a
a satisfies
| | 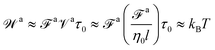 | (18) |
Eqn (18) means that
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) a
a is a strong force at which the rod is coupled only to the monomer viscosity
η0 with friction coefficient
![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif)
≈
η0l, and the work
![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) a
a performed by
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) a
a at the constant speed
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) a
a ≈
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) a
a/
![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif)
over the monomer time scale
τ0 is already comparable to the thermal energy
kBT.
The regime with the reduced friction coefficient ζa0 in eqn (15) occurs only when fa0 is above the threshold 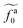 , at which the number of monomers per segment for the chain segments that affect the nanorod dynamics is
, at which the number of monomers per segment for the chain segments that affect the nanorod dynamics is
| | 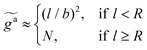 | (19) |
where
R ≈
N1/2b is the average size of melt chains. Using
eqn(10) for
ga,
eqn (11) for
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) a
a, we obtain the active force at the threshold
| | 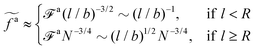 | (20) |
As a result, the active force per monomer at the threshold
| | 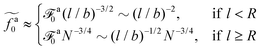 | (21) |
where
eqn (16) for
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) a0
a0 is used.
Eqn (21) shows that as the rod length increases, there is a crossover from
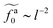
to
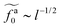
.
The scaling theory is compared with the simulation data for the systems with varying l and N. As shown in Fig. 5a, the plateau of ζa0 and the decrease of ζa0 with increasing fa0 are observed in different simulation samples. The results for different l and N can be collapsed to a master curve
| | 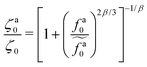 | (22) |
that goes from the plateau regime
ζa0/
ζ0 = 1 for
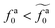
to the power-law regime
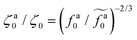
for
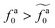
with
β quantifying the shape of the curve at
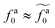
. The exponent −2/3 in the power-law regime is the result of the scaling theory (
eqn (15)).
Fig. 5b shows the collapse of all simulation data points to the master curve. To obtain the master curve,
ζa0/
ζ0 for different systems are simultaneously fit to
eqn (22). The fitting result of
β is 2.9 ± 0.6, and the best fit is used to construct the master curve (thick dashed line in
Fig. 5b). The best-fit results of
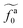
for different samples are shown in the inset to
Fig. 5b and used to rescale the corresponding
fa0 to the master curve. The successful collapse of the data points in
Fig. 5b validates the scaling theory for the power-law reduction of the friction coefficient with increasing strength of activeness (
eqn (15)).
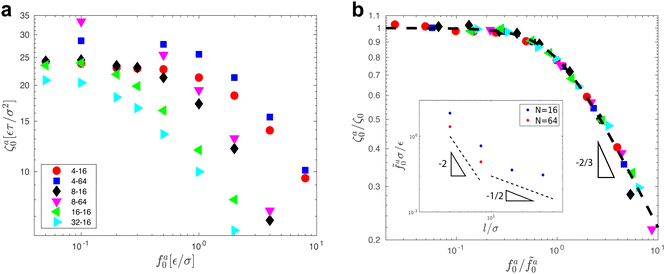 |
| | Fig. 5 (a) The monomeric friction coefficient ζa0 for the force-driven ballistic motion of an active thin nanorod in an unentangled polymer melt as a function of the active force per monomer fa0. The rod length l and the polymer melt chain length N are indicated in the format l − N. (b) Rescaling of ζa0 by the plateau value ζ0 and fa0 by 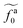 , which is threshold active force for the reduction in ζa0, results in the collapse of the data points in (a) to a master curve. The thick dashed line indicates the master curve (eqn (22)). The inset shows , which is threshold active force for the reduction in ζa0, results in the collapse of the data points in (a) to a master curve. The thick dashed line indicates the master curve (eqn (22)). The inset shows 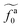 as a function of l for the nanorods in the melts of N = 16 and N = 64. The dashed lines in the inset indicate two scaling regimes in the theory. as a function of l for the nanorods in the melts of N = 16 and N = 64. The dashed lines in the inset indicate two scaling regimes in the theory. | |
As shown in the inset to Fig. 5b, the l-dependence of 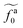 for the force-driven active nanorods in the polymer melt of N = 16 exhibits a crossover from
for the force-driven active nanorods in the polymer melt of N = 16 exhibits a crossover from 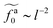 to
to 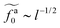 as l increases from l = 4σ slightly below R ≈ 4.7σ to l = 32σ > R. For the nanorods in the other polymer melt of N = 64, l = 4σ and l = 8σ are both smaller than R ≈ 10.1σ, and the l-dependence of
as l increases from l = 4σ slightly below R ≈ 4.7σ to l = 32σ > R. For the nanorods in the other polymer melt of N = 64, l = 4σ and l = 8σ are both smaller than R ≈ 10.1σ, and the l-dependence of 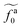 is close to the scaling relation
is close to the scaling relation 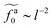 . These results agree with the scaling theory for the onset of the reduction in the friction coefficient (eqn (21)), further validating the theory.
. These results agree with the scaling theory for the onset of the reduction in the friction coefficient (eqn (21)), further validating the theory.
Along with the decrease of ζa0, there is a suppression of the rotation of the rod. We track the unit vector u(t) along the rod axis as a function of time, as visualized in Fig. 6. The range spanned by the tip of u(t) on the unit sphere decreases with increasing strength of the active force. The time-correlation function of the unit vector along the rod axis 〈u(t)·u(0)〉 is computed. The results for the simulation samples in Fig. 6 are shown in Fig. 7. Here, as in the calculation of MSD (Fig. 3), the average is taken over different rods as well as different time periods of the same length in the steady state. For vanishing fa0, the correlation function approaches 0 over a time scale comparable to the rotational relaxation time τrot = 7.4 × 104τ for the passive thermal motion, which was obtained by fitting the decay of 〈u(t)·u(0)〉 to exp(−t/τrot).43 This indicates that the strength of the active force is weak and cannot keep the rod axis around its initial orientation or equivalently the force direction. As fa0 increases, the correlation function levels off at a finite value up to the longest time scale in the simulations, indicating a stronger active force that suppresses the rotational diffusion of the rod axis. For the largest active force with fa0 = 2ε/σ, the correlation function levels off at 0.93, indicating a much reduced rotational diffusion of the nanorod. The suppression of the rotational diffusion and the cutting off of the de-correlation of rod axis with time are consistent with the force-driven nanorod being coupled to local chain segments rather than entire polymer chains.
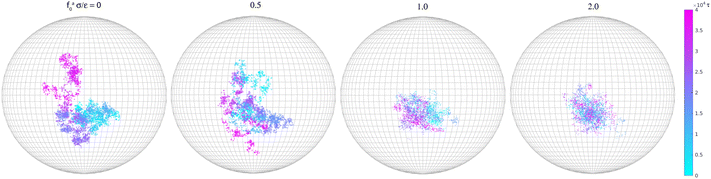 |
| | Fig. 6 Rotational trajectories of the unit vector ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (t) along the rod axis for the force-driven active nanorods of l = 32σ in polymer melts of N = 16. (t) along the rod axis for the force-driven active nanorods of l = 32σ in polymer melts of N = 16. | |
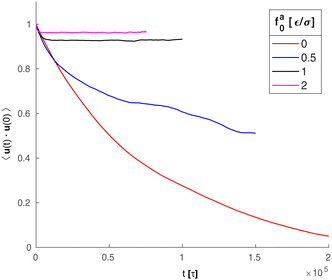 |
| | Fig. 7 Time-correlation function of the unit vector ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (t) along the rod axis for the same systems in Fig. 6. (t) along the rod axis for the same systems in Fig. 6. | |
The reduction in rotational diffusion originates from the active force being in a fixed direction. If a self-propelled active force fa0u(t) were applied instead, the force would change its direction at timescales above the rotational relaxation time of the rod axis τrot. As a result, one would expect the terminal dynamics of the self-propelled active nanorod to be different from that with a constant driving force fa0u(0). Recent Brownian dynamics simulations of self-propelled active filaments44 showed that the force-driven ballistic motion only persists to the timescale of τrot, after which the rotational diffusion of the filament randomizes the direction of self-propulsion, leading to a diffusive translational motion again.
4 Concluding remarks
By combining molecular dynamics simulations and scaling theory analysis, we demonstrate the competition between the activeness induced by a constant external force and the passive thermal motion of the nanorod that is coupled to the viscosity of an unentangled polymer melt. The activeness outcompetes the thermal motion and results in a force-driven ballistic motion with a constant speed va in the force direction for the timescales above τballistic (see Fig. 3). On the scaling level, τballistic is the timescale where the work performed by the active force wa is comparable to the thermal energy kBT (eqn (17)). With increasing strength of the active force, τballistic decreases below the terminal relaxation time τmelt of entire polymer chains, allowing only the local viscosity of the chain segments with ga monomers each and relaxation time τag ≈ τballistic < τmelt to affect the force-driven active dynamics. As a result, the friction coefficient for the friction that balances the active force decreases with increasing strength of the active force (see Fig. 4). For sufficiently strong active force, the terminal speed va is above the thermal speed of the nanorod, and therefore the force-driven ballistic motion dominates all relevant time scales. Accompanying the reduction in the friction coefficient, the increase of the active force also leads to the suppression of the rotational diffusion of the rod and a strong correlation of the rod axis over time (see Fig. 6 and 7).
Regarding the connections to experiments,28,29,62 the model of thin nanorods in the present work captures the effects of the anisotropic particle shape. Nevertheless, the model has yet to be extended to cover more aspects such as the rod thickness, which may be larger than the monomer length scale b, as well as the boundary conditions at the nanorod and polymer interface, which may involve attractive interactions between the rod and surrounding polymers and a grafted polymer brush layer that prevents the aggregation of nanorods. The steady-state motion of an active nanorod under constant external force as in the simulated model may be realized by the implementation of a nanorod with a uniformly distributed charge under an external electric field. Another way to extend the present computational and theoretical work to connect to a broader range of experiments is to include more disparate polymer matrices, such as entangled polymer melts, polymer solutions, and hydrogels.
Conceptually, the effect of the active force on the center-of-mass trajectory of a thin nanorod in an unentangled polymer melt may be compared with the effect of an external force on the conformation of a polymer chain. For a polymer chain with force of magnitude f applying at both chain ends, the random-walk conformation of an unperturbed chain is replaced by an extended array of tension blobs.63 Each tension blob contains g monomers and the blob size ξ ≈ bg1/2 is the threshold length scale that chain segments are able to adopt the random-walk conformation without being perturbed by the external tensile force. The tension blob size is determined by fξ ≈ kT, reflecting the competition between the external perturbation and the thermal energy. Similarly, for a thin nanorod under the active force of magnitude fa, the center-of-mass random-walk trajectory in the time domain for the passive dynamics of the nanorod is replaced by an extended array of “active blobs”, as illustrated in Fig. 8. Each active blob corresponds to a time scale τaballistic ≈ τag (eqn (1)) and a length scale that is comparable to the MSD〈Δr2(τag)〉aballistic ≈(vaτag)2 (eqn (8)). The random-walk trajectory at time scales below τag is not perturbed by the active force and follows the MSD for the thermal motion of the nanorod. τag and hence 〈Δr2(τag)〉aballistic are determined by wa ≈ favaτag ≈ kBT (eqn (17)), which is a balance between the external perturbation and the thermal energy. Note that the random-walk trajectories for the passive dynamics and for the force-driven active dynamics at timescales below τaballistic are not ideal 3-dimensional random walks, as the translational diffusion along the rod axis is faster than that normal to the rod axis.43 The description of the active dynamics trajectories using the language of blobs in polymer physics, as illustrated in Fig. 8, may provide a new perspective on the theory of active particles and active polymers.64
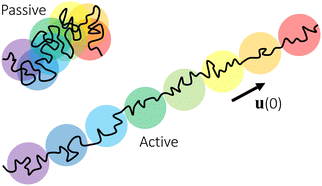 |
| | Fig. 8 Schematic illustration of the center-of-mass trajectories of thin nanorods (black lines) in unentangled polymer melts. The trajectory under an active force is a stretched array of active blobs (circles), which are segments of the trajectory over the time scale τaballistic. Colors of increasing wavelength (from violet to red) are used to indicate the time order of the active blobs. The blobs of different colors overlap along the trajectory for the passive dynamics, indicating the randomness of the thermal diffusive motion. The arrow indicates the unit vector ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (0) along the initial rod axis or equivalently the direction of the applied force. (0) along the initial rod axis or equivalently the direction of the applied force. | |
The microscopic insights provided by the molecular simulations and scaling theory may aid in the control of nanorods in functional nanorod–polymer composites using external force fields65 and the manipulation of the trajectories of one-dimensional nanomotors in the applications of bio-imaging and drug delivery.27 Additionally, the microscopic insights may also help understand the active filaments propelled by motor proteins in the cytoskeleton, RNA and DNA molecules in the transcription process within a cell, and also rod-like bacteria and viruses in biological settings.64,66,67
Author contributions
S. Zhang: methodology, software, formal analysis, investigation, data curation, visualization, review and editing of the manuscript; J. Wang: methodology, software, formal analysis, investigation, validation, and review and editing of the manuscript; T. Ge: conceptualization, supervision, writing – original draft preparation, and funding acquisition.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
T. G. acknowledges start-up funds from the University of South Carolina. This work was supported in part by the National Science Foundation EPSCoR Program under NSF Award No. OIA-1655740. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect those of the National Science Foundation. This work is partially supported by an ASPIRE grant from the Office of the Vice President for Research at the University of South Carolina. Simulations were performed on the flagship computing cluster Hyperion at the University of South Carolina.
Notes and references
- M. Moniruzzaman and K. I. Winey, Macromolecules, 2006, 39, 5194–5205 CrossRef CAS.
- H. Koerner, J. Kelley, J. George, L. Drummy, P. Mirau, N. S. Bell, J. W. Hsu and R. A. Vaia, Macromolecules, 2009, 42, 8933–8942 CrossRef CAS.
- N. McCook, B. Boesl, D. Burris and W. Sawyer, Tribol. Lett., 2006, 22, 253–257 CrossRef CAS.
- J. Shen, X. Li, L. Zhang, X. Lin, H. Li, X. Shen, V. Ganesan and J. Liu, Macromolecules, 2018, 51, 2641–2652 CrossRef CAS.
- A. Brioude, X. Jiang and M. Pileni, J. Phys. Chem. B, 2005, 109, 13138–13142 CrossRef CAS PubMed.
- P. K. Jain, S. Eustis and M. A. El-Sayed, J. Phys. Chem. B, 2006, 110, 18243–18253 CrossRef CAS PubMed.
- M. J. Hore, A. L. Frischknecht and R. J. Composto, ACS Macro Lett., 2012, 1, 115–121 CrossRef CAS PubMed.
- W. U. Huynh, J. J. Dittmer and A. P. Alivisatos, Science, 2002, 295, 2425–2427 CrossRef CAS PubMed.
- S. I. White, B. A. DiDonna, M. Mu, T. C. Lubensky and K. I. Winey, Phys. Rev. B, 2009, 79, 024301 CrossRef.
- S. I. White, R. M. Mutiso, P. M. Vora, D. Jahnke, S. Hsu, J. M. Kikkawa, J. Li, J. E. Fischer and K. I. Winey, Adv. Funct. Mater., 2010, 20, 2709–2716 CrossRef CAS.
- R. M. Mutiso, M. C. Sherrott, J. Li and K. I. Winey, Phys. Rev. B, 2012, 86, 214306 CrossRef.
- R. M. Mutiso, M. C. Sherrott, A. R. Rathmell, B. J. Wiley and K. I. Winey, ACS Nano, 2013, 7, 7654–7663 CrossRef CAS PubMed.
- X. Xu, H. Li, D. Hasan, R. S. Ruoff, A. X. Wang and D. L. Fan, Adv. Funct. Mater., 2013, 23, 4332–4338 CrossRef CAS.
- X. Yu, Y. Li, J. Wu and H. Ju, Anal. Chem., 2014, 86, 4501–4507 CrossRef CAS PubMed.
- B. Esteban-Fernández De Ávila, A. Martín, F. Soto, M. A. Lopez-Ramirez, S. Campuzano, G. M. Vásquez-Machado, W. Gao, L. Zhang and J. Wang, ACS Nano, 2015, 9, 6756–6764 CrossRef PubMed.
- S. Fu, X. Zhang, Y. Xie, J. Wu and H. Ju, Nanoscale, 2017, 9, 9026–9033 RSC.
- D. Kagan, R. Laocharoensuk, M. Zimmerman, C. Clawson, S. Balasubramanian, D. Kang, D. Bishop, S. Sattayasamitsathit, L. Zhang and J. Wang, Small, 2010, 6, 2741–2747 CrossRef CAS PubMed.
- Z. Wu, X. Lin, X. Zou, J. Sun and Q. He, ACS Appl. Mater. Interfaces, 2015, 7, 250–255 CrossRef CAS PubMed.
- M. Yu, J. Wang, Y. Yang, C. Zhu, Q. Su, S. Guo, J. Sun, Y. Gan, X. Shi and H. Gao, Nano Lett., 2016, 16, 7176–7182 CrossRef CAS PubMed.
- P. Díez, B. Esteban-Fernández De Ávila, D. E. Ramírez-Herrera, R. Villalonga and J. Wang, Nanoscale, 2017, 9, 14307–14311 RSC.
- B. Esteban-Fernández De Ávila, D. E. Ramírez-Herrera, S. Campuzano, P. Angsantikul, L. Zhang and J. Wang, ACS Nano, 2017, 11, 5367–5374 CrossRef PubMed.
- J. Wang and X. Shi, Acta Mech. Solida Sin., 2017, 30, 241–247 CrossRef.
- M. Hansen-Bruhn, B. E. F. de Ávila, M. Beltrán-Gastélum, J. Zhao, D. E. Ramírez-Herrera, P. Angsantikul, K. Vesterager Gothelf, L. Zhang and J. Wang, Angew. Chem., Int. Ed., 2018, 57, 2657–2661 CrossRef CAS PubMed.
- J. Wang, Y. Yang, M. Yu, G. Hu, Y. Gan, H. Gao and X. Shi, J. Mech. Phys. Solids, 2018, 112, 431–457 CrossRef CAS.
- C. Bao, B. Liu, B. Li, J. Chai, L. Zhang, L. Jiao, D. Li, Z. Yu, F. Ren and X. Shi, Nano Lett., 2020, 20, 1352–1361 CrossRef CAS PubMed.
- W. Bao, F. Tian, C. Lyu, B. Liu, B. Li, L. Zhang, X. Liu, F. Li, D. Li and X. Gao, Sci. Adv., 2021, 7, eaba2458 CrossRef CAS PubMed.
- J. Guo and Y. Lin, Biomater. Transl., 2020, 1, 18–32 Search PubMed.
- S. Alam and A. Mukhopadhyay, Macromolecules, 2014, 47, 6919–6924 CrossRef CAS.
- J. Choi, M. Cargnello, C. B. Murray, N. Clarke, K. I. Winey and R. J. Composto, ACS Macro Lett., 2015, 4, 952–956 CrossRef CAS PubMed.
- S.-J. Li, H.-J. Qian and Z.-Y. Lu, Phys. Chem. Chem. Phys., 2018, 20, 20996–21007 RSC.
- A. Karatrantos, R. J. Composto, K. I. Winey and N. Clarke, Macromolecules, 2019, 52, 2513–2520 CrossRef CAS.
- K. I. Morozov and A. M. Leshansky, Macromolecules, 2022, 55, 3116–3128 CrossRef CAS.
- W. Gao, S. Sattayasamitsathit, K. M. Manesh, D. Weihs and J. Wang, J. Am. Chem. Soc., 2010, 132, 14403–14405 CrossRef CAS PubMed.
- D. L. Fan, R. C. Cammarata and C. L. Chien, Appl. Phys. Lett., 2008, 92, 093115 CrossRef.
- Y. Wang, R. M. Hernandez, D. J. Bartlett, J. M. Bingham, T. R. Kline, A. Sen and T. E. Mallouk, Langmuir, 2006, 22, 10451–10456 CrossRef CAS PubMed.
- W. Gao, A. Uygun and J. Wang, J. Am. Chem. Soc., 2012, 134, 897–900 CrossRef CAS PubMed.
- M. Manjare, B. Yang and Y. P. Zhao, J. Phys. Chem. C, 2013, 117, 4657–4665 CrossRef CAS.
- X. Ma, A. C. Hortelao, A. Miguel-López and S. Sánchez, J. Am. Chem. Soc., 2016, 138, 13782–13785 CrossRef CAS PubMed.
- Z. Huang, P. Chen, G. Zhu, Y. Yang, Z. Xu and L.-T. Yan, ACS Nano, 2018, 12, 6725–6733 CrossRef CAS PubMed.
- F. B. Wyart and P. G. de Gennes, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 1, 93 CrossRef CAS.
-
M. Doi and S. F. Edwards, The theory of polymer dynamics, Oxford University Press, 1988 Search PubMed.
-
J. Happel and H. Brenner, Low Reynolds number hydrodynamics: with special applications to particulate media, Martinus Nijhoff: The Hague, 1983 Search PubMed.
- J. Wang, T. C. O'Connor, G. S. Grest, Y. Zheng, M. Rubinstein and T. Ge, Macromolecules, 2021, 54, 7051–7059 CrossRef CAS PubMed.
- S. Mandal, C. Kurzthaler, T. Franosch and H. Löwen, Phys. Rev. Lett., 2020, 125, 138002 CrossRef CAS PubMed.
- C. Kurzthaler, S. Mandal, T. Bhattacharjee, H. Löwen, S. S. Datta and H. A. Stone, Nat. Commun., 2021, 12, 7088 CrossRef CAS PubMed.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- G. S. Grest, J. Chem. Phys., 2016, 145, 141101 CrossRef PubMed.
- H.-P. Hsu and K. Kremer, J. Chem. Phys., 2016, 144, 154907 CrossRef PubMed.
- S. Lu, Z. Wu and A. Jayaraman, J. Phys. Chem. B, 2021, 125, 2435–2449 CrossRef CAS PubMed.
- S. Lu and A. Jayaraman, ACS Macro Lett., 2021, 10, 1416–1422 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- L.-H. Cai, S. Panyukov and M. Rubinstein, Macromolecules, 2011, 44, 7853–7863 CrossRef CAS PubMed.
- L.-H. Cai, S. Panyukov and M. Rubinstein, Macromolecules, 2015, 48, 847–862 CrossRef CAS PubMed.
- T. Ge, J. T. Kalathi, J. D. Halverson, G. S. Grest and M. Rubinstein, Macromolecules, 2017, 50, 1749–1754 CrossRef CAS PubMed.
- T. Ge, G. S. Grest and M. Rubinstein, Phys. Rev. Lett., 2018, 120, 057801 CrossRef PubMed.
- T. Ge and M. Rubinstein, Macromolecules, 2019, 52, 1536–1545 CrossRef CAS PubMed.
- U. Yamamoto and K. S. Schweizer, J. Chem. Phys., 2011, 135, 224902 CrossRef PubMed.
- J. T. Kalathi, U. Yamamoto, K. S. Schweizer, G. S. Grest and S. K. Kumar, Phys. Rev. Lett., 2014, 112, 108301 CrossRef PubMed.
- U. Yamamoto and K. S. Schweizer, Macromolecules, 2015, 48, 152–163 CrossRef CAS.
- C. Aponte-Rivera and M. Rubinstein, Macromolecules, 2021, 54, 1783–1800 CrossRef CAS PubMed.
- K. A. Rose, M. Molaei, M. J. Boyle, D. Lee, J. C. Crocker and R. J. Composto, J. Appl. Phys., 2020, 127, 191101 CrossRef CAS.
-
M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- R. G. Winkler and G. Gompper, J. Chem. Phys., 2020, 153, 040901 CrossRef CAS PubMed.
- M. J. Hore and R. J. Composto, Curr. Opin. Chem. Eng., 2013, 2, 95–102 CrossRef.
- M. Smith, R. Poling-Skutvik, A. H. Slim, R. C. Willson and J. C. Conrad, Macromolecules, 2021, 54, 4557–4563 CrossRef CAS.
- G. C. L. Wong, J. D. Antani, P. P. Lele, J. Chen, B. Nan, M. J. Kühn, A. Persat, J.-L. Bru, N. M. Høyland-Kroghsbo, A. Siryaporn, J. C. Conrad, F. Carrara, Y. Yawata, R. Stocker, Y. V. Brun, G. B. Whitfield, C. K. Lee, J. de Anda, W. C. Schmidt, R. Golestanian, G. A. O'Toole, K. A. Floyd, F. H. Yildiz, S. Yang, F. Jin, M. Toyofuku, L. Eberl, N. Nomura, L. A. Zacharoff, M. Y. El-Naggar, S. E. Yalcin, N. S. Malvankar, M. D. Rojas-Andrade, A. I. Hochbaum, J. Yan, H. A. Stone, N. S. Wingreen, B. L. Bassler, Y. Wu, H. Xu, K. Drescher and J. Dunkel, Phys. Biol., 2021, 18, 051501 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  ,
Jiuling
Wang
,
Jiuling
Wang
 and
Ting
Ge
and
Ting
Ge
 *
*
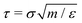 . Polymer chains of N monomers each are connected by the finitely extensible nonlinear elastic (FENE) bonds. We simulate the thin nanorods as rigid bodies made of beads identical to the monomers. To create a thin nanorod of length l, l/σ beads are placed along a straight line with regular spacing σ and grouped into a rigid body. The interaction between a bead of a nanorod and a surrounding monomer is the weakly attractive LJ potential with rc = 2.5σ, which promotes the dispersion of nanorods in the melt. The interaction between two beads from two different nanorods is the purely repulsive LJ potential with rc = 21/6σ, which prevents the aggregation of the nanorods.
. Polymer chains of N monomers each are connected by the finitely extensible nonlinear elastic (FENE) bonds. We simulate the thin nanorods as rigid bodies made of beads identical to the monomers. To create a thin nanorod of length l, l/σ beads are placed along a straight line with regular spacing σ and grouped into a rigid body. The interaction between a bead of a nanorod and a surrounding monomer is the weakly attractive LJ potential with rc = 2.5σ, which promotes the dispersion of nanorods in the melt. The interaction between two beads from two different nanorods is the purely repulsive LJ potential with rc = 21/6σ, which prevents the aggregation of the nanorods.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818
818![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818
818![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818
818![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818
818![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 909
909![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 909
909![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) com(t) −
com(t) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) com(0)]2〉 of the center of mass of the nanorod as a function of time t in the polymer melts. Fig. 3 shows 〈Δr2(t)〉 for the nanorods of l = 32σ in the polymers of N = 16 with increasing fa0. 〈Δr2(t)〉 for t < 10τ and 10τ ≤ t ≤ 104τ are computed separately. Depending on the strength of the active force, the production run for MSD in the time window 10τ < t < 104τ lasted from 4 × 104τ to 6 × 105τ. Coordinates were dumped every 10τ. For the earlier time window 0.01τ < t < 10τ, the production run lasted for 100τ, and coordinates were dumped every 0.01τ in all cases. In the calculations of MSD, the average was taken over different nanorods and different time periods of the same length in the steady state.
com(0)]2〉 of the center of mass of the nanorod as a function of time t in the polymer melts. Fig. 3 shows 〈Δr2(t)〉 for the nanorods of l = 32σ in the polymers of N = 16 with increasing fa0. 〈Δr2(t)〉 for t < 10τ and 10τ ≤ t ≤ 104τ are computed separately. Depending on the strength of the active force, the production run for MSD in the time window 10τ < t < 104τ lasted from 4 × 104τ to 6 × 105τ. Coordinates were dumped every 10τ. For the earlier time window 0.01τ < t < 10τ, the production run lasted for 100τ, and coordinates were dumped every 0.01τ in all cases. In the calculations of MSD, the average was taken over different nanorods and different time periods of the same length in the steady state.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log〈Δr2(t)〉/d
log〈Δr2(t)〉/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t = 2 to the sub-diffusive motion with α < 1 at intermediate timescales and eventually to the terminal diffusion with α = 1, in agreement with the previous simulation result.43 For fa0 > 0, the MSD is characterized by the new force-driven ballistic regime with α = 2 at long timescales. The overlap of the MSD for the active nanorods prior to the force-driven ballistic regime with the MSD for the passive dynamics of nanorods indicates that the active force is not sufficiently strong such that the nanorod dynamics are dictated by the thermal motion at short timescales. With increasing fa0, the force-driven ballistic regime begins at a shorter time. Eventually, for the largest fa0 = 2ε/σ, the force-driven ballistic regime covers the entire range of timescales explored in the simulations.
t = 2 to the sub-diffusive motion with α < 1 at intermediate timescales and eventually to the terminal diffusion with α = 1, in agreement with the previous simulation result.43 For fa0 > 0, the MSD is characterized by the new force-driven ballistic regime with α = 2 at long timescales. The overlap of the MSD for the active nanorods prior to the force-driven ballistic regime with the MSD for the passive dynamics of nanorods indicates that the active force is not sufficiently strong such that the nanorod dynamics are dictated by the thermal motion at short timescales. With increasing fa0, the force-driven ballistic regime begins at a shorter time. Eventually, for the largest fa0 = 2ε/σ, the force-driven ballistic regime covers the entire range of timescales explored in the simulations.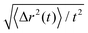 . The increase of va with increasing fa0 for the samples in Fig. 3 is shown in Fig. 4. va for fa0 = 2ε/σ is slightly above the thermal speed of the nanorod with 32 beads of mass m, which is
. The increase of va with increasing fa0 for the samples in Fig. 3 is shown in Fig. 4. va for fa0 = 2ε/σ is slightly above the thermal speed of the nanorod with 32 beads of mass m, which is 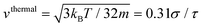 . va > vthermal indicates that the ballistic motion dominates the thermal motion at all timescales, as the displacement vat from the active motion is sufficiently large that it surpasses the displacement vthermalt from the undamped thermal ballistic motion. The increase of va with increasing fa0 can also be observed in the representative trajectories of active nanorods in Fig. 2, where the displacement over the same time of 200τ increases with increasing fa0.
. va > vthermal indicates that the ballistic motion dominates the thermal motion at all timescales, as the displacement vat from the active motion is sufficiently large that it surpasses the displacement vthermalt from the undamped thermal ballistic motion. The increase of va with increasing fa0 can also be observed in the representative trajectories of active nanorods in Fig. 2, where the displacement over the same time of 200τ increases with increasing fa0.
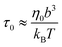
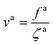
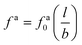

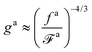
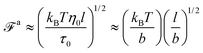
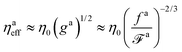
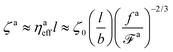
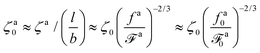
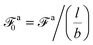
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) a satisfies
a satisfies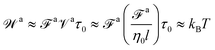
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) a is a strong force at which the rod is coupled only to the monomer viscosity η0 with friction coefficient
a is a strong force at which the rod is coupled only to the monomer viscosity η0 with friction coefficient ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) ≈ η0l, and the work
≈ η0l, and the work ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) a performed by
a performed by ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) a at the constant speed
a at the constant speed ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) a ≈
a ≈ ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) a/
a/![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) over the monomer time scale τ0 is already comparable to the thermal energy kBT.
over the monomer time scale τ0 is already comparable to the thermal energy kBT.
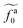 , at which the number of monomers per segment for the chain segments that affect the nanorod dynamics is
, at which the number of monomers per segment for the chain segments that affect the nanorod dynamics is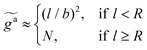
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) a, we obtain the active force at the threshold
a, we obtain the active force at the threshold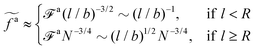
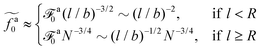
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) a0 is used. Eqn (21) shows that as the rod length increases, there is a crossover from
a0 is used. Eqn (21) shows that as the rod length increases, there is a crossover from 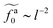 to
to 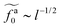 .
.
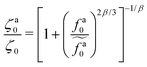
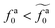 to the power-law regime
to the power-law regime 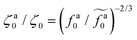 for
for 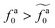 with β quantifying the shape of the curve at
with β quantifying the shape of the curve at 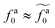 . The exponent −2/3 in the power-law regime is the result of the scaling theory (eqn (15)). Fig. 5b shows the collapse of all simulation data points to the master curve. To obtain the master curve, ζa0/ζ0 for different systems are simultaneously fit to eqn (22). The fitting result of β is 2.9 ± 0.6, and the best fit is used to construct the master curve (thick dashed line in Fig. 5b). The best-fit results of
. The exponent −2/3 in the power-law regime is the result of the scaling theory (eqn (15)). Fig. 5b shows the collapse of all simulation data points to the master curve. To obtain the master curve, ζa0/ζ0 for different systems are simultaneously fit to eqn (22). The fitting result of β is 2.9 ± 0.6, and the best fit is used to construct the master curve (thick dashed line in Fig. 5b). The best-fit results of 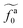 for different samples are shown in the inset to Fig. 5b and used to rescale the corresponding fa0 to the master curve. The successful collapse of the data points in Fig. 5b validates the scaling theory for the power-law reduction of the friction coefficient with increasing strength of activeness (eqn (15)).
for different samples are shown in the inset to Fig. 5b and used to rescale the corresponding fa0 to the master curve. The successful collapse of the data points in Fig. 5b validates the scaling theory for the power-law reduction of the friction coefficient with increasing strength of activeness (eqn (15)).

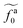 , which is threshold active force for the reduction in ζa0, results in the collapse of the data points in (a) to a master curve. The thick dashed line indicates the master curve (eqn (22)). The inset shows
, which is threshold active force for the reduction in ζa0, results in the collapse of the data points in (a) to a master curve. The thick dashed line indicates the master curve (eqn (22)). The inset shows 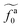 as a function of l for the nanorods in the melts of N = 16 and N = 64. The dashed lines in the inset indicate two scaling regimes in the theory.
as a function of l for the nanorods in the melts of N = 16 and N = 64. The dashed lines in the inset indicate two scaling regimes in the theory.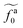 for the force-driven active nanorods in the polymer melt of N = 16 exhibits a crossover from
for the force-driven active nanorods in the polymer melt of N = 16 exhibits a crossover from 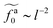 to
to 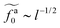 as l increases from l = 4σ slightly below R ≈ 4.7σ to l = 32σ > R. For the nanorods in the other polymer melt of N = 64, l = 4σ and l = 8σ are both smaller than R ≈ 10.1σ, and the l-dependence of
as l increases from l = 4σ slightly below R ≈ 4.7σ to l = 32σ > R. For the nanorods in the other polymer melt of N = 64, l = 4σ and l = 8σ are both smaller than R ≈ 10.1σ, and the l-dependence of 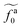 is close to the scaling relation
is close to the scaling relation 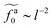 . These results agree with the scaling theory for the onset of the reduction in the friction coefficient (eqn (21)), further validating the theory.
. These results agree with the scaling theory for the onset of the reduction in the friction coefficient (eqn (21)), further validating the theory.
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (t) along the rod axis for the force-driven active nanorods of l = 32σ in polymer melts of N = 16.
(t) along the rod axis for the force-driven active nanorods of l = 32σ in polymer melts of N = 16.
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) (t) along the rod axis for the same systems in Fig. 6.
(t) along the rod axis for the same systems in Fig. 6.



