Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
All-atom simulations of bent liquid crystal dimers: the twist-bend nematic phase and insights into conformational chirality†
Gary
Yu
 and
Mark Richard
Wilson
and
Mark Richard
Wilson
 *
*
Department of Chemistry, Durham University, Lower Mountjoy, Stockton Road, Durham, UK. E-mail: mark.wilson@durham.ac.uk
First published on 25th March 2022
Abstract
The liquid crystal dimer 1,7-bis-4-(4′-cyanobiphenyl)heptane (CB7CB) is known to exhibit a nematic–nematic phase transition, with the lower temperature phase identified as the twist-bend nematic (NTB) phase. Despite the achiral nature of the mesogen, the NTB phase demonstrates emergent chirality through the spontaneous formation of a helical structure. We present extensive molecular dynamics simulations of CB7CB using an all-atom force field. The NTB phase is observed in this model and, upon heating, shows phase transitions into the nematic (N) and isotropic phases. The simulated NTB phase returns a pitch of 8.35 nm and a conical tilt angle of 29°. Analysis of the bend angle between the mesogenic units reveals an average angle of 127°, which is invariant to the simulated phase. We have calculated distributions of the chirality order parameter, χ, for the ensemble of conformers in the NTB and N phases. These distributions elucidate that CB7CB is statistically achiral but can adopt chiral conformers with no preference for a specific handedness. Furthermore, there is no change in the extent of conformational chirality between the NTB and N phases. Using single-molecule stochastic dynamics simulations in the gas phase, we study the dimer series CBnCB (where n = 6, 7, 8 or 9) and CBX(CH2)5YCB (where X/Y = CH2, O or S) in terms of the bend angle and conformational chirality. We confirm that the bent molecular shape determines the ability of a dimer to exhibit the NTB phase rather than its potential to assume chiral conformers; as |χ|max increases with the spacer length, but the even-membered dimers have a linear shape in contrast to the bent nature of dimers with spacers of odd parity. For CBX(CH2)5YCB, it is found that |χ|max increases as the bend angle of the dimer decreases, while the flexibility of the dimers remains unchanged through the series.
1 Introduction
The simplest liquid crystal mesophase is the uniaxial nematic (N) phase, which is characterised by the orientational alignment of the molecules in a preferred direction but with low positional ordering. The introduction of chirality, either by a chiral centre within the mesogen or the addition of a chiral dopant into a host N phase, results in the formation of the chiral nematic (N*) phase which features a helical structure. Independently, Meyer1 and Dozov2 predicted that liquid crystal phases with local chirality could be formed by bent achiral mesogens which was, later, supported by Memmer3 in computer simulations. Dozov proposed that a pure uniform bend in space, arising from the packing of bent molecules, is forbidden and, thus, twist or splay deformations of the local director must accompany the spontaneous bend. In the twist-bend nematic (NTB) phase, a heliconical structure is formed in which the director is tilted with respect to the helical axis, where there are equal numbers of degenerate domains of opposite handedness.The NTB phase was first discovered for 1,7-bis-4-(4′-cyanobiphenyl)heptane, CB7CB, which consists of two mesogenic units connected by a flexible spacer.4–7 The requisite bent molecular shape is exhibited in dimers with a hydrocarbon spacer of odd parity. Other dimeric mesogens,8–17 bent-core species,18,19 and supramolecular hydrogen-bonded systems20–23 have been reported to manifest the NTB phase. Despite the significant number of materials investigated, a general structure–property relationship for the NTB phase remains elusive; although, it is found that a spatially uniform curvature of the molecule is necessary to form the NTB phase regardless of the underlying chemical groups.24,25 The addition of an intrinsic chiral centre into a bent dimer resolves the globally achiral NTB into its chiral counterpart, the NTB* phase, which only contains domains according to the handedness of the chiral centre.26 By extending the length of the terminal alkyl chains, achiral dimers can exhibit a heliconical smectic (SmCTB) phase.27–29 Possible applications utilising the NTB phase such as optical devices,30–33 gels,34 photoswitchable adhesives,35 and photoalignment technology36 have been reported.
Molecular simulation is an effective tool in the study of liquid crystals.37–39 In recent years, improvements in the accuracy of force fields and increase in available computational power has greatly benefited the modelling of these systems.40 All-atom simulations have facilitated the contribution of numerous insights into liquid crystals including: structural, thermodynamic and phase-related properties of nematogens within mesophases and across the phase transitions;41 optimisation of force fields to improve representation of phase transitions and physical properties;42 calculation of molecular chirality and helical twisting powers;43–48 simulation of a biaxial nematic phase;49 predictions of the dark conglomerate phase formed by a bent-core mesogen;50 and investigations of the emergent chirality in achiral bent-core molecules.51–55 An early model for a liquid crystal dimer represented the rigid mesogenic segments with anisotropic Gay–Berne units which were connected by a flexible Lennard-Jones chain.56 Simulations using this model demonstrated the spontaneous growth of smectic phases from the isotropic liquid. A similar model, at the same resolution, displays a Nx phase which was assigned as the polar-twisted N phase.57 Further coarse-grained models, such as a crescent-shaped model of connected hard spheres58 or curved spherocylinders,59–61 successfully exhibit the NTB phase. At the fully atomistic level, conformational probability distributions for CB7CB show a broad peak centred at approximately 120° for the molecular bend angle with a minor peak at about 30° corresponding to hairpin conformers.4,16 Atomistic simulations have also captured the NTB phase and are in good agreement with experimental findings.6
In this paper, we present extensive all-atom molecular dynamics (AA MD) simulations of the bent liquid crystal dimer CB7CB. We observe the formation of the NTB phase, characterise its properties, and explore the CB7CB phase diagram as a function of temperature. The simulations provide a full description of the orientational order of molecules in the N and NTB phases and a detailed examination of the structure of CB7CB molecules in these phases. We calculate distributions of the bend angle and chirality order parameter for molecules in the N and NTB phases. Using single-molecule simulations in the gas phase, we expand the scope of the investigation to the dimer series CBnCB (where n = 6, 7, 8 or 9) and CBX(CH2)5YCB (where X/Y = CH2, O or S). The effect of the spacer length and heteroatom linkages are discussed in terms of the conformational distributions of the bend angle and their molecular chirality.
2 Computational methods
2.1 Force field
The General AMBER Force Field (GAFF) was utilised for atomistic simulations.62 The Antechamber package from AmberTools1863 was employed to generate Lennard-Jones potentials and atomic charges for the force field, with the latter employing the AM1-BCC method.64 The output GAFF topologies were converted into the necessary input files for GROMACS by the ACPYPE script.652.2 Simulation details
A bulk system was set up by randomly inserting 512 molecules of CB7CB, which were oriented with the molecular long axes aligned with the z-axis, into a box with dimensions of 8 nm × 8 nm × 16 nm. Initially, an additional improper dihedral potential (with an equilibrium angle of 180° and force constant of 25 kJ mol−1) was applied across each molecule, between the terminal nitrogen atoms and the linking carbon of the mesogenic units with the alkyl spacer and the corresponding atoms on the other cyanobiphenyl segment, to enforce an all-trans configuration of the heptane chain.All MD simulations were carried out using the GROMACS 2021.1 molecular dynamics simulation package.66 A cutoff of 1.2 nm was used for all short-range interactions and long-range electrostatics were treated with the Particle Mesh Ewald (PME) method.67 After a steepest-descent minimisation, a 100 ps pre-equilibration run in the NVT ensemble was carried out using the Berendsen thermostat followed by a 100 ps pre-equilibration in the NPT ensemble with the addition of the Berendsen barostat.68 Simulations were performed using semi-isotropic pressure coupling which allows for the x/y and z dimensions of the system to vary independently. Time constants of 1 ps and 5 ps were used for the thermostat and barostat, respectively. The system was compressed with a pressure of 100 bar for 1 ns, before an equilibration run of 500 ps was carried out using the Nosé–Hoover thermostat69,70 to maintain a constant temperature of 370 K, and the Parrinello–Rahman barostat71 to keep the pressure constant at 1 bar. A leap-frog algorithm was employed with a time step of 1 fs for equilibration with an increase to 2 fs for production simulations, where constraints were implemented using the LINCS method.72 At this point, the system exhibited a nematic phase which acted as an ideal starting configuration. A final equilibration of 1 ns was executed without the additional biasing potential to allow for equilibration of the molecular conformations and for the heliconical structure to start developing. Finally, a production simulation of 1 μs was performed. Equilibration was ensured by monitoring average values for thermodynamic and structural quantities, and checking that they were stabilised. MD simulations were carried out on the new N8 CIR supercomputer Bede, housed at Durham University, using one NVIDIA V100 GPU; achieving a performance of 180 ns day−1 on a ∼30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atom system.
000 atom system.
The concluding system at 370 K was used as the starting configuration for a heating/cooling sequence. Simulations were performed at 10 K intervals for 200 ns each in the temperature range of 350–470 K.
For the chirality order parameter calculations, the sampling of conformers was conducted via single-molecule simulations in the gas phase using a stochastic dynamics (SD) integrator at a temperature of 370 K with a standard friction constant of 0.5 ps−1. Each molecule was equilibrated for 1 ns before a 500 ns production run to obtain data with snapshots being collected in 1 ps intervals. For single-molecule MD simulations calculations there are no collisions with neighbouring molecules to exchange energy and aid molecules to traverse high conformational energy barriers. Consequently, SD provides improved conformational sampling for single molecules in comparison to standard MD thermostats.
All simulation snapshots were visualised in VMD, version 1.9.3.73
2.3 Orientational order parameter
The orientational order parameter, S2, can be determined from diagonalisation of the order tensor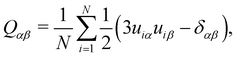 | (1) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) , of the system. The unit vector, ûi, of the molecular long axis for a molecule i can be defined by the eigenvector corresponding to the lowest eigenvalue found by diagonalising the moment of inertia tensor for a molecule
, of the system. The unit vector, ûi, of the molecular long axis for a molecule i can be defined by the eigenvector corresponding to the lowest eigenvalue found by diagonalising the moment of inertia tensor for a molecule | (2) |
2.4 Chirality order parameter
Ferrarini et al. developed a surface chirality model to determine a chirality order parameter, χ, based on a molecular isosurface which describes the coupling between the surface chirality and orientational order of the molecule.74–77 The value of χ is positive for right-handed conformers and negative for left-handed ones. Here, molecular isosurfaces were generated using the Simple Invariant Molecular Surface (SIMS) method developed by Vorobjev and Hermans.78 This utilised a rolling sphere algorithm where a spherical probe with a diameter of 5 Å produced a corresponding van der Waals surface of a molecule with a point resolution of 10 dots per Å2. Three tensors are obtained from the isosurface for the calculation of χ: the surface tensor (T), the helicity tensor (Q) and the ordering matrix (S). Numerical integration of the normal vectors over the surface points yields T, whereas integration over the molecular surface produces Q. The ordering matrix, S, is calculated by integration of an orientational distribution function involving an orienting potential describing the orientation of the solute molecule within a liquid crystal phase.46 Finally, the chirality order parameter is calculated from | (3) |
3 Results and discussion
3.1 Phase behaviour
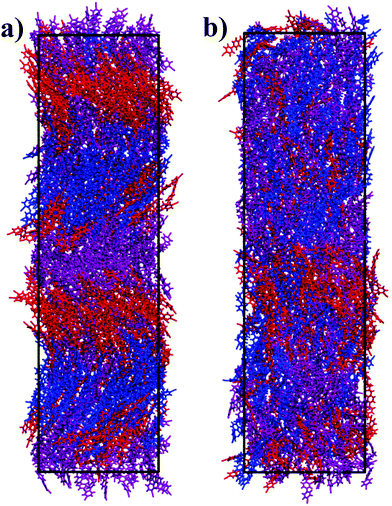
The system of 512 molecules of CB7CB at 370 K exhibited a heliconical structure that was stable for hundreds of nanoseconds. A snapshot of this simulated phase is shown in Fig. 2(a) in which molecules are coloured in blue, purple or red according to their azimuth angle (ϕ) in the range −180° ≤ ϕ < −60°, −60°≤ ϕ < 60° and 60°≤ ϕ ≤ 180°, respectively. The angle ϕ was calculated for the unit vector â which corresponds to the molecular long axis of the molecule. A second unit vector![[b with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0062_0302.gif) can be defined as the unit vector which bisects the two vectors between a terminal nitrogen atom and the centre of mass (COM) of the molecule. A schematic for these unit vectors is shown in Fig. 1. From visual inspection, a helical structure is found where the molecules are tilted with respect to the helical axis which largely coincides with the z axis of the box. It is noted that the helix found here is left-handed and that, experimentally, there are equal domains of opposite handedness.
can be defined as the unit vector which bisects the two vectors between a terminal nitrogen atom and the centre of mass (COM) of the molecule. A schematic for these unit vectors is shown in Fig. 1. From visual inspection, a helical structure is found where the molecules are tilted with respect to the helical axis which largely coincides with the z axis of the box. It is noted that the helix found here is left-handed and that, experimentally, there are equal domains of opposite handedness.
The defined unit vectors were utilised in the analysis of the system. An orientational correlation function, Sbb, can be calculated as a function of intermolecular distance along the helical axis, r‖, by79
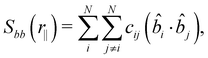 | (4) |
 | (5) |
![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) precesses about the helical axis through the system as expected in the NTB phase. This behaviour has been found for simulated phases previously.57,58 From this plot (shown in Fig. 3 for the final configuration at 370 K), it can be seen that minima/maxima occur at distances (n + 1/2)p, where n is 0, 1/2 and 1, and the pitch, p, is estimated to be 8.35 ± 0.2 nm. Our measured pitch is in good agreement with those found experimentally in the NTB phase for CB7CB of ∼8 nm.6,7
precesses about the helical axis through the system as expected in the NTB phase. This behaviour has been found for simulated phases previously.57,58 From this plot (shown in Fig. 3 for the final configuration at 370 K), it can be seen that minima/maxima occur at distances (n + 1/2)p, where n is 0, 1/2 and 1, and the pitch, p, is estimated to be 8.35 ± 0.2 nm. Our measured pitch is in good agreement with those found experimentally in the NTB phase for CB7CB of ∼8 nm.6,7
The conical tilt angle, θ, is defined as the angle between the unit vector â and the helical axis. Noting that θ(z) = ±|k|z = ±2πz/p. A histogram of θ values observed in the system is shown in Fig. 3(b), which confirms that the molecules in the simulated phase are tilted with the average conical tilt angle measured to be 29°. Our simulation result is slightly higher than the ∼25° reported experimentally.6,80,81
The simulated system at 370 K, which has been characterised as the NTB phase, was cooled/heated in order to produced a full phase diagram for the AA model. Simulations were performed in the temperature range of 350–470 K and the average orientational order parameter, 〈S2〉, was determined for unit vectors â and ![[b with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0062_0302.gif) . The results are presented in Fig. 4 in which the stability range of the NTB, N and isotropic (I) phases are indicated. Here, we define the NTB–N phase transition as the temperature at which helical ordering is lost (〈S2〉b ≈ 0) and the I phase is identified when, additionally, 〈S2〉a ≈ 0.1. It is noted that, via visual inspection, the system at 430 K appears nematic but does not satisfy the aforementioned criteria for the N phase. A simulation snapshot of the N phase for CB7CB at 440 K is shown in Fig. 2(b). For 〈S2〉b, this value diminishes slightly as the system is heated which is expected as the helix unwinds upon its approach into the N phase.80 For 〈S2〉a, the nematic-like ordering increases with temperature throughout the NTB phase until the phase transition into the N phase. This trend is observed in X-ray and polarised Raman scattering experiments and our measured values for 〈S2〉a of ∼0.35 in the NTB phase (and subsequent values in the N phase) compare favourably.81,82 However, the phase transitions in the AA model, TNTB–N = 435 K and TN–I = 460 K, occur at temperatures higher than reported7 (experimentally, TNTB–N = 376 K and TN–I = 389 K). We suggest that the force field for CB7CB produces molecules that are slightly too stiff, thus mesogens are slightly elongated favouring orientational ordering and require slightly more energy to induce conformational changes. Both effects tend to increase transition temperatures. The force field would require further optimisation of the interatomic interaction parameters to reproduce the correct phase transitions. This has been demonstrated for GAFF in studies of liquid crystals systems, where the representation of structural and phase properties have been improved.42,50,53,83
. The results are presented in Fig. 4 in which the stability range of the NTB, N and isotropic (I) phases are indicated. Here, we define the NTB–N phase transition as the temperature at which helical ordering is lost (〈S2〉b ≈ 0) and the I phase is identified when, additionally, 〈S2〉a ≈ 0.1. It is noted that, via visual inspection, the system at 430 K appears nematic but does not satisfy the aforementioned criteria for the N phase. A simulation snapshot of the N phase for CB7CB at 440 K is shown in Fig. 2(b). For 〈S2〉b, this value diminishes slightly as the system is heated which is expected as the helix unwinds upon its approach into the N phase.80 For 〈S2〉a, the nematic-like ordering increases with temperature throughout the NTB phase until the phase transition into the N phase. This trend is observed in X-ray and polarised Raman scattering experiments and our measured values for 〈S2〉a of ∼0.35 in the NTB phase (and subsequent values in the N phase) compare favourably.81,82 However, the phase transitions in the AA model, TNTB–N = 435 K and TN–I = 460 K, occur at temperatures higher than reported7 (experimentally, TNTB–N = 376 K and TN–I = 389 K). We suggest that the force field for CB7CB produces molecules that are slightly too stiff, thus mesogens are slightly elongated favouring orientational ordering and require slightly more energy to induce conformational changes. Both effects tend to increase transition temperatures. The force field would require further optimisation of the interatomic interaction parameters to reproduce the correct phase transitions. This has been demonstrated for GAFF in studies of liquid crystals systems, where the representation of structural and phase properties have been improved.42,50,53,83
 | ||
Fig. 4 Average orientational order parameter, 〈S2〉, for unit vectors â and ![[b with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0062_0302.gif) as a function of temperature. as a function of temperature. | ||
3.2 Conformational distributions and molecular chirality
The following section focuses on the conformational properties of bent dimer mesogens and their ability to exhibit chiral conformations. The bend angle of the mesogen can be defined as the angle between the unit vectors representing the para axes of the cyanobiphenyl units (i.e. the vector calculated between the nitrogen atom and the carbon atom connecting the cyanobiphenyl unit to the spacer). Based on the simulations performed in the previous section, Fig. 5 shows histograms of this bend angle for CB7CB in the N and NTB phases. In both phases, the average bend angle is found to be 127°. This is somewhat higher than the value of ∼120° determined by Monte Carlo sampling in previous single-molecule studies4,16 but in line with a bulk phase MD simulation6 value of 133°. It is found that the bend angle distribution does not change significantly between molecules in the N and NTB phases but the broadness of the peak in the N phase increases, as expected for the higher temperature. The histograms also show a minor peak at 20° corresponding to hairpin conformers. NMR experiments suggest that the conformational distribution for CB7CB does not change significantly between the N and NTB phases and that the chirality of the NTB phase is a consequence of the bent molecular shape.84 | ||
| Fig. 5 Distribution functions for the bend angle between the mesogenic units in the N and NTB phases at 440 K and 370 K, respectively. | ||
Distributions of the chirality order parameter, χ, were calculated for CB7CB for molecules in the N and NTB phases, and for a single molecule in the gas phase. These are presented in Fig. 6(a). All three plots demonstrate that CB7CB is statistically achiral (with the peaks centred at χ = 0) but can adopt chiral conformers with equal probability of left- or right-handedness (as the peaks are symmetric). This behaviour has been reported previously in single-molecule simulations of the PnOPIMB series of bent-core mesogens.52,53 The aforementioned calculations found, for similar model parameters, values of |χ|max to be ∼800 and greater whereas, in this work, we have estimated |χ|max to be ∼200 for CB7CB. The much higher |χ|max for the bent-core molecules, compared to CB7CB, may account for why P8OPIMB can form the highly twisted B4 phase which consists of helical nanofilaments.85 The ability of achiral bent-core mesogens51,52 and CB7CB86,87 to decrease the pitch of a N* phase is hypothesised to be a result of the presence of chiral conformers with high helical twisting powers.52,53 Interestingly, the distributions of χ are unchanged between the N and NTB phases, which indicates that there is no change in the molecular chirality of the conformations even as the phase gains chirality. This is in line with analogous findings for the conformational distributions.84 The analysis of the molecular chirality for a single molecule in the gas phase produces a distribution that is very similar to that from the condensed phases with the exception that the peak is broader. This is expected as there is greater freedom for the molecule to sample a wider range of conformers in the gas phase.
From Fig. 6(a), it can be seen that sampling of conformers via a single-molecule simulation provides a good approximation for the distributions of χ obtained from simulations of the liquid crystal phases. This approach is relatively facile as the full calculations, from the automated generation of the force field/input files to the acquisition of the χ distribution, takes ∼20 hours and does not require a liquid crystal phase to be equilibrated. Thus, we can expand the scope of our investigation to the series of bent dimers CBnCB (where n = 6, 7, 8 or 9) and CBX(CH2)5YCB (where X/Y = CH2, O or S). The first series of mesogens allows for the odd–even effect and the effect of the spacer length on the conformations/chirality of the molecule to be studied. The second series consists of bent dimers all with 7 heavy atoms in the spacer and considers the effect of heteroatoms in the linking chain.
The odd–even effect of the spacer on typical liquid crystalline phase behaviour is well-documented, and the NTB phase is only found for odd-membered mesogenic dimers.88–90 It is found that, in the all-trans configuration, dimers with an odd spacer will exhibit a bent molecular shape whereas an even spacer will result in a more linear shape. Moreover, the sensitivity of TNTB–N to the bend angle has been demonstrated by a generalised Maier–Saupe theory.91 Bend angle distributions for the CBnCB series are shown in Fig. 7(a). We obtain mean bend angles of 165°, 110°, 172° and 99° for n = 6, 7, 8 and 9, respectively at 370 K. Previously reported values include 166° for CB6CB,6 111–120° for CB7CB,4,16,92 and 102° for CB9CB.93 Overall, our measured values are in good agreement with previous work and the correct trend is observed. Notably, the bend angle for CB7CB in the gas phase is lower than in the N and NTB phases, which suggests that the effect of a nematic environment on the conformational distribution is significant. This indicates that single-molecule calculations, regardless of the level of theory, are not truly representative of the actual behaviour within a mesophase. This is expected as the constraints arising from the packing of molecules in the N phase will affect the conformers adopted by the mesogens as well as promote a more linear shape of the molecules.94,95 For the even-membered dimers, the dominant conformers are those with linear configurations, but there is the presence of a significant number of bent conformers with bend angles of around 85° and 130° for CB6CB and CB8CB, respectively. These bent conformers are likely to be suppressed strongly in the N phase.
 | ||
| Fig. 7 Distribution functions of the (a) bend angle and (b) chirality order parameter, χ, for CBnCB where n = 6, 7, 8 or 9. | ||
The χ distributions for the CBnCB series are presented in Fig. 7(b) and all show that the mesogens are statistically achiral but can adopt chiral conformers of opposite handedness with equal probability. The histograms for CB6CB and CB8CB are noticeably narrower than those for the dimers with odd spacers. This demonstrates that the more linear shape of the even-membered dimers results in a lower tendency to exhibit instantaneous conformations with high helical twisting powers. For n = 6, 7 and 8, |χ|max ≈ 200 but is ∼250 for CB9CB. It seems that there is a slight increase in |χ|max as the length of the spacer increases regardless of the odd/even parity of the chain. This suggests strongly that the ability to form the NTB phase for dimers with a spacer of odd parity, or only exhibit the N phase for dimers with a spacer of even parity, is dependent on the molecular shape of the mesogen and not its potential to assume chiral conformers.96
In the CBX(CH2)5YCB series (where X/Y = CH2, O or S), the NTB phase is observed for all molecules.16,92,97–99 While it is generally considered that CBO nOCB homologues mainly form the N phase, the presence of a NTB phase is indicated for CBO5OCB by changes in the optical texture upon supercooling.100,101 Here, we measure peaks in the bend angle distribution (see Fig. 8(a)) of 116° for CB6OCB, 110° for CB6SCB, 120° for CBO5OCB, 100° for CBS5SCB and 112° for CBS5OCB. Conformational sampling provides a reported value of ∼120° for CB6OCB16 and optimised geometries of dimers, with all-trans configurations of the spacer,92 give bend angles of 143° for CBO5OCB, 94° for CBS5SCB and 119° for CBS5OCB. Our results compare favourably with the exception of CBO5OCB.92 It is noted that this literature value was obtained from a single conformer, albeit the minimum energy geometry, which does not consider the flexibility of the molecule.
 | ||
| Fig. 8 Distribution functions of the (a) bend angle and (b) chirality order parameter, χ, for CBX(CH2)5YCB where X/Y = CH2, O or S. The inset shows a focused view of the plot near |χ|max. | ||
Since the CBX(CH2)5YCB (where X/Y = CH2, O or S) series all have spacer lengths of 7 heavy atoms, any differences will mostly arise from the bond angle and flexibility afforded by the heteroatom linkage. The χ distributions are presented in Fig. 8(b). Here, we observe that the distributions get broader and |χ|max increases for bent dimers in the order CBO5OCB, CB6OCB, CBS5OCB, CB6SCB to CBS5SCB. This is also the sequence of dimers going from the highest to lowest average bend angle measured here. Thus, we obtain the trend that a lower bend angle results in a higher degree of conformational chirality. Experimentally, the effect of the bend angle on TNTB–N is unclear. The sulfur-linked dimers unexpectedly exhibit a lower TNTB–N than the methylene versions despite having a smaller bend angle.92,100 As |χ|max is commensurate with the bend angle, we similarly do not observe any correlation between the presence of high χ conformers and the stability of the NTB phase or transition temperatures. The full width at half maximum of the main peaks in Fig. 8a (which is a measure of the flexibility) is ∼50° for CB7CB and all the CBX(CH2)5YCB dimers, and so it cannot be said that there is a strong link between the flexibility (i.e. polydispersity of bend angles) and TNTB–N.
4 Conclusions
In conclusion, we have presented extensive AA MD results for the bent liquid crystal dimer CB7CB. The simulations show a NTB phase, which has a pitch of 8.35 nm and a conical tilt angle of 29°. Upon heating, phase transitions into the N and I phases are observed but TNTB–N and TN–I are overestimated. We suggest that improvements to the force field could be made, according to previously reported methodologies,42,50,53,83 to better represent the transition temperatures. Analysis of the bend angle between the cyanobiphenyl units for CB7CB produces an average value of 127°, which is invariant between the NTB and N phases. Distributions of the chirality order parameter, χ, demonstrate that CB7CB is statistically achiral but can adopt chiral conformers of opposite handedness with equal probability, and that the degree of molecular chirality is unchanged between the NTB and N phases.Using single-molecule simulations in the gas phase, distributions of the bend angle and χ are determined for the series of dimers CBnCB (where n = 6, 7, 8 or 9) and CBX(CH2)5YCB (where X/Y = CH2, O or S). We obtain bend angles in good agreement with previously reported values with a simple and fast process. For CBnCB, we confirm that the ability to exhibit the NTB phase is dependent on a bent molecular shape and not from the potential of the dimer to assume chiral conformers. For CBX(CH2)5YCB, we report that a decrease in the bend angle increases |χ|max. This corresponds to an increase in the extent of instantaneous chiral conformations for dimers with higher bent molecular curvature, despite the flexibility being similar.
The workflow presented here is easily automated, could be coupled with optimised parameters for the force field, and provides a route for high-throughput analysis of various properties of liquid crystal mesogens.
Finally, we note that all-atom simulations of the type described here provide unique insights into how molecules are arranged at the molecular level in complex mesophases, such as the NTB. Future atomistic studies of other materials are likely to provide valuable insights into how molecular structure is related to the range of stability of NTB phases. The influence of subtle changes in molecular shape, interactions and flexibility is very difficult to capture within a simple coarse-grained model. However, we are currently developing bottom-up coarse-grained approaches to multiscale modelling. These approaches use conformational and through-space interactions from an underlying atomistic reference to provide new coarse-grained molecular models that incorporate flexibility and aim to capture the influence of subtle changes in molecular structure on phase behaviour.102,103 This work will facilitate the study of these fascinating liquid crystal phases on larger length and time scales.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by Durham University and EPSRC (EP/R513039/1). This work made use of the facilities, Bede, of the N8 Centre of Excellence in Computationally Intensive Research (N8 CIR) provided and funded by the N8 research partnership and EPSRC (Grant No. EP/T022167/1). The Centre is co-ordinated by the Universities of Durham, Manchester and York. The authors would also like to thank Martin Walker for providing the code to calculate the chirality order parameters.Notes and references
- R. B. Meyer, in Les Houches Summer School in Theoretical Physics, ed. R. G. Balian and G. Weil, Gordon and Breach, New York, 1976, pp. 273–373 Search PubMed.
- I. Dozov, Europhys. Lett., 2001, 56, 247–253 CrossRef CAS.
- R. Memmer, Liq. Cryst., 2002, 29, 483–496 CrossRef CAS.
- M. Cestari, S. Diez-Berart, D. A. Dunmur, A. Ferrarini, M. R. de la Fuente, D. J. B. Jackson, D. O. Lopez, G. R. Luckhurst, M. A. Perez-Jubindo, R. M. Richardson, J. Salud, B. A. Timimi and H. Zimmermann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031704 CrossRef CAS PubMed.
- C. Meyer, G. R. Luckhurst and I. Dozov, Phys. Rev. Lett., 2013, 111, 067801 CrossRef CAS PubMed.
- D. Chen, J. H. Porada, J. B. Hooper, A. Klittnick, Y. Shen, M. R. Tuchband, E. Korblova, D. Bedrov, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15931–15936 CrossRef CAS PubMed.
- V. Borshch, Y. K. Kim, J. Xiang, M. Gao, A. Jákli, V. P. Panov, J. K. Vij, C. T. Imrie, M. G. Tamba, G. H. Mehl and O. D. Lavrentovich, Nat. Commun., 2013, 4, 2635 CrossRef CAS PubMed.
- M. Sepelj, A. Lesac, U. Baumeister, S. Diele, H. L. Nguyen and D. W. Bruce, J. Mater. Chem., 2007, 17, 1154–1165 RSC.
- V. P. Panov, M. Nagaraj, J. K. Vij, Y. P. Panarin, A. Kohlmeier, M. G. Tamba, R. A. Lewis and G. H. Mehl, Phys. Rev. Lett., 2010, 105, 167801 CrossRef CAS PubMed.
- P. A. Henderson and C. T. Imrie, Liq. Cryst., 2011, 38, 1407–1414 CrossRef CAS.
- K. Adlem, M. Čopič, G. R. Luckhurst, A. Mertelj, O. Parri, R. M. Richardson, B. D. Snow, B. A. Timimi, R. P. Tuffin and D. Wilkes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022503 CrossRef CAS PubMed.
- R. J. Mandle, E. J. Davis, S. A. Lobato, C.-C. A. Vol, S. J. Cowling and J. W. Goodby, Phys. Chem. Chem. Phys., 2014, 16, 6907–6915 RSC.
- R. J. Mandle, E. J. Davis, C. T. Archbold, S. J. Cowling and J. W. Goodby, J. Mater. Chem. C, 2014, 2, 556–566 RSC.
- R. J. Mandle, E. J. Davis, C. T. Archbold, C.-C. A. Voll, J. L. Andrews, S. J. Cowling and J. W. Goodby, Chem. – Eur. J., 2015, 21, 8158–8167 CrossRef CAS PubMed.
- E. Gorecka, N. Vaupotic, A. Zep, D. Pociecha, J. Yoshioka, J. Yamamoto and H. Takezoe, Angew. Chem., Int. Ed., 2015, 54, 10155–10159 CrossRef CAS PubMed.
- D. A. Paterson, M. Gao, Y.-K. Kim, A. Jamali, K. L. Finley, B. Robles-Hernández, S. Diez-Berart, J. Salud, M. R. de la Fuente, B. A. Timimi, H. Zimmermann, C. Greco, A. Ferrarini, J. M. D. Storey, D. O. López, O. D. Lavrentovich, G. R. Luckhurst and C. T. Imrie, Soft Matter, 2016, 12, 6827–6840 RSC.
- D. A. Paterson, J. P. Abberley, W. T. A. Harrison, J. M. D. Storey and C. T. Imrie, Liq. Cryst., 2017, 44, 127–146 CAS.
- D. Chen, M. Nakata, R. Shao, M. R. Tuchband, M. Shuai, U. Baumeister, W. Weissflog, D. M. Walba, M. A. Glaser, J. E. Maclennan and N. A. Clark, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022506 CrossRef PubMed.
- S. P. Sreenilayam, V. P. Panov, J. K. Vij and G. Shanker, Liq. Cryst., 2017, 44, 244–253 CAS.
- S. M. Jansze, A. Martínez-Felipe, J. M. D. Storey, A. T. M. Marcelis and C. T. Imrie, Angew. Chem., Int. Ed., 2015, 54, 643–646 CAS.
- R. Walker, D. Pociecha, J. P. Abberley, A. Martinez-Felipe, D. A. Paterson, E. Forsyth, G. B. Lawrence, P. A. Henderson, J. M. D. Storey, E. Gorecka and C. T. Imrie, Chem. Commun., 2018, 54, 3383–3386 RSC.
- R. Walker, D. Pociecha, A. Martinez-Felipe, J. M. D. Storey, E. Gorecka and C. T. Imrie, Crystals, 2020, 10, 175 CrossRef CAS.
- R. Walker, D. Pociecha, M. Salamończyk, J. M. D. Storey, E. Gorecka and C. T. Imrie, Mater. Adv., 2020, 1, 1622–1630 RSC.
- R. J. Mandle, Soft Matter, 2016, 12, 7883–7901 RSC.
- R. Walker, Liq. Cryst. Today, 2020, 29, 2–14 CrossRef CAS.
- R. Walker, D. Pociecha, J. M. D. Storey, E. Gorecka and C. T. Imrie, Chem. – Eur. J., 2019, 25, 13329–13335 CrossRef CAS PubMed.
- J. P. Abberley, R. Killah, R. Walker, J. M. D. Storey, C. T. Imrie, M. Salamończyk, C. Zhu, E. Gorecka and D. Pociecha, Nat. Commun., 2018, 9, 228 CrossRef PubMed.
- R. Walker, D. Pociecha, G. J. Strachan, J. M. D. Storey, E. Gorecka and C. T. Imrie, Soft Matter, 2019, 15, 3188–3197 RSC.
- M. Salamończyk, N. Vaupoti, D. Pociecha, R. Walker, J. M. D. Storey, C. T. Imrie, C. Wang, C. Zhu and E. Gorecka, Nat. Commun., 2019, 10, 1922 CrossRef PubMed.
- J. Xiang, Y. Li, Q. Li, D. A. Paterson, J. M. D. Storey, C. T. Imrie and O. D. Lavrentovich, Adv. Mater., 2015, 27, 3014–3018 CrossRef CAS PubMed.
- J. Xiang, A. Varanytsia, F. Minkowski, D. A. Paterson, J. M. D. Storey, C. T. Imrie, O. D. Lavrentovich and P. Palffy-Muhoray, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12925–12928 CrossRef CAS PubMed.
- M. Mrukiewicz, O. S. Iadlovska, G. Babakhanova, S. Siemianowski, S. V. Shiyanovskii and O. D. Lavrentovich, Liq. Cryst., 2019, 46, 1544–1550 CrossRef CAS.
- S. K. Prasad, P. L. Madhuri, P. Satapathy and C. V. Yelamaggad, Appl. Phys. Lett., 2018, 112, 253701 CrossRef.
- V. Sridurai, M. B. Kanakala, C. V. Yelamaggad and G. G. Nair, Soft Matter, 2019, 15, 9982–9990 RSC.
- S. Aya, P. Salamon, D. A. Paterson, J. M. D. Storey, C. T. Imrie, F. Araoka, A. Jákli and A. Buka, Adv. Mater. Interfaces, 2019, 6, 1802032 CrossRef.
- C. Feng, J. Feng, R. Saha, Y. Arakawa, J. Gleeson, S. Sprunt, C. Zhu and A. Jákli, Phys. Rev. Res., 2020, 2, 032004 CrossRef CAS.
- C. Zannoni, Liq. Cryst., 2018, 45, 1880–1893 CrossRef CAS.
- C. Zannoni, J. Mater. Chem., 2001, 11, 2637–2646 RSC.
- P. Pasini and C. Zannoni, Advances in the Computer Simulatons of Liquid Crystals, Springer, Dordrecht, 1999 Search PubMed.
- M. P. Allen, Liq. Cryst., 2019, 117, 2391–2417 CAS.
- M. R. Wilson, Chem. Soc. Rev., 2007, 36, 1881–1888 RSC.
- N. J. Boyd and M. R. Wilson, Phys. Chem. Chem. Phys., 2015, 17, 24851–24865 RSC.
- M. J. Cook and M. R. Wilson, J. Chem. Phys., 2000, 112, 1560–1564 CrossRef CAS.
- M. R. Wilson and D. J. Earl, J. Mater. Chem., 2001, 11, 2672–2677 RSC.
- M. P. Neal, M. Solymosi, M. R. Wilson and D. J. Earl, J. Chem. Phys., 2003, 119, 3567–3573 CrossRef CAS.
- D. J. Earl and M. R. Wilson, J. Chem. Phys., 2003, 119, 10280–10288 CrossRef CAS.
- D. J. Earl and M. R. Wilson, J. Chem. Phys., 2004, 120, 9679–9683 CrossRef CAS PubMed.
- D. J. Earl, M. A. Osipov, H. Takezoe, Y. Takanishi and M. R. Wilson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 021706 CrossRef PubMed.
- J. Peláez and M. R. Wilson, Phys. Rev. Lett., 2006, 97, 267801 CrossRef PubMed.
- N. J. Boyd and M. R. Wilson, Phys. Chem. Chem. Phys., 2018, 20, 1485–1496 RSC.
- S.-Y. Jo, B.-C. Kim, S.-W. Jeon, J.-H. Bae, M. Walker, M. Wilson, S.-W. Choi and H. Takezoe, RSC Adv., 2017, 7, 1932–1935 RSC.
- B.-C. Kim, M. Walker, S.-Y. Jo, M. R. Wilson, H. Takezoe and S.-W. Choi, RSC Adv., 2018, 8, 1292–1295 RSC.
- J. S. Lintuvuori, G. Yu, M. Walker and M. R. Wilson, Liq. Cryst., 2018, 45, 1996–2009 CrossRef CAS.
- S. Shadpour, A. Nemati, N. J. Boyd, L. Li, M. E. Prévôt, S. L. Wakerlin, J. P. Vanegas, M. Salamończyk, E. Hegmann, C. Zhu, M. R. Wilson, A. I. Jákli and T. Hegmann, Mater. Horiz., 2019, 6, 959–968 RSC.
- S. Shadpour, A. Nemati, M. Salamończyk, M. E. Prévôt, J. Liu, N. J. Boyd, M. R. Wilson, C. Zhu, E. Hegmann, A. I. Jákli and T. Hegmann, Small, 2020, 16, 1905591 CrossRef CAS PubMed.
- M. R. Wilson, J. Chem. Phys., 1998, 107, 8654–8663 CrossRef.
- A. G. Vanakaras and D. J. Photinos, Liq. Cryst., 2018, 45, 2184–2196 CrossRef CAS.
- C. Greco and A. Ferrarini, Phys. Rev. Lett., 2015, 115, 147801 CrossRef PubMed.
- M. Chiappini, A. Patti and M. Dijkstra, Phys. Rev. E, 2020, 102, 040601 CrossRef CAS PubMed.
- M. Chiappini and M. Dijkstra, Nat. Commun., 2021, 12, 2157 CrossRef CAS PubMed.
- M. Chiappini, T. Drwenski, R. van Roij and M. Dijkstra, Phys. Rev. Lett., 2019, 123, 068001 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- A. Jakalian, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS PubMed.
- A. W. S. da Silva and W. F. Vranken, BMC Res. Notes, 2012, 5, 367 CrossRef PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoell, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- A. Ferrarini, G. J. Moro and P. L. Nordio, Liq. Cryst., 1995, 19, 397–399 CrossRef CAS.
- A. Ferrarini, G. J. Moro and P. L. Nordio, Mol. Phys., 1996, 87, 485–499 CrossRef CAS.
- A. Ferrarini, G. Gottarelli, P. L. Nordio and G. P. Spada, J. Chem. Soc., Perkin Trans. 2, 1999, 411–418 RSC.
- A. di Matteo, S. M. Todd, G. Gottarelli, G. Solladie, V. E. Williams, R. P. Lemieux, A. Ferrarini and G. P. Spada, J. Am. Chem. Soc., 2001, 123, 7842–7851 CrossRef CAS PubMed.
- Y. Vorobjev and J. Hermans, Biophys. J., 1997, 73, 722–732 CrossRef CAS PubMed.
- A. J. Stone, Mol. Phys., 1978, 36, 241–256 CrossRef CAS.
- C. Meyer, G. R. Luckhurst and I. Dozov, J. Mater. Chem. C, 2015, 3, 318–328 RSC.
- G. Singh, J. Fu, D. M. Agra-Kooijman, J.-K. Song, M. R. Vengatesan, M. Srinivasarao, M. R. Fisch and S. Kumar, Phys. Rev. E, 2016, 94, 060701 CrossRef PubMed.
- R. J. Mandle and J. W. Goodby, Phys. Chem. Chem. Phys., 2019, 21, 6839–6843 RSC.
- G. Yu, M. Walker and M. R. Wilson, Phys. Chem. Chem. Phys., 2021, 23, 6408–6421 RSC.
- J. W. Emsley, M. Lelli, A. Lesage and G. R. Luckhurst, J. Phys. Chem. B, 2013, 117, 6547–6557 CrossRef CAS PubMed.
- C. Zhang, N. Diorio, O. D. Lavrentovich and A. Jákli, Nat. Commun., 2014, 5, 3302 CrossRef CAS PubMed.
- A. Varanytsia and L.-C. Chien, J. Appl. Phys., 2016, 119, 014502 CrossRef.
- Y.-C. Lin, P.-C. Wu and W. Lee, Photonics Res., 2019, 7, 1258–1265 CrossRef CAS.
- C. T. Imrie and P. A. Henderson, Chem. Soc. Rev., 2007, 36, 2096–2124 RSC.
- A. Ferrarini, G. R. Luckhurst, P. L. Nordio and S. J. Roskilly, J. Chem. Phys., 1994, 100, 1460–1469 CrossRef CAS.
- G. R. Luckhurst and S. Romano, J. Chem. Phys., 1997, 107, 2557–2572 CrossRef CAS.
- C. Greco, G. R. Luckhurst and A. Ferrarini, Soft Matter, 2014, 10, 9318–9323 RSC.
- E. Cruickshank, M. Salamończyk, D. Pociecha, G. J. Strachan, J. M. D. Storey, C. Wang, J. Feng, C. Zhu, E. Gorecka and C. T. Imrie, Liq. Cryst., 2019, 46, 1595–1609 CrossRef CAS.
- E. E. Pocock, R. J. Mandle and J. W. Goodby, Soft Matter, 2018, 14, 2508–2514 RSC.
- M. R. Wilson and M. P. Allen, Liq. Cryst., 1992, 12, 157–176 CrossRef CAS.
- M. R. Wilson, Liq. Cryst., 1996, 21, 437–447 CrossRef CAS.
- C. Greco, G. R. Luckhurst and A. Ferrarini, Phys. Chem. Chem. Phys., 2013, 15, 14961–14965 RSC.
- Y. Arakawa, K. Komatsu and H. Tsuji, New J. Chem., 2019, 43, 6786–6793 RSC.
- Y. Arakawa, K. Komatsu, S. Inui and H. Tsuji, J. Mol. Struct., 2020, 1199, 126913 CrossRef CAS.
- Y. Arakawa, K. Komatsu, T. Shiba and H. Tsuji, Mater. Adv., 2021, 2, 1760–1773 RSC.
- D. A. Paterson, J. P. Abberley, W. T. A. Harrison, J. M. D. Storey and C. T. Imrie, Liq. Cryst., 2017, 44, 127–146 CAS.
- Y. Arakawa, K. Komatsu, T. Shiba and H. Tsuji, J. Mol. Liq., 2021, 326, 115319 CrossRef CAS.
- T. D. Potter, M. Walker and M. R. Wilson, Soft Matter, 2020, 16, 9488–9498 RSC.
- G. Yu and M. R. Wilson, J. Mol. Liq., 2022, 345, 118210 CrossRef CAS.
Footnote |
| † Electronic Supplementary Information (ESI) available: Simulation input files and snapshot coordinates for the NTB, nematic and isotropic phases. See DOI: 10.1039/d2sm00291d |
| This journal is © The Royal Society of Chemistry 2022 |