Subtle changes in pH affect the packing and robustness of fatty acid bilayers†
Lauren A.
Lowe
ab,
James T.
Kindt
 c,
Charles
Cranfield
c,
Charles
Cranfield
 d,
Bruce
Cornell
e,
Alexander
Macmillan
f and
Anna
Wang
d,
Bruce
Cornell
e,
Alexander
Macmillan
f and
Anna
Wang
 *ab
*ab
aSchool of Chemistry, UNSW Sydney, NSW 2052, Australia. E-mail: anna.wang@unsw.edu.au
bAustralian Centre for Astrobiology, UNSW Sydney, NSW 2052, Australia
cDepartment of Chemistry, Emory University, Atlanta, Georgia 30322, USA
dSchool of Life Sciences, University of Technology Sydney, Ultimo, NSW 2007, Australia
eSDx Tethered Membranes Pty. Ltd., Unit 6, 30-32 Barcoo Street, Roseville, NSW 2069, Australia
fKatharina Gaus Light Microscopy Facility, UNSW Sydney, NSW 2052, Australia
First published on 19th April 2022
Abstract
Connecting molecular interactions to emergent properties is a goal of physical chemistry, self-assembly, and soft matter science. We show that for fatty acid bilayers, vesicle rupture tension, and permeability to water and ions are coupled to pH via alterations to lipid packing. A change in pH of one, for example, can halve the rupture tension of oleic acid membranes, an effect that is comparable to increasing lipid unsaturation in phospholipid systems. We use both experiments and molecular dynamics simulations to reveal that a subtle increase in pH can lead to increased water penetration, ion permeability, pore formation rates, and membrane disorder. For changes in membrane water content, oleic acid membranes appear to be more than a million times more sensitive to protons than to sodium ions. The work has implications for systems in which fatty acids are likely to be found, for example in the primitive cells on early Earth, biological membranes especially during digestion, and other biomaterials.
1 Introduction
Amphiphilic molecules comprise the lipid bilayer membranes that encapsulate all living cells and even some viruses. Because of the ubiquity of such membranes, the ability to predict macroscopic outcomes from the molecular packing of the lipid bilayer membrane is a tantalising goal in membrane biophysics.1 As a soft material, the lipid bilayer has been studied both computationally and experimentally to explore a large parameter space of both physical and chemical triggers that lead to changes in material properties. For example, temperature, membrane additives, pH, and ionic strength can be used to tune a myriad of mechanical outcomes such as changes in membrane fluidity and bending rigidity. These processes, in turn, have important consequences to processes essential for life, such as membrane rupture and cell division.Simpler lipids, such as the lipids that would have existed at the emergence of life, have a weaker hydrophobic interaction than the phospholipids of modern cell membranes2 and would thus have been even more sensitive to environmental triggers. One key class of molecules are fatty acids, which are capable of forming lipid bilayer membranes at a pH near the apparent pKa. In contrast to phospholipids, which require dozens of enzymes for synthesis,3 fatty acids are some of the chemically-simplest molecules known to form lipid bilayers. Short-chained fatty acids have been found on carbonaceous chondrites,4 indicating their ability to form abiotically and potential relevance to the origins of life.5
While the crude pH-dependence of fatty acid self-assembly is well known, forming emulsions at a pH significantly below the apparent pKa and micelles significantly above the apparent pKa, our understanding of the effects of subtler changes in pH within the pH range at which vesicles form remains lacking. We recently reported that giant unilamellar vesicles (GUVs) form at a pH slightly below the pKa, but not slightly above the pKa of the fatty acid.6 Specifically for oleic acid (pKa ∼ 8.5), GUVs form at pHs between 8.1 and 8.4, and heterogeneous multilamellar vesicles (MLVs) at pHs between 8.5 and 8.8. The pH-dependent shift from GUVs to MLVs suggests that a change in fatty acid packing is occurring, and raises questions as to which other properties are changing as a function of pH.
Here we focus on a pH approximately equal to the apparent pKa of oleic acid, and probe the properties of oleic acid/oleate bilayers in this pH range. Lipid bilayers in the form of closed vesicles are of particular interest owing to their relevance in a variety of fields including synthetic biology,7 origins of life studies,8 and drug delivery.9 The effect of pH on fatty acid monolayers is also relevant for sea spray aerosols.10 Because the pH-dependent self-assembly we showed in our previous work6 is intimately linked to the pH-dependent properties in this work, and the pH-dependent self-assembly occurred for a variety of fatty acids, we expect our results here to also be applicable to a variety of fatty acids.
Using molecular dynamics simulations and experimental tools, we find that changes in lipid packing in a fatty acid bilayer system, driven by a subtle change in pH of less than one, can lead to significant changes in water penetration, rupture tension, and permeability. We find that the hydrogen bonding network of lipids in fatty acid bilayers can be disrupted by a very small increase in pH. The changes in membrane properties with small shifts in pH has major impacts on the ability of fatty acid vesicles and thus fatty-acid-based primitive cells to retain encapsulated material, and the ability of different substances to traverse fatty-acid-based membranes.
2 Methods
2.1 Chemicals
Oleic acid (Sigma Australia), Laurdan (Sigma Australia), bicine (Sigma Australia), NaOH solution (Lowy Solutions), NaCl solution (Lowy Solutions), D(+)-glucose monohydrate (Calbiochem), sucrose (Univar/Ajax Finechem), ethanol (Chem Supply), pyranine/8-hydroxypyrene-1,3,6-trisulfonic acid trisodium salt (Sigma-Aldrich) were used as received.2.2 Buffer preparation
All bicine buffer solutions were prepared from a 1 M bicine stock solution titrated with NaOH to the appropriate pH, pH confirmed on a Mettler Toledo Seven Compact pH meter.2.3 Vesicle preparation
Oleic acid SUVs were prepared by weighing approximately 100 μmoles of neat oleic acid and adding it to a 1 mL solution containing pH 8.3 200 mM bicine buffer, 50 mM NaOH and 100 mM sucrose. The exact concentration of oleic acid (∼100 mM) was calculated. The solution was left to agitate on an orbital shaker (PSU-10i Grant Bio, UK) for at least 4 hours at 110 rpm. The vesicles were then diluted into a dilution buffer containing 200 mM bicine and 100 mM sucrose to a final concentration of approximately 10 mM oleic acid. A miniextruder (Avanti Polar Lipids) was used to extrude the sample of vesicles 21 times through a polycarbonate filter with pores 100 nm in diameter.Vesicles for Laurdan GP measurements were prepared by dispersing 3.2 μL neat oleic acid into a 1 mL solution of 100 mM bicine buffer, pH 8.43. A miniextruder (Avanti Polar Lipids) was used to extrude the sample of vesicles 21 times through a polycarbonate filter with pores 100 nm in diameter. Vesicles were then diluted into dilution buffers containing 100 mM bicine at a range of different pHs to a final concentration of 1 mM oleic acid. Laurdan stock in DMSO was then added to the vesicles to a final concentration of 1 μM and the samples gently pipetted up and down to mix.
To prepare oleic acid GUVs, 100 mM oleate micelles were prepared by adding 100 μmoles of neat oleic acid to a 1 mL solution of 150 mM NaOH. 10 mM oleic acid GUVs were then prepared by adding the micelle stock to a hydration buffer containing the solute to be encapsulated. This solution contained 100 mM bicine, 500 mM sucrose and 1 mM pyranine. The solution was vortexed for 3 s and placed on an orbital shaker (PSU-10i Grant Bio, UK) for 5 days at 100 rpm.
2.4 Vesicle characterisation
Vesicle diameter was measured with DLS using a Malvern Zetasizer Nano ZS and 12 mm Square Polystyrene Cuvettes (DTS0012) (Malvern Panalytical).Laurdan GP was measured on a Cary Eclipse (Varian) fluorescence spectrophotometer using 360 nm excitation wavelength in PMMA semi-micro cuvettes that have transparency above 300 nm (BRAND).
The GP of each vesicle sample was calculated by finding the maximum fluorescence intensity of each sample at two peaks at approximately 430 nm and 500 nm. The intensity of the first peak was determined by finding the maximum intensity between 400 nm and 440 nm. The maximum of the second peak was determined by finding the maximum intensity between 440 nm and 540 nm. The average of the five intensity values about each of the maxima was calculated. These averages were designated I430 and I500 for simplicity and were substituted into eqn (1) to calculate the GP.
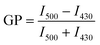 | (1) |
To compare our experimental GP values with literature, linear interpolation was used to estimate the GP of pH 8.5 oleic acid vesicles in a study conducted by Suga et al.11 GP values of vesicles at pH 8.4 and 8.8 were substituted into eqn (2) to estimate the GP of pH 8.5 vesicles.
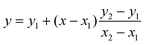 | (2) |
2.5 Electrical impedance spectroscopy
T10 tethered bilayer lipid membranes (tBLMs) were made using pre-prepared polycarbonate slides with gold sputter-coated onto the surface to form electrodes. The slides were coated with 10% benzyl disulfide octaethylene terminated by a C20 phytanyl chain which act as tethering molecules and 90% benzyl disulfide tetraethylene glycol terminated by a hydroxyl group which act as spacer molecules designed to promote phospholipid bilayer formation (SDx Tethered Membranes). tBLMs were formed using a solvent exchange procedure where the slide was air dried before 8 μL of a 3 mM solution of the oleic acid in ethanol was added to a 1 μL flow cell chamber and the excess liquid was collected in a 500 μL overflow container. After being incubated for two minutes, 3 × 100 μL of the desired electrolyte solution was added to the flow cell chamber. All subsequent membrane flushes used 3 × 100 μL of the desired electrolyte solution. This is an adaptation of a well-used protocol.12Electrolyte solutions containing 25 mM bicine and 100 mM NaCl were prepared at pH 8.3, 8.5 and 9.0.
AC impedance spectroscopy was performed using an SDx tethaPod and SDx tethaQuick software. Swept frequency impedance spectroscopy was employed using a sequential 25 mV excitation applied over the frequencies 0.1, 0.159, 0.251, 0.399, 0.634, 1.003, 1.588, 2.513, 3.991, 6.313, 10.016, 15.873, 25.176, 39.936, 55.066, 95.057, 159.236, 245.098, 409.836, 641.026, 1041.667 and 2083.333 Hz using zero bias potential. The impedance data was fitted to a simple model of a circuit containing a capacitor and resistor to represent the bilayer to determine the conductance and capacitance of the tBLM.
2.6 Molecular dynamics simulations
The simulation set up is described in detail in the Methods in Kindt et al.6 In this work packing was assessed independently within two planes, located a distance Δz above and below the center plane of the bilayer. The set of lateral positions within either plane was chosen as the midpoint of the first C–C bond in a chain to intersect the plane. Molecules that do not cross either plane in a given frame of the simulation were excluded from consideration for that frame. The order parameter for each crossing molecule j was determined as: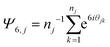 | (3) |
To estimate the tilt modulus Kθ and twist modulus Ktw from the simulation data we followed the method of Brown et al.13,14 by analysing the fluctuations of fatty acid tail tilt vectors in Fourier space. In the long wavelength/low-q limit, the following relation should hold:
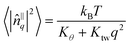 | (4) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ‖q is the longitudinal Fourier mode along wavevector q of the molecular tilt.
‖q is the longitudinal Fourier mode along wavevector q of the molecular tilt.
3 Results and discussion
3.1 Molecular dynamics simulations
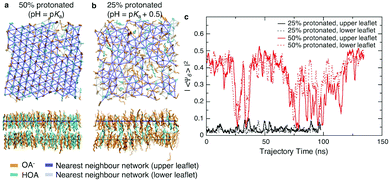
We first assessed the effect of pH on the packing of fatty acid molecules in bilayers with molecular dynamics (MD) simulations. We simulated octanoic acid bilayers at two different protonation states and thus pHs. First, at a pH equal to the apparent pKa (Fig. 1a), i.e. half the bilayer is protonated, the bilayer is highly ordered with few defects present. However, when the pH is increased by 0.5 (Fig. 1b) and the protonation state decreases to 25%, there is a notable change in packing with the bilayer looking qualitatively more disordered.To quantify the change in lipid packing, we calculated the 2D hexagonal complex order parameter Ψ6 for each chain based on the arrangement of its near neighbours (see Methods). The magnitude of the order parameter reflects how closely the arrangement of neighbours matches a regular hexagon, while its phase reflects the specific orientation of that hexagon. Averaging Ψ6 over all molecules in a given leaflet will result in a value close to zero if the orientation is uncorrelated at length scales comparable to the size of the simulation box. As shown in Fig. 1c, at the lower protonation state there is no evidence of packing orientational order on a length scale of the simulation box, while for the 50% protonated state the system shows hexagonal orientational order across the simulation box over part of the simulation trajectory, interrupted by periods of reduced order. We note that the periods of reduced order occur simultaneously for both leaflets, but this may simply reflect that the area fluctuations are forced to occur simultaneously in the two leaflets by the pressure coupling algorithm.
The hexagonal ordering is superficially reminiscent of gel-phase lipid bilayers. Phospholipids often show a sharp transition between a liquid-disordered state, in which tails are splayed and likely to contain one or more gauche torsional defects, to one or more states in which tails are elongated and packed in a hexagonal or distorted hexagonal lattice.15 The cycling between ordered and disordered states in our system, however, contrasts greatly with ordered-phase phospholipid bilayers, where the local packing may not relax over periods of hundreds of nanoseconds or more, leading to poor equilibration.16 The system is too small to determine whether the large-area limit would correspond to an isotropic liquid phase with a large but exponentially decaying correlation length or a hexatic state with quasi-long range orientational order.17,18
Finally, we might expect the packing of the fatty acid tails within the bilayer to be correlated with the mechanical properties of the membrane. We previously reported that when the pH increases from the pKa to the pKa + 0.5, the bending modulus decreases from >20 kT to 5.5 kT.6 Using the method as described in Kindt et al.6 and by Brown and coworkers,13,14 we analysed the mean square transverse orientational fluctuations (see Methods and Fig. S1, ESI†). With the limited range of q to analyse, we estimate that when the pH increases from the pKa to the pKa + 0.5 the tilt modulus Kθ decreases from 32.2 kT nm−2 to 21.7 kT nm−2. The twist modulus Ktw decreases from 5.2 kT to 1.5 kT. All values are similar to values reported for fluid-phase phospholipid bilayers which have tilt moduli ranging from 12.0–26.8 kT nm−2 and twist moduli from 2.2–5.9 kT.13,14 This shows that the decrease in membrane order is correlated with decreased resistance to deformations.
3.2 Lipid packing
To assess the impact of pH on fatty acid bilayers experimentally, we used an oleic acid/oleate system. Oleic acid has been studied widely in literature and is ideal for experiments owing to its low melting point and relatively low critical vesicle concentration.6 As previously, the shorter chain length for simulations was chosen for computational efficiency and not expected to qualitatively impact our investigation into the effects of headgroup charge on lipid packing.6We prepared oleic acid vesicles at a range of pHs and used the fluorescent probe Laurdan to monitor membrane polarity. The fluorescence spectra show two peaks (Fig. S2, ESI†), with the longer wavelength peak (near 500 nm) corresponding to a more solvent-rich state.11,19 We calculate the modified generalised polarisation (GP) using the values of intensity peaks near 430 nm and 500 nm (see Methods). Here, a GP ∼ 1 corresponds to highly solvated structures such as micelles.11
We found that GP increases with pH (Fig. 2a), likely because of increased water penetration across intact membranes as well as the formation of high-curvature structures. Because the apparent pKa of oleic acid in oleic acid bilayers is 8.5, we expect the protonation state of the bilayer to decrease from 75% to 25% as the pH increases from 8.0 to 9.0, corresponding to a trebling of the bilayer's negative charge density. The increase in Laurdan GP with pH could be a consequence of electrostatic repulsion between negatively-charged lipids allowing more water molecules to enter the bilayer. Alternatively, the average critical packing parameter of the lipids CPP = v/al is expected to decrease, owing to an increase in lipid area a while lipid volume v and length l stay the same. Such a change in CPP could result in the formation of more high-curvature monolayer structures that intrinsically have higher GP, such as micelles and transient pores,11 also increasing the Laurdan GP.
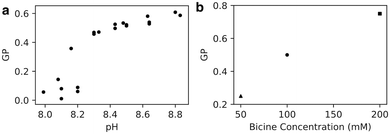 | ||
| Fig. 2 (a) Generalised polarisation (GP) of oleic acid vesicles in 100 mM bicine increases with increasing pH (n = 23). (b) GP of oleic acid vesicles at pH 8.5 increases with increasing bicine concentration. 50 mM GP from Suga et al.11 and 200 mM GP from Budin et al.19 | ||
We also note, by comparison with other work,11,19 that Laurdan GP increases with Na-bicine concentration (Fig. 2b). This observation is consistent with an increase in sodium ion concentration leading to a decrease in the apparent pKa of the membrane, thus affecting the protonation state and hence packing and subsequent properties of the membranes.6 These results highlight that although the membrane packing can be tuned with a change in ionic strength, a change in proton (or hydronium ion) concentration of Δ[H+] = 10−8–10−8.8 M ∼ 8 nM is as effective as a sodium ion concentration change of ∼150 mM for altering the membrane's water penetration.
Thus far, we have established that Laurdan probes embedded within oleic acid bilayers become more exposed to water as the pH of solution increases, consistent with simulation results indicating decreased lipid order with an increase in pH. In the next sections we consider potential consequences of such changes in lipid packing.
3.3 Permeability
We hypothesised that a change in membrane packing could alter the propensity of molecules to permeate across the membrane – the permeability. Because we have found that the packing is sensitive to salt concentration, we did not want to use the calcein shrink-swell assay because of the ionic strengths required. Instead, we adapted an AC impedance spectroscopy system, designed for phospholipids, for use with fatty acids. We prepared oleic acid tethered bilayer lipid membranes (tBLMs) and monitored changes in conductance and capacitance across the tBLMs with changes in pH. While not originally designed for supporting fatty acid bilayers, we found that when tBLMs successfully formed there were consistent results across multiple trials and experiments (Fig. S3, ESI†).Both the conductance and capacitance of oleic acid tBLMs increased with increasing pH (Fig. 3). The change in relative capacitance Cfinal/Cinitial as a function of ΔpH appears to be linear, with a change of 10% per ΔpH. Because capacitance is inversely proportional to membrane thickness, the increased capacitance at higher pHs could suggest that bilayer thickness decreases with pH.12,20,21 This is consistent with the results from previously-simulated octanoic acid bilayers, which were thinner at higher pHs6 because of increased lipid headgroup area from electrostatic repulsion. Additionally, membrane capacitance is also affected by water content.21 Part of the increased capacitance at higher pHs could reflect an increase in membrane water content, also seen in the Laurdan experiments (Fig. 2), owing to disordered lipid packing (Fig. 1).
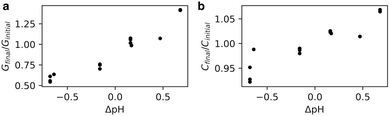 | ||
| Fig. 3 AC impedance spectroscopy performed on oleic acid tBLMs at varying pHs. Conductance (G) and capacitance (C) across tBLMs increases with an increase in pH. For further details see Fig. S3 (ESI†). | ||
There was also a noteworthy increase in membrane conductance even with small changes in pH. As conductance is proportional to ion flux through the membrane, the increased conductance at higher pHs suggests that fatty acid membranes are more permeable to ions at higher pHs. The Laurdan (Fig. 2) and molecular dynamics simulations (Fig. 1) both show increased membrane disorder at higher pHs. One consequence is that the decreased CPP of lipids upon an increase in pH could favour pore formation,22,23 which is one potential permeability mechanism in lipid bilayers.24–26 Additionally, permeability via the solubility-diffusion mechanism is strongly dependent on area per lipid27 and thus any thinning of the membrane and concomitant increase in area per lipid could lead to an increase in permeability. One other reason for increased ion conductance with an increase in pH could be an increase in sodium ion translocation via lipid flip-flop. These results echo the pH-dependent conductance changes observed in phospholipid bilayers across a large pH change (pH 9 to pH 7 and pH 5).20 Finally, we verified that for a less-permeable solute such as the trivalent molecule pyranine, the permeability is not notably pH-dependent (Fig. S4 and S5, ESI†), suggesting that pH perturbations can tune permeability to smaller species without affecting the retention of larger molecules.
3.4 Rupture tension
Thus far we have determined that an increase in pH leads to membrane thinning, as well as increased permeability to ions possibly owing to the formation of pores, increased flip-flop, or both. We hypothesised that the rupture tension would also be affected by an increase in pH, because it is a macroscopic property known to also be impacted by membrane thickness and pore formation. Rupture or lysis tension refers to the minimum tension required to be placed on a vesicle before it ruptures. Rupture tension is an important concept because it determines the ability of a cell or primitive cell to retain encapsulated genetic material and nutrients under shear or osmotic stress. We therefore sought to understand how the strength of a membrane is impacted by pH.The critical tension at which membranes rupture is usually measured by micropipette aspiration, where increasing tension is applied to a vesicle until it is seen to rupture under microscopy. The technique is complicated by two effects. First, aspiration or loading rate affects the measured rupture tension owing to the stochastic nature of pore formation.28 Second, fatty acid bilayers under tension can relieve this tension by growing at the expense of vesicles under less tension.29 This would further jeopardise the potential for clean measurements and necessitates application of tension that is faster than the rate at which membranes can grow. We therefore chose to measure rupture tension using an entirely different approach, one that applies tension rapidly.
We adopt the method of Patty and Frisken,30 who used extrusion as a method to measure the rupture tension of vesicles.30 During extrusion, multilamellar vesicles are forced through pores to yield smaller unilamellar vesicles. Because the multilamellar vesicles are significantly larger than the polycarbonate membrane pore size, they must rupture in order to pass through the pores and form smaller vesicles.30,31 Patty and coworkers found a relationship between between the final radius of extruded vesicles (Rves), rupture (lysis) tension (γ), the radius of the extrusion membrane pores (Rp) and the pressure exerted on the vesicles (P):
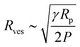 | (5) |
The radius of extruded vesicles can thus be used to estimate the relative rupture tension. To use this strategy, we prepared micrometre-sized 10 mM oleic acid vesicles encapsulating 100 mM sucrose in 200 mM bicine at pHs between 8.0 and 8.9 (Fig. S6, ESI†). These vesicles were then extruded through polycarbonate membranes with 100 nm pores to decrease their size by at least tenfold and yield unilamellar oleic acid vesicles (Fig. 4). The size of these vesicles was measured using dynamic light scattering (DLS) (Fig. 5a).
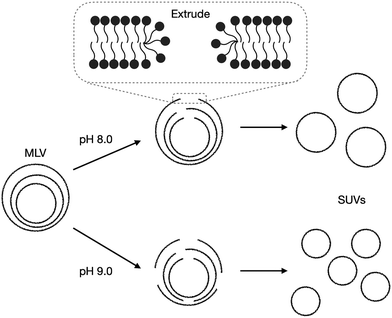 | ||
| Fig. 4 Schematic demonstrating the impact of pH on the extrusion of oleic acid vesicles. Multilamellar vesicles (MLVs) (Fig. S6, ESI†) are extruded through extrusion pores. The membranes rearrange by first forming membrane pores, rupturing, then re-forming into smaller unilamellar vesicles (SUVs). | ||
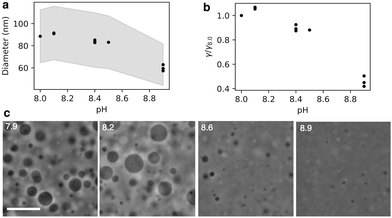
We found that the diameter of all the vesicles was smaller than the 100 nm pore size of the membranes used in the extrusion process. This is consistent with previous studies using 10 mM oleic acid vesicles in 200 mM bicine at pH 8.8, extruded through 100 nm pores.32 Despite the diameter of all the vesicles being smaller than the polycarbonate membrane pore size, a dependence of vesicle size on pH was still observed. Minimal difference in size was observed for vesicles at pH 8.0 and 8.1. Vesicles at pH 8.4 and 8.5 were slightly smaller than pH 8.1 vesicles. However, the most significant change occurred for vesicles at pH 8.9 which were approximately 30% smaller than vesicles at pH 8.1.
By eqn (5), the dependence of vesicle size on pH suggests that rupture tension is also pH dependent. In our experiments, the combined pressure associated with the extrusion process as well as the osmotic pressure exerted on the vesicle membranes owing to the encapsulated sucrose causes the vesicles to rupture. This involves the formation of pores in the bilayer to release built up membrane tension.33–35 In our experiments, the extrusion membrane pore size was consistent across all samples, and the average flow rate during the 21 extrusion passes remained constant at 100 ± 10 μL s−1. Our assumption that the applied pressures across experiments is constant is validated by the average vesicle radius after extrusion being highly reproducible at a given pH, indicating high reproducibility in the mechanics of extrusion between samples. Therefore, the change in vesicle size is a direct result of the change in rupture tension at different pHs (Fig. 5b).
The change in rupture tensions with pH is substantial, with the rupture tension of vesicles at pH 8.0–8.1 being approximately double that of vesicles at pH 8.9. By osmotically stressing the vesicles, Chen et al.29 estimated that the rupture tension of oleic acid vesicles at pH 8.5 was approximately 10 mN m−1, leading us to conclude that the rupture tension of membranes in our system are ∼10 mN m−1 at pH 8.5 and ∼5 mN m−1 at pH 8.9. This is comparable to the difference between the rupture tension of di-oleic phosphatidyl choline (diC18:1; 9.9 mN m−1) and di-linoleic phosphatidyl choline (diC18:2; 5.1 mN m−1)1 vesicles. It is intriguing that a halving in rupture tension in oleic acid vesicles can be achieved in the same bilayer membrane by simply changing the pH by 1, rather than altering the lipid composition by increasing lipid unsaturation. One potential source of error is possible variability in pressure exerted on the vesicles during extrusion, contributing an error of approximately 10% to the rupture tension if we assume the variation in flow rate is related to a variation in pressure. Additionally, the vesicle size distribution was not taken into account. However, our results were reproducible across different days and we would not expect these factors to create a factor of two in difference in rupture tension. We further confirm the significant difference in rupture tension with pH using microscopy.
We diluted 10 mM oleic acid GUVs encapsulating 500 mM sucrose into hypotonic buffers of varying pH containing no sucrose, thereby exposing the vesicles to osmotic pressure. Imaging the diluted vesicles revealed a clear difference in surviving vesicle size as a function of pH (Fig. 5c). Vesicles at pH 8.6 were notably smaller than vesicles at pH 7.9 and pH 8.2. Vesicles at pH 8.9 were even smaller than those at pH 8.6. The smaller size of the vesicles at high pHs indicates that they were unable to withstand the high osmotic pressure gradient exerted on the membrane. In other words, the vesicles at higher pHs are more prone to rupture.
There are a number of factors that contribute to the reduced rupture tension of oleic acid membranes at higher pHs. First, from the simulated bilayers (Fig. 1) we found that fatty acid bilayers at higher pHs are more disordered and have more defects present. As oleic acid has a pKa of 8.5,6 the simulated bilayers can be compared to oleic acid bilayers at a pH of 8.5 and 9.0. We can infer that vesicles at pH 9.0 will have more defects than at pH 8.5. As vesicle rupture occurs due to pore formation, and pore formation stems from the presence of hydrophobic defects in the membrane,22,23 it is perhaps not surprising that fatty acid vesicles at higher pHs are more prone to rupture because they have more packing defects (Fig. 4) and their lipids have a lower CPP as previously discussed. Another contributing factor could be the varying thickness of bilayer membranes at different pHs. The rupture tension of vesicles composed of different phospholipids is dependent on membrane thickness, with defects being more likely to form in thinner membranes, making them more prone to rupture.28 Previous molecular dynamics simulations showed fatty acid bilayers at high pHs were thinner and had a lower bending modulus than bilayers at a low pH.6 Thus fatty acid vesicles could be more prone to rupture at higher pHs because they are thinner and less rigid than vesicles at lower pHs.
4 Conclusions
We have shown, using both molecular dynamics simulations and experiments, a consistent picture of how the packing of lipid molecules in fatty acid bilayers is strongly dependent on pH. Subtle increases in pH lead to decreased hydrogen bonding and increased membrane disorder. With small increases in pH, fatty acid vesicles become more prone to water penetration and more susceptible to rupture. Additionally, fatty acid bilayers become more permeable to ions with slight increases in pH. Because fatty acid vesicles are able to encapsulate a variety of materials in their aqueous cores, including sugars, fluorescent dyes, nucleotides, nanoparticles, RNA and drug molecules,6,9,36 gaining an increased understanding of how pH affects the ability of vesicles to encapsulate and retain these materials helps enhance the effectiveness with which they are encapsulated.Improving our understanding of these properties is of particular significance in the origins of life field. Fatty acid vesicles have been proposed as model protocell systems due to the ease with which they self-assemble, their chemical simplicity and because they can be synthesised abiotically.4,6 Protocells required nutrient and waste exchange, whilst continuing to encapsulate the contents vital to the cell. Thus understanding how pH impacts the packing of fatty acid molecules in bilayer membranes and the ability of the membranes to encapsulate and permeate solutes is of particular use in understanding how protocells were able to thrive. One potential geological setting for the origin of cellular life on Earth are surficial hot springs, which often have environments of varying pH.37 Protocells moving into these pH streams would have experienced fluctuations in membrane packing, allowing nutrients or waste to enter or exit the cell without the need for the complex enzymes that regulate this process in modern cells.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. A. L. is supported by an Australian Government Research Training Program Scholarship. A. W. is the recipient of an Australian Research Council Discovery Early Career Award (DE210100291). This work was supported by the Human Frontier Science Program (RPG0029/2020 to A. W.).References
- K. Olbrich, W. Rawicz, D. Needham and E. Evans, Biophys. J., 2000, 79, 321–327 CrossRef CAS PubMed.
- A. Wang and J. W. Szostak, Emerging Top. Life Sci., 2019, 3, 537–542 CrossRef PubMed.
- M. Exterkate and A. J. Driessen, Emerging Top. Life Sci., 2019, 3, 543–549 CrossRef PubMed.
- J. G. Lawless and G. U. Yuen, Nature, 1979, 282, 396 CrossRef CAS.
- K. Morigaki and P. Walde, Curr. Opin. Colloid Interface Sci., 2007, 12, 75–80 CrossRef CAS.
- J. T. Kindt, J. W. Szostak and A. Wang, ACS Nano, 2020, 14, 14627–14634 CrossRef PubMed.
- J. C. Blain and J. W. Szostak, Annu. Rev. Biochem., 2014, 83, 615–640 CrossRef CAS PubMed.
- I. A. Chen and P. Walde, Cold Spring Harbor Perspect. Biol., 2010, 2, a002170 Search PubMed.
- L. Kumar, S. Verma, S. Kumar, D. N. Prasad and A. K. Jain, Artif. Cells, Nanomed., Biotechnol., 2017, 45, 251–260 CrossRef CAS PubMed.
- E. M. Adams, B. A. Wellen, R. Thiraux, S. K. Reddy, A. S. Vidalis, F. Paesani and H. C. Allen, Phys. Chem. Chem. Phys., 2017, 19, 10481–10490 RSC.
- K. Suga, D. Kondo, Y. Otsuka, Y. Okamoto and H. Umakoshi, Langmuir, 2016, 32, 7606–7612 CrossRef CAS PubMed.
- C. Cranfield, S. Carne, B. Martinac and B. Cornell, in Methods in Membrane Lipids, ed. D. M. Owen, Springer New York, New York, NY, 2015, pp. 45–53 Search PubMed.
- M. C. Watson, E. G. Brandt, P. M. Welch and F. L. H. Brown, Phys. Rev. Lett., 2012, 109, 028102 CrossRef PubMed.
- Z. A. Levine, R. M. Venable, M. C. Watson, M. G. Lerner, J.-E. Shea, R. W. Pastor and F. L. H. Brown, J. Am. Chem. Soc., 2014, 136, 13582–13585 CrossRef CAS PubMed.
- W.-J. Sun, R. M. Suter, M. A. Knewtson, C. R. Worthington, S. Tristram-Nagle, R. Zhang and J. F. Nagle, Phys. Rev. E, 1994, 49, 4665–4676 CrossRef CAS PubMed.
- K. Uppulury, P. S. Coppock and J. T. Kindt, J. Phys. Chem. B, 2015, 119, 8725–8733 CrossRef CAS PubMed.
- E. P. Bernard and W. Krauth, Phys. Rev. Lett., 2011, 107, 155704 CrossRef PubMed.
- S. Katira, K. K. Mandadapu, S. Vaikuntanathan, B. Smit and D. Chandler, eLife, 2016, 5, e13150 CrossRef PubMed.
- I. Budin, A. Debnath and J. W. Szostak, J. Am. Chem. Soc., 2012, 134, 20812–20819 CrossRef CAS PubMed.
- C. G. Cranfield, T. Berry, S. A. Holt, K. R. Hossain, A. P. Le Brun, S. Carne, H. Al Khamici, H. Coster, S. M. Valenzuela and B. Cornell, Langmuir, 2016, 32, 10725–10734 CrossRef CAS PubMed.
- A. Alghalayini, A. Garcia, T. Berry and C. G. Cranfield, Antibiotics, 2019, 8, 12 CrossRef CAS PubMed.
- S. A. Akimov, P. E. Volynsky, T. R. Galimzyanov, P. I. Kuzmin, K. V. Pavlov and O. V. Batishchev, Sci. Rep., 2017, 7, 12152 CrossRef PubMed.
- S. A. Akimov, P. E. Volynsky, T. R. Galimzyanov, P. I. Kuzmin, K. V. Pavlov and O. V. Batishchev, Sci. Rep., 2017, 7, 12509 CrossRef PubMed.
- S. Paula, A. G. Volkov, A. N. Van Hoek, T. H. Haines and D. W. Deamer, Biophys. J., 1996, 70, 339–348 CrossRef CAS PubMed.
- S. Paula, A. G. Volkov and D. W. Deamer, Biophys. J., 1998, 74, 319–327 CrossRef CAS PubMed.
- A. G. Volkov, S. Paula and D. W. Deamer, Bioelectrochem. Bioenerg., 1997, 42, 153–160 CrossRef CAS.
- J. F. Nagle, J. C. Mathai, M. L. Zeidel and S. Tristram-Nagle, J. Gen. Physiol., 2008, 131, 77–85 CrossRef CAS PubMed.
- E. Evans, V. Heinrich, F. Ludwig and W. Rawicz, Biophys. J., 2003, 85, 2342–2350 CrossRef CAS PubMed.
- I. A. Chen, R. W. Roberts and J. W. Szostak, Science, 2004, 305, 1474–1476 CrossRef CAS PubMed.
- P. J. Patty and B. J. Frisken, Biophys. J., 2003, 85, 996–1004 CrossRef CAS PubMed.
- D. G. Hunter and B. J. Frisken, Biophys. J., 1998, 74, 2996–3002 CrossRef CAS PubMed.
- E. Blöchliger, M. Blocher, P. Walde and P. L. Luisi, J. Phys. Chem. B, 1998, 102, 10383–10390 CrossRef.
- P.-A. Boucher, B. Joós, M. J. Zuckermann and L. Fournier, Biophys. J., 2007, 92, 4344–4355 CrossRef CAS PubMed.
- C. Taupin, M. Dvolaitzky and C. Sauterey, Biochemistry, 1975, 14, 4771–4775 CrossRef CAS PubMed.
- M. A. Idiart and Y. Levin, Phys. Rev. E, 2004, 69, 061922 CrossRef PubMed.
- L. Jin, A. E. Engelhart, K. P. Adamala and J. W. Szostak, J. Visualized Exp., 2018, 57324 Search PubMed.
- B. Damer and D. Deamer, Astrobiology, 2020, 20, 429–452 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00272h |
| This journal is © The Royal Society of Chemistry 2022 |