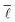Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stiffening of under-constrained spring networks under isotropic strain
Cheng-Tai
Lee
 and
Matthias
Merkel
and
Matthias
Merkel
 *
*
CNRS, Centre de Physique Théorique (CPT, UMR 7332), Turing Center for Living Systems, Aix Marseille Univ, Université de Toulon, Marseille, France. E-mail: matthias.merkel@univ-amu.fr
First published on 17th June 2022
Abstract
Disordered spring networks are a useful paradigm to examine macroscopic mechanical properties of amorphous materials. Here, we study the elastic behavior of under-constrained spring networks, i.e. networks with more degrees of freedom than springs. While such networks are usually floppy, they can be rigidified by applying external strain. Recently, an analytical formalism has been developed to predict the scaling behavior of the elastic network properties close to this rigidity transition. Here we numerically show that these predictions apply to many different classes of spring networks, including phantom triangular, Delaunay, Voronoi, and honeycomb networks. The analytical predictions further imply that the shear modulus G scales linearly with isotropic stress T close to the rigidity transition. However, this seems to be at odds with recent numerical studies suggesting an exponent between G and T that is smaller than one for some network classes. Using increased numerical precision and shear stabilization, we demonstrate here that close to the transition a linear scaling, G ∼ T, holds independent of the network class. Finally, we show that our results are not or only weakly affected by finite-size effects, depending on the network class.
Introduction
Understanding macroscopic rigidity and how it depends on the microscopic structure in amorphous materials such as fibrous networks, glasses, jammed colloids, and granular materials has been a long-standing challenge in the field. While the macroscopic mechanics of crystalline materials can be computed explicitly by exploiting their spatially periodic microscopic structure, this is not possible for disordered materials. In particular, upon deformation disordered materials generally display non-affine microscopic displacements, which are hard to predict.1–11A classical way to predict the onset of rigidity in many systems is to use Maxwell's constraint counting, which states that rigidity emerges whenever the constraints in a system outnumber its degrees of freedom.12–14 In systems with pair interactions, this is equivalent to comparing the average connectivity z, i.e. the average number of pair interactions each particle is involved in, to the number of degrees of freedom per particle, which is given by the dimension of space, D. Such systems are predicted to be rigid if z exceeds the isostatic point, z > zc := 2D. In this case the system is called over-constrained. Otherwise, for z < zc, the system is called under-constrained or sub-isostatic, and is predicted to be floppy.
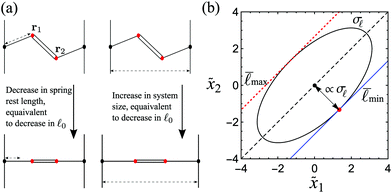
While Maxwell's constraint counting predicts under-constrained systems to be floppy, these systems can still be rigidified, either through the application of external strain or the presence of residual stresses.3,6,7,11,15–21 As a simple model to study such strain-induced rigidity, we discuss here strain-induced rigidity in athermal, under-constrained disordered spring networks.16,18,19,22–24 Strain-induced rigidification is illustrated in Fig. 1a for a network to which isotropic and shear strain has been applied.
 | ||
Fig. 1 Under-constrained spring networks can be rigidified by the external application of strain. (a) Network configurations and spring tensions for an example network under either isotropic or shear strain. (b) Change of minimal network energy E, bulk modulus B, and shear modulus G when isotropically deforming a network across the rigidity transition, which occurs at the critical strain value ε*. Below ε*, all springs can attain their rest lengths, the system is floppy, and E = B = G = 0. Beyond ε*, springs start to deviate from their rest lengths. According to ref. 18, the bulk modulus B shows a discrete jump at ε*, while G increases linearly and E increases quadratically with the distance from the transition point ε*. (c) Two types of spring potentials are used in our simulations, harmonic (left) and rope-like (right). ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 denote spring length and rest length, respectively. 0 denote spring length and rest length, respectively. | ||
The mechanism creating strain-induced rigidity has been discussed in the literature before.15,16,25,26 When approaching the transition from the floppy side, a state of self-stress (SSS) forms right at the transition. A SSS is a set of tensions that could be put on the springs without any net forces on the nodes. The SSS that appears at the rigidity transition couples to isotropic strain, and using known approaches it can be shown that this induces a jump in the bulk modulus right at the transition (Fig. 1b).14,18 Meanwhile, the shear modulus shows a continuous transition, whenever the SSS that appears at the transition has no net overlap with shear strain. Previously, the floppy side of the strain-stiffening transition was discussed in the limit where the springs are infinitely rigid.25,26 Here, we are interested in the network mechanics of the rigid side of the transition when spring constants are finite.
Recent work involving one of us proposed a theoretical approach that allows to analytically predict the behavior of the elastic properties of under-constrained materials close to the strain-induced rigidity transition.18 This approach is based on a minimal-length function that formalizes the relationship between spring lengths and the applied global strain. This minimal-length function both reflects the critical point where the network starts to rigidify and allows to predict the behavior of the elastic network properties in the rigid regime. In ref. 18, this approach was numerically verified both on models for disordered cellular materials and for packing-derived spring networks. However, it has never been explicitly tested for other classes of under-constrained spring networks.
The approach in ref. 18 allows to predict the behavior of the elastic moduli close to the transition, where the bulk modulus B shows a discontinuity, while the shear modulus G increases linearly with isotropic strain ε (Fig. 1b). One can show that as a consequence of both, one would expect the shear modulus G to linearly increase also with isotropic stress T close to the transition. This is also consistent with earlier work on stress-induced rigidity.3,15,27 However, more recent numerical work19 on under-constrained disordered spring networks suggested that the value for the scaling exponent between G and T can differ from one, depending on the class of network studied. The reason for this deviation from the analytical predictions is so far unclear. Other recent work proposed that the numerical results in ref. 18 could potentially be affected by finite-size effects caused by a diverging length scale when shearing the system.11 Could similar finite-size effects be the reason for this contradiction between predicted and numerically obtained exponents between G and T?
Here, we numerically test the predictions from ref. 18 on several different classes of athermal spring networks. These include phantom triangular, Delaunay, Voronoi, and honeycomb networks, where we study two types of spring potentials, harmonic and rope-like (Fig. 1c). In the following, we first summarize the analytical approach from ref. 18 in Section 1. We then test the analytical predictions on the four different network classes in Section 2, and show that they follow the predicted behavior (Section 2.2). In Section 2.3, we furthermore show that the scaling behavior of the coefficients appearing in the minimal-length function with connectivity z depends on the network class. We then numerically explore the scaling behavior of the shear modulus G over isotropic stress T with increased numerical precision and find a scaling exponent of one, independent of network class (Section 2.4). Finally, we show that depending on the network class, there is no or a weak system-size dependence affecting these results (Section 2.5).
1 Theoretical predictions
We start by summarizing the approach of ref. 18, which allows to predict the scaling behavior of the elastic properties of under-constrained spring networks close to the rigidity transition.In general, the formalism of ref. 18 applies to any disordered Hookean spring network of N springs, where each spring i has a different spring constant ki and rest length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0i. The energy of such a network is:
0i. The energy of such a network is:
 | (1) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is the length of spring i. The springs are connected at movable nodes, around which they can freely rotate. While the approach can be applied largely independently of the precise boundary conditions, we focus here on periodic boundary conditions with fixed system size. Unless stated otherwise, we use dimensionless quantities, where the length unit is Lc := (V/N)1/D with D being the dimension of space and V the system volume. We define the energy unit such that
i is the length of spring i. The springs are connected at movable nodes, around which they can freely rotate. While the approach can be applied largely independently of the precise boundary conditions, we focus here on periodic boundary conditions with fixed system size. Unless stated otherwise, we use dimensionless quantities, where the length unit is Lc := (V/N)1/D with D being the dimension of space and V the system volume. We define the energy unit such that 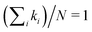 . Using dimensionless lengths will later allow us to describe the effect of isotropic strain (Section 1.3).
. Using dimensionless lengths will later allow us to describe the effect of isotropic strain (Section 1.3).
Here, to explain just the key ideas of the approach, we focus for simplicity on the special case of a network with homogeneous spring constants ki = 1 and rest lengths ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0i =
0i = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0:
0:
 | (2) |
The elastic properties of disordered networks are in general difficult to predict analytically. Formally, these elastic properties can be computed from derivatives of a minimal energy function emin(ε,γ) with respect to external isotropic strain ε or shear strain γ. This function corresponds to the minimized system energy e({rn},ε,γ) with respect to the node positions rn at constant strain variables ε,γ. However, applying strain to a disordered network generally induces non-affine displacements of the node positions, which are typically hard to predict without numerical energy minimization. To nevertheless make non-trivial predictions about the scaling of the elastic properties, ref. 18 introduced a different approach. Instead of explicitly following the node motion, progress can already be made by focusing on the relation between spring lengths and external strain.
Note that while we focus in this section on harmonic springs, the formalism can also be applied to networks with rope-like pair interactions (Fig. 1c). This is because a rope-like pair interaction can be perfectly mimicked by a chain of two or more harmonic springs18 (see also Appendix D).
1.1 Key idea
To obtain an explicit expression for emin in terms of external strain, we first transform the expression in eqn (2) into a sum of two squares: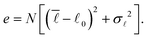 | (3) |
 and
and  are average and variance of the spring lengths, respectively.
are average and variance of the spring lengths, respectively.
The expression in eqn (3) allows us to more conveniently discuss the minimal network energy emin and its behavior once we strain the system. Because e is the sum of two squares, an energy minimum is attained whenever both  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are as small as possible. There are two possibilities. First, if there is a set of node positions such that both squares can simultaneously attain zero, then the minimal energy is zero emin = 0. Because elastic stresses and moduli correspond to derivatives of emin, the system is floppy in this parameter regime. Second, there might be no set of node positions such that both terms
are as small as possible. There are two possibilities. First, if there is a set of node positions such that both squares can simultaneously attain zero, then the minimal energy is zero emin = 0. Because elastic stresses and moduli correspond to derivatives of emin, the system is floppy in this parameter regime. Second, there might be no set of node positions such that both terms  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) can simultaneously vanish. In this regime, the system is typically rigid.
can simultaneously vanish. In this regime, the system is typically rigid.
To access the value of emin in the rigid regime, we need to understand how the system compromises between minimizing  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) in eqn (3). To this end, we first need a way to express which combinations of
in eqn (3). To this end, we first need a way to express which combinations of  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are geometrically possible. As shown in ref. 18, this can be done using a minimal-length function
are geometrically possible. As shown in ref. 18, this can be done using a minimal-length function  which returns the minimally possible
which returns the minimally possible  for a given σ
for a given σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . In other words, a combination of
. In other words, a combination of  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is geometrically possible only if:
is geometrically possible only if:
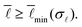 | (4) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0 it is possible to find only network configurations with
= 0 it is possible to find only network configurations with  . Thus, for
. Thus, for  the network will be floppy, because both squares in eqn (3) can simultaneously vanish, which implies that emin and its derivatives vanish. Conversely, for
the network will be floppy, because both squares in eqn (3) can simultaneously vanish, which implies that emin and its derivatives vanish. Conversely, for 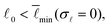 the first term in eqn (3) can not vanish with σ
the first term in eqn (3) can not vanish with σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0, because only configurations with
= 0, because only configurations with  are possible. Thus,
are possible. Thus,  is the transition point between floppy and rigid regime.
is the transition point between floppy and rigid regime.
In general, the precise functional form of  depends on the network structure. However, we showed in ref. 18 that at the transition point to first order in σ
depends on the network structure. However, we showed in ref. 18 that at the transition point to first order in σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) this function can be expanded as
this function can be expanded as
 | (5) |
 and a
and a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are constants that encode the network structure. Eqn (5) holds in the limit of small σ
are constants that encode the network structure. Eqn (5) holds in the limit of small σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , which means that the system is close to the transition point, where σ
, which means that the system is close to the transition point, where σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0. We expect that deriving expressions for
= 0. We expect that deriving expressions for 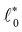 and a
and a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) from first principles is very hard for disordered networks. Besides some exceptions,
from first principles is very hard for disordered networks. Besides some exceptions, 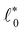 and a
and a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) will need to be determined numerically.
will need to be determined numerically.
We briefly outline how eqn (5) is a consequence of the SSS that is created at the transition point (details in ref. 18). At the transition point the N-dimensional vector of all spring lengths ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i is given by
i is given by  with e = (1,…,1). We consider a state of the network that is slightly shifted into the rigid regime, where
with e = (1,…,1). We consider a state of the network that is slightly shifted into the rigid regime, where  . One can then show that the definition of an SSS implies that
. One can then show that the definition of an SSS implies that  is perpendicular to it:18
is perpendicular to it:18
 | (6) |
 , we first decompose both
, we first decompose both  and t into parts parallel and perpendicular to
and t into parts parallel and perpendicular to 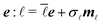 and t ∼ e + a
and t ∼ e + a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) mt, where we use the normalization m
mt, where we use the normalization m![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2 = mt2 = N. Note that this defines a
2 = mt2 = N. Note that this defines a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) as the coefficient of variation of the SSS components. We then insert both decompositions into eqn (6) and obtain:
as the coefficient of variation of the SSS components. We then insert both decompositions into eqn (6) and obtain: | (7) |
 for fixed σ
for fixed σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , the scalar product m
, the scalar product m![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ·mt needs to be maximized. In the presence of only a single SSS, m
·mt needs to be maximized. In the presence of only a single SSS, m![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) can be any normalized vector perpendicular to e, and thus m
can be any normalized vector perpendicular to e, and thus m![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ·mt is maximized by m
·mt is maximized by m![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = mt, for which eqn (7) becomes eqn (5).
= mt, for which eqn (7) becomes eqn (5).
To derive an expression for the minimal energy emin in the solid regime, we combine two parts: the energy in eqn (3) and the condition of geometrically possible combinations  in eqn (4) and (5). First, eqn (4) implies that for fixed σ
in eqn (4) and (5). First, eqn (4) implies that for fixed σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , the energy in eqn (3) is minimized when
, the energy in eqn (3) is minimized when 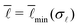 . Combining this with eqn (5), insertion into eqn (3), and minimization with respect to σ
. Combining this with eqn (5), insertion into eqn (3), and minimization with respect to σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , yields:
, yields:
 | (8) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0, and the two parameters
0, and the two parameters 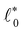 and a
and a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) that encode the network structure. Note that from eqn (8) we see that the system energy is that of a single effective spring with rest length
that encode the network structure. Note that from eqn (8) we see that the system energy is that of a single effective spring with rest length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0.
0.
1.2 Simple example network
To illustrate the ideas of the previous section, we discuss a simple example network (Fig. 2a left). The network consists of four springs with equal dimensionless spring constants k = 1 and rest lengths![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. Two of the springs are connected to fixed points (black dots) located at positions (−1/2,0) and (1/2,0), respectively. The two internal nodes (red dots) at positions rn with n = 1, 2 are movable. We will use the ideas of the previous section to derive an expression for the minimal energy emin.
0. Two of the springs are connected to fixed points (black dots) located at positions (−1/2,0) and (1/2,0), respectively. The two internal nodes (red dots) at positions rn with n = 1, 2 are movable. We will use the ideas of the previous section to derive an expression for the minimal energy emin.
For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 ≥ 1/3, there are always configurations where all springs can attain their rest lengths
0 ≥ 1/3, there are always configurations where all springs can attain their rest lengths ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i =
i = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 (Fig. 2a top). This implies that
0 (Fig. 2a top). This implies that  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0, i.e. both terms in eqn (3) can simultaneously vanish.
= 0, i.e. both terms in eqn (3) can simultaneously vanish.
Conversely, for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 < 1/3, the springs will be under tension (Fig. 2a bottom). Our 4-spring example network is simple enough so that we can explicitly minimize the energy with respect to the inner node positions rn = (xn,yn) with n = 1, 2. This will allow us to first directly test whether the minimal energy has the form predicted by eqn (8) in the previous section. The energy of our example network is
0 < 1/3, the springs will be under tension (Fig. 2a bottom). Our 4-spring example network is simple enough so that we can explicitly minimize the energy with respect to the inner node positions rn = (xn,yn) with n = 1, 2. This will allow us to first directly test whether the minimal energy has the form predicted by eqn (8) in the previous section. The energy of our example network is
 | (9) |
Here, to simplify the following discussion, we have set y1 = y2 = 0. The energy e has a global minimum at x1 = −(1 + 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0)/10, x2 = (1 + 2
0)/10, x2 = (1 + 2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0)/10, where its value is
0)/10, where its value is
 | (10) |
We now demonstrate how the minimal energy emin can instead be obtained using the ideas of the previous section. We first discuss which pairs of  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are geometrically possible. To this end, we express
are geometrically possible. To this end, we express  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) in terms of the internal degrees of freedom x1,x2:
in terms of the internal degrees of freedom x1,x2:
 | (11) |
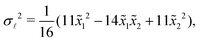 | (12) |
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 1 = x1 + 1/6 and
1 = x1 + 1/6 and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 2 = x2 − 1/6. Both eqn (11) and (12) are illustrated in Fig. 2b. Curves of constant
2 = x2 − 1/6. Both eqn (11) and (12) are illustrated in Fig. 2b. Curves of constant  correspond to lines inclined by 45, where
correspond to lines inclined by 45, where  increases as
increases as ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 1 decreases and
1 decreases and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 2 increases. Meanwhile, curves of constant σ
2 increases. Meanwhile, curves of constant σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) correspond to ellipses centered at
correspond to ellipses centered at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 1 =
1 = ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 2 = 0, whose main axes scale with σ
2 = 0, whose main axes scale with σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and are oriented at 45 angles with respect to the
and are oriented at 45 angles with respect to the ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 1 and
1 and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 2 axes.† Thus, for a given value of σ
2 axes.† Thus, for a given value of σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , any combination of x1 and x2 can give rise to values for
, any combination of x1 and x2 can give rise to values for  only in an interval between
only in an interval between  (blue solid line) and
(blue solid line) and 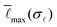 (red dashed line). The upper bound
(red dashed line). The upper bound  only exists because we set y1 = y2 = 0 before; without this constraint,
only exists because we set y1 = y2 = 0 before; without this constraint,  can become arbitrarily large for a given σ
can become arbitrarily large for a given σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) .‡ Meanwhile, the lower bound
.‡ Meanwhile, the lower bound  decreases linearly with the distance between origin (black dot) and the intersection point (red dot) in Fig. 2b, which is proportional to σ
decreases linearly with the distance between origin (black dot) and the intersection point (red dot) in Fig. 2b, which is proportional to σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . As a consequence, using eqn (11) and (12):
. As a consequence, using eqn (11) and (12): | (14) |
 and a
and a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1/3. Inserting this into eqn (8), we obtain indeed eqn (10).
= 1/3. Inserting this into eqn (8), we obtain indeed eqn (10).
In our discussion here we included the internal degrees of freedom x1, x2 to demonstrate their connection to geometrically possible combinations of  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , and to obtain explicit values for
, and to obtain explicit values for  and a
and a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . In general, however, the approach from ref. 18 does not require a discussion of internal degrees of freedom. Eqn (3)–(5) are sufficient to understand the overall system behavior close to the rigidity transition, unless one wants to derive the values of the coefficients
. In general, however, the approach from ref. 18 does not require a discussion of internal degrees of freedom. Eqn (3)–(5) are sufficient to understand the overall system behavior close to the rigidity transition, unless one wants to derive the values of the coefficients  and a
and a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) from first principles.
from first principles.
1.3 Effect of isotropic strain
We now discuss how the effect of isotropic strain ε is incorporated into the formalism. The 4-spring system in Fig. 2a transitions from floppy to rigid when decreasing the dimensionless parameter![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. Such a decrease in
0. Such a decrease in ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 can correspond either to a decrease in the dimensional spring rest length while keeping the system size constant (Fig. 2a left), or to an increase in system size while keeping the dimensional rest length constant (Fig. 2a right). Thus,
0 can correspond either to a decrease in the dimensional spring rest length while keeping the system size constant (Fig. 2a left), or to an increase in system size while keeping the dimensional rest length constant (Fig. 2a right). Thus, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 is a control parameter combining both dimensional spring rest length and isotropic strain.
0 is a control parameter combining both dimensional spring rest length and isotropic strain.
Let us consider simulations where the dimensional spring rest length L0 is kept constant, but the system size V is changing. In this case, the combined control parameter ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 encodes isotropic strain. We define (linear) isotropic strain as ε := (V/Vref)1/D − 1, where the Vref is the system volume right after creation of the network. From our length non-dimensionalization follows that we can convert between
0 encodes isotropic strain. We define (linear) isotropic strain as ε := (V/Vref)1/D − 1, where the Vref is the system volume right after creation of the network. From our length non-dimensionalization follows that we can convert between ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 and bulk strain ε via:
0 and bulk strain ε via:
 | (15) |
1.4 Effect of shear strain
To understand how shear strain enters the formalism, we first note that shearing the system does not change the energy formula eqn (3). However, shearing the system will change the set of geometrically possible combinations . Thus, shear strain needs to be included as a parameter in the minimal-length function
. Thus, shear strain needs to be included as a parameter in the minimal-length function  . In ref. 18 this function is Taylor expanded to second order in shear strain, so that eqn (5) becomes most generally:
. In ref. 18 this function is Taylor expanded to second order in shear strain, so that eqn (5) becomes most generally: | (16) |
 by
by  .
.
Note that the linear order term in ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) appears only because disordered systems with a finite size generally display a small but finite anisotropy. Eqn (16) can be simplified by removing this anisotropy through defining a new shear variable γ =
appears only because disordered systems with a finite size generally display a small but finite anisotropy. Eqn (16) can be simplified by removing this anisotropy through defining a new shear variable γ = ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) − Δγ0, where
− Δγ0, where ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) = Δγ0 is defined as the shear where the function
= Δγ0 is defined as the shear where the function  is minimal: Δγ0 = − b1/2b. Defining
is minimal: Δγ0 = − b1/2b. Defining 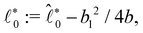 this leads to the minimal-length function:
this leads to the minimal-length function:
 | (17) |
1.5 Elastic properties near the rigidity transition
Substituting eqn (17) into eqn (3) and minimizing with respect to σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , we obtain the following explicit energy expression in terms of the control parameters
, we obtain the following explicit energy expression in terms of the control parameters ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 and γ:
0 and γ: | (18) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 (which is related to isotropic strain ε viaeqn (15)) and shear strain γ allow to derive the following quantities, here for the 2D case:18
0 (which is related to isotropic strain ε viaeqn (15)) and shear strain γ allow to derive the following quantities, here for the 2D case:18 | (19) |
 | (20) |
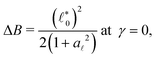 | (21) |
 | (22) |
 , a
, a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and b fully describe the macroscopic elastic behavior in this regime.
and b fully describe the macroscopic elastic behavior in this regime.
2 Numerical results
While in ref. 18 the analytical predictions in eqn (19)–(22) were numerically tested on packing-derived networks only, we test these predictions here on a set of additional network classes. These include phantom triangular and Delaunay networks (both with varying connectivity z), as well as honeycomb and Voronoi networks (which both have fixed connectivity z = 3). We probe the elastic properties of these networks under isotropic (i.e. bulk) strain.2.1 Network generation and energy minimization
Networks of freely hinging nodes are created in a periodic box following existing protocols19,28 (details in Appendix B). We probe the system by varying isotropic strain ε. Each time, we first use bisection to detect the transition point ε*, before we carry out exponential and/or linear sweeps in isotropic strain ε (details in Appendix C). To ensure high precision in our energy minimization, we use an optimized conjugate gradient scheme that allows to reduce the average residual force per degree of freedom to less than 10−12.18Right after creation, where ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) = 0, the disordered networks will generally display an anisotropy. To remove this anisotropy, we need to shear the system to the state
= 0, the disordered networks will generally display an anisotropy. To remove this anisotropy, we need to shear the system to the state ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) = Δγ0 (i.e. γ = 0, see Section 1.4). At this point, according to eqn (20), shear stress vanishes, σ = 0. Thus, the anisotropy in the networks can be numerically removed using shear stabilization.29 Shear stabilization means that shear strain is treated as an additional degree of freedom during the energy minimization. Unless stated otherwise, we always apply this method during the bisection phase to search for the transition point, so that our system right after the bisection phase is at (ε,γ) = (ε*,0). During the subsequent ε sweeps, we keep shear strain γ fixed (details in Appendix C).
= Δγ0 (i.e. γ = 0, see Section 1.4). At this point, according to eqn (20), shear stress vanishes, σ = 0. Thus, the anisotropy in the networks can be numerically removed using shear stabilization.29 Shear stabilization means that shear strain is treated as an additional degree of freedom during the energy minimization. Unless stated otherwise, we always apply this method during the bisection phase to search for the transition point, so that our system right after the bisection phase is at (ε,γ) = (ε*,0). During the subsequent ε sweeps, we keep shear strain γ fixed (details in Appendix C).
2.2 Elastic moduli close to the transition
To numerically characterize the nature of the transition, we first carry out a combination of exponential and linear sweeps around the transition point ε* (details in Appendix C). In Fig. 3, we plot bulk modulus B and shear modulus G against isotropic strain ε for single network realizations with varying connectivity z, where we use harmonic spring potentials. | ||
| Fig. 3 Behavior of bulk and shear moduli across the transition for four different classes of networks and comparison to analytical predictions. (a)–(c) Sketches of network structures of phantom triangular (a, z = 3.2, W = 10), Delaunay (b, z = 3.2, W = 12), Voronoi (c, z = 3, W = 12) and honeycomb (c, z = 3, W = 12) networks. In (a), the solid lines are springs of length one, while the dashed ones are phantom springs, i.e. springs that cross one or more nodes without being connected to them. We show phantom springs, which are actually straight, slightly curved only for better visualization. In (b), gray lines indicate the removed springs from the initial full Delaunay network, leaving the black springs in the actual network. (d)–(i) Numerically obtained bulk modulus B and shear modulus G at γ = 0 against increasing isotropic strain ε for different network classes: phantom triangular (d, g, W = 40) and Delaunay (e, h, W = 20) networks with variable connectivity z, as well as Voronoi (f, i, W = 70) and honeycomb (f, i, W = 60). Here, we use harmonic spring potentials, and we shear stabilized the networks before the ε sweeps (Appendix C). The discontinuity ΔB in the bulk modulus at the transition point and linear scaling of G predicted from eqn (21) and (22) are indicated as solid bars and solid lines, respectively. (h inset) Log-log plot of G against strain difference ε − ε*, to resolve the vicinity of the transition point ε*. Symbols are numerical data and lines are analytical predictions. | ||
At the transition, all networks show a discontinuity ΔB in the bulk modulus, while the transition is continuous in the shear modulus G. This is qualitatively consistent with our analytical predictions (Section 1.5) and the behavior of packing-derived networks.18 We also observe that for both phantom triangular and Delaunay networks the transition point ε* decreases with the average connectivity z.
To compare these data to the prediction for the bulk modulus discontinuity ΔB according to eqn (21), we need the values of 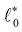 and a
and a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for our simulations. To extract
for our simulations. To extract  , we insert the transition point strain value ε* into eqn (15). To extract a
, we insert the transition point strain value ε* into eqn (15). To extract a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , we plot σ
, we plot σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) over
over  (inset of Fig. 4d) and perform a linear fit whose slope is a
(inset of Fig. 4d) and perform a linear fit whose slope is a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for small
for small  (see Appendix D). Note that for symmetry reasons, the honeycomb lattice has σ
(see Appendix D). Note that for symmetry reasons, the honeycomb lattice has σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0 and thus a
= 0 and thus a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0. The resulting predictions for the bulk modulus discontinuities ΔB are respectively indicated as horizontal bars in Fig. 3d–f. Indeed, our predictions match well the discontinuities present in the simulation data for all four network classes and all connectivities z.
= 0. The resulting predictions for the bulk modulus discontinuities ΔB are respectively indicated as horizontal bars in Fig. 3d–f. Indeed, our predictions match well the discontinuities present in the simulation data for all four network classes and all connectivities z.
Some of the data points right at the transition fall below the analytically predicted value for ΔB. These deviations occur in our data for the strain values closest to the transition point, while ΔB values of the same network at similar strain values match closely with our analytical prediction. These deviations are likely due to numerical residues, an effect that we observed before.18
For the shear modulus, eqn (22) predicts a continuous transition with a linear scaling  . Using eqn (15), this implies also a linear scaling
. Using eqn (15), this implies also a linear scaling 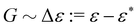 to lowest order in Δε. Indeed, this is what we observed close to the transition (inset of Fig. 4g). We indicate this linear scaling also in Fig. 3g–i. Note that for larger Δε, non-linearities in
to lowest order in Δε. Indeed, this is what we observed close to the transition (inset of Fig. 4g). We indicate this linear scaling also in Fig. 3g–i. Note that for larger Δε, non-linearities in  and in eqn (15) create deviations from this prediction.
and in eqn (15) create deviations from this prediction.
Note that both honeycomb and Voronoi networks have their transition points at ε* = 0. This means that these networks have a SSS already right at creation. While this is clearly the case for the honeycomb lattice, we show in Appendix E that it is also true for any Voronoi network.
Taken together, the elastic properties of the system close to the transition, such as the transition point ε*, the magnitude of the discontinuity ΔB in the bulk modulus, and the linear scaling coefficient for the shear modulus G, can be predicted from the coefficients 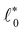 , a
, a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and b.
and b.
2.3 Scaling of 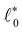 , a
, a![[small script l]](https://www.rsc.org/images/entities/h3_char_e146.gif) and b with connectivity z
and b with connectivity z
In Fig. 4, we plot the parameters  , a
, a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and b for phantom triangular, Delaunay, Voronoi, and honeycomb networks with harmonic spring potentials. For phantom triangular and Delaunay networks, we show the dependency on the connectivity z. For the disordered networks (i.e. phantom triangular, Delaunay, and Voronoi) we average each time over 50 random realizations.
and b for phantom triangular, Delaunay, Voronoi, and honeycomb networks with harmonic spring potentials. For phantom triangular and Delaunay networks, we show the dependency on the connectivity z. For the disordered networks (i.e. phantom triangular, Delaunay, and Voronoi) we average each time over 50 random realizations.
In both phantom triangular and Delaunay networks, close to the isostatic point the parameter 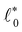 exhibits a linear dependence on Δz with a negative coefficient (Fig. 4a and b), which has also been observed in 2D packing-derived networks.18
exhibits a linear dependence on Δz with a negative coefficient (Fig. 4a and b), which has also been observed in 2D packing-derived networks.18
We also examined the z-scaling exponents of a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and b close to isostaticity (Fig. 4d, e, g and h). For a
and b close to isostaticity (Fig. 4d, e, g and h). For a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , we find for phantom triangular networks a scaling exponent of ≈0.2, for Delaunay networks, we find an exponent close to −1, while we found an exponent of −0.5 in earlier work for packing-derived networks. Meanwhile for b, we find for phantom triangular networks an exponent of ≈−0.5 or smaller, for Delaunay networks an exponent of roughly −2, while we have found before for packing-derived networks an exponent of −1. Hence, the scaling exponent of both parameters strongly depends on network class.
, we find for phantom triangular networks a scaling exponent of ≈0.2, for Delaunay networks, we find an exponent close to −1, while we found an exponent of −0.5 in earlier work for packing-derived networks. Meanwhile for b, we find for phantom triangular networks an exponent of ≈−0.5 or smaller, for Delaunay networks an exponent of roughly −2, while we have found before for packing-derived networks an exponent of −1. Hence, the scaling exponent of both parameters strongly depends on network class.
Note that for a small fraction of the Delaunay networks, we did not observe a linear scaling between σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and
and  , suggesting that the linear relation between
, suggesting that the linear relation between  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) might be violated for these networks (Appendix D). A more detailed examination suggests that this could quite possibly be due to finite numerical cutoffs required to identify the transition point, which would make us miss the regime where this scaling is linear (Appendix F). We excluded these networks from the averages shown in Fig. 4. We stress that we only found deviations from the linear
might be violated for these networks (Appendix D). A more detailed examination suggests that this could quite possibly be due to finite numerical cutoffs required to identify the transition point, which would make us miss the regime where this scaling is linear (Appendix F). We excluded these networks from the averages shown in Fig. 4. We stress that we only found deviations from the linear  scaling for Delaunay networks with harmonic springs, while we could numerically confirm the predicted linear scaling for all phantom triangular and Voronoi networks, as well as the honeycomb network.
scaling for Delaunay networks with harmonic springs, while we could numerically confirm the predicted linear scaling for all phantom triangular and Voronoi networks, as well as the honeycomb network.
2.4 The shear modulus scales linearly with isotropic stress.
In the previous Sections (1.5 and 2.2), we showed that the shear modulus G scales linearly with the isotropic strain beyond the transition point, Δε = ε −ε*. Moreover, a finite bulk modulus discontinuity at ε* implies that the isotropic stress T also scales linearly with Δε to lowest order, which can be derived form eqn (15) and (19). Hence, we would expect from the analytical predictions in Section 1 that the shear modulus scales linearly with the isotropic stress:| G ∼ Tα with α = 1. | (23) |
To resolve this contradiction between the numerical results from ref. 19 and our analytical results from Section 1 and ref. 18, we simulate here different kinds of rope-like networks with a high numerical precision, where we vary linear system size W by more than an order of magnitude. Fig. 5a shows the scaling of the shear modulus G against the isotropic stress T, both averaged over 50 realizations, for phantom triangular networks, where we used two protocols. The open symbols correspond to a protocol without any shear stabilization. This means that no shear strain was applied after the creation of the network, and the ε sweep was carried out at ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) = 0. The closed symbols correspond to a protocol where we used shear stabilization when searching for the transition point, and as a consequence the ε sweep was carried out at γ = 0 (see Sections 1.4).
= 0. The closed symbols correspond to a protocol where we used shear stabilization when searching for the transition point, and as a consequence the ε sweep was carried out at γ = 0 (see Sections 1.4).
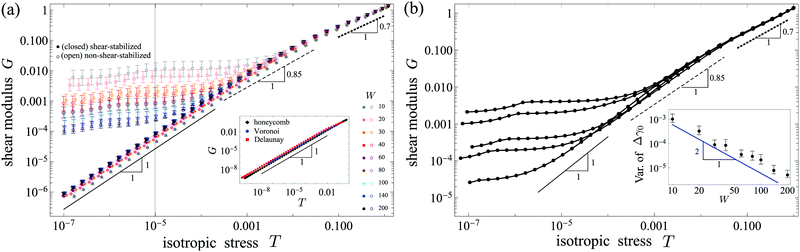 | ||
| Fig. 5 The shear modulus G scales linearly with isotropic stress T for shear-stabilized networks. Without shear stabilization an additional plateau appears at small T. (a) Dependence of G on isotropic stress T for phantom triangular networks with z = 3.2 and rope-like spring potentials for varying system size W, where we either use shear stabilization (closed circles) or not (open circles). All shear-stabilized networks show a linear scaling close to the transition point (at small T). The gray vertical line indicates the lowest T value probed in previous work.19 (a inset) The linear scaling in G(T) also appears for shear-stabilized honeycomb (W = 60), Voronoi (W = 70) and Delaunay (W = 20) networks. Error bars in panel a & inset indicate the standard error of the mean. (b) The G(T) curves for individual phantom triangular networks with z = 3.2 and W = 40 without shear stabilization also exhibit a plateau, confirming that the plateaus in panel a are not due to an averaging effect. (b inset) The variance of the network anisotropy Δγ0 (defined below eqn (16)) across different randomly generated networks for a given system size W scales inversely proportional with W2. | ||
We find that indeed, for the protocol with shear stabilization (closed symbols), the shear modulus G scales linearly with isotropic stress T over many orders of magnitude (Fig. 5a for phantom triangular networks & inset for the other network classes). This observation is independent of system size. However, without shear stabilization (open symbols), at small stress T we observe a plateau, whose value depends on system size. Away from the plateau regions the curves largely collapse for different system sizes.
The appearance of a plateau in G(T) in the protocol without shear stabilization can be readily understood from our analytical results. eqn (22) states that G is proportional to 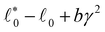 , where
, where  and γ =
and γ = ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) − Δγ0. Without shear stabilization,
− Δγ0. Without shear stabilization, ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) = 0 and so γ = −Δγ0. This implies a plateau in G that is proportional to Δγ02. In other words, the plateau in G(T) is related to the small anisotropy in the disordered networks. Shear stabilization removes this anisotropy and thus also the plateau in G(T).
= 0 and so γ = −Δγ0. This implies a plateau in G that is proportional to Δγ02. In other words, the plateau in G(T) is related to the small anisotropy in the disordered networks. Shear stabilization removes this anisotropy and thus also the plateau in G(T).
To test whether the plateaus that we find in Fig. 5a do not result form an averaging effect, we plot in Fig. 5b the same curves for individual realizations for a given system size. We find that the plateau is also present in individual simulations, and that its height fluctuates across realizations. This makes sense, because the network anisotropy Δγ0 also fluctuates across realizations. Moreover, we find that the variance of Δγ0 decreases inversely proportional to the number of springs in the system (Fig. 5b), which scales as ∼W2. Hence, the plateau in G(T) corresponds to a finite-size effect. A similar conclusion was drawn also in ref. 30 following a different line of argument.
2.5 Linear range of  shows no or weak system-size dependence
shows no or weak system-size dependence
In recent work, it was pointed out that scaling exponents in spring networks under shear strain may be affected by finite-size effects.11 In particular, it was suggested that for networks of size W, finite-size effects could affect scaling exponents when shearing the systems by Δγ ≲ W−1/ν beyond the transition point γ*, where ν > 0. This would correspond to a diverging length scale ξ ∼ |Δγ|−ν. While in this article, we probe the system mechanics with respect to isotropic strain ε instead, we still wanted to check whether such finite-size effects could affect our results.
The system mechanics with respect to isotropic strain is crucially determined by how the minimal-length function  scales with σ
scales with σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) in eqn (15) (Section 1, Appendix H). Hence, we were wondering whether the linear scaling of
in eqn (15) (Section 1, Appendix H). Hence, we were wondering whether the linear scaling of  with σ
with σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is only valid close to the transition point with strains Δε < Δεmax ∼ W−1/ν
is only valid close to the transition point with strains Δε < Δεmax ∼ W−1/ν![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for some ν
for some ν![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 0. In other words, we wondered whether the range Δεmax of linear
> 0. In other words, we wondered whether the range Δεmax of linear  scaling would algebraically decrease to zero with increasing system size W.
scaling would algebraically decrease to zero with increasing system size W.
In Fig. 6 we show the resulting dependency of Δεmax on system size W for both phantom triangular networks and packing-derived networks, both with rope-like spring potentials, where Δεmax is quantified as described in Appendix G. For the phantom networks, beyond an initial quick decrease in Δεmax for small W, we find that for W ≥ 60 our data indicates a finite-size scaling exponent in the range 1/ν![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∈ [0.04,0.35]. Thus, the range of linear scaling in the
∈ [0.04,0.35]. Thus, the range of linear scaling in the  function slowly decreases with system size. In contrast, for the packing-derived networks discussed in ref. 18, we find a range of 1/ν
function slowly decreases with system size. In contrast, for the packing-derived networks discussed in ref. 18, we find a range of 1/ν![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∈ [−0.03,0.08]. This means that the linear scaling range of
∈ [−0.03,0.08]. This means that the linear scaling range of 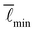 is subject to none, or at most a weak finite-size effect. Thus, intriguingly, the effect of finite-size effects on the linear scaling range of
is subject to none, or at most a weak finite-size effect. Thus, intriguingly, the effect of finite-size effects on the linear scaling range of  appears to depend on the class of network studied.
appears to depend on the class of network studied.
 | ||
Fig. 6 Plot of the isotropic strain range Δεmax = εmax − ε* within which the  function scales linearly with σ function scales linearly with σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , shown here for increasing system size W for phantom triangular networks, and for shear-stabilized packing-derived networks (inset). In both cases, we use z = 3.2 and rope-like potentials. The range Δεmax is quantified as explained in Appendix G and Fig. 9. While for W ≳ 60, the linear range of the phantom triangular networks appear to show a weak power-law dependence on W, there is no significant dependence on system size for packing-derived networks. Error bars indicate the standard error of the mean. , shown here for increasing system size W for phantom triangular networks, and for shear-stabilized packing-derived networks (inset). In both cases, we use z = 3.2 and rope-like potentials. The range Δεmax is quantified as explained in Appendix G and Fig. 9. While for W ≳ 60, the linear range of the phantom triangular networks appear to show a weak power-law dependence on W, there is no significant dependence on system size for packing-derived networks. Error bars indicate the standard error of the mean. | ||
Given that strain-controlled transitions in spring networks have been shown to be critical transitions,4,6,7,10,11,19 we wondered whether we would also observe a divergence in the fluctuations close to the transition. Focusing on the scaling behavior of a non-affine motion parameter Γ with system size W and distance to the transition point, ε − ε*, we find indeed such a divergence (Appendix G). Moreover, we also find finite-size effects with exponents of 1/νΓ ≈ 0.75 for phantom triangular networks and 1/νΓ ≈ 0.6 for packing-derived networks. Intriguingly, these exponents are very different from what we observe for the linear scaling regime of 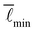 , i.e. νΓ ≠ ν
, i.e. νΓ ≠ ν![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . This suggests that the linear range of
. This suggests that the linear range of  is not controlled by the diverging length scale that controls non-affine motion. A possible reason for this is that close to the transition the non-affinity parameter Γ mostly captures motions that are (to first-order) unconstrained by spring lengths, while
is not controlled by the diverging length scale that controls non-affine motion. A possible reason for this is that close to the transition the non-affinity parameter Γ mostly captures motions that are (to first-order) unconstrained by spring lengths, while  characterizes spring length behavior.
characterizes spring length behavior.
3 Discussion
We studied the elastic behavior of sub-isostatic spring networks that are rigidified by isotropic expansion, comparing numerical simulation results with analytical predictions from ref. 18. We first summarized the approach from ref. 18, which proposed an analytical framework to predict the behavior of the elastic network properties using a minimal-length function (eqn (17)). This minimal-length function allows to map the physical problem of the strain-induced stiffening transition to the purely geometric problem of finding a minimal length. Because of this reduction to a geometric problem, we expect these results to hold quite generally for any athermal, under-constrained material with a fixed connectivity.
(eqn (17)). This minimal-length function allows to map the physical problem of the strain-induced stiffening transition to the purely geometric problem of finding a minimal length. Because of this reduction to a geometric problem, we expect these results to hold quite generally for any athermal, under-constrained material with a fixed connectivity.
The  formalism allows to make several predictions of the elastic network behavior close to the transition.18 These predictions include the rigid-floppy boundary with respect to shear and isotropic strain, the value of the bulk modulus discontinuity at the transition, the linear scaling coefficient of shear modulus with isotropic tension, the value of the shear modulus discontinuity for networks under shear strain, the coefficient of the linear shear modulus scaling beyond this transition, and the coefficient describing the anomalous Poynting effect. All of these predictions are based on the three parameters
formalism allows to make several predictions of the elastic network behavior close to the transition.18 These predictions include the rigid-floppy boundary with respect to shear and isotropic strain, the value of the bulk modulus discontinuity at the transition, the linear scaling coefficient of shear modulus with isotropic tension, the value of the shear modulus discontinuity for networks under shear strain, the coefficient of the linear shear modulus scaling beyond this transition, and the coefficient describing the anomalous Poynting effect. All of these predictions are based on the three parameters  , a
, a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and b. In other words, ref. 18 reduced the question of quantitatively predicting the elastic properties of disordered spring networks close to the transition to the question of determining these three parameters a priori, which we believe is a very hard problem that remains for future work. Currently, these parameters need to be determined numerically. However, by combining our predictions one also obtains non-trivial parameter-free predictions that apply to any athermal under-constrained material.18
and b. In other words, ref. 18 reduced the question of quantitatively predicting the elastic properties of disordered spring networks close to the transition to the question of determining these three parameters a priori, which we believe is a very hard problem that remains for future work. Currently, these parameters need to be determined numerically. However, by combining our predictions one also obtains non-trivial parameter-free predictions that apply to any athermal under-constrained material.18
A key result required to derive all our predictions is that close to the transition the minimal average spring length  depends linearly on the standard deviation of the spring lengths σ
depends linearly on the standard deviation of the spring lengths σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . We have shown that this scaling results from the appearance of a state of self-stress (SSS) at the onset of rigidity.14 We note that an equivalent linear scaling has been reported before, in a system of spheres close to the jamming point.31 However, in such a system each contact change will also change the set of SSSs. Contact changes occur also in a host of other systems, such as vitrimers.32 Hence, investigating in depth how varying connectivity affects the relation between
. We have shown that this scaling results from the appearance of a state of self-stress (SSS) at the onset of rigidity.14 We note that an equivalent linear scaling has been reported before, in a system of spheres close to the jamming point.31 However, in such a system each contact change will also change the set of SSSs. Contact changes occur also in a host of other systems, such as vitrimers.32 Hence, investigating in depth how varying connectivity affects the relation between  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is an interesting question for future research.
is an interesting question for future research.
To numerically test the predictions, we first verified the linear scaling of the minimal-length function near the transition and extracted the three parameters  , a
, a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and b for four different network classes, including phantom triangular, Delaunay, honeycomb, and Voronoi networks. Based on these parameters, we compute the bulk modulus discontinuity ΔB, which predicts well our numerical results for all network classes (Fig. 3). Moreover, we also recovered the predicted linear scaling of the shear modulus G with isotropic tension T close to the transition.
and b for four different network classes, including phantom triangular, Delaunay, honeycomb, and Voronoi networks. Based on these parameters, we compute the bulk modulus discontinuity ΔB, which predicts well our numerical results for all network classes (Fig. 3). Moreover, we also recovered the predicted linear scaling of the shear modulus G with isotropic tension T close to the transition.
Next we explored the scaling of the parameters 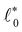 , a
, a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and b with respect to connectivity z. We found that the scaling of the parameters a
and b with respect to connectivity z. We found that the scaling of the parameters a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and b with the distance to isostaticity Δz = 4 − z strongly depends on the network class. The scaling exponent for a
and b with the distance to isostaticity Δz = 4 − z strongly depends on the network class. The scaling exponent for a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) can even change sign, varying from −1 for Delaunay networks to ≈0.2 for phantom triangular networks (Fig. 4, with an exponent of −0.5 for packing-derived networks18). The scaling exponent for b varies from −2 for Delaunay networks to −0.5 for phantom triangular networks (Fig. 4, with an exponent of −1 for packing-derived networks18). This dependency on network class is not too surprising, since the parameters
can even change sign, varying from −1 for Delaunay networks to ≈0.2 for phantom triangular networks (Fig. 4, with an exponent of −0.5 for packing-derived networks18). The scaling exponent for b varies from −2 for Delaunay networks to −0.5 for phantom triangular networks (Fig. 4, with an exponent of −1 for packing-derived networks18). This dependency on network class is not too surprising, since the parameters  , a
, a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and b depend on the microscopic network structure, which varies with network class. In contrast, the value of
and b depend on the microscopic network structure, which varies with network class. In contrast, the value of  always showed a linear dependency on Δz, where intercept and slope depend on network class.
always showed a linear dependency on Δz, where intercept and slope depend on network class.
One prediction of the formalism in ref. 18 is a linear scaling of the shear modulus G with the isotropic stress T close to the transition point: G ∼ Tα with α = 1. This is a direct consequence of the discontinuity ΔB in the bulk modulus and of the linear scaling of the shear modulus G with strain Δε. There are different ways to derive such a linear scaling (e.g. ref. 15 and 27); ref. 18 showed that it can be understood as a consequence of the linear scaling of the  function with σ
function with σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . While in Section 1.4 we make the assumption that
. While in Section 1.4 we make the assumption that 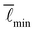 at its minimum is analytical in γ, even certain non-analytic behavior in γ would still lead to an integer exponent α (Appendix H). However, the prediction of integer α seems to be at odds with recent numerical work, which suggested that the value of α can be different from one for networks with a rope-like interaction potential, depending on the disordered nature of the network.19 In particular, ref. 19 found an exponent of α ≈ 0.85 for phantom triangular networks and α ≈ 0.9 for Delaunay networks with connectivity of z = 3.2.
at its minimum is analytical in γ, even certain non-analytic behavior in γ would still lead to an integer exponent α (Appendix H). However, the prediction of integer α seems to be at odds with recent numerical work, which suggested that the value of α can be different from one for networks with a rope-like interaction potential, depending on the disordered nature of the network.19 In particular, ref. 19 found an exponent of α ≈ 0.85 for phantom triangular networks and α ≈ 0.9 for Delaunay networks with connectivity of z = 3.2.
To reconcile the two results from ref. 18 and 19, we numerically studied the G(T) scaling with an increased numerical precision, and our results confirmed the analytically predicted scaling exponent of α = 1 in both phantom triangular and Delaunay networks (Fig. 5a and inset). We show that the result also depends on a small random anisotropy in the generated network. In the presence of such a finite anisotropy, we observed a plateau in the shear modulus G(T) for small isotropic stress T, consistent with the analytic prediction, eqn (22). This plateau disappears when using shear stabilization,29 which removes the network anisotropy by shearing the network by a shear strain Δγ0 (Section 1.4). We moreover show that the plateau disappears for larger system sizes (Fig. 5b inset). Hence, while without shear stabilization large system sizes are required to probe the behavior close to the transition, shear stabilization allows to explore this regime already for smaller systems.
We see two possible reasons for the discrepancy in the G(T) scaling between ref. 18 and 19. First, we used the conjugate gradient minimizer code developed in ref. 18, which allows us to probe the system at least two orders of magnitude closer to the transition point than ref. 19 (see gray vertical line in Fig. 5a). For instance in phantom triangular networks we observe an exponent of α < 1 for larger isotropic stress T ≳ 10−3, which seems consistent with the value of 0.85 given by ref. 19, while we observe an exponent of α = 1 for stress T smaller than that. Second, we show that a small anisotropy in the generated network can lead to a plateau in the shear modulus curve G(T), which could in turn affect the inferred scaling exponent.
Previous work suggested that finite-size effects could affect scaling exponents in spring networks.11 This can occur whenever the system size is on the order of or smaller than a length scale that diverges close to the transition point. While ref. 11 focused on shear simulations, we wanted to test whether such an effect could also arise in our isotropic-strain simulations. To this end, we numerically tested in what range around the transition point the linear scaling of the  function holds. Our results suggest that this potentially depends on the class of network studied. While in phantom triangular networks, this range decreases weakly with system size, we did not find a significant decrease in packing-derived networks. This is also consistent with Fig. 5a, which suggests that G(T) is largely independent of system size W for the range of W probed.
function holds. Our results suggest that this potentially depends on the class of network studied. While in phantom triangular networks, this range decreases weakly with system size, we did not find a significant decrease in packing-derived networks. This is also consistent with Fig. 5a, which suggests that G(T) is largely independent of system size W for the range of W probed.
Intriguingly, we found that non-affine motion Γ shows a much stronger system-size dependence, suggesting that it is controlled by a length scale that does not affect the linear range of 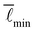 . One possible reason for this is that close to the transition point non-affine motions are to linear order unconstrained in under-constrained networks. Better understanding this difference in the finite-size scaling behavior of Γ and
. One possible reason for this is that close to the transition point non-affine motions are to linear order unconstrained in under-constrained networks. Better understanding this difference in the finite-size scaling behavior of Γ and  is an interesting avenue for future research.
is an interesting avenue for future research.
Conflicts of interest
The authors declare no conflict of interest.Appendix
A Generalization to networks with heterogeneous spring constants and rest lengths
In the main text, we focused on the case where all springs share the same rest length![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 and the same spring constant k. Here, we generalize this to networks where rest length and spring constant may differ among the springs, as in eqn (1). Similar to ref. 18, we introduce re-scaled spring lengths
0 and the same spring constant k. Here, we generalize this to networks where rest length and spring constant may differ among the springs, as in eqn (1). Similar to ref. 18, we introduce re-scaled spring lengths 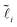 , re-scaled spring constants
, re-scaled spring constants ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) i, and an average spring rest length
i, and an average spring rest length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 in a way that allows us to rewrite eqn (1) in the form:
0 in a way that allows us to rewrite eqn (1) in the form: | (24) |
 | (25) |
 | (26) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 as the quadratic mean of the
0 as the quadratic mean of the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0i, weighted by the ki:
0i, weighted by the ki: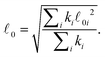 | (27) |
 | (28) |
 and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are defined as the average and standard deviation of the re-scaled spring length
are defined as the average and standard deviation of the re-scaled spring length  with the weighting factors
with the weighting factors ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) i:
i: | (29) |
B Network generation
Networks were created using the following protocols.Phantom triangular (Fig. 3a)28
Following ref. 19, a 2D triangular lattice of spacing 1 is first constructed by depositing three sets of W parallel filaments each at angles of 0°, 60° and 120° with the x-axis, respectively. To reduce the connectivity from z = 6 to values observed in e.g. collagen networks33 of 3 ≤ z < 4, we first detach at each node one filament, which is randomly chosen among the three crossing filaments. This creates a network of homogeneous connectivity z = 4. To avoid system-spanning filaments, one spring is removed at a random position on each filament, giving the average connectivity z = 4 − 6/W. To further reduce the connectivity to a defined value z, we implement an iterative procedure. At each iteration, we randomly remove only a few of the springs and then clear off all of the dangling springs and isolated islands. This is repeated until the desired connectivity z is reached.Delaunay (Fig. 3b)
Delaunay networks are constructed from W2 nodes that are placed at uncorrelated random positions in a square box of side W. The connectivity of initially z = 6 is decreased to the desired value z by employing the same protocol using random cuts as for the phantom triangular networks.Honeycomb (Fig. 3c)
We construct a network of W2/3 regular hexagons with side length 1.Voronoi (Fig. 3c)
Voronoi networks correspond to the Voronoi tessellation of W2/2 nodes at uncorrelated random positions in a square box of side W.In all four network classes, we set the dimensionless spring rest lengths ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0i to the respective initial spring lengths before any deformation is applied, i.e. at (ε,
0i to the respective initial spring lengths before any deformation is applied, i.e. at (ε,![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) ) = (0,0). We set the dimensionless spring constants as the inverse of the respective rest length at zero strain, ki = 1/
) = (0,0). We set the dimensionless spring constants as the inverse of the respective rest length at zero strain, ki = 1/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0i.
0i.
C Details of numerical strain sweeps and computation of the elastic moduli
In this paper, we exclusively carry out sweeps of isotropic strain ε. Before each sweep, we first identified the transition point ε*. To this end, we implemented a bisection scheme, which we optimized by linearly interpolating the transition point in each step. We defined networks as rigid whenever their isotropic stress T is above a cutoff value of 10−10 (two orders of magnitude above the tolerance for the residual force cutoff per degree of freedom, 10−12). We use isotropic stress T as a criterion for network rigidity, because it is much faster to compute than an elastic modulus.In the bisection to identify the transition point, we also implemented the option to perform shear stabilization to remove network anisotropy (Sections 1.4 and 2.1). This is done by treating the shear strain ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) as an additional degree of freedom during each energy minimization of the bisection process. In any case, shear stabilization was always turned off (i.e. shear remains constant) after the transition point ε* has been identified.
as an additional degree of freedom during each energy minimization of the bisection process. In any case, shear stabilization was always turned off (i.e. shear remains constant) after the transition point ε* has been identified.
We apply an exponential sweep of isotropic strain to probe the scaling behavior of network mechanics close to the transition point ε*. In particular, we probed strain values ε − ε* = 10−10+0.2k, where the step index k ranged from 0 to 51 by default, with only two exceptions. First, in Fig. 3, we apply the same exponential sweep, yet with k ranging from 0 to 7 only, which is then followed by a linear sweep. Second, for the Voronoi networks of size W = 70 (Fig. 4 and Fig. 5a inset) we needed to increase the residual force cutoff for the energy minimization to 10−10, and so we also raised the cutoff in isotropic stress T to identify the transition point to 10−8. Accordingly, we changed the sweep to the values ε − ε* = 10−8+0.2k with k ranging from 0 to 41.
We computed the elastic moduli using two different methods. For not too big networks, we diagonalized the Hessian of the system energy and used the resultant eigenvalues to compute elastic moduli.18,27,34–36 This approach produces a higher numerical precision and was suitable for typical system sizes W < 100 (Fig. 3 and 4). However, in Fig. 5 we studied networks with a large system size, and so we used a less time-intensive way of computing the shear modulus G. We computed G through a difference quotient of the shear stress over the shear strain: G(ε, γ = 0) = [σ(ε, Δ) − σ(ε, −Δ)]/2Δ, where we numerically tuned and found the optimized shear strain Δ = 5 × 10−5. We also noticed that for ε − ε* < 10−7 the shear modulus computed with this method could deviate significantly from the true value. We hence excluded these data points in Fig. 5 and the lowest isotropic stress there is accordingly T ≈ 10−7.
D Extraction of the parameters a![[small script l]](https://www.rsc.org/images/entities/h3_char_e146.gif) and b of the minimal-length function
and b of the minimal-length function
To extract a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) from numerical data, one could just directly use the
from numerical data, one could just directly use the  function (eqn (5)). However, this approach depends on the correct identification of the transition point
function (eqn (5)). However, this approach depends on the correct identification of the transition point  . While we can identify
. While we can identify  with a relatively high precision of ∼10−10, we could even remove the dependency on
with a relatively high precision of ∼10−10, we could even remove the dependency on 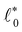 entirely when determining a
entirely when determining a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . To this end, we note that in an energy-minimized state, the energy is also minimal with respect to variation of σ
. To this end, we note that in an energy-minimized state, the energy is also minimal with respect to variation of σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , i.e. de/dσ
, i.e. de/dσ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0. From eqn (3), and using the insight that
= 0. From eqn (3), and using the insight that  in the rigid regime, the minimization condition reads:
in the rigid regime, the minimization condition reads: | (30) |
 . Taken together, we thus obtain the linear relation:
. Taken together, we thus obtain the linear relation: | (31) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and
and  (e.g.Fig. 4d inset) allows both to effectively verify the scaling of the minimal-length function (eqn (5)), and to extract the value of a
(e.g.Fig. 4d inset) allows both to effectively verify the scaling of the minimal-length function (eqn (5)), and to extract the value of a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . This approach does not involve the critical value
. This approach does not involve the critical value  which we obtain with a lower precision as compared to
which we obtain with a lower precision as compared to  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (as precise as 10−12).
(as precise as 10−12).
To extract the parameter b, we use the derived shear modulus formula (eqn (22)), instead of directly using the original minimal-length function (eqn (17)) since we do not shear the networks (i.e. γ = 0). As before, we intend not to use the critical value  . Thus, to replace the term
. Thus, to replace the term 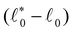 that appears in the shear modulus formula (eqn (22)), we insert eqn (31) back into the minimal-length function (eqn (5)) and obtain
that appears in the shear modulus formula (eqn (22)), we insert eqn (31) back into the minimal-length function (eqn (5)) and obtain
 | (32) |
 | (33) |
 (Fig. 4g inset).
(Fig. 4g inset).
By default we use the first 25 data points from an exponential sweep to numerically fit eqn (31) and (33) and extract the parameters a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and b. Note that a
and b. Note that a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) in Fig. 6 is defined in the very same way, based on the first 25 data points of an exponential sweep. Meanwhile in Fig. 3 we use only the first 5 data points due to a decreased step number n in the exponential sweep of isotropic strain (Appendix C).
in Fig. 6 is defined in the very same way, based on the first 25 data points of an exponential sweep. Meanwhile in Fig. 3 we use only the first 5 data points due to a decreased step number n in the exponential sweep of isotropic strain (Appendix C).
We note that rope-like spring potentials can be treated as well with the analytical framework in Section 1, which we took into account when computing  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) here. While one way to treat rope-like spring potentials was discussed in ref. 18, where each spring is subdivided into a series of shorter springs, we chose here an alternative approach. We used the fact that for rope-like spring potentials, a spring i only affects the mechanics when
here. While one way to treat rope-like spring potentials was discussed in ref. 18, where each spring is subdivided into a series of shorter springs, we chose here an alternative approach. We used the fact that for rope-like spring potentials, a spring i only affects the mechanics when ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i >
i > ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0i, while springs with
0i, while springs with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i <
i < ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0i do not contribute. Thus, to compute
0i do not contribute. Thus, to compute  and σ
and σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , whenever for any spring i the distance of the two connected nodes is smaller than the rest length
, whenever for any spring i the distance of the two connected nodes is smaller than the rest length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0i, we set the spring length to
0i, we set the spring length to ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i =
i = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0i. This redefinition of
0i. This redefinition of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i does not affect the computation of shear modulus G and tension T.
i does not affect the computation of shear modulus G and tension T.
E Any Voronoi network at creation has a state of self stress
We numerically found that Voronoi networks have a critical isotropic strain very close to zero, ε* ≈ 0. Here we show that the critical strain is indeed exactly zero, by proving that there is a state of self stress right at creation of these networks. In other words, at creation (ε = 0) these networks can sustain finite tensions in a subset of springs, while force balance is maintained at the internal nodes.The geometric structure of a Voronoi network allows for the following set of spring tensions ti (with i being a spring index) to be a state of self stress:
| ti = η |C2i− C1i|. | (34) |
 | ||
| Fig. 7 Illustration of local force balance at any node n of a Voronoi network, demonstrating that Voronoi networks have a SSS at creation. Red dots are the internal nodes, while blue dots are the neighboring random seeds used for the Voronoi tessellation. Geometrically, node n is created as the circumcenter of the local triangle (gray dashed lines) formed by these seeds, and the three local springs i, j and k (black segments) are the vertical bisectors of the respective sides. The vectors C1i and C2i refer to the two seed points at the side perpendicular to spring i (and similarly for springs j and k). The node n is force-balanced when the magnitude of the spring tensile forces (fi, fj and fk, in black arrows) follow the proportionality relation, eqn (34). These forces will form a closed triangle that is similar to the local triangle by a rotation of 90°, thus giving zero net force, see also eqn (35) and (36). | ||
To show that the set of spring tensions ti form a state of self stress, we demonstrate that they satisfy local force balance at each node. To this end, we focus here on a node n that is connected to springs i, j, k as shown in Fig. 7. The force that spring i exerts on the node n is fi = tiei, where ei is the unit tangent vector of spring i pointing away from node n. Furthermore, we have
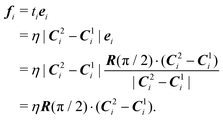 | (35) |
| fi + fj + fk = 0. | (36) |
F Apparent non-linear scaling of  in some Delaunay networks
in some Delaunay networks
For Delaunay networks with harmonic spring potentials, we observed that a fraction of the networks did not seem to follow the linear relation (31) between σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and
and  (blue and red data points in Fig. 8a inset). This is also apparent from the absence of a plateau in
(blue and red data points in Fig. 8a inset). This is also apparent from the absence of a plateau in  (compare blue and red with black data points in Fig. 8a). From our arguments in Appendix D, it follows that this non-linearity also implies a non-linear scaling of the minimal-length function
(compare blue and red with black data points in Fig. 8a). From our arguments in Appendix D, it follows that this non-linearity also implies a non-linear scaling of the minimal-length function  with σ
with σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , which would also affect the elastic network properties, eqn (19)–(22).
, which would also affect the elastic network properties, eqn (19)–(22).
We wondered whether this non-linear scaling between σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and
and 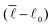 was just due to finite numerical cutoffs, or whether it reflects the real scaling behavior infinitesimally close to the transition point. Numerical limitations arise because we cannot probe the networks arbitrarily close to the true transition point. Indeed, we used a cutoff value of Tcutoff = 10−10 for the isotropic stress T to numerically identify the transition point. In other words, at the detected transition point we are already in the rigid regime by some small extent beyond the true transition point. If the plateau in
was just due to finite numerical cutoffs, or whether it reflects the real scaling behavior infinitesimally close to the transition point. Numerical limitations arise because we cannot probe the networks arbitrarily close to the true transition point. Indeed, we used a cutoff value of Tcutoff = 10−10 for the isotropic stress T to numerically identify the transition point. In other words, at the detected transition point we are already in the rigid regime by some small extent beyond the true transition point. If the plateau in 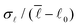 exists only close to the true transition point until some isotropic stress value Tmax < Tcutoff, we will not detect it since we missed that regime. To test if this could be the case, we created histograms of the extent Tmax of the plateau for different connectivity z (Fig. 8b). For a given network, we define Tmax as the isotropic stress of the data point at which the quotient
exists only close to the true transition point until some isotropic stress value Tmax < Tcutoff, we will not detect it since we missed that regime. To test if this could be the case, we created histograms of the extent Tmax of the plateau for different connectivity z (Fig. 8b). For a given network, we define Tmax as the isotropic stress of the data point at which the quotient  first deviates by more than 10% from the value of this quotient at the detected transition point. For networks where the plateau ends below Tcutoff, we would find with this approach Tmax ≈ Tcutoff = 10−10. If there is a significant excess of networks where we numerically do not observe a plateau, this could be an indication that there is indeed no plateau.
first deviates by more than 10% from the value of this quotient at the detected transition point. For networks where the plateau ends below Tcutoff, we would find with this approach Tmax ≈ Tcutoff = 10−10. If there is a significant excess of networks where we numerically do not observe a plateau, this could be an indication that there is indeed no plateau.
Fig. 8b shows that for Delaunay networks with harmonic springs, Tmax generally decreases with connectivity z, and that we only observe a peak around Tmax ≈ Tcutoff occur mostly for the two largest values of z. Even in these cases, the peak is not very pronounced and may very well arise from the integral of the real Tmax distribution from 0 to Tcutoff. In other words, these networks may possibly have a plateau which ends just too close to the transition point for us to detect it.
This is also consistent with the observation that most of these curves appear to collapse with the curves that do show a plateau beyond the end of the plateau (Fig. 8a). This suggests that the non-linear scaling regime just corresponds to a regime governed by higher-order terms. In future work, it will be interesting to see if these higher-order terms could also be predicted from first principles.
G Finite-size effects
In the main text, we examined the range of validity of the linear scaling of with σ
with σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . In Fig. 9 we show how we determined this range using a 10% cutoff on the ratio
. In Fig. 9 we show how we determined this range using a 10% cutoff on the ratio  . We find in Section 2.5 that this range does not or only weakly change with system size.
. We find in Section 2.5 that this range does not or only weakly change with system size.
 | ||
Fig. 9 Δεmax in Fig. 6 is defined as the strain range where the ratio 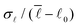 shows a deviation of less than 10% from its value a shows a deviation of less than 10% from its value a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) defined very close to the transition point (Appendix C). defined very close to the transition point (Appendix C). | ||
Strain-stiffening of spring networks has been shown to be a critical transition when using shear strain as control parameter, which includes diverging fluctuations when approaching the transition point.6,10,11,19 We wondered whether we would also observe diverging fluctuations when using isotropic strain as control parameter. Analogous to previous work,6,10,11,19 we quantify fluctuations using a non-affinity parameter Γ, which we define as:
 | (37) |
 | (38) |
Using the same networks as in Fig. 6, we numerically studied Γ(ε) and its dependence on system size. For all system sizes we observed a plateau in Γ(ε) (Fig. 10a), for both phantom triangular and packing-derived networks.
 | ||
| Fig. 10 Finite-size scaling of the non-affinity parameter Γ defined in eqn (37). (a) A plateau regime is observed in Γ at strain values close to the transition point ε*. Here we show only three example networks with W = 140 of different class. (b and c) As system size W increases, the range Δεpl of the plateau decreases as a power-law, while the plateau value Γpl increases as a power-law. The plateau range Δεpl here is defined as the strain difference between the transition point ε* and the point where Γ shows a 10% deviation from its plateau value Γpl. Error bars indicate the standard error of the mean (≈50 networks for each system size). Here we studied the same set of networks as in Fig. 6. | ||
We examined how both height Γpl and extent Δεpl of the plateau depend on system size (Fig. 10b and c). We quantified the extent Δεpl as the value of ε where Γ deviates by 10% from the plateau value, where we also performed linear interpolation between neighboring εk values. We found power law scaling with system size of both plateau value Γpl ∼ WλΓ/νΓ and plateau extent Δεpl ∼ W−1/νΓ. For the phantom triangular networks we found the plateau height exponent λΓ/νΓ ≈ 1.1 and for plateau extent 1/νΓ ≈ 0.75. For the packing-derived networks, we found the plateau height exponent λΓ/νΓ ≈ 0.5 and for plateau extent 1/νΓ ≈ 0.6.
These findings are consistent with the finite-size scaling behavior of the non-affinity parameter Γ with respect to shear strain γ:6,10,11,19 The non-affinity parameter generally diverges when approaching the transition as Γ ∼ |Δγ|−λΓ with λΓ > 0, but a diverging length scale ξΓ ∼ |Δγ|−νΓ with νΓ > 0 changes this behavior for system sizes W ≲ ξΓ. As a consequence, the non-affinity parameter Γ (γ) has a plateau whose height scales as Γpl ∼ WλΓ/νΓ, and whose extent scales as Δγpl ∼ W−1/νΓ. Here we demonstrated that this behavior also appears when using isotropic strain instead of shear strain as control parameter.
Noticeably, the 1/νΓ values are much larger than the power-law exponent 1/ν![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) that characterizes the range of the linear scaling of
that characterizes the range of the linear scaling of  (Fig. 6; for phantom triangular networks 1/ν
(Fig. 6; for phantom triangular networks 1/ν![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∈ [0.04,0.35], while for packing-derived ones 1/ν
∈ [0.04,0.35], while for packing-derived ones 1/ν![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∈ [−0.03,0.08]). This indicates that the linear scaling regime of
∈ [−0.03,0.08]). This indicates that the linear scaling regime of  is not controlled by the diverging length scale ξΓ that governs the apparent divergence of the non-affine motions.
is not controlled by the diverging length scale ξΓ that governs the apparent divergence of the non-affine motions.
H General form of the minimal length function
In eqn (5), we Taylor-expanded the minimal length function to the second order in shear strain γ, while treating the coefficient a
to the second order in shear strain γ, while treating the coefficient a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) as independent of γ. Here we discuss a more general form of
as independent of γ. Here we discuss a more general form of  that can include potentially non-analytic dependencies on γ:
that can include potentially non-analytic dependencies on γ: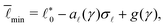 | (39) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (γ) is a function of γ. We also newly introduced the function g(γ), where we choose the convention g(0) = 0; any offset can be absorbed into
(γ) is a function of γ. We also newly introduced the function g(γ), where we choose the convention g(0) = 0; any offset can be absorbed into  . Note that eqn (39) reflects an arbitrary dependency of
. Note that eqn (39) reflects an arbitrary dependency of  on γ, while we keep the linear dependency on σ
on γ, while we keep the linear dependency on σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . Both a
. Both a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and g do not need to be analytic, but they need to be twice differentiable at γ = 0, or at least arbitrarily close to γ = 0.
and g do not need to be analytic, but they need to be twice differentiable at γ = 0, or at least arbitrarily close to γ = 0.
After minimizing the energy with respect to inner degrees of freedom and the standard deviation σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , the resultant energy e is:
, the resultant energy e is:
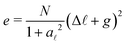 | (40) |
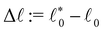 . Using G = (d2e/dγ2)|γ=0/N we then obtain for the shear modulus:
. Using G = (d2e/dγ2)|γ=0/N we then obtain for the shear modulus: | (41) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , g, and their derivatives with respect to γ.
, g, and their derivatives with respect to γ.
Note that according to eqn (19), Δ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is proportional to isotropic tension: T ∼ Δ
is proportional to isotropic tension: T ∼ Δ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , which can be understood as a consequence of the bulk modulus discontinuity. Since the Qs in eqn (41) do not depend on Δ
, which can be understood as a consequence of the bulk modulus discontinuity. Since the Qs in eqn (41) do not depend on Δ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , one already observes from this equation that any scaling G ∼ Tα needs to have α ∈ {0,1,2}. In this sense, the integer scaling exponent between G and T is inherited from the linear scaling of the
, one already observes from this equation that any scaling G ∼ Tα needs to have α ∈ {0,1,2}. In this sense, the integer scaling exponent between G and T is inherited from the linear scaling of the 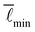 function with σ
function with σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) in eqn (39).
in eqn (39).
Which of the three values α ∈ {0,1,2} is attained depends on the coefficients Q0 to Q2 in eqn (41), which are:
Q0 = (1 + a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2)2g′2 2)2g′2 | (42) |
 | (43) |
 | (44) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) or g has a finite first or second derivative with respect to γ at γ = 0.
or g has a finite first or second derivative with respect to γ at γ = 0.
With respect to the scaling exponent α we can say that first, α = 0 only if g has a finite first derivative. This corresponds to the case where there is a discontinuity in the shear modulus at the transition point. In these cases, the SSS that appears at the transition must have finite overlap with the shear deformation, i.e. the network is asymmetric (Section 1.4, e.g. the non-shear stabilized simulations in Fig. 5). Second, α = 1 only if g′ = 0 (i.e. the network is symmetric) and g has a finite second derivative. This is the typical case that we observe for shear-stabilized networks. Third, α = 2 would appear if the network is symmetric (g′ = 0), the second derivative of g vanishes, and a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) has finite first or second derivative. This situation might appear at a bifurcation (where g′′ as bifurcation parameter crosses zero), possibly related to a structural transition in the network.
has finite first or second derivative. This situation might appear at a bifurcation (where g′′ as bifurcation parameter crosses zero), possibly related to a structural transition in the network.
Eqn (42)–(44) include first and second derivatives of g and a![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , which may formally not exist at γ = 0. An important possibility is that at least one of these four derivatives might diverge as γ → 0. However, with eqn (41) this would imply that generally also the shear modulus G diverges as γ → 0, which to our knowledge has not yet been observed in spring networks.
, which may formally not exist at γ = 0. An important possibility is that at least one of these four derivatives might diverge as γ → 0. However, with eqn (41) this would imply that generally also the shear modulus G diverges as γ → 0, which to our knowledge has not yet been observed in spring networks.
Acknowledgements
We thank Martin Lenz for fruitful discussions. We thank the Centre Interdisciplinaire de Nanoscience de Marseille (CINaM) for providing office space. The project leading to this publication has received funding from France 2030, the French Government program managed by the French National Research Agency (ANR-16-CONV-0001), and from the Excellence Initiative of Aix-Marseille University – A*MIDEX. The Centre de Calcul Intensif dAix-Marseille is acknowledged for granting access to its high-performance computing resources.References
- W. G. Ellenbroek, Z. Zeravcic, W. Van Saarloos and M. Van Hecke, EPL, 2009, 87, 6 CrossRef
.
- J. L. Silverberg, A. R. Barrett, M. Das, P. B. Petersen, L. J. Bonassar and I. Cohen, Biophys. J., 2014, 107, 1721–1730 CrossRef CAS PubMed
.
- A. J. Licup, S. Münster, A. Sharma, M. Sheinman, L. M. Jawerth, B. Fabry, D. A. Weitz and F. C. MacKintosh, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 9573–9578 CrossRef CAS PubMed
.
- J. Feng, H. Levine, X. Mao and L. M. Sander, Soft Matter, 2016, 12, 1419–1424 RSC
.
- A. S. V. Oosten, M. Vahabi, A. J. Licup, A. Sharma, P. A. Galie, F. C. MacKintosh and P. A. Janmey, Sci. Rep., 2016, 6, 19270 CrossRef
.
- A. Sharma, A. J. Licup, R. Rens, M. Vahabi, K. A. Jansen, G. H. Koenderink and F. C. MacKintosh, Phys. Rev. E, 2016, 94, 042407 CrossRef CAS PubMed
.
- A. Sharma, A. J. Licup, K. A. Jansen, R. Rens, M. Sheinman, G. H. Koenderink and F. C. Mackintosh, Nat. Phys., 2016, 12, 584–587 Search PubMed
.
- A. J. Licup, A. Sharma and F. C. Mackintosh, Phys. Rev. E, 2016, 93, 012407 CrossRef CAS PubMed
.
- K. A. Jansen, A. J. Licup, A. Sharma, R. Rens, F. C. MacKintosh and G. H. Koenderink, Biophys. J., 2018, 114, 2665–2678 CrossRef CAS PubMed
.
- J. L. Shivers, S. Arzash, A. Sharma and F. C. MacKintosh, Phys. Rev. Lett., 2019, 122, 188003 CrossRef CAS PubMed
.
- S. Arzash, J. L. Shivers and F. C. MacKintosh, Soft Matter, 2020, 169, 6784–6793 RSC
.
- J. C. Maxwell, Lond. Edinb. Dublin Philos. Mag. J. Sci., 1864, 27, 294–299 CrossRef
.
- C. Calladine, Int. J. Solids Struct., 1978, 14, 161–172 CrossRef
.
- T. C. Lubensky, C. L. Kane, X. Mao, A. Souslov and K. Sun, Rep. Prog. Phys., 2015, 78, 73901 CrossRef CAS PubMed
.
- S. Alexander, Phys. Rep., 1998, 296, 65–236 CrossRef CAS
.
- M. Wyart, H. Liang, A. Kabla and L. Mahadevan, Phys. Rev. Lett., 2008, 101, 1–4 CrossRef PubMed
.
- D. E. Ingber, N. Wang and D. Stamenović, Rep. Prog. Phys., 2014, 77, 046603 CrossRef PubMed
.
- M. Merkel, K. Baumgarten, B. P. Tighe and M. L. Manning, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 6560–6568 CrossRef CAS PubMed
.
- S. Arzash, J. L. Shivers, A. J. Licup, A. Sharma and F. C. MacKintosh, Phys. Rev. E, 2019, 99, 042412 CrossRef CAS
.
- B. Cui, G. Ruocco and A. Zaccone, Granul. Matter, 2019, 21, 69 CrossRef
.
- O. K. Damavandi, V. F. Hagh, C. D. Santangelo and M. L. Manning, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2022, 105, 025003 CrossRef CAS PubMed
.
- P. R. Onck, T. Koeman, T. van Dillen and E. van der Giessen, Phys. Rev. Lett., 2005, 95, 178102 CrossRef CAS PubMed
.
- M. Sheinman, C. P. Broedersz and F. C. MacKintosh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021801 CrossRef CAS PubMed
.
- M. F. J. Vermeulen, A. Bose, C. Storm and W. G. Ellenbroek, Phys. Rev. E, 2017, 96, 053003 CrossRef PubMed
.
- G. Düring, E. Lerner and M. Wyart, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 1–12 CrossRef PubMed
.
- R. Rens, C. Villarroel, G. Düring and E. Lerner, Phys. Rev. E, 2018, 98, 062411 CrossRef CAS
.
- M. Merkel and M. L. Manning, New J. Phys., 2018, 20, 022002 CrossRef
.
- C. P. Broedersz and F. C. MacKintosh, Soft Matter, 2011, 7, 3186–3191 RSC
.
- S. Dagois-Bohy, B. P. Tighe, J. Simon, S. Henkes and M. Van Hecke, Phys. Rev. Lett., 2012, 109, 1–5 CrossRef PubMed
.
- O. K. Damavandi, M. L. Manning and J. M. Schwarz, EPL, 2022, 138, 27001 CrossRef
.
- S. Kooij and E. Lerner, Phys. Rev. E, 2019, 100, 042609 CrossRef CAS PubMed
.
- S. Ciarella, F. Sciortino and W. G. Ellenbroek, Phys. Rev. Lett., 2018, 121, 58003 CrossRef CAS PubMed
.
- S. B. Lindström, D. A. Vader, A. Kulachenko and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 051905 CrossRef PubMed
.
- K. Huang and M. Born, Proc. R. Soc. London, Ser. A, 1950, 203, 178–194 CAS
.
- M. Born and K. Huang, Am. J. Phys., 1955, 23, 474 CrossRef
.
- A. Lemaître and C. Maloney, J. Stat. Phys., 2006, 123, 415–453 CrossRef
.
Footnotes |
| † This is because eqn (12) can be transformed into where u = ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 1 + 1 + ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 2 and w = 2 and w = ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 1 − 1 − ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 2. This is the equation of an ellipse whose main axes are diagonally oriented and scale with σ 2. This is the equation of an ellipse whose main axes are diagonally oriented and scale with σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . . |
‡ That  can become arbitrarily large for given σ can become arbitrarily large for given σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) < 1/4 can be shown explicitly by considering a subset of configurations parameterized by two scalars w and h as r1 = (−w/2,h) and r2 = (−w/2,h). Then one can show that the choice < 1/4 can be shown explicitly by considering a subset of configurations parameterized by two scalars w and h as r1 = (−w/2,h) and r2 = (−w/2,h). Then one can show that the choiceleads to the correct value for the standard deviation of the spring lengths σ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . Moreover, one can show that for this choice, the relation . Moreover, one can show that for this choice, the relationholds, and that  with with  given by eqn (14). Finally, for fixed σ given by eqn (14). Finally, for fixed σ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , the function , the function  increases monotonically with h without upper bound. increases monotonically with h without upper bound. |
| This journal is © The Royal Society of Chemistry 2022 |