Correction: Simulation of dense non-Brownian suspensions with the lattice Boltzmann method: shear jammed and fragile states

Abstract

Correction for ‘Simulation of dense non-Brownian suspensions with the lattice Boltzmann method: shear jammed and fragile states’ by Pradipto et al., Soft Matter, 2020, 16, 945–959, DOI: 10.1039/C9SM00850K.

---

The authors regret several typographical errors in the Appendix A of the original article. Firstly, although eqn (26) is correct, for completeness, it would be better rewritten as:including the equation of F^h_j, where the definitions of the variables can be found in the paper. Secondly, eqn (28) should read:

A^(ij)_αβ = X^A_ijn^(ij)_αn^(ij)_β + Y^A_ij (δ_αβ − n^(ij)_αn^(ij)_β) (28)

Thirdly, the average radius a in eqn (33)–(41) should be replaced by a_i, the radius of the i-th particle. Since, fortunately, our numerical code was based on the correct expressions, we do not need to report any changes of the results of our simulation in the paper.

Finally, we discuss whether our model based on eqn (26) is correct under the shear. This is because the lubrication resistance matrix in eqn (26) misses the shear term related to the E^∞ tensor in the correct two body lubrication resistance matrix.^1,2 We validate our simulation without the shear term in the near field by simulating two particles under simple shear to compare the simulation results with the exact solution of two body hydrodynamic interactions^1–3 in Fig. 1. We have confirmed that our LBM with lubrication corrections (eqn (26)) is sufficient to recover the exact solution, while the deviation becomes larger if we include the shear contribution in relation to E^∞ in the near field. Thus, we conclude that our treatment is correct even for the problem under the shear.

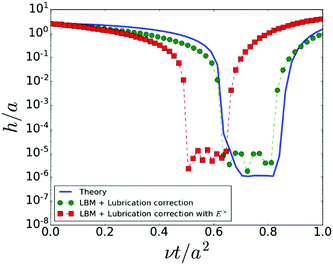Fig. 1 Plots of the time evolution of the interparticle gap h between two particles under simple shear, where green filled circles and red squares express the results by the LBM with lubrication correction in eqn (26) and the LBM with lubrication correction including E^∞ terms, respectively. The blue solid line is the exact solution of two spheres under the simple shear from ref. 1–3

We thank S. Takada for his indication of our typos and discussion on the effect of the E^∞ terms.

The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.

References

1. D. J. Jeffrey and Y. Onishi, J. Fluid Mech., 1984, 139, 261–290.
2. D. J. Jeffrey, Phys. Fluids, 1992, 4, 16–29.
3. K. Ichiki, et al. , arXiv, 2013, 1302.1461.

---