DOI:
10.1039/D1SM01811F
(Paper)
Soft Matter, 2022,
18, 4280-4304
Electric-field-induced oscillations in ionic fluids: a unified formulation of modified Poisson–Nernst–Planck models and its relevance to correlation function analysis
Received
23rd December 2021
, Accepted 1st May 2022
First published on 26th May 2022
Abstract
We theoretically investigate an electric-field-driven system of charged spheres as a primitive model of concentrated electrolytes under an applied electric field. First, we provide a unified formulation for the stochastic charge and density dynamics of the electric-field-driven primitive model using the stochastic density functional theory (DFT). The stochastic DFT integrates the four frameworks (the equilibrium and dynamic DFTs, the liquid state theory and the field-theoretic approach), which allows us to justify in a unified manner various modifications previously made for the Poisson–Nernst–Planck model. Next, we consider stationary density–density and charge–charge correlation functions of the primitive model with a static electric field. We predict an electric-field-induced synchronization between emergences of density and charge oscillations. We are mainly concerned with the emergence of stripe states formed by segregation bands transverse to the external field, thereby demonstrating the following: (i) the electric-field-induced crossover occurs prior to the conventional Kirkwood crossover without an applied electric field, and (ii) the ion concentration dependence of the decay lengths at the onset of oscillations bears a similarity to the underscreening behavior found by recent simulation and theoretical studies on equilibrium electrolytes. Also, the 2D inverse Fourier transform of the correlation function illustrates the existence of stripe states beyond the electric-field-induced Kirkwood crossover.
I. Introduction
Primitive model
Ionic fluids cover a wide range of charged materials, including solvent-in-salt electrolytes, room-temperature ionic liquids (RTILs), various colloidal dispersions, and polyelectrolytes.1,2 Recently, ionic fluids are increasingly attracting much attention, due to their diverse applications not only in chemistry and biology1 but also in renewable energy devices such as batteries, supercapacitors, and separation media.2–4 Here we consider electrolytes, RTILs, and mixtures of oppositely charged colloids under applied electric fields, as examples of symmetric ionic fluids driven by external electric fields. These appear in biological ion channels, micro/nanofluidic devices for environmental and biomedical applications, and electrolyte-immersed porous electrodes for electrochemical applications.1–4
Among models of the ionic fluids on target is a primitive model, or a symmetric collection of charged spheres whose cationic and anionic species have equal size and equal but opposite charge. The primitive model under a static electric field, with which we are concerned, has been widely used to explain the structural and dynamical properties of concentrated electrolytes driven by external electric fields in confined geometries.2,5–7
Poisson–Nernst–Planck (PNP) model
The Poisson–Nernst–Planck (PNP) model is the standard approach to describe the primitive model with a static electric field applied.2,5–7 The Nernst-Planck equation, also known as the drift-diffusion equation, treats ionic currents arising from the combination of Fick's law of diffusion due to a concentration gradient and Ohm's law for drift of ions in a gradient of Coulomb potential. The Nernst-Planck equation represents the conservation law:| | | ∂tnl(r, t) = −∇·Jl(r, t), | (1) |
where nl(r, t) (l = 1,2) denotes an instantaneous number density of either cations (l = 1) or anions (l = 2) and Jl(r, t) the associated current vector of the l-th ion density. The PNP model considers the coupled set of the Poisson and NP equations by relating nl(r, t) to the Coulomb interaction potential via the Poisson equation.
Deficiencies of the PNP model
The PNP model provides a basic description of linear response dynamics of dilute electrolytes perturbed from equilibrium. However, the original PNP model takes no account of (i) steric interactions, (ii) ion–ion Coulomb correlations, and (iii) dielectric boundary effects. Hence, the conventional PNP model is insufficient to predict various electrokinetic phenomena when ions are crowded and/or when the ion distributions are spatially inhomogeneous.5,6
For example, the PNP model is not relevant to the interfacial electrokinetic phenomena which are found not only in biological ion channels but also in advanced devices for micro/nanofluidic and electrochemical applications.5,6 Steric effects become significant in either RTILs or thin electric double layers formed at large applied voltages, which, however, are not included in the PNP model.5–16
There are also bulk properties for which the PNP model is not valid: inhomogeneous steady states have been reported by theoretical, experimental, and simulation studies in the bulk region of either electrolytes or oppositely charged colloidal mixtures driven by electric fields.13,17–20 Theoretically, on the one hand, stationary correlation functions of electric-field-driven electrolytes were calculated, suggesting a tendency to form chains of cations and anions in the external field direction at large electric fields.13 On the other hand, experimental and simulation studies have provided dynamic phase diagrams of steady states including laned, jammed or clogged, and mixed states of oppositely charged particles under DC or AC electric fields.17,18 It is well known that lane formation of like-charge particles occurs at a high enough field strength along the applied field.17,18 At the same time, previous studies have observed that bands of like-charge particles are aligned in a direction non-parallel to the applied field direction when the electric-field-driven colloidal mixtures are in jammed or mixed states.17,18
Modified PNP models: deterministic case
A variety of modified PNP (mPNP) models have thus been proposed so far; these arise either from semi-phenomenological methods5–10 or from deterministic density functional theory (DFT).11,12 The modifications have aimed to complement the above shortcomings given in (i) to (iii) as follows: (i) Steric effects are included by adding a density current, or its associated chemical potential due to non-Coulombic short-range interactions. (ii) Ion–ion Coulomb correlations are taken into account by modified Poisson equations such as higher-order Poisson equation.21–24 (iii) Dielectric boundary effects are investigated according to a generalized Born theory which evaluates solvation energy from an ionic self-energy.25
Some of the results achieved by the deterministic mPNP models are as follows:5–10 first, for biological ion channels, the numerical results have been found to agree with experimental or simulation data on the ion channel characteristics of selectivity and rectification. Next, for micro/nanofluidics, it has been demonstrated that a coupled set of the mPNP and Navier-Stokes equations is a good descriptor of the interfacial electrokinetic phenomena. These include electro-osmotic flow, streaming current, and ionic conductance in porous media or nanochannels filled with RTILs or concentrated electrolytes of high valence. Then, in terms of renewable energy technologies, the deterministic mPNP models have successfully explained differential capacitance and non-monotonic oscillatory decay of electric double layers at solid-liquid interfaces with large voltages applied to RTILs or concentrated electrolytes.
Modified PNP models: stochastic case
An alternative approach to extend the PNP dynamics to a stochastic process is the stochastic DFT (SDFT).11,26 In the SDFT, we use the Dean–Kawasaki model11,26 that contains multiplicative noise by adding a stochastic current in eqn (1). The Dean–Kawasaki equation can be linearized for fluctuating density field around a reference density.13–15,27,28 The linearized Dean–Kawasaki equation has proved relevant to describe various dynamics. It is an outstanding feature of the linearized SDFT to justify the inclusion of stochastic processes into the PNP model. The stochastic nature allows us to compute correlation functions for density and charge fluctuations around a uniform state.
Recently, the stochastic mPNP models based on the linearized SDFT have provided the following results:13–16,27,28 First, the linear Dean–Kawasaki equation has formulated ion concentration-dependent electrical conductivity. The obtained expression for conductivity reproduces the Debye–Hückel-Onsager theory and also explains the experimental results on concentrated electrolytes where the Debye–Hückel-Onsager theory breaks down.13,15,16 It should be noted that we need to use a regularized interaction potential15 and to introduce hydrodynamic interactions15,16 for explaining the high-density results;15 while this paper will justify the use of regularized form from the first principle, consideration of hydrodynamic interactions is beyond our scope. Furthermore, it is found from the analysis of correlation functions that density–density and charge–charge correlations are long-range correlated even in the steady state. The asymptotic decay of the correlation functions exhibits a power-law behavior with a dipolar character, thereby giving rise to a long-range fluctuation-induced force acting on uncharged confining plates.14
However, the above three issues (i.e., (i) to (iii) described above) have yet to be fully addressed by the stochastic mPNP models. It should also be remembered that the stochastic mPNP models have been concerned with linear response dynamics from a uniform density distribution and that there have been few systematic studies on an inhomogeneous density distribution in a steady state.28 Further modifications of the stochastic mPNP models need to be made for incorporating improvements in the deterministic mPNP models.
The aim of this paper
To summarize, the deterministic and stochastic mPNP models proposed so far are beneficial in the following respects: while the deterministic mPNP models have provided elaborate and tractable methods to include short-range correlations and interactions of Coulombic and non-Coulombic origins, the stochastic mPNP models have demonstrated the relevance to correlation function analysis on fluctuation phenomena in uniform and steady states. Integration of the deterministic and stochastic mPNP models should lead to a deeper understanding of the electrokinetic phenomena in concentrated electrolytes. To pave the way for such an elaborate mPNP model, the stochastic mPNP models need to capture the benefits of the deterministic mPNP models.
Thus, this paper serves two purposes. The first aim is to provide a unified formulation that combines the above results of the deterministic and stochastic mPNP models. From the aspect of the deterministic mPNP models, we attempt, using the unified formulation, to add the stochastic term to the deterministic mPNP equations and to derive the semi-phenomenological modifications5–10 from the first principle based on the liquid state theory. In terms of the stochastic mPNP models, on the other hand, the unified formulation justifies the inclusion of modified terms proposed by the deterministic mPNP models5–10 into the stochastic equations.13–15
The second purpose is to determine when density and charge oscillations emerge in non-equilibrium steady states. To this end, we investigate stationary correlation functions which are averaged over the plane transverse to the applied electric field. The unified mPNP model yields the stationary correlation functions at equal times, which enables us to explore crossovers from monotonic to oscillatory decay of density–density and charge–charge correlations.
The organization of this paper
In what follows, we first present the summarized results on both the unified form of mPNP models (Section II) and the correlation function analysis to investigate steady states (Section III) before going into the details.
On the one hand, Table 1 in Section II summarizes the obtained forms compared to previous formulations. The essential achievement in terms of the theoretical formalism is clarified in Section IID. As detailed in Appendix A, the hybrid framework of the field-theoretic approach, the equilibrium37,38 and dynamic11 DFTs, and the liquid state theory justifies the modified Poisson equations5–10,23,24,39–41 and the generalized Debye–Hückel equation for the self-energy.10,25
Table 1 Summary table of our formulation in comparison with previous theories on the mPNP models
On the other hand, Fig. 2 in Section III provides a schematic summary of electric-field-dependent decay length prior to the equilibrium Kirkwood crossover in the external field direction. Fig. 2 illustrates not only the emergence of stripe states formed by segregation bands transverse to the applied field direction but also the intimate connection between the electric-field-induced shift of the decay length at the steady-sate Kirkwood crossover and the underscreening behaviors19,20,29–31 observed in equilibrium electrolytes whose concentrations are higher than the conventional Kirkwood crossover point.32–36 Section IIIE presents the 2D behaviors of oscillatory correlations above the Kirkwood crossover using heat maps, which corroborates the appearance of stripe states in the presence of relatively weak electric fields.
Section IV clarifies the detailed process to analytical and numerical results of the electric-field-induced Kirkwood crossover and the decay length using a couple of models typical for the liquid state theory. In Section V, we have discussions for comparing the theoretical predictions with experimental and simulation results.
II. Formulation results on modifications of PNP model
In the first place, this section summarizes the resulting formulation, according to Table 1 (Section IIA). As seen from the equation type given in the leftmost column of Table 1, we have verified two modifications of PNP equations using the SDFT of the symmetric primitive model specified in Section IIB. In Section IIC, we present fully modified PNP equations that incorporate into the PNP model density currents due to Gaussian noise fields as well as a self-energy contribution. Section IID describes the theoretical achievements in terms of the Dean–Kawasaki model.11,26 In Section IIE, we investigate the linearized mPNP equations while neglecting the self-energy in order to obtain stationary correlation functions at equal times.
A. Comparison with previous theories
In Sections IIC and D, we will present the self-energy-modified PNP equations10 and the linear mPNP equations.13–15Table 1 compares these equation sets with previous approaches.
Self-energy-modified PNP equations.
Previous theories5–12 have made two modifications. One is to improve the Poisson equation for the Coulomb interaction potential ψ(r, t) experienced by an ion (the higher-order Poisson eqn (15)).5–10,21–24 The other is to make a self-energy correction to the Coulomb interaction term in the PNP equations (the self-energy term determined by the generalized Debye–Hückel eqn (21)),10,25 thereby providing theoretical descriptions of ionic transport in agreement with simulation results; however, these modifications are empirical, and correlation functions have been beyond the scope due to the absence of stochastic current. Meanwhile, our self-energy-modified PNP equations, derived from the basic formulation of the SDFT (see Appendix A for details), verify the stochastic dynamics and encompass the above modifications.
Linear mPNP equations.
Recently, the mPNP model covers the stochastic dynamics of density fluctuations around a uniform state while neglecting the self-energy contribution.13,14 Furthermore, a finite-spread Poisson equation has been used in an ad hoc manner depending on a charge smearing model adopted.15 The stochastic mPNP equations allow us to evaluate correlation functions, yielding either the ion concentration-dependent electrical conductivity or the long-range fluctuation-induced force.14 In this study, we confirm the stochastic mPNP equations previously used as an approximation of the self-energy-modified PNP equations.10 Accordingly, the use of the finite-spread Poisson equation13,15,24,39–41 is validated from the decomposition of the direct correlation function (DCF) to extract the weight function ω(k), implying that we can improve the finite-spread Poisson equation systematically by adopting a more appropriate function form of ω(k) other than eqn (12).
B. Model
The 3D primitive model introduces three parameters, p, σ and ε, for concentrated electrolytes with a static electric field E applied: p-valent cations and anions are modeled by equisized charged hard spheres of diameter σ immersed in a structureless and uniform dielectric medium with dielectric constant ε at a temperature T. For later convenience, the external field E represents the conventional field multiplied by e/kBT (see also the statement after eqn (A14)). Fig. 1 presents a schematic of the electric-field-driven primitive model in Cartesian coordinates where the external electric field E with its strength of E = |E| is parallel to the unit vector êx = (1,0,0)T = E/E in the direction of x-axis. There are two parallel plates in Fig. 1; however, the interplate distance is much larger than the sphere diameter, and we suppose that the finite size effect due to the presence of the plates is negligible.
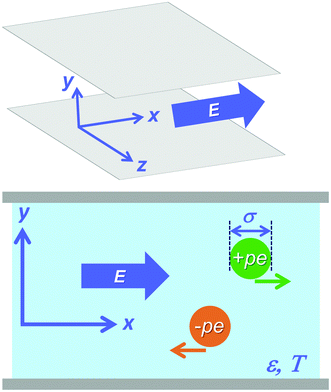 |
| | Fig. 1 A schematic of concentrated electrolytes under a static electric field E in Cartesian coordinates (top figure). The 3D primitive model is illustrated in the xy plane (lower figure). The definition of symbols is provided in the main text. | |
 |
| | Fig. 2 A schematic summary of results obtained in this study is depicted in terms of the decay length ξ(1)Decay of either monotonic decay or damped oscillatory on a log–log plot of ξ(1)Decay/ξDH = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ξ(1)Decayvs. σ/ξDH = ξ(1)Decayvs. σ/ξDH = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ where ξDH = σ where ξDH = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) −1 denotes the smeared Debye–Hückel screening length defined by eqn (36). Our numerical results of ξ(1)Decay will be given in Fig. 3 and 8. In Fig. 2, these are shown using the solid brown lines terminated at nodes A and B, and the dashed green arrow from node A to node B, or from the Kirkwood crossover at E = 0 to that under electric field (E ≠ 0). While the solid brown line terminated at node A (E = 0) converges to ξ(1)Decay/ξDH = 1 in the dilute limit, the solid brown line terminated at node B (E ≠ 0) approaches zero in the dilute limit because of the finite decay length ξ(1)Decay = (pE)−1 (see also a discussion given at the end of Section IIIA). As illustrated by the upper inset, the green vertical line through node B marks −1 denotes the smeared Debye–Hückel screening length defined by eqn (36). Our numerical results of ξ(1)Decay will be given in Fig. 3 and 8. In Fig. 2, these are shown using the solid brown lines terminated at nodes A and B, and the dashed green arrow from node A to node B, or from the Kirkwood crossover at E = 0 to that under electric field (E ≠ 0). While the solid brown line terminated at node A (E = 0) converges to ξ(1)Decay/ξDH = 1 in the dilute limit, the solid brown line terminated at node B (E ≠ 0) approaches zero in the dilute limit because of the finite decay length ξ(1)Decay = (pE)−1 (see also a discussion given at the end of Section IIIA). As illustrated by the upper inset, the green vertical line through node B marks  , or the onset of shifted Kirkwood crossover from a uniform state to a stripe state without consideration of lane formation.17,18 For comparison, we add the dashed blue line to show underscreening behavior in concentrated electrolytes without applied electric field beyond the conventional Kirkwood crossover indicated by the blue vertical line through node A; this blue line represents , or the onset of shifted Kirkwood crossover from a uniform state to a stripe state without consideration of lane formation.17,18 For comparison, we add the dashed blue line to show underscreening behavior in concentrated electrolytes without applied electric field beyond the conventional Kirkwood crossover indicated by the blue vertical line through node A; this blue line represents  , which is the conventional Kirkwood crossover value32–36 in the range of 1.0 to 1.2 for symmetric electrolytes. Recent studies20,29–31 have demonstrated that ξ(1)Decay/ξDH ∼ (σ/ξDH)χ with the exponent of χ > 1 in a damped oscillatory state. It will be seen from Fig. 3(b) and 8(b) that a similar scaling relation holds for the dashed green arrow. , which is the conventional Kirkwood crossover value32–36 in the range of 1.0 to 1.2 for symmetric electrolytes. Recent studies20,29–31 have demonstrated that ξ(1)Decay/ξDH ∼ (σ/ξDH)χ with the exponent of χ > 1 in a damped oscillatory state. It will be seen from Fig. 3(b) and 8(b) that a similar scaling relation holds for the dashed green arrow. | |
The primitive model is characterized by a pairwise interaction potential vlm(r) between charged hard spheres with a separation distance of r = |r|: v11(r), v12(r) and v22(r) represent cation-cation, cation-anion and anion-anion interactions, respectively. We have
| |  | (2) |
where
lB =
e2/(4π
εkBT) denotes the Bjerrum length, the length at which the bare Coulomb interaction between two monovalent ions is exactly
kBT. It is noted that this paper defines all of the energetic quantities, including the pairwise interaction potentials, in units of
kBT.
C. Self-energy-modified PNP equations: a full set of the resulting formulation
The conservation equation with stochastic current.
In the conservation eqn (1) of the SDFT, the ionic current Jl(r, t) consists of three parts:| |  | (3) |
where 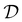 and μl[n] denote, respectively, the diffusion constant and the chemical potential as a functional of n(r, t) = (n1(r, t), n2(r, t))T, and ζ(r, t) represents an uncorrelated Gaussian noise field defined below. Incidentally, we have neglected an advection term,15,16nl(r, t)u(r, t), on the right hand side (rhs) of eqn (3) with u(r, t) denoting the solvent velocity field to satisfy the incompressibility condition ∇·u = 0; this approximation is equivalent to supposing that
and μl[n] denote, respectively, the diffusion constant and the chemical potential as a functional of n(r, t) = (n1(r, t), n2(r, t))T, and ζ(r, t) represents an uncorrelated Gaussian noise field defined below. Incidentally, we have neglected an advection term,15,16nl(r, t)u(r, t), on the right hand side (rhs) of eqn (3) with u(r, t) denoting the solvent velocity field to satisfy the incompressibility condition ∇·u = 0; this approximation is equivalent to supposing that 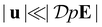 .
.
Concrete forms of density current Jl(r, t).
The first term on the rhs of eqn (3) represents the reference current directly determined by E. The chemical potential μl[n] of the second term on the rhs of eqn (3) is given by| | μl[n] = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nl(r, t) + Ul[n], nl(r, t) + Ul[n], | (4) |
using an instantaneous interaction energy Ul[n] per cation (l = 1) or anion (l = 2). Eqn (4) indicates that this part of the total current is due to contributions from ideal entropy and Coulomb interactions including steric effects. The last term on the rhs of eqn (3) corresponds to the stochastic current arising from ζ(r, t) characterized by| | | 〈ζ(r, t)ζ(r′, t′)T〉ζ = δ(r − r′)δ(t − t′), | (5) |
with the subscript “ζ” representing the Gaussian noise averaging in space and time.
Following the mPNP equations proposed so far,5–10,13–16Ul[n] is further divided into two parts:
| |  | (6) |
where (−1)
l−1ψ(
r,
t) and
u(
r,
t)/2 denote, respectively, the instantaneous interaction potential and the instantaneous self-energy per ion. We define
ψ(
r,
t) by
| | 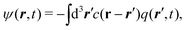 | (7) |
using the DCF
c(
r −
r′) and an instantaneous charge density,
| | | peq(r, t) = pe{n1(r, t) − n2(r, t)}. | (8) |
By definition of the DCF, the potential function
ψ(
r,
t) defined in
eqn (7) corresponds to the conventional Coulomb potential multiplied by
pe/
kBT (see also
eqn (13)). It follows that
q(
r,
t) in
eqn (7) is not an instantaneous charge density but is merely the concentration difference (
q =
n1 −
n2) as seen from
eqn (8).
Meanwhile, our resulting formulation provides the self-energy as follows:
| |  | (9) |
where bare and dressed propagators,
G0(
r −
r′) and
G(
r −
r′), are given by
| | | p2G0(r − r′) = −c(r − r′), | (10) |
| | | p2G(r − r′) = −h(r − r′), | (11) |
with
h(
r −
r′) denoting the total correlation function between ions of the same kind.
We investigate the following model forms as the DCFs:
| |  | (12) |
in the Fourier transform of the DCF given by
| |  | (13) |
where |
k| =
k. While the former expression of
ω(
k) in
eqn (12) represents the Gaussian charge smearing model
35,40 and has been used in the hypernetted chain approximation of one-component ionic fluids,
42 the latter form in
eqn (12) indicates the restriction of Coulomb interactions to the separation of |
r −
r′| >
σ with a cutoff at |
r −
r′| =
σ and is an approximate form of the modified MSA model
43 as shown in Appendix A2.
Finite-spread or higher-order Poisson equation.
Combining eqn (7), (12) and (13), we have| | 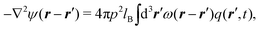 | (14) |
which will be referred to as the finite-spread Poisson equation after the finite-spread Poisson–Boltzmann equation; both equations consider the charge distribution inside a charged sphere using a weight function ω(r − r′). As shown in Appendix A2, eqn (14) transforms to| |  | (15) |
when performing the low wavenumber expansion of ω(k), similarly to the transformation from the finite-spread Poisson–Boltzmann equation to the higher-order one for one-component fluids.24Eqn (15) will be referred to as the higher-order Poisson equation5–10,21–24 for comparison with the finite-spread Poisson eqn (14), though often called either the Poisson-Fermi equation or the Bazant–Storey–Kornyshev equation.21
A generalized Debye–Hückel equation.
It follows from eqn (10)–(13) that the DCF and the total correlation function, c(r − r′) and h(r − r′), obey a modified Poisson equation and a generalized Debye–Hückel equation, respectively: we have| | | −∇2G0(r − r′) = 4πlBω(r − r′), | (16) |
whereas the Orstein–Zernike equation reads| |  | (17) |
where a generalized Debye–Hückel length κ−1(r) has been defined as| | | κ−1(r) = {4πlBp2ρ(r, t)}−1/2, | (18) |
| | | ρ(r, t) = n1(r, t) + n2(r, t). | (19) |
Eqn (16) and (17) for point charges (σ = 0) reduce, respectively, to| | | −∇2G0(r − r′) = 4πlBδ(r − r′) | (20) |
and| | | −∇2G(r − r′) + κ2(r)G(r − r′) = 4πlBδ(r − r′) | (21) |
because of| |  | (22) |
as confirmed from eqn (12). Eqn (21) corresponds to the generalized Debye–Hückel equation previously used.10,25
D. Theoretical achievement in terms of the Dean–Kawasaki model
In Appendices A and B, we prove that the Dean–Kawasaki model can be approximated by the formula given by eqn (3)–(11) for concentrated electrolytes: the hybrid framework of the equilibrium DFT and field-theoretic treatment transforms the original Dean–Kawasaki equation11,26 to a tractable expression for binary ionic fluids without ad hoc modifications. Here we clarify the theoretical achievement instead of going into the detailed formulations presented in Appendix A. It is found from eqn (A2), (B1), (B2) and (B3) that the straightforward use of the original DK model provides exactly| | 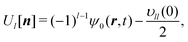 | (23) |
| |  | (24) |
It follows from eqn (3), (6) and (23) that the electrostatic contribution to ionic current reads| |  | (25) |
| |  | (26) |
because of ∇υll(0) = 0. Comparison between eqn (25) and (26) reveals that the SDFT based on the above hybrid framework justifies| |  | (27) |
in the Gaussian approximation of the auxiliary potential field (see Appendix A for details), where use has been made of the relation,  . Our achievement in terms of the theoretical formalism is essentially to validate eqn (27).
. Our achievement in terms of the theoretical formalism is essentially to validate eqn (27).
E. Linear mPNP equations and the associated correlation functions
The matrix representation.
Let us introduce two vectors, θ(r, t) and η(r, t), for having a compact form of the mPNP equation set:| |  | (28) |
| | 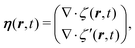 | (29) |
where ρ(r, t) and q(r, t) have been defined in eqn (19) and (8), respectively, and ζ′(r, t) satisfies the relation (5) as well as ζ(r, t). We perform the change of variables from n(r, t) to q(r, t) in the linearization of the mPNP equation set given by eqn (1) and eqn (3)–(6) with the self-energy term (9) being dropped. Thus, we obtain the stochastic currents, Jρ and Jq, from linearizing the current given by eqn (3) (see Appendix A for details):| |  | (30) |
using the smeared density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) of cations or anions. We insert the expression (30) into the conservation equation for ρ(r, t) and q(r, t):
of cations or anions. We insert the expression (30) into the conservation equation for ρ(r, t) and q(r, t):| |  | (31) |
which is Fourier transformed to| |  | (32) |
In eqn (14), the matrix to determine restoring forces is expressed as| |  | (33) |
| | 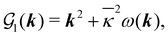 | (34) |
noting that the finite-spread Poisson eqn (14) yields| | −2![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) k2ψ(k) = −8πp2lB k2ψ(k) = −8πp2lB![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ω(k)q(−k) = − ω(k)q(−k) = −![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 2ω(k)q(−k), 2ω(k)q(−k), | (35) |
where we have defined the smeared Debye–Hückel length,| | ξDH = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) −1 ≡ (8πp2lB −1 ≡ (8πp2lB![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) )−1/2, )−1/2, | (36) |
other than κ−1(r, t) defined by eqn (18). In eqn (33), the anisotropy of the k-space is associated with the direction of applied electric field (i.e., êx = E/E) and we haveor
Density–density and charge–charge correlation functions.
One of the benefits of stochastic equations is that correlation functions are calculated straightforwardly. Here we consider density–density and charge–charge correlation functions at equal times, which are defined using the equal-time correlation matrix as follows:| |  | (40) |
In the matrix elements given by eqn (40), 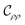 and
and  are the target correlation functions. To be precise,
are the target correlation functions. To be precise,  is the charge–charge correlation function, according to the definition of eqn (8). For brevity, however, we will refer to
is the charge–charge correlation function, according to the definition of eqn (8). For brevity, however, we will refer to  as the charge–charge correlation function.
as the charge–charge correlation function.
We focus on the steady-state solutions of the correlation functions:
| |  | (41) |
| |  | (42) |
As detailed below, these are written as
| |  | (43) |
where we have
| |  | (44) |
| |  | (45) |
and the adjugate matrix of
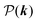
, signified by

, reads
| |  | (46) |
Eqn (44) indicates that both

and

have identical poles under the external electric field
E.
In the limit of k → 0, we have
| |  | (47) |
Then, we divide

into two parts:
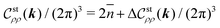
where
| |  | (48) |
is directly related to total correlation functions, or essential parts of density–density correlations.
In the limit of σ → 0, on the other hand, we have ω(k) = 1 and eqn (43) is approximated by
| |  | (49) |
in the low wavenumber region of
kx![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) −1
−1 ≪ 1 (see Appendix D for the derivation). It should be noted that
eqn (49) agrees with the expression previously obtained in a different manner
14 and that the Fourier transform of
eqn (49) has been demonstrated to provide anisotropic long-range correlation functions exhibiting a power-law behavior with a dipolar character.
14 At low field strength of
pE![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) −1
−1 ≪ 1,
eqn (49) converges to
| |  | (50) |
clarifying that low electric-field-driven electrolytes in steady states mimic weakly interacting ionic fluids without applied electric field on a large scale and that

given by
eqn (50) satisfies not only the electroneutrality but also the Stillinger–Lovett second-moment condition.
III. Correlation function analysis: electric-field-induced crossover to a damped oscillatory state
The first two subsections will be devoted to what is implied by the complicated forms (43)–(48) of correlation functions,  and
and  , especially focusing on the high wavenumber in the external field direction. While Section IIIA provides the pole equations of the correlation functions, Section IIIB clarifies the electric-field-induced oscillations when considering the solutions to the pole eqn (66), or an anisotropic crossover from monotonic to oscillatory decay of correlations along the direction of applied electric field. Before going into the numerical details of the results obtained from the pole eqn (66), Section IIIC aims to understand the relationship between the Kirkwood crossover at E = 0 and E ≠ 0 using Fig. 2, a schematic plot of the decay length ξ(1)Decay. After presenting the schematic summary, Section IIID explains how the crossover point is determined in the anisotropic approximation of the pole eqn (66). In the anisotropic approximation (53), we can analytically investigate the electric-field-induced Kirkwood crossover (see Section IV for details). Fig. 3 in Section IIID gives the numerical results on the E-dependencies of both the decay length
, especially focusing on the high wavenumber in the external field direction. While Section IIIA provides the pole equations of the correlation functions, Section IIIB clarifies the electric-field-induced oscillations when considering the solutions to the pole eqn (66), or an anisotropic crossover from monotonic to oscillatory decay of correlations along the direction of applied electric field. Before going into the numerical details of the results obtained from the pole eqn (66), Section IIIC aims to understand the relationship between the Kirkwood crossover at E = 0 and E ≠ 0 using Fig. 2, a schematic plot of the decay length ξ(1)Decay. After presenting the schematic summary, Section IIID explains how the crossover point is determined in the anisotropic approximation of the pole eqn (66). In the anisotropic approximation (53), we can analytically investigate the electric-field-induced Kirkwood crossover (see Section IV for details). Fig. 3 in Section IIID gives the numerical results on the E-dependencies of both the decay length 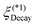 and the smeared Debye–Hückel length
and the smeared Debye–Hückel length  at the Kirkwood crossover points. Last, Section IIIE presents various results on the 2D inverse Fourier transforms of
at the Kirkwood crossover points. Last, Section IIIE presents various results on the 2D inverse Fourier transforms of  . We will see anisotropic density–density correlations reflecting the emergence of stripe states in a high-density region above the Kirkwood crossover.
. We will see anisotropic density–density correlations reflecting the emergence of stripe states in a high-density region above the Kirkwood crossover.
 |
| | Fig. 3 Comparison between the electric-field-dependent length results which are obtained from the Gaussian charge smearing model (abbreviated as “G” and represented by green lines) and the modified MSA model (abbreviated as “M” and represented by red lines). Section IVB presents the detailed formulation to obtain the results given in this figure. (a) The electric-field dependencies of the Debye–Hückel length 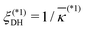 and the decay length and the decay length  at the Kirkwood crossover are shown by the plot of at the Kirkwood crossover are shown by the plot of 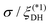 and and  against pEσ, an energetic measure of electric field strength in units of kBT. While the solid lines represent against pEσ, an energetic measure of electric field strength in units of kBT. While the solid lines represent  , the dashed lines , the dashed lines  . The related equations are as follows: green solid line (eqn (99)); green dashed line (eqn (102)); red solid and dashed lines (eqn (105) and (106)). (b) A log–log plot of . The related equations are as follows: green solid line (eqn (99)); green dashed line (eqn (102)); red solid and dashed lines (eqn (105) and (106)). (b) A log–log plot of 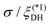 -dependencies of -dependencies of  . The dotted line, as a guide to the eye, indicates a scaling relation . The dotted line, as a guide to the eye, indicates a scaling relation  . . | |
A. Electric-field-induced synchronization between the emergences of density and charge oscillations
It is found from the denominator on the rhs of eqn (44) that the obtained correlation functions given by eqn (43)–(48) provide the following pole equations:| |  | (51) |
| | 2(k(2))2 + ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 2ω(k(2)) = 0, 2ω(k(2)) = 0, | (52) |
which remarkably apply to both density–density and charge–charge correlation functions. Namely, both density–density and charge–charge correlation functions exhibit the same behavior.
Let us discuss the concrete behaviors particularly in the anisotropic approximation of eqn (39) such that
(see Section IIIB for details). Focusing on the onset of oscillatory decay of correlations (or the Kirkwood crossover) at a fixed electric field, a summary provided in advance is threefold:
1. Simultaneous emergence of density and charge oscillations.
The weight function ω(k) multiplied by ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 2 allows us to have complex solutions to the pole eqn (51) and (52), other than purely imaginary solutions. The appearance of real solutions corresponds to the onset of oscillatory correlations. Hence, we find that eqn (51) and (52), which are equally valid for density–density and charge–charge correlations, lead to simultaneous emergence of density and charge oscillations. It is striking that the correlation function analysis directly predicts the electric-field-induced synchronization between the emergences of density and charge oscillations. The simultaneous occurrence of crossovers is in contrast to equilibrium crossover phenomena which emerge separately: the equilibrium density–density and charge–charge correlation functions exhibit the Fisher–Widom31,36,44 and Kirkwood31–36 crossovers, respectively.
2 allows us to have complex solutions to the pole eqn (51) and (52), other than purely imaginary solutions. The appearance of real solutions corresponds to the onset of oscillatory correlations. Hence, we find that eqn (51) and (52), which are equally valid for density–density and charge–charge correlations, lead to simultaneous emergence of density and charge oscillations. It is striking that the correlation function analysis directly predicts the electric-field-induced synchronization between the emergences of density and charge oscillations. The simultaneous occurrence of crossovers is in contrast to equilibrium crossover phenomena which emerge separately: the equilibrium density–density and charge–charge correlation functions exhibit the Fisher–Widom31,36,44 and Kirkwood31–36 crossovers, respectively.
2. Shifted crossover from monotonic to oscillatory decay of correlations.
We consider the case where a smallest value of the purely imaginary solution to either eqn (51) or (52) exists for| | ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ ≤ σ ≤ ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*j)σ, (*j)σ, | (54) |
with the superscripts, (*1) and (*2), of the maxima denoting the upper bounds for eqn (51) and (52), respectively. Namely, the solutions to eqn (51) and (52) become complex beyond ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ and
(*1)σ and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*2)σ, respectively. It can be readily seen from eqn (52) that
(*2)σ, respectively. It can be readily seen from eqn (52) that ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*2)σ is independent of E but is larger than the conventional Kirkwood crossover value32–36 in the range of 1.0 <
(*2)σ is independent of E but is larger than the conventional Kirkwood crossover value32–36 in the range of 1.0 < ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) *σ <1.2 for symmetric electrolytes in equilibrium where the pole equation is k2 + (
*σ <1.2 for symmetric electrolytes in equilibrium where the pole equation is k2 + (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) *)2ω(k) = 0: it follows from eqn (52) that
*)2ω(k) = 0: it follows from eqn (52) that| | 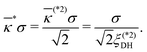 | (55) |
In contrast, eqn (51) implies that ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ depends on E and is smaller than the above Kirkwood crossover value at E = 0 due to additional screening effect measured by pE.
(*1)σ depends on E and is smaller than the above Kirkwood crossover value at E = 0 due to additional screening effect measured by pE.
3. Finite decay length in the dilute limit.
Eqn (51) and (52) are reduced to| | f1(k(1)x) ≡ (k(1)x)2 + ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 2 + (pE)2 = 0, 2 + (pE)2 = 0, | (56) |
| | f2(k(2)x) ≡ (k(2)x)2 + 0.5![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 2 = 0, 2 = 0, | (57) |
respectively, when considering the anisotropic approximation (53) and ω(k) = 1 for simplicity. In the dilute limit of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) → 0, eqn (56) yields a finite decay length ξ(1)Decay ≈ (pE)−1 (see Section IIIB for detailed derivation), whereas eqn (57) ensures the divergent behavior of the decay length ξ(2)Decay given by
→ 0, eqn (56) yields a finite decay length ξ(1)Decay ≈ (pE)−1 (see Section IIIB for detailed derivation), whereas eqn (57) ensures the divergent behavior of the decay length ξ(2)Decay given by  .
.
The non-vanishing decay length ξ(1)Decay ≈ (pE)−1 helps us to understand the physics of the decay mode on target. We explain below the decay length ξ(1)Decay ≈ (pE)−1 in terms of competing electrokinetics between electrophoresis and free diffusion. We have an electrophoresis time,  , for a variable length L because the electrophoretic velocity is given by
, for a variable length L because the electrophoretic velocity is given by  , remembering that the force pE exerted on a single ion by the applied electric field is defined in units of kBT and that the mobility is given by
, remembering that the force pE exerted on a single ion by the applied electric field is defined in units of kBT and that the mobility is given by  according to the Einstein relation. It follows that the equality between a required time for electrophoresis and free diffusion reads
according to the Einstein relation. It follows that the equality between a required time for electrophoresis and free diffusion reads
| |  | (58) |
which is equivalent to the above relation
ξ(1)Decay ≈ (
pE)
−1 when
L =
ξ(1)Decay.
Hence, eqn (58) implies that ξ(1)Decay ≈ (pE)−1 is related to an electrokinetic crossover length. In the smaller scale of L < ξ(1)Decay, free diffusion is dominant, and the electrophoretic migration path is blurred by diffusion. Meanwhile, for an electrophoresis dominant length scale L > ξ(1)Decay, fluctuations in diffusion processes become negligible in comparison with electrophoretic migration: spatial distribution of charged spheres in a steady state is mainly determined by particles migrating uniformly. This electrokinetic aspect of a steady state provides an explanation of the decay length ξ(1)Decay ≈ (pE)−1 that remains finite even in the dilute limit of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) → 0.
→ 0.
B. Electric-field-induced Kirkwood crossover
Let r⊥ be a transverse vector r⊥ = (0, y, z)T similar to k⊥ defined by eqn (39) (see also Fig. 1). The Fourier transform then reads| |  | (59) |
| |  | (60) |
We consider the real-space representations of  and
and  defined by
defined by| | 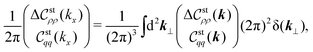 | (61) |
following the anisotropic approximation (53). Accordingly, eqn (59) and (60) are reduced, respectively, to| |  | (62) |
| |  | (63) |
using smeared correlation functions which are integrated over a cross section transverse to the applied electric field:| |  | (64) |
| |  | (65) |
Correspondingly, the pole eqn (51) and (52) are simplified, respectively, as| | (k(1)xσ)2 + (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ)2ω(k(1)x) + (pEσ)2 = 0, σ)2ω(k(1)x) + (pEσ)2 = 0, | (66) |
| | (k(2)xσ)2 + 0.5(![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ)2ω(k(2)x) = 0, σ)2ω(k(2)x) = 0, | (67) |
both of which are different not only from the Debye–Hückel-type equation,  , used in equilibrium electrolytes but also from the approximate forms (56) and (57) where ω(k) = 1.
, used in equilibrium electrolytes but also from the approximate forms (56) and (57) where ω(k) = 1.
The complex solutions k(j)xσ (j = 1,2) to eqn (66) and (67) are related, respectively, to the wavelengths μ(j) and decaying lengths ξ(j)Decay of stationary correlation functions at equal times as follows:
| | | k(j)xσ = x(j) + iy(j), | (68) |
| |  | (69) |
Thus, we have clarified that the above
expressions (62) and (63) of the anisotropic Fourier transforms satisfy the pole
eqn (66) and (67) with
eqn (68) and (69). This leads to the averaged correlation functions expressed as
| |  | (70) |
| |  | (71) |
where it is noted that both of these density–density and charge–charge correlation functions have the same wavelengths of oscillations in addition to the identical decay lengths, reflecting the above electric-field-induced synchronization.
The introduction of averaged correlation functions given by eqn (64) and (65) enables us to investigate correlations between coarse-grained planes perpendicular to the electric field without consideration of lane formation. In particular, we focus on the pole eqn (66) that predicts an electric-field-induced shift of the Kirkwood crossover from a monotonic decay state to a damped oscillatory state.
More precisely, our focus is on the electric-field-induced Kirkwood crossover between the two regions specified below. For ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ ≤
σ ≤ ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ, both solutions to eqn (66) and (67) are purely imaginary: eqn (70) and (71) read
(*1)σ, both solutions to eqn (66) and (67) are purely imaginary: eqn (70) and (71) read
| |  | (72) |
| |  | (73) |
respectively, where

and
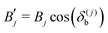
. In the range of
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ
σ >
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ
(*1)σ, on the other hand, the solution to
eqn (66) becomes complex while the solution to
(67) is purely imaginary:
eqn (72) and (73) transform to
| |  | (74) |
| |  | (75) |
respectively.
The electric-field-induced Kirkwood crossover is thus represented by the changes of the correlation functions from eqn (72) and (73) to eqn (74) and (75), which occurs at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ =
σ = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ. We further predict the Fisher–Widom crossover31,36,44 that the density and charge oscillations become obvious in the range of
(*1)σ. We further predict the Fisher–Widom crossover31,36,44 that the density and charge oscillations become obvious in the range of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ <
(*1)σ < ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ <
σ < ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*2)σ where the two decay lengths, ξ(1)Decay and ξ(2)Decay, approach each other; however, it is beyond the scope of this paper to determine the full phase diagram using the steady-state extensions of the Kirkwood and Fisher–Widom crossovers31 related to eqn (66) and (67).
(*2)σ where the two decay lengths, ξ(1)Decay and ξ(2)Decay, approach each other; however, it is beyond the scope of this paper to determine the full phase diagram using the steady-state extensions of the Kirkwood and Fisher–Widom crossovers31 related to eqn (66) and (67).
C. Relationship between E-dependent solutions to eqn (66) and the equilibrium decay length
Fig. 2 shows a schematic representation of numerical results presented in Fig. 3 and 8. In Fig. 2, the ratio of ξ(1)Decay to the smeared Debye–Hückel screening length ξDH (i.e., ξ(1)Decay/ξDH) is shown on a log–log plot as a function of σ/ξDH.
First, it is seen from Fig. 2 that the equilibrium Kirkwood crossover point32–36 located at node A shifts gradually along the green arrow with the increase of electric field strength: the dashed green arrow from node A to node B represents the numerical results shown in Fig. 3(b) and 8(b). Incidentally, node B is merely an electric-field-induced Kirkwood crossover point at an arbitrary field strength.
Next, we explain the solid brown curves in Fig. 2 terminated at nodes A and B. These curves represent the ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ-dependencies of ξ(1)Decay in a uniform state without and with applied electric field, respectively. On the one hand, ξ(1)Decay at E = 0 is identified with ξDH in the dilute limit of
σ-dependencies of ξ(1)Decay in a uniform state without and with applied electric field, respectively. On the one hand, ξ(1)Decay at E = 0 is identified with ξDH in the dilute limit of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ∼
∼ ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) 1/2 → 0 and decreases more rapidly than ξDH with increase of
1/2 → 0 and decreases more rapidly than ξDH with increase of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) in a uniform state prior to the Kirkwood crossover in equilibrium. On the other hand, there are two features as seen from the brown curve under the applied electric field (E ≠ 0): the dilute limit of ξ(1)Decay/ξDH approaches zero because of the finiteness of the decay length ξ(1)Decay in the limit of ξDH → ∞ as mentioned before, whereas the downward trend of ξ(1)Decay/ξDH, similar to the above behavior at E = 0, is observed near the electric-field-induced Kirkwood crossover.
in a uniform state prior to the Kirkwood crossover in equilibrium. On the other hand, there are two features as seen from the brown curve under the applied electric field (E ≠ 0): the dilute limit of ξ(1)Decay/ξDH approaches zero because of the finiteness of the decay length ξ(1)Decay in the limit of ξDH → ∞ as mentioned before, whereas the downward trend of ξ(1)Decay/ξDH, similar to the above behavior at E = 0, is observed near the electric-field-induced Kirkwood crossover.
Third, let us turn our attention to the dashed blue line in Fig. 2 representing a typical underscreening behavior beyond the Kirkwood line (the vertical blue line through node A) with no electric field applied. The dashed blue line in Fig. 2 depicts the following relation for a decay length ξDecay:
| |  | (76) |
according to previous simulation and theoretical studies;
20,29–31 the experimental results of
χ ≈ 3 in RTILs are beyond the scope of this study. It follows from
eqn (77) that
eqn (76) reads
| |  | (78) |
Eqn (78) implies that the decay length
ξDecay of damped oscillations for correlations becomes longer despite increasing
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
, which has been referred to as underscreening behavior without an electric field.
Remarkably, the scaling relation given by eqn (76) and (78) applies to the ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ-dependence of
σ-dependence of  at the Kirkwood crossover; the exponent χ appears close to 1.4 as will be shown in Fig. 3(b).20,29–31 Reflecting this similarity between the exponents χ of the underscreening behavior and the electric-field-induced shift for
at the Kirkwood crossover; the exponent χ appears close to 1.4 as will be shown in Fig. 3(b).20,29–31 Reflecting this similarity between the exponents χ of the underscreening behavior and the electric-field-induced shift for  , the dashed blue line in Fig. 2 is drawn as an extension of the green arrow from node A (E = 0) to node B (E ≠ 0).
, the dashed blue line in Fig. 2 is drawn as an extension of the green arrow from node A (E = 0) to node B (E ≠ 0).
Last, we focus on the vertical green line through node B in Fig. 2, indicating the condition of the electric-field-induced Kirkwood crossover from a uniform state to a stripe state. In the stripe state, we can observe a damped oscillatory decay of both density–density and charge–charge correlation functions along the direction of applied electric field in the anisotropic approximation (53). It is to be noted here that the stripe state is specified using the averaged correlation functions,  and
and  , which by definition smear out density and charge distributions on cross sections perpendicular to the applied electric field (see eqn (64) and (65)).
, which by definition smear out density and charge distributions on cross sections perpendicular to the applied electric field (see eqn (64) and (65)).
The emergence of anisotropic density and charge modulations is consistent with the previous results as follows: Theoretically, the SDFT using the Gaussian charge smearing model35,40 has provided numerical results of two-dimensional correlation functions showing a tendency to form alternating chains of cations and anions along the field direction.13 Also, according to simulation and experimental studies on oppositely charged colloids, the electric-field-driven mixtures have been found to form bands non-parallel to the field direction, other than lanes in the electric field direction, under some conditions on various dynamic phase diagrams of steady states with AC or DC fields applied.17,18 Our present findings of the emergence of stripe state thus shed light on these anisotropic inhomogeneities as related to crossover phenomena of steady-state correlations.
D. Numerical solutions to eqn (66)
Fig. 3(a) shows the electric-field effects on the Kirkwood crossover in terms of the smeared Debye–Hückel length  and a decay length
and a decay length  at the Kirkwood crossover. As detailed in Section IV, we have obtained these results using both the Gaussian charge smearing model35,40 (or the HNC approximation for one-component ionic fluids42) and the modified MSA model for the DCF,43 or its essential function ω(k) given by eqn (12). The former model is depicted by green lines, whereas the latter by red lines. All of the results in Fig. 3(a) exhibit downward trends in accordance with analytical observations made in Section IV.
at the Kirkwood crossover. As detailed in Section IV, we have obtained these results using both the Gaussian charge smearing model35,40 (or the HNC approximation for one-component ionic fluids42) and the modified MSA model for the DCF,43 or its essential function ω(k) given by eqn (12). The former model is depicted by green lines, whereas the latter by red lines. All of the results in Fig. 3(a) exhibit downward trends in accordance with analytical observations made in Section IV.
Furthermore, Fig. 3(a) allows us to make quantitative comparisons between the present two models for the DCF. First, it is confirmed from the values of  at E = 0 in Fig. 3(a) that the numerical results correctly reproduce the Kirkwood crossover points previously obtained for the Gaussian charge smearing model34,35 and the modified MSA model.29–31,34 Second, Fig. 3(a) shows that the electric-field-induced shifts of
at E = 0 in Fig. 3(a) that the numerical results correctly reproduce the Kirkwood crossover points previously obtained for the Gaussian charge smearing model34,35 and the modified MSA model.29–31,34 Second, Fig. 3(a) shows that the electric-field-induced shifts of  are similar to each other. Remembering that
are similar to each other. Remembering that 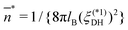 by definition (36), it is seen from the variations of
by definition (36), it is seen from the variations of  in Fig. 3(a) that, irrespective of the models adopted, the crossover densities at pEσ = 3.0 are evaluated to be less than half of those at E = 0. Last, we turn our attention to the relationship between
in Fig. 3(a) that, irrespective of the models adopted, the crossover densities at pEσ = 3.0 are evaluated to be less than half of those at E = 0. Last, we turn our attention to the relationship between  and
and  as a function of either
as a function of either ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) * or E. For a fixed strength of applied electric field, the decay length
* or E. For a fixed strength of applied electric field, the decay length  becomes shorter as the ionic solution density
becomes shorter as the ionic solution density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) *, or
*, or  , becomes larger, which is consistent with the previous results conventionally found for concentrated electrolytes prior to the Kirkwood crossover without an applied electric field.30–33 The electric-field dependencies, on the other hand, exhibit an opposite relationship between
, becomes larger, which is consistent with the previous results conventionally found for concentrated electrolytes prior to the Kirkwood crossover without an applied electric field.30–33 The electric-field dependencies, on the other hand, exhibit an opposite relationship between 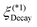 and
and  : the downward trends in Fig. 3(a) indicate that both
: the downward trends in Fig. 3(a) indicate that both  and
and  are smaller as E is larger.
are smaller as E is larger.
Fig. 3(b) demonstrates this opposite tendency using a log–log plot of 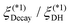 vs.
vs.  : it is seen from Fig. 3(b) that
: it is seen from Fig. 3(b) that
| |  | (79) |
for an exponent
χ larger than unity. The dotted line is a guide to the eye, indicating that
χ is close to 1.4 and is consistent with the relation 1 <
χ ≤ 1.5 previously obtained from simulation results on underscreening behaviors in RTILs beyond the Kirkwood line with no electric field applied.
20,29–31
E. The 2D inverse Fourier transforms for assessing the anisotropic approximation (53)
The last subsection of Section III presents the results of the 2D inverse Fourier transforms using heat maps, which would help us not only to understand the above analytical results concretely but also to assess the anisotropic approximation (53). We perform the 2D inverse Fourier transform of  by setting kz = 0 similar to the expressions (61), (62) and (64):
by setting kz = 0 similar to the expressions (61), (62) and (64):| | 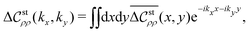 | (80) |
| |  | (81) |
In other words, the inverse Fourier transform provides the mean correlation function  as follows:
as follows:| |  | (82) |
The 2D results of the mean correlation function 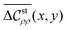 can reflect the 3D behaviors of density–density correlations when the translational symmetry of
can reflect the 3D behaviors of density–density correlations when the translational symmetry of 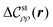 is preserved with respect to the z-direction and the correlation functions on the xy cross-sections are indistinguishable at two different z values.
is preserved with respect to the z-direction and the correlation functions on the xy cross-sections are indistinguishable at two different z values.
The setup in Fig. 1 is a plausible example to satisfy such translational symmetry. The upper figure of Fig. 1 indicates that the plate-plate distance is sufficiently smaller than the size in the z-direction, and yet we suppose that the finite-size effects are negligible because the plate-plate distance is much larger than the sphere diameter as mentioned in Section IIA. Such a system could serve as a platform for investigating the 2D inverse Fourier transforms of the 3D primitive model.
We also compare the 1D results of the mean correlation functions,  at a fixed y-coordinate value of y0 and
at a fixed y-coordinate value of y0 and  defined by eqn (64), which are related respectively to the 2D mean correlation function
defined by eqn (64), which are related respectively to the 2D mean correlation function  defined by eqn (81) as follows:
defined by eqn (81) as follows:
| |  | (83) |
| | 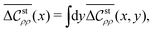 | (84) |
revealing that
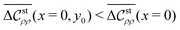
because of

(see
Fig. 5 for confirmation).
Below we provide results of the inverse Fourier transforms in Fig. 4–6, demonstrating real-space behaviors of the density–density correlation function in a high-density region such that ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ exceeds the Fisher–Widom-like crossover31,36,44 as well as the Kirkwood crossover:32–36
σ exceeds the Fisher–Widom-like crossover31,36,44 as well as the Kirkwood crossover:32–36![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ >
σ > ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*2)σ (>
(*2)σ (>![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ) is investigated (remember the discussion at the end of Section IIB). We see from Fig. 4 that stripe states illustrated in Fig. 2 are observed more clearly as
(*1)σ) is investigated (remember the discussion at the end of Section IIB). We see from Fig. 4 that stripe states illustrated in Fig. 2 are observed more clearly as ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ is larger at a fixed strength of electric field. In Fig. 5 and 6, we validate the anisotropic approximation (53) from comparing
σ is larger at a fixed strength of electric field. In Fig. 5 and 6, we validate the anisotropic approximation (53) from comparing  and
and 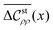 (see also eqn (83) and (84)). Furthermore, Fig. 7 shows the emergence of a lane structure with the increase of electric field strength from pEσ = 0.1 to 1.0 at a high value of
(see also eqn (83) and (84)). Furthermore, Fig. 7 shows the emergence of a lane structure with the increase of electric field strength from pEσ = 0.1 to 1.0 at a high value of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.78.
σ = 2.78.
 |
| | Fig. 4 Comparison between the 2D results of  for different conditions on ionic condition and electric field strength. The color bar on the right hand side, which is common to the three heat maps, represents the value of for different conditions on ionic condition and electric field strength. The color bar on the right hand side, which is common to the three heat maps, represents the value of  at a location (x/σ, y/σ) measured in units of sphere diameter σ. While the difference between Fig. 4(a) and (b) is ionic concentration, or at a location (x/σ, y/σ) measured in units of sphere diameter σ. While the difference between Fig. 4(a) and (b) is ionic concentration, or ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ, at an identical electrical field, an electric field effect is seen from comparing Fig. 4(b) and (c) at a same ionic concentration: (a) ( σ, at an identical electrical field, an electric field effect is seen from comparing Fig. 4(b) and (c) at a same ionic concentration: (a) (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ, pEσ) = (2.2,0.5); (b) ( σ, pEσ) = (2.2,0.5); (b) (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ, pEσ) = (2.6,0.5); (c) ( σ, pEσ) = (2.6,0.5); (c) (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ, pEσ) = (2.6,1.5). σ, pEσ) = (2.6,1.5). | |
 |
| | Fig. 5 Comparison between the 1D results of  at a fixed y-coordinate value of y0 and at a fixed y-coordinate value of y0 and  defined byeqn (64). The density–density correlation functions are plotted as functions of x/σ, the separation distance in the applied field direction measured in units of sphere diameter σ. At an identical electric field strength pEσ = 0.5, two ionic concentrations, defined byeqn (64). The density–density correlation functions are plotted as functions of x/σ, the separation distance in the applied field direction measured in units of sphere diameter σ. At an identical electric field strength pEσ = 0.5, two ionic concentrations, ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2 and 2.6, are considered in both figures: (a) the green and red solid lines depict the behaviors of σ = 2.2 and 2.6, are considered in both figures: (a) the green and red solid lines depict the behaviors of  at at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2 (green) and 2.6 (red), respectively, whereas the red dotted line represents σ = 2.2 (green) and 2.6 (red), respectively, whereas the red dotted line represents  at at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.6; (b) the green and red solid lines depict the behaviors of σ = 2.6; (b) the green and red solid lines depict the behaviors of  at at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2 and 2.6, respectively. σ = 2.2 and 2.6, respectively. | |
 |
| | Fig. 6 The green and red lines are the same results as those in Fig. 5(b): we show  over the range, 0 ≤ x/σ ≤ 20, at over the range, 0 ≤ x/σ ≤ 20, at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2 (green) and 2.6 (red) in the presence of applied electric field (pEσ = 0.5). The dashed lines correspond to the best fit of eqn (85). σ = 2.2 (green) and 2.6 (red) in the presence of applied electric field (pEσ = 0.5). The dashed lines correspond to the best fit of eqn (85). | |
Fig. 4 shows how the density–density correlation behaviors vary depending on the ionic concentration and electric field strength. The difference between Fig. 4(a) and (b) is the ionic concentration at the same electric field of pEσ = 0.5. Meanwhile, the difference between Fig. 4(b) and (c) is the strength of electric field at the same ionic condition of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.6. Fig. 4(b) can be a reference result for investigating the effects of ionic concentration and electric field strength. Fig. 4(b) exhibits the oscillatory decay behaviors in the external field direction on an xy plane, which is typical of density–density correlations in the stripe state.
σ = 2.6. Fig. 4(b) can be a reference result for investigating the effects of ionic concentration and electric field strength. Fig. 4(b) exhibits the oscillatory decay behaviors in the external field direction on an xy plane, which is typical of density–density correlations in the stripe state.
When ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ is reduced from 2.6 to 2.2 without changing the electric field strength, we obtain the result of Fig. 4(a). Comparison between Fig. 4(a) and (b) indicates the following. First, we can observe the oscillatory decays in the external field direction for both values of
σ is reduced from 2.6 to 2.2 without changing the electric field strength, we obtain the result of Fig. 4(a). Comparison between Fig. 4(a) and (b) indicates the following. First, we can observe the oscillatory decays in the external field direction for both values of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ when setting the electric field strength to be pEσ = 0.5. Furthermore, Fig. 4(a) shows that the correlation function becomes almost zero for x ≥ 5σ: The density–density correlation function becomes equal to 2
σ when setting the electric field strength to be pEσ = 0.5. Furthermore, Fig. 4(a) shows that the correlation function becomes almost zero for x ≥ 5σ: The density–density correlation function becomes equal to 2![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) δ(r) for x ≥ 5σ in contrast to the long-range correlations seen in Fig. 4(b). The different behaviors of density–density correlations suggest that the smaller
δ(r) for x ≥ 5σ in contrast to the long-range correlations seen in Fig. 4(b). The different behaviors of density–density correlations suggest that the smaller ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ is, the shorter the decay length becomes. In other words, comparison between Fig. 4(a) and (b) reveals an underscreening behavior19,20,29–31 beyond the Kirkwood condition as depicted in the schematic of Fig. 2. Fig. 4(c) further demonstrates that alignment of segregation band to the external field direction becomes clear by increasing the electric field strength to pEσ = 1.5 at
σ is, the shorter the decay length becomes. In other words, comparison between Fig. 4(a) and (b) reveals an underscreening behavior19,20,29–31 beyond the Kirkwood condition as depicted in the schematic of Fig. 2. Fig. 4(c) further demonstrates that alignment of segregation band to the external field direction becomes clear by increasing the electric field strength to pEσ = 1.5 at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.6.
σ = 2.6.
Fig. 4 has found an external field condition (pEσ = 0.5) that creates an anisotropic density modulation reflecting the stripe state as depicted in Fig. 2. This finding has justified the anisotropic approximation (53) from a qualitative point of view. We make below a quantitative assessment of the anisotropic approximation (53). To this end, we further investigate the extent to which the one-variable correlation function represents the results of Fig. 4 using Fig. 5 and 6.
Fig. 5 compares the x-dependencies of the 2D correlation function 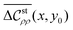 at y0, a fixed y-coordinate value, with the behaviors of the one-variable correlation function
at y0, a fixed y-coordinate value, with the behaviors of the one-variable correlation function  defined by eqn (64). Both solid lines in Fig. 5(a) show the x-dependencies at y0 = 0. The same external field condition pEσ = 0.5 is used in both results of Fig. 5(a) and (b), and the ionic conditions for the green and red lines are identical in Fig. 5(a) and (b): the green and red lines represent the results at
defined by eqn (64). Both solid lines in Fig. 5(a) show the x-dependencies at y0 = 0. The same external field condition pEσ = 0.5 is used in both results of Fig. 5(a) and (b), and the ionic conditions for the green and red lines are identical in Fig. 5(a) and (b): the green and red lines represent the results at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2 and 2.6, respectively.
σ = 2.2 and 2.6, respectively.
It is noted that the value of the vertical axis in Fig. 5(a) is one-tenth of that in Fig. 5(b) due to the different definitions of the two correlation functions as clarified by eqn (83) and (84). Nevertheless, the behaviors bear resemblances. First, these two functions, 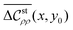 and
and  , exhibit oscillatory decay behaviors, and we will make a quantitative comparison using Fig. 6. They also share the feature of correlation value that becomes smaller with the decrease of ionic concentration from
, exhibit oscillatory decay behaviors, and we will make a quantitative comparison using Fig. 6. They also share the feature of correlation value that becomes smaller with the decrease of ionic concentration from ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.6 to 2.2. Furthermore, we observe that the oscillations disappear faster for the green line than for the red line in both Fig. 5(a) and (b), which corresponds to the underscreening behavior suggested by Fig. 4.
σ = 2.6 to 2.2. Furthermore, we observe that the oscillations disappear faster for the green line than for the red line in both Fig. 5(a) and (b), which corresponds to the underscreening behavior suggested by Fig. 4.
The solid lines in Fig. 5(a) are the results at a fixed y-coordinate: y0 = 0. The specific value of y0 raises the question as to whether or not the above similarity of solid lines in Fig. 5(a) and (b) is a coincidence. To address this question, the red dashed line shows the x-dependency of the two-variable function at y0/σ = 5 when pEσ = 0.5 and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2. We can see that the period of the dashed red line is close to that of the solid red line. However, the initial phase is different from that at y0/σ = 0, and the correlation value is reduced considerably even at x/σ = 0 as y0/σ varies from 0 to 5. The latter difference implies that the x-dependency of
σ = 2.2. We can see that the period of the dashed red line is close to that of the solid red line. However, the initial phase is different from that at y0/σ = 0, and the correlation value is reduced considerably even at x/σ = 0 as y0/σ varies from 0 to 5. The latter difference implies that the x-dependency of  near y0/σ = 0 greatly contributes to the one-variable correlation function
near y0/σ = 0 greatly contributes to the one-variable correlation function  defined by eqn (64), which is why the two solid lines in Fig. 5(a) reproduce the one-variable function behaviors in Fig. 5(b).
defined by eqn (64), which is why the two solid lines in Fig. 5(a) reproduce the one-variable function behaviors in Fig. 5(b).
Let us consider a simple asymptotic form determined by a single decay length ξDecay and oscillation period μ:
| | 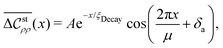 | (85) |
which is fitted to the results of
Fig. 5(b) instead of
eqn (70). While the solid lines in
Fig. 6, which are the same as those of
Fig. 5(b), are shown over the range 0 ≤
x/
σ ≤ 20, the dashed lines in
Fig. 6 correspond to the best fit of
eqn (85). The best-fit parameter sets are as follows:(
A,
ξDecay,
μ,
δa) = (0.6 × 10
−2, 2.0, 5.6, 1.1) at
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ
σ = 2.2, whereas (
A,
ξDecay,
μ,
δa) = (1.3 × 10
−2, 2.5, 3.8, 0.4) at
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ
σ = 2.6. The best-fit periods,
μ = 5.6 and 3.8, reflect the oscillatory behaviors seen from
Fig. 6. Meanwhile, the best-fit decay length
ξDecay extends from 2
σ to 2.5
σ with the increase of
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ
σ from 2.2 to 2.6, which is a quantitative result of underscreening behavior. Evaluating the exponent
χ defined by
eqn (79) from this increase in
ξDecay, we have 2 <
χ < 3; it is interesting to note that the present exponent is larger than the equilibrium exponent (1 <
χ ≤ 1.5) previously obtained from the MSA of the 3D primitive model but is close to the exponent experimentally obtained.
19
Last, we consider the 2D inverse Fourier transforms of  when increasing
when increasing ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ to 2.78. The strengths of the applied electric field are pEσ = 0.1 (Fig. 7(a)) and pEσ = 1.0 (Fig. 7(b)). The heat maps in Fig. 7 reveal the oscillatory 2D patterns due to the suppression of decaying behaviors. On the one hand, even at the weak electric field strength of pEσ = 0.1, Fig. 7(a) shows that segregation bands of ions with the same sign are deformed along the x-axis, the external field direction, though the stripe state remains a good approximation in the region of y/σ ≤ 5. On the other hand, at pEσ = 1.0, Fig. 7(b) demonstrates the emergence of lane structure formed by aligned bands, revealing that the anisotropic approximation (53) becomes invalid far beyond the electric-field-induced Kirkwood crossovers.
σ to 2.78. The strengths of the applied electric field are pEσ = 0.1 (Fig. 7(a)) and pEσ = 1.0 (Fig. 7(b)). The heat maps in Fig. 7 reveal the oscillatory 2D patterns due to the suppression of decaying behaviors. On the one hand, even at the weak electric field strength of pEσ = 0.1, Fig. 7(a) shows that segregation bands of ions with the same sign are deformed along the x-axis, the external field direction, though the stripe state remains a good approximation in the region of y/σ ≤ 5. On the other hand, at pEσ = 1.0, Fig. 7(b) demonstrates the emergence of lane structure formed by aligned bands, revealing that the anisotropic approximation (53) becomes invalid far beyond the electric-field-induced Kirkwood crossovers.
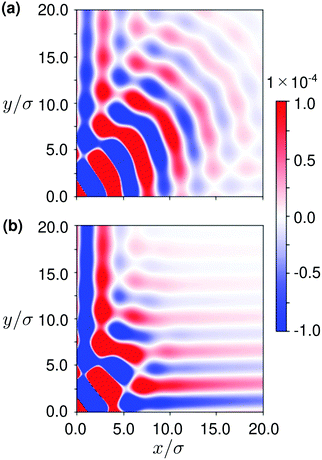 |
| | Fig. 7 Comparison between the 2D results of  at different electric field strengths: (a) pEσ = 0.1 and (b) pEσ = 1.0. The same ionic condition at different electric field strengths: (a) pEσ = 0.1 and (b) pEσ = 1.0. The same ionic condition ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.78 is adopted in both results. σ = 2.78 is adopted in both results. | |
 |
| | Fig. 8 Comparison between Fig. 2 (a schematic summary) and numerical results of the modified MSA model. (a) The graphical representation of the solution to u(y*) = v(y*) given by eqn (105) and (106), respectively. Eqn (105) provides 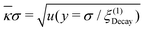 , the ξ(1)Decay-dependence of , the ξ(1)Decay-dependence of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ, which varies depending on the electric field strength measured by pEσ. The colored solid lines represent these dependencies for pEσ = 0 (green), pEσ = 1.5 (orange), and pEσ = 3 (red). Meanwhile, the blue dashed line shows another dependence of σ, which varies depending on the electric field strength measured by pEσ. The colored solid lines represent these dependencies for pEσ = 0 (green), pEσ = 1.5 (orange), and pEσ = 3 (red). Meanwhile, the blue dashed line shows another dependence of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ on ξ(1)Decay/σ which is given by σ on ξ(1)Decay/σ which is given by  (see eqn (106)). The three intersection points are indicated by brown circles, giving both the Debye–Hückel lengths (see eqn (106)). The three intersection points are indicated by brown circles, giving both the Debye–Hückel lengths  at the electric-field-induced crossovers and the Kirkwood decay lengths at the electric-field-induced crossovers and the Kirkwood decay lengths  at different field strengths. (b) Numerical results summarized in Fig. 2. In this figure, the at different field strengths. (b) Numerical results summarized in Fig. 2. In this figure, the ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ-dependencies of ξ(1)Decay are depicted by the solid lines colored green (pEσ = 0), blue (pEσ = 1), orange (pEσ = 1.5), and red (pEσ = 3), from top to bottom, on a log–log plot of ξ(1)Decay/ξDH = σ-dependencies of ξ(1)Decay are depicted by the solid lines colored green (pEσ = 0), blue (pEσ = 1), orange (pEσ = 1.5), and red (pEσ = 3), from top to bottom, on a log–log plot of ξ(1)Decay/ξDH = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ξ(1)Decayvs. σ/ξDH = ξ(1)Decayvs. σ/ξDH = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ. The brown circles mark the termination points of these lines representing the Kirkwood crossover points at each electric-field strength, and the rightmost circle A corresponds to node A in Fig. 2, the Kirkwood crossover point at E = 0. The location shift of brown circles with the increase of E is indicated by the dashed green arrow, showing an electric-field-induced shift of the Kirkwood crossover. For comparison, the dotted line delineates the scaling relation, σ. The brown circles mark the termination points of these lines representing the Kirkwood crossover points at each electric-field strength, and the rightmost circle A corresponds to node A in Fig. 2, the Kirkwood crossover point at E = 0. The location shift of brown circles with the increase of E is indicated by the dashed green arrow, showing an electric-field-induced shift of the Kirkwood crossover. For comparison, the dotted line delineates the scaling relation,  , as well as that in Fig. 3(b). , as well as that in Fig. 3(b). | |
IV. Details on the determination of the electric-field-induced Kirkwood crossovers in the anisotropic approximation
We perform the correlation function analysis, especially focusing on the pole eqn (66). In Section IVA, we see that discriminant analysis of a quadratic equation becomes available to investigate the solution to eqn (66), irrespective of the function forms of ω(k), as a result of the small kxσ-expansion of the key function ω(k). Section IVB provides concrete results of both the Gaussian charge smearing model and the modified MSA model for clarifying how the results in Fig. 3 are obtained.
A. A general approximation of eqn (66) for evaluating the Kirkwood crossover point
Expanding ω(k) with respect to k(1)xσ, we have a general form,| | | ω(k(1)x) ≈ 1 − α1(k(1)xσ)2 + α2(k(1)xσ)4, | (86) |
as seen from eqn (12); for instance, α1 = 1/2 and α2 = 1/8 for the Gaussian charge smearing model,35,40 and α1 = 1/2 and α2 = 1/24 for the modified MSA model.43Eqn (66) then reduces to the quadratic equation for  :
:| |  | (87) |
It follows from eqn (68) that| | | (k(1)xσ)2 = x2 − y2 + 2ixy | (88) |
where x and y are related to the decay length ξ(1)Decay and wavelength μ(1) as defined in eqn (69). Eqn (69) and (88) imply that discriminant analysis of eqn (87) is found useful to determine the Kirkwood crossover point where the correlation functions change from monotonic (μ(1) = 0) to oscillatory (μ(1) ≠ 0) decay. As mentioned in eqn (54), the imaginary solution 2ixy disappears at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ because of x = 0, or μ(1) → ∞: the Kirkwood crossover occurs when exceeding
(*1)σ because of x = 0, or μ(1) → ∞: the Kirkwood crossover occurs when exceeding ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ.
(*1)σ.
We find approximate forms of the solution to the discriminant equation of eqn (87) as follows:
| |  | (89) |
| |  | (90) |
see Appendix E for these derivations. Plugging the modified MSA coefficients,
α1 = 1/2 and
α2 = 1/24, into the relation
(89) for
E = 0, we have
| |  | (91) |
which is in good agreement with the Kirkwood crossover values previously obtained for the primitive model in the absence of applied electric field.
29–33
Eqn (89) and (90) imply that the Debye–Hückel length  at the Kirkwood crossover becomes longer as E is larger. Namely, the crossover density
at the Kirkwood crossover becomes longer as E is larger. Namely, the crossover density  becomes lower with the increase of E; eqn (90) predicts that both charge–charge and density–density oscillations are observed even in a dilute electrolyte upon applying a high electric field.
becomes lower with the increase of E; eqn (90) predicts that both charge–charge and density–density oscillations are observed even in a dilute electrolyte upon applying a high electric field.
B. Analytical and numerical results
Gaussian charge smearing model35,40.
First, we consider the Gaussian charge smearing model. This model is represented by 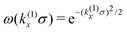 in eqn (12). Then, eqn (66) is rewritten as
in eqn (12). Then, eqn (66) is rewritten as| |  | (92) |
| | | 2τ = (k(1)xσ)2 + (pE)2σ2. | (93) |
It is convenient to transform eqn (92) and (93) to| |  | (94) |
| | | 2τ = x2 − y2 + (pE)2σ2 + 2ixy, | (95) |
which can be rewritten as| | 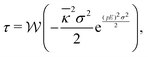 | (96) |
using the Lambert function  35 defined by
35 defined by  .
.
Focusing on the principal branch of the Lambert function,35 it is found that the Kirkwood crossover point satisfies the relations,
| |  | (97) |
similar to those at
E = 0.
Eqn (97) transforms to
| |  | (99) |
or
| |  | (100) |
for the crossover density
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
*.
Eqn (99) verifies the above approximate result
(90), whereas
eqn (100) enables us to make an analytical prediction that the increase of
E results in the decrease of
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
*. Inserting
eqn (98) into
eqn (95), we have
| | 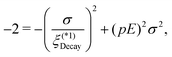 | (101) |
or
| |  | (102) |
because of
x = 0 at the Kirkwood crossover.
Eqn (100) and (102) state that, as
E is larger, Coulomb interactions are more short-ranged despite the decrease in the Kirkwood crossover density
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif)
* given by
eqn (100). In other words, our target mode

describes an aspect of electric-field-induced screening which is enhanced by the applied electric field (see also the last paragraph of Section IIIA for the underlying physics).
Relationship between the results in Fig. 8 and the present results given by eqn (99), (102), (105) and (106).
Thus, we have obtained the formulation to find the results in Fig. 8(a). On the one hand, eqn (99) and (102) yield  (or
(or ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ) and
(*1)σ) and  of the Gaussian charge smearing model, respectively. On the other hand, eqn (105) and (106) are solved numerically to find
of the Gaussian charge smearing model, respectively. On the other hand, eqn (105) and (106) are solved numerically to find 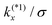 , or the inverse of
, or the inverse of  in the modified MSA,43 and we can easily calculate
in the modified MSA,43 and we can easily calculate ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ from
(*1)σ from  using eqn (105). The same results as those of Fig. 8(a) are presented on a log–log plot in Fig. 8(b), further indicating that, in the range of
using eqn (105). The same results as those of Fig. 8(a) are presented on a log–log plot in Fig. 8(b), further indicating that, in the range of  , the
, the  -dependencies of
-dependencies of  exhibit a scaling relation
exhibit a scaling relation  with χ being close to 1.4, which is similar to eqn (76) previously found for concentrated electrolytes.20,29–31
with χ being close to 1.4, which is similar to eqn (76) previously found for concentrated electrolytes.20,29–31
V Discussion and conclusions
This paper has demonstrated the usefulness of the SDFT13–15 on concentrated electrolytes under steady electric fields, which is summarized in Table 1 and Fig. 2. While Table 1 has provided a detailed summary of our stochastic mPNP model in comparison with previous mPNP models,5–15 we would like to make additional three remarks related to the schematic summary of Fig. 2.
(i) The weight function ω(k) in terms of the Kirkwood crossover
It has been proved that we can extend the mPNP models to consider the stochastic process, thereby allowing us to obtain stationary equal-time correlation functions which include the key function ω(k) as seen from eqn (43)–(48). To be noted, the Kirkwood crossover does not occur without ω(k) given by eqn (12); therefore, it is indispensable to incorporate either the finite-spread Poisson eqn (14) or the generalized Debye–Hückel eqn (17) into the stochastic mPNP models for predicting the onset of oscillatory decay of correlations.
(ii) Stripe states
An oscillatory state along the field direction (a stripe state) as given in Fig. 2 is stationary as long as lane formation is not favored. The stripe state is consistent with some previous findings of inhomogeneous steady states such as alternating chains of cations and anions along the applied field direction in electrolytes13 and non-parallels bands in oppositely charged colloidal mixtures17,18 (see the last paragraph of Section IIIC). Incidentally, it has been found that the lane structure17 clearly appears in concentrated electrolytes at a moderate condition such that ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ ≈ 1.6 and p2lB/σ = 1 by adding to the mPNP equations a fluctuating advection term due to interparticle interactions.45
σ ≈ 1.6 and p2lB/σ = 1 by adding to the mPNP equations a fluctuating advection term due to interparticle interactions.45
(iii) Fisher–Widom crossover between two Kirkwood crossovers
Above the Kirkwood crossover condition of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ >
σ > ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ, we have smeared correlation functions,
(*1)σ, we have smeared correlation functions,  and
and  , which are given by the sum of oscillatory and monotonic decay functions (i.e., eqn (74) and (75)). Furthermore, the monotonic decay parts of correlation functions subsequently become oscillatory when
, which are given by the sum of oscillatory and monotonic decay functions (i.e., eqn (74) and (75)). Furthermore, the monotonic decay parts of correlation functions subsequently become oscillatory when ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ goes beyond
σ goes beyond ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*2)σ which is related to the equilibrium Kirkwood crossover value
(*2)σ which is related to the equilibrium Kirkwood crossover value ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) *σ as eqn (55). This crossover phenomenon suggests the possibility of simultaneous occurrence of the Fisher–Widom crossover31,36,44 for density–density and charge–charge correlations in the range of
*σ as eqn (55). This crossover phenomenon suggests the possibility of simultaneous occurrence of the Fisher–Widom crossover31,36,44 for density–density and charge–charge correlations in the range of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ ≤
(*1)σ ≤ ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ ≤
σ ≤ ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*2)σ though the full phase diagram of steady states for electric-field-driven electrolytes remains to be determined. For the concrete understanding of anisotropic density modulations in stripe states, Section IIIE presents various results on the 2D density–density correlations beyond the Fisher–Widom crossover. As confirmed from Fig. 4 and 7, there are some electric field conditions that create stripe states formed by segregation bands transverse to the external field direction.
(*2)σ though the full phase diagram of steady states for electric-field-driven electrolytes remains to be determined. For the concrete understanding of anisotropic density modulations in stripe states, Section IIIE presents various results on the 2D density–density correlations beyond the Fisher–Widom crossover. As confirmed from Fig. 4 and 7, there are some electric field conditions that create stripe states formed by segregation bands transverse to the external field direction.
It is still necessary to investigate whether experimental and simulation studies can find an electric-field-induced shift of the Kirkwood crossover from monotonic to oscillatory decay of density–density and charge–charge correlations in the applied electric field direction. Therefore, let us make three comparisons in terms of realizability.
Although the primitive model has been used for investigating concentrated electrolytes, we would like to see the interaction parameters of RTILs and colloidal nano-particle dispersions as well as concentrated electrolytes. For instance, let us consider (p, σ, ε, lB) = (1, 0.7, 10, 5.6) for RTILs46 and (10, 10, 80, 0.7) for colloidal nano-particle dispersions as adequate parameters of valence p, diameter σ [nm], dielectric constant ε, and the Bjerrum length lB [nm] at room temperature T = 300 K. Accordingly, we have p2lB/σ = 8 (RTILs) and p2lB/σ = 7 (nano-particle dispersions), and the use of eqn (7) and (13) can be justified because the relation (A25) barely holds.
Next, we evaluate a realistic range of electric field strength. At pEσ = 1.5, we have E ≈ 5.5 × 107 V m−1 for the RTILs (i.e., (p, σ) = (1,0.7)) and E ≈ 3.8 × 105 V m−1 for the nano-particles (i.e., (p, σ) = (10,10)). These are plausible values according to previous simulation and experimental studies as follows: molecular dynamics simulations of RTILs have revealed that E ∼ 107 V m−1 corresponds to a boundary value beyond which RTILs are reorganized into nematic-like order and exhibit anisotropic dynamics,47 whereas, for colloidal dispersions, a magnitude of E ∼ 105 V m−1 is within the possible range when referring to segregation of oppositely charged colloidal particles into bands perpendicular to the direction of external AC field.17,18
Last, let us evaluate the electric-field-induced Kirkwood crossover densities at pEσ = 1.5. We have obtained that ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) *σ is equal to 1.04 (pEσ = 0) and that
*σ is equal to 1.04 (pEσ = 0) and that ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ ≈ 0.82 (pEσ = 1.5) when adopting the modified MSA model.43 It follows that the Kirkwood crossover density varies from 0.30 M (pEσ = 0) to 0.19 M (pEσ = 1.5) for an RTIL (1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide) diluted with propylene carbonate where we set (p, σ, ε, lB) = (1,0.4,65,0.88). The former density (0.30 M) agrees well with experimental and simulation results19,20 with no electric field applied, whereas the validity of density difference (0.30–0.19 = 0.11 M) due to the external electric field needs to be assessed in future.
(*1)σ ≈ 0.82 (pEσ = 1.5) when adopting the modified MSA model.43 It follows that the Kirkwood crossover density varies from 0.30 M (pEσ = 0) to 0.19 M (pEσ = 1.5) for an RTIL (1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide) diluted with propylene carbonate where we set (p, σ, ε, lB) = (1,0.4,65,0.88). The former density (0.30 M) agrees well with experimental and simulation results19,20 with no electric field applied, whereas the validity of density difference (0.30–0.19 = 0.11 M) due to the external electric field needs to be assessed in future.
Conflicts of interest
There are no conflicts to declare.
Appendix A. Details on modifications of the PNP model presented in Section II
We provide the detailed formulations of the results in Section II by dividing this section into four parts: general formulation of two-component fluids (Appendix A1), two modifications of the Poisson equation (Appendix A2), formulations of stochastic currents for electric-field-driven electrolytes (Appendix A3), and outline of deriving stationary correlation functions at equal times (Appendix A4). In Appendix A1, the functional-integral representation of the Dean–Kawasaki model reveals that the Gaussian approximation of the free energy difference between non-equilibrium and equilibrium free energies yields the self-energy-modified current of each component in mixtures. In Appendix A2, we validate the approximate form (7) of interaction potential ψ(r, t) for the primitive model using the modified MSA43 model, and also demonstrate for the modified MSA model that the finite-spread Poisson equation obtained from this expression (7) leads to the higher-order Poisson eqn (15) due to the small kσ-expansion. In Appendix A3, we show that the self-energy-modified current given by eqn (3)–(6) is obtained from combining the results in Appendix A2 and that linearization of this current corresponds to the first-order expansion of non-equilibrium chemical potential around a uniform density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) . Appendix A4 explains that the stationary condition (A45) imposed on a general matrix form of equal-time correlation functions yields density–density and charge–charge correlation functions given by eqn (43)–(48).
. Appendix A4 explains that the stationary condition (A45) imposed on a general matrix form of equal-time correlation functions yields density–density and charge–charge correlation functions given by eqn (43)–(48).
1 General formulation
Stochastic current in the Dean–Kawasaki model.
The stochastic equations for the density fields nl(r, t) (l = 1,2) have been formulated based on the Dean–Kawasaki model.11,26 We have, according to the Dean–Kawasaki model, the conservation eqn (1) for nl(r, t) by introducing the stochastic current Jl(r, t): the Dean–Kawasaki model provides a general form of the stochastic current Jl(r, t) expressed as| |  | (A1) |
| |  | (A2) |
We can see from eqn (A1) and (A2) that there are two features of the Dean–Kawasaki model, compared with the dynamic DFT based on the deterministic density-functional equation: (i) the deterministic current, the first term on the rhs of eqn (A1), is nonlinear with respect to nl(r, t) in general and is determined by a constrained free energy 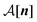 , instead of the equilibrium free energy functional;37,38 (ii) addition of the stochastic current, the second term on the rhs of eqn (A1), helps us to describe fluctuating phenomena.
, instead of the equilibrium free energy functional;37,38 (ii) addition of the stochastic current, the second term on the rhs of eqn (A1), helps us to describe fluctuating phenomena.
Functional-integral representation of constrained free energy  .
It has been shown that the constrained free energy
.
It has been shown that the constrained free energy  as a functional of given density fields n(r, t) = (n1(r, t), n2(r, t))T can be expressed by considering fluctuating potential fields ϕ(r, t) = (ϕ1(r, t), ϕ2(r, t))T, which are conjugate to n(r,t), in addition to an adjusted potential field ϕdftl(r, t) similar to that of the equilibrium DFT.37,38 Extending the previous result24,28 to the expression for two-component systems (see Appendix B for details), we have
as a functional of given density fields n(r, t) = (n1(r, t), n2(r, t))T can be expressed by considering fluctuating potential fields ϕ(r, t) = (ϕ1(r, t), ϕ2(r, t))T, which are conjugate to n(r,t), in addition to an adjusted potential field ϕdftl(r, t) similar to that of the equilibrium DFT.37,38 Extending the previous result24,28 to the expression for two-component systems (see Appendix B for details), we have| |  | (A3) |
with the following constraint imposed by the canonical ensemble:| | 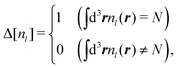 | (A4) |
where the total number of either anions or cations is equally N. The free-energy functional F[n, ϕ] in the exponent of eqn (A3) is defined using the grand potential of the primitive model with an imaginary external field iϕ(r) applied, and can be divided into two parts (see Appendix B for details):| | | F[n, ϕ] = F[n,0] + ΔF[n, ϕ]. | (A5) |
The free-energy functional F[n,0] in the absence of fluctuating potential reduces to the intrinsic Helmholtz free energy, a key thermodynamic quantity in the equilibrium DFT.37,38 It follows that F[n,0] is related to the chemical potential μeq in equilibrium through the following stationary equation:| |  | (A6) |
where a non-equilibrium chemical potential μ0l[n] is a functional of n(r, t) because the external potential distribution φdftl(r, t) is adjusted to identify nl(r, t) with the equilibrium density as is the case with the equilibrium DFT (see Appendix B for details).37,38
Decomposition of the stochastic current given by eqn (A1).
It follows from eqn (A2)–(A6) that| | | μl[n] = μ0l[n] + μδl[n] − μN, | (A7) |
| | 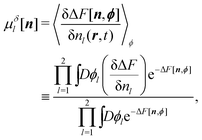 | (A8) |
where μN corresponds to the Lagrange multiplier to enforce the constraint Δ[nl] given by eqn (A4). Correspondingly, the stochastic current Jl(r, t) can be decomposed into three parts:| |  | (A9) |
where eqn (A1), (A7) and (A8) provide| |  | (A10) |
| |  | (A11) |
While the expression (116) indicates that J0l(r, t) is the conventional current used in the deterministic density-functional equation, the additional current Jδl(r, t) is obtained from eqn (A2), (A7) and (A8).
Here we adopt the Ramakrishnan–Yussouf functional38 as the equilibrium free energy F[n, 0], yielding
| |  | (A12) |
with
clm(
r −
r′) denoting the DCF between the
l-th and
m-th ions.
Eqn (A12) yields
J0l(
r,
t) for electric-field-driven electrolytes in the presence of an applied steady potential
Ψ(
r) as well as the interaction potential,
| |  | (A13) |
which is a time-varying potential due to the time dependence of
nm(
r′,
t). Combining
eqn (A10), (A12) and (A13), we have
| |  | (A14) |
where the applied electric field
E ≡ −∇
Ψ(
r) generates, in units of
kBT, an external force (−1)
l−1pE exerted on a cation (
l = 1) or an anion (
l = 2).
Self-energy contribution10,25.
We evaluate the free-energy difference ΔF[n, ϕ] in the Gaussian approximation, or the Gaussian expansion around the equilibrium free-energy functional F[n, 0] with the density distributions being fixed at n(r, t). Namely, ΔF[n, ϕ] is expressed by the quadratic term of fluctuating ϕ-fields:| |  | (A15) |
where the  -matrix is given by
-matrix is given by| | 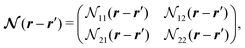 | (A16) |
| |  | (A17) |
using the total correlation functions hlm (r − r′) between the l-th and m-th ions. As detailed in Appendix C, combination of eqn (A8) and (A15) yields eqn (9):| |  | (A18) |
It follows from eqn (A11) and (A18) that| |  | (A19) |
where use has been made of the identity, hll(0) = −1 independent of nl(r, t), in the last equality.
2. Modified Poisson equations given by eqn (14) and (15)
The DCF form given by eqn (12) and (13).
In the modified MSA,43 the DCF is of the following form:| |  | (A20) |
| | | flm(k) = fclm(k) + fhlm(k), | (A21) |
| | fclm(k) = (−1)l+mp2lB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kσ), cos(kσ), | (A22) |
| |  | (A23) |
where flm(k) is separated into two parts, fclm and fhlm. Eqn (A21) reduces to| | flm(k) ≈ fclm(k) = (−1)l+mp2lB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kσ) cos(kσ) | (A24) |
when| | 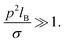 | (A25) |
Namely, the above expression of the DCF given by eqn (12) and (13) is verified in the modified MSA43 under the condition (A25). It is noted that the approximation (A24) applies to the primitive model because fclm(k) represents Coulomb interactions including steric effects.15 The relation (A25) corresponds to the strong-coupling condition for one-component plasma, implying that the strong Coulomb interactions justify the negligibility of fhlm given by eqn (A23). In this paper, we have supposed that, in general, the simplified form (13) applies to aqueous electrolytes if only because of p2lB/σ > 1 (see Section V for a more detailed comparison between the relation (A25) and experimental conditions).
Finite-spread Poisson equation: derivation of eqn (14)13,15,24,39–41.
The two interaction potentials, ψ1(r, t) and ψ2(r, t), have been defined in eqn (A13); however, the approximate form of the DCF given by eqn (13) justifies that| | | ψ(r, t) = ψ1(r, t) = −ψ2(r, t). | (A26) |
Thus, the expression (7) of ψ(r, t) has been verified by eqn (A26), and the approximate form (13) follows the notations of| | | c11(r, t) = c22(r, t) = c(r, t), | (A27) |
| | | c12(r, t) = c21(r, t) = −c(r, t), | (A28) |
thereby leading to the finite-spread Poisson eqn (14).
Higher-order Poisson equation: derivation of eqn (15)5–10,21–24.
We perform the small kσ-expansion of ω(k) in eqn (13), yielding| |  | (A29) |
irrespective of the model forms given by eqn (12). It follows from eqn (7), (8), (12) and (13) that the Fourier transform of the Poisson equation reads| |  | (A30) |
which is further reduced to| |  | (A31) |
in the small kσ-expansion: (1 − k2σ2/2)−1 ≈ 1 + k2σ2/2. The real-space representation of eqn (A31) is the higher-order Poisson eqn (15).
3. Stochastic mPNP currents given by eqn (3) and (30)
Derivation of linear mPNP current given by eqn (30)13–15.
Let νl(r, t) be the density difference:| | νl(r, t) = nl(r, t) − ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) . . | (A34) |
To linearize the self-energy-modified current given by eqn (3), we expand the chemical potential μl around n1(r, t) = n2(r, t) = ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (or q ≡ 0) to the first order in νl(r, t):
(or q ≡ 0) to the first order in νl(r, t):| |  | (A35) |
with μl[![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ] denoting μl[
] denoting μl[![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ] = μl[(
] = μl[(![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ,
, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) )T]. Since we have
)T]. Since we have| |  | (A36) |
neglecting the contribution from the triplet DCF, eqn (A35) simply reads| |  | (A37) |
Combining eqn (3) and (A37), the mPNP current becomes, to the lowest order,| |  | (A38) |
We also note that| | | ∇ρ(r, t) = ∇{ν1(r, t) + ν2(r, t)}, | (A39) |
| | | ∇q(r, t) = ∇{ν1(r, t) − ν2(r, t)}. | (A40) |
Thus, eqn (A38)–(A40) lead to the stochastic currents, Jρ = J1 + J2 and Jq = J1 − J2, given by eqn (30).
4 Equal-time correlation functions given by eqn (43)–(46)
Stationary condition of equal-time correlation matrix.
The compact form (32) of the stochastic equation is solved to obtain13,15| |  | (A41) |
It follows from eqn (5) and (29) that| |  | (A42) |
Plugging eqn (A41) and (A42) into the definition (40) of the equal-time correlation matrix, we have| |  | (149) |
where the relation (A42) generates the following matrix:| |  | (A44) |
It has been shown that the stationary condition 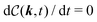 for the expression (A43) reads13,15
for the expression (A43) reads13,15| | 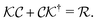 | (A45) |
The four matrix elements of  , or the four kinds of correlation functions in eqn (40), can be determined by four simultaneous equations arising from the above stationary condition (A45) (see Appendix D for details).
, or the four kinds of correlation functions in eqn (40), can be determined by four simultaneous equations arising from the above stationary condition (A45) (see Appendix D for details).
Density–density and charge–charge correlation functions at equal times: derivation scheme of eqn (43)–(48).
We are concerned with the stationary density–density and charge–charge correlation functions at equal times,  and
and  , among the matrix elements of
, among the matrix elements of  . As detailed in Appendix D, the solution to eqn (A45) reads
. As detailed in Appendix D, the solution to eqn (A45) reads| |  | (A46) |
where 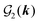 has been defined in eqn (45), and the matrix elements of
has been defined in eqn (45), and the matrix elements of  is given by
is given by| | 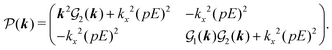 | (A47) |
Obviously, eqn (A46) and (A47) transform to eqn (43)–(48).
Appendix B. Details on the constrained free energy  of a given density distribution n(r, t)
of a given density distribution n(r, t)
We consider the overdamped dynamics of ions with the total number N of charged spheres being fixed. Hence, the constrained free-energy functional  of a given density distribution nl(r, t) (l = 1,2) is defined for the canonical ensemble using the contour integral over a complex variable w = eμ:28
of a given density distribution nl(r, t) (l = 1,2) is defined for the canonical ensemble using the contour integral over a complex variable w = eμ:28| |  | (B1) |
| |  | (B2) |
| |  | (B3) |
In eqn (B1), the Dirac delta functional represents the constraint on the original density distribution 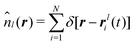 . It has been shown for one-component fluid that the constrained free energy functional is expressed by the functional integral over a fluctuating potential field. Similarly, we have
. It has been shown for one-component fluid that the constrained free energy functional is expressed by the functional integral over a fluctuating potential field. Similarly, we have| | 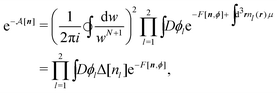 | (B4) |
where| |  | (B5) |
and the superscript “dft” denotes the equilibrium DFT37 according to which the external field φdftl(r) is used for ensuring that the equilibrium density found from the grand potential Ω[φ] is equated with nl(r):| | 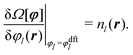 | (B6) |
The free-energy functional F[n, 0] in the absence of fluctuating ϕ-field corresponds to the intrinsic Helmholtz free energy that is related to the grand potential Ω[φdft] through the Legendre transform using the external field φdftl(r):| |  | (B7) |
as well as the equilibrium DFT.
Appendix C. Derivation of μδl given by eqn (A18)
Let us introduce the potential–potential correlation matrix Φ that represents the set of potential–potential correlation functions defined by| |  | (C1) |
| |  | (C2) |
where 〈Φlm(r − r′)〉ϕ is related to the DCF function clm(r − r′) as| |  | (C3) |
The average, 〈ϕl(r)ϕm(r′)〉ϕ, has been performed over the fluctuating potential field as| |  | (C4) |
following the expression (A8). Hence, eqn (C4) yields eqn (C3) as far as the Gaussian functional form (A15) for ΔF[n, ϕ] is concerned. It is found from eqn (A17) and (C3) that the Ornstein–Zernike equations for two-component liquids read| |  | (C5) |
indicating that the Fourier-transformed matrix Φ(−k) is the inverse of density–density correlation matrix  .
.
Considering that  for the density–density correlation function
for the density–density correlation function  defined by eqn (A17), eqn (A15) leads to
defined by eqn (A17), eqn (A15) leads to
| |  | (C6) |
To evaluate the above functional derivatives, we introduce the following notations: it follows from
eqn (A17) that
| |  | (C7) |
with which we have
| |  | (C8) |
using
Φ(1)lm, a derivative of
Φlm, defined by
eqn (C7) and (C8). At the same time, it is also useful to consider the following functional derivative:
| |  | (C9) |
where use has been made of the expression
(C3) in the last two equalities.
The unknown functional 〈Φ(1)lm〉ϕ is related to 〈Φlm〉(1)ϕ, given by eqn (C9), as
| |  | (C10) |
stating that 〈
Φ(1)lm〉
ϕ can be equated with 〈
Φlm〉
(1)ϕ in the approximation of 〈
AB〉
ϕ ≈ 〈
A〉
ϕ〈
B〉
ϕ for
A =
Φlm and
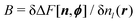
. Thus, we obtain
| |  | (C11) |
from plugging
eqn (C9) and (C10) into the second term in the last line of
eqn (C8).
Meanwhile, we have
| |  | (C12) |
Hence, the combination of
eqn (C11) and (C12) gives
| |  | (C13) |
and
| | 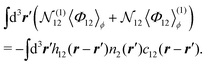 | (C14) |
Considering the Ornstein–Zernike equation,
| |  | (C15) |
the sum of
eqn (C13) and (C14) leads to
| |  | (C16) |
Thus, the resulting form
(A18) of
μδl has been verified.
Appendix D. Solving the steady-state eqn (A45)
We calculate the matrix elements of  and
and  , using a simplified form of
, using a simplified form of| |  | (D1) |
with α = k2, 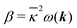 and
and 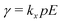 . It follows that
. It follows that| | 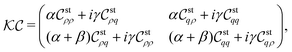 | (D2) |
| |  | (D3) |
The sum of eqn (D2) and (D3) provides the steady-state eqn (A45) which consists of the four kinds of equations for correlation functions as follows:| | 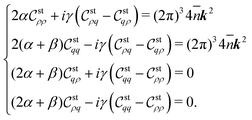 | (D4) |
It is easy to find from the last two equations of the above set that 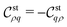 and
and| |  | (D5) |
Substituting eqn (D5) into the first two equations of eqn (D4), we have| |  | (D6) |
which reads| |  | (D7) |
and| |  | (D8) |
In the matrix elements, we note that  and
and  . Hence, the above expressions (D7) and (D8) are found to be equivalent to eqn (A46) and (A47).
Eqn (43)–(46) are combined into a single form,
. Hence, the above expressions (D7) and (D8) are found to be equivalent to eqn (A46) and (A47).
Eqn (43)–(46) are combined into a single form,| | 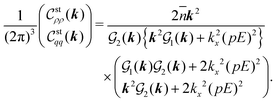 | (D9) |
The three propagators,  ,
,  and
and  , can be simply approximated by
, can be simply approximated by 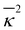 when considering the small wavevector region of
when considering the small wavevector region of  at a moderate field strength of
at a moderate field strength of  . This approximation allows eqn (D9) to be reduced to
. This approximation allows eqn (D9) to be reduced to| |  | (D10) |
whose rearrangement leads to eqn (49).
The discriminant analysis of eqn (87) provides the determining equation for the Debye–Hückel length  on the Kirkwood crossover:
on the Kirkwood crossover:| |  | (E1) |
with  . Eqn (87) reads the following quadratic equation,
. Eqn (87) reads the following quadratic equation,| |  | (E2) |
for  . The solution X to eqn (E2) is
. The solution X to eqn (E2) is| |  | (E3) |
At a low field strength of  , the numerator on the rhs of eqn (E3) is approximated by
, the numerator on the rhs of eqn (E3) is approximated by| |  | (E4) |
whereas we have| |  | (E5) |
for the high field strength of  . While the approximate form (E4) of the numerator results in the expression (89), the limiting result (90) is valid due to eqn (E5).
. While the approximate form (E4) of the numerator results in the expression (89), the limiting result (90) is valid due to eqn (E5).
Acknowledgements
The author thanks the anonymous referees for their valuable comments and suggestions.
References
-
(a) Y. Levin, Rep. Prog. Phys., 2002, 65, 1577 CrossRef CAS;
(b)
D. Andelman, Introduction to Electrostatics in Soft and Biological Matter, in Soft Condensed Matter Physics in Molecular and Cell Biology, ed. W. C. K. Poon and D. Andelman, CRC Press, 2006 Search PubMed.
-
(a)
H. Bruus, Theoretical Microfluidics, Oxford University Press, Oxford, 2007 Search PubMed;
(b) R. B. Schoch, J. Han and P. Renaud, Rev. Mod. Phys., 2008, 80, 839 CrossRef CAS;
(c) L. Bocquet and E. Charlaix, Chem. Soc. Rev., 2010, 39, 1073–1095 RSC.
-
(a) H. Weingärtner, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef PubMed;
(b) M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036 CrossRef CAS PubMed;
(c) R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS PubMed.
-
(a) C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, Chem. Soc. Rev., 2015, 44, 7484–7539 RSC;
(b) T. M. Gür, Energy Environ. Sci., 2018, 11, 2696–2767 RSC.
-
(a) M. S. Kilic, M. Z. Bazant and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 02150 Search PubMed;
(b) B. D. Storey and M. Z. Bazant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 056303 CrossRef PubMed;
(c) T. R. Ferguson and M. Z. Bazant, J. Electrochem. Soc., 2012, 159, A1967 CrossRef CAS;
(d) M. Schmuck and M. Z. Bazant, SIAM J. Appl. Math., 2015, 75, 1369–1401 CrossRef;
(e) J. P. de Souza, C. M. Chow, R. Karnik and M. Z. Bazant, Phys. Rev. E, 2021, 104, 044802 CrossRef CAS PubMed.
-
(a) D. Gillespie, W. Nonner and R. S. Eisenberg, J. Phys.: Condens. Matter, 2002, 14, 12129 CrossRef CAS;
(b) B. Eisenberg, Y. Hyon and C. Liu, J. Chem. Phys., 2010, 133, 104104 CrossRef PubMed;
(c) T. L. Horng, T. C. Lin, C. Liu and B. Eisenberg, J. Phys. Chem. B, 2012, 116, 11422–11441 CrossRef CAS PubMed;
(d) J. L. Liu and B. Eisenberg, J. Chem. Phys., 2014, 141, 12B640_1 Search PubMed;
(e) J. L. Liu and B. Eisenberg, Entropy, 2020, 22, 550 CrossRef CAS PubMed.
-
(a) B. Corry, S. Kuyucak and S. H. Chung, Biophys. J., 2000, 78, 2364–2381 CrossRef CAS PubMed;
(b) B. Corry, S. Kuyucak and S. H. Chung, Biophys. J., 2003, 84, 3594–3606 CrossRef CAS PubMed;
(c) Q. Zheng and G. W. Wei, J. Chem. Phys., 2011, 134, 194101 CrossRef PubMed;
(d) C. Maffeo, S. Bhattacharya, J. Yoo, D. Wells and A. Aksimentiev, Chem. Rev., 2012, 112, 6250–6284 CrossRef CAS PubMed.
-
(a) A. Yochelis, J. Phys. Chem. C, 2014, 118, 5716–5724 CrossRef CAS;
(b) N. Gavish, D. Elad and A. Yochelis, J. Phys., Lett., 2018, 9, 36–42 CAS.
-
(a) M. Burger, B. Schlake and M. T. Wolfram, Nonlinearity, 2012, 25, 961 CrossRef;
(b) A. A. Lee, S. Kondrat, D. Vella and A. Goriely, Phys. Rev. Lett., 2015, 115, 106101 CrossRef PubMed;
(c) C. Wang, J. Bao, W. Pan and X. Sun, Electrophoresis, 2017, 38, 1693–1705 CrossRef CAS PubMed;
(d) S. Fleischmann, J. B. Mitchell, R. Wang, C. Zhan, D. E. Jiang, V. Presser and V. Augustyn, Chem. Rev., 2020, 120, 6738–6782 CrossRef CAS PubMed;
(e) S. H. Amrei, G. H. Miller, K. J. Bishop and W. D. Ristenpart, Soft Matter, 2020, 16, 7052–7062 RSC;
(f) M. Schammer, B. Horstmann and A. Latz, J. Electrochem. Soc., 2021, 168, 026511 CrossRef CAS;
(g) A. Gupta, P. J. Zuk and H. A. Stone, Phys. Rev. Lett., 2020, 125, 076001 CrossRef CAS PubMed;
(h) F. Henrique, P. J. Zuk and A. Gupta, Soft Matter, 2022, 18, 198–213 RSC.
-
(a) Z. Xu, M. Ma and P. Liu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 013307 CrossRef PubMed;
(b) P. Liu, X. Ji and Z. Xu, SIAM J. Appl. Math., 2018, 78, 226–245 CrossRef;
(c) M. Ma, Z. Xu and L. Zhang, SIAM J. Appl. Math., 2021, 81, 1645–1667 CrossRef;
(d) M. Ma, Z. Xu and L. Zhang, Phys. Rev. E, 2021, 104, 035307 CrossRef CAS PubMed.
- M. te Vrugt, H. Löwen and R. Wittkowski, Adv. Phys., 2020, 69, 121–247 CrossRef.
-
(a) U. M.-B. Marconi, S. Melchionna and I. Pagonabarraga, J. Chem. Phys., 2013, 138, 244107 CrossRef PubMed;
(b) J. Jiang, D. Cao, D. E. Jiang and J. Wu, J. Phys.: Condens. Matter, 2014, 26, 284102 CrossRef PubMed;
(c) C. Zhan, C. Lian, Y. Zhang, M. W. Thompson, Y. Xie, J. Wu, P. R.-C. Kent, P. T. Cummings, D. Jiang and D. J. Wesolowski, Adv. Sci., 2017, 4, 1700059 CrossRef PubMed;
(d) H. Gao and C. Xiao, Europhys. Lett., 2018, 124, 58002 CrossRef;
(e) S. Babel, M. Eikerling and H. Löowen, J. Phys. Chem. C, 2018, 122, 21724–21734 CrossRef CAS.
-
(a) V. Démery and D. S. Dean, J. Stat. Mech.: Theo. Exp., 2016, 2016, 023106 CrossRef;
(b) A. Poncet, O. Bénichou, V. Démery and G. Oshanin, New J. Phys., 2017, 118, 118002 Search PubMed.
-
(a) S. Mahdisoltani and R. Golestanian, Phys. Rev. Lett., 2021, 126, 158002 CrossRef CAS PubMed;
(b) S. Mahdisoltani and R. Golestanian, New J. Phys., 2021, 23, 073034 CrossRef.
- Y. Avni, R. M. Adar, D. Andelman and H. Orland, Phys. Rev. Lett., 2022, 128, 098002 CrossRef CAS PubMed.
-
(a) J. P. Péraud, A. J. Nonaka, J. B. Bell, A. Donev and A. L. Garcia, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10829–10833 CrossRef PubMed;
(b) A. Donev, A. J. Nonaka, C. Kim, A. L. Garcia and J. B. Bell, Phys. Rev. Fluids, 2019, 4, 043701 CrossRef;
(c) A. Donev, A. L. Garcia, J. P. Péraud, A. J. Nonaka and J. B. Bell, Curr. Opin. Electrochem., 2019, 13, 1–10 CrossRef CAS.
-
(a) J. Chakrabarti, J. Dzubiella and H. Löwen, Phys. Rev. E: Stat.,
Nonlinear, Soft Matter Phys., 2004, 70, 012401 CrossRef CAS PubMed;
(b) H. Löwen, Soft Matter, 2010, 6, 3133–3142 RSC.
-
(a) T. Vissers, A. van Blaaderen and A. Imhof, Phys. Rev. Lett., 2011, 106, 228303 CrossRef PubMed;
(b) M. Ikeda, H. Wada and H. Hayakawa, Europhys. Lett., 2012, 99, 68005 CrossRef CAS;
(c) K. Klymko, P. L. Geissler and S. Whitelam, Phys. Rev. E, 2016, 94, 022608 CrossRef PubMed;
(d) C. Reichhardt and C. J.-O. Reichhardt, Soft Matter, 2018, 14, 490–498 RSC;
(e) B. Li, Y. L. Wang, G. Shi, Y. Gao, X. Shi, C. E. Woodward and J. Forsman, ACS Nano, 2021, 15, 2363–2373 CrossRef CAS PubMed.
-
(a) M. A. Gebbie, H. A. Dobbs, M. Valtiner and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7432–7437 CrossRef CAS PubMed;
(b) A. A. Lee, D. Vella, S. Perkin and A. Goriely, J. Phys. Chem. Lett., 2015, 6, 159–163 CrossRef CAS PubMed;
(c) A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed;
(d) M. A. Gebbie, A. M. Smith, H. A. Dobbs, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Chem. Commun., 2017, 53, 1214–1224 RSC;
(e) A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Phys. Rev. Lett., 2017, 119, 026002 CrossRef PubMed;
(f) P. Gaddam and W. Ducker, Langmuir, 2019, 35, 5719–5727 CrossRef CAS PubMed;
(g) C. S. Perez-Martinez and S. Perkin, Soft Matter, 2019, 15, 4255–4265 RSC.
-
(a) G. Feng, M. Chen, S. Bi, Z. A. Goodwin, E. B. Postnikov, N. Brilliantov, M. Urbakh and A. A. Kornyshev, Phys. Rev. X, 2019, 9, 021024 CAS;
(b) N. Anousheh, F. J. Solis and V. Jadhao, AIP Adv., 2020, 10, 125312 CrossRef CAS;
(c) S. W. Coles, C. Park, R. Nikam, M. Kanduc, J. Dzubiella and B. Rotenberg, J. Phys. Chem. B, 2020, 124, 1778–1786 CAS;
(d) J. Zeman, S. Kondrat and C. Holm, Chem. Commun., 2020, 56, 15635–15638 RSC;
(e) J. Zeman, S. Kondrat and C. Holm, J. Chem. Phys., 2021, 155, 204501 CrossRef CAS PubMed;
(f) E. Krucker-Velasquez and J. W. Swan, J. Chem. Phys., 2021, 155, 134903 CrossRef CAS PubMed.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102 CrossRef PubMed.
-
(a) R. P. Misra, J. P. de Souza, D. Blankschtein and M. Z. Bazant, Langmuir, 2019, 35, 11550–11565 CrossRef CAS PubMed;
(b) J. P. de Souza, Z. A.-H. Goodwin, M. McEldrew, A. A. Kornyshev and M. Z. Bazant, Phys. Rev. Lett., 2020, 125, 116001 CrossRef CAS PubMed;
(c) J. P. de Souza and M. Z. Bazant, J. Phys. Chem. C, 2020, 124, 11414–11421 CrossRef CAS.
-
(a) S. Buyukdagli and R. Blossey, J. Phys.: Condens. Matter, 2016, 28, 343001 CrossRef CAS PubMed;
(b) R. Blossey, A. C. Maggs and R. Podgornik, Phys. Rev. E, 2017, 95, 060602 CrossRef CAS PubMed;
(c) C. D. Santangelo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041512 CrossRef PubMed;
(d) M. M. Hatlo and L. Lue, Soft Matter, 2009, 5, 125–133 RSC;
(e) M. M. Hatlo and L. Lue, Europhys. Lett., 2010, 89, 25002 CrossRef;
(f) T. Xiao and X. Song, J. Phys. Chem. A, 2021, 125, 2173–2183 CrossRef CAS PubMed.
-
H. Frusawa, J. Stat. Mech.: Theory Exp., 2021, 2021, 013213 Search PubMed.
-
(a) Z. G. Wang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021501 CrossRef PubMed;
(b) M. Ma and Z. Xu, J. Chem. Phys., 2014, 141, 244903 CrossRef PubMed;
(c) R. Wang and Z. G. Wang, J. Chem. Phys., 2015, 142, 104705 CrossRef PubMed;
(d) R. Wang and Z. G. Wang, J. Chem. Phys., 2016, 144, 134902 CrossRef PubMed;
(e) H. Frusawa, Phys. Rev. E, 2020, 101, 012121 CrossRef CAS PubMed.
-
(a) T. Munakata, J. Phys. Soc. Jpn., 1989, 58, 2434–2438 CrossRef;
(b) K. Kawasaki, Physica A, 1994, 208, 35–64 CrossRef;
(c) D. S. Dean, J. Phys. A: Math. Gen., 1996, 29, L613 CrossRef CAS;
(d) H. Frusawa and R. Hayakawa, J. Phys. A: Math. Gen., 2000, 33, L155 CrossRef;
(e) V. Démery, O. Bénichou and H. Jacquin, New J. Phys., 2014, 16, 053032 CrossRef;
(f) P. H. Chavanis, Entropy, 2019, 21, 1006 CrossRef.
-
(a) T. Leonard, B. Lander, U. Seifert and T. Speck, J. Chem. Phys., 2013, 139, 204109 CrossRef CAS PubMed;
(b) H. Jacquin, B. Kim, K. Kawasaki and F. van Wijland, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022130 CrossRef PubMed;
(c) N. Bidhoodi and S. P. Das, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 012325 CrossRef PubMed;
(d) D. S. Dean, B. S. Lu, A. C. Maggs and R. Podgornik, Phys. Rev. Lett., 2016, 116, 240602 CrossRef PubMed;
(e) M. Krüger and D. S. Dean, J. Chem. Phys., 2017, 146, 134507 CrossRef PubMed;
(f) J. F. Lutsko, Sci. Adv., 2019, 5, eaav7399 CrossRef CAS PubMed;
(g) L. Tociu, É. Fodor, T. Nemoto and S. Vaikuntanathan, Phys. Rev. X, 2019, 9, 4 Search PubMed.
-
(a) H. Frusawa, J. Phys. A: Math. Theor., 2019, 52, 065003 CrossRef CAS;
(b) H. Frusawa, Entropy, 2020, 22, 34 CrossRef PubMed;
(c) H. Frusawa, Soft Matter, 2021, 17, 8810–8831 RSC.
-
(a) B. Rotenberg, O. Bernard and J. P. Hansen, J. Phys.: Condens. Matter, 2018, 30, 054005 CrossRef PubMed;
(b) F. Coupette, A. A. Lee and A. Härtel, Phys. Rev. Lett., 2018, 121, 075501 CrossRef CAS PubMed;
(c) R. Kjellander, Soft Matter, 2019, 15, 5866–5895 CAS;
(d) R. Kjellander, Phys. Chem. Chem. Phys., 2020, 22, 23952–23985 RSC;
(e) C. W. Outhwaite and L. B. Bhuiyan, J. Chem. Phys., 2021, 155, 014504 CrossRef CAS PubMed;
(f)
A. Ciach and O. Patsahan, 2021, arXiv preprint, arXiv:2102.00878.
-
(a) R. M. Adar, S. A. Safran, H. Diamant and D. Andelman, Phys. Rev. E, 2019, 100, 042615 CrossRef CAS PubMed;
(b) Y. Avni, R. M. Adar and D. Andelman, Phys. Rev. E, 2020, 101, 010601 CrossRef CAS PubMed.
- P. Cats, R. Evans, A. Härtel and R. van Roij, J. Chem. Phys., 2021, 154, 124504 CrossRef CAS PubMed.
- J. G. Kirkwood and J. C. Poirier, J. Phys. Chem., 1954, 58, 591–596 CrossRef CAS.
-
(a) P. Attard, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1993, 48, 3604 CrossRef CAS PubMed;
(b) J. Ennis, R. Kjellander and D. J. Mitchell, J. Chem. Phys., 1995, 102, 975 CrossRef CAS;
(c) B. P. Lee and M. E. Fisher, Europhys. Lett., 1997, 39, 611 CrossRef CAS;
(d) O. Patsahan and A. Ciach, J. Phys.: Condens. Matter, 2007, 19, 236203 CrossRef;
(e) J. Janecek and R. R. Netz, J. Chem. Phys., 2009, 130, 074502 CrossRef PubMed.
- P. B. Warren and A. Vlasov, J. Chem. Phys., 2014, 140, 084904 CrossRef PubMed.
-
(a) P. B. Warren, A. Vlasov, L. Anton and A. J. Masters, J. Chem. Phys., 2013, 138, 204907 CrossRef PubMed;
(b) D. Frydel, J. Chem. Phys., 2016, 145, 184703 CrossRef PubMed;
(c) D. Frydel and M. Ma, Phys. Rev. E, 2016, 93, 062112 CrossRef PubMed.
-
(a) R. J.-F. Leote de Carvalho and R. Evans, Mol. Phys., 1994, 83, 619–654 CrossRef;
(b) A. J. Archer, D. Pini, R. Evans and L. Reatto, J. Chem. Phys., 2007, 126, 014104 CrossRef CAS PubMed.
-
(a) R. Evans, Adv. Phys., 1979, 28, 143–200 CrossRef CAS;
(b) J. Wu, AIChE J., 2006, 52, 1169–1193 CrossRef CAS;
(c) J. Wu and Z. Li, Annu. Rev. Phys. Chem., 2007, 58, 85–112 CrossRef CAS PubMed.
- T. V. Ramakrishnan and M. Yussouff, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 2775 CrossRef CAS.
- D. Frydel, Adv. Chem. Phys., 2016, 160, 209–260 CrossRef CAS.
-
(a) Y. G. Chen, C. Kaur and J. D. Weeks, J. Phys. Chem. B, 2004, 108, 19874 CrossRef CAS;
(b) Y. G. Chen and J. D. Weeks, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7560 CrossRef CAS PubMed.
-
(a) H. Frusawa, Phys. Rev. E, 2018, 98, 052130 CrossRef CAS;
(b) N. V. Brilliantov, J. M. Rubí and Y. A. Budkov, Phys. Rev. E, 2020, 101, 042135 CrossRef CAS PubMed;
(c) Y. A. Budkov, Phys. Chem. Chem. Phys., 2020, 22, 14756–14772 RSC.
- K. C. Ng, J. Chem. Phys., 1974, 61, 2680 CrossRef CAS.
-
(a) L. M. Varela, M. Perez-Rodriguez, M. Garcia, F. Sarmiento and V. Mosquera, J. Chem. Phys., 1999, 111, 10986–10997 CrossRef CAS;
(b) L. M. Varela, M. Garcia and V. Mosquera, Phys. Rep., 2003, 382, 1–111 CrossRef CAS;
(c) L. M. Varela, M. Perez-Rodriguez, M. Garcia, F. Sarmiento and V. Mosquera, J. Chem. Phys., 1998, 109, 1930–1938 CrossRef CAS.
- M. E. Fisher and B. Wiodm, J. Chem. Phys., 1969, 50, 3756–3772 CrossRef CAS.
- H. Frusawa, Entropy, 2022, 24, 500 CrossRef PubMed.
-
(a) T. Singh and A. Kumar, J. Phys. Chem. B, 2008, 112, 12968–12972 CrossRef CAS PubMed;
(b) A. Rybinska-Fryca, A. Sosnowska and T. Puzyn, J. Mol. Liq., 2018, 260, 57–64 CrossRef CAS.
-
(a) R. Shi and Y. Wang, J. Phys. Chem. B, 2013, 117, 5102–5112 CrossRef CAS PubMed;
(b) Y. L. Wang, B. Li, S. Sarman, F. Mocci, Z. Y. Lu, J. Yuan, A. Laaksonen and M. D. Fayer, Chem. Rev., 2020, 120, 5798–5877 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article

![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ξ(1)Decayvs. σ/ξDH =
ξ(1)Decayvs. σ/ξDH = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ where ξDH =
σ where ξDH = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) −1 denotes the smeared Debye–Hückel screening length defined by eqn (36). Our numerical results of ξ(1)Decay will be given in Fig. 3 and 8. In Fig. 2, these are shown using the solid brown lines terminated at nodes A and B, and the dashed green arrow from node A to node B, or from the Kirkwood crossover at E = 0 to that under electric field (E ≠ 0). While the solid brown line terminated at node A (E = 0) converges to ξ(1)Decay/ξDH = 1 in the dilute limit, the solid brown line terminated at node B (E ≠ 0) approaches zero in the dilute limit because of the finite decay length ξ(1)Decay = (pE)−1 (see also a discussion given at the end of Section IIIA). As illustrated by the upper inset, the green vertical line through node B marks
−1 denotes the smeared Debye–Hückel screening length defined by eqn (36). Our numerical results of ξ(1)Decay will be given in Fig. 3 and 8. In Fig. 2, these are shown using the solid brown lines terminated at nodes A and B, and the dashed green arrow from node A to node B, or from the Kirkwood crossover at E = 0 to that under electric field (E ≠ 0). While the solid brown line terminated at node A (E = 0) converges to ξ(1)Decay/ξDH = 1 in the dilute limit, the solid brown line terminated at node B (E ≠ 0) approaches zero in the dilute limit because of the finite decay length ξ(1)Decay = (pE)−1 (see also a discussion given at the end of Section IIIA). As illustrated by the upper inset, the green vertical line through node B marks  , or the onset of shifted Kirkwood crossover from a uniform state to a stripe state without consideration of lane formation.17,18 For comparison, we add the dashed blue line to show underscreening behavior in concentrated electrolytes without applied electric field beyond the conventional Kirkwood crossover indicated by the blue vertical line through node A; this blue line represents
, or the onset of shifted Kirkwood crossover from a uniform state to a stripe state without consideration of lane formation.17,18 For comparison, we add the dashed blue line to show underscreening behavior in concentrated electrolytes without applied electric field beyond the conventional Kirkwood crossover indicated by the blue vertical line through node A; this blue line represents  , which is the conventional Kirkwood crossover value32–36 in the range of 1.0 to 1.2 for symmetric electrolytes. Recent studies20,29–31 have demonstrated that ξ(1)Decay/ξDH ∼ (σ/ξDH)χ with the exponent of χ > 1 in a damped oscillatory state. It will be seen from Fig. 3(b) and 8(b) that a similar scaling relation holds for the dashed green arrow.
, which is the conventional Kirkwood crossover value32–36 in the range of 1.0 to 1.2 for symmetric electrolytes. Recent studies20,29–31 have demonstrated that ξ(1)Decay/ξDH ∼ (σ/ξDH)χ with the exponent of χ > 1 in a damped oscillatory state. It will be seen from Fig. 3(b) and 8(b) that a similar scaling relation holds for the dashed green arrow.

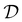 and μl[n] denote, respectively, the diffusion constant and the chemical potential as a functional of n(r, t) = (n1(r, t), n2(r, t))T, and ζ(r, t) represents an uncorrelated Gaussian noise field defined below. Incidentally, we have neglected an advection term,15,16nl(r, t)u(r, t), on the right hand side (rhs) of eqn (3) with u(r, t) denoting the solvent velocity field to satisfy the incompressibility condition ∇·u = 0; this approximation is equivalent to supposing that
and μl[n] denote, respectively, the diffusion constant and the chemical potential as a functional of n(r, t) = (n1(r, t), n2(r, t))T, and ζ(r, t) represents an uncorrelated Gaussian noise field defined below. Incidentally, we have neglected an advection term,15,16nl(r, t)u(r, t), on the right hand side (rhs) of eqn (3) with u(r, t) denoting the solvent velocity field to satisfy the incompressibility condition ∇·u = 0; this approximation is equivalent to supposing that 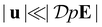 .
.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nl(r, t) + Ul[n],
nl(r, t) + Ul[n],
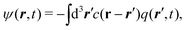



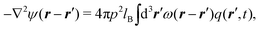



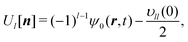




 . Our achievement in terms of the theoretical formalism is essentially to validate eqn (27).
. Our achievement in terms of the theoretical formalism is essentially to validate eqn (27).

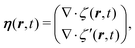

![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) of cations or anions. We insert the expression (30) into the conservation equation for ρ(r, t) and q(r, t):
of cations or anions. We insert the expression (30) into the conservation equation for ρ(r, t) and q(r, t):


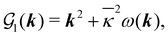
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) k2ψ(k) = −8πp2lB
k2ψ(k) = −8πp2lB![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ω(k)q(−k) = −
ω(k)q(−k) = −![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 2ω(k)q(−k),
2ω(k)q(−k),![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) −1 ≡ (8πp2lB
−1 ≡ (8πp2lB![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) )−1/2,
)−1/2,
 and
and  are the target correlation functions. To be precise,
are the target correlation functions. To be precise,  is the charge–charge correlation function, according to the definition of eqn (8). For brevity, however, we will refer to
is the charge–charge correlation function, according to the definition of eqn (8). For brevity, however, we will refer to  as the charge–charge correlation function.
as the charge–charge correlation function.





 , signified by
, signified by  , reads
, reads
 and
and  have identical poles under the external electric field E.
have identical poles under the external electric field E.

 into two parts:
into two parts: 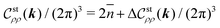 where
where

![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) −1 ≪ 1 (see Appendix D for the derivation). It should be noted that eqn (49) agrees with the expression previously obtained in a different manner14 and that the Fourier transform of eqn (49) has been demonstrated to provide anisotropic long-range correlation functions exhibiting a power-law behavior with a dipolar character.14 At low field strength of pE
−1 ≪ 1 (see Appendix D for the derivation). It should be noted that eqn (49) agrees with the expression previously obtained in a different manner14 and that the Fourier transform of eqn (49) has been demonstrated to provide anisotropic long-range correlation functions exhibiting a power-law behavior with a dipolar character.14 At low field strength of pE![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) −1 ≪ 1, eqn (49) converges to
−1 ≪ 1, eqn (49) converges to
 given by eqn (50) satisfies not only the electroneutrality but also the Stillinger–Lovett second-moment condition.
given by eqn (50) satisfies not only the electroneutrality but also the Stillinger–Lovett second-moment condition.
 and
and  , especially focusing on the high wavenumber in the external field direction. While Section IIIA provides the pole equations of the correlation functions, Section IIIB clarifies the electric-field-induced oscillations when considering the solutions to the pole eqn (66), or an anisotropic crossover from monotonic to oscillatory decay of correlations along the direction of applied electric field. Before going into the numerical details of the results obtained from the pole eqn (66), Section IIIC aims to understand the relationship between the Kirkwood crossover at E = 0 and E ≠ 0 using Fig. 2, a schematic plot of the decay length ξ(1)Decay. After presenting the schematic summary, Section IIID explains how the crossover point is determined in the anisotropic approximation of the pole eqn (66). In the anisotropic approximation (53), we can analytically investigate the electric-field-induced Kirkwood crossover (see Section IV for details). Fig. 3 in Section IIID gives the numerical results on the E-dependencies of both the decay length
, especially focusing on the high wavenumber in the external field direction. While Section IIIA provides the pole equations of the correlation functions, Section IIIB clarifies the electric-field-induced oscillations when considering the solutions to the pole eqn (66), or an anisotropic crossover from monotonic to oscillatory decay of correlations along the direction of applied electric field. Before going into the numerical details of the results obtained from the pole eqn (66), Section IIIC aims to understand the relationship between the Kirkwood crossover at E = 0 and E ≠ 0 using Fig. 2, a schematic plot of the decay length ξ(1)Decay. After presenting the schematic summary, Section IIID explains how the crossover point is determined in the anisotropic approximation of the pole eqn (66). In the anisotropic approximation (53), we can analytically investigate the electric-field-induced Kirkwood crossover (see Section IV for details). Fig. 3 in Section IIID gives the numerical results on the E-dependencies of both the decay length 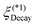 and the smeared Debye–Hückel length
and the smeared Debye–Hückel length  at the Kirkwood crossover points. Last, Section IIIE presents various results on the 2D inverse Fourier transforms of
at the Kirkwood crossover points. Last, Section IIIE presents various results on the 2D inverse Fourier transforms of  . We will see anisotropic density–density correlations reflecting the emergence of stripe states in a high-density region above the Kirkwood crossover.
. We will see anisotropic density–density correlations reflecting the emergence of stripe states in a high-density region above the Kirkwood crossover.

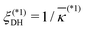 and the decay length
and the decay length  at the Kirkwood crossover are shown by the plot of
at the Kirkwood crossover are shown by the plot of 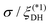 and
and  against pEσ, an energetic measure of electric field strength in units of kBT. While the solid lines represent
against pEσ, an energetic measure of electric field strength in units of kBT. While the solid lines represent  , the dashed lines
, the dashed lines  . The related equations are as follows: green solid line (eqn (99)); green dashed line (eqn (102)); red solid and dashed lines (eqn (105) and (106)). (b) A log–log plot of
. The related equations are as follows: green solid line (eqn (99)); green dashed line (eqn (102)); red solid and dashed lines (eqn (105) and (106)). (b) A log–log plot of 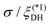 -dependencies of
-dependencies of  . The dotted line, as a guide to the eye, indicates a scaling relation
. The dotted line, as a guide to the eye, indicates a scaling relation  .
.
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 2ω(k(2)) = 0,
2ω(k(2)) = 0,![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 2 allows us to have complex solutions to the pole eqn (51) and (52), other than purely imaginary solutions. The appearance of real solutions corresponds to the onset of oscillatory correlations. Hence, we find that eqn (51) and (52), which are equally valid for density–density and charge–charge correlations, lead to simultaneous emergence of density and charge oscillations. It is striking that the correlation function analysis directly predicts the electric-field-induced synchronization between the emergences of density and charge oscillations. The simultaneous occurrence of crossovers is in contrast to equilibrium crossover phenomena which emerge separately: the equilibrium density–density and charge–charge correlation functions exhibit the Fisher–Widom31,36,44 and Kirkwood31–36 crossovers, respectively.
2 allows us to have complex solutions to the pole eqn (51) and (52), other than purely imaginary solutions. The appearance of real solutions corresponds to the onset of oscillatory correlations. Hence, we find that eqn (51) and (52), which are equally valid for density–density and charge–charge correlations, lead to simultaneous emergence of density and charge oscillations. It is striking that the correlation function analysis directly predicts the electric-field-induced synchronization between the emergences of density and charge oscillations. The simultaneous occurrence of crossovers is in contrast to equilibrium crossover phenomena which emerge separately: the equilibrium density–density and charge–charge correlation functions exhibit the Fisher–Widom31,36,44 and Kirkwood31–36 crossovers, respectively.
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ ≤
σ ≤ ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*j)σ,
(*j)σ,![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ and
(*1)σ and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*2)σ, respectively. It can be readily seen from eqn (52) that
(*2)σ, respectively. It can be readily seen from eqn (52) that ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*2)σ is independent of E but is larger than the conventional Kirkwood crossover value32–36 in the range of 1.0 <
(*2)σ is independent of E but is larger than the conventional Kirkwood crossover value32–36 in the range of 1.0 < ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) *σ <1.2 for symmetric electrolytes in equilibrium where the pole equation is k2 + (
*σ <1.2 for symmetric electrolytes in equilibrium where the pole equation is k2 + (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) *)2ω(k) = 0: it follows from eqn (52) that
*)2ω(k) = 0: it follows from eqn (52) that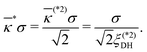
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ depends on E and is smaller than the above Kirkwood crossover value at E = 0 due to additional screening effect measured by pE.
(*1)σ depends on E and is smaller than the above Kirkwood crossover value at E = 0 due to additional screening effect measured by pE.
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 2 + (pE)2 = 0,
2 + (pE)2 = 0,![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 2 = 0,
2 = 0,![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) → 0, eqn (56) yields a finite decay length ξ(1)Decay ≈ (pE)−1 (see Section IIIB for detailed derivation), whereas eqn (57) ensures the divergent behavior of the decay length ξ(2)Decay given by
→ 0, eqn (56) yields a finite decay length ξ(1)Decay ≈ (pE)−1 (see Section IIIB for detailed derivation), whereas eqn (57) ensures the divergent behavior of the decay length ξ(2)Decay given by  .
.
 , for a variable length L because the electrophoretic velocity is given by
, for a variable length L because the electrophoretic velocity is given by  , remembering that the force pE exerted on a single ion by the applied electric field is defined in units of kBT and that the mobility is given by
, remembering that the force pE exerted on a single ion by the applied electric field is defined in units of kBT and that the mobility is given by  according to the Einstein relation. It follows that the equality between a required time for electrophoresis and free diffusion reads
according to the Einstein relation. It follows that the equality between a required time for electrophoresis and free diffusion reads
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) → 0.
→ 0.

 and
and  defined by
defined by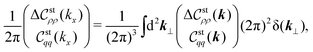




![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ)2ω(k(1)x) + (pEσ)2 = 0,
σ)2ω(k(1)x) + (pEσ)2 = 0,![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ)2ω(k(2)x) = 0,
σ)2ω(k(2)x) = 0, , used in equilibrium electrolytes but also from the approximate forms (56) and (57) where ω(k) = 1.
, used in equilibrium electrolytes but also from the approximate forms (56) and (57) where ω(k) = 1.



![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ ≤
σ ≤ ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ, both solutions to eqn (66) and (67) are purely imaginary: eqn (70) and (71) read
(*1)σ, both solutions to eqn (66) and (67) are purely imaginary: eqn (70) and (71) read

 and
and  . In the range of
. In the range of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ >
σ > ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ, on the other hand, the solution to eqn (66) becomes complex while the solution to (67) is purely imaginary: eqn (72) and (73) transform to
(*1)σ, on the other hand, the solution to eqn (66) becomes complex while the solution to (67) is purely imaginary: eqn (72) and (73) transform to

![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ =
σ = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ. We further predict the Fisher–Widom crossover31,36,44 that the density and charge oscillations become obvious in the range of
(*1)σ. We further predict the Fisher–Widom crossover31,36,44 that the density and charge oscillations become obvious in the range of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ <
(*1)σ < ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ <
σ < ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*2)σ where the two decay lengths, ξ(1)Decay and ξ(2)Decay, approach each other; however, it is beyond the scope of this paper to determine the full phase diagram using the steady-state extensions of the Kirkwood and Fisher–Widom crossovers31 related to eqn (66) and (67).
(*2)σ where the two decay lengths, ξ(1)Decay and ξ(2)Decay, approach each other; however, it is beyond the scope of this paper to determine the full phase diagram using the steady-state extensions of the Kirkwood and Fisher–Widom crossovers31 related to eqn (66) and (67).![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ-dependencies of ξ(1)Decay in a uniform state without and with applied electric field, respectively. On the one hand, ξ(1)Decay at E = 0 is identified with ξDH in the dilute limit of
σ-dependencies of ξ(1)Decay in a uniform state without and with applied electric field, respectively. On the one hand, ξ(1)Decay at E = 0 is identified with ξDH in the dilute limit of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ∼
∼ ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) 1/2 → 0 and decreases more rapidly than ξDH with increase of
1/2 → 0 and decreases more rapidly than ξDH with increase of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) in a uniform state prior to the Kirkwood crossover in equilibrium. On the other hand, there are two features as seen from the brown curve under the applied electric field (E ≠ 0): the dilute limit of ξ(1)Decay/ξDH approaches zero because of the finiteness of the decay length ξ(1)Decay in the limit of ξDH → ∞ as mentioned before, whereas the downward trend of ξ(1)Decay/ξDH, similar to the above behavior at E = 0, is observed near the electric-field-induced Kirkwood crossover.
in a uniform state prior to the Kirkwood crossover in equilibrium. On the other hand, there are two features as seen from the brown curve under the applied electric field (E ≠ 0): the dilute limit of ξ(1)Decay/ξDH approaches zero because of the finiteness of the decay length ξ(1)Decay in the limit of ξDH → ∞ as mentioned before, whereas the downward trend of ξ(1)Decay/ξDH, similar to the above behavior at E = 0, is observed near the electric-field-induced Kirkwood crossover.

![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) , which has been referred to as underscreening behavior without an electric field.
, which has been referred to as underscreening behavior without an electric field.
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ-dependence of
σ-dependence of  at the Kirkwood crossover; the exponent χ appears close to 1.4 as will be shown in Fig. 3(b).20,29–31 Reflecting this similarity between the exponents χ of the underscreening behavior and the electric-field-induced shift for
at the Kirkwood crossover; the exponent χ appears close to 1.4 as will be shown in Fig. 3(b).20,29–31 Reflecting this similarity between the exponents χ of the underscreening behavior and the electric-field-induced shift for  , the dashed blue line in Fig. 2 is drawn as an extension of the green arrow from node A (E = 0) to node B (E ≠ 0).
, the dashed blue line in Fig. 2 is drawn as an extension of the green arrow from node A (E = 0) to node B (E ≠ 0). and
and  , which by definition smear out density and charge distributions on cross sections perpendicular to the applied electric field (see eqn (64) and (65)).
, which by definition smear out density and charge distributions on cross sections perpendicular to the applied electric field (see eqn (64) and (65)). and a decay length
and a decay length  at the Kirkwood crossover. As detailed in Section IV, we have obtained these results using both the Gaussian charge smearing model35,40 (or the HNC approximation for one-component ionic fluids42) and the modified MSA model for the DCF,43 or its essential function ω(k) given by eqn (12). The former model is depicted by green lines, whereas the latter by red lines. All of the results in Fig. 3(a) exhibit downward trends in accordance with analytical observations made in Section IV.
at the Kirkwood crossover. As detailed in Section IV, we have obtained these results using both the Gaussian charge smearing model35,40 (or the HNC approximation for one-component ionic fluids42) and the modified MSA model for the DCF,43 or its essential function ω(k) given by eqn (12). The former model is depicted by green lines, whereas the latter by red lines. All of the results in Fig. 3(a) exhibit downward trends in accordance with analytical observations made in Section IV.
 at E = 0 in Fig. 3(a) that the numerical results correctly reproduce the Kirkwood crossover points previously obtained for the Gaussian charge smearing model34,35 and the modified MSA model.29–31,34 Second, Fig. 3(a) shows that the electric-field-induced shifts of
at E = 0 in Fig. 3(a) that the numerical results correctly reproduce the Kirkwood crossover points previously obtained for the Gaussian charge smearing model34,35 and the modified MSA model.29–31,34 Second, Fig. 3(a) shows that the electric-field-induced shifts of  are similar to each other. Remembering that
are similar to each other. Remembering that 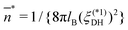 by definition (36), it is seen from the variations of
by definition (36), it is seen from the variations of  in Fig. 3(a) that, irrespective of the models adopted, the crossover densities at pEσ = 3.0 are evaluated to be less than half of those at E = 0. Last, we turn our attention to the relationship between
in Fig. 3(a) that, irrespective of the models adopted, the crossover densities at pEσ = 3.0 are evaluated to be less than half of those at E = 0. Last, we turn our attention to the relationship between  and
and  as a function of either
as a function of either ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) * or E. For a fixed strength of applied electric field, the decay length
* or E. For a fixed strength of applied electric field, the decay length  becomes shorter as the ionic solution density
becomes shorter as the ionic solution density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) *, or
*, or  , becomes larger, which is consistent with the previous results conventionally found for concentrated electrolytes prior to the Kirkwood crossover without an applied electric field.30–33 The electric-field dependencies, on the other hand, exhibit an opposite relationship between
, becomes larger, which is consistent with the previous results conventionally found for concentrated electrolytes prior to the Kirkwood crossover without an applied electric field.30–33 The electric-field dependencies, on the other hand, exhibit an opposite relationship between 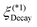 and
and  : the downward trends in Fig. 3(a) indicate that both
: the downward trends in Fig. 3(a) indicate that both  and
and  are smaller as E is larger.
are smaller as E is larger.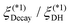 vs.
vs.  : it is seen from Fig. 3(b) that
: it is seen from Fig. 3(b) that
 by setting kz = 0 similar to the expressions (61), (62) and (64):
by setting kz = 0 similar to the expressions (61), (62) and (64):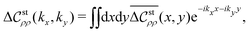

 as follows:
as follows:
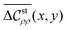 can reflect the 3D behaviors of density–density correlations when the translational symmetry of
can reflect the 3D behaviors of density–density correlations when the translational symmetry of 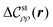 is preserved with respect to the z-direction and the correlation functions on the xy cross-sections are indistinguishable at two different z values.
is preserved with respect to the z-direction and the correlation functions on the xy cross-sections are indistinguishable at two different z values.
 at a fixed y-coordinate value of y0 and
at a fixed y-coordinate value of y0 and  defined by eqn (64), which are related respectively to the 2D mean correlation function
defined by eqn (64), which are related respectively to the 2D mean correlation function  defined by eqn (81) as follows:
defined by eqn (81) as follows:
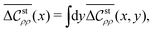
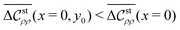 because of
because of  (see Fig. 5 for confirmation).
(see Fig. 5 for confirmation).
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ exceeds the Fisher–Widom-like crossover31,36,44 as well as the Kirkwood crossover:32–36
σ exceeds the Fisher–Widom-like crossover31,36,44 as well as the Kirkwood crossover:32–36![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ >
σ > ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*2)σ (>
(*2)σ (>![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ) is investigated (remember the discussion at the end of Section IIB). We see from Fig. 4 that stripe states illustrated in Fig. 2 are observed more clearly as
(*1)σ) is investigated (remember the discussion at the end of Section IIB). We see from Fig. 4 that stripe states illustrated in Fig. 2 are observed more clearly as ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ is larger at a fixed strength of electric field. In Fig. 5 and 6, we validate the anisotropic approximation (53) from comparing
σ is larger at a fixed strength of electric field. In Fig. 5 and 6, we validate the anisotropic approximation (53) from comparing  and
and 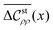 (see also eqn (83) and (84)). Furthermore, Fig. 7 shows the emergence of a lane structure with the increase of electric field strength from pEσ = 0.1 to 1.0 at a high value of
(see also eqn (83) and (84)). Furthermore, Fig. 7 shows the emergence of a lane structure with the increase of electric field strength from pEσ = 0.1 to 1.0 at a high value of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.78.
σ = 2.78.
 for different conditions on ionic condition and electric field strength. The color bar on the right hand side, which is common to the three heat maps, represents the value of
for different conditions on ionic condition and electric field strength. The color bar on the right hand side, which is common to the three heat maps, represents the value of  at a location (x/σ, y/σ) measured in units of sphere diameter σ. While the difference between Fig. 4(a) and (b) is ionic concentration, or
at a location (x/σ, y/σ) measured in units of sphere diameter σ. While the difference between Fig. 4(a) and (b) is ionic concentration, or ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ, at an identical electrical field, an electric field effect is seen from comparing Fig. 4(b) and (c) at a same ionic concentration: (a) (
σ, at an identical electrical field, an electric field effect is seen from comparing Fig. 4(b) and (c) at a same ionic concentration: (a) (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ, pEσ) = (2.2,0.5); (b) (
σ, pEσ) = (2.2,0.5); (b) (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ, pEσ) = (2.6,0.5); (c) (
σ, pEσ) = (2.6,0.5); (c) (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ, pEσ) = (2.6,1.5).
σ, pEσ) = (2.6,1.5).
 at a fixed y-coordinate value of y0 and
at a fixed y-coordinate value of y0 and  defined byeqn (64). The density–density correlation functions are plotted as functions of x/σ, the separation distance in the applied field direction measured in units of sphere diameter σ. At an identical electric field strength pEσ = 0.5, two ionic concentrations,
defined byeqn (64). The density–density correlation functions are plotted as functions of x/σ, the separation distance in the applied field direction measured in units of sphere diameter σ. At an identical electric field strength pEσ = 0.5, two ionic concentrations, ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2 and 2.6, are considered in both figures: (a) the green and red solid lines depict the behaviors of
σ = 2.2 and 2.6, are considered in both figures: (a) the green and red solid lines depict the behaviors of  at
at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2 (green) and 2.6 (red), respectively, whereas the red dotted line represents
σ = 2.2 (green) and 2.6 (red), respectively, whereas the red dotted line represents  at
at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.6; (b) the green and red solid lines depict the behaviors of
σ = 2.6; (b) the green and red solid lines depict the behaviors of  at
at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2 and 2.6, respectively.
σ = 2.2 and 2.6, respectively.
 over the range, 0 ≤ x/σ ≤ 20, at
over the range, 0 ≤ x/σ ≤ 20, at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2 (green) and 2.6 (red) in the presence of applied electric field (pEσ = 0.5). The dashed lines correspond to the best fit of eqn (85).
σ = 2.2 (green) and 2.6 (red) in the presence of applied electric field (pEσ = 0.5). The dashed lines correspond to the best fit of eqn (85).![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.6. Fig. 4(b) can be a reference result for investigating the effects of ionic concentration and electric field strength. Fig. 4(b) exhibits the oscillatory decay behaviors in the external field direction on an xy plane, which is typical of density–density correlations in the stripe state.
σ = 2.6. Fig. 4(b) can be a reference result for investigating the effects of ionic concentration and electric field strength. Fig. 4(b) exhibits the oscillatory decay behaviors in the external field direction on an xy plane, which is typical of density–density correlations in the stripe state.![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ is reduced from 2.6 to 2.2 without changing the electric field strength, we obtain the result of Fig. 4(a). Comparison between Fig. 4(a) and (b) indicates the following. First, we can observe the oscillatory decays in the external field direction for both values of
σ is reduced from 2.6 to 2.2 without changing the electric field strength, we obtain the result of Fig. 4(a). Comparison between Fig. 4(a) and (b) indicates the following. First, we can observe the oscillatory decays in the external field direction for both values of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ when setting the electric field strength to be pEσ = 0.5. Furthermore, Fig. 4(a) shows that the correlation function becomes almost zero for x ≥ 5σ: The density–density correlation function becomes equal to 2
σ when setting the electric field strength to be pEσ = 0.5. Furthermore, Fig. 4(a) shows that the correlation function becomes almost zero for x ≥ 5σ: The density–density correlation function becomes equal to 2![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) δ(r) for x ≥ 5σ in contrast to the long-range correlations seen in Fig. 4(b). The different behaviors of density–density correlations suggest that the smaller
δ(r) for x ≥ 5σ in contrast to the long-range correlations seen in Fig. 4(b). The different behaviors of density–density correlations suggest that the smaller ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ is, the shorter the decay length becomes. In other words, comparison between Fig. 4(a) and (b) reveals an underscreening behavior19,20,29–31 beyond the Kirkwood condition as depicted in the schematic of Fig. 2. Fig. 4(c) further demonstrates that alignment of segregation band to the external field direction becomes clear by increasing the electric field strength to pEσ = 1.5 at
σ is, the shorter the decay length becomes. In other words, comparison between Fig. 4(a) and (b) reveals an underscreening behavior19,20,29–31 beyond the Kirkwood condition as depicted in the schematic of Fig. 2. Fig. 4(c) further demonstrates that alignment of segregation band to the external field direction becomes clear by increasing the electric field strength to pEσ = 1.5 at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.6.
σ = 2.6.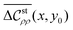 at y0, a fixed y-coordinate value, with the behaviors of the one-variable correlation function
at y0, a fixed y-coordinate value, with the behaviors of the one-variable correlation function  defined by eqn (64). Both solid lines in Fig. 5(a) show the x-dependencies at y0 = 0. The same external field condition pEσ = 0.5 is used in both results of Fig. 5(a) and (b), and the ionic conditions for the green and red lines are identical in Fig. 5(a) and (b): the green and red lines represent the results at
defined by eqn (64). Both solid lines in Fig. 5(a) show the x-dependencies at y0 = 0. The same external field condition pEσ = 0.5 is used in both results of Fig. 5(a) and (b), and the ionic conditions for the green and red lines are identical in Fig. 5(a) and (b): the green and red lines represent the results at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2 and 2.6, respectively.
σ = 2.2 and 2.6, respectively.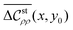 and
and  , exhibit oscillatory decay behaviors, and we will make a quantitative comparison using Fig. 6. They also share the feature of correlation value that becomes smaller with the decrease of ionic concentration from
, exhibit oscillatory decay behaviors, and we will make a quantitative comparison using Fig. 6. They also share the feature of correlation value that becomes smaller with the decrease of ionic concentration from ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.6 to 2.2. Furthermore, we observe that the oscillations disappear faster for the green line than for the red line in both Fig. 5(a) and (b), which corresponds to the underscreening behavior suggested by Fig. 4.
σ = 2.6 to 2.2. Furthermore, we observe that the oscillations disappear faster for the green line than for the red line in both Fig. 5(a) and (b), which corresponds to the underscreening behavior suggested by Fig. 4.![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2. We can see that the period of the dashed red line is close to that of the solid red line. However, the initial phase is different from that at y0/σ = 0, and the correlation value is reduced considerably even at x/σ = 0 as y0/σ varies from 0 to 5. The latter difference implies that the x-dependency of
σ = 2.2. We can see that the period of the dashed red line is close to that of the solid red line. However, the initial phase is different from that at y0/σ = 0, and the correlation value is reduced considerably even at x/σ = 0 as y0/σ varies from 0 to 5. The latter difference implies that the x-dependency of  near y0/σ = 0 greatly contributes to the one-variable correlation function
near y0/σ = 0 greatly contributes to the one-variable correlation function  defined by eqn (64), which is why the two solid lines in Fig. 5(a) reproduce the one-variable function behaviors in Fig. 5(b).
defined by eqn (64), which is why the two solid lines in Fig. 5(a) reproduce the one-variable function behaviors in Fig. 5(b).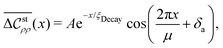
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.2, whereas (A, ξDecay,μ, δa) = (1.3 × 10−2, 2.5, 3.8, 0.4) at
σ = 2.2, whereas (A, ξDecay,μ, δa) = (1.3 × 10−2, 2.5, 3.8, 0.4) at ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.6. The best-fit periods, μ = 5.6 and 3.8, reflect the oscillatory behaviors seen from Fig. 6. Meanwhile, the best-fit decay length ξDecay extends from 2σ to 2.5σ with the increase of
σ = 2.6. The best-fit periods, μ = 5.6 and 3.8, reflect the oscillatory behaviors seen from Fig. 6. Meanwhile, the best-fit decay length ξDecay extends from 2σ to 2.5σ with the increase of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ from 2.2 to 2.6, which is a quantitative result of underscreening behavior. Evaluating the exponent χ defined by eqn (79) from this increase in ξDecay, we have 2 < χ < 3; it is interesting to note that the present exponent is larger than the equilibrium exponent (1 < χ ≤ 1.5) previously obtained from the MSA of the 3D primitive model but is close to the exponent experimentally obtained.19
σ from 2.2 to 2.6, which is a quantitative result of underscreening behavior. Evaluating the exponent χ defined by eqn (79) from this increase in ξDecay, we have 2 < χ < 3; it is interesting to note that the present exponent is larger than the equilibrium exponent (1 < χ ≤ 1.5) previously obtained from the MSA of the 3D primitive model but is close to the exponent experimentally obtained.19
 when increasing
when increasing ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ to 2.78. The strengths of the applied electric field are pEσ = 0.1 (Fig. 7(a)) and pEσ = 1.0 (Fig. 7(b)). The heat maps in Fig. 7 reveal the oscillatory 2D patterns due to the suppression of decaying behaviors. On the one hand, even at the weak electric field strength of pEσ = 0.1, Fig. 7(a) shows that segregation bands of ions with the same sign are deformed along the x-axis, the external field direction, though the stripe state remains a good approximation in the region of y/σ ≤ 5. On the other hand, at pEσ = 1.0, Fig. 7(b) demonstrates the emergence of lane structure formed by aligned bands, revealing that the anisotropic approximation (53) becomes invalid far beyond the electric-field-induced Kirkwood crossovers.
σ to 2.78. The strengths of the applied electric field are pEσ = 0.1 (Fig. 7(a)) and pEσ = 1.0 (Fig. 7(b)). The heat maps in Fig. 7 reveal the oscillatory 2D patterns due to the suppression of decaying behaviors. On the one hand, even at the weak electric field strength of pEσ = 0.1, Fig. 7(a) shows that segregation bands of ions with the same sign are deformed along the x-axis, the external field direction, though the stripe state remains a good approximation in the region of y/σ ≤ 5. On the other hand, at pEσ = 1.0, Fig. 7(b) demonstrates the emergence of lane structure formed by aligned bands, revealing that the anisotropic approximation (53) becomes invalid far beyond the electric-field-induced Kirkwood crossovers.
 at different electric field strengths: (a) pEσ = 0.1 and (b) pEσ = 1.0. The same ionic condition
at different electric field strengths: (a) pEσ = 0.1 and (b) pEσ = 1.0. The same ionic condition ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ = 2.78 is adopted in both results.
σ = 2.78 is adopted in both results.
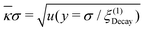 , the ξ(1)Decay-dependence of
, the ξ(1)Decay-dependence of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ, which varies depending on the electric field strength measured by pEσ. The colored solid lines represent these dependencies for pEσ = 0 (green), pEσ = 1.5 (orange), and pEσ = 3 (red). Meanwhile, the blue dashed line shows another dependence of
σ, which varies depending on the electric field strength measured by pEσ. The colored solid lines represent these dependencies for pEσ = 0 (green), pEσ = 1.5 (orange), and pEσ = 3 (red). Meanwhile, the blue dashed line shows another dependence of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ on ξ(1)Decay/σ which is given by
σ on ξ(1)Decay/σ which is given by  (see eqn (106)). The three intersection points are indicated by brown circles, giving both the Debye–Hückel lengths
(see eqn (106)). The three intersection points are indicated by brown circles, giving both the Debye–Hückel lengths  at the electric-field-induced crossovers and the Kirkwood decay lengths
at the electric-field-induced crossovers and the Kirkwood decay lengths  at different field strengths. (b) Numerical results summarized in Fig. 2. In this figure, the
at different field strengths. (b) Numerical results summarized in Fig. 2. In this figure, the ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ-dependencies of ξ(1)Decay are depicted by the solid lines colored green (pEσ = 0), blue (pEσ = 1), orange (pEσ = 1.5), and red (pEσ = 3), from top to bottom, on a log–log plot of ξ(1)Decay/ξDH =
σ-dependencies of ξ(1)Decay are depicted by the solid lines colored green (pEσ = 0), blue (pEσ = 1), orange (pEσ = 1.5), and red (pEσ = 3), from top to bottom, on a log–log plot of ξ(1)Decay/ξDH = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ξ(1)Decayvs. σ/ξDH =
ξ(1)Decayvs. σ/ξDH = ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ. The brown circles mark the termination points of these lines representing the Kirkwood crossover points at each electric-field strength, and the rightmost circle A corresponds to node A in Fig. 2, the Kirkwood crossover point at E = 0. The location shift of brown circles with the increase of E is indicated by the dashed green arrow, showing an electric-field-induced shift of the Kirkwood crossover. For comparison, the dotted line delineates the scaling relation,
σ. The brown circles mark the termination points of these lines representing the Kirkwood crossover points at each electric-field strength, and the rightmost circle A corresponds to node A in Fig. 2, the Kirkwood crossover point at E = 0. The location shift of brown circles with the increase of E is indicated by the dashed green arrow, showing an electric-field-induced shift of the Kirkwood crossover. For comparison, the dotted line delineates the scaling relation,  , as well as that in Fig. 3(b).
, as well as that in Fig. 3(b). :
:
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ because of x = 0, or μ(1) → ∞: the Kirkwood crossover occurs when exceeding
(*1)σ because of x = 0, or μ(1) → ∞: the Kirkwood crossover occurs when exceeding ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ.
(*1)σ.



 at the Kirkwood crossover becomes longer as E is larger. Namely, the crossover density
at the Kirkwood crossover becomes longer as E is larger. Namely, the crossover density  becomes lower with the increase of E; eqn (90) predicts that both charge–charge and density–density oscillations are observed even in a dilute electrolyte upon applying a high electric field.
becomes lower with the increase of E; eqn (90) predicts that both charge–charge and density–density oscillations are observed even in a dilute electrolyte upon applying a high electric field.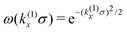 in eqn (12). Then, eqn (66) is rewritten as
in eqn (12). Then, eqn (66) is rewritten as

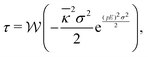
 35 defined by
35 defined by  .
.



![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) *. Eqn (99) verifies the above approximate result (90), whereas eqn (100) enables us to make an analytical prediction that the increase of E results in the decrease of
*. Eqn (99) verifies the above approximate result (90), whereas eqn (100) enables us to make an analytical prediction that the increase of E results in the decrease of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) *. Inserting eqn (98) into eqn (95), we have
*. Inserting eqn (98) into eqn (95), we have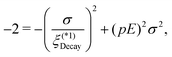

![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) * given by eqn (100). In other words, our target mode
* given by eqn (100). In other words, our target mode  describes an aspect of electric-field-induced screening which is enhanced by the applied electric field (see also the last paragraph of Section IIIA for the underlying physics).
describes an aspect of electric-field-induced screening which is enhanced by the applied electric field (see also the last paragraph of Section IIIA for the underlying physics).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cosh
cosh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y − i sin
y − i sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sinh
sinh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y, eqn (66) reads
y, eqn (66) reads![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 2σ2cos
2σ2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cosh
cosh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y = y2 − (pE)2σ2 − x2,
y = y2 − (pE)2σ2 − x2,![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) 2σ2
2σ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh
sinh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y = 2xy,
y = 2xy,

 .
.
 and
and  as a function of y = σ/ξ(1)Decay including the Kirkwood crossover value y*. While there is a single line of
as a function of y = σ/ξ(1)Decay including the Kirkwood crossover value y*. While there is a single line of  in Fig. 8(a), the curves of
in Fig. 8(a), the curves of  are depicted using different values of pEσ = 0, 1.5 and 3. We can see from Fig. 8(a) that the intersection points of these curves (three brown circles located at the intersections in Fig. 8(a)) is determined by u(y*) = v(y*) and is located at the maximum of
are depicted using different values of pEσ = 0, 1.5 and 3. We can see from Fig. 8(a) that the intersection points of these curves (three brown circles located at the intersections in Fig. 8(a)) is determined by u(y*) = v(y*) and is located at the maximum of  as a function of y; actually, it is easily confirmed that u(y*) = v(y*) is nothing but the maximum condition for
as a function of y; actually, it is easily confirmed that u(y*) = v(y*) is nothing but the maximum condition for  . We find from a series of intersection points
. We find from a series of intersection points  for different field strengths in Fig. 8(a) that the modified MSA model43 exhibits a similar trend observed in the above Gaussian charge smearing model:35 the maxima of
for different field strengths in Fig. 8(a) that the modified MSA model43 exhibits a similar trend observed in the above Gaussian charge smearing model:35 the maxima of  decrease with increase of E. That is, the Debye–Hückel length
decrease with increase of E. That is, the Debye–Hückel length  at the electric-field-induced crossover is larger as the decay length
at the electric-field-induced crossover is larger as the decay length  at the Kirkwood crossover is smaller due to the increase of E. These dependencies are in qualitative agreement with eqn (99) and (102) of the Gaussian charge smearing model.
at the Kirkwood crossover is smaller due to the increase of E. These dependencies are in qualitative agreement with eqn (99) and (102) of the Gaussian charge smearing model. (or
(or ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ) and
(*1)σ) and  of the Gaussian charge smearing model, respectively. On the other hand, eqn (105) and (106) are solved numerically to find
of the Gaussian charge smearing model, respectively. On the other hand, eqn (105) and (106) are solved numerically to find 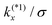 , or the inverse of
, or the inverse of  in the modified MSA,43 and we can easily calculate
in the modified MSA,43 and we can easily calculate ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ from
(*1)σ from  using eqn (105). The same results as those of Fig. 8(a) are presented on a log–log plot in Fig. 8(b), further indicating that, in the range of
using eqn (105). The same results as those of Fig. 8(a) are presented on a log–log plot in Fig. 8(b), further indicating that, in the range of  , the
, the  -dependencies of
-dependencies of  exhibit a scaling relation
exhibit a scaling relation  with χ being close to 1.4, which is similar to eqn (76) previously found for concentrated electrolytes.20,29–31
with χ being close to 1.4, which is similar to eqn (76) previously found for concentrated electrolytes.20,29–31
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ ≈ 1.6 and p2lB/σ = 1 by adding to the mPNP equations a fluctuating advection term due to interparticle interactions.45
σ ≈ 1.6 and p2lB/σ = 1 by adding to the mPNP equations a fluctuating advection term due to interparticle interactions.45
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ >
σ > ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ, we have smeared correlation functions,
(*1)σ, we have smeared correlation functions,  and
and  , which are given by the sum of oscillatory and monotonic decay functions (i.e., eqn (74) and (75)). Furthermore, the monotonic decay parts of correlation functions subsequently become oscillatory when
, which are given by the sum of oscillatory and monotonic decay functions (i.e., eqn (74) and (75)). Furthermore, the monotonic decay parts of correlation functions subsequently become oscillatory when ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ goes beyond
σ goes beyond ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*2)σ which is related to the equilibrium Kirkwood crossover value
(*2)σ which is related to the equilibrium Kirkwood crossover value ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) *σ as eqn (55). This crossover phenomenon suggests the possibility of simultaneous occurrence of the Fisher–Widom crossover31,36,44 for density–density and charge–charge correlations in the range of
*σ as eqn (55). This crossover phenomenon suggests the possibility of simultaneous occurrence of the Fisher–Widom crossover31,36,44 for density–density and charge–charge correlations in the range of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ ≤
(*1)σ ≤ ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) σ ≤
σ ≤ ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*2)σ though the full phase diagram of steady states for electric-field-driven electrolytes remains to be determined. For the concrete understanding of anisotropic density modulations in stripe states, Section IIIE presents various results on the 2D density–density correlations beyond the Fisher–Widom crossover. As confirmed from Fig. 4 and 7, there are some electric field conditions that create stripe states formed by segregation bands transverse to the external field direction.
(*2)σ though the full phase diagram of steady states for electric-field-driven electrolytes remains to be determined. For the concrete understanding of anisotropic density modulations in stripe states, Section IIIE presents various results on the 2D density–density correlations beyond the Fisher–Widom crossover. As confirmed from Fig. 4 and 7, there are some electric field conditions that create stripe states formed by segregation bands transverse to the external field direction.
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) *σ is equal to 1.04 (pEσ = 0) and that
*σ is equal to 1.04 (pEσ = 0) and that ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (*1)σ ≈ 0.82 (pEσ = 1.5) when adopting the modified MSA model.43 It follows that the Kirkwood crossover density varies from 0.30 M (pEσ = 0) to 0.19 M (pEσ = 1.5) for an RTIL (1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide) diluted with propylene carbonate where we set (p, σ, ε, lB) = (1,0.4,65,0.88). The former density (0.30 M) agrees well with experimental and simulation results19,20 with no electric field applied, whereas the validity of density difference (0.30–0.19 = 0.11 M) due to the external electric field needs to be assessed in future.
(*1)σ ≈ 0.82 (pEσ = 1.5) when adopting the modified MSA model.43 It follows that the Kirkwood crossover density varies from 0.30 M (pEσ = 0) to 0.19 M (pEσ = 1.5) for an RTIL (1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide) diluted with propylene carbonate where we set (p, σ, ε, lB) = (1,0.4,65,0.88). The former density (0.30 M) agrees well with experimental and simulation results19,20 with no electric field applied, whereas the validity of density difference (0.30–0.19 = 0.11 M) due to the external electric field needs to be assessed in future.![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) . Appendix A4 explains that the stationary condition (A45) imposed on a general matrix form of equal-time correlation functions yields density–density and charge–charge correlation functions given by eqn (43)–(48).
. Appendix A4 explains that the stationary condition (A45) imposed on a general matrix form of equal-time correlation functions yields density–density and charge–charge correlation functions given by eqn (43)–(48).


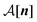 , instead of the equilibrium free energy functional;37,38 (ii) addition of the stochastic current, the second term on the rhs of eqn (A1), helps us to describe fluctuating phenomena.
, instead of the equilibrium free energy functional;37,38 (ii) addition of the stochastic current, the second term on the rhs of eqn (A1), helps us to describe fluctuating phenomena.
 .
It has been shown that the constrained free energy
.
It has been shown that the constrained free energy  as a functional of given density fields n(r, t) = (n1(r, t), n2(r, t))T can be expressed by considering fluctuating potential fields ϕ(r, t) = (ϕ1(r, t), ϕ2(r, t))T, which are conjugate to n(r,t), in addition to an adjusted potential field ϕdftl(r, t) similar to that of the equilibrium DFT.37,38 Extending the previous result24,28 to the expression for two-component systems (see Appendix B for details), we have
as a functional of given density fields n(r, t) = (n1(r, t), n2(r, t))T can be expressed by considering fluctuating potential fields ϕ(r, t) = (ϕ1(r, t), ϕ2(r, t))T, which are conjugate to n(r,t), in addition to an adjusted potential field ϕdftl(r, t) similar to that of the equilibrium DFT.37,38 Extending the previous result24,28 to the expression for two-component systems (see Appendix B for details), we have
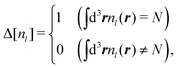

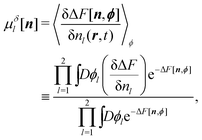







 -matrix is given by
-matrix is given by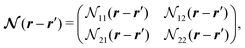




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kσ),
cos(kσ),
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kσ)
cos(kσ)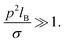




![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) .
.![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (or q ≡ 0) to the first order in νl(r, t):
(or q ≡ 0) to the first order in νl(r, t):
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ] denoting μl[
] denoting μl[![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ] = μl[(
] = μl[(![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ,
, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) )T]. Since we have
)T]. Since we have






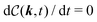 for the expression (A43) reads13,15
for the expression (A43) reads13,15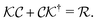
 , or the four kinds of correlation functions in eqn (40), can be determined by four simultaneous equations arising from the above stationary condition (A45) (see Appendix D for details).
, or the four kinds of correlation functions in eqn (40), can be determined by four simultaneous equations arising from the above stationary condition (A45) (see Appendix D for details).
 and
and  , among the matrix elements of
, among the matrix elements of  . As detailed in Appendix D, the solution to eqn (A45) reads
. As detailed in Appendix D, the solution to eqn (A45) reads
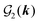 has been defined in eqn (45), and the matrix elements of
has been defined in eqn (45), and the matrix elements of  is given by
is given by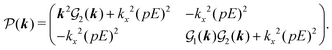
 of a given density distribution n(r, t)
of a given density distribution n(r, t) of a given density distribution nl(r, t) (l = 1,2) is defined for the canonical ensemble using the contour integral over a complex variable w = eμ:28
of a given density distribution nl(r, t) (l = 1,2) is defined for the canonical ensemble using the contour integral over a complex variable w = eμ:28


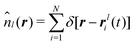 . It has been shown for one-component fluid that the constrained free energy functional is expressed by the functional integral over a fluctuating potential field. Similarly, we have
. It has been shown for one-component fluid that the constrained free energy functional is expressed by the functional integral over a fluctuating potential field. Similarly, we have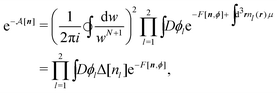

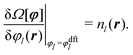






 .
.
 for the density–density correlation function
for the density–density correlation function  defined by eqn (A17), eqn (A15) leads to
defined by eqn (A17), eqn (A15) leads to




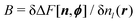 . Thus, we obtain
. Thus, we obtain


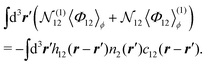


 and
and  , using a simplified form of
, using a simplified form of
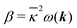 and
and 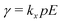 . It follows that
. It follows that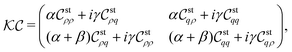

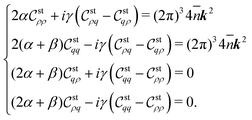
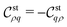 and
and



 and
and  . Hence, the above expressions (D7) and (D8) are found to be equivalent to eqn (A46) and (A47).
. Hence, the above expressions (D7) and (D8) are found to be equivalent to eqn (A46) and (A47).
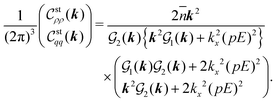
 ,
,  and
and  , can be simply approximated by
, can be simply approximated by 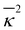 when considering the small wavevector region of
when considering the small wavevector region of  at a moderate field strength of
at a moderate field strength of  . This approximation allows eqn (D9) to be reduced to
. This approximation allows eqn (D9) to be reduced to
 on the Kirkwood crossover:
on the Kirkwood crossover:
 . Eqn (87) reads the following quadratic equation,
. Eqn (87) reads the following quadratic equation,
 . The solution X to eqn (E2) is
. The solution X to eqn (E2) is
 , the numerator on the rhs of eqn (E3) is approximated by
, the numerator on the rhs of eqn (E3) is approximated by

 . While the approximate form (E4) of the numerator results in the expression (89), the limiting result (90) is valid due to eqn (E5).
. While the approximate form (E4) of the numerator results in the expression (89), the limiting result (90) is valid due to eqn (E5).

