Dynamics of elastic, nonheavy spheres sedimenting in a rectangular duct

Abstract

Understanding of sedimentation dynamics of particles in bounded fluids is of crucial importance for a wide variety of processes. While there is a profound knowledge base regarding the sedimentation of rigid solid particles, the fundamental principles of sedimentation dynamics of elastic spheres in bounded fluids are not well understood. This especially applies to nonheavy spheres, whose density is close to that of the surrounding medium and which therefore show extended inertial effects upon acceleration. Here, we present model experiments of the sedimentation dynamics of deformable, nonheavy spheres in the presence of walls. Despite the deformations of the particles being small, the particle dynamics of elastic spheres differed fundamentally from that of rigid spheres. Initially, the sedimentation of elastic spheres is comparable with the sedimentation of rigid spheres. From a characteristic onset position of about 10·R, deformability effects kick in and a second acceleration appears. Finally, the deformable spheres reach a terminal sedimentation velocity. The softer the spheres are (in terms of Young's elastic modulus), the higher the terminal velocity is. In the present setup, a terminal velocity up to 9% higher than the velocity for comparable rigid spheres was reached. By analyzing the obtained data, insights into the dynamics are given that could serve as basic approaches for modelling the dynamics of elastic spheres in bounded fluids.

---

1 Introduction

Solid sedimentation in liquids due to gravity is a widely used process in civil and environmental engineering. In a variety of applications, like in wastewater treatment or in food industry, sedimentation is used specifically as for example separation method.¹ In other applications, such as in the ink and paint industry, sedimentation of solid pigments is an undesirable effect that must be avoided. Profound knowledge and modelling of fluid-particle dynamics of sedimentation is therefore essential and it is the basis for the design of these processes. The calculation and design of such processes is mostly based on the assumption of spherical, heavy and rigid particles. However, both in nature and in applications, the assumption of rigid and heavy particles is often not valid. For example, microplastics or microgels, such as silicone particles, are in many cases soft and deformable. Further, biological particles cannot be treated as rigid and heavy particles since, for example, fungal capsules or cell membranes are deformable.² Wastewater treatment plants have been designed in the past mostly using rigid particle sedimentation for design calculations. But in the process, increasing amounts of microplastics enter the wastewater. Shape factors and empirical formulations are used to account for the sedimentation velocity of microplastics, which obviously differs from that of other heavier particles.³ Furthermore, several polymers have a density in the range of that of water, i.e. the density ratio is in the range of unity. These particles are called nonheavy particles. Studies show that a significant proportion of microplastics cannot be removed from wastewater in sewage treatment plants and end up in the environment.⁴ The motion of biological particles such as bacteria or blood cells in flows is often described using, e.g. challenging soft capsule models or, e.g. flexible bond models in CFD-DEM simulations.^5,6 It is assumed, that elastic solid beads could also serve as good models for biological particles.⁷ Additionally, such soft particle models are of particular interest in the field of microfluids, like transportation of soft particles through rectangular micro ducts. Here, however, not only the link between shape, material properties (deformability) and fluid dynamics plays a role, but also the influence of the surrounding walls.^8–11

While the literature regarding the dynamics of rigid particles is vast and consolidated, the research and knowledge regarding the dynamics of elastic particles is still incomplete in places and it remains of great interest to the scientific community.^7,12 Even comparatively simple particle dynamics, such as the sedimentation of elastic spheres in an unbounded fluid, is only described in basic theory or is based on numerical calculations.^13,14 Thereby, it is well known from related fields like liquid–liquid separation, for example in drop settling or bubble rise in fluids, that the deformation of dispersed particles has a significant influence on the particle dynamics.^15,16 There are numerous studies, experimental as well as numerical and theoretical, which relate the dynamics under deformation to characteristic quantities like, e.g., viscous forces, cohesion forces or hydrostatic pressure.^17–20

However, relationships between sedimentation velocity and elastic properties are still missing. Basic research is necessary at this point. Therefore, we perform sedimentation experiments, which allow insights into the dynamics of elastic solid spheres at low Reynolds numbers in a rectangular duct. Trajectories and resulting dynamics are recorded on a macroscopic scale. With the data obtained, both the transient and the steady-state sedimentation of deformable solid particles under wall influence can be quantitatively determined and related to the deformability.

2 Theoretical background

A rigid spherical particle with radius R, volume V_P and density ρ_P sediments due to gravitational acceleration g with velocity U_P in an unbounded fluid. The fluid density is ρ and the fluid dynamic viscosity η. Furthermore, the particle starts from rest at t = 0 s and, initially, the fluid velocity field around the particle is |U| = 0 m s⁻¹. In the stationary state the particle sediments in the Stokes regime wier Re_P = 2U_PRρη⁻¹ ≪ 1. The equation of motion of a nonheavy particle with a particle-to-fluid density ratio γ = ρ_P/ρ → 1⁺ (quasi neutrally buoyant particles) can be described with the Basset–Boussinesq–Oseen (BBO) equation according to Basset, Boussinesq and Oseen.^21–23 The BBO equation results from the force balance around the particle with F_I + F_g + F_Buoyancy + F_St + F_AM + F_B = 0 (see Fig. 1(a)). The differential equation for the particle velocity U_P in direction of the gravitational acceleration reads as^15,24

Fig. 1 (a) Force balance around a spherical particle at different times during sedimentation; (b) exemplary velocity curve of a sedimenting sphere with particle-to-fluid density ratio γ ≫ 1 (heavy) and one with particle-to-fluid density ratio γ → 1 (nonheavy).

The overdot denotes a time-derivate and s is a dummy time variable for integration. The term on the left side of eqn (1) is the inertial force F_I. The inertial force is equaled by the gravitational force F_g and the buoyancy F_Buoyancy. F_St denotes the drag force resulting from Stokes's law.²⁵ The third term on the right is the added mass force F_AM which arises because the acceleration of the particle requires acceleration of the fluid surrounding it. The fourth term is the Basset history force F_B. The Basset history force includes past acceleration and represents the effect of the diffusion of vorticity around the sphere due the temporal delay in boundary layer development.^15,26

When a rigid particle starts sedimenting from rest, it first undergoes a transient phase until it reaches a stationary, terminal sedimentation velocity. The two acceleration forces F_AM and F_B lead to a more extended transient phase compared to heavy particles (see Fig. 1(b)). In the steady state (dU_P/dt = 0), where the gravitational force and buoyancy balance the drag and the acceleration forces vanish, eqn (1) results in the terminal Stokes velocity

The previous equations are valid for particles sedimenting in an unbounded fluid. The influence of walls on the terminal velocity of a rigid sphere between parallel plane walls was first treated by Faxén.²⁷ A detailed overview of empirical equations and of mathematical methods for calculating the influence of walls on particle dynamics is given by Happel and Brenner.²⁸ In principle, the following statement can be made: if particles sediment in the presence of walls, drag exerted on the sphere is increased and thus the terminal velocity is reduced. While there are numerous empirical as well as theoretical approaches to calculate drag coefficient corrections for cylindrical pipes, drag corrections for confined spaces with plane walls are mostly based on computational studies. For example, in a computational study, Swan and Brady calculated the terminal velocity of a spherical particle sedimenting along a channel with two parallel walls in dependence of the wall distance.²⁹ Since they assume the space between the two walls as infinite, the real terminal velocity is estimated to be even lower. These effects would be expected in confined spaces like in a rectangular duct. Hensley and Papavassiliou performed CFD simulations to calculate the drag exerted on a sphere moving in the center of a square microduct with width W.³⁰ For a spherical particle that moves with Re_P = 0.1 in a square microduct they proposed a correction of the Stokes's drag. Using their correction factor, the particle velocity in a rectangular duct reduces to

In contrast to rigid solid particles, there is little knowledge available with respect to deformable, elastic solid particles. In 1980, Murata derived an expression for the terminal sedimentation velocity of an elastic sphere in an unbounded fluid. According to Murata's calculations, when a sphere sediments in the low Reynolds number regime with Re_P ≪ 1, it deforms into a prolate spheroid in direction of the gravitational acceleration.¹³ This deformation into a prolate spheroid would reduce the drag acting on the elastic body. Hence, the terminal sedimentation velocity increases.²⁸ By series expansion with the perturbation parameter α and in terms of specific constants K₀ and K₁, Murata derived the following expression for the terminal sedimentation velocity of an elastic sphere

In this equation, the terminal velocity for rigid particles is extended by an elastic component of the terminal velocity Δ_el,M. The perturbation parameter α relates the viscous stresses to the elastic, mechanical stresses with α = U_StηG⁻¹R⁻¹ ≪ 1. α can therefore be interpreted as dimensionless elastocapillary number and, since it is much smaller than unity, small deformations are assumed. The elastic constants K₀ and K₁ are calculated from the solid material properties (K_0,1 = f(G, λ, ρ_P, R, g)). G and λ denote Lamé's constants with G = E[2(1 + ν)]⁻¹ and λ = Eν[(1 + ν)(1 − 2ν)]⁻¹. E represents Young's elastic modulus and ν the Poisson's ratio of the elastic solid material.

To the best of our knowledge, the theoretically derived velocity from eqn (4) has not yet been verified by experimental data. Furthermore, it is not known whether the equation, or the increase in sedimentation velocity respectively, is analogous in the case of sedimentation in a bounded fluid. It is not yet known whether walls as in a rectangular duct have an additional influence not captured by Murata's calculations.

In the following, we hence investigate the sedimentation of elastic spheres under small deformation and in a bounded fluid domain.

3 Methods

3.1. Experimental setup

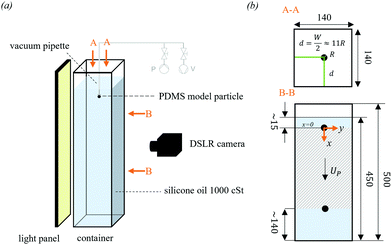
Sedimentation of rigid and elastic model particles was performed in a rectangular duct. As a vessel for the experiments, a glass container of 140 mm × 140 mm × 500 mm (W × D × H) was used, see Fig. 2.

Fig. 2 (a) Schematic experimental setup: spherical particles sediment in a rectangular container with square base in silicone oil with a nominal viscosity of 1000 cSt. The particles were immersed hanging on a vacuum pipette. By flooding the pipette with air, the spheres were released; (b) dimensions (in mm) and coordinates: (A–A) top view and (B–B) view from optical axis. The particles were placed in the center of the container so that the wall distance to all walls is d ≈ 11R. In the standard experiments the spheres were immersed around 15 mm deep. The origin of coordinates which is used in the evaluation lies in the center of the sphere after it was completely detached from the pipette. Dashed area: measurement range.

The container was filled up to a height of around 450 mm with silicone oil which is a Newtonian fluid. The silicone oil had a nominal viscosity of 1000 cSt. The choice of the model particle size together with the choice of a high viscosity liquid ensured that Re_P is always much smaller than 1. This condition allowed to investigate the same conditions as small, elastic microparticles would experience in aqueous liquids. The spheres were hold with a pipette under weak vacuum and then immersed in the liquid. The wall distance of the sphere center to all sides was about d ≈ 11R (see Fig. 2(b)). After immersion, the vacuum was released. The sphere began to fall without rotation due to gravity. This ensured that the spheres began to sediment at an initial velocity of U_P,0 = 0 ms⁻¹ (starting from rest). High-resolution videos of the sedimentation experiments were recorded by a DSLR camera (Nikon® D7200 with Sigma® 50 mm f1.4 objective lens). Subsequently, the velocities were evaluated with a self-programmed image processing tool in MATLAB. The tool tracked the centroid of the recorded pixel disc in each image extracted from the video at fixed timesteps and calculated the velocity. During the experiments, the container with silicone oil was illuminated from the opposite side of the camera by a collimated light panel. This ensured a straight projection of the model particle recorded by the camera sensor and allowed for the assumption, that the recorded centroid of the disc corresponds to the center of mass of the sphere.

3.2. Model particle fabrication

Elastic model particles were fabricated from polydimethylsiloxane (PDMS) by casting. To vary Young's modulus of the particles, mixtures of two PDMS types were prepared in different mixing ratios. The fabrication procedure was based on the report by Palchesko et al.³¹ First, base blends of commercially available PDMS elastomer Sylgard^TM 184 (Dow Corning®) and PDMS Dielectric Gel Sylgard^TM 527 (Dow Corning®) were prepared according to the manufacturer's specifications. The recommended mixing ratios (Sylgard 184 silicone oil: curing agent in a 10 : 1 ratio; Sylgard 527 part A: part B in a 1 : 1 ratio) were used. Each base blend was colored black with 1 w% iron oxide powder. The production of base blends in the recommended mixing ratio ensured that complete cross-linking could take place for both components. This is of crucial importance for the mechanical stability of the mixture of both PDMS types. Each base blend was degassed. Hereafter, the base blends were mixed with each other in a 1 : 1 ratio and a 1 : 5 ratio, respectively. Pure Sylgard 184, respectively the again degassed mixtures of Sylgard 184 and Sylgard 527, were poured into a mould for hemispheres. The hemisphere moulds had a diameter of 12 mm. The casted hemispheres were hardened for 12 h at 60 °C. For at least another 36 h, they were cured at room temperature. Two hemispheres were bonded together with a thin film of the corresponding newly produced PDMS compound avoiding ridges and asymmetries. The bonded spheres were cured for at least another 48 h at room temperature. The shape deviation of the bonded hemispheres compared to a perfect sphere with radius R was evaluated prior to the experiments with high-resolution images. For all experiments it was shown that the measured area corresponds well to the calculated area of a disc with radius R resulting from circle fitting. Hence, shape factors of the model particles do not differ notably from a value of 1.

In the standard case, experiments were performed with the spheres in the dry state after fabrication. For comparison, spheres that had remained in silicone oil after the first experiment showed slight swelling effects. It was observed that size, weight and consequently the density of the sphere changed over time. This suggests that the spheres swell by diffusion of the silicone oil into the elastomer-gel matrix. However, a significant change in the material properties was only observed after the spheres had been immersed in the oil for at least two days. Consequently, swelling effects are not to be expected during the short period of the experiment. A defined initial state could be ensured for the experiments.

To compare soft PDMS spheres with rigid spheres whose density is in a range comparable to that of PDMS, spheres made of epoxy resin were fabricated. Blends of Casting Resin MS 1000 by Weicon® were mixed according to the manufacturer's recommendations and colored black with 1 w% iron oxide powder. The same hemisphere moulds as for the soft spheres were used to cast the hemispheres. The hemispheres were hardened according to the manufacturer's recommendation. The following steps were analogous to the fabrication of the soft spheres.

3.3. Material properties

The solid density of the spheres was determined directly after the sedimentation experiments. This ensured to be able to correctly represent the current state of the density. The solid density was determined using a hydrostatic balance (Sartorius® ENTRIS BCE 224i-1s analytical balance + density determination kit YDK03 for determination of solid and liquid densities). The balance has a readability of 0.1 mg. Density measurements were performed in distilled water. The density of silicone oil was also determined hydrostatically at room temperature. The corresponding material data for the solid and liquid density can be found in Table 1. The dynamic viscosity η of the silicone oil under experimental conditions was measured to be about 980 mPa s using a rotational viscometer (IKA® Rotavisc lo-vi).

Table 1 Measured material properties

Material properties
a According to manufacturer information.
Liquid density	ρ	971.28 ± 0.134	kg m^−3
Liquid dynamic viscosity	η	0.9797 ± 0.012	Pa s
Solid densities
Epoxy resin	ρ Epoxy	1159.21 ± 1.17	kg m^−3
Sylgard 184	ρ SYL184	1040.01 ± 1.90	kg m^−3
Sylgard 184 : 527 1 : 1	ρ MIX11	1004.75 ± 1.32	kg m^−3
Sylgard 184 : 527 1 : 5	ρ MIX15	987.59 ± 1.90	kg m^−3
Young's moduli
Epoxy resin	E Epoxy	2.9^a	GPa
Sylgard 184	E SYL184	1712 ± 82.55	kPa
Sylgard 184 : 527 1 : 1	E MIX11	936 ± 33.44	kPa
Sylgard 184 : 527 1 : 5	E MIX15	135 ± 13.14	kPa

---

The elastic material properties were determined experimentally by means of compression tests. Cylindrical specimens of the PDMS mixtures also used in the model experiments were fabricated. The compression tests were in accordance with DIN ISO 7743:2016-08.³² A Schenk Trebel RSA25 universal testing machine with a piezoelectric load cell and potentiometric displacement sensor was used to record the force-displacement measurement data in a displacement-controlled test (v_Δl = 10 mm min⁻¹), see Fig. 8 in the appendix. To avoid friction effects, silicone oil with a viscosity of 1000 cSt was used as lubricant. The Young's elastic modulus of each specimen was determined from the slope of the compressive stress–strain curve in the linear-elastic range of small deformations. The experimentally determined averaged Young's moduli are shown in Table 1.

4 Results and discussion

4.1. Velocity measurements

4.1.1. Reference: rigid spheres. Results for the velocity measurements of the nonheavy rigid spheres made of epoxy resin show typical velocity curves for rigid particles under wall influence, see Fig. 3. As expected, sedimentation shows two phases. After the initial, transient phase the rigid spheres reach the terminal velocity, the second phase of sedimentation dynamics.

Fig. 3 Dimensionless velocity plotted over the transient time scale of a sphere which starts sedimentation from rest. The sphere was made of epoxy resin with E_■ = 2.9 GPa, ρ_P,■ = 1159.21 ± 1.17 kg m⁻³, R_■ = 6 × 10⁻³ m, Re_P,■ = 0.179, γ_■ = 1.19; inset: absolute values of the measured particle velocity plotted over time.

The results are presented as absolute U_P–t diagram and in a dimensionless representation. As will be shown, the experiments with varying elasticity are not directly comparable on the dimensional time scale. The difference in density between materials and the mixtures lead to much faster sedimentation for the rigid spheres compared to the elastic spheres. Anyway, the dimensional quantities are shown for the sake of completeness.

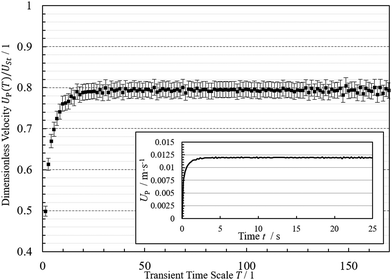
The nondimensionalization of the velocity is performed by U_St from eqn (2) as characteristic scale. The dimensionless velocity is plotted over the time scale resulting from the viscous diffusion time. This dimensionless time is also known as transient time scale T.³³

The measured terminal velocity of the rigid sphere is Ū_P,term,■ = 11.9 mm s⁻¹. The terminal Stokes velocity resulting from the measured material properties after eqn (2) is U_St,■ = 15.0 ± 0.4 mm s⁻¹. Hence, the measured terminal velocity in the experiment is reduced to about 80% of the velocity in an unbounded fluid. This is due to wall effects stemming from the four container walls, even though the particle sediments more than 11 times its radius away from the walls. This reduction is in accordance with existing literature data based on calculations. For example, according to Swan and Brady's numerical calculations, a particle would reach a terminal velocity of approximately 85–90% of the Stokes velocity when the sphere sediments at a distance of d ≈ 11R between two infinite walls.²⁹

Since in their calculations just two parallel walls were assumed, a reduction to a value in the measured range of our experiments with four walls is realistic. Specifically with respect to four walls, a good agreement of the experimental values is obtained with eqn (3) stemming from the increase in drag. With the correction factor found by Hensley and Papavassiliou in CFD simulations, a dimensionless velocity of U_P,corr/U_St = 0.82 is expected for the width of the container of 140 mm and a radius of 6 mm.³⁰

Because the investigated particles classify as nonheavy, the transient phase is more extended than it would be the case for the sedimentation of particles with high particle-to-fluid-density ratio γ ≫ 1. Solving the differential eqn (1) with respect to U_P neglecting the Basset history force, the theoretical terminal velocity for the epoxy resin spheres would be reached after about 0.1 seconds. In contrast, the experimental determined terminal velocity is reached after a time of about 3 seconds during the sphere sediments about 30 mm = 5R. Correspondingly, in the present case, initial effects like the added mass force and the Basset history force must be considered to describe the complete sedimentation dynamics adequately.

4.1.2. Elastic, deformable spheres. Velocity curves of elastic, deformable spheres significantly differ from those of the rigid spheres. Elasticity affects both the dynamic evolution of sedimentation as well as the terminal sedimentation velocity. This effect is the stronger the lower the Young's modulus E becomes, see Fig. 4(a–c).

Fig. 4 Dimensionless velocity plotted over the transient time scale of a sphere which starts sedimentation from rest made of (a) Sylgard 184 with E_◆ = 1712 ± 82.55 kPa, ρ_P,◆ = 1040.01 ± 1.9 kg m⁻³, R_◆ = 0.00593 m, Re_P,◆ = 0.061, γ_◆ = 1.07; (b) Sylgard 184:Sylgard 527 in a 1 : 1 mixing ratio with E_▲ = 936 ± 33.44 kPa, ρ_P,▲ = 1004.75 ± 1.32 kg m⁻³, R_▲ = 0.00598 m, Re_P,▲ = 0.032, γ_▲ = 1.03; (c) Sylgard 184 : Sylgard 527 in a 1 : 5 mixing ratio with E_● = 135 ± 13.14 kPa, ρ_P,● = 987.59 ± 1.9 kg m⁻³, R_● = 0.006 m, Re_P,● = 0.016, γ_● = 1.02; insets (a–c): absolute values of the measured particle velocities plotted over time; (d) schematic of elastic particle sedimentation showing the four phases of sedimentation.

While the differences in the sedimentation of rigid and elastic spheres are not yet obvious at first glance for the PDMS spheres with the highest Young's modulus of E_SYL184 = 1712 kPa (Fig. 4(a)), a reduction of the Young's modulus by about half (E_MIX11 = 936 kPa, Fig. 4(b)) already leads to a clearer visibility of the differences. The additional influence of elasticity is most evident with the lowest Young's modulus of E_MIX15 = 135 ± 13.14 kPa (Fig. 4(c)). It is evident that the sphere's increase in velocity is not uniform but happens in several stages. For the softest sphere, no clear steady-state condition was established within the measuring range. Based on the last measured values from T ≈ 1800(t ≈ 260 s), a terminal velocity of Ū_P,term,● ≈ 1.2 mm s⁻¹ can be estimated. These values exceed the actual measuring range (cf.Fig. 2(b)). The measuring range was selected in such a way that there is at least 140 mm (same as width and depth of the container) of space to the ground to exclude ground effects such as deceleration of the sphere. Values below the measuring range were nevertheless recorded by the camera and were considered in this case. All measured averaged terminal velocities and calculated Stokes's terminal velocities can be found in Table 2.

Table 2 Velocity measurements

E (kPa)	Ū P,term (mm s^−1)	U St (mm s^−1)
1712 ± 8255	4.5 ± 0.0	5.4 ± 0.2
936 ± 33.44	2.2 ± 0.0	2.7 ± 0.1
135 ± 13.14	1.2 ± 0.0	1.3 ± 0.04

---

In the following, we divide the sedimentation of the elastic spheres in four phases (Fig. 4(d)). The phases are: (I) the transient acceleration and (II) the first plateau. The dimensionless velocity on the first plateau is comparable with the dimensionless velocity of the rigid spheres as will be discussed in Section 4.2. The rigid plateau is followed by phase (III), the second acceleration. Ultimately, the elastic spheres reach phase (IV), a second plateau on which the elastic spheres reach their terminal sedimentation velocity. The principles and distinguishing features of the individual phases will be discussed in detail below.

The error bars shown in Fig. 3 and 4 were calculated by means of systematic and statistical measurement errors. Systematic errors in our measurements include, for example, measurement inaccuracies of the measuring instruments or errors when scaling the data from image velocimetry (pixels to real length units). Statistical measurement errors include the deviations within multiple measurements of a measured quantity. Here, the error analysis was carried out just for the terminal Stokes velocity. The representation of the uncertainty for the time scale T was omitted at this point for the sake of clarity.

Furthermore, only single experiments are presented in the figures. Experiments were performed with different specimens fabricated from each material and at least two measurements were performed for each specimen. Only experiments in which the sphere sedimented without rotation were considered. It was shown that the experiments are consistent and reproducible in terms of quality and quantity within the scope of the deviations described above.

It should also be noted that the starting point for velocity measurement is the first image where the sphere is completely detached from the vacuum pipette. This inevitably leads to the fact that the time T = 0 may differ between the individual experiments (depending on the time step size selected for the evaluation).

4.2. Phase I & II: transient acceleration, rigid plateau and elastic time scale

When the dynamics of rigid and elastic spheres are compared, similarities arise during the initial phases. First, all soft model particles presumably reach a first plateau (II) after a first, transient acceleration phase (I). This plateau lies at a value between ∼0.8 and ∼0.83 considering the mean value of the dimensionless velocity in this range. This velocity is just the same as the terminal velocity of the rigid spheres within the uncertainty of the measurements. It is hence reasonable to assume that all particles – both rigid and soft – initially reach the same reduced stationary state, which is only due to the wall influence.

However, the velocity-time behavior of the different spheres is not directly comparable to each other due to the different density ratios following from the individual mixing ratios (Table 1) needed to fabricate spheres of varying elasticity. Consequently, inertial influences are different for each type of sphere, see the different slopes of the velocity curves for different elasticities at low times in Fig. 5(a). For a better overview, we slightly shifted all curves within the measurement uncertainty to a reference value of 0.81 within the second phase. To make the experimental data of all experiments comparable on the time scale, the time delay of the increase due to inertia must be eliminated. One way to do this is reported by R. B. Moorman in 1955 in his dissertation.³⁴ If the transient range is resolved, an inflection point of the velocity-time curve appears. This point marks the time from which the frictional forces become more significant and ultimately more dominant than the inertial forces in the transient range. Experimentally Moorman determined this inflection point to be located at about 60% of the terminal velocity, i.e. U_P/U_St ≈ 0.6 at the corresponding time T_0.6. R.B. Moorman could map similar curves from the sedimentation of rigid spheres on a universal curve upon scaling T with T_0.6.³³ Following the same procedure, also the sedimentation velocities for elastic spheres fall on top of each other within the first two phases (Fig. 5(b)).

Fig. 5 (a) Dimensionless velocities of the experiments from Fig. 3 and 4 (■ epoxy resin, Sylgard 184, Mix 1 : 1, Mix 1 : 5) fitted to a value of 0.81 at the first plateau and plotted against the transient time scale; (b) interpolated dimensionless velocities of the experiments from Fig. 3 and 4 (— epoxy resin, Sylgard 184, Mix 1 : 1, Mix 1 : 5) adjusted to a value of 0.81 at the first plateau and plotted against the characteristic time ratio T/T_0.6. The interpolation was performed with cubic B-splines for the sake of clarity of the representation.

Attaining this universal curve supports the assumption that at the beginning of the sedimentation, elastic spheres follow the same principles as rigid spheres: inertial and frictional forces determine the transient acceleration until a steady state is reached. For the investigated spheres, any elastic effects obviously kick in at a time scale that is larger than the time scale for establishing this first plateau.

In the experiments, after reaching the first plateau, all curves of the elastic spheres start to rise again from a characteristic time ratio of T/T_0.6 ≈ 20 (see Fig. 5(b)). This allows an estimation and calculation of a time t_el with

From this time on, an elastic effect leads to a significant change in the particle dynamics and to an increase in the sedimentation velocity due to elasticity. Furthermore, t_el marks the end of the second sedimentation phase.

It should be mentioned that the normalization after Moorman in Fig. 5 was performed with respect to the sedimentation velocity in an unbounded fluid (U_P/U_St ≈ 0.6). It remains to be clarified whether in the case of wall influence and consequently lower velocities, the inflection point shifts accordingly, here to a point for T at U_P/U_St ≈ 0.6 × 0.81. Experimentally, the consequences for T_0.6 are not large due to the steep increase in velocity. An experimental investigation of this inflection point would however require a large temporal resolution of the transient phase and is a potential field for further investigations. In the present case, the chosen approach is viable insofar as a mapping of the curves on top of each other could be established.

4.3. Phase III: second acceleration

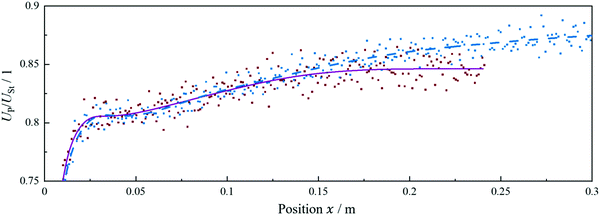
As described above, a second, elastic acceleration starts about the characteristic time t_el. Alternatively, the sedimentation velocity can be considered as a function of position in the direction of gravitational acceleration (Fig. 6). All elastic spheres sediment with a velocity comparable to the rigid sphere's velocity until the position x_el ≈ 10·R is reached. At this characteristic elastic onset position, the second acceleration begins. The extension of the second acceleration, i.e. the distance Δx_el between the characteristic onset x_el and the second plateau with the final velocity Ū_P,term, depends on the elasticity of the sphere. The more deformable (E↓) the sphere is, the longer is the distance Δx_el until the stationary state is reached. For the present data, the length of the second acceleration phase due to elasticity can be approximately described in terms of the sphere radius R as function of the Young's Modulus E (in Pa)

Fig. 6 Interpolated dimensionless velocities of the experiments from Fig. 3 and 4 (— epoxy resin, Sylgard 184, Mix 1 : 1, Mix 1 : 5, Mix 1 : 5 deep immersed) fitted to a value of 0.81 at the first plateau and plotted against the position x within the measuring range (x <0.3 m) – rigid sedimentation behavior is found until position x_el ≈ 10·R is reached.

As already described in Section 4.1.2., the sphere with the lowest Young's modulus only reached the terminal velocity at the last measured values that are not part of the measuring range (x < 0.3 m). For this reason, the second plateau of the softest sphere is not visible in Fig. 6. It is possible that the second acceleration phase has not yet been fully completed by this sphere.

4.4. Phase IV: second plateau – elastic terminal velocity

After the second acceleration discussed in the section before, the fourth phase of sedimentation of elastic spheres starts. In this final phase, the elastic spheres reach the terminal sedimentation velocity. The more deformable the spheres are, the faster are the spheres and the higher is the measured increase in velocity relative to the first plateau (see Fig. 6). The measured relative increase to the rigid sedimentation velocity Δ_el,exp reaches up to nearly 9% for the softest spheres (exact values see Table 3).

Table 3 Experimental values of Δ_el,exp and theoretical values of Δ_el,M calculated with a Poisson's ratio of ν = 0.491

E (kPa)	Δ el,exp (%)	Δ el,M (%)	0.025 Δel,Mα^−2 (%)
1712	1.39	1.24 × 10^−10	1.30
936	2.71	2.60 × 10^−10	3.37
135	8.96	7.65 × 10^−9	8.64

---

To our knowledge, no equation exists describing the increase in velocity of elastic spheres in a bounded fluid. There is merely the expression proposed by Murata for sedimentation in an unbounded fluid (eqn (4)). It predicts an increase to the terminal Stokes velocity of Δ_el,M.¹³ Hence, the increase in sedimentation velocity obtained experimentally is not directly comparable to the sedimentation velocity for elastic spheres proposed by Murata in eqn (4). However, a comparison of Murata's predicted increase and the experimentally obtained increase can be used to shed light on possible additional wall influences on the increase in velocity. In general, the terminal velocity of an elastic sphere can be thought to be influenced by the sphere's shape that evolves according to its elasticity.

A deformation may already occur in an unbounded fluid. Furthermore, additional wall-related forces may occur. It is known that bodies moving close to an elastic wall are subjected to an additional elastic lift force away from the wall as well as to an altered drag force.^35,36 Similar forces might also occur during sedimentation of soft bodies in a bounded fluid.

The increase according to Murata Δ_el,M can be determined using known material parameters. No exact measured values for the Poisson's ratio of the PDMS mixtures are available. Therefore, the increase according to Murata was calculated for various Poisson's ratios. Based on measurements for pure Sylgard 184, it is assumed that the Poisson's ratio of all mixtures has a value between ν = 0.490 and ν = 0.499.³⁷ The percentage increase from the experimental data is calculated from the mean values of the velocities of the first plateau and the second plateau.

Comparing the calculated increase according to Murata's equation to the measured increase in the experiments, shows that the values fundamentally differ in the order of magnitude, but slightly correlate in the prefactor (see Table 3). The measured increase in velocity relative to the first plateau is up to a factor 10¹⁰ higher than the percentage increase predicted by Murata. In total, the increase according to Murata Δ_el,M in an unbounded fluid is almost negligible for Poisson's ratios in the previously mentioned range. In contrast, the measured increase of nearly 9% is not negligible, particularly with regard to applications. Exemplarily, Table 3 shows the percentage increases Δ_el,M for a Poisson's ratio of 0.491 assumed for all PDMS mixtures.

Although the values of Δ_el do not fit to each other at the first glance, a closer look on the measured increase compared to the predicted increase shows that they just seem to differ by a factor α⁻² and some constant C(ν) which depends on the Poisson's ratio (see Fig. 7).

Δ_el,exp ≈ C(ν)·α⁻²·Δ_el,M (8)

Fig. 7 Experimental determined and by factor α⁻²·C(ν) fitted values of the velocity increase to the rigid velocity plotted against the Young's modulus E.

Calculation of the specific constants K₀ and K₁ from Murata's equation suggests that the sphere deforms into a prolate ellipsoid while sedimentation. Yet, this deformation is small, since the perturbation parameter α (viscous stresses vs. mechanical stresses) ≪ 1. In order to evaluate deformation during the experiments, the isoperimetric quotient was determined for each timestep. It is defined as (4·area·π)/perimeter² and gives the ratio of the measured area to the area of a disc with the same perimeter as the perimeter measured for the particles. Large deformation of the particle would lead to a change in the isoperimetric quotient over time. In our experiments, this ratio was found to be constant over time for all experiments. Consistently, no apparent deformation could be detected with the optical resolution of our measurement method, where also α ≪ 1.

Also, elastohydrodynamic lubrication theories, which predict wall lift and drag forces, typically consider small surface deformations that are not easily observable. At the same time, the effect of such wall-related forces is macroscopically significant. From the comparison of Murata's calculation in an unbounded fluid and the experiments in a bounded fluid, it is hence likely that wall-related forces influence the terminal velocity. After all, if lift-forces existed on the particle, they could pinch together the particle from all four sides.

4.5. Influencing factors and future directions

In order to further investigate the effect of walls on the terminal sedimentation velocity, more experiments are needed especially with varying radius to container size ratios. Experiments already show that this would require either very large container dimensions or the development of a specialized particle release mechanism. Experiments with spheres of R ≈ 4 mm made from the 1 : 5 mixture of Sylgard 184 and Sylgard 527 showed that such small spheres are not heavy enough to overcome adhesion to the pipette on their own. Pushing the spheres however leads to completely different initial conditions and hence sedimentation dynamics.

In addition, PIV experiments or CFD simulations might help to shed light on the hydrodynamic mechanisms under wall influence by visualizing the fluid streamlines. The plane container walls and the four corners of the container could lead to an altered flow profile around the sphere compared to the axisymmetric profile assumed for unbounded sedimentation in the Stokes flow regime. In the case of elastic spheres, these asymmetries in the hydrodynamics could cause elastohydrodynamic lift forces and the pinch already mentioned in Section 4.4. Furthermore, coupled fluid-structure mechanics interaction (FSI) simulations might help to investigate and to understand these elastohydrodynamic interactions. Such FSI simulations could also shed light on the magnitude of deformation caused by the hydrodynamic forces which could not be resolved with the optics used in the experiments.

Also, the pressure in the system might play a role since it could in principle deform the particles. To check any possible influence of hydrostatic pressure on the elastohydrodynamic acceleration, experiments with a larger immersion depth were performed (violet curve in Fig. 6). The same sphere as considered in Section 4.1.2 that has a Young's modulus of 135 kPa was immersed about 55 mm deeper before release. No influence of the hydrostatic pressure (at least not at this immersion depths) could be observed for phases I and II and also not for the beginning of phase III. This is consistent with the assumptions and also with the behavior of rigid spheres, like which the elastic spheres behave during the initial times. Deeper immersed spheres however do not reach the same terminal velocity as initially less immersed spheres (see Fig. 9 in the appendix). This saturation takes place significantly before any possible influence of the bottom of the container would be assumed (x >0.24 m). Hence, the length of elastohydrodynamic acceleration as described in eqn (7) may depend on further variables that remain to be investigated.

Fig. 8 Stress–strain curve of four cycles (load and unloading) of a test with a cylinder fabricated from a Sylgard 184 and Sylgard 527 in a 1 : 5 mixing ratio lubricated with silicone oil; Since no standard bodies for testing were used and the recorded displacement of the sensor is not adjusted to the sample height, there are intercepts (curve does not start at point (0/0)). To determine Young's moduli and thereby exclude initial and frictional effects, in this example the slopes of in total 0.0.5 absolute strain in the range of small deformations are determined by a linear fit (here in the range [0.025;0.075])

Fig. 9 Measured dimensionless velocity and interpolation curves of experiments of spheres with Young's modulus E_MIX15 = 135 ± 13.14 kPa (– – – Mix 1 : 5 immersed 15 mm deep, — Mix 1 : 5 immersed 70 mm deep) fitted to a value of 0.81 at the first plateau and plotted against the position x within the measuring range (x< 0.3 m for 15 mm immersion; x< 0.24 m for 70 mm immersion).

Under the here investigated conditions, the sedimentation dynamics of elastic particles could be well described in four phases. Both the characteristic elastic time t_el and the characteristic onset position x_el show a dependence on the particle radius. Especially in the case of small and highly deformable particles, it could be possible that elastic effects would kick in earlier. Then it would no longer be possible to distinguish between the acceleration phases and effectively two phases would be observed. However, the resulting overall time of acceleration to reach the terminal velocity would still be much longer than in the case of comparable rigid particles.

5 Conclusion

In this paper, we presented experimentally derived characteristics of sedimentation of elastic, deformable and nonheavy spheres in a rectangular duct. The experiments gave fundamental insights into the fluid-particle dynamics of elastic particles in bounded fluids and at low Reynolds numbers. We observed that the sedimentation of elastic spheres under the influence of walls differs fundamentally from that of rigid spheres.

Sedimentation of rigid and elastic spheres with a radius of 6 mm was performed in a rectangular duct at low Reynolds numbers. Sedimentation dynamics of rigid spheres was as expected. Velocities of ∼81% of the Stokes velocity were measured for the rigid spheres. The reduction of the velocity is due to the influence of the four surrounding plane walls in the rectangular duct. The measured reduction in velocity was expected and agrees with theoretical calculations from literature. The experiments with the elastic model particles showed a completely different velocity-time behavior, or velocity-displacement behavior respectively, than rigid particles. It appears that elastic effects kick in at a comparatively large time scale, such that the sedimentation of elastic spheres could be described by four phases instead of two phases as for solid particles. The first phase showed a transient acceleration and the second phase a first velocity plateau that corresponds to the dimensionless velocity of the rigid spheres. Thereafter, for all elastic spheres a second acceleration began after a distance of about 10R. This characteristic onset position corresponds to a time of t_el ≈ 20T_0.6·4ρR²η⁻¹. From this characteristic time on, the elasticity has a significant influence on the sedimentation of elastic spheres in the bounded fluid. The third phase of sedimentation showed further acceleration that depends strongly on the Young's modulus. The more deformable the spheres were, the longer the second acceleration lasted and the further the distance was until the terminal velocity of the second plateau was reached. It was shown, that the softest spheres sedimented more than 50R until the terminal velocity of the second plateau was reached. Furthermore, the measured percentage increase Δ_el,exp compared to the rigid velocity plateau was found to be up to 9%. This long-term unsteady behavior and the much higher terminal velocities both are relevant for calculations, but they also have a significant impact on applications, e.g. process design, since these deviations from the known rigid particle behavior are not negligible.

With the help of our experimental data and the characteristic quantities obtained so far, it is already possible to make some easy-to-calculate statements about the expected terminal velocity of elastic (micro-)particles under wall influence. Our findings and their discussions regarding the gaps that still exist, also encourage a great deal of further research. Our findings can be used as a basis for following investigations in this area, which in our opinion, especially with respect to the associated applications, has been little studied experimentally but also theoretically in the past. In particular, we see a lot of potential in conducting further experiments with more variations of Young's modulus and of the ratio of the radius to the duct size. Even sedimentation of elastic spheres in an unbounded fluid remains to be investigated experimentally. An overarching goal for the future would be the modeling of the relationship between the elastic material parameters and the particle dynamics. With the help of analytical expressions of the forces acting on particles or the sedimentation velocity as a function of the Young's modulus, the computational effort, e.g. for CFD simulations including elastic particle dynamics, would be greatly reduced.

Conflicts of interest

The authors report no conflict of interest.

Appendix

Acknowledgements

Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 172116086 – SFB 926. The experiments were performed in frame of subproject A10 “Elastohydrodynamic interactions of particles flowing over microstructured surfaces” in the Collaborative Research Center 926 (CRC926 MICOS). Thanks to our CRC926 collaboration partners from the Working Group Materials Testing (AWP), Technische Universität Kaiserslautern, D-67663 Kaiserslautern, Germany under Prof. Eberhard Kerscher (subproject B04 of CRC926). Special thanks to Markus Burmeister (AWP) for material testing of the elastic specimens and for the editorial support.

Notes and references

1. A. De, Sedimentation Process and Design of Settling Systems, Springer, New Delhi, 2017.
2. G. R. D. S. Araújo, N. B. Viana, F. Gómez, B. Pontes and S. Frases, Cell Surf., 2019, 5, 100028.
3. W. E. Dietrich, Water Resour. Res., 1982, 1615–1626.
4. P. U. Iyare, S. K. Ouki and T. Bond, Environ. Sci.: Water Res. Technol., 2020, 6, 2664–2675.
5. D. Barthès-Biesel, Annu. Rev. Fluid Mech., 2016, 48, 25–52.
6. A. N. Balachandran Nair, S. Pirker, T. Umundum and M. Saeedipour, Comput. Part. Mech., 2020, 593–601.
7. M. M. Villone and P. L. Maffettone, Rheol. Acta, 2019, 58, 109–130.
8. M. M. Villone, Microfluid. Nanofluid., 2019, 23, 47.
9. M. de Corato, F. Greco, G. D’Avino and P. L. Maffettone, J. Chem. Phys., 2015, 142, 194901.
10. T. Tohme, P. Magaud and L. Baldas, Micromachines, 2021, 12, 277.
11. K. Patel and H. Stark, Soft Matter, 2021, 17, 4804–4817.
12. M. Bukowicki, M. Gruca and M. L. Ekiel-Jeżewska, J. Fluid Mech., 2015, 767, 95–108.
13. T. Murata, J. Phys. Soc. Jpn., 1980, 48, 1738–1745.
14. S. Takeuchi, Y. Yuki, A. Ueyama and T. Kajishima, Int. J. Numer. Methods Fluids, 2010, 64, 1084–1101.
15. R. Clift, J. Grace and M. Weber, Bubbles, Drops, and Particles, Acad. Press., New York, 1978.
16. H. A. Stone, Annu. Rev. Fluid Mech., 1994, 26, 65–102.
17. J. Tsamopoulos, Y. Dimakopoulos, N. Chatzidai, G. Karapetsas and M. Pavlidis, J. Fluid Mech., 2008, 601, 123–164.
18. R. Nimmagadda, J. Braz. Soc. Mech. Sci. Eng., 2020, 42, 526.
19. A. Cioncolini and M. Magnini, Fluids, 2021, 6, 437.
20. A. R. Wadhwa, V. Magi and J. Abraham, Phys. Fluids, 2007, 19, 113301.
21. A. B. Basset, A Treatise on Hydrodynamics, George Bell and Sons, London, 1888.
22. J. V. Boussinesq, Theorie analytique de la chaleur, Gauthier-Villars, Paris, 2nd edn, 1903.
23. C. W. Oseen, Neuere Methoden und Ergebnisse in der Hydrodynamik, Akademische Verlagsgesellschaft M. B. H., Leipzig, 1927.
24. T.-J. Chang and B. C. Yen, J. Eng. Mech., 1998, 1193–1199.
25. G. G. Stokes, Trans. Cambridge Philos. Soc., 1851, 8–106.
26. E. E. Michaelides, J. Fluids Eng., 1997, 119, 233–247.
27. H. Faxén, Ann. Phys., 1922, 89–119.
28. J. Happel and H. Brenner, Low Reynolds number hydrodynamics. With special applications to particulate media, Kluwer Acad, Publ, Dordrecht, 5th edn, 1983.
29. J. W. Swan and J. F. Brady, Phys. Fluids, 2010, 22, 103301.
30. Z. D. Hensley and D. V. Papavassiliou, Ind. Eng. Chem. Res., 2014, 53, 10465–10474.
31. R. N. Palchesko, L. Zhang, Y. Sun and A. W. Feinberg, PLoS One, 2012, 7, e51499.
32. DIN ISO 7743:2016-08, Rubber, vulcanized or thermoplastic – Determination of compression stress–strain properties (ISO 7743:2011).
33. M. Tashibana and K. Kitasho, Memoirs of the Faculty of Engineering Fukui University, 1976.
34. R. B. Moorman, Motion of a Spherical Particle in the Accelerated Portion of Free Fall, PhD Dissertation, 1955.
35. J. Urzay, S. G. Llewellyn Smith and B. J. Glover, Phys. Fluids, 2007, 19, 103106.
36. A. Kargar-Estahbanati and B. Rallabandi, Phys. Rev. Fluids, 2021, 6, 03400.
37. A. Müller, M. C. Wapler and U. Wallrabe, Soft Matter, 2019, 15, 779–784.

---