 Open Access Article
Open Access ArticlePassive high-frequency microrheology of blood†
Jose Rafael
Guzman-Sepulveda‡
 a,
Mahed
Batarseh
a,
Ruitao
Wu
a,
William M.
DeCampli
bc and
Aristide
Dogariu
a,
Mahed
Batarseh
a,
Ruitao
Wu
a,
William M.
DeCampli
bc and
Aristide
Dogariu
 *a
*a
aCREOL, The College of Optics and Photonics, University of Central Florida, 4304 Scorpius, Orlando, Florida 32816, USA. E-mail: adogariu@creol.ucf.edu; Tel: +1 407 823 6839
bPediatric Cardiothoracic Surgery, The Heart Center, Arnold Palmer Hospital for Children, Orlando, Florida, USA
cCollege of Medicine, University of Central Florida, Orlando, Florida, USA
First published on 13th March 2022
Abstract
Indicative of various pathologies, blood properties are under intense scrutiny. The hemorheological characteristics are traditionally gauged by bulk, low-frequency indicators that average out critical information about the complex, multi-scale, and multi-component structure. In particular, one cannot discriminate between the erythrocytes contribution to global rheology and the impact of plasma. Nevertheless, in their fast stochastic movement, before they encounter each other, the erythrocytes probe the subtle viscoelasticity of their protein-rich environment. Thus, if these short time scales can be resolved experimentally, the plasma properties could be determined without having to separate the blood components; the blood is practically testing itself. This microrheological description of blood plasma provides a direct link between the composition of whole blood and its coagulability status. We present a parametric model for the viscoelasticity of plasma, which is probed by the erythrocytes over frequency ranges of kilohertz in a picoliter-sized volume. The model is validated both in vitro, using artificial hemo-systems where the composition is controlled, as well as on whole blood where continuous measurements provide real-time information. We also discuss the possibility of using this passive microrheology as an in vivo assay for clinically relevant situations where the blood clotting condition must be observed and managed continuously for diagnosis or during therapeutic procedures at different stages of hemostatic and thrombotic processes.
1. Introduction
Understanding how blood and its components react to external mechanical stimuli has been a reliable source of information for understanding and treating diseases. The complex rheology of blood is critical since it correlates with a number of pathological conditions and it is also a convenient way to monitor the effects of pharmaceutical therapies.1–3 As an example, anomalies in the rheology of blood plasma, which are well-known to occur in both acute and chronic conditions,4,5 including hypertension6–8 and diabetes,9–11 can be used as markers and risk factors due to their underlying relationship with the concentration of fibrinogen and other macromolecules in plasma.12,13Most important transformations of the rheological properties of blood occur during coagulation. This delicate process is dominated, aside from platelet adhesion, by different mechanisms of fibrin polymerization.14,15 Controlling the subtle balance between fibrin polymerization and dissolution is critical in a variety of clinical settings where the coagulation status of blood needs to be managed dynamically. Such settings include, for instance, cardiovascular surgery requiring cardiopulmonary bypass (CPB), any major surgery in patients with coagulation disorders, extracorporeal life support (ECLS), extracorporeal membrane oxygenation (ECMO), catheter-based interventional procedures, and haemodialysis, among others. These circumstances require continuously measuring and effectively managing the coagulation status (viscoelasticity), which can cause catastrophic thrombosis and haemorrhage despite using “adequate anticoagulation therapies”.16–18
The majority of conventional coagulation assays rely on in vitro macroscopic rheological measurements, which are indicative of low-frequency mechanical properties. These approaches use external mechanical stimuli to controllably deform the fluid at low rates of a few to tens of Hertz and over at least millimeter-sized spatial scales. Moreover, these assays are provocative and non-physiologic in nature because the coagulation process is induced by external stimuli.19–22 The sample condition is assessed based on the changes in the bulk mechanical properties of the blood as the coagulation cascade is accelerated. The detailed molecular composition and its structural dynamics are all included in the effective, macroscopic properties of viscoelasticity. This approach is usually sufficient to describe common homogeneous fluids but misses some details in the case of complex, multi-component fluids such as blood. A brief survey of the various hemorheological assays is provided in the ESI† S1.
Microrheology, on the other hand, is concerned with how viscoelastic materials flow at much smaller spatial and temporal scales.23 In this framework, physical details at submicron and even molecular scales are probed over a large spectrum of frequencies.24 In this regard, we note that a microrheological measurement can be performed by active or passive means, depending on whether the probe particles are externally moved or driven solely by thermal forces. Moreover, a passive measurement can also make use of the intrinsic existence of particulates that can act as natural probes for their surroundings. In the general case of complex heterogeneous fluids, the homogenization of the mechanical properties is intrinsically scale-dependent.25 Thus, microrheology is not an alternative to traditional rheological measurements but rather a complementary description; it describes the microscopic scales of complex fluids. In the case of blood, microscale measurements could examine, for example, the viscoelasticity associated with the underlying molecular composition e.g., fibrin and other proteins,26,27 while isolating the influence of the much larger erythrocytes.
In this paper, we present a parametric description of the microrheological properties of plasma. The simple and robust parametric description is based on the standard Maxwell model of viscoelastic fluids and describes the local viscoelasticity properties over frequency ranges that are accessible through light scattering measurements. Most importantly, the erythrocytes themselves act as passive probes for the microrheological properties of plasma. We demonstrate that the parameters of the microrheological model can be used to monitor, in a condensed yet informative manner, the connection between the blood composition and its coagulability, which, in turn, can be used in clinical situations where the status of blood needs to be monitored and managed continuously.
2. Materials and methods
2.1. Sample preparation
2.2. Experimental procedure
 with f being the frequency, ai the relative amplitude,
with f being the frequency, ai the relative amplitude,  , and νi the representative relaxation time of the i-th population, respectively. Two Lorentzian components (N = 2) were sufficient to describe the shape of P(f) in all cases. The spectral decomposition of P(f) was then used to calculate the mean squared displacement (MSD) of the diffusing particles (RBCs),
, and νi the representative relaxation time of the i-th population, respectively. Two Lorentzian components (N = 2) were sufficient to describe the shape of P(f) in all cases. The spectral decomposition of P(f) was then used to calculate the mean squared displacement (MSD) of the diffusing particles (RBCs),  , where q = 2k0
, where q = 2k0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n
n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2) is the magnitude of the scattering vector, with
sin(θ/2) is the magnitude of the scattering vector, with  and θ = π rad in our reflection geometry, and n is the refractive index of the medium. Then, the MSD was used to estimate the complex viscoelastic moduli for tracers of known size. According to the approach described in ref. 30, 31, the magnitude of the viscoelastic modulus is determined as
and θ = π rad in our reflection geometry, and n is the refractive index of the medium. Then, the MSD was used to estimate the complex viscoelastic moduli for tracers of known size. According to the approach described in ref. 30, 31, the magnitude of the viscoelastic modulus is determined as  , where
, where  is the logarithmic slope of the MSD curve. Then, we extracted (i) the elastic component, G′(ω) = |G*(ω)|cos(πα(ω)/2), (ii) the viscous component, G′′(ω) = |G*(ω)|sin(πα(ω)/2), and also (iii) the loss tangent, tan
is the logarithmic slope of the MSD curve. Then, we extracted (i) the elastic component, G′(ω) = |G*(ω)|cos(πα(ω)/2), (ii) the viscous component, G′′(ω) = |G*(ω)|sin(πα(ω)/2), and also (iii) the loss tangent, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ(ω) = G′′(ω)/G′(ω). Details about the retrieval of the parameters of the Maxwell model starting from the measured P(f) can be found in the ESI.†
δ(ω) = G′′(ω)/G′(ω). Details about the retrieval of the parameters of the Maxwell model starting from the measured P(f) can be found in the ESI.†
3. Results and discussion
3.1. High-frequency micro-rheological model of blood
Complex fluids, such as blood, are viscoelastic and they can store and release energy. Moreover, their response to mechanical stimuli depends on both the amplitude and the frequency of the stimulus, as well as its duration and the way it is applied spatially.32,33 Additionally, because of their multi-component composition, their rheological properties are mesoscopic in nature as they depend on both the spatial and temporal scales at which the different components interact with one another. In this regard, the complex fluid components contribute in different ways at different scales such that macro-rheological properties describe bulk characteristics averaged over larger spatial scales, at lower frequencies, while micro-rheological properties refer to the fluid's response over a broad range of high frequencies in microscopic domains.Blood is a biological complex fluid consisting mainly of a concentrated aqueous suspension of RBCs, which comprise about 45% of the total mass and are suspended in plasma, a liquid medium containing around 92% of water and 8% of macromolecules, proteins, and trace amounts of other materials. Because of their high concentration, the macroscopic rheological properties of whole blood are largely determined by RBCs as well as their aggregates, including clusters, rouleaux, and clots.1 Moreover, the rheological properties of blood can also be highly non-stationary and can change rapidly over time, as it happens during coagulation.20 Recent efforts in hemorheology have focused mainly on modelling bulk rheological properties of blood under different regimes of active deformation i.e., steady flow and transient shear, typically outside the linear viscoelastic regime, where large deformations take place,34 with special attention to the contributions of RBC deformability and rouleaux formation.35,36 Ultimately, accounting for these contributions in bulk hemorheology can lead to diagnosis of diseases such as sickle cell anaemia, among others.1 A microscopic hemorheological measurement, on the other hand, can examine the viscoelasticity of plasma, associated with its underlying molecular composition, within a narrow window of spatial and temporal scales where the influence of the RBCs is removed. In this regard, it has been recently shown that even plasma itself exhibits a non-Newtonian behaviour due to the presence of macromolecules regardless of their small concentration.37,38 Thus, even for a microscopic description, a non-Newtonian viscoelastic fluid must be considered.
To quantitatively parametrize the frequency response of the effective local viscoelasticity, we use a standard form of a two-fluid rheological Maxwell model comprising a purely-viscous component (Newtonian solvent) and a single, effective viscoelastic component,32,39,40 as illustrated schematically in Fig. 1. Within the frame of this model, the viscoelastic response can be described in terms of the real and imaginary parts of the frequency-dependent complex viscoelastic moduli. As such, the frequency (ω) dependence of the elastic modulus (energy storage, G′(ω)) and the viscous modulus (energy dissipation, G′′(ω)), can be expressed as:
 | (1) |
 | (2) |
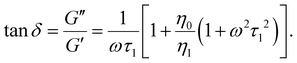 | (3) |
The loss tangent relates to the material's fluidity; it approaches infinity for a purely viscous material and is zero for a perfectly elastic material. As expressed in eqn (1)–(3), the viscoelastic response is parametrized in terms of the background viscosity η0 and a single effective viscoelastic element with viscosity η1 and relaxation time τ1 = η1/k1, where k1 refers to the spring constant associated to a purely elastic material.32,39,40
Similar Maxwell models are used in traditional bulk rheology where the macroscopic measurements are interpreted equivalently in terms of the complex viscosity.1,2,34 Notably, more complicated versions of the Maxwell rheological models with a larger number of viscoelastic elements have been used to account for larger-scale effects such as RBCs deformability as well as the formation of rouleaux and clusters,35,36 and even in attempts to describe the properties of blood clots in the context of viscoelastic solids.41,42 Maxwell-based descriptions have also been used to quantify the motion of Brownian particles in viscoelastic fluids.43,44 In Fig. 1 we schematically illustrate that the transition from a baseline condition either towards coagulation (from state A to state B) or towards anti-coagulation (from state A to state C) can be accounted by the same model, by following the changes in the triad of Maxwell parameters (η0,η1,τ1).
In this microrheological model of blood, independent RBCs act as effectively rigid probes whose Brownian motion reveals the viscoelastic properties of their immediate surroundings. When the probes are rigid and non-interacting, one can estimate the high-frequency range for which this simple microscopic description is valid. For instance, a spherical probe suspended in a fluid with effective viscosity ν and at temperature T explores diffusively, in a time t, an effective area given by the MSD, 〈Δr2(t)〉 = Defft. In standard Stokes–Einstein formulation, the effective diffusion coefficient is  , where kB is the Boltzmann constant, and dh is the hydrodynamic diameter of the probe particle. In normal conditions, RBCs have an average volume of about 90 fL with a surface area of about 136 μm2, and can swell up to a spherical shape of about 150 fL without membrane distension.45,46 A sphere with equivalent volume would have a diameter dh ≈ 5.56 μm. Regardless of the specific value taken for the viscosity of plasma e.g., in normal conditions or heparinized,5 and the detailed type of RBC packing,47 at 37 °C, an RBC-equivalent sphere needs several hundreds of seconds to diffuse over its own diameter. Based on this simple argument, one can safely conclude that if an independent RBC diffuses during 1–100 ms, which represents a frequency range of 10 Hz–1 kHz, at physiological conditions, it explores diffusively less than 10% of its own diameter. This means that for frequencies higher than 10 Hz, the response is determined by the immediate surroundings of a typical RBC. Thus, such a high-frequency microrheology measurement effectively examines only the viscoelastic properties of plasma. We would like to emphasize that, strictly, this picture where the RBCs test their environment and the influence of larger aggregates is removed, is valid only within the narrow window of spatial and temporal scales explained above, which can be accessed through light scattering measurements.
, where kB is the Boltzmann constant, and dh is the hydrodynamic diameter of the probe particle. In normal conditions, RBCs have an average volume of about 90 fL with a surface area of about 136 μm2, and can swell up to a spherical shape of about 150 fL without membrane distension.45,46 A sphere with equivalent volume would have a diameter dh ≈ 5.56 μm. Regardless of the specific value taken for the viscosity of plasma e.g., in normal conditions or heparinized,5 and the detailed type of RBC packing,47 at 37 °C, an RBC-equivalent sphere needs several hundreds of seconds to diffuse over its own diameter. Based on this simple argument, one can safely conclude that if an independent RBC diffuses during 1–100 ms, which represents a frequency range of 10 Hz–1 kHz, at physiological conditions, it explores diffusively less than 10% of its own diameter. This means that for frequencies higher than 10 Hz, the response is determined by the immediate surroundings of a typical RBC. Thus, such a high-frequency microrheology measurement effectively examines only the viscoelastic properties of plasma. We would like to emphasize that, strictly, this picture where the RBCs test their environment and the influence of larger aggregates is removed, is valid only within the narrow window of spatial and temporal scales explained above, which can be accessed through light scattering measurements.
As mentioned before, microrheology complements the information provided by bulk rheology because it examines the contribution of microscopic complex fluid components (plasma and macromolecules) while effectively isolating the influence of the RBCs and their aggregates. An experimental verification that the RBCs can be treated as rigid particles over the spatial and temporal scales of interest is shown below, in Section 3.3.1.
3.2. Optical microrheology
Optical approaches can provide measurements of mechanical responses in the frequency range of interest because the characteristic correlation time of the light scattered by complex fluids, in general, lies in that range.48 Microrheological information can be accessed optically by different approaches such as diffusing-wave spectroscopy,31,49,50 particle tracking,49,51 interference microscopy,52 and speckle correlation.53–55 The spatial and temporal scales at which the viscoelastic properties are measured in those approaches depend on the experimental implementation. Also, as mentioned before, these microrheological measurements can be performed passively or actively, depending on whether the motion of the probes has an intrinsic thermal origin or is driven by an additional external force. Moreover, in a passive measurement, one can also take advantage of the intrinsic presence of particulate components to perform the measurement, without the need to introduce probe particles. Thus, in our approach of using the RBCs as probes of their environment, one can say that the blood is practically testing itself.Recently, we have demonstrated that the coherence-gated DLS technique used here, is capable of passively measuring microrheological properties of blood.56 We showed that sensing dynamics at submicron scales allow discriminating between different coagulation states. Also, the optical fiber-based measurement system can be incorporated into standard vascular access devices that allow testing without isolating a blood sample and without having to externally trigger the coagulation cascade. Thus, this optical microrheology procedure overcomes the main constraints of macroscopic rheological assays.
A brief description of our experimental setup is given above, in Section 2.2, and more details are provided in the ESI,† (Section S2).
3.3. Use of the parametric Maxwell model
The interpretation of the microscopic viscoelastic properties of plasma within the frame of the Maxwell model requires the RBC to be rigid and independent from each other, within the frequency range of our interest. In this section, we first demonstrate the validity of this assumption, and then use our parametrization approach in different settings, including some that are relevant for clinical scenarios. We show that the Maxwell parameters capture variations in the status of blood and, in simplified in vitro hemo-systems, they can be associated to specific structural components. We also show that the model's parameters can be used to follow long-term processes such as the natural, incipient coagulation of normal blood. We emphasize that coagulation was not induced, in any case, by any external agent.As can be seen in Fig. 2(a), measured P(f) from freshly drawn whole blood as well as from a control sample of 50% RBC and 1 mg mL−1 fibrinogen in PBS are very well described by a single Lorentzian function. This is the hallmark of a rigid spherical particle diffusing normally in a purely viscous fluid.48,58 Moreover, we present in Fig. 2(b)P(f) measured in the same fibrinogen solution after replacing the RBCs with polystyrene particles of 1 um. All measurements shown in Fig. 2 were performed at the physiological temperature of 37 °C, without altering the natural rigidity of the RBCs membrane, and with the same settings (from 1 Hz to 10 kHz, 1 Hz resolution, and integration time of 30 seconds) on a freshly prepared sample. The fact that P(f) is Lorentzian in all cases, verifies that the RBCs can be treated as rigid probes of their own environment. Thus, using the measured P(f) to estimate the microscopic viscoelasticity is valid such that the model's parameters indeed reflect the plasma viscoelasticity within the narrow window of spatiotemporal scales of our measurements.
The outcome of this control experiment is summarized in Fig. 3. The temporal evolution of the three parameters in the Maxwell model is shown in Fig. 3(a) for the case when the polymerization was activated with 0.02 units per mL thrombin. The detailed steps for retrieving the parameters of the Maxwell model can be found in the ESI,† (Section S3). Thrombin was added at the beginning of the measurement, t = 0, and one can see that as the polymerization evolves in time, the background Newtonian viscosity η0 drops. At the same time, the contribution of the viscoelastic element (η1,τ1) gradually increases, especially the relaxation time τ1. This behavior together with the evident saturation of the process can be understood as a consequence of the conservation of the total amount of fibrinogen. Initially, the dispersed fibrinogen molecules contribute together with the water molecules but, as the polymerization progresses, they gradually build up the viscoelastic component τ1 due to fibrin formation.
 | ||
| Fig. 3 Viscoelasticity evolution during controlled coagulation. (a) Temporal evolution of the Maxwell model parameters (η0, η1, τ1) for a suspension of 50% RBC in PBS with fibrinogen after adding thrombin (final concentration is 0.02 units per mL). The band on the curve is the standard deviation from the sliding window along the curve. The Maxwell parameters are extracted from fitting the complex viscoelastic moduli measured to eqn (1)–(3) simultaneously. (b) Effect of thrombin concentration on the rate of change of ηo and τ1, θηo and θτ1, respectively. | ||
Taking advantage of the continuous nature of our measurement, one can also evaluate the rate of fibrin production and, therefore, assess the role of thrombin in this process. To this end, we illustrate in Fig. 3(b) the rate at which the Maxwell parameters evolve as a function of thrombin concentration. For instance, the rate of change of τ1 surges in a highly nonlinear fashion with increasing thrombin concentration, which is indicative of the faster formation of the fibrin network. The same is evident in the changing rate of η0, which decreases due to the depletion of the number of free fibrinogen molecules contributing to η0. We also note that there is only a minor influence of the thrombin concentration on η1 related to fibrin formation, which is the result of the constant amount of fibrinogen in our simplified hemo-system. Thus, the results, in this simplified hemo-system, demonstrate that the parameters can indeed capture the changes on specific structural components. In the following, we will show that this microrheological approach can be used to monitor the coagulation status of whole blood, including clinically relevant situations where the coagulation status of blood needs to be monitored continuously and managed dynamically.
 | ||
| Fig. 4 (a) Typical long-term evolution of the parameters of the Maxwell rheological model acquired continuously during the incipient coagulation. Parameters evolution for the entire patient population: (b) the viscous components η0 and η1, (c) the relaxation time of the viscoelastic element, τ1, and (d) the purely elastic k1 calculated based on the ratio viscous coefficient η1 and the relaxation time τ1 (see text for details). The interpatient variability is represented by the error bars that indicate the standard deviation across the 23 subjects; time t = 0 is the starting of the DLS measurement immediately after the blood draw. The Maxwell parameters are extracted from fitting complex viscoelastic moduli measured simultaneously to eqn (1)–(3). | ||
In the particular case illustrated in Fig. 4(a), one can see that, both viscous components, η0 and η1, have initially a similar value but, gradually, split apart as incipient coagulation takes place. The main changes are reflected in the viscoelastic components, while the background viscosity ηo remains relatively constant. More importantly, the clear increase of the parameter τ1 indicates a progressive steady increase of the viscoelastic element. Recall that the fitting parameter τ1 represents the characteristic relaxation time of the viscoelastic element, and it is a composite parameter defined as the ratio of the viscous coefficient and the spring constant i.e., τ1 = η1/k1.
To illustrate the global trends for the entire population of patients, the results at relevant time marks are summarized in Fig. 4(b)–(d). The error bars represent the standard deviation across all patients. Notably, similar behavior is observed in the cohort of patients: initially, η0 and η1 overlap significantly but, with time, they split apart; η1 increases and η0 decreases slightly, implying that while η0 remains relatively constant, η1 increases as the blood coagulate. After about 10 min, the two parameters are clearly distinct from each other in the entire population (the error bars do not overlap anymore).
The increase in τ1 observed in the specific case shown in Fig. 4(a) is not so evident for the entire population in Fig. 4(c). Also, as can be seen in Fig. 4(c), the initial values of τ1 vary significantly across the population indicating a large variability in the initial elastic component among the patients. However, as coagulation progresses, this variability decreases indicating that samples with disparate initial conditions evolve towards a similar state, as indicated by the gradual decrease of the error bars. Regarding the associated elastic component of the viscoelastic element, k1, a clear increase is now evident over the entire population, as seen in Fig. 4(d). This indicates that the state towards which the entire population transitions is characterized by a larger elastic component, as expected during the process of incipient coagulation. We would like to emphasize again that the blood is macroscopically fluid at all times during this measurement. In addition, these findings can be seen in the time evolution of the distribution of the viscoelastic parameters across the entire population of patients in the ESI† (Section S4 and Fig. S4).
The experiments summarized in Fig. 4 illustrate the viscoelastic changes due to incipient, natural coagulation. We have further tested our model in a clinically relevant scenario by comparing two states of coagulation at early stages, namely natural coagulation and a state of full systemic anticoagulation (pharmaceutical intervention for anticoagulation therapies). This study, which is detailed in the ESI,† (Section S5), demonstrates that the same model can describe both positive (coagulation) and negative (anti-coagulation) viscoelastic changes, which occur naturally or are being purposely induced during external interventions.
Lastly, we would like to bring the attention towards the rather different levels of molecular complexity between the simplified hemo-system and whole blood. Strictly, this disparity precludes a direct comparison between the experimental results, however, a consistent interpretation of the results within the frame of our viscoelastic model is still possible. For instance, in the case of full systemic anticoagulation (ESI†), τ1 decreases drastically because of the significant reduction of the elastic component of the fluid, i.e., shorter relaxation time. Moreover, during the incipient stages of coagulation, when the fibrin polymerization is barely starting, τ1 increases only slightly but η1 captures the net effect in the form of an increased viscosity (Fig. 4). Finally, when fibrin polymerizes and aggregates start being formed, one can see that the elements that contribute to the background viscosity η0 start to transform and gradually build up the elastic component τ1, which is characterized by a longer relaxation time (Fig. 3). More refined associations with other macromolecules and plasma proteins are possible and will be the subject of future work. Nevertheless, the present results demonstrate that the proposed microrheological model captures the main viscoelasticity features of blood plasma and suggest that a structural description is feasible in terms of the parametric Maxwell model.
4. Conclusions
Understanding the complex rheology of blood is critical not only for diagnosing several pathological conditions and for monitoring the effects of certain pharmaceutical therapies,1,2,34 but also because its major role in a variety of clinical settings where the coagulation status of blood needs to be continuously managed. Unfortunately, common coagulation assays are not always suited for this purpose. The bulk rheological measurements are typically end-point tests and performed in vitro, under non-physiological conditions, involving strong external stimuli19, and typically outside the linear viscoelastic regime.34 A microrheological measurement, on the other hand, can be used to passively retrieve the local viscoelasticity of a complex fluid. In the case of blood, the spatiotemporal scales of interest are those where the effective viscoelasticity of the RBCs’ immediate surroundings are tested by the RBCs themselves. In this paper, we introduced a rheological parametric model that describes the microscopic viscoelasticity of blood over such narrow window of spatiotemporal scales.The parametric model was validated by optical microrheology measurements in laboratory-controlled conditions and in clinical environments involving both natural, intrinsic processes and external interventions. The parametric description allows for a clear discrimination between different conditions of the incipient stages of whole-blood coagulation. Moreover, the parametric model also permits following the short-term progressing action of anticoagulant treatment. These results strongly suggest that the proposed parametrization can be effectively used to describe the coagulation status of whole blood, continuously and quantitatively, even in the absence of external coagulation triggers.
Microrheological properties of blood can be accessed continuously, in vivo directly while operating in clinical settings.56 Because viscoelastic properties of blood are probed at different scales, it should not be expected for a DLS-based microscopic measurement to reproduce the traces of macroscopic hemorheology assays as ACT or TEG. In fact, the information is provided at complementary spatiotemporal scales. The microrheological model demonstrated here provides a quantitative physical description of blood mechanical properties over a broad frequency range in terms of the complex viscoelastic moduli. Moreover, the outcome of the proposed approach, where the effective microscopic viscoelasticity of plasma is retrieved, can be used as input for more complex models where the multiscale response of blood is attributed to specific contributions.34–36
The microrheological model used in the present work is general and not specific to optical measurements. Nevertheless, from a practical standpoint, the all-optical-fiber implementation of the coherence-gated DLS technique has a number of key advantages such as measurement flexibility, easy access, and incorporation with standard vascular access devices. Without having to prepare samples and externally trigger the coagulation cascade, optical microrheology can overcome the typical limitations associated with the macroscopic rheological measurements and coagulation assays.
In our experiments, we report absolute measurements on untreated fresh samples of whole blood, which leads to a large inter-patient variability. This demonstrates the sensitivity of a coherence-gated DLS measurement but certainly complicates a direct inter-patient analysis. By taking advantage of an intra-patient normalization i.e., normalization of a patient's response to their own initial conditions, one can implement differential analysis that permits a more proper inter-patient comparison.56,59 A complete inter-patient analysis will be the subject of a future report.
We would also like to mention that, as the mechanical properties of blood are inferred passively at microscopic scales, the effective viscoelasticity of plasma can be related to the underlying chemical composition. This was demonstrated here by using simplified hemo-systems, where the polymerization of fibrinogen into fibrin was controlled. A more detailed study of the impact of the chemical composition on the microscopic rheological properties could provide detailed information about the macromolecular composition, as suggested by the in vitro experiments presented. For example, additional structural assays such as thrombin-antithrombin complexes and fibrinopeptides could be conducted to assess the chemical composition of blood and to further associate the physical parameters of the viscoelastic model with specific molecular complexes in plasma.
Finally, the general, quantitative description of blood viscoelasticity can be based on passive in vivo measurements as we illustrated here in the context of cardiovascular surgeries. Moreover, the parametric description we introduced can form the basis for a new class of in vivo assays for clinically relevant situations where the blood status needs to be monitored in real-time and managed continuously.
Author contributions
JRGS, MB, RW preformed the experiments, processed and analyzed data. AD designed and directed the research. WD directed the clinical research and contributed to data analysis. All authors contributed to writing the paper.Funding
This work was partially supported by the National Institutes of Health and the National Heart, Lung and Blood Institute under grant number 5R21HL124486.Conflicts of interest
The authors declare no conflict-of-interest.Notes and references
- O. K. Baskurt, M. R. Hardeman and M. D. W. Rampling, Handbook of hemorheology and hemodynamics, IOS press, 2007, vol. 69 Search PubMed.
- G. P. Galdi, et al., Hemodynamical flows, Delhi Book Store, 2008 Search PubMed.
- G. Chen, et al., Regulation of blood viscosity in disease prevention and treatment., Chin. Sci. Bull., 2012, 57(16), 1946–1952 CrossRef.
- J. Harkness, The viscosity of human blood plasma; its measurement in health and disease., Biorheology, 1971, 8(3–4), 171–193 CAS.
- G. Késmárky, et al., Plasma viscosity: a forgotten variable., Clin. Hemorheol. Microcirc., 2008, 39(1–4), 243–246 Search PubMed.
- R. L. Letcher, et al., Direct relationship between blood pressure and blood viscosity in normal and hypertensive subjects: role of fibrinogen and concentration., Am. J. Med., 1981, 70(6), 1195–1202 CrossRef CAS PubMed.
- S. MacRury, et al., Association of hypertension with blood viscosity in diabetes, Diabetic Med., 1988, 5(9), 830–834 CrossRef CAS PubMed.
- A. Raine, Hypertension, blood viscosity, and cardiovascular morbidity in renal failure: implications of erythropoietin therapy, Lancet, 1988, 331(8577), 97–100 CrossRef.
- D. E. McMillan, Further observations on serum viscosity changes in diabetes mellitus, Metabolism, 1982, 31(3), 274–278 CrossRef CAS PubMed.
- G. Lowe, et al., Increased blood viscosity in diabetic proliferative retinopathy, Diabetes Res., 1986, 3(2), 67–70 CAS.
- A. Barnes, Rheology of diabetes mellitus, Clinical Blood Rheology, 1988, 1, 163–187 Search PubMed.
- E. Ernst, Plasma fibrinogen—an independent cardiovascular risk factor, J. Intern. Med., 1990, 227(6), 365–372 CrossRef CAS PubMed.
- E. Ernst and K. L. Resch, Fibrinogen as a cardiovascular risk factor: a meta-analysis and review of the literature, Ann. Intern. Med., 1993, 118(12), 956–963 CrossRef CAS PubMed.
- J. W. Weisel and R. I. Litvinov, Mechanisms of fibrin polymerization and clinical implications. Blood, Journal of the American Society of Hematology, 2013, 121(10), 1712–1719 CAS.
- J. W. Weisel and R. I. Litvinov, Fibrin formation, structure and properties, in Fibrous proteins: structures and mechanisms. 2017, Springer, pp. 405–456 Search PubMed.
- H. J. Dalton, et al., Factors associated with bleeding and thrombosis in children receiving extracorporeal membrane oxygenation, Am. J. Respir. Crit. Care Med., 2017, 196(6), 762–771 CrossRef CAS PubMed.
- S. M. Hastings, et al., Sources of circuit thrombosis in pediatric extracorporeal membrane oxygenation, ASAIO J., 2017, 63(1), 86–92 CrossRef CAS PubMed.
- J. R. Neal, et al., Using daily plasma-free hemoglobin levels for diagnosis of critical pump thrombus in patients undergoing ECMO or VAD support, J. Extra-Corpor. Technol., 2015, 47(2), 103 Search PubMed.
- S. M. Bates and J. I. Weitz, Coagulation assays, Circulation, 2005, 112(4), e53–e60 CrossRef PubMed.
- P. Evans, et al., Rheometry and associated techniques for blood coagulation studies, Med. Eng. Phys., 2008, 30(6), 671–679 CrossRef CAS PubMed.
- D. M. Funk, Coagulation assays and anticoagulant monitoring, Hematology 2010, the American Society of Hematology Education Program Book, 2012, 1, pp. 460–465 Search PubMed.
- M. D. Lancé, A general review of major global coagulation assays: thrombelastography, thrombin generation test and clot waveform analysis, Thromb. J., 2015, 13(1), 1 CrossRef PubMed.
- T. A. Waigh, Microrheology of complex fluids, Rep. Prog. Phys., 2005, 68(3), 685 CrossRef.
- T. M. Squires and T. G. Mason, Fluid mechanics of microrheology, Annu. Rev. Fluid Mech., 2010, 42, 413–438 CrossRef.
- F. MacKintosh and C. Schmidt, Microrheology, Curr. Opin. Colloid Interface Sci., 1999, 4(4), 300–307 CrossRef CAS.
- R. R. Aure, et al., Damped White Noise Diffusion with Memory for Diffusing Microprobes in Ageing Fibrin Gels, Biophys. J., 2019, 117(6), 1029–1036 CrossRef CAS PubMed.
- P. Domínguez-García, et al., Filamentous and step-like behavior of gelling coarse fibrin networks revealed by high-frequency microrheology, Soft Matter, 2020, 16(17), 4234–4242 RSC.
- J. Y. Chang, et al., Thrombin specificity: Selective cleavage of antibody light chains at the joints of variable with joining regions and joining with constant regions, Eur. J. Biochem., 1985, 151(2), 225–230 CrossRef CAS PubMed.
- F. Putnam, The Plasma Proteins V3: Structure, Function, and Genetic Control, Elsevier, 2012 Search PubMed.
- T. G. Mason, Estimating the viscoelastic moduli of complex fluids using the generalized Stokes–Einstein equation, Rheol. Acta, 2000, 39(4), 371–378 CrossRef CAS.
- T. G. Mason and D. A. Weitz, Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids, Phys. Rev. Lett., 1995, 74(7), 1250 CrossRef CAS PubMed.
- N. Thien, Understanding Viscoelasticity: Basics of Rheology, Springer-Verlag, Berlin, 2002 Search PubMed.
- J. M. Krishnan, A. P. Deshpande and P. S. Kumar, Rheology of complex fluids, Springer, 2010 Search PubMed.
- A. N. Beris, et al., Recent advances in blood rheology: A review, Soft Matter, 2021, 10591–10613 RSC.
- J. S. Horner, et al., Investigation of blood rheology under steady and unidirectional large amplitude oscillatory shear, J. Rheol., 2018, 62(2), 577–591 CrossRef CAS.
- J. S. Horner, et al., Measurements of human blood viscoelasticity and thixotropy under steady and transient shear and constitutive modeling thereof, J. Rheol., 2019, 63(5), 799–813 CrossRef CAS.
- M. Brust, et al., Rheology of human blood plasma: Viscoelastic versus Newtonian behavior, Phys. Rev. Lett., 2013, 110(7), 078305 CrossRef CAS PubMed.
- S. Varchanis, et al., How viscoelastic is human blood plasma?, Soft Matter, 2018, 14(21), 4238–4251 RSC.
- S. P. Marques and G. J. Creus, Rheological models: integral and differential representations, in Computational Viscoelasticity, Springer, 2012, pp. 11–21 Search PubMed.
- D. Gutierrez-Lemini, Engineering viscoelasticity, Springer, 2014 Search PubMed.
- C. Schmitt, A. H. Henni and G. Cloutier, Characterization of blood clot viscoelasticity by dynamic ultrasound elastography and modeling of the rheological behavior, J. Biomech., 2011, 44(4), 622–629 CrossRef PubMed.
- T. H. van Kempen, et al., A constitutive model for developing blood clots with various compositions and their nonlinear viscoelastic behavior, Biomech. Model. Mechanobiol., 2016, 15(2), 279–291 CrossRef PubMed.
- J. Van der Gucht, et al., Brownian particles in supramolecular polymer solutions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67(5), 051106 CrossRef CAS PubMed.
- M. Grimm, S. Jeney and T. Franosch, Brownian motion in a Maxwell fluid, Soft Matter, 2011, 7(5), 2076–2084 RSC.
- M. L. Turgeon, Clinical hematology: theory and procedures, Lippincott Williams & Wilkins, 2005 Search PubMed.
- C. E. McLaren, et al., Statistical and graphical evaluation of erythrocyte volume distributions, Am. J. Physiol.: Heart Circ. Physiol., 1987, 252(4), H857–H866 CrossRef CAS PubMed.
- W. Russel, Review of the role of colloidal forces in the rheology of suspensions, J. Rheol., 1980, 24(3), 287–317 CrossRef CAS.
- B. J. Berne and R. Pecora, Dynamic light scattering: with applications to chemistry, biology, and physics, Courier Corporation, 1976 Search PubMed.
- T. G. Mason, et al., Particle tracking microrheology of complex fluids, Phys. Rev. Lett., 1997, 79(17), 3282 CrossRef CAS.
- T. Mason, H. Gang and D. Weitz, Rheology of complex fluids measured by dynamic light scattering, J. Mol. Struct., 1996, 383(1–3), 81–90 CrossRef CAS.
- F. Amblard, et al., Subdiffusion and anomalous local viscoelasticity in actin networks, Phys. Rev. Lett., 1996, 77(21), 4470 CrossRef CAS PubMed.
- F. Gittes, et al., Microscopic viscoelasticity: shear moduli of soft materials determined from thermal fluctuations, Phys. Rev. Lett., 1997, 79(17), 3286 CrossRef CAS.
- Z. Hajjarian and S. K. Nadkarni, Evaluating the viscoelastic properties of tissue from laser speckle fluctuations, Sci. Rep., 2012, 2, 316 CrossRef PubMed.
- Z. Hajjarian, M. M. Tripathi and S. K. Nadkarni, Optical Thromboelastography to evaluate whole blood coagulation, J. Biophotonics, 2015, 8(5), 372–381 CrossRef CAS PubMed.
- Z. Hajjarian, et al., Laser speckle rheology for evaluating the viscoelastic properties of hydrogel scaffolds, Sci. Rep., 2016, 6, 37949 CrossRef CAS PubMed.
- J. Guzman-Sepulveda, et al., Real-time intraoperative monitoring of blood coagulability via coherence-gated light scattering, Nat. Biomed. Eng., 2017, 1(2), 0028 CrossRef CAS.
- G. Popescu, et al., Imaging red blood cell dynamics by quantitative phase microscopy, Blood Cells, Mol., Dis., 2008, 41(1), 10–16 CrossRef CAS PubMed.
- H. Cummings and E. Pike, Photon Correlation and Light-Beating Spectroscopy, Vol. 3 of NATO Advanced Study Institute Series B: Physics, Plenum, New York, 1974 Search PubMed.
- M. Batarseh, et al., Passive Coagulability Assay Based on Coherence-Gated Light Scattering, Hemato, 2020, 1(2), 49–59 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01726h |
| ‡ Current address: Center for Research and Advanced Studies of the National Polytechnic Institute (CINVESTAV Unidad Monterrey). Apodaca, Nuevo Leon, Mexico. |
| This journal is © The Royal Society of Chemistry 2022 |


