Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding slow compression and decompression of frictionless soft granular matter by network analysis†
Stefan
Luding
 a,
Kianoosh
Taghizadeh
a,
Kianoosh
Taghizadeh
 *ab,
Chao
Cheng
*ab,
Chao
Cheng
 c and
Lou
Kondic
c and
Lou
Kondic
 c
c
aMSM, TFE-ET, MESA+, University of Twente, PO Box 217, 7500AE Enschede, The Netherlands. E-mail: k.taghizadehbajgirani@utwente.nl
bInstitute of Applied Mechanics (CE), SC SimTech, University of Stuttgart, Germany
cDepartment of Mathematical Sciences, New Jersey Institute of Technology, University Heights, Newark, NJ 07102, USA
First published on 16th February 2022
Abstract
We consider dense granular systems in three spatial dimensions exposed to slow compression and decompression, below, during, above and well above jamming. The evolution of granular systems under slow deformation is non-trivial and involves smooth, continuous, reversible (de)compression periods, interrupted by fast, discontinuous, irreversible transition events. These events are often, but not always, associated with rearrangements of particles and of the contact network. How many particles are involved in these transitions between two states can range from few to almost all in the system. An analysis of the force network that is built on top of the contact network is carried out using the tools of persistent homology. Results involve the observation that kinetic energy is correlated with the intensity of rearrangements, while the evolution of global mechanical measures, such as pressure, is strongly correlated with the evolution of the topological measures quantifying loops in the force network. Surprisingly, some transitions are clearly detected by persistent homology even though motion/rearrangement of particles is much weaker, i.e., much harder to detect or, in some cases, not observed at all.
1 Introduction
In non-Newtonian systems, complex fluids,1 colloidal suspensions,2 and especially granular matter in its flowing states,3 the system's macroscopic transport properties are not constants but depend on various state-variables such as the volume fraction and the granular temperature.4 This interdependence and the presence of energy dissipation is at the origin of many interesting phenomena like clustering,5 shear-band formation,6 jamming/un-jamming,7,8 dilatancy,9 shear-thickening2,10,11 or shear-jamming.8,12,13 While granular gases are very well described by kinetic theory,4 dense granular fluids and granular solids are much harder to understand, in particular since they can transit from fluid-like flowing states to static, reversibly elastic ones. How and why they achieve this is still under debate, e.g., by irreversible (plastic) deformations,14–19 related also to creep/relaxation phenomena,9,20–22 and many other mechanisms.In this paper, we focus on the compression (loading) and decompression (unloading) of three dimensional dense, solid-like granular packings of frictionless soft particles, which allow to study a wide range of volume fractions, resembling soft rubber, or gel particles. Goal is a better understanding of precisely how these packings respond to (de)compression. For tiny deformations (isotropic strain), the considered systems can, and mostly do, behave fully elastically and reversibly. However, for larger strains, irreversible events occur that involve some dynamics (motion, rearrangement) of the particles.23–28 In analysis of these events, in addition to classical measures (pressure, energy, coordination number), we find it insightful to consider explicitly also the force networks, describing the interparticle interactions on a scale between particles and system size. By now it is well accepted that the static and dynamic properties of these networks are closely related to mechanical properties of the whole granular sample; the examples include granular samples exposed to vibrations/tapping29,30 or pullout of an intruder from a granular sample.31 It is therefore important to be able to describe the properties of these networks in ways that are simple enough but also precise and more detailed than the classical measures alone, and that can be applied in three spatial dimensions (3D) rather than the rich 2D network analysis of recent years, see e.g. ref. 32–38 and the references therein. This is not an easy task since the force networks are built on top of contact networks, which for a deformed system evolve dynamically together interfering with each other.
While there are various approaches that could be used to describe the considered networks, they often do not satisfy some of the above requirements. In the present work, we focus on application of persistent homology (PH), which is a technique based on computational topology allowing for a concise description of 3D weighted networks, and is therefore appropriate for description of force networks, where the role of weight is played by the magnitude of the forces between granular particles. PH allows for a significant data reduction, since it describes a complicated weighted network in terms of point clouds, known as persistent diagrams, PDs, that contain information about the connectivity of the contact/force networks, and how such connectivity depends on the force magnitude. One strength of this approach is that all force magnitudes can be considered at once. This being said, the concept of a force threshold is inherent in PD calculations and the information about the connectivity for different thresholds is readily available, see ref. 39 for in-depth discussion in the context of granular matter, and40 for an introduction to computational homology, of which PH is an important part.
PDs have been used extensively for a number of systems involving weighted networks, ranging from social41 to fluid dynamics42 and material science context.43,44 While applications to granular systems are still rather limited, the approach based on PDs has been used for the systems exposed to compression,45,46 vibrations,30,47,48 or shear.49 In the present work, we will illustrate some of the strengths of this approach, including its ability to easily carry out analysis/computations in 3D, as well as to consider evolving networks, including computing their differences. The computations are carried out using the GUDHI library.50
Before closing this introduction, we point out that in the present work we also consider relative large volume fractions, that may lead to large particle deformations, which in turn could produce new contacts between particles. Recently, there have been a few studies to tackle the realistic behavior of highly deformable particles both numerically51–56 and experimentally.27,57–59 In the present paper the soft-DEM numerical approach is used to model the compaction of “soft” elastic grains; in this approach the change of shape of the grains is neglected. Since the focus of the present study is to understand the force networks using persistence analysis and DEM simulations, which is already a complex enough investigation, detailed analysis involving deformable particles using multi-particle contact methods will remain a subject of a future study.
The remainder of this paper is structured as follows: After introducing both DEM and PD methods in Section 2, we proceed to discuss the results. Section 3 focuses on a preliminary discussion of the observations based on classical measures (pressure, energy), involving the irreversible events occurring frequently during both compression (loading) and decompression (unloading) of the considered granular systems. In Section 4 we present the results obtained based on PDs, as well as by relating the quantities derived from PDs to the classical measures. Section 5 is devoted to summary, conclusions and outlook.
2 Methods
2.1 Discrete element method
The approach towards the microscopic understanding of macroscopic particulate material behaviour is the modelling of particles using the so-called discrete element method (DEM), a numerical scheme originally formulated and developed by Cundall et al.60 DEM is a straightforward implementation to solve the equations of motion for the translational and rotational (not used here) degrees of freedom for a system of many interacting particles: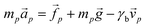 | (1) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) p, velocity
p, velocity  and acceleration
and acceleration  . It is subjected to two kinds of forces, one due to contacts with other particles (
. It is subjected to two kinds of forces, one due to contacts with other particles (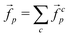 ) and one due to volume forces (i.e. due to gravity acceleration,
) and one due to volume forces (i.e. due to gravity acceleration, ![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) , neglected in this study), as well as global background damping of motion with coefficient γb.
, neglected in this study), as well as global background damping of motion with coefficient γb.
The basis of DEM consists of the force laws that relate the interaction force to the overlap of two particles. This force can be decomposed into a normal and tangential component ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) cp =
cp = ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) n +
n + ![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) t. With known normal and tangential forces acting on all particles, one can numerically integrate the equations of motion, eqn (1), and obtain the position of particles in future time-steps. Next, we will describe the simple-most force law used in this research, ignoring tangential forces.
t. With known normal and tangential forces acting on all particles, one can numerically integrate the equations of motion, eqn (1), and obtain the position of particles in future time-steps. Next, we will describe the simple-most force law used in this research, ignoring tangential forces.
 | (2) |
 is the normal unit vector pointing from particle q to particle p.
is the normal unit vector pointing from particle q to particle p.
The linear spring-dashpot contact force law is a further simplification in DEM:61–65
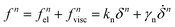 | (3) |
 ) of interacting particles with the viscoelastic damping constant for normal contact viscosity γn which is a intrinsic model parameter accounting for energy dissipation. This model implies that the spherical particles do not deform during the simulation and considers binary contacts only through a single point during their collisions.
) of interacting particles with the viscoelastic damping constant for normal contact viscosity γn which is a intrinsic model parameter accounting for energy dissipation. This model implies that the spherical particles do not deform during the simulation and considers binary contacts only through a single point during their collisions.
 = 2000 or
= 2000 or 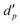 = 2, are used in the simulations shown in this paper. For working with units, there are two alternatives: either one can read the numbers in chosen units‡ or the units are chosen based on physical properties to achieve non-dimensional quantities. The latter option is adopted here, i.e., the unit of length is chosen as the mean particle diameter,
= 2, are used in the simulations shown in this paper. For working with units, there are two alternatives: either one can read the numbers in chosen units‡ or the units are chosen based on physical properties to achieve non-dimensional quantities. The latter option is adopted here, i.e., the unit of length is chosen as the mean particle diameter,  , so that 〈dp〉 = 1 is the dimensionless diameter. The second unit is the material density,
, so that 〈dp〉 = 1 is the dimensionless diameter. The second unit is the material density, 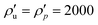 , so that one has the dimensionless density, ρ = ϕ, and thus the unit of mass,
, so that one has the dimensionless density, ρ = ϕ, and thus the unit of mass,  , i.e., the particle mass, mp = (π/6). For the third unit one has several choices, where we adopt here the units of elastic stress,
, i.e., the particle mass, mp = (π/6). For the third unit one has several choices, where we adopt here the units of elastic stress,  , with the linear normal contact stiffness,
, with the linear normal contact stiffness,  = 105, which yields the dimensionless stress
= 105, which yields the dimensionless stress 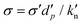 , and results in the unit of time
, and results in the unit of time  . In the chosen units, the dimensionless linear stiffness is
. In the chosen units, the dimensionless linear stiffness is  , and the linear contact viscosity,
, and the linear contact viscosity,  = 103, becomes
= 103, becomes  , with background viscosity,
, with background viscosity,  = 102, or γb =
= 102, or γb = 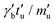 = 4 × 10−4.
= 4 × 10−4.
The consequent physically relevant properties are the restitution coefficient r = exp(−ηntc) ≈ 0.855, with damping factor ηn = γn/(2m12), reduced mass, m12 = 0.063, and contact duration, 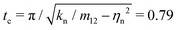 , or
, or  , all considered for a contact between the largest and the smallest particle, with the larger viscous damping time-scale, tv = 2m12/γn ≈ 5, and the even larger background damping time-scale tb = 2m12/γb ≈ 50. Note that this choice of units corresponds to setting
, all considered for a contact between the largest and the smallest particle, with the larger viscous damping time-scale, tv = 2m12/γn ≈ 5, and the even larger background damping time-scale tb = 2m12/γb ≈ 50. Note that this choice of units corresponds to setting 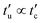 , so that the dimensionless time-scale collapses simulations with different stiffness, in the elastic regime.67,68
, so that the dimensionless time-scale collapses simulations with different stiffness, in the elastic regime.67,68
To prepare samples, first particles are randomly placed in a 3D simulation box with a periodic boundary condition at a low volume fraction, well below jamming (transition from liquid- to solid-like behavior). Then, the simulation box is compressed homogeneously from all directions, up to volume fraction ϕmax ≈ 0.9, and then decompressed. Simulations are carried out using an isotropic strain-rate, 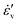 = 1.05 × 10−6, i.e.,
= 1.05 × 10−6, i.e., 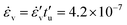 , for both loading and un-loading. In the following sections, we will present a few typical particle simulations from loading–unloading cycles, with the goal to zoom into this slow rate data, to display the dynamics of what is going on during plastic, irreversible re-arrangement events; results from different rates were reported in ref. 69.
, for both loading and un-loading. In the following sections, we will present a few typical particle simulations from loading–unloading cycles, with the goal to zoom into this slow rate data, to display the dynamics of what is going on during plastic, irreversible re-arrangement events; results from different rates were reported in ref. 69.
2.2 Persistent homology (PH)
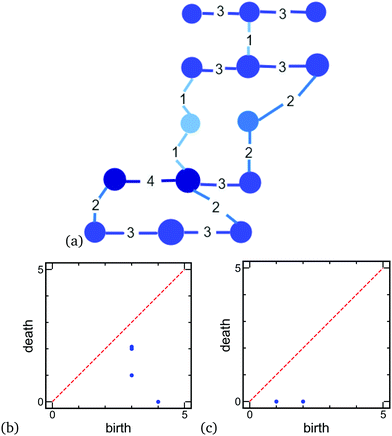
For the present purpose, one could think of PH as a tool for describing a complicated weighted network (such as the one describing interaction forces between the particles) in the form of diagrams, so called persistence diagrams (PDs). These diagrams are obtained by filtration, i.e. thresholding the strength of the interactions between particles. For the present purpose, this strength is quantified by the normal interaction forces. Then, the simplest PD, which we refer to as β0 PD, essentially traces how ‘structures’ (could be thought of as ‘force chains’, without attempting to define them) appear as a filtration level is decreased, or disappear as two structures merge (β0 stands here for the 0th Betti number that essentially counts the number of components or ‘chains’). In three spatial dimensions (3D), there are three Betti numbers, β0, β1 (counting loops), and β2, counting enclosed 3D structures, and therefore also three PDs. Since in the present context β2 structures are rarely present, we will not discuss them further, and will focus on β0 and β1 PDs. We note, and will discuss later in this section, that PDs contain the information which is significantly more detailed than the Betti numbers, since they tell us about connectivity of the components, and not only about their numbers.To illustrate how PDs encode the information about a force network, Fig. 1 shows a toy example of a simple network and the corresponding PDs. Fig. 1(a) shows a small set of particles (nodes) interacting by a force represented by the numerical values (intensity) along the edges connecting the nodes. The PDs keep track of how components appear and disappear as the force threshold is decreased from the highest value (4 in the present example) down to the lowest value (here 1). To explain how PDs are produced, let us first focus on β0 PD. The first component (single edge) with value of 4 is the first one that appears at level 4 and, by convention, never disappears (or dies), leading to the point with coordinate (4, 0) on β0 PD. On the level 3, we note that the existing component (4) becomes larger (this is not encoded in the PD, since connectivity has not changed), and three more components appear. On level 2, two of these components connect to the existing component (4) and therefore these two components disappear, or die, leading to a double point at (3, 2). Finally, on the level 1, another component from the level 3 connects to the existing component, leading to the point (3, 1). Since at level 1 all the nodes are connected, and there is just a single component existing, β0 PD is complete. We note that this PD contains the information about the number of components and their connectivity for all considered thresholds, which is a major difference to the Betti number, β0, which is threshold dependent (in this example, there is one component on level 4, four components on level 3, two components on level 2, and one component on level 1). All of this is encoded in the β0 PD, and we leave to the reader, as simple exercise, to extract the Betti numbers listed above directly from this persistence diagram.
Turning now our attention to the loops and β1 PD, we see in Fig. 1(a) that we need to go down to the threshold level 2 to form a loop (a loop forms when the weakest link appears; in this case we have two edges with the force 2 in the loop in the lower part of the figure). This loop has coordinates (2, 0) in β1 PD. Then, on level 1, another loop (central) closes, leading to the (1, 0) point in β1 PD. In the present simple toy example we do not observe disappearing or dying of loops: in a more complicated network, bigger loops ‘die’ when they get (completely) filled by edges of non-zero strength. In a granular system, this could correspond to the formation of crystalline zones, where eventually all neighboring particles interact by non-zero contact forces in a hexagonal network; see ref. 39 for further discussion of this point.
We conclude this brief discussion of PDs by pointing out one important feature: one can show that PDs are stable, in the sense that small changes of the underlying network lead to small changes of a PD; such a result can not be proven, e.g., for Betti numbers.39 In practical terms, and in the context of granular physics, this means that small errors in measuring forces between particles would lead only to correspondingly small errors in the measures derived from the PDs.
It should not come as a surprise that the PDs resulting from simulations of a large number of granular particles are significantly more complicated than the ones resulting from the toy example.
While there are many possible measures that could be introduced, one simple choice is based on the idea that there are two appropriate measures/numbers (i) points (generators) in a diagram, and (ii) the threshold range over which a point persists – both describing the force network. Using landscape as an analogy, the number of points in β0 PD specifies the number of (mountain) peaks, and their lifespan (see below) describes how well developed these peaks are, or, to push the landscape analogy further, how high they are compared to the ‘valleys’ that surround them. The lifespan ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) , is introduced as the difference between birth (B) and death (D), coordinates, so
, is introduced as the difference between birth (B) and death (D), coordinates, so ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) = B − D. Both measures could be combined into one by defining the total persistence, TP, as a sum of all lifespans. Then, for our toy example shown in Fig. 1, β0 TP = 8, and β1 TP = 3. We will be using TP later in the paper to quantify the force networks obtained from DEM simulations.
= B − D. Both measures could be combined into one by defining the total persistence, TP, as a sum of all lifespans. Then, for our toy example shown in Fig. 1, β0 TP = 8, and β1 TP = 3. We will be using TP later in the paper to quantify the force networks obtained from DEM simulations.
During the last decade, the software for computing PDs and additional measures has been developed by a number of research groups and made publicly available. All the results presented in the present work were computed using the GUDHI library.50
3 Classical analysis of DEM results
In this section we compare the loading and unloading branches at the full range of volume fractions. Focus here is on DEM particle simulation output/information, whereas in the next section, the properties of force networks and their relation to the classical measures are discussed.
Fig. 2 shows the dimensionless pressure,  plotted against volume fraction ϕ. On the scale of the whole compression/decompression cycle, the differences in pressures between the branches are rather small, and the pressure curves look rather smooth. As we will, in what follows, zoom into these curves, rich structures show up to be explored deeper. The symbols in the figure show the location of some of the events which we will consider in more detail. It is worth mentioning that the (isotropic) inertial number for these simulations is of the order of 10−5, already for rather small p ≥ 10−4. Note that while faster compression rates lead to different results, simulations with slower deformation rates (not shown here for brevity),69 are practically identical on this scale, confirming that the simulations shown in Fig. 2 are in the quasi-static, rate-independent regime.
plotted against volume fraction ϕ. On the scale of the whole compression/decompression cycle, the differences in pressures between the branches are rather small, and the pressure curves look rather smooth. As we will, in what follows, zoom into these curves, rich structures show up to be explored deeper. The symbols in the figure show the location of some of the events which we will consider in more detail. It is worth mentioning that the (isotropic) inertial number for these simulations is of the order of 10−5, already for rather small p ≥ 10−4. Note that while faster compression rates lead to different results, simulations with slower deformation rates (not shown here for brevity),69 are practically identical on this scale, confirming that the simulations shown in Fig. 2 are in the quasi-static, rate-independent regime.
 | ||
| Fig. 2 Pressure plotted against volume fraction, ϕ, for loading (L, red) and unloading (UL, blue). The symbols indicate the locations of three selected simulation event windows, for both L and UL, as circles and triangles, respectively, see Table 1. | ||
Note that volume fractions in Fig. 2 go as high as 0.9. Recent studies56 have shown that classical DEM is not accurate at such high compression, due to extreme deformations, so that particles are not spherical anymore, with additional, multiple contacts established. Different methods, e.g., DEM-FEM coupling, could be used to simulate high volume fractions,52,70,71 however such methods are computationally costly. For simplicity, in the present work we stick to classical DEM, following the phenomenology in a qualitative way, leaving more quantitative considerations of the influence of the change of particle shape (and other aspects related to large volume fractions) to other studies53 and future research.
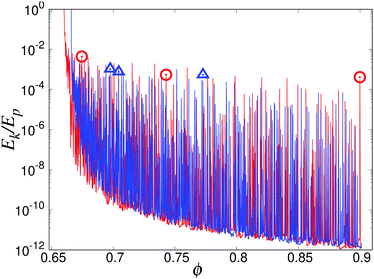
Fig. 3 shows the energy ratio (kinetic to potential), Ek/Ep, of the system during loading and unloading. It is a known fact that the energy ratio is one way to identify jamming: it drops rapidly below unity at jamming,7 while it sharply increases at unjamming, but at a different, larger value of ϕ. This figure also illustrates that the process of loading and unloading is not smooth. Slow isotropic deformations results in an energy ratio base-line Ek/Ep ∝ ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) 2v ≪ 1. But the kinetic energy is also characterized by numerous events, i.e., peaks of energy ratios up to Ek/Ep ≈ 10−3, still well below unity. This indicates that the system remains jammed even though a considerable kinetic energy shows up rapidly and decays (exponentially) fast, after each event. A closer zoom into some selected events follows below.
2v ≪ 1. But the kinetic energy is also characterized by numerous events, i.e., peaks of energy ratios up to Ek/Ep ≈ 10−3, still well below unity. This indicates that the system remains jammed even though a considerable kinetic energy shows up rapidly and decays (exponentially) fast, after each event. A closer zoom into some selected events follows below.
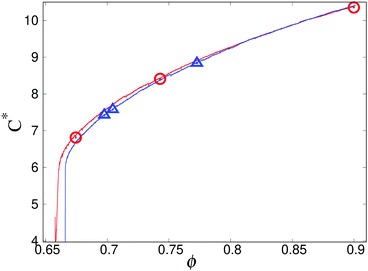
Next, we consider the coordination number C* which is related to the contact number per particle C = 2M/N (given the total number of contacts M) by C* = C/(1 − fr), in which fr is the fraction of rattlers. Fig. 4 shows that the coordination number, C*, is quite similar for the loading and unloading branches, most different at the lower volume fractions, close to jamming and unjamming. On this scale, like for pressure, the tiny fluctuations, variations and differences can be seen only when zooming in to the data, as we will do in the next subsection. It must be noted that large deformations may lead to development of new contacts between particles51,53 and that considering the influence of these newly developed contacts on the results in this paper remains to be carried out in the future study.
3.1 Loading and unloading events
To proceed further, three different windows of volume fraction for both loading and unloading branches were selected.We proceed by comparing the loading and unloading branches at a few different selected values of ϕ so to be able to zoom into windows of Δϕ = ±0.0012 around the events marked in Fig. 2–4 and summarized in Table 1.
| ϕ | p | E k/Ep | C* | |
|---|---|---|---|---|
| L1 | 0.674492 | 0.0105787 | 0.00437983 | 6.81299 |
| L2 | 0.742856 | 0.0872874 | 0.000538789 | 8.4115 |
| L3 | 0.899943 | 0.3411 | 0.000410461 | 10.3534 |
| UL1 | 0.772703 | 0.124572 | 0.000540811 | 8.83516 |
| UL2 | 0.704472 | 0.035903 | 0.000752957 | 7.57317 |
| UL3 | 0.697589 | 0.0285596 | 0.00104019 | 7.42286 |
Fig. 5 shows the pressures around the selected values of ϕ at which events take place. We note that p, differs significantly between loading (L) and unloading (UL). Only the last event on the loading branch is followed by an elastic regime that is exactly, reversibly traced back during unloading from the maximum volume fraction, ϕmax = 0.9013, confirming reversibility for small enough strain and strain rates.
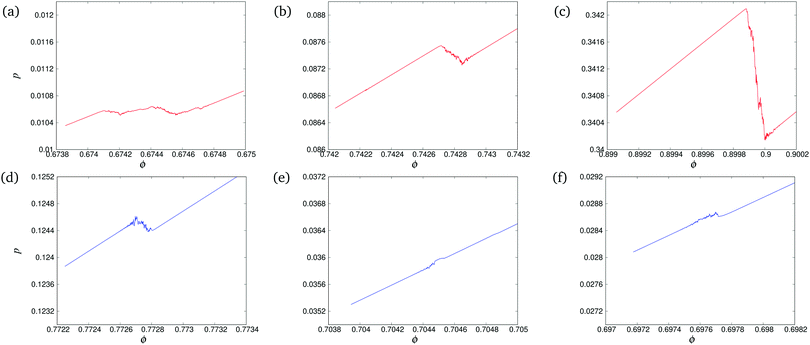 | ||
Fig. 5 Pressure, p, plotted against volume fraction, ϕ, from the same data as in Fig. 2, zooming into three events on each branch ( and and  symbols), for loading (L, red) and unloading (UL, blue). The same color/symbols are applied to Fig. 6 and 7. (a) L1, (b) L2, (c) L3, (d) UL1, (e) UL2, (f) UL3, see Table 1. symbols), for loading (L, red) and unloading (UL, blue). The same color/symbols are applied to Fig. 6 and 7. (a) L1, (b) L2, (c) L3, (d) UL1, (e) UL2, (f) UL3, see Table 1. | ||
All the events are characterized by (sometimes tiny, sometimes large) changes in pressure: for L we always observe pressure drops, while for UL, we also observe increases in pressure (note that the UL figures need to be viewed from right to left since ϕ is decreasing). As we will see in what follows, other considered quantities show significant changes during the event windows considered in Fig. 5, even when the pressure changes are almost invisible.
Fig. 6 shows the energy ratio, Ek/Ep, for the zoom-in windows. We find that this ratio is more sensitive to a change of ϕ than pressure. Note that the energy ratios during loading and unloading do not follow the same trend – even if ϕ is the same. This is not surprising, since the sample configuration has changed. We note that each event is followed by an exponential decrease in energy ratio. The corresponding dissipation rates (data not shown) depend on the restitution coefficient as ∝(1 − r2) and, somewhat, increase with volume fraction, due to an increased number of contacts,
 | ||
| Fig. 6 Kinetic to potential energy ratio, Ek/Ep, plotted against volume fraction, ϕ, from the same events as in Fig. 5. | ||
Fig. 7 shows the coordination number, C*, for the same data range as in Fig. 5 and 6. Similar to the energy ratio shown in Fig. 6, the coordination number plot reveals irreversible rearrangements during events, showing that the events (at least the ones considered in this figure) correspond to changes of the microstructure (coordination number) associated with plastic, irreversible deformations of the granular sample (in contrast to elastic, reversible deformations during which the coordination number varies continuously (i.e., outside of the event window, without significant jumps). We will discuss later in the paper also situations where events could occur without particle rearrangements, therefore without strong changes of the Ek/Ep ratio, or the coordination number.
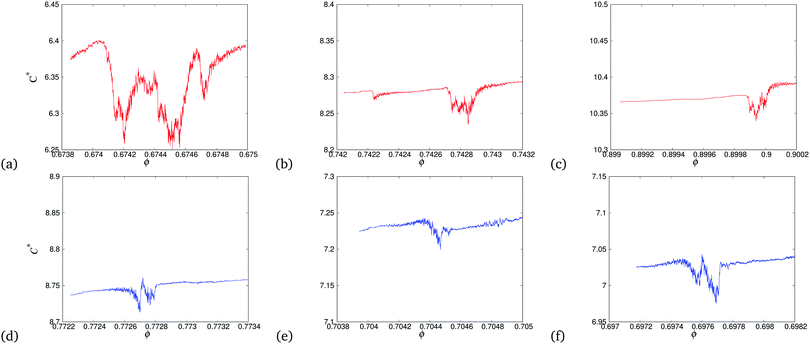 | ||
| Fig. 7 Coordination number, C*, plotted against volume fraction, ϕ, from the same events as in Fig. 5. | ||
For the events considered so far, Fig. 7 shows that an event always starts with a coordination number decrease. This is due to rearrangements of particles, which leads to an increase of the Ek/Ep ratio, as can be seen in Fig. 6. For an explanation why such kinetic energy (and displacement) fluctuations result in a drop of coordination number, see the discontinuous generalized distance probability density functions in ref. 72. Once an event is completed, the coordination number typically recovers close to its original, elastic trend, sometimes below (a and b), sometimes above (c–f).
3.2 Events force networks
In Fig. 8, force networks are plotted during events, for the loading branch only, with a threshold set such that the plots have similar volume fraction, even with a few holes/gaps that indicate extended islands of weak contacts only. The intensity of forces is color coded the same way in all plots, where blue, green, red range from low to high forces.The four snapshots shown in Fig. 8 for each of the events L1 (ϕ = 0.6735), L2 (ϕ = 0.7427), and L3 (ϕ = 0.899), are equally spaced within the event window, Δϕ ≈ 0.00023, so that biggest changes are expected between the two middle panels. However, given the rather small relative changes in pressure during events, also the force intensity change is practically invisible, and only a few modifications of edges are visible. This observation brings us to the conclusion that the visualisation of the force network is not very helpful to understand the evolution during events; further analysis of these networks based on persistent homology method will be discussed in Section 4. Before that, we discuss briefly the non-affine displacement.
3.3 Non-affine displacements during events
The main difficulty in describing the mechanics of granular materials is how to deal with disorder. The simplest approach is to ignore disorder altogether, and attempt to gain insight based on ordered, crystalline packings.73 This assumption considers a uniform strain at all scales, with the displacement field of the grains following the macroscopic deformation, so-called affine motion. However, a number of studies74–80 have shown the failure of only considering affine motion in describing the mechanical behavior of granular packings.The basic idea of elastic theories relevant to granular packings is that the macroscopic work done deforming the system is equal to the sum of the work done on the level of each grain–grain contact. The latter scale has to be replaced by a suitable split to average (affine) and fluctuating (deviating, non-affine) quantities. Thus, the displacement of a particle can be written as:
| Δxi = xi(t + Δt) −xi(t) = Δxiaffine + Δxireversible + Δxievents, | (4) |
Next we focus on the non-affine displacement from before to after an event, which involves Δxi − Δxiaffine. The reversible non-affine displacement is typically much smaller than the irreversible event displacement, so that we do not attempt to separate it off (data for Δxireversible not shown here separately).
In order to visualize the evolution during the events, the non-affine displacement of all particles during the events (from ϕ = 0.673 to 0.899) is plotted as thin lines with a stretch factor in Fig. 9. The figure shows the events from the loading branch for the system with periodic boundary conditions (grey bars). The particles with displacement above a certain threshold are plotted in color, whereas the particles with little displacement are omitted. The first and the last event are remarkable, since they show up strongest, both with a strong displacement of many particles, covering the whole system. It was found that in the low volume fraction case, the system is not yet fully jammed and the event is the superposition of several smaller sequential events. Even for very large ϕ, significant events can occur, even though the system is already strongly jammed/over-compressed. Also some events show considerably less particles involved. However, in all cases the whole system is involved, indicating possible relevance of finite size effects.
Fig. 10 shows an event from the unloading branch starting at ϕ = 0.899 until ϕ = 0.673. For unloading, the first event (left) is very weak, almost not showing up for the given thresholds, and also the last event (right) is rather weak. The three marked/selected events in the middle show different characteristic patterns well above the threshold. All events involve groups of particles of order of half system size, indicating that these are almost system spanning events, with possible relation to the finite size of the system. Additionally, comparing non-affine figures for loading and unloading events, it is found that the non-affinity is more pronounced for loading than for unloading events.
4 Force network analysis based on persistent homology
4.1 Global view
The force networks, see Fig. 8 for examples, are difficult to analyze visually. As discussed in the Introduction and Section 2, persistent diagrams, PDs, provide one complementary approach to understand granular packings under slow deformations more quantitatively. Fig. 11 shows an example of β0 and β1 PDs for volume fraction ϕ = 0.6739. Before proceeding with their quantification, we note a couple of issues that need to be considered when computing PDs for a complicated 3D network: (i) one needs to decide how to treat the forces across periodic boundaries: in our implementation, we treat these forces in the same way as all the other ones, resembling a system without wall-induced inhomogeneities or boundaries; (ii) one needs to decide how to treat so-called trivial loops formed by three particles in contact: in the current implementation, as a choice, these loops are ignored, what in practical terms means that larger loops can ‘die’ when they get completely filled by trivial loops. The interested reader is referred to ref. 39 for more details. | ||
Fig. 11 Examples of persistence diagrams, PDs, for (a) components (clusters), β0, and (b) for loops (cycles), β1 for ϕ = 0.6739. The axes show the force level at which a structure appears (B = birth) and disappears (D = death). The lifespan ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) = B − D (distance from diagonal marked as green horizontal line) illustrates the force threshold range over which a structure persists. See ESI† for animations showing the evolution from ϕ = 0.6739 to ϕ = 0.6750 (discussed later in Fig. 14–16). = B − D (distance from diagonal marked as green horizontal line) illustrates the force threshold range over which a structure persists. See ESI† for animations showing the evolution from ϕ = 0.6739 to ϕ = 0.6750 (discussed later in Fig. 14–16). | ||
The PDs are essentially point clouds, and one needs to come up with appropriate measures to quantify their features that describe the corresponding contact- and force-network in granular matter. As discussed already in Section 2, a particularly simple quantification of the connectivity properties of the underlying networks is obtained when the information contained in the PDs is compressed into a simple measure, i.e., total persistence, TP, which could be considered separately for components (‘chains’) and loops. Fig. 12 shows TP for components (β0) and for loops (β1), together with the pressure (already plotted in Fig. 2) for both loading and unloading branches. TP for β1 (TP1) closely follows the pressure, while TP for β0 (TP0) is much more noisy. In particular, while the loading pressure is always larger than the unloading one, the same does not apply to TP0. We note that the evolution of TP0 is particularly nonuniform for large ϕ's, suggesting significant changes in the force network.
 | ||
| Fig. 12 Loading (solid line) and unloading (dashed line) branches of pressure (black), TP β0 (TP0, red), TP β1 (TP1, blue). | ||
Next, the finer features of both pressure and TP are discussed. Before that, however, we quantify the correlation between pressure and TP, by computing their correlation functions. Since the data are rather noisy, we consider the data averaged over a moving window, as described next.
The moving correlation between the two time series x(t) and y(t) is calculated by first finding the covariance between the subseries xi and yi in the moving window centered at time = t0,
 | (5) |
 is a selected window which centers at t0 and w is the total number of data points in
is a selected window which centers at t0 and w is the total number of data points in  . Also,
. Also, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) t0, ȳt0 are the means of xi, yi, respectively. The standard deviation,
t0, ȳt0 are the means of xi, yi, respectively. The standard deviation,  , of xi at time t0 is
, of xi at time t0 is | (6) |
 . Then, using the standard deviations, the appropriately normalized correlation function is
. Then, using the standard deviations, the appropriately normalized correlation function is | (7) |
Fig. 13 shows the correlations between the pressure and total persistence TP (separately for TP0 and for TP1). We immediately observe that the correlation between pressure and TP1 is very high, in particular for large values of ϕ. The correlation decreases for a few isolated events, which we discuss further below, but even for those events the correlation is still very strong. This result suggests that the properties of the loops in the force network are strongly correlated with the pressure.38 On the other hand, the correlation between TP0 and pressure is much more pronounced, in particular during the rapid isolated events showing as negative peaks in the correlation curve, indicating strong anti-correlation. Therefore, the topological properties of the components are much less representative of the pressure in the system. We proceed by discussing in more detail the fines structures of the evolution during selected events on the loading and unloading branches.
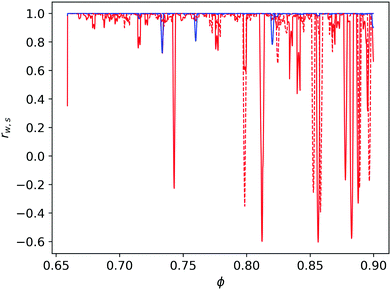 | ||
| Fig. 13 (Normalized) correlation coefficient between pressure, TP0 (red) and TP1 (blue) for loading (solid line) and unloading (dashed line) with w = 15. | ||
4.2 Analysis of the events
As already discussed in Section 3.1, and further illustrated by Fig. 13, a considerable number of events (tens or hundreds, depending on how an ‘event’ is defined) occur – in particular during loading. In what follows, we discuss further the evolution of the force networks for the events already considered in Fig. 5–7, with the goal of understanding such events more precisely.We focus first on loading and consider (on a much finer scale now) pressure and total persistence, TP. Fig. 14 shows the results, where all quantities are normalized by their value at the peak of the event. Pressure is plotted as Δp = (p − p*)/p*, where p* is the reference value as marked with symbols on Fig. 2 and reported in Table 1. Total persistence, TP, is plotted as ΔTP = (TP − TP*)/TP*, where TP* is the total persistence of corresponding volume fraction given in Table 1. Even on this very fine scale, and during the event itself, TP1 closely follows the pressure. TP0 changes much more dramatically, showing that the topology of the force network changes during an event, but not all of these changes resemble pressure modifications.
Note that a single PD provides information about the state of the system, at a given time, and therefore does not include any information about the dynamics. Another crucial feature of the PDs comes handy here: PDs live in a metric space, and therefore could be compared, see ref. 39 for a more detailed discussion of this point. This means that one can define a concept of distance between PDs, which could be thought of as a minimum (Euclidean) distance by which the points in one diagram need to be adjusted to map them exactly to each other; if the number of points in two PDs is different, the extra points are mapped orthogonally to the diagonal.
One type of distance which is often used is the degree q Wasserstein distance, Wq(PD, PD′), which is essentially the Lq norm of the minimum distance required to map the points from PD to PD′ (minimized over all possible mappings). The value of q puts emphasis on larger differences between the points, for q > 1, or on smaller ones, for q < 1. We use q = 2 in the present work and refer the reader to ref. 39 for a more detailed discussion of this concept.
Fig. 15 shows the same event from Fig. 14, but from a different perspective. Here we plot the distance between the persistence diagrams, together with the relative change of the kinetic energy of the particles, scaled by the peaks, such as ΔEratio = (Ek/Ep)/(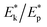 ) − 1, where
) − 1, where  are given in Table 1. Likewise other parameters, W2 distances were scaled using of the peak value of the event such as
are given in Table 1. Likewise other parameters, W2 distances were scaled using of the peak value of the event such as 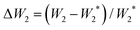 ). We see that the changes in W2 distances follow the changes in kinetic energy, although not too closely.
). We see that the changes in W2 distances follow the changes in kinetic energy, although not too closely.
The fact that the W2 distances before and after an event are similar in Fig. 15 inspires another question: is the topology of the force network before and after an event similar? To answer this question, we compute heat maps, which show the distances between all the persistence diagrams describing force networks during an event. Fig. 16 shows these heat maps (both for W2β0 and W2β1 distances) for event L1. This figure shows the heat maps as a (symmetric) square matrix, where the color of element (i, j) illustrates the distance between this element and the (i, i) one (here i counts rows, and j counts columns of the heat map); by definition, the elements on the diagonal are zero. We see that the distances between the elements progressively increase as we move away from the diagonal, meaning that the topological properties of the system before and after the event are significantly different. The blue square regions (top left and bottom right) show that before and after the event, the distances between the PDs are very small (compared to the changes during the event itself). The difference from before to after an event is considerable, however, as indicated by the dark red color in the off-diagonal corners.
 | ||
| Fig. 16 (a) Heat map (a symmetric matrix) of ΔW2 for β0 of the event L1, where the color of element (i, j) illustrates the normalized distance of PDs for β0 between ϕ = ϕi and ϕ = ϕj, normalized by the same reference value used in Fig. 15, (b) normalized ΔW2 for β1 distance. The minimal steps between i and j are Δϕ ≈ 0.00014. | ||
To complete the discussion of the loading phase, Fig. 17 shows the results for events L2 and L3. We see that the general features of the results are similar as already discussed in the context of event L1 – only these events at larger volume fractions are narrower, more localized. While TP1 closely follows the pressure, TP0 could increase or decrease during an event. Therefore, a general pattern emerges: properties of the loops that form in the force networks as characterized by TP1 (which combines the number of loops and their ‘intensity’ (distance from the diagonal), are closely related to the material response, as quantified by the pressure.
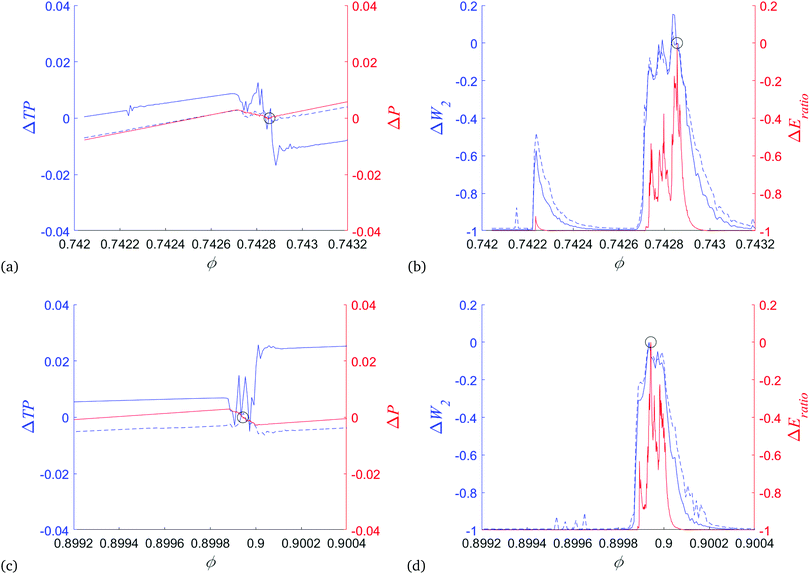 | ||
| Fig. 17 (a) L2, ΔTP0, ΔTP1 and Δp, (b) L2, ΔW2 of β0 and β1 and ΔEratio; (c) L3, ΔTP0, ΔTP1 and Δp, (d) L3, ΔW2 of β0 and β1 and ΔEratio, following the same format as in Fig. 14 and 15. | ||
Next, we proceed by discussing unloading. Fig. 12 already suggested that this phase is smoother than the loading one, with lesser and weaker events, at least on the coarse scale. On the fine scale, we consider the same three events as in Fig. 5–7, with the results shown in Fig. 18. The general features of the results are similar to the ones observed for loading, with TP1 closely following the pressure, and TP0 evolving in a much more dramatic fashion, either increasing or decreasing during an event. The relative changes are behaving similar to the kinetic energy ratio.
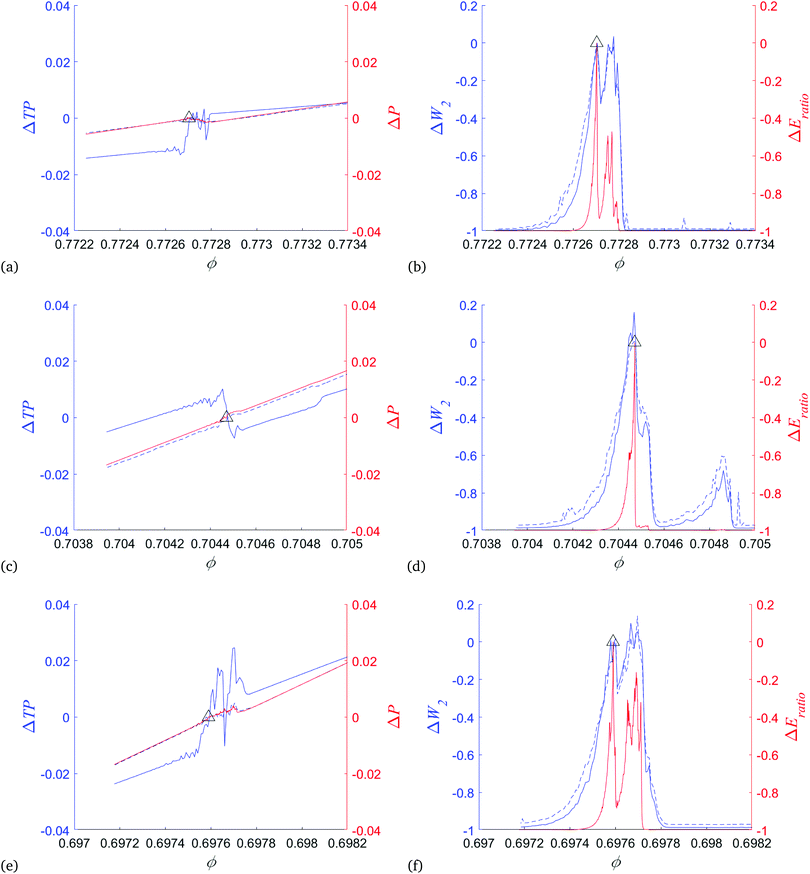 | ||
| Fig. 18 (a) UL1, ΔTP0, ΔTP1, and Δp, (b) UL1, ΔW2 of β0 and β1, and ΔEratio; (c) UL2, ΔTP0, ΔTP1, and Δp, (d) UL2, ΔW2 of β0 and β1, and ΔEratio; (e) UL3, ΔTP0, ΔTP1, and Δp, (f) UL3, ΔW2 of β0 and β1, and ΔEratio, following the same format as in Fig. 14 and 15. | ||
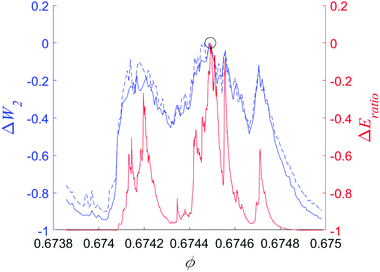
Fig. 18(c) and (d) show an interesting feature at ϕ ≈ 0.7049, where the distances between PDs show changes in the topology of force networks, although kinetic energy is unchanged – showing that changes in the topology can occur even without any motion of the particles. Note that also the coordination number is not changing much, see Fig. 7 bottom-centre, however, with stronger fluctuations.
Further results could be used to quantify the changes occurring during events by considering in more detail the ingredients that define TP: average lifespan of generators and their numbers. However, these additional results do not show obvious common features of the events. Further research, perhaps including a more detailed analysis of the persistence diagrams may be needed to better understand the details of the force network evolution during plastic events for either loading or unloading.
To conclude, we use the fact that a significant amount of information can be condensed in a visually simple-to-digest form using heat maps, and show in Fig. 19 and 20 the heat maps for a set of ten loading and unloading events. Fig. 19 shows that the distances are becoming larger as the system progresses to larger ϕ's during the loading, and Fig. 20 shows that the distances are becoming smaller for smaller ϕ's while unloading. The bigger the blue and red squares, in most higher volume fraction cases, the sharper the event is localized in strain (volume change), whereas only a few events closer to jamming are not localized, diffuse, or overlapping multiple events. Generic features of the heat-map results do not appear to change significantly between loading and unloading, or between components and loops.
 | ||
| Fig. 20 W 2 β 0 (top) and W2β1 (bottom) heat maps in log-scale for ten selected events during unloading; left to right, ϕ = 0.886, 0.866, 0.842, 0.798, 0.773, 0.761, 0.751, 0.729, 0.697, 0.694. | ||
Finally, we comment on the aspect, which has not been discussed extensively so far: while most of the events that we analyzed involve considerable particle dynamics, i.e., a significant kinetic to potential energy ratio, there are also events which involve only rearrangements of the force networks, with much weaker particle motion (data not shown, orders of magnitude smaller energy ratios). To illustrate this feature of the results, Fig. 21 shows the distances between consecutive persistence diagrams and the energy ratio for two selected loading/unloading windows. Careful inspection shows that while most of the events do involve changes of both W2 and Ek/Ep, there are a few events where only changes in W2 are present, showing that force networks can change while particles remain stationary.
 | ||
| Fig. 21 Energy ratio (red solid) and W2 distances for β0 (blue solid) and β1 (blue dashed) for loading (a) and unloading (b) against volume fraction, ϕ, for a range between 0.68 and 0.695. | ||
5 Summary and conclusion
In this paper, the process of slow compression (loading) and decompression (unloading) was studied for a three dimensional granular model system of soft particles. While below jamming the system evolution is irreversible (fluid-like), one main finding is that above jamming, both loading and unloading proceed via either reversible (elastic-) or irreversible (plastic-solid-like) processes. While the former are smooth and reversible, the latter are associated with rapid events, with serious rearrangements of the particle micro-structure, their positions and contacts, with associated particle dynamics (kinetic energy). However, there are also events that are associated with the changes in force networks persistence diagrams (PDs) only, without similarly strong particles dynamics (kinetic to potential energy ratio).The analysis of the force networks is carried out using PDs, a technique that can quantify the evolution during both reversible and irreversible processes. While PDs allow the extraction of a number of features of the underlying force networks, here we focus mostly on the most condensed measure, the total persistence, TP. It encodes information about complex weighted three dimensional (3D) networks into a single number. Even under such extreme information reduction, we find that TP provides interesting insights about the underlying force network and its evolution. In particular, we find that the changes of the mechanical pressure are strongly correlated with the TP computed for the loops that spontaneously form in evolving force networks during (de)compression. This finding suggests that the force network loops play a significant role in determining the mechanical system properties.
Further insights regarding the evolving force networks can be obtained by comparing consecutive system configurations. Such a comparison is made meaningful by computing the differences between the persistence diagrams that describe the main features of the underlying network. The difference, known as Wasserstein distance, shows that the force network experiences a significant change during the events discussed above, with strongly different force networks before and after an event. It should be emphasized that for obtaining such simple but insightful results, the data reduction provided by PH is crucial. This data reduction leads inevitably to an information loss, however we find that even under the most dramatic data compression, the emerging information still allows for reaching useful and relevant insights.
Future work should be devoted to a more quantitative analysis of strongly compressed and sheared frictional, soft granular packings – in the same spirit as present – where the deformability is fully taken into account, and also developing new approaches to consider such strong deformation of real particles, far beyond the validity of the over-simplified Hertzian based models. We expect that further significant insights into the micro-mechanics of soft granular matter, using further detailed features of PDs (like generators life-spans and numbers). Particularly interesting is the influence of inter-particle friction on the force networks, which could be better understood by a simultaneous analysis of the properties of both normal and tangential force networks.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
CC and LK acknowledge support by the US Army Research Office Grant No. W911NF1810184. SL and KT acknowledge funding from the German Science Foundation (DFG) through the project STE-969/16-1 within the SPP 1897 “Calm, Smooth and Smart”.Notes and references
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, 1986 Search PubMed.
- A. Nicolas, E. E. Ferrero, K. Martens and J.-L. Barrat, Deformation and flow of amorphous solids: An updated review of mesoscale elastoplastic models, Rev. Mod. Phys., 2018, 90(4), 045006 CrossRef CAS.
- H. M. Jaeger, S. R. Nagel and R. P. Behringer, Granular solids, liquids, and gases, Rev. Mod. Phys., 1996, 68(4), 1259–1273 CrossRef.
- T. Pöschel and S. Luding, Granular gases, Springer Science & Business Media, 2001, vol. 564 Search PubMed.
- S. Luding, Towards dense, realistic granular media in 2D, Nonlinearity, 2009, 22(12), R101–R146 CrossRef.
- M. Lätzel, S. Luding, H. J. Herrmann, D. W. Howell and R. P. Behringer, Comparing simulation and experiment of a 2D granular Couette shear device, Eur. Phys. J. E, 2003, 11(4), 325–333 CrossRef PubMed.
- F. Göncü, O. Durán and S. Luding, Jamming in frictionless packings of spheres: determination of the critical volume fraction, AIP Conference Proceedings “Powders and Grains”, 2009, vol. 1145, pp. 531–534.
- D. Bi, J. Zhang, B. Chakraborty and R. P. Behringer, Jamming by shear, Nature, 2011, 480(7377), 355–358 CrossRef CAS PubMed.
- J. Ren, J. A. Dijksman and R. P. Behringer, Reynolds Pressure and Relaxation in a Sheared Granular System, Phys. Rev. Lett., 2013, 110, 18302 CrossRef PubMed.
- R. Mari, R. Seto, J. F. Morris and M. M. Denn., Discontinuous shear thickening in brownian suspensions by dynamic simulation, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(50), 15326–15330 CrossRef CAS PubMed.
- A. Singh, R. Mari, M. M. Denn and J. F. Morris, A constitutive model for simple shear of dense frictional suspensions, J. Rheol., 2018, 62, 457 CrossRef CAS.
- N. Kumar and S. Luding, Memory of jamming-multiscale models for soft and granular matter, Granul. Matter, 2016, 18(3), 1–21 Search PubMed.
- D. Wang, J. Ren, J. A. Dijksman, H. Zheng and R. P. Behringer, Microscopic origins of shear jamming for 2d frictional grains, Phys. Rev. Lett., 2019, 120(20), 208004 CrossRef PubMed.
- I. Einav and A. M. Puzrin, Pressure-dependent elasticity and energy conservation in elastoplastic models for soils, J. Geotech. Geoenviron. Eng., 2004, 130(1), 81–92 CrossRef.
- R. G. Wan, M. Pinheiro and P. J. Guo, Elastoplastic modelling of diffuse instability response of geomaterials, Int. J. Numer. Anal. Meth. Geomech., 2011, 35(2), 140–160 CrossRef.
- M. L. Manning and A. J. Liu, Vibrational modes identify soft spots in a sheared disordered packing, Phys. Rev. Lett., 2011, 107(10), 108302 CrossRef CAS PubMed.
- Q. Zhang and K. Kamrin, Microscopic description of the granular fluidity field in nonlocal flow modeling, Phys. Rev. Lett., 2017, 118, 058001 CrossRef PubMed.
- A. A. Long, D. V. Denisov, P. Schall, T. C. Hufnagel, X. Gu, W. J. Wright and K. A. Dahmen, From critical behavior to catastrophic runaways: comparing sheared granular materials with bulk metallic glasses, Granul. Matter, 2019, 21(4), 1–8 Search PubMed.
- E. Alaei, B. Marks and I. Einav, A hydrodynamic-plastic formulation for modelling sand using a minimal set of parameters, J. Mech. Phys. Solids, 2021, 151, 104388 CrossRef.
- J. Brujić, C. Song, P. Wang, C. Briscoe, G. Marty and H. A. Makse., Measuring the Coordination Number and Entropy of a 3D Jammed Emulsion Packing by Confocal Microscopy, Phys. Rev. Lett., 2007, 98, 248001 CrossRef PubMed.
- O. I. Imole, M. Paulick, V. Magnanimo, M. Morgeneyer, B. E. Montes, M. Ramaioli, A. Kwade and S. Luding, Slow stress relaxation behavior of cohesive powders, Powder Technol., 2016, 293, 82–93 CrossRef CAS.
- E. Ando, J. Dijkstra, E. Roubin, C. Dano and E. Boller, A peek into the origin of creep in sand, Granul. Matter, 2019, 21, 11 CrossRef PubMed.
- T. T. T. Nguyen, T. Doanh, A. Le Bot and D. Dalmas., High-temporal-resolution quasideterministic dynamics of granular stick-slip, Sci. Rep., 2021, 11(1), 1–11 CrossRef PubMed.
- T. Doanh, N. Abdelmoula, L. Gribaa, T. T. T. Nguyên, S. Hans, C. Boutin and A. Le Bot, Dynamic instabilities under isotropic drained compression of idealized granular materials, Acta Geotechnica, 2017, 12(3), 657–676 CrossRef.
- T. Doanh, A. Le Bot, N. Abdelmoula, L. Gribaa, S. Hans and C. Boutin, Unexpected collapses during isotropic consolidation of model granular materials, C. R. Mec., 2016, 344(2), 69–77 CrossRef.
- D. Cui, W. Wu, W. Xiang, T. Doanh, Q. Chen, S. Wang, Q. Liu and J. Wang, Stick-slip behaviours of dry glass beads in triaxial compression, Granul. Matter, 2017, 19(1), 1–18 CrossRef CAS.
- P. Yu, S. Frank-Richter, A. Börngen and M. Sperl, Monitoring three-dimensional packings in microgravity, Granul. Matter, 2014, 16(2), 165–173 CrossRef.
- S. Frank-Richter, Disordered binary granular packings in three dimensions, PhD thesis, Heinrich-Heine-Universität, Düsseldorf, 2014.
- R. Arévalo, L. A. Pugnaloni, I. Zuriguel and D. Maza, Contact network topology in tapped granular media, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022203 CrossRef PubMed.
- L. Kondic, M. Kramár, L. A. Pugnaloni, C. Manuel Carlevaro and K. Mischaikow, Structure of force networks in tapped particulate systems of disks and pentagons. ii. persistence analysis, Phys. Rev. E, 2016, 93, 062903 CrossRef CAS PubMed.
- S. Shah, C. Cheng, P. Jalali and L. Kondic, Failure of confined granular media due to pullout of an intruder: from force networks to a system wide response, Soft Matter, 2020, 16, 7685–7695 RSC.
- D. S. Bassett, E. T. Owens, K. E. Daniels and M. A. Porter, Influence of network topology on sound propagation in granular materials, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 041306 CrossRef PubMed.
- D. M. Walker and A. Tordesillas, Taxonomy of granular rheology from grain property networks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 011304 CrossRef PubMed.
- S. Sarkar, D. Bi, J. Zhang, R. P. Behringer and B. Chakraborty, Origin of rigidity in dry granular solids, Phys. Rev. Lett., 2013, 111, 068301 CrossRef PubMed.
- L. Bo, R. Mari, C. Song and H. A. Makse, Cavity method for force transmission in jammed disordered packings of hard particles, Soft Matter, 2014, 10, 7379–7392 RSC.
- A. Tordesillas, S. T. Tobin, M. Cil, K. Alshibli and R. P. Behringer, Network flow model of force transmission in unbonded and bonded granular media, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 062204 CrossRef PubMed.
- C. Giusti, L. Papadopoulos, E. T. Owens, K. E. Daniels and D. S. Bassett, Topological and geometric measurements of force-chain structure, Phys. Rev. E, 2016, 94, 032909 CrossRef PubMed.
- R. C. Ball and R. Blumenfeld, Stress field in granular systems: loop forces and potential formulation, Phys. Rev. Lett., 2002, 88(11), 115505 CrossRef PubMed.
- M. Kramár, A. Goullet, L. Kondic and K. Mischaikow, Quantifying force networks in particulate systems, Phys. D, 2014, 283, 37–55 CrossRef.
- T. Kacynksi, K. M. Mischaikow and M. Mrozek, Computational Homology, Springer, 2004 Search PubMed.
- D. Taylor, F. Klimm, H. A. Harrington, M. Kramar, K. Mischaikow, M. A. Porter and P. J. Mucha, Topological data analysis of contagion maps for examining spreading processes on networks, Nat. Commun., 2015, 6, 1–11 Search PubMed.
- M. Kramár, R. Levanger, J. Tithof, B. Suri, M. Xu, M. Paul, M. F. Schatz and K. Mischaikow., Analysis of Kolmogorov flow and Rayleigh-Bénard convection using persistent homology, Phys. D, 2016, 334, 82–98 CrossRef.
- A. Hirata, L. J. Kang, T. Fujita, B. Klumov, K. Matsue, M. Kotani, A. R. Yavari and M. W. Chen., Geometric frustration of icosahedron in metallic glasses, Science, 2013, 341(6144), 376–379 CrossRef CAS PubMed.
- Y. Hiraoka, T. Nakamura, A. Hirata, E. G. Escolar, K. Matsue and Y. Nishiura, Hierarchical structures of amorphous solids characterized by persistent homology, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(26), 7035–7040 CrossRef CAS PubMed.
- L. Kondic, A. Goullet, C. S. O'Hern, M. Kramar, K. Mischaikow and R. P. Behringer, Topology of force networks in compressed granular media, Europhys. Lett., 2012, 97, 54001 CrossRef.
- M. Kramár, A. Goullet, L. Kondic and K. Mischaikow, Evolution of force networks in dense particulate media, Phys. Rev. E, 2014, 90, 052203 CrossRef PubMed.
- S. Ardanza-Trevijano, I. Zuriguel, R. Arévalo and D. Maza, Topological analysis of tapped granular media using persistent homology, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 052212 CrossRef CAS PubMed.
- L. A. Pugnaloni, C. M. Carlevaro, M. Kramár, K. Mischaikow and L. Kondic, Structure of force networks in tapped particulate systems of disks and pentagons. i. clusters and loops, Phys. Rev. E, 2016, 93, 062902 CrossRef PubMed.
- M. Gameiro, A. Singh, L. Kondic, K. Mischaikow and J. F. Morris, Interaction network analysis in shear thickening suspensions, Phys. Rev. Fluids, 2020, 5, 034307 CrossRef.
- Gudhi library – topological data analysis and geometric inference in higher dimension, https://gudhi.inria.fr/.
- N. Brodu, J. A. Dijksman and R. P. Behringer., Multiple-contact discrete-element model for simulating dense granular media, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91(3), 032201 CrossRef PubMed.
- S. Nezamabadi, T. H. Nguyen, J.-Y. Delenne and F. Radjai, Modeling soft granular materials, Granul. Matter, 2017, 19(1), 1–12 CrossRef CAS.
- K. Giannis, C. Schilde, J. H. Finke, A. Kwade, M. A. Celigueta, K. Taghizadeh and S. Luding, Stress based multi-contact model for discrete-element simulations, Granul. Matter, 2021, 23(2), 1–14 Search PubMed.
- S. Nezamabadi, M. Ghadiri, J.-Y. Delenne and F. Radjai, Modelling the compaction of plastic particle packings, Comput. Part. Mech., 2021, 1–8 Search PubMed.
- D. Cantor, M. Cárdenas-Barrantes, I. Preechawuttipong, M. Renouf and E. Azéma, Compaction model for highly deformable particle assemblies, Phys. Rev. Lett., 2020, 124(20), 208003 CrossRef CAS PubMed.
- M. Cárdenas-Barrantes, D. Cantor, J. Barés, M. Renouf and E. Azéma, Three-dimensional compaction of soft granular packings, Soft Matter, 2022, 18, 312–321 RSC.
- J. Brujić, A. F. Edwards, D. V. Grinev, I. Hopkinson, D. Brujić and H. A. Makse, 3d bulk measurements of the force distribution in a compressed emulsion system, Faraday Discuss., 2003, 123, 207–220 RSC.
- J. Brujic, P. Wang, C. Song, D. L. Johnson, O. Sindt and H. A. Makse, Granular dynamics in compaction and stress relaxation, Phys. Rev. Lett., 2005, 95(12), 128001 CrossRef PubMed.
- J. Barés, N. Brodu, H. Zheng and J. A. Dijksman, Transparent experiments: releasing data from mechanical tests on three dimensional hydrogel sphere packings, Granul. Matter, 2020, 22(1), 1–7 CrossRef.
- P. A. Cundall and O. D. L. Strack, A discrete numerical model for granular assemblies, Géotechnique, 1979, 29(1), 47–65 CrossRef.
- H. P. Zhang and H. A. Makse, Jamming transition in emulsions and granular materials, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 11301 CrossRef CAS PubMed.
- K. L. Johnson, Contact mechanics, Cambridge University Press, 1987 Search PubMed.
- S. Luding, Introduction to discete element methods: Basics of contact force models and how to perform the micro-marco transition to continuum theory, Eur. J. Environ. Civ. Eng., 2008, 12(7–8), 785–826 CrossRef.
- C. Thornton, S. J. Cummins and P. W. Cleary, An investigation of the comparative behaviour of alternative contact force models during elastic collisions, Powder Technol., 2011, 210(3), 189–197 CrossRef CAS.
- K. Taghizadeh, S. Luding and V. Magnanimo, Dem applied to soil mechanics, ALERT Doctoral School 2017 Discrete Element Modeling, 2017, p. 129.
- S. Luding, Objective constitutive relations from DEM, in Seehäfen für Containerschiffe zukünftiger Generationen, ed. J. Grabe, TUHH, Germany, 2008, pp. 173–182 Search PubMed.
- A. Singh, V. Magnanimo, K. Saitoh and S. Luding, Effect of cohesion on shear banding in quasistatic granular materials, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90(2), 022202 CrossRef PubMed.
- D. Vescovi and S. Luding, Merging fluid and solid granular behavior, Soft Matter, 2016, 12(41), 8616–8628 RSC.
- S. Luding, How does static granular matter re-arrange for different isotropic strain rate?, Powders and Grains, 2021, vol. 249, p. 10001 Search PubMed.
- M. Cárdenas-Barrantes, D. Cantor, J. Barés, M. Renouf and E. Azéma, Micromechanical description of the compaction of soft pentagon assemblies, Phys. Rev. E, 2021, 103(6), 062902 CrossRef PubMed.
- S. Nezamabadi, F. Radjai, J. Averseng and J.-Y. Delenne, Implicit frictional-contact model for soft particle systems, J. Mech. Phys. Solids, 2015, 83, 72–87 CrossRef.
- K. Saitoh, V. Magnanimo and S. Luding, Master equation for the probability distribution functions of overlaps between particles in two dimensional granular packings, Soft Matter, 2015, 11, 1253–1258 RSC.
- A. Merkel and S. Luding, Enhanced micropolar model for wave propagation in ordered granular materials, Int. J. Solids Struct., 2017, 106–107, 91–105 CrossRef CAS.
- H. A. Makse, N. Gland, D. L. Johnson and L. Schwartz, Granular packings: Nonlinear elasticity, sound propagation, and collective relaxation dynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 61302 CrossRef PubMed.
- E. Somfai, J. N. Roux, J. H. Snoeijer, M. van Hecke and W. van Saarloos, Elastic wave propagation in confined granular systems, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 21301 CrossRef PubMed.
- N. P. Kruyt, I. Agnolin, S. Luding and L. Rothenburg, Micromechanical study of elastic moduli of loose granular materials, J. Mech. Phys. Solids, 2010, 58(9), 1286–1301 CrossRef.
- M. H. Khalili, J.-N. Roux, J.-M. Pereira, S. Brisard and M. Bornert, Numerical study of one-dimensional compression of granular materials. i. stress-strain behavior, microstructure, and irreversibility, Phys. Rev. E, 2017, 95(3), 032907 CrossRef PubMed.
- I. Agnolin and N. P. Kruyt, On the elastic moduli of two-dimensional assemblies of disks: Relevance and modeling of fluctuations in particle displacements and rotations, Comput. Math. Appl., 2008, 55(2), 245–256 CrossRef.
- K. Taghizadeh, H. Steeb, V. Magnanimo and S. Luding, Elastic waves in particulate glass-rubber mixture: experimental and numerical investigations/studies, EPJ Web Conf., 2017, 140, 12019 CrossRef.
- H. A. Makse, N. Gland, D. L. Johnson and L. M. Schwartz, Why effective medium theory fails in granular materials, Phys. Rev. Lett., 1999, 83(24), 5070 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01689j |
‡ Units could be, e.g., length, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) u = 0.5 × 10−3 m, time, u = 0.5 × 10−3 m, time, ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) u = 10−5 s, and mass, u = 10−5 s, and mass, ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) u = 1.25 × 10−10 kg, to match experimental values: u = 1.25 × 10−10 kg, to match experimental values: ![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) p = p =  mm, mm, 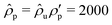 kg m−3, etc., see ref. 66. kg m−3, etc., see ref. 66. |
| This journal is © The Royal Society of Chemistry 2022 |