Open Access Article
Open Access ArticleProbing the dynamics of turbid colloidal suspensions using differential dynamic microscopy†
Reece
Nixon-Luke
 a,
Jochen
Arlt
a,
Jochen
Arlt
 b,
Wilson C. K.
Poon
b,
Wilson C. K.
Poon
 b,
Gary
Bryant
b,
Gary
Bryant
 *a and
Vincent A.
Martinez
*a and
Vincent A.
Martinez
 *b
*b
aSchool of Science, RMIT University, Melbourne, Victoria 3000, Australia. E-mail: gary.bryant@rmit.edu.au
bSUPA, School of Physics and Astronomy, The University of Edinburgh, Peter Guthrie Tait Road, Edinburgh, EH9 3FD, UK. E-mail: vincent.martinez@ed.ac.uk
First published on 11th February 2022
Abstract
Few techniques can reliably measure the dynamics of colloidal suspensions or other soft materials over a wide range of turbidities. Here we systematically investigate the capability of Differential Dynamic Microscopy (DDM) to characterise particle dynamics in turbid colloidal suspensions based on brightfield optical microscopy. We measure the Intermediate Scattering Function (ISF) of polystyrene microspheres suspended in water over a range of concentrations, turbidities, and up to 4 orders of magnitude in time-scales. These DDM results are compared to data obtained from both Dynamic Light Scattering (DLS) and Two-colour Dynamic Light Scattering (TCDLS). The latter allows for suppression of multiple scattering for moderately turbid suspensions. We find that DDM can obtain reliable diffusion coefficients at up to 10 and 1000 times higher particle concentrations than TCDLS and standard DLS, respectively. Additionally, we investigate the roles of the four length-scales relevant when imaging a suspension: the sample thickness L, the imaging depth z, the imaging depth of field DoF, and the photon mean free path ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . More detailed experiments and analysis reveal the appearance of a short-time process as turbidity is increased, which we associate with multiple scattering events within the imaging depth of the field. The long-time process corresponds to the particle dynamics from which particle-size can be estimated in the case of non-interacting particles. Finally, we provide a simple theoretical framework, ms-DDM, for turbid samples, which accounts for multiple scattering.
. More detailed experiments and analysis reveal the appearance of a short-time process as turbidity is increased, which we associate with multiple scattering events within the imaging depth of the field. The long-time process corresponds to the particle dynamics from which particle-size can be estimated in the case of non-interacting particles. Finally, we provide a simple theoretical framework, ms-DDM, for turbid samples, which accounts for multiple scattering.
1 Introduction
The measurement of particle size in suspension is of fundamental importance in a wide range of applications such as quality control1 and the development of advanced materials for drug delivery.2,3 The size and shape of micron-sized particles can be measured by optical microscopy. Scanning and transmission electron microscopy (EM) can be used for nanoparticles. In both cases, hundreds of particles must be measured for reliable statistics,4 which is therefore too time consuming for routine use. EM has the additional constraint that particles are measured in the dry state, which can lead to an underestimate of the size of core–shell type particles in solution.5,6 Cryo-EM methods avoid the need for drying and can provide high resolution for individual particles, but are again too time consuming for routine analysis.7On the other hand, scattering techniques are ideal for characterising suspended nanoparticles: they are non-destructive and suitable for a variety of solvents, including physiologically relevant media. Static light scattering (SLS), small angle X-ray scattering (SAXS) and small angle neutron scattering (SANS) all rely on the fact that the angle-dependent scattered intensity is sensitive to the particle composition, size and shape.8 They have been used to characterise a broad range of complex particles in solution such as drug delivery systems2 and solid-lipid nanoparticles.3 However, these techniques require specialised instrumentation and considerable expertise in analysis.
Unlike the methods mentioned so far, dynamic light scattering (DLS) measures particle size via particle dynamics.9,10 Standard DLS does so by measuring the temporal autocorrelation function (ACF) of the far-field scattered intensity at a specified scattering vector ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , which specifies the length scale l = 2π/q (with q = ‖
, which specifies the length scale l = 2π/q (with q = ‖![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ‖) at which the particle dynamics are being probed.
‖) at which the particle dynamics are being probed.
For diffusive monodisperse spheres, the ACF decays exponentially with a characterisitic time that depends inversely on the particle size provided that the detected photons have only been scattered once. Thus conventional DLS only works when the turbidity is negligible either because the concentration is low, or because the solvent and particles have very similar refractive indices. Dynamics in concentrated samples may also be probed, but only after care is taken to eliminate multiple scattering by refractive index matching.11 This is not possible for most samples, so methods have been developed to suppress the signal from multiple scattering, such as two-colour DLS (TCDLS)12 and 3D DLS.13,14 The synchrotron-based analogue of DLS, XPCS, does not suffer from multiple scattering, but is only available at central facilities and suffers from beam-damage problems.15 Finally, diffusing wave spectroscopy (DWS) deals with multiple scattering by seeking to model it explicitly to extract particle mean squared displacements from turbid systems, but requires knowledge of the hard-to-measure photon mean free path and gives no information on the q-dependant dynamics.16
Differential dynamic microscopy (DDM) is a relatively new technique for characterising particle dynamics in solution.17,18 The method extracts dynamical information by measuring the spatio-temporal intensity fluctuations from microscopy movies. Interestingly, recent studies have shown that DDM5,19–22 and related techniques such as heterodyne near-field scattering23 and confocal DDM24,25 appear to be less affected by multiple scattering than DLS, making it possible to investigate concentrated suspensions of colloids22 or micro-organisms26 without index matching.
However, the physical origins of DDM's insensitivity to multiple scattering remain unclear. The sample turbidity is, as in DWS, characterised by the photon mean free path ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , which is a function of the particle size and shape, refractive indices of the particles and solvent, and the particle volume fraction ϕ. However, there are three other relevant length scales characterising the experimental implementation of DDM: the sample thickness L, the imaging depth z, the imaging depth of field, DoF, Fig. 1. The range of turbidities over which DDM is applicable must depend on the three dimensionless ratios (L/
, which is a function of the particle size and shape, refractive indices of the particles and solvent, and the particle volume fraction ϕ. However, there are three other relevant length scales characterising the experimental implementation of DDM: the sample thickness L, the imaging depth z, the imaging depth of field, DoF, Fig. 1. The range of turbidities over which DDM is applicable must depend on the three dimensionless ratios (L/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , z/
, z/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , DoF/
, DoF/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ).
).
Here, we investigate this dependence systematically in dilute colloids by tuning L and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , in the latter case via the particle radius R and volume fraction ϕ. We first compare DDM with DLS and TCDLS and discuss its advantages and limitations. We find that DDM can reliably size particles at up to ≈25× higher particle concentrations than TCDLS. We then investigate the roles of the length scales mentioned above, extending previous studies18,27,28 to turbid samples. We find the emergence of a short-time decay process that appears as ϕ increases, which we associate with multiple-scattering events. We examine the source of this process and provide a simple theoretical framework for DDM that accounts for multiple scattering.
, in the latter case via the particle radius R and volume fraction ϕ. We first compare DDM with DLS and TCDLS and discuss its advantages and limitations. We find that DDM can reliably size particles at up to ≈25× higher particle concentrations than TCDLS. We then investigate the roles of the length scales mentioned above, extending previous studies18,27,28 to turbid samples. We find the emergence of a short-time decay process that appears as ϕ increases, which we associate with multiple-scattering events. We examine the source of this process and provide a simple theoretical framework for DDM that accounts for multiple scattering.
2 Theoretical background
2.1 Turbidity
A sample is described as turbid if there is a significant probability of a photon being scattered more than once in traversing it. One way to quantify turbidity is to compare the photon mean free path![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) to the relevant sample dimension L. The mean free path scales with the scattering cross-section of individual scatterers σ and their number density as
to the relevant sample dimension L. The mean free path scales with the scattering cross-section of individual scatterers σ and their number density as ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∝ 1/(σϕ). For simple spherical scatterers, as considered here, σ can be computed from Mie theory in terms of the particles' radius, their (complex) refractive index and that of the suspending medium, and the incident wavelength.29,30
∝ 1/(σϕ). For simple spherical scatterers, as considered here, σ can be computed from Mie theory in terms of the particles' radius, their (complex) refractive index and that of the suspending medium, and the incident wavelength.29,30
Scattering can be considered as a Poisson process, and the probability that a photon gets scattered n times can be estimated from the mean number of scattering events
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = L/ = L/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = −ln(T/T0), = −ln(T/T0), | (1) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ≪ 1 it is sufficient to consider only single scattering events. In general, however, singly-scattered photons (P1) represent only a fraction of the total scattered light (Psc):
≪ 1 it is sufficient to consider only single scattering events. In general, however, singly-scattered photons (P1) represent only a fraction of the total scattered light (Psc):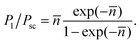 | (2) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = L/
= L/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1/5, multiple scattering already contributes ≈10%, and becomes dominant for L/
= 1/5, multiple scattering already contributes ≈10%, and becomes dominant for L/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≳ 1.3. Multiple scattering speeds up the decay of the intensity ACF measured in DLS.31 However, this effect is difficult to quantify except in the extreme DWS limit.16
≳ 1.3. Multiple scattering speeds up the decay of the intensity ACF measured in DLS.31 However, this effect is difficult to quantify except in the extreme DWS limit.16
2.2 Dynamic light scattering
For completeness, we briefly review DLS, which is well established.9,10 In a conventional DLS experiment, one measures the normalised intensity ACF of the scattered light at a given scattering angle θ:| gDLS(q, τ) = 1 + β2|f(q, τ)|2 | (3) |
 is the magnitude of the scattering vector
is the magnitude of the scattering vector ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) defined by θ, with λ the laser wavelength and n the refractive index of the solvent. For non-interacting mono-disperse Brownian spheres,
defined by θ, with λ the laser wavelength and n the refractive index of the solvent. For non-interacting mono-disperse Brownian spheres,| f(q, τ) = exp(−τ/τr) | (4) |
| D0 = kBT/6πηR, | (5) |
2.3 Two-colour dynamic light scattering
Details on TCDLS can be found elsewhere;12,32 we quote the key result. In a TCDLS experiment, one measures the scattered intensity at two distinct wavelengths but the same![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) . Cross-correlation of the two scattered intensities (XCF) allows suppression of the multiple scattering and yields the ISF:
. Cross-correlation of the two scattered intensities (XCF) allows suppression of the multiple scattering and yields the ISF:| gTCDLS(q, τ) = 1 + β2βOV2βMS2|f(q,τ)|2, | (6) |
2.4 Differential dynamic microscopy
g(s)DDM (![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , τ) = 〈|I( , τ) = 〈|I(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , t + τ) − I( , t + τ) − I(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , t)|2〉t , t)|2〉t | (7) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , t) is the Fourier transform of the recorded image I(
, t) is the Fourier transform of the recorded image I(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t), with
, t), with ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) the pixel position in the image, and brackets denote averaging over t. In transmission microscopy, the image is formed by the incident light I0 traversing the pure solvent minus the light scattered by particles in the object plane, Is, giving rise to a spatio-temporally varying measured intensity I:34
the pixel position in the image, and brackets denote averaging over t. In transmission microscopy, the image is formed by the incident light I0 traversing the pure solvent minus the light scattered by particles in the object plane, Is, giving rise to a spatio-temporally varying measured intensity I:34I(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) = I0( , t) = I0(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) − Is( , t) − Is(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) , t) | (8) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t). Note that for bright field microscopy Is can be locally negative but is positive when averaged over the field of view. Using eqn (8), eqn (7) becomes
, t). Note that for bright field microscopy Is can be locally negative but is positive when averaged over the field of view. Using eqn (8), eqn (7) becomes | (9) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) = 2〈|ΔI0(
) = 2〈|ΔI0(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) )|2〉. In practice, B represents the instrumental noise and is a combination of the incident light and camera uncorrelated noises. For isotropic motion and under appropriate optical conditions, so that the scattered intensity fluctuations are proportional to the density fluctuations (ΔIs ∝ Δρ), eqn (7) yields the ISF via33,34
)|2〉. In practice, B represents the instrumental noise and is a combination of the incident light and camera uncorrelated noises. For isotropic motion and under appropriate optical conditions, so that the scattered intensity fluctuations are proportional to the density fluctuations (ΔIs ∝ Δρ), eqn (7) yields the ISF via33,34| g(s)DDM(q, τ) = A(q)[1 − f(q, τ)] + B(q). | (10) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (q)|2S(q) is the amplitude of the static signal of the sample, where S(q) is the structure factor and
(q)|2S(q) is the amplitude of the static signal of the sample, where S(q) is the structure factor and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (q) is the single particle amplitude combining the effects of the particle form factor P(q) and the optical transfer function T(q) of the imaging system, which can be seen as the contrast of the particles in the image. For non-interacting particles and negligible turbidity, A ∝ ϕ as previously demonstrated.26
(q) is the single particle amplitude combining the effects of the particle form factor P(q) and the optical transfer function T(q) of the imaging system, which can be seen as the contrast of the particles in the image. For non-interacting particles and negligible turbidity, A ∝ ϕ as previously demonstrated.26
I(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) = I0( , t) = I0(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) − Is( , t) − Is(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) − Im( , t) − Im(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) , t) | (11) |
 | (12) |
| g(m)DDM(q, τ) = A(m)(q)[1 − αf(q, τ) − (1 − α)f(m)(q, τ)] + B(m)(q) | (13) |
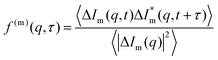 the normalised correlation function of the multiply-scattered intensity fluctuations, and B(m)(q) = B(q) + B×. The signal amplitude A(m)(q) = 2(〈|ΔIs(q)|2〉 + 〈|ΔIm(q)|2〉) can be independently estimated using eqn (1), which accounts for the attenuation of the intensity reaching the detector, and the definition of A(q) from eqn (10):
the normalised correlation function of the multiply-scattered intensity fluctuations, and B(m)(q) = B(q) + B×. The signal amplitude A(m)(q) = 2(〈|ΔIs(q)|2〉 + 〈|ΔIm(q)|2〉) can be independently estimated using eqn (1), which accounts for the attenuation of the intensity reaching the detector, and the definition of A(q) from eqn (10):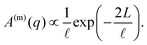 | (14) |
3 Materials and methods
3.1 Microsphere solutions and turbidity measurement
Stock solutions of charge stabilized polystyrene spheres of diameter 250, 210 and 140 nm (Bangs Labs, Fishers, IN, PS02N) were prepared at a range of concentrations, and are designated SYS250, SYS210 and SYS140 respectively. Sample volume fractions were calculated using the manufacturers specification of the stock mass fraction (10%) and particle density, and prepared via serial dilution. The suspensions were prepared with ϕ logarithmically spaced from 0.001 to 10%. Exact ϕ values for the various samples are shown in Table S1 of the ESI.† At most of these values, we expect few particle interactions, so that D(ϕ) ≈ D0.3.2 DLS and TCDLS
Measurements were performed on an ALV TCDLS instrument. Samples were contained in a cylindrical cuvette of 4 mm inner diameter (LSI Instruments), and held in a scattering vat temperature controlled to 22 °C. Data was recorded for two minutes at θ = 30° in both autocorrelation (ACF, eqn (3)), and cross-correlation (XCF, eqn (6)) modes. For single scattering samples, the intensity ACF and XCF exhibit the same decay rate, but the XCF has a reduced amplitude12 caused by the incomplete overlap of the scattered and detected volumes. For turbid samples, the amount of multiple scattering can therefore be quantified by TCDLS intercept, i.e. the reduction in the instrumental prefactor in eqn (6) from its nominal (single scattering) value as found from the limits τ → 0 of gTCDLS(τ) and gDLS(τ). The ACF and XCF were fitted using eqn (3) and (6), respectively, and eqn (4).3.3 Differential dynamic microscopy
DDM experiments were performed using an Olympus IX-71 microscope equipped with a Mikrotron MC-1362 camera connected to a Euresys Grablink Full frame grabber card. The camera is equipped with a 1280 × 1024 pixel CMOS sensor with 14 μm square pixels. Bright field images were taken with a 60×/0.7 objective using Köhler illumination with a reduced numerical aperture of ≈0.3. Under these conditions the imaged pixel size is ≈0.24 μm per pixel, which corresponds approximately to the diameter of the largest particles considered in this study. Samples were loaded into rectangular capillary tubes (Vitrocom, 4 or 8 mm width) and sealed with vaseline. We used different inner capillary heights (400, 200 and 100 μm) to explore the effects of sample thickness L. Measurements commenced after a minimum of one minute equilibration. Unless otherwise stated, samples were imaged near the midway point between the inner top and bottom walls. To avoid saturating the camera, the illumination intensity and/or exposure time was tuned to maintain the average intensity of the images in the middle range.Most of the videos were recorded using a frame rate of 100 fps, but for some of the samples we also acquired movies at 1000 fps in order to investigate the emergence of short-time processes. A table showing the conditions used for all experiments is in the ESI† (Table S2). A bespoke LABVIEW program was used to calculate the DICFs from the videos based on eqn (7), which were then fitted using eqn (4) and (10). The resulting fitted D(q) were then averaged over the range 1.5 < q < 4 μm−1, where reliable fitting were obtained, to yield the averaged diffusion coefficient D. The amplitude of the signal 〈A〉 (ϕ) was obtained by normalising the fitted A(q, ϕ) to an arbitrary reference sample A(q, ϕ0) and then averaged over the above q range.
3.4 Measurements of turbidity, transmission, and photon mean free path ![[small script l]](https://www.rsc.org/images/entities/h3_char_e146.gif)
Turbidity is a function of the sample thickness L and the photon mean free path ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (eqn (1)), and thus the volume fraction ϕ. Fig. 2 shows the visual appearance of the SYS250 suspensions in cylindrical tubes (4 mm diameter) used for DLS and TCDLS measurements and of the SYS210 suspensions in 400 μm-height capillaries used for DDM measurements, both as a function of concentration.
(eqn (1)), and thus the volume fraction ϕ. Fig. 2 shows the visual appearance of the SYS250 suspensions in cylindrical tubes (4 mm diameter) used for DLS and TCDLS measurements and of the SYS210 suspensions in 400 μm-height capillaries used for DDM measurements, both as a function of concentration.
 | ||
| Fig. 2 Pictures of (top) SYS250 particle suspensions in cylindrical tubes (4 mm diameter) used for DLS & TCDLS measurements and (bottom) SYS210 in 400 μm-height capillaries used for DDM measurements, both with increasing ϕ from left to right. See Table S2 (ESI†) for values of concentration. Top image: Highest ϕ ≈ 1.6%. Pictures were recorded using a Huawei Mate 10 Pro camera with a blue background. | ||
We quantified the turbidity by measuring the light transmitted through the sample (eqn (1)), which can be estimated from the mean intensity of microscope images, provided that these are recorded with the same illumination settings.5 We therefore recorded sets of movies covering a wide range of ϕ using identical illumination settings (but tuning the exposure time to compensate for the limited dynamic range of our camera). These movies allowed us to estimate transmission as well as the relative amplitude of the DDM signal as a function of ϕ (Section S2, ESI†). The transmission measurements were validated using an additional custom-made setup based on laser-light rather than white light (Section S4, ESI†).
4 Results
4.1 DDM versus DLS and TCDLS
Typical results for gDLS and gTCDLS are presented in Section S3 (ESI†), and for gDDM in Fig. 3 for SYS250 at several ϕ. Fitting these functions using eqn (3), (6) or (10) in combination with eqn (4) yields the diffusion coefficients measured using DLS, TCDLS, and DDM for SYS250 and SYS140 as a function of ϕ, Fig. 4. The values are normalised against the reference value obtained from averaging DLS and TCDLS results at low concentration: D0(SYS250) = 1.87 ± 0.04 μm2 and D0(SYS140) = 3.30 ± 0.10 μm2. The TCDLS intercept (prefactor in eqn (6)) is a measure of multiple scattering and shown as (*) symbols using the right-hand axis. As the concentration is increased, multiple scattering and thus turbidity increases as visually observed from images of the DLS tubes, Fig. 2, and confirmed through the decrease of the TCDLS intercept, Fig. 4. | ||
| Fig. 3 Typical DICFs, gDDM(q, τ), obtained from DDM as a function of delay time τ at q ≈ 1 μm−1 measured for several volume fractions of SYS250. Lines are fits using eqn (10) and (4). The corresponding movies (100 fps, 1024 × 1024 pixels, 20) were recording at variable incident intensity to maximise the signal amplitude. | ||
We find four regimes of behaviour as ϕ increases. Regime 1 is the single-scattering regime, where the TCDLS intercept remains at its nominal value of ≈0.6, i.e., only singly-scattered light is being detected. In this regime, all techniques return similar D(ϕ).
In regime 2, the intercept drops as ϕ increases, indicating an increase in multiple scattering. This produces faster intensity fluctuations, so that D(ϕ) measured by DLS increases. As TCDLS suppresses contributions from multiple scattering, it still returns a valid (constant) D(ϕ) in this regime.
In regime 3, the TCDLS intercept drops to zero as there are not enough single-scattered photons reaching the detector. Note that TCDLS now measures noise and delivers a null rather than false result, contrasting with DLS in regime 2. In this regime, DDM carried out using glass capillaries with L = 400 μm (blue open symbols) is able to return an accurate D(ϕ) up to ϕ = 2.5%. This limit is 25× higher than for TCDLS, and will be discussed further in Section 4.3. The multiple scattering contribution to DDM in this regime will be discussed in Section 4.2.
In regime 4, samples in L = 400 μm DDM capillaries appear extremely turbid, Fig. 2, and only a small fraction of incident light is transmitted. Even with the microscope light source set to maximum, only a very low signal is detected on the camera. The resulting DICFs are approximately τ-independent: the noise term B(m)(q) overwhelms the amplitude of the DDM signal A(q), eqn (13).
Significantly, using a thinner capillary, L = 100 μm, allowed measurements of D(ϕ) up to ϕ ≈ 10%, which is the undiluted stock solution, Fig. 4a (open blue symbol). This finding will be discussed in detail later (Section 4.2).
Results collected using a smaller particle size (SYS140), Fig. 4b, confirms these findings, although regime boundaries shift to higher ϕ. This is consistent with eqn (1), as one expects ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) to increase when R decreases (see Section 4.2). Now, regime 4 is beyond the highest concentration studied, so DDM is able to deliver reliable D(ϕ) over the whole of our concentration regime. Note that, as expected, D increases slightly with ϕ due to particle interactions.35
to increase when R decreases (see Section 4.2). Now, regime 4 is beyond the highest concentration studied, so DDM is able to deliver reliable D(ϕ) over the whole of our concentration regime. Note that, as expected, D increases slightly with ϕ due to particle interactions.35
These results demonstrate that the maximum ϕ measurable with DDM is a function of both the sample thickness L/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and the particle radius R/
and the particle radius R/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . They highlight the importance of measuring the photon mean free path
. They highlight the importance of measuring the photon mean free path ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) to fully identify and understand the limitations of DDM and its practical use for turbid samples.
to fully identify and understand the limitations of DDM and its practical use for turbid samples.
4.2 Simultaneous measurements of DDM and photon mean free path ![[small script l]](https://www.rsc.org/images/entities/h3_char_e146.gif)
By recording sets of movies with identical illumination settings we can quantify the transmission as a function of ϕ directly from the DDM movies (see Methods). Fig. 5a (main plot) shows results for SYS210 and L = 400 μm, with D(ϕ) shown in the inset. From the measured transmission we estimated ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (ϕ) using eqn (1), shown in Fig. 5b together with validating values extracted using a laser-based experimental setup (see Section S4, ESI†). Our measured
(ϕ) using eqn (1), shown in Fig. 5b together with validating values extracted using a laser-based experimental setup (see Section S4, ESI†). Our measured ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are also in good agreement with values predicted from Mie theory (Section S4, ESI†) up to ϕ ≈ 0.7%. At ϕ ≥ 0.7%, the relative transmission increasingly deviates from an exponential decay, Fig. 5a, suggesting significant contributions from multiple scattering and leading to an over-estimation of
are also in good agreement with values predicted from Mie theory (Section S4, ESI†) up to ϕ ≈ 0.7%. At ϕ ≥ 0.7%, the relative transmission increasingly deviates from an exponential decay, Fig. 5a, suggesting significant contributions from multiple scattering and leading to an over-estimation of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , Fig. 5b.
, Fig. 5b.
 | ||
Fig. 5 (a) Transmission, measured directly from DDM movies, as a function of volume fraction ϕ for SYS210 with L = 400 μm. Dotted line: Guide to the eye. Solid line: Exponential fit with exponent −L/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = −ϕ/(0.49%). Dashed line: Estimated transmission for a thinner capillary with L = 100 μm. Inset: Corresponding measured diffusion coefficient D/D0, with D0 = 2.14 μm2 s−1. Arrows show the last volume fraction for which D was measurable. Grey area: Limit in transmission (≈6–7%) above which DDM delivers reliable measurements. (b) photon mean free path = −ϕ/(0.49%). Dashed line: Estimated transmission for a thinner capillary with L = 100 μm. Inset: Corresponding measured diffusion coefficient D/D0, with D0 = 2.14 μm2 s−1. Arrows show the last volume fraction for which D was measurable. Grey area: Limit in transmission (≈6–7%) above which DDM delivers reliable measurements. (b) photon mean free path ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) obtained from transmission measurements of (circles) DDM movies and (diamonds) laser-based setup as a function of ϕ for SYS210. Lines are predictions of obtained from transmission measurements of (circles) DDM movies and (diamonds) laser-based setup as a function of ϕ for SYS210. Lines are predictions of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) from Mie scattering theory for the three particle size as indicated. The red horizontal lines indicate the sample thickness for our light scattering (dotted – L = 4 mm) and DDM experiments (dashed – L = 400 μm). Inset: Normalised signal amplitude 〈A〉 versus ϕ using ϕ0 ≈ 0.1% as reference. Line is fit to the data using eqn (14). The red and blue areas define the regimes of single scattering and emerging multiple scattering, respectively, for DDM experiments with L = 400 μm. from Mie scattering theory for the three particle size as indicated. The red horizontal lines indicate the sample thickness for our light scattering (dotted – L = 4 mm) and DDM experiments (dashed – L = 400 μm). Inset: Normalised signal amplitude 〈A〉 versus ϕ using ϕ0 ≈ 0.1% as reference. Line is fit to the data using eqn (14). The red and blue areas define the regimes of single scattering and emerging multiple scattering, respectively, for DDM experiments with L = 400 μm. | ||
Our results indicate that DDM measurements of D are reliable up to ϕ = 4% (inset Fig. 5a), corresponding to L/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≈ 10 (using predicted
≈ 10 (using predicted ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values). In other words, although most of the detected light has been scattered more than once, DDM can still deliver reliable D values down to ≈6–7% transmission (grey area in Fig. 5a).
values). In other words, although most of the detected light has been scattered more than once, DDM can still deliver reliable D values down to ≈6–7% transmission (grey area in Fig. 5a).
To further understand DDM for turbid samples, it is useful to identify the volume fraction ϕs, corresponding to the ϕ-boundary between single scattering regime and when multiple scattering emerges.
At low ϕ, where particle interactions are negligible and S(q) → 1, we expect from eqn (14) that 〈A〉 ∝ ϕ if multiple scattering can be neglected. This is indeed the case, Fig. 5b (inset). However, non-linearity, and indeed non-monotonicity, is observed at higher ϕ. These deviations arise from multiple scattering, which start to emerge at the threshold of ϕs ≈ 0.1%, corresponding to ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (ϕs) ≈ 1.6 mm for SYS210, Fig. 5b. In other words, multiple scattering starts to affect the (static) DDM signal amplitude when L/
(ϕs) ≈ 1.6 mm for SYS210, Fig. 5b. In other words, multiple scattering starts to affect the (static) DDM signal amplitude when L/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) → 1/4, where single scattering constitutes ≈88% of the signal. This value agrees with that found by a second approach based on TCDLS data (Section S5, ESI†).
→ 1/4, where single scattering constitutes ≈88% of the signal. This value agrees with that found by a second approach based on TCDLS data (Section S5, ESI†).
4.3 Effects of sample thickness L and imaging depth z
We next investigate the effects of L and z and show that increasing length scales decreases the amplitude of the static DDM signal.![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∝ 1/ϕ, we expect the multiple-scattering threshold to scale as ϕs ∝ 1/L. Fig. 6 shows that this is at least qualitatively correct: 〈A〉 deviates from a linear ϕ-dependency at increasing ϕs values when L is reduced from 400 to 100 μm. As a consequence, DDM is able to measure D reliably at concentrations up to that of the stock solutions, ϕ ≈ 10%, when using L = 100 μm (inset). Fitting the normalised 〈A〉 with eqn (14) gives good quantitative agreement, so that the increase in overall signal is indeed due to a reduction in multiple scattering events.
∝ 1/ϕ, we expect the multiple-scattering threshold to scale as ϕs ∝ 1/L. Fig. 6 shows that this is at least qualitatively correct: 〈A〉 deviates from a linear ϕ-dependency at increasing ϕs values when L is reduced from 400 to 100 μm. As a consequence, DDM is able to measure D reliably at concentrations up to that of the stock solutions, ϕ ≈ 10%, when using L = 100 μm (inset). Fitting the normalised 〈A〉 with eqn (14) gives good quantitative agreement, so that the increase in overall signal is indeed due to a reduction in multiple scattering events.
 | ||
| Fig. 6 Effect of thickness L on DDM measurements (100 fps) for SYS250. (main) amplitude of DDM signal 〈A〉 normalised to an arbitrary reference sample A0 at ϕ ≈ 0.1% and L = 400 μm versus ϕ for L = 100, 200, 400 μm. All Movies were recorded with fixed illumination and varying exposure time, except for (△) for which exposure time was fixed and illumination adjusted. Note that the normalisation takes into account differences in exposure time. Dotted line shows a slope of 1. Inset shows the corresponding measured D/D0 for the higher ϕ. Arrows define the highest ϕ at which DDM delivered a successful measurement. Lines are fits using eqn (14). | ||
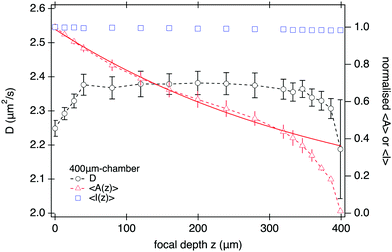 | ||
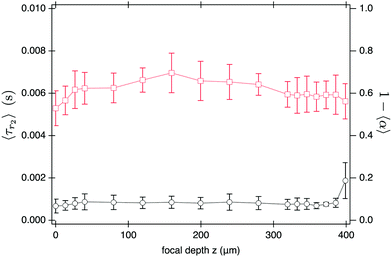
| Fig. 7 DDM measurements (100 fps) as a function of focal depth z of the imaging plane for SYS210. (left-axis) D and (right-axis) amplitude 〈A〉 and mean intensity 〈I〉, normalised to their corresponding value at z = 0, versus z for L = 400 μm at ϕ = 1.6%. Continuous line is an exponential fit to the normalised amplitude using eqn (14) for z ≤ 200 μm yielding a characteristic length-scale of z0 ≈ 380 μm. | ||
This does not, however, mean that DDM should be performed at as small z as possible to maximise signal. Fig. 7 shows that the measured diffusivity remains constant throughout the central region of the sample, but starts to decrease from z ≈ 50 μm, dropping by ≲5% close to the bottom interface. As we show in Section S6 (ESI†), this drop in diffusivity is far too large and long range to be explained by hydrodynamic interactions with the wall, but instead is mostly caused by sedimenting aggregate clusters. Thus experimental constraints, such as sample purity, might require a fairly large ‘safe distance’ from the sample edges. Selecting a sample twice as high and imaging near its mid plane18 will optimise DDM performance for turbid samples.
4.4 A short-time process and the depth of field
Fig. 3 shows that the DICF at short delay times (τ = 0.01 s), increases with ϕ. It has been suggested in a related study using heterodyne defocused DLS23 that such an increase simply reflects a rise in the noise term B(m) in eqn (13). We believe that it is in fact a signature of correlations in the multiply scattered light.To show this, we recorded movies at 1000 fps, 10× higher than in any experiment reported so far, giving access to DICFs at one decade shorter τ. This reveals a second correlated process at short time, as shown for q = 0.65 μm−1 in Fig. 8. We identify this as the f(m)(q, τ) term in our ms-DDM result, eqn (13) due to correlated fluctuations in the multiply-scattered intensity.
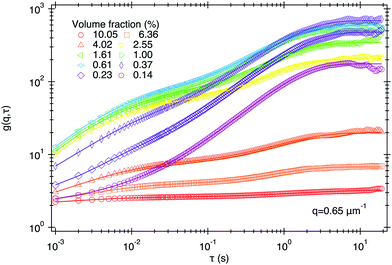 | ||
| Fig. 8 DICFs of SYS250 at q = 0.65 μm−1 recorded at a higher frame rate (1000 fps) with L = 100 μm revealing a 2nd decorrelation process at short delays, which at this q is much faster than diffusion and has a very low amplitude (note log scale for amplitude). Lines are fits based on eqn (15). | ||
We fit these DICFs with a double generalised exponential:
| g(q, τ) = A(q)[1 − αe−(τ/τr1)β1 − (1 − α)e−(τ/τr2)β2] + B(q) | (15) |
Fig. 9 shows the q-averaged values, 〈tr2〉 and 1 − 〈α〉, as functions of ϕ at three values of L. Over this ϕ range, we find a constant β2 ≈ 0.8 ± 0.1. As ϕ (and therefore turbidity) increases, we find that the short-time process speeds up (main figure) and its relative amplitude increases (inset). This is consistent with our identification of this short-time process with the f(m)(q, τ) term eqn (13).
 | ||
| Fig. 9 Average decay time of the short-time process (main) and relative fractional contribution (inset) as a function of volume fraction for data presented in Fig. 8. Error bars are standard deviation of the mean obtained in the range 0.3 ≤ q ≤ 1 μm−1. | ||
Interestingly, the time-scale, 〈τr2〉, and amplitude, 1 − 〈α〉, of the fast process do not seem to change with the sample thickness L, Fig. 9; nor do they depend on the imaging depth z, Fig. 10. This suggests that the short-time process mainly depends on the thickness of the imaged sample region, i.e. the DoF.
5 Discussion
In order to rationalise our experimental findings it is useful to divide the sample thickness L into three regions, I, II and III as introduced in Fig. 1. Each of these regions affects DDM measurements in a different way.The depth of field, DoF, defines the imaging region (II) centred around the object plane. The intensity fluctuations, ΔI, in the images captured by the camera are dominated by scattering within this region. As such, only light scattered in this region and reaching the camera contributes to the DDM signal, as was already pointed out in the earliest discussion of the technique.18 Increasing the sample thickness L beyond the DoF (and thus introducing regions I and III) generates no extra useful DDM signal. For dilute samples, there is no detrimental effect of these regions either, and larger sample thickness can offer experimental advantages such as ease of loading, handling and focusing, avoidance of boundary effects and signal distortions due to sedimenting ‘impurities’ within the sample.
However, once the suspension is turbid enough, a significant fraction of light scattered by the sample is no longer collected by the objective. The light detected by the camera is reduced by its passage through the complete sample thickness L. Our measurements for different sample thickness (Fig. 6) confirm that the drop of DDM signal amplitude with increasing volume fraction is controlled by the sample thickness L and is in quantitative agreement with eqn (14). Thus both regions I and III introduce extra attenuation, which can lead to premature failure of DDM measurements.
Our measurements for varying imaging depth z (Fig. 7) reveal a secondary effect of the near-objective region III, as z controls the thickness of the layer through which light from the object plane has to propagate to reach the camera. Apart from scattered light no longer reaching the camera, this region of the sample can also scatter light which had been scattered in the object plane (region II) to reach the camera at random positions (e.g. orange ray (d) in Fig. 1). This reduces the contrast, ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (q), of the particles in the image. We observe an exponential reduction of the DDM signal amplitude with the thickness of region III, z (Fig. 7), with a characteristic length scale z0 ≈ 380 μm ≈ 4
(q), of the particles in the image. We observe an exponential reduction of the DDM signal amplitude with the thickness of region III, z (Fig. 7), with a characteristic length scale z0 ≈ 380 μm ≈ 4![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) .
.
Our experimental investigation of the emergent short-time process highlights that the ‘extraneous’ sample regions I and III only affect the static DDM signal (〈A〉), but have no measurable effect on the dynamic DDM signal (g(q, τ)). This might at first appear surprising, especially when noticing that the short-time process is detectable at volume fractions where ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is still much larger than the depth of field (i.e. ≲10 μm) visually perceived from direct imaging. However, the DoF strongly depends on the Fourier wavenumber q and typically increases with decreasing q.18 We have verified, using a recently introduced experimental protocol,36 that our measured DoF is indeed a strongly decreasing function of q (Section S7, ESI†). For example, we find DoF ≈ 20 μm at q = 0.5 μm−1 and DoF ≈ 4 μm at (q = 3 μm−1). These values are comparable to
is still much larger than the depth of field (i.e. ≲10 μm) visually perceived from direct imaging. However, the DoF strongly depends on the Fourier wavenumber q and typically increases with decreasing q.18 We have verified, using a recently introduced experimental protocol,36 that our measured DoF is indeed a strongly decreasing function of q (Section S7, ESI†). For example, we find DoF ≈ 20 μm at q = 0.5 μm−1 and DoF ≈ 4 μm at (q = 3 μm−1). These values are comparable to ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) values (Fig. 5) at the higher volume fractions considered in this study. We may therefore expect that the f(m)(q, τ) term in eqn (13) should become important at low q (large DoF). Observation of the DICFs at ϕ = 1.6% for several q values (Section S8, ESI†) suggests the short-time process emerges at q ≲ 1.2 μm−1 for which DoF ≈ 10 μm, i.e. DoF(q)/
values (Fig. 5) at the higher volume fractions considered in this study. We may therefore expect that the f(m)(q, τ) term in eqn (13) should become important at low q (large DoF). Observation of the DICFs at ϕ = 1.6% for several q values (Section S8, ESI†) suggests the short-time process emerges at q ≲ 1.2 μm−1 for which DoF ≈ 10 μm, i.e. DoF(q)/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) > 1/7, using
> 1/7, using ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (ϕ = 1.6%, SYS250) ≈ 70 μm (Fig. 5).
(ϕ = 1.6%, SYS250) ≈ 70 μm (Fig. 5).
Interestingly, this ‘dynamical’ threshold DoF/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≈ 1/7 for the emergence of the short-time process corresponds to 7% multiple scattering contribution to the overall signal, eqn (2), in good agreement with the 12% static threshold (Section 4.2).
≈ 1/7 for the emergence of the short-time process corresponds to 7% multiple scattering contribution to the overall signal, eqn (2), in good agreement with the 12% static threshold (Section 4.2).
From a TCDLS perspective, the relevant length-scale is the sample thickness L (or diameter of the DLS tube) because a DLS measurement relies on a well defined scattering angle. Assuming multiple scattering affects TCDLS and DDM measurements in a similar way, we would expect the ratio of the highest concentration measurable by DDM and TCDLS to corresponds approximately to the ratio LTCDLS/LDDM. However, we found a significantly higher ratio of ≈25 for LTCDLS/LDDM = 10 (see Section 4.1). This finding suggests that DDM is indeed more efficient than a DLS-based setup in its capability to work at smaller relevant length-scales, here (L, z, DoF).
While this discussion and our current study pertains entirely to scattering, the same analysis should also be applicable to strongly absorbing particles. In this case, the light absorbed by the particles is equivalent to the scattering events in regions I and III that give rise to light not being collected by the camera.
6 Conclusion
We have demonstrated that DDM correctly characterises the dynamics of much more strongly scattering samples than TCDLS. This improved performance is mainly due to the fact that DDM is able to work with smaller length-scales that can be controlled when performing the experiments. As a consequence, we found that DDM successfully measures particle dynamics at volume fractions up to 10 and 1000 times higher particle concentrations than TCDLS and standard DLS, respectively.Multiple scattering effects do still affect the practice of DDM. In particular, we have shown that it contributes a short-time process that complicates data interpretation. Our results suggest that the length scale that controls the emergence of this process is the depth of field rather than the sample thickness L. In practice, these complications can be avoided by only using data at sufficiently high q, say ≳1 μm−1, and long enough delay time, say ≳0.01 s. With these provisos, we conclude that DDM should be a robust method for characterising turbid suspensions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We were funded by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program: AdG 340877-PHYSAPS, PoC 862559-NoChapFI, and European Soft Matter Infrastructure (731019-EUSMI). All data used are available via Edinburgh DataShare at https://doi.org/10.7488/ds/3404.Notes and references
- L. Peltonen, Adv. Drug Delivery Rev., 2018, 131, 101–115 CrossRef CAS PubMed.
- J. T. Xu, Q. Fu, J. M. Ren, G. Bryant and G. G. Qiao, Chem. Commun., 2013, 49, 33–35 RSC.
- R. M. Shah, J. P. Mata, G. Bryant, L. de Campo, A. Ife, A. V. Karpe, S. R. Jadhav, D. S. Eldridge, E. A. Palombo and I. H. Harding, Part. Part. Syst. Charact., 2019, 36, 1800359 CrossRef.
- H. J. Schöpe, O. Marnette, W. van Megen and G. Bryant, Langmuir, 2007, 23, 11534–11539 CrossRef PubMed.
- K. Eitel, G. Bryant and H. J. Schöpe, Langmuir, 2020, 36, 10320 CrossRef PubMed.
- A. Sanchez-Ferrer, R. P. Carney, F. Stellacci, R. Mezzenga and L. Isa, Langmuir, 2015, 31, 11179–11185 CrossRef CAS PubMed.
- G. Yu, R. Yan, C. Zhang, C. Mao and W. Jiang, Small, 2015, 11, 5157–5163 CrossRef CAS PubMed.
- B. Chu and T. Liu, J. Nanopart. Res., 2000, 2, 29–41 CrossRef CAS.
- B. Berne and R. Pecora, Dynamic Light Scattering: with applications to chemistry, biology, and physics, Courier Corporation, 2000 Search PubMed.
- W. Brown, Dynamic Light Scattering: the method and some applications, Faraday Discussions, Oxford University Press, USA, 1993 Search PubMed.
- G. Bryant, T. Mortensen, S. Henderson, S. Williams and W. van Megen, J. Colloid Interface Sci., 1999, 216, 401–408 CrossRef CAS PubMed.
- P. Segrè, W. V. Megen, P. Pusey, K. Schätzel and W. Peters, J. Mod. Opt., 1995, 42, 1929–1952 CrossRef.
- L. B. Aberle, P. Hulstede, S. Wiegand, W. Schroer and W. Staude, Appl. Opt., 1998, 37, 6511–6524 CrossRef CAS PubMed.
- E. Overbeck and C. Sinn, J. Mod. Opt., 1999, 46, 303–326 CrossRef.
- V. Martinez, J. Thijssen, F. Zontone, W. van Megen and G. Bryant, J. Chem. Phys., 2011, 134, 054505 CrossRef CAS PubMed.
- G. Maret, Curr. Opin. Colloid Interface Sci., 1997, 2, 251–257 CrossRef CAS.
- R. Cerbino and V. Trappe, Phys. Rev. Lett., 2008, 100, 188102 CrossRef.
- F. Giavazzi, D. Brogioli, V. Trappe, T. Bellini and R. Cerbino, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031403 CrossRef PubMed.
- K. He, M. Spannuth, J. C. Conrad and R. Krishnamoorti, Soft Matter, 2012, 8, 11933–11938 RSC.
- Y. Gao, J. Kim and M. E. Helgeson, Soft Matter, 2015, 11, 6360–6370 RSC.
- P. Edera, D. Bergamini, V. Trappe, F. Giavazzi and R. Cerbino, Phys. Rev. Mater., 2017, 1, 073804 CrossRef.
- A. Pal, V. A. Martinez, T. H. Ito, J. Arlt, J. J. Crassous, W. C. K. Poon and P. Schurtenberger, Sci. Adv., 2020, 6, eaaw9733 CrossRef CAS PubMed.
- M. A. Escobedo-Sanchez, L. F. Rojas-Ochoa, M. Laurati and S. U. Egelhaaf, Soft Matter, 2017, 13, 5961–5969 RSC.
- P. J. Lu, F. Giavazzi, T. E. Angelini, E. Zaccarelli, F. Jargstorff, A. B. Schofield, J. N. Wilking, M. B. Romanowsky, D. A. Weitz and R. Cerbino, Phys. Rev. Lett., 2012, 108, 218103 CrossRef PubMed.
- T. Sentjabrskaja, E. Zaccarelli, C. De Michele, F. Sciortino, P. Tartaglia, T. Voigtmann, S. U. Egelhaaf and M. Laurati, Nat. Commun., 2016, 7, 11133 CrossRef CAS PubMed.
- J. Arlt, V. A. Martinez, A. Dawson, T. Pilizota and W. C. K. Poon, Nat. Commun., 2018, 9, 768 CrossRef PubMed.
- M. S. Safari, M. A. Vorontsova, R. Poling-Skutvik, P. G. Vekilov and J. C. Conrad, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 1–12 CrossRef PubMed.
- D. M. Wulstein, K. E. Regan, R. M. Robertson-Anderson and R. McGorty, Opt. Express, 2016, 24, 20881 CrossRef CAS PubMed.
- T. Wriedt, in Mie Theory: A Review, ed. W. Hergert and T. Wriedt, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, pp. 53–71 Search PubMed.
- H. Du, Appl. Opt., 2004, 43, 1951–1956 CrossRef PubMed.
- G. Bryant, H. Schotman and J. C. Thomas, Part. Part. Syst. Charact., 1998, 15, 170–173 CrossRef CAS.
- G. Bryant, S. Martin, A. Budi and W. van Megen, Langmuir, 2003, 19, 616–621 CrossRef CAS.
- L. G. Wilson, V. A. Martinez, J. Schwarz-Linek, J. Tailleur, G. Bryant, P. N. Pusey and W. C. K. Poon, Phys. Rev. Lett., 2011, 106, 018101 CrossRef CAS PubMed.
- M. Reufer, V. A. Martinez, P. Schurtenberger and W. C. K. Poon, Langmuir, 2012, 28, 4618–4624 CrossRef CAS PubMed.
- C. M. Trotter and D. N. Pinder, J. Chem. Phys., 1981, 75, 118–127 CrossRef CAS.
- S. Aime and L. Cipelletti, Soft Matter, 2019, 15, 213–226 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01598b |
| This journal is © The Royal Society of Chemistry 2022 |