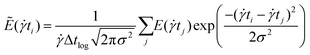Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermally fluctuating, semiflexible sheets in simple shear flow†
Kevin S.
Silmore
 *,
Michael S.
Strano
*,
Michael S.
Strano
 and
James W.
Swan
and
James W.
Swan

Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: silmore@mit.edu
First published on 22nd December 2021
Abstract
We perform Brownian dynamics simulations of semiflexible colloidal sheets with hydrodynamic interactions and thermal fluctuations in shear flow. As a function of the ratio of bending rigidity to shear energy (a dimensionless quantity we denote S) and the ratio of bending rigidity to thermal energy, we observe a dynamical transition from stochastic flipping to crumpling and continuous tumbling. This dynamical transition is broadened by thermal fluctuations, and the value of S at which it occurs is consistent with the onset of chaotic dynamics found for athermal sheets. The effects of different dynamical conformations on rheological properties such as viscosity and normal stress differences are also quantified. Namely, the viscosity in a dilute dispersion of sheets is found to decrease with increasing shear rate (shear-thinning) up until the dynamical crumpling transition, at which point it increases again (shear-thickening), and non-zero first normal stress differences are found that exhibit a local maximum with respect to temperature at large S (small shear rate). These results shed light on the dynamical behavior of fluctuating 2D materials dispersed in fluids and should greatly inform the design of associated solution processing methods.
I. Introduction
Increasingly, researchers are turning to solution processing methods for 2D materials,1–15 yet fundamental knowledge of the dynamical behavior of 2D materials in flow and how such behavior correlates with macroscopic rheological properties and coupled fluid dynamical responses is still lacking. The behavior of rigid ellipsoidal particles suspended in fluids at low Reynolds number was famously studied by Jeffery,16 Hinch and Leal,17–19 and Batchelor20,21 among others. Flexible particles, though, such as polymers22 or semiflexible sheets, exhibit far more complex behavior compared to their rigid counterparts. In previous work,23 we studied the dynamical behavior of thin, athermal, semiflexible sheets in simple shear flow as a function of two dominant variables: the initial orientation of a flat sheet about the flow axis, ϕ, and the dimensionless ratio (denoted S) of bending rigidity, κ, to shear strength given by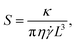 | (1) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate, and L is the characteristic radius of the sheet in a flat state. We observed elastic buckling for sheets oriented initially near the flow-vorticity plane, as well as transitions from quasi-Jeffery behavior to transient tumbling to chaotic, continuous tumbling as S decreases (or as shear strength relative to bending rigidity increases). While the athermal sheets considered in our previous work may serve as a valuable model for macroscopic sheets dispersed in viscous fluids or stiff, large-aspect-ratio nanomaterials like graphene (for which the effective bending rigidity is significantly larger than the thermal energy, kBT), stochastic thermal fluctuations can substantially alter the dynamics. In this work, we sought to explore the effects of thermal fluctuations on the dynamical behavior of sheets under shear at low Reynolds number.
is the shear rate, and L is the characteristic radius of the sheet in a flat state. We observed elastic buckling for sheets oriented initially near the flow-vorticity plane, as well as transitions from quasi-Jeffery behavior to transient tumbling to chaotic, continuous tumbling as S decreases (or as shear strength relative to bending rigidity increases). While the athermal sheets considered in our previous work may serve as a valuable model for macroscopic sheets dispersed in viscous fluids or stiff, large-aspect-ratio nanomaterials like graphene (for which the effective bending rigidity is significantly larger than the thermal energy, kBT), stochastic thermal fluctuations can substantially alter the dynamics. In this work, we sought to explore the effects of thermal fluctuations on the dynamical behavior of sheets under shear at low Reynolds number.
Since the 1980s, the equilibrium and statistical mechanical properties of sheets (or “tethered membranes” as they are often called to distinguish them from fluid membranes that lack fixed connectivity) has been widely studied from theoretical,24–31 computational,32–40 and experimental41–43 viewpoints. Much of this work has focused on a phase transition from a flat state to a crumpled state as kBT/κ is increased, a transition that does not exist for polymers, the 1D analogue of tethered membranes. Another notable difference between polymers and tethered membranes is the lack of an upper critical dimension beyond which self-avoidance effects become negligible (dc = 4 for polymers).28 In fact, most evidence presented to date points to the lack of a crumpling transition for self-avoiding membranes (despite theoretical predictions) and the presence of a rough but flat state at all temperatures.32,34,39,41 Additionally, due to thermal fluctuations, thermalized tethered membranes exhibit a wavevector-dependent renormalized bending rigidity, κr(q) ∼ κ(q/qth)−ηκ, where q is the wavevector magnitude and qth is the inverse length scale below which thermal fluctuations affect the bending rigidity and ηκ ≈ 0.8 is the anomalous dimension.24 It should be noted, then, that throughout this work, most results will be reported in terms of the “bare” bending rigidity, κ.
There are still certain unresolved questions about the equilibrium properties of sheets, and there are even more open questions about the dynamics of colloidal sheets, in part due to the few studies that have focused on such a system. Notable previous works on the subject, though, include the following. Xu and Green44,45 studied the behavior of sheets under shear and biaxial extension and found slight shear-thinning at large shear strengths. Babu and Stark46 studied the fluctuations of tethered sheets in fluids via stochastic rotation dynamics, confirming predicted scaling laws of Frey and Nelson26 (i.e., that the intermediate scattering function exhibits sub-diffusive scaling that reflects the self-similar roughness of the fluctuating surface). Additionally, Dutta and Graham47 classified the dynamical states of athermal Miura-patterned sheets, and Yu and Graham48 studied “compact–stretch” transitions of athermal elastic sheets under extensional flow via the method of regularized Stokeslets.
In this work, we study the behavior of a thermalized “bead-spring” sheet model immersed in a low-Reynolds-number simple shear flow. Such sheets can be considered asymptotically thin from the hydrodynamic point of view and are relatively inextensible compared to out-plane bending modes (i.e., they have large Föppl–von Kármán numbers). We conduct Brownian dynamics simulations with hydrodynamic interactions, quantify geometric properties of the sheets, and estimate the viscosity contributions and first normal stress differences as a function of S and the dimensionless temperature, kBT/κ. In particular, we look at the orientational covariance matrix of sheet normals, calculate minimum-volume bounding ellipsoids over time, and use such ellipsoids to estimate the aforementioned rheological properties. We find that as S decreases, there is a dynamical transition from intermittent stochastic flipping to continuous tumbling in a crumpled state, in line with our previous study of athermal sheets.23 Finally, scaling predictions for flipping statistics (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtflip ∼ (kBT/κ)−1/3S−1/3 and Var[
Δtflip ∼ (kBT/κ)−1/3S−1/3 and Var[![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtflip] ∼ (kBT/κ)−2/3S−2/3) are made with the aid of a first passage time model, and all are found to match simulation data well.
Δtflip] ∼ (kBT/κ)−2/3S−2/3) are made with the aid of a first passage time model, and all are found to match simulation data well.
II. Model and methods
Similar to the model employed in our previous work,23 hexagonal sheets of circumradius L = 38a were constructed by creating a surface triangulation with edges of length l = 2a for a total of N = 1141 vertices or “beads”. The length scale a, here, is the smallest coarse-grained length scale at which relative motion and thermal fluctuations of the sheet are resolved.Here, we summarize briefly the forces acting between the beads (see ref. 23 for further details). Bending forces were captured by dihedral forces over each pair of neighboring triangles Δi and Δj of the sheet surface as:
Ubend(Δi, Δj) = κ(1 − ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) i· i·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) j), j), | (2) |
where κ is the bending rigidity and ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) i and
i and ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) j are consistently oriented triangle normals.35,49–51 This “discrete” value of κ can be mapped to a bending rigidity of an equivalent continuum sheet,
j are consistently oriented triangle normals.35,49–51 This “discrete” value of κ can be mapped to a bending rigidity of an equivalent continuum sheet, 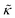 , via
, via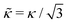 .51 Harmonic bonds of the form
.51 Harmonic bonds of the form
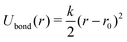 | (3) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) L and r0 = 2a, where η and
L and r0 = 2a, where η and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) are the viscosity and shear rate of the surrounding fluid, respectively. Like the bending rigidity, this value of k can be mapped to a 2D Young's modulus, Y, of an equivalent continuum sheet via
are the viscosity and shear rate of the surrounding fluid, respectively. Like the bending rigidity, this value of k can be mapped to a 2D Young's modulus, Y, of an equivalent continuum sheet via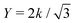 .35 All of the sheets considered consequently exhibited much softer out-of-plane bending compared to in-plane stretching, with large Föppl–von Kármán (FvK) numbers (FvK = YL2/κ) between 104 and 106. Consequently, we do not consider the FvK number to be a relevant dimensionless group for the phenomena observed.
.35 All of the sheets considered consequently exhibited much softer out-of-plane bending compared to in-plane stretching, with large Föppl–von Kármán (FvK) numbers (FvK = YL2/κ) between 104 and 106. Consequently, we do not consider the FvK number to be a relevant dimensionless group for the phenomena observed.
Hard-sphere interactions between all non-neighboring beads were approximated via the pair potential,
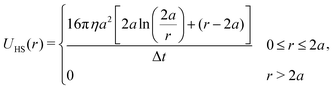 | (4) |
Brownian dynamics with hydrodynamic interactions was employed to model the motion of all of the beads with the following governing stochastic differential equation:
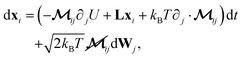 | (5) |
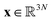 is a stacked vector of N particle coordinates, “∂j” denotes ∂/∂xj, U = Ubend + Ubond + UHS is the total potential energy, and (L)mn =
is a stacked vector of N particle coordinates, “∂j” denotes ∂/∂xj, U = Ubend + Ubond + UHS is the total potential energy, and (L)mn = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) δm1δn2 is the 3 × 3 velocity gradient tensor. Repeated indices are summed over.
δm1δn2 is the 3 × 3 velocity gradient tensor. Repeated indices are summed over. 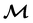 is the mobility tensor, which maps forces on particle j to particle i and accounts for fluid-mediated interactions between the particles. We set the mobility tensor equal to the well-known Rotne–Prager–Yamakawa (RPY) tensor,54,55 which is given analytically by:
is the mobility tensor, which maps forces on particle j to particle i and accounts for fluid-mediated interactions between the particles. We set the mobility tensor equal to the well-known Rotne–Prager–Yamakawa (RPY) tensor,54,55 which is given analytically by: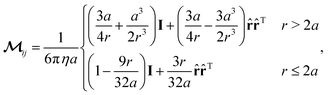 | (6) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) is a unit vector pointing from particle i to particle j. For the RPY tensor, the divergence term
is a unit vector pointing from particle i to particle j. For the RPY tensor, the divergence term 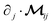 is equal to 0. Finally,
is equal to 0. Finally, 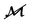 is a matrix that satisfies
is a matrix that satisfies 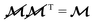 , and W is a vector of independent, standard Wiener processes. The last term of eqn (5) represents thermal fluctuations, and the action of
, and W is a vector of independent, standard Wiener processes. The last term of eqn (5) represents thermal fluctuations, and the action of  is computed efficiently via a Lanczos iteration procedure.56,57 The RPY tensor accounts for far-field, pairwise hydrodynamic interactions between two spheres in an unbounded domain and is able to serve as a “regularized” Stokeslet for composite-bead objects56,58 such as the sheets studied in this work. Hydrodynamically, the sheets in this work behave as if they were asymptotically thin because the beads are constructed to lie on a 2D manifold. Although this leads to Jeffery orbits of infinite period, thermal fluctuations in this work represent the dominant cause of sheet flipping and would remain so even for sheets of finite but small relative thickness h/L. Additionally, the RPY beads that comprise the sheet can be considered an approximation of a “no-slip” surface, which means the effects of slip on the dynamics (which can be important for small nanomaterials12,59) are neglected.
is computed efficiently via a Lanczos iteration procedure.56,57 The RPY tensor accounts for far-field, pairwise hydrodynamic interactions between two spheres in an unbounded domain and is able to serve as a “regularized” Stokeslet for composite-bead objects56,58 such as the sheets studied in this work. Hydrodynamically, the sheets in this work behave as if they were asymptotically thin because the beads are constructed to lie on a 2D manifold. Although this leads to Jeffery orbits of infinite period, thermal fluctuations in this work represent the dominant cause of sheet flipping and would remain so even for sheets of finite but small relative thickness h/L. Additionally, the RPY beads that comprise the sheet can be considered an approximation of a “no-slip” surface, which means the effects of slip on the dynamics (which can be important for small nanomaterials12,59) are neglected.
As mentioned in the introduction, length-scale-dependent thermal renormalization of the bending rigidity is important in systems of thermally fluctuating 2D sheets.24 Such renormalization effects are thus often associated with significant finite-size scaling and, in practice, also depend on the coarse-graining length scale employed. In this work, we focus on a sheet model of a particular size, so future work exploring a finite-size scaling analysis of the dynamical results presented is warranted. It is worth noting, though, that several recent works60–63 exploring the finite-temperature buckling transition of 2D sheets lend support to the idea that several results in this work may very well apply directly to sheets of different sizes as long as properly renormalized elastic constants are used (see Conclusions for additional discussion).
Eqn (5) was integrated via an Euler–Maruyama scheme with a timestep of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δt = 5 × 10−4 using a custom plugin adapted from ref. 56 for the HOOMD-blue molecular simulation package64 on graphics processing units (NVIDIA GTX 980s and 1080s). Practically, values of κ and kBT/κ were varied while
Δt = 5 × 10−4 using a custom plugin adapted from ref. 56 for the HOOMD-blue molecular simulation package64 on graphics processing units (NVIDIA GTX 980s and 1080s). Practically, values of κ and kBT/κ were varied while ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) was set to 1 for the given timestep. The initial conformation for each simulation was a flat sheet rotated by θ = 5° about the vorticity axis from the flow-vorticity plane, and 6 independent runs of length
was set to 1 for the given timestep. The initial conformation for each simulation was a flat sheet rotated by θ = 5° about the vorticity axis from the flow-vorticity plane, and 6 independent runs of length ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t = 1000 for each set of parameters were conducted with different random seeds.
t = 1000 for each set of parameters were conducted with different random seeds.
III. Flipping behavior
For rigid, athermal, and axisymmetric ellipsoidal particles, the period of the Jeffery orbit is determined by the aspect ratio of the particle,16 and thermal fluctuations cause the particles to diffuse across different orbits.19 With flexible sheets as well, thermal fluctuations cause sheets to interact with different streamlines of the shear flow and stochastically flip. Fig. 1 shows snapshots of sheets with different values of dimensionless bending rigidity, S, and different dimensionless temperatures, kBT/κ. Additional movies of sheets can be found in the ESI.† In general, the stiffest sheets examined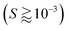 fluctuate about the flat state in the flow-vorticity plane and flip at stochastic intervals while the softest sheets
fluctuate about the flat state in the flow-vorticity plane and flip at stochastic intervals while the softest sheets 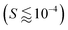 crumple and tumble continuously.
crumple and tumble continuously.
More quantitatively, Fig. 2 shows the distribution of times between flips, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtflip, for the entire range of S values considered in this work and at different temperatures. Specifically, these “times between flips” were calculated as the time between distinct peaks in the bending energy. Bending energies (i.e., the sum of all dihedral energies) were calculated every
Δtflip, for the entire range of S values considered in this work and at different temperatures. Specifically, these “times between flips” were calculated as the time between distinct peaks in the bending energy. Bending energies (i.e., the sum of all dihedral energies) were calculated every ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtlog = 0.1 units of time, and peaks were automatically extracted from all sheet trajectories by (1) smoothing the data via discrete convolution with a Gaussian of variance σ2 = 10 as:
Δtlog = 0.1 units of time, and peaks were automatically extracted from all sheet trajectories by (1) smoothing the data via discrete convolution with a Gaussian of variance σ2 = 10 as:
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δt = 1 exceeded 0.01, that the peak height above min
Δt = 1 exceeded 0.01, that the peak height above min![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ẽ was greater than 0.1(max
Ẽ was greater than 0.1(max![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ẽ − min
Ẽ − min![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ẽ), and that the distance in time from the last peak was at least
Ẽ), and that the distance in time from the last peak was at least ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t = 2, which is much smaller than the time to flip from the initial orientation).
t = 2, which is much smaller than the time to flip from the initial orientation).
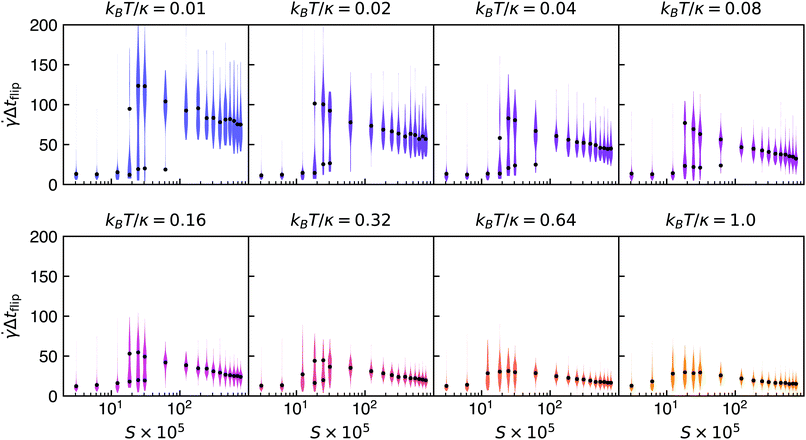
From this data presented in Fig. 2, one can glean several conclusions. First, the time between flips, in general, decreases as temperature increases. This behavior should not be surprising, since with larger amplitude fluctuations, there is a larger probability that the sheet will interact with a streamline that induces a sufficiently strong drag force to cause the sheet to flip. Second, the flipping time distributions are much wider for smaller dimensionless temperatures, which is consistent with stochastic first-passage-time-like behavior that will be discussed further below. Third, and perhaps most interestingly, there appears to be a discontinuous transition to a crumpled state with fast flipping times as S decreases. That these fast flipping times are indeed associated with a geometrically crumpled state will be discussed shortly. In fact, for temperatures less than approximately kBT/κ = 0.64, this transition from stochastic flipping to continuous tumbling manifests itself as the appearance and disappearance of discrete modes as S is varied. Without a priori knowledge of the distribution of these flipping times, a truncated Gaussian mixture model was fitted to the data for each S with the EM algorithm.65 The means of such a model for values of 1.5 × 10−4 < S < 10−3 are displayed in Fig. 2 if the Bayesian Information Criterion (BIC) difference between a bimodal mixture or single truncated Gaussian was less than −2 as a way of quantifying the discrete modes. For higher temperatures, the transition is much more gradual, and the different flipping and continuously tumbling modes are indistinguishable. The location of the transition around S ≈ 2 × 10−4 is consistent with the crumpling/chaos transition found for athermal sheets in our previous work,23 and the fact that the transition becomes more “rounded” around this athermal crumpling transition is consistent with previous work on the rounding of the buckling transition for flexible filaments.66 However, such “rounding” could also be attributed to finite-size effects similar to those seen in the classic equilibrium crumpling transition67,68 and warrants more investigation. It should also be noted that the nature of this crumpling/chaos transition is more complex than a buckling transition, the first of which occurs at much larger value of S ≈ 5.3 × 10−3 for athermal sheets oriented near the flow-vorticity plane.23 This complexity somewhat precludes the typical eigenfunction decomposition and linear stability analysis used to analyze dynamical transitions. Consequently, a more rigorous analytical theory describing such thermal “rounding” in future work would be quite valuable. Additionally, possible “critical slowing down” of the dynamical crumpling transition in the thermodynamic limit (i.e., as sheet size increases) represents an interesting avenue for exploration.
Flipping/tumbling frequencies of semiflexible polymers have been studied both experimentally69–71 and theoretically.72–74 Notably, it has been found that polymer tumbling in the flow-gradient plane for stiff polymers or large Weissenberg numbers (where Wi = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ1 and τ1 is the longest relaxation time) is determined by diffusion to a critical angle, θc, followed by advection-dominated flipping. Furthermore, θc ∼ Wi−1/3 and DrΔtdiff ∼ Wi−2/3, where Dr is the rotational diffusivity of the stiff polymer. A similar analysis can be performed for sheets at large values of S and small values of kBT/κ, such that bending rigidity is sufficiently large compared to both the shear strength and thermal energy. Unlike the typical analysis for polymers or dumbbells, motion in all directions—not just in the flow-gradient plane—could be especially relevant for a sheet. For small deviations away from the athermal flat state in the flow-vorticity plane, Jeffery's equations for an asymptotically thin, oblate spheroid become:
τ1 and τ1 is the longest relaxation time) is determined by diffusion to a critical angle, θc, followed by advection-dominated flipping. Furthermore, θc ∼ Wi−1/3 and DrΔtdiff ∼ Wi−2/3, where Dr is the rotational diffusivity of the stiff polymer. A similar analysis can be performed for sheets at large values of S and small values of kBT/κ, such that bending rigidity is sufficiently large compared to both the shear strength and thermal energy. Unlike the typical analysis for polymers or dumbbells, motion in all directions—not just in the flow-gradient plane—could be especially relevant for a sheet. For small deviations away from the athermal flat state in the flow-vorticity plane, Jeffery's equations for an asymptotically thin, oblate spheroid become:
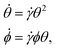 | (7) |
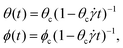 | (8) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )−1. It is also clear that motion in the ϕ-direction does not introduce any additional time scales to the problem. Thus, balancing this advective time scale with the characteristic diffusive time scale, θc2/Dr, yields the familiar scaling:
)−1. It is also clear that motion in the ϕ-direction does not introduce any additional time scales to the problem. Thus, balancing this advective time scale with the characteristic diffusive time scale, θc2/Dr, yields the familiar scaling:θc ∼ (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /Dr)−1/3, /Dr)−1/3, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtdiff ∼ ( Δtdiff ∼ (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /Dr)1/3. /Dr)1/3. | (9) |
Now, given that Dr ∼ kBT/(ηL3) for a sheet of characteristic radius L, it is possible to rewrite the scaling for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtdiff as
Δtdiff as
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtdiff ∼ (kBT/κ)−1/3S−1/3. Δtdiff ∼ (kBT/κ)−1/3S−1/3. | (10) |
Furthermore, following Harasim et al.,75 the time between flips can be represented as the sum of two contributions as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtflip =
Δtflip = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (Δtdiff + Δtadv), where Δtadv is the time required for the sheet to flip due to advective motion from the imposed flow after reaching the critical locus of orientational angles (i.e., all of critical values of (θ,ϕ)). For small θc, the advective time should scale with 1/θc from Jeffery's equations, implying that
(Δtdiff + Δtadv), where Δtadv is the time required for the sheet to flip due to advective motion from the imposed flow after reaching the critical locus of orientational angles (i.e., all of critical values of (θ,ϕ)). For small θc, the advective time should scale with 1/θc from Jeffery's equations, implying that ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtadv, and ultimately
Δtadv, and ultimately ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtflip as well should scale as (kBT/κ)−1/3S−1/3.
Δtflip as well should scale as (kBT/κ)−1/3S−1/3.
Fig. 3 shows the (empirical) mean time between flips scaled by (kBT/κ)1/3S1/3, which should be constant with S in the realm of applicability of the above analysis. And indeed, for the smallest temperatures and largest values of S plotted in Fig. 3, the data is approximately constant with S and consistent with the proposed scaling. That the scaled mean time between flips deviates from a constant value for both small values of S and larger relative temperatures is unsurprising. The proposed scaling argument is only valid for asymptotically stiff sheets undergoing small thermal fluctuations. More flexible sheets and sheets that adopt more corrugated configurations due to larger thermal fluctuations should flip more readily and exhibit smaller times between flips given that fluctuations out of plane should enhance interaction with the shear flow.
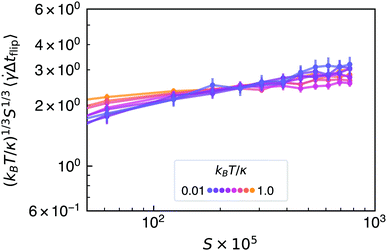 | ||
| Fig. 3 Scaled mean time between flips (see Fig. 2). Error bars represent two standard errors of the means across data from all independent runs, and lines are drawn to guide the eye. | ||
Considering that rigid sheets aligned in the flow-vorticity plane and subjected to small thermal fluctuations need to diffuse to the locus of critical orientations before advection dominates, it is natural to consider a first passage time model to understand both the mean of the time between flips as well as the variance of the time between flips. Consider a Brownian particle initially located at x = 0 and diffusing in the domain x ∈ [−θc, θc] with diffusivity Dr Let x = −θc be a reflecting (Neumann) boundary condition, and let x = θc represent an absorbing (Dirichlet) boundary condition. Clearly, such a particle is meant to represent the orientation of the sheet, and the boundary conditions model the interaction of the sheet with the flow, with absorption at the right representing the transition from diffusion to advection. As shown in Appendix A, both the mean first passage time to the right boundary and the variance about the mean can be calculated analytically as
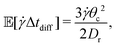 | (11) |
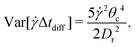 | (12) |
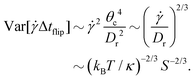 | (13) |
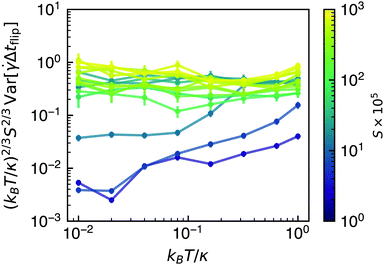 | ||
| Fig. 4 Scaled variance of the time between flips (see Fig. 2). Error bars represent two standard errors across data from all independent runs, and lines are drawn to guide the eye. | ||
IV. Conformational behavior
As S decreases, there is a transition from stochastic flipping to crumpling/continuous tumbling that is consistent with the transition to chaotic crumpling found for athermal sheets in our previous work.23 The dynamics of crumpling 2D sheets (both athermal and thermal) in different contexts has also received attention in recent years.77,78 In order to study the conformational behavior of sheets as a function of S and (kBT/κ), we consider two geometric quantities: minimum-volume bounding ellipsoids and orientational covariance matrices. Minimum-volume bounding ellipsoids of sheets were calculated for snapshots of sheet configurations every![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtsnap = 0.25 units of time via the following (dual) convex optimization problem:79
Δtsnap = 0.25 units of time via the following (dual) convex optimization problem:79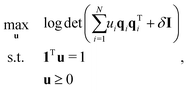 | (14) |
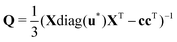 , c = Xu*, and X = [x1,…,xN]. As used in our previous work,23 the orientational covariance matrix describes the spread of the unit normals of triangles across the sheet about a mean orientation. The mean orientation of a sheet lives on the unit sphere like all of the unit normals and is consequently calculated via the weighted Fréchet mean,80
, c = Xu*, and X = [x1,…,xN]. As used in our previous work,23 the orientational covariance matrix describes the spread of the unit normals of triangles across the sheet about a mean orientation. The mean orientation of a sheet lives on the unit sphere like all of the unit normals and is consequently calculated via the weighted Fréchet mean,80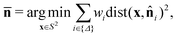 | (15) |
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) i is the normal of triangle i, wi is the area of triangle i, and
i is the normal of triangle i, wi is the area of triangle i, and 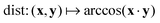 is the Riemannian distance between two points on the sphere. The (weighted) orientational covariance matrix, then, is given by:
is the Riemannian distance between two points on the sphere. The (weighted) orientational covariance matrix, then, is given by: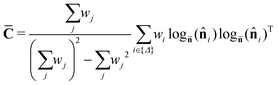 | (16) |
![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) : S2 → T
: S2 → T![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) S2 is the logarithmic map and maps points on the sphere to the tangent plane at
S2 is the logarithmic map and maps points on the sphere to the tangent plane at ![[n with combining macron]](https://www.rsc.org/images/entities/b_char_006e_0304.gif) . The orientational covariance matrix can be further characterized using its two eigenvalues, λ1 and λ2, or their sum and difference. Physically, the sum represents the total degree of crumpling, and the magnitude of the difference relative to the sum indicates the anisotropy of crumpling (see Fig. 8 of ref. 23 for an illustration).
. The orientational covariance matrix can be further characterized using its two eigenvalues, λ1 and λ2, or their sum and difference. Physically, the sum represents the total degree of crumpling, and the magnitude of the difference relative to the sum indicates the anisotropy of crumpling (see Fig. 8 of ref. 23 for an illustration).
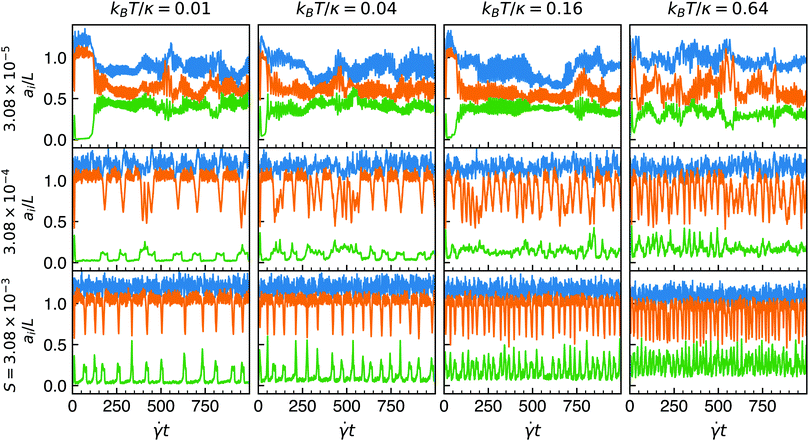
Fig. 5 shows the three semiaxis lengths of minimum-volume bounding ellipsoids over time for several different values of S and kBT/κ, both spanning two orders of magnitude. For the stiffest sheets (larger S) featured in Fig. 5 (the bottom two rows), the stochastic flipping discussed in the previous section is immediately evident as peaks in the semiaxis lengths. During flipping events, the largest semiaxis length does not change appreciably, but the two smallest semiaxis lengths tend to approach each other, moreso for the stiffest sheet. Geometrically, this means stiffer sheets are more “cigar”-like during flipping events, whereas softer sheets are more flattened. It is also important to note that the basal length of the smallest semiaxis increases with temperature, which reflects the fact that greater thermal fluctuations serve to increase the effective thickness about the flat state in the flow-vorticity plane. For S = 3.08 × 10−5 (the top row of Fig. 5), the sheet is crumpled and continuously tumbles, as evidenced by the qualitatively and quantitatively different behavior of the semiaxis lengths. All three semiaxis lengths are much closer together for all time compared to the sheets of larger S, indicating a bounding ellipsoid that is “closer” to a sphere (i.e., less anisotropic), and there are no discrete flipping events that occur. Additionally, one can see that the time required for the sheet to adopt the crumpled conformation from the flat initial condition at time ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t = 0 generally decreases with increasing temperature, indicating that thermal fluctuations help induce crumpling in sheets that are strongly sheared.
t = 0 generally decreases with increasing temperature, indicating that thermal fluctuations help induce crumpling in sheets that are strongly sheared.
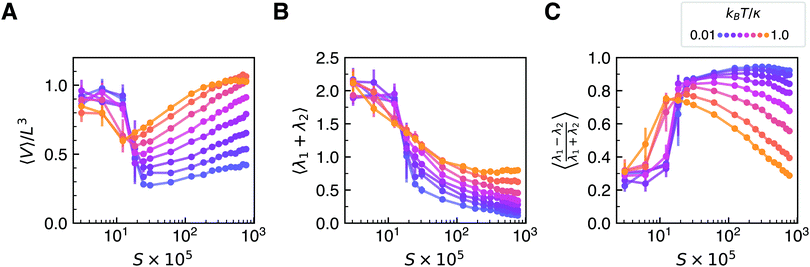
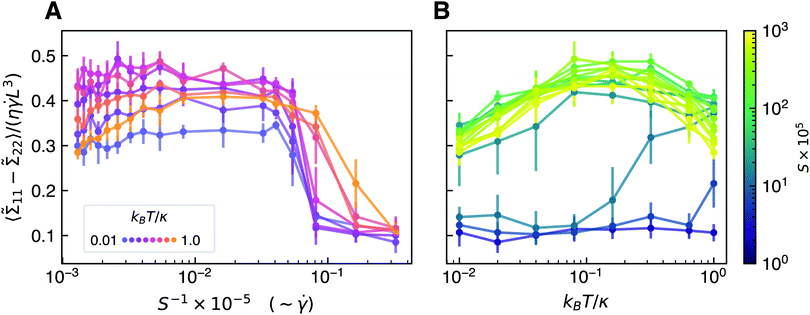
Fig. 6 shows the time-averaged volume of minimum-volume bounding ellipsoids as well as the time-averaged eigenvalues of ![[C with combining macron]](https://www.rsc.org/images/entities/b_char_0043_0304.gif) as a function of S and kBT/κ. First, in all three panels of Fig. 6, the transition to crumpling and tumbling around S ≈ 2 × 10−4 is quite evident as is the smoothing or “rounding” of the transition as temperature increases. One can see in panel A of Fig. 6 that for values of S above the dynamical crumpling transition, the time-averaged bounding volume generally increases with S at constant temperature and increases with temperature at constant S. In light of the stochastic flipping data in Fig. 6 and analysis above, this behavior can largely be attributed to greater flipping frequencies with increasing S and kBT/κ and the larger associated bounding volumes of sheets during flips. Interestingly, for the largest value of S featured in Fig. 6A, the volume decreases when approaching kBT/κ = 1, which further indicates that sufficiently strong thermal fluctuations in the presence of shear can induce more compact conformations, as is the case with the classic equilibrium “crumpling transition” (distinct from the dynamical crumpling transition in S discussed in this work) in tethered-membranes without self-avoidance.24 Whether there is a relationship between this non-monotonic geometric behavior and the equilibrium crumpling transition is an interesting question that may be explored in future work.
as a function of S and kBT/κ. First, in all three panels of Fig. 6, the transition to crumpling and tumbling around S ≈ 2 × 10−4 is quite evident as is the smoothing or “rounding” of the transition as temperature increases. One can see in panel A of Fig. 6 that for values of S above the dynamical crumpling transition, the time-averaged bounding volume generally increases with S at constant temperature and increases with temperature at constant S. In light of the stochastic flipping data in Fig. 6 and analysis above, this behavior can largely be attributed to greater flipping frequencies with increasing S and kBT/κ and the larger associated bounding volumes of sheets during flips. Interestingly, for the largest value of S featured in Fig. 6A, the volume decreases when approaching kBT/κ = 1, which further indicates that sufficiently strong thermal fluctuations in the presence of shear can induce more compact conformations, as is the case with the classic equilibrium “crumpling transition” (distinct from the dynamical crumpling transition in S discussed in this work) in tethered-membranes without self-avoidance.24 Whether there is a relationship between this non-monotonic geometric behavior and the equilibrium crumpling transition is an interesting question that may be explored in future work.
Panels B and C of Fig. 6 show the time-averaged sum and the normalized difference of the eigenvalues of the orientational covariance matrix, ![[C with combining macron]](https://www.rsc.org/images/entities/b_char_0043_0304.gif) . While the sum indicates the total degree of variance of the normals across the sheet about the mean orientation (and hence total degree of crumpling), the normalized difference represents the degree to the which the sheet deforms anisotropically. For example, a normalized eigenvalue difference of 1.0 corresponds to a sheet creased in one direction and exhibiting zero curvature in the direction orthogonal to the crease. In panel B, one can see, as expected, that the total degree of crumpling increases monotonically as S decreases for all temperatures and increases sharply around the dynamical crumpling/continuous tumbling transition. The total degree of crumpling also increases with temperature and can likely be attributed to the amplitude of the thermal fluctuations themselves.
. While the sum indicates the total degree of variance of the normals across the sheet about the mean orientation (and hence total degree of crumpling), the normalized difference represents the degree to the which the sheet deforms anisotropically. For example, a normalized eigenvalue difference of 1.0 corresponds to a sheet creased in one direction and exhibiting zero curvature in the direction orthogonal to the crease. In panel B, one can see, as expected, that the total degree of crumpling increases monotonically as S decreases for all temperatures and increases sharply around the dynamical crumpling/continuous tumbling transition. The total degree of crumpling also increases with temperature and can likely be attributed to the amplitude of the thermal fluctuations themselves.
In panel C, one can see that larger thermal fluctuations lead to more isotropically crumpled conformations for all values of S above the dynamical crumpling/continuous tumbling transition. Somewhat counterintuitively, the relative degree of anisotropy in deformation decreases with S at the highest temperatures but increases with S at the lowest temperatures. This behavior may be explained as follows. At high dimensionless temperatures, sheets are flipping quite frequently due to strong thermal fluctuations, and larger directional shear forces relative to bending forces (as S decreases) should induce more anisotropy in the deformations during flipping. At low dimensionless temperatures, sheets are flipping relatively infrequently and already deforming with large anisotropy as they fold over in the flow (see movies in the Supporting Information). Greater bending rigidity as S increases (regardless of shear strength), then, should promote more anisotropic folding, which is in line with our conclusions for athermal sheets.23 In other words, at large kBT/κ, conformational behavior is dominated mostly by the interplay of thermal fluctuations and shear flow, whereas for small kBT/κ, conformational behavior is dominated mostly by the interplay of bending rigidity and shear flow. The ratio kBT/κ, after all, indicates which energy scale is more relevant.
V. Rheological properties
For a dilute suspension of force-free rigid particles, Batchelor21 showed that the total stress is given by: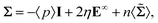 | (17) |
where p is the pressure, E∞ = (L + LT)/2 is the imposed rate-of-strain tensor, n is the number concentration of particles, and 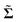 is the stresslet (denoted with
is the stresslet (denoted with 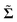 to avoid confusion with S, as it is usually denoted in the literature). The stresslet represents the symmetric part of the first moment of the force distribution on a particle.81,82 Importantly, all of the angle brackets here represent volume averages, and in an abuse of notation, we conflate the meaning of these angle brackets with the others throughout this paper that represent time averages under the assumption that they should be equal (i.e., ergodicity holds).
to avoid confusion with S, as it is usually denoted in the literature). The stresslet represents the symmetric part of the first moment of the force distribution on a particle.81,82 Importantly, all of the angle brackets here represent volume averages, and in an abuse of notation, we conflate the meaning of these angle brackets with the others throughout this paper that represent time averages under the assumption that they should be equal (i.e., ergodicity holds).
The calculation of the stress (and consequently viscosity) from immersed boundary simulations of flexible materials, such as those conducted in this work, is challenging. The Kirkwood–Riseman methodology83 is often used to model the viscosity of polymer chains, but there are certain mathematical issues (viz., singularities) associated with its use that are often underappreciated.84 As such, we chose to use the minimum-volume bounding ellipsoids discussed above to estimate the transport properties of sheets. Namely, the stresslet, 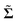 , of the bounding ellipsoid at each snapshot was calculated numerically using the formulas found in Kim and Karrila81 with rotational velocities set to those dictated by Jeffery's equations16 for force- and torque-free ellipsoids in Stokes flow. If the sheet were rigid or if the beads comprising the sheet were force-free, then the energy dissipated by the bounding ellipsoid and its viscosity would be rigorous upper bounds to those of the sheet.81,85 However, given that the beads are not force-free due to bending and stretching forces, the energy dissipated by the ellipsoid should be considered an approximate upper bound to that of the sheet, capturing the dominant hydrodynamic contributions to the stress due to changes in sheet conformation.
, of the bounding ellipsoid at each snapshot was calculated numerically using the formulas found in Kim and Karrila81 with rotational velocities set to those dictated by Jeffery's equations16 for force- and torque-free ellipsoids in Stokes flow. If the sheet were rigid or if the beads comprising the sheet were force-free, then the energy dissipated by the bounding ellipsoid and its viscosity would be rigorous upper bounds to those of the sheet.81,85 However, given that the beads are not force-free due to bending and stretching forces, the energy dissipated by the ellipsoid should be considered an approximate upper bound to that of the sheet, capturing the dominant hydrodynamic contributions to the stress due to changes in sheet conformation.
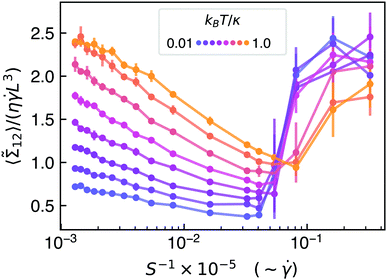
Fig. 7 shows the time-averaged off-diagonal “flow-gradient” entry of the minimum-volume bounding ellipsoid stresslet. Physically, the increase in the effective viscosity of a dilute suspension of sheets should grow linearly with this quantity as described in eqn (17). In Fig. 7, this dimensionless stress is plotted against S−1 instead of S in order to make it more amenable to typical rheological interpretation since S−1 is proportional to the shear rate for fixed bending rigidity. For values of S above the dynamical crumpling/continuously tumbling transition, the stresslet contribution to the viscosity increases with temperature and decreases with shear rate. Past the transition, though, the viscosity contribution begins to increase again. This non-monotonic behavior implies that dilute suspensions of semiflexible sheets should be shear-thinning up to to a dimensionless shear rate around S−1 ≈ 5 × 103, at which point the suspension exhibits crumpling-induced shear-thickening. Interestingly, dilute suspensions of graphene oxide, a material with a bending rigidity of κ/kBT ≈ 1 at room temperature,86 have indeed been found to exhibit peculiar behavior of shear-thinning followed by shear-thickening.87 In fact, Fig. 7 in ref. 87 also demonstrates temperature-dependent viscosity effects that are qualitatively very similar to those depicted in Fig. 4 of this work. Although Zhang et al.87 do not claim such behavior is due to conformational changes, we believe it is a strong possibility that merits further investigation.
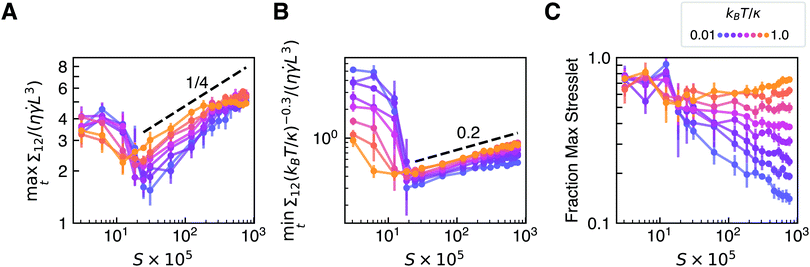
For most values of S examined, sheets do not tumble like rigid platelets, and there is a complicated balance between geometrical conformations and time spent flipping that affects the observed stresslet contribution to the viscosity (see Appendix B). However, as shown in Fig. 8, an empirical power-law fit of the form 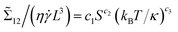 , where c1 = 8.55, c2 = 0.236, and c3 = 0.263, seems to collapse the data before the dynamical crumpling transition well. These constants were calculated via a weighted least-squares fit to the power-law functional form using run-averaged data with S > 2.5 × 10−4 and errors equal to the standard errors of the mean among the independent runs. Assuming independent, Gaussian-distributed errors and a uniform prior, Monte Carlo sampling yielded the following 95% equal-tailed credible intervals for the fitting parameters: c1 ∈ [8.45, 8.67], c2 ∈ [0.2338, 0.2379], c3 ∈ [0.2616, 0.2647]. This scaling with S0.236 is largely attributable to the size of the “U-turn” radius of the sheet as it flips, which theory75 predicts should scale as S1/4
, where c1 = 8.55, c2 = 0.236, and c3 = 0.263, seems to collapse the data before the dynamical crumpling transition well. These constants were calculated via a weighted least-squares fit to the power-law functional form using run-averaged data with S > 2.5 × 10−4 and errors equal to the standard errors of the mean among the independent runs. Assuming independent, Gaussian-distributed errors and a uniform prior, Monte Carlo sampling yielded the following 95% equal-tailed credible intervals for the fitting parameters: c1 ∈ [8.45, 8.67], c2 ∈ [0.2338, 0.2379], c3 ∈ [0.2616, 0.2647]. This scaling with S0.236 is largely attributable to the size of the “U-turn” radius of the sheet as it flips, which theory75 predicts should scale as S1/4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (see Appendix B). In terms of shear rate, it is expected, then, that the contribution to viscosity (in the relevant regime of S) should exhibit a power-law scaling exponent with respect to shear rate of −0.236, or, equivalently, an exponent value of 0.764 for the power-law fluid model.22
(see Appendix B). In terms of shear rate, it is expected, then, that the contribution to viscosity (in the relevant regime of S) should exhibit a power-law scaling exponent with respect to shear rate of −0.236, or, equivalently, an exponent value of 0.764 for the power-law fluid model.22
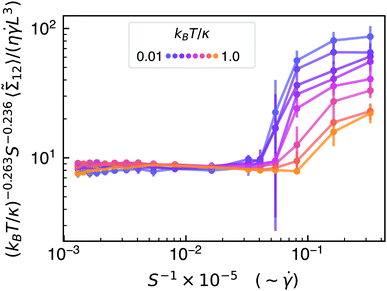 | ||
| Fig. 8 Scaled, time-averaged dimensionless stresslet contribution to the viscosity (see Fig. 7) as a function of dimensionless bending rigidity, S, and dimensionless temperature, kBT/κ. Error bars represent two standard errors of the mean between the independent runs, and lines are drawn to guide the eye. | ||
Regarding the zero-shear viscosity of dilute suspensions of sheets, a power-law fluid model is not appropriate. In fact, it is challenging to calculate such a quantity with the computational model of an asymptotically thin sheet studied in this work. Consider the following: for small kBT/κ, as shear rate approaches zero, neither the shear flow nor thermal fluctuations are perturbing the sheet much away from a flat conformation. One may expect, then, that κ becomes irrelevant and that the Péclet number, Pe = S−1(kBT/κ)−1, becomes the relevant dimensionless group. As shear rate approaches zero, the orientations of the effectively rigid sheets would be uniformly distributed, and the the suspension viscosity would be given by the orientationally averaged stresslet, which, in turn, depends significantly on the thickness of the sheets. For large kBT/κ, the zero-shear viscosity would be related to equilibrium sheet conformations, which may be dependent on the chemistry of particular experimental systems of interest.43
In addition to viscosity, first normal stress differences can be calculated using the stresslet data from the minimum-volume bounding ellipsoids. Fig. 9 shows the time-averaged first normal stress difference as a function of S and kBT/κ. As a function of S, the first normal stress difference is greatest for values of S above the dynamical crumpling transition (low shear rates) and decreases rapidly for continuously tumbling, crumpled sheets past the transition. This behavior is consistent with the orientational covariance data presented in Fig. 6 in that first normal stresses differences are most prominent for highly anisotropic particles but sheets beyond the dynamical crumpling transition are more isotropically crumpled. Suspensions of spherical particles, after all, do not exhibit any normal stress differences. Panel B of Fig. 9 shows that, as a function of temperature, stochastically flipping sheets with S values above the dynamical crumpling transition exhibit a local maximum of normal stress between kBT/κ = 0.1 to 0.3. This non-monotonic behavior in temperature is likely due to the fact that both average volume and degree of anisotropic crumpling affect the first normal stress difference. Again, from Fig. 6, one can see opposite trends with respect to temperature for the total degree of crumpling (as measured by the sum of the eigenvalues) and the relative anisotropy of deformation (as measured by the normalized difference of the eigenvalues). That is, qualitatively, the balance between these two quantities leads to the observed local maximum.
VI. Conclusions
Numerical immersed boundary simulations of semiflexible sheets subjected to thermal fluctuations and ambient simple shear flow were conducted over a range of values for dimensionless bending rigidity, S = κ/(πη![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) L3), and dimensionless temperature, kBT/κ. A dynamical transition from stochastic flipping to indefinitely crumpled and continuously tumbling sheets was identified at a value of S ≈ 2 × 10−4, which is consistent with the transition to chaotic crumpling and tumbling found in athermal sheets.23 Scaling arguments similar to those found in the tumbling polymer literature were used to characterize the mean time between flips (
L3), and dimensionless temperature, kBT/κ. A dynamical transition from stochastic flipping to indefinitely crumpled and continuously tumbling sheets was identified at a value of S ≈ 2 × 10−4, which is consistent with the transition to chaotic crumpling and tumbling found in athermal sheets.23 Scaling arguments similar to those found in the tumbling polymer literature were used to characterize the mean time between flips (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtdiff ∼ (kBT/κ)−1/3S−1/3) for stochastically flipping sheets that were stiff relative to both shear strength and thermal fluctuations. Additionally, a 1D first passage time model was constructed and successfully applied to explain the scaling of the variance of the flipping time distributions (Var[
Δtdiff ∼ (kBT/κ)−1/3S−1/3) for stochastically flipping sheets that were stiff relative to both shear strength and thermal fluctuations. Additionally, a 1D first passage time model was constructed and successfully applied to explain the scaling of the variance of the flipping time distributions (Var[![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Δtflip] ∼ (kBT/κ)−2/3S−2/3).
Δtflip] ∼ (kBT/κ)−2/3S−2/3).
Geometric and conformational behavior was quantified via the calculation of minimum-volume bounding ellipsoids as well as orientational covariance matrices describing the spread of normals across the sheet about a mean orientation. Stresslets were calculated for minimum-volume bounding ellipsoids over time in order to estimate the viscosity and first normal stress difference for dilute suspensions of semiflexible sheets. In particular, up to the dynamical crumping/continuously tumbling transition, suspensions were shear-thinning, and at higher shear rates beyond the dynamical crumpling transition, suspensions were shear-thickening. We also observed nonzero first normal stress differences that exhibited a local maximum in temperature and decreased sharply with increasing shear rate beyond the dynamical crumpling transition due to less anisotropy in the dynamically crumpled/continuously tumbling state.
Although the effects of thermal-fluctuation-induced bending rigidity renormalization were mentioned in the introduction, they were not explicitly considered in this work. In particular, the “bare” dimensionless bending rigidity was used in all analyses even though thermal fluctuations are known to induce a length-scale-dependent renormalized bending rigidity. With differently sized sheets, instead of scaling with κ and L3, one may predict that S should scale like 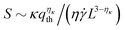 for large Föppl–von Kármán (FvK) numbers (i.e., sheets with bending modes much softer than stretching modes), where ηκ ≈ 0.8 and
for large Föppl–von Kármán (FvK) numbers (i.e., sheets with bending modes much softer than stretching modes), where ηκ ≈ 0.8 and 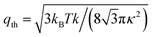 is an inverse thermal length scale.24,35 Future work that more concretely examines these effects and, namely, whether the bending rigidity in all of the scaling analyses and in the governing dimensionless parameter S could simply be replaced by its renormalized counterpart would be especially valuable.
is an inverse thermal length scale.24,35 Future work that more concretely examines these effects and, namely, whether the bending rigidity in all of the scaling analyses and in the governing dimensionless parameter S could simply be replaced by its renormalized counterpart would be especially valuable.
Between the viscosity and the first normal stress difference, it is clear that the dynamical and conformational behavior of colloidal 2D materials explored in this work contributes to a rich variety of non-Newtonian rheological properties. Importantly, this behavior can be exploited to design responsive soft materials and appropriately tune solution processing protocols for 2D materials depending on the application. We believe the fundamental advances of this work will greatly inform future theoretical work on sheet dynamics as well as experimental design.
Conflicts of interest
There are no conflicts to declare.Appendix A: first passage time model
Consider a Brownian particle with diffusivity Dr initially located in the center of the domain [−θc, θc] with a reflecting boundary condition on the left and an absorbing boundary condition on the right. The evolution of the probability distribution of the particle over time is governed by the following Fokker–Planck equation: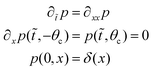 | (A1) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = Drt. An infinite series solution for p is given by:
= Drt. An infinite series solution for p is given by: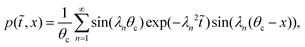 | (A2) |
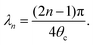 | (A3) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) is defined as
) is defined as 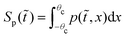 , and the associated first passage time distribution is defined as f(
, and the associated first passage time distribution is defined as f(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) = − dSp/d
) = − dSp/d![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) . Analytically, f(
. Analytically, f(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) can also be represented by an infinite series:
) can also be represented by an infinite series: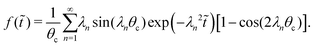 | (A4) |
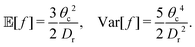 | (A5) |
Appendix B: Stresslet analysis
Fig. 10 shows the maximum and minimum instantaneous dimensionless stresslet contributions to the viscosity as well as the fraction of time spent with instantaneous stresslet values in the top 75% of those attained (i.e., time that can largely be attributed to flipping or crumpling in the flow), all averaged over the six independent runs. The minimum instantaneous stresslet values in panel B are scaled by the dimensionless temperature to a certain power, as explained below.In panel A of Fig. 10, it can be seen that the maximum instantaneous off-diagonal stresslet values attained are not a strong function of dimensionless temperature. For “intermediate” values of S that represent sheets that are not approaching infinite stiffness (i.e., most of the range of values examined beyond that of the dynamical crumpling transition), this behavior can be explained with geometric reasoning and a force balance. Following the arguments of Harasim et al.75 for understanding the “U-turn” radius of a tumbling polymer, balancing the hydrodynamic force on a “U-turn” in a flipping sheet with the bending moment of the “U-turn” yields the following scaling for the radius of curvature:
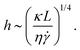 | (B1) |
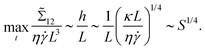 | (B2) |
Panel B shows the minimum instantaneous off-diagonal stresslet values attained, which can be attributed physically to thermal height fluctuations of flat sheets in the flow-vorticity plane (for those sheets with S values above the dynamical crumpling transition). By a similar argument, given that the bounding ellipsoid stresslet scales like hL2 and using known results24,35 for the average height fluctuations of a thermalized tethered membrane:
 | (B3) |
Panel C of Fig. 10 shows the fraction of time spent with instantaneous stresslet values in the top 75% of those attained, which is one measure of the fraction of time spent flipping or at least “disturbing” the ambient shear flow. While the dependence on S and dimensionless temperature over the full range of S examined is complicated, it is this quantity when multiplied by the maximum instantaneous stresslet values in panel A that results in the empirical power-law scaling in S and kBT/κ seen in Fig. 8. The minimum instantaneous stresslet values are approximately an order of magnitude smaller than the time-averaged stresslet values. Thus, the weak dependence on S (or, equivalently, FvK number) seen in panel B due to the choice of harmonic bond potential strength negligibly impacts the observed time-averaged stresslet contribution to the viscosity. That is, the observed viscosity scaling should be expected to hold for a given material with a constant FvK number over a relevant range of dimensionless shear rates (S−1).
Acknowledgements
This work was adapted from a chapter of a thesis written by one of the authors.88 K.S.S. was supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Department of Energy Computational Science Graduate Fellowship under Award Number DE-FG02-97ER25308. M.S.S. was supported by the Department of Energy, Office of Science, Basic Energy Sciences under grant No. DE-FG02-08ER46488 Mod 0008. J.W.S. was supported by NSF Career Award No. CBET-1554398. The authors would like to thank G. McKinley, P. Doyle, and N. Fakhri for helpful discussions.This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
This work is dedicated to James Swan, who tragically and unexpectedly passed away while this work was under review. Jim was a devoted colleague, advisor, husband, father, teacher, and friend. He was a scholar of the highest caliber with infallible integrity. His knowledge across diverse areas was remarkable. His eagerness to tackle challenging problems was infectious. And, notably, he was a caring mentor and wonderful listener. Hopefully, some of the seemingly endless joy he found in scientific inquiry is reflected in this work. To have to write this dedication now is surreal, and to say he will be greatly missed is an understatement.
References
- J. Stafford, A. Patapas, N. Uzo, O. K. Matar and C. Petit, Towards scale-up of graphene production via nonoxidizing liquid exfoliation methods, AIChE J., 2018, 64(9), 3246–3276 CrossRef CAS.
- A. Ambrosi and M. Pumera, Exfoliation of layered materials using electrochemistry, Chem. Soc. Rev., 2018, 47(19), 7213–7224 RSC.
- J. N. Coleman, M. Lotya, A. O’Neill, S. D. Bergin, P. J. King and U. Khan, et al., Two-dimensional nanosheets produced by liquid exfoliation of layered, Mater. Sci., 2011, 331(6017), 568–571 CAS.
- V. Nicolosi, M. Chhowalla, M. G. Kanatzidis, M. S. Strano and J. N. Coleman, Liquid exfoliation of layered, Mater. Sci., 2013, 340(6139), 1226419 Search PubMed.
- E. Varrla, C. Backes, K. R. Paton, A. Harvey, Z. Gholamvand and J. McCauley, et al., Large-scale production of size-controlled MoS2 nanosheets by shear exfoliation, Chem. Mater., 2015, 27(3), 1129–1139 CrossRef CAS.
- S. A. Mallory, C. Valeriani and A. Cacciuto, Anomalous dynamics of an elastic membrane in an active fluid, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92(1), 012314 CrossRef CAS PubMed.
- T. Gibaud, C. N. Kaplan, P. Sharma, M. J. Zakhary, A. Ward and R. Oldenbourg, et al., Achiral symmetry breaking and positive Gaussian modulus lead to scalloped colloidal membranes, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(17), E3376–E3384 CrossRef CAS PubMed.
- F. Ding, J. Liu, S. Zeng, Y. Xia, K. M. Wells and M. P. Nieh, et al., Biomimetic nanocoatings with exceptional mechanical, barrier, and flame-retardant properties from large-scale one-step coassembly, Sci. Adv., 2017, 3(7), e1701212 CrossRef PubMed.
- F. Tardani, W. Neri, C. Zakri, H. Kellay, A. Colin and P. Poulin, Shear rheology control of wrinkles and patterns in graphene oxide films, Langmuir, 2018, 34(9), 2996–3002 CrossRef CAS PubMed.
- P. Davidson, C. Penisson, D. Constantin and J. C. P. Gabriel, Isotropic, nematic, and lamellar phases in colloidal suspensions of nanosheets, Proc. Natl. Acad. Sci. U. S. A., 2018, 201802692 Search PubMed.
- A. Laskar, O. E. Shklyaev and A. C. Balazs, Designing self-propelled, chemically active sheets: Wrappers, flappers, and creepers, Sci. Adv., 2018, 4(12), eaav1745 CrossRef CAS PubMed.
- C. Kamal, S. Gravelle and L. Botto, Hydrodynamic slip can align thin nanoplatelets in shear flow, Nat. Commun., 2020, 11(1), 2425 CrossRef CAS PubMed.
- M. Pezzulla, E. F. Strong, F. Gallaire and P. M. Reis, Deformation of porous flexible strip in low and moderate reynolds number flows, Phys. Rev. Fluids, 2020, 5(8), 084103 CrossRef.
- A. R. Klotz, B. W. Soh and P. S. Doyle, Equilibrium structure and deformation response of 2D kinetoplast sheets, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(1), 121–127 CrossRef CAS PubMed.
- P. Liu, A. T. Liu, D. Kozawa, J. Dong, J. F. Yang and V. B. Koman, et al., Autoperforation of 2D materials for generating two-terminal memristive Janus particles, Nat. Mater., 2018, 17(11), 1005–1012 CrossRef CAS PubMed.
- G. B. Jeffery, The Motion of Ellipsoidal Particles Immersed 14 in a Viscous Fluid, Proc. R. Soc. London, Ser. A, 1922, 102(715), 161–179 Search PubMed.
- E. J. Hinch and L. G. Leal, The effect of brownian motion on the rheological properties of a suspension of non-spherical particles, J. Fluid Mech., 1972, 52(04), 683 CrossRef.
- E. J. Hinch and L. G. Leal, Rotation of small non-axisymmetric particles in a simple shear flow, J. Fluid Mech., 1979, 92(3), 591–607 CrossRef.
- L. G. Leal and E. J. Hinch, The effect of weak Brownian rotations on particles in shear flow, J. Fluid Mech., 1971, 46(04), 685 CrossRef.
- G. K. Batchelor, Slender-body theory for particles of arbitrary cross-section in Stokes flow, J. Fluid Mech., 1970, 44(3), 419–440 CrossRef.
- G. K. Batchelor, The stress system in a suspension of force-free particles, J. Fluid Mech., 1970, 41(3), 545–570 CrossRef.
- R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, 2nd edn, New York, Wiley, 1987 Search PubMed.
- K. S. Silmore, M. S. Strano and J. W. Swan, Buckling, crumpling, and tumbling of semiflexible sheets in simple shear flow, Soft Matter, 2021, 17(18), 4707–4718 RSC.
- D. Nelson, T. Piran and S. Weinberg, Statistical Mechanics of Membranes and Surfaces, 2nd edn, World Scientific, 2004 Search PubMed.
- J. A. Aronovitz and T. C. Lubensky, Fluctuations of solid membranes, Phys. Rev. Lett., 1988, 60(25), 2634–2637 CrossRef PubMed.
- E. Frey and D. L. Nelson, Dynamics of flat membranes and flickering in red blood cells, J. Phys. I, 1991, 1(12), 1715–1757 CrossRef CAS.
- Y. Kantor, M. Kardar and D. R. Nelson, Statistical mechanics of tethered surfaces, Phys. Rev. Lett., 1986, 57(7), 791–794 CrossRef CAS PubMed.
- M. Kardar and D. R. Nelson, Statistical mechanics of self-avoiding tethered manifolds, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(2), 966–982 CrossRef PubMed.
- D. R. Nelson and L. Peliti, Fluctuations in membranes with crystalline and hexatic order, J. Phys., 1987, 48(7), 1085–1092 CrossRef CAS.
- M. Paczuski, M. Kardar and D. R. Nelson, Landau theory of the crumpling transition, Phys. Rev. Lett., 1988, 60(25), 2638–2640 CrossRef PubMed.
- A. Košmrlj and D. R. Nelson, Response of thermalized ribbons to pulling and bending, Phys. Rev. B, 2016, 93(12), 125431 CrossRef.
- F. F. Abraham, W. E. Rudge and M. Plischke, Molecular dynamics of tethered membranes, Phys. Rev. Lett., 1989, 62(15), 1757–1759 CrossRef CAS PubMed.
- F. F. Abraham and D. R. Nelson, Diffraction from polymerized membranes, Science, 1990, 249(4967), 393–397 CrossRef CAS PubMed.
- M. J. Bowick, A. Cacciuto, G. Thorleifsson and A. Travesset, Universality classes of self-avoiding fixed-connectivity membranes, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 5(2), 149–160 CrossRef CAS.
- M. J. Bowick, A. Košmrlj, D. R. Nelson and R. Sknepnek, Non-Hookean statistical mechanics of clamped graphene ribbons, Phys. Rev. B, 2017, 95(10), 104109 CrossRef.
- G. Gompper and D. M. Kroll, Fluctuations of polymerized, fluid and hexatic membranes: Continuum models and simulations, Curr. Opin. Colloid Interface Sci., 1997, 2(4), 373–381 CrossRef CAS.
- G. S. Grest and I. B. Petsche, Molecular dynamics simulations of self-avoiding tethered membranes with attractive interactions: Search for a crumpled phase, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50(3), R1737–R1740 CrossRef CAS PubMed.
- J. S. Ho and A. Baumgärtner, Self-avoiding tethered membranes, Phys. Rev. Lett., 1989, 63(12), 1324 CrossRef PubMed.
- M. Plischke and D. Boal, Absence of a crumpling transition in strongly self-avoiding tethered membranes, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(9), 4943–4945 CrossRef PubMed.
- A. Tröster, High-precision Fourier Monte Carlo simulation of crystalline membranes, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(10), 104112 CrossRef.
- M. S. Spector, E. Naranjo, S. Chiruvolu and J. A. Zasadzinski, Conformations of a tethered membrane: Crumpling in graphitic oxide?, Phys. Rev. Lett., 1994, 73(21), 2867–2870 CrossRef CAS PubMed.
- X. Wen, C. W. Garland, T. Hwa, M. Kardar, E. Kokufuta and Y. Li, et al., Crumpled and collapsed conformation in graphite oxide membranes, Nature, 1992, 355(6359), 426–428 CrossRef CAS.
- P. Li, S. Wang, F. Meng, Y. Wang, F. Guo and S. Rajendran, et al., Conformational scaling relations of two-dimensional macromolecular graphene oxide in solution, Macromolecules, 2020, 53(23), 10421–10430 CrossRef CAS.
- Y. Xu and M. J. Green, Brownian dynamics simulations of nanosheet solutions under shear, J. Chem. Phys., 2014, 141(2), 024905 CrossRef PubMed.
- Y. Xu and M. J. Green, Brownian dynamics simulation of two-dimensional nanosheets under biaxial extensional flow, J. Polym. Sci., Part B: Polym. Phys., 2015, 53(17), 1247–1253 CrossRef CAS.
- S. B. Babu and H. Stark, Dynamics of semi-flexible tethered sheets, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34(12), 136 CrossRef CAS PubMed.
- S. Dutta and M. D. Graham, Dynamics of Miura-patterned foldable sheets in shear flow, Soft Matter, 2017, 13(14), 2620–2633 RSC.
- Y. Yu and M. D. Graham, Coil-stretch-like transition of elastic sheets in extensional flows, Soft Matter, 2021, 17(3), 543–553 RSC.
- X. Bian, S. Litvinov and P. Koumoutsakos, Bending models of lipid bilayer membranes: Spontaneous curvature and area-difference elasticity, Comput. Methods Appl. Mech. Eng., 2020, 359, 112758 CrossRef.
- A. Guckenberger and S. Gekle, Theory and algorithms to compute helfrich bending forces: A review, J. Phys.: Condens. Matter, 2017, 29(20), 203001 CrossRef PubMed.
- G. Gompper and D. M. Kroll, Random surface discretizations and the renormalization of the bending rigidity, J. Phys. I, 1996, 6(10), 1305–1320 CrossRef.
- D. M. Heyes and J. R. Melrose, Brownian dynamics simulations of model hard-sphere suspensions, J. Non-Newtonian Fluid Mech., 1993, 46(1), 1–28 CrossRef CAS.
- K. S. Silmore and J. W. Swan, Collective mode brownian dynamics: A method for fast relaxation of statistical ensembles, J. Chem. Phys., 2020, 152(9), 094104 CrossRef CAS PubMed.
- J. Rotne and S. Prager, Variational treatment of hydrodynamic interaction in polymers, J. Chem. Phys., 1969, 50(11), 4831–4837 CrossRef CAS.
- H. Yamakawa, Transport properties of polymer chains in dilute solution: Hydrodynamic interaction, J. Chem. Phys., 1970, 53(1), 436–443 CrossRef CAS.
- A. M. Fiore, F. Balboa Usabiaga, A. Donev and J. W. Swan, Rapid sampling of stochastic displacements in Brownian dynamics simulations, J. Chem. Phys., 2017, 146(12), 124116 CrossRef PubMed.
- E. Chow and Y. Saad, Preconditioned Krylov subspace methods for sampling multivariate Gaussian distributions, SIAM J. Sci. Comput., 2014, 36(2), A588–A608 CrossRef.
- J. W. Swan and G. Wang, Rapid calculation of hydrodynamic 15 and transport properties in concentrated solutions of colloidal particles and macromolecules, Phys. Fluids, 2016, 28(1), 011902 CrossRef.
- C. Kamal, S. Gravelle and L. Botto, Effect of hydrodynamic slip on the rotational dynamics of a thin brownian platelet in shear flow, J. Fluid Mech., 2021, 919, A1 CrossRef CAS.
- P. Z. Hanakata, S. S. Bhabesh, M. J. Bowick, D. R. Nelson and D. Yllanes, Thermal buckling and symmetry breaking in thin ribbons under compression, Extreme Mech. Lett., 2021, 44, 101270 CrossRef.
- P. Le Doussal and L. Radzihovsky, Thermal buckling transition of crystalline membranes in a field, Phys. Rev. Lett., 2021, 127(1), 015702 CrossRef CAS PubMed.
- A. Morshedifard, M. Ruiz-García, M. J. Abdolhosseini Qomi and A. Košmrlj, Buckling of thermalized elastic sheets, J. Mech. Phys. Solids, 2021, 149, 104296 CrossRef.
- S. Shankar and D. R. Nelson, Thermalized buckling of isotropically compressed thin sheets, Phys. Rev. E, 2021, 104(5), 054141 CrossRef CAS PubMed.
- J. A. Anderson, J. Glaser and S. C. Glotzer, HOOMD-blue: A Python package for high-performance molecular dynamics and hard particle Monte Carlo simulations, Comput. Mater. Sci., 2020, 173, 109363 CrossRef CAS.
- C. M. Bishop, Pattern Recognition and Machine Learning. Information Science and Statistics, Springer, New York, 2006 Search PubMed.
- H. Manikantan and D. Saintillan, Buckling transition of a semiflexible filament in extensional flow, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92(4), 041002 CrossRef PubMed.
- R. Cuerno, R. Gallardo Caballero, A. Gordillo-Guerrero, P. Monroy and J. J. Ruiz-Lorenzo, Universal behavior of crystalline membranes: Crumpling transition and Poisson ratio of the flat phase, Phys. Rev. E, 2016, 93(2), 022111 CrossRef CAS PubMed.
- D. Yllanes, S. S. Bhabesh, D. R. Nelson and M. J. Bowick, Thermal crumpling of perforated two-dimensional sheets, Nat. Commun., 2017, 8(1), 1381 CrossRef PubMed.
- C. M. Schroeder, R. E. Teixeira, E. S. G. Shaqfeh and S. Chu, Characteristic periodic motion of polymers in shear flow, Phys. Rev. Lett., 2005, 95(1), 018301 CrossRef PubMed.
- D. E. Smith, H. P. Babcock and S. Chu, Single-polymer dynamics in steady shear flow, Science, 1999, 283(5408), 1724–1727 CrossRef CAS PubMed.
- S. Gerashchenko and V. Steinberg, Statistics of tumbling of a single polymer molecule in shear flow, Phys. Rev. Lett., 2006, 96(3), 038304 CrossRef PubMed.
- R. G. Winkler, Semiflexible polymers in shear flow, Phys. Rev. Lett., 2006, 97(12), 128301 CrossRef PubMed.
- C. C. Huang, G. Sutmann, G. Gompper and R. G. Winkler, Tumbling of polymers in semidilute solution under shear flow, Europhys. Lett., 2011, 93(5), 54004 CrossRef.
- I. S. Dalal, N. Hoda and R. G. Larson, Multiple regimes of deformation in shearing flow of isolated polymers, J. Rheol., 2012, 56(2), 305–332 CrossRef CAS.
- M. Harasim, B. Wunderlich, O. Peleg, M. Kröger and A. R. Bausch, Direct observation of the dynamics of semiflexible polymers in shear flow, Phys. Rev. Lett., 2013, 110(10), 108302 CrossRef PubMed.
- M. Chertkov, I. Kolokolov, V. Lebedev and K. Turitsyn, Polymer statistics in a random flow with mean shear, J. Fluid Mech., 2005, 531, 251–260 CrossRef CAS.
- D. Yllanes, D. R. Nelson and M. J. Bowick, Folding pathways to crumpling in thermalized elastic frames, Phys. Rev. E, 2019, 100(4), 042112 CrossRef CAS PubMed.
- J. Andrejevic, L. M. Lee, S. M. Rubinstein and C. H. Rycroft, A model for the fragmentation kinetics of crumpled thin sheets, Nat. Commun., 2021, 12(1), 1470 CrossRef CAS PubMed.
- P. Kumar and E. A. Yildirim, Minimum-volume enclosing ellipsoids and core sets, J. Optim. Theory Appl., 2005, 126(1), 1–21 CrossRef.
- X. Pennec, Intrinsic statistics on riemannian manifolds: Basic tools for geometric measurements, J. Math. Imaging Vis., 2006, 25(1), 127 CrossRef.
- S. Kim and S. J. Karrila, Microhydrodynamics: Principles and Selected Applications, Dover Publications, Mineola, NY, 2005 Search PubMed.
- É. Guazzelli and J. F. Morris, A Physical Introduction to Suspension Dynamics, Cambridge University Press, 2011 Search PubMed.
- J. G. Kirkwood and J. Riseman, The intrinsic viscosities and diffusion constants of flexible macromolecules in solution, J. Chem. Phys., 1948, 16(6), 565–573 CrossRef CAS.
- R. Zwanzig, J. Kiefer and G. H. Weiss, On the validity of the Kirkwood–Riseman theory, Proc. Natl. Acad. Sci. U. S. A., 1968, 60(2), 381–386 CrossRef CAS PubMed.
- A. Nir, H. F. Weinberger and A. Acrivos, variational inequalities for a body in a viscous shearing flow, J. Fluid Mech., 1975, 68(4), 739–755 CrossRef.
- P. Poulin, R. Jalili, W. Neri, F. Nallet, T. Divoux and A. Colin, et al., Superflexibility of graphene oxide, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(40), 11088–11093 CrossRef CAS PubMed.
- X. Zhang, Y. Tang, X. Wang, J. Zhang, D. Guo and X. Zhang, Dispersion and rheological properties of aqueous graphene suspensions in presence of nanocrystalline cellulose, J. Polym. Environ., 2018, 26(8), 3502–3510 CrossRef CAS.
- K. S. Silmore, From Spheres to Sheets: Colloidal Hydrodynamics, Thermodynamics, and Statistical Inference, PhD thesis, Massachusetts Institute of Technology, 2021.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01510a |
| This journal is © The Royal Society of Chemistry 2022 |