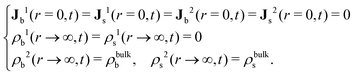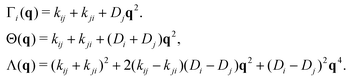Open Access Article
Open Access ArticleActive interaction switching controls the dynamic heterogeneity of soft colloidal dispersions
Michael
Bley
a,
Pablo I.
Hurtado
bc,
Joachim
Dzubiella
*ad and
Arturo
Moncho-Jordá
 *ce
*ce
aPhysikalisches Institut, Albert-Ludwigs-Universität Freiburg, Hermann-Herder Straße 3, D-79104 Freiburg, Germany. E-mail: joachim.dzubiella@physik.uni-freiburg.de
bDepartamento de Electromagnetismo y Física de la Materia, Universidad de Granada, Campus Fuentenueva S/N, 18071 Granada, Spain
cInstitute Carlos I for Theoretical and Computational Physics, Facultad de Ciencias, Universidad de Granada, Campus Fuentenueva S/N, 18071 Granada, Spain. E-mail: moncho@ugr.es
dResearch Group for Simulations of Energy Materials, Helmholtz-Zentrum Berlin für Materialien und Energie, D-14109 Berlin, Germany
eDepartamento de Física Aplicada, Universidad de Granada, Campus Fuentenueva S/N, 18071 Granada, Spain
First published on 1st December 2021
Abstract
We employ Reactive Dynamical Density Functional Theory (R-DDFT) and Reactive Brownian Dynamics (R-BD) simulations to investigate the dynamics of a suspension of active soft Gaussian colloids with binary interaction switching, i.e., a one-component colloidal system in which every particle stochastically switches at predefined rates between two interaction states with different mobility. Using R-DDFT we extend a theory previously developed to access the dynamics of inhomogeneous liquids [Archer et al., Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 040501] to study the influence of the switching activity on the self and distinct part of the Van Hove function in bulk solution, and determine the corresponding mean squared displacement of the switching particles. Our results demonstrate that, even though the average diffusion coefficient is not affected by the switching activity, it significantly modifies the non-equilibrium dynamics and diffusion coefficients of the individual particles, leading to a crossover from short to long times, with a regime for intermediate times showing anomalous diffusion. In addition, the self-part of the van Hove function has a Gaussian form at short and long times, but becomes non-Gaussian at intermediates ones, having a crossover between short and large displacements. The corresponding self-intermediate scattering function shows the two-step relaxation patters typically observed in soft materials with heterogeneous dynamics such as glasses and gels. We also introduce a phenomenological Continuous Time Random Walk (CTRW) theory to understand the heterogeneous diffusion of this system. R-DDFT results are in excellent agreement with R-BD simulations and the analytical predictions of CTRW theory, thus confirming that R-DDFT constitutes a powerful method to investigate not only the structure and phase behavior, but also the dynamical properties of non-equilibrium active switching colloidal suspensions.
1 Introduction
Responsive materials like polymers adapt to external stimuli (i.e. temperature, pH, or food) and change their shape and conformation accordingly.1–5 The environment-dependent size of responsive materials can change by a factor of two or three typically.6 Examples of this are globular proteins, in which their conformation and phase behavior can be tuned by changes in the local environment and protein–protein attractive interaction.7,8 These colloidal systems and their responsiveness can be used for tailor-made functionality such as core–shell nano-reactors for selective catalysis3,4 or controlled drug release,1,2 but also lay the foundation for adaptive and intelligent systems.9 Due to the switching of properties such as size or interactions, these compounds can exhibit a complex and rich anomalous diffusion behavior different to the classical Einstein–Smoluchowski picture of a random walk leading to a mean squared displacement (MSD) entirely linear in time ∝ t.10,11 The effective diffusion coefficient D thus changes with the observed time scale. This anomalous diffusion appears for example in various biological systems and during the transport of particles through membranes,12–22 where both sub- and superdiffusive regions are observed.Heterogeneous diffusion is also reported in a variety of amorphous materials, from low density gels to dense glasses.23–28 In most cases such dynamic heterogeneity can be explained by the presence of different particle arrest mechanisms at play. These mechanisms may range from the bonding of particles to the giant (percolating) component of a low density physical gel, which traps particles in a localized region during a long time,29–32 to the steric hindrance induced by crowding effects in glasses, which lead to strong dynamic heterogeneities.25,26 Moreover, different arrest mechanisms can also compete, leading to complex relaxation behaviors.33–36 In all cases the observed heterogeneous diffusion is related to the coexistence of fast and slow diffusing particles in the system of interest. These observations suggest that active colloidal systems where particles can stochastically change their internal state, and hence their mobility, may also lead to heterogeneous diffusion properties.
In this work, we investigate a non-equilibrium active system formed by soft colloids in which individual particles stochastically switch between two interaction states (or sizes), denoted as big (b) and small (s), at predefined rates kbs and ksb. Such a system constitutes a good model for bistable bacteria that use switching to tune structural and dynamical heterogeneities for their function,37,38 as well as for soft active or vesicles fluctuating between two states.39–42 It could also be applied to study the structure and phase behavior of conformationally fluctuating biopolymers,43–45 in particular two-state proteins switching between native and non-native states.7,8 In future it may be extendable to even study soft micromachines with a programmable morphology.46
In our previous works, we studied the structural properties and phase behavior of this active switching system by using a non-equilibrium reactive density functional theory (R-DDFT)47,48 and reactive Brownian dynamics simulations (R-BD).49,50 Flavors of R-DDFT have been recently applied to predict the propagation of virus spreading51,52 and for describing the growth of tumors.53 High switching rates lead to mixing of systems which phase separate in equilibrium conditions, whereas low, non-zero switching rates lead to the observation of temporal clusters representing local and temporal phase separation. Here, we extend the R-DDFT framework by means of the test-particle method developed by Archer et al.54 to investigate the non-equilibrium steady-state dynamics of actively switching particles in the bulk. Different, but constant diffusion coefficients are assigned to the two particle sizes. This method provides a new pathway for accessing the dynamics of particles switching between two diffusion coefficients. Moreover, we develop a phenomenological Continuous Time Random Walk theory (CTRW)24,25,55 to describe the heterogeneous dynamics of this system. Whereas for R-BD the MSD and the diffusive behavior can be determined directly from the simulated trajectories even at non-equilibrium, accessing the dynamics through R-DDFT requires the calculation of the van-Hove distribution of displacements, G(r,t).56,57 This function, defined as the probability density of finding a particle at time t at location r from the origin given that there was a particle at the origin at time t = 0, characterizes dynamical phenomena on a nanoscopic scale. It is especially important in the study of dynamics involved in liquid-crystal, glass-like and/or sol–gel transitions.24,25,58
The paper is organized as follows. First, we describe the theoretical frameworks used for accessing the van Hove function and the MSDs (R-DDFT, CTRW, and R-BD). In the second part, we discuss the effects that active switching has on the self and distinct parts of the van Hove functions and on the time evolution of the self-intermediate incoherent scattering functions. Finally, the MSDs obtained with R-DDFT are compared with R-BD and CTRW predictions, reporting good agreement between all three approaches for all switching activities investigated.
2 Theory
2.1 Reactive dynamical density functional theory for active switching colloids
We consider an active system in which each individual particle can instantaneously switch between two possible states of different size: big (b) or a small (s). Particles in state b spontaneously convert into state s at some pre-defined rate kbs (units of time−1). Similarly, particles in state s switch into particles of state b at rate ksb. At certain time, the active system resembles a binary mixture of big and small particles. The interaction between a pair of Gaussian particles is given by59| βuij = εije−r2/σij2 with i, j = s, b, | (1) |
| System | ε bb | ε ss | ε bs | σ b/σs | σ bs/σs | ρ T σ s 3 | x s | D b/Ds |
|---|---|---|---|---|---|---|---|---|
| S1 | 2.0 | 2.0 | 2.0 | 2.0 | 1.5 | 0.239 | 0.8 | 0.5 |
| S2 | 2.0 | 2.0 | 2.0 | 2.0 | 1.5 | 0.239 | 0.2 | 0.01 |
If the system is immersed inside an external field, the density profiles become inhomogeneous. We denote uexti(r) (i = b, s) as the external potentials acting on the big and small colloids at position r (we assume a general case in which the external potential is different for each particle state). These potentials arise from applied external forces (such as electrostatic or gravitational fields) or simply represent the effect of confining walls or a single fixed particle. We denote ρb(r,t) and ρs(r,t) as the number density of colloids in the big and small state at position r at time t, respectively.
The time evolution of a non-equilibrium system of active switching Brownian particles can be predicted by the so-called Reactive Dynamical Density Functional Theory (R-DDFT). Within this theoretical framework, the time evolution of ρi(r,t) (i = b, s) obey the following set of differential equations47–50,53,66
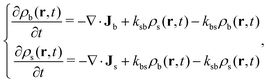 | (2) |
The first term on the right side, −∇·Ji, provides the change of particle concentrations due to diffusion, where Ji are the time and position-dependent diffusive fluxes caused by gradient in particle concentrations and chemical potential. They are given by
| Ji = −Di[∇ρi(r,t) + ρi(r,t)β∇(uexti(r) +μexi(r,t))] i = b, s, | (3) |
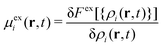 . Fex[{ρi(r,t)}] is the equilibrium excess free energy functional with the equilibrium density profiles replaced by the non-equilibrium ones ρi(r,t). The equilibrium and non-equilibrium properties of soft Gaussian particles described by eqn (1) are well represented by the mean-field excess free energy functional for colloidal mixtures of two states,
. Fex[{ρi(r,t)}] is the equilibrium excess free energy functional with the equilibrium density profiles replaced by the non-equilibrium ones ρi(r,t). The equilibrium and non-equilibrium properties of soft Gaussian particles described by eqn (1) are well represented by the mean-field excess free energy functional for colloidal mixtures of two states,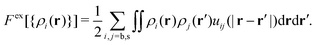 | (4) |
Please note that this mean-field approximation is equivalent to the so-called random phase approximation (RPA) for the direct correlation functions, given by cij(|r − r′|) = −δ2Fex/δρi(r)δρj(r′) = −βuij(|r − r′|).57 This approximation becomes remarkably accurate at high particle densities.61
The other two terms on the right hand of eqn (2) account for the production and disappearance of each particle state due to active switching. This process occurs locally, so the conversion rate of colloids in the big state into the small state at some specific location r only depends on the local concentrations of both species at position r. The switching between one to the other state is assumed to occur instantaneously, or at least within a time scale much shorter than the typical diffusion time of the particles. In addition, we do not impose any compressibility constraint because our study is restricted to very soft particles that can fully overlap.
In the region far away from the external perturbation (bulk), the density profiles tend to be homogeneous. We define the composition parameters of the mixture as
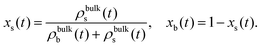 | (5) |
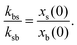 | (6) |
The switching activity, a, is defined as the ratio between the typical characteristic big-to-small conversion time, τswitch = kbs−1, and the Brownian diffusion time for small particles, τB = σs2/Ds. Therefore,
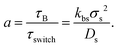 | (7) |
In the absence of switching activity (a = 0), the R-DDFT equations reduce to the classical DDFT equations for non-active binary mixture of Brownian colloids, i.e. ∂ρi(r,t)/∂t = −∇·Ji (i = b, s).67–69 For a ≪ 1, the b ⇌ s conversion rate is very slow, so the time evolution of the density profiles is dominated by the diffusion. In this case, switching events happening at some specific location are scarce, and the corresponding change in particle concentrations is rapidly compensated by the diffusive fluxes that balance the effect of the activity. In the opposite limit, a ≫ 1, the switching rate is so large that the diffusion is not fast enough to compensate its effects, so the exchange activity dominates. In this limit, particles in states b and s cannot be distinguished because they do not have enough time to diffuse and reorganize according to the applied external potentials. Consequently, both density profiles converge to each other, and the nonequilibrium system behaves as an effective one-component system that can be described by a single effective pair potential in equilibrium.49,50
If the applied external potentials do not depend on time, the R-DDFT equations lead in the limit t → ∞ to steady-state density profiles, 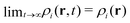 . For a = 0, this final steady state corresponds to the equilibrium, which means that the resulting density profiles are the ones of an equilibrium binary mixture. However, it is important to emphasize that this is not the case for a > 0. For active systems, the final steady-state density profiles are not the equilibrium ones, even though they are time-independent. It may be shown that thermodynamic properties depend on the diffusion coefficients of the particles, reflecting the fact that the system is not in equilibrium.49
. For a = 0, this final steady state corresponds to the equilibrium, which means that the resulting density profiles are the ones of an equilibrium binary mixture. However, it is important to emphasize that this is not the case for a > 0. For active systems, the final steady-state density profiles are not the equilibrium ones, even though they are time-independent. It may be shown that thermodynamic properties depend on the diffusion coefficients of the particles, reflecting the fact that the system is not in equilibrium.49
The microstructure of the system in bulk suspension is also affected by the switching activity. The non-equilibrium steady-state partial radial distribution functions gij(r) of the active system can be deduced making use of the Percus test particle route and extending the above described 2-states R-DDFT procedure to a 4-states R-DDFT.49,50
In the next subsections we describe how the R-DDFT method can be generalized to access the dynamics of active suspensions of switching Gaussian colloids. For this purpose, we start describing the simpler non-active one-component system and then extend the procedure to incorporate the active switching.
2.2 Dynamics of a non-active one-component system of Gaussian colloids
Here, we consider a homogeneous one-component system formed by N particles inside a volume V at temperature T. The bulk number density is ρbulk = N/V. Particles interact via a pairwise interaction potential u(r). The van Hove distribution of displacements for a one-component uniform fluid is defined as56,57,70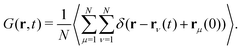 | (8) |
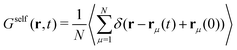 | (9) |
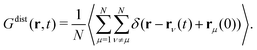 | (10) |
For t = 0, we find that the self-part is
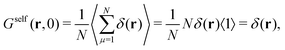 | (11) |
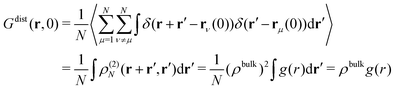 | (12) |
The standard Density Functional Theory (DFT) together with the Percus' test particle route can be used to access g(r):57,71 a single test particle is fixed at the origin r = 0, acting as an external potential for the rest of particles, so uext(r) = u(r). Solving the DFT equations for the colloidal fluid exposed to the influence of this external potential leads to a inhomogeneous one-body density distribution of colloids around the central one, ρ(r). The corresponding radial distribution function is given by g(r) = ρ(r)/ρbulk.
The van Hove function in bulk for an homogeneous system can be obtained using the DDFT framework, as proposed by Archer et al.54 According to their scheme, the system of N particles is separated into two groups that will be called self (group 1) and distinct (group 2). The self group consist of only one single test particle located at r = 0 at time t = 0. On the other hand, the distinct group is formed by the remaining N − 1 particles around the test particle. With this strategy, our originally one-component system becomes a binary two-component mixture, in which the pair interactions are given by
| u12(r) = u22(r) = u(r), u11(r) = 0. | (13) |
The time evolution of both distributions, ρ1(r,t) and ρ2(r,t), can be obtained solving the classical DDFT differential equations to this mixture
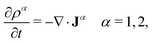 | (14) |
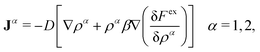 | (15) |
| Gself(r,t) = ρ1(r,t), Gdist(r,t) = ρ2(r,t). | (16) |
As time increases, Gself(r,t) broadens into a Gaussian-shaped curve. Conversely, Gdist(r,t) becomes flatter as time evolves. In the limit t → ∞ or r → ∞, the self part tends to zero whereas the distinct part converges to the uniform distribution,
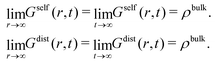 | (17) |
The MSD of the particles is obtained as an integral of Gself(r,t),
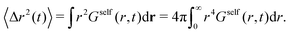 | (18) |
2.3 Dynamics of an active system of switching Gaussian colloids
For active systems each individual particle is able to switch from two states, b and s. The method shown before can be entirely adapted to this new situation. We assume that at time t = 0 the system has already reached the steady state. The steady-state radial distribution functions of the active system can be obtained using the 4-states R-DDFT with the Test Particle Route.49,50,72 This leads to the (non-equilibrium) steady-state radial distribution functions, gij(r) (i = b, s), which provide the probability density of finding a particle in state j at a distance r from another particle in the state i. Therefore, ρbulkjgij(r) represents the density of particles in state j at a distance r from a central particle in state i.Using a similar procedure than the one followed for the one-component system, we split the system into the self and distinct part (denoted again by superindex 1 and 2). The self-part represents a single test particle located at r = 0 at time t = 0, whereas the distinct one corresponds to the rest of particles. Pair interactions between self and distinct particles in states b and s are
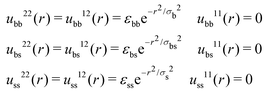 | (19) |
If the test particle located at r = 0 at time t = 0 is in the b-state, then
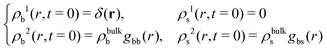 | (20) |
Conversely, if the test central particle is in the s-state, the initial conditions are
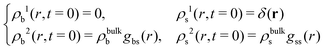 | (21) |
As t increases, the four density profiles evolve in time. Their time evolution is governed by two processes: the diffusion due to gradients of the chemical potential, and the switching events that cause the appearance/disappearance of particle states. The four coupled R-DDFT equations that control this time evolution can be obtained extending eqn (2)
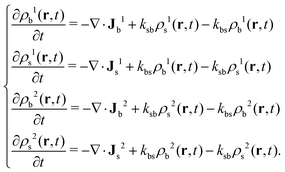 | (22) |
The diffusive fluxes are given by
| Jαi = −Di[∇ραi + ραiβ∇μex,αi] α = 1,2, i = b, s, | (23) |
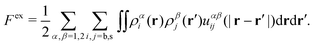 | (24) |
Performing the functional differentiation leads to the following explicit expression for the excess chemical potential
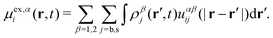 | (25) |
The R-DDFT equations are solved with the initial conditions given by eqn (20) (if the test central particle in the b-state) or eqn (21) (if the test central particle in the s-state). In addition, we need to impose the boundary conditions in r = 0 and r → ∞,
To study the dynamics of this active switching system (eqn (8)), we decompose the self-part of the van Hove function as:
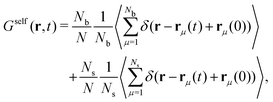 | (26) |
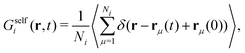 | (27) |
| Gself(r,t) = xbGselfb(r,t) + xsGselfs(r,t). | (28) |
We can identify the self-part of the van Hove with the particle densities of component 1, i.e.
| Gselfb(r,t) = ρb1(r,t) + ρs1(r,t), | (29) |
The corresponding MSD of the particles in the b-state is
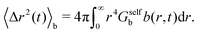 | (30) |
The same procedure can be followed starting from a test particle in the s-state located at the origin to calculate Gselfs(r,t) and 〈Δr2(t)〉s.
The average MSD of the system is
| 〈Δr2(t)〉ave = xb〈Δr2(t)〉b + xs〈Δr2(t)〉s | (31) |
Finally, the self-intermediate scattering function, routinely measured in light scattering experiments to characterize dynamics of colloidal systems, is
| Fself(q,t) = xsFselfs(q,t) + xbFselfb(q,t). | (32) |
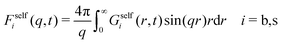 | (33) |
3 An exactly solvable continuous time random walk model for active switching colloids
In this section we describe a theoretical approach based on a Continuous Time Random Walk model (CTRW) to gain new insights on the complex diffusion of active switching colloids. In this approach the system is viewed as a heterogeneous assembly of big (b) and small (s) colloids which can stochastically switch from one state to another at constant rates. We are interested in particular in the distribution of particle displacements, i.e. the self-part of the van Hove distribution function Gself(r,t) defined in eqn (9), which measures the probability that a given colloid has traveled a distance r in a time t. To account for the interplay between the colloids bare diffusion and their switching activity, we first define gi(r,t) as the probability density function for a colloid to make a displacement r in a time t, provided it is in state i = s, b during the whole time interval [0,t]. In addition, let pi(t) be the probability that a colloid in state i switches for the first time to the complementary state j at time t, and define the cumulative distribution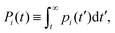 | (34) |
Now, if Gselfi(r,t) is the probability that a colloid initially in state i travels a distance r in a time t, we can write the following recurrence in the steady state
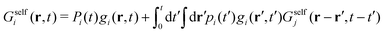 | (35) |
| Gselfi(r,t) = Pi(t)gi(r,t) + [Δi ° Gselfj](r,t), | (36) |
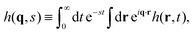 | (37) |
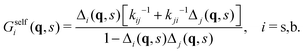 | (38) |
The colloids Brownian dynamics suggests to use diffusive expressions for the bare propagators,
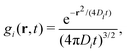 | (39) |
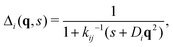 | (40) |
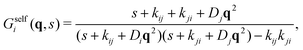 | (41) |
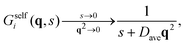 | (42) |
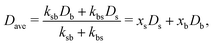 | (43) |
Inverting now the Laplace transform in eqn (41), we obtain the partial self-intermediate scattering function of particles initially in the i-state
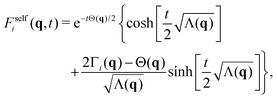 | (44) |
The full scattering function is obtained from eqn (32). From this expression we can further compute analytically the average MSD, 〈Δr2(t)〉ave, as
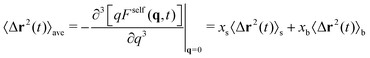 | (45) |
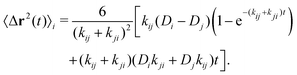 | (46) |
It is important to emphasize here that the CTRW approach neglects particle–particle interactions, so it is expected to provide good predictions for the single particle dynamics only for diluted or weakly interacting colloidal systems. For strongly interacting systems, the CTRW theory could still be applied assuming that the values of Db and Ds are given by the effective long-time concentration-dependent diffusion coefficients.
4 Reactive brownian dynamics (R-BD) computer simulations
In addition to the R-DDFT calculation and the CTRW theory described above, we performed reactive Brownian Dynamics simulations (R-BD) for all systems as in our previous work.50 R-BD allows direct access to the dynamics and diffusion coefficients for validating the results of our R-DDFT while bypassing the extensive calculations of the self and distinct part of the van Hove function. The equation of motion for a particle μ in the particle-resolved simulations using the overdamped Langevin equation is written as| ξμṙμ = −∇U(rμ) + R(t), | (47) |
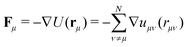 . All particle positions are updated after each time interval Δt using the Euler–Maruyama propagation scheme,74 that is
. All particle positions are updated after each time interval Δt using the Euler–Maruyama propagation scheme,74 that is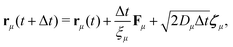 | (48) |
| pbs = 1 − e−kbsΔt, psb = 1 − e−ksbΔt. | (49) |
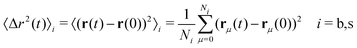 | (50) |
5 Results and discussion
We apply our generalized R-DDFT method to deduce the particle dynamics of two representative systems, S1 and S2, specified in Table 1. In particular, the interaction strengths are in all cases given by εij = 2 (in kBT units). This value represents quite well the repulsion strength between two overlapping linear polymers and soft colloidal hydrogels immersed in a good solvent.61 The resulting soft interaction not only allows partial overlap of particles, but also the full overlap of their centres of mass, especially for large particle concentration. Therefore, our system behaves as a weakly interacting fluid.The interaction parameters and total particle bulk concentration of systems S1 and S2 are exactly the same, but the composition (xs) and the diffusion coefficient of the particles in the b-state (Db) are different. In particular, for system S1 the particle diffusivities follow the Stokes–Einstein relation, Db = (σs/σb)Ds = 0.5Ds, whereas for system S2 both particles have very dissimilar diffusivities, namely Db = 0.01Ds. In addition, a composition of xs = 0.2 has been chosen for system S2 in order to emphasize the distinction between the different dynamic regimes of the mean squared displacement obtained for different switching activities. In both systems, the kinetic rate constants fulfill the condition given by eqn (6), i.e. kbs/ksb = xs/xb, in order to preserve the relative bulk composition of colloids in b and s states.
5.1 Results for system S1
The calculation is initiated assuming that the distinct parts of the van Hove function at time t = 0, ρi2(t,t = 0), are given by the corresponding steady-states radial distribution functions of the active colloidal system (eqn (20) if the test central particle is in the b-state, or 21 if it is in the s-state). For this purpose, we first need to solve the 4-state R-DDFT equations to calculate the steady-state radial distribution functions of the active system, gij(r), obtained in the limit t → ∞.49,50 We emphasize again that the steady-state distributions only agree with the equilibrium distributions geqij(r) for a = 0. Otherwise (for a > 0) the steady state corresponds to a time-independent non-equilibrium configuration.For the self-part, a very short initial time t = t0 = 5 × 10−5τB is used to approximate the singular δ-function of ρi1(r,t = 0) by a very sharp Gaussian distribution
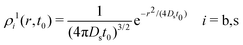 | (51) |
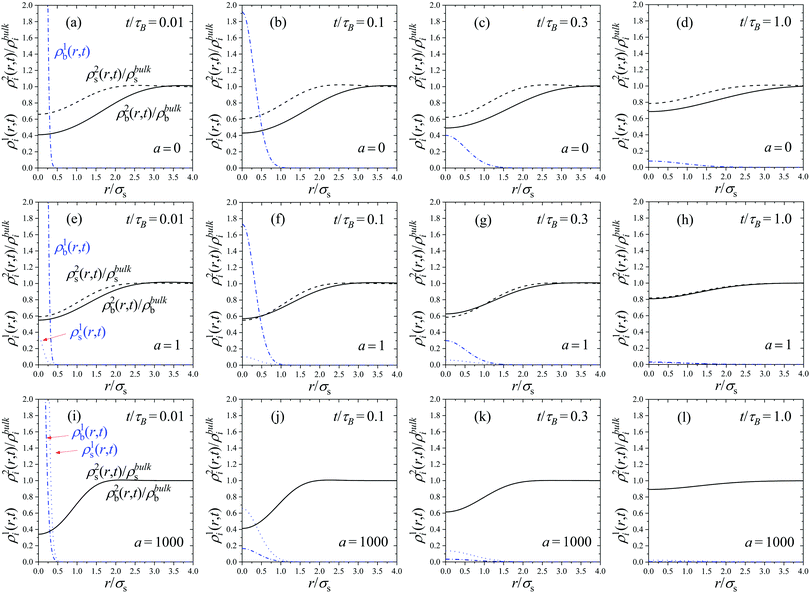
Fig. 1 shows the time dependent density profiles ραi(r,t) for system S1 of Table 1 obtained assuming that at time t = 0 there was a particle in the b-state located in the origin. The twelve plots represent the results for three different activity rates (a = 0, 1 and 1000) and four times (t/τB = 0.01, 0.1, 0.3 and 1). All times are normalized by the Brownian time, τB = σs2/Ds.
We first examine the plots for a = 0, which correspond to a non-active equilibrium mixture of non-switching big and small Gaussian colloids (see Fig. 1(a)–(d)). Since switching is forbidden, the central big test particle remains in the b-state all the time during the diffusion process. The time evolution of the self and distinct part are very similar to the ones observed in one-component systems.54 The initial delta peak of the self part, ρb1(r,t), broadens as time increases. Conversely, the distinct parts providing the density profiles of surrounding particles in the b and s states tend to be more uniform. Indeed, the initial depletion region of ρi2(r,t) close to the origin is progressively reduced, and becomes flatter as time evolve. In the limit t → ∞ or r → ∞, the self part tends to zero whereas the distinct part converges to the uniform distribution.
This behavior changes if we consider active switching systems (a > 0). In this case, particles not only diffuse, but they are also able to switch between states b and s. For instance, if the system starts with a test big particle at t = 0 (so ρb1(r,0) = δ(r) and ρs1(r,0) = 0), it means that for larger times some fraction of this initial distribution broadens by diffusion, but other part switches to create particles in the s-state, leading to time-dependent density distributions for particles in both states, ρb1(r,t) and ρs1(r,t). This effect, which constitutes a new exclusive feature of active switching colloids, can be clearly observed in Fig. 1. Indeed, for a > 0, the initial δ-distribution of ρb1(r,t) not only spreads, but also generates a new distribution of small colloids, ρs1(r,t), indicating that the central particle has switched from the b-state to the s-state. As shown by Fig. 1(e)–(h), this effect is small for a = 1 at times below t/τB = 1, but it becomes more important for longer times. Conversely, For a = 1000 (Fig. 1(i)–(l)), the switching rate is so fast that it gives rise a large peak of particles in the s-state at very short times. We have shown in our earlier works that, in the limit of a fast switching rate, the system behaves as an effective one-component system in which all particles interact with the same effective pair potential.49,50 As a consequence, both density profiles rapidly converge to a common shape, with ρs1(r,t) = (xs/xb)ρb1(r,t). The same happens for the distinct part of the van Hove function, ρs2(r,t) = (xs/xb)ρb2(r,t).
Increasing the particle concentration, ρT, entails a gradual reduction of the correlation hole of the radial distribution functions and an increase of the degree of particle overlap, typical in systems composed by soft Gaussian colloids. In other words, the system approaches the ideal gas-like behavior in the limit of large ρT. Consequently, the results for the dynamics are not affected either by concentration effects in the limit of dense colloidal suspension.
5.2 Results for the dynamically more asymmetric system S2
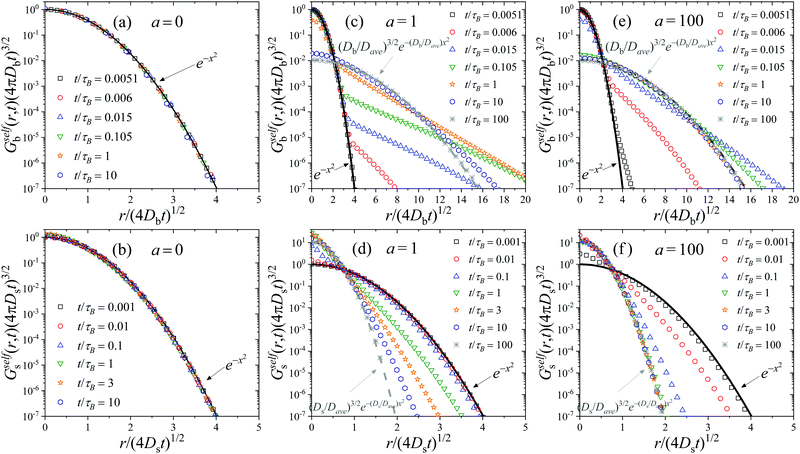
In order to really understand the role of the diffusion coefficients on the dynamic behavior of the active system, we have performed the same calculations, but using system S2 shown in Table 1. System S2 has similar features than system S1, but with a very important difference: the diffusion coefficient of colloids in the b-state is chosen to be very small compared to the one for particles in the s-state, Db = 0.01Ds, resembling the features of systems with highly heterogeneous dynamics.24 We calculate the self-part of the van Hove function Gselfb(r,t) (see eqn (29)), starting with a test particle in the b-state located at r = 0 at time t = 0. The same calculation is repeated choosing a test particle initially in the s-state to determine Gselfs(r,t).Fig. 2(a) shows Gselfb(r,t) obtained for a binary colloidal system S2 in equilibrium (a = 0). In particular, we plot the scaled functions (4πDbt)3/2Gselfb(r,t) against the scaled distance, x = r/(4Dbt). As observed, all the curves for different times collapse in a common form given by e−x2, which indicates that the diffusion process of the test big particle follows a Gaussian distribution with a diffusion coefficient given by Db. The same conclusion is found if we consider a test particle in the s-state and plot the scaled (4πDst)3/2Gselfs(r,t) against x = r/(4Dst), as shown in Fig. 2(b). Therefore, we conclude that the time-dependent distribution of displacement of the particles in a non-active (a = 0) equilibrium fluid mixture of interacting Gaussian colloids obeys the well-known Gaussian distribution
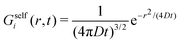 | (52) |
This scaling behavior breaks down for active switching system. Fig. 2(c) and (d) illustrate exactly the same scaled functions for system S2 at several times, but turning on the non-equilibrium switching activity rate at a = 1. Fig. 2(c) corresponds to the self-part of the van Hove function for a test particle in the b-state at t = 0. For very short times, t ≪ τB/a, the big test particle still preserves its identity, so it follows the Gaussian distribution of displacements given by eqn (52), with a diffusion coefficient D = Db. However, for intermediate times, t ∼ τB/a, Gselfb(r,t) is not Gaussian any more. In fact, it follows different distributions for short and large displacements, showing a non-Gaussian tail with a well-defined shoulder that represents the crossover from one behavior to the other. In particular, large displacements have a much larger probability to occur compared to the Gaussian prediction. This is due to the fact that the original test particle in the b has already switched to a faster s-state. Clearly, Gselfb(r,t) exhibits a bimodal character suggesting the existence of slow particles and faster diffusing particles. This dynamic behavior resembles the one observed in heterogeneous diffusion of reversible attractive colloidal gels, in which the system is formed by a coexistence of slow percolating cluster of connected droplets and fast, more freely diffusing droplets, with a dynamic exchange between the two families set by polymer moves.24 In our case, this lack of Gaussianity is a clear signature of the non-equilibrium activity introduced by the particle switching. Note that similar heterogeneous dynamics has been also observed in a wide variety of systems with Brownian yet non-Gaussian diffusion.75–77
For very long times, (t ≫ τB/a), the initial big test particle has experienced many switching events between b and s, and vice versa. In this limit, Gselfb(r,t) recovers again the Gaussian behavior (cf.eqn (52)), but with an average diffusion coefficient given by the mean of the individual diffusion coefficients weighted by the kinetic rate constants. This is exactly the prediction derived within the CTRW theory described in Section 3 for the self-part of the van Hove distribution in the long-time large-lengthscale limit (see eqn (43)).
A similar behavior is found for Gselfb(r,t) (see Fig. 2(d)). For short times (t ≪ τB/a), the small test particle located at r = 0 has not yet experienced any switching event, so Gselfs(r,t) follows a Gaussian distribution with D = Ds. At intermediate times, the Gaussian behavior is lost. In this case, large displacements have smaller probability to occur compared to the Gaussian dependence, indicating that the test particle is now diffusing slower due to the switching from s to b-state. For large enough elapsed times, the occurrence of multiple switching events between both particle states finally leads to a new Gaussian distribution with D = Dave.
The same transient behavior is found increasing the activity rate to a = 100. The only difference is that, in this case, switching events befall 100 times faster, so the transition from the short-time Gaussian regime to the long-time one arises at much shorter times. This effect can be clearly observed in Fig. 2(e) and (f), where Gselfi(r,t) becomes non-Gaussian for t ≪τB.
5.3 Intermediate scattering function
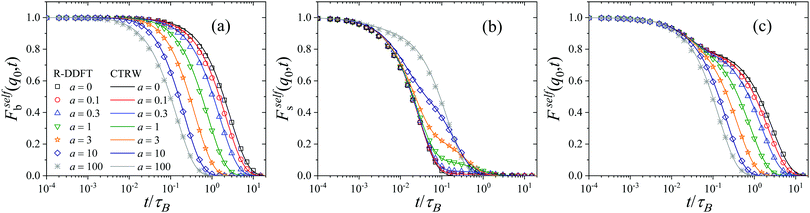
An observable of direct experimental relevance is the self-intermediate scattering function Fself(q,t), as well as its partial components Fselfi(q,t) (i = s, b) defined in eqn (33). These functions characterize the system dynamical relaxation at the single-particle level for different wave vectors q, or equivalently at lengthscales inversely proportional to |q|. Fig. 3 shows Fself(q,t) as well as Fselfb(q,t) and Fselfs(q,t) for qσs = 6 and system S2, as obtained within the R-DDFT approach together with the CTRW prediction (eqn (32), (33) and (44)). Focusing first on the small (s) colloids, note that they exhibit a fast initial relaxation, as captured by the quick initial decay of Fselfs(q,t), see Fig. 3(b), on a time scale related to their relatively large diffusion constant Ds. However, the active state switching eventually kicks in, triggering a slower relaxation for initially small particles which have switched to the big (b) state, with much smaller diffusion constant Db = 10−2Ds. This gives rise to a plateau in Fselfs(q,t) at intermediate timescales. Interestingly, the height of the plateau decreases with decreasing activity a. Indeed, for small activity the time between switching events s → b is large, so most small colloids have time to diffusively relax in the medium before a switching event slows down their dynamics, leading to small plateau height. Conversely, for large activities a ≫ 1 very few small colloids have time to relax before switching to the big (slow) state, and hence the amplitude of the plateau is large in this case.On the other hand, for big (b) colloids Fselfb(q,t) exhibits a simpler relaxation pattern, see Fig. 3(a). In this case the initial relaxation of big colloids is already slow, as expected from their low bare diffusivity, and this relaxation can be only accelerated by switching events to the small (s) state. In this way Fselfb(q,t) exhibits no secondary relaxation plateau, and the relaxation timescale for b-colloids decreases with increasing activity. The combined relaxation of small and big active colloids gives rise to a typical two-step relaxation pattern for the global incoherent scattering function Fself(q,t) = xbFselfb(q,t) + xsFselfs(q,t), see Fig. 3(c), with a plateau at intermediate timescales with a height proportional to xb = 1 − xs, the fraction of big (i.e. slow) colloids in the stationary suspension. The relaxation timescale to the plateau is controlled by the small colloids fast bare diffusivity, while the global relaxation timescale decreases with increasing activity, as expected. Interestingly, similar two-step relaxation patterns for Fself(q,t) have been widely observed for a broad family of soft materials with heterogeneous dynamics, as e.g. glasses, dense granular media, and gels.23–36
The lines in Fig. 3 correspond to the CTRW prediction given by eqn (44), and the agreement with R-DDFT results is excellent in all cases, capturing in full detail the complex relaxation dynamics of the active colloidal suspension. This striking agreement (also observed below for MSDs and other dynamical quantities) strongly suggests that the soft colloidal interactions seem to play no significant role in the diffusive and local relaxation properties of the active suspension, at least for the weak particle interaction explored in this paper. We expect interactions to become more important for larger values of εij. These interactions can be however taken into account within the CTRW model here introduced via renormalized diffusive propagators.
5.4 Mean squared displacements (MSDs) and R-BD trajectories
The relaxation dynamics and diffusive behavior at short and long timescales can be further understood by analyzing the MSD of the colloids. Fig. 4 shows the average MSD of system S2, 〈Δr2(t)〉ave (calculated from eqn (31)) for a = 0, 1 and 1000 obtained from the R-DDFT predictions and from R-BD simulations. Interestingly, theoretical and simulation data of the global MSD for these three activity rates collapse after a short transient in the same common linear dependence, given by 〈Δr2(t)〉ave = 6Davet, with Dave = xbDb + xsDs being the average diffusion coefficient of the active system. In other words, from a global point of view, the system dynamics is Brownian and can be apparently modeled by a single average diffusion constant that is always the same regardless the activity rate, a. This is however in stark contrast with the non-Gaussian character of the diffusive dynamics captured by the self-part of the global and partial van Hove distributions of displacements (see Fig. 2 and the associated discussion). Therefore, the active colloidal mixture studied here exhibits the hallmarks of the Brownian yet non-Gaussian diffusion phenomenon already described in other heterogeneous materials.75–77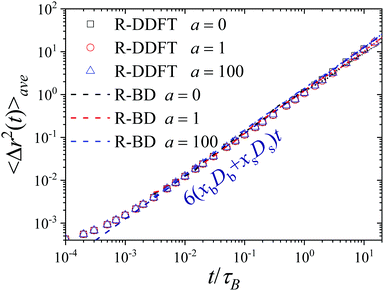 | ||
| Fig. 4 Average MSD of the active switching system as a function of time for system S2 for a = 0, 1 and 100. Symbols are R-DDFT predictions, whereas dashed lines denote R-BD results. | ||
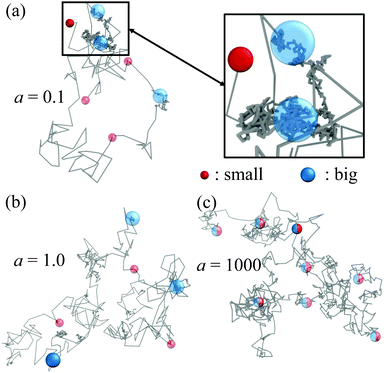
To better understand this phenomenon, we explore some representative single-particle trajectories. Fig. 5 contains a set of selected trajectories for a single, actively switching particle, at different switching activities a. The lower a is, the longer the particle stays in a given state b or s, and thus the larger the explored regions with the corresponding diffusion coefficients Ds or Db. Since Db ≪ Ds, big particles diffusively explore relatively small volumes (see Fig. 5(a)), leading to local quasi-arrested dynamics, while small particles can travel further away exploring larger volumes for the same time interval.
For small activities, or equivalently large switching time intervals, the dynamics is clearly intermittent and heterogeneous, characterized by large diffusion intervals punctuated with quasi-arrested periods when colloids switch to the big state, resulting in general in a highly heterogeneous distribution of particle displacements. When the activity increases, see Fig. 5(b) for a = 1.0, the dynamical heterogeneity of the trajectory is less apparent as state switching events are more frequent and regions of fast and slow diffusion cannot be clearly delimited, leading to a more homogeneous distribution of displacement vectors. At much larger switching activities (a = 1000, Fig. 5(c)), the switching intervals become sufficiently small to show a behavior close to an effective one component (EOC) system,50 where the macroscopic characterization of our systems revealed almost indistinguishable properties for big and small particles. However, here we still see a non-uniform distribution of displacements showing that the states remain distinguishable on a microscopic level for a single particle.
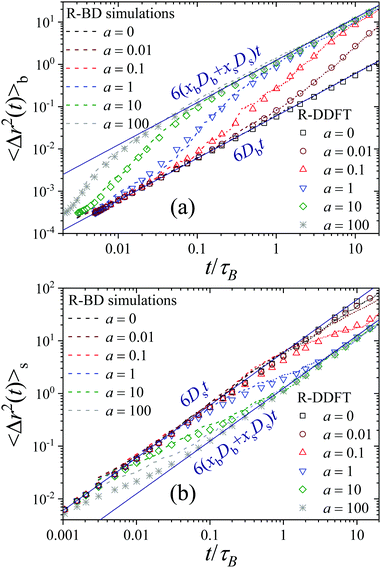
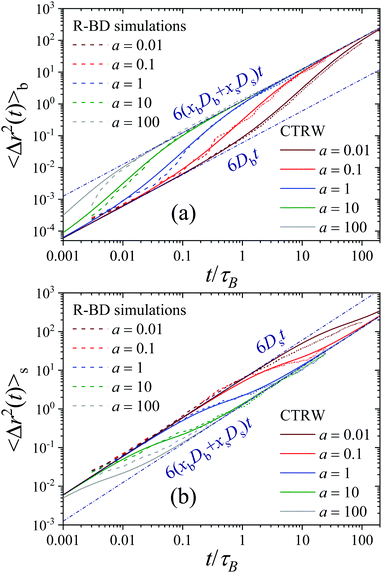
In order to quantify the heterogeneous dynamics shown by the active switching particles, we now study the MSD of colloids in a particular internal state (b or s) for different activities from a = 0 to a = 100. Fig. 6(a) shows 〈Δr2(t)〉b for a test particle initially in the b-state (system S2), obtained through eqn (30). Empty symbols correspond to R-DDFT predictions while dashed lines are results from R-BD simulations. For a = 0, the big test particle remains in the b-state all the time, so the MSD corresponds to a standard diffusive motion of a Brownian colloid with diffusion coefficient Db, i.e., 〈Δr2(t)〉b = 6Dbt. However, the situation changes as soon as particle switching is activated. For a > 0, the big particle preserves its identity for times well below the switching timescale, t ≪ τB/a. Subsequently, for intermediate times t ∼ τB/a, switching events to the small (s) state significantly accelerate the dynamics of the (initially big) test particle, leading to a superdiffusive transient regime. Finally, for large enough times, t ≫ τB/a, after many switching events back and forth between the b and s states and viceversa, an effective diffusive regime is reached with an average diffusion constant Dave = xbDb + xsDs,
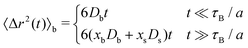 | (53) |
The R-DDFT theoretical predictions show an excellent agreement with R-BD simulation data (dashed lines in Fig. 6(a)), thus confirming that our adapted R-DDFT represents a trustful method to investigate the dynamical properties of non-equilibrium active switching systems. Furthermore, Fig. 7(a) shows a comparison of the MSD for an initially-big particle obtained in R-BD simulations for different activities, and the exact prediction obtained from the CTRW theory developed in Section 3 (see eqn (46)). As for the self-intermediate scattering functions of Fig. 3, the agreement between simulations and the phenomenological CTRW theory is also excellent. This includes both the short- and long-time asymptotic diffusive regimes with different diffusivities, but also the transient superdiffusive dynamics for initially-big particles which are accelerated by stochastic switching to the s-state.
Similar asymptotic behaviors are observed for the MSD of a test particle that was in the s-state at t = 0, see Fig. 6(b). In this case
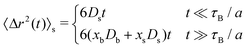 | (54) |
In this way, the overall (effective) Brownian behavior of the global MSD, see Fig. 4, results from the superposition of clearly non-Brownian dynamics of both small and big particles, which sub- and super-diffuse at intermediate times as a result of the switching activity. This anomalous diffusion properties at intermediate times are also reflected in the non-Gaussian behavior of the self-part of the van Hove displacement distribution functions (full and partial), as shown in Fig. 2.
6 Conclusions
We deduced an adapted reactive mean-field dynamical density functional theory (R-DDFT), a phenomenological continuous-time random walk (CTRW) theory, and performed Brownian dynamics (R-BD) computer simulations, to investigate the dynamical properties of an active fluid of switching Gaussian colloids in the steady-state regime. For this purpose, the R-DDFT method has been generalized using the method proposed by Archer et al.,54 in which the self-parts and the distinct-parts of the van Hove dynamic correlation function of an active system are identified with the one-body density distributions of a mixture that evolve in time according to the R-DDFT. We show that interaction switching activity not only has an important effect on the structural properties and phase behavior of the active system,49,50 but also induces a profound change of its dynamical properties, leading to a heterogeneous diffusion.The time-dependent distribution of displacements of particles initially in the b and s-state (i.e. the self-parts of the van Hove correlation functions Gselfb(r,t) and Gselfs(r,t), respectively) follow the well-known Gaussian distribution for t ≪ τB/a, with a diffusion coefficient given D = Db and D = Ds, respectively. For intermediate times, t ∼ τB/a, both distributions lose the Gaussian dependence, exhibiting a well-defined crossover that separates the behavior for short and large particle displacements. This phenomenon is entirely caused by the non-equilibrium switching activity, which induces the formation of a bimodal distribution of displacements (slow/big and fast/small particles, respectively). For long enough times, t ≫ τB/a, the large number of switching events finally leads again to a Gaussian distribution, but with an effective diffusion coefficient given by the the average of the individual ones, Dave = xbDb + xsDs. This heterogeneous diffusion is also observed in the self-intermediate scattering functions of the solution, of direct experimental relevance. In particular, a secondary relaxation plateau emerges whose height gives a measure of the fraction of colloids in the big (i.e. slow) state, and whose relaxation timescale is directly linked with the colloidal activity.
The transition involved in the dynamics of the individual particles is also manifested in the corresponding MSDs (〈Δr2(t)〉b and 〈Δr2(t)〉s for test particles in states b and s, respectively). Indeed, particles originally in the b-state (s-state) exhibit Brownian motion with a diffusion coefficient that shifts from D = Db (Ds) for short times to D = Dave for long times. For intermediate times, t ∼ τB/a, the MSD depicts an anomalous behavior (super-diffusive for particles in the b-state and sub-diffuse for particle in s-state) connecting both dynamic regimes. Theoretical predictions obtained with R-DDFT and CTRW for the MSD of the switching interaction particles show excellent quantitative agreement with those of our reactive Brownian dynamics computer simulations (R-BD).
We believe our model applies to biological systems such as switching bistable bacteria which use switching to control structural and dynamic heterogeneity and with that collective function37,38 or synthetic realizations in, e.g., active hydrogels.39–42
Our study on switching colloids inspires many future works, e.g., open questions concern the nature of the non-equilibrium thermodynamics (heat and entropy in these system), the violation of the fluctuation–dissipation theorem, and more first-principle approaches of our rather phenomenological model, e.g., based on active versions of the recently introduced responsive colloids (RCs) model78,79 involving continuous bimodal landscape for the particle size distribution.80 Such a treatment may lead to position and concentration dependent switching rates with nontrivial consequences on position-dependent structure and dynamics of the active dispersions. It would be also interesting to investigate the dynamic properties of switching colloids with larger interaction strengths, εij. In this regime, previous simulation studies performed in one-component fluids of Gaussian colloids report a non-monotonic density dependence of the long-time diffusion coefficient, which reaches a minimum value at some intermediate particle concentration.81,82 This reduction of the long-time diffusion coefficient induced by particle interactions should also be present in our two-state mixture of active soft colloids. Finally, quantification of collective phenomena such as interdiffusion is also an interesting topic for future studies.83 This could in principle be obtained from examination of the time evolution of the distinct-part of the van Hove function (see Fig. 1). Close to equilibrium (a = 0) interdiffusion is expected to play a big role in mixing, while for increasing activity its role diminishes as the particles switch before diffusing, i.e. switching accelerates the interdiffusion process.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. B. and J. D. acknowledge support by the state of Baden-Württemberg through bwHPCand the German Research Foundation (DFG) through grant no INST 39/963-1 FUGG (bw – ForCluster NEMO) and by the Deutsche Forschungsgemeinschaft (DFG) via grant WO 2410/2-1 within the framework of the Research Unit FOR 5099 “Reducing complexity of nonequilibrium” (project No. 431945604). P. I. H. and A. M.-J acknowledge the financial support provided by the Spanish Ministry and Agencia Estatal de Investigación (AEI) through Grants PID2020-113681GB-I00 and FIS2017-84256-P, the Junta de Andalucía and European Regional Development Fund – Consejería de Conocimiento, Investigación y Universidad, Junta de Andalucía (Projects PY20-00241, A-FQM-90-UGR20, A-FQM-175-UGR18 and SOMM17/6105/UGR), and the program Visiting Scholars of the University of Granada (Project PPVS2018-08). Finally, we thank Nils Göth for inspiring discussions and useful comments, and the computational resources and assistance provided by PROTEUS, the supercomputing center of Institute Carlos I for Theoretical and Computational Physics at the University of Granada, Spain.References
- A. Bajpai, S. K. Shukla, S. Bhanu and S. Kankane, Prog. Polym. Sci., 2008, 33, 1088–1118 CrossRef CAS.
- M. A. C. Stuart, W. T. S. Huck, J. Genzer, M. Müller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk, M. Urban, F. Winnik, S. Zauscher, I. Luzinov and S. Minko, Nat. Mater., 2010, 9, 101 CrossRef PubMed.
- P. Hervés, M. Pérez-Lorenzo, L. M. Liz-Marzán, J. Dzubiella, Y. Lu and M. Ballauff, Chem. Soc. Rev., 2012, 41, 5577–5587 RSC.
- S. Wu, J. Dzubiella, J. Kaiser, M. Drechsler, X. Guo, M. Ballauff and Y. Lu, Angew. Chem., Int. Ed., 2012, 51, 2229–2233 CrossRef CAS PubMed.
- P. Theato, B. S. Sumerlin, R. K. O'Reilly and T. H. Epps, III, Chem. Soc. Rev., 2013, 42, 7055–7056 RSC.
- R. Schroeder, A. A. Rudov, L. A. Lyon, W. Richtering, A. Pich and I. I. Potemkin, Macromolecules, 2015, 48, 5914–5927 CrossRef CAS.
- J. Stegen and P. van der Schoot, Soft Matter, 2015, 11, 2036–2045 RSC.
- J. Stegen and P. van der Schoot, J. Chem. Phys., 2015, 142, 244901 CrossRef CAS PubMed.
- A. Walther, Adv. Mater., 2019, n/a, 1905111 Search PubMed.
- A. Einstein, Ann. Phys., 1905, 322, 549–560 CrossRef.
- E. Frey and K. Kroy, Ann. Phys., 2005, 14, 20–50 CrossRef CAS.
- R. Metzler and J. Klafter, Phys. Rep., 2000, 339, 1–77 CrossRef CAS.
- B. Wang, S. M. Anthony, S. C. Bae and S. Granick, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15160–15164 CrossRef CAS PubMed.
- B. Wang, J. Kuo, S. C. Bae and S. Granick, Nat. Mater., 2012, 11, 481–485 CrossRef CAS PubMed.
- F. Höfling and T. Franosch, Rep. Prog. Phys., 2013, 76, 046602 CrossRef PubMed.
- G. Kwon, B. J. Sung and A. Yethiraj, J. Phys. Chem. B, 2014, 118, 8128–8134 CrossRef CAS PubMed.
- M. V. Chubynsky and G. W. Slater, Phys. Rev. Lett., 2014, 113, 098302 CrossRef PubMed.
- S. K. Ghosh, A. G. Cherstvy and R. Metzler, Phys. Chem. Chem. Phys., 2015, 17, 1847–1858 RSC.
- R. Jain and K. L. Sebastian, J. Phys. Chem. B, 2016, 120, 3988–3992 CrossRef CAS PubMed.
- R. Metzler, Biophys. J., 2017, 112, 413–415 CrossRef CAS PubMed.
- N. Gnan and E. Zaccarelli, Nat. Phys., 2019, 15, 683–688 Search PubMed.
- E. Yamamoto, T. Akimoto, A. Mitsutake and R. Metzler, Phys. Rev. Lett., 2021, 126, 128101 CrossRef CAS PubMed.
- R. Richert, J. Phys.: Condens. Matter, 2002, 14, R703–R738 CrossRef CAS.
- P. I. Hurtado, L. Berthier and W. Kob, Phys. Rev. Lett., 2007, 98, 135503 CrossRef PubMed.
- P. Chaudhuri, L. Berthier and W. Kob, Phys. Rev. Lett., 2007, 99, 060604 CrossRef PubMed.
- In Dynamical Heterogeneities in Glasses, Colloids and Granular Materials, ed. L. Berthier, G. Biroli, J. P. Bouchaud, L. Cipelletti and W. van Saarloos, Oxford University Press, 2011 Search PubMed.
- D. Levis and L. Berthier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062301 CrossRef PubMed.
- W. Wang, A. G. Cherstvy, X. Liu and R. Metzler, Phys. Rev. E, 2020, 102, 012146 CrossRef CAS PubMed.
- E. D. Gado, A. Fierro, L. de Arcangelis and A. Coniglio, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 051103 CrossRef.
- E. Zaccarelli, S. V. Buldyrev, E. L. Nave, A. J. Moreno, I. Saika-Voivod, F. Sciortino and P. Tartaglia, Phys. Rev. Lett., 2005, 94, 218301 CrossRef CAS PubMed.
- E. D. Gado and W. Kob, Phys. Rev. Lett., 2007, 98, 028303 CrossRef PubMed.
- E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101 CrossRef.
- E. Zaccarelli and W. C. K. Poon, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15203–15208 CrossRef CAS PubMed.
- P. Chaudhuri, L. Berthier, P. I. Hurtado and W. Kob, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 040502 CrossRef PubMed.
- N. Khalil, A. de Candia, A. Fierro, M. P. Ciamarra and A. Coniglio, Soft Matter, 2014, 10, 4800–4805 RSC.
- P. Chaudhuri, P. I. Hurtado, L. Berthier and W. Kob, J. Chem. Phys., 2015, 142, 174503 CrossRef PubMed.
- N. Q. Balaban, J. Merrin, R. Chait, L. Kowalik and S. Leibler, Science, 2004, 305, 1622–1625 CrossRef CAS PubMed.
- D. Dubnau and R. Losick, Mol. Microbiol., 2006, 61, 564–572 CrossRef CAS PubMed.
- R. Yoshida, T. Takahashi, T. Yamaguchi and H. Ichijo, J. Am. Chem. Soc., 1996, 118, 5134–5135 CrossRef CAS.
- T. Heuser, E. Weyandt and A. Walther, Angew. Chem., Int. Ed., 2015, 54, 13258–13262 CrossRef CAS PubMed.
- L. Heinen, T. Heuser, A. Steinschulte and A. Walther, Nano Lett., 2017, 17, 4989–4995 CrossRef CAS PubMed.
- H. Che, S. Cao and J. C. M. van Hest, J. Am. Chem. Soc., 2018, 140, 5356–5359 CrossRef CAS PubMed.
- Y. Shin and C. P. Brangwynne, Science, 2017, 357, 1253 CrossRef CAS PubMed.
- U. B. Choi, J. J. McCann, K. R. Weninger and M. E. Bowen, Structure, 2011, 19, 566–576 CrossRef CAS PubMed.
- S. Dhiman, A. Jain and S. J. George, Angew. Chem., Int. Ed., 2017, 56, 1329–1333 CrossRef CAS PubMed.
- H.-W. Huang, M. S. Sakar, A. J. Petruska, S. Pané and B. J. Nelson, Nat. Commun., 2016, 7, 12263 CrossRef CAS PubMed.
- S. C. Glotzer, E. A. Di Marzio and M. Muthukumar, Phys. Rev. Lett., 1995, 74, 2034–2037 CrossRef CAS PubMed.
- J. F. Lutsko and G. Nicolis, Soft Matter, 2016, 12, 93–98 RSC.
- A. Moncho-Jordá and J. Dzubiella, Phys. Rev. Lett., 2020, 125, 078001 CrossRef PubMed.
- M. Bley, J. Dzubiella and A. Moncho-Jordá, Soft Matter, 2021, 17, 7682–7696 RSC.
- M. te Vrugt, J. Bickmann and R. Wittkowski, Nat. Commun., 2020, 11, 5576 CrossRef CAS PubMed.
- M. te Vrugt, J. Bickmann and R. Wittkowski, J. Phys. Commun., 2021, 5, 055008 CrossRef.
- H. M. Al-Saedi, A. J. Archer and J. Ward, Phys. Rev. E, 2018, 98, 022407 CrossRef CAS PubMed.
- A. J. Archer, P. Hopkins and M. Schmidt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 040501 CrossRef PubMed.
- E. W. Montroll and G. H. Weiss, J. Math. Phys., 1965, 6, 167–181 CrossRef.
- L. Van Hove, Phys. Rev., 1954, 95, 249–262 CrossRef CAS.
- J.-P. Hansen and I. McDonald, Theory of Simple Liquids, Academic Press, 4th edn, 2013 Search PubMed.
- G. L. Hunter and E. R. Weeks, Rep. Prog. Phys., 2012, 75, 066501 CrossRef PubMed.
- F. H. Stillinger, J. Chem. Phys., 1976, 65, 3968–3974 CrossRef CAS.
- A. A. Louis, P. G. Bolhuis, J. P. Hansen and E. J. Meijer, Phys. Rev. Lett., 2000, 85, 2522–2525 CrossRef CAS PubMed.
- A. A. Louis, P. G. Bolhuis and J. P. Hansen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 62, 7961–7972 CrossRef CAS PubMed.
- A. Scotti, S. Bochenek, M. Brugnoni, M. A. Fernandez-Rodriguez, M. F. Schulte, J. E. Houston, A. P. H. Gelissen, I. I. Potemkin, L. Isa and W. Richtering, Nat. Commun., 2019, 10, 1418 CrossRef CAS PubMed.
- R. G. Winkler, D. A. Fedosov and G. Gompper, Curr. Opin. Colloid Interface Sci., 2014, 19, 594–610 CrossRef CAS.
- J. Dzubiella and C. N. Likos, J. Phys.: Condens. Matter, 2003, 15, L147–L154 CrossRef CAS.
- A. J. Archer, J. Phys.: Condens. Matter, 2005, 17, 1405–1427 CrossRef CAS.
- Y. Liu and H. Liu, AIChE J., 2020, 66, e16824 CAS.
- U. M. B. Marconi and P. Tarazona, J. Chem. Phys., 1999, 110, 8032–8044 CrossRef CAS.
- A. J. Archer and R. Evans, J. Chem. Phys., 2004, 121, 4246–4254 CrossRef CAS PubMed.
- M. te Vrugt, H. Löwen and R. Wittkowski, Adv. Phys., 2020, 69, 121–247 CrossRef.
- P. Hopkins, A. Fortini, A. J. Archer and M. Schmidt, J. Chem. Phys., 2010, 133, 224505 CrossRef PubMed.
- J. K. Percus, Phys. Rev. Lett., 1962, 8, 462–463 CrossRef.
- P. Hopkins and M. Schmidt, J. Phys.: Condens. Matter, 2011, 23, 325104 CrossRef PubMed.
- W. Kob and H. C. Andersen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1995, 51, 4626–4641 CrossRef CAS PubMed.
- D. L. Ermak and J. A. McCammon, J. Chem. Phys., 1978, 69, 1352–1360 CrossRef CAS.
- A. V. Chechkin, F. Seno, R. Metzler and I. M. Sokolov, Phys. Rev. X, 2017, 7, 021002 Search PubMed.
- R. Pastore, A. Ciarlo, G. Pesce, F. Greco and A. Sasso, Phys. Rev. Lett., 2021, 126, 158003 CrossRef CAS PubMed.
- J. M. Miotto, S. Pigolotti, A. V. Chechkin and S. Roldán-Vargas, Phys. Rev. X, 2021, 11, 031002 CAS.
- Y.-C. Lin, B. Rotenberg and J. Dzubiella, Phys. Rev. E, 2020, 102, 042602 CrossRef CAS PubMed.
- U. Baul and J. Dzubiella, J. Phys.: Condens. Matter, 2021, 33, 174002 CrossRef CAS PubMed.
- U. Baul, N. Goeth and J. Dzubiella, arXiv: https://arxiv.org/abs/2109.11454, 2021.
- P. Mausbach and H.-O. May, Fluid Ph. Equilibria, 2006, 249, 17–23 CrossRef CAS.
- H. Wensink, H. Löwen, M. Rex, C. Likos and S. van Teeffelen, Comput. Phys. Commun., 2008, 179, 77–81 CrossRef CAS.
- J. Horbach, S. K. Das, A. Griesche, M.-P. Macht, G. Frohberg and A. Meyer, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 174304 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |