Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reinforcement learning reveals fundamental limits on the mixing of active particles†
Dominik
Schildknecht
 *a,
Anastasia N.
Popova
b,
Jack
Stellwagen
c and
Matt
Thomson
d
*a,
Anastasia N.
Popova
b,
Jack
Stellwagen
c and
Matt
Thomson
d
aBiology and Biological Engineering, California Institute of Technology, Pasadena, CA, USA. E-mail: dominik.schildknecht@gmail.com
bApplied and Computational Mathematics, California Institute of Technology, Pasadena CA, USA
cSchool of Computer Science, Carnegie Mellon University, Pittsburgh, PA, USA
dBiology and Biological Engineering, California Institute of Technology, Pasadena, CA, USA. E-mail: mthomson@caltech.edu
First published on 13th December 2021
Abstract
The control of far-from-equilibrium physical systems, including active materials, requires advanced control strategies due to the non-linear dynamics and long-range interactions between particles, preventing explicit solutions to optimal control problems. In such situations, Reinforcement Learning (RL) has emerged as an approach to derive suitable control strategies. However, for active matter systems, it is an important open question how the mathematical structure and the physical properties determine the tractability of RL. In this paper, we demonstrate that RL can only find good mixing strategies for active matter systems that combine attractive and repulsive interactions. Using analytic results from dynamical systems theory, we show that combining both interaction types is indeed necessary for the existence of mixing-inducing hyperbolic dynamics and therefore the ability of RL to find homogeneous mixing strategies. In particular, we show that for drag-dominated translational-invariant particle systems, mixing relies on combined attractive and repulsive interactions. Therefore, our work demonstrates which experimental developments need to be made to make protein-based active matter applicable, and it provides some classification of microscopic interactions based on macroscopic behavior.
1 Introduction
Mixing is crucial in applications ranging from large-scale chemical processes in industries such as petroleum or food2 down to microscopic scales, including microfluidic applications in medicine.3,4 However, microscopic mixing is challenging because microscale systems are typically drag-dominated, therefore, efficient mixing strategies are not obvious. While current microfluidic solutions exist for microscopic mixing and material transport, they rely on external pumps, prefabricated device geometries,5–8 and (active) additives9–11 so that they are limited in their reconfigurability. In contrast, natural cells use the self-organization of interacting components to make microscopic transport and mixing more compact and energy-efficient.12To better understand nature, and to replicate it for applications, researchers started to study so-called active matter. Here, active matter refers to systems of proteins or other particles that continuously consume energy to achieve non-equilibrium dynamics, which can self-organize to achieve specific tasks. In particular, recent work suggested using active matter to achieve macroscopic tasks, such as generating fluid flows,13–15 flow rectification,16 and equilibration of glassy systems.17
The unsolved scientific challenge is how to assemble the existing (microscopic) active matter systems to achieve macroscopic results such as mixing and material transport. While recently, machine learning was applied to various topics in active matter (see ref. 18 for a review), the literature on active matter control is limited. While in macroscopic systems, where individual agent properties can be controlled, various goals could be achieved, such as navigation through fluids at various Reynolds numbers19–25 and self-organization emerging in a multi-agent setting to solve several tasks,26–31 using microscopic systems to achieving macroscopic behavior is challenging. Indeed, while some limited control was achieved, such as the ability to generate simple fluid flows,13–16,32 achieve global particle momentum,33 and accelerated equilibration of otherwise glassy systems,17 control strategies for more complex scenarios are absent. The reason for this challenging behavior is that active matter systems are interaction-dominated, so strategies have to exert indirect control via agent–agent interactions rather than single–agent properties. Therefore, finding successful strategies to achieve macroscopic goals requires advanced control methods, including policy-based reinforcement learning.
The key question we address in this paper is finding control strategies for the macroscopic task of mixing using protein-based active matter systems. In particular, we focus on finding mixing strategies of active particles by applying RL to our recent numerical active matter model.1 If we find good mixing solutions for the active particles, these strategies could then be implemented experimentally to induce mixing in the surrounding medium, for example, via fluid–matter interactions. For our model of active particles, we observe that while RL fails to learn good strategies if only attractive or repulsive interactions are available, RL finds good strategies if attractive and repulsive interactions can be combined. We analyze this puzzling behavior using dynamical systems theory, particularly theory to hyperbolic dynamics and Anosov diffeomorphisms,34 to prove that mixed interactions are indeed necessary to render the problem solvable. Our results, therefore, provide a guideline to make protein-based active matter applicable and answer the question of how different interactions can lead to macroscopic behavior asked in a recent review.18
2 Methods
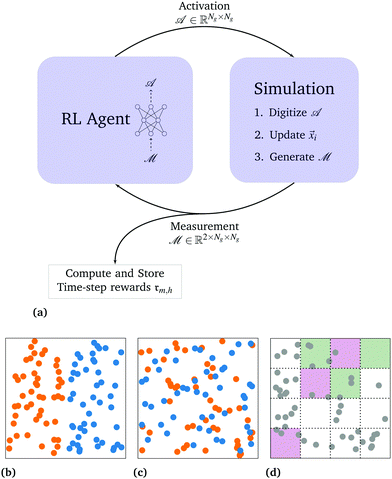
The simulation loop is shown in Fig. 1a The reinforcement learning agent and the simulation interact by exchanging information. In particular, the reinforcement learning system controls the simulation by providing the activations for each bin![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) . The simulation performs an update and provides the reinforcement learning algorithm with the measurement tensor
. The simulation performs an update and provides the reinforcement learning algorithm with the measurement tensor ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) , which is additionally used to compute the rewards. In this section, we will describe this process in more detail. In particular, we describe the simulation engine in Section 2.1, the reward function in Section 2.2, and the reinforcement learning framework in Section 2.3.
, which is additionally used to compute the rewards. In this section, we will describe this process in more detail. In particular, we describe the simulation engine in Section 2.1, the reward function in Section 2.2, and the reinforcement learning framework in Section 2.3.
2.1 Simulation and reinforcement learning environment
In this work, we will start by applying RL to a specific microscopic model of active matter. In particular, we want to select a sufficiently simple model to be amenable to RL while at the same time being suitable to describe various problems central to microscopic material transport and active matter. Microscopic models are often drag-dominated35 and can be classified into continuum theories10,11,15,36–40 and particle-based models.1,41–43 While continuum theories are often preferred due to their analytic properties, we chose a particle-based model because they tend to be quicker to simulate small- and medium-sized systems, and therefore more amenable to RL requiring many simulations. In addition, since we are interested in general properties, a phenomenological model is sufficient, and we used the simulation platform proposed by us in ref. 1. It should be noted that our results will be generalized to a larger array of models in Section 4.Our model1 required only attractive interactions to describe the existing experimental platform.14,15,44 However, this restriction will turn out to limit mixing. Hence, an extended model is introduced as follows: the system consists of Np particles in two dimensions indexed by i, which can be in three states: attractive-activated (pai = 1, pri = 0), repulsive-activated (pai = 0, pri = 1), or inactivated (pai = 0, pri = 0). Particles can be activated if they were previously inactivated by being in the corresponding activation area (which will form our control input) and deactivate back to the inactivated state with a rate λ. Activated particles interact with other similar-activated particles by a spring potential.‡ The system's dynamics is described by the equations of motion
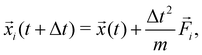 | (1a) |
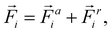 | (1b) |
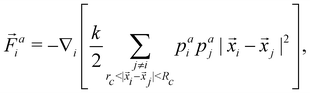 | (1c) |
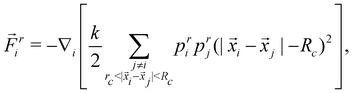 | (1d) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i(t) is the position of particle i at time t, and
i(t) is the position of particle i at time t, and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) i is the total force acting on it. The total force
i is the total force acting on it. The total force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) i is split into attractive and repulsive contributions, and at every times step, at least one of them vanishes because at least one of pai and pri is 0. It should be noted that the attractive and the repulsive force incorporate the same spring constant k, lower truncation rc, and upper truncation Rc, and differ only by their rest length being 0 or Rc for the attractive and repulsive force, respectively. It should be noted that eqn (1) describes drag-dominated particles, because while these equations were derived from an inertial description, the limit of infinitely strong drag was taken to ensure numerical stability for large time-steps.1
i is split into attractive and repulsive contributions, and at every times step, at least one of them vanishes because at least one of pai and pri is 0. It should be noted that the attractive and the repulsive force incorporate the same spring constant k, lower truncation rc, and upper truncation Rc, and differ only by their rest length being 0 or Rc for the attractive and repulsive force, respectively. It should be noted that eqn (1) describes drag-dominated particles, because while these equations were derived from an inertial description, the limit of infinitely strong drag was taken to ensure numerical stability for large time-steps.1
Using this model of drag-dominated particle dynamics with controllable pairwise spring interactions, we built an RL environment using OpenAI gym.45 In particular, Np = 96 particles are initialized randomly in a box with periodic boundary conditions, asserting an equal number of particles on the two halves of the system (for future reference, tagged “left” and “right”). The system is then integrated according to eqn (1) with a time-step of Δt = 0.05 for Nt = 100 time-steps. A sketch of the initial condition can be found in Fig. 1b, and an example of a target state is depicted in Fig. 1c. The detailed simulation parameters can be found in the ESI.† The observation and control spaces are introduced by using an Ng × Ng = 4 × 4 square grid, as depicted in Fig. 1d. In particular, observations are given to the algorithm by providing a separate count for each tag (corresponding to the orange and blue colors in Fig. 1b and c) and each bin. The system is controlled by associating each square of the binning to either activation area or none at all so that the action space at every time-step is 34×4 ≈43 × 106 dimensional if both interactions are included.§
It should be noted that the individual simulations are relatively small at only 96 particles and a coarse binning in a 4 × 4 grid. We chose such small system sizes because the individual simulations are run many thousands of times, and as such, they need to run very quickly. Nevertheless, because the scaling of an individual simulation is only ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (Np2), future work could easily extend to larger particle numbers. In contrast, due to the exponential scaling of the action space with grid resolution, increasing the spatial resolution would slow down learning, and possibly more advanced methods such as curriculum learning would need to be implemented to achieve fine-grained control. However, the main result of this paper, namely the necessity of two types of interactions, will continue to hold independent of the number of particles or the grid resolution, as we will show in Section 4.
(Np2), future work could easily extend to larger particle numbers. In contrast, due to the exponential scaling of the action space with grid resolution, increasing the spatial resolution would slow down learning, and possibly more advanced methods such as curriculum learning would need to be implemented to achieve fine-grained control. However, the main result of this paper, namely the necessity of two types of interactions, will continue to hold independent of the number of particles or the grid resolution, as we will show in Section 4.
2.2 Reward functions
To apply RL, we need to measure how well mixed a given state is, i.e., we need to define a functional giving a configuration as depicted in Fig. 1b a low score and one as in Fig. 1c a high score. Various approaches could be taken to define such a function: one could use variations of the continuous mix-norm46–49 or an adversarial neural network approach to distinguish a well-mixed state from a segregated state. However, as we will demonstrate in Section 4, the main results of our paper will be unaffected by the choice of the reward function, and hence, the compute-intensive reward functions can be replaced by a simpler one. In particular, we use the measurement tensor![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) , which describes the particle count with a specific tag per bin. Hence,
, which describes the particle count with a specific tag per bin. Hence, ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) has the indices (tag, x-bin, y-bin), where tag ∈ {l, r}, and x-bin and y-bin ∈ {1, 2,…,Ng}. Then, we define the mixing reward at a specific time-step as
has the indices (tag, x-bin, y-bin), where tag ∈ {l, r}, and x-bin and y-bin ∈ {1, 2,…,Ng}. Then, we define the mixing reward at a specific time-step as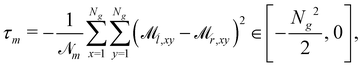 | (2) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) and τm for easier notation. In eqn (2), the minus sign ensures that the reward is larger for well-mixed states, and
and τm for easier notation. In eqn (2), the minus sign ensures that the reward is larger for well-mixed states, and ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) m = (Np/Ng)2 is chosen so that the reward for the initial state is −1 on average. It should be noted that the minimal value of τm is much smaller than −1 and is attained if all “left” particles are in one bin and all “right” particles in another.
m = (Np/Ng)2 is chosen so that the reward for the initial state is −1 on average. It should be noted that the minimal value of τm is much smaller than −1 and is attained if all “left” particles are in one bin and all “right” particles in another.
Since only using eqn (2) will lead to degenerate solutions that collapse all particles to dense clusters, we use an additional (time-step) homogeneity reward, constructed analogously to eqn (2):
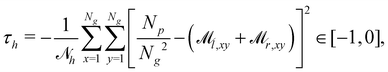 | (3) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) l,ij +
l,ij + ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) r,ij) to the average number of particles
r,ij) to the average number of particles 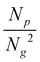 per bin. Here,
per bin. Here, 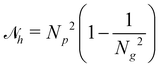 so that the most inhomogeneous solution, namely all particles in a single bin, has a reward of −1. It should be noted that
so that the most inhomogeneous solution, namely all particles in a single bin, has a reward of −1. It should be noted that ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) m and
m and ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) h are chosen so that τm and τh are −1 in the typical situation they should avoid, namely the segregated initial state, and a completely collapsed state, respectively. As such, using these values of
h are chosen so that τm and τh are −1 in the typical situation they should avoid, namely the segregated initial state, and a completely collapsed state, respectively. As such, using these values of ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) m and
m and ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) h provides a natural normalization.
h provides a natural normalization.
We introduce the episode rewards as the mean over the time-step rewards for an entire episode:
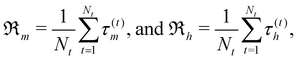 | (4) |
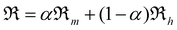 using the parameter α ∈ [0, 1] to tune between weighting more homogeneous or more mixed solutions continuously.
using the parameter α ∈ [0, 1] to tune between weighting more homogeneous or more mixed solutions continuously.
2.3 Reinforcement learning framework
Because the action space is large (34×4 ≈ 43 × 106 for combined interactions), conventional control theory techniques are intractable due to Bellman's curse of dimensionality.50 Similarly, the action space is also too large for value-based RL methods, so that we use a policy-based algorithm. In particular, we use the rllib implementation51 of Proximal Policy Optimization (PPO).52In the RL agents, we use a neural network, which gets as input the tensor ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) . The neural network itself then consists of three convolutional layers (with 32, 64, and 256 channels, and kernel sizes 3, 3, and 4, respectively), and a dense layer with Ng × Ng output neurons. The simulation uses the value of these output neurons to determine if a bin should be activated by thresholding.
. The neural network itself then consists of three convolutional layers (with 32, 64, and 256 channels, and kernel sizes 3, 3, and 4, respectively), and a dense layer with Ng × Ng output neurons. The simulation uses the value of these output neurons to determine if a bin should be activated by thresholding.
The hyperparameters for PPO were tuned automatically during training using ray tune's Population Based Training (PBT)53 with 16 agents. Using PBT, unstable solutions could be overcome, and we observed converged strategies in all training situations. Additional hyperparameters required for PBT can be found in the ESI.†
3 Results
3.1 Attractive interactions
Experimentally, a controllable active matter system with attractive interactions is already available,14,15,44 so this case is analyzed first. In Fig. 2a, we show the average episode reward of each of the 16 agents as a function of training time as a solid line, with the minimal and maximal episode reward during the batch providing an error band. It should be noted that while the training resulted in some average increase in reward, the span of rewards is still large. Additionally, we can also observe that agents failing due to some instabilities, as seen by a sharp drop in the reward, can recover due to using PBT. Therefore, the data allows for qualitative analysis, but visual inspection needs to confirm the quality of a strategy¶ in a specific instance. In Fig. 2b, an exemplary time series for a converged strategy is shown, where the emergent strategy collapses all particles into a dense cluster. While this strategy is not a good mixer in the common sense, the solution optimizes eqn (2). In particular, if all particles collapse to a cluster in a single bin, then this bin has a balanced number of “left” and “right”, so that for this cell![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) l,ij =
l,ij = ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) r,ij = Np/2, and the difference is 0. All other cells are empty so that for these cells
r,ij = Np/2, and the difference is 0. All other cells are empty so that for these cells ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) l,ij =
l,ij = ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) r,ij = 0 again leading to a vanishing difference, and hence τ = 0·τh + 1·τm = 0 is optimal.
r,ij = 0 again leading to a vanishing difference, and hence τ = 0·τh + 1·τm = 0 is optimal.
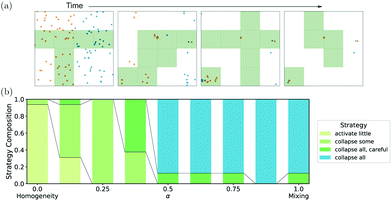 | ||
| Fig. 2 Training with only attractive interactions achieves only collapsed clusters: In (a), the mean episode reward of the 16 agents training at α = 1 is shown in solid lines, with minimal and maximal episode rewards as an error band. It can be observed that while training converged, reward variations were still substantial, and several dips in reward were recovered using PBT. In (b), an exemplary time series for only mixing-focused training (α = 1) is shown, in which a collapse of the particle density can be observed. The panels are enumerated from 1 to 4, corresponding to the time-steps 0, 20, 40, and 60, respectively. (A curated list of time series for all attractive-interaction strategies can be found in Fig. S4, ESI†). In (c), the composition of emergent strategies at various values of α is shown, where all the intermediate emergent strategies are taking over continuously. However, no emergent strategy displays a homogeneous mixing. | ||
To overcome the trivial “collapse all”-solution, α can be reduced so that homogeneity is weighted in. For the extreme case of α = 0, where the algorithm optimizes for homogeneity only, almost no particles were activated as the initial condition already has a high homogeneity. We called this emerging strategy “activate little”, which also did not lead to homogeneous mixing. We analyzed the behavior for intermediate values of α by performing additional simulations at 7 additional values of α (to a total of 9), and we hand-labeled the last validation video for each of the 16 PBT agents. It should be noted, that hand-labeling produced interpretable strategies, but that a quantitative analysis of the activation dynamics (cf. Fig. S7 and S8, ESI†) shows that the activation patterns can be roughly classified into groups consistent with our hand-labeling procedure. The results of the emergent strategy composition are plotted as a function of α in Fig. 2c. There we can observe that for intermediate values of α, we observed two additional strategies. Firstly, for some simulations at 0 ≤ α < 0.5, a “collapse some”-strategy emerged, which focuses on collecting dense particle clusters of opposite tags to remedy the worst bins, but leaves most of the other parts of the system inactivated. Secondly, for various values of α, we observed a “collapse all, careful”-strategy similar to the “collapse all”-strategy in that it tries to collect all particles into a single bin. However, it does so over longer periods of time (typically taking more than half of the simulation time) in order to avoid intermediate dense clusters, particularly if these dense clusters are of a single color. As an additional feature of this strategy, due to giving the system longer times to react, the “collapse all, careful”-strategy tends to be more thorough in collapsing all particles in a single bin compared to the “collapse all”-strategy, that mainly focuses on speed. While the exact details, i.e., which strategy emerges for which value of α, will depend on a variety of factors such as the number of bins Ng × Ng, the initial condition, and the subjective assessment during the hand-labeling (cf. ESI† Section SC), we can observe two main results: firstly, the strategies continuously transform from one to another by tuning α. Secondly, none of the observed strategies achieves a homogeneous mixed state.
Therefore, using only attractive interactions, no strategy emerged that provides a solution similar to our target, as depicted in Fig. 1c, even when varying α. Indeed, we will show in Section 4 that no reward-shaping could overcome this problem, as attractive interactions are insufficient to arrive at a homogeneous and mixed state.
3.2 Repulsive interactions
While not yet implemented in the experimental platform, a repulsive–interactions system could be engineered by introducing another motor protein type. Using repulsive interactions only, a more homogeneous mixing strategy exists than in the attractive-only case: a typical time series for the mixing focused α = 1 case is shown in Fig. 3a, where we observe that the emergent strategy is the “activate one side”-strategy. For Ng = 4 and with periodic boundary conditions, every bin is a boundary bin between the two sides of the initial configuration. As such, every particle expelled from one side enters the other without contracting to a cluster. Two features of this mixing solution should be highlighted: first, this strategy again maximizes by reducing the homogeneity of the system. Second, mixing is only facilitated by exploiting the boundary conditions.
by reducing the homogeneity of the system. Second, mixing is only facilitated by exploiting the boundary conditions.
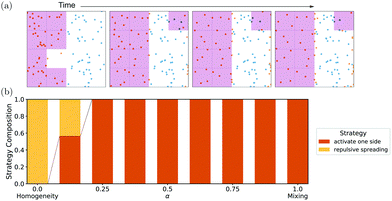 | ||
| Fig. 3 Training with repulsive interactions has a dominant strategy using the periodic boundary conditions to achieve mixing: in (a), an exemplary time series for only mixing-focused training (α = 1) is shown, in which activation of one side of the system can be observed, using the periodic boundary conditions to facilitate mixing. (A curated list of time series of all repulsive-interaction strategies can be found in Fig. S5, ESI†). In (b), the different emergent strategies are shown, demonstrating that the “activate one side”-strategy is dominant over most of the α-parameter space. | ||
For α = 0, i.e., maximizing the homogeneity of the system, the network uses repulsive interactions in more densely populated bins to achieve homogenization beyond the initial condition (“repulsive spreading”-strategy). However, as becomes clear from Fig. 3b, this spreading strategy only emerges very close to α = 0 and is quickly overtaken by the “activate one side” strategy (cf. Fig. S7 and S8, ESI†). Indeed, the homogeneity reward strongly punishes dense clusters as emergent in the “collapse all”-strategy but only weakly punishes a situation where only half of the cells become empty. Hence, the “activate one side”-strategy is dominant over large parts of the α-parameter-space. While the “activate one side”-strategy achieves some mixing with the repulsive-only interactions, the strategy is not tunable, and it heavily relies on the periodic boundary conditions. Indeed, we will demonstrate in Section 4 that phase-space-limiting boundary conditions (such as periodic boundary conditions) are required to facilitate mixing with repulsive interactions only.
3.3 Combined interactions
In contrast to the previous cases, using both interaction types, we will achieve a tunable mixing strategy that can achieve both homogeneity and mixing without exploiting the boundary conditions. Starting with the α = 1 case, we observe the “collapse all”-strategy emerging once more. However, already for α = 1, the network sometimes uses repulsive interactions to spread dense particle clusters, only to attract them again. Because this cycle typically occurs multiple times, we call these strategies oscillatory, and they emerge in different flavors. For large α, the emergent strategy still collapses particles to a dense cluster (see Fig. 4a) in a strategy we term “oscillation w/collapse”. For smaller α, the strategies still use oscillations but avoid very dense clusters in a strategy we call “oscillations w/o collapse”, depicted in Fig. 4b. Finally, for α = 0, the RL algorithm finds an “attractive-repulsive spreading”-strategy which homogenizes the system using both interaction types to spread dense cells and collapse in less populated cells.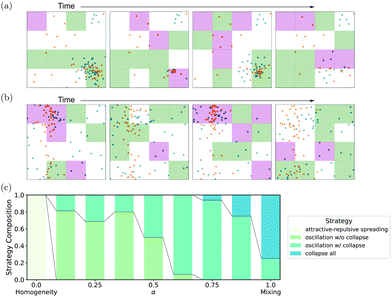 | ||
| Fig. 4 Training on a system with both interactions achieves homogeneous mixing by alternating attractive and repulsive interactions: in (a and b), two exemplary time series for oscillation strategies are shown, with and without collapse, respectively. (A curated list of time series for all combined-interaction strategies can be found in Fig. S6, ESI†). In (c), the fraction of runs with a particular strategy at various values of α is shown, with various emergent strategies continuously transforming into each other. | ||
Overall, an interesting strategy evolution as a function of α emerges using both interactions, as shown in Fig. 4c. In particular, a smooth transition from one strategy to the next can be observed (maybe with exception to the “attractive-repulsive spreading”-strategy), and various intermediate strategies produce well-mixed states without relying on boundary conditions. It should be noted that the actual emergent strategies depend on various factors and are to a degree subjective due to the hand-labeling procedure. Indeed, both oscillatory strategies and the “collapse all”-strategy are similar (cf. the more quantitative analysis presented in Fig. S7 and S8, ESI†), and their differences are can mainly be attributed to when a spread of a dense cluster occurs. As such, this classification relies on the hand-labeling procedure to correlate the particle configuration with the activation pattern. However, we can observe some general features: namely, the strategy evolution is mostly continuous, and the existence of a homogeneous mixing strategy seemed to depend mainly on the interaction set. This result is surprising as attractive or repulsive interactions alone are insufficient to produce efficient mixing, but the combination of both is sufficient. We can now analyze the success-failure pattern of RL to find efficient strategies using dynamical systems theory to analyze the problem more closely. Doing so will reveal that the necessity of combined interactions is not a specific feature of the model in eqn (1) but a much more general statement about different models.
4 Theoretical analysis
In the numerical results presented in Section 3, we observed that only the combination of attractive and repulsive interactions led to homogeneously mixed states and that tweaking the reward function did not find a suitable solution for restricted interaction sets. While these results are limited in their applicability to the model described by eqn (1), here, we will demonstrate how these results can be generalized using dynamical system theory and ergodic theory. Indeed, mixing is studied mathematically as a subdiscipline of ergodic theory, where (weak) mixing is a stronger form of ergodicity, i.e., ergodicity is a necessary but not sufficient condition for mixing (see textbooks54–56). In particular, we will use that if a map is an Anosov diffeomorphism, it will induce (weak) mixing,34,57 to show that homogeneous mixing in drag-dominated translational-invariant particle systems can only occur in systems with attractive and repulsive interactions.We start by reconsidering the model in eqn (1). Without truncating the sums, the equations of motion are
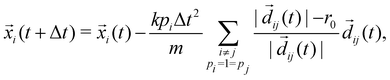 | (5) |
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) ij(t) =
ij(t) = ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i(t) −
i(t) − ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) j(t). Hence, the updates without periodic boundary conditions can be written as a matrix-vector multiplication:
j(t). Hence, the updates without periodic boundary conditions can be written as a matrix-vector multiplication: ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) (t + Δt) = M
(t + Δt) = M![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) (t), where
(t), where ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ∈
∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2Np is the collection of all particle positions. It should be noted that M depends on which particles are activated (hence making it time-dependent), and on
2Np is the collection of all particle positions. It should be noted that M depends on which particles are activated (hence making it time-dependent), and on ![[X with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0058_20d1.gif) (making the update non-linear). However, both dependencies are small since
(making the update non-linear). However, both dependencies are small since 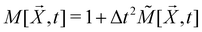 , where Δt ≪ 1, and
, where Δt ≪ 1, and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) describes the particle–particle interactions.
describes the particle–particle interactions.
The long-term evolution of the system can be analyzed by considering the eigenvalues λi of M at every time-step. Namely, ergodicity (and therefore mixing) requires the update to be measure-preserving in phase space,56 meaning that the determinant det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M = Πiλi has to be 1. Suppose the update map M is sufficiently (namely C2) differentiable, has eigenvalues smaller and larger than 1, but maintains a determinant of 1. Then, the map is so-called Anosov, is guaranteed to mix the phase space (i.e., the 2 × Np-dimensional space),34,57 and as such it is expected to mix the projection in the 2-dimensional real space.
M = Πiλi has to be 1. Suppose the update map M is sufficiently (namely C2) differentiable, has eigenvalues smaller and larger than 1, but maintains a determinant of 1. Then, the map is so-called Anosov, is guaranteed to mix the phase space (i.e., the 2 × Np-dimensional space),34,57 and as such it is expected to mix the projection in the 2-dimensional real space.
Therefore, if we understand the spectrum of M (i.e., the set of all eigenvalues), strong statements about mixing can be achieved. The update matrix M can be expressed as
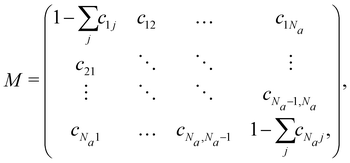 | (6a) |
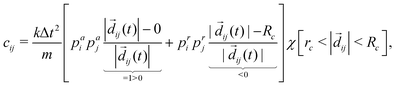 | (6b) |
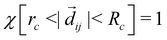 if the condition in the brackets is met and 0 otherwise, ensuring that only particles in the interaction range interact. While eqn (6b) is specific to the force model described by eqn (1), it should be noted that the form of M shown in eqn (6a) is quite general. Namely, M having a row sum 1 and small off-diagonal elements will generally arise for particle-based drag-dominated translational-invariant systems.35 Indeed, only the general form of M shown in eqn (6a) is required to derive the necessary results about the spectrum, and hence all the following results are valid for a large class of models.
if the condition in the brackets is met and 0 otherwise, ensuring that only particles in the interaction range interact. While eqn (6b) is specific to the force model described by eqn (1), it should be noted that the form of M shown in eqn (6a) is quite general. Namely, M having a row sum 1 and small off-diagonal elements will generally arise for particle-based drag-dominated translational-invariant systems.35 Indeed, only the general form of M shown in eqn (6a) is required to derive the necessary results about the spectrum, and hence all the following results are valid for a large class of models.
Because M is symmetric, all eigenvalues are real.|| Because of Gershgorin's circle theorem58, the spectrum of M
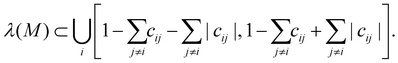 | (7) |
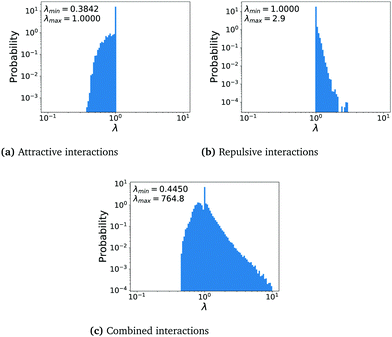
Using eqn (7) for attractive interactions where cij ≥ 0: 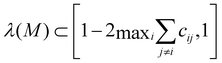 so that the largest possible eigenvalue is 1, while all other eigenvalues are less than 1. Therefore, det
so that the largest possible eigenvalue is 1, while all other eigenvalues are less than 1. Therefore, det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ≤ 1 and iterating M on any initial vector will either collapse the phase space direction (associated eigenvalue λ < 1) or leave it invariant (associated eigenvalue λ = 1). Hence, with only attractive interactions, the system will only be able to collapse, never leading to homogeneous mixing.
M ≤ 1 and iterating M on any initial vector will either collapse the phase space direction (associated eigenvalue λ < 1) or leave it invariant (associated eigenvalue λ = 1). Hence, with only attractive interactions, the system will only be able to collapse, never leading to homogeneous mixing.
Analogously, for repulsive interactions, where cij ≤ 0, 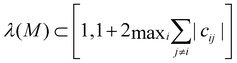 so that all eigenvalues are larger or equal to 1, and det
so that all eigenvalues are larger or equal to 1, and det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ≥ 1. Therefore, without phase-space-limiting boundary conditions, the phase space is expanding, never leading to homogeneous mixing. However, with periodic boundary conditions, phase space is limited and can be folded into itself. Thus, the successful mixing with only repulsive interactions presented in Section 3.2 was only possible due to the periodic boundary conditions.
M ≥ 1. Therefore, without phase-space-limiting boundary conditions, the phase space is expanding, never leading to homogeneous mixing. However, with periodic boundary conditions, phase space is limited and can be folded into itself. Thus, the successful mixing with only repulsive interactions presented in Section 3.2 was only possible due to the periodic boundary conditions.
Finally, for attractive and repulsive interactions, the off-diagonal elements are around 0 but can have either sign** so that the eigenvalues of M lie around 1 (more precisely 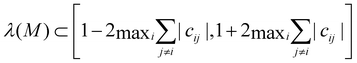 ). While it is not guaranteed that the determinant will be 1, the updates now can induce hyperbolic dynamics, i.e., phase space stretching in some directions and compressing in others, bringing the dynamics closer to an Anosov diffeomorphism, hence being able to induce mixing in agreement with our successful mixing simulations in Section 3.3. Furthermore, our results indicate that in order to optimize mixing, the determinant should be close to 1. This optimal mixing could be achieved in future work by tuning α dynamically during training by monitoring the average determinant.
). While it is not guaranteed that the determinant will be 1, the updates now can induce hyperbolic dynamics, i.e., phase space stretching in some directions and compressing in others, bringing the dynamics closer to an Anosov diffeomorphism, hence being able to induce mixing in agreement with our successful mixing simulations in Section 3.3. Furthermore, our results indicate that in order to optimize mixing, the determinant should be close to 1. This optimal mixing could be achieved in future work by tuning α dynamically during training by monitoring the average determinant.
The results on the eigenvalue spectra can be verified numerically: additional simulations at 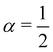 were performed for all three interaction cases. We analyzed the update matrices of the last validation runs for each of the agents at every time point of the simulation and plotted their eigenvalue frequency as histograms in Fig. 5. Indeed, we observe the bounded spectra for limited interaction sets while the system with combined interactions exhibits a more balanced eigenvalue spectrum. While the spectrum for combined interactions in Fig. 5c is not entirely balanced around 1, and the determinant is larger than 1, the matrix is closer to describe an Anosov diffeomorphism and can describe one if necessary. In particular, the oscillatory strategies discussed in Section 3.3 alternate attractive and repulsive interactions to achieve eigenvalues larger and smaller than 1 over multiple time-steps (cf. Fig. S9, ESI†). In conclusion, we indeed observe the predicted eigenvalue spectra throughout all simulations, clearly demonstrating why limited interaction sets cannot provide mixing, whereas the combined interaction set can.
were performed for all three interaction cases. We analyzed the update matrices of the last validation runs for each of the agents at every time point of the simulation and plotted their eigenvalue frequency as histograms in Fig. 5. Indeed, we observe the bounded spectra for limited interaction sets while the system with combined interactions exhibits a more balanced eigenvalue spectrum. While the spectrum for combined interactions in Fig. 5c is not entirely balanced around 1, and the determinant is larger than 1, the matrix is closer to describe an Anosov diffeomorphism and can describe one if necessary. In particular, the oscillatory strategies discussed in Section 3.3 alternate attractive and repulsive interactions to achieve eigenvalues larger and smaller than 1 over multiple time-steps (cf. Fig. S9, ESI†). In conclusion, we indeed observe the predicted eigenvalue spectra throughout all simulations, clearly demonstrating why limited interaction sets cannot provide mixing, whereas the combined interaction set can.
5 Conclusion
This paper analyzed a challenging control problem arising for active matter components, where control cannot be exerted over individual agents or particles but merely over their pairwise interaction. In particular, we attempted to find efficient microscopic mixing strategies for active particles using policy-based RL, where we observed that RL only finds efficient mixing strategies for models with combined attractive and repulsive interactions but not for those with only one type of interaction. This peculiar success/failure pattern was then analyzed using dynamical systems theory, particularly theory to hyperbolic dynamics, on the update matrix M to prove that both types of interactions are required to induce mixing in arbitrary drag-dominated translational-invariant particle models. Finally, the mathematical results on M were confirmed in additional training runs, demonstrating why RL could only solve the problem with both interaction types.The results of this paper suggest further work in two areas: first, our results could be transferred to the experimental system14,15,43 to verify that mixing of active particles can induce mixing in the surrounding medium via fluid–matter interactions. While the experimental platform is not yet ready, since it lacks an additional repulsive light-controllable motor protein, our paper provides a clear and feasible guideline for necessary developments to the platform to enable active–matter-based mixing. As such, we hope to provide the necessary motivation for the field to develop a dual-controlled active–matter system.
Second, the strategies we found should be further refined for actual applications. While some computational effort could be saved by tuning α dynamically to match a unit determinant, future simulations should use a higher grid resolution, a larger number of particles, better boundary conditions, and more realistic particle–particle interactions to produce realistic strategies. While such refined simulations are highly interesting, their computational demand will undoubtedly be more extensive, so that we expect more advanced machine learning approaches such as transfer learning or curriculum learning to be necessary. Nevertheless, we are confident that our work paves the way for future applications of RL to this area of study, namely control of complex interaction-dominated active matter systems.
Author contributions
DS and MT conceived the project. DS, ANP, and JS wrote the simulation environment. DS performed the simulations and analyzed the results. DS and MT wrote the manuscript with input from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Arjuna Subramanian, Jerry Wang, Pranav Bhamidipati, Ivan Jimenez, Jeremy Bernstein, Dr Guannan Qu, Dr Christopher Miles, and Dr Shahriar Shadkhoo for scientific discussions and feedback on the manuscript. We thank Inna-Marie Strazhnik for help with the figures. We acknowledge funding through the Foundational Questions Institute and Fetzer Franklin Fund through FQXi 1816, the Packard Foundation (2019-69662), and the Heritage medical research institute. ANP acknowledges additional funding through the SFP SURF program.References
- D. Schildknecht and M. Thomson, New J. Phys., 2021, 23, 083001 CrossRef.
- E. L. Paul, V. Atiemo-Obeng and S. Kresta, Handbook of Industrial Mixing, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2003 Search PubMed.
- P. M. Valencia, O. C. Farokhzad, R. Karnik and R. Langer, Nat. Nanotechnol., 2012, 7, 623–629 CrossRef CAS PubMed.
- P. Neužil, S. Giselbrecht, K. Länge, T. J. Huang and A. Manz, Nat. Rev. Drug Discovery, 2012, 11, 620–632 CrossRef PubMed.
- A. D. Stroock, S. K. W. Dertinger, A. Ajdari, I. Mezic, H. Stone and G. M. Whitesides, Science, 2002, 295, 647–651 CrossRef CAS PubMed.
- H. Y. Gan, Y. C. Lam, N. T. Nguyen, K. C. Tam and C. Yang, Microfluid. Nanofluid., 2006, 3, 101–108 CrossRef.
- J. S. Kuo and D. T. Chiu, Annu. Rev. Anal. Chem., 2011, 4, 275–296 CrossRef CAS PubMed.
- J. Ortega-Casanova, J. Fluids Struct., 2016, 65, 1–20 CrossRef.
- A. Groisman and V. Steinberg, Nature, 2001, 410, 905–908 CrossRef CAS PubMed.
- D. Saintillan and M. J. Shelley, Phys. Rev. Lett., 2008, 100, 1–4 CrossRef PubMed.
- D. Saintillan and M. J. Shelley, Phys. Fluids, 2008, 20, 123304 CrossRef.
- M. Guo, A. J. Ehrlicher, M. H. Jensen, M. Renz, J. R. Moore, R. D. Goldman, J. Lippincott-Schwartz, F. C. Mackintosh and D. A. Weitz, Cell, 2014, 158, 822–832 CrossRef CAS PubMed.
- D. Marenduzzo and E. Orlandini, Soft Matter, 2010, 6, 774 RSC.
- Z. Qu, D. Schildknecht, S. Shadkhoo, E. Amaya, J. Jiang, H. J. Lee, D. Larios, F. Yang, R. Phillips and M. Thomson, Commun. Phys., 2021, 4, 198 CrossRef.
- Z. Qu, J. Jiang, H. J. Lee, R. Phillips, S. Shadkhoo and M. Thomson, 2021, arXiv: 2101.08464v1, pp. 1–8.
- J. Stenhammar, R. Wittkowski, D. Marenduzzo and M. E. Cates, Sci. Adv., 2016, 2, e1501850 CrossRef PubMed.
- A. K. Omar, Y. Wu, Z.-G. Wang and J. F. Brady, ACS Nano, 2019, 13, 560–572 CrossRef CAS PubMed.
- F. Cichos, K. Gustavsson, B. Mehlig and G. Volpe, Nat. Mach. Intell., 2020, 2, 94–103 CrossRef.
- G. Reddy, A. Celani, T. J. Sejnowski and M. Vergassola, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E4877–E4884 CrossRef CAS PubMed.
- S. Colabrese, K. Gustavsson, A. Celani and L. Biferale, Phys. Rev. Lett., 2017, 118, 158004 CrossRef PubMed.
- S. Muiños-Landin, A. Fischer, V. Holubec and F. Cichos, Sci. Robot., 2021, 6, eabd9285 CrossRef PubMed.
- G. Reddy, J. Wong-Ng, A. Celani, T. J. Sejnowski and M. Vergassola, Nature, 2018, 562, 236–239 CrossRef CAS PubMed.
- S. Verma, G. Novati and P. Koumoutsakos, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5849–5854 CrossRef CAS PubMed.
- L. Biferale, F. Bonaccorso, M. Buzzicotti, P. C. D. Leoni and K. Gustavsson, Chaos, 2019, 29, 103138 CrossRef CAS PubMed.
- E. Schneider and H. Stark, EPL, 2019, 127, 64003 CrossRef.
- C.-H. Yu and R. Nagpal, Twenty-Fourth AAAI Conference on Artificial Intelligence (AAAI), 2010.
- M. Rubenstein, A. Cornejo and R. Nagpal, Science, 2014, 345, 795–799 CrossRef CAS PubMed.
- Y. Yang, R. Luo, M. Li, M. Zhou, W. Zhang and J. Wang, 35th International Conference on Machine Learning, ICML 2018, 2018, pp. 8869-8886.
- M. Durve, F. Peruani and A. Celani, Phys. Rev. E, 2020, 102, 012601 CrossRef CAS PubMed.
- K. Zhang, Z. Yang and T. Baar, in Handbook of Reinforcement Learning and Control, ed. K. G. Vamvoudakis, Y. Wan, F. L. Lewis and D. Cansever, Springer International Publishing, Cham, 2021, pp. 321–384 Search PubMed.
- S. Chennakesavalu and G. M. Rotskoff, J. Chem. Phys., 2021, 155, 194114 CrossRef CAS PubMed.
- M. M. Norton, P. Grover, M. F. Hagan and S. Fraden, Phys. Rev. Lett., 2020, 125, 178005 CrossRef CAS PubMed.
- M. J. Falk, V. Alizadehyazdi, H. Jaeger and A. Murugan, 2021, arXiv: 2105.04641, pp. 1–11.
- D. V. Anosov, Proc. Steklov Inst. Math., 1967, 90, 235 Search PubMed.
- P. M. Chaikin and T. C. Lubensky, Principles of Condensed Matter, Cambridge University Press, Cambridge, 1995, ch. 7 Search PubMed.
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, 1993 Search PubMed.
- J. F. Joanny, F. Jülicher, K. Kruse and J. Prost, New J. Phys., 2007, 9, 422 CrossRef.
- L. Giomi, M. C. Marchetti and T. B. Liverpool, Phys. Rev. Lett., 2008, 101, 198101 CrossRef PubMed.
- L. Giomi, Phys. Rev. X, 2015, 5, 031003 Search PubMed.
- P. J. Foster, S. Fürthauer, M. J. Shelley and D. J. Needleman, eLife, 2015, 4, 1–21 CrossRef PubMed.
- H. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- F. Nédélec and D. Foethke, New J. Phys., 2007, 9, 427 CrossRef.
- T. D. Ross, H. J. Lee, Z. Qu, R. A. Banks, R. Phillips and M. Thomson, Nature, 2019, 572, 224–229 CrossRef CAS PubMed.
- G. Brockman, V. Cheung, L. Pettersson, J. Schneider, J. Schulman, J. Tang and W. Zaremba, arXiv, 2016, 1–4 Search PubMed.
- C. R. Doering and J. L. Thiffeault, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 1–4 CrossRef PubMed.
- J.-L. Thiffeault, Nonlinearity, 2012, 25, R1–R44 CrossRef.
- C. J. Miles and C. R. Doering, Nonlinearity, 2018, 31, 2346–2359 CrossRef.
- C. J. Miles and C. R. Doering, J. Nonlinear Sci., 2018, 28, 2153–2186 CrossRef CAS.
- R. Bellman, Dynamic Programming, Princeton University Press, 1957 Search PubMed.
- E. Liang, R. Liaw, P. Moritz, R. Nishihara, R. Fox, K. Goldberg, J. E. Gonzalez, M. I. Jordan and I. Stoica, 35th International Conference on Machine Learning, ICML 2018, 2018, pp. 3053–3062.
- J. Schulman, F. Wolski, P. Dhariwal, A. Radford and O. Klimov, arXiv, 2017, 1–12 Search PubMed.
- R. Liaw, E. Liang, R. Nishihara, P. Moritz, J. E. Gonzalez and I. Stoica, arXiv, 2018, https://arxiv.org/abs/1807.05118 Search PubMed.
- P. Walters, An Introduction to Ergodic Theory, Springer-Verlag, New York, 1982 Search PubMed.
- D. Kerr and H. Li, Ergodic Theory. Independence and Dichotomies, Springer International Publishing, 2017 Search PubMed.
- J. Hawkins, Ergodic Dynamics, Springer International Publishing, Cham, 2021, vol. 289 Search PubMed.
- M. Brin and G. Stuck, Introduction to Dynamical Systems, Cambridge University Press, 2010, ch. 6, pp. 141–152 Search PubMed.
- S. Gershgorin, Bull. Acad. Sci. URSS, Cl. Sci. Phys.-Math., 1931, 749–754 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional details to the simulations, and supplemental figures. The code for the simulation can be found in ref. 1, and the OpenAI gym environment can be found on https://github.com/domischi/SpringBoxDDPG. The data and analysis scripts are accessible. See DOI: 10.1039/d1sm01400e |
| ‡ I.e., attractive-activated particles only interact with other attractive-interacted particles, and repulsive-activated particles only interact with other repulsive-activated particles. |
| § If only one interaction type is included, the action space at every time-step is 24×4 ≈ 65 × 103 dimensional. |
| ¶ It should be noted that we define a strategy to summarize all actions of an agent throughout an entire simulation. In contrast, one could consider motifs, i.e., actions an agent performs during a short time period. However, most strategies observed in this paper can be described by a single motif which is used continuously, or at most two that alternate. |
| || For non-symmetric matrices, the argument would be analogous, limiting the discussion to the absolute value of the eigenvalue. |
| ** Per row, each off-diagonal will have the same sign, as only the same activation states interact with each other. However, due to the possibility of changing the interaction state, the same row can have an opposite sign at different times. |
| This journal is © The Royal Society of Chemistry 2022 |